Study on Cavitation Flow Structure Evolution in the Hump Region of Water-Jet Pumps Under the Valley Condition
Abstract
1. Introduction
2. Research on Numerical Simulation Method
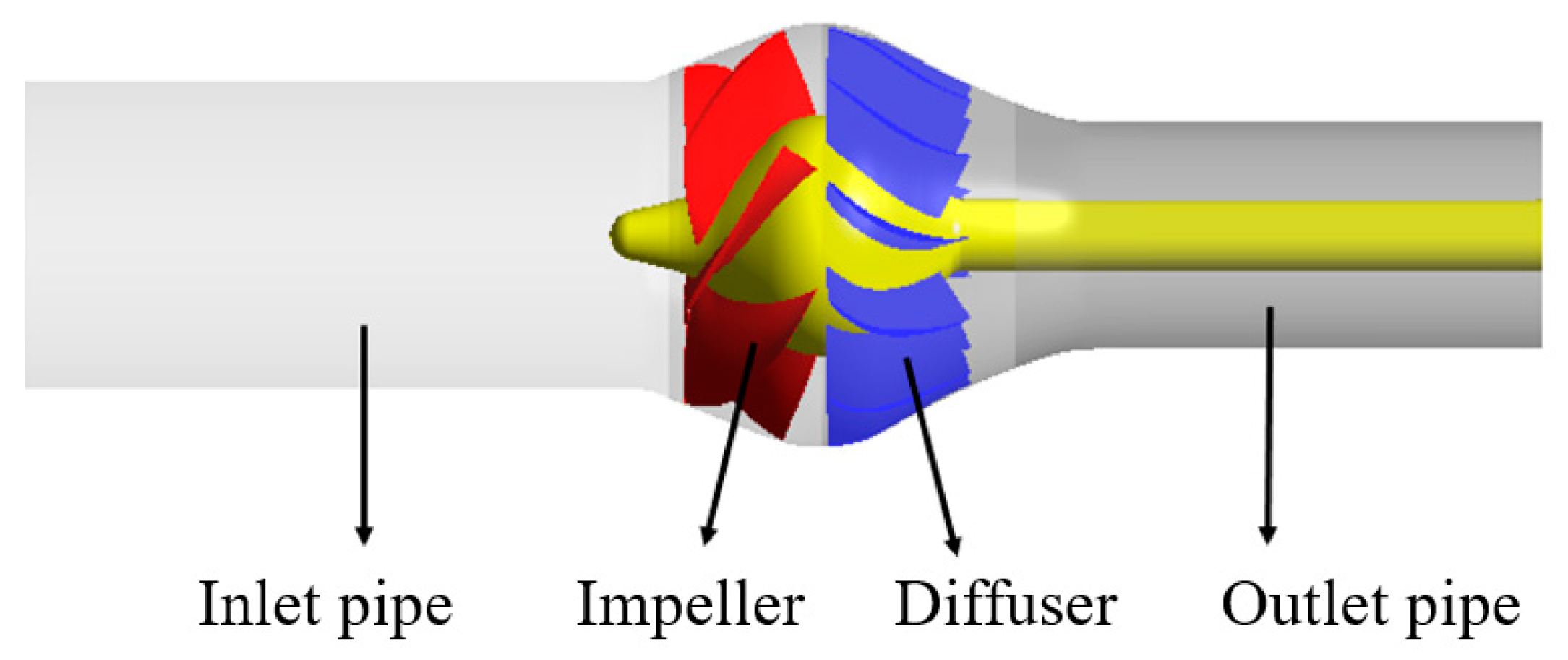
2.1. Numerical Calculation Model
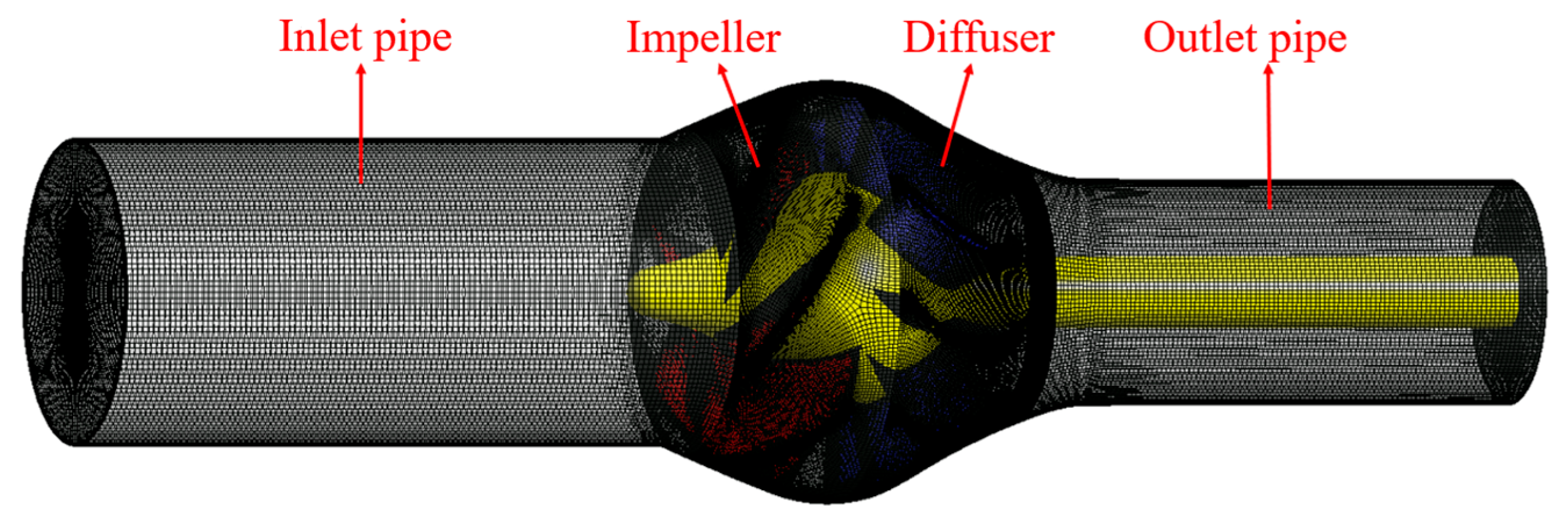
2.2. Mesh Generation
2.3. Control Equation
- (1)
- Continuity equation
- (2)
- Momentum conservation equation
2.4. Turbulence Model
2.5. Cavitation Model
2.6. Boundary Condition
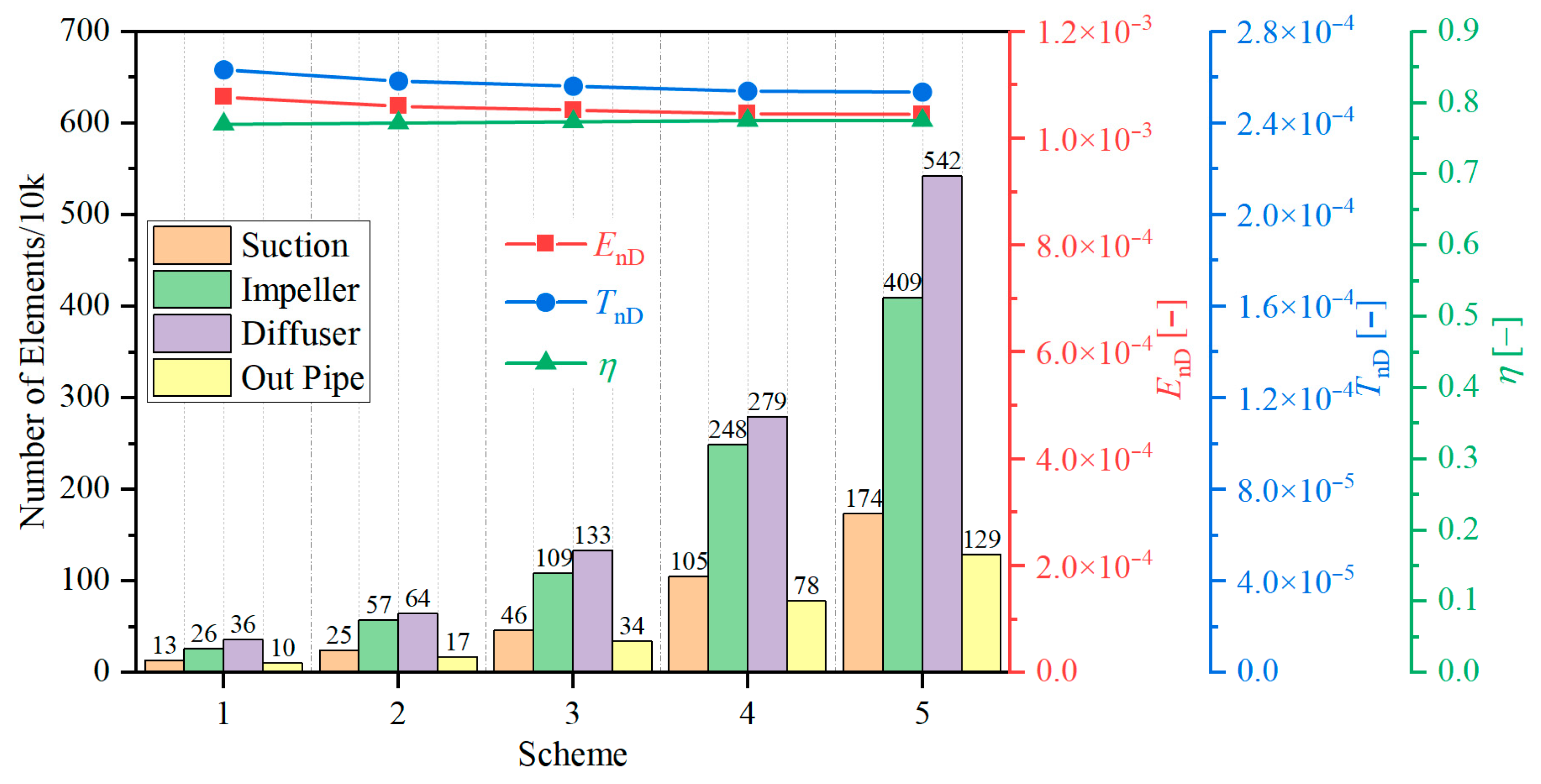
2.7. Mesh Independence Verification
3. Cavitation Experiment
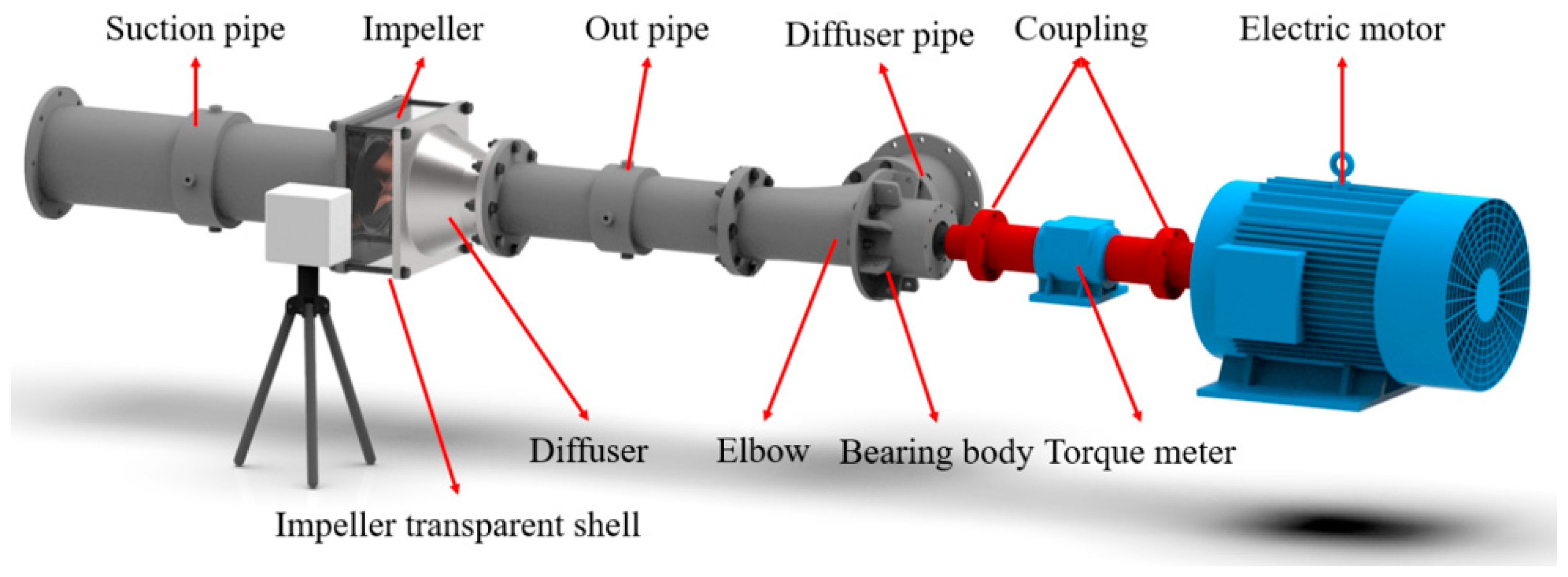
3.1. Cavitation Experiment Test
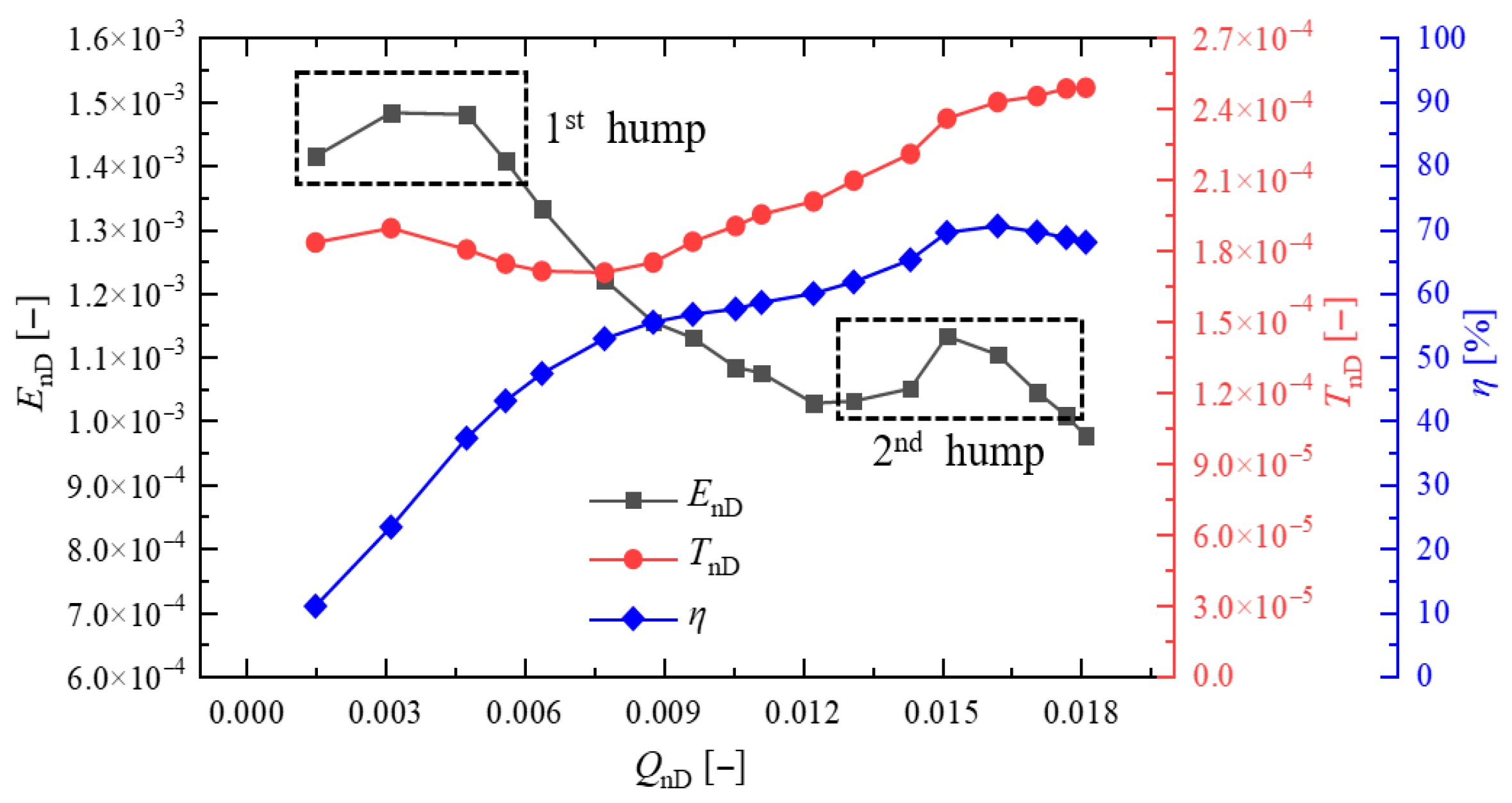
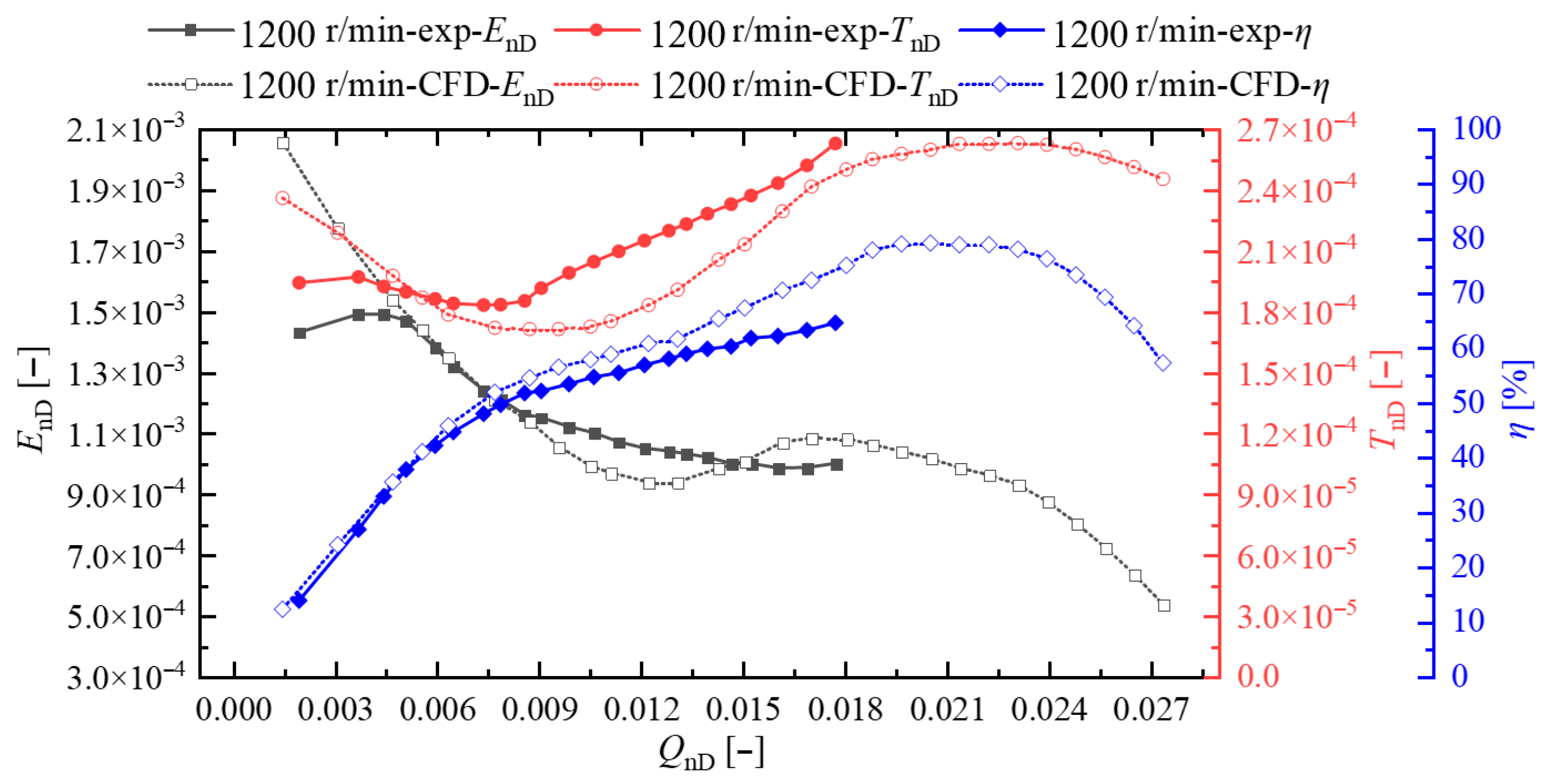
3.2. Analysis of Hydraulic Performance Experiment Results
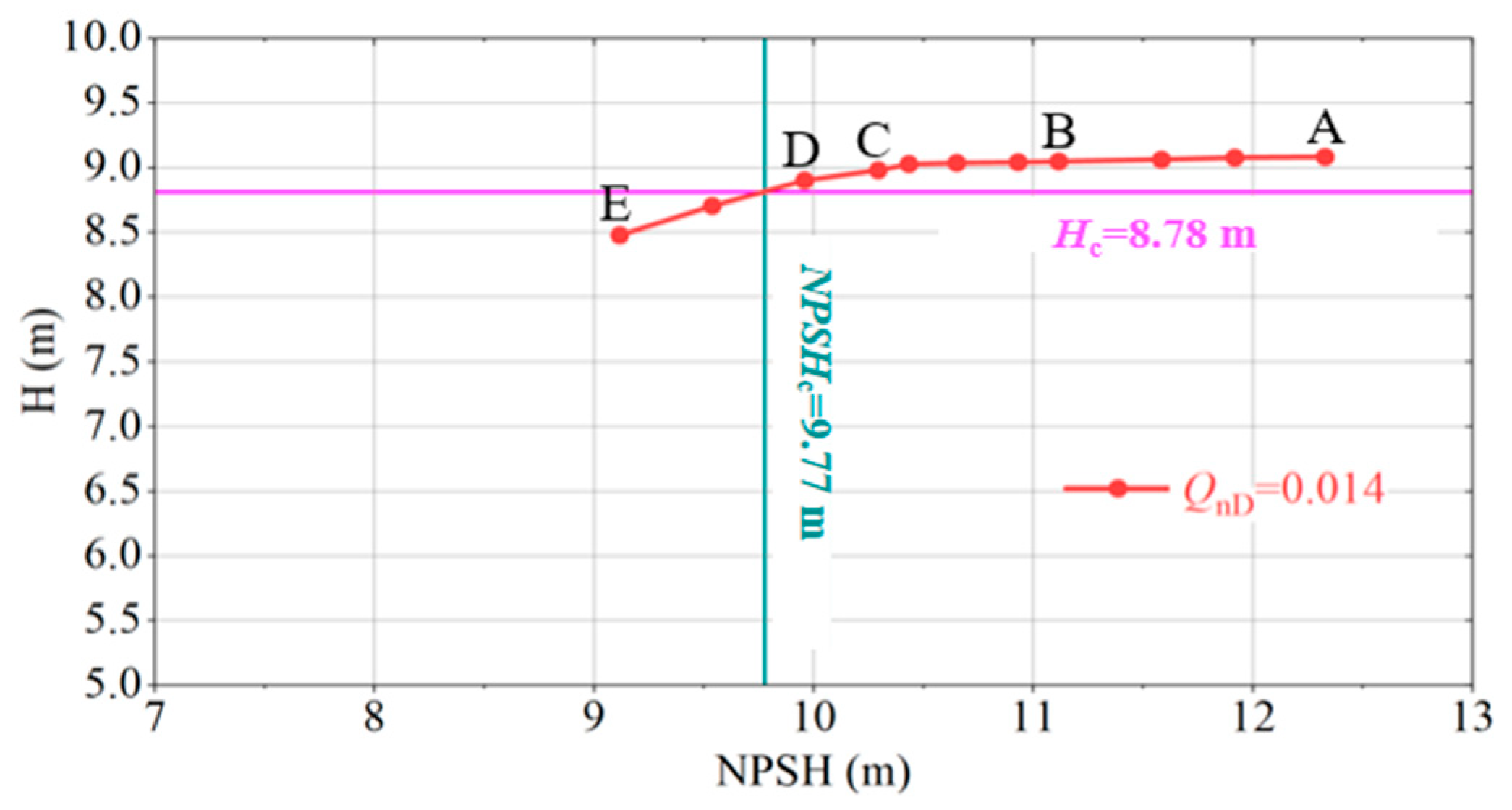
3.3. Analysis of Cavitation Performance Experiment Results
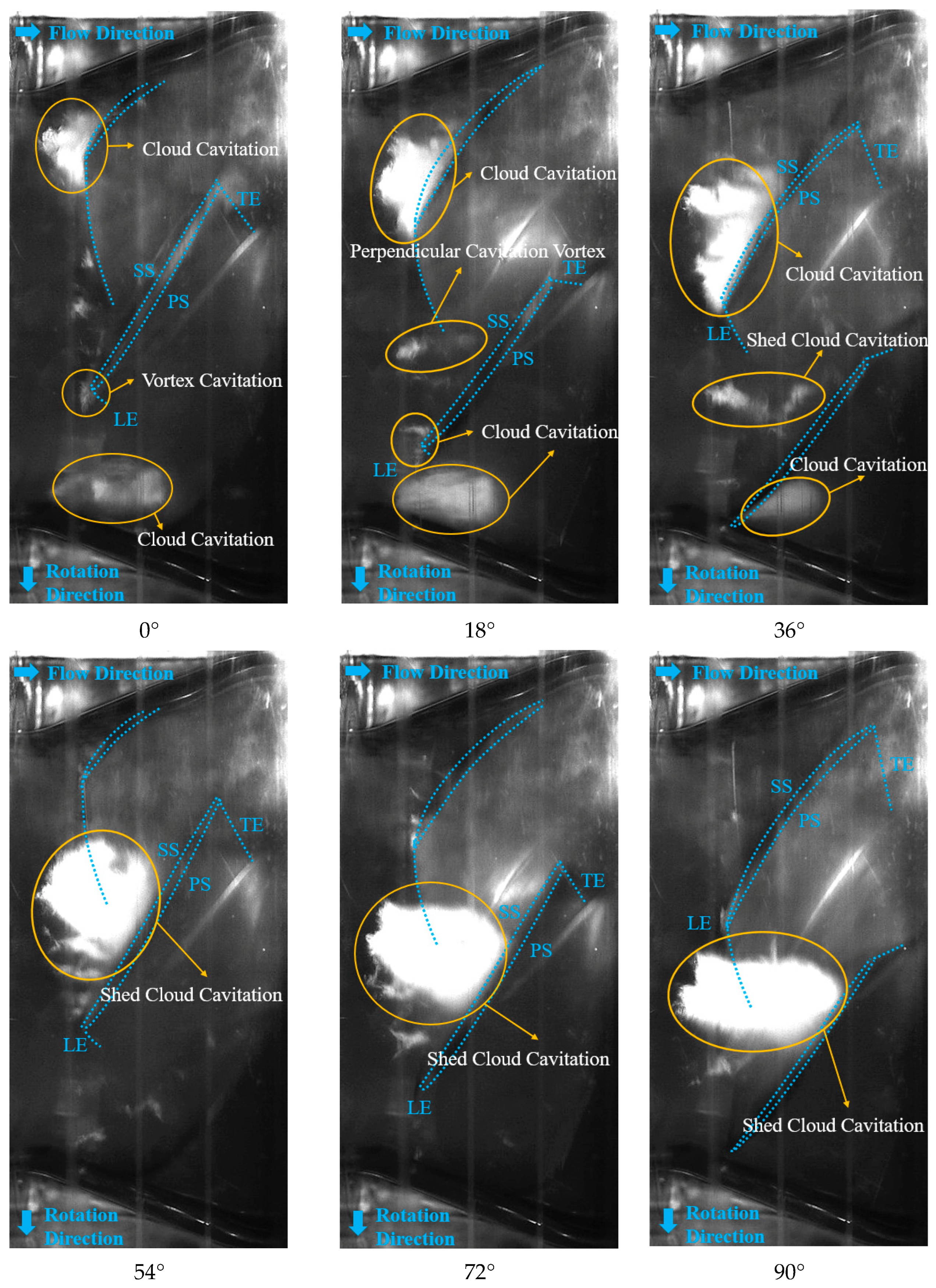
4. Evolution of Cavitation Flow Structure
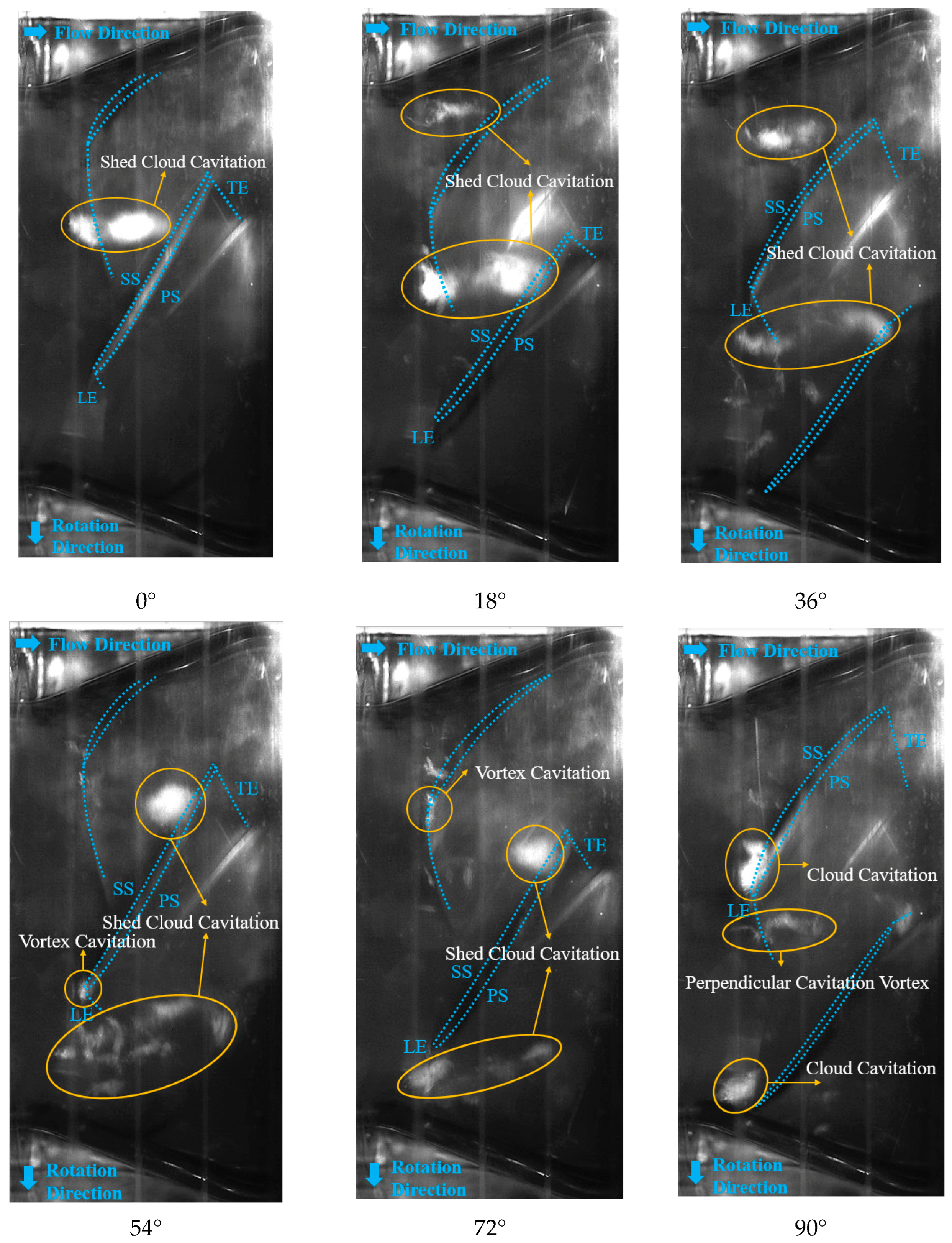
4.1. Cavitation Inception Stage
4.2. Cavitation Development Transition Stage
4.3. First Critical Cavitation Stage
4.4. Critical Cavitation Stage
4.5. Breakdown Cavitation Stage
5. Evolution of Flow Structure in the Pump
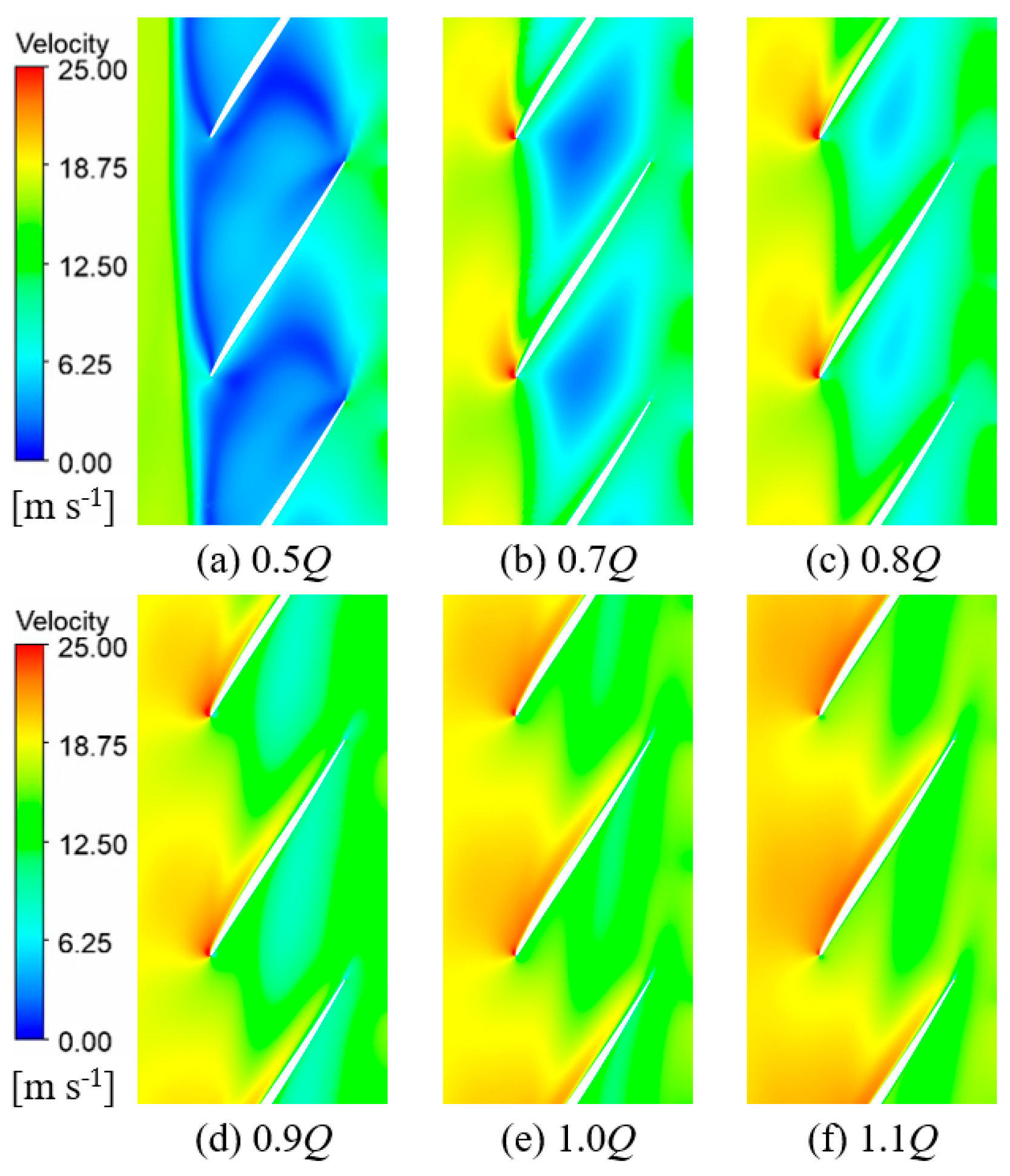
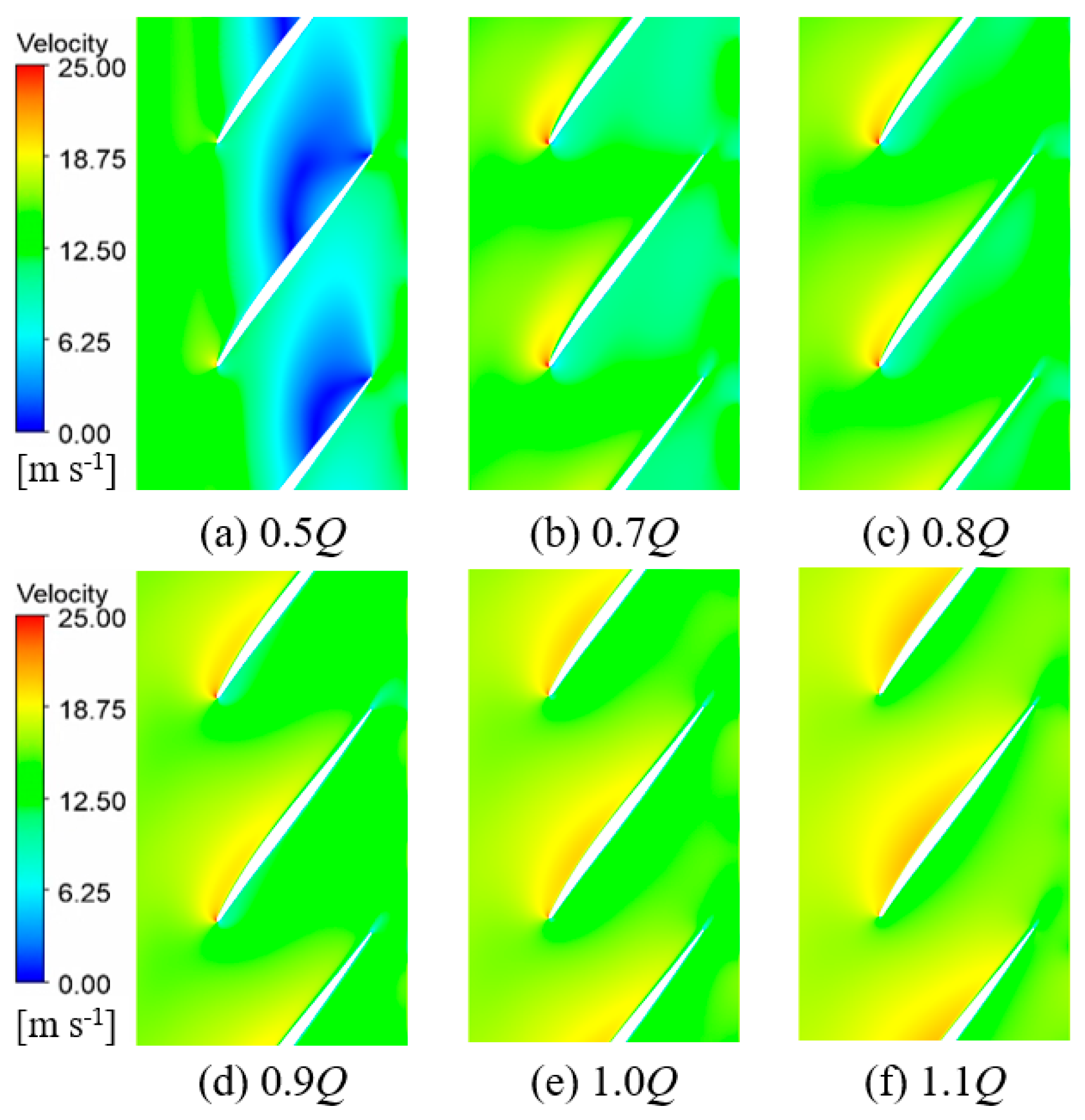
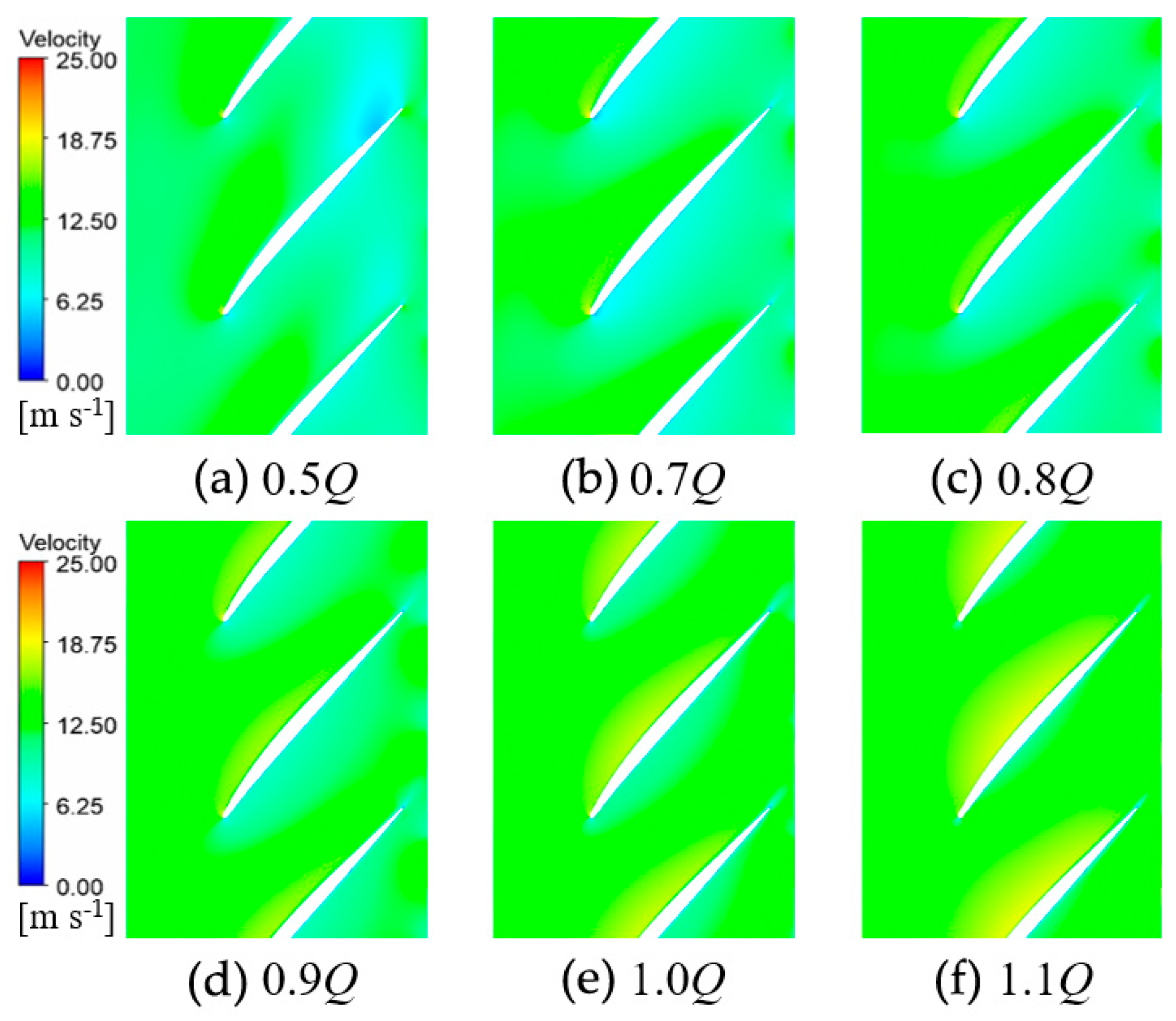
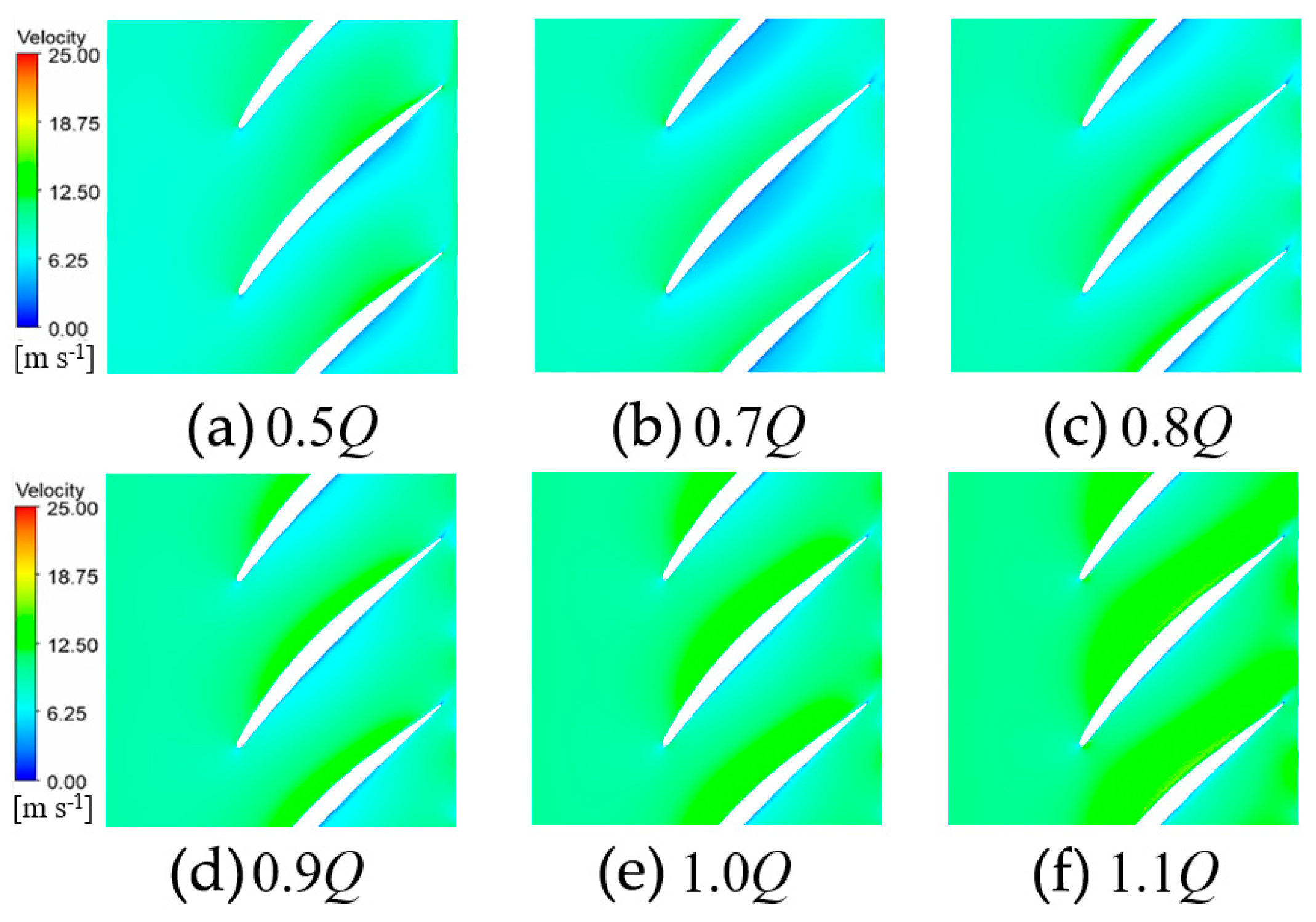
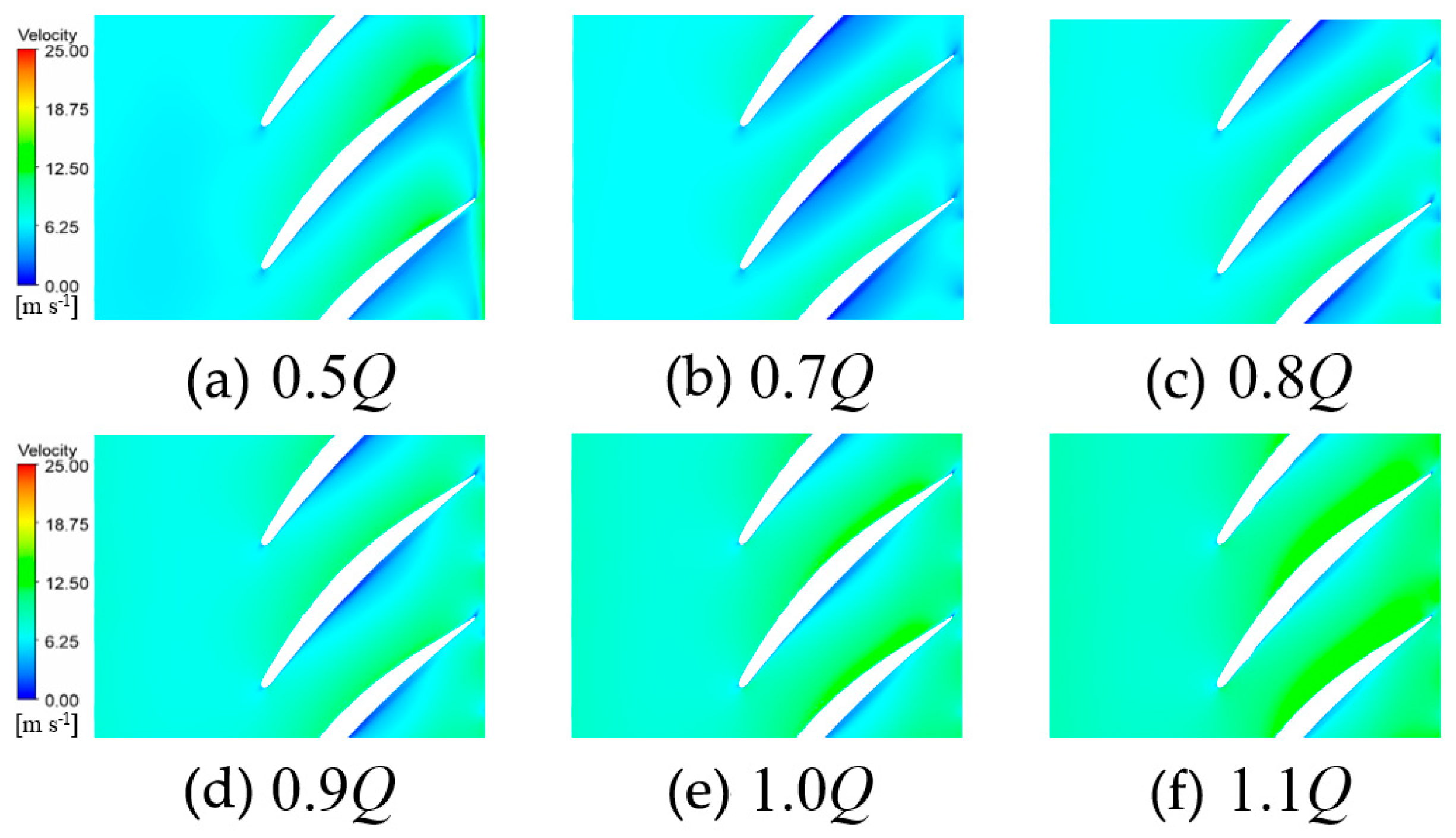
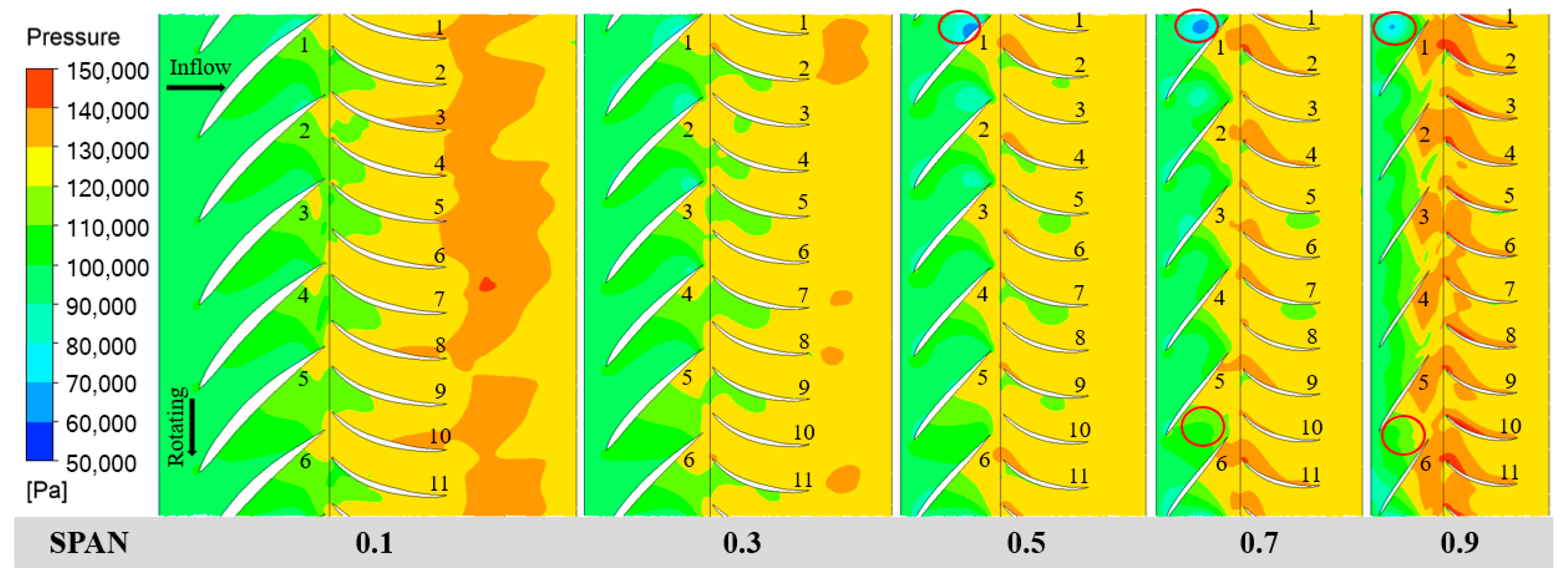
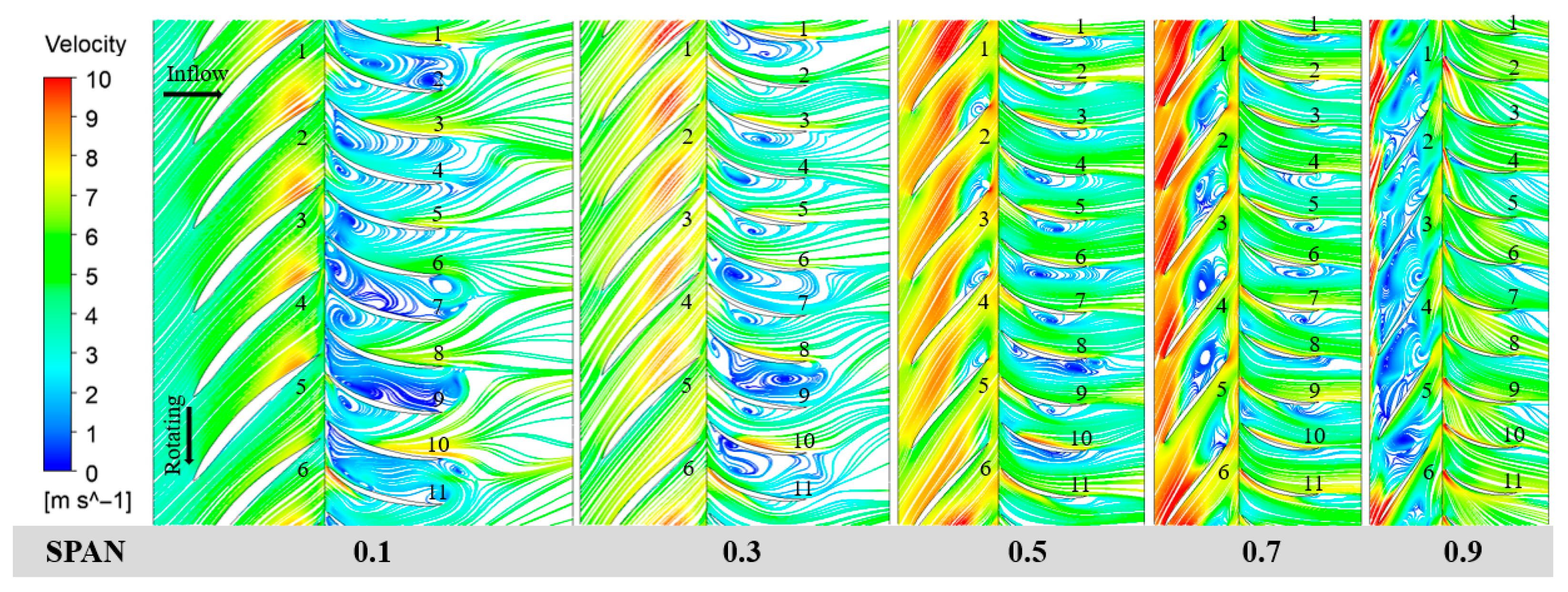
5.1. Analysis of Velocity Distribution Characteristics in Different Span Sections
5.2. Analysis of Pressure Distribution Characteristics
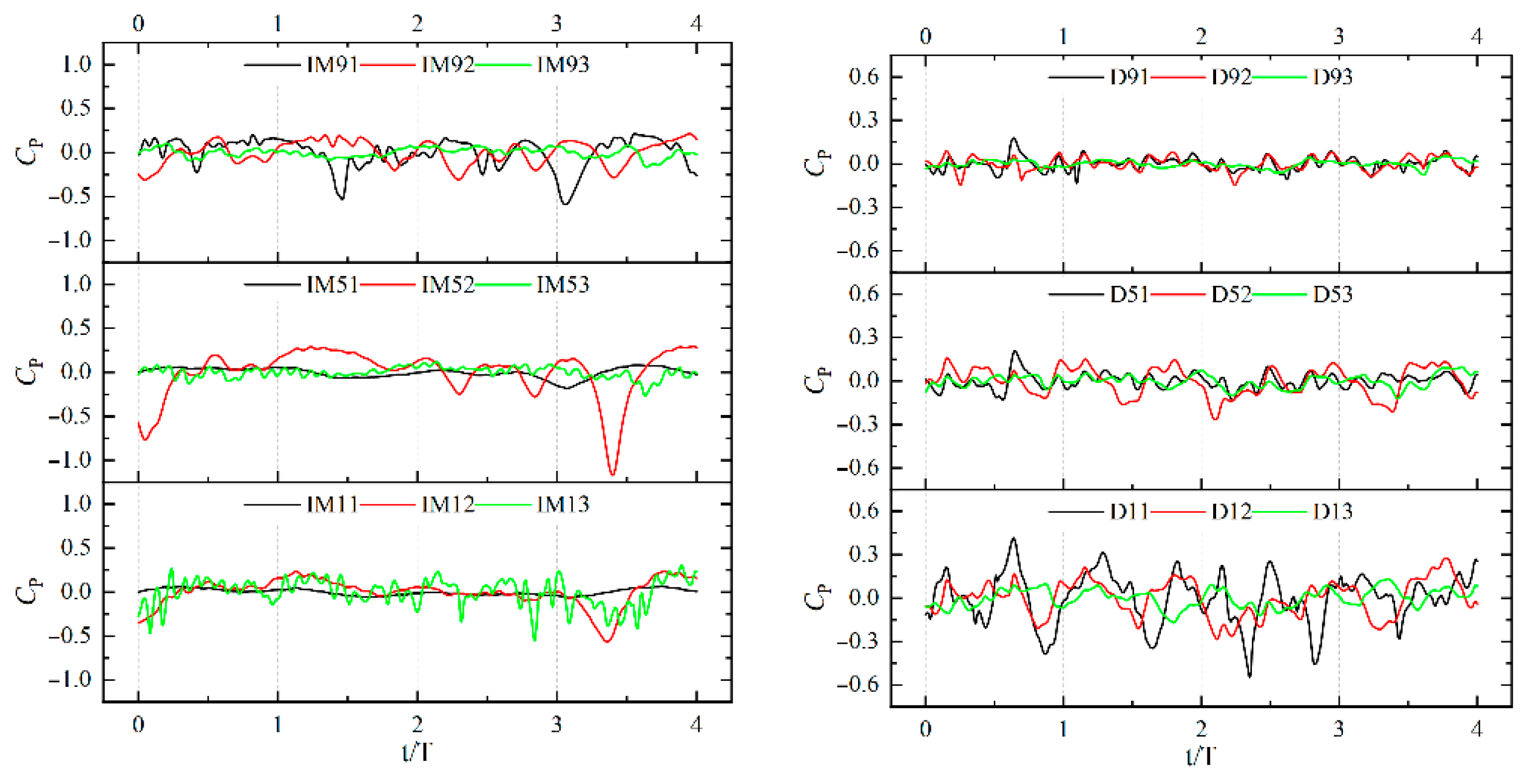
5.3. Coupling Mechanisms of Pressure Fluctuations and Cavitation
5.4. Driving Mechanism of Re-Entrant Jets on Cavitation
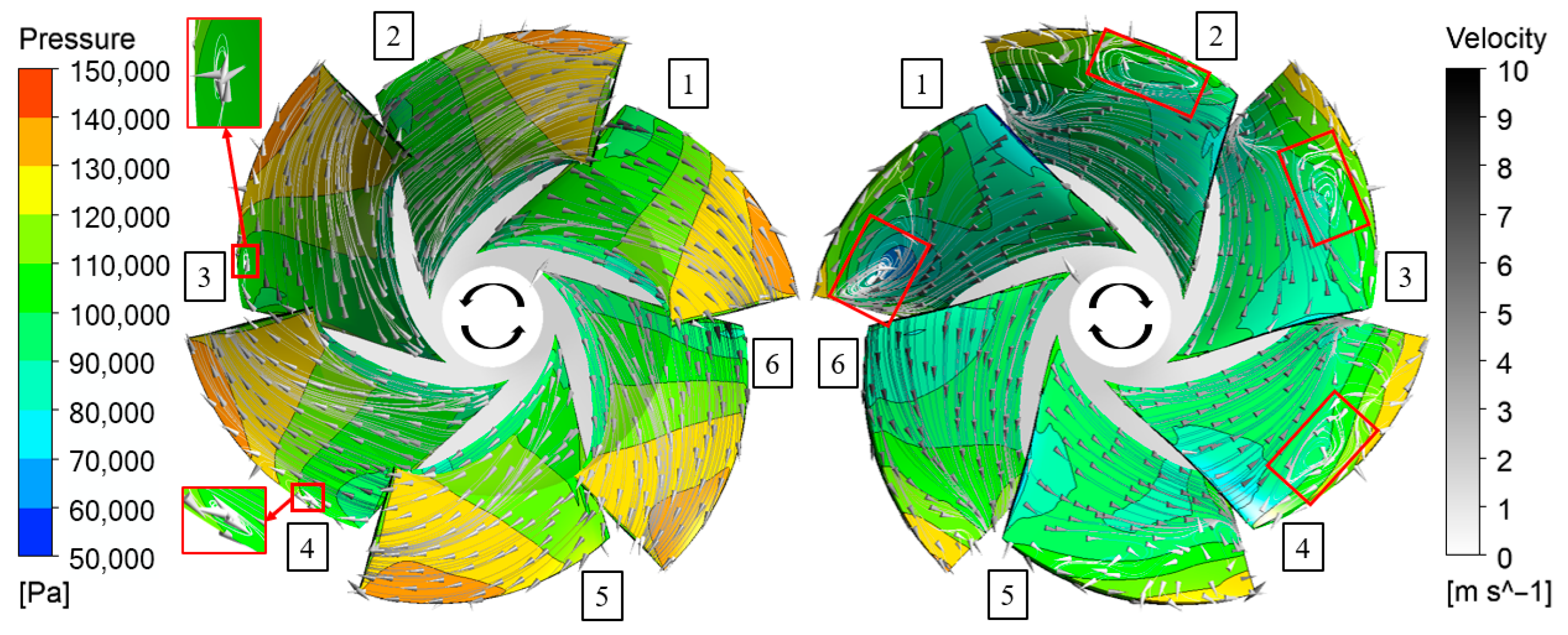
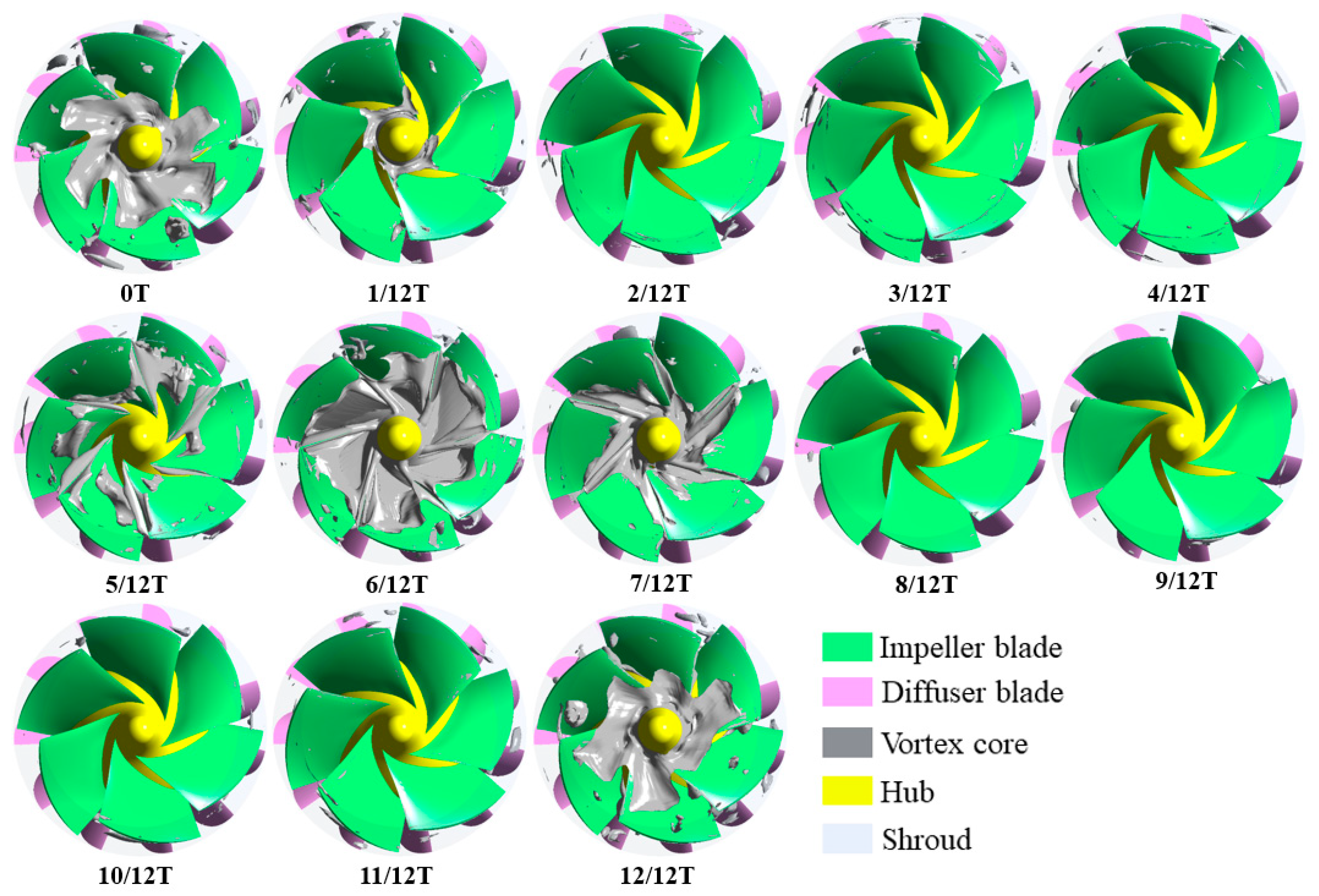
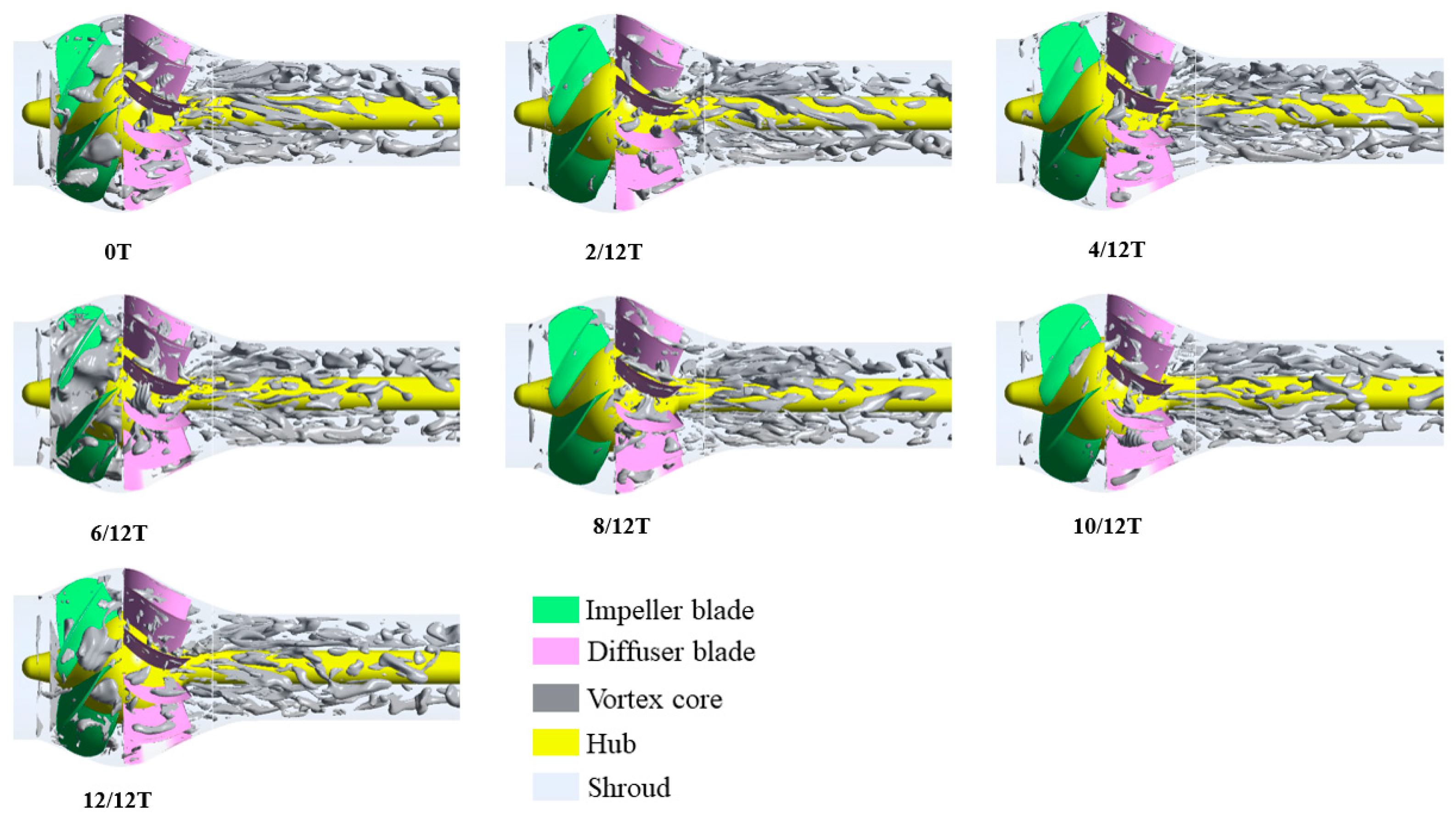
5.5. Distribution of Vortex Cores in the Pump
6. Numerical Simulation Results and Experimental Comparison
7. Conclusions
- (1)
- Hydraulic and cavitation performance curves under the hump valley condition (QnD = 0.014) were obtained. Different cavitation development stages were defined based on variations in head and cavitation flow structure.
- (2)
- Under the valley condition, the cavitation patterns in different development stages mainly include vortex cavitation, cloud cavitation, and perpendicular cavitation vortex. In the inception stage, cavitation initiates as vortex cavitation at the inlet edge of the impeller rim, evolves into cloud cavitation, and then detaches to form a perpendicular cavitation vortex at the center of the flow channel. In the development transition stage, cloud cavitation and perpendicular cavitation vortex dominate, with the cavity size increasing. In the first critical stage, adjacent flow channels exhibit significant differences in cavitation extent; cloud cavitation detaches and moves downstream as the impeller rotates, with cavitation vortex blocking 2/3 of some channels. In the critical stage, one flow channel is nearly blocked by cavitation, while the other is circumferentially blocked by 1/3. In the breakdown stage, the cavitation patterns resemble those in the critical stage but with a larger cavity size and higher blockage, further reducing pump performance.
- (3)
- Under the valley condition, the impeller and diffuser contain more small-scale vortex structures with higher overall vortex core strength, whereas the full flow domain exhibits lower overall vortex core strength but larger individual vortex cores. Additionally, flow velocity distributions at various flow rates and spanwise sections (from blade tip to root) indicate that deviations in flow rate from the design point readily induce low-velocity regions, recirculation, and boundary layer separation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| NPSH | Net positive suction head |
| QnD | non-dimensional flow coefficient |
| EnD | non-dimensional energy coefficient |
| TnD | non-dimensional torque coefficient |
| CFD | Computational fluid dynamics |
| SST | Shear stress transport |
References
- Huang, S.; Song, Y.; Yin, J.; Xu, R.; Wang, D. Research on pressure pulsation characteristics of a reactor coolant pump in hump region. Ann. Nucl. Energy 2022, 178, 109325. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Z. Optimization design of hump phenomenon of low specific speed centrifugal pump based on CFD and orthogonal test. Sci. Rep. 2022, 12, 12121. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Feng, X.; Liu, X.; Peng, T.; Chen, Z.; Wang, Z. The suppression of hump instability inside a pump turbine in pump mode using water injection control. Processes 2023, 11, 1647. [Google Scholar] [CrossRef]
- Liu, H.; Ma, Y.; Yan, W. Study and optimization of hump shaped performance characteristics of low specific speed centrifugal pump. Process Equip. Pip. 2018, 55, 58–61. (In Chinese) [Google Scholar]
- Liu, Y.; Chen, D.J.; Wang, D.Z.; Zhang, J.G.; Hu, Y.Y.; Ran, H.J. Seismic calculation and analysis of a long-axis multi-stage molten salt pump used in solar thermal power station. J. Vib. Shock 2021, 40, 148–155, 170. [Google Scholar]
- Li, W.; Ping, Y.; Shi, W.; Ji, L.; Li, E.; Ma, L. Research progress in rotating stall in mixed-flow pumps with guide vane. J. Drain. Irrig. Mach. Eng. 2019, 37, 737–745. (In Chinese) [Google Scholar]
- Li, E.; Li, W.; Shi, W.; Ma, L.; Yang, Z. Research on stall discrimination of a mixed-flow water jet pump in hump region. J. Cent. South Univ. Sci. Technol. 2020, 51, 2643–2652. (In Chinese) [Google Scholar]
- Li, E. Research on Flow Instability Mechanism of a Mixed-Flow Water Jet Pump. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2020. (In Chinese). [Google Scholar]
- Ye, W.; Ikuta, A.; Chen, Y.; Miyagawa, K.; Luo, X. Numerical simulation on role of the rotating stall on the hump characteristic in a mixed flow pump using modified partially averaged Navier-Stokes model. Renew. Energy 2020, 166, 91–107. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Liu, C.; Han, W. Study on unsteady internal flow characteristics in hump zone of mixed flow pump turbine. J. Gansu Sci. 2017, 29, 54–58. (In Chinese) [Google Scholar]
- Yang, J.; Yuan, S.; Pavesi, G.; Chun, L.; Zhou, Y. Study of hump instability phenomena in pump turbine at large partial flow conditions on pump mode. J. Mech. Eng. 2016, 52, 170–178. (In Chinese) [Google Scholar] [CrossRef]
- Qian, C.; Weimin, F.; Longcai, Z.; Na, L. Effects of inlet guide vane on characteristics of backflow vortex in hump region of axial flow pump. Trans. Chin. Soc. Agric. Mach. 2016, 47, 8–14. (In Chinese) [Google Scholar]
- Long, Y.; Zhu, R.; Wang, D. A cavitation performance prediction method for pumps PART1-Proposal and feasibility. Nucl. Eng. Technol. 2020, 52, 2471–2478. [Google Scholar] [CrossRef]
- Long, Y.; An, C.; Zhu, R.; Chen, J. Research on hydrodynamics of high velocity regions in a water-jet pump based on experimental and numerical calculations at different cavitation conditions. Phys. Fluids 2021, 33, 045124. [Google Scholar] [CrossRef]
- Yun, L.; Yan, Z.; Jianping, C.; Rongsheng, Z.; Dezhong, W. A cavitation performance prediction method for pumps: Part2-sensitivity and accuracy. Nucl. Eng. Technol. 2021, 53, 3612–3624. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, M.; Zhou, Z.; Zhong, J.; An, C.; Chen, Y.; Wan, C.; Zhu, R. Research on cavitation wake vortex structures near the impeller tip of a water-jet pump. Energies 2023, 16, 1576. [Google Scholar] [CrossRef]
- Kumar, A.; Ghobadian, A.; Nouri, J. Numerical simulation and experimental validation of cavitating flow in a multi-hole diesel fuel injector. Int. J. Engine Res. 2022, 23, 958–973. [Google Scholar] [CrossRef]
- Akira, S.; Shigeo, H.; Akio, T. Effects of cavitation in a nozzle on liquid jet atomization. Int. J. Heat Mass Transf. 2008, 50, 3575–3582. [Google Scholar]
- Huang, B.; Wang, G.; Zhao, Y. Numerical simulation unsteady cloud cavitating flow with a filter-based density correction model. J. Hydrodyn. 2014, 26, 26–36. [Google Scholar] [CrossRef]
- Zhang, R. Research on incipient cavitation performance of axial flow pumps. Trans. Chin. Soc. Agric. Mach. 1994, 3, 38–44. [Google Scholar]
- Van der Westhuizen, W.B. Cavitation erosion effects, due to off design operation of boiler reed pumps in 600 MW power station. In Proceedings of the Institution of Mechanical Engineers: International Conference on Cavitation, Cambridge, UK, 9–11 December 1992; pp. 249–262. [Google Scholar]
- Hua, H.; He, Y. Experimental Study on Scale Effects of Developed Cavitation. In Proceedings of the 2nd Asian Conference on Fluid Mech, Beijing, China, 25–29 October 1983. [Google Scholar]
- Subar, B.H. Investigation of Tip-Wall Vortex Cavitation in An Axial-Flow Pump; AD-A134357; Naval Sea Systems Command: Washington, DC, USA, 1983. [Google Scholar]
- Li, S.; Gu, C.; Miao, Y. Visual experimental study on cavitation characteristics in centrifugal pump. Pump Technol. 1997, 5, 14–20. (In Chinese) [Google Scholar]
- Li, S.; Gu, C.; Miao, Y. Experimental study on cavitation visualization of centrifugal pump with front inducer. Fluid Mach. 1997, 10, 3–7. (In Chinese) [Google Scholar]
- Huang, R.; Zhang, R.; Wang, Y.; Luo, X.; Zhu, L. Experimental and numerical investigations into flow features in an intake duct for the waterjet propulsion under mooring conditions. Acta Mech. Sin. 2021, 37, 826–843. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, K.Y. Analysis and Optimization of a Vaned Diffuser in a Mixed Flow Pump to Improve Hydrodynamic Performance. J. Fluids Eng. 2012, 134, 071104. [Google Scholar] [CrossRef]
- Gong, B.; Zhu, H.L.; Chen, X.H.; Yin, J.L.; Li, N.; Wang, D.Z. Numerical and experimental study of tip leakage vortex structures and dynamics in a mixed-flow waterjet pump. J. Phys. Conf. Ser. 2024, 2752, 012103. [Google Scholar] [CrossRef]
- Zhao, G. Research on the Mechanisms of Cavitation-Excited Forces and It’s Stablities Control in a Waterjet Pump. Ph.D. Thesis, Zhenjiang University, Hangzhou, China, 2022. [Google Scholar]
- Arakeri, V.H. Viscous effects on the position of cavitation separation from smooth bodies. J. Fluid Mech. 1975, 68, 779–799. [Google Scholar] [CrossRef]
- Ceccio, S.L.; Brennen, C.E. Dynamics of attached cavities on bodies of revolution. ASME J. Fluids Eng. 1992, 114, 93–99. [Google Scholar] [CrossRef]
- Xu, S.; Long, X.-P.; Ji, B.; Li, G.-B.; Song, T. Vortex dynamic characteristics of unsteady tip clearance cavitation in a waterjet pump determined with different vortex identification methods. J. Mech. Sci. Technol. 2019, 33, 5901–5912. [Google Scholar] [CrossRef]
- Huang, R.; Wang, Y.; Du, T.; Luo, X.; Zhang, W.; Dai, Y. Mechanism analyses of the unsteady vortical cavitation behaviors for a waterjet pump in a non-uniform inflow. Ocean Eng. 2021, 233, 108798. [Google Scholar] [CrossRef]
- Long, Y.; Zhou, Z.; Zhong, J.; Han, H. Experimental study on evolution of cavitation flow structure in hump region of waterjet pump. J. Appl. Fluid Mech. 2024, 17, 2734–2744. [Google Scholar] [CrossRef]
- Long, Y.; Zheng, Y.; Han, H.; Zhong, J.; Zhu, R. Research on hydraulic optimization design method of water-jet propulsion pump considering hump index. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 377. [Google Scholar] [CrossRef]
- Han, H.; Long, Y.; Zhong, J. Research on the internal flow difference between peak and valley conditions of water jet propulsion pump during working at hump region. J. Mar. Sci. Eng. 2024, 12, 258. [Google Scholar] [CrossRef]
- Liu, M.; Long, Y.; Zheng, Y.; Zhong, J.; Yin, H. Research on the Comparison of the Flow Evolution Mechanisms of a Water-Jet Pump Between Valley and Peak Conditions. J. Mar. Sci. Eng. 2024, 12, 2352. [Google Scholar] [CrossRef]
- Liu, M.; Long, Y.; Yin, H.; Tian, C.; Zhong, J. Research on Energy Dissipation Mechanism of Hump Characteristics Based on Entropy Generation and Coupling Excitation Mechanism of Internal Vortex Structure of Waterjet Pump at Hump Region. J. Mar. Sci. Eng. 2025, 13, 442. [Google Scholar] [CrossRef]
- Li, D.; Qin, Y.; Wang, J.; Zhu, Y.; Wang, H.; Wei, X. Optimization of blade high-pressure edge to reduce pressure fluctuations in pump-turbine hump region. Renew. Energy 2022, 181, 24–38. [Google Scholar] [CrossRef]
- Wang, H.; Wu, G.; Wu, W.; Wei, X.; Chen, Y.; Li, H. Numerical simulation and analysis of the hump district of Francis pump-turbine. J. Hydroelectr. Eng. 2012, 31, 253–258. (In Chinese) [Google Scholar]
- Menter, F.R. Improved two-equation k-omega turbulence models for aerodynamic flows. NASA Tech. Memo. 1992, 93, 103975. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the ICMF 2004 International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004. [Google Scholar]

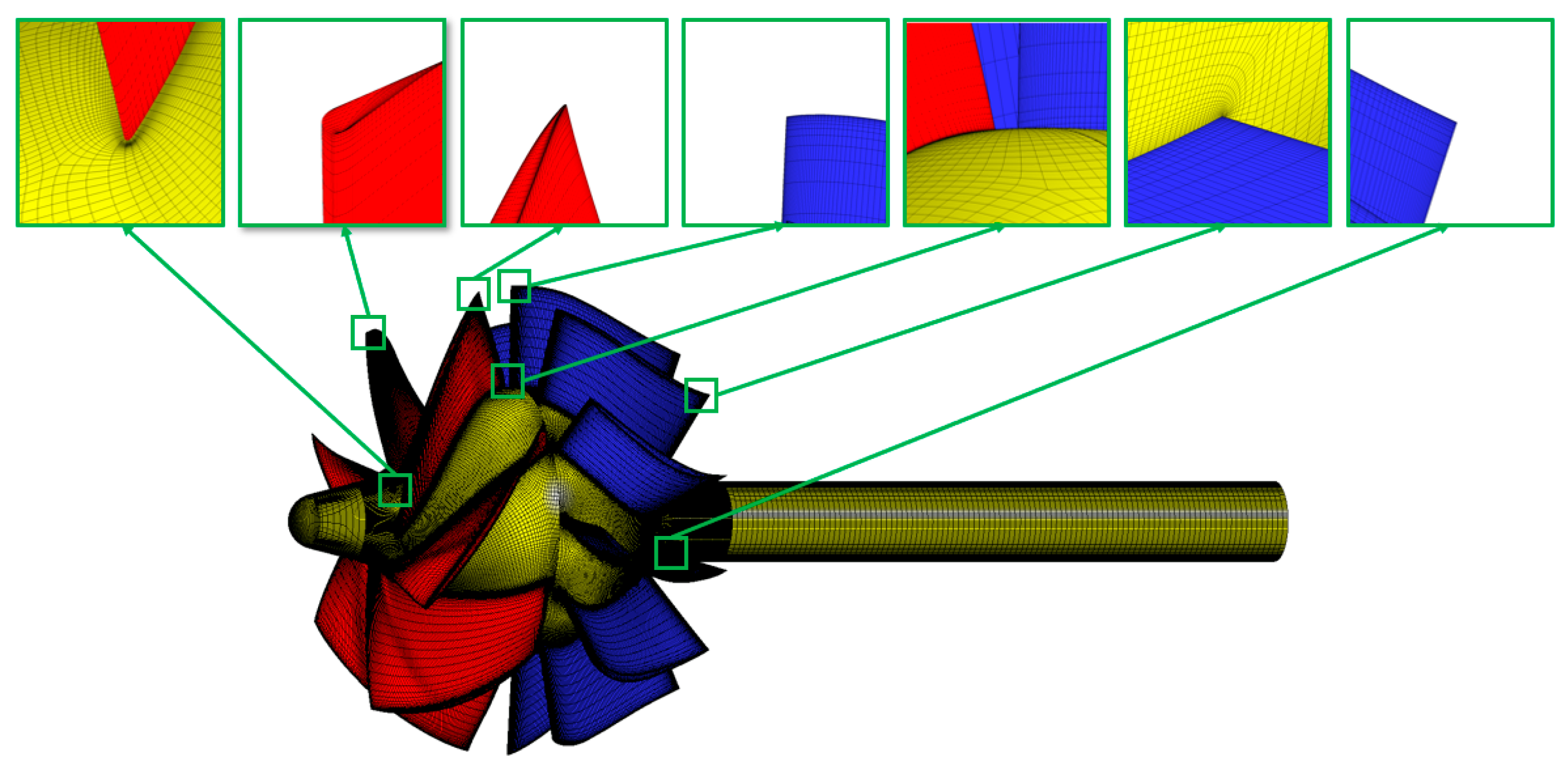





| Component | Wall | Minimum Wall Value | Maximum Wall Value | Average Wall Value | Average Component Value |
|---|---|---|---|---|---|
| Inlet pipe | Pipe wall | 1.083 | 15.882 | 4.110 | 4.151 |
| Deflector | 1.168 | 17.727 | 6.549 | ||
| Impeller | Hub | 0.038 | 4.739 | 2.004 | 3.504 |
| Blade | 0.051 | 15.673 | 4.212 | ||
| Edge | 0.131 | 10.202 | 3.198 | ||
| Diffuser | Hub | 0.049 | 7.150 | 2.075 | 3.714 |
| Blade | 0.041 | 10.330 | 4.035 | ||
| Edge | 0.131 | 10.202 | 3.937 | ||
| Outlet pipe | Shaft | 5.495 | 12.737 | 8.000 | 7.518 |
| Pipe wall | 5.323 | 9.857 | 7.368 |
| Liquid Phase | Water at 25 °C |
|---|---|
| turbulence calculation | SST k-ω turbulence model |
| impeller fluid domain | rotating domain |
| other fluid domain | stationary domain |
| inlet boundary condition | total pressure inlet |
| outlet boundary condition | mass flow rate |
| wall boundary condition | no-slip wall condition |
| impeller shroud | reverse rotating wall |
| remaining wall | stationary wall |
| interface between rotating and stationary | frozen rotor |
| differential scheme | high order |
| iterations | 1000 |
| convergence criterion | 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Long, Y.; Liu, M.; Han, H.; Wang, K.; Zhong, J.; Long, Y. Study on Cavitation Flow Structure Evolution in the Hump Region of Water-Jet Pumps Under the Valley Condition. J. Mar. Sci. Eng. 2025, 13, 1598. https://doi.org/10.3390/jmse13081598
Zheng Y, Long Y, Liu M, Han H, Wang K, Zhong J, Long Y. Study on Cavitation Flow Structure Evolution in the Hump Region of Water-Jet Pumps Under the Valley Condition. Journal of Marine Science and Engineering. 2025; 13(8):1598. https://doi.org/10.3390/jmse13081598
Chicago/Turabian StyleZheng, Yingying, Yun Long, Min Liu, Hanqiao Han, Kai Wang, Jinqing Zhong, and Yun Long. 2025. "Study on Cavitation Flow Structure Evolution in the Hump Region of Water-Jet Pumps Under the Valley Condition" Journal of Marine Science and Engineering 13, no. 8: 1598. https://doi.org/10.3390/jmse13081598
APA StyleZheng, Y., Long, Y., Liu, M., Han, H., Wang, K., Zhong, J., & Long, Y. (2025). Study on Cavitation Flow Structure Evolution in the Hump Region of Water-Jet Pumps Under the Valley Condition. Journal of Marine Science and Engineering, 13(8), 1598. https://doi.org/10.3390/jmse13081598







