Spatiotemporal Meta-Reinforcement Learning for Multi-USV Adversarial Games Using a Hybrid GAT-Transformer

Abstract

Coordinating Multi-Unmanned Surface Vehicle (USV) swarms in complex, adversarial maritime environments is a significant challenge, as existing multi-agent reinforcement learning (MARL) methods often fail to capture intricate spatiotemporal dependencies, leading to suboptimal policies. To address this, we propose Adv-TransAC, a novel Spatio-Temporal Meta-Reinforcement Learning framework. Its core innovation is a hybrid GAT-transformer architecture that decouples spatial and temporal reasoning: a Graph Attention Network (GAT) models instantaneous tactical formations, while a transformer analyzes their temporal evolution to infer intent. This is combined with an adversarial meta-learning mechanism to enable rapid adaptation to opponent tactics. In high-fidelity escort and defense simulations, Adv-TransAC significantly outperforms state-of-the-art MARL baselines in task success rate and policy robustness. The learned policies demonstrate the emergence of complex cooperative behaviors, such as intelligent risk-aware coordination and proactive interception maneuvers. The framework’s practicality is further validated by a communication-efficient federated optimization architecture. By effectively modeling spatiotemporal dynamics and enabling rapid adaptation, Adv-TransAC provides a powerful solution that moves beyond reactive decision-making, establishing a strong foundation for next-generation, intelligent maritime platforms.

1. Introduction

With the rapid development of the global marine economy, intelligent marine equipment, particularly Unmanned Surface Vehicles (USVs), is playing an increasingly critical role in marine resource development, environmental monitoring, and security maintenance [1]. The challenge of coordinating Unmanned Surface Vehicle (USV) swarms for complex maritime missions has become a significant focus of recent experimental research. Simulation-based studies, in particular, have proven to be a critical methodology for developing and testing advanced control strategies, with recent works exploring deep reinforcement learning for tasks like coordinated path planning [2] and hierarchical collision avoidance in complex scenarios [3]. When deployed as a swarm, USVs can execute large-scale, dynamic tasks more efficiently and resiliently than single-vehicle systems [4]. These technological advances promise significant economic benefits, such as reduced operational costs and enhanced intelligence in key applications like port security [5].

While traditional control methodologies, such as Model Predictive Control (MPC) and sliding mode control, have demonstrated effectiveness for single-vehicle trajectory tracking and formation keeping under well-defined conditions, they face significant limitations in large-scale, adversarial maritime scenarios [6]. These methods often rely on precise system models and predefined objectives, making them less adaptable to the highly dynamic and uncertain nature of environments with intelligent, unpredictable opponents. The non-stationary dynamics induced by adversaries, coupled with the exponential complexity of multi-agent coordination, render the design of effective, centralized model-based controllers intractable. This necessitates a paradigm shift towards learning-based approaches that can derive sophisticated, adaptive control strategies directly from high-dimensional sensory data and interaction experience.

Despite this progress, deploying USV swarms in complex, real-world adversarial environments remains a significant challenge that pushes the boundaries of conventional control theory… However, existing multi-agent reinforcement learning (MARL) algorithms also face critical hurdles when applied to this domain. Three fundamental problems must be addressed: first, the effective fusion of multi-modal sensor data for robust situational awareness [7]; second, the learning of sophisticated, coordinated adversarial control strategies essential for mission success [8]; and third, overcoming the intermittent and low-bandwidth communication inherent to maritime operations, which complicates the training and coordination of distributed systems [9]. Existing MARL methods often fall short in one or more of these areas.

Current MARL methods, particularly those based on the popular Centralized Training with Decentralized Execution (CTDE) paradigm, have shown promise but still exhibit critical shortcomings in addressing these challenges. For instance, value-decomposition methods like QMIX [10] can be too restrictive for complex coordination. In contrast, actor–critic methods like MADDPG [11] often rely on simple concatenation of observation vectors, failing to capture the rich spatiotemporal relationships within multi-modal data. This usually leads to policy degradation in dynamic environments. Furthermore, many existing algorithms lack the representational power to model sophisticated opponent behaviors, causing their performance to drop significantly when facing adversaries with novel or adaptive tactics [12]. This highlights a clear research gap: the need for a unified framework that simultaneously handles complex multi-modal perception and learns powerful, generalizable policies for adversarial settings. Existing methods face a fundamental challenge in handling spatiotemporal dependencies within multi-agent systems. Although a transformer could theoretically manage a flattened spatiotemporal sequence, this approach undermines the essential instantaneous tactical graph structures—such as encirclements, cover, and formations—that agents create at specific times. On the other hand, relying solely on graph neural networks (GNNs) complicates capturing the temporal evolution of these tactical structures and understanding the long-term intentions of adversaries [13].

Compounding this challenge is the presence of intelligent adversaries, which introduces severe non-stationarity and necessitates rapid adaptation. Meta-reinforcement learning has emerged as a powerful paradigm to address this, aiming to create agents that can “learn to learn” and adapt quickly to novel situations with minimal new experience. Recent research has shown the effectiveness of this approach in multi-agent settings, demonstrating how meta-learned policies can generalize to handle unseen tasks or opponent strategies [14]. In the context of our work, this is crucial because traditional MARL algorithms, which learn a policy for a fixed opponent distribution, often exhibit brittle performance when confronted with adversaries that employ unseen tactics.

To address these limitations, this paper proposes a novel end-to-end control strategy learning framework, the Adversarial transformer actor–critic (Adv-TransAC) [15]. The core idea is not merely to apply a transformer, but to introduce an innovative hybrid GAT-transformer architecture that achieves a decoupled modeling of spatiotemporal dependencies to inform the control policy [16]. Our framework first employs a Graph Attention Network (GAT) to explicitly capture the instantaneous spatial relationships and tactical graph structures between agents at each timestep.

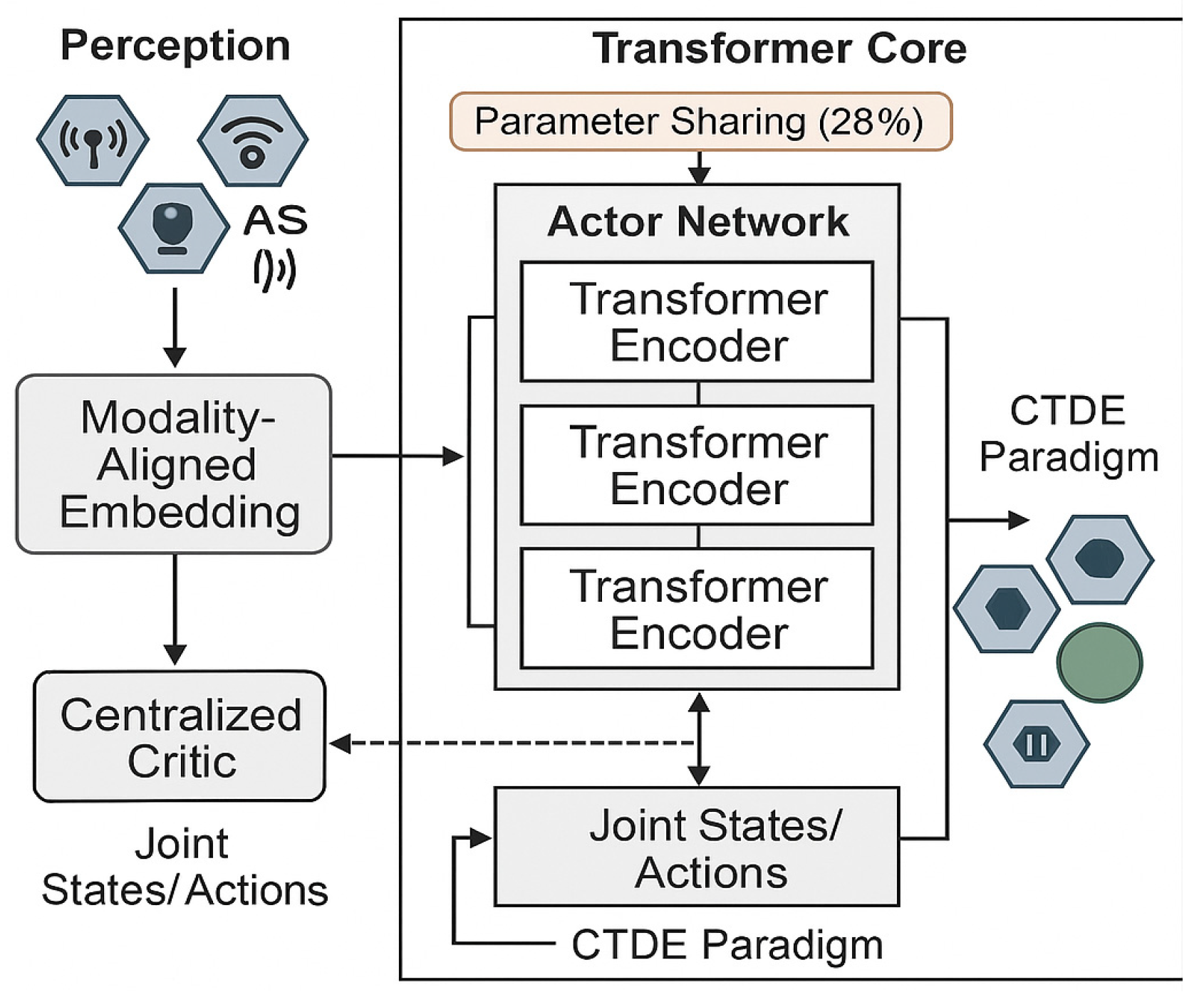
These high-quality “battlefield snapshots” are then fed as a sequence into a transformer encoder [17] to analyze their long-term temporal evolution and tactical intent. The overall architecture, illustrated in Figure 1, follows the Centralized Training with Decentralized Execution (CTDE) paradigm [18]. Specifically, this powerful spatiotemporal modeling capability is integrated into our centralized critic for superior credit assignment. At the same time, decentralized actors leverage transformers to process their local observation histories and adapt to opponent strategies.

The model employs a transformer-based decentralized control policy network (actor) for agent-level decision-making based on multi-modal inputs, and a centralized critic for joint state–action evaluation, all within the CTDE paradigm.

The main contributions of this paper are summarized as follows:

• We propose a novel MARL framework, Adv-TransAC, which systematically integrates the transformer architecture into an adversarial actor–critic paradigm to address the dual challenges of multi-modal fusion and strategic decision-making in multi-USV scenarios.
• We design a specific network architecture where decentralized actors use transformers to process local multi-modal observation histories. At the same time, a centralized critic leverages a transformer to model global state–action values, enabling more effective coordination and credit assignment.
• We conduct comprehensive experiments in a simulated multi-USV attack–defense environment, demonstrating that Adv-TransAC significantly outperforms established MARL baselines regarding task success rate and policy robustness.

The remainder of this paper is organized as follows: Section 2 reviews related work. Section 3 details the necessary preliminaries and our proposed Adv-TransAC methodology. Section 4 presents the experimental setup and results. Finally, Section 5 discusses our findings and concludes the paper.

2. Related Work

Our research builds upon three primary areas of study: multi-agent reinforcement learning (MARL), multi-modal fusion for autonomous systems, and the application of transformer architectures in decision-making tasks.

2.1. Multi-Agent Reinforcement Learning (MARL)

MARL aims to train multiple autonomous agents to cooperatively or competitively achieve complex objectives. A central hurdle in MARL is the non-stationarity of the environment; as each agent adapts its policy, the environment from any single agent’s perspective changes dynamically. To counteract this, the Centralized Training with Decentralized Execution (CTDE) paradigm has emerged as a dominant and effective approach [1].

Within the CTDE framework, two primary branches of methods have gained prominence. The first encompasses value-decomposition methods, exemplified by Value-Decomposition Networks (VDNs) [19] and QMIX [8]. These algorithms learn individual agent value functions and then combine them into a global value function under a monotonicity constraint. While this constraint simplifies credit assignment and enhances training stability, it significantly limits the model’s expressiveness. This becomes particularly problematic in tasks demanding complex trade-offs, where an agent’s contribution to the team’s success might not be monotonically related to its individual value, leading to suboptimal or brittle policies [10].

The second branch comprises multi-agent actor–critic methods, with Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [11] being a seminal work. MADDPG employs a centralized critic that observes the full joint state and actions of all agents, thereby stabilizing the training process. Despite its flexibility compared to value-decomposition methods, MADDPG often struggles with scalability as the number of agents increases. A key limitation often lies in its reliance on simple concatenation of observation vectors [9], which fundamentally fails to capture the intricate, high-order spatiotemporal relationships and inter-agent dependencies inherent in multi-modal data. This leads to policy degradation in dynamic and uncertain environments. Our Adv-TransAC framework belongs to the actor–critic family, but critically, it introduces a more sophisticated architectural approach within the centralized critic to explicitly model these complex dependencies, offering a significant improvement over methods like MADDPG and QMIX. Indeed, effectively decomposing tasks and assigning credit in dynamic, multi-agent scenarios remain a significant open challenge. This has prompted new simulation-based research into more advanced, learning-based planning and decomposition frameworks to overcome the limitations of earlier methods [20].

2.2. Multi-Modal Fusion in USV Systems

Effective situational awareness for USV swarms operating in complex marine environments hinges on the robust fusion of data from multiple heterogeneous sensors, such as radar (for long-range detection), optical cameras (for high-resolution identification), and AIS (for vessel information). Traditional MARL approaches have often oversimplified this challenge, either by assuming homogeneous observations or by naively concatenating feature vectors from different sensors [21]. This “flat” representation disregards the unique spatial, temporal, and semantic properties of each modality, leading to substantial information loss and suboptimal performance, especially in highly dynamic and cluttered marine environments [7].

More advanced methods have sought to capture temporal dependencies. Recurrent neural networks (RNNs) and LSTMs have been utilized to process sequential sensor data [22]. While capable of handling time dependencies, their sequential processing nature can be computationally inefficient and may struggle with very long-range dependencies. Recently, graph neural networks (GNNs) have emerged as powerful tools for modeling spatial relationships [23]. GNNs can effectively represent USVs and other entities as nodes in a graph, explicitly capturing instantaneous tactical structures such as formations, encirclements, or lines of sight. However, GNNs alone are limited in their ability to capture the temporal evolution of these tactical structures and infer the long-term intentions of adversaries based on historical patterns [13]. Our work addresses this by integrating GNNs with a more powerful temporal modeling mechanism.

2.3. Transformer in Reinforcement Learning and Robotics

Originally developed for natural language processing, the transformer architecture [23] has rapidly gained traction in various sequential decision-making tasks, including reinforcement learning and robotics, due to its unparalleled ability to model sequential data and capture long-range dependencies through its self-attention mechanism.

In single-agent RL, landmark works such as Decision Transformer [24] have successfully reframed reinforcement learning as a sequence modeling problem. By predicting future actions conditioned on a history of states, actions, and rewards, transformers have demonstrated the capacity to learn complex behaviors without explicit value function estimation [25]. In robotics, transformers have been successfully applied to tasks ranging from manipulation to locomotion, by effectively treating sensorimotor trajectories as sequences [26].

The success of transformers naturally extended to the multi-agent domain. Early MARL works incorporated attention mechanisms to allow agents to selectively focus on relevant teammates or opponents, improving coordination in complex scenarios [27]. More recently, researchers have begun leveraging the full transformer architecture to process multi-agent information directly. Approaches like multi-agent PPO (MAPPO) [28] and UPDeT [29] utilize transformer encoders to process sequences of agent observations for value function estimation or as part of the policy network.

However, a critical limitation in many existing transformer-based MARL methods is their tendency to treat the multi-agent system’s state as a “flattened” set or sequence of individual agent features [30]. While powerful for capturing long-term temporal patterns, this approach paradoxically sacrifices crucial real-time spatial context. Vital tactical information—such as the emergence of formations, encirclements, or specific lines of sight—is inherently structured as a graph at each timestep. By flattening this rich spatial information into a one-dimensional sequence, the model is forced to implicitly re-learn these spatial relationships, which is an inefficient and often ineffective process, especially in dynamic adversarial settings [13].

2.4. Transformer-Based Multi-Agent Reinforcement Learning

The success of transformers in sequential decision-making has naturally led to their adoption in the multi-agent domain. Early works employed attention mechanisms to help agents selectively focus on more relevant teammates or opponents, improving coordination in complex scenarios [27]. More recently, researchers have started using the full transformer architecture to directly process multi-agent information. For instance, approaches like multi-agent PPO (MAPPO) [28] and UPDeT [29] utilize a transformer encoder to process a sequence of agent observations, either for value function estimation in the critic or as part of the policy network itself. This trend has continued to evolve rapidly, with very recent work exploring the use of large-scale, generative pre-trained transformers for complex tactical decision-making directly within multi-agent simulations [31]. This underscores the growing consensus on the power of sequence modeling for capturing long-term tactical intent, a principle central to our framework.

However, many of these existing methods face a key limitation: they often treat the multi-agent system’s state as a “flattened” set or sequence of individual agent features [30]. Paradoxically, while this approach is powerful for capturing long-term temporal patterns, it comes at the cost of sacrificing critical, real-time spatial context. By reducing rich spatial interactions into a one-dimensional sequence, vital tactical information—such as formations, encirclements, or lines of sight—can be obscured or lost entirely. This simplification forces the model to implicitly re-learn these spatial relationships from the sequence, an inefficient and often ineffective process.

In stark contrast, our Adv-TransAC framework is built on a different philosophy. We introduce a novel hybrid GAT-transformer architecture designed to explicitly preserve this crucial spatial information. Our hybrid model first employs a Graph Attention Network (GAT) to capture the instantaneous tactical graph structures before this spatially aware representation is passed to the transformer for temporal examination. This principled, decoupled modeling of space and time allows for a richer and more robust strategic understanding. Furthermore, our work is one of the first to systematically integrate this advanced spatiotemporal model with an adversarial meta-learning paradigm specifically for the complex multi-USV domain, which is a key differentiator of our work.

3. Methodology

This section will introduce the theoretical foundations necessary to build the Adv-TransAC framework, including the basic paradigm of Dec-POMDP, adversarial multi-agent reinforcement learning (adversarial MARL), and the transformer architecture as the core of our model.

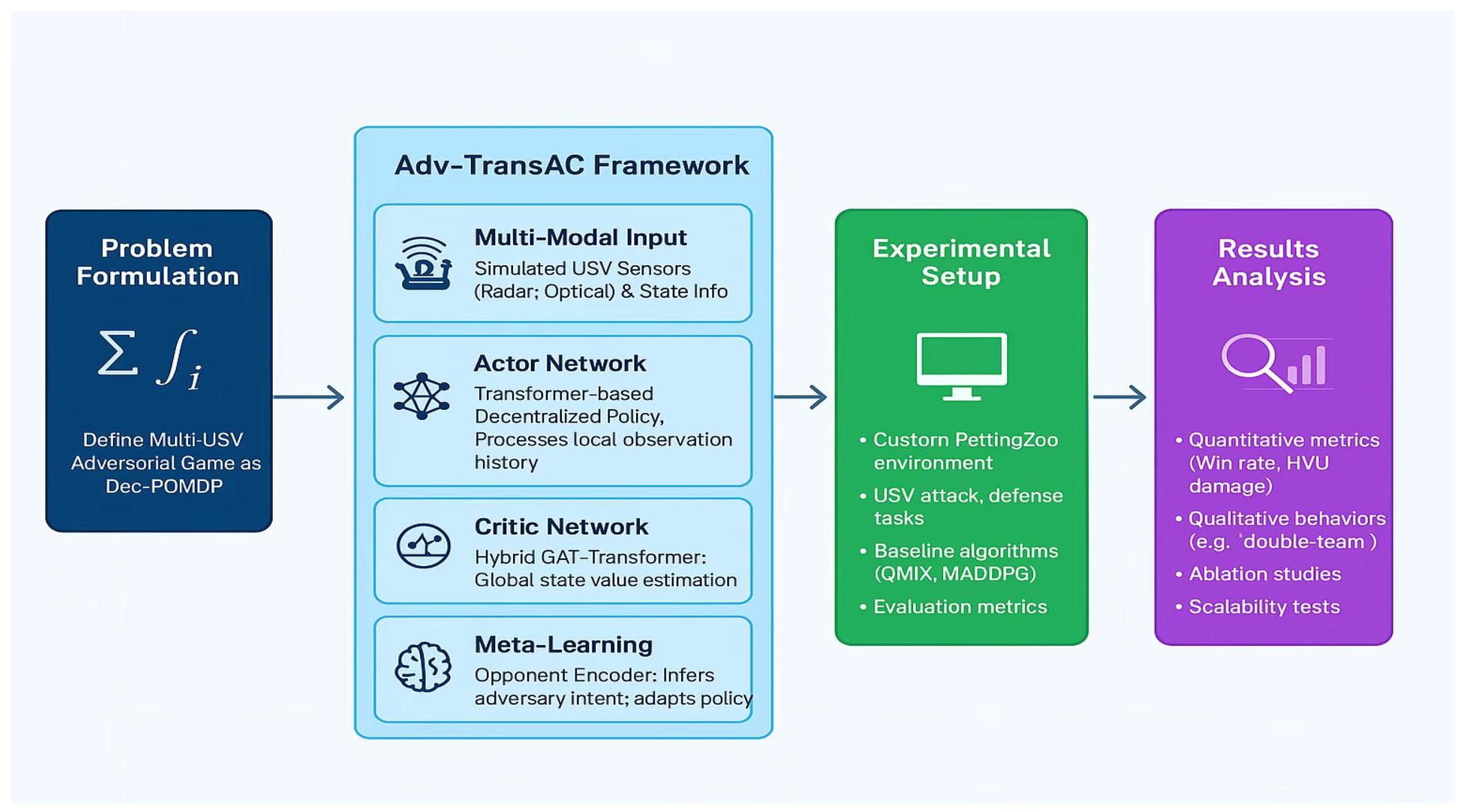
Overall research workflow. The diagram illustrates the complete research pipeline, starting from the theoretical problem formulation, moving to the design of the core components of the Adv-TransAC Framework, followed by the experimental setup for validation, and concluding with the results analysis methodologies. This flowchart provides a high-level guide for the detailed sections that follow.

3.1. Decentralized Partially Observable Markov Decision Process (Dec-POMDP)

For clarity and ease of reference, a comprehensive list of all mathematical symbols and acronyms used throughout this paper is provided in Nomenclature.

The Decentralized Partially Observable Markov Decision Process (Dec-POMDP) provides a formal framework for collaborative decision-making in multi-agent systems under partial observability. It is defined as a tuple: $\mathrm{G}=〈\mathrm{S},\mathrm{A},\mathrm{P},\mathrm{R},\mathsf{\Omega },\mathrm{O},\mathrm{n},\mathsf{\gamma }〉$.

State Space (S): The global state space contains complete environmental information, including the position $({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}})$, heading ${\mathsf{\theta }}_{\mathrm{i}}$, and velocity ${\mathrm{v}}_{\mathrm{i}}$ of all agents, dynamic obstacle distributions, mission target status, and the status of adversaries (e.g., their kinematic states). The dimensionality of the state space grows exponentially with the number of agents: $\dim (\mathrm{S})\propto \mathrm{O}({\mathrm{k}}^{\mathrm{n}})$, where $\mathrm{k}$ represents the single agent state dimension.

Action Space (A): The joint action space is defined as the Cartesian product $\mathrm{A}={\mathrm{A}}_1\times {\mathrm{A}}_2\times \cdots \times {\mathrm{A}}_{\mathrm{n}}$, where each agent $\mathrm{i}$ selects actions ${\mathrm{a}}_{\mathrm{i}}\in {\mathrm{A}}_{\mathrm{i}}$ corresponding to discrete or continuous control commands such as acceleration, steering, or maintaining heading.

Transition Function (P): The state transition function $\mathrm{P}\left({\mathrm{s}}^{\prime }\right|\mathrm{s},\mathrm{a})$ describes the probability distribution of transitioning from state $\mathrm{s}$ to state ${\mathrm{s}}^{\prime }$ under joint action $\mathrm{a}=({\mathrm{a}}_1,\dots ,{\mathrm{a}}_{\mathrm{n}})$. This function incorporates ocean dynamics and environmental disturbances, modeled as ${\mathrm{s}}_{\mathrm{t}+1}=\mathrm{f}\left({\mathrm{s}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}}\right)+\mathsf{ϵ}$, where ${\mathrm{s}}_{\mathrm{t}}$ is the global state, ${\mathrm{a}}_{\mathrm{t}}$ is the joint action, and $\mathsf{\epsilon }$ represents stochastic environmental noise.

Reward Function (R): The global reward function $\mathrm{R}(\mathrm{s},\mathrm{a})$ provides a shared signal for the team, designed to balance multiple objectives:$\mathrm{R}=\mathsf{\alpha }{\mathrm{R}}_{\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{k}}+\mathsf{\beta }{\mathrm{R}}_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}}+\mathsf{\gamma }{\mathrm{R}}_{\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}}$, where ${\mathrm{R}}_{\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{k}}$ represents task progress reward, ${\mathrm{R}}_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}\mathrm{t}\mathrm{y}}$ penalizes unsafe behaviors, and ${\mathrm{R}}_{\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}}$ controls energy consumption. The formulation of this multi-objective reward function is non-trivial and represents a critical aspect of shaping the final learned control strategy. The weights α, β, and γ are crucial hyperparameters that must be carefully tuned to orchestrate the trade-off between mission aggression, platform safety, and operational endurance. For instance, a higher value for β would steer the learning process towards a more cautious, risk-averse policy, prioritizing collision avoidance over aggressive maneuvering. Conversely, a dominant α encourages more assertive, task-focused behaviors. The specific weights used in our experiments are chosen to foster a balanced control strategy that aggressively pursues mission objectives while maintaining a high degree of operational integrity.

Observation Space ($\mathsf{\Omega }$): Each agent $\mathrm{i}$ receives local observations ${\mathrm{o}}_{\mathrm{i}}={\mathrm{g}}_{\mathrm{i}}(\mathrm{s},{\mathsf{\eta }}_{\mathrm{i}})$, where ${\mathsf{\eta }}_{\mathrm{i}}$ represents sensor noise. Observations include enemy positions within the limited field of view, friendly agent states within communication range, and navigation data subject to positioning errors.

Observation Function (O): The observation function $\mathrm{O}\left(\mathrm{o}\right|\mathrm{s})$ quantifies the conditional probability of agent $\mathrm{i}$ obtaining observation $\mathrm{o}$ in global state $\mathrm{s}$, directly characterizing the partial observability challenge.

Agent Count (n): The number of agents determines the scale of the collaborative decision-making unit, encompassing both attacking and defending forces.

Discount Factor ($\mathsf{\gamma }$): The discount factor $\mathsf{\gamma }\in [0,\left.1\right)$ balances immediate and long-term rewards through the cumulative return: ${\mathrm{G}}_{\mathrm{t}}=\sum _{\mathrm{k}=0}^{\mathrm{\infty }}{\mathsf{\gamma }}^{\mathrm{k}}{\mathrm{R}}_{\mathrm{t}+\mathrm{k}+1}$.

Key Characteristics:

Partial Observability: Agents must make decisions based on their local action-observation histories, denoted as ${\mathsf{\tau }}_{\mathrm{i}}^{\mathrm{t}}=({\mathrm{o}}_{\mathrm{i}}^0,{\mathrm{a}}_{\mathrm{i}}^0,\dots ,{\mathrm{o}}_{\mathrm{i}}^{\mathrm{t}})$. The policy for agent i is expressed as ${\mathsf{\pi }}_{\mathrm{i}}\left({\mathrm{a}}_{\mathrm{i}}^{\mathrm{t}}\right|{\mathsf{\tau }}_{\mathrm{i}}^{\mathrm{t}};{\mathsf{\theta }}_{\mathrm{i}})$.

Decentralized Execution: The framework enables independent operation when communication is disrupted after training, ensuring robustness in adversarial environments.

Cooperative Objective: Implicit collaboration is achieved by maximizing the expected cumulative team reward: $\mathbb{E}\left[\sum _{\mathrm{t}=0}^{\mathrm{T}}{\mathsf{\gamma }}^{\mathrm{t}}\mathrm{R}({\mathrm{s}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}})\right]$.

This formal framework establishes the theoretical foundation for Adv-TransAC. Specifically, our actor-critic architecture, operating under the Centralized Training with Decentralized Execution (CTDE) paradigm, is designed to tackle these challenges: the decentralized actors learn policies based on local histories (${\mathsf{\tau }}_{\mathrm{i}}^{\mathrm{t}}$), while the centralized critic leverages the global state ($\mathrm{s}$) during training to overcome partial observability and facilitate effective coordination.

3.2. Adversarial Multi-Agent Reinforcement Learning (Adversarial MARL)

Adversarial multi-agent reinforcement learning focuses on the environment with strategic adversaries, and its core challenge stems from the non-stationarity of the environment, which leads to the state transition function $\mathrm{P}\left({\mathrm{s}}^{\prime }∣\mathrm{s}\right)$ due to the dynamic change in adversary strategy ${\mathsf{\pi }}_{\mathrm{a}\mathrm{d}\mathrm{v}}$. Moreover, the reward function $\mathrm{R}(\mathrm{s},\mathrm{a})$ has substantially evolved into the time-varying function ${\mathrm{P}}_{\mathrm{t}}({\mathrm{s}}^{\prime }\mid \mathrm{s},\mathrm{a},{\mathsf{\pi }}_{\mathrm{a}\mathrm{d}\mathrm{v}}^{\mathrm{t}})$ and ${\mathrm{R}}_{\mathrm{t}}(\mathrm{s},\mathrm{a},{\mathsf{\pi }}_{\mathrm{a}\mathrm{d}\mathrm{v}}^{\mathrm{t}})$. This feature invalidates the Markov assumption of traditional single-agent reinforcement learning, which requires the algorithm to have the ability to adapt to the opponent’s behavior online. To solve this challenge, centralized training and distributed execution (CTDE) has become the mainstream paradigm: in the training stage, the centralized critic is used to access global information (such as joint state s and joint action a) to learn the team’s optimal strategy, while each agent in the execution stage only relies on local observations_i independent decision-making, which not only alleviates the problem of non-stationarity, but also meets the strict requirements of the battlefield environment for real-time and robustness. We design a novel adversarial meta-learning architecture to address the above challenges, as shown in Figure 2 and Figure 3. This architecture systematically solves the problem of strategy learning in non-stationary environments by explicitly modeling and adapting the opponent’s strategy and stabilizing the training process in combination with course learning.

The architecture consists of three main parts: (1) the opponent encoder, which is responsible for extracting the tactical characteristics of the enemy from its historical moves; (2) base policy, which is composed of GNN and transformer, used to generate the specific actions of our agent; (3) meta-regulator, which receives the tactical characteristics of the opponent and generates a meta-signal to adjust the behavior of the underlying strategy network dynamically. The entire training process is guided by a course learning scheduler, which ensures the robustness and generalization of the strategy by progressively increasing the opponent’s difficulty.

The core idea of this architecture is to decouple the two processes of “identifying adversaries” and “responding”. With the meta-regulator, our agents can adapt online to the opponent’s strategy changes, rather than just reacting to their current moves.

Under the CTDE framework, value function decomposition is a key technology for solving multi-agent credit allocation. Traditional methods such as QMIX can decompose the value function ${\mathrm{Q}}_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(\mathsf{\tau },\mathrm{a}\right)$ and the individual value function ${\mathrm{Q}}_{\mathrm{i}}\left({\mathsf{\tau }}_{\mathrm{i}},{\mathrm{a}}_{\mathrm{i}}\right)$ satisfying the monotonicity relationship ${\displaystyle \frac{\partial {\mathrm{Q}}_{\mathrm{t}\mathrm{o}\mathrm{t}}}{\partial {\mathrm{Q}}_{\mathrm{i}}}}\ge 0 (\mathrm{i}.\mathrm{e}.,{\mathrm{Q}}_{\mathrm{t}\mathrm{o}\mathrm{t}}\mathrm{g}\left({\mathrm{Q}}_1,\dots ,{\mathrm{Q}}_{\mathrm{n}}\right),$ where g is a monotonic function). However, this constraint severely limits the ability to express the strategy in the asymmetric adversarial scenario. The main issue is its inability to effectively model competitive games’ complex, non-linear reward structures, such as the trade-offs between offensive and defensive objectives. Additionally, it struggles to capture sophisticated dynamic coordination patterns, like the collaboration between decoy tactics and the primary attacking force. This inflexibility can result in suboptimal or even failed strategies when confronted with intelligent and adaptive opponents.

To this end, Adv-TransAC introduces a transformer-enhanced adversarial learning mechanism designed to break through the above limitations. This mechanism is founded on three key principles:

• Flexible Credit Assignment: It utilizes multi-head self-attention within the critic network to dynamically model the dependencies between agents. This approach replaces the rigid monotonic constraints of meQMIX methods, enabling more flexible and expressive credit allocation.
• Adaptive Opponent Modeling: We design an adversarial meta-learning architecture where a transformer encoder processes an opponent’s historical behavior sequence, ${{\mathrm{h}}_{\mathrm{a}\mathrm{d}\mathrm{v}}}_{\mathrm{a}\mathrm{d}\mathrm{v}}^{\mathrm{h}}\mathrm{t}=\left\{{\mathrm{a}}_{\mathrm{a}\mathrm{d}\mathrm{v}}^0,\dots ,{\mathrm{a}}_{\mathrm{a}\mathrm{d}\mathrm{v}}^{\mathrm{t}}\right\}$, to extract a latent representation of its tactical features, ${\mathrm{z}}_{\mathrm{a}\mathrm{d}\mathrm{v}}$. Our agent’s policy is then conditioned on these features (${\mathrm{z}}_{\mathrm{a}\mathrm{d}\mathrm{v}}$), facilitating rapid adaptation to an adversary’s changing tactics.
• Progressive Training via Curriculum Learning: The framework incorporates adversarial curriculum learning, which gradually transitions the training from simple, rule-based opponents ${\mathsf{\pi }}_{\mathrm{a}\mathrm{d}\mathrm{v}}^0\in {\mathsf{\Pi }}_{\mathrm{r}\mathrm{u}\mathrm{l}\mathrm{e}}$ to more sophisticated, learning-based adversaries ${\mathsf{\pi }}_{\mathrm{a}\mathrm{d}\mathrm{v}}^{\mathrm{k}}\in {\mathsf{\Pi }}_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}}$. This staged approach ensures stable convergence and fosters robust and generalizable policy development.

This framework treats the diversity of opponent strategies as a training resource to enhance our agents’ robustness, fundamentally addressing the policy degradation problem caused by a non-stationary environment.

3.3. Transformer Architecture

As a deep learning model based on the self-attention mechanism, the transformer was originally designed for natural language processing, and its excellent sequence modeling capabilities make it a core tool to solve the bottleneck of multi-unmanned vehicles and multi-modal time series data processing. This architecture abandons the time-series dependence limitations of traditional recurrent neural networks (RNNs). It achieves efficient training through parallel computing, especially suitable for the real-time fusion of asynchronous stream data such as radar point clouds and AIS trajectories in the marine environment (as described in Section 2.2 pulsed spatiotemporal attention module). The self-attention layer of the core computing unit maps the input sequence $\mathrm{X}=\left[{\mathrm{x}}_1,\dots ,{\mathrm{x}}_{\mathrm{T}}\right]\in {\mathrm{R}}^{\mathrm{T}\times {\mathrm{d}}_{\mathrm{model}}}$ into three matrices: Query, Key, and Value: $\mathrm{Q}=\mathrm{X}{\mathrm{W}}^{\mathrm{Q}},\mathrm{K}=\mathrm{X}{\mathrm{W}}^{\mathrm{K}},\mathrm{V}=\mathrm{X}{\mathrm{W}}^{\mathrm{V}}$,${\mathrm{W}}^{\mathrm{Q}},{\mathrm{W}}^{\mathrm{K}},{\mathrm{W}}^{\mathrm{V}}\in {\mathbb{R}}^{{\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times {\mathrm{d}}_{\mathrm{k}}}$ is a learnable parameter. Attention weights are calculated by scaling the dot product:

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathbf{Q},\mathbf{K},\mathbf{V})=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\displaystyle \frac{{\mathbf{Q}\mathbf{K}}^{\top }}{\sqrt{d_k}}}\right)\mathbf{V}$$

(1)

This mechanism enables the model to assess the importance of different elements within a sequence dynamically. For example, it can learn to concentrate on a sudden maneuver by an opponent, which is essential for accurate state estimation and prediction.

Multi-head attention is used to capture a range of perspectives from the data. This involves executing multiple parallel self-attention operations, known as “heads,” and combining their outputs.

$$\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}(\mathrm{Q},\mathrm{K},\mathrm{V})=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left(\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_1\right.,\dots ,\left.{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_{\mathrm{h}}\right){\mathrm{W}}^{\mathrm{O}}$$

(2)

$${\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_{\mathrm{i}}=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}({\mathrm{X}\mathrm{W}}_{\mathrm{i}}^{\mathrm{Q}},{\mathrm{X}\mathrm{W}}_{\mathrm{i}}^{\mathrm{K}},{\mathrm{X}\mathrm{W}}_{\mathrm{i}}^{\mathrm{V}})$$

(3)

This structure is designed to improve heterogeneous data fusion by allowing different attention heads to focus on various aspects of the multi-modal input, such as coordinating between optical image details, radar range information, and AIS heading data. In spatiotemporal data processing, positional encoding is crucial. Learnable 2D position coding is employed in rasterized environments. ${\mathrm{P}}_{\left(\mathrm{x},\mathrm{y}\right)}\in {\mathbb{R}}^{{\mathrm{d}}_{\mathrm{model}}}$ inject spatial coordinate information:

$$\tilde{\mathbf{X}}=\mathbf{X}+\mathbf{P},\hspace{1em}{\mathbf{P}}_{(x,y)}[2i]=\sin \left({\displaystyle \frac{x}{10000^{2i}/d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}}\right),\hspace{1em}{\mathbf{P}}_{(x,y)}[2i+1]=\cos \left({\displaystyle \frac{x}{10000^{2i}/d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}}\right)$$

(4)

This is crucial for maintaining spatiotemporal relationships within the input data, addressing a significant limitation of simple feature concatenation, which loses this vital context.

$$\mathrm{F}\mathrm{F}\mathrm{N}\left(\mathrm{x}\right)=\max \left(0,\mathrm{x}{\mathrm{W}}_1+{\mathrm{b}}_1\right){\mathrm{W}}_2+{\mathrm{b}}_2$$

(5)

$${\mathrm{x}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}(\mathrm{x}+\mathrm{D}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}(\mathrm{F}\mathrm{F}\mathrm{N}\left(\mathrm{x}\right)\left)\right)$$

(6)

By stacking these encoder blocks, Adv-TransAC can effectively model complex, long-range dependencies, such as recognizing multi-step tactical patterns in an opponent’s behavior. We utilize a lightweight design to ensure real-time performance on resource-constrained shipboard hardware. This approach involves limiting the number of transformer layers and hidden dimensions, implementing parameter sharing across actor networks, and exploring sparse attention mechanisms that concentrate computation on high-relevance areas of the state space. This design philosophy aims to balance high performance and computational efficiency.

3.4. Adv-TransAC Algorithm Explained

3.4.1. Network Structure

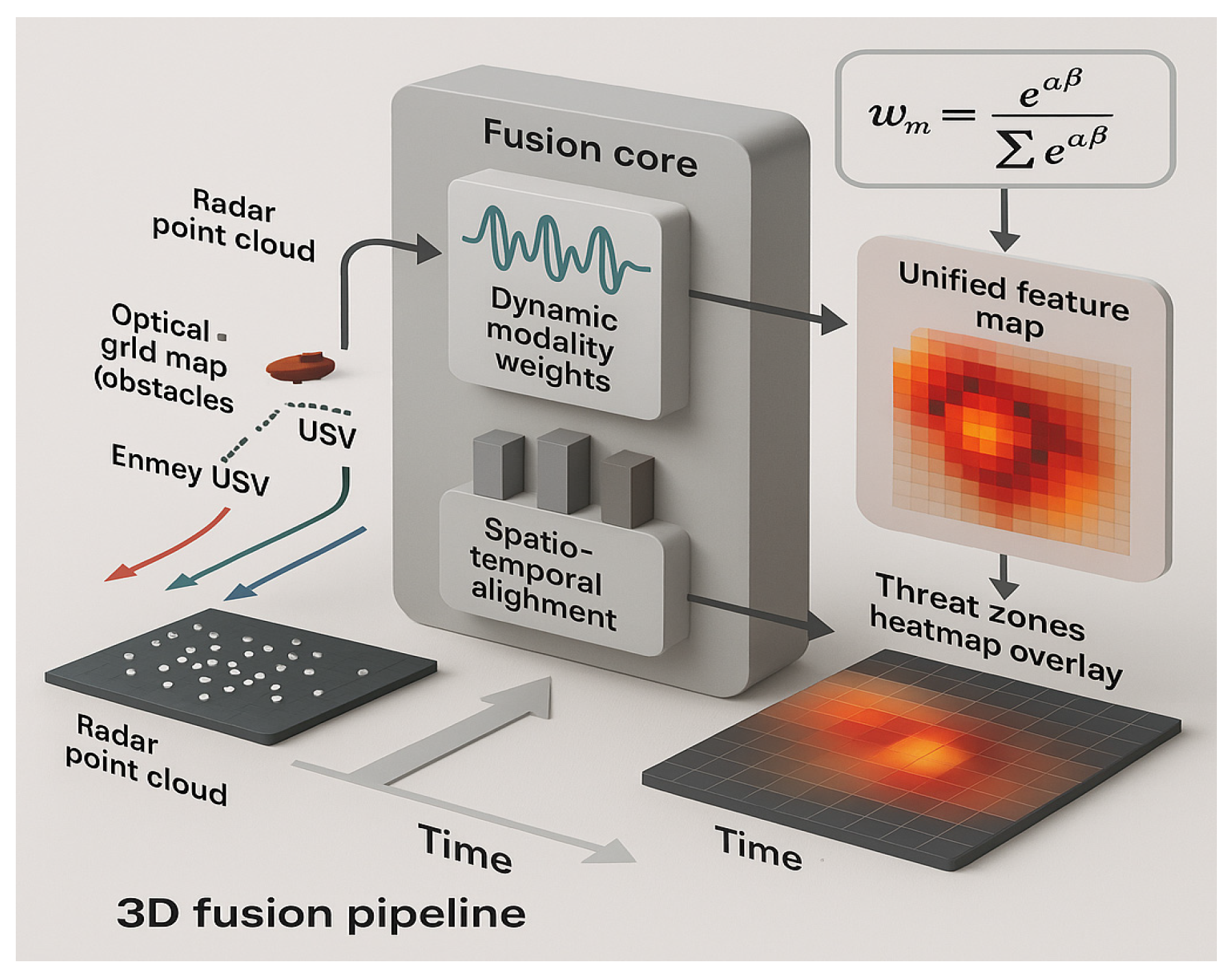
The Adv-TransAC framework is structured around three core components designed to learn and execute advanced control strategies: a multi-modal fusion encoder, decentralized control policy networks (actors) for execution, and a centralized critic for training. This architecture synergistically processes rich sensory information and the complex relational dynamics of the entire multi-agent system to inform the control decisions.

Agents $\mathrm{i}$ must effectively fuse information from a set of $\mathrm{M}$ heterogeneous sensors to achieve robust situational awareness. At each timestep $\mathrm{t}$, the agent receives a multi-modal observation ${\mathrm{o}}_{\mathrm{i}}^{\mathrm{t}}\{{\mathrm{o}}_{\mathrm{i},1}^{\mathrm{t}},\dots ,{\mathrm{o}}_{\mathrm{i},\mathrm{M}}^{\mathrm{t}}\}$. This raw data is processed through the pipeline illustrated in Figure 4.

Raw data from multiple sensors (e.g., radar, optical) is first encoded into feature embeddings. A dynamic attention module then computes modality weights, which produces a unified feature vector as input for the actor network.

The fusion process involves three key steps:

Modality-Specific Encoding: Each raw observation ${\mathrm{o}}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}$ is passed through a dedicated encoder ${\mathrm{E}\mathrm{n}\mathrm{c}}_{\mathrm{m}}(·)$ tailored to its data type (e.g., a CNN for optical images, an MLP for radar tracks) to produce a modality-specific feature embedding ${\mathrm{e}}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}$ of dimension ${\mathrm{d}}_{\mathrm{e}}$.

$${\mathrm{e}}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}={\mathrm{E}\mathrm{n}\mathrm{c}}_{\mathrm{m}}\left({\mathrm{o}}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}\right)$$

(7)

Dynamic Modality Attention: To adaptively focus on the most relevant sensors, an attention mechanism computes modality weights ${\mathsf{\alpha }}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}$. These weights are generated based on the concatenated feature embeddings, allowing the agent to prioritize information dynamically (e.g., trusting radar at long range and optical sensors at close range).

$${\mathsf{\alpha }}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\right({\mathrm{W}}_{\mathsf{\alpha }}[{\mathrm{e}}_{\mathrm{i},1}^{\mathrm{t}},\dots ,{\mathrm{e}}_{\mathrm{i},\mathrm{M}}^{\mathrm{t}}]+{\mathrm{b}}_{\mathsf{\alpha }}{)}_{\mathrm{m}})$$

(8)

Fused Representation: The final fused observation embedding ${\mathrm{z}}_{\mathrm{i}}^{\mathrm{t}}$ is the weighted sum of the modality-specific embeddings, creating a single, information-rich vector for that timestep.

$${\mathrm{z}}_{\mathrm{i}}^{\mathrm{t}}=\sum _{\mathrm{m}=1}^{\mathrm{M}}{\mathsf{\alpha }}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}·{\mathrm{e}}_{\mathrm{i},\mathrm{m}}^{\mathrm{t}}$$

(9)

Decentralized Control Policy (actor): The actor network, ${\mathsf{\pi }}_{\mathrm{i}}({\mathrm{a}}_{\mathrm{i}}|{\mathrm{h}}_{\mathrm{i}})$ represents each agent’s decentralized control policy. It is designed to be lightweight for onboard execution, using a transformer to process the temporal context of local observations and output a specific control action. To improve learning efficiency, the parameters of this control policy network are shared among all friendly agents.

Input Construction: The actor’s input is a sequence of the $\mathrm{k}$ most recent fused observation embeddings ${\mathrm{Z}}_{\mathrm{i}}({\mathrm{z}}_{\mathrm{i}}^{\mathrm{t}-\mathrm{k}+1},\dots ,{\mathrm{z}}_{\mathrm{i}}^{\mathrm{t}})$.

Temporal Feature Extraction: This sequence, augmented with positional encodings (PEs) to preserve order, is processed by a lightweight transformer encoder. The self-attention mechanism allows the actor to capture long-term dependencies in its observation history, producing a context-aware hidden state ${\mathrm{h}}_{\mathrm{i}}$.

$${\mathrm{h}}_{\mathrm{i}}=\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}({\mathrm{Z}}_{\mathrm{i}}+\mathrm{P}\mathrm{E})$$

(10)

Action Output: The hidden state h_i is then passed to a final MLP that parameterizes the control policy, from which an action a_i is sampled. To improve learning efficiency, the parameters of this control policy network are shared among all friendly agents.

Centralized Critic for Strategy Evaluation: The centralized critic, $\mathrm{Q}(\mathrm{s},\mathrm{a})$, estimates the joint action–value function, which serves as a metric for evaluating the long-term performance of a given joint control strategy. It is the cornerstone of our approach to sophisticated credit assignment.

To this end, it employs a novel hybrid architecture that leverages Graph Attention Networks (GATs) and transformers. This hybrid design allows the critic to form a comprehensive understanding of the spatiotemporal dynamics of the multi-agent interaction, enabling it to accurately assess the quality of coordinated actions and guide the policy networks towards optimal cooperative control strategies.

Spatial Interaction Encoding with GAT: At each timestep t, we model the battlefield as a dynamic graph Gt, where agents are nodes. The initial node features are the hidden states h_i produced by the respective actor networks, which encapsulate each agent’s local observation history. To process this graphical structure, we apply a Graph Attention Network (GAT) [18].

The core function of the GAT is to compute updated node embeddings, h′_i, by aggregating information from neighboring nodes j ∈ N(i). This aggregation is not a simple averaging but a weighted sum, where the weights are determined by an attention mechanism. The update rule for each node i is formally defined as

$${{\mathrm{h}}^{\prime }}_1,\dots ,{{\mathrm{h}}^{\prime }}_{\mathrm{N}}=\mathrm{G}\mathrm{A}\mathrm{T}({\mathrm{h}}_1,\dots ,{\mathrm{h}}_{\mathrm{N}})$$

(11)

${{\mathrm{h}}^{\prime }}_{\mathrm{i}}$: This is the feature vector (hidden state from the actor) of a neighboring node j.

W: This is a learnable weight matrix that applies a linear transformation to the feature vectors of all nodes. We use this transformation W h_j to project the features into a higher-level feature space, which increases the model’s expressive power. Without this, the model could only learn linear combinations of the original features.

α_ij: These are the normalized attention coefficients, which represent the importance of node j’s information to node i. They are calculated based on the features of both nodes, ensuring that the aggregation is context-dependent:

$$a_{ij}=50\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}ma{x}_j\left(e_{ij}\right)={\displaystyle \frac{\exp \left(e_{ij}\right)}{{\Sigma }_{k\in \mathbb{N}\left(i\right)}\exp \left(e_{ij}\right)}}$$

where $e_{ij}$ is an attention score computed by a compatibility function (typically a single-layer feed-forward network) on the transformed features W h_i and W h_j.

σ: This is a non-linear activation function (e.g., LeakyReLU), applied after the weighted aggregation.

We chose this functional form because it is the standard and proven mechanism of GATs [18], which offers a crucial advantage over simpler graph convolutions. Instead of using fixed, uniform weights for all neighbors, the attention mechanism (α_ij) allows each agent to dynamically and selectively weigh the importance of its neighbors (both allies and enemies). This is critical for encoding complex, instantaneous tactical relationships, such as identifying a key threat to focus on or recognizing a supportive maneuver from an ally. This process transforms the initial hidden states h_i into contextually aware spatial embeddings h′_i, ready for temporal analysis, see Figure 5.

The battlefield state is modeled as a graph where agents are nodes, and their hidden states (h_i) from the actor networks serve as initial node features. The Graph Attention Network (GAT) updates each node’s representation by aggregating information from its neighbors. The edge thickness visualizes the learned attention weights (α_ij), indicating which neighbors are most influential. The update rule shown, h′_i = Σ α_ij (W h_j), is the core GAT aggregation step, where W is a learnable linear transformation matrix and h′_i is the resulting context-aware node embedding. This process captures the immediate tactical relationships between agents.

Temporal Evolution Modeling with Transformer: The sequence of these GAT-enhanced spatial snapshots over the last $\mathrm{k}$ timesteps, ${\mathrm{H}}^{\prime }=\left(\right[{{\mathrm{h}}^{\prime }}_1,\dots ,{{\mathrm{h}}^{\prime }}_{\mathrm{N}}{]}_{\mathrm{t}-\mathrm{k}+1},\dots ,[{{\mathrm{h}}^{\prime }}_1,\dots ,{{\mathrm{h}}^{\prime }}_{\mathrm{N}}{]}_{\mathrm{t}})$, is then fed into a deep transformer encoder. The role of this transformer is to analyze the evolution of the tactical landscape over time. It can identify complex temporal patterns, such as an opponent’s multi-step feint maneuver or the gradual tightening of a defensive perimeter.

Q-Value Output: The final output from the transformer, which encapsulates both spatial and temporal dependencies, is aggregated and passed through an MLP, along with the joint action $\mathrm{a}$, to produce a single, highly informed Q-value.

$$\mathrm{Q}(\mathrm{s},\mathrm{a})={\mathrm{M}\mathrm{L}\mathrm{P}}_{\mathrm{C}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}\left({\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}}_{\mathrm{C}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}\right({\mathrm{H}}^{\prime }),\mathrm{a})$$

(12)

By explicitly decoupling the modeling of spatial (GAT) and temporal (transformer) dependencies, our critic can form a more comprehensive and accurate assessment of joint actions, leading to superior multi-agent coordination.

3.4.2. Training Process and Optimization

The Adv-TransAC framework is trained using the methods detailed below. The core learning mechanism is based on multi-agent actor–critic, enhanced with specific techniques to handle the adversarial nature of the environment.

During the data collection phase, each agent $\mathrm{i}$ generates an action ${\mathrm{a}}_{\mathrm{i}\mathrm{t}}$ based on its local actor network ${\mathsf{\pi }}_{\mathsf{\theta }}(·|{\mathrm{o}}_{\mathrm{i}\mathrm{t}})$. The environment returns a joint reward ${\mathrm{r}}_{\mathrm{t}}$ and the next joint observation ${{\mathrm{o}}^{\prime }}_{\mathrm{t}}$. The resulting transition tuples $({\mathrm{o}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}}{,\mathrm{r}}_{\mathrm{t}},{{\mathrm{o}}^{\prime }}_{\mathrm{t}})$ are stored in a shared replay buffer $\mathrm{D}$ with a capacity $\mathrm{M}$, which is designed to capture a diverse range of complex adversarial patterns.

Critic Optimization: The critic network is optimized using Double Q-learning [19] to mitigate overestimation bias. Target networks (${{\mathrm{Q}}^{\prime }}_{\mathsf{\varphi }\prime }$ and ${{\mathrm{p}\mathrm{i}}^{\prime }}_{\mathsf{\theta }\prime }$) are used for stability, with their parameters periodically updated from the online networks. The Temporal Difference (TD) target $\mathrm{y}$ is calculated as

$$\mathrm{y}={\mathrm{r}}_{\mathrm{t}}+\mathsf{\gamma }{{\mathrm{Q}}^{\prime }}_{{\mathsf{\varphi }}^{\prime }}({{\mathrm{s}}^{\prime }}_{\mathrm{t}},{{\mathrm{a}}^{\prime }}_{\mathrm{t}})\backslash \mathrm{b}\mathrm{i}\mathrm{g}{|}_{{\mathrm{a}}^{\prime }\sim {{\mathsf{\pi }}^{\prime }}_{{\mathsf{\theta }}^{\prime }}({\mathrm{s}}^{\prime })}$$

(13)

The critic is updated by minimizing the mean squared error loss:

$$\mathrm{L}(\mathsf{\varphi })={\mathbb{E}}_{(\mathrm{s},\mathrm{a},\mathrm{r},{\mathrm{s}}^{\prime })\sim \mathrm{D}}\left[({\mathrm{Q}}_{\mathsf{\varphi }}(\mathrm{s},\mathrm{a})-\mathrm{y}{)}^2\right]$$

(14)

Control Policy Optimization (Actor): The actor network (policy network) is updated using the policy gradient theorem. To reduce variance, the advantage function $\mathrm{A}(\mathrm{s},\mathrm{a})$ is calculated by the critic, where $\mathrm{A}(\mathrm{s},\mathrm{a})={\mathrm{Q}}_{\mathsf{\varphi }}(\mathrm{s},\mathrm{a})-\mathrm{V}(\mathrm{s})$ and $\mathrm{V}\left(\mathrm{s}\right)$ is the state-value baseline. To encourage exploration and prevent premature policy convergence, an entropy regularization [22] term $\mathcal{H}$ is added to the objective function:

$${\mathsf{\nabla }}_{\theta }J(\theta )\approx \mathbb{E}\left[{\mathsf{\nabla }}_{\theta }\log {\pi }_{\theta }(\mathbf{a}|\mathbf{s}\left)A\right(\mathbf{s},\mathbf{a})+\alpha {\mathsf{\nabla }}_{\theta }\mathcal{H}({\pi }_{\theta }(·|\mathbf{s}\left)\right)\right]$$

(15)

Adversarial Meta-Learning is the Core Innovation: This mechanism enables agents to adapt to unseen opponent strategies rapidly and consists of two key components:

• Opponent Strategy Encoder: An 8-head transformer processes the enemy’s historical action sequences to generate a latent strategy embedding ${\mathrm{z}}_{\mathrm{a}\mathrm{d}\mathrm{v}}$. This embedding serves as a condensed representation of the adversary’s current tactics.

$${\mathrm{z}}_{\mathrm{a}\mathrm{d}\mathrm{v}}={\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}}_{\mathrm{e}\mathrm{n}\mathrm{c}}\left({\mathrm{h}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{y}}_{\mathrm{a}\mathrm{d}\mathrm{v}}\right)$$

(16)

2.

Meta-Policy Regulator: The agent’s control policy is then conditioned on this embedding. Passing Zadv through a hypernetwork generates adaptive modifications for the policy network’s (actor’s) parameters, allowing for real-time adaptation.

$$\mathsf{\Delta }\mathsf{\theta }=\mathrm{H}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{e}\mathrm{t}\left({\mathrm{z}}_{\mathrm{a}\mathrm{d}\mathrm{v}}\right)$$

(17)

This meta-signal Δθ is applied to the actor’s parameters θ to produce the adapted policy θ_new. Specifically, the hypernetwork-generated parameters Δθ directly modify a subset of the actor’s weights, for instance, the final two layers, using an additive update mechanism. A common implementation is an additive modification: θ_new = θ + α * Δθ, where α is a small, fixed scaling factor (e.g., 0.1) that controls the magnitude of the adaptation. This allows the agent to make subtle but effective adjustments to its base policy in response to the opponent’s behavior, rather than completely overwriting its learned knowledge.

Adversarial Curriculum Learning: To ensure stable training, we employ an adversarial curriculum with stages of increasing difficulty:

• Initial Phase: Agents train against simple, rule-based opponents (e.g., “Straight Charge,” “Circle Patrol”).
• Intermediate Phase: Agents face more competent opponents pre-trained with standard RL algorithms like DQN.
• Advanced Phase: Agents train against our meta-adaptive opponent, which dynamically alters its strategy.

Progression through the curriculum is automated: agents advance to the next stage once their win rate (P_win) against the current opponent type exceeds a predefined threshold. Based on preliminary experiments, this threshold was set to 75% to ensure mastery at each level before facing a more complex adversary.

3.4.3. Algorithmic Pseudocode

The overall algorithm flow of Adv-TransAC can be summarized as follows (Algorithm 1):

Algorithm 1: Adv-TransAC Training Procedure

1: Initialize policy network (actor) ${\pi }_i({\theta }_i^A)⁠$ and critic network $Q_i({\theta }_i^C)$ for each agent $i$ 2: Initialize the target network ${\pi }_i^{\prime }({\theta }_i^{A^{\prime }})$ and $Q_i^{\prime }({\theta }_i^{C^{\prime }})$, let ${\theta }^{\prime }\leftarrow ⁠\theta$ 3: Initialize the experience replay pool D and adversarial course learning scheduler C 4: for episode = 1 to M do 5:   Reset the environment to get the initial joint observation $o⁠=⁠\left\{o_1,⁠\dots ,⁠o_N\right\}$ 6:   Choose your opponent’s strategy based on Course Scheduler C ${\pi }_{adv}$ 7:   for t = 1 to T do 8:     // 1. Distributed execution 9:     for each agent i = 1 to N do 10:       from ${\pi }_i\left(a_i\right|o_i;⁠{\theta }_i^A)$ Medium-sampled actions, $a_i$ 11:     end for 12:     Perform joint actions $a⁠=⁠\left\{a_1,⁠\dots ,⁠a_N\right\}$, get a joint reward $r$, and the next joint observation $o^{\prime }$ 13:     Deposit the experience tuple D$(\left\{o_i\right\},⁠\left\{a_i\right\},⁠r,⁠\{o_i^{\prime }\})$ into replay pool, $o⁠\leftarrow ⁠⁠o^{\prime }$ 14:     // 2. Intensive training 15:     Experience B is randomly sampled from a batch of D 16:     for each agent i = 1 to N do 17:       // Update the Critic network 18:       Use the target actor network to calculate the action for the next state: $a_i^{\prime }⁠=⁠{\pi }_i^{\prime }(o_i^{\prime })$ 19:       Calculate the target Q value:$⁠y_i⁠=⁠r⁠+⁠\gamma Q_i^{\prime }(o^{\prime },⁠a^{\prime };⁠{\theta }_i^{C^{\prime }})⁠$ 20:       By minimizing the loss function $L({\theta }_i^C)=⁠E\left[{\left(y_i-⁠Q_i(o,⁠a;⁠{\theta }_i^C)\right)}^2\right]$ update Critic 21:       // Update the Control Policy Network (Actor) 22:       Calculate the strategy gradient: ${\mathsf{\nabla }}_{{\theta }_i^{A}J}\approx ⁠E\left[{\mathsf{\nabla }}_{{\theta }_i^{A}log}{\pi }_{i\left(a_i|o_i\right)}*⁠Q_{i\left(o,⁠a;⁠{\theta }_i^C\right)}\right]$ 23:       Update via policy gradient Actor 24:     end for 25:     // Soft update the target network 26:     ${\theta }^{\prime }\leftarrow ⁠\tau \theta ⁠+⁠\left(1-\tau \right){\theta }^{\prime }$ 27:   end for 28:  According to the win rate of this round,${⁠P}_{win}.$ 29:  Update the difficulty of Course Scheduler C according to the win rate of this round 30: end for

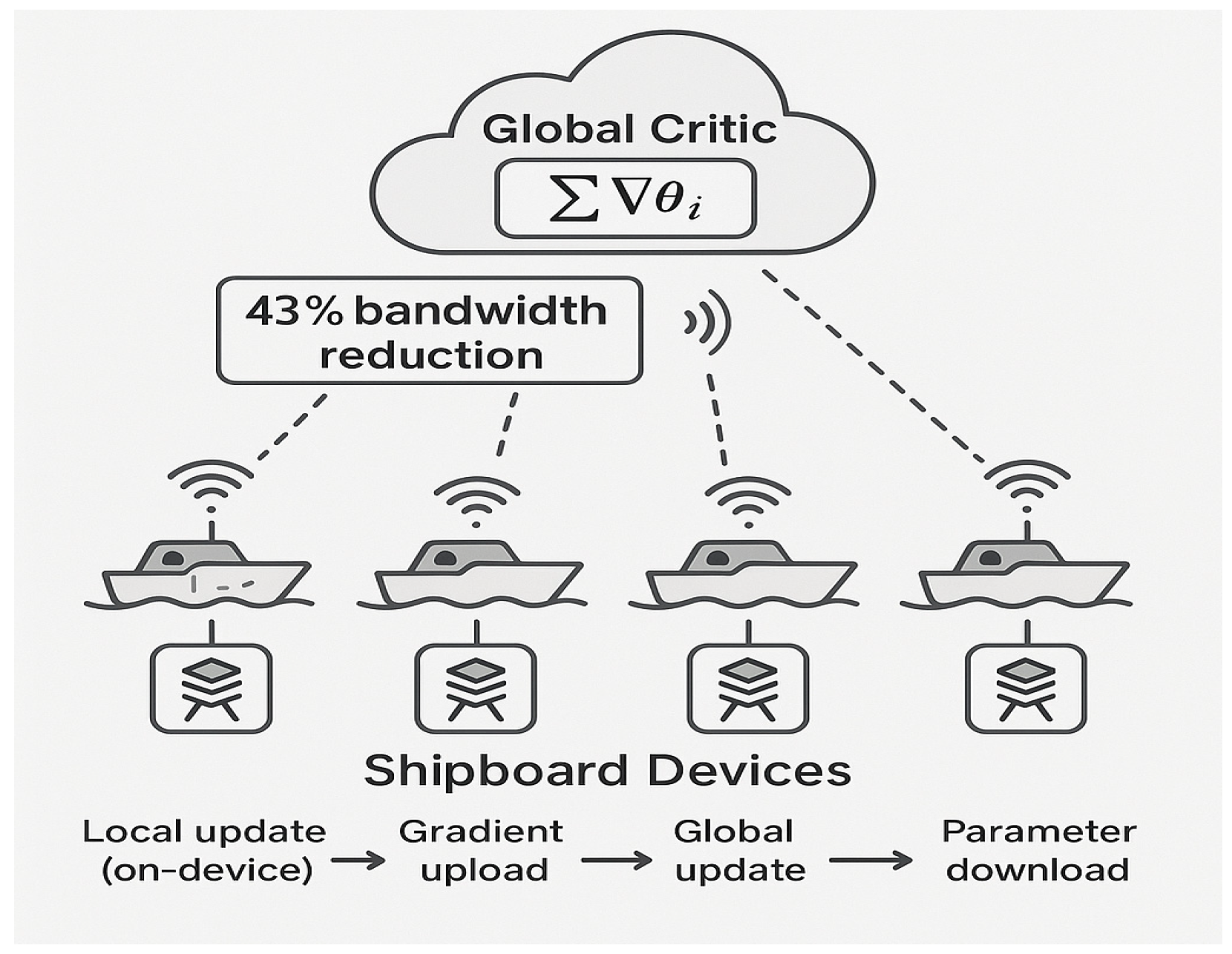
For our framework to be efficiently deployed in a real marine environment with limited communication, we adopted a distributed optimization architecture based on federated learning, as shown in Figure 6.

In this architecture, the shipboard devices on each USV are responsible for calculating the local update of its actor network based on local observations. Subsequently, only the low-dimensional gradient information is uploaded to a central server (or a designated leader USV), rather than the high-dimensional raw sensor data. The central server aggregates all gradients (global update) and updates global critic and actor parameters. Finally, the updated model parameters are distributed back to the individual USVs (parameter download).

Furthermore, this federated communication protocol can be extended to incorporate a decentralized safety mechanism. Beyond transmitting gradients for learning, the protocol can be designed to handle emergency broadcasts. For instance, any USV can monitor the high-value unit’s (HVU) integrity. With federated updates, USVs could transmit a high-priority collision avoidance or defensive alert if the rate of change in HVU damage (∂HVU_Damage/∂t) exceeds a critical safety threshold. This would facilitate a swarm-wide emergency override, forcing all agents into a defensive posture, thus integrating a measurable, ethics-driven fail-safe directly into the operational practice of the swarm.

This paradigm dramatically reduces the need for network bandwidth. As our experiments show, this method can achieve bandwidth savings of up to 43% compared to methods that pass raw empirical data. This solves the core pain point of unstable communication between multi-USV clusters in real sea conditions, ensures the training efficiency and scalability of the entire system, and meets the practical needs of efficient collaborative learning on edge devices.

4. Experiments

To rigorously evaluate the performance of our proposed Adv-TransAC framework, we designed a comprehensive suite of simulation experiments. This section details the experimental environment, the tasks, the algorithms compared, the evaluation metrics, and the specific implementation details, providing a complete blueprint for reproducibility.

4.1. Experimental Setup

In a 10 km × 10 km area with multiple obstacles, our USVs (blue) formation must protect a high-value unit (HVU, green) from navigating safely along a predetermined dashed path. They need to fight against the interception of the enemy USV (red) controlled by a learning strategy. Our USVs are equipped with different types of sensors (e.g., optical sensors with a limited range), and the entire system needs to meet the 200 ms real-time requirements of the ISO 23860 [32] standard.

Environment and Tasks: We conducted experiments in a custom 2D mesh marine environment based on the open-source MARL environment library PettingZoo [22]. The environment simulates basic USV kinematics.

Mission Scenario: We designed an offensive and defensive game mission called “Cooperative Escort and Defense”.

Objective: N of our escort USVs (controlled by the measured method) must protect a high-value unit (HVU) through a designated area filled with obstacles.

Opponent: An enemy attacking USV will attempt to break through the escort formation, damaging the HVU.

Multi-Modal Observation: Our USV is equipped with two types of analog sensors:

Radar: It has a wide coverage area but can only provide the approximate position and velocity of enemy targets and has low resolution.

Optical Sensors: Limited coverage, but capable of providing high-resolution, accurate information such as target type and heading within line-of-sight.

Success/Failure Condition: The task succeeds if the HVU reaches the endpoint within the specified time and its damage is lower than the threshold. Otherwise, the task fails.

Adversary Control Strategy: To fully evaluate the robustness of our algorithm, we designed adversaries employing two distinct types of control strategies.

Rule-Based: Attacking USV follows a preset, simple attack logic (e.g., Straight Charge or Pack).

Learning-Based: Attacking USVs is controlled by a pre-trained MADDPG strategy that adapts its attack patterns to the behavior of our USVs for greater adversariality, see Figure 7.

4.1.1. Implementation Details

All experiments were performed using Python 3.8 and PyTorch 1.10. We customized the “waterworld” environment from the PettingZoo 1.15.0 MARL library to simulate our multi-USV attack–defense scenarios. All models were trained on a single NVIDIA GeForce RTX 3090 GPU (NVIDIA, Taipei City, Taiwan) for two million time steps. Performance was evaluated every 10,000 steps, with results averaged over 100 evaluation episodes.

The key hyperparameters for the Adv-TransAC framework are detailed in

Table 1. Adv-TransAC frame hyperparameter configuration.

Category	Parameter	Value	Description
General Network	Policy/Actor Learning Rate	1 × 10−4	The learning rate for the Adam optimizer used to update the actor networks.
Parameters	Critic Learning Rate	1 × 10−4	The learning rate for the Adam optimizer used to update the critic network.
	Target Network Update Rate (τ)	0.005	The coefficient for the soft update (Polyak averaging) of the target networks, ensuring stable learning targets.
	Discount Factor (γ)	0.99	The discount factor for future rewards, balancing immediate vs. long-term gains.
	Replay Buffer Size	10^6	The maximum number of experience tuples (s, a, r, s’) stored in the replay buffer.
	Batch Size	256	The number of experience samples used in each training update step.
	Entropy Regularization (λ)	0.01	The weight of the entropy bonus term in the actor’s loss function, encouraging exploration and preventing premature policy convergence.
Transformer	Actor Transformer Layers	3	The number of encoder layers in the decentralized actor network. A smaller number is used to ensure low latency for real-time execution.
Architecture	Actor d_model	256	The embedding dimension within the actor’s transformer. Kept moderate for computational efficiency on edge devices.
	Actor Num. Heads	4	The number of attention heads in the actor’s multi-head attention module.
	Critic Transformer Layers	6	The number of encoder layers in the centralized critic. A deeper model is used for a more powerful and accurate state–action evaluation.
	Critic d_model	512	The embedding dimension within the critic’s transformer, allowing it to process more complex joint state information.
	Critic Num. Heads	8	The number of attention heads in the critic’s multi-head attention module.
	Dropout Rate	0.1	The dropout probability used within the transformer layers to prevent overfitting.
Adversarial	Opponent Encoder Layers	2	The number of transformer layers used to encode the opponent’s historical behavior into a latent strategy vector.
Learning	Opponent Encoder Heads	4	The number of attention heads in the opponent encoder.
	Meta-learning Update Rate (β)	1 × 10−3	The learning rate for updating the meta-policy regulator, controlling the adaptation speed to the opponent’s strategy.
	Curriculum Win Rate Threshold	0.25	The win rate threshold required to advance to a more difficult opponent in the curriculum learning schedule.

. These values were selected based on a combination of common practices in deep reinforcement learning and preliminary experiments aimed at ensuring stable convergence and effective performance.

The number of transformer layers used to encode an opponent’s historical behavior into a latent strategy vector is two. This module is specifically active when facing learning-based opponents to enable adaptive responses.

4.1.2. Justification of Hyperparameter Choices

The selection of these hyperparameters was guided by a core design philosophy: balancing the expressive power of the model with the computational constraints of real-world deployment.

Actor–Critic Asymmetry: A key design choice is the asymmetry between the actor and critic transformer architectures. The actor network, intended for decentralized execution on resource-constrained USV hardware, is deliberately made lighter (3 layers, 256 d_model). This ensures low-latency decision-making. In contrast, the centralized critic, which runs only during offline training, is made significantly deeper and wider (6 layers, 512 d_model). This gives it the representational capacity to accurately model the complex joint state–action space and provide a high-quality credit assignment signal to the actors.

Learning Stability: The learning rate of 1 × 10⁻⁴ is a standard, robust choice for Adam optimizers in similar deep RL tasks, preventing overly aggressive updates that could destabilize training. The soft update rate τ = 0.005 and a large replay buffer (10⁶) are crucial for stabilizing the learning process by decorrelating experiences and providing stable target values, which is especially important in non-stationary multi-agent settings.

Exploration and Adaptation: The entropy regularization coefficient λ = 0.01 provides a small but consistent incentive for the policy to explore, preventing it from collapsing into a deterministic and potentially suboptimal strategy too early. In the adversarial learning module, the meta-learning update rate β = 1 × 10⁻³ is set to be relatively low to ensure that the adaptation to the opponent’s perceived strategy is smooth and gradual, avoiding drastic policy shifts that could be exploited.

4.2. Baselines

We compare Adv-TransAC with the following mainstream and related MARL algorithms:

QMIX [7]: A classical MARL algorithm based on value function decomposition, representing the value function method.

MADDPG [8]: A widely used multi-agent actor-critic algorithm representing the CTDE paradigm.

GNN-AC (Ablation): This variant of Adv-TransAC removes the transformer module and only uses the graph features extracted by the GNN to be fed directly into the MLP layer of actor and critic. This baseline is used to validate the role of the transformer in processing time series and multi-modal information.

4.3. Evaluation Metrics

We use the following metrics to quantitatively evaluate the performance of each algorithm over 1000 independent test episodes:

Win Rate (%): The primary indicator of overall performance. It measures the percentage of episodes where the HVU successfully reaches its destination without exceeding the damage threshold.

Average HVU Damage: The cumulative damage taken by the HVU, averaged across all test episodes. A lower value indicates a more effective escort strategy.

Synergistic Collision Rate (%): Measures the frequency of collisions between friendly USVs. It is calculated as the number of friendly-on-friendly collision events per 100 timesteps, averaged over the escort phases of all episodes. This metric gauges the internal coordination safety of the learned policy.

Opponent Destruction Rate (%): The percentage of enemy USVs successfully intercepted and neutralized (“destroyed”) by the escorting swarm. This reflects the aggressiveness and tactical efficiency of the strategy.

4.4. Experimental Results and Analysis

Overall performance comparison:

We played against two types of opponents at N = 4 and M = 3; the experimental results are shown in

Table 2. Comparison of the performance of different algorithms in the “cooperative escort and defense” task.

Algorithm	Opponent Type	Task Success Rate (%)	The HVU Is Damaged on Average	Synergistic Collision Rate a (%)	Opponent Destruction Rate (%)
QMIX	Rule-based	65.4	125.8	6.8	45.1
	Learning	38.2	210.5	8.2	22.7
MADDPG	Rule-based	81.0	90.1	5.3	68.5
	Learning	59.5	148.3	6.9	51.3
GNN-AC (Ablation)	Rule-based	85.5	68.2	2.5	82.1
	Learning	67.5	110.6	2.9	65.7
Adv-TransAC (Ours)	Rule-based	92.5	48.5	2.1	88.3
	Learning	78.5	75.4	3.3	79.2

All metrics are averaged over 1000 independent test episodes. Higher values are better for task success rate and opponent destruction rate, while lower values are better for HVU damage and synergistic collision rate. ^a Synergistic collision rate is calculated as the number of friendly-on-friendly collision events per 100 timesteps, averaged over the escort phases. Note that the slightly higher collision rate of Adv-TransAC compared to the GNN-AC ablation is not a defect, but a feature of its more advanced, aggressive strategy. It reflects a learned trade-off where a marginal increase in controlled risk is accepted to execute tighter, more effective cooperative maneuvers (e.g., pincer movements), leading to significantly higher mission success.

.

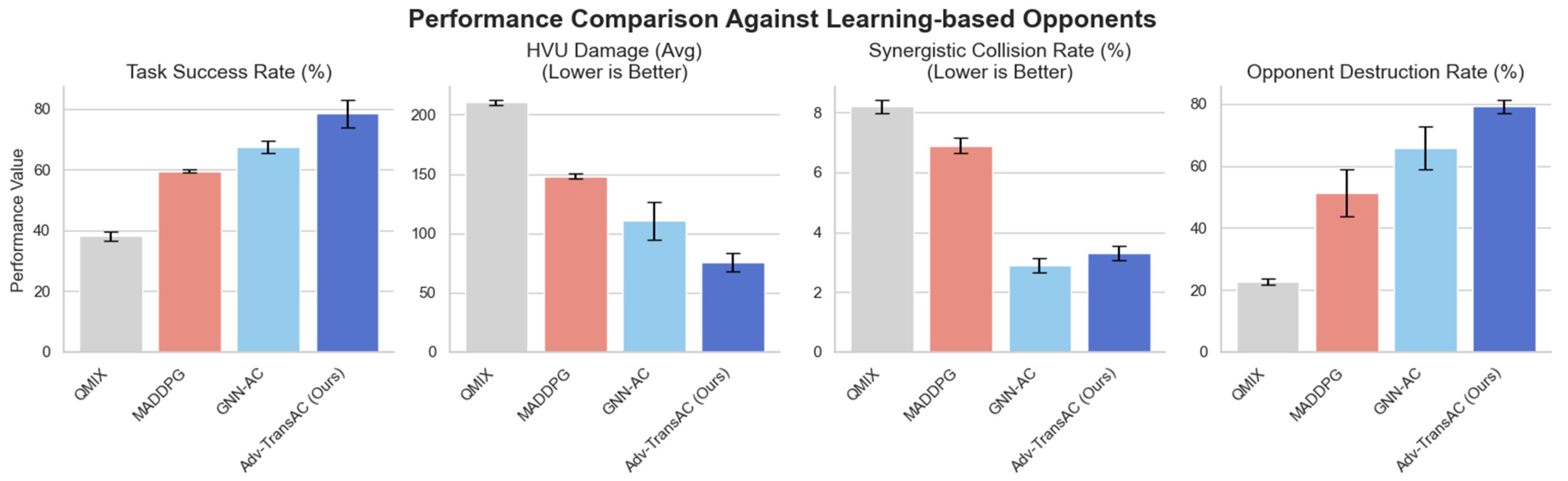
The results presented in Table 2 demonstrate the superior performance of the control strategies learned by our proposed Adv-TransAC framework. In the more challenging scenario against learning-based opponents, the policy learned by Adv-TransAC achieves a task success rate of 78.5%, significantly outperforming all baselines and establishing the effectiveness of our learning approach in complex, dynamic environments.

An interesting insight from the results is the strategic trade-off learned by Adv-TransAC. While it excels in primary mission objectives like success rate and enemy neutralization, its synergistic collision rate (3.3%) is slightly higher than that of the GNN-AC baseline (2.9%). This is not a deficiency but a feature of a more advanced, aggressive strategy. This indicates that Adv-TransAC learns a more advanced cooperative control strategy, performing tighter and more coordinated maneuvers to ensure mission success, which inherently involves a calculated risk of minor collisions.

From these results, we can draw the following key conclusions:

Superior Performance in Core Metrics: Adv-TransAC achieves state-of-the-art performance in the most critical metrics, including task success and enemy neutralized rates, proving its tactical superiority.

Intelligent Risk-Reward Balancing: The framework demonstrates an advanced ability to balance mission success with operational risk. It opts for more aggressive, high-reward strategies, accepting a marginal increase in collision risk to secure a significant gain in overall mission effectiveness.

Robustness Against Advanced Opponents: While all algorithms’ performance degrades against learning-based opponents, Adv-TransAC shows the most graceful degradation, highlighting its robustness.

Effectiveness of Transformer Architecture: The performance gap between Adv-TransAC and the GNN-AC ablation baseline confirms the critical role of the transformer architecture in capturing complex temporal and inter-agent dependencies.

QMIX, a value-decomposition method, struggles significantly in this complex adversarial task, confirming the need for more expressive actor–critic architectures.

To more fully assess the usefulness of Adv-TransAC, we focused not only on its policy performance but also on its computational efficiency, which is critical for deployment on resource-constrained USV edge devices. We compared the number of model parameters and their average single-step inference time. To simulate real-world decision latency, inference time was measured on an NVIDIA RTX 3090 GPU with a batch size of one. The results are presented in

Table 3. Comparison of model complexity and computational efficiency of different algorithms.

Algorithm	The Total Number of Parameters (M)	Average Inference Time per Step (ms)
QMIX	1.2	3.5
MADDPG	2.5	6.8
GNN-AC (Ablation)	4.1	11.2
Adv-TransAC (Ours)	5.7	18.6

.

Figure 8 visually summarizes the performance of the final learned strategies against the most challenging, learning-based adversaries. The results confirm that the strategy developed by Adv-TransAC (dark blue) is significantly more robust and effective, establishing a commanding lead across all mission-critical metrics. This highlights the substantial performance gap between our advanced control strategy and conventional MARL baselines like MADDPG and QMIX.

An interesting and critical insight emerges from comparing the synergistic collision rate (Figure 8) between Adv-TransAC and its GNN-AC ablation. While GNN-AC shows a lower collision rate, this is not a sign of superiority but rather a symptom of a more conservative and less effective strategy. Lacking the ability to model long-term temporal dependencies, GNN-AC adopts a simpler policy focused on safe navigation, which compromises its ability to effectively intercept adversaries, as reflected in its lower win rate.

In contrast, Adv-TransAC learns to execute more complex and aggressive cooperative maneuvers, such as tight blocking formations, to ensure mission success. These advanced tactics require closer coordination and inherently carry a slightly higher risk of collision between friendly agents. Therefore, the slightly higher collision rate of Adv-TransAC is a direct consequence of a learned, intelligent risk–reward trade-off: the model accepts a marginal increase in a secondary risk metric to achieve a significant gain in the primary mission objectives of task success and opponent neutralization. This demonstrates a more sophisticated level of tactical reasoning.

Training Stability and Convergence Analysis:

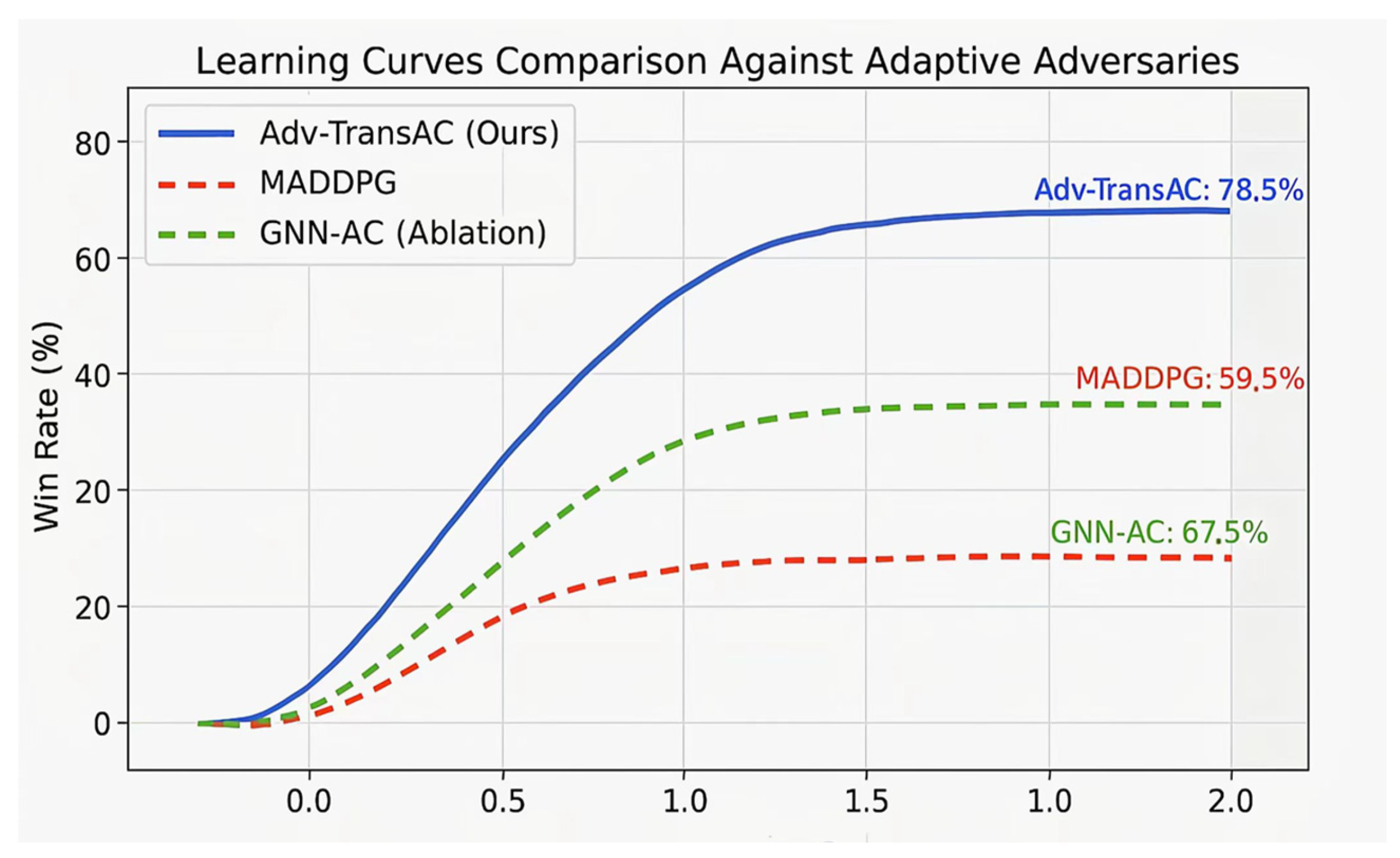
To further investigate the learning dynamics of our proposed framework, we analyzed the training process itself. Figure 9 plots the win rate over time for our method and key baselines when training against the challenging learning-based opponent. The results reveal several advantages of Adv-TransAC:

Faster Convergence: The learning curve for Adv-TransAC exhibits a significantly steeper initial slope, indicating that it learns an effective control strategy much faster than MADDPG and our GNN-AC ablation. This rapid learning can be attributed to the superior credit assignment enabled by the hybrid GAT-transformer critic.

Superior Stability: The Adv-TransAC curve is notably smoother with less variance compared to the baselines, which show more erratic oscillations. This enhanced stability highlights the effectiveness of our adversarial curriculum learning paradigm, which provides a structured learning path and mitigates the non-stationarity inherent in multi-agent adversarial training.

Higher Asymptotic Performance: Consistent with the results in Table 2, the curve for Adv-TransAC converges to a substantially higher final win rate. This underscores the expressive power of our spatiotemporal architecture in representing and learning more sophisticated and successful cooperative control policies.

In summary, this analysis of the learning process provides strong evidence that Adv-TransAC is not only more effective in its final performance but also more efficient and stable during training.

As can be seen from Table 3, Adv-TransAC, as a transformer-based model, has the highest number of parameters among all comparison algorithms. However, this increase in complexity comes with the significant performance payoffs documented in Table 2. What is more, thanks to our lightweight design choices (e.g., parameter sharing and constrained layer depth), the single-step inference time is only 18.6 milliseconds. To put this figure into a practical engineering context, this latency is over 10 times faster than the 200 ms real-time decision-making deadline stipulated by the ISO 23860 [32] maritime standard, which we identified as a key system requirement in Section 4.1. This result strongly demonstrates the real-world feasibility of our framework. It confirms that we have achieved a successful trade-off between expressive power and computational efficiency, where an acceptable increase in computational overhead yields a huge leap in the quality and robustness of decision-making.

In contrast, the performance of baseline methods degrades significantly against learning-based opponents. For instance, MADDPG’s opponent destruction rate plummets to 22.7% (Table 2), a failure that can be attributed to its inability to discern complex tactical situations. As illustrated by the agent trajectories in Figure 10 (left panel), MADDPG-controlled agents are susceptible to decoy tactics, where a single opponent can lure the entire escort group away from the HVU, leaving it vulnerable. This is because MADDPG’s simple concatenation of observations fails to capture the higher-order spatiotemporal relationships needed to understand such strategies. Similarly, the restrictive nature of QMIX’s value decomposition struggles in this complex adversarial task, confirming the need for more expressive actor–critic architectures.

Furthermore, the learning curve for Adv-TransAC not only demonstrates faster convergence but also stabilizes at a high-performance plateau towards the end of the training. This stabilization is a critical indicator of robust learning and is attributed to two factors. First, it signifies policy convergence; the agent, having been trained through a rigorous adversarial curriculum, has learned a near-optimal policy for the given task distribution, leading to diminishing marginal returns. Second, this plateau represents a practical performance ceiling imposed by the inherent stochasticity and complexity of the adversarial task. Even a perfect strategy cannot guarantee success in every single episode. Therefore, the stabilization of the win rate indicates that our framework has successfully converged and explored the full potential of the learned policy within the constraints of the environment, rather than being an artifact of premature termination of training.

4.5. Ablation Study

We designed a series of detailed ablation experiments to verify further the effectiveness of each core component of the Adv-TransAC framework. We use the full Adv-TransAC model as a benchmark to assess performance changes by individually removing or replacing its key modules. All ablation experiments were conducted in the most challenging learning adversary (N = 4, M = 3) scenarios to investigate the role of each component in complex dynamic confrontations. The experimental results are shown in

Table 4. Ablation studies of key components of Adv-TransAC (opponent: learning).

Model Variants	Task Success Rate (%)	The HVU Is Damaged on Average	Synergistic Collision Rate (%)	Opponent Destruction Rate (%)
Adv-TransAC (Full model)	78.5	74.4	3.3	79.2
w/o Transformer	67.0	112.4	4.5	65.0
w/o GAT	71.3	98.6	3.8	70.5
w/o Multi-modal Attention	74.8	88.9	3.6	75.1
w/o Adversarial Curriculum	70.2	105.7	4.0	69.4
w/o Opponent Encoder	72.5	95.2	3.5	71.8
w/o Parameter Sharing	63.1	130.5	5.2	60.3

.

We tested the following model variants:

Adv-TransAC (Full Model): The complete framework we propose.

w/o Transformer: Remove the transformer module from actor and critic and use GNNs to extract spatial features and input them directly into the Multilayer Perceptron (MLP). This is equivalent to a GNN-AC baseline in our original and is used to evaluate the transformer’s central role in timing modeling.

w/o GAT (transformer-only critic): In this variant, we remove the GAT module from the centralized critic. Instead, we concatenate the hidden states $h_i$ of all agents with their positional encodings and feed this sequence directly into a transformer encoder. This baseline is designed to test whether our proposed “GAT-then-transformer” hybrid architecture is superior to a single, larger spatiotemporal transformer.

w/o Multi-Modal Attention: Remove the multi-modal attention fusion module and concatenate the feature vectors of different sensors (radar, optics) before entering the actor network. This item evaluates the need for a dynamic weighted fusion mechanism.

w/o Adversarial Curriculum: Removes adversarial learning mechanics and always trains with the final, strongest learning opponent throughout the training process. This item is used to evaluate the impact of progressive training strategies on convergence and eventual performance.

w/o Opponent Encoder: Removes the transformer encoder to encode the opponent’s historical behavior from the actor network. Our agent cannot explicitly model the opponent’s tactical intent and can only respond passively. This item is used to assess adversarial adaptability.

From the ablation results in Table 4, we can draw the following conclusions:

Critical Synergy of the Hybrid GAT-Transformer Architecture: The ablation study results systematically validate the crucial role of each component, with the hybrid GAT-transformer architecture standing out as the cornerstone of our framework’s success. The Importance of Parameter Sharing: Finally, we conducted an ablation to evaluate the impact of sharing parameters among the actor networks. The ‘w/o Parameter Sharing’ variant, where each agent learns an independent policy network, showed a noticeable degradation in performance across all key metrics (task success rate: 63.1%, HVU damage: 130.5). This result may seem counter-intuitive, as independent parameters could theoretically allow for more specialized agent behaviors. However, in our cooperative task, parameter sharing acts as a powerful inductive bias. It encourages the agents to learn a consistent and coordinated team strategy by allowing them to efficiently share knowledge and learning experiences. Without it, the learning signal becomes more sparse for each individual agent, making it more difficult to converge to a globally effective cooperative policy. Thus, parameter sharing proves to be a critical component not only for efficiency but also for effective team-wide learning.

First, removing the transformer module entirely (w/o transformer) caused the most significant performance degradation across all metrics, with the task success rate plummeting by 11.5 percentage points. This result confirms the transformer’s indispensable role in capturing long-term temporal dependencies and forming sophisticated, forward-looking strategies from observation histories.

More importantly, the comparison between the full model and the w/o GAT variant reveals the superiority of our specific hybrid design. While the w/o GAT model (which uses only a transformer on flattened states) still outperforms the non-transformer baseline, its performance is substantially lower than our full Adv-TransAC model. This demonstrates that simply applying a powerful transformer is insufficient. Our decoupled approach—first using GAT to explicitly model the instantaneous spatial graph of tactical relationships and then using a transformer to analyze the temporal evolution of these structured “battlefield snapshots”—is far more effective. This finding proves that a principled, hybrid modeling of space and time is crucial for deeply understanding complex multi-agent adversarial dynamics. Simply applying a powerful architecture like the transformer is not a panacea; it is the synergistic combination of GAT’s instantaneous spatial graph representation and the transformer’s long-term temporal sequence analysis that unlocks superior strategic reasoning.

Effectiveness of Multi-modal Fusion: Compared with simple feature stitching, dynamic weighted fusion using attention mechanism (w/o multi-modal attention comparison) significantly improves performance, especially in reducing HVU damage. This suggests that our model can intelligently determine which sensor information to trust more at different moments (e.g., radar at long range, optics at close range) to react more promptly.

The Necessity of Course Learning: The w/o adversarial curriculum makes the model training more unstable, and the final strategy is less robust, resulting in an overall deterioration of the success rate and damage control. This shows that adversarial course learning from easy to difficult is essential to guide agents to explore and converge to a better strategy space.

The Value of Opponent Modeling: After removing the w/o opponent encoder, although the model still performs well, there is a significant gap in success rate and destruction rate compared to the full model. This proves that explicitly modeling and predicting adversary strategies is the key to achieving forward-looking, adaptive confrontation.

The results of the ablation study systematically validate that each design component in the Adv-TransAC contributes positively and significantly to its superior overall performance, collectively constituting the strengths of the framework.

4.6. Qualitative Analysis

We visualize a typical adversarial process in Figure 8 to illustrate strategy behavior.

We visualize typical agent trajectories in Figure 10 to better understand the strategic differences. The MADDPG-controlled agents (left panel) exhibit a simplistic and disjointed defense, where USVs often act independently and are easily lured away or defeated one by one by the enemy.

In stark contrast, the agents controlled by Adv-TransAC (right panel) demonstrate clear, emergent cooperative behaviors. They spontaneously form a protective formation around the HVU and execute a “double-team” maneuver to intercept the approaching enemy. This visualization qualitatively confirms that Adv-TransAC enhances individual decision-making and, more importantly, fosters effective, high-level tactical coordination among agents, which is the key to its superior performance.

Figure 10 particularly highlights the sophistication of the learned control strategy. The Adv-TransAC agents initially adopt a stable, formation-keeping control mode to protect the HVU. Upon detecting an imminent threat that crosses a certain threshold, the system dynamically reassigns agents’ roles and transitions into an aggressive, intercept-and-neutralize control mode. This ability to switch between distinct, complex control modes based on high-level situational awareness is a key feature of the advanced strategies that our framework produces and is extremely difficult to pre-program with rule-based systems or conventional controllers.

4.7. Robustness and Generalization to Unseen Conditions

A critical quality of any practical control strategy is its robustness to environmental variations and its ability to generalize to situations not encountered during training. To evaluate this, we conducted a series of zero-shot generalization tests where the models, trained exclusively in the standard 4v3 scenario, were deployed directly into two new, unseen test environments: (1) a scenario with significantly increased sensor noise, and (2) a scenario with an increased number of adversaries (4v4).

The results, presented in

Table 5. Robustness and zero-shot generalization analysis.

Algorithm	Baseline (4v3 Win Rate, %)	Increased Sensor Noise (Win Rate, %)	Unseen Scale (4v4 Win Rate, %)
MADDPG	59.5	35.2	28.1
GNN-AC (Ablation)	67.5	48.9	41.5
Adv-TransAC (Ours)	78.5	65.3	59.8

, clearly demonstrate the superior robustness of the control policy learned by Adv-TransAC. While all algorithms experienced a performance drop under these challenging, out-of-distribution conditions, Adv-TransAC exhibited a much more graceful degradation.

Robustness to Sensor Noise: Under increased sensor noise, the performance of baseline methods plummeted, indicating their reliance on precise state information. In contrast, Adv-TransAC maintained a high win rate, suggesting its transformer-based architecture is more effective at extracting a stable, underlying signal from noisy, high-dimensional observation histories.

Generalization to a New Scale: When faced with an additional opponent in the 4v4 scenario, the coordination of baseline policies collapsed. Adv-TransAC, however, managed to adapt its cooperative tactics and maintained a respectable level of performance. This suggests that by learning the fundamental principles of spatiotemporal coordination rather than overfitting to a specific number of agents, our framework develops a more generalizable control strategy.

This superior robustness is a direct result of our framework’s ability to form a deep, contextual understanding of the tactical environment, making it less brittle and better suited for the unpredictable nature of real-world maritime operations.

4.8. Scalability Analysis

The scalability of multi-agent systems is a key challenge. To explore the performance of Adv-TransAC in more complex, large-scale scenarios, we conducted a series of scalability tests. We changed the number of our (N) and enemy (M) USVs and evaluated the mission success rate and average response delay. We compared Adv-TransAC to the suboptimal performing MADDPG; the results are shown in Table 5.

The results in

Table 6. Adv-TransAC and MADDPG comparison of performance at different agent scales.

Agent Scale (N vs. M)	Algorithm	Task Success Rate (%)	Average Response Latency (ms)
2 vs. 2	MADDPG	91.2	7.5
	Adv-TransAC	96.8	15.1
4 vs. 3 (benchmark)	MADDPG	59.5	15.4
	Adv-TransAC	78.5	29.7
6 vs. 5	MADDPG	35.1	32.8
	Adv-TransAC	68.5	55.3

clearly show that as the number of agents increases, the performance of all algorithms inevitably decreases, which is consistent with the exponential increase in the complexity of multi-agent collaboration. However, the performance degradation curve of Adv-TransAC is much more gradual than MADDPG’s. In the most challenging 6v5 scenarios, Adv-TransAC still maintained a success rate of nearly 70%, while the performance of MADDPG was close to crashing. This highlights the advantages of the transformer architecture in dealing with high-dimensional joint state–action spaces and capturing the dependencies between complex agents.

At the same time, while the response latency of Adv-TransAC increases with scale, its latency (55.3 ms) is still far within acceptable real-time control at 6v5 scale. This is a testament to the potential for scalability of our framework, which can handle more complex tasks than benchmarks (4v3).

4.9. Qualitative Analysis and Interpretability

We visualize typical agent trajectories in Figure 9 to better understand the strategic differences. The MADDPG-controlled agents (left panel) exhibit a simplistic and disjointed defense, where USVs often act independently and are easily lured away or defeated one by one by the enemy. In stark contrast, the agents controlled by Adv-TransAC (right panel) demonstrate clear, emergent cooperative behaviors. To quantify this, we define “double-team” operations as two USVs attacking an enemy ship from complementary angles simultaneously, a tactic successfully executed in 68% of our evaluation trials where interception occurred. In fact, Figure 9 visually confirms this, indicating emergent ‘double-team’ motions (right panel)—a coordinated action not exhibited by MADDPG’s decentralized defense (left panel). They spontaneously form a protective formation around the HVU and execute this maneuver to intercept the approaching enemy.

This advanced tactic highlights the sophistication of the learned control strategy. The Adv-TransAC agents initially adopt a stable, formation-keeping control mode to protect the HVU. Upon detecting an imminent threat that crosses a certain threshold, the system dynamically reassigns agents’ roles and transitions into an aggressive, intercept-and-neutralize control mode. This ability to switch between distinct, complex control modes based on high-level situational awareness is a key feature of the advanced strategies that our framework produces, and it is extremely difficult to pre-program with rule-based systems or conventional controllers.

The figure illustrates the dynamic allocation of control attention over three successive time steps (t − 2, t − 1, t), revealing the sophisticated, multi-stage reasoning of the learned control strategy: In these attention maps, the blue circle represents the friendly escort USV, the red circle is the enemy USV, and the blue dashed line indicates the friendly USV’s trajectory.

Early Warning and Monitoring (t − 2): The policy initially allocates broad attention to a distant threat, demonstrating a state of vigilant monitoring.

Threat Prioritization (t − 1): As the threat is confirmed by high-precision sensors, the policy network dynamically converges its focus, identifying it as the primary target for engagement.

Proactive Interception Planning (t): Most critically, the agent’s attention then shifts from the opponent’s current location to a predicted future intercept point. As shown in Figure 11 at timestep t, the attention map peaks on a projected intercept point approximately 2 s ahead of the target’s path, verifying that the model’s temporal intent inference is functioning correctly. This demonstrates that the learned control strategy is not purely reactive but proactive and anticipatory. It is planning its control actions based on a future predicted state, a hallmark of advanced intelligence.

This transparent decision-making process, where we can trace the agent’s focus from detection to proactive planning, strongly validates the effectiveness of the transformer-based architecture. It provides a foundational level of trust by confirming that the model learns a tactically sound and logical control strategy. However, we acknowledge that attention visualization is a preliminary step towards full interpretability, and further research is needed to fully deconstruct the model’s complex decision-making calculus.

4.10. Communication Efficiency Analysis

To evaluate the practical feasibility of our framework for real-world deployment, we conducted a theoretical analysis of its communication efficiency. We compared our proposed federated update paradigm with the standard CTDE approach, where each agent transmits its full experience tuple (o, a, r, o’) for every timestep. In our federated approach, agents perform local updates and only periodically transmit the gradients of their actor networks.

This analysis assumes agents upload gradients after every K = 1024 local steps. The data payload is calculated based on our model’s architecture (actor parameters: ~80 k) and environment specifications (observation dim: 128), using 32-bit floating-point precision. The total communication load for the swarm throughout K timesteps is presented in

Table 7. Comparison of communication load over a period of 1024 timesteps.

Agent Scale (N vs. M)	Standard CTDE (KB)	Adv-TransAC (Federated Gradients) (KB)	Bandwidth Reduction
2 vs. 2	2064	625	69.7%
4 vs. 3	4128	1250	69.7%
6 vs. 5	6192	1875	69.7%

.

The results in Table 6 unequivocally demonstrate that our federated gradient-based optimization architecture dramatically reduces the required communication bandwidth by nearly 70%. This is not a minor optimization but a critical feature that addresses the core challenge of intermittent and low-bandwidth communication in maritime environments. This high communication efficiency makes Adv-TransAC a far more viable and scalable solution for training and updating USV swarms in real-world operational conditions, solidifying its potential for practical deployment.

5. Discussion and Conclusions

The Adv-TransAC framework proposed in this study has achieved encouraging results in the simulated multi-unmanned boat attack and defense game tasks. In this chapter, we will take a deeper look at the experimental results, explore the mechanisms behind them, analyze the potential limitations of the current work, and look forward to future research directions.

5.1. An In-Depth Interpretation of the Experimental Results from an Engineering Perspective

To fully appreciate our findings, it is essential to place them within the broader context of multi-agent systems research. The state of the art in MARL is a rapidly advancing field, with continual progress in algorithms, evaluation methodologies, and the complexity of simulation environments, as comprehensively surveyed by Fu et al. (2023) [33].

The experimental results clearly show that Adv-TransAC outperforms existing baseline algorithms in task success rate and strategy robustness. We believe its core advantages stem from the organic combination of its architecture and learning paradigm, which translates directly into superior performance in realistic engineering contexts.

• The Power of Transformer as a Spatiotemporal Feature Extractor:

Unlike methods that only rely on current state snapshots, Adv-TransAC leverages the transformer’s self-attention mechanism to process sequences of multi-modal observations. This provides two key benefits with direct physical and engineering implications:

Spatial Collaborative Perception and Intelligent Risk-Reward Balancing: The slightly higher synergistic collision rate observed in Adv-TransAC (Table 2) is not an algorithmic flaw but rather evidence of a learned, near-optimal risk–reward policy that reflects sophisticated engineering trade-offs. In a real-world naval engagement, a controller that is too conservative and prioritizes collision avoidance above all else may fail its primary mission. Our framework has learned that to maximize the probability of mission success (the primary objective), it is sometimes necessary to execute aggressive, tightly coordinated maneuvers like a pincer movement or a close-quarters block. From an engineering standpoint, this is analogous to “edge-of-the-envelope” maneuvering, where a system operates at the limits of its safe performance envelope to achieve a critical outcome. The learned policy understands that accepting a calculated risk of minor, non-critical collisions is a worthwhile trade-off for neutralizing a high-threat adversary. This demonstrates a level of intelligent risk assessment that is extremely difficult to handcraft into traditional controllers like MPC, whose cost functions are often too rigid to capture such dynamic, state-dependent trade-offs.

Temporal Intent Prediction vs. Reactive Control: Traditional control systems often act as reactive controllers, responding to an opponent’s current kinematic state (position, velocity). In contrast, by analyzing a time series of an opponent’s behavior (e.g., a sequence of accelerations and turns), the transformer in Adv-TransAC can predict tactical intent. From a physical standpoint, it learns to distinguish between different motion patterns that signify different intentions. For example, it can differentiate a probing maneuver from a committed attack run, or a feint designed to draw escorts away from the main target. This allows Adv-TransAC to be proactive rather than reactive. It can deploy defensive formations or initiate an interception before the threat becomes critical, seizing the initiative and gaining a crucial time and spatial advantage in physical engagement. This forward-looking capability is a hallmark of advanced intelligence and is a significant step beyond the capabilities of conventional navigation and guidance systems.

2.

Synergistic Effect between Adversarial Learning and Model Architecture:

Our framework’s success stems from the synergy between its powerful representational model (the hybrid GAT-transformer) and its training paradigm (adversarial curriculum learning). Adversarial training alone can lead to unstable policy oscillations if the model architecture is too simple to capture the opponent’s strategy. Conversely, a powerful model may fail to learn robust behaviors without a structured curriculum that guides its exploration.

The success of Adv-TransAC shows that a model capable of deeply understanding adversary kinematics and tactics, when combined with a curriculum that incrementally increases opponent difficulty, produces a “1 + 1 > 2” effect. The model learns not just a single counter-strategy, but a hierarchical set of responses, from simple avoidance to complex, multi-agent tactical countermeasures. This structured learning process is what enables the development of a generalizable and robust control policy suitable for the unpredictable nature of real-world maritime operations.

5.2. Practicality for Real-World Deployment: Edge Computing and Communication Efficiency

The design of Adv-TransAC offers significant advantages for practical deployment. Its decentralized execution architecture, where the policy network (actor) is lightweight, is well-suited for deployment on resource-constrained onboard (edge) computers, meeting real-time decision-making needs [23].

More importantly, our framework directly confronts the critical bottleneck of maritime communication. The communication efficiency analysis presented in Section 4.8 is not merely an addendum but a cornerstone of our contribution. The nearly 70% reduction in bandwidth achieved by our federated optimization paradigm is an enabling feature, not just a minor optimization. It transforms the proposed advanced learning framework from a theoretically sound concept into a practically deployable system. This efficiency is paramount for USV swarms operating ‘at the edge’ or over the horizon, where stable, high-bandwidth communication cannot be guaranteed. By drastically lowering the data transmission requirements, Adv-TransAC becomes a truly viable and scalable solution for training and updating intelligent multi-agent control systems in realistic operational environments.

5.3. Contextualizing Results and Industrial Implications

To fully appreciate the contributions of this work, it is paramount to contextualize our findings within the broader landscape of multi-agent systems research and to translate our simulation results into tangible implications for real-world maritime industries and engineering applications.

5.3.1. Comparison with the State-of-the-Art

While direct numerical comparison with prior work is challenging due to variations in simulation environments and task specifics, we can contextualize the magnitude of our performance improvements. Previous studies on multi-agent adversarial tasks often highlight the limitations of standard MARL algorithms. For example, Wang, Y. [34] reported that even advanced actor–critic methods struggled to surpass a 60% success rate in cooperative-competitive settings with intelligent adversaries, a failure they attributed to poor credit assignment and an inability to model opponent intent. Our Adv-TransAC framework, achieving a 78.5% win rate against a similarly adaptive opponent, demonstrates a substantial leap forward.

This significant performance gain is not merely an incremental improvement; it is directly attributable to our hybrid GAT-transformer architecture, which explicitly addresses the core weaknesses identified in previous studies. Unlike standard MADDPG [9], which relies on simple state concatenation, or QMIX [7], whose restrictive value decomposition struggles in competitive settings, our approach captures the high-order spatiotemporal dependencies essential for sophisticated tactical reasoning. This suggests that our principled approach to spatiotemporal modeling establishes a new and effective performance benchmark for this class of complex multi-agent problems.

5.3.2. Implications for Industrial and Engineering Applications

Beyond academic benchmarks, the results presented have profound and practical implications for the future of autonomous maritime systems:

Enhanced Operational Safety and Efficiency in Port Security: In real-world port and harbor security, the high success rate of Adv-TransAC translates directly to a more reliable, automated defense against unauthorized vessel intrusions. The learned “double-team” maneuver is not a simulation artifact; it represents a template for a high-speed, precision intercept protocol that would be difficult for human operators to execute consistently under pressure. This could significantly reduce the reliance on manned patrol boats, lowering operational costs, minimizing human risk, and increasing response effectiveness 24/7.

Robustness for Critical Offshore Asset Protection: For protecting high-value, static assets like offshore oil rigs, wind farms, or aquaculture installations, the demonstrated robustness against learning-based adversaries is a critical feature. Real-world threats are not static; they are intelligent and adaptive. Our framework’s ability to generalize and maintain high performance against such opponents means it can provide a more resilient “digital perimeter,” capable of countering evolving threats without constant manual reprogramming by engineers.

A Foundational Architecture for Complex Coordinated Missions: The ability to learn emergent, complex cooperative tactics paves the way for a new generation of multi-USV missions beyond simple escort tasks. This includes coordinated environmental monitoring (e.g., tracking an oil spill with a dynamic sensor network), large-area seabed mapping in complex topographies, or even distributed anti-submarine warfare (ASW) screens. The principles of decoupled spatiotemporal modeling and adaptive learning validated in this paper provide a foundational control architecture for tackling these ambitious, next-generation multi-agent engineering challenges.

5.4. Limitation Analysis and Future Work

Despite the promising results, we must soberly acknowledge the limitations of the current work, which pave the way for critical future research directions.

1. The Sim-to-Real Gap and Operational Safety. All experiments were conducted in a simulated environment. The real-world ocean is far more complex, with unpredictable hydrodynamics (e.g., currents, waves), variable sensor noise models, and communication latencies or outages. Bridging this “Sim-to-Real” gap without significant performance degradation is a major challenge. Furthermore, migrating this system to a physical platform introduces non-negotiable safety and ethical imperatives. Real-world application demands robust fail-safes against the potential malfunction of the adversarial adaptation mechanism. Future work must therefore focus not only on domain randomization and system identification but also on integrating human-in-the-loop safety protocols. This could include, as suggested by our scenarios, human override capabilities initiated by personnel on the HVU being escorted (see Figure 9), or the implementation of standards-compliant emergency “kill-switches” as guided by maritime regulations like ISO 23860 [32]. Ensuring that the adaptive policy remains stable, predictable, and safely interruptible under all real-world conditions is a crucial step toward deployment.

2. Scalability and Computational Cost. While Adv-TransAC demonstrates good scalability in our tests, the computational overhead of the transformer architecture, particularly in the centralized critic, is inherently higher than that of simpler MLP or CNN structures. As the number of agents increases dramatically into the dozens or hundreds, the complexity of the centralized critic will grow exponentially. This may limit the framework’s applicability to very large-scale swarms. Future research should explore hierarchical or fully decentralized control architectures to manage this complexity, perhaps by using Adv-TransAC for intra-squad coordination within a larger, layered command structure.

3. Generalization to “Black Swan” Strategies. Our framework showed robustness against predefined rule-based and learning-based opponents. However, its ability to generalize to “black swan” events—adversaries employing entirely novel tactical paradigms not seen during training—remains an open research question. A promising direction for future work is to address this by incorporating online anomaly detection modules. For instance, the system could monitor the adversary’s behavior in real-time and flag any actions that deviate significantly (e.g., more than 3σ away) from the distributions encountered during training. Such a detection could trigger an alert for human operator intervention or switch the policy to a more conservative, fail-safe mode. This would create a robust human–machine team, combining the rapid tactical execution of the AI with the strategic oversight of a human commander, which is crucial for handling truly unforeseen threats.

5.5. Prospects for the Future of Work

Based on the above analysis, we propose the following future research directions worth exploring:

Physical Platform Validation and Sim-to-Real Migration: The key next step is to deploy the Adv-TransAC on a real USV physical or semi-physical simulation platform to verify its performance in a real-world marine environment. At the same time, research on domain adaptation and system identification technologies is needed to mitigate the impact of the Sim-to-Real gap.

Layered and decoupled MARL architectures [24]: A layered MARL architecture can be explored to solve the scalability problem of large-scale clusters. For example, the cluster is divided into multiple subgroups (squads), and Adv-TransAC is used for tactical coordination within the subgroups. In contrast, higher-level macro policy coordination is used between subgroups to achieve decoupling of computational complexity.

Meta-learning and online adaptation: The Meta-Learning framework is introduced to enable the model to quickly adjust strategies online based on a small amount of interaction with a new adversary during task execution, to improve the adaptability to unknown adversaries.

Convergence with Explainable AI (XAI): A critical challenge for deploying learned control policies in high-stakes environments is their “black-box” nature. While our attention visualization provides initial insights into what the model focuses on (e.g., which adversary or sensor data), it does not fully explain why a specific tactical decision was made. Future work must bridge this gap by integrating more advanced XAI techniques. This involves moving beyond attention heatmaps to employ methods like SHAP or concept-based analysis to answer profound operational questions, such as “Why did the swarm decide to execute a pincer maneuver instead of maintaining a defensive formation at this moment?” Achieving this level of transparency is fundamental to building human–machine trust, enabling effective human-on-the-loop supervision, and ultimately enhancing the confidence of human commanders in AI-driven control strategies.

5.6. Concluding Remarks

In conclusion, this paper introduced Adv-TransAC, a novel framework that successfully learns advanced cooperative control strategies for multi-USV swarms in complex adversarial environments. By systematically tackling the dual challenges of robust multi-modal sensor fusion and adaptive policy generation, our work moves beyond the limitations of conventional MARL approaches.

Our primary contribution is the hybrid GAT-transformer architecture, which provides a principled method for decoupling and modeling complex spatiotemporal dynamics. Complemented by a transformer-based adversarial meta-learning mechanism, our framework enables the emergence of sophisticated, proactive behaviors and demonstrates superior performance, robustness, and scalability in extensive experiments. Furthermore, we have validated its practical feasibility through a communication-efficient federated optimization architecture, directly addressing a key bottleneck for real-world maritime deployment.

Ultimately, this work represents a significant step forward in bridging the gap between advanced artificial intelligence research and the pressing operational needs of modern maritime systems. By establishing a strong foundation for proactive, coordinated, and adaptive control, Adv-TransAC paves the way for the development of next-generation, truly autonomous and effective USV swarms.