Scour Near Offshore Structures—Part 2: Practical Scour Model
Abstract
1. Introduction
2. Scouring Processes
2.1. General
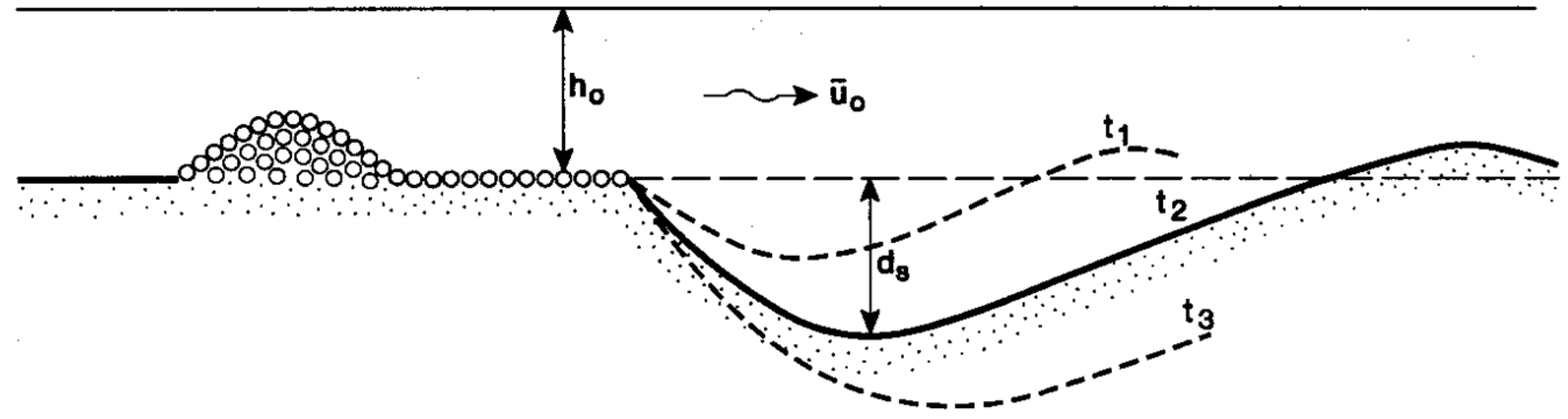
- Clear-water scour: The approach velocity is slightly below the (critical) flow velocity for initiation of motion (ucr); the upstream flow has no sediment load; and scour is initiated by the flow velocity increase around the upstream half of the pile and the extra turbulence and associated vortices generated in the lee zone of the pile.
- Live-bed scour: The approach velocity is higher than the (critical) flow velocity for initiation of motion (ucr); the upstream flow has a sediment load; and the sediment transport capacity around the pile is substantially higher than upstream.
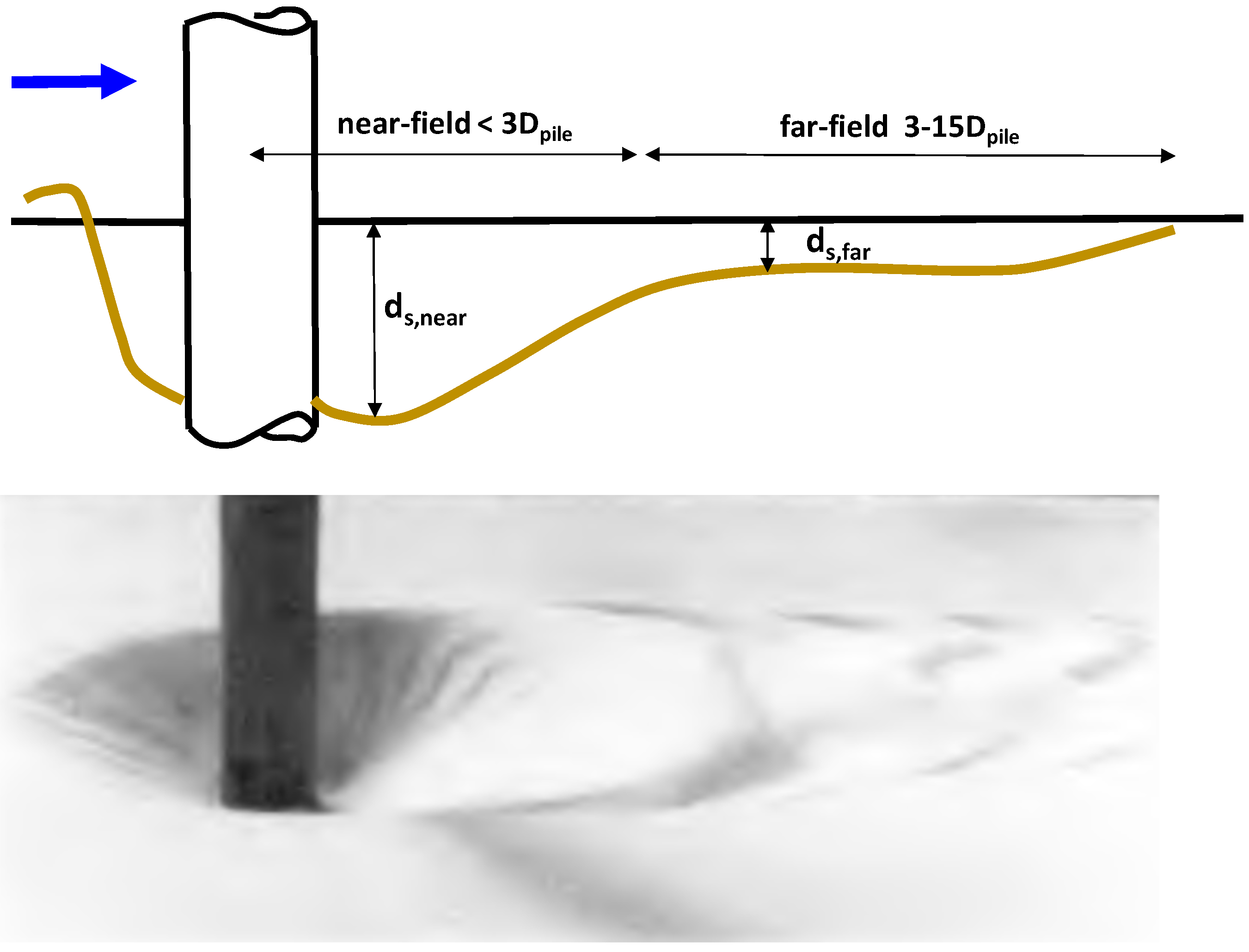
- Near-field zone: within a distance of 3 to 5 times the length or height scale of the structure/obstacle from the source location, where a deep scour hole is generated;
- Far-field zone: where a shallow scour hole is generated gradually, reducing to zero further away from the structure; erosion in this zone is often masked by the presence of migrating bed forms (mega-ripples, dune-type forms).
2.2. Berms and Sills
2.3. Pile-Type Structures
3. Description of SEDTUBE Scour Model
3.1. General
3.2. Model Equations
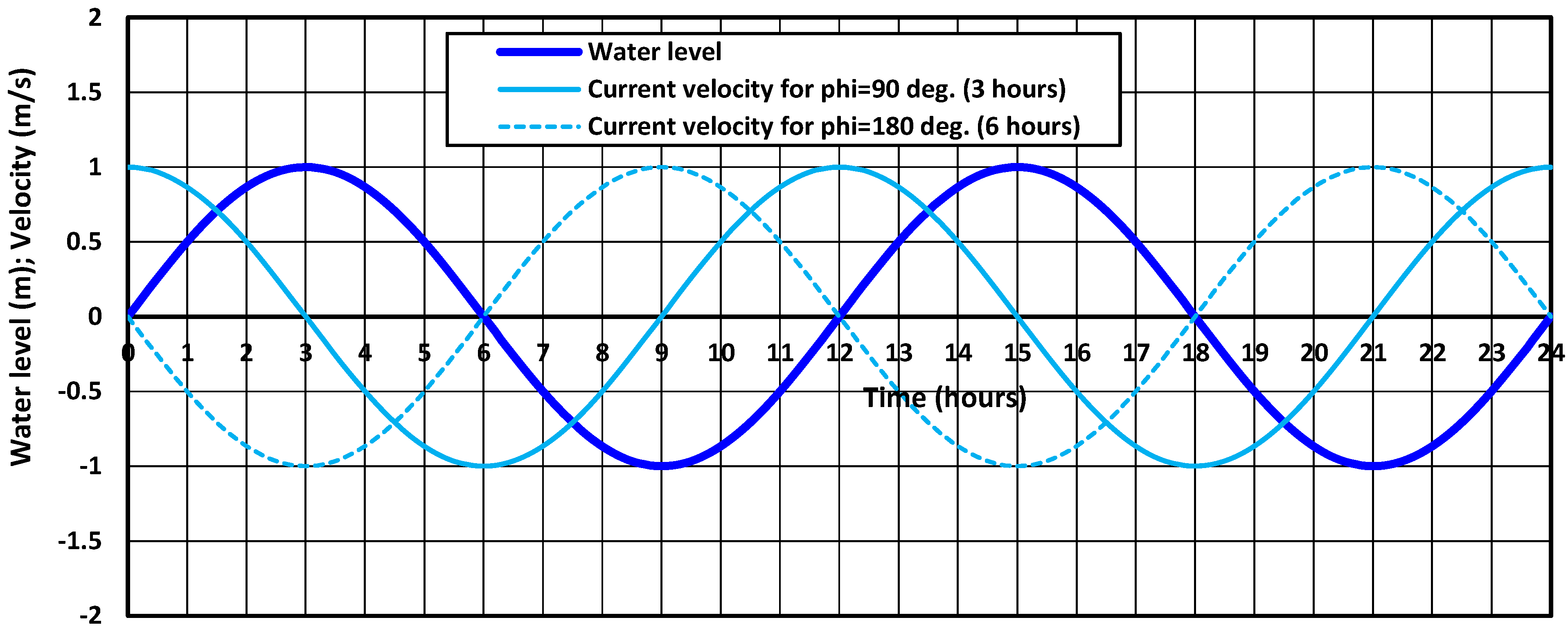
3.2.1. Tidal Flow
3.2.2. Effective Flow Velocity for Sediment Transport
3.2.3. Sediment Transport
3.2.4. Bed Level Changes
0.5 γsmooth(zb,i+1,t − 2zb,i,t + zb,i−1,t)]/[2 bi ∆x(1 − ε)ρs]
- No sand is present on the hard layer: sand transport along the hard layer is constant (Qs,i+1 = Qs,i and Qb,e,I = Qb,i−1);
- Sufficient sand is present on the hard layer: the erosion is computed by Equations (12)–(15);
- Insufficient sand is present on the hard layer or the potential erosion thickness (∆zb) is larger than the sand layer thickness (∆zhard): the sand transport is adjusted; see Equation (16).
3.2.5. Input and Output Parameters
- Water depth values and hard-layer values of bed profile (m);
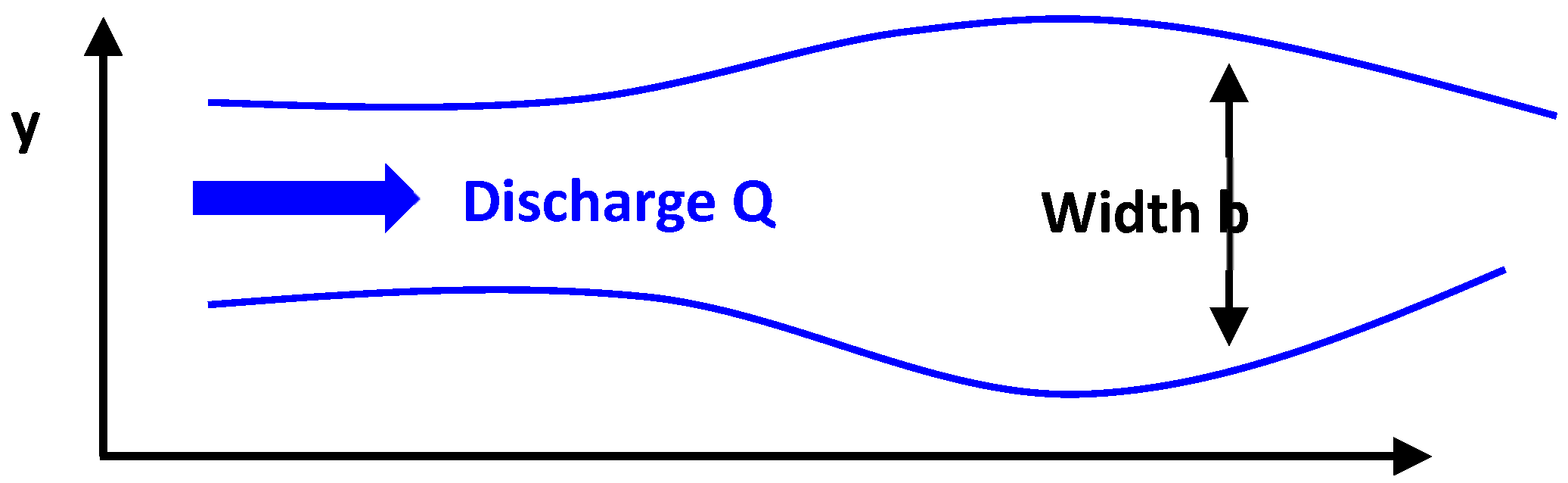
- Stream tube width values (m);
- x-coordinate values of bed profile (m);
- Grid size values (variable) along domain (m);
- Storm setup above mean sea level (m);
- Tidal amplitude η1,max (m) of M1 tide and η2,max (m) of S1 tide mean flow velocity umo (m/s);
- Maximum (peak) tidal flow velocity u1,max (m/s) of M1 tide and u2,max (m/s) of S1 tide;
- Phase lag φ (hours);
- Tidal period Ttide1 (hours) of M1 tide and Ttide2 of S1 tide;
- Significant wave height Hs (m) and period Tp (s) and duration (days) of each wave condition;
- Water temperature (Celsius); ρw, density of seawater (kg/m3); and ρs, density of sediment (kg/m3);
- Porosity of bed material (-); sand d50, d90 (m);
- ws, settling velocity of suspended sediment for sand (m/s);
- ucr, critical depth-averaged velocity (m/s);
- pfines, percentage fines < 63 µm (%);
- ks, bed roughness (m);
- γbed, (gamb) calibration parameter bed load transport, default (-);
- γsus, (gams) calibration parameter suspended load transport, default = 1 (-);
- γeff, (game) calibration factor effective velocity of waves, default = 1 (-);
- γbh, (gambh) calibration factor for turbulence adjustment distance, default = 1 (-);
- αad, (alfad) coefficient of suspended load adjustment factor, range 0.1–0.3 (-);
- ro, turbulence coefficient (-);
- xr, position from where turbulence coefficient is active (m);
- bh, length scale (width or height) of upstream obstacle/strucure on bed (m);
- ∆t, time step (s);
- γsmooth, (gamsb) bed smoothing factor (-);
- iswr, switch (0/1) equilibrium transport zero transport at boundaries (-);
- resfle, output selection parameters.
4. Validation of SEDTUBE Model
4.1. General
- Laboratory cases:
- -
- Scour downstream of bed protection (no upstream structure);
- -
- Scour downstream of rock berm and bed protection.
- Field cases:
- -
- Scour downstream of culvert in the Eastern Scheldt (NL);
- -
- Scour downstream of rock berm structure, Morecambe Bay, UK;
- -
- Sedimentation in trial dredge trench in the Western Scheldt estuary, NL.
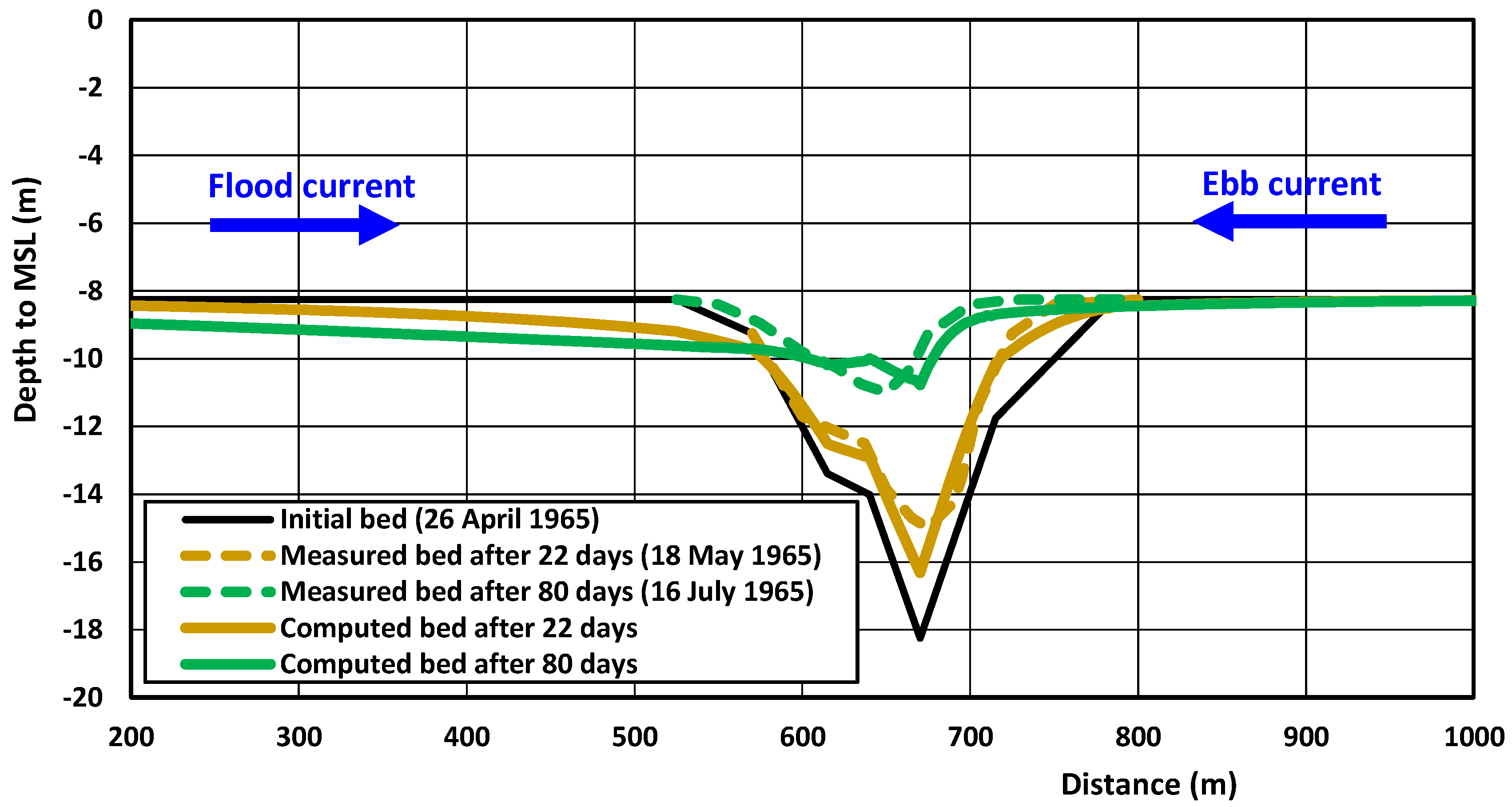
4.2. Laboratory Case—Scour Downstream of Bed Protection (No Upstream Structure)
4.3. Laboratory Case—Scour Downstream of Rock Berm and Bed Protection
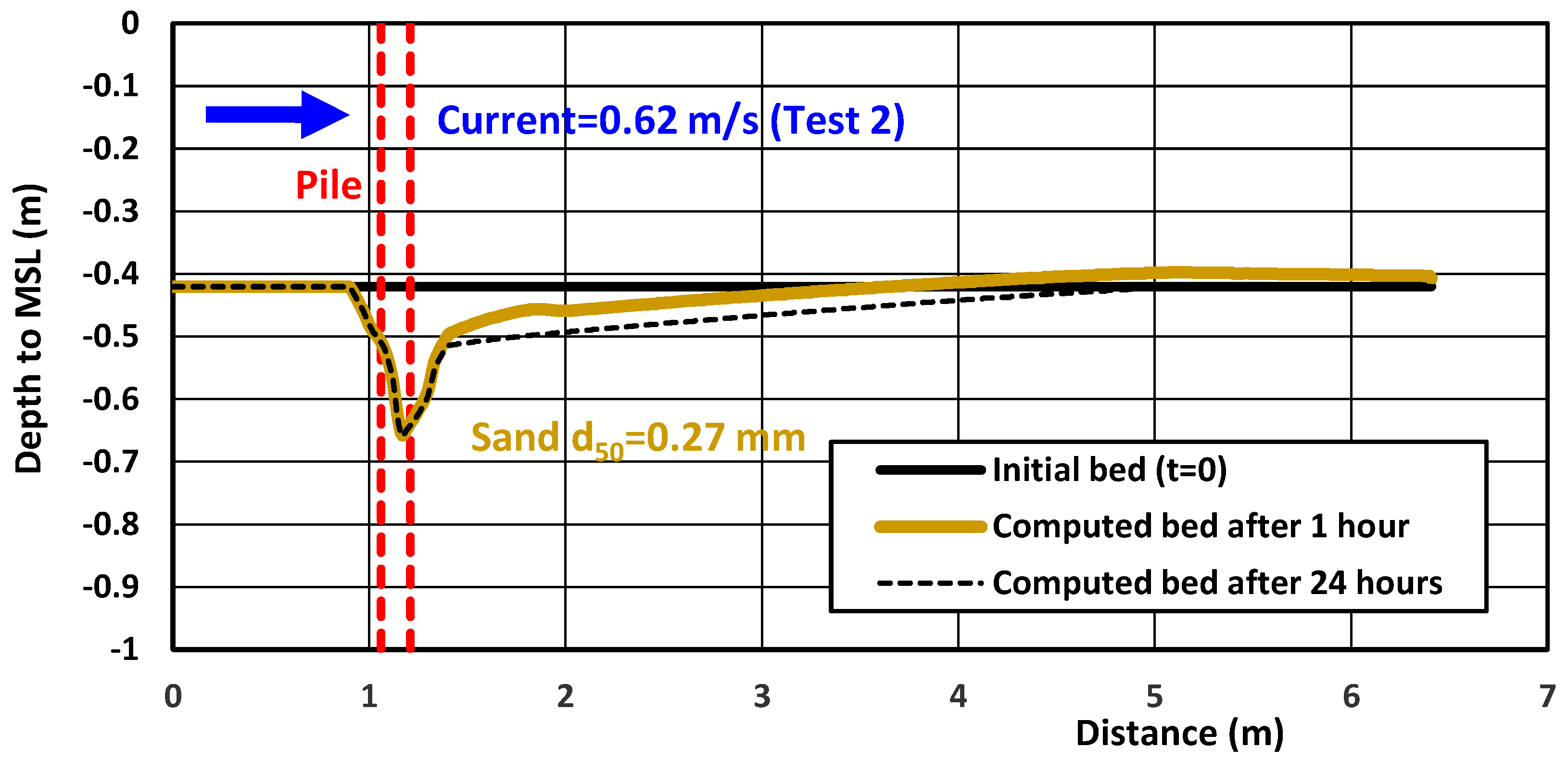
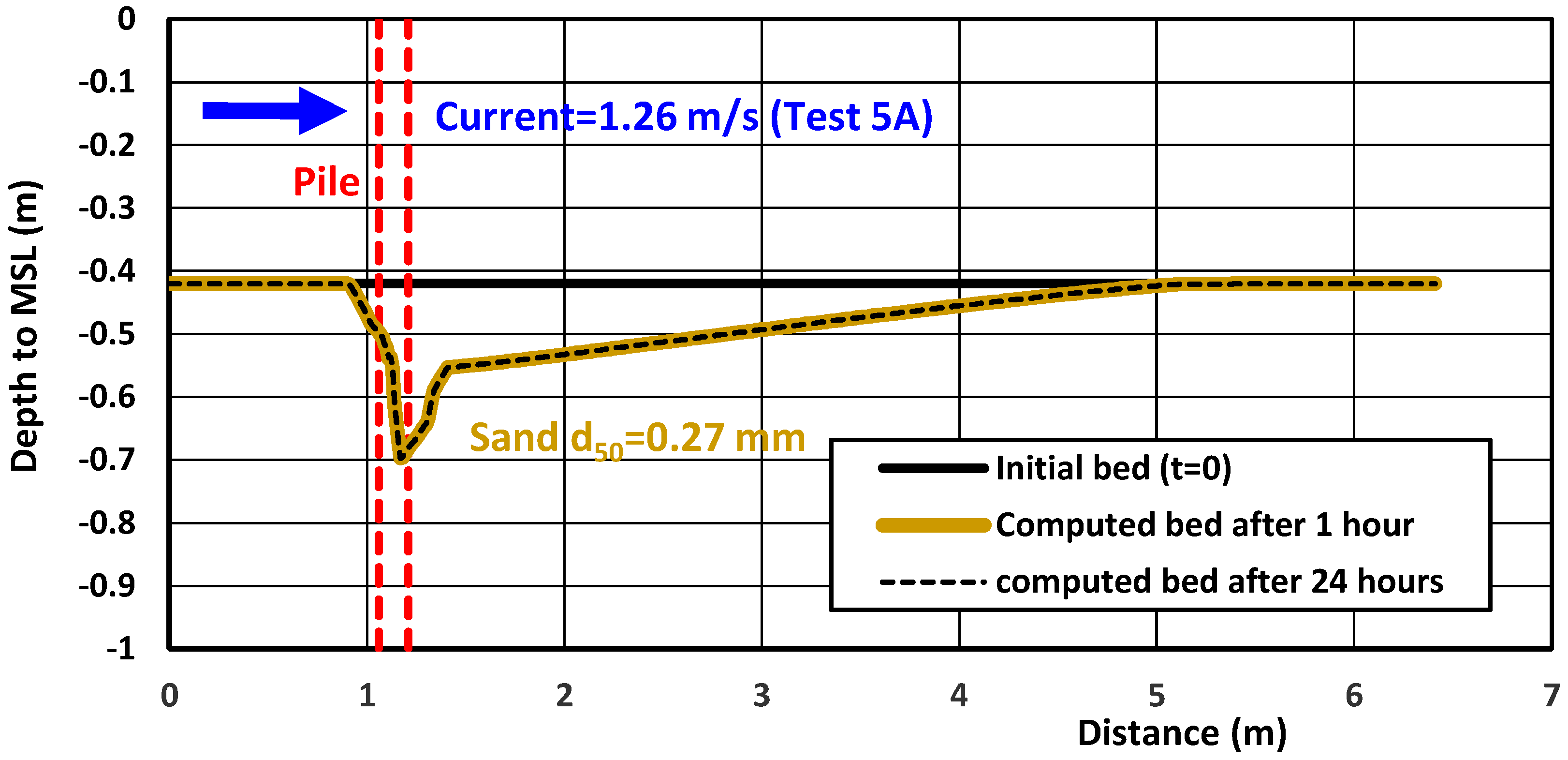
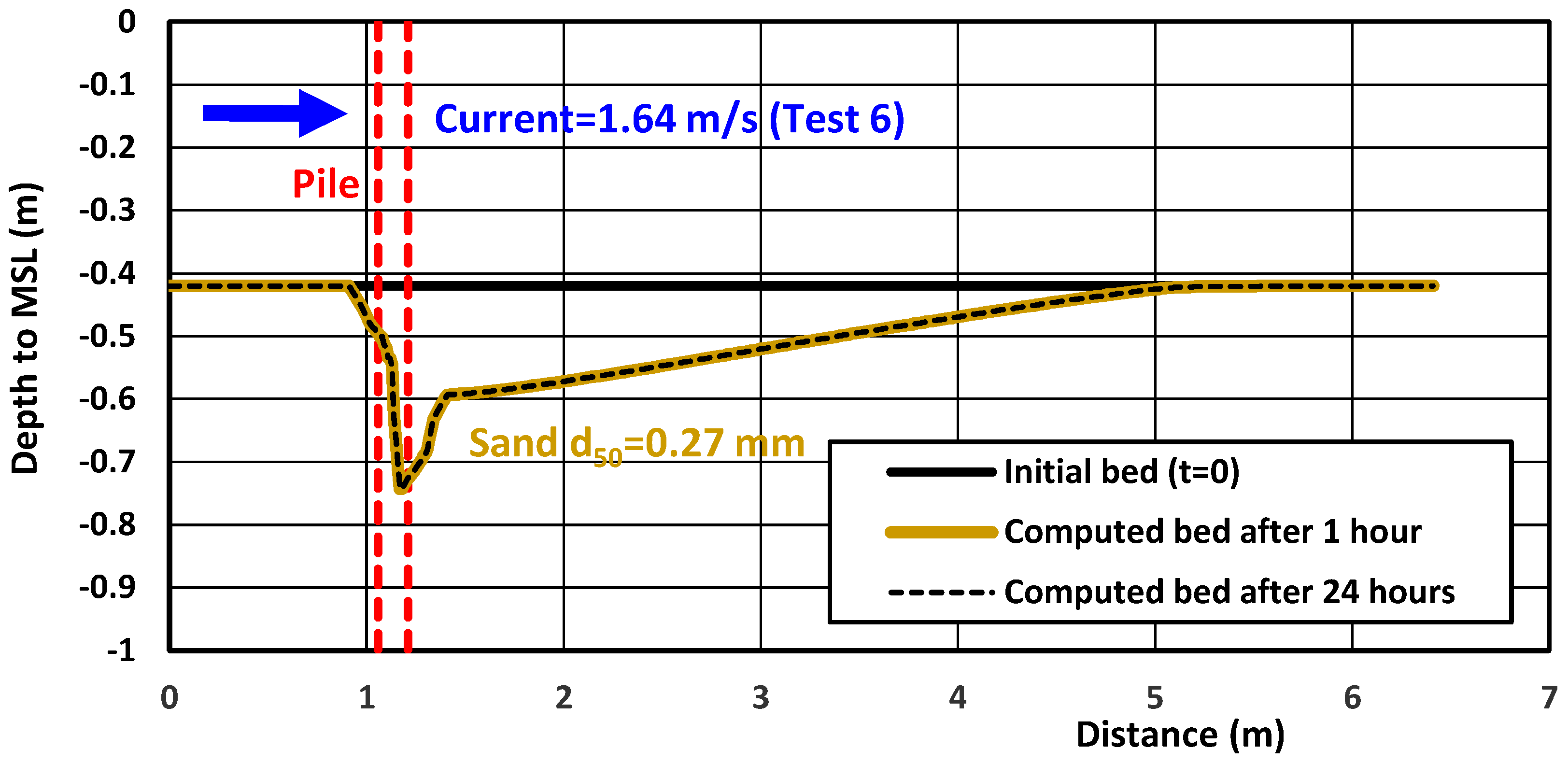
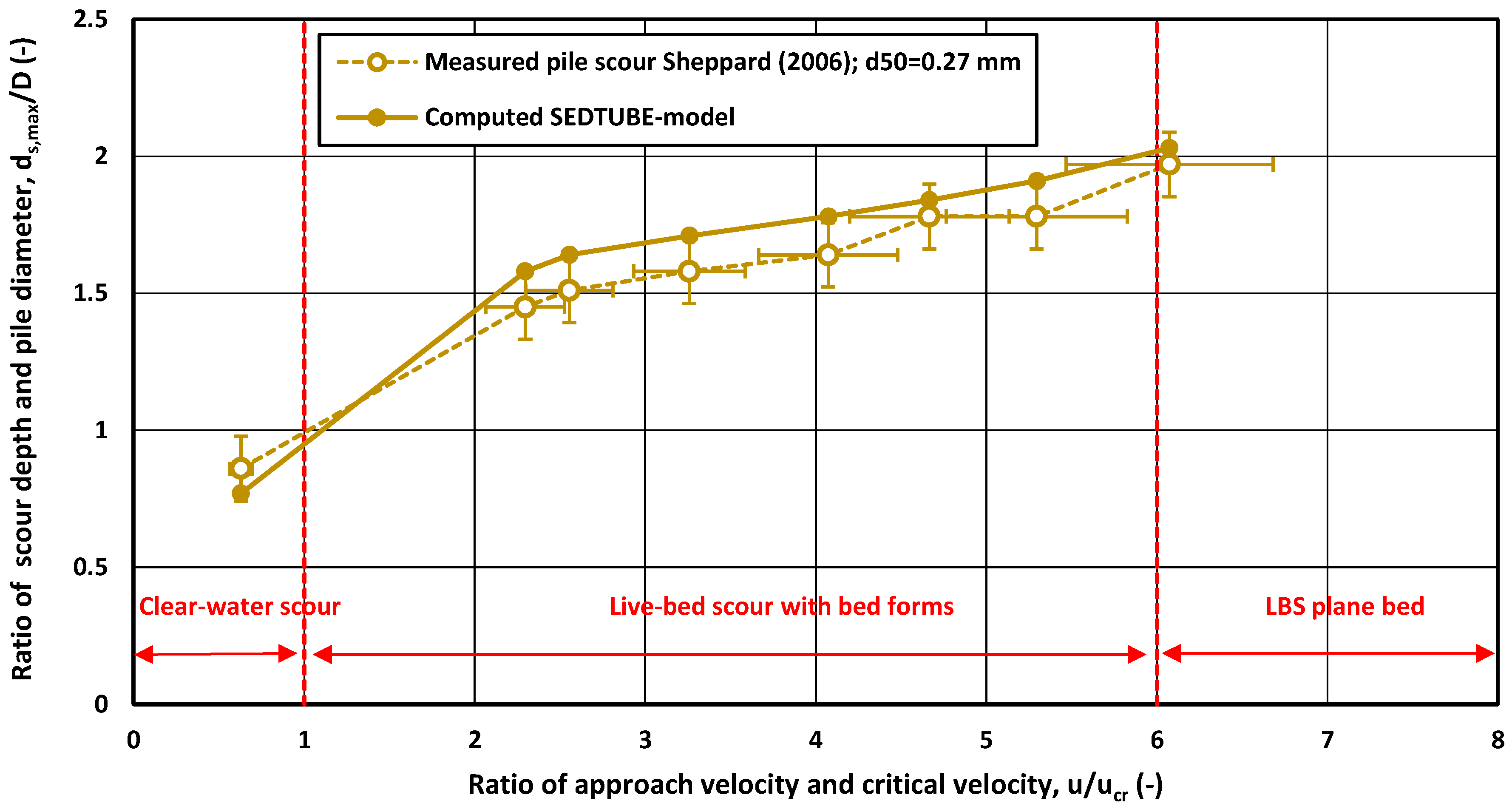
4.4. Laboratory Case—Scour Around Piles in Uni-Directional Flow
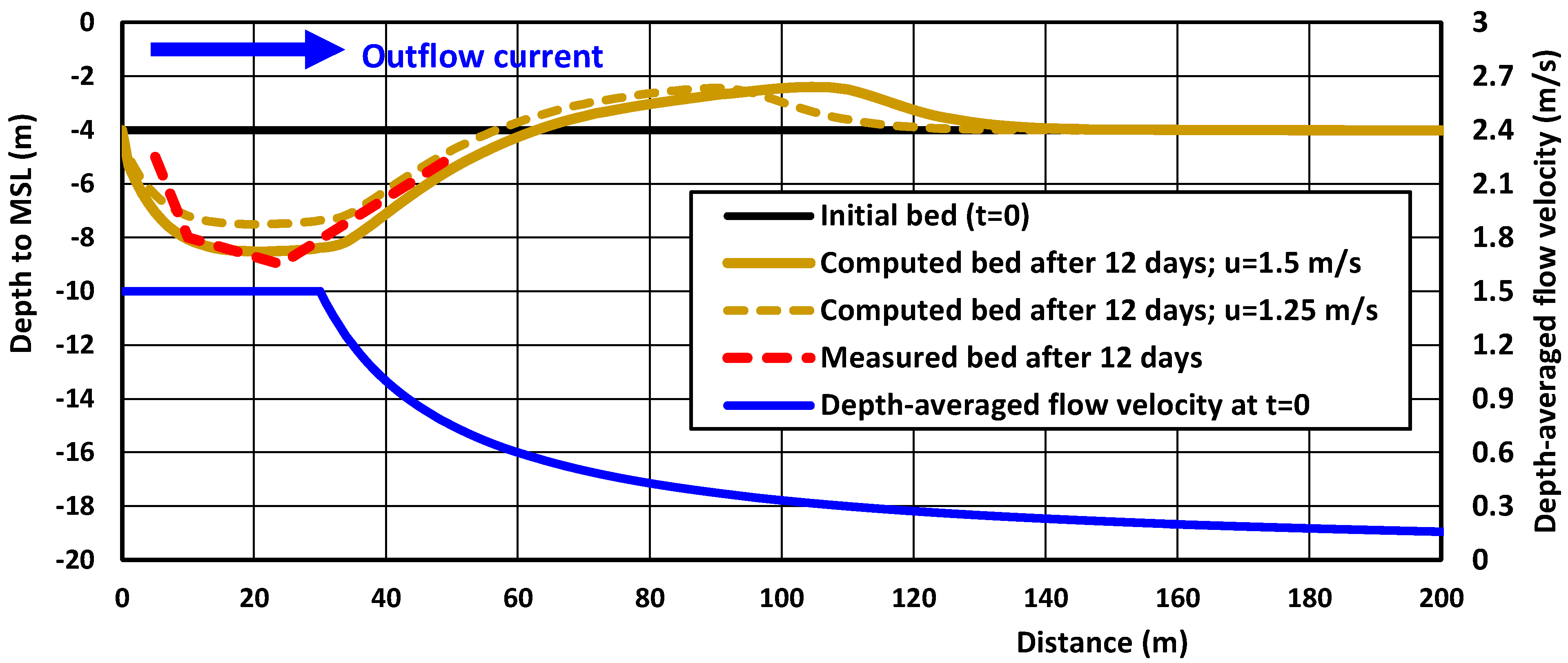
4.5. Field Case—Scour Around Pile in Tidal Flow—Scroby Sands, UK
4.6. Scour Downstream of Culvert in Eastern Scheldt, The Netherlands
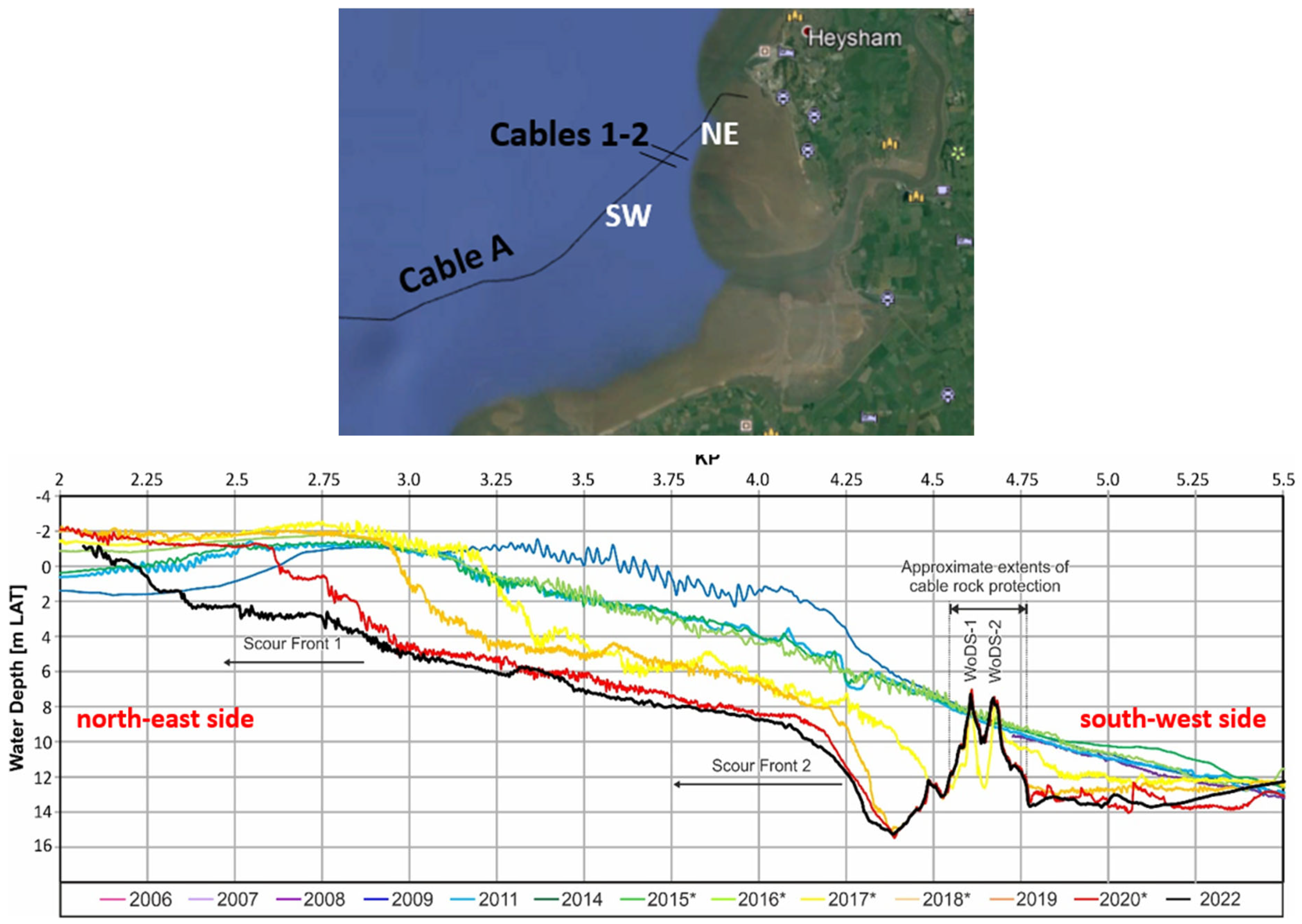
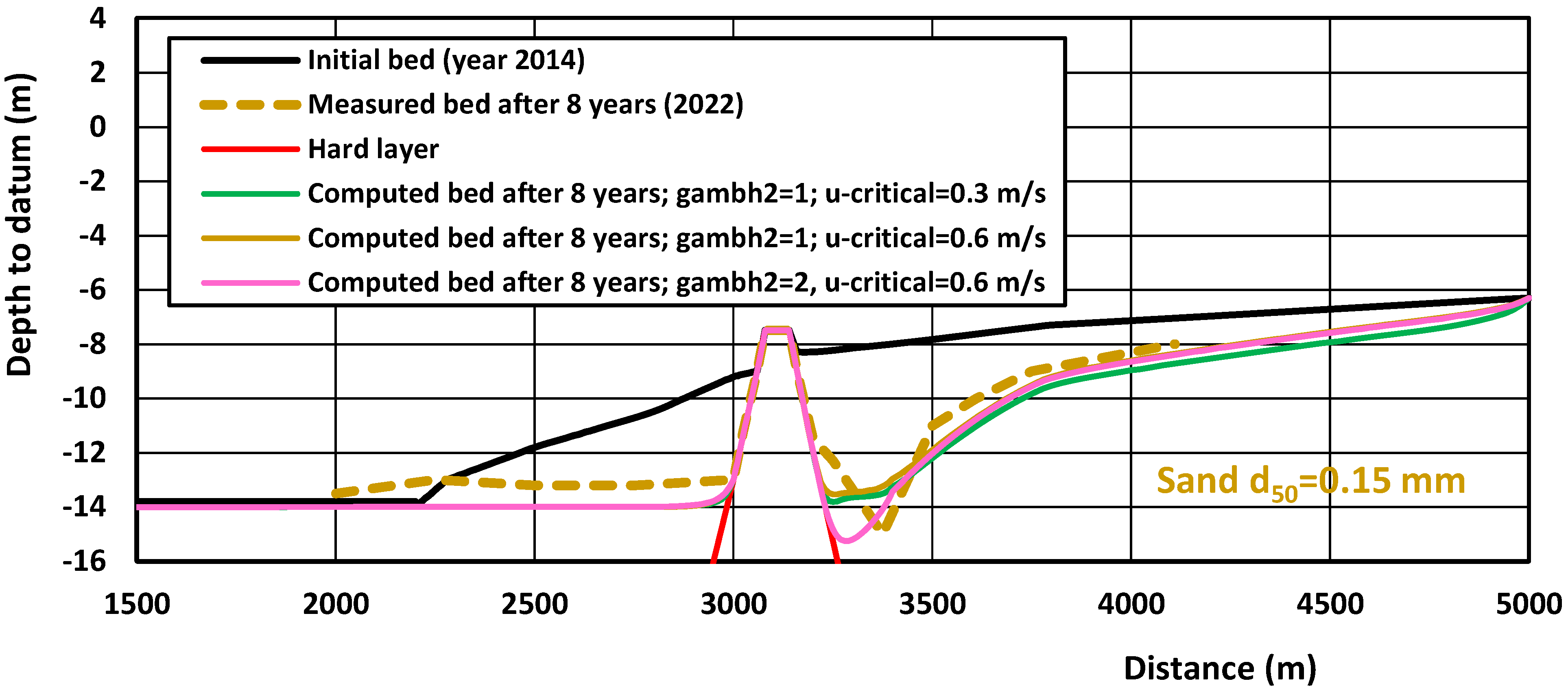
4.7. Scour Downstream of Rock Berm Structure, Morecambe Bay, UK
4.8. Sedimentation in Trial Dredge Trench in Western Scheldt Estuary, The Netherlands
5. Summary, Applications, and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Rijn, L.C.; Geleynse, N.; Perk, L.; Schoonhoven, D. Scour near Offshore Monopiles, Jacket-Type and Caisson-Type Structures. J. Mar. Sci. Eng. 2025, 13, 266. [Google Scholar] [CrossRef]
- Melville, B. The Physics of Local Scour at Bridge Piers. In Proceedings of the Fourth International Conference on Scour and Erosion, Tokyo, Japan, 4–8 November 2008. [Google Scholar]
- Liang, B.; Du, S.; Pan, X.; Zhang, L. Local Scour for Vertical Piles in Steady Currents: Review of Mechanisms, Influencing Factors and Empirical Equations. J. Mar. Sci. Eng. 2020, 8, 4. [Google Scholar] [CrossRef]
- Gong, E.; Chen, S.; Chen, X.; Guan, D.; Zhang, J. Large-scale experimental study on scour around both slender and large monopiles under irregular waves. Water Sci. Eng. 2025. [Google Scholar] [CrossRef]
- Garcia, K.; Jordan, C.; Melling, G.; Schendel, A.; Welzel, M.; Schlurmann, T. Scour variability across offshore wind farms (OWFs): Understanding site-specific scour drivers as a step towards assessing potential impacts on the marine environment. Wind. Energy Sci. 2025. [Google Scholar] [CrossRef]
- Cui, J.; Bao, T.; Ding, X.; Tang, C.; Li, T.; Zhou, W. Scour predictions, monitoring and protection measures for offshore wind turbines; recent advancements and insights. Ocean. Eng. 2025, 339, 122194. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Y.; Jia, J.; Zhang, J. Experimental and Numerical Study on Local Scour of Pile Group Foundations for Offshore Wind Turbines Under Wave-Current Interactions. China Ocean 2025, 39, 493–503. [Google Scholar] [CrossRef]
- Duan, B.; Wang, D.; Qin, C.; Duan, L. Local Scour Around Marine Structures: A comprehensive review of influencing factors, prediction methods, and future directions. Buildings 2025, 15, 2125. [Google Scholar] [CrossRef]
- Rudolph, D.; Raaijmakers, T.; Stam, C.J. Time-Dependent Scour Development Under Combined Current and Wave Conditions, Hindcast of Field Measurements. In Proceedings of the 4th International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008. [Google Scholar]
- Raaijmakers, T.C.; Van Velzen, G.; Riezebos, H.J. Dynamic Scour Prediction for Offshore Monopiles. In Proceedings of the 7th International Conference Scour and Erosion, Perth, Australia, 2–4 December 2014. [Google Scholar]
- Whitehouse, R.S.J. Marine Scour at Large Foundations. In Proceedings of the 2nd International Conference on Scour and Erosion, Singapore, 14–17 November 2004. [Google Scholar]
- Whitehouse, R.; Harris, J.; Sutherland, J.; Rees, J. An Assessment of Field Data for Scour at Offshore Wind Turbine Foundations. In Proceedings of the Fourth International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008. [Google Scholar]
- Whitehouse, R.; Harris, J.; Sutherland, J. Evaluating scour at marine gravity structures. HR Wallingford. ICE-Marit. Eng. 2012, 164, 143–157. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.; Zhang, N.; Zhao, H.; Liu, L.; Huang, K.; Chen, X. Local Scour Mechanism of Offshore Wind Power Pile Foundation Based on CFD-DEM. J. Mar. Sci. Eng. 2022, 10, 1724. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M.; Verheij, H.J. Scour Manual; Balkema Publishing Company: Rotterdam, The Netherlands, 1997. [Google Scholar]
- Breusers, H.N.C.; Raudkivi, A.J. Scouring Hydraulic Structures Design Manual Series; CRC Press: Boca Raton, FL, USA, 2020; Volume 2, ISBN 978-1000108507. [Google Scholar] [CrossRef]
- Breusers, H.N.C. Two-Dimensional Scour in Loose Sediments; Delft Hydraulics: Delft, The Netherlands, 1967; Publ. 64. [Google Scholar]
- Breusers, H.N.C.; Nicollet, G.; Shen, H.W. Local scour around cylindrical piers. J. Hydr. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Van der Meulen, T.; Vinjé, J.J. Three-Dimensional Local Scour in Non-Cohesive Sediments. In Proceedings of the 15th Congress IAHR, Sao Paulo, Brazil, 27 July–1 August 1975; Volume 2, p. B33. [Google Scholar]
- Dietz, J.W. Kolkbildung in Feinen oder Leichten Sohlmaterialien bei Strömendem Abfluss Mitteilungen Heft 155; TU: Hannover, Germany, 1969; pp. 1–121. [Google Scholar]
- Schoppman, B. Strömungs—Und Transportmechanismen Einer Fortschreitenden Auskolkung. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, 1972. [Google Scholar]
- Van Rijn, L.C. Principles of Sedimentation and Erosion Engineering in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 2005. Available online: www.aquapublications.nl (accessed on 1 August 2025).
- Deltares. Sutrench-Model: Two-Dimensional Vertical Mathematical Model for Suspended Sediment Transport by Currents and Waves. In Report S488 Part IV; Deltares: Delft, The Netherlands, 1985. [Google Scholar]
- Van Rijn, L.C. Mathematical modelling of suspended sediment in nonuniform flows. J. Hydraul. Eng. ASCE 1986, 112, 433–455. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Principles of Fluid Flow and Surface Waves in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 2011. Available online: www.aquapublications.nl (accessed on 1 August 2025).
- Eysink, W.; Vermaas, H. Computational Method to Estimate the Sedimentation in Dredged Channels And harbour Basins in Estuarine Environments. In Proceedings of the International Conference on Coastal and Port Engineering in Developing Countries, 1st International Association for Hydraulic Research, Colombo, Sri Lanka, 20–26 March 1983. [Google Scholar]
- Van Rijn, L.C. Unified view of sediment transport by currents and waves, I: Initiation of motion, bed roughness, and bed-load transport. J. Hydraul. Eng. 2007, 133, 649–667. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993. Available online: www.aquapublications.nl (accessed on 1 August 2025).
- Van Rijn, L.C. Unified view of sediment transport by currents and waves, II: Suspended transport. J. Hydraul. Eng. 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M. Concentration and Flow Velocity Measurements in a Local Scour Hole; Department of Civil Engineering, Delft University of Technology: Delft, The Netherlands, 1990; Report 4–90. [Google Scholar]
- Deltares. Systematic Study of 2D and 3D Scour Downstream of Structures (in Dutch); Deltares: Delft, The Netherlands, 1972; Report M648–863. [Google Scholar]
- Sheppard, D.M.; Miller, W. Live-Bed local pier scour experiments. J. Hydraul. Eng. ASCE 2006, 132, 635–642. [Google Scholar] [CrossRef]
- Sheppard, D.M. Large Scale and Live Bed Local Pier Scour Experiments (Phase 1); Florida Department of Transportation FDOT: Tallahassee, FL, USA, 2003; Final Report.
- Høgedal, M.; Hald, T. Scour assessment and design for scour for monopile foundations for offshore wind turbines. Cph. Offshore Wind 2005, 1–10. [Google Scholar]
- Üşenti, B. Scour Hole Formation for Lateral Non-Uniform Flow in Non-Cohesive Sediments. Master’s Thesis, Department of Civil Engineering, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- GEO-4D. Barrow Offshore Wind Farm Export cable WoDS Crossing. In Factual Survey Results Report No: P1063-DC-H015; Unit 5; RAC Estate: Faringdon, UK, 2022. [Google Scholar]
- Deltares. Numerical Model for Non-Steady Suspended Transport (in Dutch). In Report R975 Part II; Deltares: Delft, The Netherlands, 1977. [Google Scholar]
- Deltares. Computation of Siltation in Dredged Trenches. In Report R1267 Part V; Deltares: Delft, The Netherlands, 1980. [Google Scholar]
- Kerssens, P.J.M.; Prins, A.; Van Rijn, L.C. Model for suspended sediment transport. J. Hydraul. Div. ASCE 1979, 105, 461–476. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sedimentation of dredged channels by currents and waves. J. Waterw. Port Coast. Ocean. Eng. ASCE 1986, 112, 541–559. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Meijer, K.; Dumont, K.; Fordeyn, J. Practical 2DV modelling of deposition and erosion of sand and mud in dredged Channels due to currents and waves. J. Waterw. Port Coast. Ocean. Eng. 2024, 150, 04024002. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Meijer, K.; Dumont, K.; Fordeyn, J. Simulation of sand and mud transport processes in currents and waves by time-dependent 2DV model. Int. J. Sediment Res. 2024, 40, 1–14. [Google Scholar] [CrossRef]
- Wang, G. PIV-Experiment and CFD Simulation of Flow Around Cylinder. Master’s Thesis, Department of Civil Engineering, University of Texas, Austin, TX, USA, 2015. [Google Scholar]


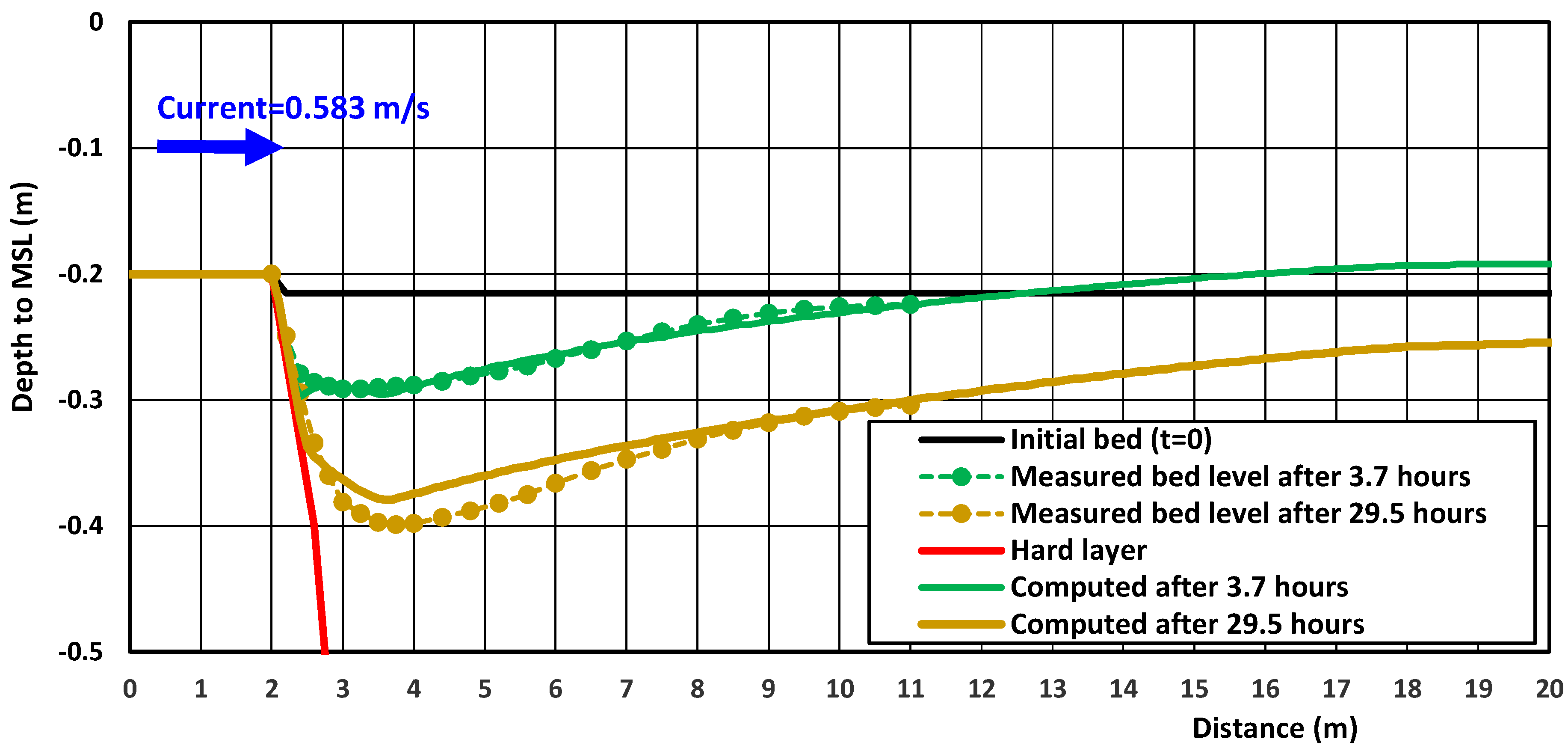
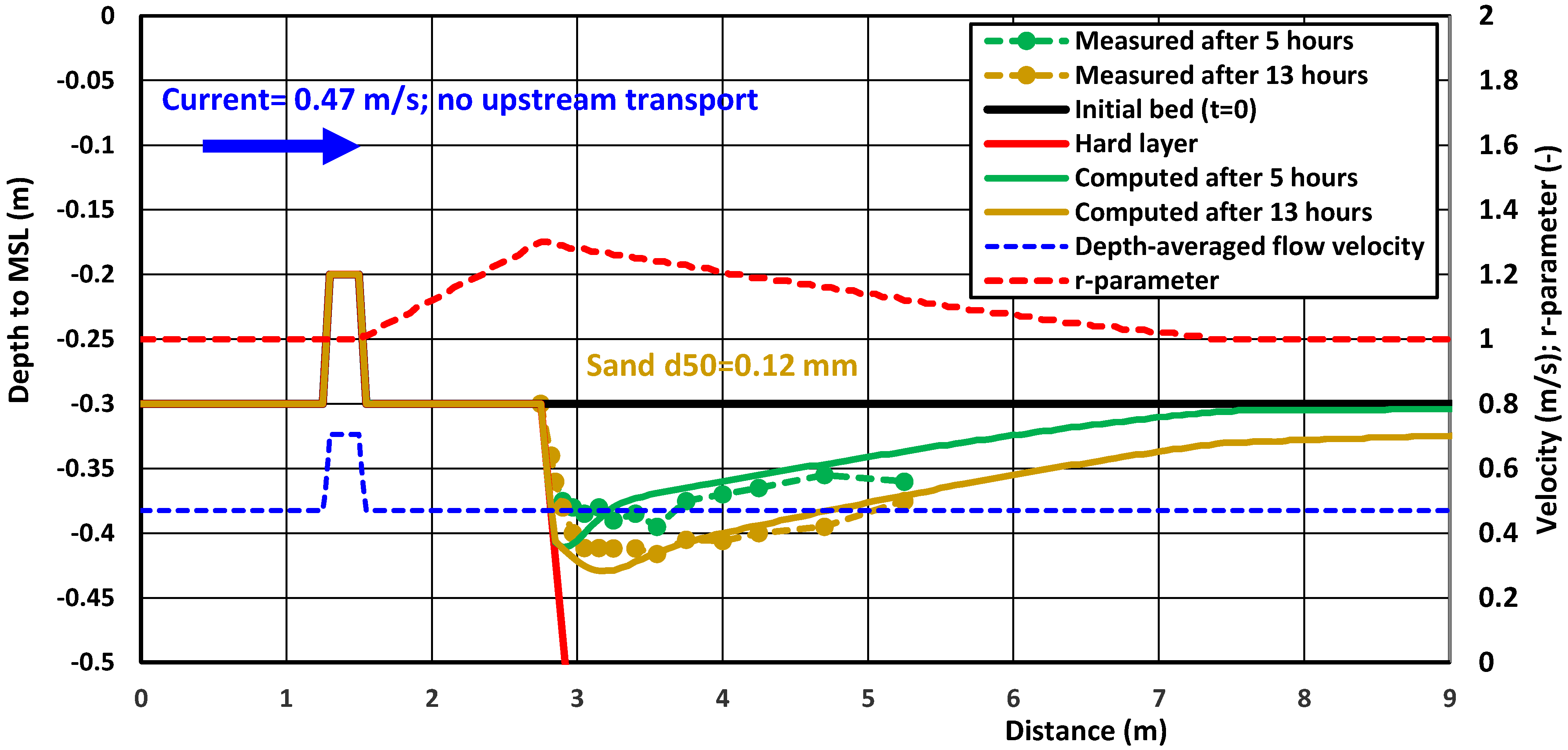
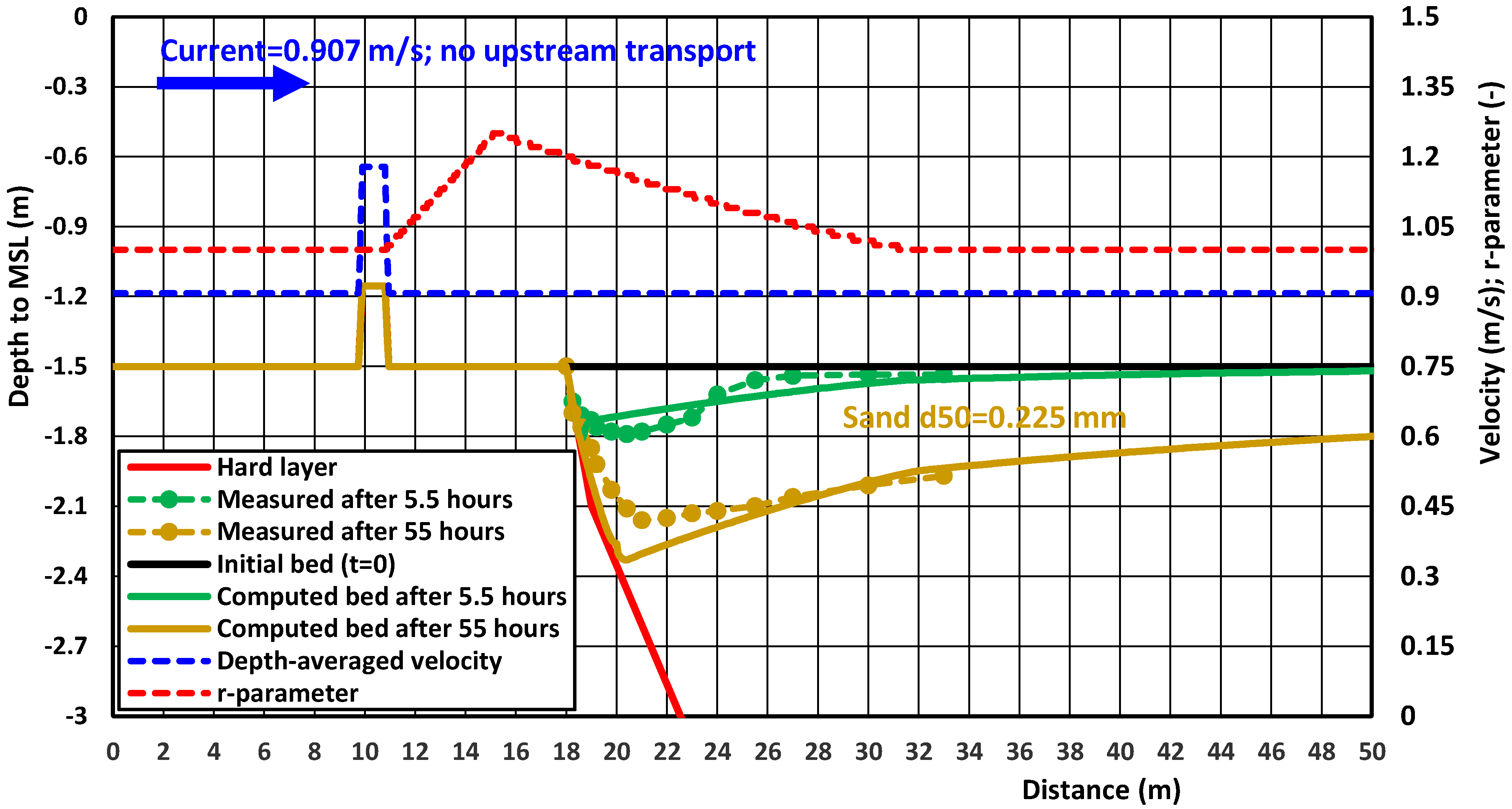
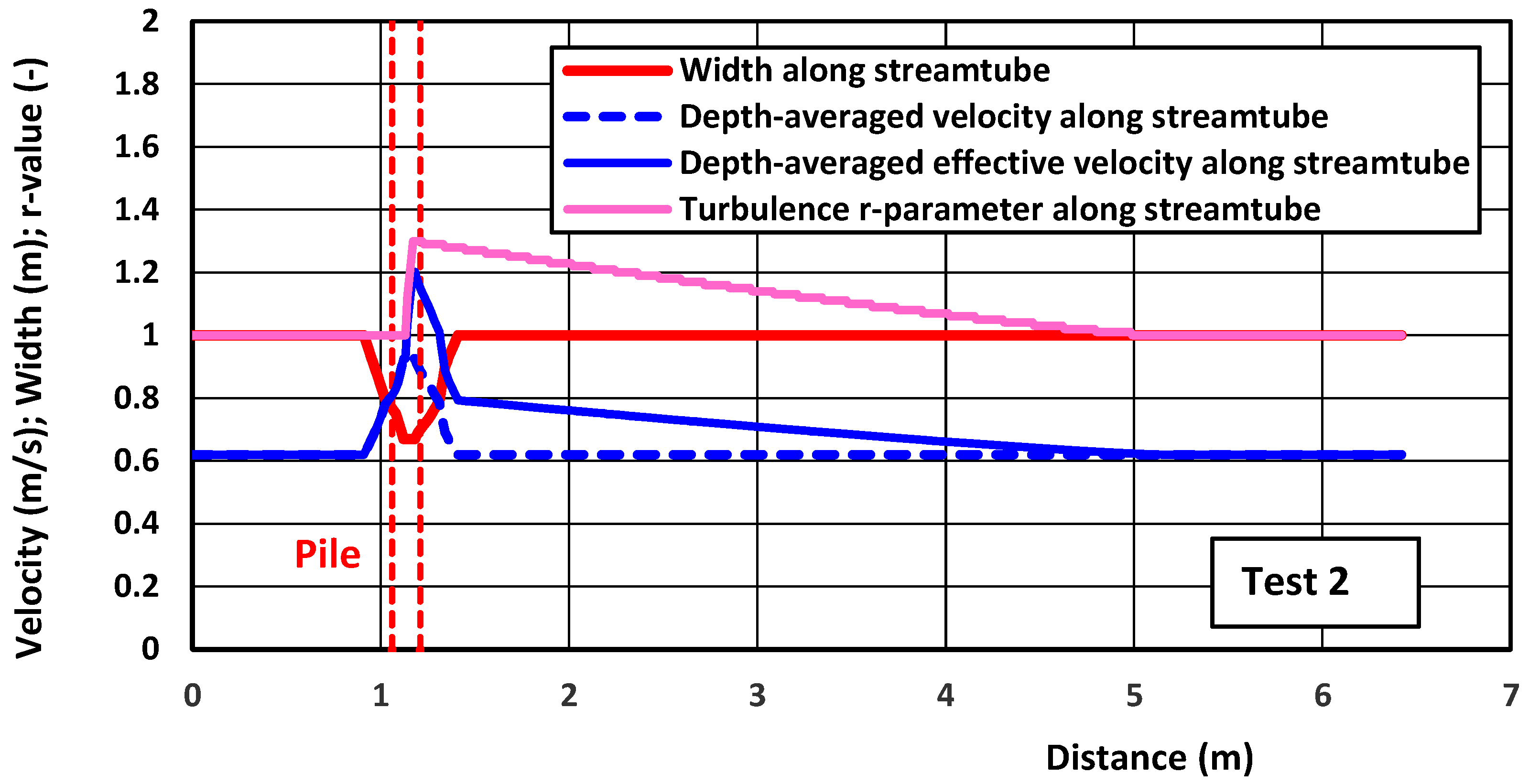
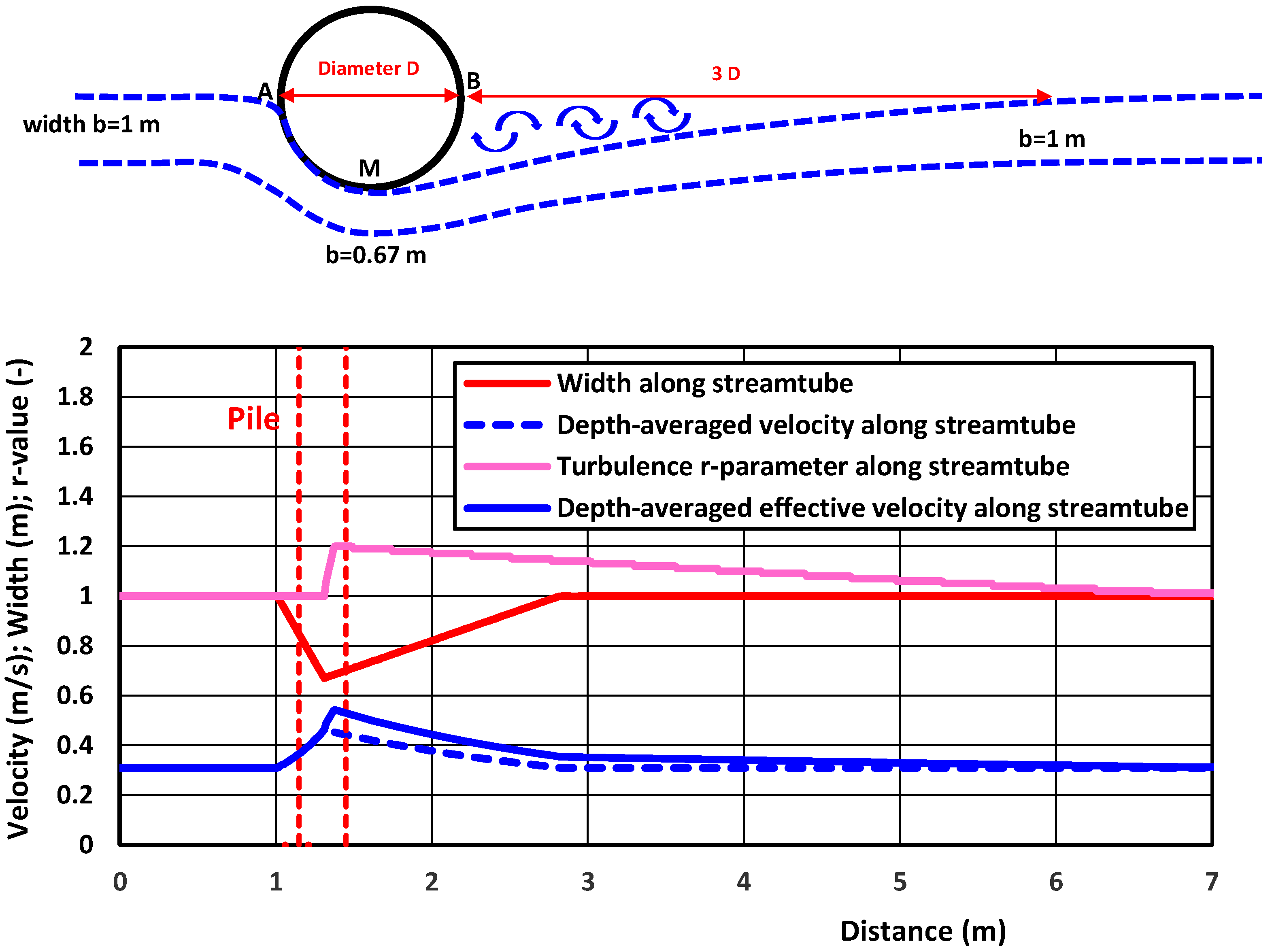
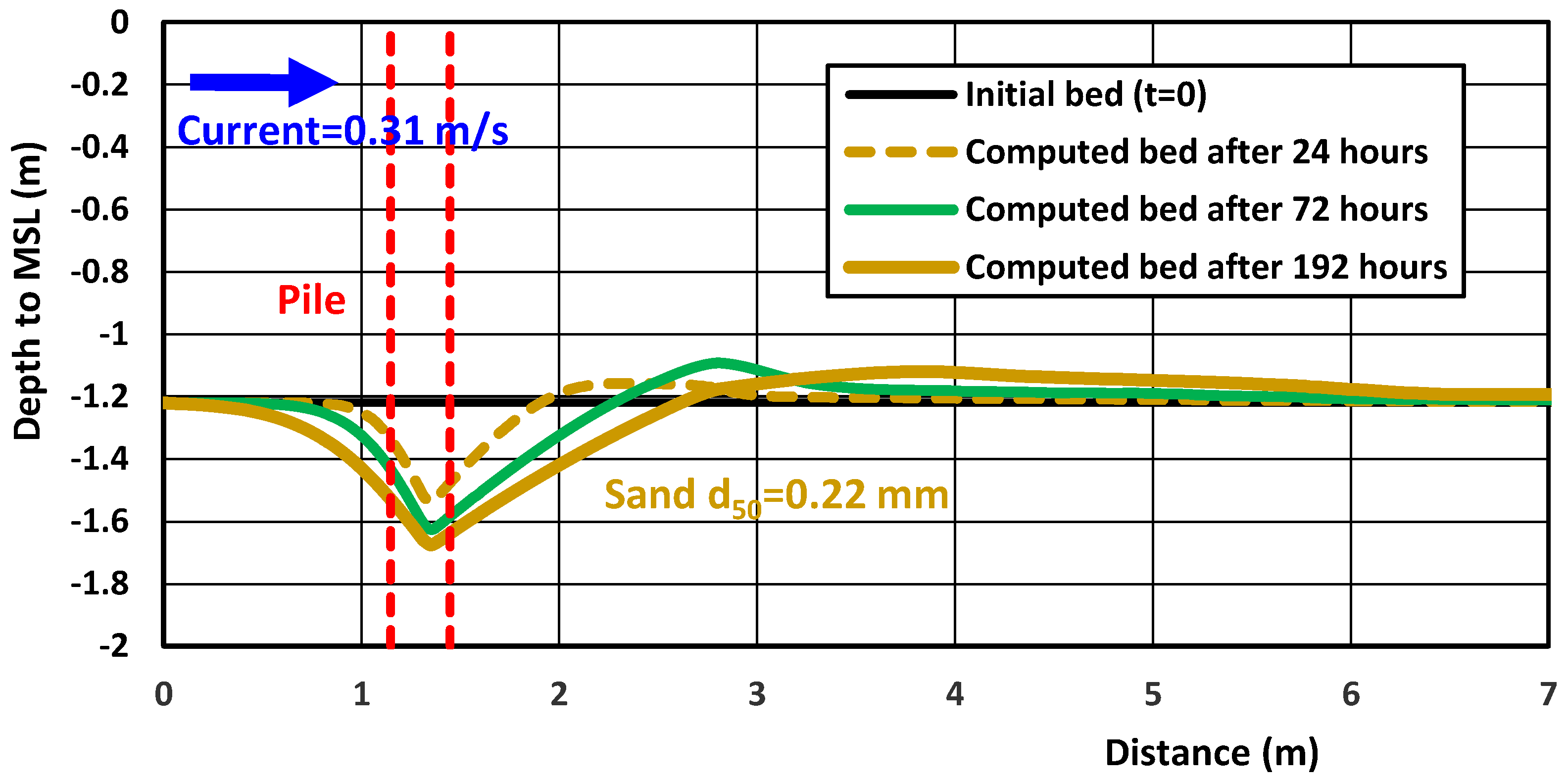
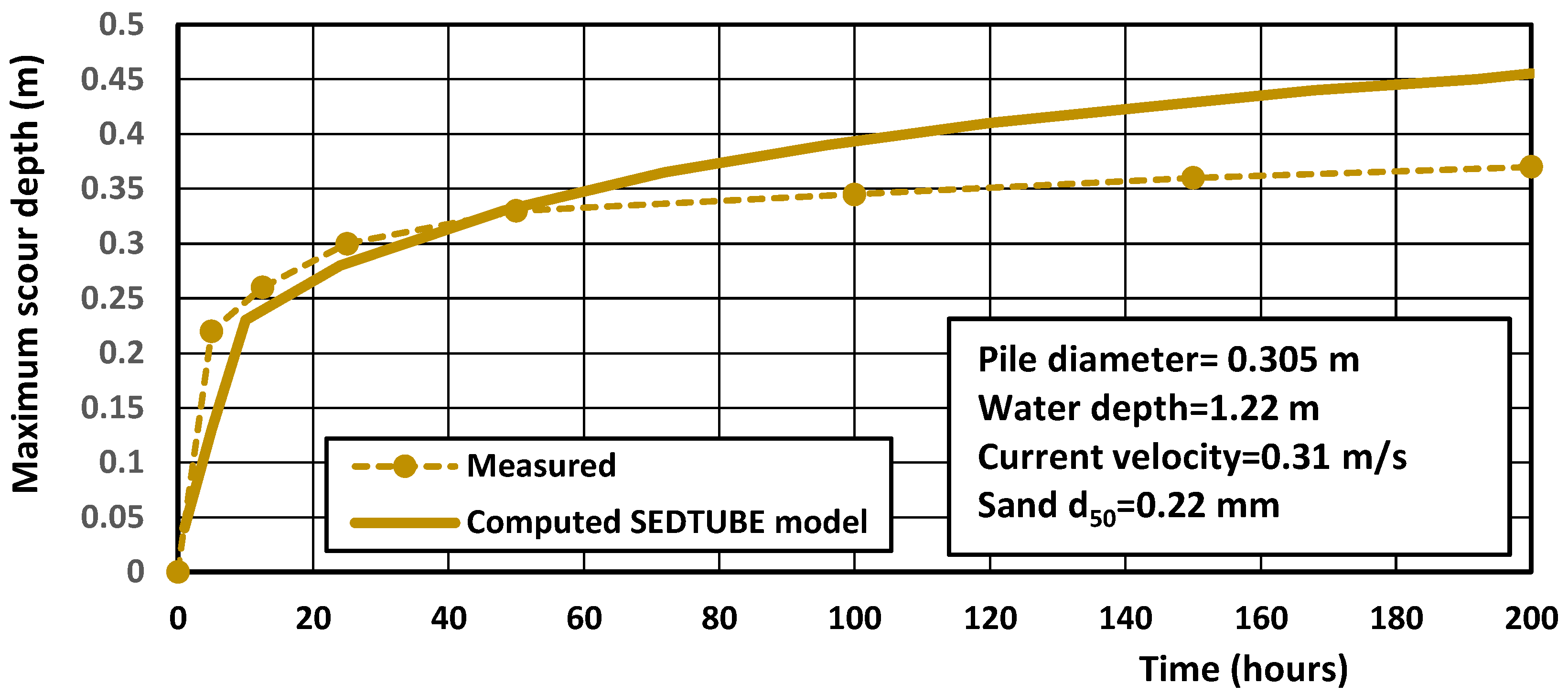
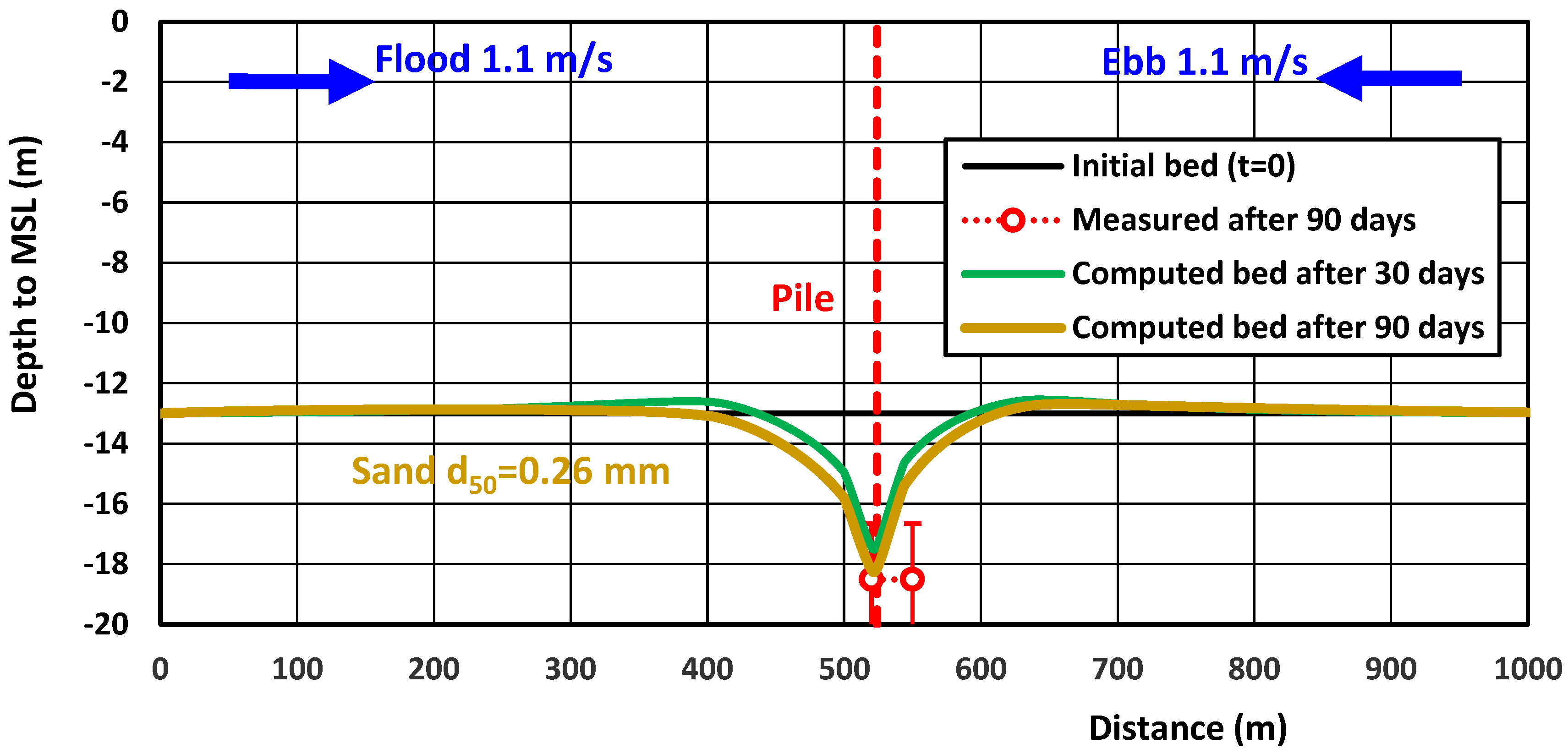


| Parameter | Test C60 |
|---|---|
| Water depth outside to SWL (m) | 0.2 |
| Initial bed (m) | −0.015 m below bed protection |
| Stream tube width (m) | 1 |
| Storm setup (m) | 0 |
| Tidal amplitude (m); tidal period (hours); phase difference (hours) | 0; 0; 0 (no tide) |
| Depth-averaged flow velocity; peak tidal velocity (m/s) | 0.583 |
| Significant wave height (m), period (s), and duration (days) | 0; 0; 0 (no waves) |
| Water temperature (°C) and bed porosity (-) | 15; 0.4 |
| Fluid and sediment density (kg/m3) | 1000; 2650 |
| Bed material d50; d90 (mm) | 0.165; 0.21 |
| Fall velocity (m/s); critical velocity (m/s) | 0.015; computed by model |
| Percentage fines (%) | 0 |
| Bed roughness (m) | 0.01 |
| Calibration factor (scaling) bed load transport γb (-) | 1. (default) |
| Calibration factor (scaling) suspended transport γs (-) | 1. (default) |
| Scaling coefficient effective velocity γe (-) | 1. (default) |
| Coefficients adjustment length turbulence γbh1, γbh2 (-) | 1.6; 2 |
| Coefficient adjustment suspended transport αA (-) | 0.2 |
| Turbulence enhancement coefficient ro (-) | 0.3 |
| Longitudinal coordinate of turbulence source, xr (m) | 2 |
| Sediment transport value at boundaries x = 0, iswr (-) | 0 (no transport at x = 0) |
| Bed smoothing coefficient γsmooth (-) | 0.00001 |
| Grid size (m) and time step (s) | 0.1; 60 |
| File | SEDTUBETESTC60 |
| Parameter | Test S11-12B | Test S20-3 |
|---|---|---|
| Water depth outside to SWL (m) | 0.3 | 1.5 |
| Initial bed (m) | flat bed | flat bed |
| Stream tube width (m) | 1 | 1 |
| Storm setup (m) | 0 | |
| Tidal amplitude (m); tidal period (hours); phase difference (hours) | 0; 0; 0 (no tide) | 0; 0; 0 (no tide) |
| Depth-averaged flow velocity; peak tidal velocity (m/s) | 0.47 | 0.907 |
| Significant wave height (m), period (s), and duration (days) | 0; 0; 0 (no waves) | 0; 0; 0 (no waves) |
| Water temperature (°C) and bed porosity (-) | 15; 0.4 | 15; 0.4 |
| Fluid and sediment density (kg/m3) | 1000; 2650 | 1000; 2650 |
| Bed material d50; d90 (mm) | 0.12; 0.25 | 0.225; 0.5 |
| Fall velocity (m/s) | 0.01 | 0.02 |
| Percentage fines (%) | 0 | 0 |
| Bed roughness (m) | 0.01 | 0.03 |
| Calibration factor (scaling) bed load transport γb (-) | 0.6 (default) | 0.4 (default) |
| Calibration factor (scaling) suspended transport γs (-) | 0.6 (default) | 0.4 (default) |
| Scaling coefficient effective velocity γe (-) | 1. (default) | 1. (default) |
| Coefficients adjustment length turbulence γbh1, γbh2 (-) | 2.5; 1.5 | 2.5; 1.5 |
| Coefficient adjustment suspended transport αA (-) | 0.2 | 0.2 |
| Turbulence enhancement coefficient ro (-) | 0.3 | 0.25 |
| Longitudinal coordinate of turbulence source, xr (m) | 1.5 | 10.8 |
| Height of obstacle at bed, dobst (m) | 0.1 m | 0.35 m |
| Sediment transport value at boundaries x = 0, iswr (-) | 0 | 0 |
| Bed smoothing γsmooth (-), grid size (m), timestep (s) | 0.01; 0.1; 60 | 0.01; 0.1; 60 |
| File | SEDTUBEBERM11 | SEDTUBEBERM20 |
| Test | Current (m/s) | Measured Scour Depth (m) | Test Period (hours) | Computed Scour Depth (m) | Bed and Suspended Load Coefficients (-) | Turbulence Parameter Settings | Adjustment Suspended Load αA (-) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| ro (-) | γbh1 (-) | γbh2 (-) | xr (m) | |||||||
| 1 | 0.17 | 0.13 | 29 | 0.1 | 1 (default) | 0.3 | 0.1 | 1 | 1.12 | 0.2 |
| 2 | 0.62 | 0.22 | 5.1 | 0.24 | 1 (default) | 0.3 | 0.1 | 1 | 1.12 | 0.2 |
| 8 | 0.69 | 0.23 | 24.5 | 0.25 | 1 (default) | 0.35 | 0.1 | 1 | 1.12 | 0.2 |
| 3 | 0.88 | 0.24 | 7.4 | 0.26 | 1 (default) | 0.4 | 0.1 | 1 | 1.12 | 0.2 |
| 4 | 1.10 | 0.25 | 7.8 | 0.27 | 1 (default) | 0.45 | 0.1 | 1 | 1.12 | 0.2 |
| 5A | 1.26 | 0.27 | 4.3 | 0.28 | 1 (default) | 0.5 | 0.1 | 1 | 1.12 | 0.2 |
| 5B | 1.43 | 0.27 | 1.6 | 0.29 | 1 (default) | 0.6 | 0.1 | 1 | 1.12 | 0.2 |
| 6 | 1.64 | 0.3 | 1.7 | 0.31 | 1 (default) | 0.7 | 0.1 | 1 | 1.12 | 0.2 |
| Test | Current (m/s) | Measured Scour Depth (m) | Computed Scour Depth (m) | Bed and Suspended Load Coefficients (-) | Turbulence Parameter Settings | Adjustment Suspended Load αA (-) | |||
|---|---|---|---|---|---|---|---|---|---|
| ro (-) | γbh1 (-) | γbh2 (-) | xr (m) | ||||||
| 12 | 0.31 | 0.37 after 200 h | 0.45 after 200 h | 0.7 | 0.2 | 0.1 | 1 | 1.3 | 0.2 |
| Cases | Type of Upstream Structure | Type of Flow | Water Depth; Flow Velocity h (m) u (m/s) | Sediment Bed d50 (mm) pfines (%) | Calibration Coefficients Bed Load and Suspended Load γb; γs (-) | Turbulence Parameters | |||
|---|---|---|---|---|---|---|---|---|---|
| ro (-) | γbh1 (-) | γbh2 (-) | |||||||
| L | Scour downstream of bed protection Test C60 (Hoffmans) [15] | bed protection | UDF | 0.2; 0.583 | 0.165; 0 | 1 | - | - | - |
| L | Scour downstream of berm Test S11-12B (Deltares) [31] | berm | UDF | 0.3; 0.47 | 0.12; 0 | 0.6 | 0.3 | 2.5 | 1.5 |
| L | Scour downstream of berm Test S20-3 (Deltares) [31] | berm | UDF | 1.5; 0.907 | 0.225; 0 | 0.4 | 0.25 | 2.5 | 1.5 |
| L | Scour around pile Test 1–8 (Sheppard–Miller) [32] | pile | UDF | 0.42; 0.17/1.64 | 0.27; 0 | 1 | 0.3–0.7 | 0.1 | 1 |
| L | Scour around pile (Sheppard) [33] | pile | UDF | 1.22; 0.31 | 0.22; 0 | 0.7 | 0.2 | 0.1 | 1 |
| F | Scour around pile, Scroby Sands (UK) | pile | TF | 13; 1.1 | 0.26; 5 | 1.0 | 0.35 | 0.1 | 1.5 |
| F | Scour downstream of culvert, Eastern Scheldt (NL) | culvert | UDF | 4; 1.25/1.5 | 0.13; 0 | 1.5 | 0.3 | 1 | 1 |
| F | Scour around berm Morceambe Bay (UK) | Berm | TF | 6 to 14; 0.6/1.4 | 0.15; 30 | 1.0 | 0.5 | 0.5 | 1–2 |
| F | Sedimentation trench Western Scheldt (NL) | none | TF | 8.25; 0.8/1.05 | 0.18; 0 | 1.2 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Rijn, L.C.; Meijer, K.L. Scour Near Offshore Structures—Part 2: Practical Scour Model. J. Mar. Sci. Eng. 2025, 13, 1583. https://doi.org/10.3390/jmse13081583
van Rijn LC, Meijer KL. Scour Near Offshore Structures—Part 2: Practical Scour Model. Journal of Marine Science and Engineering. 2025; 13(8):1583. https://doi.org/10.3390/jmse13081583
Chicago/Turabian Stylevan Rijn, L. C., and K. L. Meijer. 2025. "Scour Near Offshore Structures—Part 2: Practical Scour Model" Journal of Marine Science and Engineering 13, no. 8: 1583. https://doi.org/10.3390/jmse13081583
APA Stylevan Rijn, L. C., & Meijer, K. L. (2025). Scour Near Offshore Structures—Part 2: Practical Scour Model. Journal of Marine Science and Engineering, 13(8), 1583. https://doi.org/10.3390/jmse13081583





