Abstract
Efficient cleaning of floating waste using an intelligent unmanned surface vehicle is an important development trend in inland water governance. Path planning is the core of the decision-making module for unmanned surface vehicle waste cleaning and is key to achieving autonomous operation of the unmanned surface vehicle. However, due to the complexity and dynamic changes of the water surface environment, unmanned surface vehicle path planning methods for floating waste face challenges such as small size, uncertainty, and uneven distribution of floating waste. In response to the above issues, this article studies the problem of insufficient integration and low efficiency between existing path planning algorithms and target-perception modules, and designs an efficient overall path planning method for floating-waste cleaning by an unmanned surface vehicle. This method transforms the path planning problem of floating-waste cleaning unmanned surface vehicle into a Traveling Salesman Problem by setting global patrol points and tracking local targets, and proposes an improved ant colony algorithm, IACO, to solve the Traveling Salesman Problem. This article is based on the TSPLIB dataset and practical applications for experiments. The experimental results show that the proposed method has average optimal path lengths of 75.930 m, 446.555 m, and 703.759 m on the Ulysses22, eil51, and st70 datasets, respectively, which are reduced by 0.355 m, 4.108 m, and 13.575 m compared to the benchmark.
1. Introduction
Floating-waste pollution in aquatic environments is a global issue that poses a significant threat to ecological balance, aquatic life, and the development of tourism [1]. With the rapid advancement of sensor technologies and artificial intelligence, autopilot systems for unmanned surface vehicles (USVs) have emerged as a key research focus. The perception module utilizes various sensors, including cameras, LiDAR, radar, ultrasonic sensors, etc., to perceive and interpret the surrounding environment, thereby providing accurate information for the decision-making module. The decision-making module processes the data received from the perception module and performs high-level planning tasks such as mission assignment and path planning. The control module then translates these planning decisions into executable control actions, such as steering and propulsion. In this context, target perception refers to the USV’s ability to recognize, detect, and understand relevant objects or targets in its surroundings. Path planning, on the other hand, involves determining an optimal navigation route based on task requirements and environmental perception, making it a core function of the decision-making system. Therefore, the development of efficient and accurate path planning algorithms that can tightly integrate with real-time target detection systems is of paramount importance for enabling autonomous and effective USV operations in dynamic aquatic environments.
USV path planning involves computing and determining an optimal route from a starting point to a target location, based on environmental data acquired through onboard sensors and the mission requirements of the USV. Path planning can generally be divided into two categories, namely, global path planning and local path planning. An optimal path is typically one that minimizes travel time while avoiding collisions with obstacles. For floating-waste cleaning missions, effective USV path planning often requires a combination of both global and local strategies. Global path planning is carried out after acquiring map information and aims to cover the entire water area efficiently. In contrast, local path planning operates in real time by continuously sensing the surrounding environment—particularly the locations of floating waste—while the USV navigates along the global path.
Traditional path planning algorithms include Dijkstra’s algorithm [2], the A* algorithm [3], the D* Lite algorithm [4], and the artificial potential field method [5], among others. These algorithms typically perform path planning by searching for optimal routes on graphs or by sampling the environment to generate waypoints. Numerous researchers, both domestically and internationally, have refined and extended these classical algorithms to support path planning for the USV. For instance, Guan et al. [6] proposed a dynamic path planning algorithm for the USV that combines the global optimality of the A* algorithm with the real-time responsiveness of the dynamic window approach. This method dynamically generates global paths and ensures smooth navigation toward the target. To further enhance planning speed and reduce navigation time, Zhang et al. [7] introduced an adaptive hybrid dynamic step-size and target-attraction RRT (AHDSTAF-RRT) algorithm. This approach improves obstacle avoidance and search efficiency through a dynamic step-size mechanism, incorporates target-attraction to guide path growth, and automatically switches between narrow and open-area modes, depending on environmental features. It also applies path pruning and interpolation to produce smoother trajectories. However, these classical path planning algorithms commonly suffer from several limitations, such as high computational complexity, susceptibility to becoming stuck in local optima, poor adaptability to dynamic environments, and insufficient path smoothness. More critically, they typically operate independently from the perception module, lacking tight, real-time integration with object detection results. This makes it difficult to effectively handle the challenges posed by dynamically changing positions and uneven distribution of floating debris.
Biologically inspired optimization algorithms, such as the particle swarm optimization (PSO) algorithm [8], artificial fish swarm algorithm [9], genetic algorithm (GA) [10], and ant colony optimization (ACO) algorithm [11], exhibit strong parallel computing capabilities, enhanced global optimization performance, better robustness, and improved path smoothness. These advantages enable them to effectively address the limitations of traditional path planning methods. Cai et al. [12] proposed an ant colony algorithm (FA-ACA) based on the firefly algorithm optimization. The method optimizes the core parameters of the ACO algorithm (namely, pheromone heuristic factor , expectation heuristic factor , and volatility coefficient ) through the adaptive search mechanism of the firefly population, and dynamically adjusts the parameter combinations using the brightness comparison mechanism of fireflies to address the problem that the traditional ACO algorithm is sensitive to the initial parameters. Secondly, the elite strategy is introduced to enhance the pheromone update intensity of the optimal path, and the step factor of the firefly algorithm is dynamically optimized using the parameter adaptive adjustment formula to avoid the local oscillation phenomenon. Wu et al. [13] proposed an autonomous planning method for USV navigation paths based on a hybrid ant colony algorithm. The algorithm addresses the problems of poor initial search efficiency in the ant colony algorithm and combines it with the particle swarm algorithm to improve search efficiency, thereby reducing the time required for path planning.
Among these algorithms, the firefly algorithm is easy to implement and possesses strong global search capabilities; however, it tends to fall into local optima, exhibits slower convergence rates, and is highly sensitive to parameter settings. The particle swarm optimization (PSO) algorithm is simpler to implement and requires less computational memory, but it often suffers from loss of population diversity and premature convergence to local optima. The genetic algorithm (GA) is flexible and can be effectively combined with other algorithms, demonstrating strong global search ability; however, it generally requires longer computation times and exhibits weaker local search performance. The ant colony optimization (ACO) algorithm is a heuristic optimization method that simulates the foraging behavior of ants. First, ACO exhibits inherent parallelism, as multiple artificial ants simultaneously explore the solution space during execution. Second, ACO employs a hybrid search strategy, combining greedy heuristics and pheromone-guided exploration, striking a balance between global and local search. This enables the algorithm to converge rapidly toward local optima while retaining the capability to escape local traps and seek global optima. Despite its high search efficiency and strong global optimization ability, ACO suffers from slow convergence in its early stages and may experience chaotic behavior. Furthermore, all the aforementioned algorithms share common limitations, including insufficient integration between path planning and perception modules, a lack of coherence, and limited adaptability to dynamic environments.
Based on the above discussion, although existing path planning methods have improved in optimization capability and computational speed, they still face significant challenges when addressing the actual needs of unmanned surface vehicles for cleaning floating garbage. Our research can effectively address these limitations; first, existing algorithms lack close integration with perception modules and coherence, making it difficult to adapt to environmental changes; second, the algorithms themselves have inherent defects such as slow convergence and susceptibility to local optima. To address these limitations, this paper proposes an improved ant colony algorithm and designs an integrated path planning method for USV. The main contributions of this paper are as follows:
- A complete path planning framework is designed for the floating-waste-cleaning USV, incorporating both global patrol path planning and local cleaning path planning. The overall path planning problem is transformed into a Traveling Salesman Problem (TSP) by setting global patrol points and using floating-waste location data obtained from the perception module.
- An improved ant colony optimization (ACO) algorithm is proposed, integrating genetic algorithm (GA) strategies with ACO to address floating-waste detection and navigation on the water surface. This hybrid approach leverages the strengths of both algorithms, improving convergence speed and reducing the risk of falling into local optima.
- An adaptive pheromone evaporation coefficient mechanism is designed to dynamically adjust the evaporation rate, thereby increasing the robustness of the algorithm and enhancing its global search capability.
The rest of this paper is organized as follows. In Section 2, we introduce the improved ant colony algorithm for floating-waste-cleaning USV, detailing the system architecture and TSP modeling approach. In Section 3, we present comprehensive experimental validations, including algorithm parameter analysis, ablation studies on TSPLIB datasets, benchmark comparisons with other heuristic algorithms, and real-world application evaluations for both global patrol and local cleanup scenarios. In Section 4, we provide a systematic summary of the entire work and an outlook for future work.
2. Path Planning Method Based on Improved Ant Colony Algorithm
In this paper, a path planning method for the floating-waste-cleaning USV is designed in conjunction with the perception module. The overall system architecture is illustrated in Figure 1. The proposed method mainly consists of two core components, namely, global patrol path planning and local cleaning path planning. First, the USV performs global patrol path planning using a full-coverage strategy [14,15]. By defining global patrol points, the problem is modeled as a Traveling Salesman Problem (TSP) [16], and an improved ant colony optimization (ACO) algorithm is applied to determine the optimal global patrol route. Second, as the USV follows the globally planned path, it continuously detects and tracks floating-waste targets via the perception module. Once the locations of all detected targets are obtained, a second TSP is formulated for local cleaning path planning, and the improved ACO algorithm is again applied to compute an efficient local route for waste collection. By combining global and local path planning, the proposed approach enables the USV to efficiently complete its cleaning tasks, maximize resource utilization, and achieve reliable and effective performance in dynamic water environments.
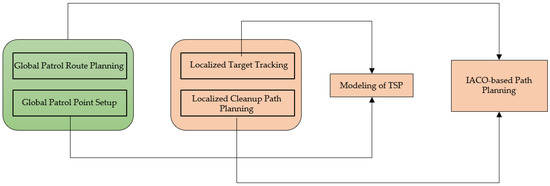
Figure 1.
Architecture of path planning for a floating-waste-cleaning USV.
The Traveling Salesman Problem (TSP) is classified as an NP-hard problem, meaning that no known algorithm can solve it optimally in polynomial time. For large-scale instances, heuristic algorithms are typically employed to obtain approximate optimal solutions. In this paper, an improved ant colony optimization (IACO) algorithm is proposed. The IACO enhances the traditional ant colony optimization (ACO) algorithm by integrating it with a genetic algorithm (GA), leveraging the complementary strengths of both approaches.
2.1. Modeling the Traveler Problem
The Traveling Salesman Problem (TSP) is a classic combinatorial optimization problem, where the objective is to determine the shortest possible route that visits each given city exactly once and returns to the starting point.
In this paper, both global patrol path planning and local cleanup path planning are modeled as instances of the Traveling Salesman Problem (TSP) within a two-dimensional water surface coordinate system, based on the setting of global patrol points and local target tracking. By utilizing the coordinate positions of the global patrol points and local target points, and calculating the distances between each pair of points, the TSP for both global and local planning can be formulated as the task of finding the shortest possible route that visits all global patrol or local target points exactly once and returns to the starting point. The mathematical formulation of the TSP is given as follows:
Equation (1) is the objective function of the mathematical model, and is the function to solve the shortest path, where n denotes the total number of patrol points or target points, and denotes the distance between the patrol point or target point and patrol point or target point . is the access variable, which takes the value of 0 or 1, and denotes whether it goes from point to point or not. Equation (2) shows the constraints, where the first constraint indicates that each point must be visited and can be visited only once. The last two constraints are used to eliminate sub-loops, and is an auxiliary variable.
2.1.1. Global Patrol Point Setup
The latitude and longitude coordinates are obtained by setting the cruising point on the high-definition satellite map, as shown in Figure 2. By counting the real data labels of Texas Instruments’ 77 GHz millimeter-wave radar, its maximum sensing distance is about 14.7 m. According to the conversion relationship between latitude and longitude and distance, in the case of equal latitude, the distance difference is about 10 m for every 0.0001 degree of longitude; in the case of equal longitude, the distance difference is about 11 m for every 0.0001 degree of latitude. In this paper, a grid line with a longitude interval of 0.00015 degrees (distance interval of about 15 m) and a latitude interval of 0.00015 degrees (distance interval of about 16.5 m) is set up to define global patrol points for the working waters of the floating-waste-cleaning USV. Taking a lake on campus as an example, the global patrol point is set as the red point in Figure 3, and the specific settings are shown in Figure 3. The grid lines are drawn according to the latitude and longitude intervals, and the grid points falling into the lake are set as global patrol points. The corresponding latitude and longitude coordinates are obtained, which can be converted to the world coordinate system to find the distance between each patrol point. Therefore, the global path planning problem of floating-waste-cleaning USV can be modeled as the TSP problem of global patrol points, i.e., solving the shortest path that visits all patrol points (all patrol points are visited once).
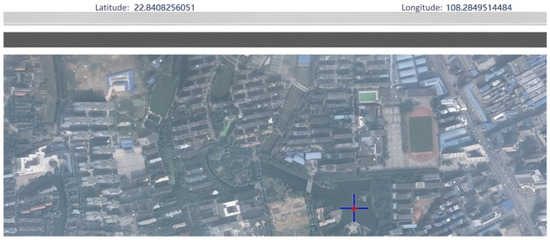
Figure 2.
Satellite map demonstration.

Figure 3.
Global patrol point.
2.1.2. Local Target Perception
As the floating-waste-cleaning USV follows the planned global patrol route, it continuously detects floating-waste targets through its perception module. In this paper, a sensor fusion algorithm combining radar and vision is adopted to achieve accurate detection and tracking of floating waste on the water surface. Specifically, the YOLO-Float target detection algorithm [17] is used to obtain the orientation and distance information of the detected targets, enabling effective real-time perception.
YOLO-Float is an improved version of the YOLOv5 target detection algorithm, specifically designed for detecting floating waste on the water surface. It enhances small target feature extraction through the introduction of the low-level representation enhancement module (LREM), which reduces the loss of small object information during the downsampling process in the backbone network. In addition, the attention fusion module (AFM) is employed to fuse feature maps of different resolutions, thereby enhancing the model’s adaptability to complex backgrounds and improving detection accuracy. YOLO-Float is tailored for small object detection and background noise suppression, making it more effective in dynamic water surface environments. The overall framework of YOLO-Float is illustrated in Figure 4.
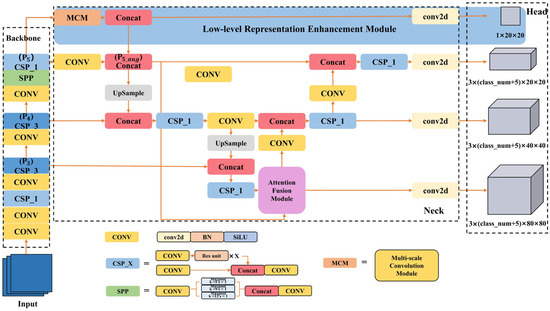
Figure 4.
The architecture of the YOLO-Float.
The sensing algorithm based on the fusion of radar and vision sensors achieves multi-dimensional target perception by leveraging the complementary strengths of both sensors. The vision sensor provides high-resolution color and texture information for accurate target classification, while the radar offers three-dimensional spatial data, such as target orientation, distance, and velocity, through point cloud measurements. By employing multi-sensor data fusion techniques, the algorithm integrates the fine-grained perceptual capabilities of the vision sensor with the radar’s strong anti-interference and environmental adaptability. This fusion not only compensates for the limitations of individual sensors but also significantly enhances the overall robustness and accuracy of the perception system. The detailed algorithmic flowchart is illustrated in Figure 5.
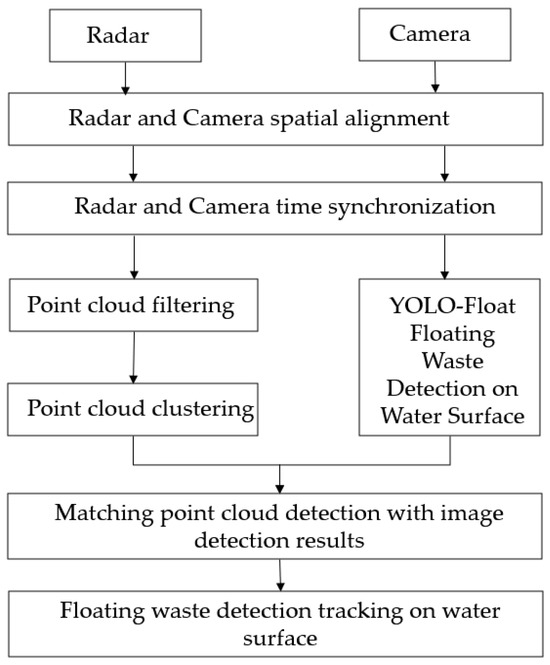
Figure 5.
Fusion sensing methodology flow.
The sensing module continuously tracks detected targets and assigns each a unique identification (ID). It is stipulated that once the floating-waste-cleaning USV detects targets, it continues moving in the current direction until the positional information of all tracked targets is acquired. Using a video sequence from the FloW-RI [18] dataset as an example, the complete process of local target tracking is illustrated in Figure 6. Figure 6a presents the detection result of the radar and camera fusion algorithm, and the detected target contains both point cloud position information and image detection frames. Figure 6b presents the radar and camera detection tracking results, which contain the image detection frame and ID identification. Figure 6c presents the localized target tracking result, which updates the position information of the tracked target according to the radar and camera fusion algorithm detection result. The red circular dots in the figure represent patrol route points, indicating the locations where the USV first detected floating waste. The green square dots indicate the target points with newly acquired position information, obtained by updating the position information after the fusion algorithm detects a new waste target and matches it to the tracking target ID. The gray square point indicates the target point for which position information has been acquired. The blue point indicates the current location of the USV. While the USV continues to travel in its current direction, the fusion algorithm detects targets with IDs 2, 1, 4, 7, 6, and 5, and obtains their corresponding position information. At this time, the position information of all tracking targets is obtained, and the distance between each target point can be obtained according to the position information of each target point, after which the local target tracking is finished. In this paper, the local path planning problem of the floating-waste-cleaning USV is modeled as a TSP problem with local target points, aiming to find the shortest path that visits each target exactly once.
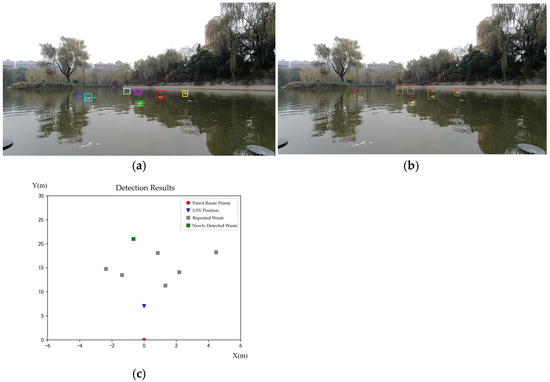
Figure 6.
Local target tracking. (a) Fusion algorithm detection results. (b) Detection tracking results. (c) Local target tracking results.
2.2. Improved Ant Colony Algorithm IACO
Ant colonies coordinate their actions by releasing and sensing pheromones during their food search process. Specifically, ants deposit a chemical substance called pheromone along the paths they traverse to locate food sources. When choosing a path, ants tend to prefer those with higher pheromone concentrations, enabling the colony to find food more quickly and efficiently. Similarly, the ant colony (ACO) algorithm simulates this behavior by controlling the probability of ants selecting a particular path based on pheromone intensity, which is mathematically represented by the following formula:
Among them, denotes the probability that ant chooses to move from path point to path point at time . This probability depends on two variables, namely, the pheromone concentration and the heuristic function . Specifically, represents the pheromone intensity on the path from point to point at time , while encodes prior knowledge, defined as the inverse of the distance between points and . Parameters and represent the relative influence of the pheromone concentration and heuristic function, respectively, and are used to balance their contributions. Ant maintains a tabu list, denoted as , which contains all the path points it has already visited. Once all points have been visited, the ant completes a tour. After all ants complete their respective tours, the pheromone concentration on each path is updated according to the following equation:
where is the pheromone volatilization coefficient, taking the value range of (0, 1). is the pheromone increment, which indicates the pheromone increment of all ants on path in this iteration, and the formula of is expressed as follows:
where is a constant, denotes the total length of the path traveled by ant in this iteration; it can be seen that when the total length of the path traveled by the ants is shorter, the pheromone increment is larger, the pheromone concentration of the path becomes larger, the probability of the subsequent ants choosing the increases, the number of ants choosing the path increases, and the increase in the number of ants also increases the pheromone concentration of the shortest path. It can be seen that the ant colony algorithm utilizes the positive feedback mechanism to help the ant colony find the optimal solution.
This paper proposes an improved algorithm that integrates crossover and mutation operations from genetic algorithms into the basic ant colony optimization algorithm. This integration enhances the global search capability of the ant colony algorithm, preventing premature convergence to local optima. Additionally, new pheromone update terms are introduced to accelerate the convergence speed of the algorithm.
In each iteration, the specific operation involves identifying the child ants that have traversed the shortest total paths within the current cycle. The paths taken by these ants represent the better solutions of that iteration. Crossover and mutation operations are then applied to these ants to reorganize and generate new offspring. Through crossover, the offspring inherit the superior traits of the parent ants, which accelerates the convergence process. Meanwhile, mutation introduces novel genetic information, enhancing randomness and helping the algorithm escape local optima. For the crossover operation, two parent ants are randomly paired from the selected ants. Two crossover points are then randomly determined, and the segments between these points are exchanged between the paired parents. The resulting offspring are subsequently completed to form new ants. Regarding mutation, this paper employs an inversion mutation strategy. Two mutation points are randomly selected, and the path segment between these points in each offspring ant is reversed, producing mutated ants. The formula for updating the pheromone information in the ant colony optimization algorithm after integration with the genetic algorithm is as follows:
where denotes the pheromone increment of newborn child ants on path in this iteration. Compared with the original pheromone update formula, the new term can both increase the pheromone concentration on the excellent paths, which makes the algorithm converge, and broaden the exploration space of the ant colony, which increases the stochasticity and global search ability. The specific improved ant colony algorithm IACO process is shown in Figure 7:
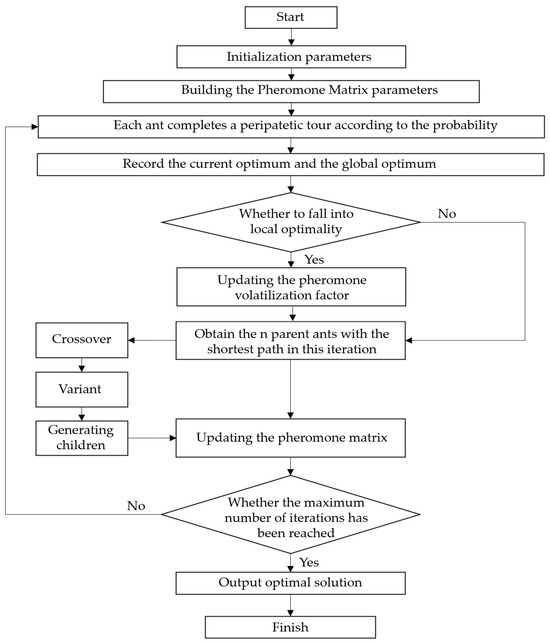
Figure 7.
Improved ant colony algorithm IACO flowchart.
2.3. Improvement of Pheromone Volatilization Coefficients
The pheromone volatilization coefficient in the ant colony optimization (ACO) algorithm controls the rate at which pheromone evaporates. A small volatilization coefficient indicates that pheromone concentrations accumulated on previously explored paths remain high, increasing the likelihood of those paths being selected again and, thus, accelerating the algorithm’s convergence. Conversely, a large volatilization coefficient results in greater pheromone evaporation on previously traversed paths, reducing the probability of reselecting these paths and thereby enhancing the randomness and global search capability of the algorithm. It is evident that the pheromone volatilization coefficient plays a critical role in the algorithm’s performance. However, the basic ant colony algorithm typically employs a fixed volatilization coefficient, which may cause the algorithm to become trapped in local optima and impair its overall effectiveness. To address this limitation, this paper proposes an adaptive pheromone volatilization coefficient that dynamically adjusts the evaporation rate, thereby improving the robustness and global search ability of the algorithm. The formula for calculating the adaptive pheromone volatilization coefficient is as follows:
Based on the recommendations in Ref. [19] and the convergence process of Bayesian parameter optimization [20], this paper adopts this setting and verifies it in the parameter selection section below, where is the value of the pheromone volatilization coefficient at the initial moment, which is set to 0.1 in this paper; is the adjustment factor, which is set to 0.4 in this paper; is the current iteration number, and is the total iteration number.
3. Experimental Results and Analysis
This paper experimentally verifies the effectiveness of the improved ant colony (IACO) algorithm. First, ablation experiments of the proposed IACO are performed on ulysses22, eil51, and st70 datasets from the publicly available Traveling Salesman Problem Library (TSPLIB) [21] to validate the contribution of each improvement module. Second, comparative experiments between the IACO and other heuristic algorithms are conducted on the same datasets to demonstrate the superiority of IACO. Finally, the performance of the IACO is evaluated through application case studies involving global patrol and local cleanup tasks, providing an objective and comprehensive assessment of its effectiveness.
3.1. Algorithm Parameter Selection
The selection of algorithm parameters significantly influences the performance of the proposed method. Parameters and represent the weighting factors for pheromone intensity and heuristic information, respectively. When and are excessively large, the search process overly depends on one type of information, which may cause the algorithm to become trapped in local optima. Conversely, values that are too small can result in slow convergence.
Parameter denotes the number of ants selected in each iteration with the shortest total paths for crossover and mutation operations. A large value of increases computational complexity and may lead to premature convergence or excessive randomness, thereby reducing the algorithm’s stability. On the other hand, a small limits the global search capability, making the algorithm prone to local optima and slow convergence. Therefore, should be carefully adjusted according to the problem scale, computational resources, and empirical tuning.
Let denote the initial value of the pheromone volatilization coefficient, and is the regulating factor. If the volatilization coefficient is set too high, the search efficiency decreases due to excessive evaporation of pheromones. Conversely, if it is too low, solution diversity may be reduced, potentially hindering convergence to the optimal solution.
The selection of algorithm parameters critically influences solution quality and convergence efficiency. Traditional empirical tuning often yields suboptimal configurations; therefore, IACO systematically determines the ideal hyperparameters on the st70 dataset using Bayesian optimization and Gaussian process expectation improvement (GP-EI). This data-driven approach balances exploration and exploitation of the parameter space while minimizing evaluation costs. The specific parameter convergence process is shown in Figure 8.
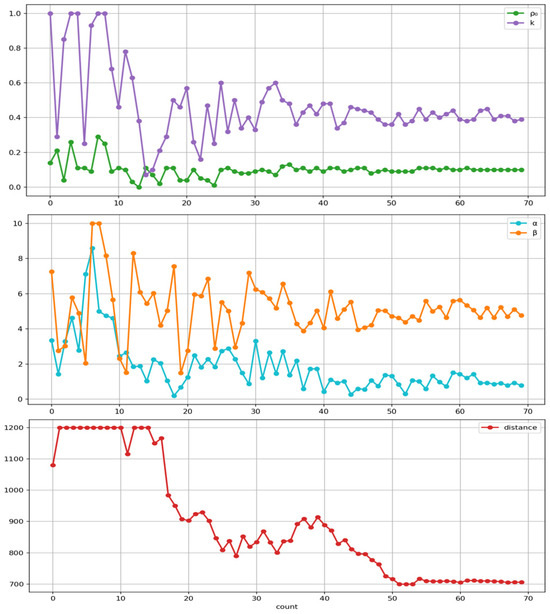
Figure 8.
Bayesian optimization hyperparameter optimization process.
In this study, based on the convergence results, the initial pheromone volatilization coefficient is set to 0.1, a relatively small value that helps preserve pheromone trails over time and thereby supports algorithm convergence. The regulating factor is set to 0.4, which effectively balances the algorithm’s convergence speed and global search capability. During the iterative process, when the global best path length becomes less than or equal to the best individual path length in the current iteration, it indicates that the algorithm may have fallen into a local optimum. At this point, the pheromone volatilization coefficient is increased using the adaptive update formula. Raising the coefficient accelerates pheromone evaporation, reducing the influence of historical accumulation, enhancing randomness, improving global search ability, and helping the algorithm escape local optima. The variation curve of the adaptive pheromone volatilization coefficient is illustrated in Figure 9.
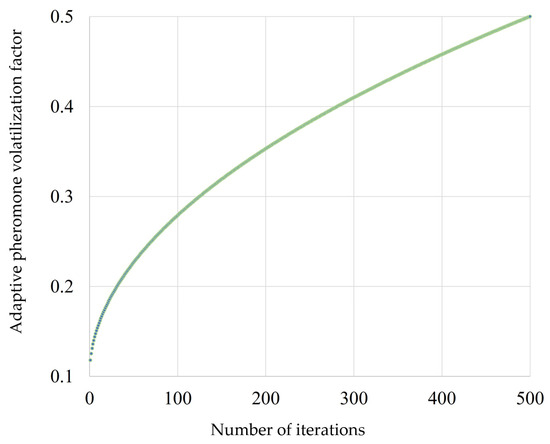
Figure 9.
Adaptive pheromone volatilization coefficient variation curve.
Selecting appropriate parameter values is critical to ensuring the stability of the algorithm and the quality of the optimal solution. In this study, parameters are tuned based on the principles discussed above and the parameter optimization. After a comprehensive evaluation of solution quality, convergence speed, and algorithmic stability, the final parameter settings are determined as follows: the number of ants in the colony is set to 50; the maximum number of iterations is 500; the importance factors for pheromone concentration and heuristic information are set to 1 and 5, respectively; the constant is set to 1; the number of offspring ants selected for crossover and mutation operations per iteration is 10; the initial pheromone volatilization coefficient is set to 0.1; and the regulation factor is set to 0.4.
3.2. Evaluation Indicators
For each dataset, multiple experiments are conducted using different path planning algorithms. In each experiment, the best path generated by the corresponding algorithm and its associated path length are recorded. Based on these results, the mean, minimum, and variance of the path lengths are computed to evaluate algorithm performance. The performance of a path planning algorithm is assessed using these three statistical metrics. Specifically, the mean path length reflects the overall quality of the paths produced; a smaller mean value indicates that, on average, the algorithm generates shorter paths across multiple runs, demonstrating better average performance. The mean path length is defined by Equation (8):
where is the number of experiments; in this paper, the experiments are set to 10 times. is the path length of the best path obtained from experiment . The minimum value of the path length is used to evaluate the optimization ability of the path planning algorithm, and a smaller minimum value indicates that the path planning algorithm has a stronger optimization ability. The minimum value of the path length is defined in Equation (9):
The variance of the path length is used to evaluate the stability and robustness of the path planning algorithm. A smaller variance indicates that the algorithm performs more consistently across different datasets, demonstrating higher robustness and better adaptability. The variance of the path length is defined in Equation (10):
3.3. Ablation Experiments on the TSPLIB Dataset
To evaluate the effectiveness of the improved ant colony optimization (IACO) algorithm and thoroughly analyze the contribution of each enhancement module, this study conducts a series of ablation experiments with the following configurations: (1) the baseline ant colony optimization (ACO) algorithm; (2) ACO-I, which incorporates genetic algorithm operations (crossover and mutation); (3) ACO-II, which introduces an adaptive pheromone volatilization coefficient; and (4) the fully enhanced improved ant colony optimization (IACO) algorithm. The datasets ulysses22, eil51, and st70 contain 22, 51, and 70 nodes, respectively. The ablation experiment results for the IACO algorithm are presented in Table 1.

Table 1.
Ablation of experiments on TSPLIB datasets.
The basic parameters of all four models are kept consistent; the number of ants is set to 50, the maximum number of iterations is 500, the importance factors of pheromone concentration and heuristic function are set to 1 and 5, respectively, and the constant coefficient is set to 1. Each model is tested on the ulysses22, eil51, and st70 datasets with 10 independent experimental runs. For each configuration, the mean, minimum, and variance of the resulting path lengths are computed. After incorporating the genetic algorithm, the ACO-I model shows significant improvements compared to the baseline ACO. Specifically, the mean path lengths are reduced by 0.355 m, 4.108 m, and 13.575 m on the ulysses22, eil51, and st70 datasets, respectively. The minimum path lengths are reduced by 0.436 m, 1.339 m, and 11.401 m, while the variances decrease by 0.130, 25.370, and 49.851, respectively. These results demonstrate that the integration of genetic operations enhances both the optimization ability and the stability of the ACO algorithm. When introducing the adaptive pheromone volatilization coefficient, the ACO-II model also outperforms the baseline. The mean path lengths are reduced by 0.128 m, 3.287 m, and 2.510 m on the ulysses22, eil51, and st70 datasets, respectively. Similarly, the minimum path lengths decrease by 0.099 m, 1.243 m, and 1.838 m, while the variances drop by 0.064, 6.340, and 11.296, respectively. These results indicate improvements in the algorithm’s average performance and robustness due to the adaptive volatility mechanism. Furthermore, the fully improved IACO model, which integrates both the genetic algorithm and the adaptive pheromone volatilization coefficient, achieves the best performance across all evaluation metrics and datasets. This indicates that IACO has superior global search capability, stronger optimization performance, higher stability, and better reliability in solving path planning problems.
Furthermore, the convergence speed and optimization capability of the algorithms can be more intuitively observed by comparing the evolution curves of the optimal path length from a single experimental run of the IACO and ACO algorithms. Figure 10 illustrates the convergence trajectories of both algorithms on the ulysses22, eil51, and st70 datasets. It is evident from the figure that the IACO algorithm demonstrates a faster convergence rate and stronger optimization performance compared to the ACO algorithm. Across datasets of varying scales, the IACO consistently outperforms the ACO, indicating superior robustness. These results confirm that the improved IACO algorithm achieves enhanced performance. The integration of the genetic algorithm and the adaptive pheromone volatilization coefficient contributes to faster convergence and more effective global search capabilities, thereby reducing the risk of the algorithm becoming trapped in local optima.
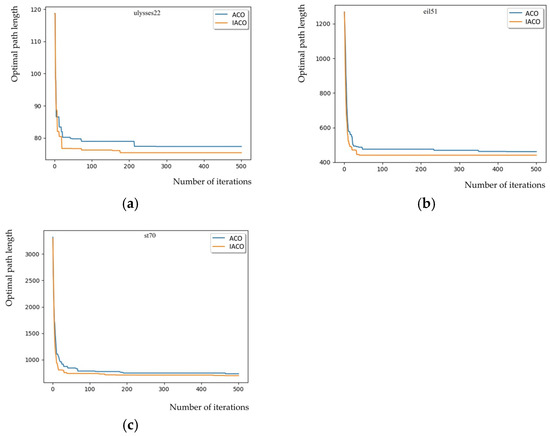
Figure 10.
Change curves on ulysses22, eil51, st70 dataset. (a) ulysses22. (b) eli51. (c) st70.
3.4. Comparison Experiments on the TSPLIB Dataset
In this paper, IACO is compared with other heuristic algorithms on the TSPLIB dataset, containing the ant colony (ACO) algorithm, particle swarm (PSO) algorithm [8], genetic algorithm (GA) [10], simulated annealing (SA) algorithm [22], tabu search (TS) algorithm [23], and improvement of artificial fish swarming algorithm [24]; the results of the experiments are shown in Table 2.

Table 2.
Comparison of experiments on TSPLIB datasets.
To evaluate the performance of IACO, comparative experiments were conducted on the ulysses22, eil51, and st70 datasets, each repeated 10 times. For each algorithm, the mean, minimum, and variance of the optimal path lengths were computed. The results demonstrate that IACO consistently achieves the best overall performance across all three datasets. Specifically, IACO yields lower mean, minimum, and variance values for the optimal path length compared to the other algorithms, indicating superior optimization capability, stability, and robustness. Furthermore, the performance of IACO remains stable regardless of dataset size, suggesting its strong generalization ability and broader applicability. These results confirm that IACO outperforms the comparative algorithms in both effectiveness and reliability.
3.5. Perception and Fusion Algorithm Verification
To rigorously validate the efficacy of YOLO-Float for floating-waste detection, comprehensive comparative experiments were conducted on the FloW-RI dataset, with detailed experimental results presented in Table 3.

Table 3.
Comparison experiment on FloW-RI with image detection.
Benchmarking against mainstream YOLO variants, including YOLOv5, YOLOv6, YOLOv7, and YOLOX under identical training protocols, reveals YOLO-Float’s superior performance; it achieves a state-of-the-art mAP of 44.7%, surpassing YOLOv5 by 2.6% and YOLOX by 1.9%. Particularly significant is its 43.1% mAP at a strict IoU threshold of 0.75, representing a 9.1% absolute improvement over YOLOv5 in high-precision localization. These enhancements directly originate from the low-level representation enhancement module and attention fusion module, which effectively overcome challenges of small-target detection and complex background interference characteristic of aquatic environments. Furthermore, YOLO-Float attains a 52.1% mAR—the highest among compared models—demonstrating exceptional capability to minimize missed detections critical for comprehensive waste coverage. With 91.8 million parameters and real-time inference at 35 FPS on embedded platforms, Jetson Xavier NX, the algorithm demonstrates an optimal balance between accuracy and efficiency for deployment on resource-constrained unmanned surface vessels. These quantifiable advancements in detection precision, recall robustness, and operational efficiency collectively justify our selection of YOLO-Float as the core perception module for unmanned surface vessels dedicated to floating-waste detection.
To validate the effectiveness of the radar and camera fusion algorithm for detecting floating debris on water surfaces, experiments were conducted in this section using the FloW-RI dataset. Four fusion algorithms based on different methodological implementations were adopted for comparative analysis to verify the performance of the proposed fusion approach. The comparison methods are summarized in Table 4.

Table 4.
Comparison of different point cloud clustering and matching methods.
Method 1 employs no point cloud clustering, directly projecting 3D point clouds onto 2D images for matching. Method 2 utilizes DBSCAN [25] for point cloud clustering, matching projected point cloud bounding boxes with image detection bounding boxes using maximum intersection over union (IoU). Method 3 adopts density-based HDBSCAN [26] clustering with 1/d-based association matching. Method 4 employs density-based OPTICS [27] clustering with 1/d-based association matching. Our method employs density-based OPTICS clustering with 1/d-based association matching. All methods employ YOLO-Float for image object detection, and their detection performance is summarized in Table 5.

Table 5.
Comparison experiment on FloW-RI.
As shown in Table 5, the proposed method outperforms the other four comparative algorithms in directional error , distance error , positional error , and miss rate . Method 1 exhibits significant spatiotemporal misalignment due to direct point-cloud-to-image mapping, resulting in high localization errors, with measuring 0.107 m and Loss at 44.3%. The proposed method substantially reduces all error metrics; decreases 0.471°, decreases 0.042 m, decreases 0.083 m, and decreases 34.59%, demonstrating superior localization and association matching. Method 2 achieves positional accuracy comparable to the proposed method, with measuring 0.021 m, but its increases to 71%. The 1/d-based association matching strategy adopted in this work overcomes the failure of maximum IoU matching under synchronization deviations, decreasing by 61.29%. Methods 3 and 4 exhibit higher errors, with Method 3’s Loss increasing to 80.66%. This indicates DBSCAN provides superior robustness and target extraction accuracy over HDBSCAN and OPTICS in aquatic environments characterized by uneven point cloud density and significant noise. In conclusion, the adopted detection and fusion methodology effectively detects and localizes floating debris on water surfaces.
3.6. Global Patrol and Local Cleanup Example Application Validation
To preliminarily validate the feasibility of the proposed algorithm in real-world environments, the algorithm was deployed and tested on a Jetson Xavier NX development board. Due to inter-algorithm communication requirements, the deployment was implemented using the Robot Operating System (ROS). YOLO-Float visual detection, fusion perception algorithms, and the improved ant colony optimization (IACO) path planning algorithm were packaged as ROS nodes, with communication established through ROS topic publishers and subscribers. The main operational nodes are illustrated in Figure 11.
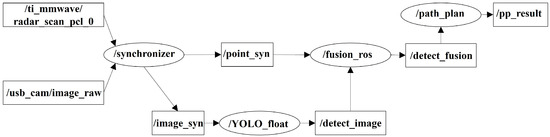
Figure 11.
Main nodes of the algorithm.
For preliminary performance evaluation, a campus lake was selected as a representative testing environment. The global patrol algorithm configured 23 patrol points within this environment. For local target-oriented scenarios, real-time images of the lake area captured by cameras identified floating debris targets, serving as application cases for local target cleanup. Path planning for both scenarios utilized the improved ant colony optimization (IACO) algorithm. The generated planning paths are shown in Figure 12 and Figure 13. The real-time closed-loop performance was quantitatively validated through latency measurements in Table 6, confirming operational feasibility for dynamic water environments. As demonstrated, the IACO algorithm produced reasonable and efficient paths in both global and local planning contexts within this specific test scenario, yielding shorter and more optimized paths. The total system latency of 85 ms enables responsive navigation control at USV operational speeds, demonstrating compliance with real-time requirements for floating-waste cleaning missions, and revealing its potential for such applications.
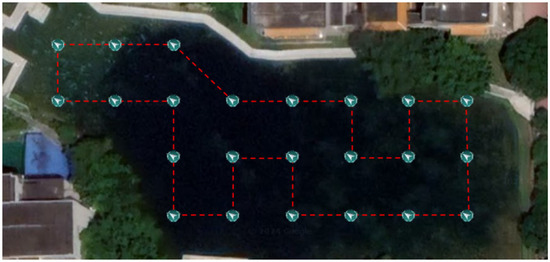
Figure 12.
Global patrol path planning results.
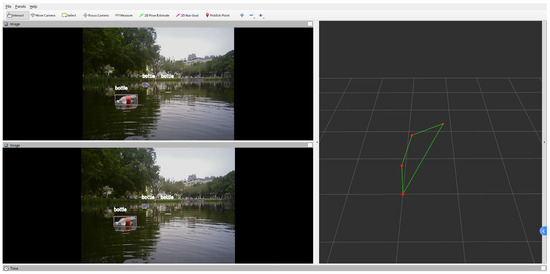
Figure 13.
Localized goal path planning results.

Table 6.
Real-time closed-loop latency measurements.
It should be noted that this experiment focused on a single campus lake scenario for preliminary validation of system feasibility. Future research will expand testing to more diverse aquatic environments (e.g., urban waterways, wetland parks) to assess adaptability and robustness under varied conditions.
Collectively, the experimental validation establishes compelling evidence for the efficacy of our integrated approach. Algorithmically, IACO consistently outperforms seven state-of-the-art heuristic methods across three benchmark datasets, achieving path length reductions up to 13.575 m with faster convergence, demonstrating superior optimization capability and computational efficiency. Perceptually, the YOLO-Float and radar-camera fusion framework achieves 44.7% mAP detection accuracy and 0.024 m localization precision, overcoming challenges of aquatic small-target detection while maintaining real-time operation at 35 FPS. Systematically, hardware deployment confirms closed-loop feasibility with 85 ms total latency, successfully coordinating perception-planning modules in dynamic environments. These quantitatively validated capabilities—spanning algorithmic innovation, sensor fusion robustness, and edge-computing practicality—collectively substantiate the solution’s readiness for real-world floating-waste cleaning operations.
4. Conclusions
This paper models the path planning challenge for a floating-waste-cleaning USV as a Traveling Salesman Problem, integrating global patrol points and local target tracking. Our proposed improved ant colony optimization algorithm enhances traditional ACO by incorporating genetic algorithm operations—mutation and crossover—alongside adaptive pheromone volatility coefficients. This dual innovation accelerates convergence in large-scale environments while preventing local optima traps. Critically, experimental validation demonstrates IACO’s superiority—on TSPLIB datasets, it achieves path length reductions of 0.355 m in ulysses22, 4.108 m in eil51, and 13.575 m in st70 compared to baseline ACO. Real-world deployment on a Jetson Xavier NX platform confirms operational viability with 85 ms closed-loop latency, enabling efficient waste collection in campus lake scenarios.
Despite these advances, limitations warrant consideration. Current testing assumes static environments without addressing dynamic obstacles like moving boats. Energy consumption optimization and edge device computational constraints present additional challenges. Consequently, future work will prioritize dynamic obstacle avoidance mechanisms, distributed computing architectures for large-scale deployments, and energy-aware heuristic integration, specifically extending IACO for cooperative path planning in complex aquatic environments.
Author Contributions
Conceptualization, Y.L. and S.Y.; methodology, C.T., R.W. and Y.L.; software, C.T. and R.W.; validation, C.T. and R.W.; writing—original draft preparation, C.T., D.G. and Y.L.; writing—review and editing, C.T., D.G., Y.L. and R.W.; supervision, R.W.; project administration, Y.L. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Laboratories of Sensing and Application of Intelligent Optoelectronic System in Sichuan Provincial Universities (Grant No. ZNGD2206), the Youth Fund Project of Hebei Province Higher Education Science Research (Grant No. QN2024209), Sichuan Province Engineering Technology Research Center of Modern Agriculture Equipment (Grant No. XDNY2023-005), and Key Laboratory of Advanced Manufacturing Technology of the Ministry of Education (Grant No. GZUAMT2021KF[04]). The APC was funded by Yong Li.
Data Availability Statement
FloW-RI dataset: https://orca-tech.cn/datasets/FloW/FloW-RI (accessed on 1 May 2025); TSPLIB dataset: http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95 (accessed on 22 April 2025).
Acknowledgments
The authors thank the Guangxi Key Laboratory of the Intelligent Control and Maintenance of Power Equipment for the device support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rangel-Buitrago, N.; Williams, A.T.; Neal, W.J.; Gracia, C.A.; Micallef, A. Litter in Coastal and Marine Environments. Mar. Pollut. Bull. 2022, 177, 113546. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Li, L.; Wu, W.; Jiao, Y. Application of Improved Dijkstra Algorithm in Intelligent Ship Path Planning. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 4926–4931. [Google Scholar]
- Zhang, H.; Tao, Y.; Zhu, W. Global Path Planning of Unmanned Surface Vehicle Based on Improved A-Star Algorithm. Sensors 2023, 23, 6647. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Yang, M.; Zhao, Z.; Wang, X.; Bai, Y.; Wu, J.; Xu, J. Path Planning of Unmanned Surface Vessel in an Unknown Environment Based on Improved D*Lite Algorithm. Ocean. Eng. 2022, 266, 112873. [Google Scholar] [CrossRef]
- Fan, X.; Guo, Y.; Liu, H.; Wei, B.; Lyu, W. Improved Artificial Potential Field Method Applied for AUV Path Planning. Math. Probl. Eng. 2020, 2020, 6523158. [Google Scholar] [CrossRef]
- Guan, W.; Wang, K. Autonomous Collision Avoidance of Unmanned Surface Vehicles Based on Improved A-Star and Dynamic Window Approach Algorithms. IEEE Intell. Transport. Syst. Mag. 2023, 15, 36–50. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, D.; Gu, J.; Li, F. A Path-Planning Strategy for Unmanned Surface Vehicles Based on an Adaptive Hybrid Dynamic Stepsize and Target Attractive Force-RRT Algorithm. JMSE 2019, 7, 132. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial Fish Swarm Algorithm: A Survey of the State-of-the-Art, Hybridization, Combinatorial and Indicative Applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, J.; Xu, L.; Wang, J. Cooperative Path Planning Study of Distributed Multi-Mobile Robots Based on Optimised ACO Algorithm. Robot. Auton. Syst. 2024, 179, 104748. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, H.; Liu, B. Path Planning of Agricultural Information Collection Robot Integrating Ant Colony Algorithm and Particle Swarm Algorithm. IEEE Access 2024, 12, 50821–50833. [Google Scholar] [CrossRef]
- Ai, B.; Jia, M.; Xu, H.; Xu, J.; Wen, Z.; Li, B.; Zhang, D. Coverage Path Planning for Maritime Search and Rescue Using Reinforcement Learning. Ocean Eng. 2021, 241, 110098. [Google Scholar] [CrossRef]
- Krishna Lakshmanan, A.; Elara Mohan, R.; Ramalingam, B.; Vu Le, A.; Veerajagadeshwar, P.; Tiwari, K.; Ilyas, M. Complete Coverage Path Planning Using Reinforcement Learning for Tetromino Based Cleaning and Maintenance Robot. Autom. Constr. 2020, 112, 103078. [Google Scholar] [CrossRef]
- Pop, P.C.; Cosma, O.; Sabo, C.; Sitar, C.P. A Comprehensive Survey on the Generalized Traveling Salesman Problem. Eur. J. Oper. Res. 2024, 314, 819–835. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Gao, D.; Liu, Z. A Floating-Waste-Detection Method for Unmanned Surface Vehicle Based on Feature Fusion and Enhancement. JMSE 2023, 11, 2234. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhu, J.; Jiang, M.; Fu, J.; Pang, C.; Wang, P.; Sankaran, K.; Onabola, O.; Liu, Y.; Liu, D.; et al. Flow: A Dataset and Benchmark for Floating Waste Detection in Inland Waters. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path Planning Optimization of Indoor Mobile Robot Based on Adaptive Ant Colony Algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Reinelt, G. TSPLIB—A Traveling Salesman Problem Library. ORSA J. Comput. 1991, 3, 376–384. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J. Simulated Annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Gendreau, M. An Introduction to Tabu Search. In Handbook of Metaheuristics; Glover, F., Kochenberger, G.A., Eds.; International Series in Operations Research & Management Science; Kluwer Academic Publishers: Boston, MA, USA, 2003; Volume 57, pp. 37–54. ISBN 978-1-4020-7263-5. [Google Scholar]
- Cheng, C.; Li, H.-F.; Bao, C.-H. Hybrid Artificial Fish Algorithm to Solve TSP Problem. In Proceedings of the 6th International Asia Conference on Industrial Engineering and Management Innovation: Innovation and Practice of Industrial Engineering and Management (Volume 2), Tianjin, China, 25–26 July 2015; Springer: Berlin/Heidelberg, Germany, 2016; pp. 275–285. [Google Scholar]
- Im, S.; Kim, D.; Cheon, H.; Ryu, J. Object Detection and Tracking System with Improved DBSCAN Clustering Using Radar on Unmanned Surface Vehicle. In Proceedings of the 2021 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12 October 2021; pp. 868–872. [Google Scholar]
- Stewart, G.; Al-Khassaweneh, M. An Implementation of the HDBSCAN* Clustering Algorithm. Appl. Sci. 2022, 12, 2405. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P. OPTICS: Ordering Points to Identify the Clustering Structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).