Radar Target Detection in Sea Clutter Based on Two-Stage Collaboration
Abstract
1. Introduction
- 1.
- This paper introduces a two-stage detection paradigm, providing a new direction for controllable false alarm in radar target detection. Experimental results also demonstrate the effectiveness of the proposed method.
- 2.
- This paper presents a radar echo embedding module and a high-level reconstruction module. Combining these two network architectures can achieve high-level feature extraction of radar echoes.
- 3.
- An open dataset for X-band pulse compression radar is established. We will open source these data in batches in the future.
2. Related Works
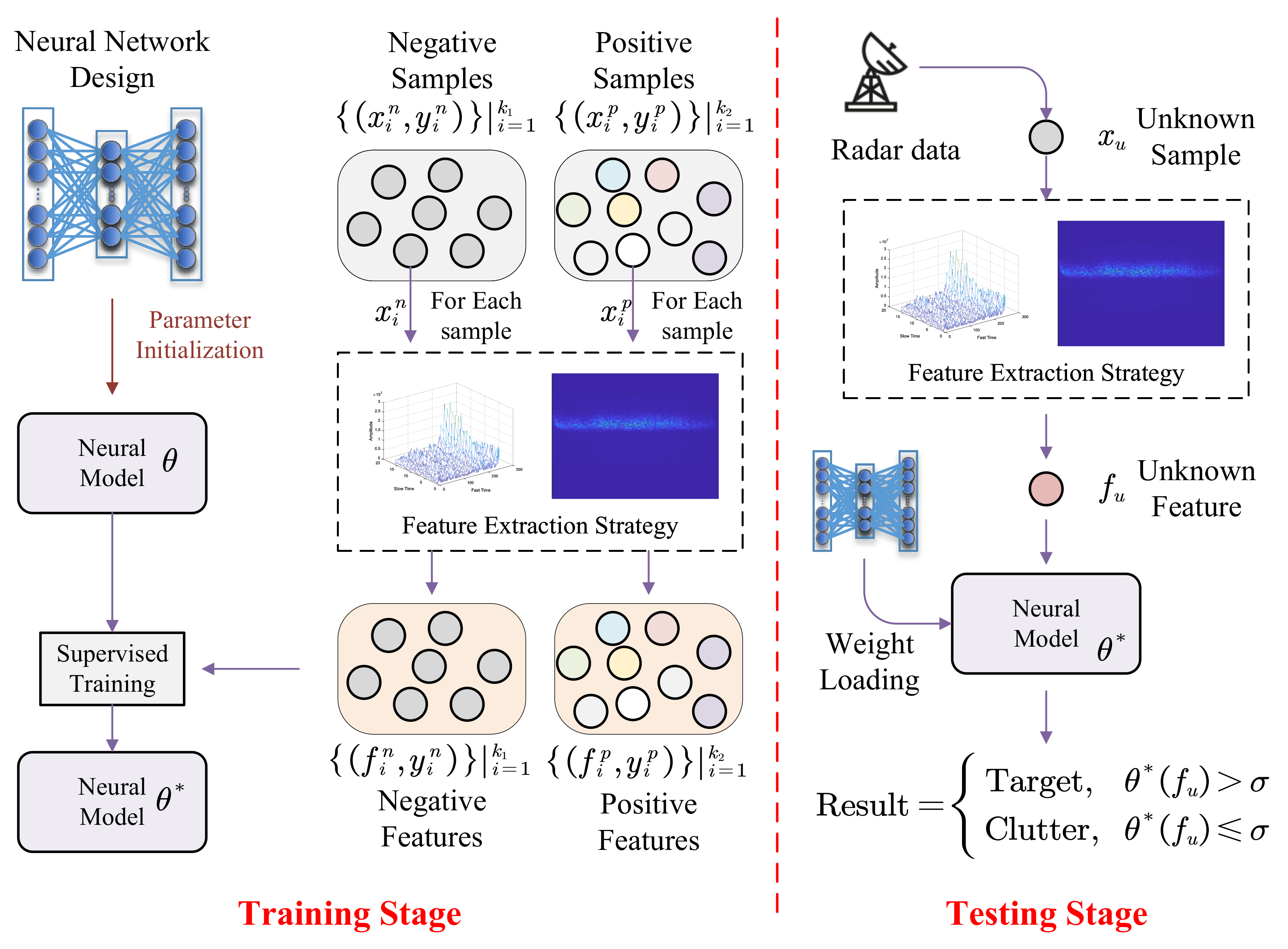
3. Methodology
3.1. Radar Target Signal Model
3.2. Anchor Box Extraction
3.3. Fine-Grained Prediction
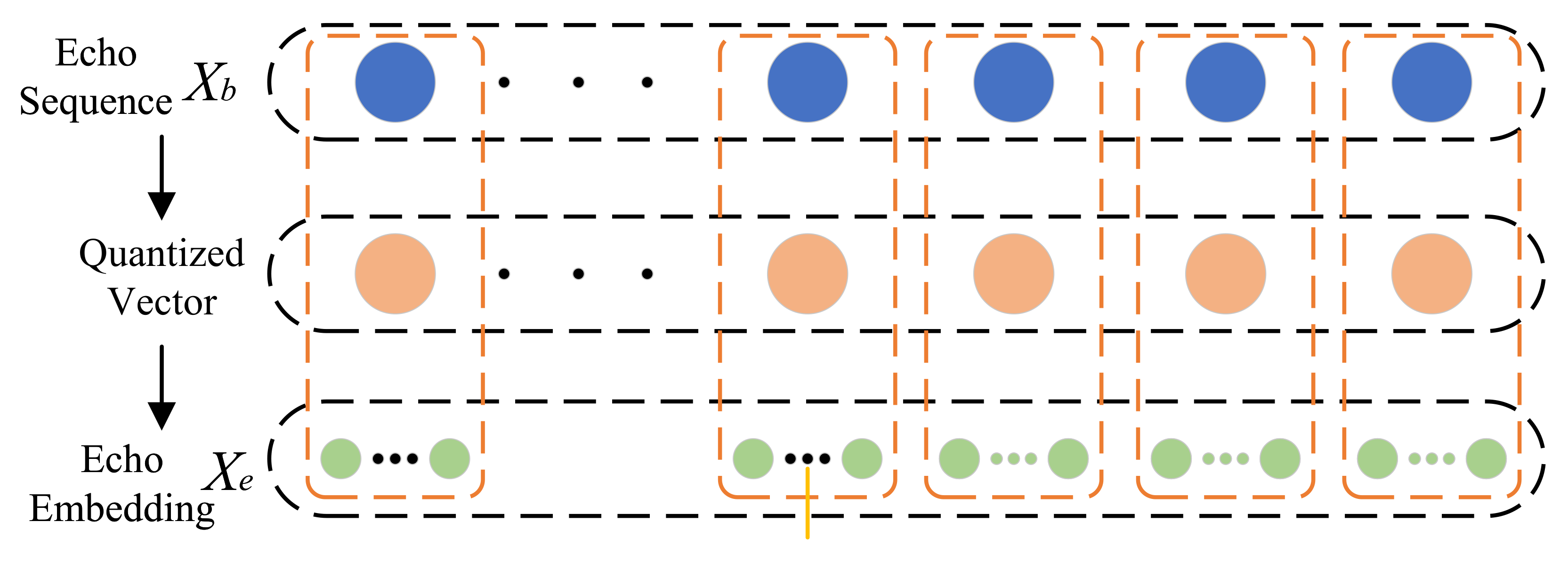
3.3.1. Echo Embedding
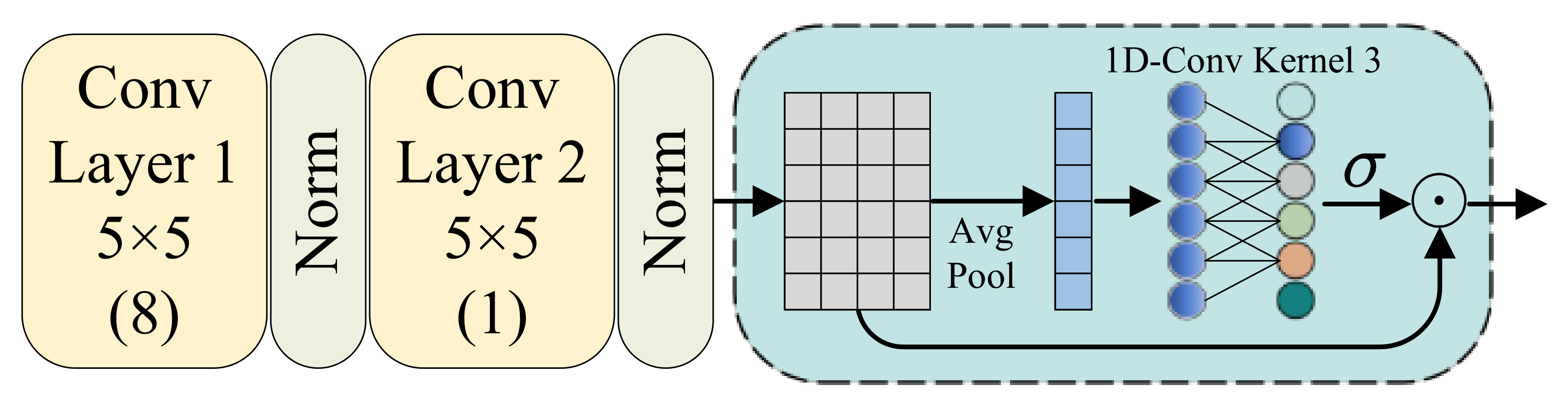
3.3.2. High-Level Reconstruction
3.3.3. Linear Prediction
4. Experiments and Discussions
4.1. Experimental Settings
4.1.1. Radar Deployment
4.1.2. Dataset Description
4.1.3. Comparison Algorithms
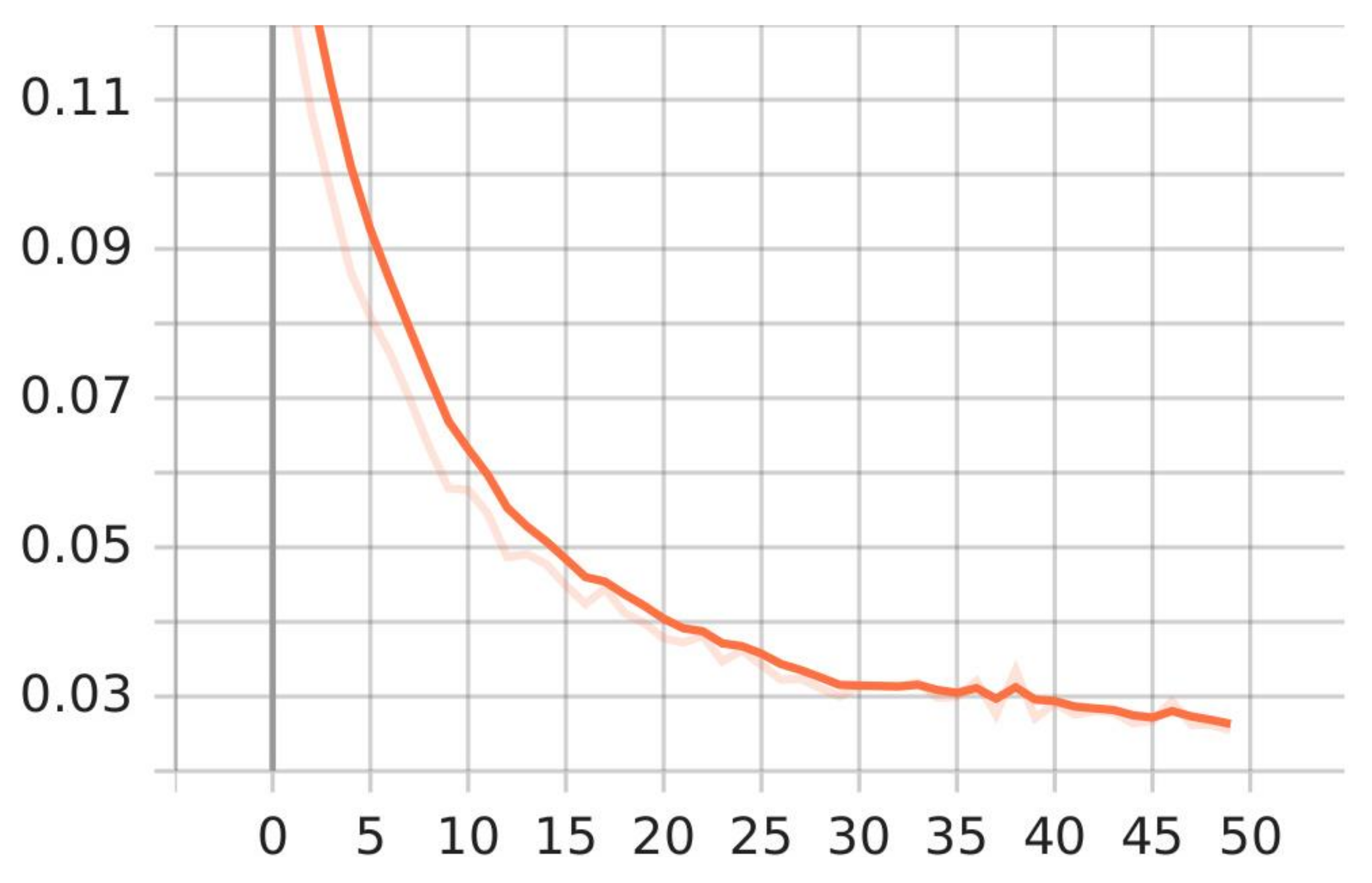
4.2. Ablation Study
4.3. Detection Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, S.; Zhu, J.; Jiang, J.; Shui, P. Sea-Surface Floating Small Target Detection by Multifeature Detector Based on Isolation Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 704–715. [Google Scholar] [CrossRef]
- Yan, K.; Bai, Y.; Wu, H.C.; Zhang, X. Robust Target Detection Within Sea Clutter Based on Graphs. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7093–7103. [Google Scholar] [CrossRef]
- Liu, N.; Dong, Y.; Wang, G.; Ding, H.; Huang, Y.; Guan, J.; Chen, X.; He, Y. Sea-detecting X-band radar and data acquisition program. J. Radars 2019, 8, 656. [Google Scholar]
- Rosenberg, L. Sea-Spike Detection in High Grazing Angle X-Band Sea-Clutter. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4556–4562. [Google Scholar] [CrossRef]
- Huang, W.; Liu, X.; Gill, E.W. Ocean Wind and Wave Measurements Using X-Band Marine Radar: A Comprehensive Review. Remote Sens. 2017, 9, 1261. [Google Scholar] [CrossRef]
- Shui, P.L.; Li, D.C.; Xu, S.W. Tri-feature-based detection of floating small targets in sea clutter. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1416–1430. [Google Scholar] [CrossRef]
- Xu, S.; Zheng, J.; Pu, J.; Shui, P. Sea-Surface Floating Small Target Detection Based on Polarization Features. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1505–1509. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, G.; Dong, Y.; Bai, Y. Floating Small Target Detection in Sea Clutter Using Mean Spectral Radius. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4023405. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Bao, Z.; He, Y. Detection and Extraction of Target With Micromotion in Spiky Sea Clutter Via Short-Time Fractional Fourier Transform. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1002–1018. [Google Scholar] [CrossRef]
- Bi, X.; Guo, S.; Yang, Y.; Shu, Q. Adaptive Target Extraction Method in Sea Clutter Based on Fractional Fourier Filtering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5115609. [Google Scholar] [CrossRef]
- Chen, X.; Su, N.; Huang, Y.; Guan, J. False-Alarm-Controllable Radar Detection for Marine Target Based on Multi Features Fusion via CNNs. IEEE Sens. J. 2021, 21, 9099–9111. [Google Scholar] [CrossRef]
- Wang, J.; Li, S. Maritime Radar Target Detection in Sea Clutter Based on CNN with Dual-Perspective Attention. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3500405. [Google Scholar] [CrossRef]
- Su, N.; Chen, X.; Guan, J.; Huang, Y. Maritime Target Detection Based on Radar Graph Data and Graph Convolutional Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4019705. [Google Scholar] [CrossRef]
- Chen, S.; Feng, C.; Huang, Y.; Chen, X.; Li, F. Small Target Detection in X-Band Sea Clutter Using the Visibility Graph. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5115011. [Google Scholar] [CrossRef]
- Qu, Q.; Wang, Y.L.; Liu, W.; Li, B. A False Alarm Controllable Detection Method Based on CNN for Sea-Surface Small Targets. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4025705. [Google Scholar] [CrossRef]
- Wan, H.; Tian, X.; Liang, J.; Shen, X. Sequence-Feature Detection of Small Targets in Sea Clutter Based on Bi-LSTM. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4208811. [Google Scholar] [CrossRef]
- Wang, J.; Li, S. SALA-LSTM: A novel high-precision maritime radar target detection method based on deep learning. Sci. Rep. 2023, 13, 12125. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, W.; Jin, M. Spectral Norm Based Mean Matrix Estimation and Its Application to Radar Target CFAR Detection. IEEE Trans. Signal Process. 2019, 67, 5746–5760. [Google Scholar] [CrossRef]
- Maali, A.; Mesloub, A.; Djeddou, M.; Mimoun, H.; Baudoin, G.; Ouldali, A. Adaptive CA-CFAR threshold for non-coherent IR-UWB energy detector receivers. IEEE Commun. Lett. 2009, 13, 959–961. [Google Scholar] [CrossRef]
- Gao, G.; Liu, L.; Zhao, L.; Shi, G.; Kuang, G. An Adaptive and Fast CFAR Algorithm Based on Automatic Censoring for Target Detection in High-Resolution SAR Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1685–1697. [Google Scholar] [CrossRef]
- Messali, Z.; Soltani, F.; Sahmoudi, M. Robust radar detection of CA, GO and SO CFAR in Pearson measurements based on a non linear compression procedure for clutter reduction. Signal Image Video Process. 2008, 2, 169–176. [Google Scholar] [CrossRef]
- Xiang, J.; Lv, X.; Fu, X.; Yun, Y. Detection and Estimation Algorithm for Marine Target With Micromotion Based on Adaptive Sparse Modified-LV’s Transform. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5108617. [Google Scholar] [CrossRef]
- Gao, C.; Tao, R.; Kang, X. Weak Target Detection in the Presence of Sea Clutter Using Radon-Fractional Fourier Transform Canceller. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5818–5830. [Google Scholar] [CrossRef]
- Li, Y.; Xie, P.; Tang, Z.; Jiang, T.; Qi, P. SVM-Based Sea-Surface Small Target Detection: A False-Alarm-Rate-Controllable Approach. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1225–1229. [Google Scholar] [CrossRef]
- Jing, H.; Cheng, Y.; Wu, H.; Wang, H. Radar Target Detection With Multi-Task Learning in Heterogeneous Environment. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4021405. [Google Scholar] [CrossRef]
- Xi, C.; Liu, R. Detection of Small Floating Target on Sea Surface Based on Gramian Angular Field and Improved EfficientNet. Remote Sens. 2022, 14, 4364. [Google Scholar] [CrossRef]
- Su, N.; Chen, X.; Guan, J.; Li, Y. Deep CNN-Based Radar Detection for Real Maritime Target Under Different Sea States and Polarizations. In Proceedings of the Cognitive Systems and Signal Processing—4th International Conference, ICCSIP 2018, Beijing, China, 29 November–1 December 2018; Revised Selected Papers, Part II. Springer: Berlin/Heidelberg, Germany, 2018; Volume 1006, pp. 321–331. [Google Scholar]
- Si, X.; Zhang, C.; Li, S.; Liang, J. Source-free domain adaptation for unsupervised radar-based human activity recognition. Pattern Recognit. 2026, 169, 111866. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, X.; Xia, Z.; Xu, F. Human Activity Recognition Trained on Simulated Millimeter-Wave Radar Data With Domain Adaptation. IEEE Trans. Instrum. Meas. 2025, 74, 2525513. [Google Scholar] [CrossRef]
- Hernangómez, R.; Bjelakovic, I.; Servadei, L.; Stanczak, S. Unsupervised Domain Adaptation across FMCW Radar Configurations Using Margin Disparity Discrepancy. In Proceedings of the 30th European Signal Processing Conference, EUSIPCO 2022, Belgrade, Serbia, 29 August–2 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1566–1570. [Google Scholar]
- Liu, J.; Zeng, D.; Li, L.; Lin, H.; Tian, X. Source-Free Domain Adaptation for Millimeter Wave Radar Based Human Activity Recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP 2024, Seoul, Republic of Korea, 14–19 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 7120–7124. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, W.; Jiang, C. A survey of word embeddings based on deep learning. Computing 2020, 102, 717–740. [Google Scholar] [CrossRef]
- OpenStreetMap. Available online: https://www.openstreetmap.org/ (accessed on 5 May 2024).
- Van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]

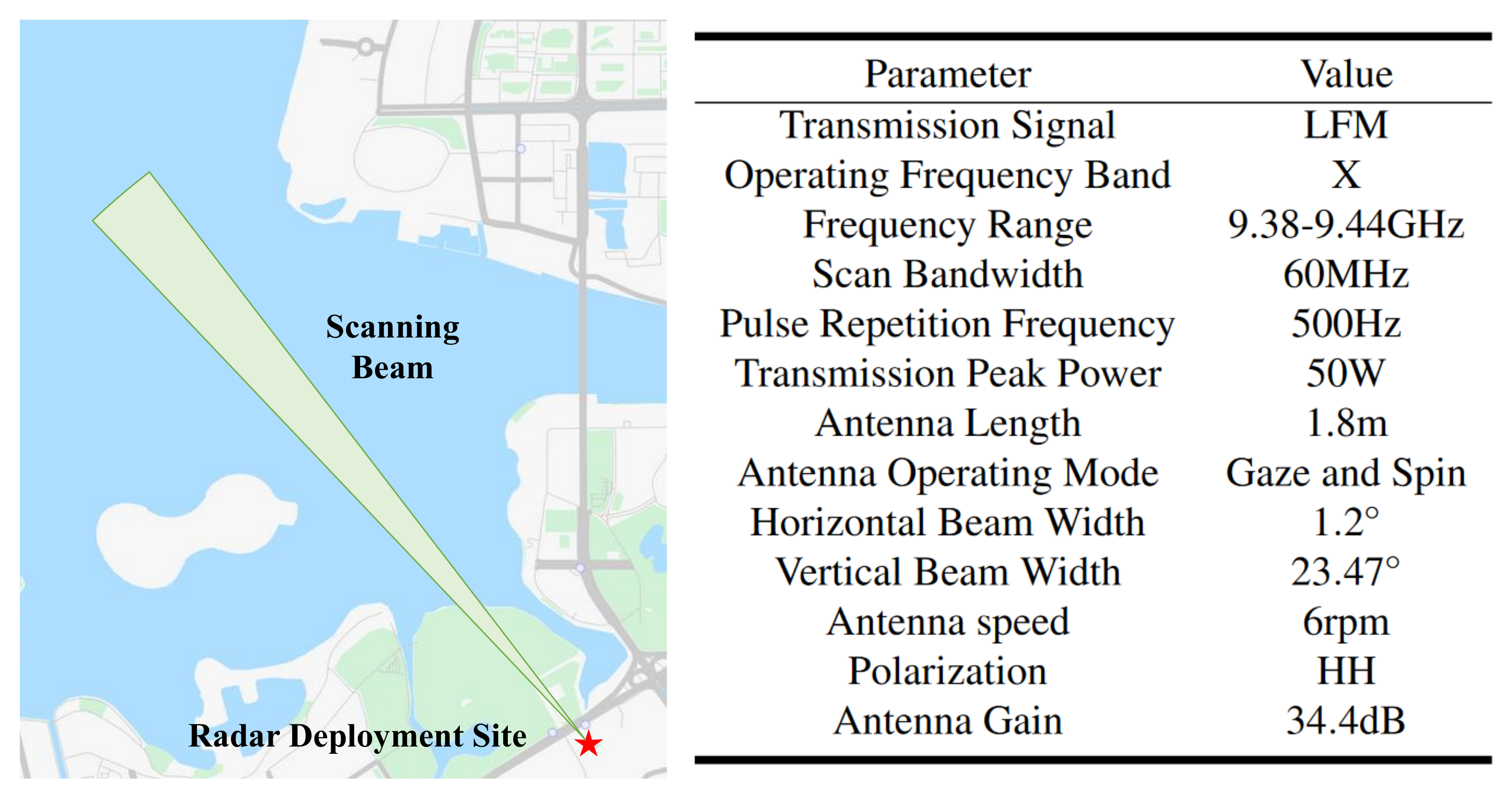



| Month | Mostly Cloudy/Sunny | Thunderstorm/Rain | Wind Speed |
|---|---|---|---|
| February | 15 days | 13 days | 20–49 km/h |
| March | 23 days | 8 days | 29–38 km/h |
| April | 13 days | 17 days | 20–38 km/h |
| July | 15 days | 16 days | 20–49 km/h |
| Index | Model Variant | Accuracy |
|---|---|---|
| ♯1 | Remove echo embedding module | 86.06% |
| ♯2 | Remove high-level reconstruction module | 94.55% |
| ♯3 | Only linear prediction module | 88.47% |
| ♯4 | Change embedding size to 64 | 95.18% |
| ♯5 | Change the quantification interval to 4096 | 95.41% |
| ♯6 | Change the block size to 3×3 | 94.79% |
| ♯7 | The whole method | 95.42% |
| Metric | Detection Method | Dataset | ||
|---|---|---|---|---|
| D1 | D2 | D3 | ||
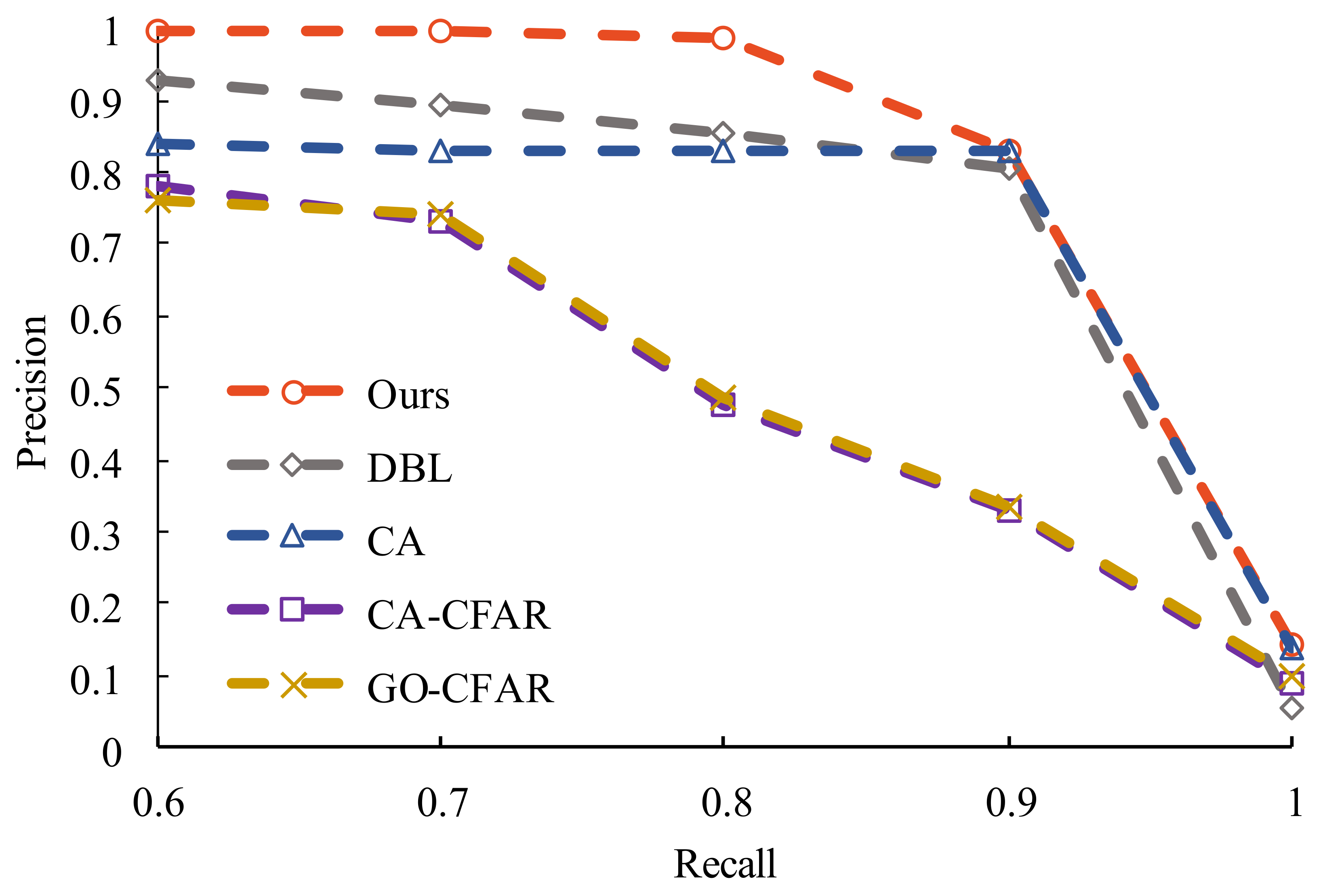
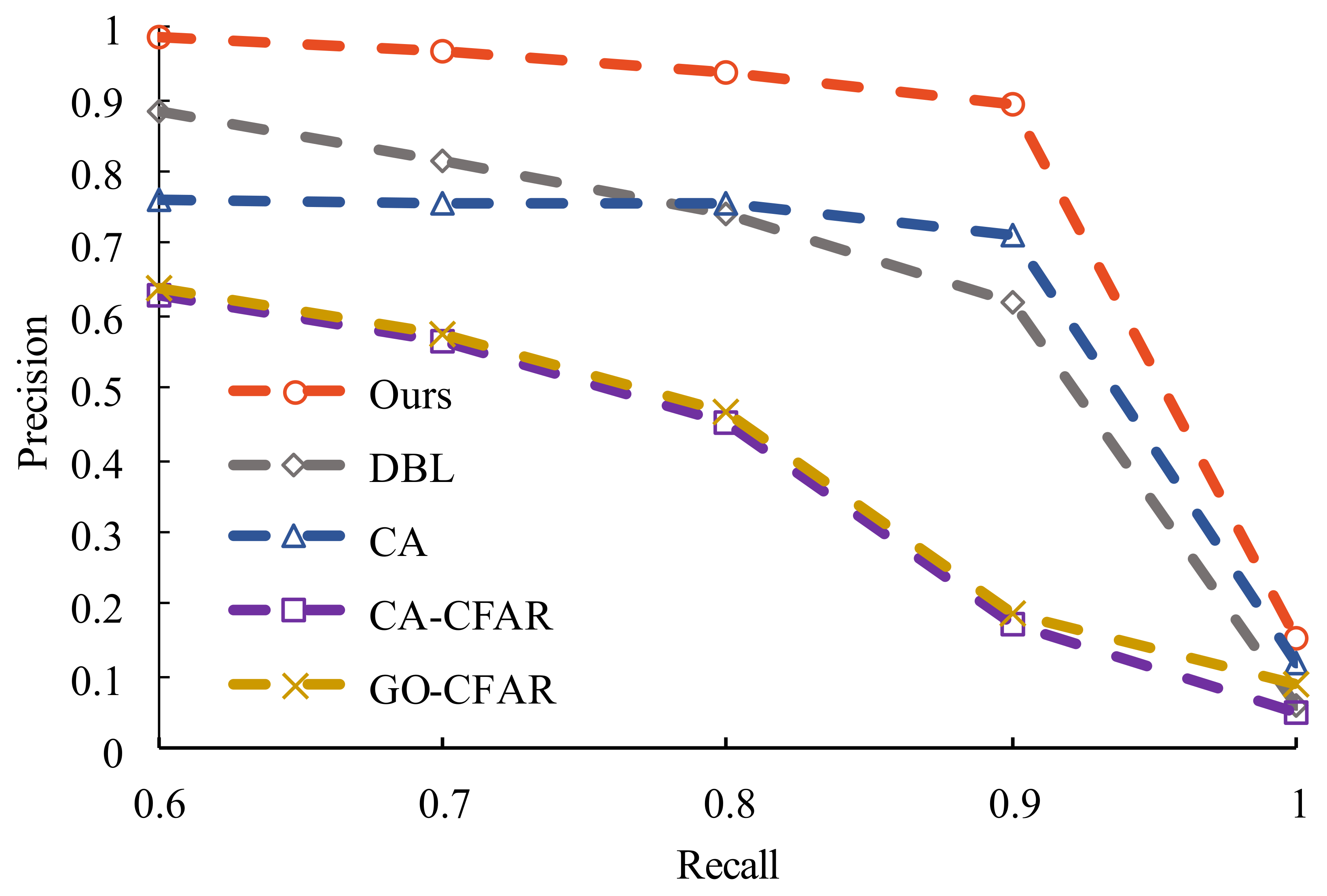
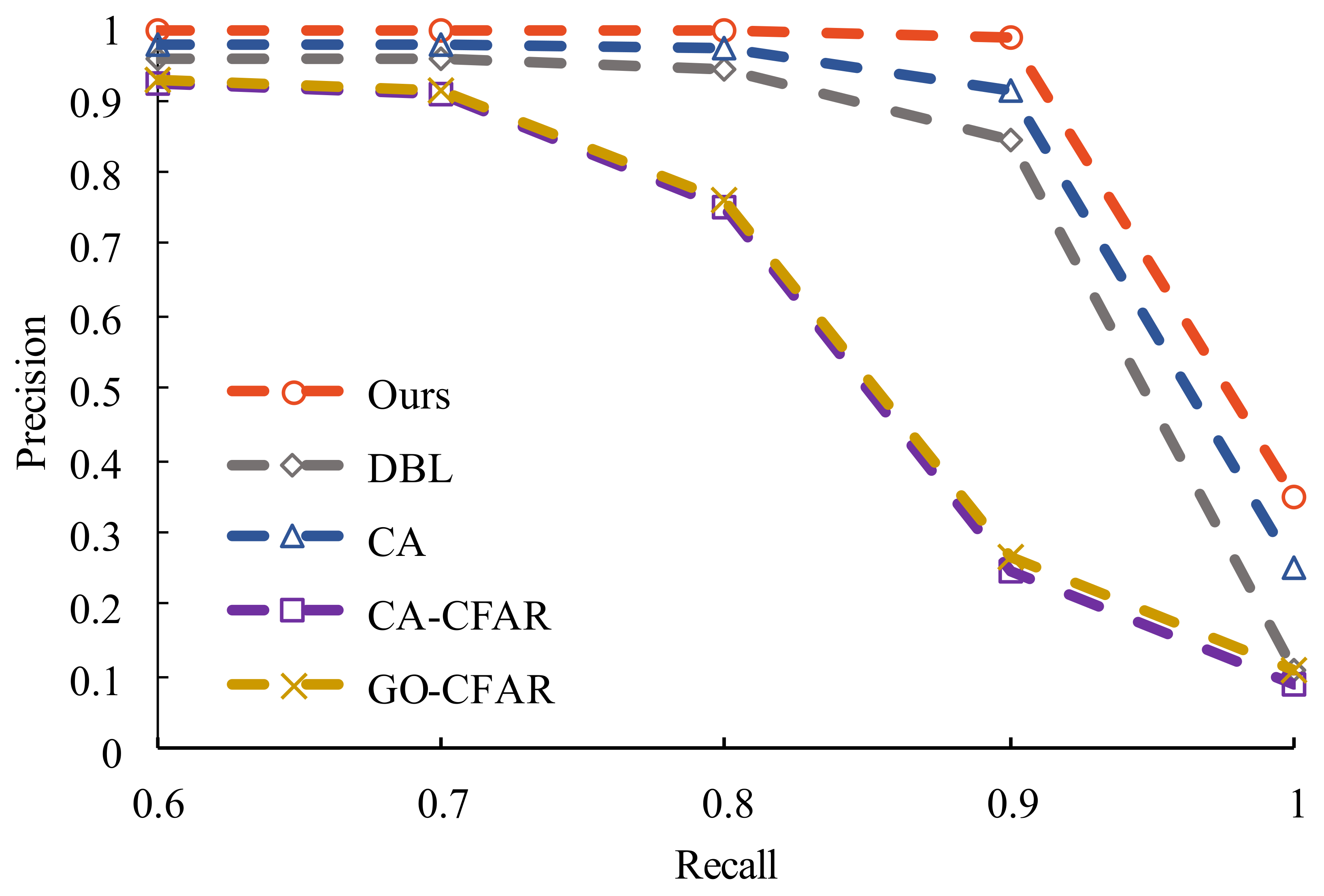
| Precision | CA-CFAR | 34.29% | 31.75% | 74.33% |
| GO-CFAR | 40.75% | 39.58% | 80.45% | |
| CA [12] | 50.38% | 48.03% | 73.99% | |
| DBL [16] | 87.06% | 76.45% | 96.48% | |
| Ours | 92.65% | 90.17% | 96.78% | |
| Recall (DP) | CA-CFAR | 91.43% | 81.08% | 85.19% |
| GO-CFAR | 80.00% | 78.38% | 81.48% | |
| CA [12] | 98.91% | 98.34% | 94.57% | |
| DBL [16] | 91.43% | 91.89% | 88.89% | |
| Ours | 97.14% | 99.08% | 93.83% | |
| FAR | CA-CFAR | 2.99% | 3.46% | 2.65% |
| GO-CFAR | 2.92% | 3.37% | 2.58% | |
| CA [12] | 1.02% | 1.25% | 0.71% | |
| DBL [16] | 0.16% | 0.35% | 0.08% | |
| Ours | 0.43% | 0.28% | 0.57% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xiao, T.; Liu, P. Radar Target Detection in Sea Clutter Based on Two-Stage Collaboration. J. Mar. Sci. Eng. 2025, 13, 1556. https://doi.org/10.3390/jmse13081556
Wang J, Xiao T, Liu P. Radar Target Detection in Sea Clutter Based on Two-Stage Collaboration. Journal of Marine Science and Engineering. 2025; 13(8):1556. https://doi.org/10.3390/jmse13081556
Chicago/Turabian StyleWang, Jingang, Tong Xiao, and Peng Liu. 2025. "Radar Target Detection in Sea Clutter Based on Two-Stage Collaboration" Journal of Marine Science and Engineering 13, no. 8: 1556. https://doi.org/10.3390/jmse13081556
APA StyleWang, J., Xiao, T., & Liu, P. (2025). Radar Target Detection in Sea Clutter Based on Two-Stage Collaboration. Journal of Marine Science and Engineering, 13(8), 1556. https://doi.org/10.3390/jmse13081556






