A Systematic Evaluation of the New European Wind Atlas and the Copernicus European Regional Reanalysis Wind Datasets in the Mediterranean Sea
Abstract
1. Introduction
2. Data and Methodology
2.1. Copernicus European Regional Reanalysis (CERRA)
- The assimilation of additional observations, available from the observing system, throughout the reanalysis period in order to represent more accurately the atmospheric conditions. These observations are obtained from ECMWF’s Meteorological Archival and Retrieval System (MARS) and the European Centre File Storage system (ECFS), and include conventional (e.g., synoptic surface observations, drifting buoys, ships) and other observations, such as scatterometer and radiance observations [35].
- The Ensemble Data Assimilation (EDA) system coupled with the deterministic CERRA system to regularly estimate the background error covariance matrix (B-Matrix) with flow-dependency updates [36] to sufficiently represent errors when changes in the weather regime are detected.
2.2. New European Wind Atlas (NEWA)
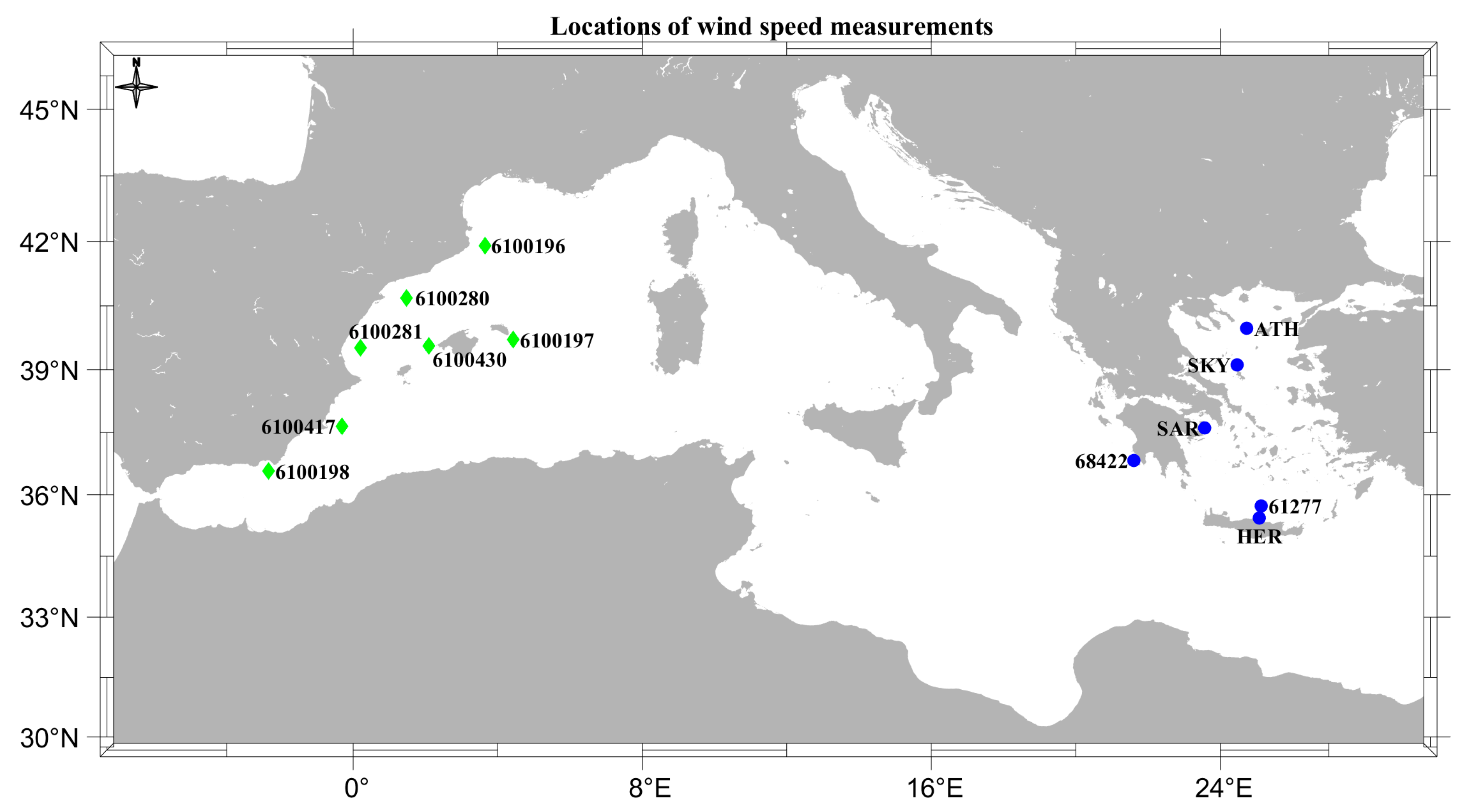
2.3. In Situ Wind Measurements
2.4. Methodology
3. Numerical Results
3.1. Overall Evaluation
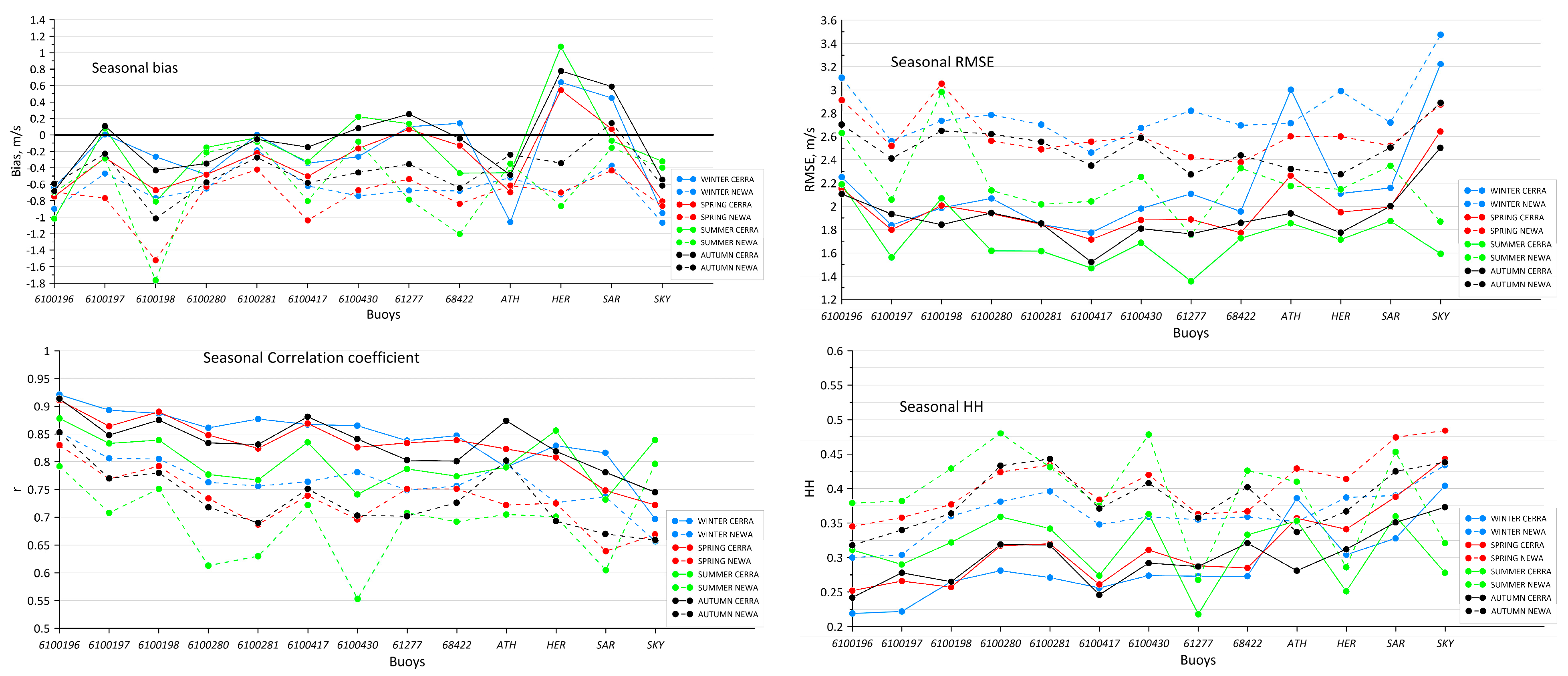
- The performance of CERRA remains better than the performance of NEWA. Specifically, the values for CERRA are smaller than the corresponding values for NEWA for all locations. CERRA also outperforms NEWA with regards to for all locations except for 6100196, ATH, HER and SAR. The values of for CERRA are higher and the values of are smaller than the corresponding values for NEWA for all locations. The values of and for CERRA are smaller than the corresponding values for NEWA (except for 6100430 for and 6100417 and SKY for ).
- The results for the interpolated point (see Equation (1)) show overall better agreement with the buoy measurements for both datasets. Specifically, the and values are smaller for all locations and both datasets (except for 6100281/NEWA). values are always greater (or equal) for all locations and both datasets except for HER/NEWA). The values of and are always smaller (or equal) for all locations and both datasets (except for 6100430/NEWA as regards and 6100417-SKY/NEWA as regards ). The only case where the results of the closest point have been slightly improved refers to for NEWA: the bias has been improved for seven locations (6100196, 6100197, 6100281, 6100417, 6100430, ATH, and SKY).
- buoy measurements collocated with CERRA, (),
- CERRA wind dataset (),
- buoy measurements collocated with NEWA (), and
- NEWA wind dataset ().
3.2. Seasonal Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Let it be clarified beforehand that, in contrast with CERRA, NEWA is not a reanalysis product. |
| 2 | Specifically, wind data for the buoys 6100196, 6100197, 6100198, 6100280, 6100281, 6100417, 6100430, 61277, and 68422 have been obtained via the Copernicus Marine Service; wind data for the buoys Athos (ATH), Heraklion (HER), Saronikos (SAR) and Skyros (SKY) have been obtained via the POSEIDON monitoring, forecasting and information system for the Greek Seas. |
| 3 | The roughness length depends on the prevailing sea state characteristics (significant wave height and wave age) and the wind speed. |
| 4 | Negative values of the differences imply a smaller bias for CERRA wind dataset. |
References
- Soukissian, T.; Papadopoulos, A.; Skrimizeas, P.; Karathanasi, F.; Axaopoulos, P.; Avgoustoglou, E.; Kyriakidou, H.; Tsalis, C.; Voudouri, A.; Gofa, F.; et al. Assessment of offshore wind power potential in the Aegean and Ionian Seas based on high-resolution hindcast model results. AIMS Energy 2017, 5, 268–289. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Karathanasi, F.E.; Zaragkas, D.K. Exploiting offshore wind and solar resources in the Mediterranean using ERA5 reanalysis data. Energy Convers. Manag. 2021, 237, 114092. [Google Scholar] [CrossRef]
- Kardakaris, K.; Boufidi, I.; Soukissian, T. Offshore Wind and Wave Energy Complementarity in the Greek Seas Based on ERA5 Data. Atmosphere 2021, 12, 1360. [Google Scholar] [CrossRef]
- Zheng, C.-W.; Xiao, Z.-N.; Peng, Y.-H.; Li, C.-Y.; Du, Z.-B. Rezoning global offshore wind energy resources. Renew. Energy 2018, 129, 1–11. [Google Scholar] [CrossRef]
- Zheng, C.W.; Pan, J. Assessment of the global ocean wind energy resource. Renew. Sustain. Energy Rev. 2014, 33, 382–391. [Google Scholar] [CrossRef]
- Medina-Lopez, E.; McMillan, D.; Lazic, J.; Hart, E.; Zen, S.; Angeloudis, A.; Bannon, E.; Browell, J.; Dorling, S.; Dorrell, R.M.; et al. Satellite data for the offshore renewable energy sector: Synergies and innovation opportunities. Remote Sens. Environ. 2021, 264, 112588. [Google Scholar] [CrossRef]
- Soukissian, T.; Karathanasi, F.; Axaopoulos, P. Satellite-Based Offshore Wind Resource Assessment in the Mediterranean Sea. IEEE J. Ocean. Eng. 2017, 42, 73–86. [Google Scholar] [CrossRef]
- Li, X.; Mitsopoulos, P.; Yin, Y.; Peña, M. SARAL-AltiKa Wind and Significant Wave Height for Offshore Wind Energy Applications in the New England Region. Remote Sens. 2021, 13, 57. [Google Scholar] [CrossRef]
- Ahsbahs, T.; Badger, M.; Volker, P.; Hansen, K.S.; Hasager, C.B. Applications of satellite winds for the offshore wind farm site Anholt. Wind Energy Sci. 2018, 3, 573–588. [Google Scholar] [CrossRef]
- de Baar, J.; Nhat Luu, L.; van der Schrier, G.; van den Besselaar, E.; Garcia-Marti, I. Recent improvements in the E-OBS gridded data set for daily mean wind speed over Europe in the period 1980–2021. In Proceedings of the EMS Annual Meeting 2022, Bonn, Germany, 4–9 September 2022. [Google Scholar]
- Zhang, H.; Jeffrey, S.; Carter, J. Improved quality gridded surface wind speed datasets for Australia. Meteorol. Atmos. Phys. 2022, 134, 85. [Google Scholar] [CrossRef]
- Gualtieri, G. Analysing the uncertainties of reanalysis data used for wind resource assessment: A critical review. Renew. Sustain. Energy Rev. 2022, 167, 112741. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L. Projections of extreme storm surge levels along Europe. Clim. Dyn. 2016, 47, 3171–3190. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Characterization of wind resource in China from a new perspective. Energy 2019, 167, 994–1010. [Google Scholar] [CrossRef]
- He, J.; Chan, P.W.; Li, Q.; Lee, C.W. Spatiotemporal analysis of offshore wind field characteristics and energy potential in Hong Kong. Energy 2020, 201, 117622. [Google Scholar] [CrossRef]
- Salvação, N.; Guedes Soares, C. Wind resource assessment offshore the Atlantic Iberian coast with the WRF model. Energy 2018, 145, 276–287. [Google Scholar] [CrossRef]
- Schimanke, S.; Ridal, M.; Le Moigne, P.; Berggren, L.; Undén, P.; Randriamampianina, R.; Andrea, U.; Bazile, E.; Bertelsen, A.; Brousseau, P.; et al. CERRA Sub-Daily Regional Reanalysis Data for Europe on Single Levels from 1984 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Bonn, Germany, 2021; Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-cerra-single-levels?tab=overview (accessed on 10 January 2025).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Galanaki, E.; Giannaros, C.; Agathangelidis, I.; Cartalis, C.; Kotroni, V.; Lagouvardos, K.; Matzarakis, A. Validating the Copernicus European Regional Reanalysis (CERRA) Dataset for Human-Biometeorological Applications. Environ. Sci. Proc. 2023, 26, 111. [Google Scholar] [CrossRef]
- Hadjipetrou, S.; Kyriakidis, P. High-Resolution Wind Speed Estimates for the Eastern Mediterranean Basin: A Statistical Comparison Against Coastal Meteorological Observations. Wind 2024, 4, 311–341. [Google Scholar] [CrossRef]
- Rouholahnejad, F.; Meyer, P.; Gottschall, J. Collocating wind data: A case study on the verification of the CERRA dataset. J. Phys. Conf. Ser. 2024, 2875, 012016. [Google Scholar] [CrossRef]
- Pelosi, A. Performance of the Copernicus European Regional Reanalysis (CERRA) dataset as proxy of ground-based agrometeorological data. Agric. Water Manag. 2023, 289, 108556. [Google Scholar] [CrossRef]
- Jourdier, B.; Diaz, C.; Dubus, L. Evaluation of CERRA for wind energy applications. In Proceedings of the EMS Annual Meeting 2023, Bratislava, Slovakia, 4–9 September 2023. [Google Scholar]
- Spangehl, T.; Borsche, M.; Niermann, D.; Kaspar, F.; Schimanke, S.; Brienen, S.; Möller, T.; Brast, M. Intercomparing the quality of recent reanalyses for offshore wind farm planning in Germany’s exclusive economic zone of the North Sea. Adv. Sci. Res. 2023, 20, 109–128. [Google Scholar] [CrossRef]
- Hahmann, A.N.; Sīle, T.; Witha, B.; Davis, N.N.; Dörenkämper, M.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; Olsen, B.T.; et al. The making of the New European Wind Atlas—Part 1: Model sensitivity. Geosci. Model Dev. 2020, 13, 5053–5078. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Murcia, J.P.; Koivisto, M.J.; Luzia, G.; Olsen, B.T.; Hahmann, A.N.; Sørensen, P.E.; Als, M. Validation of European-scale simulated wind speed and wind generation time series. Appl. Energy 2022, 305, 117794. [Google Scholar] [CrossRef]
- Kalverla, P.C.; Holtslag, A.A.M.; Ronda, R.J.; Steeneveld, G.-J. Quality of wind characteristics in recent wind atlases over the North Sea. Q. J. R. Meteorol. Soc. 2020, 146, 1498–1515. [Google Scholar] [CrossRef]
- Meyer, P.J.; Gottschall, J. How do NEWA and ERA5 compare for assessing offshore wind resources and wind farm siting conditions? J. Phys. Conf. Ser. 2022, 2151, 012009. [Google Scholar] [CrossRef]
- Araveti, S.; Quintana, C.A.; Kairisa, E.; Mutule, A.; Adriazola, J.P.S.; Sweeney, C.; Carroll, P. Wind Energy Assessment for Renewable Energy Communities. Wind 2022, 2, 325–347. [Google Scholar] [CrossRef]
- Jourdier, B. Evaluation of ERA5, MERRA-2, COSMO-REA6, NEWA and AROME to simulate wind power production over France. Adv. Sci. Res. 2020, 17, 63–77. [Google Scholar] [CrossRef]
- Ridal, M.; Bazile, E.; Le Moigne, P.; Randriamampianina, R.; Schimanke, S.; Andrae, U.; Berggren, L.; Brousseau, P.; Dahlgren, P.; Edvinsson, L.; et al. CERRA, the Copernicus European Regional Reanalysis system. Q. J. R. Meteorol. Soc. 2024, 150, 3385–3411. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Randriamampianina, R. The Impact of Assimilating Satellite Radiance Observations in the Copernicus European Regional Reanalysis (CERRA). Remote Sens. 2021, 13, 426. [Google Scholar] [CrossRef]
- El-Said, A.; Brousseau, P.; Ridal, M.; Randriamampianina, R. Towards Full Flow-Dependence: New Temporally Varying EDA Quotient Functionality to Estimate Background Errors in CERRA. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002637. [Google Scholar] [CrossRef]
- Calamia, J. Where the wind blows. New Sci. 2017, 234, 31–33. [Google Scholar] [CrossRef]
- Karagali, I.; Hahmann, A.N.; Badger, M.; Hasager, C.; Mann, J. New European wind atlas offshore. J. Phys. Conf. Ser. 2018, 1037, 052007. [Google Scholar] [CrossRef]
- Mann, J.; Angelou, N.; Arnqvist, J.; Callies, D.; Cantero, E.; Chávez Arroyo, R.; Courtney, M.; Cuxart, J.; Dellwik, E.; Gottschall, J.; et al. Complex terrain experiments in the New European Wind Atlas. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375. [Google Scholar] [CrossRef] [PubMed]
- Olsen, B.T.; Hahmann, A.N.; Sempreviva, A.M.; Badger, J.; Jørgensen, H.E. An intercomparison of mesoscale models at simple sites for wind energy applications. Wind Energy Sci. 2017, 2, 211–228. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Olsen, B.T.; Witha, B.; Hahmann, A.N.; Davis, N.N.; Barcons, J.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; et al. The Making of the New European Wind Atlas—Part 2: Production and evaluation. Geosci. Model Dev. 2020, 13, 5079–5102. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Chronis, G.T.; Nittis, K.; Diamanti, C. Advancement of Operational Oceanography in Greece: The Case of the Poseidon System. J. Atmos. Ocean Sci. 2002, 8, 93–107. [Google Scholar] [CrossRef]
- Copernicus Marine in Situ tac Data Management Team, NetCDF Format Manual Version 2.0.0. 2023, p. 28. Available online: https://archimer.ifremer.fr/doc/00488/59938/ (accessed on 10 January 2025).
- Mears, C.A.; Smith, D.K.; Wentz, F. Comparison of Special Sensor Microwave Imager and buoy-measured wind speeds from 1987 to 1997. J. Geophys. Res. 2001, 106, 719–729. [Google Scholar] [CrossRef]
- Peng, G.; Zhang, H.-M.; Frank, H.P.; Bidlot, J.-R.; Higaki, M.; Stevens, S.; Hankins, W.R. Evaluation of Various Surface Wind Products with OceanSITES Buoy Measurements. Weather Forecast. 2013, 28, 1281–1303. [Google Scholar] [CrossRef]
- Shu, Z.R.; Li, Q.S.; He, Y.C.; Chan, P.W. Observations of offshore wind characteristics by Doppler-LiDAR for wind energy applications. Appl. Energy 2016, 169, 150–163. [Google Scholar] [CrossRef]
- Hansen, F.V. Surface Roughness Lengths; U.S. Army Research Laboratory, White Sands Missile Range: Las Cruces, NM, USA, 1993; pp. 1–40. [Google Scholar]
- Mortensen, N.G.; Landberg, L.; Troen, I.; Petersen, E.L. Wind Analysis and Application Program (WAsP)–User’s Guide (Tech. Rep. I-666(EN)); Risø National Laboratory: Roskilde, Denmark, 1993. [Google Scholar]
- Kim, Y.-H.; Lim, H.-C. Effect of island topography and surface roughness on the estimation of annual energy production of offshore wind farms. Renew. Energy 2017, 103, 106–114. [Google Scholar] [CrossRef]
- Golbazi, M.; Archer, C.L. Methods to Estimate Surface Roughness Length for Offshore Wind Energy. Adv. Meteorol. 2019, 2019, 5695481. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Problems in RMSE-based wave model validations. Ocean Model. 2013, 72, 53–58. [Google Scholar] [CrossRef]
- Hanna, S.R.; Heinold, D.W. Development and Application of a Simple Method for Evaluating Air Quality Models; American Petroleum Institute: Washington, DC, USA, 1985. [Google Scholar]
| Season | North Aegean | South Aegean | ||
|---|---|---|---|---|
| CERRA | ERA5 | CERRA | ERA5 | |
| Winter | 1.65 | 2.88 | 1.21 | 1.01 |
| Spring | 1.34 | 2.42 | 1.69 | 2.29 |
| Summer | 1.13 | 2.79 | 1.65 | 2.25 |
| Autumn | 1.37 | 2.62 | 1.70 | 2.43 |
| Buoy Code | Latitude (o) | Longitude (o) | Measurement Period | Overlapping Time Periods | |
|---|---|---|---|---|---|
| CERRA | NEWA | ||||
| 6100196 | 41.9000 | 3.6500 | 27 March 2001–18 November 2024 | 2001–2020 | 2009–2018 |
| 6100197 | 39.7100 | 4.4200 | 29 April 1993–30 November 2024 | 1993–2020 | 2009–2018 |
| 6100198 | 36.5700 | –2.3400 | 27 March 1998–30 November 2024 | 1998–2020 | 2009–2018 |
| 6100280 | 40.6900 | 1.4700 | 20 August 2004–30 November 2024 | 2004–2020 | 2009–2018 |
| 6100281 | 39.5100 | 0.2000 | 15 September 2005–13 November 2024 | 2005–2020 | 2009–2018 |
| 6100417 | 37.6500 | –0.3100 | 18 July 2006–30 November 2024 | 2006–2020 | 2009–2018 |
| 6100430 | 39.5600 | 2.0900 | 29 November 2006–30 November 2024 | 2006–2020 | 2009–2018 |
| 61277 | 35.7263 | 25.1307 | 28 May 2007–21 November 2024 | 2007–2020 | 2009–2018 |
| 68422 | 36.8288 | 21.6068 | 9 November 2007–1 April 2023 | 2007–2020 | 2009–2018 |
| ATH | 39.9750 | 24.7294 | 25 May 2000–26 November 2022 | 2000–2020 | 2009–2018 |
| HER | 35.4342 | 25.0792 | 15 July 2016–29 October 2024 | 2016–2020 | 2016–2018 |
| SAR | 37.6099 | 23.5669 | 27 August 2007–1 August 2019 | 2007–2019 | 2009–2018 |
| SKY | 39.1130 | 24.4640 | 28 August 2007–18 July 2012 | 2000–2012 | 2009–2012 |
| # | (m/s) | (m/s) | (m/s) | (m/s) | (%) | (%) | (m/s) | (m/s) | (m/s) | (m/s) | (m/s) | (m/s) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6100196 | 33782 | 6.91 | 7.69 | 5.70 | 6.46 | 70.0 | 62.7 | 27.9 | 28.8 | 16.5 | 17.0 | 19.9 | 20.4 |
| 6100197 | 50912 | 6.04 | 6.05 | 5.47 | 5.44 | 59.8 | 56.0 | 24.5 | 22.7 | 13.1 | 12.6 | 16.3 | 15.8 |
| 6100198 | 48341 | 6.03 | 6.56 | 5.47 | 6.14 | 62.1 | 59.2 | 22.2 | 24.3 | 12.8 | 13.4 | 15.9 | 16.7 |
| 6100280 | 43592 | 5.04 | 5.40 | 4.36 | 4.62 | 67.0 | 62.7 | 21.4 | 22.5 | 11.7 | 12.1 | 14.9 | 15.2 |
| 6100281 | 38111 | 5.02 | 5.09 | 4.36 | 4.36 | 64.2 | 61.7 | 21.1 | 20.6 | 11.2 | 11.3 | 14.1 | 13.8 |
| 6100417 | 37063 | 5.41 | 5.73 | 4.97 | 5.31 | 57.4 | 53.6 | 19.9 | 19.7 | 11.2 | 11.5 | 13.8 | 14.0 |
| 6100430 | 36647 | 5.30 | 5.33 | 4.70 | 4.69 | 61.7 | 60.1 | 23.0 | 22.1 | 11.7 | 11.6 | 14.7 | 14.9 |
| 61277 | 24523 | 6.14 | 5.99 | 5.89 | 5.72 | 50.9 | 47.9 | 20.9 | 19.1 | 11.8 | 11.2 | 14.6 | 13.8 |
| 68422 | 24375 | 5.36 | 5.49 | 4.97 | 5.12 | 58.1 | 55.6 | 20.7 | 20.6 | 11.2 | 11.1 | 14.1 | 14.3 |
| ATH | 44736 | 5.30 | 5.94 | 4.54 | 5.18 | 69.5 | 61.7 | 24.5 | 21.9 | 12.4 | 13.0 | 16.2 | 16.1 |
| HER | 8734 | 6.12 | 5.33 | 6.09 | 5.39 | 49.3 | 50.4 | 20.1 | 18.2 | 10.9 | 9.5 | 14.1 | 12.9 |
| SAR | 21407 | 5.15 | 4.90 | 4.81 | 4.62 | 60.1 | 56.5 | 19.3 | 19.0 | 10.7 | 9.7 | 13.1 | 12.5 |
| SKY | 10676 | 5.63 | 6.26 | 5.10 | 5.87 | 62.3 | 55.5 | 20.9 | 21.3 | 12.1 | 12.6 | 15.2 | 15.6 |
| # | (m/s) | (m/s) | (m/s) | (m/s) | (%) | (%) | (m/s) | (m/s) | (m/s) | (m/s) | (m/s) | (m/s) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6100196 | 76427 | 6.94 | 7.65 | 5.70 | 6.43 | 69.6 | 64.6 | 26.7 | 27.4 | 16.4 | 17.7 | 19.9 | 21.8 |
| 6100197 | 98096 | 6.08 | 6.51 | 5.47 | 6.03 | 59.8 | 55.1 | 24.8 | 25.3 | 13.1 | 13.3 | 16.4 | 16.9 |
| 6100198 | 89363 | 6.11 | 7.36 | 5.70 | 7.22 | 61.6 | 54.5 | 23.0 | 25.1 | 12.8 | 14.2 | 15.9 | 17.6 |
| 6100280 | 113775 | 5.02 | 5.53 | 4.36 | 4.73 | 66.9 | 63.5 | 21.9 | 24.7 | 11.7 | 12.8 | 14.7 | 16.6 |
| 6100281 | 99809 | 5.02 | 5.26 | 4.36 | 4.53 | 63.8 | 62.4 | 21.1 | 24.3 | 11.2 | 11.7 | 13.9 | 15.1 |
| 6100417 | 92900 | 5.40 | 6.15 | 4.97 | 5.86 | 57.9 | 52.1 | 19.9 | 22.4 | 11.2 | 11.9 | 13.8 | 14.8 |
| 6100430 | 94425 | 5.32 | 5.81 | 4.91 | 5.28 | 61.4 | 58.5 | 24.8 | 22.4 | 11.7 | 12.3 | 14.7 | 15.8 |
| 1277 | 20009 | 6.05 | 6.62 | 5.84 | 6.50 | 51.4 | 47.4 | 20.9 | 21.6 | 11.8 | 12.3 | 14.4 | 15.2 |
| 8422 | 22851 | 5.37 | 6.22 | 4.97 | 6.02 | 58.4 | 53.3 | 20.7 | 25.6 | 11.2 | 12.1 | 14.1 | 15.4 |
| ATH | 31509 | 5.50 | 5.92 | 4.71 | 5.31 | 65.7 | 60.6 | 22.5 | 23.7 | 12.6 | 12.7 | 16.0 | 16.0 |
| HER | 6102 | 6.07 | 6.69 | 5.96 | 6.86 | 51.1 | 49.7 | 20.1 | 24.0 | 11.2 | 12.1 | 14.4 | 15.3 |
| SAR | 21048 | 5.15 | 5.34 | 4.79 | 4.94 | 60.3 | 59.5 | 19.3 | 21.4 | 10.7 | 11.2 | 13.1 | 14.4 |
| SKY | 10455 | 5.62 | 6.35 | 5.09 | 6.01 | 62.4 | 55.9 | 20.9 | 22.4 | 12.1 | 12.8 | 15.2 | 16.4 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 2.172 | 2.827 | –0.780 | –0.713 | 0.912 | 0.844 | 1.604 | 2.120 | 0.293 | 0.394 | 0.252 | 0.330 |
| 6100197 | 1.781 | 2.391 | –0.009 | –0.435 | 0.872 | 0.788 | 1.292 | 1.779 | 0.295 | 0.387 | 0.259 | 0.339 |
| 6100198 | 1.971 | 2.856 | –0.534 | –1.250 | 0.877 | 0.784 | 1.461 | 2.203 | 0.315 | 0.420 | 0.273 | 0.379 |
| 6100280 | 1.895 | 2.534 | –0.360 | –0.515 | 0.849 | 0.740 | 1.410 | 1.920 | 0.369 | 0.495 | 0.312 | 0.420 |
| 6100281 | 1.794 | 2.462 | –0.072 | –0.241 | 0.841 | 0.714 | 1.315 | 1.850 | 0.357 | 0.489 | 0.307 | 0.423 |
| 6100417 | 1.618 | 2.354 | –0.324 | –0.755 | 0.868 | 0.752 | 1.197 | 1.789 | 0.293 | 0.413 | 0.258 | 0.369 |
| 6100430 | 1.840 | 2.533 | –0.024 | –0.486 | 0.839 | 0.723 | 1.361 | 1.901 | 0.347 | 0.467 | 0.302 | 0.406 |
| 61277 | 1.791 | 2.334 | 0.151 | –0.575 | 0.826 | 0.738 | 1.303 | 1.688 | 0.291 | 0.374 | 0.270 | 0.339 |
| 68422 | 1.829 | 2.461 | –0.129 | –0.847 | 0.826 | 0.744 | 1.362 | 1.868 | 0.340 | 0.430 | 0.299 | 0.384 |
| ATH | 2.245 | 2.451 | –0.643 | –0.423 | 0.829 | 0.775 | 1.592 | 1.830 | 0.406 | 0.439 | 0.344 | 0.375 |
| HER | 1.855 | 2.477 | 0.796 | –0.623 | 0.834 | 0.723 | 1.450 | 1.792 | 0.274 | 0.395 | 0.296 | 0.357 |
| SAR | 2.001 | 2.517 | 0.254 | –0.192 | 0.777 | 0.681 | 1.524 | 1.921 | 0.385 | 0.488 | 0.354 | 0.430 |
| SKY | 2.536 | 2.828 | –0.636 | –0.721 | 0.753 | 0.700 | 1.623 | 1.926 | 0.436 | 0.486 | 0.380 | 0.424 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 2.200 | 2.828 | −0.804 | −0.709 | 0.910 | 0.843 | 1.622 | 2.121 | 0.296 | 0.395 | 0.255 | 0.331 |
| 6100197 | 1.784 | 2.396 | 0.004 | −0.434 | 0.872 | 0.787 | 1.294 | 1.782 | 0.295 | 0.388 | 0.260 | 0.339 |
| 6100198 | 1.981 | 2.869 | −0.534 | −1.266 | 0.876 | 0.784 | 1.468 | 2.213 | 0.317 | 0.422 | 0.274 | 0.380 |
| 6100280 | 1.918 | 2.544 | −0.371 | −0.525 | 0.846 | 0.739 | 1.426 | 1.927 | 0.373 | 0.496 | 0.315 | 0.421 |
| 6100281 | 1.829 | 2.461 | −0.111 | −0.215 | 0.837 | 0.714 | 1.338 | 1.847 | 0.364 | 0.489 | 0.312 | 0.424 |
| 6100417 | 1.622 | 2.355 | −0.320 | −0.752 | 0.868 | 0.752 | 1.198 | 1.789 | 0.294 | 0.413 | 0.259 | 0.037 |
| 6100430 | 1.887 | 2.534 | −0.154 | −0.475 | 0.831 | 0.723 | 1.392 | 1.902 | 0.356 | 0.047 | 0.310 | 0.406 |
| 61277 | 1.808 | 2.338 | 0.122 | −0.577 | 0.823 | 0.737 | 1.312 | 1.691 | 0.294 | 0.375 | 0.272 | 0.340 |
| 68422 | 1.874 | 2.468 | −0.231 | −0.853 | 0.823 | 0.744 | 1.394 | 1.874 | 0.347 | 0.431 | 0.304 | 0.385 |
| ATH | 2.259 | 2.452 | −0.640 | −0.401 | 0.827 | 0.775 | 1.602 | 1.830 | 0.409 | 0.440 | 0.346 | 0.376 |
| HER | 2.051 | 2.507 | 1.151 | −0.673 | 0.828 | 0.728 | 1.623 | 1.810 | 0.277 | 0.398 | 0.338 | 0.360 |
| SAR | 2.002 | 2.540 | 0.254 | −0.212 | 0.777 | 0.679 | 1.525 | 1.935 | 0.385 | 0.492 | 0.354 | 0.433 |
| SKY | 2.543 | 2.832 | −0.636 | −0.720 | 0.752 | 0.699 | 1.633 | 1.930 | 0.438 | 0.487 | 0.382 | 0.043 |
| Buoy | (W/m2) | Relative Difference % | ||||
|---|---|---|---|---|---|---|
| 6100196 | 559.701 | 662.476 | 559.580 | 689.487 | −18.362 | −23.215 |
| 6100197 | 303.229 | 283.048 | 308.756 | 346.157 | 6.655 | −12.113 |
| 6100198 | 309.574 | 374.687 | 317.960 | 477.538 | −21.033 | −50.188 |
| 6100280 | 206.834 | 233.209 | 203.087 | 259.759 | −12.752 | −27.905 |
| 6100281 | 190.242 | 190.123 | 188.398 | 215.610 | 0.063 | −14.444 |
| 6100417 | 204.459 | 226.621 | 205.257 | 270.951 | −10.839 | −32.006 |
| 6100430 | 213.590 | 213.585 | 214.737 | 264.035 | 0.002 | −22.957 |
| 61277 | 261.397 | 230.168 | 253.010 | 308.039 | 11.947 | −21.750 |
| 68422 | 203.865 | 208.952 | 205.399 | 286.709 | −2.495 | −39.586 |
| ATH | 251.887 | 300.366 | 260.548 | 290.285 | −19.246 | −11.413 |
| HER | 248.682 | 168.855 | 251.954 | 326.835 | 32.100 | −29.720 |
| SAR | 185.093 | 148.965 | 184.987 | 207.414 | 19.519 | −12.124 |
| SKY | 254.582 | 305.446 | 254.598 | 321.297 | −19.979 | −26.198 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 1.880 | 2.748 | −0.049 | −0.332 | 0.707 | 0.619 | 1.420 | 2.067 | 0.209 | 0.441 | 0.012 | 0.026 |
| 6100197 | 2.333 | 2.640 | 1.102 | 0.812 | 0.642 | 0.587 | 1.715 | 1.931 | 0.315 | 0.467 | 0.032 | 0.040 |
| 6100198 | 1.819 | 2.533 | −0.026 | −0.270 | 0.695 | 0.570 | 1.327 | 1.851 | 0.249 | 0.473 | 0.018 | 0.034 |
| 6100280 | 2.162 | 3.144 | 0.450 | 0.432 | 0.635 | 0.543 | 1.604 | 2.417 | 0.369 | 0.802 | 0.032 | 0.068 |
| 6100281 | 2.080 | 3.155 | 0.802 | 1.004 | 0.608 | 0.458 | 1.524 | 2.420 | 0.316 | 0.776 | 0.033 | 0.080 |
| 6100417 | 1.778 | 2.590 | 0.381 | 0.442 | 0.643 | 0.487 | 1.319 | 1.931 | 0.261 | 0.562 | 0.024 | 0.051 |
| 6100430 | 2.238 | 2.923 | 0.705 | 0.667 | 0.634 | 0.496 | 1.625 | 2.146 | 0.374 | 0.672 | 0.036 | 0.061 |
| 61277 | 2.227 | 2.456 | 1.368 | 0.646 | 0.613 | 0.545 | 1.697 | 1.770 | 0.252 | 0.464 | 0.037 | 0.043 |
| 68422 | 2.066 | 2.368 | 0.698 | 0.140 | 0.650 | 0.586 | 1.483 | 1.727 | 0.328 | 0.484 | 0.033 | 0.042 |
| ATH | 1.974 | 2.806 | 0.377 | 1.004 | 0.692 | 0.546 | 1.437 | 2.036 | 0.290 | 0.527 | 0.023 | 0.049 |
| HER | 2.667 | 2.494 | 1.995 | 0.448 | 0.656 | 0.576 | 2.166 | 1.771 | 0.272 | 0.509 | 0.063 | 0.045 |
| SAR | 2.810 | 2.995 | 1.936 | 1.061 | 0.511 | 0.463 | 2.292 | 2.347 | 0.374 | 0.707 | 0.076 | 0.079 |
| SKY | 1.949 | 2.520 | 0.611 | 0.741 | 0.663 | 0.570 | 1.355 | 1.848 | 0.274 | 0.463 | 0.025 | 0.042 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 1.892 | 2.617 | 0.174 | −0.443 | 0.613 | 0.524 | 1.436 | 1.987 | 0.190 | 0.360 | 0.010 | 0.019 |
| 6100197 | 2.501 | 2.712 | 1.301 | 0.907 | 0.533 | 0.502 | 1.845 | 1.985 | 0.303 | 0.437 | 0.030 | 0.035 |
| 6100198 | 1.923 | 2.615 | −0.038 | −0.238 | 0.618 | 0.520 | 1.426 | 1.890 | 0.252 | 0.459 | 0.017 | 0.031 |
| 6100280 | 2.180 | 3.099 | 0.557 | 0.282 | 0.568 | 0.457 | 1.586 | 2.328 | 0.328 | 0.704 | 0.027 | 0.053 |
| 6100281 | 2.110 | 3.298 | 0.946 | 1.119 | 0.564 | 0.405 | 1.537 | 2.505 | 0.275 | 0.752 | 0.028 | 0.072 |
| 6100417 | 1.812 | 2.738 | 0.468 | 0.530 | 0.582 | 0.415 | 1.335 | 2.023 | 0.241 | 0.568 | 0.021 | 0.048 |
| 6100430 | 2.390 | 3.080 | 0.828 | 0.852 | 0.558 | 0.407 | 1.715 | 2.233 | 0.372 | 0.647 | 0.033 | 0.055 |
| 61277 | 2.429 | 2.580 | 1.577 | 0.777 | 0.563 | 0.510 | 1.874 | 1.880 | 0.255 | 0.453 | 0.037 | 0.039 |
| 68422 | 2.141 | 2.371 | 0.737 | 0.168 | 0.605 | 0.561 | 1.534 | 1.749 | 0.314 | 0.434 | 0.029 | 0.034 |
| ATH | 1.974 | 3.011 | 0.612 | 1.255 | 0.648 | 0.479 | 1.428 | 2.165 | 0.240 | 0.515 | 0.019 | 0.046 |
| HER | 2.964 | 2.772 | 2.135 | 0.436 | 0.620 | 0.492 | 2.344 | 2.046 | 0.333 | 0.570 | 0.064 | 0.045 |
| SAR | 3.085 | 3.056 | 2.180 | 1.028 | 0.461 | 0.396 | 2.516 | 2.374 | 0.390 | 0.679 | 0.077 | 0.068 |
| SKY | 2.082 | 2.683 | 0.820 | 0.959 | 0.616 | 0.543 | 1.416 | 1.961 | 0.261 | 0.447 | 0.023 | 0.039 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 2.252 | 3.104 | −0.639 | −0.898 | 0.921 | 0.853 | 1.630 | 2.314 | 0.252 | 0.346 | 0.219 | 0.300 |
| 6100197 | 1.838 | 2.560 | 0.005 | −0.469 | 0.893 | 0.806 | 1.363 | 1.881 | 0.249 | 0.341 | 0.222 | 0.304 |
| 6100198 | 1.987 | 2.734 | −0.265 | −0.768 | 0.887 | 0.805 | 1.439 | 2.060 | 0.313 | 0.420 | 0.265 | 0.360 |
| 6100280 | 2.068 | 2.786 | −0.482 | −0.652 | 0.861 | 0.763 | 1.564 | 2.141 | 0.323 | 0.441 | 0.281 | 0.381 |
| 6100281 | 1.844 | 2.702 | 0.001 | −0.188 | 0.877 | 0.756 | 1.370 | 2.047 | 0.315 | 0.459 | 0.271 | 0.396 |
| 6100417 | 1.774 | 2.463 | −0.345 | −0.619 | 0.867 | 0.764 | 1.321 | 1.865 | 0.290 | 0.391 | 0.256 | 0.348 |
| 6100430 | 1.981 | 2.673 | −0.264 | −0.741 | 0.865 | 0.781 | 1.459 | 1.987 | 0.317 | 0.411 | 0.274 | 0.359 |
| 61277 | 2.108 | 2.822 | 0.099 | −0.674 | 0.838 | 0.749 | 1.542 | 2.069 | 0.301 | 0.398 | 0.273 | 0.355 |
| 68422 | 1.956 | 2.696 | 0.142 | −0.680 | 0.847 | 0.756 | 1.475 | 2.020 | 0.302 | 0.404 | 0.273 | 0.359 |
| ATH | 3.002 | 2.714 | −1.058 | −0.517 | 0.790 | 0.796 | 2.004 | 2.039 | 0.450 | 0.409 | 0.386 | 0.352 |
| HER | 2.111 | 2.991 | 0.639 | −0.723 | 0.829 | 0.726 | 1.593 | 2.236 | 0.308 | 0.438 | 0.304 | 0.387 |
| SAR | 2.158 | 2.720 | 0.449 | −0.375 | 0.816 | 0.737 | 1.644 | 2.087 | 0.350 | 0.447 | 0.328 | 0.390 |
| SKY | 3.223 | 3.475 | −0.949 | −1.066 | 0.697 | 0.657 | 2.105 | 2.368 | 0.452 | 0.486 | 0.404 | 0.434 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 2.155 | 2.912 | −0.748 | −0.694 | 0.911 | 0.830 | 1.583 | 2.181 | 0.295 | 0.412 | 0.252 | 0.345 |
| 6100197 | 1.799 | 2.520 | −0.278 | −0.768 | 0.864 | 0.769 | 1.330 | 1.927 | 0.304 | 0.404 | 0.266 | 0.358 |
| 6100198 | 2.006 | 3.053 | −0.672 | −1.521 | 0.890 | 0.792 | 1.471 | 2.370 | 0.290 | 0.406 | 0.257 | 0.377 |
| 6100280 | 1.937 | 2.562 | −0.482 | −0.628 | 0.848 | 0.734 | 1.438 | 1.942 | 0.375 | 0.498 | 0.317 | 0.424 |
| 6100281 | 1.846 | 2.491 | −0.220 | −0.421 | 0.824 | 0.687 | 1.364 | 1.892 | 0.371 | 0.499 | 0.320 | 0.434 |
| 6100417 | 1.715 | 2.556 | −0.503 | −1.038 | 0.869 | 0.739 | 1.278 | 1.956 | 0.292 | 0.420 | 0.261 | 0.384 |
| 6100430 | 1.883 | 2.599 | −0.164 | −0.671 | 0.826 | 0.696 | 1.400 | 1.982 | 0.358 | 0.478 | 0.311 | 0.420 |
| 61277 | 1.888 | 2.422 | 0.068 | −0.536 | 0.834 | 0.751 | 1.380 | 1.795 | 0.321 | 0.411 | 0.288 | 0.363 |
| 68422 | 1.773 | 2.378 | −0.129 | −0.837 | 0.839 | 0.751 | 1.304 | 1.798 | 0.323 | 0.407 | 0.285 | 0.367 |
| ATH | 2.264 | 2.601 | −0.696 | −0.615 | 0.823 | 0.722 | 1.657 | 1.969 | 0.424 | 0.502 | 0.357 | 0.429 |
| HER | 1.950 | 2.600 | 0.544 | −0.699 | 0.808 | 0.725 | 1.501 | 1.980 | 0.352 | 0.475 | 0.341 | 0.414 |
| SAR | 1.994 | 2.520 | 0.071 | −0.432 | 0.748 | 0.639 | 1.512 | 1.917 | 0.436 | 0.543 | 0.388 | 0.474 |
| SKY | 2.644 | 2.875 | −0.806 | −0.864 | 0.722 | 0.669 | 1.793 | 2.088 | 0.520 | 0.566 | 0.443 | 0.484 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 2.189 | 2.630 | −1.017 | −0.697 | 0.878 | 0.792 | 1.633 | 1.999 | 0.351 | 0.448 | 0.311 | 0.379 |
| 6100197 | 1.562 | 2.058 | 0.078 | −0.288 | 0.833 | 0.708 | 1.152 | 1.558 | 0.321 | 0.429 | 0.290 | 0.382 |
| 6100198 | 2.069 | 2.982 | −0.809 | −1.763 | 0.839 | 0.751 | 1.578 | 2.347 | 0.361 | 0.439 | 0.322 | 0.429 |
| 6100280 | 1.618 | 2.137 | −0.152 | −0.214 | 0.777 | 0.613 | 1.197 | 1.614 | 0.412 | 0.542 | 0.359 | 0.480 |
| 6100281 | 1.616 | 2.017 | −0.033 | −0.082 | 0.767 | 0.630 | 1.182 | 1.519 | 0.382 | 0.474 | 0.342 | 0.431 |
| 6100417 | 1.470 | 2.043 | −0.326 | −0.803 | 0.835 | 0.722 | 1.094 | 1.585 | 0.306 | 0.407 | 0.274 | 0.375 |
| 6100430 | 1.686 | 2.253 | 0.222 | −0.083 | 0.741 | 0.553 | 1.261 | 1.709 | 0.387 | 0.520 | 0.363 | 0.478 |
| 61277 | 1.358 | 1.754 | 0.135 | −0.787 | 0.787 | 0.708 | 1.058 | 1.327 | 0.225 | 0.264 | 0.218 | 0.268 |
| 68422 | 1.726 | 2.328 | −0.465 | −1.203 | 0.774 | 0.692 | 1.310 | 1.836 | 0.371 | 0.445 | 0.333 | 0.426 |
| ATH | 1.855 | 2.174 | −0.460 | −0.350 | 0.790 | 0.705 | 1.396 | 1.658 | 0.408 | 0.468 | 0.353 | 0.410 |
| HER | 1.715 | 2.146 | 1.075 | −0.864 | 0.856 | 0.701 | 1.422 | 1.505 | 0.190 | 0.290 | 0.251 | 0.286 |
| SAR | 1.873 | 2.348 | −0.071 | −0.157 | 0.732 | 0.605 | 1.415 | 1.803 | 0.399 | 0.500 | 0.360 | 0.453 |
| SKY | 1.593 | 1.869 | −0.321 | −0.398 | 0.839 | 0.796 | 1.136 | 1.373 | 0.312 | 0.362 | 0.278 | 0.321 |
| Buoy | (m/s) | (m/s) | (m/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | N | C | N | C | N | C | N | C | N | C | N | |
| 6100196 | 2.106 | 2.703 | −0.682 | −0.592 | 0.914 | 0.853 | 1.574 | 2.031 | 0.283 | 0.380 | 0.242 | 0.318 |
| 6100197 | 1.934 | 2.411 | 0.107 | −0.229 | 0.848 | 0.770 | 1.349 | 1.764 | 0.308 | 0.383 | 0.278 | 0.340 |
| 6100198 | 1.842 | 2.649 | −0.430 | −1.014 | 0.875 | 0.780 | 1.382 | 2.051 | 0.304 | 0.405 | 0.265 | 0.364 |
| 6100280 | 1.944 | 2.621 | −0.347 | −0.577 | 0.834 | 0.718 | 1.454 | 1.995 | 0.374 | 0.508 | 0.319 | 0.433 |
| 6100281 | 1.853 | 2.555 | −0.053 | −0.274 | 0.831 | 0.690 | 1.343 | 1.917 | 0.368 | 0.511 | 0.318 | 0.443 |
| 6100417 | 1.522 | 2.351 | −0.149 | −0.582 | 0.881 | 0.751 | 1.117 | 1.773 | 0.280 | 0.422 | 0.246 | 0.371 |
| 6100430 | 1.809 | 2.589 | 0.083 | −0.456 | 0.841 | 0.703 | 1.334 | 1.930 | 0.329 | 0.465 | 0.292 | 0.408 |
| 61277 | 1.763 | 2.274 | 0.253 | −0.354 | 0.803 | 0.702 | 1.265 | 1.621 | 0.303 | 0.395 | 0.287 | 0.358 |
| 68422 | 1.859 | 2.439 | −0.043 | −0.644 | 0.801 | 0.726 | 1.368 | 1.825 | 0.362 | 0.459 | 0.321 | 0.402 |
| ATH | 1.940 | 2.321 | −0.487 | −0.239 | 0.874 | 0.802 | 1.442 | 1.688 | 0.328 | 0.389 | 0.281 | 0.337 |
| HER | 1.774 | 2.276 | 0.776 | −0.342 | 0.819 | 0.693 | 1.377 | 1.632 | 0.285 | 0.405 | 0.312 | 0.367 |
| SAR | 2.002 | 2.505 | 0.588 | 0.143 | 0.781 | 0.670 | 1.549 | 1.905 | 0.353 | 0.464 | 0.351 | 0.425 |
| SKY | 2.503 | 2.890 | −0.544 | −0.615 | 0.745 | 0.659 | 1.546 | 1.928 | 0.425 | 0.496 | 0.373 | 0.438 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soukissian, T.; Apostolou, V.; Koutri, N.-E. A Systematic Evaluation of the New European Wind Atlas and the Copernicus European Regional Reanalysis Wind Datasets in the Mediterranean Sea. J. Mar. Sci. Eng. 2025, 13, 1445. https://doi.org/10.3390/jmse13081445
Soukissian T, Apostolou V, Koutri N-E. A Systematic Evaluation of the New European Wind Atlas and the Copernicus European Regional Reanalysis Wind Datasets in the Mediterranean Sea. Journal of Marine Science and Engineering. 2025; 13(8):1445. https://doi.org/10.3390/jmse13081445
Chicago/Turabian StyleSoukissian, Takvor, Vasilis Apostolou, and Natalia-Elona Koutri. 2025. "A Systematic Evaluation of the New European Wind Atlas and the Copernicus European Regional Reanalysis Wind Datasets in the Mediterranean Sea" Journal of Marine Science and Engineering 13, no. 8: 1445. https://doi.org/10.3390/jmse13081445
APA StyleSoukissian, T., Apostolou, V., & Koutri, N.-E. (2025). A Systematic Evaluation of the New European Wind Atlas and the Copernicus European Regional Reanalysis Wind Datasets in the Mediterranean Sea. Journal of Marine Science and Engineering, 13(8), 1445. https://doi.org/10.3390/jmse13081445







