A Heave Motion Prediction Approach Based on Sparse Bayesian Learning Incorporated with Empirical Mode Decomposition for an Underwater Towed System
Abstract
1. Introduction
- A simplified heave motion model of a towing ship is developed based on strip theory, and an approach for parameter estimation is proposed, thereby enhancing the prediction reliability and model adaptability.
- The EMD is employed to eliminate the high-frequency noise of the measurement data to restore low-frequency towing ship motion. Meanwhile, the SBL is utilized to train the weight parameters in the built model to predict heave motion, which not only reconstruct heave motion from non-stationary sensor signals with noise but also prevent overfitting.
- The depth compensation of the towed vehicle is then performed using the predicted heave motion. Moreover, the compensation results show that the predicted depth compensation effect of the towed vehicle is significantly superior to that without prediction.
2. System Modeling and Problem Formulation
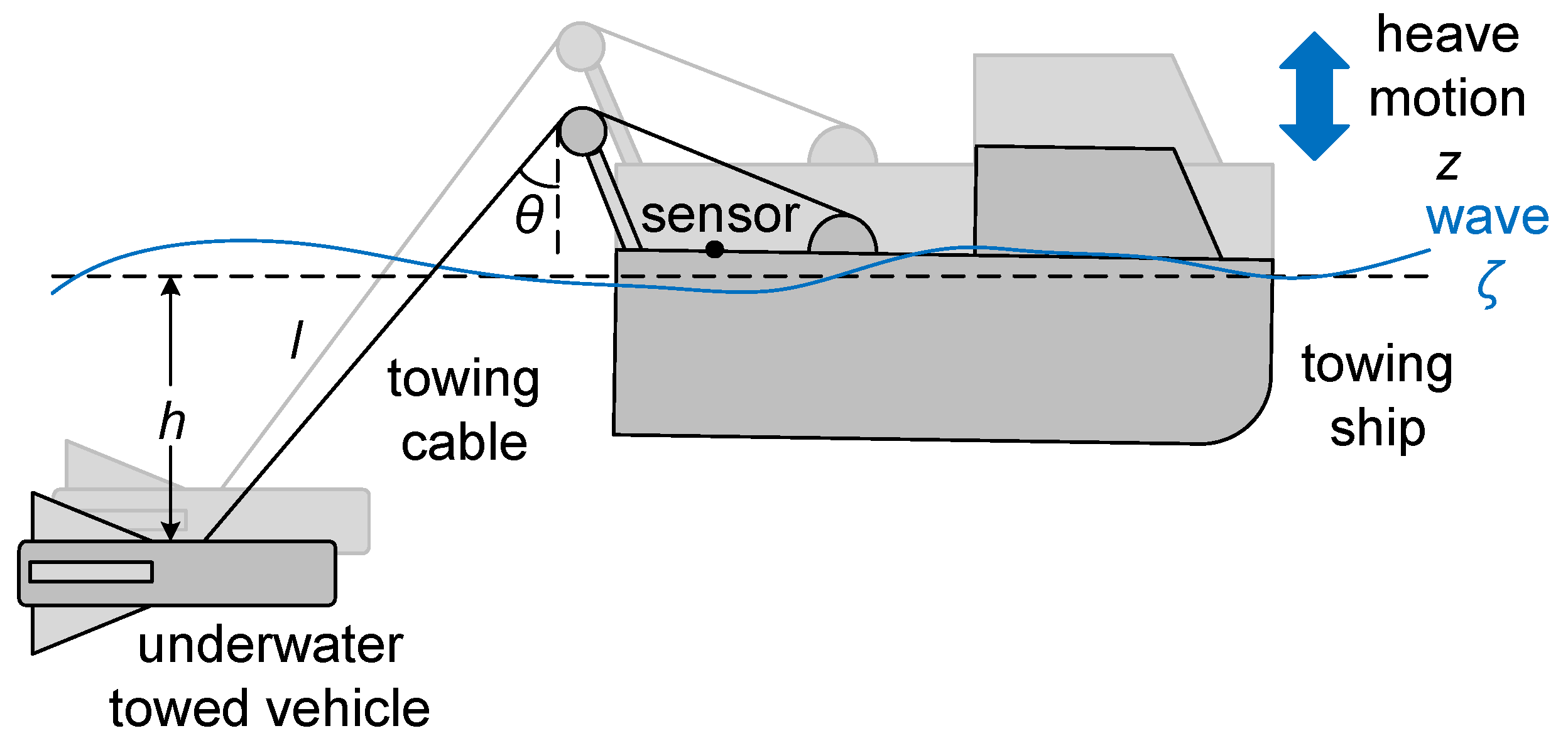
2.1. System Modeling
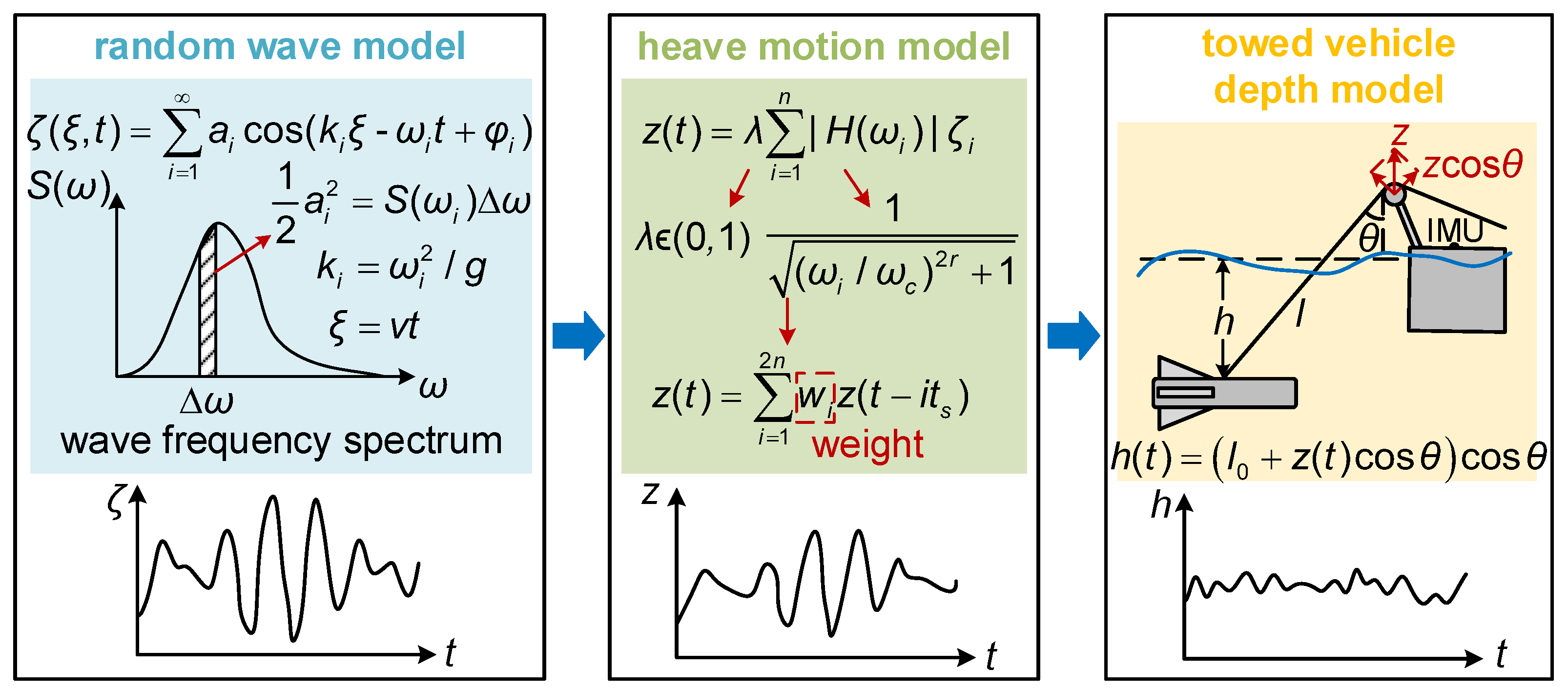
2.1.1. Random Wave Model
2.1.2. Heave Motion Model with Random Surface Wave
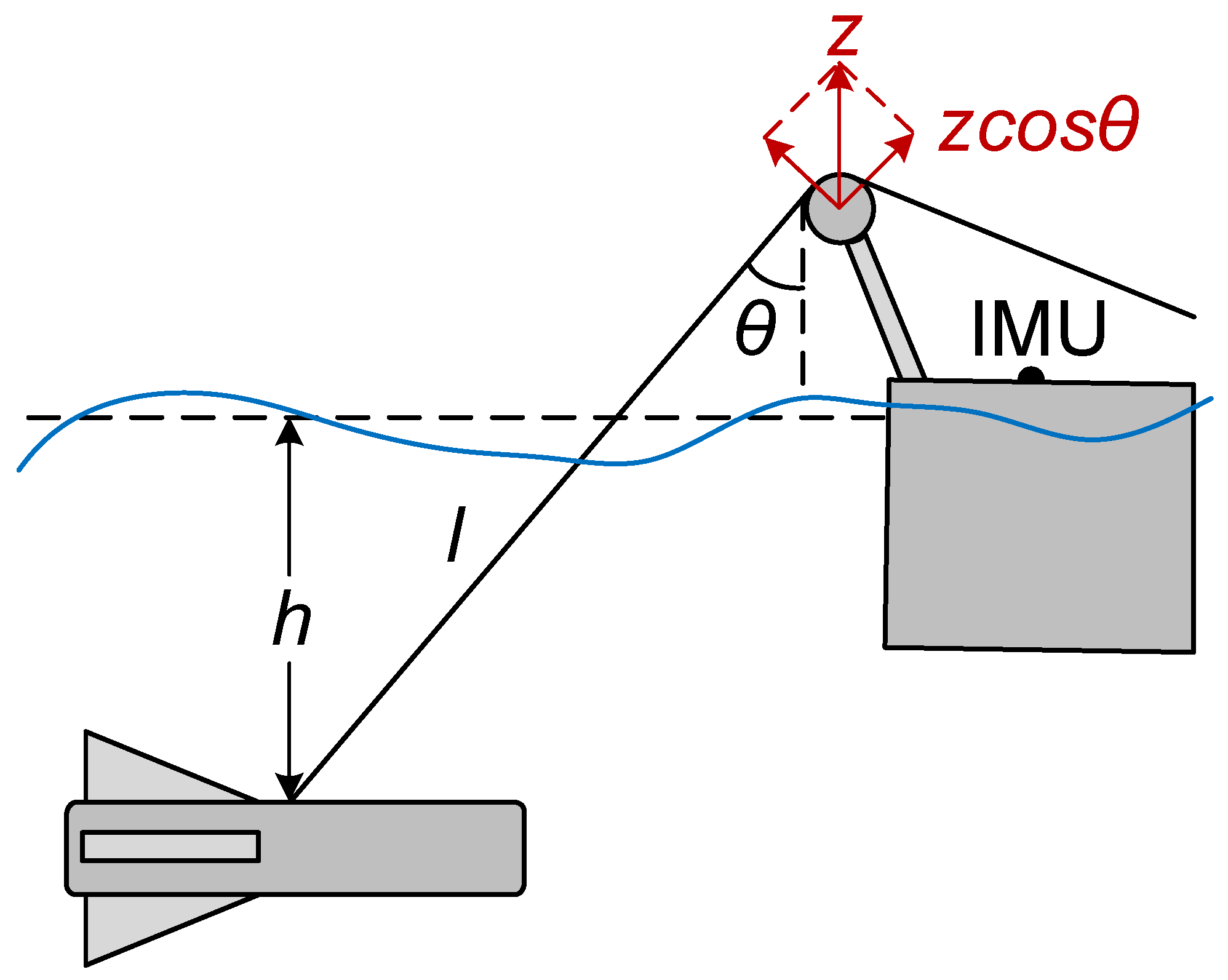
2.1.3. The Depth Model of the Towed Vehicle
2.2. Problem Formulation
3. EMD-SBL for Heave Motion Prediction
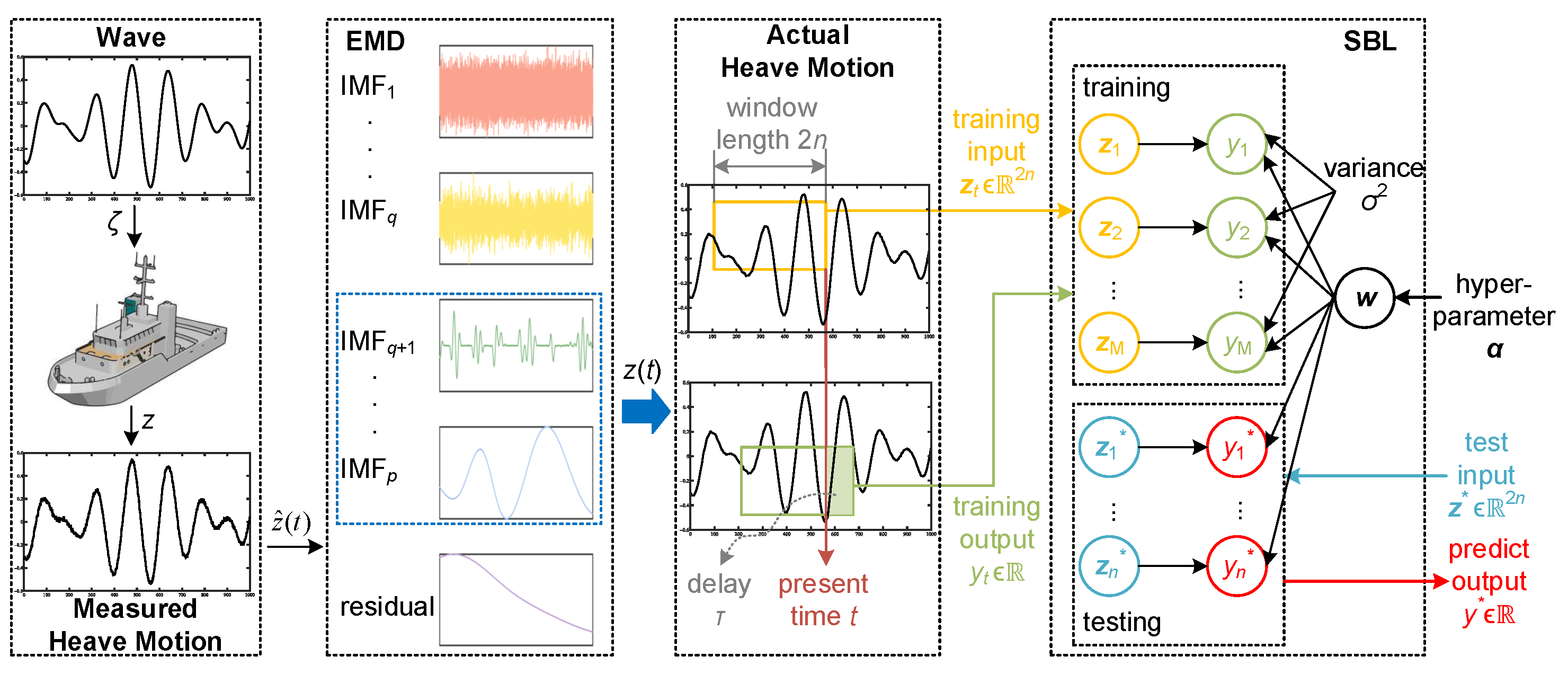
3.1. Overview of EMD-SBL
3.2. Empirical Mode Decomposition
3.3. Heave Motion Prediction Based on Sparse Bayesian Learning
4. Results and Discussion
4.1. Experiment Setup
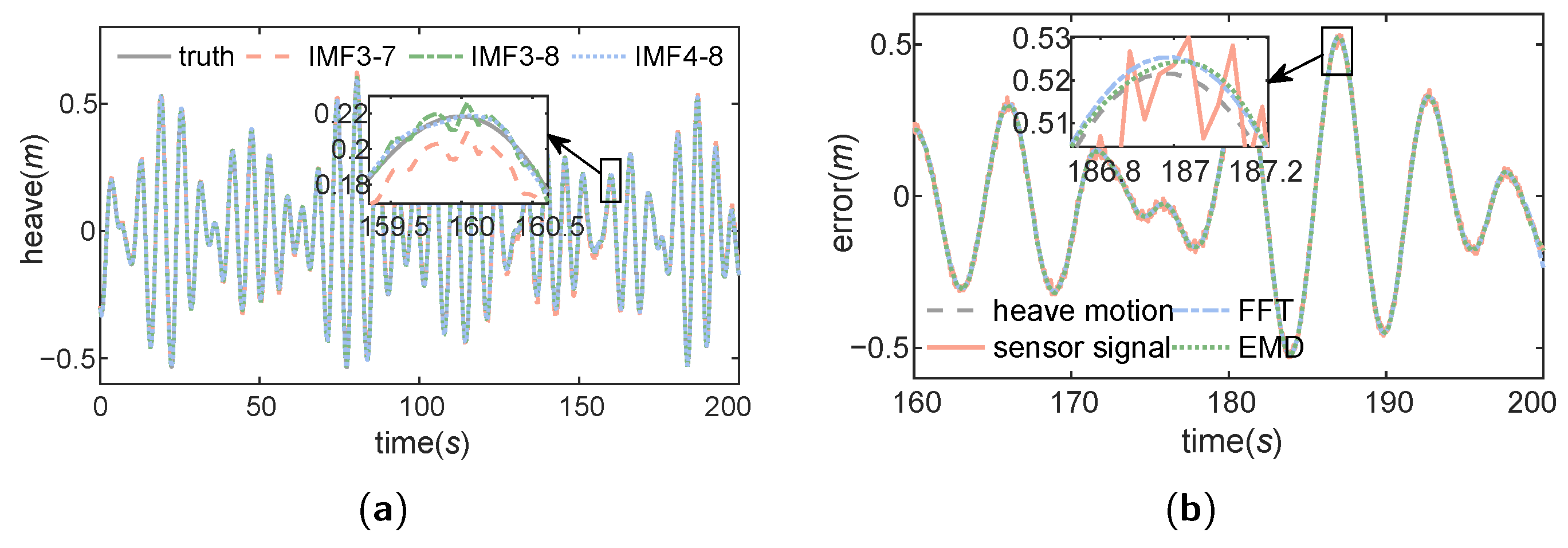
4.2. EMD Ablation Experiments
4.3. Training Results of the EMD-SBL-Based Heave Motion Prediction Model
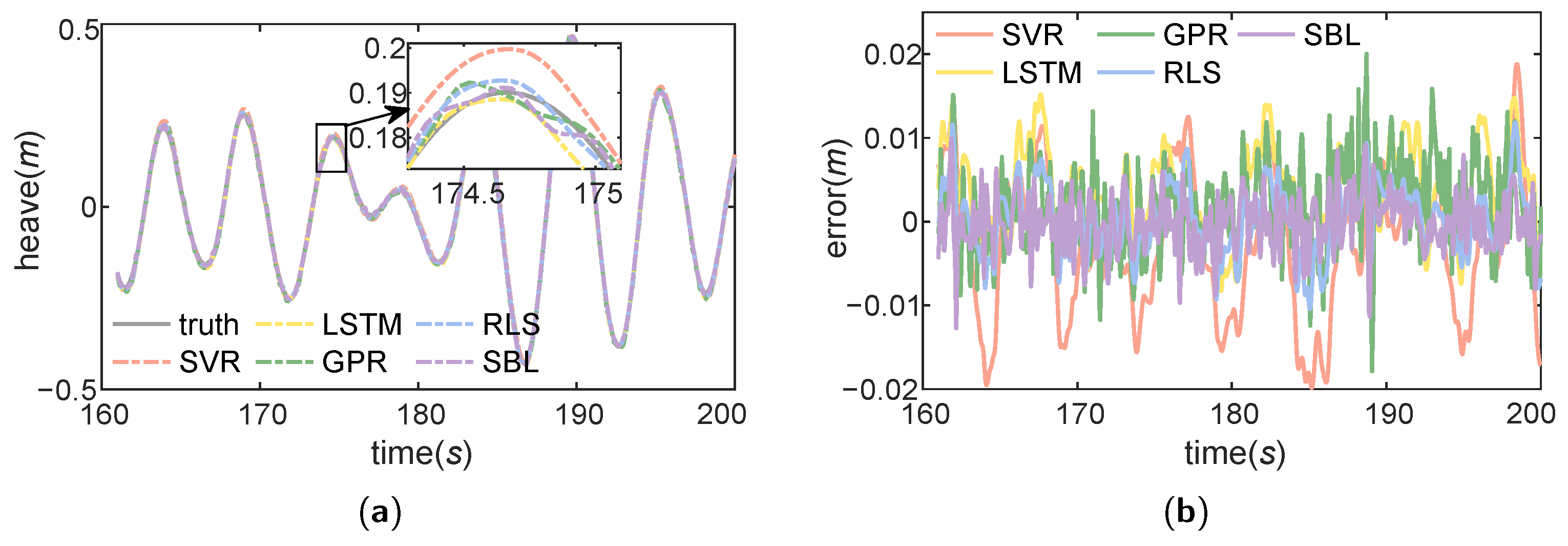
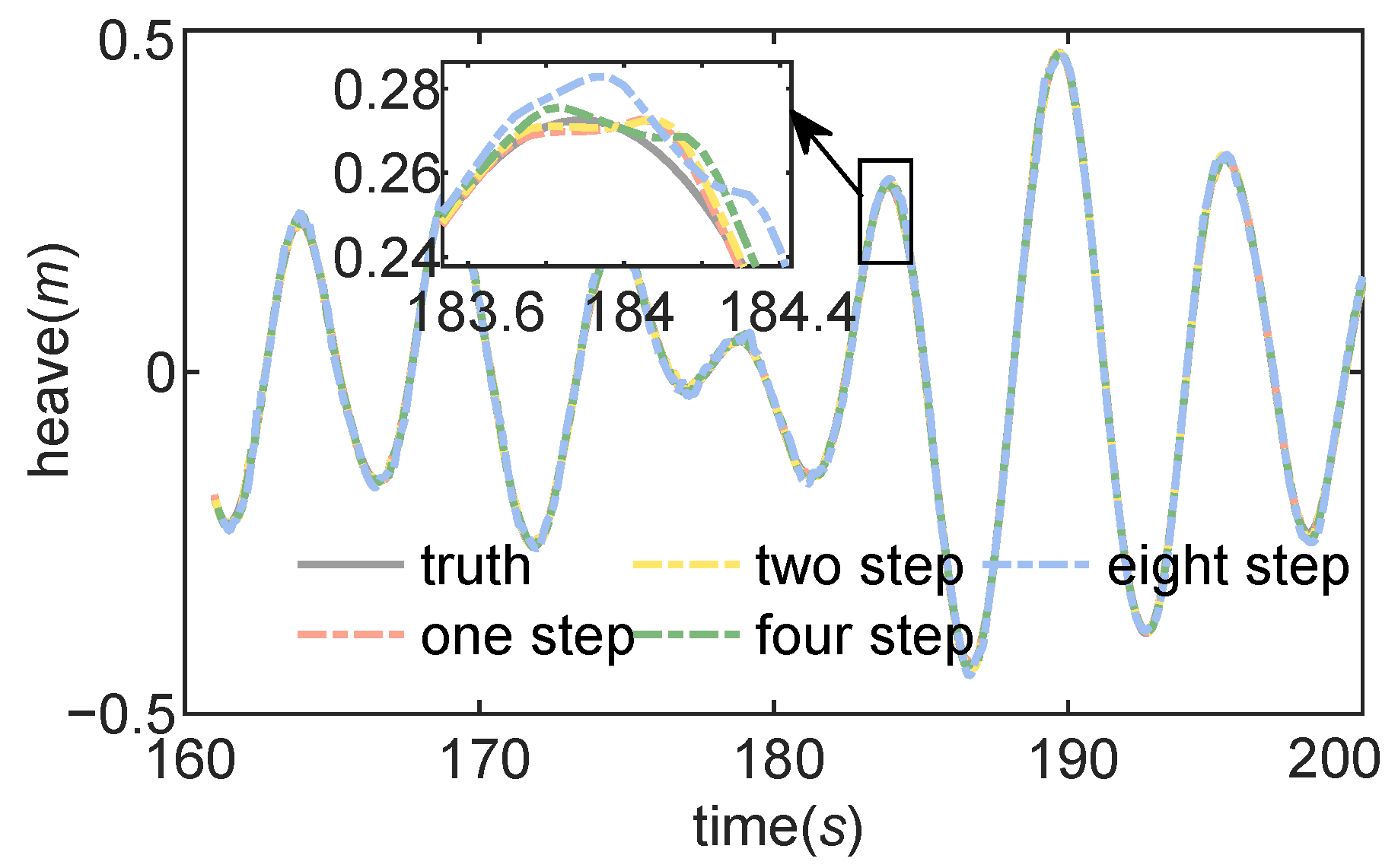
4.4. Heave Motion Prediction Experiments
4.5. Towed Vehicle Depth Compensation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UTS | Underwater towed system |
| SBL | Sparse Bayesian learning |
| EMD | Empirical mode decomposition |
| AR | Autoregressive moving |
| ARMA | Autoregressive moving average model |
| ARIMA | Autoregressive integrated moving average model |
| SVG | Support vector regression |
| GPR | Gaussian process regression |
| RANS | Reynolds-averaged Navier–Stokes methods |
| IMF | Intrinsic mode function |
| FFT | Fast Fourier transform |
| LSTM | Long short-term memory |
| RLS | Recursive least square |
| MAE | Mean absolute error |
| RMSE | Root mean square error |
| STD | Standard deviation |
References
- Yang, X.; Wu, J.; Li, Q.; Lv, H. Numerical simulation of depth tracking control of an underwater towed system coupled with wave–ship interference. J. Mar. Sci. Eng. 2021, 9, 874. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Xu, K.; Song, D.; Xia, Y.; Xu, G. Motion Control of a Flexible-Towed Underwater Vehicle Based on Dual-Winch Differential Tension Coordination Control. J. Mar. Sci. Eng. 2025, 13, 1120. [Google Scholar] [CrossRef]
- Woodacre, J.K.; Bauer, R.J.; Irani, R.A. A review of vertical motion heave compensation systems. Ocean. Eng. 2015, 104, 140–154. [Google Scholar] [CrossRef]
- Tang, G.; Yao, X.; Li, F.; Wang, Y.; Hu, X. Prediction about the vessel’s heave motion under different sea states based on hybrid PSO-ARMA model. Ocean. Eng. 2022, 263, 112247. [Google Scholar] [CrossRef]
- Majidian, H.; Enshaei, H.; Howe, D. Online short-term ship response prediction with dynamic buffer window using transient free switching filter. Ocean. Eng. 2024, 294, 116701. [Google Scholar] [CrossRef]
- Jiang, H.; Duan, S.L.; Huang, L.M.; Han, Y.; Yang, H.; Ma, Q.W. Scale effects in AR model real-time ship motion prediction. Ocean. Eng. 2020, 203, 107202. [Google Scholar] [CrossRef]
- Xu, D.W.; Wang, Y.D.; Jia, L.M.; Qin, Y.; Dong, H.H. Real-time road traffic state prediction based on ARIMA and Kalman filter. Front. Inf. Technol. Electron. Eng. 2017, 18, 287–302. [Google Scholar] [CrossRef]
- Ge, Y.; Qin, M.J.; Niu, Q.T. Prediction of Ship Motion Attitude Based on BP Network. In Proceedings of the 2017 29th Chinese Control and Decision Conference (Ccdc), Chongqing, China, 28–30 May 2017; pp. 1596–1600. [Google Scholar] [CrossRef]
- Li, Z.Y.; Dong, J.; Song, Z.K.; Zhang, H.C.; Guo, Y.B. Prediction of Ship Roll Motion Based on Combination of Phase Space Reconstruction Theory and Elman Network. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 31 July–4 August 2016; pp. 686–689. [Google Scholar] [CrossRef]
- Yin, J.C.; Perakis, A.N.; Wang, N. A real-time ship roll motion prediction using wavelet transform and variable RBF network. Ocean. Eng. 2018, 160, 10–19. [Google Scholar] [CrossRef]
- Tang, G.; Lei, J.M.; Shao, C.T.; Hu, X.; Cao, W.D.; Men, S.Y. Short-Term Prediction in Vessel Heave Motion Based on Improved LSTM Model. IEEE Access 2021, 9, 58067–58078. [Google Scholar] [CrossRef]
- Tian, R.; Li, X.M.; Ma, Z.Y.; Liu, Y.X.; Wang, J.X.; Wang, C. LDformer: A parallel neural network model for long-term power forecasting. Front. Inf. Technol. Electron. Eng. 2023, 24, 1287–1301. [Google Scholar] [CrossRef]
- Nie, Z.H.; Shen, F.; Xu, D.J.; Li, Q.H. An EMD-SVR model for short-term prediction of ship motion using mirror symmetry and SVR algorithms to eliminate EMD boundary effect. Ocean. Eng. 2020, 217, 107927. [Google Scholar] [CrossRef]
- Ouyang, Z.L.; Zou, Z.J. Nonparametric modeling of ship maneuvering motion based on Gaussian process regression optimized by genetic algorithm. Ocean. Eng. 2021, 238, 109699. [Google Scholar] [CrossRef]
- Amini-Afshar, M.; Bingham, H.B. Added resistance using Salvesen-Tuck-Faltinsen strip theory and the Kochin function. Appl. Ocean. Res. 2021, 106, 102481. [Google Scholar] [CrossRef]
- Chen, J.P.; Zhu, D.X. Numerical Simulations of Wave-Induced Ship Motions in Time Domain by a Rankine Panel Method. J. Hydrodyn. 2010, 22, 373–380. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, T.; Wang, X. Hydrodynamic Analysis and Motions of Ship with Forward Speed via a Three-Dimensional Time-Domain Panel Method. J. Mar. Sci. Eng. 2021, 9, 87. [Google Scholar] [CrossRef]
- Tang, K.; Wang, J.X.; Chen, X.; Jiang, D.P.; Li, Y.L. Nonlinear ship motion with forward speed in waves based on 3D time domain hybrid Green function method. Eng. Anal. Bound. Elem. 2021, 123, 107–121. [Google Scholar] [CrossRef]
- Gadelho, J.F.M.; Rodrigues, J.M.; Lavrov, A.; Soares, C.G. Heave and sway hydrodynamic coefficients of ship hull sections in deep and shallow water using Navier-Stokes equations. Ocean. Eng. 2018, 154, 262–276. [Google Scholar] [CrossRef]
- Richter, M.; Schaut, S.; Walser, D.; Schneider, K.; Sawodny, O. Experimental validation of an active heave compensation system: Estimation, prediction and control. Control Eng. Pract. 2017, 66, 1–12. [Google Scholar] [CrossRef]
- Küchler, S.; Mahl, T.; Neupert, J.; Schneider, K.; Sawodny, O. Active Control for an Offshore Crane Using Prediction of the Vessel’s Motion. IEEE/ASME Trans. Mechatronics 2011, 16, 297–309. [Google Scholar] [CrossRef]
- Xia, D.W.; Geng, J.; Huang, R.X.; Shen, B.Q.; Hu, Y.; Li, Y.T.; Li, H.Q. A distributed EEMDN-SABiGRU model on Spark for passenger hotspot prediction. Front. Inf. Technol. Electron. Eng. 2023, 24, 1316–1331. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
- Calnan, C.; Bauer, R.J.; Irani, R.A. Reference-Point Algorithms for Active Motion Compensation of Towed Bodies. IEEE J. Ocean. Eng. 2019, 44, 1024–1040. [Google Scholar] [CrossRef]
- Vegte, J.V.D. Fundamentals of Digital Signal Processing; Publishing House of Electronics Industry: Beijing, China, 2003; pp. 293–298. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar] [CrossRef]
- Pierson, W.J., Jr.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Xu, C.Z.; Zou, Z.J. Online Prediction of Ship Roll Motion in Waves Based on Auto-Moving Gird Search-Least Square Support Vector Machine. Math. Probl. Eng. 2021, 2021, 2760517. [Google Scholar] [CrossRef]



| Wind Speed (m/s) | (rad/s) | (rad/s) |
|---|---|---|
| 7 | 1.044989 | 7.047480 |
| 11 | 0.664988 | 4.484760 |
| 15 | 0.487659 | 3.288826 |
| Descriptions | Parameter | Value | Unit |
|---|---|---|---|
| Sampling period | s | ||
| Simulation time | t | 200 | s |
| Velocity of towing ship | v | 2 | m/s |
| Wind speed | u | m/s | |
| Gravitational acceleration | g | m/s2 | |
| Harmonic number of waves | n | 12 | / |
| Amplitude attenuation coefficient | / | ||
| Cut-off frequency of low-pass filter | Hz | ||
| Low-pass filter order | r | 1 | / |
| Descriptions | Parameter | Value |
|---|---|---|
| Data number of data set | M | 5000 |
| Data number of testing set | N | 1000 |
| Window length | 24 | |
| Number of delayed sampling cycles | k |
| MAE (m) | 0.01080 | 0.00303 | 0.00238 |
| RMSE (m) | 0.01253 | 0.00387 | 0.00304 |
| SBL | FFT-SBL | EMD-SBL | |
|---|---|---|---|
| MAE (m) | 0.00440 | 0.00334 | 0.00239 |
| RMSE (m) | 0.00553 | 0.00407 | 0.00307 |
| 1.65985 | −0.63717 | 0 | −0.00170 | 0.00689 | 0.00272 |
| −0.00125 | 0 | 0 | −0.00792 | 0 | −0.00653 |
| −0.00794 | −0.00526 | 0 | −0.00550 | 0 | 0 |
| 0 | −0.00352 | 0 | 0 | 0 | 0.00240 |
| Wind Speed | Evaluation | Data-Based Methods | Model-Based Methods | |||
|---|---|---|---|---|---|---|
| (m/s) | (m) | SVR | LSTM | GPR | RLS | SBL |
| MAE | 0.00694 | 0.00521 | 0.00425 | 0.00332 | 0.00252 | |
| u = 7 m/s | RMSE | 0.00871 | 0.00643 | 0.00532 | 0.00408 | 0.00320 |
| STD | 0.20007 | 0.19875 | 0.19848 | 0.19855 | 0.19795 | |
| MAE | 0.02299 | 0.01772 | 0.01429 | 0.00390 | 0.00258 | |
| u = 11 m/s | RMSE | 0.03487 | 0.03277 | 0.02252 | 0.00498 | 0.00325 |
| STD | 0.53159 | 0.52349 | 0.50551 | 0.51569 | 0.51690 | |
| MAE | 0.03108 | 0.02966 | 0.02583 | 0.00502 | 0.00267 | |
| u = 15 m/s | RMSE | 0.03966 | 0.03800 | 0.03307 | 0.00594 | 0.00341 |
| STD | 1.06264 | 1.05958 | 1.02100 | 1.04961 | 1.04642 | |
| k | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| MAE (m) | 0.00252 | 0.00264 | 0.00330 | 0.00619 |
| RMSE (m) | 0.00320 | 0.00334 | 0.00410 | 0.00752 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.-F.; Yan, H.-C.; Xu, J.-B. A Heave Motion Prediction Approach Based on Sparse Bayesian Learning Incorporated with Empirical Mode Decomposition for an Underwater Towed System. J. Mar. Sci. Eng. 2025, 13, 1427. https://doi.org/10.3390/jmse13081427
Lu Z-F, Yan H-C, Xu J-B. A Heave Motion Prediction Approach Based on Sparse Bayesian Learning Incorporated with Empirical Mode Decomposition for an Underwater Towed System. Journal of Marine Science and Engineering. 2025; 13(8):1427. https://doi.org/10.3390/jmse13081427
Chicago/Turabian StyleLu, Zhu-Fei, Heng-Chang Yan, and Jin-Bang Xu. 2025. "A Heave Motion Prediction Approach Based on Sparse Bayesian Learning Incorporated with Empirical Mode Decomposition for an Underwater Towed System" Journal of Marine Science and Engineering 13, no. 8: 1427. https://doi.org/10.3390/jmse13081427
APA StyleLu, Z.-F., Yan, H.-C., & Xu, J.-B. (2025). A Heave Motion Prediction Approach Based on Sparse Bayesian Learning Incorporated with Empirical Mode Decomposition for an Underwater Towed System. Journal of Marine Science and Engineering, 13(8), 1427. https://doi.org/10.3390/jmse13081427





