Unsteady Hydrodynamic Calculation and Characteristic Analysis of Voith–Schneider Propeller with High Eccentricity
Abstract
1. Introduction
2. Principles and Methods
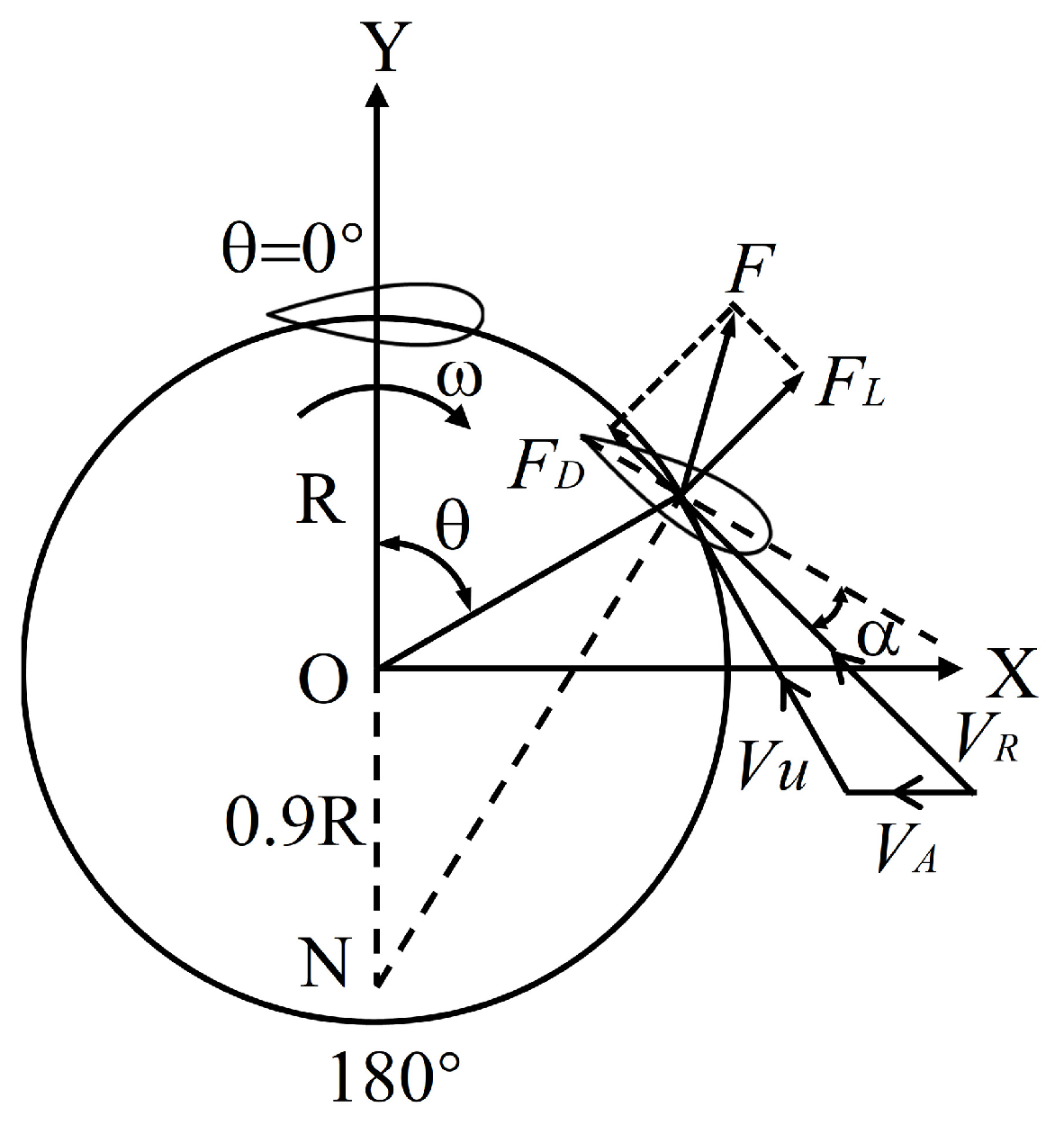
2.1. Working Principles
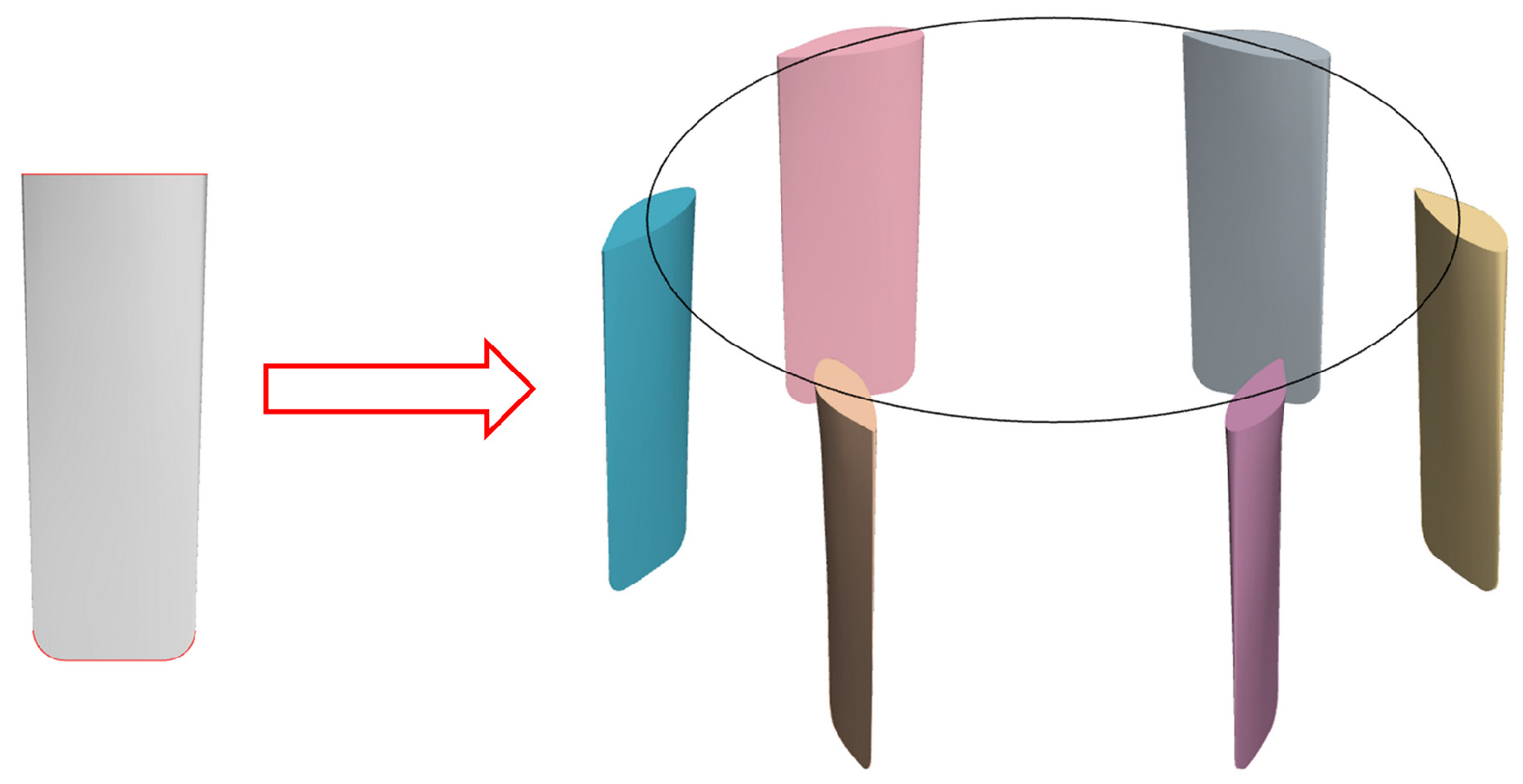
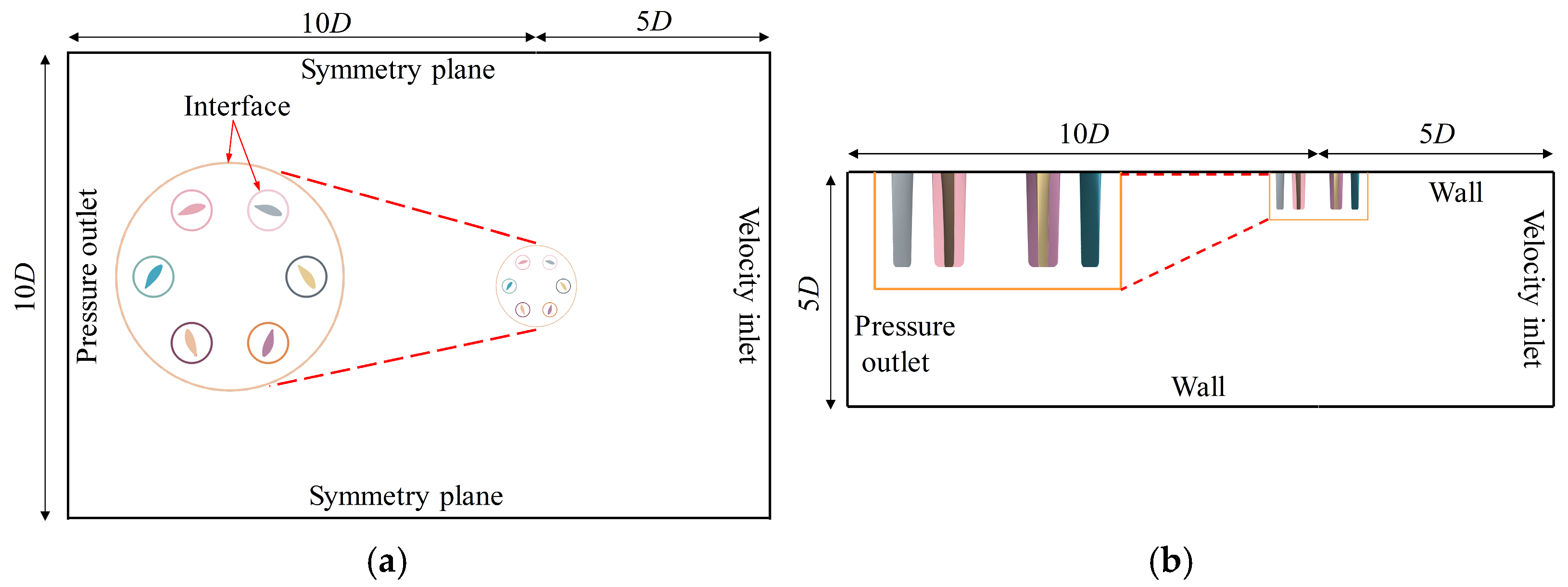
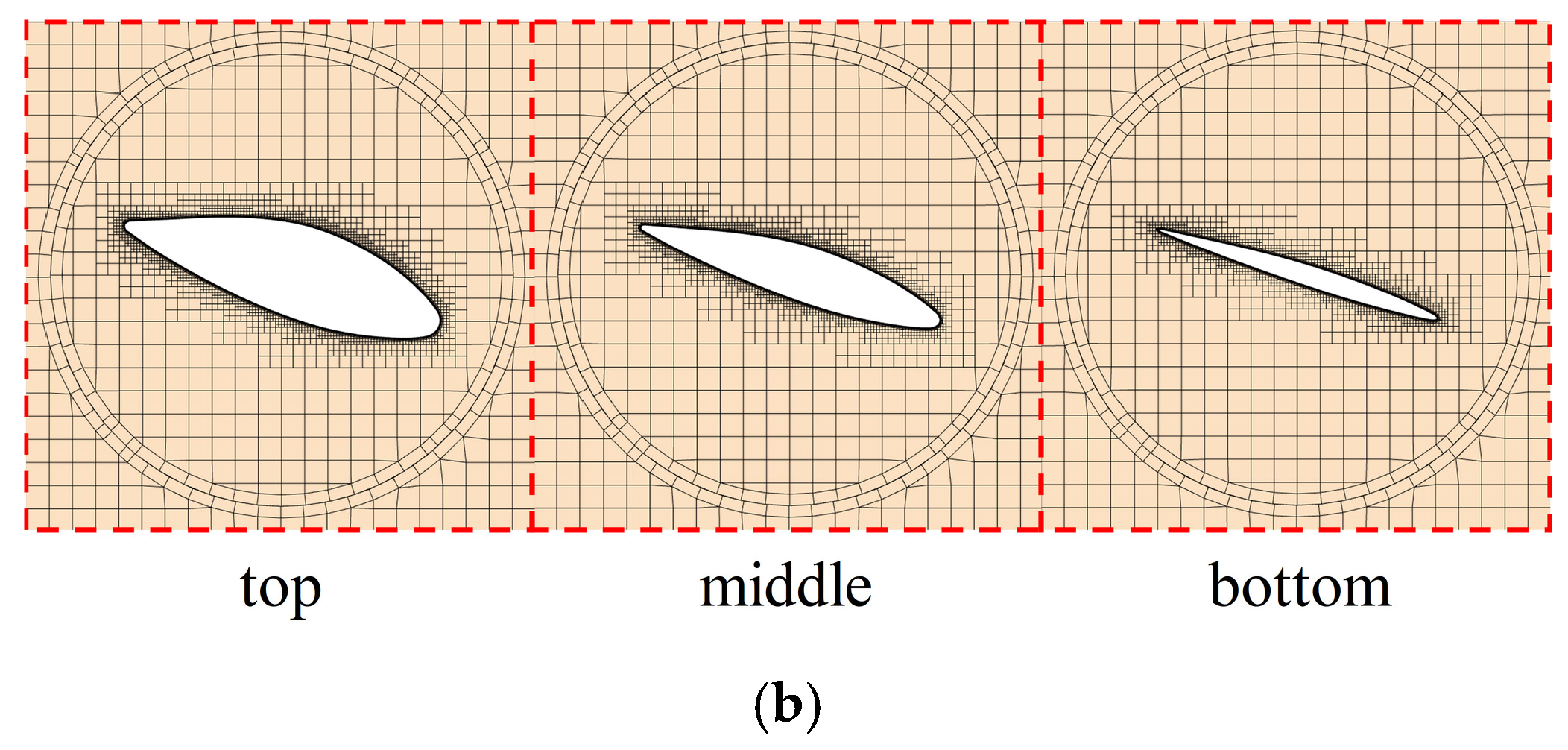
2.2. Numerical Simulation Methods
3. Results
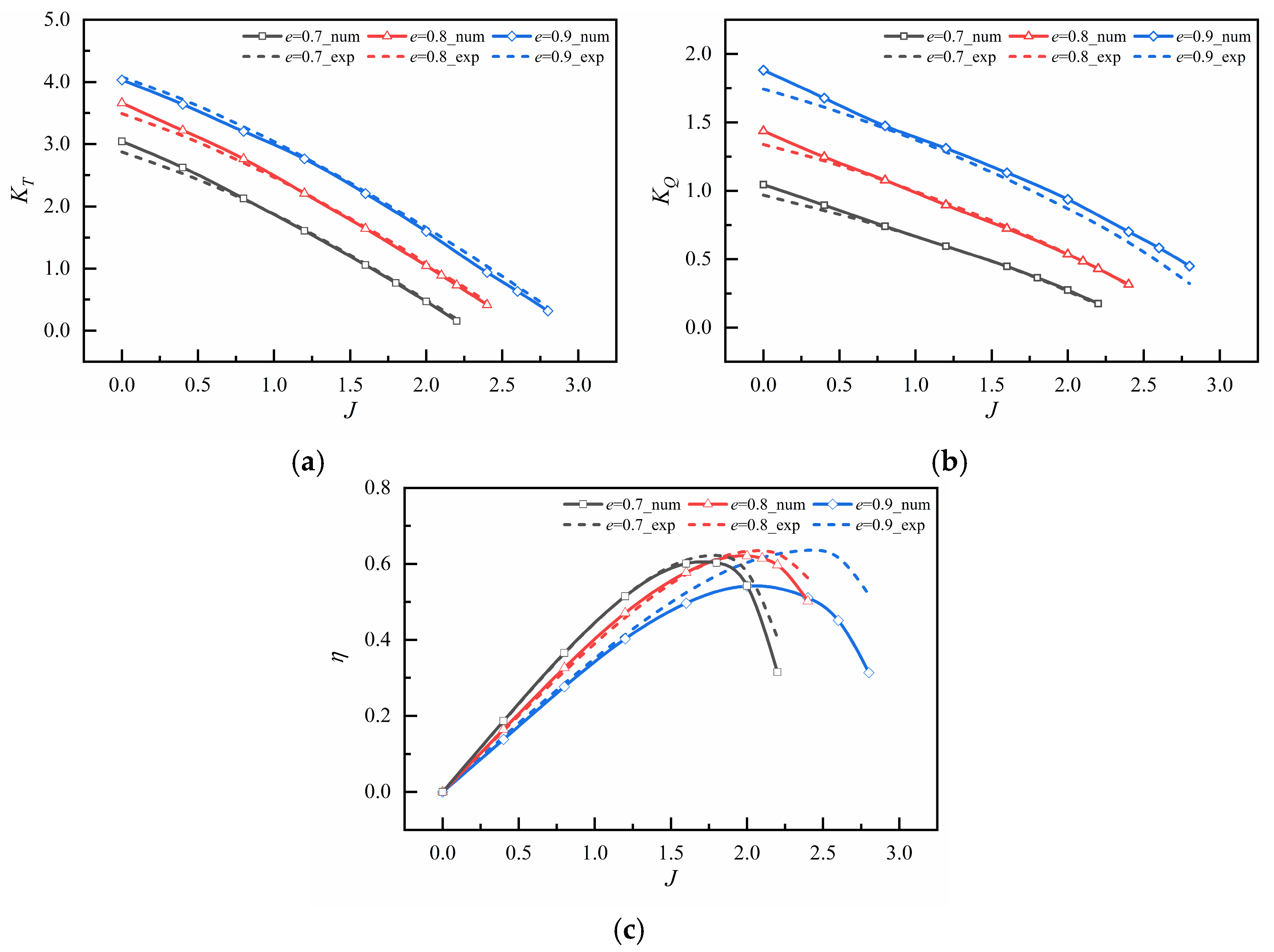
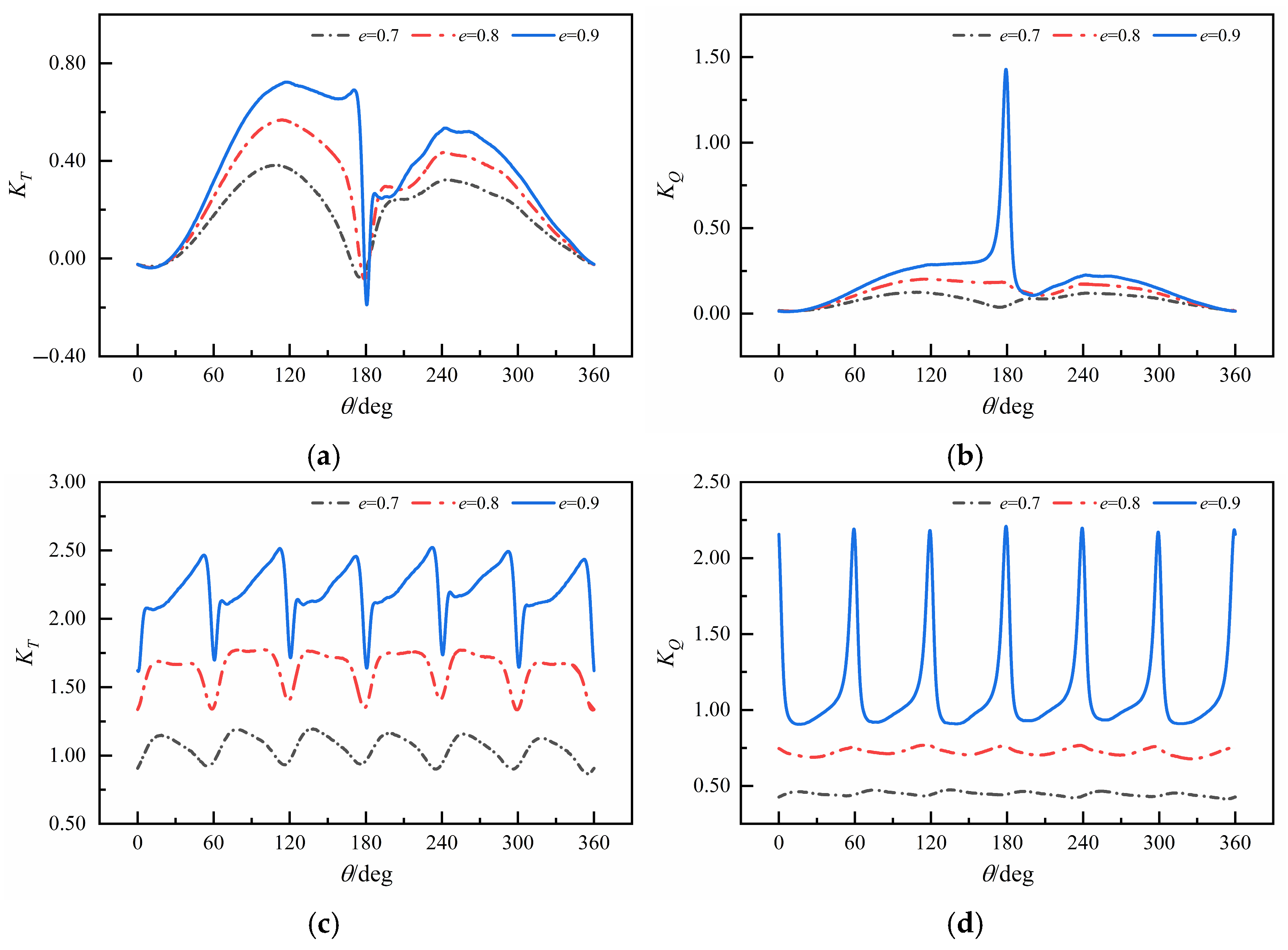
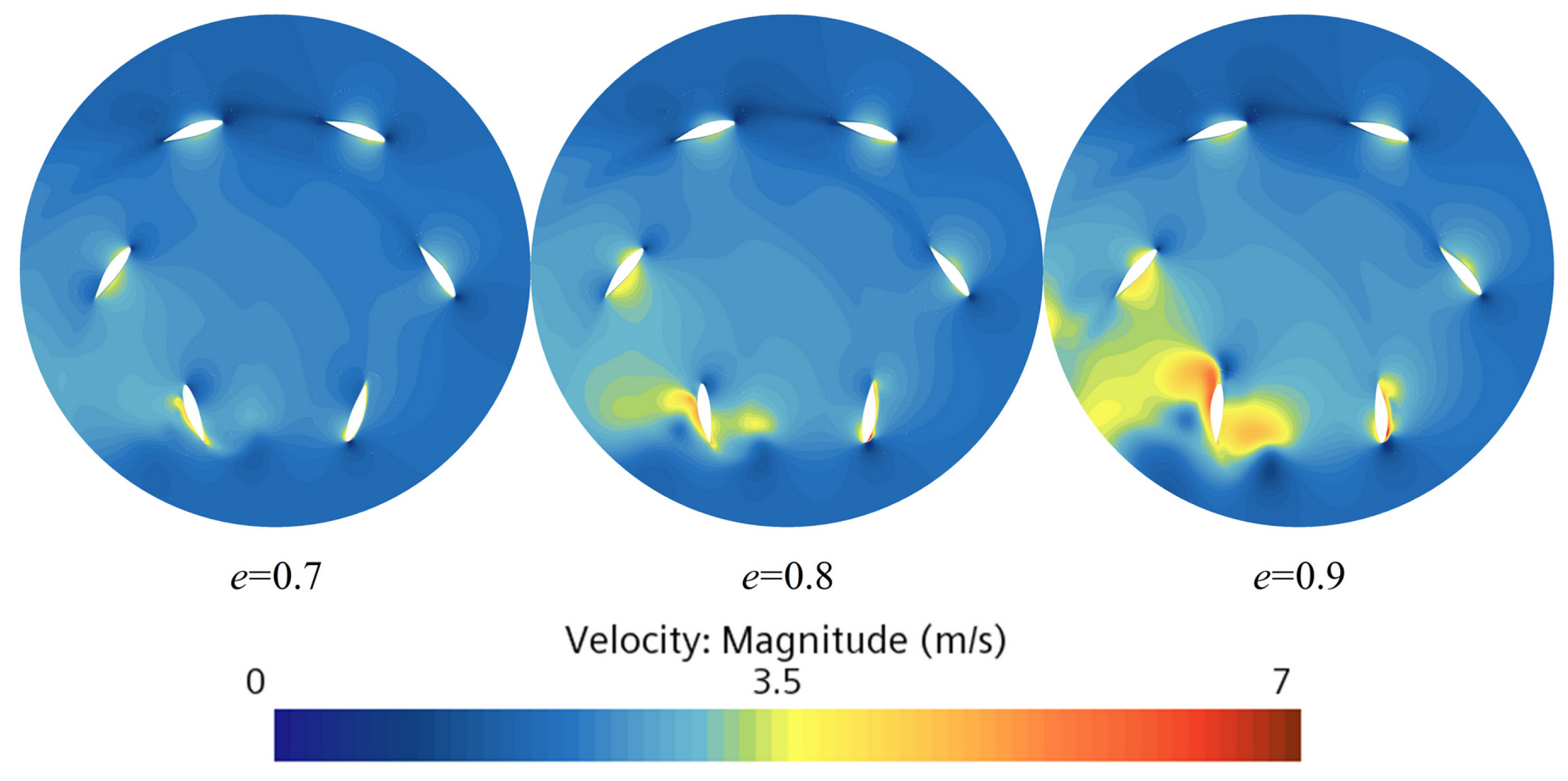
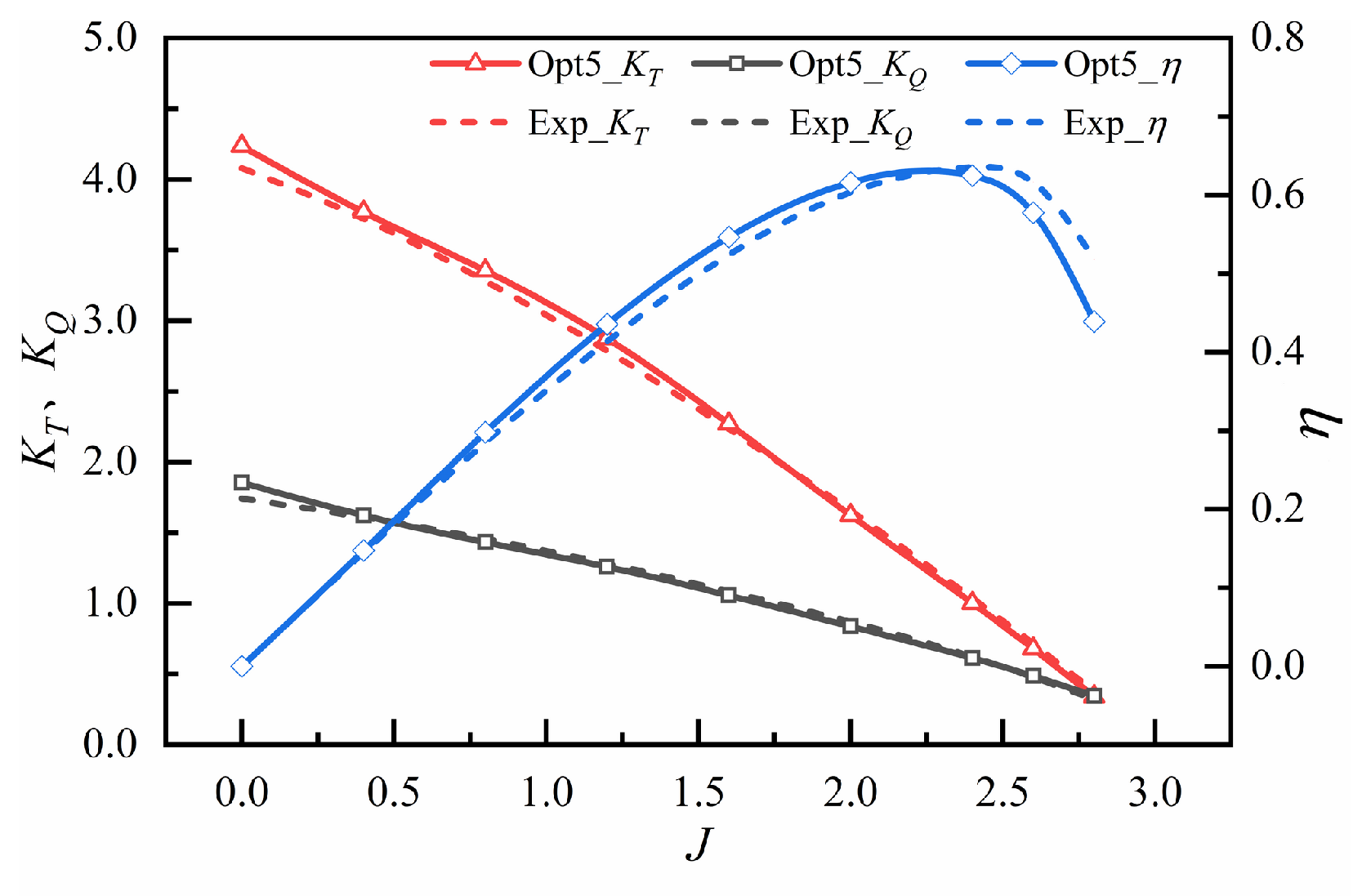
3.1. Open-Water Performance Analysis
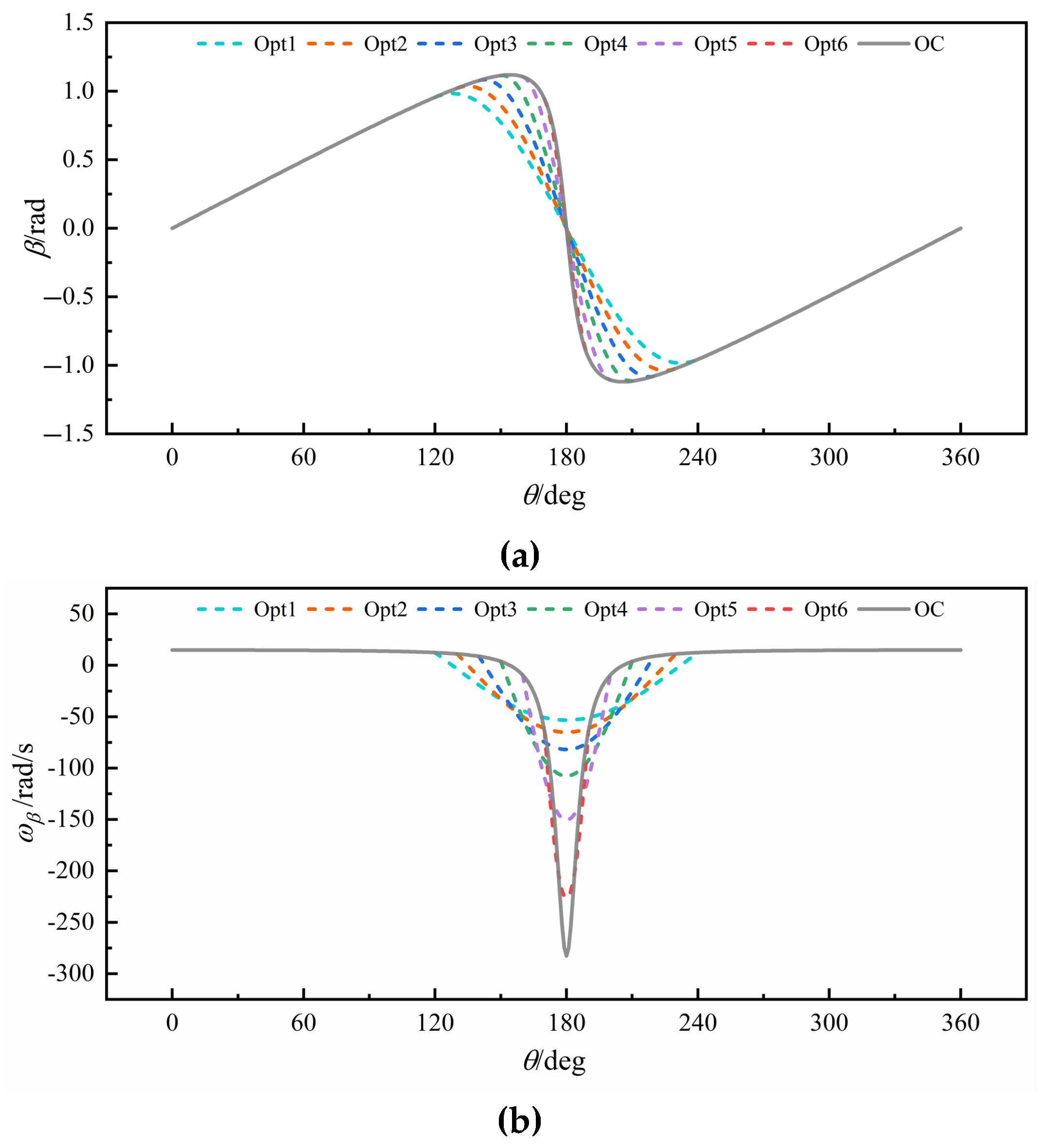
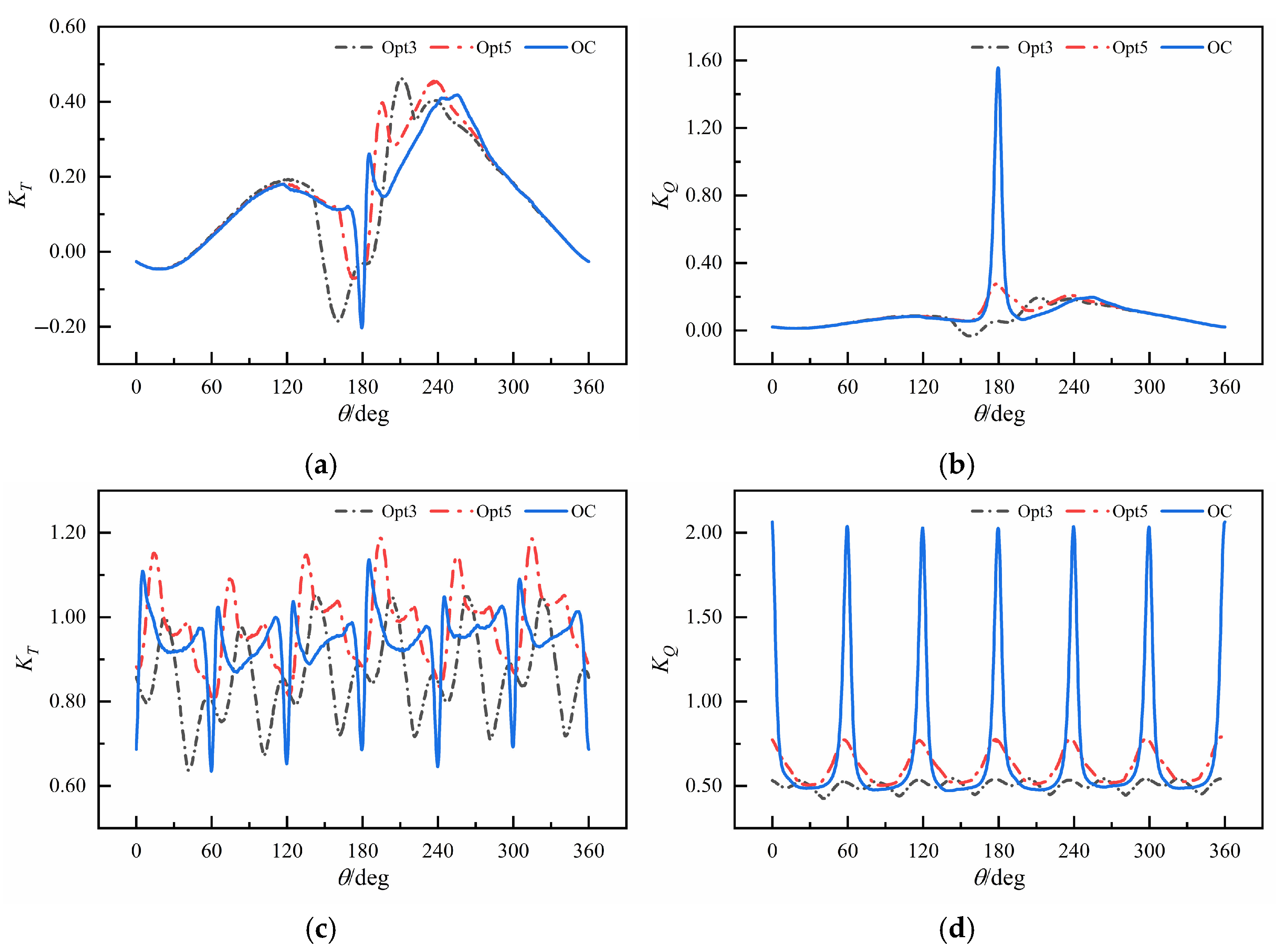
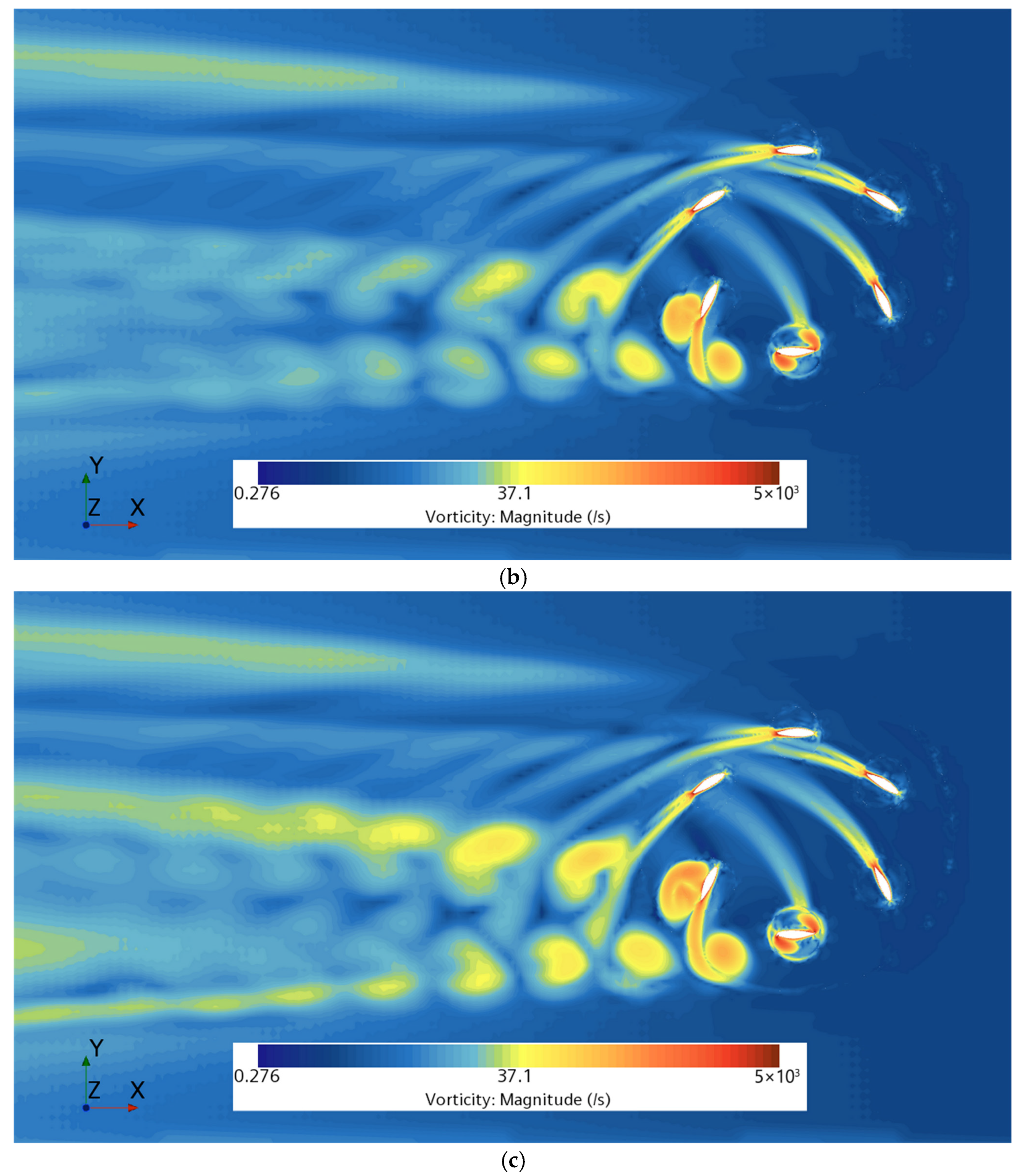
3.2. Investigation of Blade Steering Curve
4. Conclusions
- Under the high-eccentricity condition (e = 0.9), the amplitude of the blade self-rotation angular velocity of the VSP increases significantly. When blades pass near the eccentric point, strong unsteady hydrodynamic pulsation occurs, and the torque acting on the blades increases substantially, leading to a decrease in propulsion efficiency at high eccentricity.
- Limited by the executability of the cam control mechanism, the VSP blades during rapid flipping in the experiment did not strictly adhere to the “normal intersection principle”. Therefore, in the design of high-performance VSPs, the amplitude of the blade self-rotation angular velocity should be constrained according to different control methods.
- The appropriate design of the Blade Steering Curve can substantially improve the hydrodynamic performance. At J = 2.4, the Opt-5 curve generated via the sinusoidal fitting strategy enables a 25.19% reduction in overall thrust pulsation, an 81.94% reduction in overall torque pulsation, a 4.67% increase in thrust, a 12.74% reduction in torque, and a 19.95% improvement in efficiency for the VSP.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Huang, H.; Leng, J.; Chen, L.; Huang, J. The Design and Application of a New Vertical-Axis Ship Propeller. In Proceedings of the OCEANS 2015-MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; IEEE: Washington, DC, USA, 2015; pp. 1–4. [Google Scholar]
- Desai, M.; Gokhale, R.; Halder, A.; Benedict, M.; Young, Y.L. Augmenting Maneuverability of UUVs with Cycloidal Propellers. Young 2020, 1, 3. [Google Scholar]
- Sarchin, T.H.; Tryner, H.G. Cycloidal Propulsion and Control for Ship Handling Tugs. Nav. Eng. J. 1970, 82, 52–69. [Google Scholar] [CrossRef]
- Taniguchi, K. Sea Trial Analysis of the Vertical Axis Propellers. In Fourth Symposium on Naval Hydrodynamics: Propulsion Hydroelasticity; Office of Naval Research and Web Institute of Naval Architecture: Washington, DC, USA, 1962; pp. 27–31. [Google Scholar]
- Haberman, W.L.; Harley, E.E. Performance of Vertical Axis (Cycloidal) Propellers Calculated by Taniguchi’s Method. In Hydromechanics Laboratory Research and Development Report 1564; Report No. SR0090101; David Taylor Model Basin: Washington, DC, USA, 1961. [Google Scholar]
- Zhu, D.M. A Computational Method for Cycloidal Propellers. Int. Shipbuild. Prog. 1981, 28, 102–111. [Google Scholar] [CrossRef]
- Ficken, N.L.; Dickerson, M.C. Experimental Performance and Steering Characteristics of Cycloidal Propellers; Defense Technical Information Center: Fort Belvoir, VA, USA, 1969. [Google Scholar]
- Bartels, J.; Jürgens, D. Latest Developments in Voith Schneider Propulsion Systems. In Proceedings of the 18th International Tug & Salvage Convention, Miami, FL, USA, 26–29 April 2004. [Google Scholar]
- Bartels, J.-E.; Jürgens, D. The Voith Schneider Propeller: Current Applications and New Developments; Voith Turbo Marine GmbH: Heidenheim, Germany, 2006. [Google Scholar]
- Bakhtiari, M.; Ghassemi, H.; Sakaki, A.; He, G. Optimisation Scheme Applied to the Voith-Schneider Propulsion System Using Genetic Algorithm. Ships Offshore Struct. 2021, 16, 650–658. [Google Scholar] [CrossRef]
- Li, T.; Hu, J.; Wang, Y.; Zhang, W.; Mao, Y.; Guo, C. Hydrodynamic Analysis of Cycloidal Propellers. Ships Offshore Struct. 2022, 17, 2116–2129. [Google Scholar] [CrossRef]
- Sun, Z.; Li, H.; Liu, Z.; Wang, W.; Zhang, G.; Zong, Z.; Jiang, Y. Study on Hydrodynamic Performance of Cycloidal Propeller with Flap at the Trailing Edge. Ocean. Eng. 2021, 237, 109657. [Google Scholar] [CrossRef]
- Hu, J.; Yan, Q.; Sun, S.; Li, F.; Ma, J. Numerical Simulation to Assess Hydrodynamic Performance of Cycloidal Propellers during Maneuvering. Ocean. Eng. 2023, 273, 113931. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Z.; Zhang, G.; Sun, Y. Study on Thrust Directional Steadiness of Cycloidal Propeller. Ocean. Eng. 2023, 287, 115840. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Chen, Q.; Ma, C. Research on Efficiency Optimization of the Voith-Schneider Propeller Based on Motion Curve Parameter Control. Ocean. Eng. 2024, 299, 117136. [Google Scholar] [CrossRef]
- Jürgens, B.; Fork, W. The Fascination of the Voith-Schneider Propeller: History and Engineering; Koehlers Verlagsgesellschaft mbH: Minden, Germany, 2002; ISBN 3-7822-0859-5. [Google Scholar]
- Jürgens, D.; Palm, M.; Singer, S.; Urban, K. Numerical Optimization of the Voith-Schneider® Propeller. Z Angew. Math. Mech. 2007, 87, 698–710. [Google Scholar] [CrossRef]
- Zhai, S.; Jin, S.; Chen, J.; Liu, Z.; Song, X. CFD-Based Multi-Objective Optimization of the Duct for a Rim-Driven Thruster. Ocean. Eng. 2022, 264, 112467. [Google Scholar] [CrossRef]
- Nakonechny, B.V. Design of a 9-Inch Cycloidal Propeller Model Unit and Some Experimental Results; No. NSRDC-3150. 1974. Available online: https://apps.dtic.mil/sti/citations/ADA005768 (accessed on 21 July 2025).








| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Diameter | D | 22.86 | cm |
| Avg. Chord | 4.026 | cm | |
| Max. Chord | 4.328 | cm | |
| Length | L | 11.43 | cm |
| Revolution speed | n | 5 | rps |
| Mesh | Mesh Size (mm) | Mesh Count (M) | KT | Exp | Error (%) |
|---|---|---|---|---|---|
| 1—Very fine | 1.4 | 14.3 | 0.791 | 0.787 | 0.508 |
| 2—Fine | 1.7 | 10.0 | 0.790 | 0.787 | 0.381 |
| 3—Medium | 2.0 | 7.5 | 0.788 | 0.787 | 0.127 |
| 4—Coarse | 2.4 | 5.4 | 0.783 | 0.787 | −0.508 |
| 5—Very coarse | 2.8 | 4.2 | 0.774 | 0.787 | −1.652 |
| Mesh | RG | PG | CG | UG%S |
|---|---|---|---|---|
| 1–2–3 | 0.500 | 2.001 | 1.001 | 0.127% |
| 2–3–4 | 0.400 | 2.645 | 1.501 | 0.339% |
| 3–4–5 | 0.555 | 1.697 | 0.800 | 0.798% |
| BSC | Fitting Interval (deg) | Max Angle (rad) | Max Angular Velocity (rad/s) |
|---|---|---|---|
| Opt1 | 120–240 | 0.9834 | −53.2870 |
| Opt2 | 130–230 | 1.0374 | −65.0843 |
| Opt3 | 140–220 | 1.0842 | −81.8950 |
| Opt4 | 150–210 | 1.1156 | −107.5383 |
| Opt5 | 160–200 | 1.1198 | −150.4127 |
| Opt6 | 170–190 | 1.1198 | −226.9734 |
| OC | — | 1.1198 | −282.7433 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Xue, W.; Liu, W.; Chen, Q. Unsteady Hydrodynamic Calculation and Characteristic Analysis of Voith–Schneider Propeller with High Eccentricity. J. Mar. Sci. Eng. 2025, 13, 1407. https://doi.org/10.3390/jmse13081407
Liu Z, Xue W, Liu W, Chen Q. Unsteady Hydrodynamic Calculation and Characteristic Analysis of Voith–Schneider Propeller with High Eccentricity. Journal of Marine Science and Engineering. 2025; 13(8):1407. https://doi.org/10.3390/jmse13081407
Chicago/Turabian StyleLiu, Zhihua, Weixin Xue, Wentao Liu, and Qian Chen. 2025. "Unsteady Hydrodynamic Calculation and Characteristic Analysis of Voith–Schneider Propeller with High Eccentricity" Journal of Marine Science and Engineering 13, no. 8: 1407. https://doi.org/10.3390/jmse13081407
APA StyleLiu, Z., Xue, W., Liu, W., & Chen, Q. (2025). Unsteady Hydrodynamic Calculation and Characteristic Analysis of Voith–Schneider Propeller with High Eccentricity. Journal of Marine Science and Engineering, 13(8), 1407. https://doi.org/10.3390/jmse13081407






