Berth Allocation and Quay Crane Scheduling in Port Operations: A Systematic Review
Abstract
1. Introduction
- 1.
- Offering a comprehensive summary of the current status of berth allocation and quay crane assignment and scheduling for container terminals, analyzing the berth layout, vessels arrivals, crane handling, sustainability and green infrastructure in port operations, objective function, model formulation, policy trade-offs, solution approach and model performance evaluation associated with different model types.
- 2.
- Providing a detailed discussion on current issues associated with models applied to berth allocation, quay crane assignment, and scheduling.
- 3.
- Outlining the outcomes and identifying future research directions in relation to berth allocation, quay crane assignment, and scheduling.
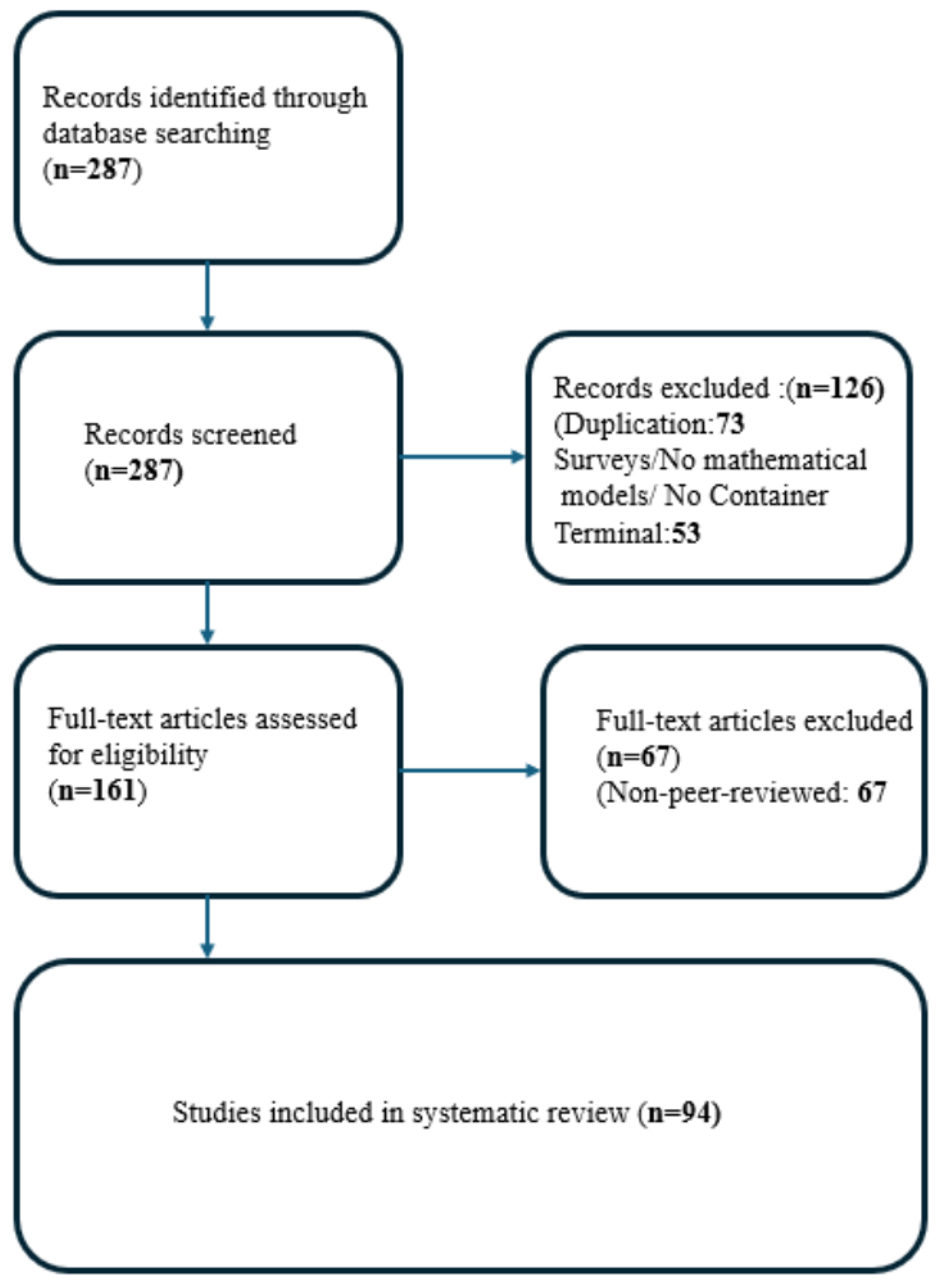
2. Review Methodology
3. Results
3.1. Current Status of BAP, QCAP and QCSP
3.1.1. Inputs and Configuration for BAP, QCAP, and QCSP
3.1.2. BAP, QCAP, and QCSP Mathematical Model Formulation
- i: set of vessels.
- j: set of berths.
- k: set of quay cranes.
- t: Time index .
- : Arrival time of vessel i.
- : Length of vessel i.
- : Maximum number of quay cranes available at berth j.
- : Handling time for vessel i when quay crane k is assigned at berth j.
- : Length of berth j.
- : Water depth of vessel i.
- : Draft of vessel i.
- : Cost of setting crane k for vessel i.
- : Desired departure time of vessel i.
- : Penalty for exceeding the desired departure time of vessel i.
- : Start time of service for vessel i.
- : Departure time of service for vessel i.
- : Waiting time of vessel i.
- is the weight of waiting time,
- is the weight of service time,
- is the weight of the penalty cost for exceeding the desired departure time,
- is the weight of crane setup cost.
- 1.
- Berth Allocation Constraints
- (a)
- Each vessel is assigned to exactly one berth:
- (b)
- Vessel assignments must not exceed berth length:
- (c)
- Vessel its serviced after its arrival:
- (d)
- Vessel draft can not be more than water depth:
- 2.
- Quay Crane Allocation Constraints
- (a)
- Each crane can work on one vessel at a time:
- (b)
- The number of quay cranes allocated to a vessel cannot exceed the maximum available at its assigned berth:
- (c)
- Quay cranes are only allocated to vessels assigned to a berth:
- 3.
- Quay Crane Scheduling Constraints
- (a)
- Quay cranes allocated to adjacent vessels should not interfere:
- (b)
- Quay crane must work the entire period until the end of service:
- i: set of vessels.
- q: set of quay cranes.
- t: time index .
- : Arrival time of vessel i.
- : Length of vessel i.
- N: Total number of quay cranes available.
- : Handling time for vessel i.
- P: Total length of the quay.
- : Starting berth position of vessel i.
- : Number of quay cranes assigned to vessel i is at time t.
- : Start time of service for vessel i.
- : Departure time of service for vessel i.
- : Waiting time of vessel i.
- : Maximum number of quay cranes for vessel i.
- : Maximum number of quay cranes available at time t.
- is the weight of waiting time;
- is the weight of service time;
- is the weight of the crane setup.
- 1.
- Berth Allocation Constraints
- (a)
- Vessel must be fully accommodated within the quay:
- (b)
- Vessel is serviced after its arrival:
- 2.
- Quay Crane Allocation Constraints (QCAP and QCSP)
- (a)
- Each vessel can be assigned a limited number of cranes:
- (b)
- At any time t, the total number of cranes assigned across all vessels cannot exceed the maximum available:
- (c)
- Quay cranes can be assigned to only one vessel at a time:
3.1.3. BAP, QCAP, and QCSP Solution Approach
4. Discussion
- 1.
- Uncertainty handlingSeveral studies fall short in adequately addressing uncertainties, including weather variations, mechanical failures, schedule adjustments, vessel congestion, equipment malfunctions, and fluctuations in cargo volume [33,68,81]. While Xiang et al. [81] examine BAP, QCAP, and QCSP under uncertainty, they lack robust techniques to effectively manage uncertainties such as adverse weather conditions and disruptions.
- 2.
- Limited sustainability impact and multi-objective optimizationsFew studies consider multi-objective optimization models for the BAP, QCAP, and QCSP. Many studies tend to overlook environmental, economic, and social factors like emissions, carbon tax, energy, and safety, focusing instead solely on efficiency constraints. Chargui et al. [32], Alnaqbi et al. [25], and El-Boghdadly et al. [39] concentrate exclusively on efficiencies, such as minimizing service time, handling time, and costs, without considering the impact on sustainability. Many models do not effectively integrate green infrastructure, such as shore power and renewable energy, nor do they adequately balance economic and environmental objectives.
- 3.
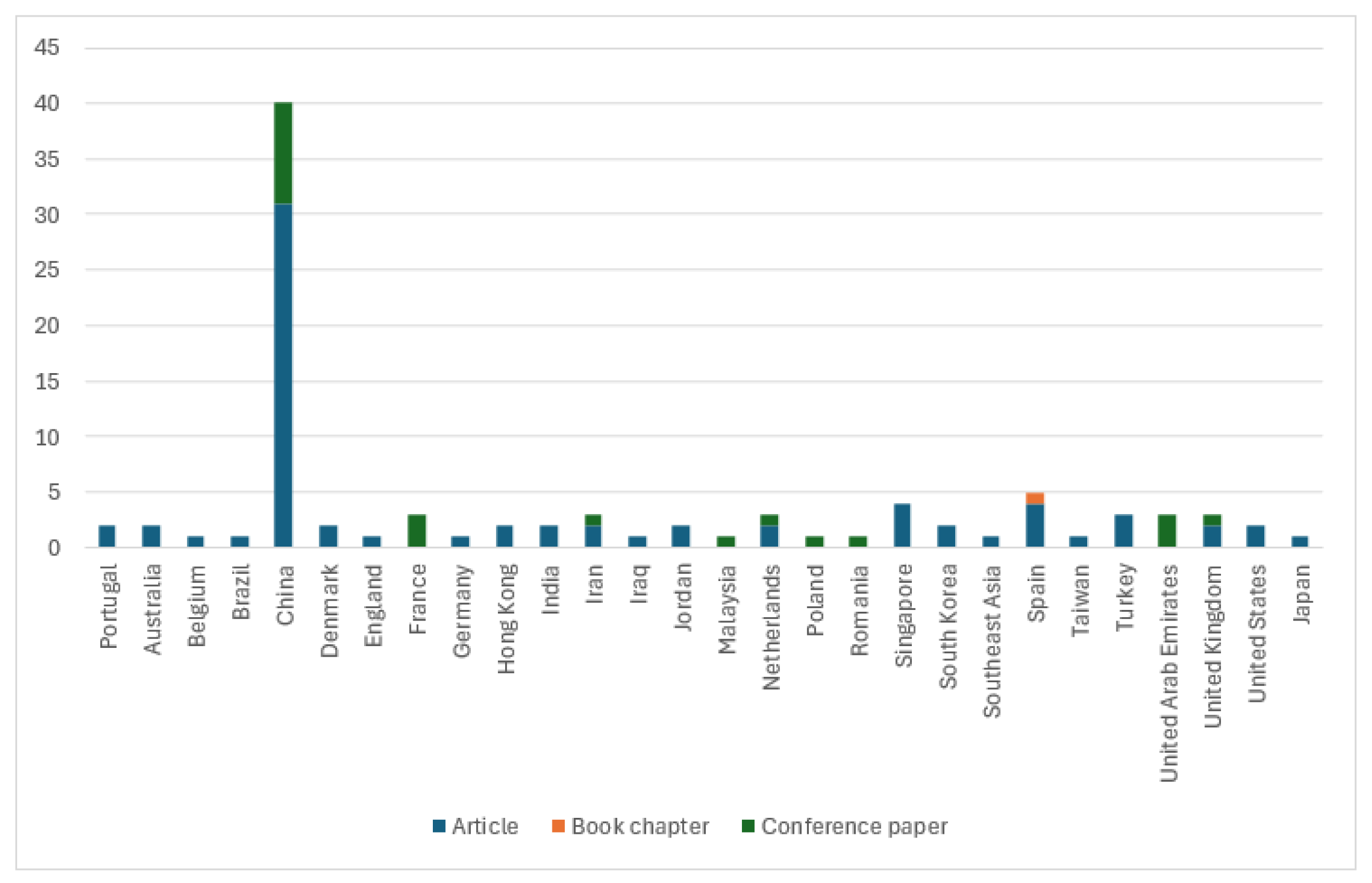
- Narrow global coverageAmong the selected articles for review, none addressed berth allocation problems within the sub-Saharan African region, indicating a significant research gap in this area. Most studies tend to focus on China, as illustrated in Figure 3.
- 4.
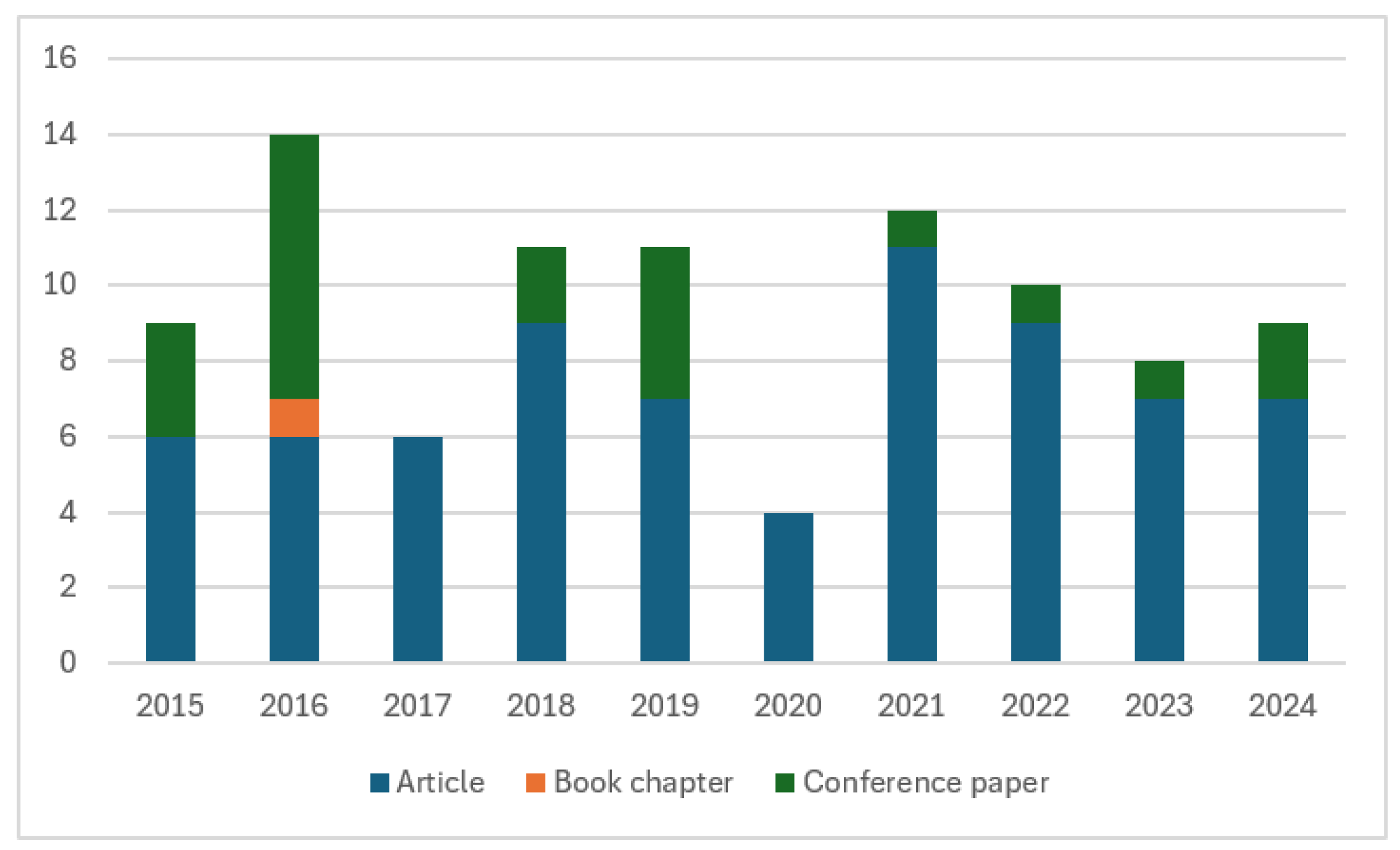
- Real-world data and real-time adaptabilityThe majority of the studies utilized simulated data to model BAP, QCAP, and QCSP. Very few studies employed real-world data, while others combined both real-world and simulated data. This reliance on simulation has resulted in a lack of benchmark data, raising concerns about the generalizability of the models. Despite advances in adaptive scheduling, many solutions still lack full real-time implementation due to reliance on predefined scenarios or delayed data updates. This limitation hinders responsiveness to sudden disruptions, which is a practical challenge in port management.
- 5.
- IntegrationDuring the review period, most papers focused on the integration of the BAP and QCAP. However, very few addressed the integration with the QCSP, yard operations, or storage. As an example, the study by Al-Refaie and Abedalqader [26], Woo et al. [78], and Chargui et al. [33] did not take into account the integration of the BAP with other related issues in the terminal, such as the yard and container stacking.
- 1.
- Innovative mechanism to handle uncertaintiesFuture research should emphasize the introduction of new algorithms, such as reinforcement learning, stochastic models, robust optimization techniques, and hybrid algorithms that combine metaheuristics with exact methods. These advancements aim to tackle uncertainties, disruptions, and sustainability objectives while also accommodating large-scale terminal operations.
- 2.
- Inclusion of Policy trade-offThe majority of the paper did not address policy trade-offs; instead, most studies concentrated on efficiency objectives, such as minimizing completion time, waiting time, and service time, without considering conflicting objectives and regulatory requirements. Future research should incorporate objectives that focus on efficiency while also addressing other important factors, such as sustainability, safety, costs, and other unspecified considerations.
- 3.
- Multi-objective optimization and integration with other port operationsMost current studies aim to minimize total turnaround time. However, in real-world scenarios, various objectives often come into play, such as minimizing waiting time, reducing energy consumption, and maximizing revenue. Future research should concentrate on developing multi-objective optimization models for the BAP that can accommodate these diverse objectives. One possible direction is to extend the model to consider multiple quays instead of a single quay.
- 4.
- Incorporating machine learning and AI techniquesMachine learning and AI techniques, including deep learning and reinforcement learning, have shown promising results in addressing various optimization problems. Future research could aim to apply these techniques to BAP, QCAP, and QCSP to improve the performance and efficiency of algorithms. Rodrigues and Agra [68] emphasize the potential of machine learning approaches, such as neural networks, to enhance predictions of vessel arrival times. Overall, advancing the applications of machine learning could significantly improve berth allocation algorithms. Research should aim to enhance automation in crane scheduling and berth allocation by utilizing the Internet of Things (IoT), artificial intelligence (AI), and machine learning for automated guided vehicles (AGVs). This approach aligns with the increasing trend toward the development of intelligent ports and smart terminal management.
- 5.
- Real-world DataFuture research could focus on developing algorithms that adapt to real-time data and can be tested in real-world scenarios. This would enable dynamic adjustments to berth allocation and crane assignment plans. Additionally, the study could be expanded to include actual data from port terminals to validate the models and enhance their practical application.
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BAP | berth assignment problem |
| QCAP | quay crane allocation problem |
| QCSP | quay crane scheduling problem |
| SA | simulated annealing |
| PSO | particle swarm optimization |
| GA | genetic algorithms |
| GP | genetic programming |
| IGA | improved genetic algorithms |
| CSA | cuckoo search algorithm |
| BMO | bird mating optimizer |
| SWO | squeaky wheel optimization |
| MOGA | multiobjective genetic algorithm |
| MILP | mixed-integer linear programming |
| Three-stage opt | three-stage optimization |
| DES + MPC | discrete event simulation with model predictive control |
| chaotic Quantum SSA | chaotic quantum social spider algorithm |
| GRASP | greedy randomized adaptive search procedure |
| VNS | variable neighborhood search |
| BRKGA | biased random-key genetic algorithm |
| NSGA-II | non-dominated sorting genetic algorithm II |
| Stochastic (CTMC) | stochastic modeling with continuous-time Markov chain |
| ACO | ant colony optimization |
| EA | evolutionary algorithm |
| ALNS | adaptive large neighborhood search |
| RTPSO | real-time particle swarm optimization |
| ILP | integer linear programming |
| MBCO | multi-objective bacterial colony optimization |
| Online alg (4/3-comp) | online algorithm with 4/3-competitive ratio |
| MORHCO | multi-objective robust hydrologic cycle optimization |
References
- Bouzekri, H.; Alpan, G.; Giard, V. A dynamic hybrid Berth Allocation Problem with routing constraints in bulk ports. In IFIP Advances in Information and Communication Technology, Proceedings of the IFIP International Conference on Advances in Production Management Systems, Novi Sad, Serbia, 30 August–3 September 2020; Springer: Cham, Switzerland, 2020; pp. 250–258. [Google Scholar]
- Lassoued, R.; Elloumi, A. The discrete and dynamic berth allocation problem in bulk port. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1976–1980. [Google Scholar]
- Hoffarth, L.; Voß, S. Berth allocation in a container terminal: Development of a decision support system. In Proceedings of the Operations Research Proceedings, Melbourne, VIC, Australia, 9–18 June 1993; pp. 89–95. [Google Scholar]
- Lim, A. The berth planning problem. Oper. Res. Lett. 1998, 22, 105–110. [Google Scholar] [CrossRef]
- Meersmans, P.J.M.; Dekker, R. Operations Research Supports Container Handling; Technical report; Erasmus University Rotterdam: Rotterdam, The Netherlands, 2001. [Google Scholar]
- Vis, I.F.; De Koster, R. Transshipment of containers at a container terminal: An overview. Eur. J. Oper. Res. 2003, 147, 1–16. [Google Scholar] [CrossRef]
- Steenken, D.; Voß, S.; Stahlbock, R. Container terminal operation and operations research-a classification and literature review. OR Spectr. 2004, 26, 3–49. [Google Scholar]
- Vacca, I.; Bierlaire, M.; Salani, M. Optimization at container terminals: Status, trends and perspectives. In Proceedings of the Swiss Transport Research Conference, Ascona, Switzerland, 12–14 September 2007. [Google Scholar]
- Stahlbock, R.; Voß, S. Operations research at container terminals: A literature update. OR Spectr. 2008, 30, 1–52. [Google Scholar] [CrossRef]
- Park, Y.M.; Kim, K.H. A scheduling method for berth and quay cranes. OR Spectr. 2003, 25, 1–23. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2010, 202, 615–627. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Raeesi, R.; Sahebjamnia, N.; Mansouri, S.A. The synergistic effect of operational research and big data analytics in greening container terminal operations: A review and future directions. Eur. J. Oper. Res. 2023, 310, 943–973. [Google Scholar] [CrossRef]
- Naeem, D.; Gheith, M.; Eltawil, A. A comprehensive review and directions for future research on the integrated scheduling of quay cranes and automated guided vehicles and yard cranes in automated container terminals. Comput. Ind. Eng. 2023, 179, 109149. [Google Scholar] [CrossRef]
- Aslam, S.; Michaelides, M.P.; Herodotou, H. A survey on computational intelligence approaches for intelligent marine terminal operations. IET Intell. Transp. Syst. 2024, 18, 755–793. [Google Scholar] [CrossRef]
- Xie, H.; Ambrosino, D. Operations Research, Machine Learning, and Integrated Techniques for Decision Problems in the Seaside Area of Container Terminals. Oper. Res. Forum 2025, 6, 1–51. [Google Scholar] [CrossRef]
- Rodrigues, F.; Agra, A. Berth allocation and quay crane assignment/scheduling problem under uncertainty: A survey. Eur. J. Oper. Res. 2022, 303, 501–524. [Google Scholar] [CrossRef]
- Correcher, J.F.; Perea, F.; Alvarez-Valdes, R. The berth allocation and quay crane assignment problem with crane travel and setup times. Comput. Oper. Res. 2024, 162, 106468. [Google Scholar] [CrossRef]
- Iris, Ç.; Lalla-Ruiz, E.; Lam, J.S.L.; Voß, S. Mathematical programming formulations for the strategic berth template problem. Comput. Ind. Eng. 2018, 124, 167–179. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Sun, Q.; Zhen, L.; Xiao, L.; Tan, Z. Recoverable robustness considering carbon tax in weekly berth and quay crane planning. In Smart Innovation, Systems and Technologies, Proceedings of the Smart Transportation Systems 2019, Auckland, New Zealand, 27–30 October 2019; Springer: Singapore, 2019; pp. 75–84. [Google Scholar]
- Abou Kasm, O.; Diabat, A.; Cheng, T. The integrated berth allocation, quay crane assignment and scheduling problem: Mathematical formulations and a case study. Ann. Oper. Res. 2020, 291, 435–461. [Google Scholar] [CrossRef]
- Agra, A.; Oliveira, M. MIP approaches for the integrated berth allocation and quay crane assignment and scheduling problem. Eur. J. Oper. Res. 2018, 264, 138–148. [Google Scholar] [CrossRef]
- Aljasmi, A.; Kaabi, R.A.; Hassani, N.A. A static-hybrid berth allocation problem with multi ship crane scheduling. In Proceedings of the 2016 7th International Conference on Information, Intelligence, Systems & Applications (IISA), Chalkidiki, Greece, 13–15 July 2016. [Google Scholar] [CrossRef]
- Alnaqbi, B.; Alrubaiai, H.; Alawi, S.A. Combination of a dynamic-hybrid berth allocation problem with a quay crane scheduling problem. In Proceedings of the 2016 7th International Conference on Information, Intelligence, Systems & Applications (IISA), Chalkidiki, Greece, 13–15 July 2016. [Google Scholar] [CrossRef]
- Al-Refaie, A.; Abedalqader, H. Optimal Quay Crane Assignment and Scheduling in Port’s Container Terminals. Jordan J. Mech. Ind. Eng. 2021, 15, 153–167. [Google Scholar]
- Al-Refaie, A.; Abedalqader, H. Optimal berth allocation under regular and emergent vessel arrivals. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2021, 235, 642–656. [Google Scholar] [CrossRef]
- Cahyono, R.T.; Flonk, E.J.; Jayawardhana, B. Dynamic berth and quay crane allocation for multiple berth positions and quay cranes. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 3262–3267. [Google Scholar]
- Cahyono, R.T.; Flonk, E.J.; Jayawardhana, B. Discrete-event systems modeling and the model predictive allocation algorithm for integrated berth and quay crane allocation. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1321–1331. [Google Scholar] [CrossRef]
- Cao, X.; Yang, Z.Y.; Hong, W.C.; Xu, R.Z.; Wang, Y.T. Optimizing Berth-quay Crane Allocation considering Economic Factors Using Chaotic Quantum SSA. Appl. Artif. Intell. 2022, 36, 2073719. [Google Scholar] [CrossRef]
- Cereser, B.L.H.; de Oliveira, A.R.L.; Moretti, A.C. A mathematical model and solution method for the berth allocation problem with variable handling time and continuous time horizon. Pesqui. Oper. 2022, 42, e261709. [Google Scholar] [CrossRef]
- Chargui, K.; Zouadi, T.; El Fallahi, A.; Reghioui, M.; Aouam, T. Berth and quay crane allocation and scheduling with worker performance variability and yard truck deployment in container terminals. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102449. [Google Scholar] [CrossRef]
- Chargui, K.; Zouadi, T.; Sreedharan, V.R.; El Fallahi, A.; Reghioui, M. A novel robust exact decomposition algorithm for berth and quay crane allocation and scheduling problem considering uncertainty and energy efficiency. Omega 2023, 118, 102868. [Google Scholar] [CrossRef]
- Correcher, J.F.; Alvarez-Valdes, R. A biased random-key genetic algorithm for the time-invariant berth allocation and quay crane assignment problem. Expert Syst. Appl. 2017, 89, 112–128. [Google Scholar] [CrossRef]
- Dai, Y.; Li, Z.; Wang, B. Optimizing Berth Allocation in Maritime Transportation with Quay Crane Setup Times Using Reinforcement Learning. J. Mar. Sci. Eng. 2023, 11, 1025. [Google Scholar] [CrossRef]
- De Oliveira, J.P.R.; Barbosa, J.D.; Lamprou, M. Multi-objective optimization of the quay crane assignment and scheduling problem: Time and movement optimization. In Proceedings of the 2016 7th International Conference on Information, Intelligence, Systems & Applications (IISA), Chalkidiki, Greece, 13–15 July 2016; pp. 1–7. [Google Scholar]
- Dhingra, V.; Roy, D.; de Koster, R.B.M. A cooperative quay crane-based stochastic model to estimate vessel handling time. Flex. Serv. Manuf. J. 2017, 29, 97–124. [Google Scholar] [CrossRef]
- El-boghdadly, T.; Bader-El-Den, M.; Jones, D.F. A genetic programming algorithm for the berth and quay crane allocation problem. In Proceedings of the IEEE International Conference on Advanced Logistics and Transport, Kraków, Poland, 1–3 June 2016. [Google Scholar]
- El-Boghdadly, T.; Bader-El-Den, M.; Jones, D. Evolving local search heuristics for the integrated berth allocation and quay crane assignment problem. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 2880–2887. [Google Scholar] [CrossRef]
- Expósito-Izquiero, C.; Lalla-Ruiz, E.; Lamata, T.; Melián-Batista, B.; Moreno-Vega, J.M. Fuzzy optimization models for seaside port logistics: Berthing and quay crane scheduling. Stud. Comput. Intell. 2016, 613, 323–343. [Google Scholar] [CrossRef]
- Fatemi-Anaraki, S.; Tavakkoli-Moghaddam, R.; Abdolhamidi, D.; Vahedi-Nouri, B. Simultaneous waterway scheduling, berth allocation, and quay crane assignment: A novel matheuristic approach. Int. J. Prod. Res. 2021, 59, 7576–7593. [Google Scholar] [CrossRef]
- Fu, Q.; Cai, C. Berth and Quay Crane Scheduling Optimization Based on Improved Genetic Algorithm. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 2138–2142. [Google Scholar] [CrossRef]
- Han, X.; Gong, X.; Jo, J. A new continuous berth allocation and quay crane assignment model in container terminal. Comput. Ind. Eng. 2015, 89, 15–22. [Google Scholar] [CrossRef]
- Hoseini, S.F.; Omran, M.M.; Márquez, A.C.; Makui, A. Simultaneous optimisation of seaside operations in container terminals: A case study of the Iranian Rajaee port. Int. J. Shipp. Transp. Logist. 2018, 10, 587–617. [Google Scholar] [CrossRef]
- Idris, N.; Zainuddin, Z.M. A simultaneous integrated model with multiobjective for continuous berth allocation and quay crane scheduling problem. In Proceedings of the 2016 International Conference on Industrial Engineering, Management Science and Application (ICIMSA), Jeju, Republic of Korea, 23–26 May 2016. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S. Improved formulations and an adaptive large neighborhood search heuristic for the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 123–147. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Optimal energy management and operations planning in seaports with smart grid while harnessing renewable energy under uncertainty. Omega 2021, 103, 102445. [Google Scholar] [CrossRef]
- Jiachen, X.; Guoyou, S. A study of integrated continuous berth allocation and quay crane scheduling. In Proceedings of the 2022 2nd Conference on High Performance Computing and Communication Engineering (HPCCE 2022), Harbin, China, 16–18 December 2022; Volume 12605. [Google Scholar] [CrossRef]
- Jiang, M.; Feng, J.; Zhou, J.; Zhou, L.; Ma, F.; Wu, G.; Zhang, Y. Multi-Terminal Berth and Quay Crane Joint Scheduling in Container Ports Considering Carbon Cost. Sustainability 2023, 15, 5018. [Google Scholar] [CrossRef]
- Jiao, X.; Zheng, F.; Liu, M.; Xu, Y. Integrated berth allocation and time-variant quay crane scheduling with tidal impact in approach channel. Discret. Dyn. Nat. Soc. 2018, 2018, 9097047. [Google Scholar] [CrossRef]
- Lalita, T.; Murthy, G. Compact ILP formulations for a class of solutions to berth allocation and quay crane scheduling problems. OPSEARCH 2022, 59, 413–439. [Google Scholar] [CrossRef]
- Lalla-Ruiz, E.; Expósito-Izquierdo, C.; De Armas, J.; Melián-Batista, B.; Moreno-Vega, J.M. Migrating Birds Optimization for the Seaside Problems at Maritime Container Terminals. J. Appl. Math. 2015, 2015, 781907. [Google Scholar] [CrossRef]
- Li, Z.; Li, S. An integrated model and enhanced quantum annealing algorithm for berth allocation and quay crane scheduling problem. EasyChair 2021, 10. [Google Scholar] [CrossRef]
- Li, Y.; Chu, F.; Zheng, F.; Kacem, I. Integrated Berth Allocation and Quay Crane Assignment With Uncertain Maintenance Activities. In Proceedings of the 2019 International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Z.; Chu, F. A mathematical model for container port integrated scheduling and optimization problem. In Proceedings of the 2015 International Conference on Logistics, Informatics and Service Sciences (LISS), Barcelona, Spain, 27–29 July 2015. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, L.; Zhang, C. Behavior perception-based disruption models for berth allocation and quay crane assignment problems. Comput. Ind. Eng. 2016, 97, 258–275. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Li, S. Rolling horizon based robust optimization method of quayside operations in maritime container ports. Ocean Eng. 2022, 256, 111505. [Google Scholar] [CrossRef]
- Ma, H.L.; Wang, Z.; Chung, S.H.; Chan, F.T. The impacts of time segment modeling in berth allocation and quay crane assignment on terminal efficiency. Ind. Manag. Data Syst. 2019, 119, 968–992. [Google Scholar] [CrossRef]
- Ma, H.; Chan, F.T.; Chung, S. A fast approach for the integrated berth allocation and quay crane assignment problem. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 2076–2087. [Google Scholar] [CrossRef]
- Malekahmadi, A.; Alinaghian, M.; Hejazi, S.R.; Assl Saidipour, M.A. Integrated continuous berth allocation and quay crane assignment and scheduling problem with time-dependent physical constraints in container terminals. Comput. Ind. Eng. 2020, 147, 106672. [Google Scholar] [CrossRef]
- Nishimura, E. Yard and berth planning efficiency with estimated handling time. Marit. Bus. Rev. 2020, 5, 5–29. [Google Scholar] [CrossRef]
- Niu, B.; Liu, Q.; Wang, Z.; Tan, L.; Li, L. Multi-objective bacterial colony optimization algorithm for integrated container terminal scheduling problem. Nat. Comput. 2021, 20, 89–104. [Google Scholar] [CrossRef]
- Olteanu, S.; Costescu, D.; Ruscǎ, A.; Oprea, C. A genetic algorithm for solving the quay crane scheduling and allocation problem. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 042045. [Google Scholar] [CrossRef]
- Pan, J.; Xu, Y.; Zhang, G. Online integrated allocation of berths and quay cranes in container terminals with 1-lookahead. J. Comb. Optim. 2018, 36, 617–636. [Google Scholar] [CrossRef]
- Ran, L.; Cheng, Y.; Zhang, G. Two-stage robust optimization for the integrated dynamic berth allocation and quay crane scheduling problem under uncertainty. Eng. Optim. 2024, 32, 425–452. [Google Scholar] [CrossRef]
- Ren, J.; Shang, X.T.; Cao, J.X. A genetic algorithm for the integrated berth allocation and quay crane scheduling problem in container terminals. In Proceedings of the 2015 4th International Conference on Sensors, Measurement and Intelligent Materials, Shenzhen, China, 27–28 December 2015; pp. 1036–1040. [Google Scholar]
- Ren, J.; Cao, J.; Xue, C.C. The Continuous Berth Allocation and Quay Crane Assignment Problem Based on the Operational General Time Loss of Vessels. In Proceedings of the 17th COTA International Conference of Transportation Professionals, Shanghai, China, 7–9 July 2017; pp. 1358–1367. [Google Scholar]
- Rodrigues, F.; Agra, A. An exact robust approach for the integrated berth allocation and quay crane scheduling problem under uncertain arrival times. Eur. J. Oper. Res. 2021, 295, 499–516. [Google Scholar] [CrossRef]
- Salhi, A.; Alsoufi, G.; Yang, X. An evolutionary approach to a combined mixed integer programming model of seaside operations as arise in container ports. Ann. Oper. Res. 2019, 272, 69–98. [Google Scholar] [CrossRef]
- Samrout, M.; Sbihi, A.; Yassine, A. Solving an Integrated Bi-objective Container Terminal Integrated Planning with Transshipment Operations. In Metaheuristics; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 14754 LNCS; Springer: Cham, Switzerland, 2024; pp. 380–386. [Google Scholar] [CrossRef]
- Shang, X.T.; Cao, J.X.; Ren, J. A robust optimization approach to the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 44–65. [Google Scholar] [CrossRef]
- Tang, M.; Ji, B.; Fang, X.; Yu, S.S. Discretization-strategy-based solution for berth allocation and quay crane assignment problem. J. Mar. Sci. Eng. 2022, 10, 495. [Google Scholar] [CrossRef]
- Tang, S.; Xu, S.; Gao, J.; Ma, M.; Liao, P. Effect of Service Priority on the Integrated Continuous Berth Allocation and Quay Crane Assignment Problem after Port Congestion. J. Mar. Sci. Eng. 2022, 10, 1259. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Fatemi-Anaraki, S.; Abdolhamidi, D.; Vahedi-Nouri, B. Integrated Waterway Scheduling, Berth Allocation and Quay Crane Assignment Problem by Using a Hybrid Flow Shop Concept. In Proceedings of the 2019 International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019. [Google Scholar] [CrossRef]
- Türkoğulları, Y.B.; Taşkın, Z.C.; Aras, N.; Altınel, İ.K. Optimal berth allocation, time-variant quay crane assignment and scheduling with crane setups in container terminals. Eur. J. Oper. Res. 2016, 254, 985–1001. [Google Scholar] [CrossRef]
- Venturini, G.; Iris, Ç.; Kontovas, C.A.; Larsen, A. The multi-port berth allocation problem with speed optimization and emission considerations. Transp. Res. Part D Transp. Environ. 2017, 54, 142–159. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X.; Meng, Q. Joint berth allocation and quay crane assignment under different carbon taxation policies. Transp. Res. Part B Methodol. 2018, 117, 18–36. [Google Scholar] [CrossRef]
- Woo, S.H.; Park, H.J.; Cho, S.W.; Kim, K.H. Proactive berth scheduling with data-driven buffer time in container terminals. Int. Trans. Oper. Res. 2024, 31, 2875–2902. [Google Scholar] [CrossRef]
- Wu, F.; Jiang, Z.; Zhang, R.; Zhang, X. Approximation algorithms for scheduling monotonic moldable tasks on multiple platforms. J. Sched. 2023, 26, 383–398. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C.; Miao, L. A bi-objective robust model for berth allocation scheduling under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 294–319. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C.; Miao, L. Reactive strategy for discrete berth allocation and quay crane assignment problems under uncertainty. Comput. Ind. Eng. 2018, 126, 196–216. [Google Scholar] [CrossRef]
- Xingchi, W.; Caimao, T.; Junliang, H. Integrated Optimization of Berth Allocation and Quay Crane Assignment under Uncertainty. In Proceedings of the 2019 International Conference on Advances in Construction Machinery and Vehicle Engineering (ICACMVE), Changsha, China, 14–16 May 2019; pp. 11–16. [Google Scholar]
- Yang, J.; Gao, H.; Liu, W.; Liu, T. A novel strategy for berth and quay crane allocation under disruption in container terminal. Int. J. Innov. Comput. Inf. Control 2016, 12, 1535–1551. [Google Scholar]
- Yin, W.; Xu, B.; Yang, Y. Integrated Allocation and Scheduling Problem for Berth and Quay Crane in U-shaped Container Port under Spatio-temporal Asynchronous Propagation. In Proceedings of the 2022 International Symposium on Sensing and Instrumentation in 5G and IoT Era (ISSI), Shanghai, China, 17–18 November 2022; pp. 47–52. [Google Scholar] [CrossRef]
- Yu, J.; Tang, G.; Voß, S.; Song, X. Berth allocation and quay crane assignment considering the adoption of different green technologies. Transp. Res. Part E Logist. Transp. Rev. 2023, 176, 103185. [Google Scholar] [CrossRef]
- Yu, T.; Qiang, Z.; Benfei, Z. A genetic algorithm based on spatiotemporal conflict between continuous berth-allocation and time-varying specific crane assignment. Eng. Optim. 2019, 51, 390–411. [Google Scholar] [CrossRef]
- Yu, S.; Wang, B.; Zhang, S.; Zhen, L. Berth Allocation in Transshipment Ports by Considering Quay Crane Coverage and Ship Fuel Consumption. Asia-Pac. J. Oper. Res. 2022, 39, 2150028. [Google Scholar] [CrossRef]
- Yu, M.; Liu, X.; Ji, X.; Ren, Y.; Guo, W. Integrated berth allocation and quay crane assignment and scheduling problem under the influence of various factors. IET Collab. Intell. Manuf. 2024, 6, e70001. [Google Scholar] [CrossRef]
- Yuping, W.; Zhe, X.; Youfang, H.; Yangyang, H.; Tianyi, G. Study of continuous berth allocation algorithm based on fairness maximization. J. Eng. Sci. Technol. Rev. 2017, 10, 116–127. [Google Scholar] [CrossRef]
- Zhao, W.; Qiu, Q.; Zhao, H.; Bian, X.; Yu, H.; Liu, J.; Mei, X. Multi-population for Multi-objective Genetic Algorithm with Adaptive Information Sharing Strategy for Berth Allocation and Quay Crane Assignment Problems. In Proceedings of the GECCO ’24 Companion: Proceedings of the Genetic and Evolutionary Computation Conference Companion, Melbourne, VIC, Australia, 14–18 July 2024; pp. 387–390. [Google Scholar] [CrossRef]
- Zheng, F.; Qiao, L.; Liu, M. An online model of berth and quay crane integrated allocation in container terminals. In Combinatorial Optimization and Applications; Lecture Notes in Computer Science (Including Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2015; Volume 9486, pp. 721–730. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, J.; Liu, B. Integrated continuous berth allocation and quay crane scheduling under tidal influence at container terminal. Jisuanji Jicheng Zhizao Xitong/Comput. Integr. Manuf. Syst. 2018, 24, 2599–2611. [Google Scholar] [CrossRef]
- Zhong, H.; Lian, Z.; Xue, B.; Niu, B.; Qu, R.; Zhou, T. An integrated container terminal scheduling problem with different-berth sizes via multiobjective hydrologic cycle optimization. Int. J. Intell. Syst. 2022, 37, 11909–11925. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Wu, W.; Han, X.L.; Niravong, J. Integration of berth allocation and quay crane assignment in tidal container ports. J. Donghua Univ. 2015, 32, 559–564 and 570. [Google Scholar]
- He, J.; Wang, Y.; Tan, C.; Yu, H. Modeling berth allocation and quay crane assignment considering QC driver cost and operating efficiency. Adv. Eng. Inform. 2021, 47, 101252. [Google Scholar] [CrossRef]
- He, J. Berth allocation and quay crane assignment in a container terminal for the trade-off between time-saving and energy-saving. Adv. Eng. Inform. 2016, 30, 390–405. [Google Scholar] [CrossRef]
- Tasoglu, G.; Yildiz, G. Simulated annealing based simulation optimization method for solving integrated berth allocation and quay crane scheduling problems. Simul. Model. Pract. Theory 2019, 97, 101948. [Google Scholar] [CrossRef]
- Li, F.; Sheu, J.B.; Gao, Z.Y. Solving the continuous berth allocation and specific quay crane assignment problems with quay crane coverage range. Transp. Sci. 2015, 49, 968–989. [Google Scholar] [CrossRef]
- Fazli, M.; Fathollahi-Fard, A.M.; Tian, G. Addressing a coordinated quay crane scheduling and assignment problem by red deer algorithm. Int. J. Eng. 2019, 32, 1186–1191. [Google Scholar]
- Nourmohammadzadeh, A.; Voß, S. A robust multiobjective model for the integrated berth and quay crane scheduling problem at seaside container terminals. Ann. Math. Artif. Intell. 2022, 90, 831–853. [Google Scholar] [CrossRef]
- Chu, L.; Zhang, J.; Chen, X.; Yu, Q. Optimization of Integrated Tugboat–Berth–Quay Crane Scheduling in Container Ports Considering Uncertainty in Vessel Arrival Times and Berthing Preferences. J. Mar. Sci. Eng. 2024, 12, 1541. [Google Scholar] [CrossRef]
- Li, M.Z.; Jin, J.G.; Lu, C.X. Real-time disruption recovery for integrated berth allocation and crane assignment in container terminals. Transp. Res. Rec. 2015, 2479, 49–59. [Google Scholar] [CrossRef]
- Wu, E.; Zhu, J. Integrated proactive-reactive approach and a hybrid adaptive large neighborhood search algorithm for berth and quay crane scheduling under uncertain combination. J. Ind. Manag. Optim. 2023, 19, 5612–5640. [Google Scholar] [CrossRef]
- Tan, C.; He, J. Integrated proactive and reactive strategies for sustainable berth allocation and quay crane assignment under uncertainty. Ann. Oper. Res. 2025, 349, 879–910. [Google Scholar] [CrossRef]
- Lu, H.; Lu, X. Joint Optimization of Berths and Quay Cranes Considering Carbon Emissions: A Case Study of a Container Terminal in China. J. Mar. Sci. Eng. 2025, 13, 148. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Zhang, J.; Zeng, Y.; Fan, C. Bi-Objective Optimization for Joint Time-Invariant Allocation of Berths and Quay Cranes. Appl. Sci. 2025, 15, 3035. [Google Scholar] [CrossRef]
- Hsu, H.P.; Chiang, T.L.; Wang, C.N.; Fu, H.P.; Chou, C.C. A hybrid GA with variable quay crane assignment for solving berth allocation problem and quay crane assignment problem simultaneously. Sustainability 2019, 11, 2018. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C. An almost robust optimization model for integrated berth allocation and quay crane assignment problem. Omega 2021, 104, 102455. [Google Scholar] [CrossRef]
- Wen, D.; Li, X.; Ren, X.; Ji, M.; Long, Q. Optimisation of berth and quay crane joint scheduling considering efficiency and energy consumption. Int. J. Shipp. Transp. Logist. 2023, 17, 487–505. [Google Scholar] [CrossRef]
- Jiang, M.; Ma, F.; Zhang, Y.; Lv, S.; Pei, Z.; Wu, G. Collaborative scheduling optimization of container port berths and cranes under low-carbon environment. Sustainability 2024, 16, 2985. [Google Scholar] [CrossRef]
- Cai, L.; Li, W.; Zhou, B.; Li, H.; Yang, Z. Robust multi-equipment scheduling for U-shaped container terminals concerning double-cycling mode and uncertain operation time with cascade effects. Transp. Res. Part C Emerg. Technol. 2024, 158, 104447. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, C.; Shi, J.; Lim, G.; Wu, Y. Optimal Port Microgrid Scheduling Incorporating Onshore Power Supply and Berth Allocation Under Uncertainty. Appl. Energy 2022, 313, 118856. [Google Scholar] [CrossRef]
- Jiang, M.; Zhou, J.; Feng, J.; Zhou, L.; Ma, F.; Wu, G. Integrated Berth and Crane Scheduling Problem Considering Crane Coverage in Multi-Terminal Tidal Ports under Uncertainty. J. Mar. Sci. Eng. 2022, 10, 506. [Google Scholar] [CrossRef]
- Golias, M.M.; Boilé, M.; Theofanis, S.; Taboada, H.A. A multi-objective decision and analysis approach for the berth scheduling problem. Int. J. Inf. Technol. Proj. Manag. (IJITPM) 2010, 1, 54–73. [Google Scholar] [CrossRef][Green Version]
- Imai, A.; Nishimura, E.; Papadimitriou, S. The dynamic berth allocation problem for a container port. Transp. Res. Part B Methodol. 2001, 35, 401–417. [Google Scholar] [CrossRef]
- Kim, K.H.; Moon, K.C. Berth scheduling by simulated annealing. Transp. Res. Part B Methodol. 2003, 37, 541–560. [Google Scholar] [CrossRef]
- Guan, Y.; Cheung, R.K. The berth allocation problem: Models and solution methods. OR Spectr. 2004, 26, 75–92. [Google Scholar] [CrossRef]

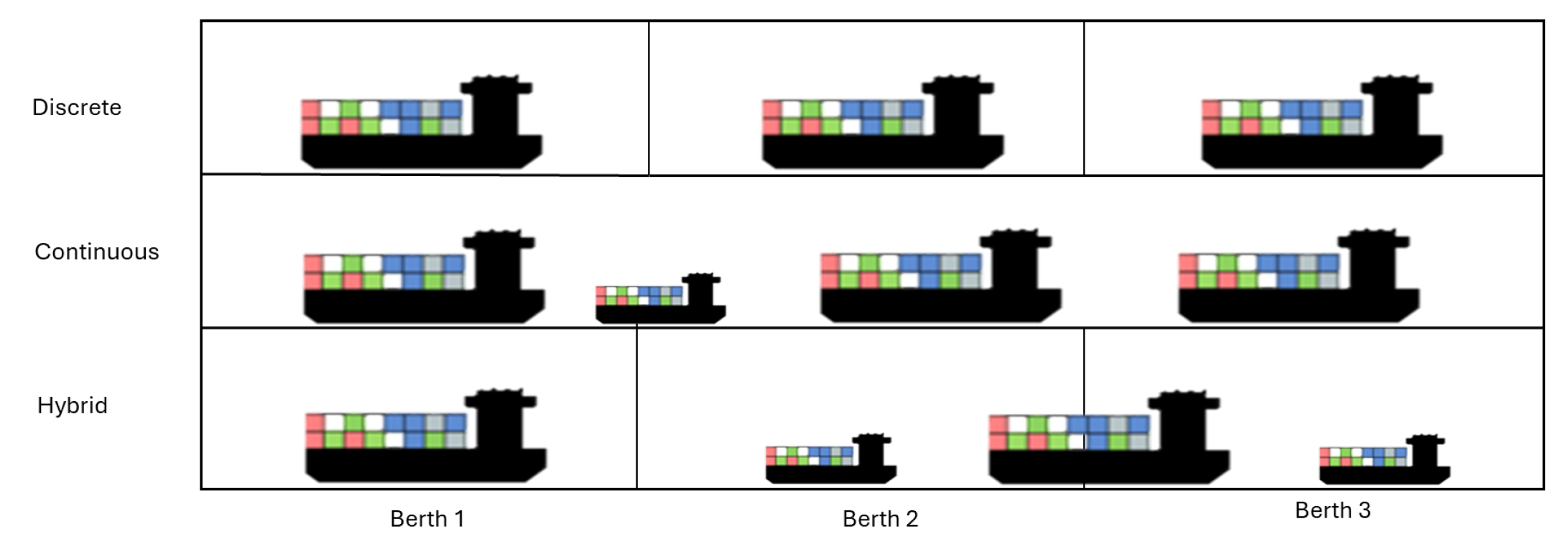


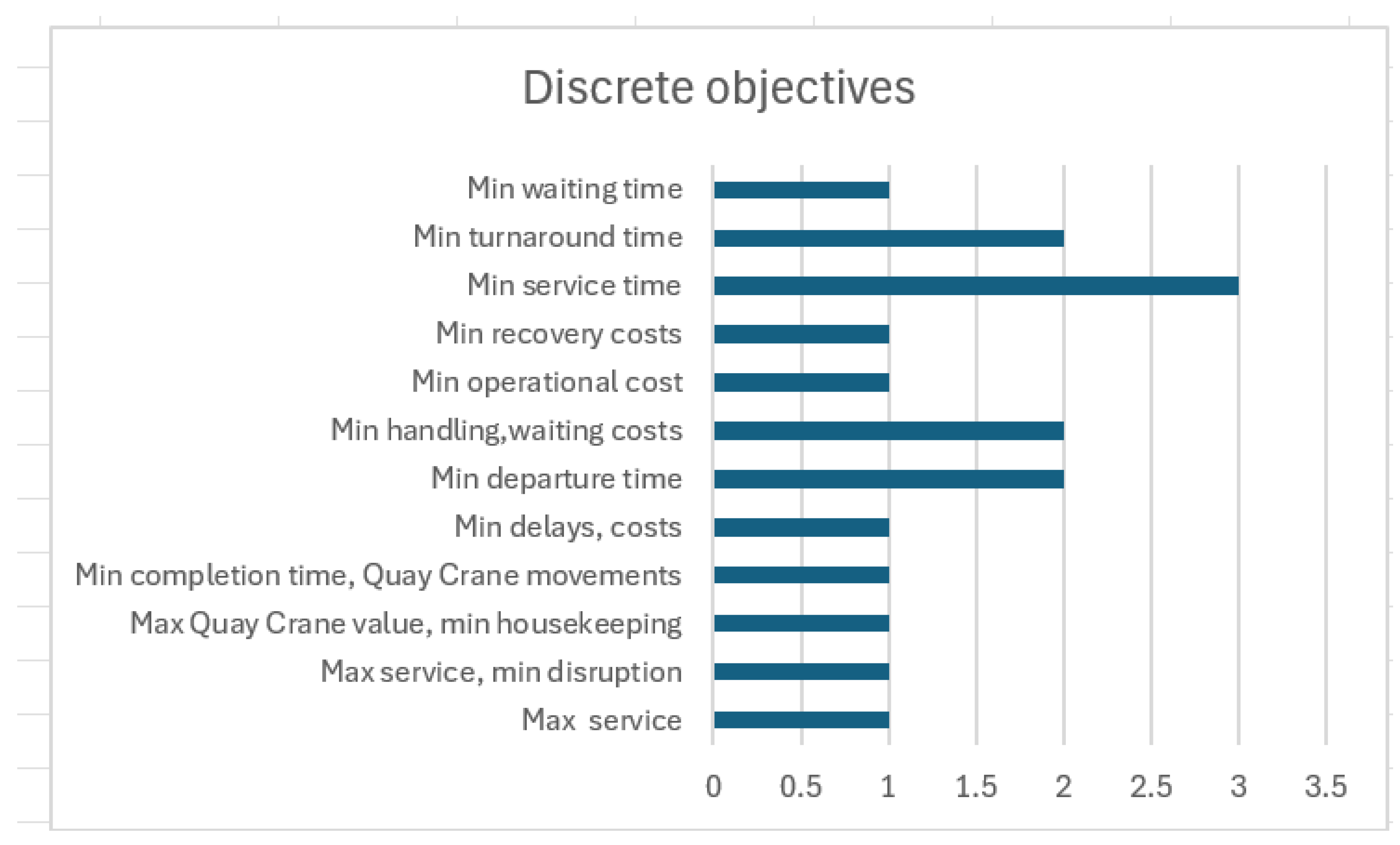

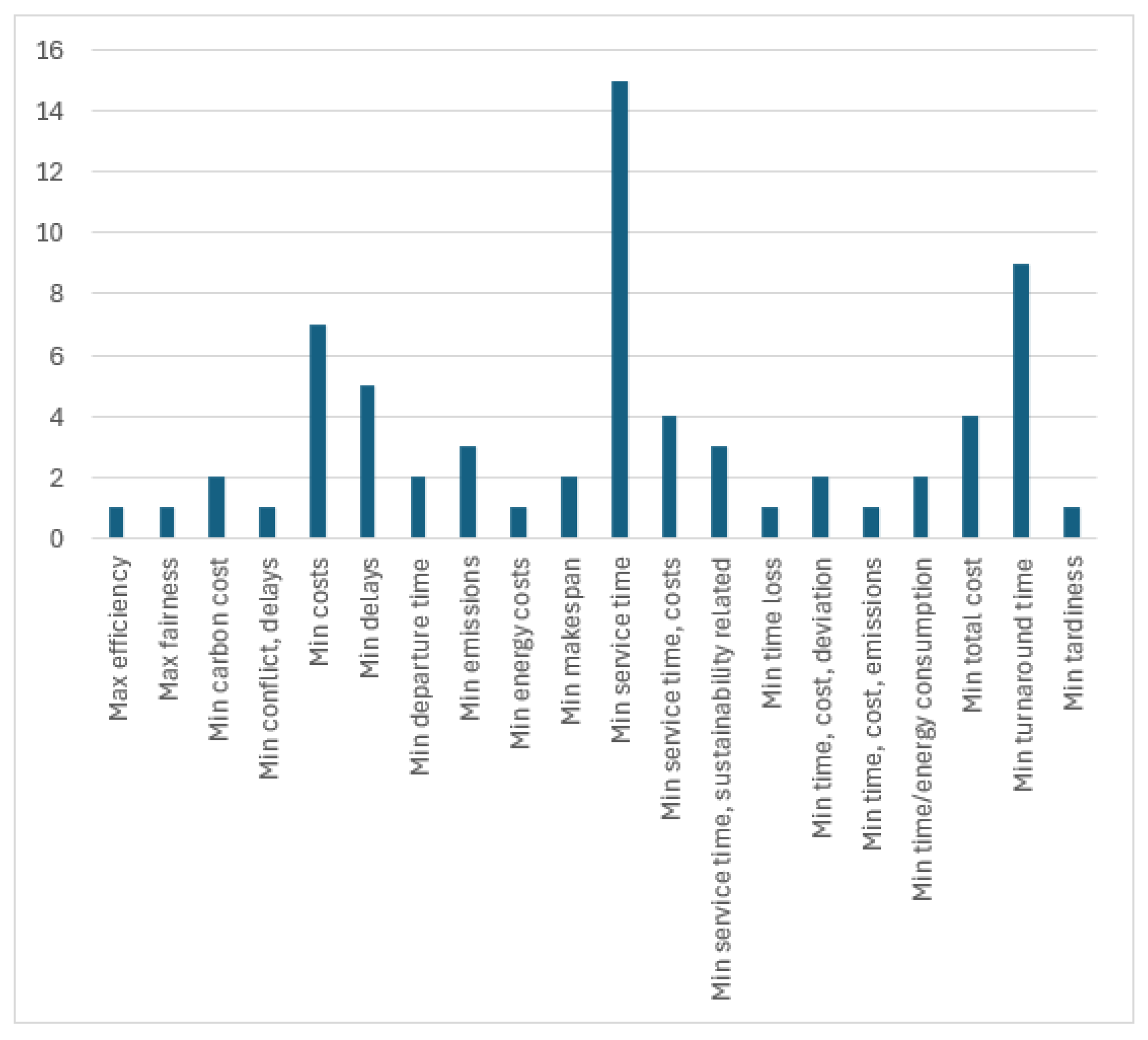
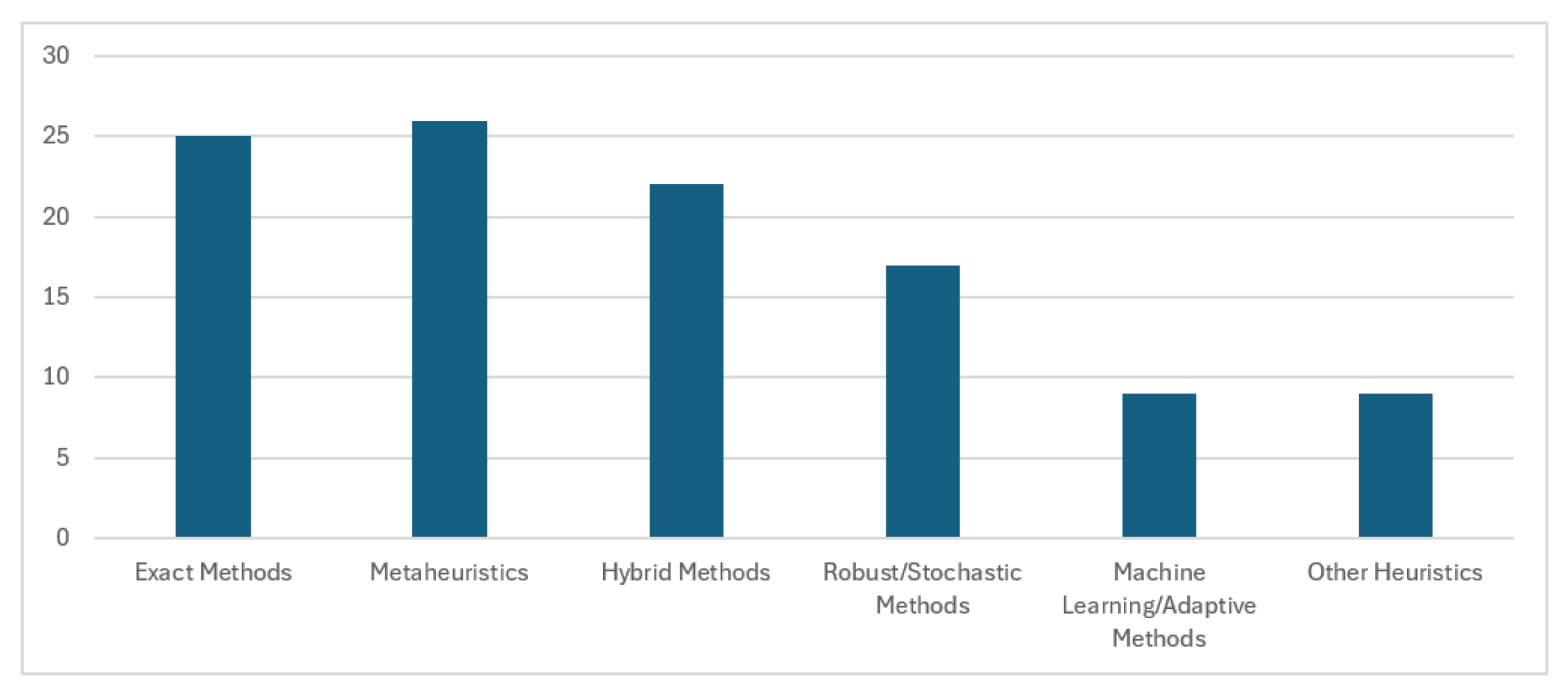
| Reference | Berth Layout | Arrival Process | Objective | Solution Approach | Handling of Crane |
|---|---|---|---|---|---|
| Correcher et al. [18] | Continuous | Dynamic | Min service time, setup costs | MILP | Variable |
| Iris et al. [19] | Continuous | Static | Min service time | MILP | Fixed |
| Iris and Lam [20] | Continuous | Stochastic | Min costs | Robust MILP | Variable,QCSP |
| Sun et al. [21] | Continuous | Stochastic | Min costs (carbon tax) | Robust MILP | Variable |
| Abou Kasm et al. [22] | Continuous | Dynamic | Min flow time, tardiness | MILP + Gurobi | Variable |
| Agra and Oliveira [23] | Discrete | Dynamic | Max QC value, min housekeeping | MIP + Tabu | Variable,QCSP |
| Aljasmi et al. [24] | Hybrid | Static | Min service time | GA-based heuristic | Variable |
| Alnaqbi et al. [25] | Hybrid | Dynamic | Min waiting/handling time | GA | Variable |
| Al-Refaie and Abedalqader [26] | Discrete | Stochastic | Max emergent service | Three-stage opt | Fixed,QCSP |
| Al-Refaie and Abedalqader [27] | Discrete | Stochastic | Max emergent service, min disruption | Three-stage opt | Variable,QCSP |
| Cahyono et al. [28] | Discrete | Dynamic | Min handling/waiting costs | DES + MPC | Variable |
| Cahyono et al. [29] | Discrete | Dynamic | Min handling/waiting costs | DES + MPC | Variable |
| Cao et al. [30] | Continuous | Dynamic | Min costs | Chaotic Quantum SSA | Variable,QCSP |
| Cereser et al. [31] | Continuous | Dynamic | Min total cost | GRASP | Variable |
| Chargui et al. [32] | Discrete | Dynamic | Min departure time | MILP + VNS | Variable |
| Chargui et al. [33] | Continuous | Stochastic | Min worst-case costs | Robust decomposition | Fixed |
| Correcher and Alvarez-Valdes [34] | Continuous | Static | Min service time | BRKGA | Variable |
| Dai et al. [35] | Continuous | Stochastic | Min turnaround time, setup costs | MILP + RL | Variable,QCSP |
| De Oliveira et al. [36] | Discrete | Static | Min completion time, QC movements | NSGA-II | Variable |
| Dhingra et al. [37] | Discrete | Stochastic | Estimate handling time | Stochastic (CTMC) | Variable,QCSP |
| El-boghdadly et al. [38] | Continuous | Dynamic | Min service time | GP | Variable,QCSP |
| El-Boghdadly et al. [39] | Continuous | Dynamic | Min service time | GP | Variable |
| Expósito-Izquiero et al. [40] | Continuous | Stochastic | Min service time, max robustness | Fuzzy MILP | Variable |
| Fatemi-Anaraki et al. [41] | Continuous | Dynamic | Min service time | Matheuristic (GA + ACO) | Fixed |
| Fu and Cai [42] | Continuous | Dynamic | Min service time | GA | Variable |
| Han et al. [43] | Continuous | Dynamic | Min service time | Branch-and-price | Variable |
| Hoseini et al. [44] | Hybrid | Stochastic | Min service time, costs | Simulation-based EA | Variable |
| Idris and Zainuddin [45] | Continuous | Stochastic | Min service/waiting time | MO meta-heuristic | Variable |
| Iris et al. [46] | Continuous | Dynamic | Min service time | ALNS | Variable |
| Iris and Lam [47] | Continuous | Stochastic | Min energy costs | MILP + Heuristic | Variable,QCSP |
| Jiachen and Guoyou [48] | Continuous | Stochastic | Min turnaround time | RTPSO | Variable |
| Jiang et al. [49] | Continuous | Stochastic | Min carbon cost, delays | Robust MILP + ALNS | Variable |
| Jiao et al. [50] | Continuous | Dynamic | Min turnaround time | ILP + GA/PSO/SA | Variable |
| Lalita and Murthy [51] | Hybrid | Static/Dynamic | Min service time, costs | Compact ILP | Fixed |
| Lalla-Ruiz et al. [52] | Continuous | Dynamic | Min service time | MBO | Variable |
| Li and Li [53] | Continuous | Dynamic | Min service time | Quantum Annealing | Variable,QCSP |
| Li et al. [54] | Continuous | Stochastic | Min turnaround time | Stochastic ILP + SAA | Variable |
| Liu et al. [55] | Discrete | Dynamic | Min operational cost | MIP + GA | Variable |
| Liu et al. [56] | Continuous | Stochastic | Min turnaround time (disruptions) | MIP + GA-SA | Variable |
| Liu et al. [57] | Continuous | Stochastic | Min departure delays | Robust + CCG | Variable |
| Ma et al. [58] | Continuous | Dynamic | Max efficiency | MILP + Heuristic | Variable,QCSP |
| Ma et al. [59] | Continuous | Dynamic | Min service time | GA-based heuristic | Variable |
| Malekahmadi et al. [60] | Continuous | Dynamic | Min turnaround time | RTPSO | Variable |
| Nishimura [61] | Discrete | Stochastic | Min waiting time, AGV use | PSO | Variable |
| Niu et al. [62] | Continuous | Dynamic | Min time, cost, deviation | MBCO | Variable |
| Olteanu et al. [63] | Discrete | Dynamic | Min completion time | GA | Variable |
| Pan et al. [64] | Continuous | Dynamic | Min makespan | Online heuristic | Variable |
| Ran et al. [65] | Continuous | Stochastic | Min departure time (worst-case) | Two-stage robust + CCG | |
| Ren et al. [66] | Continuous | Dynamic | Min turnaround time | GA | Variable,QCSP |
| Ren et al. [67] | Continuous | Dynamic | Min time loss | MILP | Variable |
| Rodrigues and Agra [68] | Continuous | Stochastic | Min worst-case completion | Two-stage robust + MOSA | Fixed |
| Salhi et al. [69] | Continuous | Stochastic | Min service time, costs | MIP + EA | Variable |
| Samrout et al. [70] | Continuous | Dynamic | Min service time, transshipment costs | NSGA-III | Fixed |
| Shang et al. [71] | Continuous | Stochastic | Min delays | Robust MILP | Variable |
| Tang et al. [72] | Discrete | Dynamic | Min service time | Discretization + Heuristic | Fixed,QCSP |
| Tang et al. [73] | Continuous | Dynamic | Min weighted delay | GA | Variable |
| Tavakkoli-Moghaddam et al. [74] | Continuous | Dynamic | Min turnaround time | MIP + Mb-MOKA | Variable |
| Türkoğulları et al. [75] | Continuous | Dynamic | Min service time, setup costs | MILP | Variable |
| Venturini et al. [76] | Continuous | Stochastic | Min emissions, costs | MILP | Variable,QCSP |
| Wang et al. [77] | Continuous | Dynamic | Min costs (carbon tax) | MILP | Variable,QCSP |
| Woo et al. [78] | Continuous | Dynamic | Min delays | Data-driven heuristic | Variable |
| Wu et al. [79] | Abstract | Deterministic | Min makespan | Approx alg | Variable |
| Xiang et al. [80] | Discrete | Dynamic | Min service time | MILP | Fixed,QCSP |
| Xiang et al. [81] | Discrete | Stochastic | Min turnaround time | MIP + Heuristic | Variable,QCSP |
| Xingchi et al. [82] | Continuous | Stochastic | Min delays | Robust MILP | Variable |
| Yang et al. [83] | Discrete | Stochastic | Min recovery costs | Heuristic/meta-heuristic | Variable |
| Yin et al. [84] | Continuous | Dynamic | Min service time | MILP + GA | Fixed |
| Yu et al. [85] | Continuous | Stochastic | Min emissions, delays | MILP + GA | Variable |
| Yu et al. [86] | Continuous | Dynamic | Min conflict, delays | GA | Variable |
| Yu et al. [87] | Continuous | Dynamic | Min service time, fuel use | Spatiotemporal + BB | Variable |
| Yu et al. [88] | Continuous | Stochastic | Min delays, max safety | MO-GA + SA | Variable |
| Yuping et al. [89] | Continuous | Stochastic | Max fairness | Fairness heuristic | Variable,QCSP |
| Zhao et al. [90] | Continuous | Stochastic | Min time, cost, emissions | MO-GA | Variable |
| Zheng et al. [91] | Hybrid | Dynamic | Min makespan | Online alg (4/3-comp) | Fixed |
| Zheng et al. [92] | Continuous | Dynamic | Min turnaround time | ILP + GA/HPSO/HSA | Fixed |
| Zhong et al. [93] | Continuous | Dynamic | Min time, cost, deviation | MORHCO | Variable |
| Lu et al. [94] | Continuous | Dynamic | Min waiting/handling time | MILP + heuristic | Variable,QCSP |
| He et al. [95] | Continuous | Dynamic | Min cost, max efficiency | MILP | Variable |
| He [96] | Continuous | Dynamic | Min time/energy consumption | Multi-objective optimization | Variable |
| Tasoglu and Yildiz [97] | Discrete | Stochastic | Min total cost/time | Simulated annealing | Variable,QCSP |
| Li et al. [98] | Continuous | Dynamic | Min service time, max coverage | Heuristic | Variable |
| Fazli et al. [99] | Discrete | Dynamic | Min makespan | Red Deer Algorithm | Variable |
| Nourmohammadzadeh and Vo [100] | Continuous | Stochastic | Min cost/time, max robustness | Robust multi-objective | Variable,QCSP |
| Chu et al. [101] | Continuous | Stochastic | Min total cost, max preference | MILP + heuristic | Variable |
| Li et al. [102] | Discrete/Continuous | Dynamic | Min disruption time | Real-time heuristic | Variable |
| Wu and Zhu [103] | Continuous | Stochastic | Min delay, max reliability | Hybrid ALNS | Variable |
| Tan and He [104] | Continuous | Stochastic | Min emissions/time, max sustainability | Proactive-reactive model | Variable |
| Lu and Lu [105] | Continuous | Dynamic | Min carbon emissions/time | Multi-objective GA | Variable |
| Zhang et al. [106] | Discrete | Static | Min cost/time, max utilization | Bi-objective optimization | Fixed, time-invariant |
| Hsu et al. [107] | Discrete/Continuous | Dynamic | Min total time | Hybrid GA | Variable |
| Xiang and Liu [108] | Continuous | Stochastic | Min cost/time, max robustness | Almost robust optimization | Variable |
| Wen et al. [109] | Continuous | Dynamic | Min energy/time, max efficiency | Optimization model | Variable |
| Jiang et al. [110] | Continuous | Dynamic | Min carbon emissions/time | Collaborative optimization | Variable |
| Cai et al. [111] | Discrete | Stochastic | Min total time, max robustness | Robust scheduling | Variable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makhado, N.; Paepae, T.; Sejeso, M.; Harley, C. Berth Allocation and Quay Crane Scheduling in Port Operations: A Systematic Review. J. Mar. Sci. Eng. 2025, 13, 1339. https://doi.org/10.3390/jmse13071339
Makhado N, Paepae T, Sejeso M, Harley C. Berth Allocation and Quay Crane Scheduling in Port Operations: A Systematic Review. Journal of Marine Science and Engineering. 2025; 13(7):1339. https://doi.org/10.3390/jmse13071339
Chicago/Turabian StyleMakhado, Ndifelani, Thulane Paepae, Matthews Sejeso, and Charis Harley. 2025. "Berth Allocation and Quay Crane Scheduling in Port Operations: A Systematic Review" Journal of Marine Science and Engineering 13, no. 7: 1339. https://doi.org/10.3390/jmse13071339
APA StyleMakhado, N., Paepae, T., Sejeso, M., & Harley, C. (2025). Berth Allocation and Quay Crane Scheduling in Port Operations: A Systematic Review. Journal of Marine Science and Engineering, 13(7), 1339. https://doi.org/10.3390/jmse13071339






