Advances of Complex Marine Environmental Influences on Underwater Vehicles
Abstract
1. Introduction
2. Influences of Surface Waves
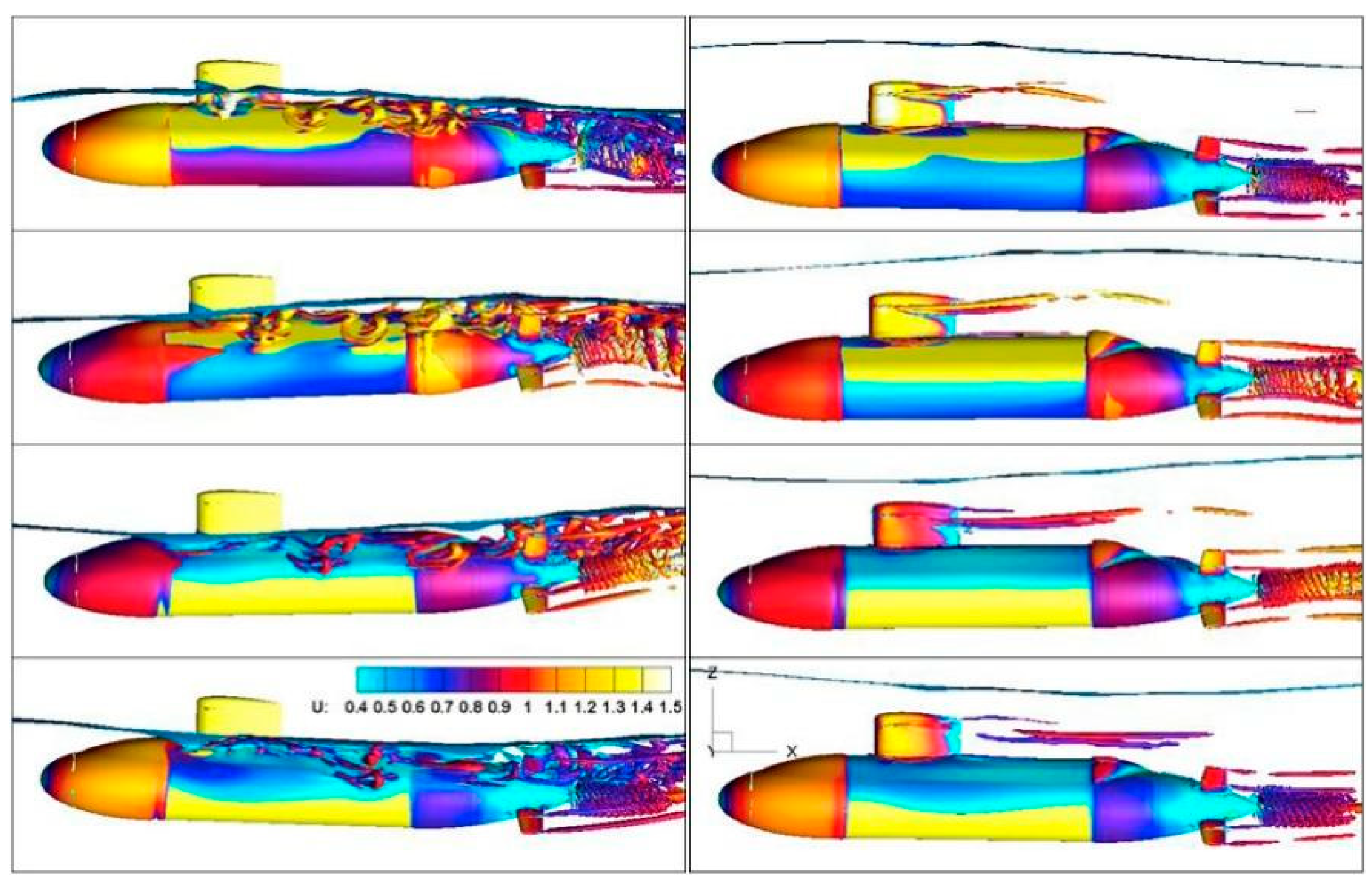
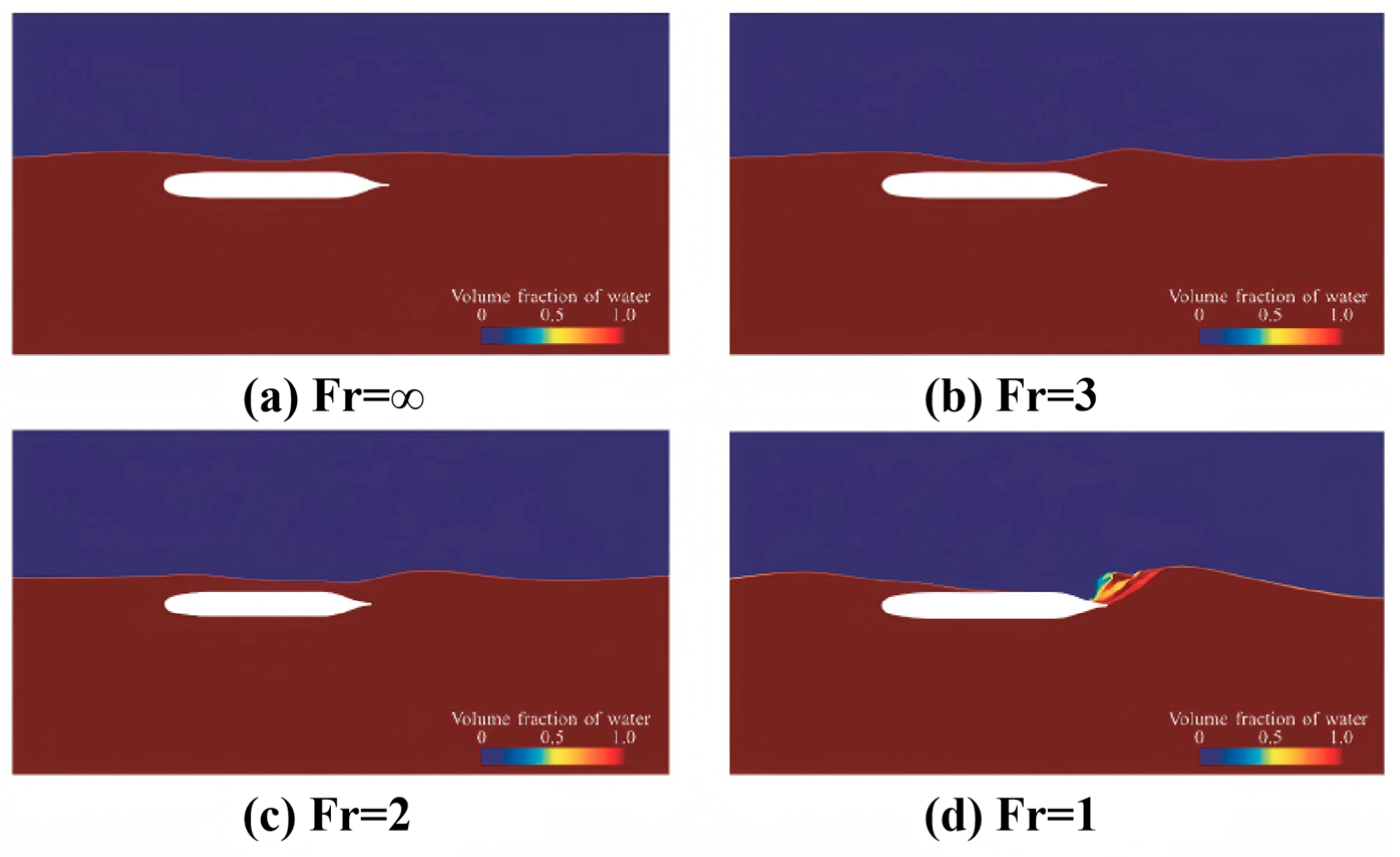
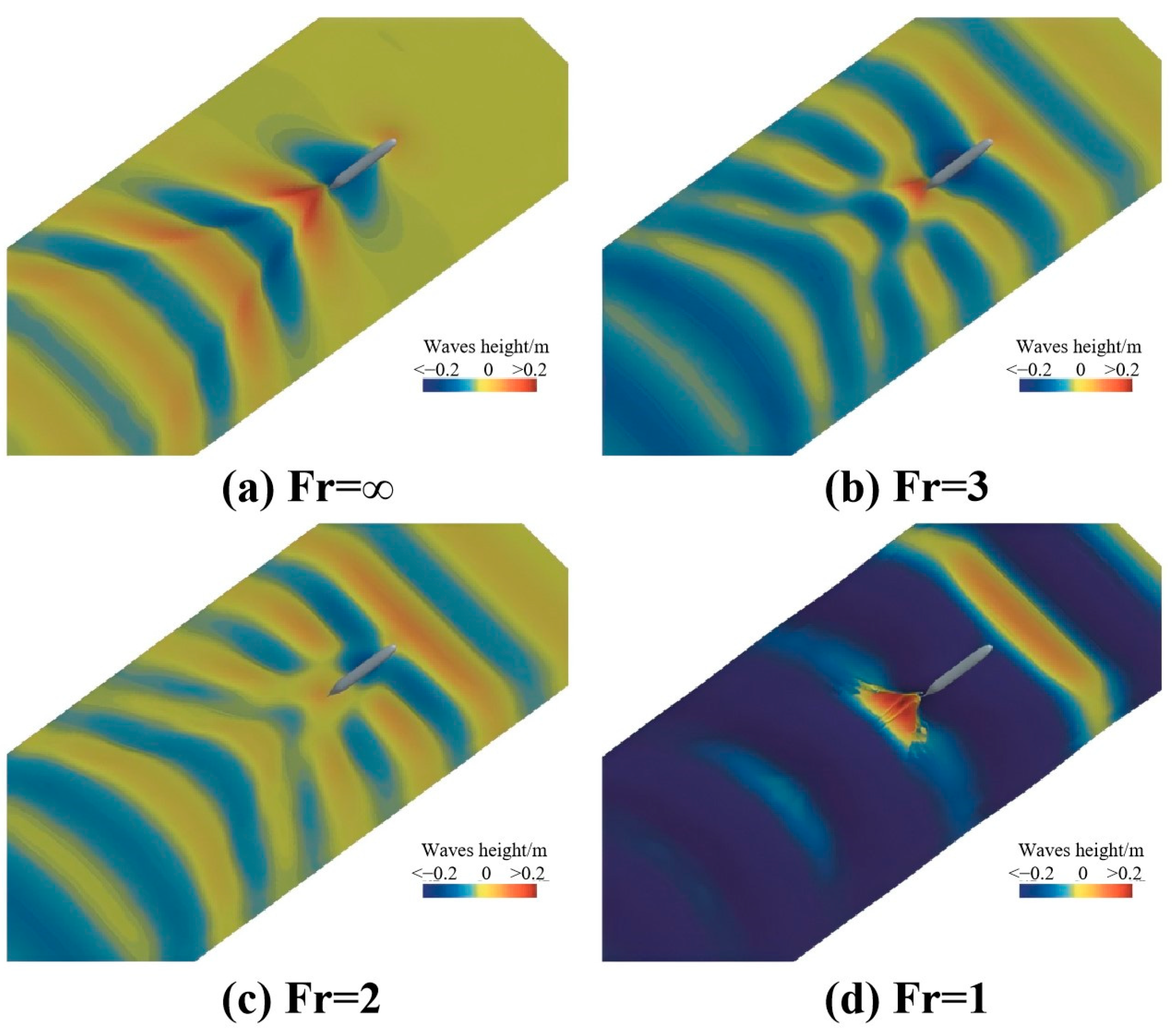
2.1. Near-Surface Navigation in Surface Waves
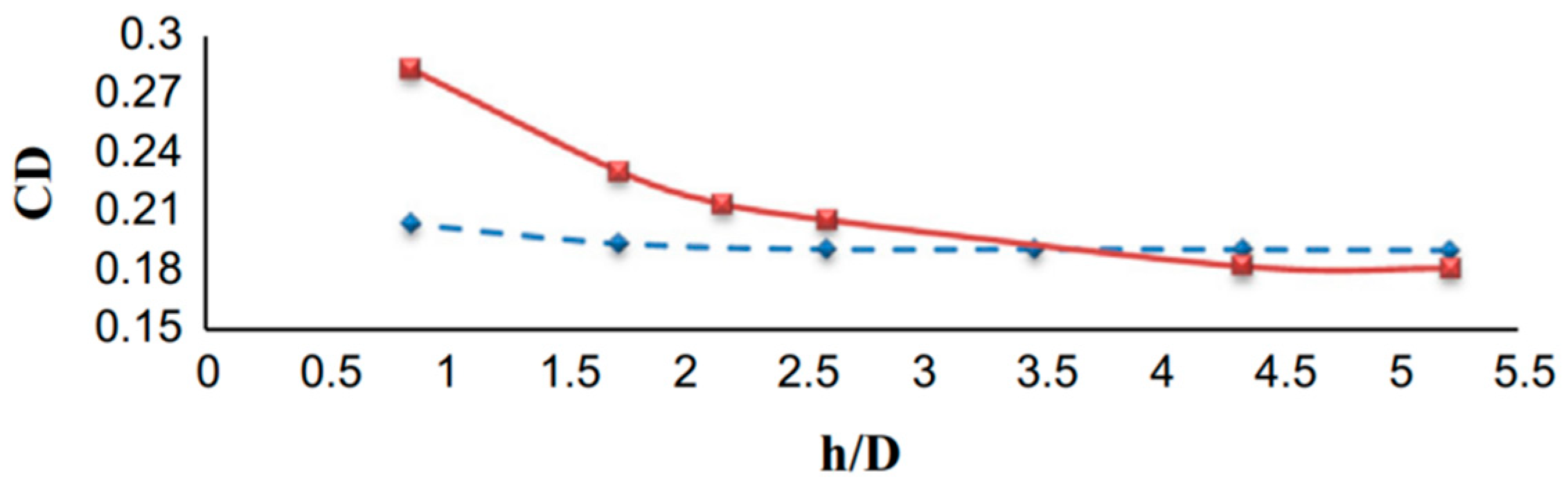
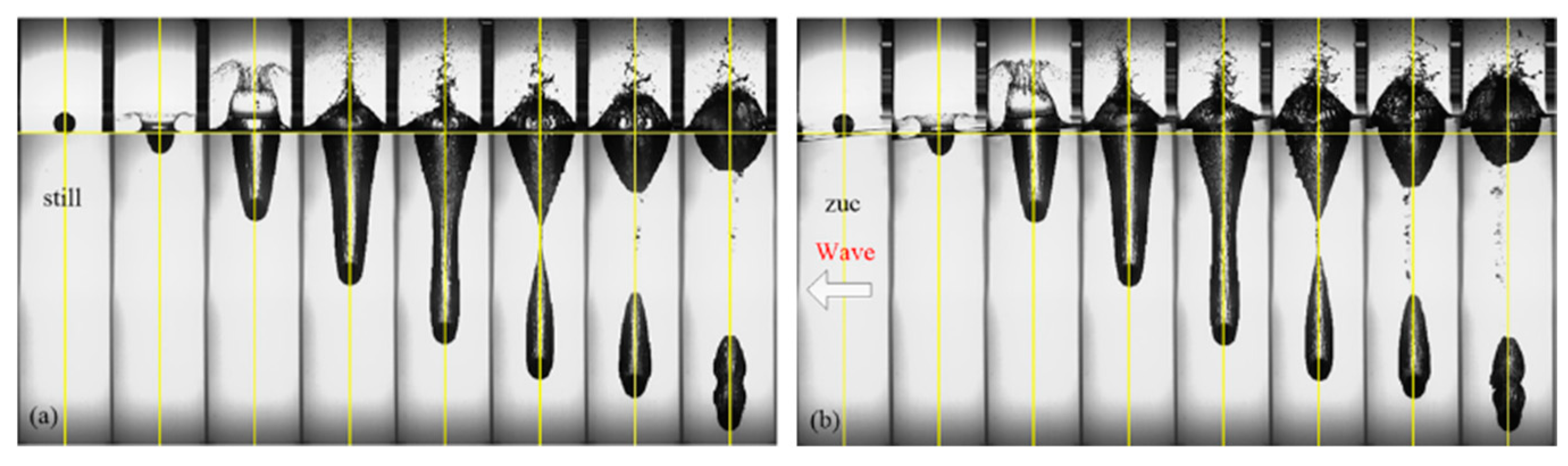
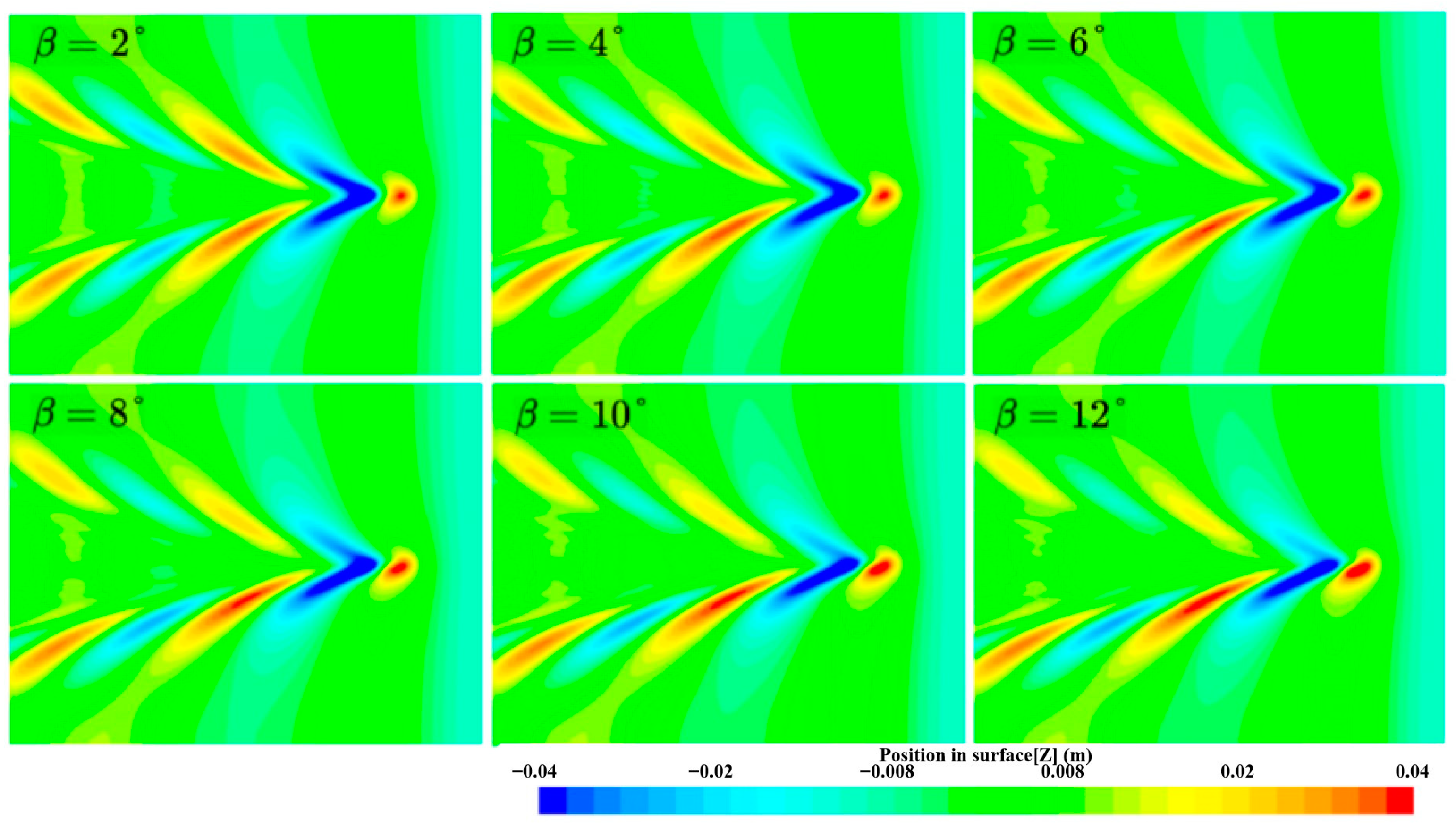
2.2. Water-Exit in Surface Waves
2.3. Water Entry in Surface Waves
3. Influences of Ocean Currents
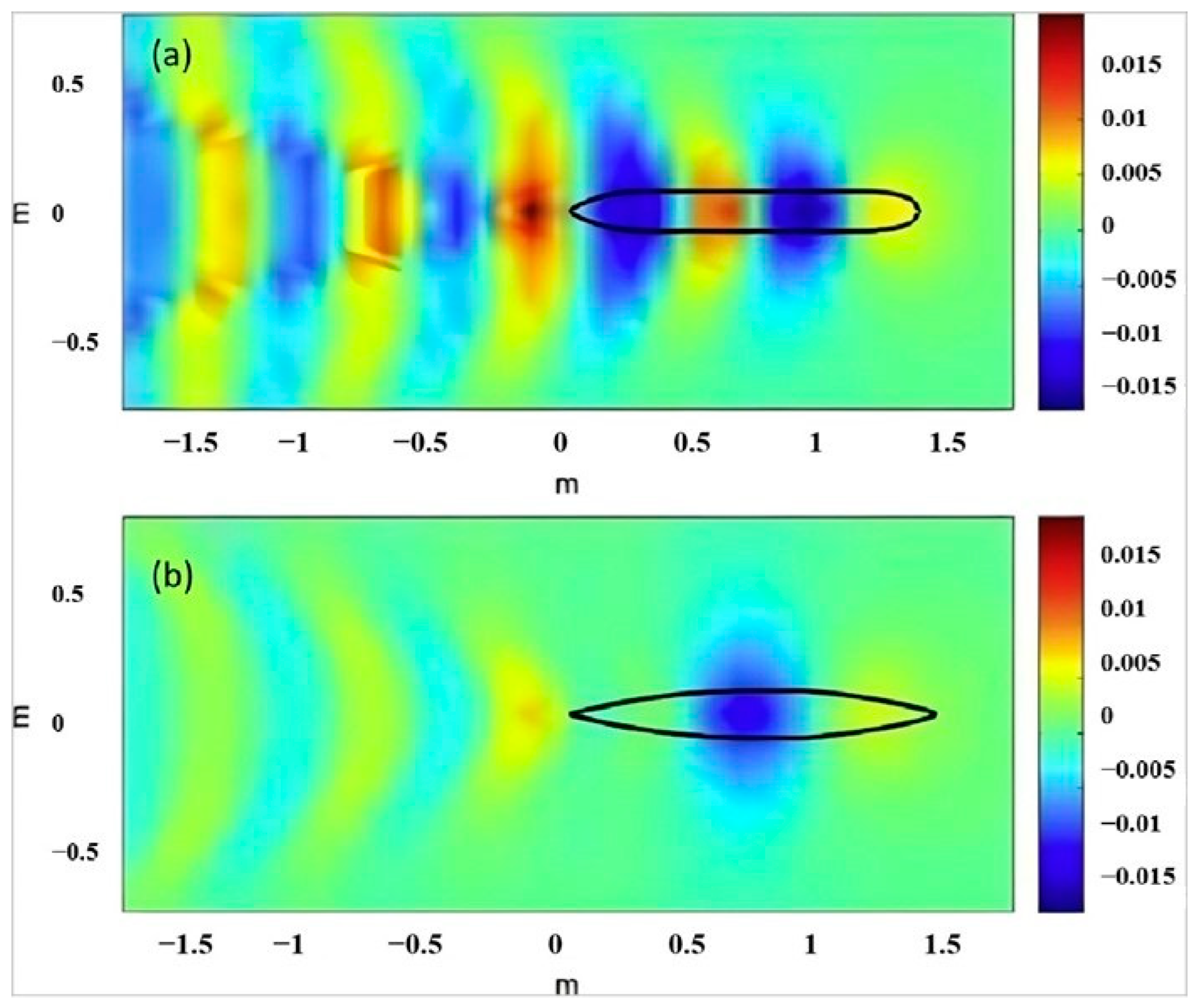
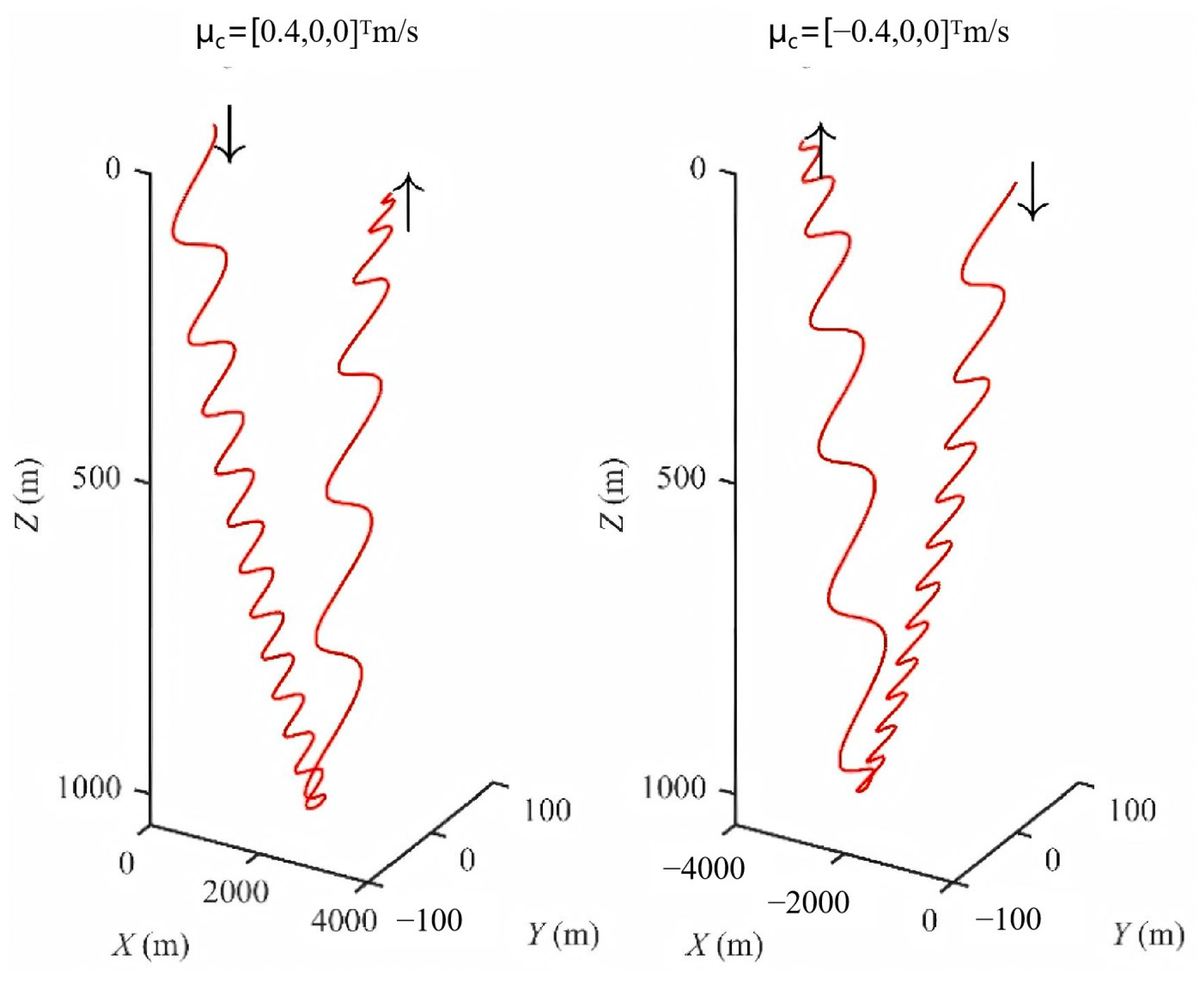
3.1. Influences on Navigation State
3.2. Influences on Path Planning
- (1)
- A* algorithm: The A* algorithm is an effective method for solving the shortest path in static road networks. Perdomo proposed a CTS-A* (Constant-Time Surfacing A*) algorithm based on the A* algorithm [74]. The advantage of this algorithm lies in its ability to handle current information effectively, but its limitations are severe, and the algorithm fails in dynamic current settings. Redondo et al. [75] further improved this algorithm by introducing time into the algorithm and integrating the time-varying trajectory of the underwater vehicle using the time-varying 2D current field provided by the regional ocean model. The improved method ensures the optimality of the paths obtained when uncertainties such as current eddies are taken into account. Also in the 2D case, Josep Isem et al. [76] proposed a low-energy underwater path planning method based on the A* and ND algorithms. The advantage of this method is that it is suitable for complex environments such as strong currents and can effectively avoid static or dynamic obstacles to obtain an optimal path. All of the above algorithms are limited to two-dimensional conditions. They are not applicable to three-dimensional situations. In contrast, Zhou et al. [77] applied the CTS-A* iterative algorithm to the path planning of an underwater vehicle based on the constructed current field. This has been demonstrated in sea trials with single and multi-path currents.
- (2)
- Wavefront Algorithm: This method is based on the graph search theory. It is a blind search algorithm for solving the shortest path problem from the start point to the end point on a known map. Soulignac et al. [78] proposed a sliding wavefront expansion method based on the wave matrix algorithm. The advantage of this algorithm is that it ensures accuracy, efficiency, and global optimality of the path by combining an appropriate cost function with successive optimization techniques, but the algorithm is not applied to the 3D case. Chinmay and Pierre [79] proposed a wavefront algorithm for time-varying current path planning in a current environment. This algorithm takes into account the unknown and real-time nature of currents in the real ocean environment, which provides better accuracy and adaptability.
- (3)
- Level set algorithm: Level set is a numerical technique for interface tracking and shape modeling, which has the advantage of allowing the numerical computation of evolving curved surfaces on Cartesian grids without parameterizing the curved surfaces. Tomaszewski et al. [80] investigated the problem of efficient path planning for an underwater vehicle traversing a current field in a real ocean by using the level set method. The method can effectively reduce the time and energy consumption of traversing paths. However, the traditional level set method is slow, so Liu [81] improved it and proposed an improved narrowband level set method suitable for path planning. Based on the improved level set, a two-dimensional and three-dimensional path planning method considering the influence of ocean currents is developed. It is characterized by its ability to effectively utilize the downstream currents, avoid the strong currents and obstacle areas in the reverse direction, and reach the target point in the shortest time. But the limitations of this algorithm are clearer: Its planned route considers only the time-optimal route without considering the path length and energy consumption, while the time-varying characteristics of the current are not considered in the three-dimensional path planning.
- (4)
- Artificial potential field method: This method was first proposed by Khatib [82]. He applied it to the field of path planning for mobile robots. The underwater vehicle moves to the target point under the joint action of gravitational force and repulsive force. The gravitational field is generated by the target point and the repulsive field is generated by the obstacles. However, the traditional artificial potential field methods are not easy to obtain the optimal path; for example, such methods suffer from the local extreme value problem and are ineffective or even invalid in complex current environments [83]. Therefore, for the path planning problem under the influence of sea currents, most of them adopt the improved or hybrid artificial potential field method. Cao et al. [84] combined the artificial potential field method and ant colony algorithm and then proposed a path planning algorithm under a sea current environment. This algorithm can effectively avoid the local extreme value problem of the artificial potential field method. Yang et al. [85] introduced the velocity potential field function into the artificial potential field method, transforming the static potential field into a dynamic potential field, and combined with the kinematic properties and constraints of the underwater vehicle to obtain an expression for the obstacle influence radius, overcame the limitations of local extremes and target unreachability.
- (5)
- Ant colony algorithm: Italian scientists Dorigo et al. [86] proposed this algorithm inspired by the characteristics of foraging behavior of ant colonies in nature, which is a kind of intelligent bionic optimization algorithm. Liu et al. [87] improved the ant colony algorithm by considering the role of factors such as sea currents and used the energy consumption of sailing to guide colony evolution. Compared to the unimproved method, the navigation time was significantly improved. The traditional ant colony path planning method has the disadvantage of slow convergence speed. To overcome this disadvantage, Fu et al. [88] introduced artificial potential field heuristic factors into the ant colony algorithm to obtain the Artificial Potential Field Ant Colony Algorithm (APF-ACO). The method uses the cell to reflect the regional physical elements and quantifies the physical ocean phenomena in the form of a cost function to realize the extensive use of the ocean sound velocity environment, the ocean density environment, and the current environment, on the basis of which the optimal path is designed. As a result of this improvement, the convergence speed of the algorithm is effectively enhanced. Furthermore, the integration of the Delaunay triangle decompositions into the ACO optimization algorithm can also achieve the effective use of current information [89] and has a faster convergence rate.
- (6)
- Particle Swarm Optimization Algorithm: This is a simulation algorithm based on the flock aggregation model used to solve the problems of how birds avoid collision and adjust neighboring birds’ speed. Compared with the particle swarm algorithm, the quantum particle swarm algorithm shows better ability in the ocean current environment [90]. Based on the quantum particle swarm algorithm principle, Zou et al. [91] proposed an ocean current path planning method suitable for high-dimensional situations. However, the method fails when there are complex obstacles and currents in the environment. In fact, the marine environment is constantly changing, so there is a high probability that the underwater vehicle will encounter new obstacles while tracking the global path. To solve the multi-objective path planning problem for underwater vehicles under uncertain sea currents and uncertain hazard sources, Gu [92] proposed an interval-based multi-objective quantum particle swarm algorithm, which works well for route planning by interval optimization under constant current conditions, changing current conditions, and dynamic obstacle conditions.
4. Influences of Ocean Stratification
4.1. Influences on Navigation State
4.2. Influences of Stealth Performance
5. Influences of Oceanic Internal Waves
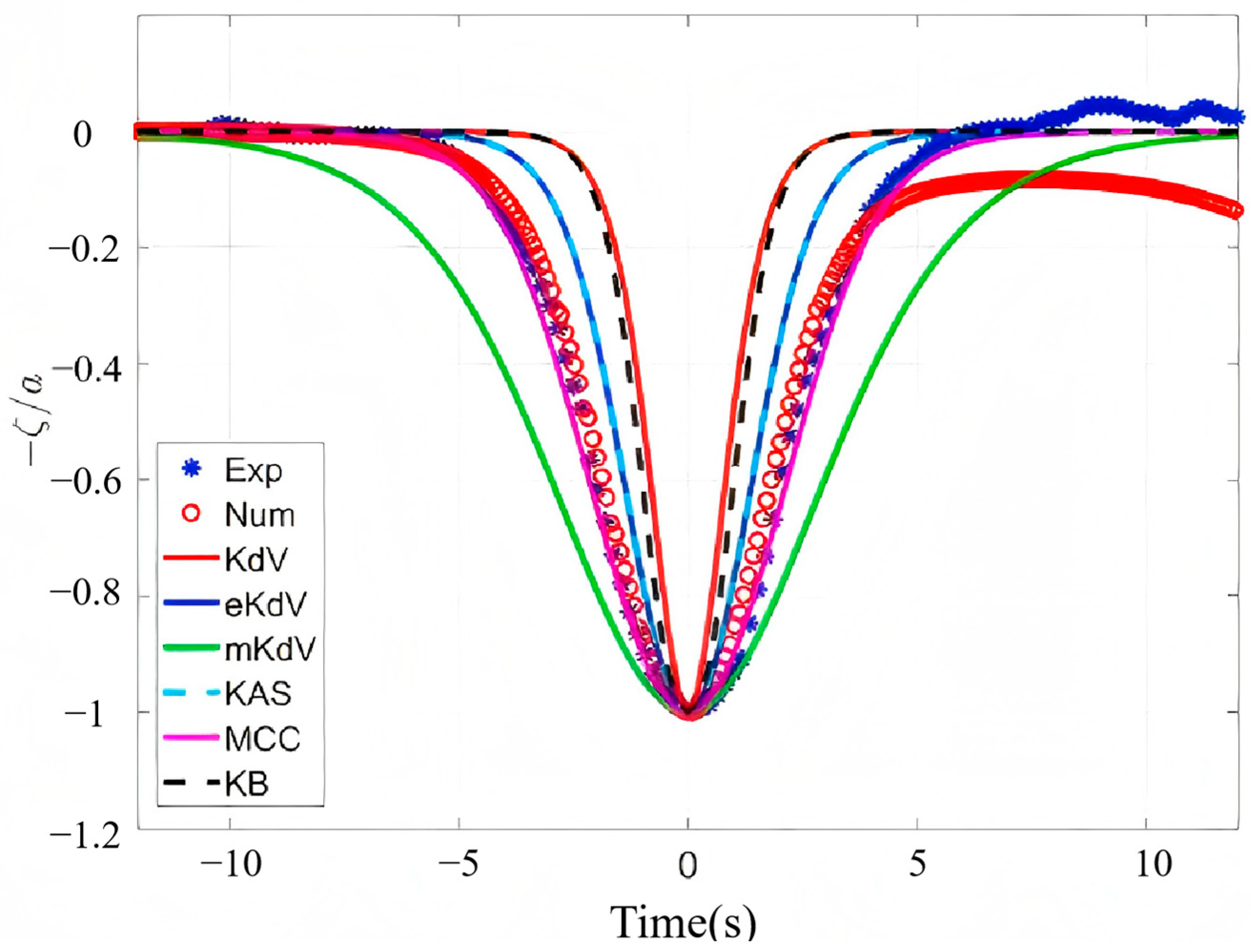
5.1. Internal Wave Theory
5.2. Experiments
5.3. Numerical Simulation
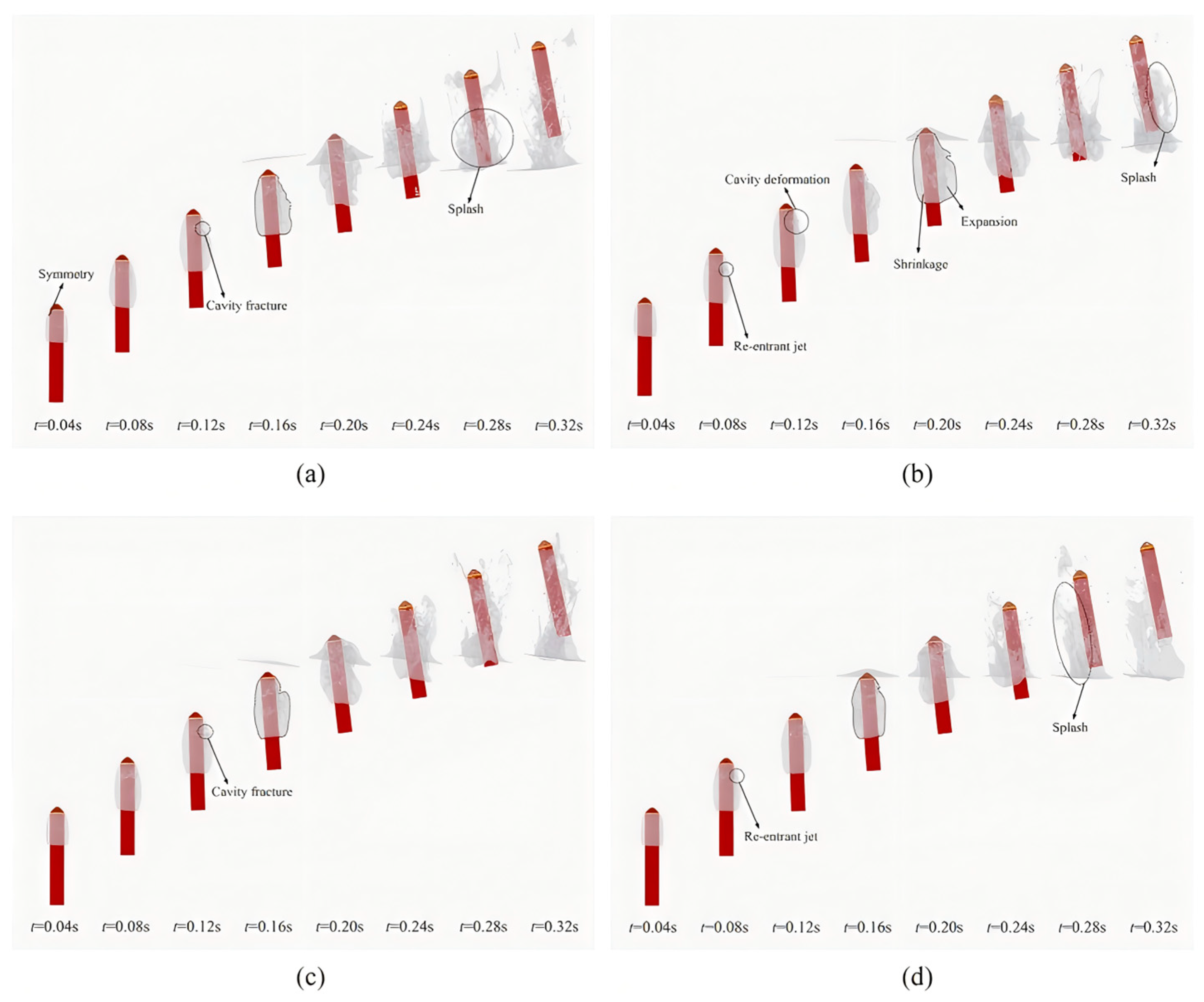
- (1)
- The motion response of a submarine located above and at the pycnocline is more affected under the action of internal solitary waves. The effect on the loading characteristics of the submarine increases as it moves closer to the pycnocline.
- (2)
- The speed of response of the submerged body motion and the peak size of the load applied are mainly affected by the amplitude of the wave. The larger the amplitude of the internal solitary waves, the faster the response of the submerged body motion and the larger the peak value of the load applied.
- (3)
- Under the influence of internal solitary waves, a self-propelled body is more susceptible to runaway phenomena and force surge compared to a suspended body. Additionally, the peak load on the submerged body increases at higher speeds.
6. Conclusions
- (1)
- The effects of waves on underwater vehicles cover near-surface stabilization, out-of-water motion, and in-water motion. Wave forces, drift effects, and attitude perturbations together affect the stability of near-surface vehicles. Waves change the shape of the evacuation, the vehicle trajectory, and the variables at the entry point, which increase the complexity and risk of exiting the water; in the presence of waves, the entry process will be accompanied by complex flow phenomena, such as the evolution of the cavitation, splashing, and vortex distribution, which leads to increased difficulty in entering the water. The current research mainly focuses on the principle of the influence of waves, the load and motion characteristics of the underwater vehicle, and the evolution of the flow field, and there are fewer studies on how to reduce the influence of waves, the control strategy in the waves, and the rapid selection of suitable exit and entry positions, which can be further researched in the future.
- (2)
- The presence of currents mainly affects parameters such as course direction, speed, pressure distribution, and hydrodynamic characteristics of the underwater vehicle, which can interfere with positioning and navigation performance, and ultimately reduce the accuracy of its path planning. At present, scholars have established a complete motion model of the underwater vehicle in the sea current environment, on the basis of which they have summarized the influence law of the sea current on the operation state, and improved the existing path planning algorithms and put forward some path planning methods which are applicable to the ocean current environment. With the rapid development of artificial intelligence in recent years, the integration of multiple algorithms and the introduction of deep learning and other technologies can significantly improve the path planning ability; therefore, the development of a multi-algorithm collaborative model based on machine learning is the main direction for the development of the path planning problem.
- (3)
- Density stratification can lead to the phenomenon of “sea cliffs”, which can have a serious impact on the loads on the vehicles, as well as cause anomalies in the wake of the vehicle and affect the shape of the free surface, which greatly increases the risk of exposure for the vehicle. After more than a century of research, scholars now have a clear understanding of the influence law of density stratification on the loading of the vehicle and the evolution process of the wake field. However, current research focuses on simplified or ideal environments and models. Further research and development of numerical, computational, and experimental methods are needed in the future to study the actual density jump layer and complex vehicles.
- (4)
- At present, the research on the influence of internal waves on underwater vehicles is relatively systematic, and scholars have conducted deep research in theoretical studies, physical experiments, and numerical simulations. Using experimental and CFD methods, the mechanism of internal wave effects on the underwater vehicle is revealed based on various internal wave models, such as KdV, MCC, DJL, etc. The influence of various parameters is explored. However, there are still some aspects that deserve further exploration. In terms of internal wave experiments, it is now possible to generate stably propagating internal waves in the laboratory based on a variety of methods, and to conduct some experiments on the interaction of internal waves with simple structural objects. Due to the limitations of scale, equipment, and other conditions, there is a lack of experimental studies on the interaction of internal waves with complex structures or self-propelled bodies, and further research work is still needed. In terms of numerical simulation studies, most of the studies are carried out on the underwater vehicle itself, and there are few studies on the interaction between internal waves and the attachments, which deserves the attention of scholars.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.M. Influence of main ocean environments on the navigation of underwater vehicles. CAAI Trans. Intell. Syst. 2015, 10, 316–323. [Google Scholar]
- Carrica, P.M.; Kim, Y.; Martin, J.E. Near-surface self propulsion of a generic submarine in calm water and waves. Ocean Eng. 2019, 183, 87–105. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, H.; Lang, J.; Xing, L. Safety Analysis of Initial Separation Phase for AUV Deployment of Mission Payloads. J. Mar. Sci. Eng. 2024, 12, 608. [Google Scholar] [CrossRef]
- Xing, B.; Yu, M.; Liu, Z.; Tan, Y.; Sun, Y.; Li, B. A Review of Path Planning for Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2023, 11, 1556. [Google Scholar] [CrossRef]
- Cao, L.; Pan, Y.; Gao, G.; Li, L.; Wan, D. Review on the Hydro- and Thermo-Dynamic Wakes of Underwater Vehicles in Linearly Stratified Fluid. J. Mar. Sci. Eng. 2024, 12, 490. [Google Scholar] [CrossRef]
- He, Z.; Wu, W.; Wang, J.; Ding, L.; Chang, Q.; Huang, Y. Investigations into Motion Responses of Suspended Submersible in Internal Solitary Wave Field. J. Mar. Sci. Eng. 2024, 12, 596. [Google Scholar] [CrossRef]
- Gao, J.L.; Mi, C.L.; Song, Z.W.; Liu, Y.Y. Transient gap resonance between two closely-spaced boxes triggered by nonlinear focused wave groups. Ocean Eng. 2024, 305, 117938. [Google Scholar] [CrossRef]
- Khader, M.H. Effects of Wave Drag on Submerged Bodies. Houille Blanche 1979, 8, 465–470. [Google Scholar] [CrossRef]
- Suriben, K.M.; Yeager, K.I.; Klamo, J. Experimental Study of the Drag and Wave-Induced Surge Forces on an Underwater Vehicle Operating Near the Surface. In Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering, OMAE, Hamburg, Germany, 5–10 June 2022; Volume 5B. [Google Scholar]
- Mansoorzadeh, S.; Javanmard, E. An investigation of free surface effects on drag and lift coefficients of an autonomous underwater vehicle (AUV) using computational and experimental fluid dynamics methods. J. Fluids Struct. 2014, 51, 161–171. [Google Scholar] [CrossRef]
- Battista, T.; Valentinis, F.; Woolsey, C. A Maneuvering Model for an Underwater Vehicle Near a Free Surface—Part II: Incorporation of the Free-Surface Memory. IEEE J. Ocean. Eng. 2023, 48, 740–751. [Google Scholar] [CrossRef]
- Valentinis, F.; Battista, T.; Woolsey, C. A Maneuvering Model for an Underwater Vehicle Near a Free Surface—Part III: Simulation and Control Under Waves. IEEE J. Ocean. Eng. 2023, 48, 752–777. [Google Scholar] [CrossRef]
- Fang, M.C.; Chang, P.E.; Luo, J.H. Wave effects on ascending and descending motions of the autonomous underwater vehicle. Ocean Eng. 2006, 33, 1972–1999. [Google Scholar] [CrossRef]
- Kim, C.H.; Chou, F.S.; Tein, D. Motions and hydrodynamic loads of a ship advancing in oblique waves. Trans. Soc. Nav. Archit. Mar. Eng. 1980, 88, 225–256. [Google Scholar]
- Fang, M.C.; Lee, M.L.; Lee, C.K. The simulation of water shipping for a ship advancing in large longitudinal waves. J. Ship Res. 1993, 37, 126–137. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, Z.; Wang, Y. On the motion analysis of autonomous underwater vehicles under arbitrary waves. In Proceedings of the 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022. [Google Scholar]
- Guo, J.; Lin, Y.; Wang, Y.; Lin, P.; Li, H.; Huang, H.; Chen, Y. Numerical research on hydrodynamic characteristics of the disk-shaped autonomous underwater vehicle near free surface. Ocean Eng. 2023, 288, 116175. [Google Scholar] [CrossRef]
- Shi, Z.Q.; Zou, Y.C.; You, C.X. Seakeeping investigations of a cross-domain vehicle with the capability of high-speed cruising in waves. Ocean Eng. 2024, 308, 118282. [Google Scholar] [CrossRef]
- Tolliver, J. Studies on Submarine Control for Periscope Depth Operations. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 1996. [Google Scholar]
- Manimaran, R. Hydrodynamic investigations on the performance of an underwater remote operated vehicle under the wave using OpenFOAM. Ships Offshore Struct. 2022, 17, 2186–2202. [Google Scholar] [CrossRef]
- Alvarez, A.; Bertram, V.; Gualdesi, L. Hull hydrodynamic optimization of autonomous underwater vehicles operating at snorkeling depth. Ocean Eng. 2009, 36, 105–112. [Google Scholar] [CrossRef]
- Pan, G.; Liu, Y.N.; Du, X.X.; Malik, S.A. Computational Analysis and Prediction of Wave Forces on Portable Underwater Vehicle. Acta Armamentarii 2014, 35, 371–378. [Google Scholar]
- Chen, Z.; Jiao, J.; Wang, S. CFD-FEM simulation of water entry of a wedged grillage structure into Stokes waves. Ocean Eng. 2023, 275, 114159. [Google Scholar] [CrossRef]
- Chen, Z.; Jiao, J.; Wang, Q.; Wang, S. CFD-FEM Simulation of Slamming Loads on Wedge Structure with Stiffeners Considering Hydroelasticity Effects. J. Mar. Sci. Eng. 2022, 10, 1591. [Google Scholar] [CrossRef]
- Qi, C.; Lyu, X.J.; Wang, X.; Ye, H.; Shi, H.J.; Wan, Z.H. Experimental and numerical studies on vertical water entry of a cylinder under the influence of current. Phys. Fluids 2024, 36, 033322. [Google Scholar] [CrossRef]
- Greenhow, M.; Moyo, S. Water entry and exit of horizontal circular cylinders. Philos. Trans. R. Soc. Lond. 1997, 355, 551–563. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Fang, X.; Wu, X.; Du, T. On the internal collapse phenomenon at the closure of cavitation bubbles in a deceleration process of underwater vertical launching. Appl. Ocean Res. 2016, 56, 157–165. [Google Scholar] [CrossRef]
- Wu, Q.G.; Ni, B.Y.; Bai, X.L.; Cui, B.; Sun, S.L. Experimental study on large deformation of free surface during water exit of a sphere. Ocean Eng. 2017, 140, 369–376. [Google Scholar] [CrossRef]
- Guo, C.; Liu, T.; Hao, H.; Chang, X. Evolution of water column pulled by partially submerged spheres with different velocities and submergence depths. Ocean Eng. 2019, 187, 106087. [Google Scholar] [CrossRef]
- Zhou, B.J.; Zhao, Z.J.; Dai, Q. Numerical study on the cavity dynamics of water entry and exit for a high-speed projectile crossing a wave. Phys. Fluids 2024, 36, 063321. [Google Scholar] [CrossRef]
- Quan, X.B.; Kong, D.C.; Li, Y. Wave simulation and its effects on the exceeding water process of the underwater vehicle. J. Harbin Inst. Technol. 2011, 43, 5. [Google Scholar]
- Zhu, K.; Chen, H.L.; Liu, L.H. Effect of Wave Phase on Hydrodynamic Characteristics of Underwater Vehicle out of Water. Acta Armamentarii 2014, 35, 355–361. [Google Scholar]
- Qin, N.; Lu, C.; Li, J. Numerical investigation of characteristics of water-exit ventilated cavity collapse. J. Shanghai Jiaotong Univ. 2016, 21, 530–540. [Google Scholar] [CrossRef]
- Zhi, M.Y.; Ma, G.H.; Ren, Z.Y. Analysis of the influence of regular waves on the water-exiting attitude parameters of underwater vehicle. Astronaut. Syst. Eng. Technol. 2022, 6, 15–26. [Google Scholar]
- Zhang, S.; Xu, H.; Sun, T.Z.; Duan, J.X. Water-exit dynamics of a ventilated underwater vehicle in wave environments with a combination of computational fluid dynamics and machine learning. Phys. Fluids 2024, 36, 023312. [Google Scholar] [CrossRef]
- Zhang, C.X. Dynamics modeling and simulation of water-exit course of small submarine-launched missile under wave disturbance. J. Natl. Univ. Def. Technol. 2015, 6, 91–95. [Google Scholar]
- Jo, S.M.; Lee, H.M.; Kwon, O.J. Prediction of surficial pressure loading for an underwater projectile using CFD-based database. Int. J. Aeronaut. Space Sci. 2018, 19, 618–625. [Google Scholar] [CrossRef]
- Worthington, A.M.; Cole, R.S.V. Impact with a liquid surface studied by the aid of instantaneous photography. Philos. Trans. R. Soc. Lond. Ser. A 1897, 189, 137–148. [Google Scholar]
- Xu, L.; Wang, Z.Q.; Lv, H.Q. Exploring the load characteristics and structural responses of a high-speed vehicle entering water. Phys. Fluids 2024, 36, 027124. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Hou, Z.; Sun, T.Z. Numerical simulation of the effect of waves on cavity dynamics for oblique water entry of a cylinder. J. Hydrodyn. 2020, 32, 1178–1190. [Google Scholar] [CrossRef]
- Sun, S.Y.; Chen, H.L.; Xu, G. Water Entry of a Wedge into Waves in Three Degrees Offreedom. Pol. Marit. Res. 2019, 26, 117–124. [Google Scholar] [CrossRef]
- Zhao, C.Z.; Wang, Q.; Lu, H.C.; Liu, H. Vertical water entry of a hydrophobic sphere into waves: Numerical computations and experiments. Phys. Fluids 2023, 35, 073324. [Google Scholar] [CrossRef]
- Von Karman, T. The Impact on Seaplane Floats During Landing; National Advisory Committee for Aeronautics: Washington, DC, USA, 1929; pp. 1–8. [Google Scholar]
- Wagner, H. Phenomena associated with impacts and sliding on liquid surfaces. Z. Angew. Math. Mech. 1932, 12, 193–215. [Google Scholar] [CrossRef]
- Korobkin, A. Asymptotic theory of liquid–solid impact. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1997, 355, 507–522. [Google Scholar] [CrossRef]
- Scolan, Y.M.; Korobkin, A. Energy distribution from vertical impact of a three-dimensional solid body onto the flat free surface of an ideal fluid. J. Fluid Struct. 2003, 17, 275–286. [Google Scholar] [CrossRef]
- Zhao, R.; Faltinsen, O.; Aarsnes, J. Water entry of arbitrary two-dimensional sections with and without flow separation. In Proceedings of the 21st Symposium on Naval Hydrodynamics; National Academy Press: Washington, DC, USA, 1996; pp. 408–423. [Google Scholar]
- Yang, L.; Xiang, J.B.; Zhang, S.X. Compressibility effects on cavity dynamics and shock waves in high-speed water entry. Phys. Fluids 2024, 36, 042104. [Google Scholar] [CrossRef]
- Wang, X.; Qi, C.; Liu, C. Experimental study on the cavity dynamics of a sphere entering flowing water. Phys. Fluids 2024, 36, 022102. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, C.Z.; Lu, H.C. Experimental observation on water entry of a sphere in regular wave. Theor. Appl. Mech. Lett. 2023, 13, 100473. [Google Scholar] [CrossRef]
- Tang, W.H.; Hong, Y.; Gong, Z.X. Experimental Study on Cavity Evolution During Oblique Water Entry of a Slender Axisymmetric Body at Constant Speed in Progressive Waves. In Proceedings of the 31st International Ocean and Polar Engineering Conference, Rhodes, Greece, 20–25 June 2021; pp. 1745–1751. [Google Scholar]
- Wang, C.; Huang, Q.G.; Lu, L. Numerical investigation of water entry characteristics of a projectile in the wave environment. Ocean Eng. 2024, 294, 116821. [Google Scholar] [CrossRef]
- Wu, X.; Chang, X.; Liu, S. Numerical study on the water entry impact forces of an air-launched underwater glider under wave conditions. Shock Vib. 2022, 2022, 4330043. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, T.; Wu, B.; Wang, F.; Tong, M. Numerical study of wave effect on water entry of a three-dimensional symmetric wedge. Ocean Eng. 2022, 50, 110800. [Google Scholar] [CrossRef]
- Li, Z.Y.; Hu, H.B.; Wang, C. Hydrodynamics and stability of oblique water entry in waves. Ocean Eng. 2024, 292, 116506. [Google Scholar] [CrossRef]
- Fan, S.; Woolsey, C.A. Dynamics of underwater gliders in currents. Ocean Eng. 2014, 84, 249–258. [Google Scholar] [CrossRef]
- Yin, C.Y. Submarine Launched Missile Launch and Exit Load Study. Master’s thesis, Northwestern Polytechnical University, Xi’an, China, 2004. [Google Scholar]
- Zhao, C.J. The Simulation on Exceeding Tube Process of an Underwater Vehicle Consider Factors such as Boat Speed. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Fang, P.P. 6-DOF Motion Simulation of Autonomous Underwater Vehicles Considering the Influence of Lateral Flow. Master’s Thesis, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- Chen, Y. Hydrodynamic Characterization of Navigational Bodies in Complex Marine Environments. Master’s Thesis, Harbin Engineering University, Harbin, China, 2012. [Google Scholar]
- Yang, H.; Sun, L.Q.; Liu, Y. 3D numerical simulation on water entry of cylindrical under wave and stream action. J. Ship Mech. 2015, 19, 1186–1196. [Google Scholar]
- Chen, J.; Lv, H. Study on the Effects of Environment on Buoyancy Speed and Emergence Posture of Nautical Bodies. Equip. Manuf. Technol. 2023, 2, 24–30. [Google Scholar]
- Aguiar, A.P.; Pascoal, A.M. Dynamic positioning and way-point tracking of underactuated AUVs in the presence of ocean currents. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002. [Google Scholar]
- Refsnes, J.E.; Pettersen, K.Y.; Sorensen, A.J. Control of slender body underactuated AUVs with current estimation. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 43–50. [Google Scholar]
- Borhaug, E.; Pivano, L.; Pettersen, K.Y.; Johansen, T.A. A Model-Based Ocean Current Observer for 6DOF Underwater Vehicles. IFAC Proc. Vol. 2007, 40, 169–174. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, W.; Yu, X.; Yang, S.; Zhang, L. Quantitative evaluation of motion performances of underwater gliders considering ocean currents. Ocean Eng. 2021, 236, 109501. [Google Scholar] [CrossRef]
- Merckelbach, L.; Smeed, D.; Griffiths, G. Vertical Water Velocities from Underwater Gliders. J. Atmos. Ocean. Technol. 2010, 27, 547–563. [Google Scholar] [CrossRef]
- Haghi, P. Adaptive Position and Attitude Tracking of an AUV in the Presence of Ocean Current Disturbances. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 741–746. [Google Scholar]
- Aguiar, A.P.; Pascoal, A.M. Way-Pont Tracking of autonomous underwater vehicle in heading and depth attitude via self-adaptive fuzzy PID controller. J. Mar. Sci. Technol. 2015, 20, 559–578. [Google Scholar]
- Fan, S.S. Research on Underwater Glider Dynamic Modeling, Motion Analysis and Controller Design in Currents. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2013. [Google Scholar]
- Hu, W.F. Numerical Simulation of Course-Keeping for Autonomous Underwater Vehicle Under Current Disturbance. Master’s Thesis, Dalian Maritime University, Dalian, China, 2020. [Google Scholar]
- Abdurahman, B.; Savvaris, A.; Tsourdos, A. Switching LOS guidance with speed allocation and vertical course control for path-following of unmanned underwater vehicles under ocean current disturbances. Ocean Eng. 2019, 182, 412–426. [Google Scholar] [CrossRef]
- Zhang, R.; He, B.; Wang, Y.; Ma, W.; Yang, S. Recent advances in path planning for underwater gliders: A comprehensive review. Ocean Eng. 2024, 299, 117166. [Google Scholar] [CrossRef]
- Enrique, F.; Jorge, C.; Daniel, H. Path Planning for Gliders Using Regional Ocean Models: Application of Pinzon Path Planner with the ESEOAT Model and the Ru27 Trans-Atlantic Flight Data. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, Australia, 24–27 May 2010; pp. 1–10. [Google Scholar]
- Wang, X.C.; Yi, C.; Thompson, D.R. Multi-model ensemble forecasting and glider path planning in the mid-Atlantic bight. Cont. Shelf Res. 2013, 63, S223–S234. [Google Scholar] [CrossRef]
- Isern-González, J.; Hernández-Sosa, D.; Fernández-Perdomo, E. Obstacle avoidance in underwater glider path planning. J. Phys. Agents 2012, 1, 11–20. [Google Scholar] [CrossRef]
- Zhou, H.X.; Zeng, Z.; Lian, L. Adaptive re-planning of AUVs for environmental sampling missions: A fuzzy decision support system based on multi-objective particle swarm optimization. Int. J. Fuzzy Syst. 2018, 20, 650–671. [Google Scholar] [CrossRef]
- Soulignac, M. Feasible and Optimal Path Planning in Strong Current Fields. IEEE Trans. Robot. 2011, 27, 89–98. [Google Scholar] [CrossRef]
- Chinmay, S.K.; Pierre, F.J.L. Three-dimensional time-optimal path planning in the ocean. Ocean Model. 2020, 152, 101644. [Google Scholar]
- Tomaszewski, C.; Abhinav, V.; Paul, S. Planning Efficient Paths through Dynamic Flow Fields in Real World Domains. In Proceedings of the 2013 OCEANS—San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–5. [Google Scholar]
- Sun, T.L. Research on Path Planning Method of AUV Considering the Influence of Ocean Current. Master’s Thesis, Harbin Engineering University, Harbin, China, 2016. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, D.Q. Path Planning for Autonomous Underwater Vehicle Based on Artificial PotentialField and Velocity Synthesis. Control Eng. China 2015, 22, 418–424. [Google Scholar]
- Cao, J. Research on Path Planning Methods for AUVs in Complex Environments. Master’s Thesis, Ocean University of China, Qingdao, China, 2011. [Google Scholar]
- Yang, M.; Wang, Y.H.; Wang, S.X. Motion parameter optimization for gliding strategy analysis of underwater gliders. Ocean Eng. 2019, 191, 106502. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: An autocatalytic optimizing process. Clustering 1991, 3, 340. [Google Scholar]
- Liu, G.; Liu, P.; Mu, W. A Path Optimization Algorithm for AUV Using an Improved Ant Colony Algorithm with Optimal Energy Consumption. J. Xi’an Jiaotong Univ. 2016, 50, 93–98. [Google Scholar]
- Fu, J.; Lv, T.; Li, B. Three-Dimensional Underwater Path Planning of Submarine Considering the Real Marine Environment. IEEE Access 2022, 10, 37016–37029. [Google Scholar] [CrossRef]
- Cheng, K.X.; Zheng, Z.; Lian, L. Path planning of multi-modal underwater vehicle for adaptive sampling using Delaunay spatial partition-ant colony optimization. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans, Kobe, Japan, 28–31 May 2018; pp. 1–8. [Google Scholar]
- Wang, H.L.; Wang, C.L.; Zhang, C.L. Path Planning of Saucer-type Autonomous Underwater Glider Based on AQPSO Algorithm. Ship Eng. 2020, 42, 13–19. [Google Scholar]
- Zou, M.K.; Yu, F.; Lv, C.Y. Path planning for autonomous underwater vehicles by using QPSO. CAAI Trans. Intell. Syst. 2013, 8, 221–225. [Google Scholar]
- Gu, J.Y. A Thesis Submitted in Fulfillment of the Requirements for the Degree of Master of Engineering. Master’s Thesis, Jiangsu University of Science and Technology, Suzhou, China, 2022. [Google Scholar]
- Zhang, J.H.; Huang, H.F.; Hu, K. Study on Influence of Pycnocline on Submarine Maneuverability and Countermeasures. J. Sichuan Ordnance 2021, 4, 118–122. [Google Scholar]
- Fourdrinoy, J.; Dambrine, J.; Petcu, M. The dual nature of the dead-water phenomenology: Nansen versus Ekman wave-making drags. Proc. Natl. Acad. Sci. USA 2020, 29, 16770–16775. [Google Scholar] [CrossRef]
- Ekman, V.W. The Norwegian North Polar Expedition, 1893–1896 Scientific Results. Nature 1904, 1823, 549–550. [Google Scholar]
- Grue, J. Nonlinear dead water resistance at subcritical speed. Phys. Fluids 2015, 8, 082103. [Google Scholar] [CrossRef]
- Hudimac, A.A. Ship Waves in A Stratified Ocean. J. Fluid Mech. 1961, 2, 229–243. [Google Scholar] [CrossRef]
- Motygin, O.V.; Kuznetsov, N.G. The wave resistance of a two-dimensional body moving forward in a two-layer fluid. J. Eng. Math. 1997, 1, 53–72. [Google Scholar] [CrossRef]
- Miloh, T.; Tulin, M.P.; Zilman, G. Dead-water effects of a ship moving in stratified seas. J. Offshore Mech. Arct. Eng. 1993, 2, 105–110. [Google Scholar] [CrossRef]
- Yeung, R.W.; Nguyen, T.C. Waves generated by a moving source in a two-layer ocean of finite depth. J. Eng. Math. 1999, 1–2, 85–107. [Google Scholar] [CrossRef]
- Sturova, I.V. Radiation instability of a circular cylinder in a uniform flow of a two-layer fluid. J. Appl. Math. Mech. 1997, 6, 957–965. [Google Scholar] [CrossRef]
- Mercier, M.J.; Vasseur, R.; Dauxois, T. Resurrecting dead-water phenomenon. Nonlinear Process. Geophys. 2011, 2, 193–208. [Google Scholar] [CrossRef]
- Gou, Y.; Zhang, X.W.; Xu, W.B. Experimental study of towing resistance of box structure in two-layer flow. In Proceedings of the 18th China Ocean (Onshore) Engineering Symposium, Zhoushan, China, 23–25 September 2017; pp. 475–479. [Google Scholar]
- Esmaeilpour, M.; Martin, J.E.; Carrica, P.M. Computational Fluid Dynamics Study of the Dead Water Problem. J. Fluids Eng.-Trans. ASME 2018, 3, 031203. [Google Scholar] [CrossRef]
- Cao, L.S.; Gao, G.; Guo, E.K.; Wan, D.C. Hydrodynamic performances and wakes induced by a generic submarine operating near the free surface in continuously stratified fluid. J. Hydrodyn. 2023, 3, 396–406. [Google Scholar] [CrossRef]
- Huang, F.; Meng, Q.; Cao, L. Wakes and free surface signatures of a generic submarine in the homogeneous and linearly stratified fluid. Ocean Eng. 2022, 250, 111062. [Google Scholar] [CrossRef]
- Lu, W. Investigation on the Resistance and Wave-Maker of Submarine Traveling in a Stratified Marine Environment. Master’s Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Liu, S.; He, G.; Wang, Z. Resistance and flow field of a submarine in a density stratified fluid. Ocean Eng. 2020, 217, 107934. [Google Scholar] [CrossRef]
- Zhang, Q.; Gou, Y.; Sun, J. Numerical study on the resistance characteristics of structural “dead water” in two-layer fluids. In Proceedings of the 19th China Ocean (Shore) Engineering Symposium, Chongqing, China, 11–13 October 2019. [Google Scholar]
- Liu, S.; He, G.H.; Wang, W. Effect of Appendages on Hydrodynamic Characteristics of Submarine in Stratified Fluid. Acta Armamentarii 2021, 1, 108–117. [Google Scholar]
- Baines, P.G. Upstream blocking and airflow over mountains. Annu. Rev. Fluid Mech. 1987, 19, 75–95. [Google Scholar] [CrossRef]
- Bonneton, P.; Chomaz, J.M.; Hopfinger, E.J. Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 1993, 254, 23–40. [Google Scholar] [CrossRef]
- Sutyrin, G.G.; Radko, T. The fate of pancake vortices. Phys. Fluids 2017, 29, 031701. [Google Scholar] [CrossRef]
- Luo, F.; Shuai, C.; Du, Y. Thermal characteristics of vehicle wake induced by the interaction between hydrodynamic wake and cold skin. Ocean Eng. 2023, 267, 113272. [Google Scholar] [CrossRef]
- Keller, J.B.; Munk, W.H. Internal Wave Wakes of a Body Moving in a Stratified Fluid. Phys. Fluids 1970, 13, 1425–1431. [Google Scholar] [CrossRef]
- Voisin, B. Internal wave generation in uniformly stratified fluids. Part 2. Moving point sources. J. Fluid Mech. 1994, 261, 333–374. [Google Scholar] [CrossRef]
- Zhu, R.C.; Gao, Y.; Miao, G.P.; Yao, Z.C. Green’s function of internal waves in uniformly stratified fluid. J. Shanghai Jiaotong Univ. 2016, 50, 265–271. [Google Scholar]
- Radko, T. Ship Waves in a Stratified Fluid. J. Ship Res. 2001, 45, 1–12. [Google Scholar] [CrossRef]
- Allen, H. Schooley a1 and R. W. Stewart a2. Experiments with a self-propelled body submerged in a fluid with a vertical density gradient. J. Fluid Mech. 1963, 15, 83–96. [Google Scholar]
- Hopfinger, E.; Flor, J.-B.; Chomaz, J.M.; Bonneton, P. Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp. Fluids 1991, 11, 255–261. [Google Scholar] [CrossRef]
- Chomaz, J.M.; Bonneton, P.; Hopfinger, E.J. The structure of the near wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 1993, 254, 1–21. [Google Scholar] [CrossRef]
- Zhao, X.Q.; Wei, G.; Wu, N. Experimental study of small spheres generating trailing internal waves in linearly stratified fluids. In Proceedings of the Ninth National Hydrodynamics Conference and the Twenty-Second National Symposium on Hydrodynamics, Chengdu, China, 17–20 August 2009; pp. 418–423. [Google Scholar]
- Wei, G.; Wu, N.; Xu, X.H. Experiments on the generation of internal waves by a hemispheroid in a linearly stratified fluid. Acta Phys. Sin. 2011, 4, 352–358. [Google Scholar]
- Wang, J.; You, Y.X.; Hu, T.Q. The characteristics of internal waves excited by towed bodies with different aspect ratios in a stratified fluid. Chin. Sci. Bull. 2012, 8, 606–617. [Google Scholar] [CrossRef]
- Ma, H.; Ma, B.; Zhang, R. Theoretical and experimental research on object motion wake in stratified fluid. J. Univ. Sci. Technol. China 2000, 30, 677–684. [Google Scholar]
- Bidokhti, A.A. Flow Visualization of Internal Waves and Wakes of a Streamlined Body in a Stratified Fluid. J. Appl. Fluid Mech. 2016, 9, 635–641. [Google Scholar] [CrossRef]
- Niu, M.; Ding, Y.; Ma, W. Research on the numerical simulation methods of continuously stratified flows based on thermal density current model. J. Ship Mech. 2017, 21, 941–949. [Google Scholar]
- Ding, Y.; Duan, F.; Han, P.; Niu, M. Research on the relationship between moving patterns of submerged body and the features of induced internal waves in two-layer fluid. J. Ship Mech. 2016, 20, 523–529. [Google Scholar]
- Ma, W.; Li, Y.; Ding, Y. Numerical simulations of linearly stratified flow past submerged bodies. Pol. Marit. Res. 2018, 25, 68–77. [Google Scholar] [CrossRef]
- Ma, W.; Li, Y.; Ding, Y.; Duan, F. Numerical investigation of internal wave and free surface wave induced by the DARPA Suboff moving in a strongly stratified fluid. Ships Offshore Struct. 2020, 15, 587–604. [Google Scholar] [CrossRef]
- Yang, Z.C.; Chen, K.; Li, Y.H. Modulation effects of submarine internal wake waves on free surface divergence field. Phys. Fluids 2023, 35, 062109. [Google Scholar]
- Shi, C.; Cheng, X.; Liu, Z. Numerical Simulation of the Maneuvering Motion Wake of an Underwater Vehicle in Stratified Fluid. J. Mar. Sci. Eng. 2022, 10, 1672. [Google Scholar] [CrossRef]
- Yao, W.G.; Zhang, H.; Jiang, D.W. The transformation mechanisms of vortex structures on vortex-induced vibration of an elastically mounted sphere by Lorentz force. Ocean Eng. 2023, 280, 114436. [Google Scholar] [CrossRef]
- Osborne, A.R.; Burch, T.L. Internal solitons in the Andaman Sea. Science 1980, 208, 451–460. [Google Scholar] [CrossRef]
- Cai, S.Q.; Gan, Z.J. Progress in the study of isolated intrathecal waves in the northern part of the South China Sea. Prog. Earth Sci. 2001, 16, 215–219. [Google Scholar]
- Xu, Z.H.; Liu, K.; Yin, B.S. Long-range propagation and associated variability of internal tides in the South China Sea. J. Geophys. Res. Ocean. 2016, 121, 8268–8286. [Google Scholar] [CrossRef]
- Grimshaw, R.; Wang, C.X.; Li, L. Modelling of polarity change in a nonlinear internal wave train in Laoshan Bay. J. Phys. Oceanogr. 2016, 46, 965–974. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, W.; Tian, J.; Yang, Q. Mooring observations of internal solitary waves in the deep basin west of Luzon Strait. Acta Oceanol. Sin. 2014, 33, 82–89. [Google Scholar] [CrossRef]
- Horn, D.A.; Imberger, J. The degeneration of large-scale interfacial gravity waves in lakes. J. Fluid Mech. 2001, 434, 181–207. [Google Scholar] [CrossRef]
- Simmons, H.; Chang, M.H.; Chang, Y.T.; Chao, S.-Y.; Fringer, O.; Jackson, C.; Ko, D.S. Modeling and prediction of internal waves in the South China Sea. Oceanography 2011, 24, 88–99. [Google Scholar] [CrossRef]
- Cheng, L.; Du, P.; Wang, C.; Xie, Z.L.; Hu, H.B.; Chen, X.P.; Li, Z.Y.; Yuan, Z.M. Tuning control parameters of underwater vehicle to minimize the influence of internal solitary waves. Ocean Eng. 2024, 310, 118681. [Google Scholar] [CrossRef]
- Dauxois, T.; Peyrard, M. Physics of Solitons; Cambridge University Press: Cambridge, UK, 2006; Chapter 1. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Koop, C.G.; Butler, G. An investigation of internal solitary waves in a two-fluid system. J. Fluid Mech. 1981, 112, 225–251. [Google Scholar] [CrossRef]
- Segur, H.; Hammack, J.L. Soliton models of long internal waves. J. Fluid Mech. 1982, 118, 285–304. [Google Scholar] [CrossRef]
- Benjamin, B.T. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 1967, 29, 559–592. [Google Scholar] [CrossRef]
- Ono, H. Wave propagation in an inhomogeneous anharmonic lattice. J. Phys. Soc. Jpn. 1972, 32, 332–336. [Google Scholar] [CrossRef]
- Helfrich, K.R.; Melville, W.K. On long nonlinear internal waves over slope-shelf topography. J. Fluid Mech. 1986, 167, 285–308. [Google Scholar] [CrossRef]
- Helfrich, K.R.; Melville, W.K. Review of dispersive and resonant effects in internal wave propagation. In Physical Oceanography of Sea Straits; Springer: Dordrecht, The Netherlands, 1990; pp. 391–420. [Google Scholar]
- Helfrich, K.R.; Melville, W.K. Long nonlinear internal waves. Annu. Rev. Fluid Mech. 2006, 38, 395–425. [Google Scholar] [CrossRef]
- Michallet, H.; Barthelemy, E. Experimental study of interfacial solitary waves. J. Fluid Mech. 1998, 366, 159–177. [Google Scholar] [CrossRef]
- Choi, W.; Camassa, R. Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 1999, 396, 1–36. [Google Scholar] [CrossRef]
- Miyata, M. An internal solitary wave of large amplitude. Deep Sea Res. Part B. Oceanogr. Lit. Rev. 1985, 33, 210. [Google Scholar]
- Miyata, M. Long internal waves of large amplitude. In Nonlinear Water Waves; Springer: Berlin/Heidelberg, Germany, 1988; pp. 399–406. [Google Scholar]
- Camassa, R.; Chol, W.; Michallet, H. On the realm of validity of strongly nonlinear asymptotic approximations for internal waves. J. Fluid Mech. 2006, 549, 1. [Google Scholar] [CrossRef]
- Huang, W.H.; You, Y.X.; Wang, X. Wave-making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth. Acta Phys. Sin. 2013, 62, 084705. [Google Scholar] [CrossRef]
- Cui, J.; Dong, S.; Wang, Z. Study on applicability of internal solitary wave theories by theoretical and numerical method. Appl. Ocean Res. 2021, 111, 102629. [Google Scholar] [CrossRef]
- Fructus, D.; Grue, J. Fully nonlinear solitary waves in a layered stratified fluid. J. Fluid Mech. 2004, 505, 323–347. [Google Scholar] [CrossRef]
- Stastna, M.; Lamb, K.G. Large fully nonlinear internal solitary waves: The effect of background current. Phys. Fluids 2002, 14, 2987–2999. [Google Scholar] [CrossRef]
- Lamb, K.G. A numerical investigation of solitary internal waves with trapped cores formed via shoaling. J. Fluid Mech. 2002, 451, 109–144. [Google Scholar] [CrossRef]
- Stastna, M. Internal Waves in the Ocean; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Wang, Z.; Yuan, C. Oceanic internal solitary waves in three-layer fluids of great depth. Acta Mech. Sin. 2022, 38, 1–14. [Google Scholar] [CrossRef]
- Walker, L.R. Interfacial solitary waves in a two-fluid medium. Phys. Fluids 1973, 16, 1796–1804. [Google Scholar] [CrossRef]
- Huang, W.H.; You, Y.X.; Wang, X. Internal Solitary Wave Loads Experiments and Its Theoretical Model for a Cylindrical Structure. Chin. J. Theor. Appl. Mech. 2013, 45, 716–728. [Google Scholar]
- Chen, C.Y.; Hsu, J.R.C.; Chen, C.W. Generation of internal solitary wave by gravity collapse. J. Mar. Sci. Technol. 2007, 15, 1. [Google Scholar] [CrossRef]
- Wei, G.; Du, H.; Xu, X.H.; Zhang, Y.; Qu, Z.; Hu, T.; You, Y. Experimental investigation of the generation of large-amplitude internal solitary wave and its interaction with a submerged slender body. Sci. China Phys. Mech. Astron. 2014, 57, 301–310. [Google Scholar] [CrossRef]
- Du, H.; Wei, G.; Wang, S.D. Experimental study of elevation-and depression-type internal solitary waves generated by gravity collapse. Phys. Fluids 2019, 31, 102104. [Google Scholar] [CrossRef]
- Ermanyuk, E.V.; Gavrilov, N.V. Experimental Study of the Dynamic Effect of an Internal Solitary Wave on a Submerged Circular Cylinder. J. Appl. Mech. Tech. Phys. 2005, 46, 800–806. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Y.; Lv, H. An Experimental Study of Wave-Resistance of a Horizontal Cylinder in Internal Waves. Period. Ocean Univ. China 2007, 1, 1–6. [Google Scholar]
- Xu, X.H.; Hu, T.Q.; Wei, G. Experimental investigations on the interaction of internal waves with a submerged body in a stratified fluid. J. Hydrodyn. 2011, 26, 186–193. [Google Scholar]
- Wei, G.; Du, H.; Qu, Z.Y. Measurement and analysis of the effect of internal isolated waves on the kinematic properties of an elongated submerged body. In Proceedings of the 14th Academic Conference on Modern Mathematics and Mechanics, Zhangjiajie, China, 17 August 2014; pp. 45–46. [Google Scholar]
- Ji, M.; Chen, K.; You, Y. Experimental study of wave loading by internal solitary waves on a submerged slender body. In Proceedings of the 39th International Conference on Ocean, Offshore and Arctic Engineering, Virtual, 3–7 August 2020; Paper No. V06BT06A059. ISBN 978-0-7918-8438-6. [Google Scholar]
- Wang, S.D.; Wei, G.; Du, H. Experimental investigation of the wave-flow structure of an oblique internal solitary wave and its force exerted on a slender body. Ocean Eng. 2020, 201, 107057. [Google Scholar] [CrossRef]
- Xie, Z.L.; Jiao, J.; Zhao, B.; Xu, F.C. Theoretical and experimental research on the effect of bi-directional misalignment on the static and dynamic characteristics of a novel bearing. Mech. Syst. Signal Process. 2024, 208, 111041. [Google Scholar] [CrossRef]
- Xie, Z.; Li, J.; Tian, Y.; Du, P.; Zhao, B.; Xu, F. Theoretical and experimental study on influences of surface texture on lubrication performance of a novel bearing. Tribol. Int. 2024, 193, 109351. [Google Scholar] [CrossRef]
- Chen, X. Forces on Bodies Exerted by Internal Wavesin Stratified Fluids. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2007. [Google Scholar]
- Du, H.; Wei, G.; Zeng, W.H. Experimental investigation on the kinematics characteristic of submerged slender body under internal solitary wave of depression. J. Ship Mech. 2017, 21, 8. [Google Scholar]
- Chen, M.; Chen, K.; You, Y.X. Experimental investigation of internal solitary wave forces on a semi-submersible. Ocean Eng. 2017, 141, 205–214. [Google Scholar] [CrossRef]
- Ocean University of China. An Experimental System for the Interaction Between Internal Waves and Submerged Bodies CN201810114516.7, 3 September 2019.
- Harbin Institute of Technology (Weihai). Measurement System and Measurement Method for Submerged Body Encountering Internal Isolated Wave Test with Double Rod Connection CN202110436236.X, 20 July 2021.
- People’s Liberation Army University of National Defence Science and Technology. An Embedded Force Measurement Method for Underwater Structures with Internal Isolated Wave Action CN202211064910.7, 9 September 2024.
- Huang, M.M.; Zhang, N.; Zhu, A.J. Hydrodynamic loads and motion features of a submarine with interaction of internal solitary waves. J. Ship Mech. 2019, 23, 531–540. [Google Scholar]
- Chen, J.; You, Y.X.; Liu, X.D. Numerical simulation of interaction of internal solitary waves with a moving submarine. J. Hydrodyn. 2010, 25, 344–351. [Google Scholar]
- Xie, J.; Jian, Y.; Yang, L. Strongly nonlinear internal soliton load on a small vertical circular cylinder in two-layer fluids. Appl. Math. Model. 2010, 34, 2089–2101. [Google Scholar] [CrossRef]
- Li, G.Y. Numerical Simulation of Interaction of Three-Dimensional Internal Solitary Waves with the Structure in a Stratified Flow. Master’s Thesis, South China University of Technology, Guangzhou, China, 2012. [Google Scholar]
- Guan, H.; Wei, G.; Du, H. Hydrodynamic properties of interactions of three-dimensional internal solitary waves with submarine. J. Army Eng. Univ. PLA 2012, 13, 577–582. [Google Scholar]
- Yang, F. Study on the Interaction Between Internal Solitary Waves and the Submerged Body. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2017. [Google Scholar]
- Du, H.; Wei, G.; Gu, M. Experimental investigation of the load exerted by nonstationary internal solitary waves on a submerged slender body over a slope. Appl. Ocean. Res. 2016, 59, 216–223. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Chen, T. Numerical Investigation of Internal Solitary Wave Forces on Submarines in Continuously Stratified Fluids. J. Mar. Sci. Eng. 2021, 9, 1374. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, T.; Yu, L. Penetration depth of the dynamic response of seabed induced by internal solitary waves. Appl. Ocean Res. 2019, 90, 101867. [Google Scholar] [CrossRef]
- Chen, C.Y. An experimental study of stratifified mixing caused by internal solitary waves in a two-layered flfluid system over variable seabed topography. Ocean Eng. 2007, 34, 1995–2008. [Google Scholar] [CrossRef]
- Gong, S.K.; Gao, J.L.; Mao, H.F. Investigations on fluid resonance within a narrow gap formed by two fixed bodies with varying breadth ratios. China Ocean Eng. 2023, 37, 962–974. [Google Scholar] [CrossRef]
- Gao, J.-L.L.; Yu, J.; Wang, J.H. Study on Transient Gap Resonance with Consideration of the Motion of Floating Body. China Ocean Eng. 2022, 6, 994–1006. [Google Scholar] [CrossRef]
- 170 Cai, S.; Long, X.; Gan, Z. A method to estimate the forces exerted by internal solitons on cylindrical piles. Ocean Eng. 2003, 30, 673–689. [Google Scholar] [CrossRef]
- Xie, J.; Xu, J.; Cai, S. A numerical study of the load on cylindrical piles exerted by internal solitary waves. J. Fluids Struct. 2011, 27, 1252–1261. [Google Scholar] [CrossRef]
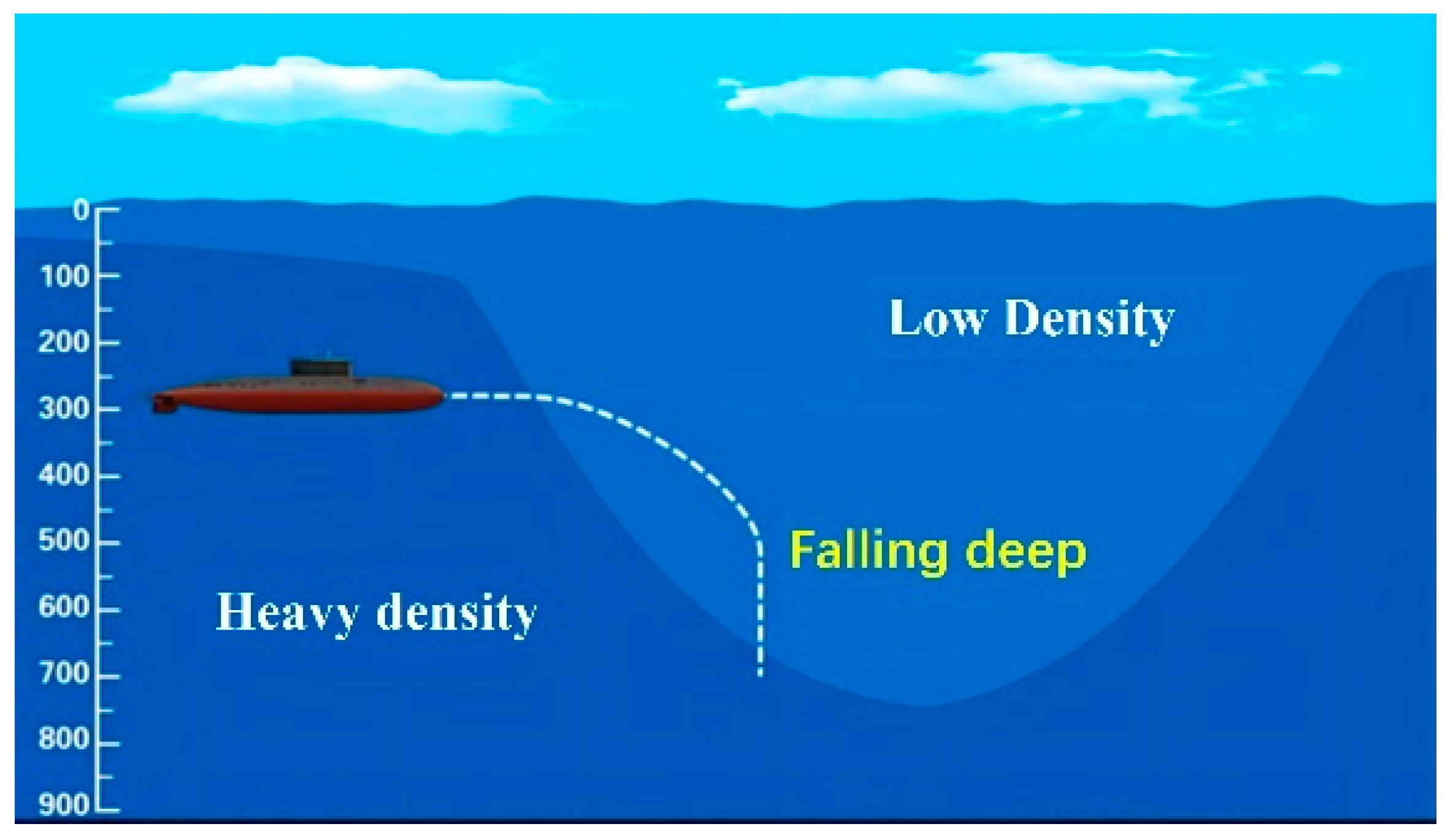
- Wang, C.; Wang, J.; Liu, Q. Dynamics and “falling deep” mechanism of submerged floating body under internal solitary waves. Ocean Eng. 2023, 288, 116058. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, C.; Guo, B.B.; Liang, Q.Y.; Xie, Z.L.; Yuan, Z.M.; Chen, X.P.; Hu, H.B.; Du, P. Numerical investigation on the interaction between large-scale continuously stratified internal solitary wave and moving submersible. Appl. Ocean Res. 2024, 145, 103938. [Google Scholar] [CrossRef]
- Wang, J.R.; He, Z.Y.; Xie, B.T. Numerical investigation on the interaction between internal solitary wave and self-propelled submersible. Phys. Fluids 2023, 35, 107119. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, H.; Du, P.; Chen, X.; Li, Z.; Wang, C.; Cheng, L.; Tang, Z. Detection of an internal solitary wave by the un-derwater vehicle based on machine learning. Phys. Fluids 2022, 34, 115137. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, H.B.; Guo, B.B.; Liang, Q.Y.; Zhang, F.; Chen, X.P.; Xie, Z.L.; Du, P. Predicting shear stress distribution on structural surfaces under internal solitary wave loading: A deep learning perspective. Phys. Fluids 2024, 36, 035153. [Google Scholar] [CrossRef]
- Cheng, L.; Du, P.; Hu, H.B. Control of underwater suspended vehicle to avoid ‘falling deep’ under the influence of internal solitary waves. Ships Offshore Struct. 2023, 19, 1349–1367. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Hu, Y.; Wang, X.; Gao, Y. Experimental study on interaction between the internal solitary wave and a hydrofoil based on the spectral proper orthogonal decomposition. Phys. Fluids 2023, 35, 112118. [Google Scholar]

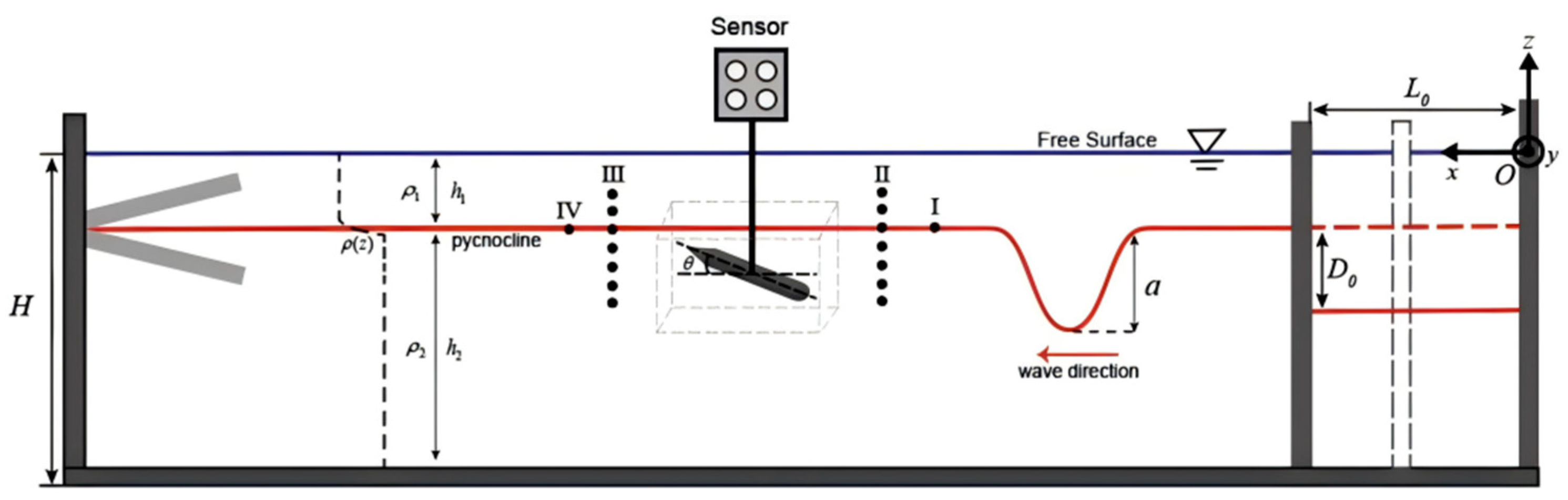
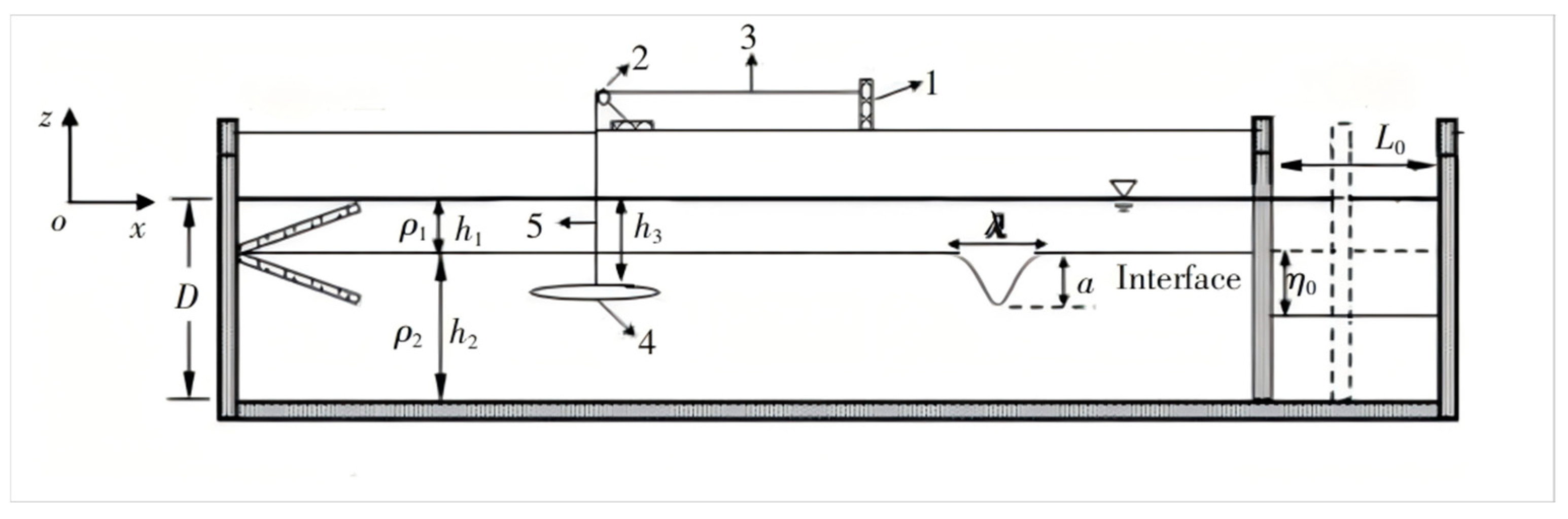
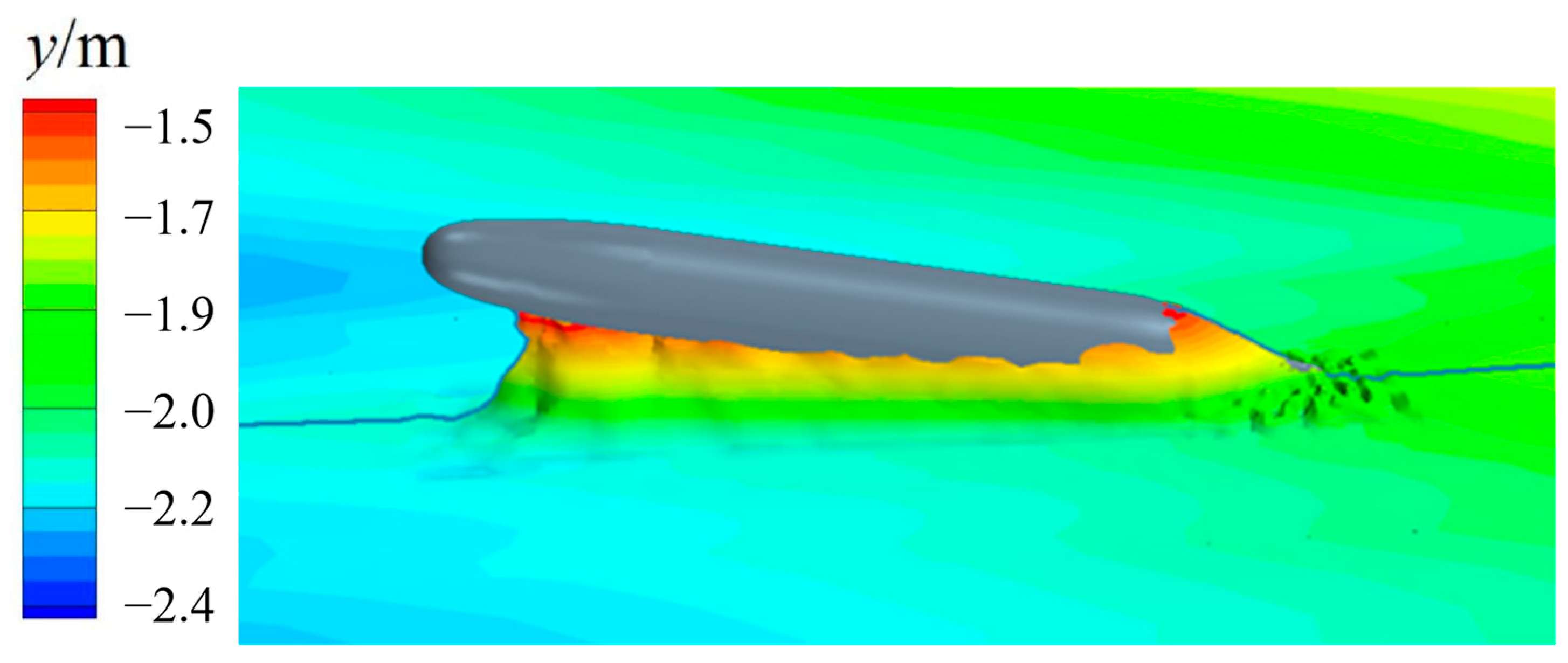

| Method Name | Principle or Technology | Advantages | Disadvantages |
|---|---|---|---|
| A* algorithm | Maintenance of actual and predicted distances | Fast convergence and high stability | May fail under dynamic conditions |
| Wavefront Algorithm | Graph search theory | Good accuracy and adaptability | Requires known maps |
| Level set algorithm | Categorize and compare | Interface tracking and shape modeling | Slow convergence |
| Artificial potential field method | Gravitational and repulsive field interactions | Simple principle | Existence of localized extremes |
| Ant colony algorithm | Foraging behavior of ants | More Intelligent | Slow convergence |
| Particle Swarm Optimization Algorithm | Bird Aggregation Modeling | Simple structure, easy to implement | May fail under dynamic conditions |
| Model Name | Creator | Fluid Type | Range of Application |
|---|---|---|---|
| KdV | Korteweg G. de.Vries | two-layer fluid | weak nonlinearity shallow |
| eKdV | Helfrich Melville | two-layer fluid | medium nonlinear shallow |
| mKdV | Michallet Barthelemy | two-layer fluid | medium nonlinear shallow |
| MCC | Miyata Choi Camassa | two-layer fluid three-layer fluid | strongly nonlinear deepwater |
| DJL | Dubreil Jacotin Long | continuously stratified fluid | strongly nonlinear shallow/deepwater |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Hu, H.; Ouahsine, A.; Lu, H.; Li, Z.; Yuan, Z.; Du, P. Advances of Complex Marine Environmental Influences on Underwater Vehicles. J. Mar. Sci. Eng. 2025, 13, 1297. https://doi.org/10.3390/jmse13071297
Zhao S, Hu H, Ouahsine A, Lu H, Li Z, Yuan Z, Du P. Advances of Complex Marine Environmental Influences on Underwater Vehicles. Journal of Marine Science and Engineering. 2025; 13(7):1297. https://doi.org/10.3390/jmse13071297
Chicago/Turabian StyleZhao, Sen, Haibao Hu, Abdellatif Ouahsine, Haochen Lu, Zhuoyue Li, Zhiming Yuan, and Peng Du. 2025. "Advances of Complex Marine Environmental Influences on Underwater Vehicles" Journal of Marine Science and Engineering 13, no. 7: 1297. https://doi.org/10.3390/jmse13071297
APA StyleZhao, S., Hu, H., Ouahsine, A., Lu, H., Li, Z., Yuan, Z., & Du, P. (2025). Advances of Complex Marine Environmental Influences on Underwater Vehicles. Journal of Marine Science and Engineering, 13(7), 1297. https://doi.org/10.3390/jmse13071297










