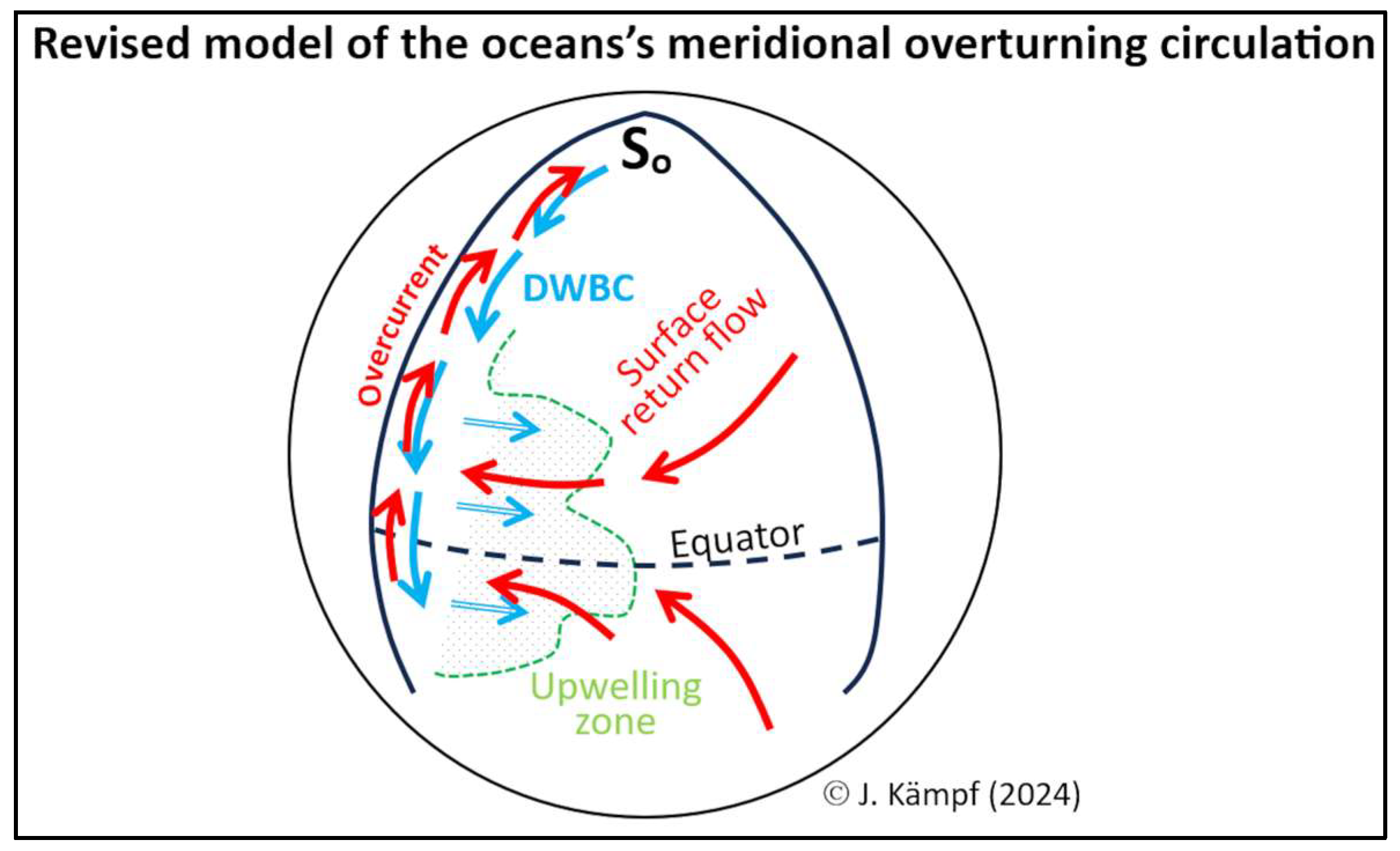
A Revised Model of the Ocean’s Meridional Overturning Circulation
Abstract
1. Introduction
2. Methodology
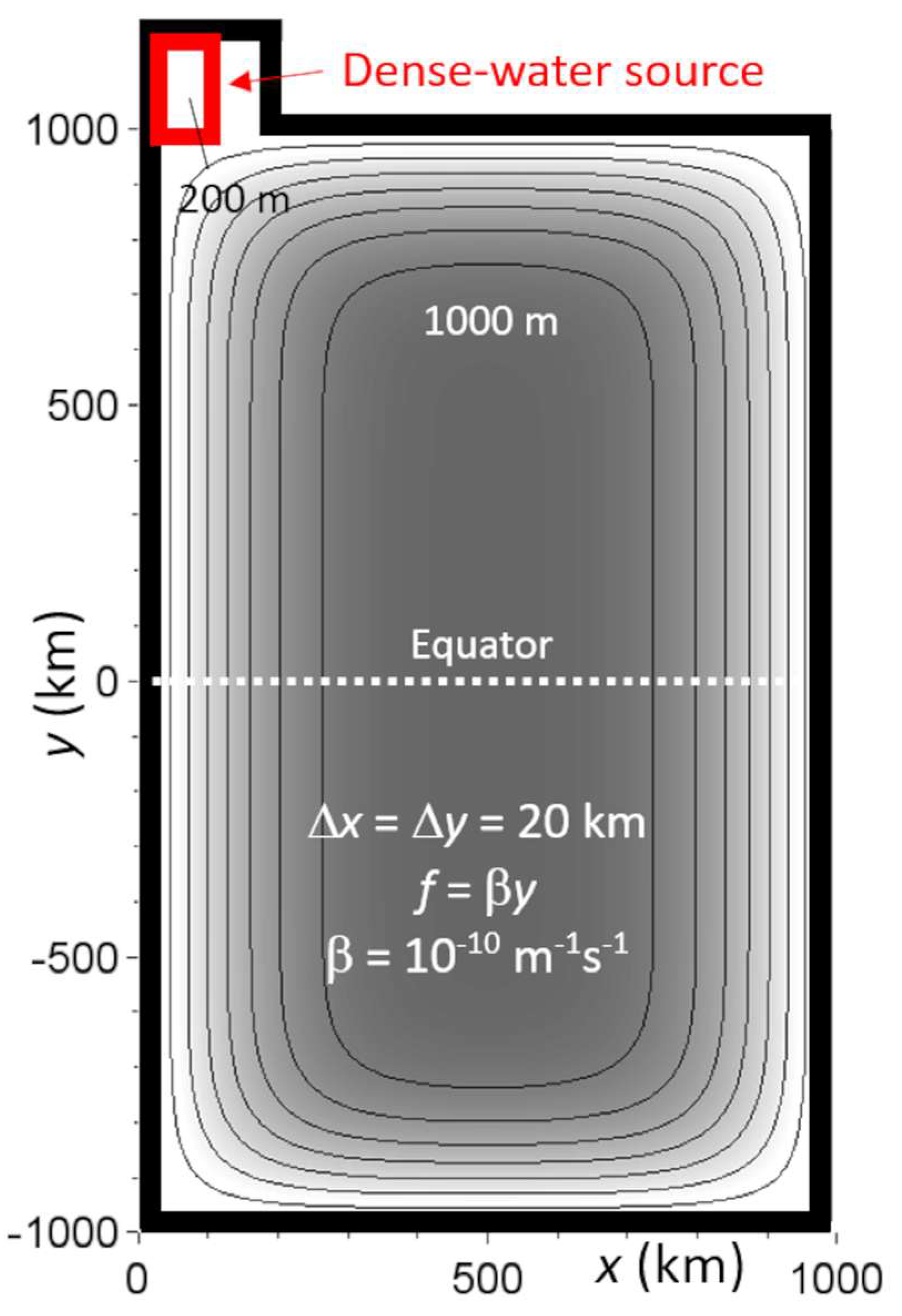
2.1. Model Description
2.2. Experimental Design
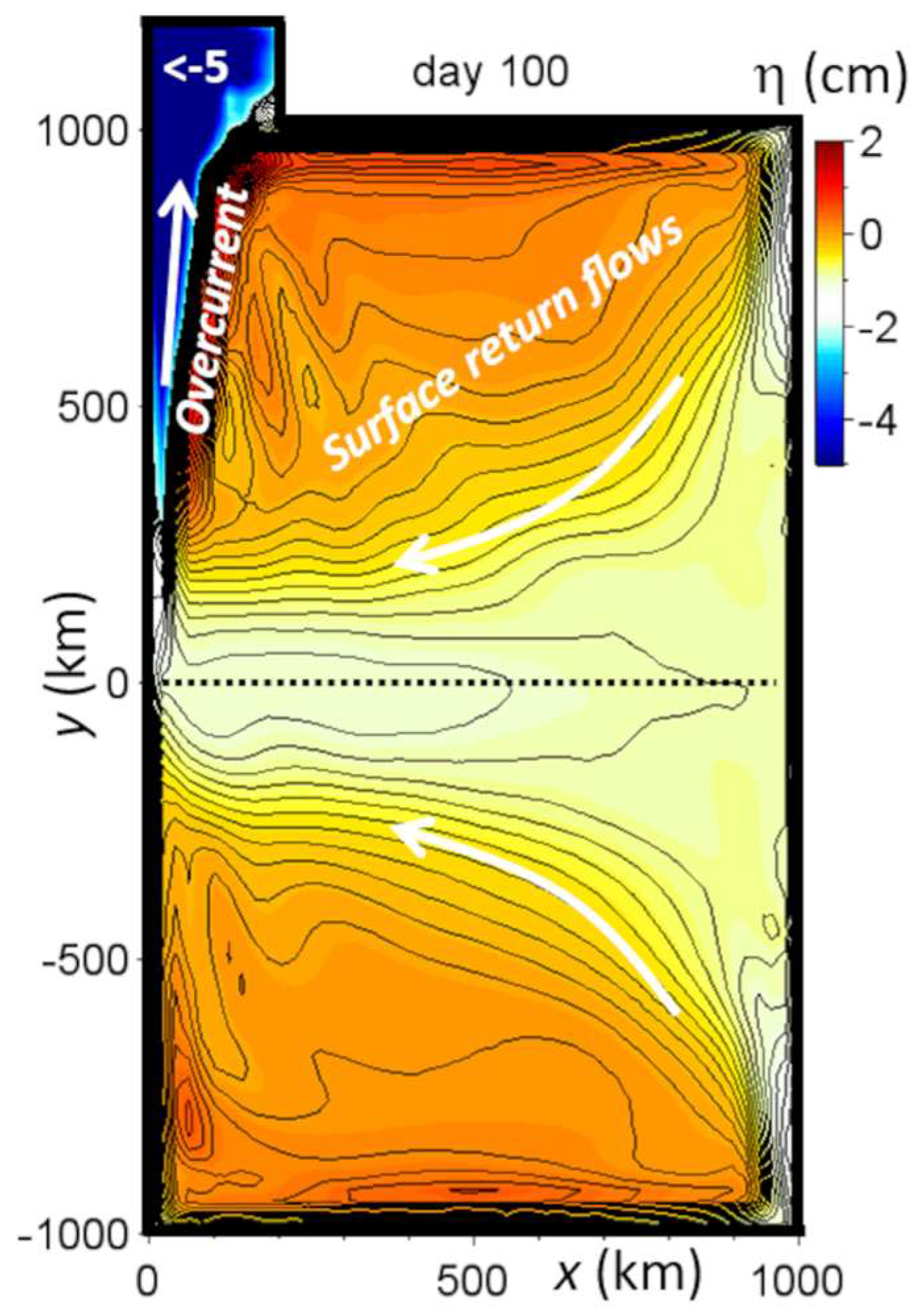
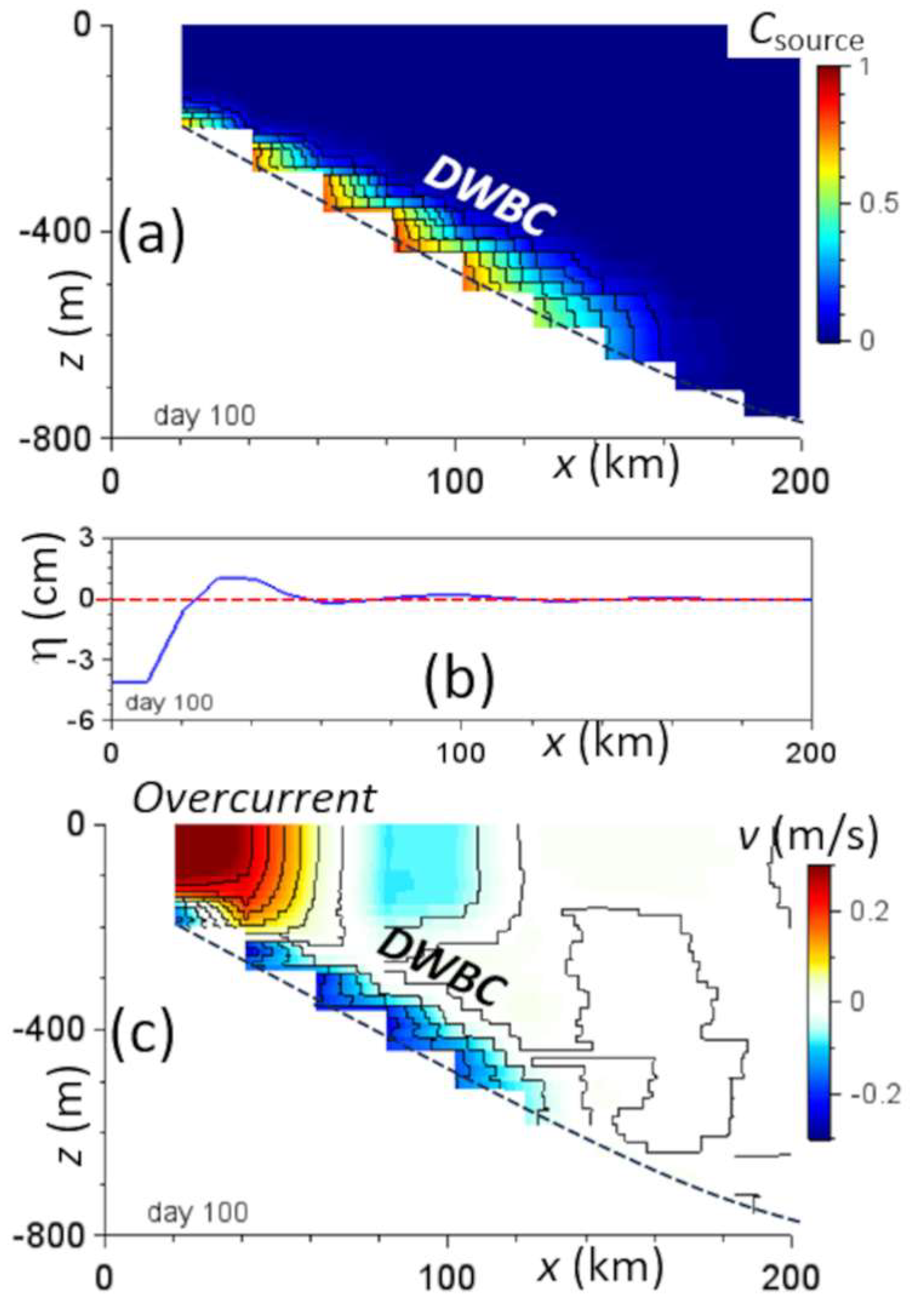
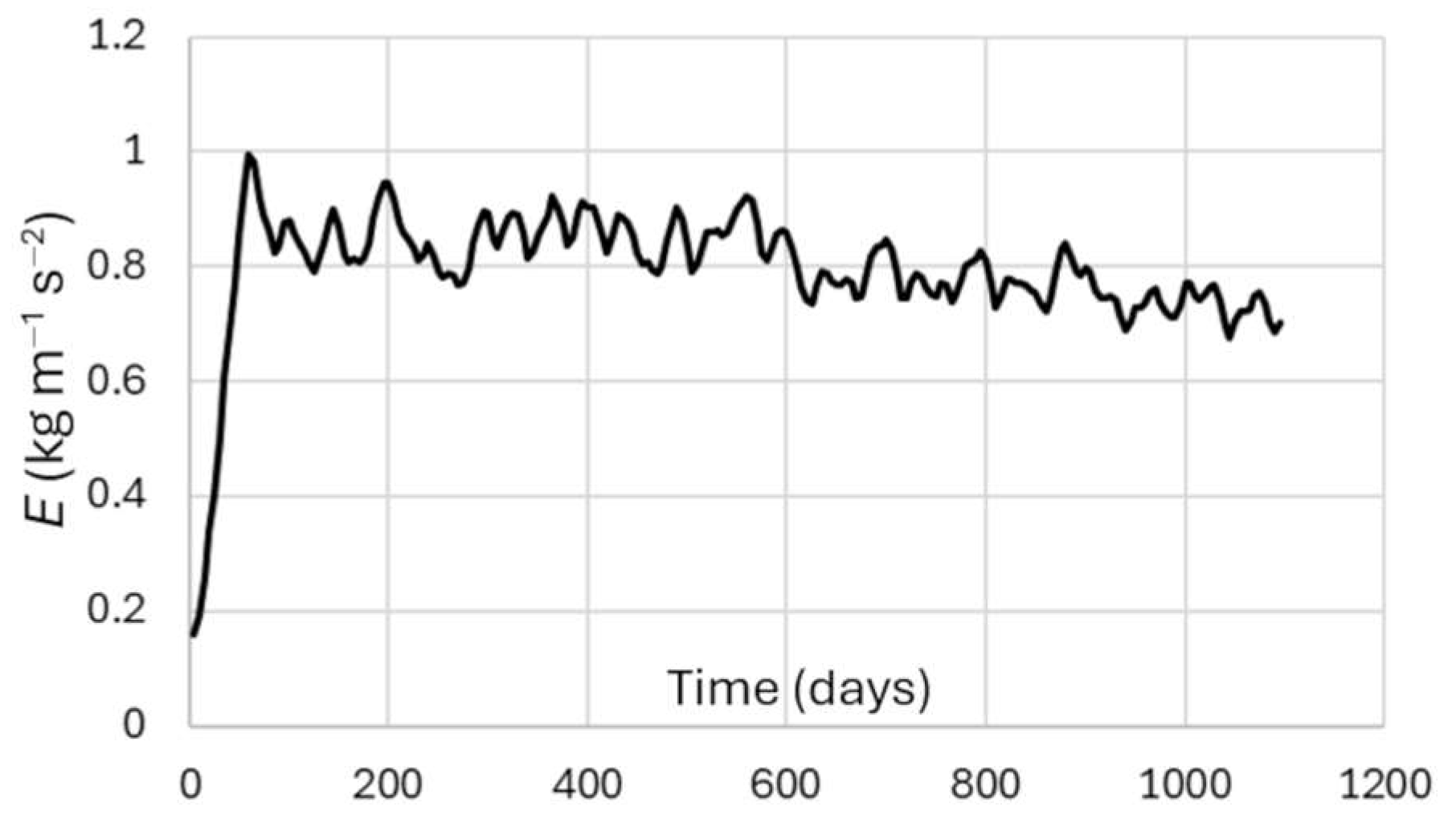
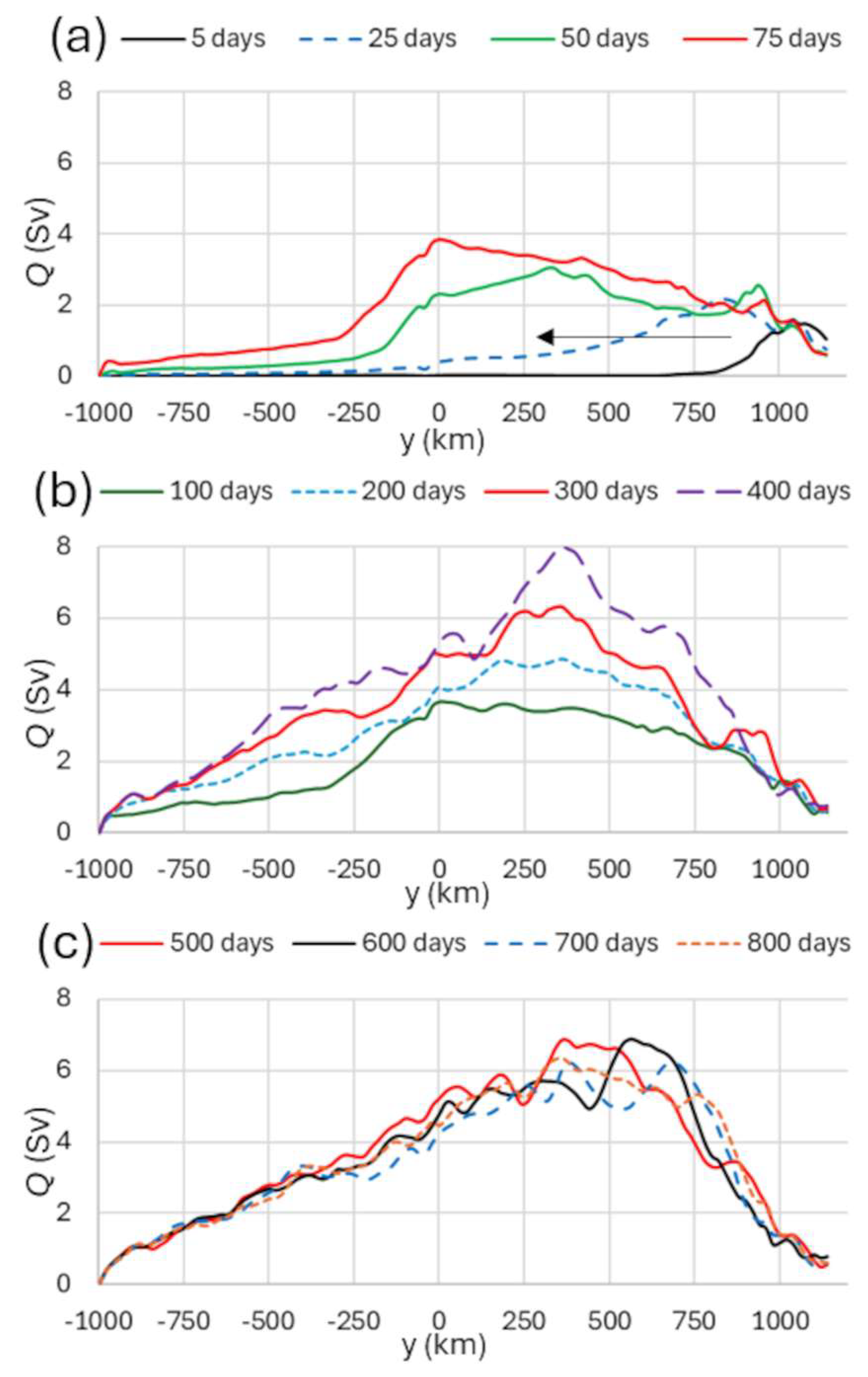
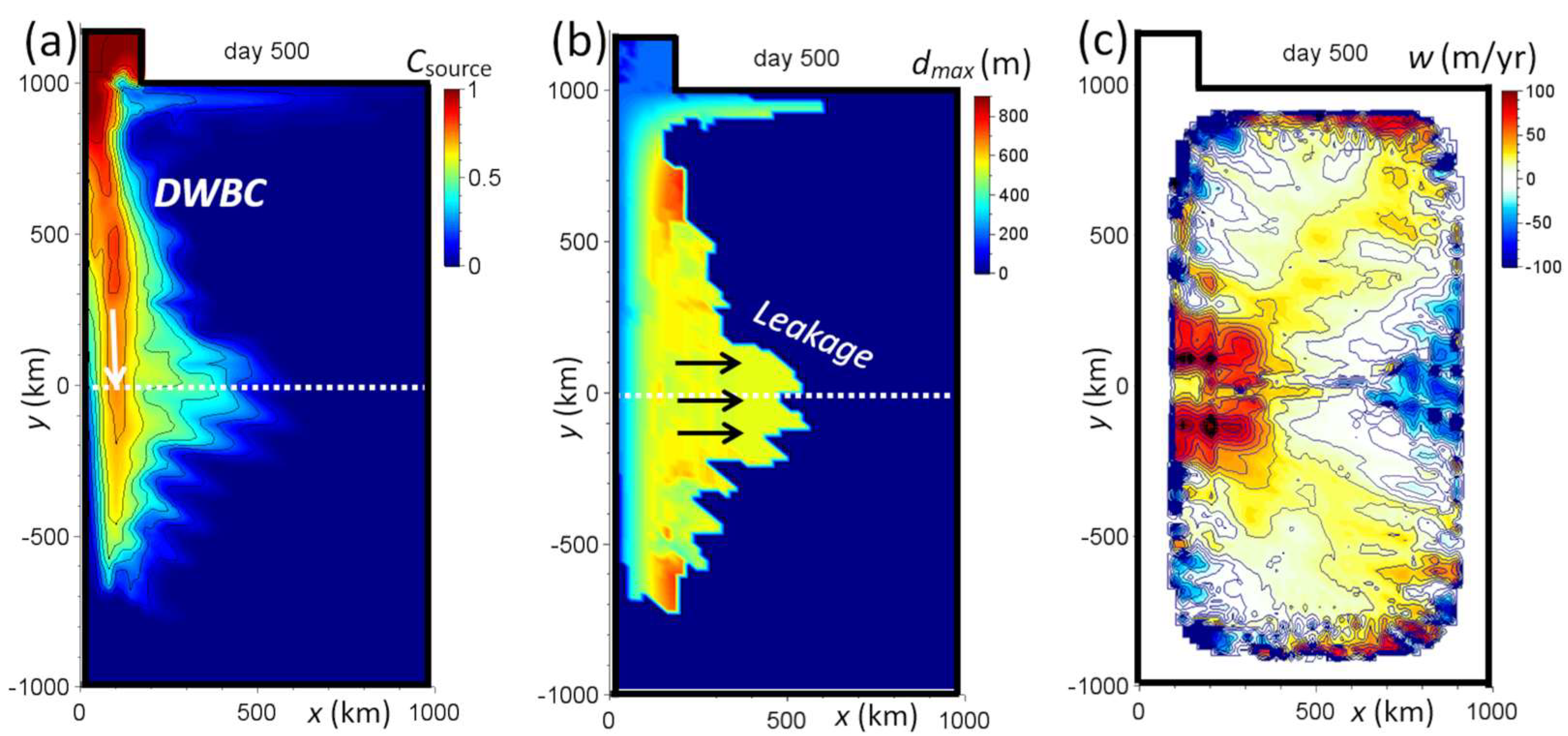
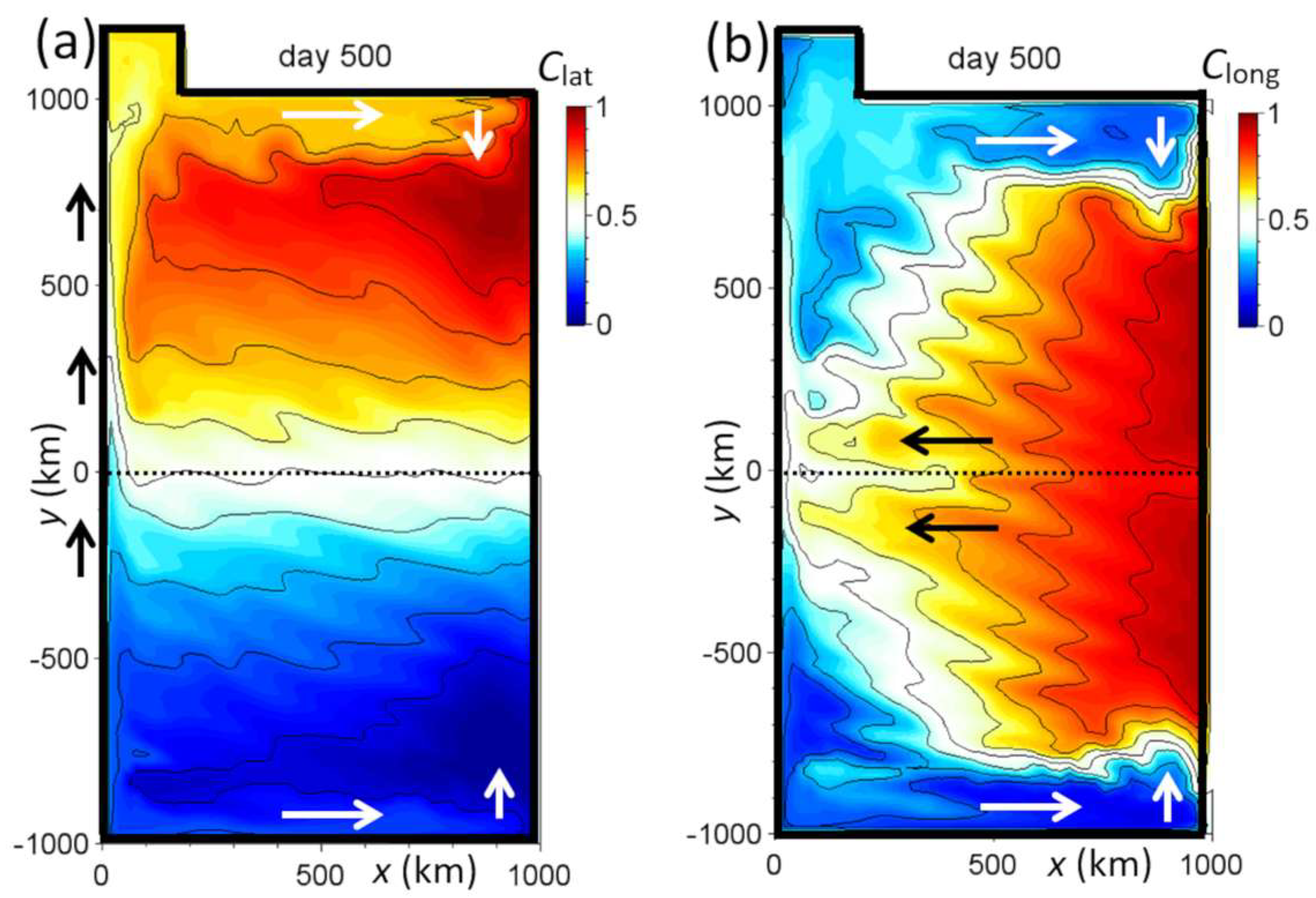
3. Results and Discussion
4. Final Discussion
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tomczak, M.; Godfrey, J.S. Regional Oceanography: An Introduction, 2nd ed.; Daya Publishing House: Delhi, India, 2003; 390p. [Google Scholar]
- Stommel, H.; Arons, A.B. On the abyssal circulation of the world ocean: I. Stationary planetary flow patterns on a sphere. Deep-Sea Res. 1960, 6, 140–154. [Google Scholar] [CrossRef]
- Stommel, H.; Arons, A.B. On the abyssal circulation of the world ocean: II. An idealized model of the circulation pattern and amplitude in oceanic basins. Deep-Sea Res. 1960, 6, 217–233. [Google Scholar] [CrossRef]
- Stommel, H.; Arons, A.B.; Faller, A.J. Some examples of stationary flow patterns in bounded basins. Tellus 1958, 10, 179–187. [Google Scholar] [CrossRef]
- Ferrari, R.; Mashayek, A.; McDougall, T.J.; Nikurashin, M.; Campin, J. Turning ocean mixing upside down. J. Phys. Oceanogr. 2016, 46, 2239–2261. [Google Scholar] [CrossRef]
- Wunsch, C. A simplified ocean physics? Revisiting Abyssal Recipes. J. Phys. Oceanogr. 2023, 53, 1387–1400. [Google Scholar] [CrossRef]
- Pedlosky, J. Ocean Circulation Theory; Springer: New York, NY, USA, 2004; 453p. [Google Scholar]
- Munk, W.H. Abyssal recipes. Deep-Sea Res. Oceanogr. Abstr. 1966, 13, 707–730. [Google Scholar] [CrossRef]
- Waterhouse, A.F.; MacKinnon, J.A.; Nash, J.D.; Alford, M.H.; Kunze, E.; Simmons, H.L.; Polzin, K.L.; Laurent, L.C.S.; Sun, O.M.; Pinkel, R.; et al. Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate. J. Phys. Oceanogr. 2014, 44, 1854–1872. [Google Scholar] [CrossRef]
- Gregg, M.C. Ocean Mixing; Cambridge University Press: Cambridge, UK, 2021; 378p. [Google Scholar]
- Moum, J.N. Variations in ocean mixing from seconds to years. Ann. Rev. Mar. Sci. 2021, 13, 201–226. [Google Scholar] [CrossRef]
- Burchard, H.; Alford, M.; Chouksey, M.; Dematteis, G.; Eden, C.; Giddy, I.; Klingbeil, K.; Boyer, A.L.; Olbers, D.; Pietrzak, J.; et al. Linking Ocean Mixing and Overturning Circulation. Bull. Am. Meteorol. Soc. 2024, 105, E1265–E1274. [Google Scholar] [CrossRef]
- Polzin, K.L. An abyssal recipe. Ocean Model. 2009, 30, 298–309. [Google Scholar] [CrossRef]
- Cessi, P. The global overturning circulation. Annu. Rev. Mar. Sci. 2019, 11, 249–270. [Google Scholar] [CrossRef] [PubMed]
- Holland, W.R. Ocean tracer distributions. I. A preliminary numerical experiment. Tellus 1971, 23, 371–392. [Google Scholar] [CrossRef]
- Veronis, G. The role of models in tracer studies. In Numerical Models of Ocean Circulation 1975, Proceedings of a symposium held at Durham, New Hampshire, Durham, NH, USA, 17–20 October 1972; National Academy of Sciences: Washington, DC, USA; pp. 133–146.
- McDougall, T.; Church, J. Pitfalls with the numerical representation of isopycnal and diapycnal mixing. J. Phys. Oceanogr. 1985, 17, 1950–1964. [Google Scholar] [CrossRef]
- Cox, M.; Bryan, K. A numerical model of the ventilated thermocline. J. Phys. Oceanogr. 1984, 14, 674–687. [Google Scholar] [CrossRef]
- Redi, M.H. Oceanic isopycnal mixing by coordinate rotation. J. Phys. Oceanogr. 1982, 12, 1154–1158. [Google Scholar] [CrossRef]
- Cox, M.D. An eddy-resolving numerical model of the ventilated thermocline: Time dependence. J. Phys. Oceanogr. 1987, 17, 1044–1056. [Google Scholar] [CrossRef]
- Gough, W.A.; Lin, C.A. Isopycnal mixing and the Veronis effect in an ocean general circulation model. J. Mar. Res. 1995, 53, 189–199. [Google Scholar] [CrossRef]
- Lazar, A.; Madec, G.; Delecluse, P. The deep interior downwelling, the Veronis effect, and mesoscale tracer transport parameterizations in an OGCM. J. Phys. Oceanogr. 1999, 29, 2945–2961. [Google Scholar] [CrossRef]
- Gent, P.R.; McWilliams, J.C. Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 1990, 20, 150–155. [Google Scholar] [CrossRef]
- Böning, C.W.; Holland, W.R.; Bryan, F.O.; Danabasoglu, G.; McWilliams, J.C. An overlooked problem in model simulations of the thermohaline circulation and heat transport in the Atlantic Ocean. J. Clim. 1995, 8, 515–523. [Google Scholar] [CrossRef]
- Danabasoglu, G.; McWilliams, J.C. Sensitivity of the global ocean circulation to parameterizations of mesoscale tracer transports. J. Clim. 1995, 8, 2967–2987. [Google Scholar] [CrossRef]
- Weaver, A.J.; Eby, M. On the numerical implementation of advection schemes for use in conjunction with various mixing parameterizations in the GFDL ocean model. J. Phys. Oceanogr. 1997, 27, 369–377. [Google Scholar] [CrossRef]
- Kawase, M. Establishment of deep ocean circulation driven by deep-water production. J. Phys. Oceanogr. 1987, 17, 2294–2317. [Google Scholar] [CrossRef]
- Hautala, S.L.; Riser, S.T. A simple model of abyssal circulation, including effects of wind, buoyancy, and topography. J. Phys. Oceanogr. 1989, 19, 596–611. [Google Scholar] [CrossRef]
- Straub, D.N.; Rhines, P.B. Effects of large-scale topography on abyssal circulation. J. Mar. Res. 1990, 48, 223–253. [Google Scholar] [CrossRef]
- Straub, D.N.; Killworth, P.D.; Kawase, M. A simple model of mass-driven abyssal circulation over a general bottom topography. J. Phys. Oceanogr. 1993, 23, 1454–1469. [Google Scholar] [CrossRef]
- Karcher, M.; Lippert, A. Spin-up and breakdown of source-driven deep North Atlantic flow over realistic bottom topography. J. Geophys. Res. 1994, 99, 12357–12373. [Google Scholar] [CrossRef]
- Spall, M.A. Large-Scale Circulations Forced by Localized Mixing over a Sloping Bottom. J. Phys. Oceanogr. 2001, 31, 2369–2384. [Google Scholar] [CrossRef]
- Andersson, H.C.; Veronis, G. Thermohaline circulation in a two-layer model with sloping boundaries and a mid-ocean ridge. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2004, 51, 93–106. [Google Scholar] [CrossRef]
- Luyten, P.J.; Jones, J.E.; Proctor, R.; Tabor, A.; Tett, P.; Wild-Allen, K. COHERENS-A Coupled Hydrodynamical-Ecological Model for Regional and Shelf Seas: User Documentation; MUMM Report; Management Unit of the North Sea: Brussels, Belgium, 1999; 914p, Available online: https://uol.de/f/5/inst/icbm/ag/physoz/download/from_emil/COHERENS/print/userguide.pdf (accessed on 10 June 2025).
- Kämpf, J. Advanced Ocean Modelling; Springer: Berlin/Heidelberg, Germany, 2010; pp. 125–127. [Google Scholar]
- Blumberg, A.F.; Mellor, G.L. A description of a three-dimensional coastal ocean circulation model. In Three-Dimensional Coastal Ocean Models Coastal and Estuarine Sciences; Heaps, N.S., Ed.; American Geophysical Union: Washington, DC, USA, 2013; Volume 4, pp. 1–16. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. I: The basic experiment. Mon. Weath. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Backhaus, J.O. Application of a transient reduced gravity plume model to the Denmark Strait Overflow. J. Geophys. Res. 1994, 99, 12375–12396. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Beckers, J.-M. Introduction to Geophysical Fluid Dynamics, 2nd ed.; Academic Press: Cambridge, MA, USA, 2011; 875p. [Google Scholar]
- Kämpf, J. Cascading-driven upwelling in submarine canyons at high latitudes. J. Geophys. Res. 2005, 110, C02007. [Google Scholar] [CrossRef]
- Weaver, A.J.; Middleton, J.H. An analytic model for the Leeuwin Current of West Australia. Cont. Shelf Res. 1990, 10, 105–122. [Google Scholar] [CrossRef]
- Jochumsen, K.; Moritz, M.; Nunes, N.; Quadfasel, D.; Larsen, K.M.H.; Hansen, B.; Valdimarsson, H.; Jonsson, S. Revised transport estimates of the Denmark Strait overflow. J. Geophys. Res. Oceans 2017, 122, 3434–3450. [Google Scholar] [CrossRef]
- Richardson, P.L.; Fratantoni, D.M. Float trajectories in the deep western boundary current and deep equatorial jets of the tropical Atlantic. Deep-Sea Res. Part II Top. Stud. Oceanogr. 1999, 46, 305–333. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaempf, J. A Revised Model of the Ocean’s Meridional Overturning Circulation. J. Mar. Sci. Eng. 2025, 13, 1244. https://doi.org/10.3390/jmse13071244
Kaempf J. A Revised Model of the Ocean’s Meridional Overturning Circulation. Journal of Marine Science and Engineering. 2025; 13(7):1244. https://doi.org/10.3390/jmse13071244
Chicago/Turabian StyleKaempf, Jochen. 2025. "A Revised Model of the Ocean’s Meridional Overturning Circulation" Journal of Marine Science and Engineering 13, no. 7: 1244. https://doi.org/10.3390/jmse13071244
APA StyleKaempf, J. (2025). A Revised Model of the Ocean’s Meridional Overturning Circulation. Journal of Marine Science and Engineering, 13(7), 1244. https://doi.org/10.3390/jmse13071244





