Analytical and Experimental Investigation of a Three-Module VLFS Connector Based on an Elastic Beam Model
Abstract
1. Introduction
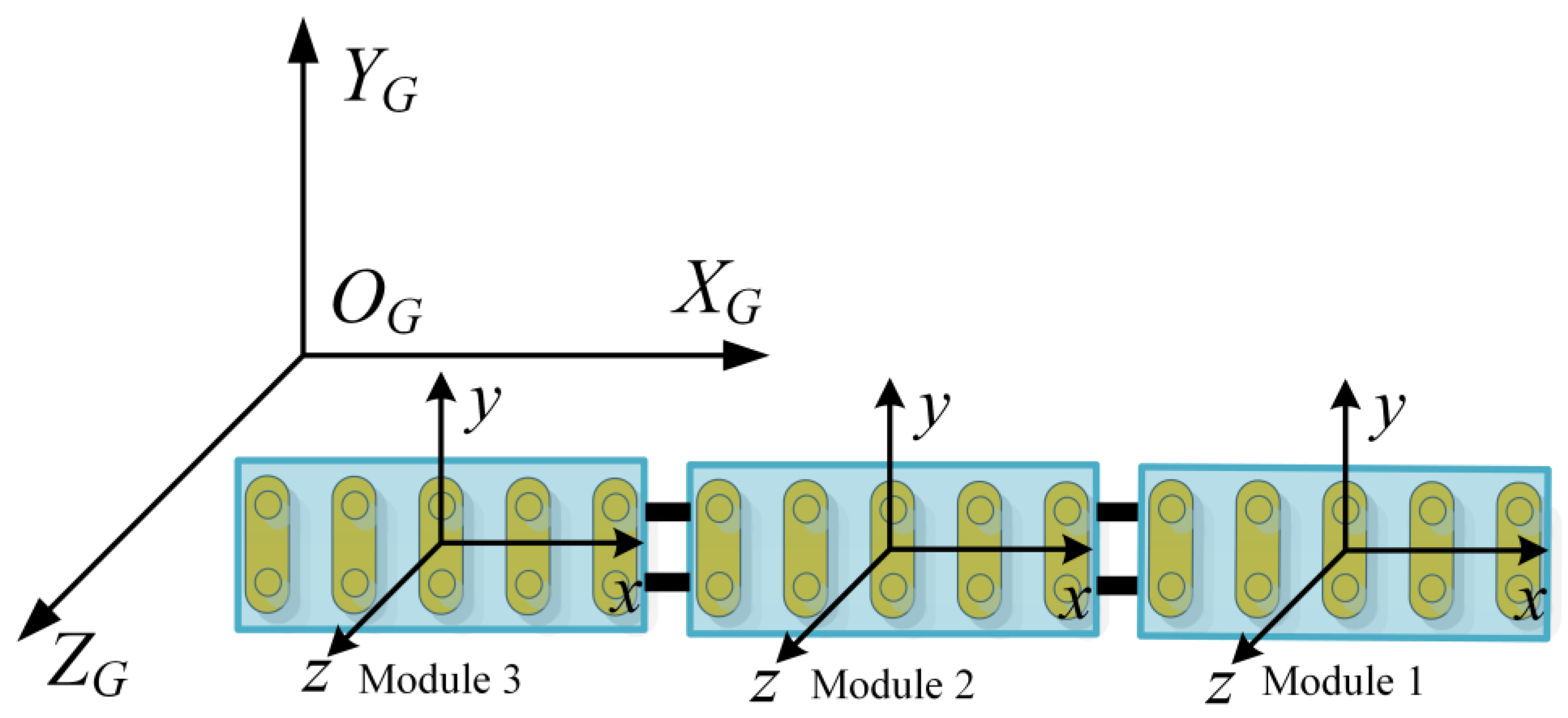
2. Mathematical Modeling of a VLFS
2.1. Hydrodynamic Model for VLFS Modules
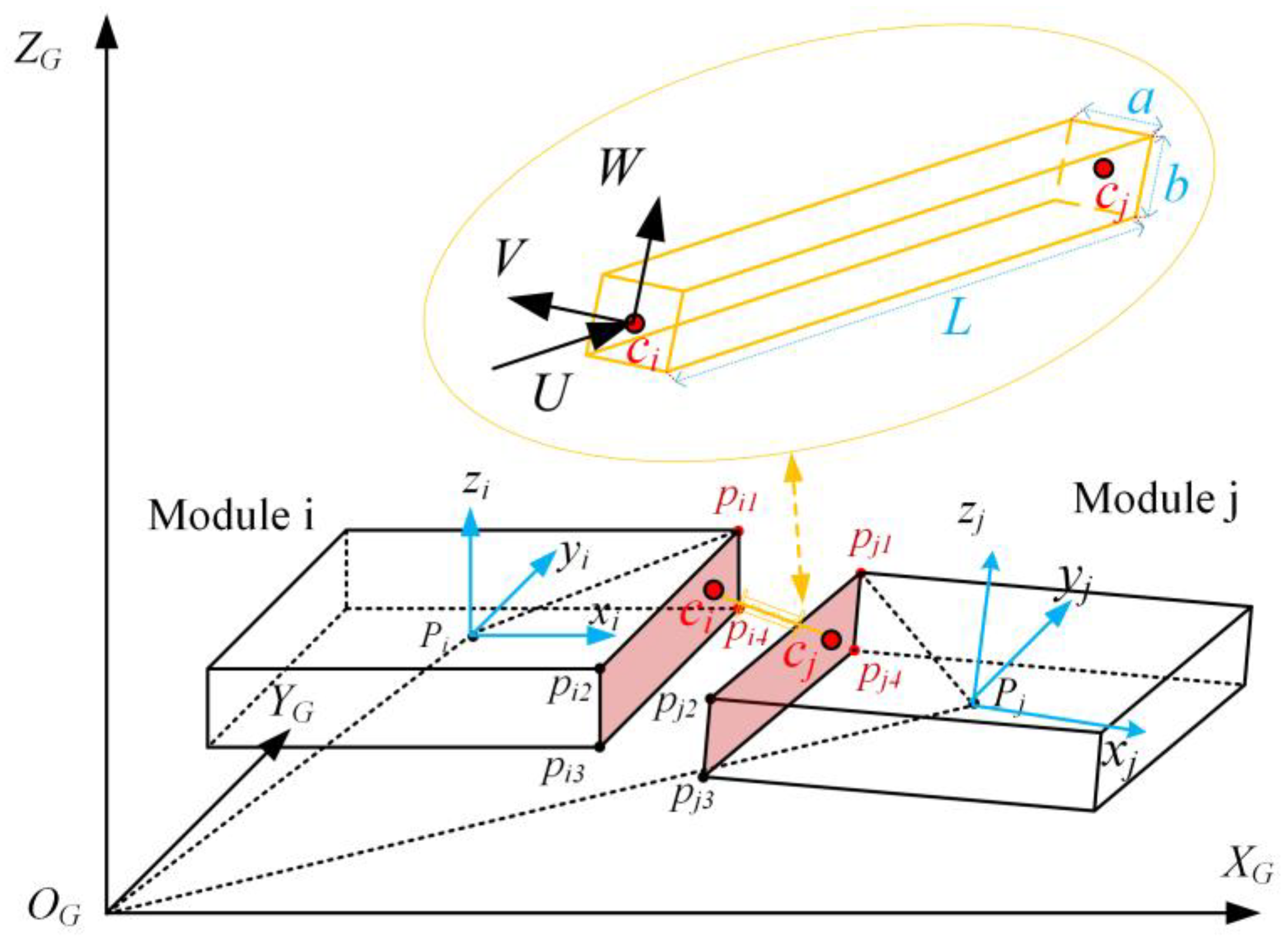
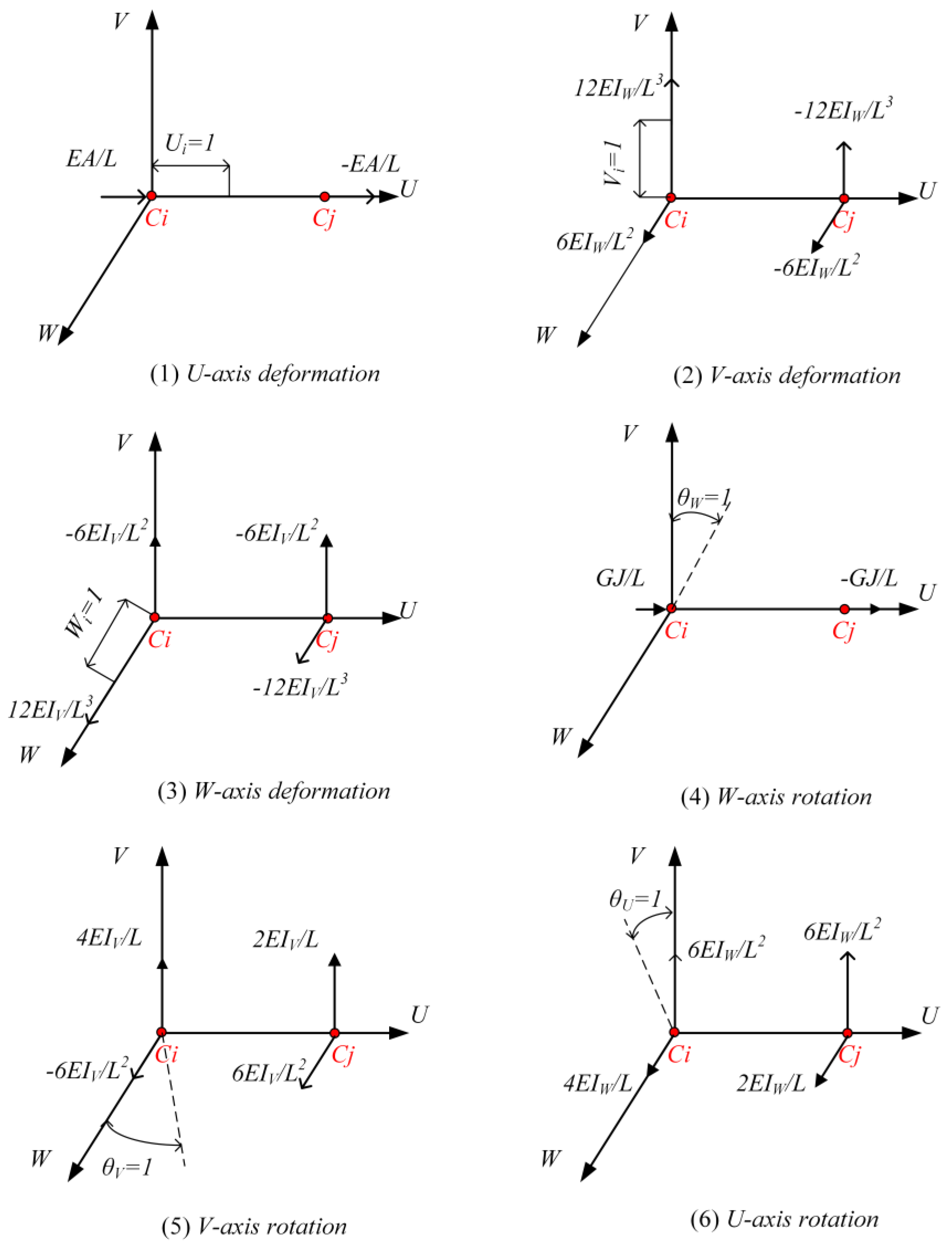
2.2. General Elastic Beam Model for VLFS Connectors
3. Validation of the Proposed Connector Mechanical Model
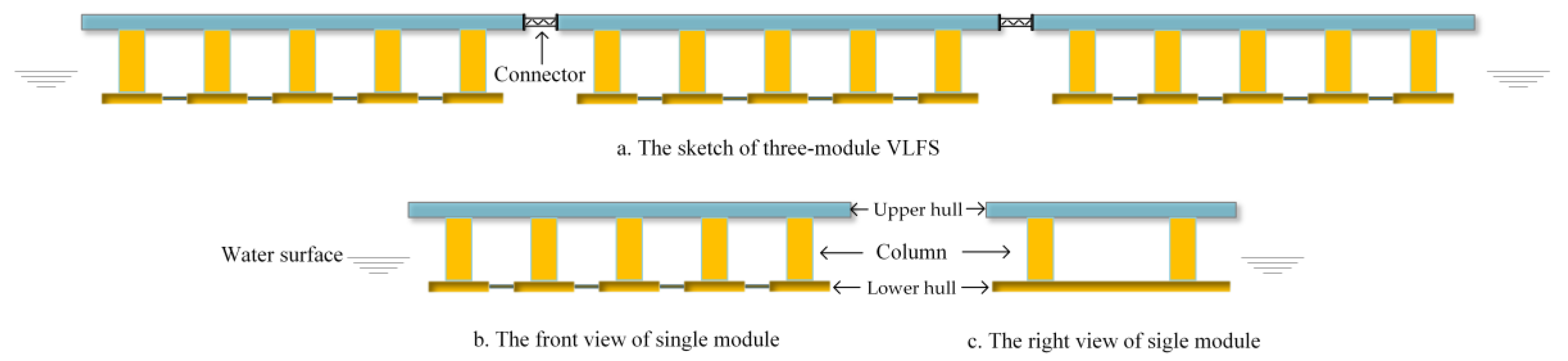
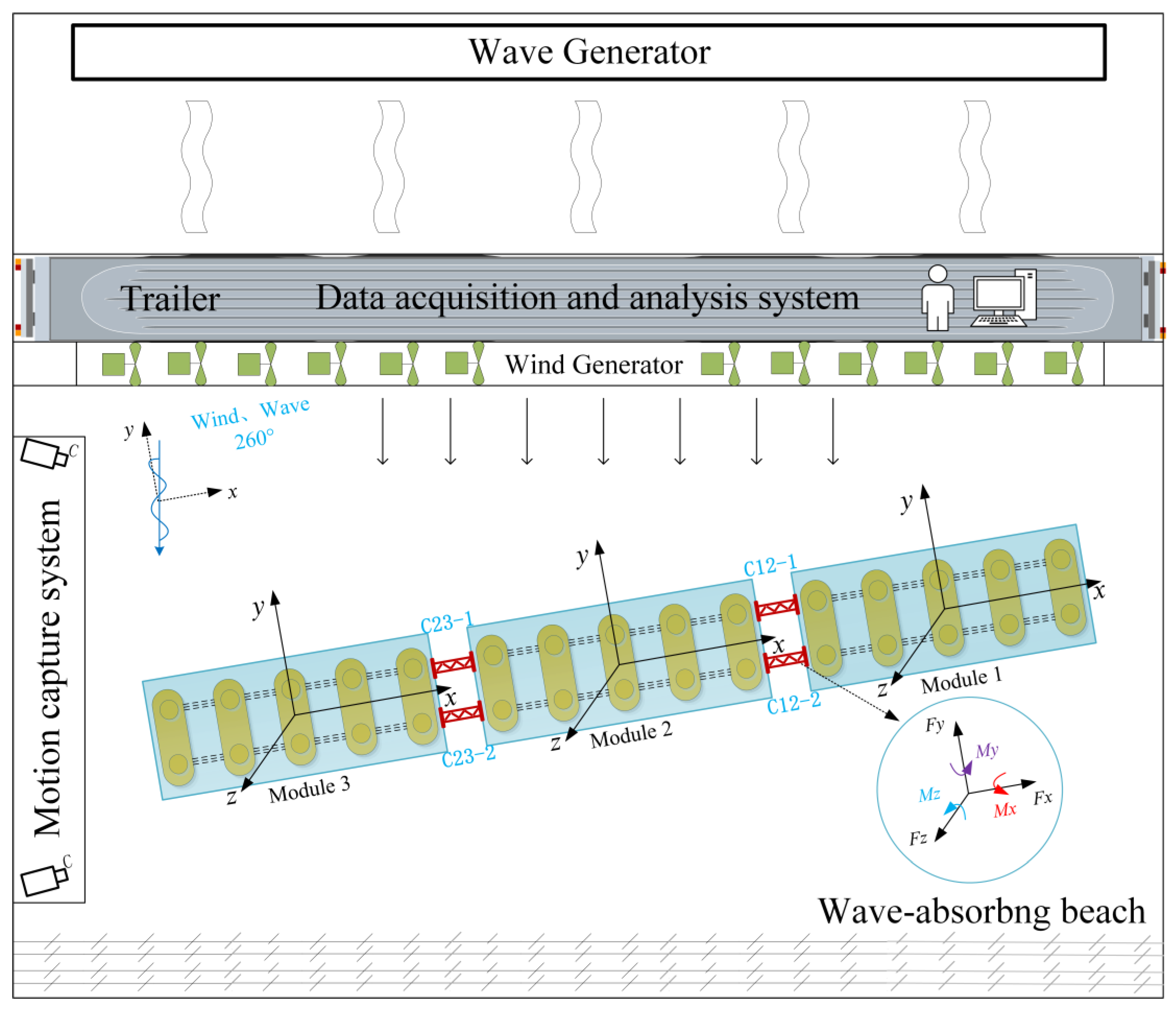
3.1. Parameters of the VLFS
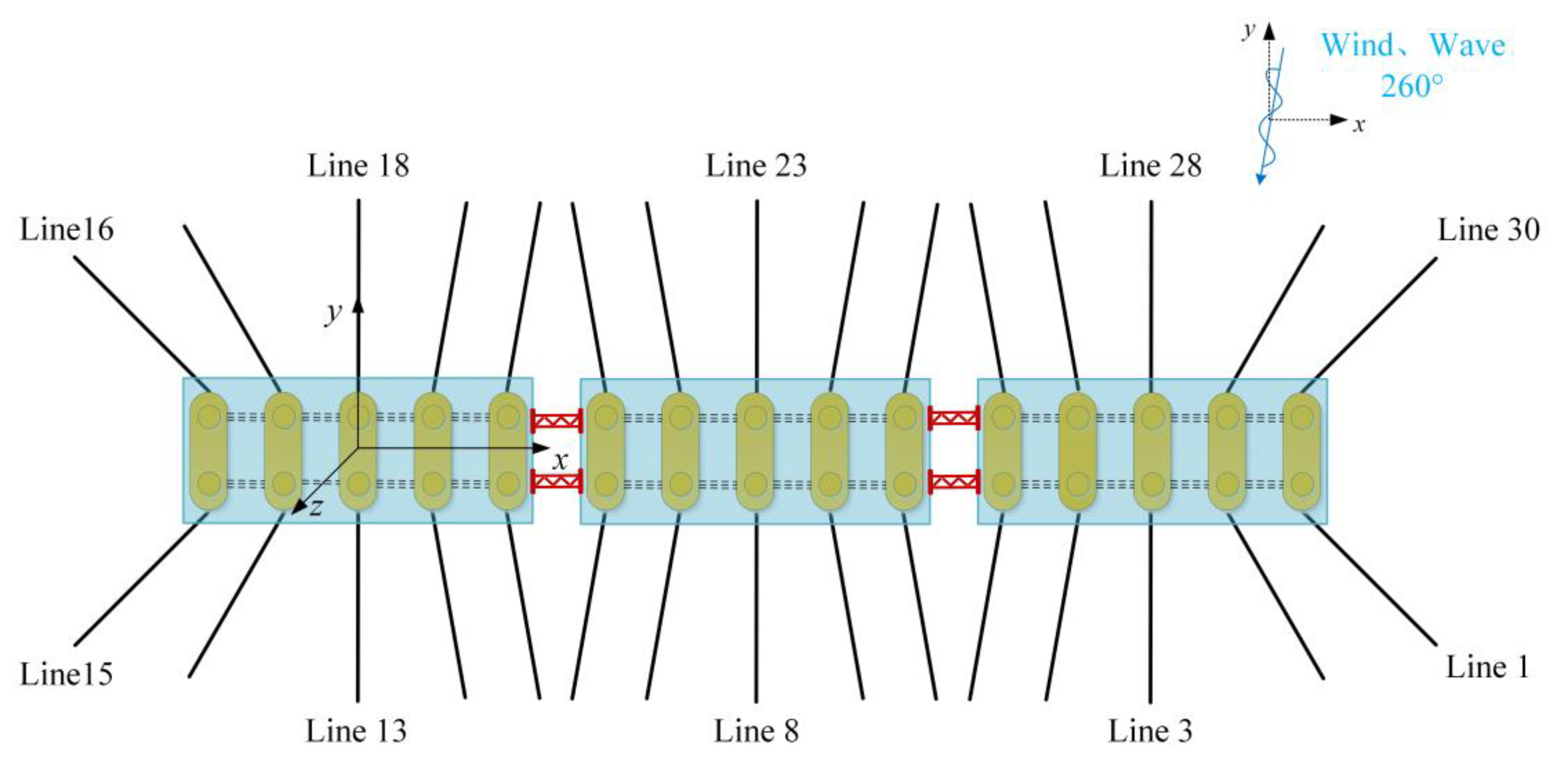
3.2. Setting of the Experimental Parameters
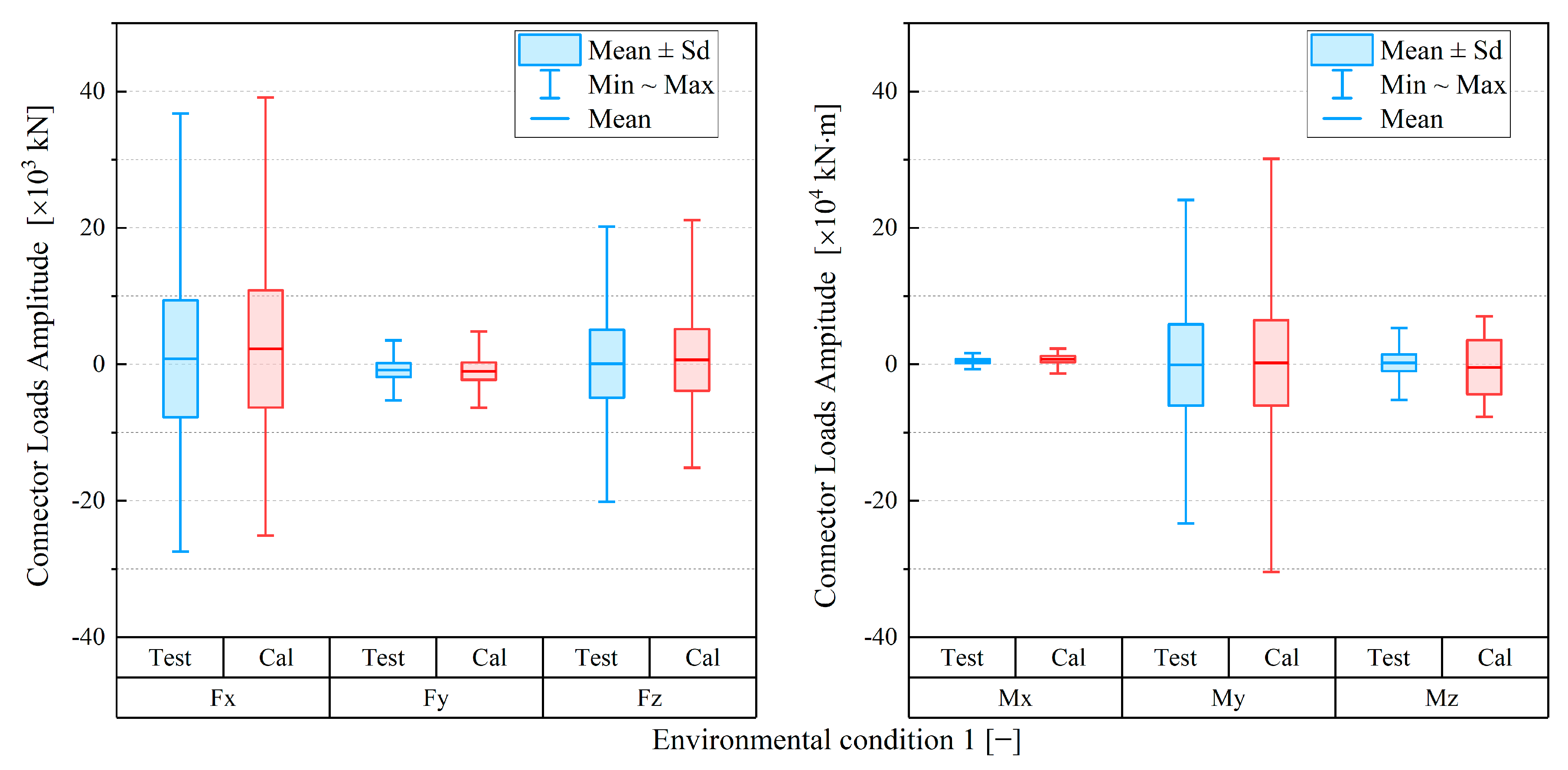
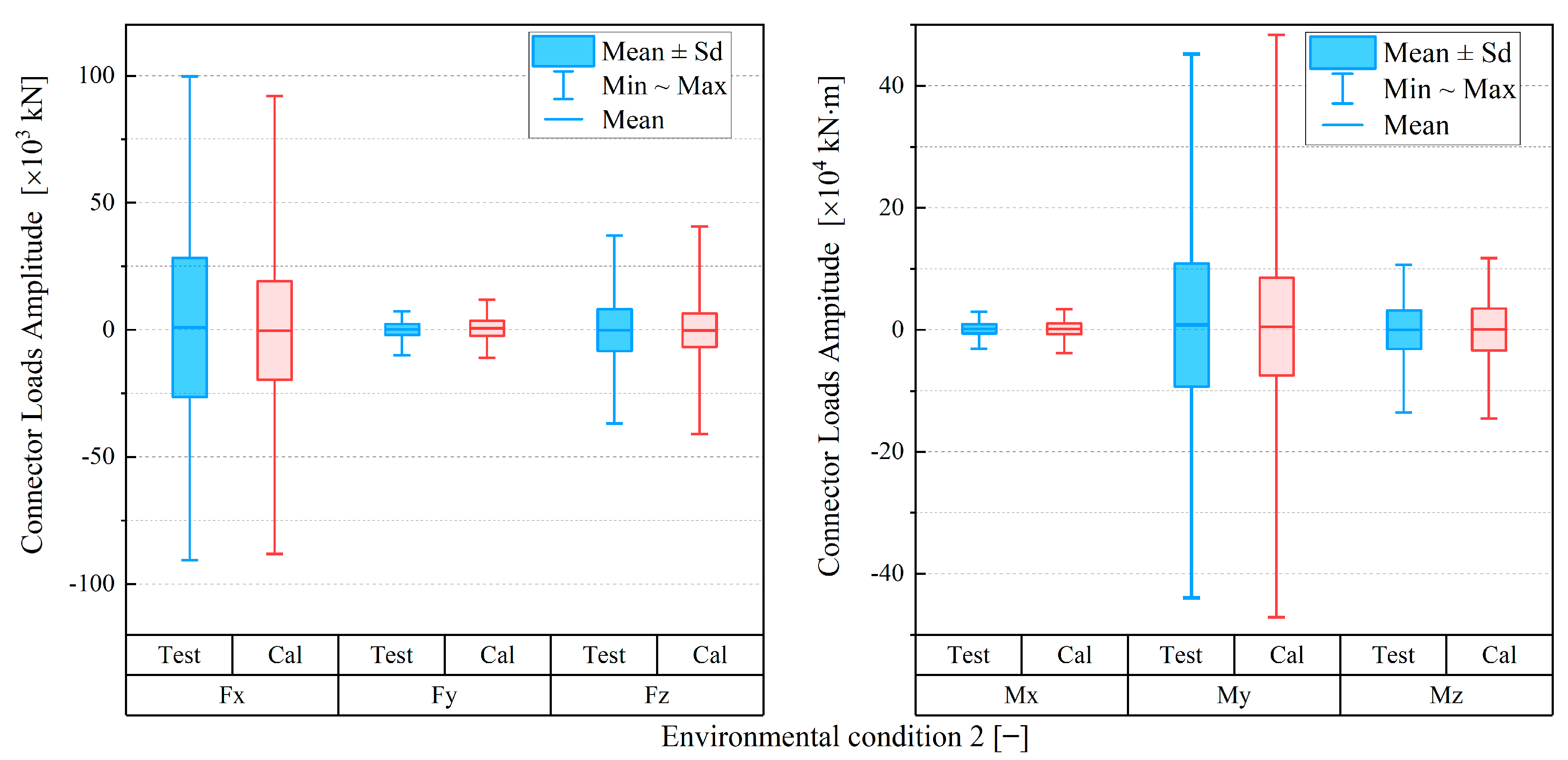
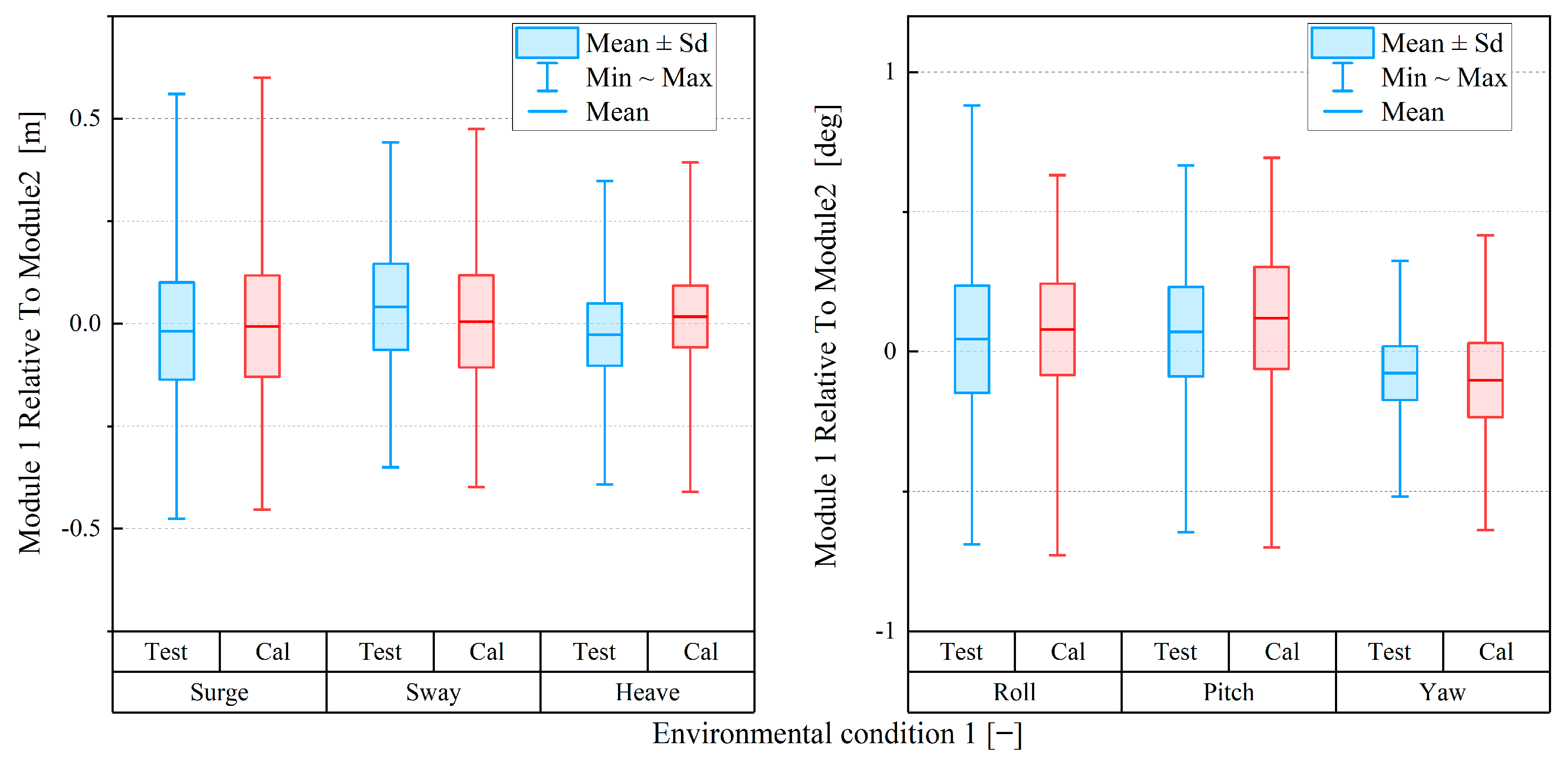
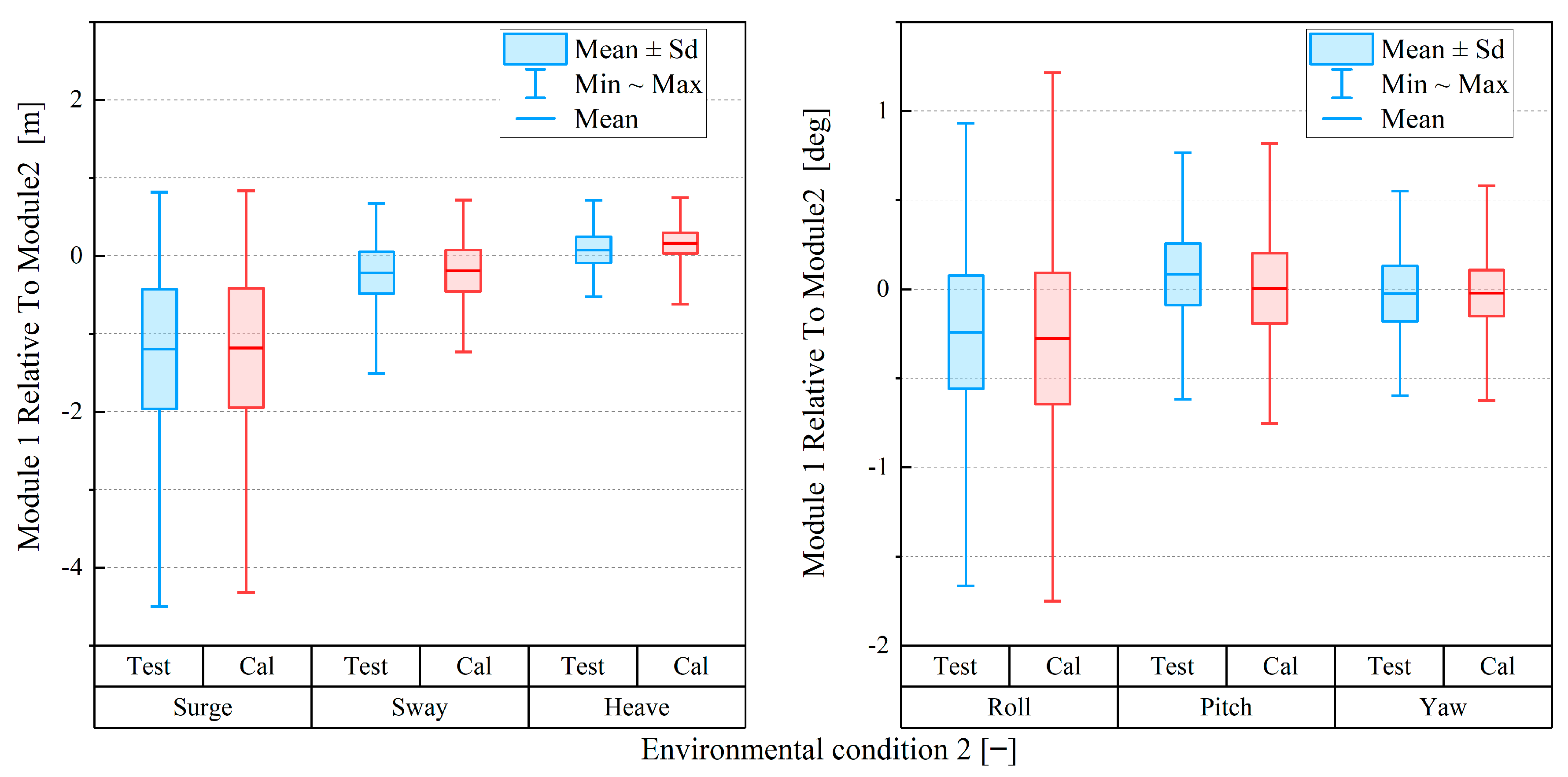
3.3. Verification Results
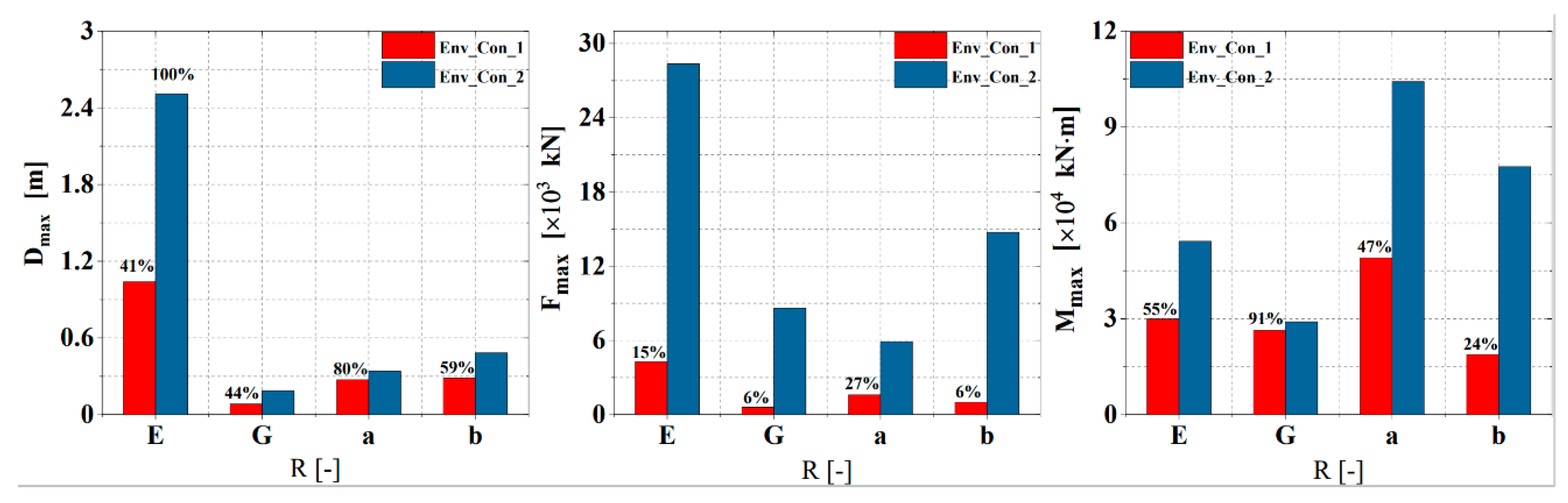
4. Connector Parameter Analysis and Optimization
4.1. VLFS Motion Normalization
4.2. Connector Load Normalization
4.3. Setting of the Orthogonal Analysis Strategy
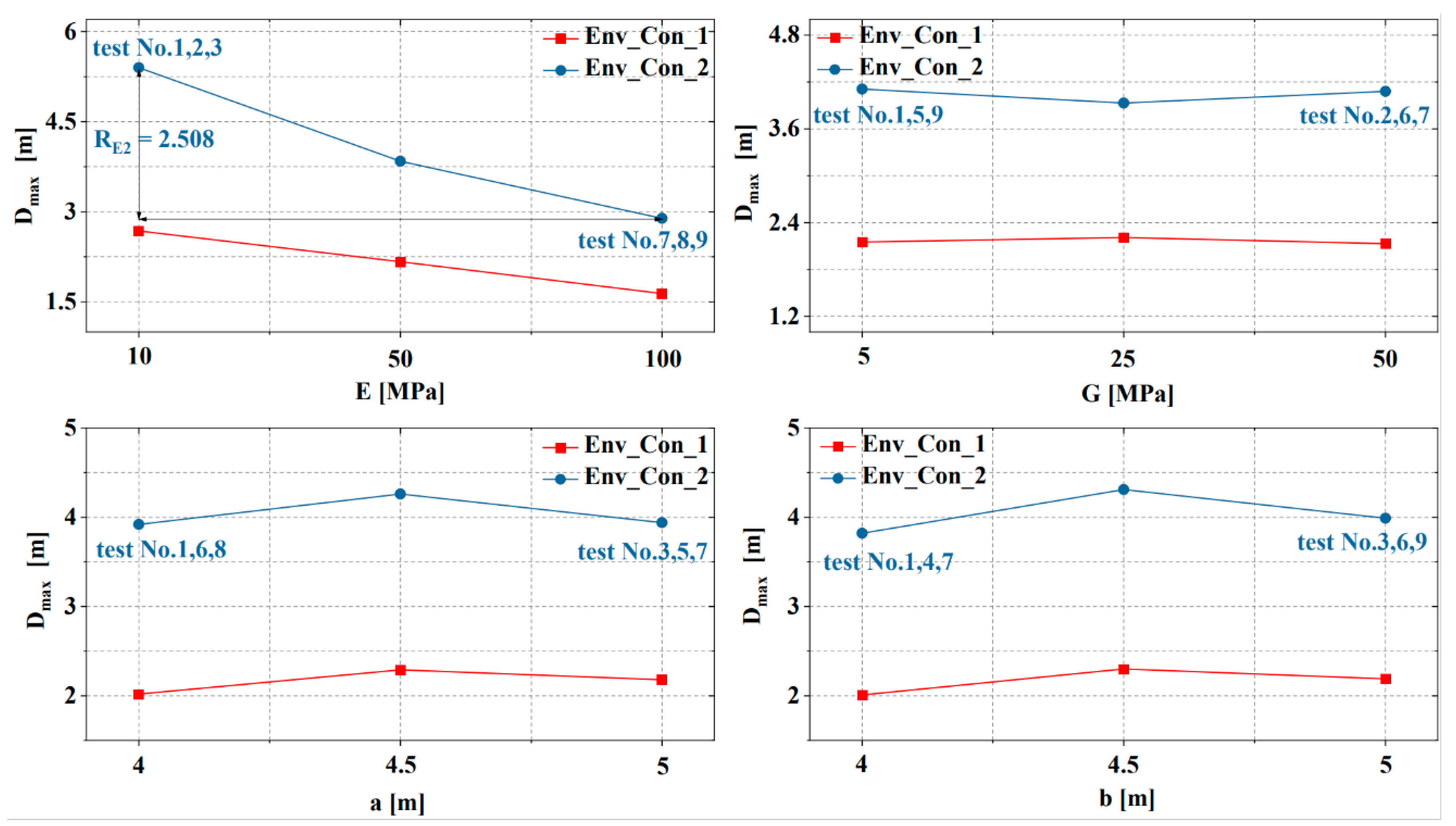
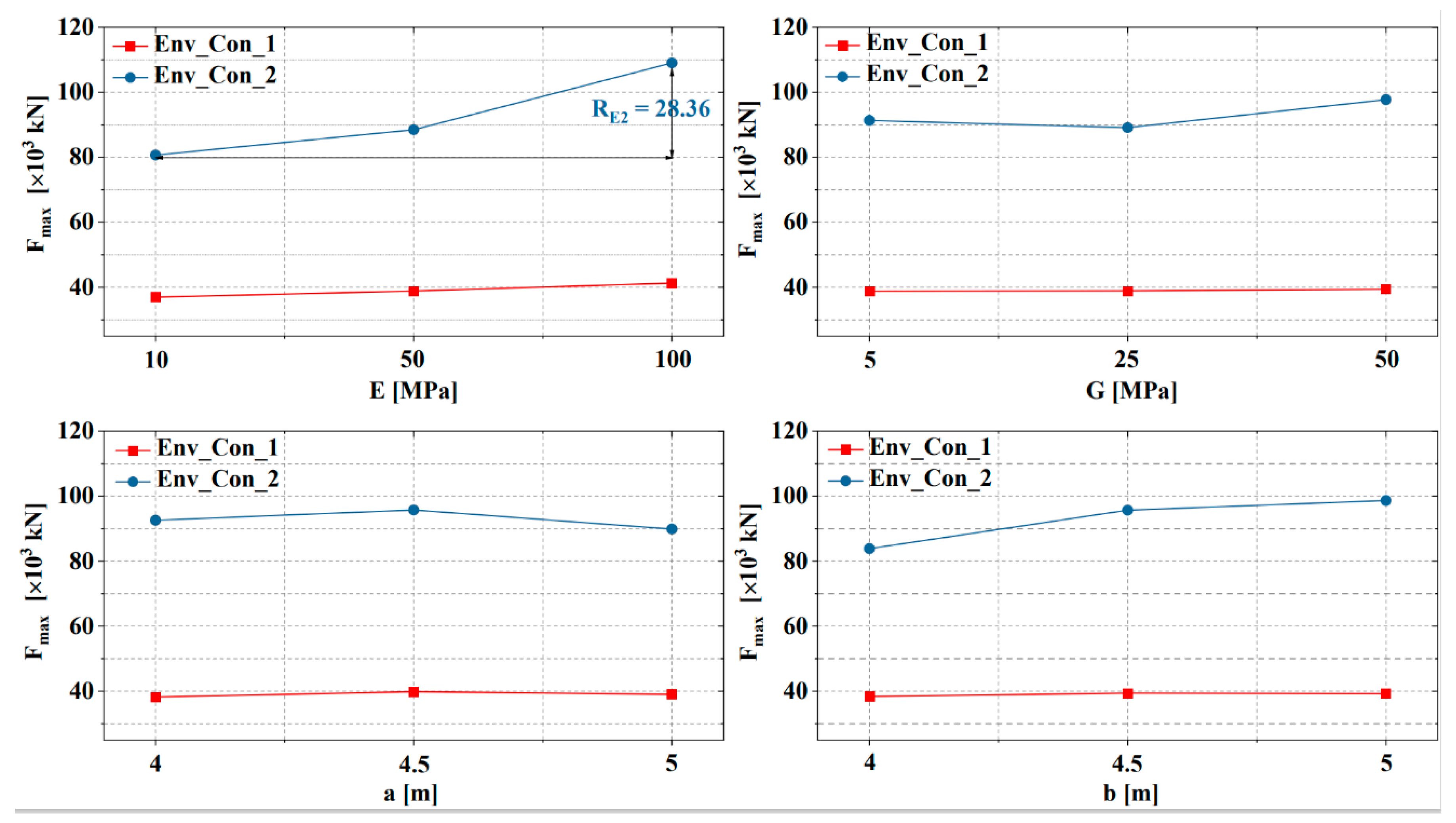
4.4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Armstrong, E.R. Sea Station. U.S. Patent 1,511,153, 7 October 1924. [Google Scholar]
- Armstrong, E.R. The seadrome project for transatlantic airways. Seadrome Pat. Wilmington 1943. [Google Scholar]
- Wu, C. Wave-induced connector loads and connector design considerations for the mobile offshore base. In Proceedings of the International Workshop on Very Large Floating Structures, SRI, Hayama, Japan, 25–28 November 1996. [Google Scholar]
- Pratt, J.A.; Priest, T.; Castaneda, C.J. Offshore Pioneers: Brown & Root and the History of Offshore Oil and Gas; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Figari, J.G. Floating Airport and Method of Its Construction. U.S. Patent 3,913,336, 21 October 1975. [Google Scholar]
- Maeda, H.; Masuda, K.; Miyajima, S.; Ikoma, T. Hydroelastic responses of pontoon type very large floating offshore structure. J. Soc. Nav. Archit. Jpn. 1995, 1995, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Wung, C.C.; Manetas, M.; Ying, J. Hydrodynamic computational tools validation against mobile offshore base (mob) model testing. In Proceedings of the 3rd 505 International Workshop on Very Large Floating Structures, Honolulu, HI, USA, 22–24 September 1999; pp. 538–545. [Google Scholar]
- Wang, D.; Ertekin, R.C.; Riggs, H.R. Three-dimensional hydroelastic response of a very large floating structure. Int. J. Offshore Polar Eng. 1991, 1, 307–316. [Google Scholar]
- Kim, B.W.; Hong, S.Y.; Kyoung, J.H.; Cho, S.K. Evaluation of bending moments and shear forces at unit connections of very large floating structures using hydroelastic and rigid body analyses. Ocean Eng. 2007, 34, 1668–1679. [Google Scholar] [CrossRef]
- Riggs, H.; Ertekin, R.; Mills, T. Impact of stiffness on the response of a multimodule mobile offshore base. Int. J. Offshore Polar Eng. 1999, 9, 126–133. [Google Scholar]
- Zhang, H.; Xu, D.; Xia, S.; Wu, Y. A new concept for the stability design of floating airport with multiple modules. Procedia IUTAM 2017, 22, 221–228. [Google Scholar] [CrossRef]
- Wu, Y.s.; Ding, J.; Tian, C.; Li, Z.w.; Ling, H.j.; Ma, X.z.; Gao, J.l. Numerical analysis and model tests of a three-module VLFS deployed near islands and reefs. J. Ocean Eng. Mar. Energy 2018, 4, 111–122. [Google Scholar] [CrossRef]
- Riggs, H.; Ertekin, R.; Mills, T. Characteristics of the wave response of mobile offshore bases. In Proceedings of the 18th International Conference on Offshore Mechanics and Arctic Engineering, St. John’s, NL, Canada, 11–16 July 1999; pp. 1–9. [Google Scholar]
- Riggs, H.; Ertekin, R. Response characteristics of serially connected semisubmersibles. J. Ship Res. 1999, 43, 229–240. [Google Scholar] [CrossRef]
- Xu, D.L.; Zhang, H.C.; Qi, E.R.; Hu, J.J.; Wu, Y.S. On study of nonlinear network dynamics of flexibly connected multi-module very large floating structures. In Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 1805–1814. [Google Scholar]
- Zhang, H.; Xu, D.; Lu, C.; Qi, E.; Hu, J.; Wu, Y. Amplitude death of a multi-module floating airport. Nonlinear Dyn. 2015, 79, 2385–2394. [Google Scholar] [CrossRef]
- Shi, Q.; Xu, D.; Zhang, H.; Zhao, H.; Wu, Y. Optimized stiffness combination of a flexible-base hinged connector for very large floating structures. Mar. Struct. 2018, 60, 151–164. [Google Scholar] [CrossRef]
- Michailides, C.; Loukogeorgaki, E.; Angelides, D.C. Response analysis and optimum configuration of a modular floating structure with flexible connectors. Appl. Ocean Res. 2013, 43, 112–130. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, H.; Liu, C.; Xu, D.; Shi, Q.; Liu, J.; Zou, W.; Wu, Y. Connector configuration effect on the dynamic characteristics of multi-modular floating structure. J. Ocean Eng. Sci. 2024, 9, 517–527. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Shen, K.; Lu, M.; Ren, X.; Cui, L.; Zhang, Y. A discrete-module-beam hydroelasticity method with finite element theory in analyzing VLFS in different engineering scenarios. Ocean Eng. 2024, 307, 118121. [Google Scholar]
- Chen, Y.; Wei, Z.; Gu, X.; Ni, X.; Lu, Y.; Geng, Y.; Ding, J.; Wang, S. Numerical and experimental studies on a 2-module VLFS with hinged connector. Ocean Eng. 2024, 310, 118552. [Google Scholar]
- Cummins, W.E. The impulse response functions snd ship motion. Schiffstechnik 1962, 9, 101–109. [Google Scholar]
- Cai, S.; Bao, G.; Ma, X.; Wu, W.; Bian, G.B.; Rodrigues, J.J.; de Albuquerque, V.H.C. Parameters optimization of the dust absorbing structure for photovoltaic panel cleaning robot based on orthogonal experiment method. J. Clean. Prod. 2019, 217, 724–731. [Google Scholar] [CrossRef]



| Term | Parameter | VLFS | Term | Parameter | VLFS |
|---|---|---|---|---|---|
| Upper hull | Length/m | 300 | Inertia radius | Roll/m | 28.47 |
| Width/m | 100 | Pitch/m | 86.31 | ||
| Height/m | 6 | Yaw/m | 89.77 | ||
| Lower hull | Length/m | 96 | Others | Draught/m | 12 |
| Width/m | 30 | Displacement/t | 93,614 | ||
| Height/m | 5 | Center of gravity/m | 12 | ||
| Columns | Cross-section | Circle | |||
| Radius/m | 9 | ||||
| Height/m | 16 |
| Connector | Young’s Modulus | Shear Modulus | Cross-Section | Length | |
|---|---|---|---|---|---|
| E/MPa | G/MPa | a/m | b/m | Lc/m | |
| - | 50 | 25 | 5 | 5 | 6 |
| No. | Significant Wave | Spectrum Peak | Wind |
|---|---|---|---|
| Height [m] | Period [s] | [m/s] | |
| 1 | 3 | 7.48 | 10 |
| 2 | 5 | 9.66 | 36 |
| No. | Young’s Modulus | Shear Modulus | Cross-Section | Length | |
|---|---|---|---|---|---|
| E [MPa] | G [MPa] | a [m] | b [m] | Lc [m] | |
| 1 | 10 | 5 | 4 | 4 | 6 |
| 2 | 10 | 50 | 4.5 | 4.5 | 6 |
| 3 | 10 | 25 | 5 | 5 | 6 |
| 4 | 50 | 25 | 4.5 | 4 | 6 |
| 5 | 50 | 5 | 5 | 4.5 | 6 |
| 6 | 50 | 50 | 4 | 5 | 6 |
| 7 | 100 | 50 | 5 | 4 | 6 |
| 8 | 100 | 25 | 4 | 4.5 | 6 |
| 9 | 100 | 5 | 4.5 | 5 | 6 |
| Connector | (m) | () | () | |||
|---|---|---|---|---|---|---|
| Env_Con_1 | Env_Con_2 | Env_Con_1 | Env_Con_2 | Env_Con_1 | Env_Con_2 | |
| 1 | 2.37 | 3.11 | 5.33 | 17.57 | 30.99 | 63.77 |
| 2 | 2.91 | 3.59 | 8.53 | 22.92 | 33.96 | 88.58 |
| 3 | 2.77 | 3.11 | 7.12 | 20.02 | 36.42 | 95.27 |
| 4 | 2.19 | 2.26 | 8.92 | 19.76 | 28.91 | 68.78 |
| 5 | 2.3 | 2.47 | 9.01 | 21.8 | 34.24 | 82.68 |
| 6 | 2.01 | 2.25 | 8.66 | 24.8 | 32.11 | 72.19 |
| 7 | 1.47 | 1.58 | 11.02 | 25.58 | 38.13 | 75.92 |
| 8 | 1.68 | 1.77 | 10.73 | 27.06 | 30.97 | 69.83 |
| 9 | 1.78 | 1.9 | 12.08 | 29.14 | 35.13 | 76.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, X.; Xu, S.; Wang, L. Analytical and Experimental Investigation of a Three-Module VLFS Connector Based on an Elastic Beam Model. J. Mar. Sci. Eng. 2025, 13, 1148. https://doi.org/10.3390/jmse13061148
Wang Y, Wang X, Xu S, Wang L. Analytical and Experimental Investigation of a Three-Module VLFS Connector Based on an Elastic Beam Model. Journal of Marine Science and Engineering. 2025; 13(6):1148. https://doi.org/10.3390/jmse13061148
Chicago/Turabian StyleWang, Yongheng, Xuefeng Wang, Shengwen Xu, and Lei Wang. 2025. "Analytical and Experimental Investigation of a Three-Module VLFS Connector Based on an Elastic Beam Model" Journal of Marine Science and Engineering 13, no. 6: 1148. https://doi.org/10.3390/jmse13061148
APA StyleWang, Y., Wang, X., Xu, S., & Wang, L. (2025). Analytical and Experimental Investigation of a Three-Module VLFS Connector Based on an Elastic Beam Model. Journal of Marine Science and Engineering, 13(6), 1148. https://doi.org/10.3390/jmse13061148






