Abstract
As a novel energy-saving and maneuvering device for ships, the gate rudder system (GRS) functions similarly to an accelerating duct. While providing additional thrust, its independently controllable rudder blades on either side of the propeller also enhance ship maneuverability. The GRS was first fully implemented on a container ship in Japan, demonstrating improved propulsion efficiency, fuel savings, and excellent performance in maneuvering, noise, and vibration reduction. In recent years, extensive research has been conducted on the hydrodynamic performance, acoustic characteristics, and energy-saving effects of the GRS. However, certain gaps remain in the research, such as a lack of systematic studies on optimal GRS design in the publicly available literature. Only Ahmet Yusuf Gurkan has investigated the sensitivity of propulsion performance to parameters such as rudder angle, rudder X-shift, rudder tip skewness, and blade tip chord ratio. Therefore, this study employs the JBC benchmark vessel and adopts a coupled CFD-CAESES approach to develop a matching optimization design for the GRS. The influence of geometric parameters—including GRS airfoil camber, maximum camber position, chord length, thickness, distance from the leading edge to the propeller plane, and the gap between the GRS and propeller blades—on ship propulsion performance is investigated. The sensitivity of these design variables to propulsion performance is analyzed, and the optimal GRS design is selected to predict and evaluate its energy-saving effects. This research establishes a rapid and comprehensive CFD-based optimization methodology for GRS matching design. The findings indicate that the gap between the GRS and propeller, the distance from the GRS to the stern, and the airfoil camber of the GRS significantly contribute to various performance responses. After GRS installation, the viscous pressure resistance of the JBC ship decreases, resulting in an 8.05% energy-saving effect at the designated speed.
1. Introduction
Since the onset of the 21st century, marine environmental pollution has become increasingly severe, and excessive energy consumption has emerged as a major obstacle to sustainable development. Improving ship energy efficiency to reduce carbon emissions can fundamentally address this issue. To this end, the International Maritime Organization (IMO) introduced regulations such as the Energy Efficiency Design Index (EEDI) and the Energy Efficiency Operational Indicator (EEOI) in 2008 [1]. To lower the EEDI, the maritime industry has explored various solutions, primarily focusing on reducing ship resistance, enhancing propulsion efficiency, or developing new energy sources. Among these, the most convenient approach is the installation of energy-saving devices (ESDs). In 2011, Japanese scholar Kuribayashi proposed a novel ESD—the gate rudder [2]. The gate rudder is an innovative ESD technology [3], consisting of a propeller flanked by two asymmetrically shaped rudders on either side. These rudder blades can be controlled independently. Compared to conventional rudder–propeller systems, the gate rudder offers superior maneuverability. Additionally, the two rudder blades encircle the propeller at the top and sides, creating a ducted effect that generates extra thrust during navigation, effectively replacing the additional drag caused by traditional rudders [4].
Upon its introduction, the gate rudder concept attracted significant research interest, leading to a series of numerical simulations, model tests, and full-scale studies. One of the pioneering studies was the NOAH (No More Artistic Hull) project by Japan’s National Maritime Research Institute (NMRI) [5]. This project revealed that the gate rudder has an energy-saving potential of 7–8%. For ships with high block coefficients (Cb) or low length-to-beam ratios, the energy-saving potential can reach 6–8%, with a return on investment of approximately one year. In 2013, Professor Sasaki first applied the gate rudder to a 6 m long ship with a block coefficient of 0.66 and conducted model tests. The results demonstrated an energy-saving effect exceeding 10%. In 2018, Sasaki et al. investigated the propulsion efficiency of ships equipped with the gate rudder system [4]. By analyzing model tests, CFD simulations, and full-scale data from two container ships, they found that a well-designed gate rudder system could significantly improve the effective wake fraction compared to conventional rudder–propeller configurations. The gate rudder alters the flow field around the stern, optimizing the wake distribution on the propeller plane.
In November 2017, the world’s first gate rudder system was installed on the 2400 GT container ship “Shigenobu” [6]. Sasaki et al. conducted full-scale trials in Japan’s Seto Inland Sea, comparing the ship’s performance with its sister ship “Sakura”, which was equipped with a conventional rudder. The results showed that “Shigenobu” achieved approximately 14% better energy efficiency than “Sakura”. Notably, “Shigenobu” exhibited significantly reduced stern wake, warranting further research into the gate rudder’s impact on wake characteristics [7].
In 2019, Sasaki and colleagues conducted a comprehensive reanalysis of voyage logs from the sister vessels “Shigenobu” and “Sakura” dating back to November 2017. Operating under nearly identical conditions along Japan’s northeastern coastal routes, these ships provided comparative datasets encompassing critical parameters such as speed, fuel consumption, and power output. The analysis demonstrated that “Shigenobu” not only maintained superior performance in calm conditions but achieved remarkable efficiency gains exceeding 30% during adverse weather operations, highlighting the system’s exceptional environmental adaptability.
Recently, research on gate rudder systems has continued to advance, with significant focus on numerical simulations of hydrodynamic performance. A 2020 study by Tacar Z et al. employed RANS-based CFD analysis using two different scale models and full-scale data from the same container ship to investigate the gate rudder’s impact on vessel performance [4]. Their numerical simulations utilizing the SST k-ω turbulence model demonstrated reasonable accuracy in predicting ship resistance and effective power. Compared to conventional rudder systems, vessels equipped with gate rudders showed substantially reduced brake power requirements, confirming the system’s potential as an effective energy-saving device for reducing fuel consumption and GHG emissions. Further investigations by Zhai Shu-cheng et al. in 2022 employed CFD methods to analyze hydrodynamic characteristics including the lift–drag properties of the rudder itself, hull resistance, and propeller performance [8]. Their findings revealed that the gate rudder’s flow acceleration effect caused a 1.8% increase in hull resistance due to pressure reduction at the stern, while simultaneously reducing rudder resistance by 2.7% through thrust generation. The accelerated flow also led to decreased propeller loading under identical rotation speeds, with thrust and torque reductions of 17.7% and 9.8%, respectively. The 2023 GATERS project study by Köksal et al. pioneered power extrapolation methods for retrofitted vessels with gate rudder systems, incorporating analysis of hull aging, surface roughness, and biofouling effects. This research addressed a critical gap in retrofit applications, demonstrating how hull degradation can significantly diminish the gate rudder’s energy-saving performance and emphasizing the need for separate consideration of these factors in power predictions. Wout Opdam’s 2024 [9] investigation of gate rudder hydrodynamics during straight sailing and drifting conditions revealed that when operating at drift angles, one rudder blade generates positive thrust due to the angle of attack with incoming flow, which is typically counterbalanced by increased drag on the opposite blade. That same year, Köksal et al. conducted model tests under the EU H2020 GATERS project to evaluate hull–propeller–gate rudder interactions in both calm water and oblique wave conditions. Their comparative analysis with conventional rudder systems confirmed the gate rudder’s maintenance of efficiency in complex seaways, providing crucial experimental evidence for energy-efficient design in varied operating conditions.
Research on gate rudder systems has also extended to scale-effect investigations, where significant discrepancies between full-scale computational results and model-scale test predictions have revealed substantial scaling effects unique to this configuration. A 2019 study by Noriyuki Sasaki et al. identified that the gate rudder’s distinctive stern arrangement leads to more pronounced scaling effects compared to conventional rudder systems [10]. At model scale, the relatively low Reynolds numbers result in predominantly laminar flow characteristics around the gate rudder assembly, causing strong adverse effects on the lift and drag coefficients of the rudder blades. Their analysis demonstrated that the scaling behavior of wake flow differs fundamentally between gate rudder-equipped vessels and those with conventional systems, necessitating the decomposition of measured propeller advance speed into two components with distinct scaling methodologies. Subsequent research in 2021 by Sasaki and Atlar revealed that the gate rudder blades’ displacement effect increases pressure near the stern, while propeller action modifies this hydrodynamic interaction [11,12]. The resulting stern pressure recovery reduces the pressure drop induced by propeller operation—a phenomenon directly linked to thrust deduction. This interaction enables significant minimization of the thrust deduction factor. Continuing this line of inquiry, Sasaki’s 2023 work further established that the gate rudder’s thrust deduction factor exhibits marked scale effects [13], confirming that model tests failing to account for scaling phenomena would yield inaccurate performance predictions. A 2022 numerical analysis by Md Daluar Hussain systematically compared hydrodynamic performance across three scales including full dimensions, demonstrating that full-scale gate rudders generate substantially greater thrust than scaled models. These collective findings underscore the system’s capacity for enhanced thrust generation and superior propulsive performance at operational scales.
The acoustic performance characteristics of gate rudder systems have also attracted significant research attention. A 2023 investigation by Özsayan et al. employed combined experimental and numerical approaches to systematically evaluate the system’s effects on cavitation and underwater radiated noise (URN), with comprehensive comparisons against conventional rudder systems (CRSs). Their results demonstrated that the gate rudder configuration achieves remarkable 10 dB reductions in high-frequency-URN spectra, primarily attributed to optimized propeller loading and cavitation control through the gate rudder’s unique flow conditioning mechanism. Building upon these findings, a 2024 study by Santić et al. conducted under the EU H2020 GATERS project implemented multi-dimensional testing protocols incorporating particle image velocimetry (PIV), cavitation observation, and acoustic measurements. This rigorous experimental framework successfully elucidated the coupled hydrodynamic–acoustic mechanisms of gate rudder operation while providing scientifically validated performance benchmarks against conventional systems, thereby establishing crucial technical foundations for engineering applications.
Current research prioritizes hydrodynamic performance prediction, with limited focus on GRS design parameters. In 2022, Ahmet Yusuf Gurkan [14] optimized blade angles and propeller–rudder spacing, identifying rudder angle as the most sensitive parameter. In 2024, Sasaki advocated redesigning hull forms around optimized GRS configurations. Building upon previous research, this study conducts a comprehensive optimization of gate rudder parameters including airfoil camber, maximum camber position, chord length, thickness, distance from the leading edge to propeller plane, and rudder–propeller clearance. Through parametric modeling and sensitivity analysis, we determine the optimal configuration and evaluate its hydrodynamic performance, flow-field effects, and energy-saving potential to establish a foundation for future gate rudder research.
2. Research Object
This study employs a scaled model of the Japan Bulk Carrier (JBC), one of the standard ship models provided at the 2015 Tokyo CFD Workshop, which included comprehensive resistance and self-propulsion test data [15]. The principal dimensions of the JBC hull and MP. 687 propeller are summarized in Table 1 and Table 2, respectively.

Table 1.
Principal particulars of JBC ship model.

Table 2.
Principal geometric parameters of MP. 687 propeller.
The numerical simulation conditions in this study were determined based on the experimental test conditions provided by the 2015 Tokyo Workshop on Naval Hydrodynamics. Table 3 presents the test conditions for the resistance tests of the JBC ship model.

Table 3.
Test conditions for calm water resistance tests.
3. Numerical Calculation Method and Verification
Numerical calculations were performed for the resistance of the JBC ship model, the open-water performance of the MP687 propeller, and the self-propelled condition of the hull–propeller system. For the resistance calculation, since the JBC ship model is symmetric about the centerline plane, only the port side of the hull was calculated to save computational resources and improve efficiency. The size of the computational domain is shown in Figure 1, with dimensions in the length, width, and height directions as follows: −2.5 < X/Lpp < 2, 0 < Y/Lpp < 2.5, −2 < Z/Lpp < 1, where Lpp is the length between perpendiculars. For the physical model, the SST k-ω turbulence model was selected. The VOF method was used to capture the free surface, and the VOF wave damping option was activated to eliminate reflected waves caused by boundaries. The time step Δt was set to Lpp/v. For boundary conditions, the inlet, top boundary, bottom boundary, and side boundaries were set as velocity inlets with a velocity value of 1.179 m/s; the outlet was set as a pressure outlet with a pressure value of 0 Pa; the ship’s centerplane was set as a symmetry plane; and all other boundaries were set as walls. For the self-propulsion simulation, since the model no longer had symmetry, a full-hull calculation was required. The computational domain remained the same as in the resistance simulation, except that the symmetry plane was removed. For the resistance calculation, the base mesh size on the hull surface was set to 0.09 m, and the Y+ value on the hull was set to 60. Volume control was used to locally refine the free surface, Kelvin wake, hull feature lines, and areas with high curvature changes (bow and stern). For the propeller open-water performance calculation, the base surface grid size was set to 0.09135 m (0.45D), and local refinement was applied to the hub and blade tip regions. The propeller boundary layer used prism layer grids with 8 prism layers, and the dimensionless thickness y+ of the first near-wall layer on the propeller blades was set to 1. For the self-propulsion calculation, the same grid generation strategy was applied to both the hull and propeller. The grid distribution in different regions is shown in Figure 2. The final mesh consisted of approximately 7.46 million cells in the stationary domain, 0.38 million cells in the rotating domain, and a total of approximately 7.84 million cells in the entire computational domain.

Figure 1.
Computational domain for self-propulsion numerical simulation.
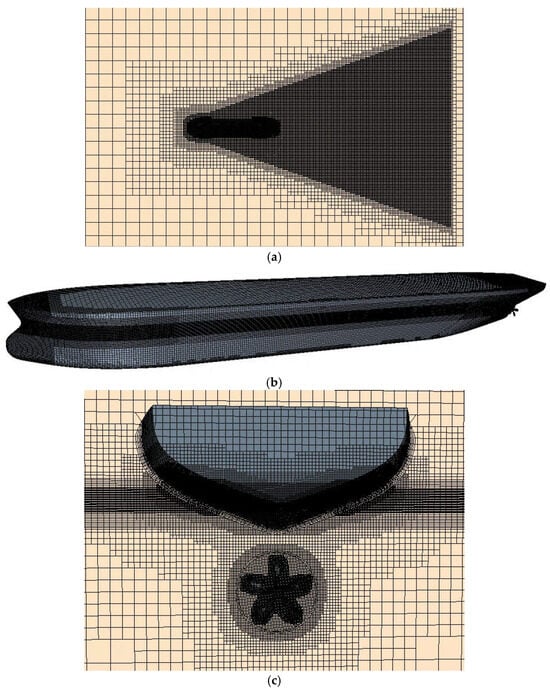
Figure 2.
Mesh distribution in different computational domains: (a) free-surface mesh; (b) hull-surface mesh; (c) boundary-layer mesh.
To verify the accuracy of the numerical method, three sets of grids with a grid growth rate of were generated for the ship model resistance calculation and propeller open-water performance calculation, respectively, and grid convergence verification analysis was conducted. The calculation results are shown in Table 4 and Table 5. From Table 4 and Table 5, it can be seen that the fluctuation ranges of the resistance calculation values and propeller open-water performance calculation values for the three sets of grids are very small, indicating that this numerical method and grid generation strategy can effectively predict the resistance of the JBC ship model and the open-water performance of the MP. 687 propeller. Considering the computational cost of the grids, the medium grid density was selected for subsequent research. Table 6 presents a comparison between the experimental data of JBC ship resistance and simulation results under the medium grid scale. The error of the total resistance coefficient is 0.793%, and the error of the residual resistance coefficient is 3.01%, both within acceptable error ranges. Figure 3 shows the open-water curves of the propeller calculated with medium grid density. It can be observed that the overall error between the simulation results and experimental values is controlled within 5%.

Table 4.
Resistance calculation results based on three grid sets.

Table 5.
Hydrodynamic parameter results of propeller under three grid sets (J = 0.5).

Table 6.
Comparison between experimental data and simulation results for JBC ship model resistance.
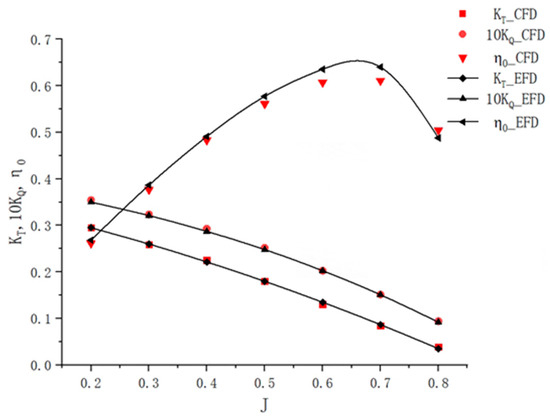
Figure 3.
Comparison between numerical and experimental results of propeller open-water performance.
The self-propulsion numerical simulation of the JBC hull–propeller system was conducted based on the calculation conditions provided by the 2015 Tokyo Workshop on Naval Hydrodynamics. The computational results were compared with the experimental data published by the workshop to verify the reliability of the present numerical method. Table 7 presents the numerical results of the JBC ship model’s resistance, thrust deduction force, propeller thrust, and torque in calm water, along with the corresponding model test results. The comparison shows that the simulation errors for ship model resistance, thrust deduction force, propeller thrust, and torque are all within 5%.

Table 7.
Comparison between numerical and experimental results for JBC ship model self-propulsion.
4. Gate Rudder Matching Optimization Design
4.1. Fully Parametric Modeling of Gate Rudder
The matching optimization design of the gate rudder for the target ship and propeller was conducted using the coupled CAESES 5 and Simcenter STAR-CCM+ 2020.3 (15.06.007-R8) software platform. For the complete hull–propeller–rudder system, both the hull and propeller were imported as standard models, requiring only the gate rudder to be fully parametrically modeled in CAESES. The workflow for the fully parametric modeling of the gate rudder is shown in Figure 4. The process begins with importing the JBC ship model and MP. 687 propeller to determine the modeling position of the gate rudder, followed by defining the 2D airfoil profile of the rudder blades. Then, parametric curves describing the radial distribution of the 2D blade sections are defined, and finally, the 3D geometric model of the gate rudder is generated.
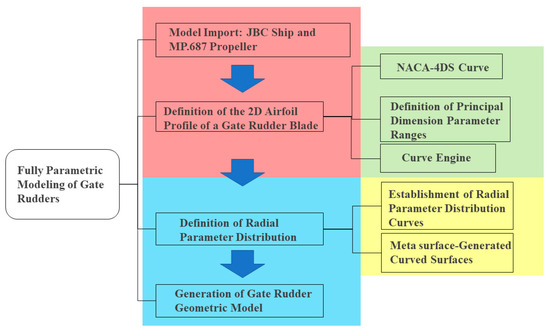
Figure 4.
Gate rudder parametric modeling process.
The detailed modeling process is as follows:
- (1)
- First, as is vividly shown in Figure 5, import the geometric models of the JBC ship and MP. 687 propeller to determine the modeling position of the gate rudder.
 Figure 5. Hull and propeller geometric model in CAESES.
Figure 5. Hull and propeller geometric model in CAESES. - (2)
- Use the NACA-4DS Curve in CAESES to generate the Curve Engine for this asymmetric airfoil, Figure 6 shows the 2D airfoil profile of the gate rudder.
 Figure 6. Definition of the 2D airfoil profile for the gate rudder blade.
Figure 6. Definition of the 2D airfoil profile for the gate rudder blade. - (3)
- After establishing the characteristic curves of the airfoil profile, draw the distribution curves of the characteristic parameters according to their radial distribution. Four characteristic parameters are defined: chord length, thickness, camber, and maximum camber position (camber pos). Their distribution curves are established to control the radial variation of the airfoil. Then, create the radial curves of the gate rudder to control the extrusion path of the airfoil, Figure 7 illustrates the characteristic parameter distribution curves of the gate rudder.
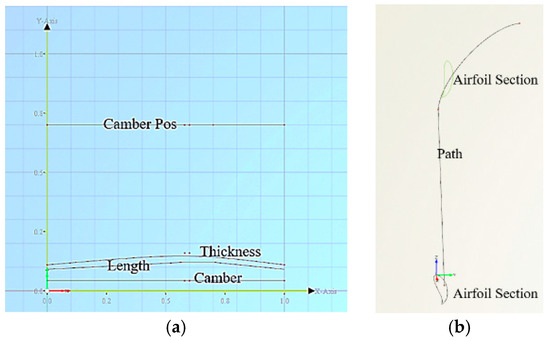 Figure 7. Distribution curves of characteristic parameters for the gate rudder. (a) Distribution curves of characteristic parameters. Four characteristic parameters are defined: chord length, thickness, camber, and maximum camber position (camber pos). (b) Path curves, with the radial curves of the gate rudder created to control the extrusion path of the airfoil.
Figure 7. Distribution curves of characteristic parameters for the gate rudder. (a) Distribution curves of characteristic parameters. Four characteristic parameters are defined: chord length, thickness, camber, and maximum camber position (camber pos). (b) Path curves, with the radial curves of the gate rudder created to control the extrusion path of the airfoil. - (4)
- Combine the Meta Surface, Curve Engine, and BRep functions to achieve the radial distribution of the 2D airfoil profile. Furthermore, establish the enclosed surface of the gate rudder geometric model, as shown in Figure 8, to generate a complete parametric gate rudder model. Figure 9 shows the arrangement of the gate rudder at the stern of the JBC ship.
 Figure 8. Fully parametric model of the gate rudder.
Figure 8. Fully parametric model of the gate rudder. Figure 9. Arrangement of the gate rudder at the stern.
Figure 9. Arrangement of the gate rudder at the stern.
4.2. Experimental Design and Parameter Optimization
The Design of Experiments (DOE) serves as a methodology to develop appropriate schemes based on predetermined objectives, providing a rational and effective approach for acquiring information and data, with extensive applications in scientific research and engineering. Currently, the most widely used experimental design method in CAESES software is the Sobol sequence [16].
This section selects six design variables for the matching optimization of the gate rudder: the chord length, thickness, camber, and maximum camber position of the 2D airfoil profile, the fore–aft position of the gate rudder relative to the propeller, and the clearance between the gate rudder and propeller blades. This study primarily considers these six parameters, ensuring that the gate rudder blade profile forms an asymmetric airfoil and that the gate rudder size is approximately 120–140% of the propeller diameter. The selected variables and their variation ranges are presented in Table 8.

Table 8.
Variables and their variation ranges.
After determining the experimental design method, variables, and their ranges, the variable-parameter simulation for the gate rudder can be conducted. This study employs a coupled approach with CAESES 5 and Simcenter STAR-CCM+ 2020.3 (15.06.007-R8) software. The self-propulsion condition for the JBC ship has been previously specified with a speed of v = 1.179 m/s, Fr = 0.142, and a propeller rotation rate of 7.8 rps. Therefore, this section performs variable-parameter self-propulsion calculations for the integrated JBC ship–MP. 687 propeller–gate rudder system based on the self-propulsion setup of the JBC hull–propeller system.
The number of samples for the experimental design should be appropriately selected based on the number of design variables and the complexity of the problem [17]. The sample size selection follows Equation (1), which recommends the number of sample points when the number of design variables ranges from 5 to 10:
where N is the number of samples and n is the number of design variables.
This study involves six design variables. To enhance the reliability of subsequent parameter sensitivity analysis, the sample size was increased to appropriately 40. Upon completion of the calculations, 32 valid samples were obtained. The parameter values for each case are listed in Table 9.

Table 9.
Sample parameters.
To more intuitively display the distribution of parameters such as hull resistance, propeller thrust, propeller torque, and thrust generated by the gate rudder across the samples, scatter plots are presented in Figure 10. The plots demonstrate that after installing the gate rudder, the total hull resistance decreases, and the gate rudder generates additional thrust. Since the gate rudder consists of two asymmetric airfoil rudders positioned on either side of the propeller, creating a ducted effect, the thrust produced by the propeller decreases.
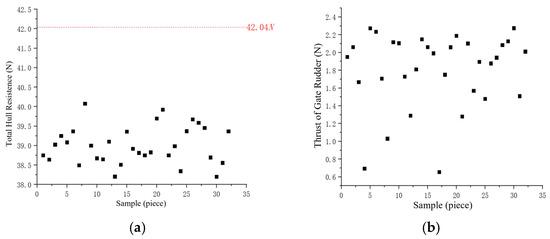
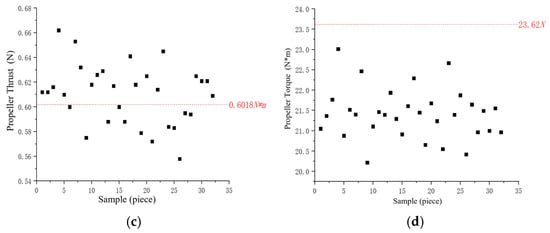
Figure 10.
Sample point distribution. (a) Total hull resistance. (b) Thrust generated by gate rudder. (c) Propeller thrust. (d) Propeller torque.
Typically, the energy-saving effect of ducted energy-saving devices is evaluated based on the hull’s utilization of propeller power, using one of two methods: propulsion efficiency assessment or propeller power assessment. The latter method, which compares power changes with and without the energy-saving device, is more reasonable and intuitive for this study due to the numerous and complex parameters involved in gate rudder optimization, along with unknown parameter correlations. This approach focuses on torque variations.
Through the extraction of torque values from the 32 samples of the gate rudder experimental design, Sample No. 25 with the minimum torque was selected. Table 10 presents the calculation results for this optimal sample. The results indicate that after installing the gate rudder, hull resistance changes slightly and the gate rudder provides additional thrust leading to reduced total resistance, while both propeller thrust and torque decrease.

Table 10.
Calculation results for minimum-torque sample.
4.3. Sensitivity Analysis of Gate Rudder Parameters
Based on the 32 gate rudder samples obtained using the Sobol experimental design method and their corresponding hull resistance, gate rudder thrust, propeller thrust, and torque values, a complete sample set was established. A multiple linear regression model was constructed for each sample point using SIMULIA Isight 2022 software, expressed by the equation below. Sensitivity analysis was performed on the fitted polynomial to determine the sensitivity of each gate rudder characteristic parameter to the aforementioned parameters.
For n sets of samples, the multiple linear regression forms a matrix represented as
Here, ε represents random error, where
To intuitively display the percentage contribution of each output parameter (chord length, thickness, camber, maximum camber position, propeller–rudder clearance, etc.) to the responses (hull resistance, gate rudder thrust, propeller thrust, and torque), the results are presented in bar charts. These charts reflect the percentage contribution of all terms in the fitted model to each response, with blue bars indicating positive effects and red bars indicating negative effects.
As shown in Figure 11, hull resistance gradually decreases with increases in the clearance between the gate rudder and propeller and the maximum camber position, chord length, thickness, and camber of the gate rudder airfoil. Conversely, hull resistance increases as the gate rudder leading edge moves closer to the stern. These parameter variations should be carefully considered during gate rudder design.
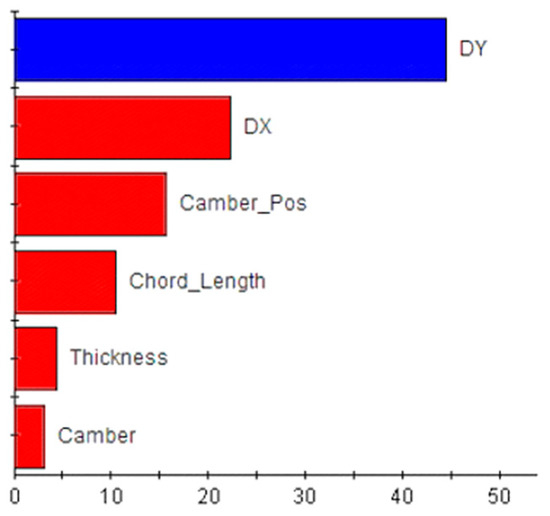
Figure 11.
Sensitivity of hull resistance.
Figure 12 shows that the thrust generated by the gate rudder decreases with increases in the distance between the gate rudder and stern, airfoil thickness, and maximum camber position. In contrast, the thrust increases with increases in the clearance between the gate rudder and propeller, chord length, and camber. The clearance between the gate rudder and propeller has the most significant impact on thrust generation, contributing approximately 57%. Therefore, this variable should be prioritized during design.
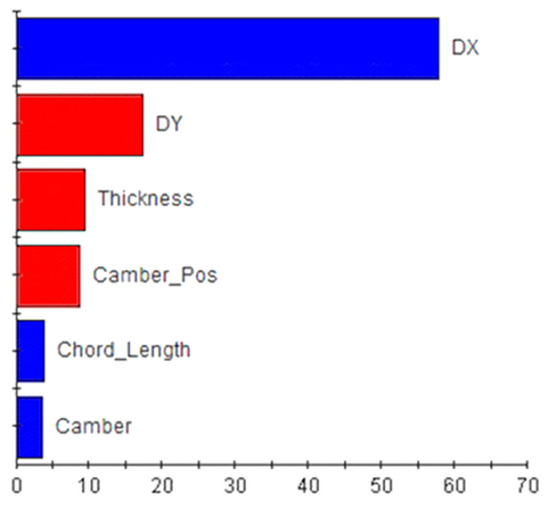
Figure 12.
Sensitivity of gate rudder thrust.
Figure 13 indicates that propeller thrust decreases with increases in chord length, camber, propeller–rudder clearance, thickness, and maximum camber position, with sensitivity gradually diminishing. The distance between the gate rudder and stern has the greatest influence on propeller thrust sensitivity, accounting for 38%.
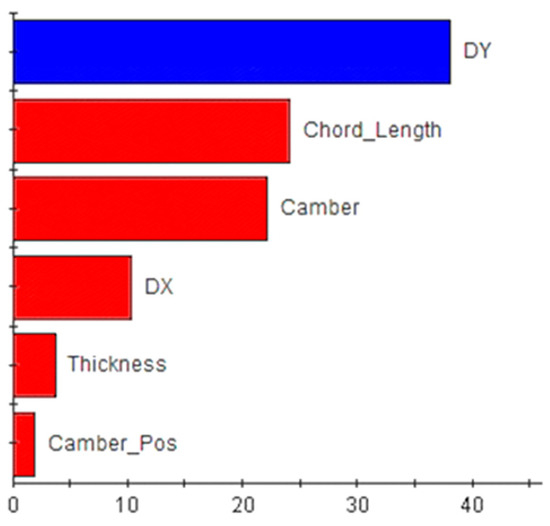
Figure 13.
Sensitivity of propeller thrust.
Figure 14 reveals that, constrained by sample parameters and their ranges, all parameters except airfoil thickness exhibit a negative correlation with propeller torque. As these parameters increase, propeller torque decreases. The camber of the gate rudder airfoil has the most substantial impact, contributing 42%. Thus, this parameter should be emphasized during design.
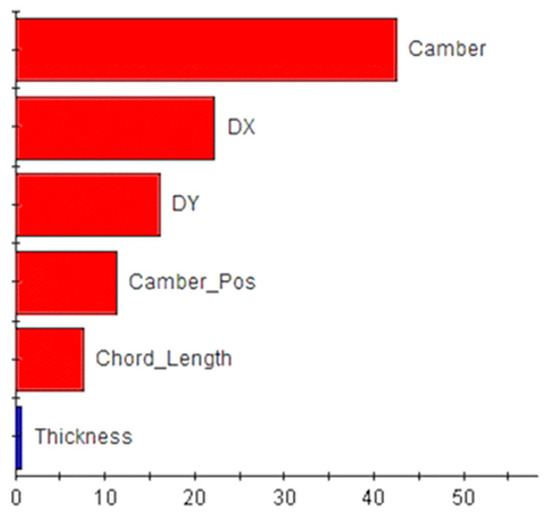
Figure 14.
Sensitivity of propeller torque.
Overall, the clearance between the gate rudder and propeller, the distance between the gate rudder and stern, and the camber of the gate rudder airfoil significantly influence the responses. The main effects of these three parameters on propeller torque are analyzed separately.
In Figure 15, the left panel displays the main-effect plot of the gate rudder airfoil on propeller torque (point–line diagram), while the right panel presents the fitted curve. The analysis reveals that within a reasonable parameter range, increased airfoil camber leads to reduced propeller torque and the improved energy-saving performance of the gate rudder system.
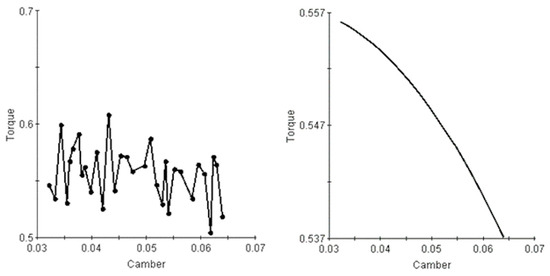
Figure 15.
Main effect of gate rudder airfoil camber on torque.
Figure 16 presents the main-effect plot of the clearance parameter between the gate rudder and propeller on propeller torque. The left panel presents the point–line plot, and the right panel shows the fitted curve. The fitted curve indicates a minimum torque value within the clearance range of 0.02–0.035 (or 0.2 R–0.35 R). Thus, maintaining the clearance within this range optimizes the energy-saving effect, consistent with findings in the literature that the gate rudder should be positioned 1.2 R–1.4 R from the propeller.
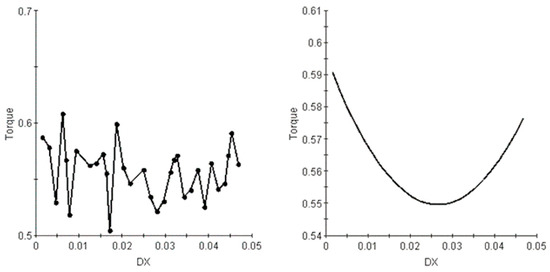
Figure 16.
Main effect of propeller–rudder clearance on torque.
Figure 17 shows the main-effect plot of the distance parameter between the gate rudder leading edge and propeller plane on propeller torque. The analysis shows that torque reaches a maximum within the distance range of 0.021–0.031 (or 0.2 R–0.3 R). Therefore, this range should be avoided during gate rudder design.
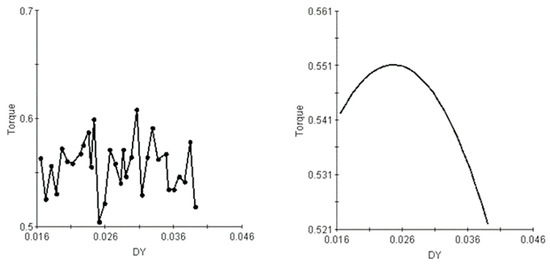
Figure 17.
Main effect of the distance between the gate rudder leading edge and propeller plane on torque.
5. Study on the Flow-Field Influence and Energy-Saving Mechanism of the Gate Rudder
5.1. Influence of Gate Rudder on Propeller Open-Water Performance
This section investigates the open-water performance of the gate rudder–propeller system using the optimal gate rudder model obtained in the previous chapter, which exhibits the highest compatibility with the JBC ship model and MP. 687 propeller. The key parameters of the optimized gate rudder are listed in Table 11, with some parameters expressed in terms of the propeller radius R.

Table 11.
Key parameters of the gate rudder.
The open-water performance curves are shown in Figure 18. Under open-water conditions, both the thrust coefficient (KT) and torque coefficient (10 KQ) of the propeller with the gate rudder are lower than those of the standalone MP. 687 propeller. This is attributed to the gate rudder’s acceleration effect on the surrounding flow. Notably, the gate rudder generates thrust at advance coefficients (J) below 0.4 but produces drag at J > 0.4. As J increases, the gate rudder’s contribution shifts from thrust to drag, with the drag magnitude gradually rising.
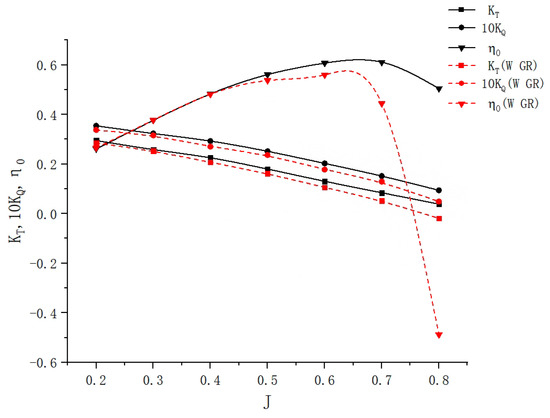
Figure 18.
Open-water performance curves of the gate rudder–propeller system.
5.2. Influence of Gate Rudder on Bare-Hull Hydrodynamic Performance
Resistance calculations were performed for the JBC ship model under three configurations: bare hull, hull with conventional rudder, and hull with gate rudder. The simulation conditions align with the 2015 Tokyo Workshop on Naval Hydrodynamics (Fr = 0.142, Re = 7.46 × 106).
As appendages, both rudders introduce additional resistance. Let R0, RGR, and RCR denote the resistances of the bare hull, gate rudder, and conventional rudder, respectively. The total resistance R for each configuration is summarized in Table 12. At Fr = 0.142, the conventional rudder slightly increases resistance (RCR = 0.168 N), while the gate rudder’s resistance is marginally higher (RGR = 0.206 N). However, the gate rudder reduces the hull’s resistance (R0) and total resistance (R), unlike the conventional rudder.

Table 12.
Resistance components for different configurations.
5.3. Energy-Saving Effect and Mechanism of Gate Rudder
5.3.1. Energy-Saving Performance
To investigate the energy-saving effects of gate rudders, based on previous hull–propeller integrated self-propulsion simulations, both gate rudders and conventional rudders were installed at the stern for comparative analysis. Compared to the computational domain of the hull–propeller integrated model, the computational domain of the hull–propeller–rudder integrated model incorporates an additional rudder component. Figure 19 illustrates the mesh generation for the hull–propeller–gate rudder integrated model, where Figure 19a shows the grid distribution around the gate rudder at the stern, Figure 19b presents the surface mesh of the propeller blades in the stern region, and Figure 19c details the mesh topology of the gate rudder assembly. Figure 20 displays the meshing scheme for the hull–propeller–conventional rudder integrated model, with Figure 20a depicting the grid structure covering the bow, stern, and adjacent flow fields, and Figure 20b focusing on the rotating-domain mesh refinement in the propeller stern region. The simulations maintained consistent y+ values (<5) for turbulence modeling accuracy, with optimized boundary-layer meshes using prismatic elements (growth rates ≤ 1.2) and sliding mesh interfaces for propeller motion. This computational approach enables the systematic evaluation of hydrodynamic interactions and energy consumption differences between rudder configurations under identical operating conditions.
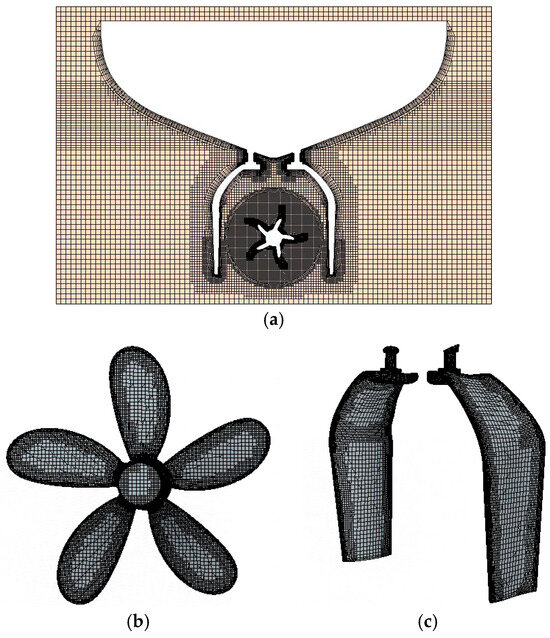
Figure 19.
Mesh configuration of the integrated hull–propeller–gate rudder system: (a) mesh generation of the gate rudder at the stern section; (b) surface mesh discretization of propeller blades; (c) surface mesh topology of gate rudder components.
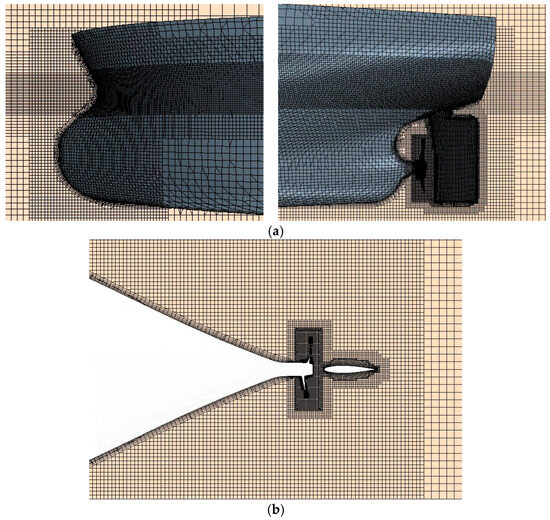
Figure 20.
Mesh configuration of the integrated hull–propeller–conventional rudder system: (a) mesh discretization of bow and stern sections; (b) rotating-domain mesh generation.
Table 13 presents a comparison of hydrodynamic performance calculations between the hull–propeller integrated self-propulsion model and the hull–propeller–rudder integrated model. The results show that installing rudders slightly increases hull resistance. While the conventional rudder generates drag behind the propeller, the gate rudder produces thrust. Consequently, the total resistance of the ship model increases by 2.97% with the conventional rudder but decreases by 5.69% with the gate rudder. After installing the conventional rudder, both the thrust and torque of the propeller increase—propeller thrust rises by 14.61% and torque by 13.99%. In contrast, with the gate rudder installed, both propeller thrust and torque decrease—thrust reduces by 13.72% and torque by 7.33%. This indicates that the gate rudder creates a ducted flow effect near the propeller area, generating partial thrust while accelerating the water flow at the propeller disk, thereby reducing propeller thrust. Additionally, some of the propeller’s trailing vortices are transferred to the gate rudder, forming circulation on the gate rudder and consequently reducing propeller torque and wake losses.

Table 13.
Comparison of hydrodynamic performance calculation results.
Table 14 shows the decomposition of resistance components under different rudder configurations. The data reveal that frictional resistance increases after rudder installation due to the increased wetted surface area. However, with the gate rudder installed, the ship’s total resistance decreases by 5.69%, with residual resistance decreasing by 16.84%, which is the primary reason for the overall resistance reduction with gate rudders.

Table 14.
Resistance components under different rudder configurations.
To conduct a more detailed analysis of the variations in viscous pressure resistance and wave-making resistance within the residual resistance components, additional overlapping grid calculations were performed for both the JBC hull–propeller configuration and the JBC hull–propeller–gate rudder configuration at a specified speed, based on the previously described computational methodology. These calculations neglected free-surface effects and consequently excluded wave-making resistance, with the resulting total ship resistance comprising only frictional resistance and viscous pressure resistance, as presented in Table 15. The results demonstrate that viscous pressure resistance constitutes the primary component of residual resistance. After installing the gate rudder, frictional resistance increased by 1.03%, while viscous pressure resistance decreased by 37%, leading to an overall reduction in total hull resistance. When considering free-surface effects, the presence of the gate rudder reduced residual resistance by 2.72 N compared to the rudderless configuration. In calculations excluding free-surface effects, the viscous pressure resistance decreased by 5.35 N with the gate rudder installed. These findings indicate that while the gate rudder causes slight increases in both frictional resistance and wave-making resistance, the substantial reduction in viscous pressure resistance results in a net decrease in total ship resistance.

Table 15.
Overlapping grid calculation results.
Figure 21 presents the self-propulsion test curves for configurations with gate rudders and conventional rudders, respectively. Using Z = 18.2 N as the reference value, the self-propulsion points were determined through interpolation on the numerical self-propulsion test curves. The self-propulsion points for both rudder configurations are listed in Table 16.
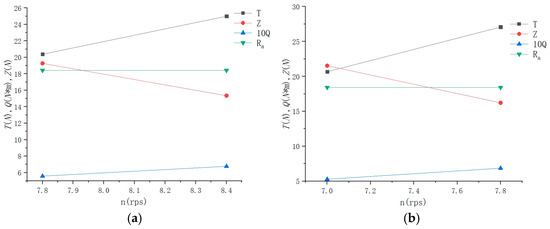
Figure 21.
Self-propulsion test curves under different rudder configurations: (a) gate rudder—the self-propulsion test curves for configurations with gate rudders; (b) conventional rudder—the self-propulsion test curves for configurations with conventional rudders.

Table 16.
Self-propulsion points for different rudder configurations.
By equating the thrust coefficient KT between the self-propelled condition and open-water condition of the propeller, the advance coefficient J, torque coefficient 10 KQ, and efficiency η at the self-propulsion point can be determined through interpolation on the propeller’s open-water characteristic curve. The numerical simulation results provide the self-propulsion factors under different rudder configurations, including the effective wake fraction, thrust deduction coefficient, relative rotative efficiency, hull efficiency, and overall propulsive efficiency, as systematically listed in Table 17.

Table 17.
Numerical self-propulsion factor analysis results.
The data reveal that the gate rudder configuration reduces the total resistance coefficient Ct by 5.69%, while the conventional rudder increases it by 2.96%, demonstrating the gate rudder’s effectiveness in reducing ship resistance. As established in previous analysis, this reduction primarily stems from a significant decrease in viscous pressure resistance. Wake analysis indicates that the conventional rudder increases the wake fraction due to flow-blocking effects behind the propeller, whereas the gate rudder reduces the wake fraction by accelerating flow around the propeller region.
A comparative analysis of propeller performance under JBC self-propulsion conditions reveals that the gate rudder configuration improves propeller efficiency by 36.57% relative to conventional rudders. The relative rotative efficiency shows a 1.01% enhancement, while hull efficiency decreases by 21.66% with gate rudder installation. An evaluation of overall propulsive efficiency across configurations indicates that the rudderless condition achieves peak efficiency, confirming that both rudder types incur certain efficiency penalties. However, the gate rudder demonstrates a significant 8.05% improvement in total propulsive efficiency ηD compared to conventional rudders. Consequently, the JBC model equipped with gate rudders exhibits clear advantages in energy-efficient propulsion, achieving measurable energy savings of 8.05%. The self-propulsion factors presented in Table 17 show strong correlation with empirical observations, validating the numerical methodology’s accuracy.
5.3.2. Influence on Stern Flow Field
Figure 22 shows the schematic diagram of six cross-sections extracted from the stern to the bow along the hull, with the propeller disk plane serving as the reference plane.

Figure 22.
Schematic diagram of cross-section locations.
Figure 23 presents the axial effective wake fraction distributions at the stern for four configurations: bare hull, hull–propeller, hull–propeller–conventional rudder, and hull–propeller–gate rudder, with the wake fraction defined by Equation (5). The results show that in rudderless conditions, the wake fraction distribution remains highly symmetrical, indicating symmetric flow characteristics. With rudders installed, the flow field becomes asymmetric—the incoming flow near the hull ahead of the propeller clearly shifts leftward at Section 4 (where the stern lines begin to converge) after passing through the port-side flow field. Both conventional and gate rudder configurations exhibit similar asymmetric wake fraction distributions, demonstrating that both rudder types induce flow asymmetry in the incoming stream ahead of the propeller, reducing flow velocity on the port side while increasing velocity on the starboard side.
where VA represents the axial velocity at the cross-section, and V0 denotes the freestream velocity.
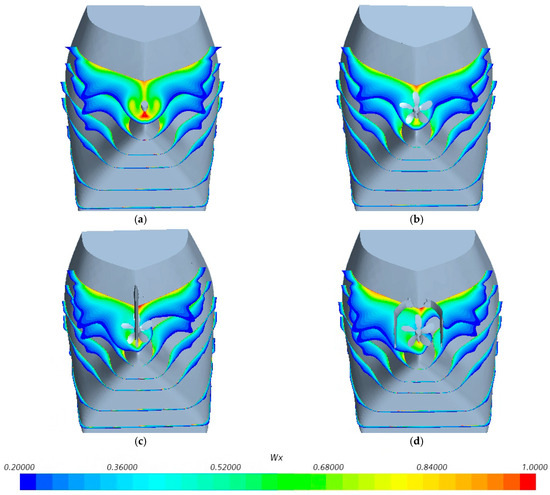
Figure 23.
Wake distribution at the stern under different configurations: (a) bare hull; (b) hull–propeller configuration; (c) hull–propeller–conventional rudder; (d) hull–propeller–gate rudder.
Figure 24 presents detailed views of the local flow field at the stern for both conventional rudder and gate rudder configurations. As shown in Figure 24a, when equipped with a conventional rudder, a distinct water flow passes directly above the propeller along the hull bulb root, ultimately forming part of the ship’s visible wake. Figure 24b reveals that with the gate rudder installed, the flow direction of this bulb-root water stream is partially altered, with a portion now entering the propeller disk. This redirection effectively increases the water flow velocity in certain areas of the propeller disk, resulting in improved propeller efficiency.
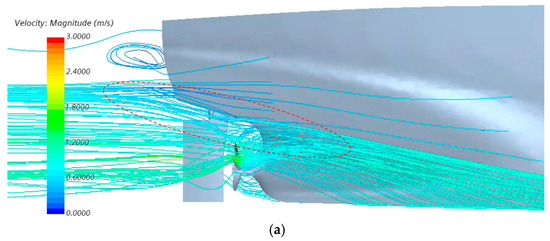
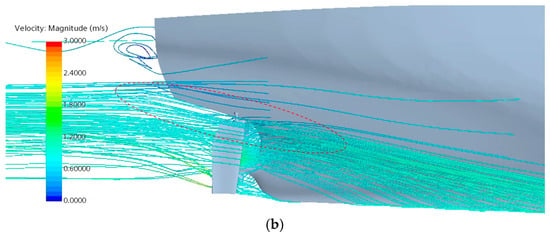
Figure 24.
Local-flow-field details at stern with different rudder configurations: (a) flow-field details with conventional rudder; (b) flow-field details with gate rudder.
5.3.3. Influence on Propeller Wake
Figure 25 presents the numerically computed stern flow fields for four configurations: bare hull, hull–gate rudder (resistance calculation), hull–propeller, and hull–propeller–gate rudder (self-propulsion calculation). The results reveal that when propeller effects are not considered, the stern flow field exhibits complete symmetry. Both conventional and gate rudder installations increase flow velocity in the rudder area while decreasing velocity near the stern region.
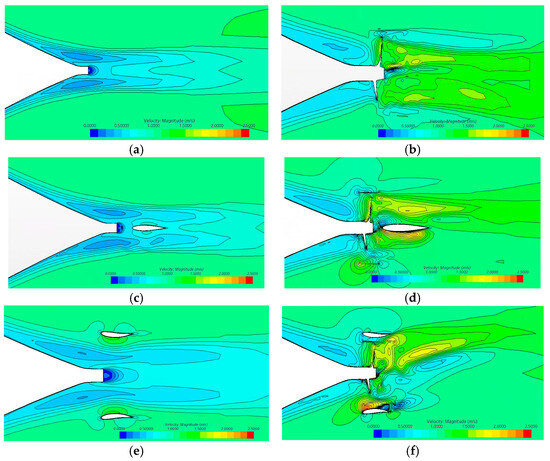
Figure 25.
Stern-flow-field distribution with different configurations: (a) bare hull; (b) hull–propeller integrated; (c) hull–conventional rudder; (d) hull–propeller–conventional rudder integrated; (e) hull–gate rudder integrated; (f) hull–propeller–gate rudder integrated.
When accounting for propeller influence and propeller–rudder interactions, the flow field clearly displays asymmetric characteristics: the low-velocity zone near the stern expands significantly, and fluid velocity increases after passing through the propeller. With either conventional or gate rudders installed, the interaction between the propeller and rudder further amplifies the asymmetry of the propeller wake. The gate rudder’s unique design modifies this interaction pattern, converting part of the asymmetric losses into useful thrust enhancement.
Figure 26 presents the dimensionless axial velocity distributions at three key axial positions (X/D = 0.05 upstream of propeller, propeller disk plane, and X/D = −0.05 downstream) for three self-propelled configurations: hull–propeller only, hull–propeller–conventional rudder, and hull–propeller–gate rudder. The velocity fields are viewed in the stern-to-bow direction, with all velocities normalized by the ship’s forward speed V0. The results demonstrate how conventional and gate rudders differentially modify the propeller’s inflow and outflow characteristics compared to the rudderless baseline case.
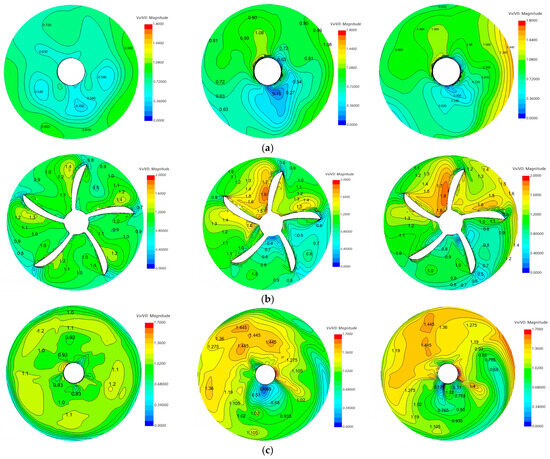
Figure 26.
Dimensionless axial velocity distribution in self-propulsion condition: (a) pre-propeller plane (X/D = 0.05); (b) propeller disk plane; (c) post-propeller plane (X/D = −0.05).
Figure 26a reveals that after rudder installation, the wake distribution at the pre-propeller cross-section increases compared to the rudderless condition, with smaller wake fractions near the propeller shaft area and gradually increasing dimensionless axial velocities outward from the shaft axis. Due to propeller effects, the wake distribution at this section becomes asymmetric. Compared to conventional rudders, the gate rudder configuration demonstrates higher dimensionless axial velocities at the pre-propeller section, indicating its significant flow acceleration effect on the incoming stream. Figure 26b shows that regardless of rudder presence, the propeller blade tips operate within sharply varying wake regions. In rudderless conditions, distinct high-velocity wake zones appear at mid-chord positions on the blade backs. This pattern changes with rudder installation—the upper blade sections experience increased wake while lower sections show reduced wake. Both conventional and gate rudders produce similar wake distributions across the propeller disk, with notably enhanced wake in upper blade regions and slightly diminished wake in lower sections. Figure 26c presents the dimensionless axial velocity distribution at the post-propeller section (X/D = −0.05), where wake velocities show significant overall reduction compared to the propeller disk plane. The wake distribution pattern remains consistent with the disk plane, maintaining larger wake fractions in upper propeller regions and smaller fractions below. Compared to rudderless operation, rudder-equipped configurations exhibit substantially increased wake velocities in the propeller slipstream, representing notable energy losses that critically reduce overall propulsive efficiency. The gate rudder demonstrates superior performance in this regard, with more pronounced wake reduction behind the propeller than conventional rudders, confirming its ability to recover partial energy from the propeller slipstream and deliver measurable energy-saving benefits.
6. Conclusions
Using a coupled CFD and CAESES platform approach, this study developed a matching design of the gate rudder for the JBC ship model and MP. 687 propeller. A sensitivity analysis was performed of various geometric parameters of the gate rudder (including rudder height, width, propeller–rudder clearance, airfoil profile, etc.), and the energy-saving effects and mechanisms of the designed gate rudder were analyzed. The main conclusions are as follows:
- (1)
- Among the design variables, the clearance between the gate rudder and propeller, the distance between the gate rudder and stern, and the camber of the gate rudder airfoil make significant contributions to various responses. Through a main-effect analysis of the relationship between the gate rudder–propeller clearance and propeller torque, it is recommended to maintain the gate rudder–propeller clearance within the range of 0.2 R~0.35 R, where the gate rudder demonstrates better energy-saving effects.
- (2)
- Under open-water conditions, the angle of attack between water flow and the gate rudder section varies with different advance coefficients. As the advance coefficient increases, the angle of attack between incoming flow and the gate rudder section gradually increases, causing the force generated by the gate rudder to change from positive thrust to negative drag.
- (3)
- After the installation of the gate rudder, the ship’s frictional resistance and wave-making resistance slightly increase, while the viscous pressure resistance decreases significantly, resulting in an overall reduction in total ship resistance. The gate rudder can provide thrust equivalent to about 6.7% of the hull resistance, while both propeller thrust and torque decrease. Compared with the installation of a conventional rudder, the JBC ship model with a gate rudder achieves an energy-saving effect of 8.05%.
- (4)
- After the installation of either a conventional rudder or gate rudder on the JBC ship model, the stern wake and propeller wake distribution become asymmetric, with significantly increased wake velocity causing energy loss. The gate rudder can guide part of the stern water flow into the upper side of the propeller disk, improving propeller efficiency. Moreover, compared with the conventional rudder, the wake behind the propeller is more significantly reduced after the installation of the gate rudder, indicating that the gate rudder can recover some energy from the propeller wake, demonstrating certain energy-saving effects.
- (5)
- All computational and experimental investigations in this study were conducted at model scale without accounting for scale effects. Subsequent research could incorporate scale-effect considerations into model-scale computations and experiments, while also extending to full-scale and even multi-scale computational model testing.
Author Contributions
Conceptualization, C.W. (Chunhui Wang); methodology, L.L.; software, writing—original draft preparation, Q.G.; data curation, F.G.; software, validation, formal analysis, Z.W.; editing, visualization, C.W. (Chao Wang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the Nature Scientific Foundation of Heilongjiang Province of China (YQ2022E015).
Data Availability Statement
Data are contained within the article.
Acknowledgments
This research was supported by Harbin Engineering University, where their towing tank and related laboratories were used for the experiments. The authors would like to express sincere gratitude to those who supported this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, W.; Huang, G. Energy-Saving Technologies in Ship Hydrodynamics; Shanghai Jiao Tong University Press: Shanghai, China, 2018; pp. 3–36. [Google Scholar]
- Sasaki, N.; Kuribayashi, S.; Asaumi, N.; Fukazawa, M.; Nonaka, T.; Turkmen, S.; Atlar, M. Measurements and calculations of gate rudder performance. In Proceedings of the International Conference on Advanced Model Measurement Technology for the Maritime Industry, Glasgow, UK, 11–13 October 2017; pp. 358–388. [Google Scholar]
- Sasaki, N.; Atlar, M.; Kuribayashi, S. Advantages of twin rudder system with asymmetric wing section aside a propeller: The new hull form with twin rudders utilizing duct effects. J. Mar. Sci. Technol. 2016, 21, 297–308. [Google Scholar] [CrossRef]
- Tacar, Z.; Sasaki, N.; Atlar, M.; Korkut, E. An investigation into effects of Gate Rudder® system on ship performance as a novel energy-saving and manoeuvring device. Ocean. Eng. 2020, 218, 108250. [Google Scholar] [CrossRef]
- Sasaki, N. ZEUS and NOAH projects of NMRI. In Proceedings of the Third International Symposium on Marine Propulsors, Lauceston, Australia, 5–8 May 2013; pp. 324–330. [Google Scholar]
- Sasaki, N.; Kuribayashi, S.; Atlar, M. Gate rudder. In Proceedings of the Third International Naval Architecture and Maritime Symposium-INTNAM, Istanbul, Turkey, 24–25 April 2018; pp. 89–108. [Google Scholar]
- Sasaki, N.; Kuribayashi, S.; Atlar, M. GATE RUDDER®. In Proceedings of the 3rd International Symposium on Naval Architecture and Maritime (INT-NAM), Istanbul, Turkey, 23–25 April 2018; pp. 24–25. [Google Scholar]
- Zhai, S.; Zhang, R.; Song, J.; Chen, L.Q.; Liu, D.C. The numerical investigation of the hydrodynamic performance of a new twin rudder system. In Proceedings of the International Symposium of Marine Propulsors smp’2022, Wuxi, China, 17–21 October 2022; pp. 17–21. [Google Scholar]
- Wout, O.; Bijlard, M.; van Esch, B.; Melissaris, T.; Wärtsilä Netherlands BV. Hydrodynamic Characteristics of a Gate Rudder During Straight-sailing and Sailing with a Ship Drift Angle. In Proceedings of the 26th Numerical Towing Tank Symposium (NuTTS), Mülheim an der Ruhr, Germany, 23–25 October 2024. [Google Scholar]
- Sasaki, N.; Kuribayashi, S.; Fukazawa, M.; Atlar, M. Towards a realistic estimation of the powering performance of a ship with a gate rudder system. J. Mar. Sci. Eng. 2020, 8, 43. [Google Scholar] [CrossRef]
- Sasaki, N.; Atlar, M. Scale effect of gate rudder. In Proceedings of the Sixth International Symposium on Marine Propulsors, Rome, Italy, 26–30 May 2019. [Google Scholar]
- Sasaki, N.; Yazawa, M. Joint Sea Trial of Ships with Gate Rudder® and Conventional Rudder. In Proceedings of the Royal Institution of Naval Architects Full Scale Ship Performance Online Conference, Online, 10–11 February 2021. [Google Scholar]
- Sasaki, N.; Atlar, M. Gate rudder and ship design. In Proceedings of the 8th International Symposium on Marine Propulsors, Smp 2024, Berlin, Germany, 17–20 March 2024; Norwegian University of Science and Technology, Department of Marine Technology: Trondheim, Norway, 2024; pp. 311–325. [Google Scholar]
- Gürkan, A.Y.; Ünal, U.O.; Aktaş, B.; Atlar, M. An investigation into the gate rudder system design for propulsive performance using design of experiment method. Ship Technol. Res. 2023, 71, 199–212. [Google Scholar] [CrossRef]
- National Maritime Research Institute (NMRI). Tokyo 2015: A Workshop on CFD in Ship Hydrodynamics [EB/OL]. 2015. Available online: http://www.t2015.nmri.go.jp (accessed on 13 August 2021).
- Sobol, I. Distribution of points in a cube approximate evaluation of integrals. USSR Comput. Maths. Math. Phys. 1967, 7, 86–112. (In English) [Google Scholar] [CrossRef]
- Schmit, L.A.; Farshi, B. Some Approximation Concepts for Structural Synthesis. AIAA J. 1974, 12, 692–699. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).