Novel Polarization Construction Method and Synchronization Algorithm for Underwater Acoustic Channel Under T-Distribution Noise Environment
Abstract
1. Introduction
- (1)
- Aiming at the multipath and time-varying characteristics, we present a novel, robust and efficient polar code construction method using the base-adversarial polarization weight (BPW) algorithm, named the NREPCC method, for the UWAC channel. Meanwhile, to subsequently validate the NREPCC method, we built the polar-coded UWAC OFDM system model.
- (2)
- Combined with a more realistic t-distribution noise model, an improved synchronization algorithm is proposed for packet detection, which effectively enhances the communication efficiency and stability of the polar-coded UWAC OFDM system.
- (3)
- We thoroughly validate and comprehensively assess the performance of the proposed polar construction method and the polar-coded UWAC OFDM scheme with detailed theoretical analysis and numerical simulation experiments.
2. Related Work
- Inclusion criteria:
- (1)
- Studies focusing on UWA OFDM communication systems, particularly those addressing multipath effects and time-varying channel characteristics.
- (2)
- Research on polar code construction methods, especially those tailored for non-Gaussian noise environments.
- (3)
- Works published in high-quality journals or conferences within the last five years.
- Exclusion criteria:
- (1)
- Studies that do not directly address UWA OFDM communication or polar code construction.
- (2)
- Research that lacks experimental validation or relies solely on theoretical analysis without practical application.
- (3)
- Works published in non-peer-reviewed venues or those with limited relevance to our research objectives.
3. Polar Codes
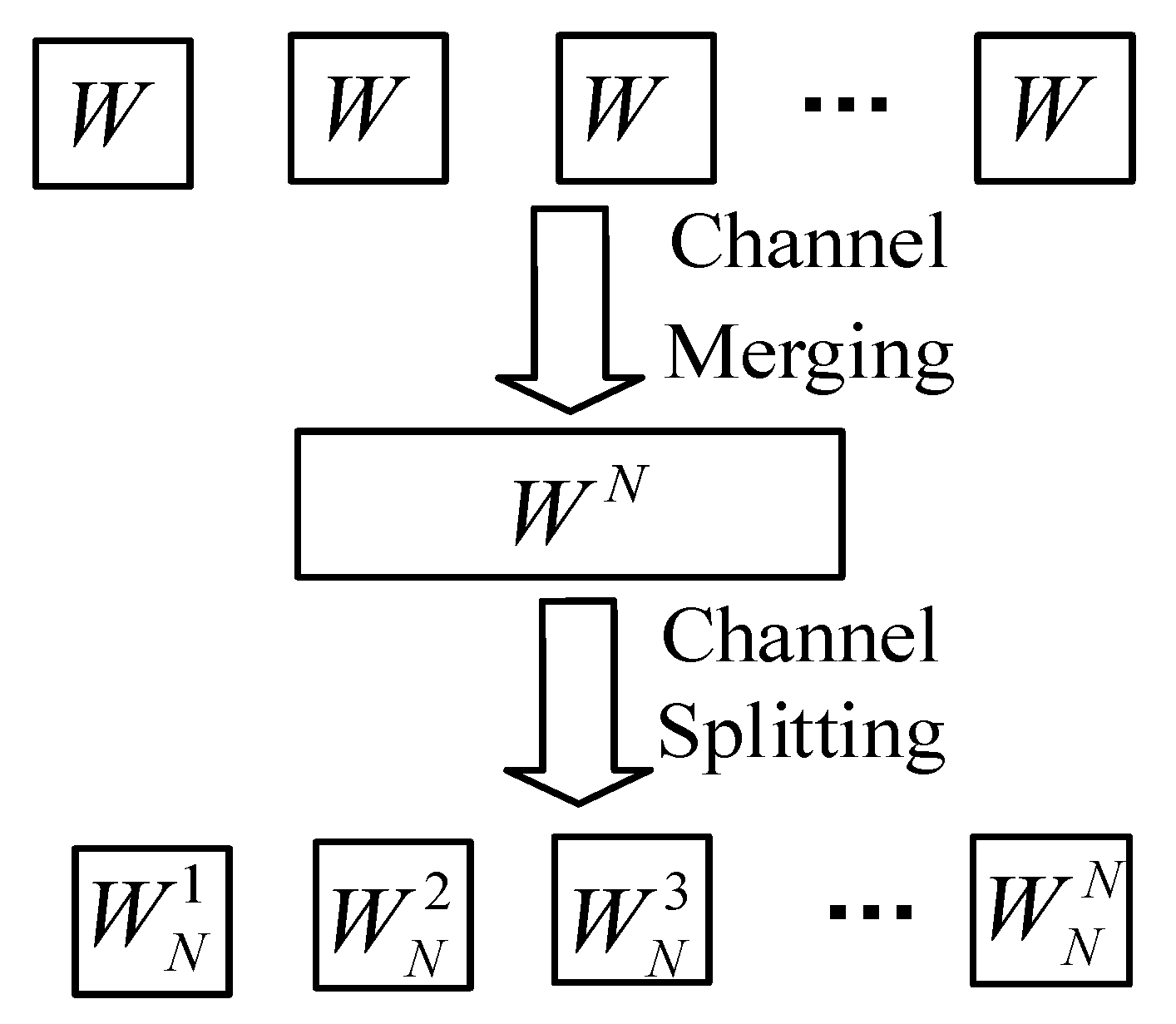
3.1. Channel Polarization Principle
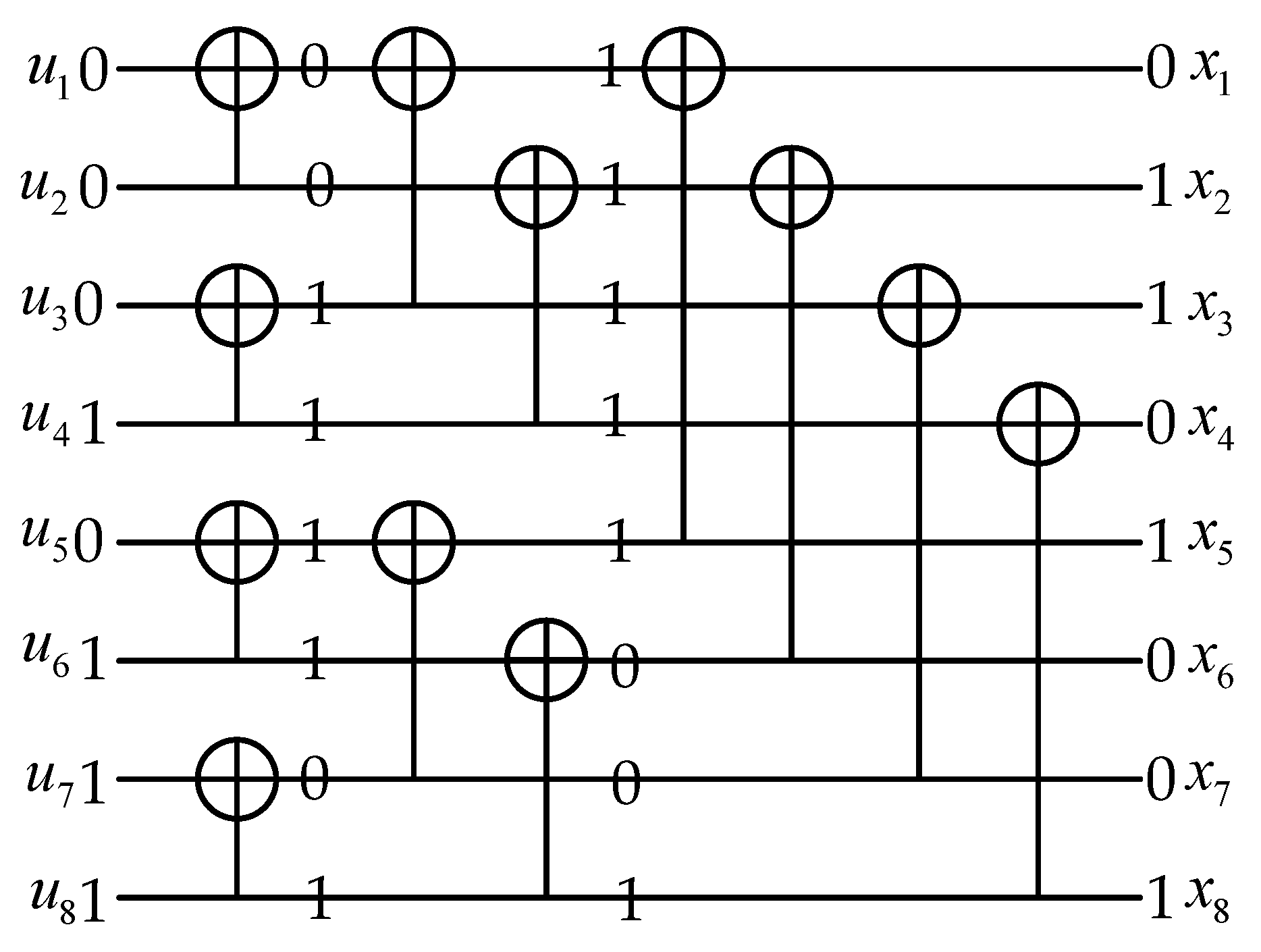
3.2. Polar Codes Encoding and Decoding
4. A Novel Polar Code Construction Method for the UWA Channel
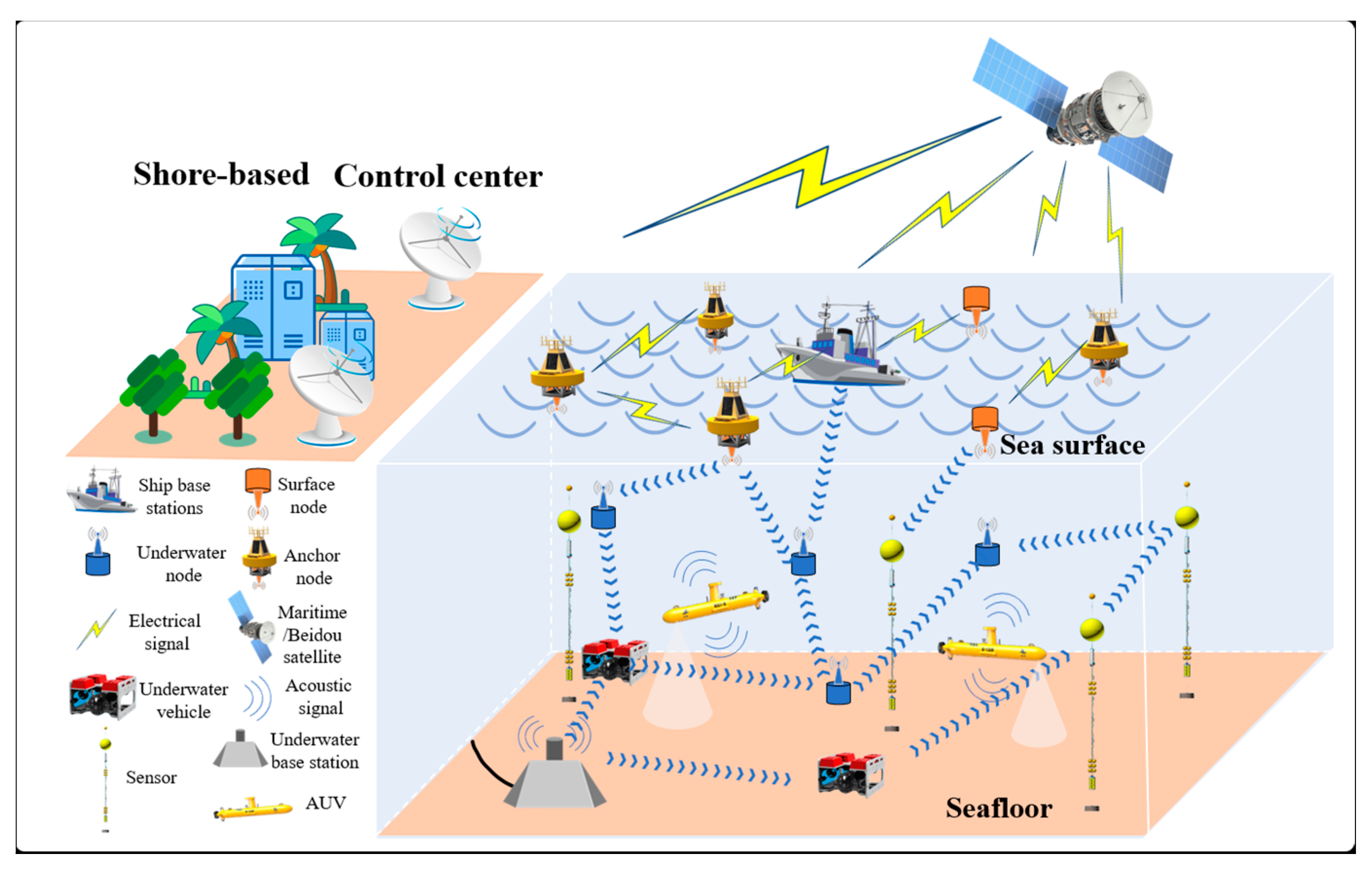
4.1. Underwater Acoustic Channel
4.2. Novel Polar Code Construction Method for the UWA Channel
5. Polar-Coded UWAC OFDM System Model and Improved Synchronization Algorithm
5.1. Ocean Noise Model
5.2. System Structure
5.3. Synchronization Algorithm
6. Simulation and Analysis
6.1. Synchronization Algorithm Robustness Verification
6.2. Effectiveness Verification of Polarization Construction Methods
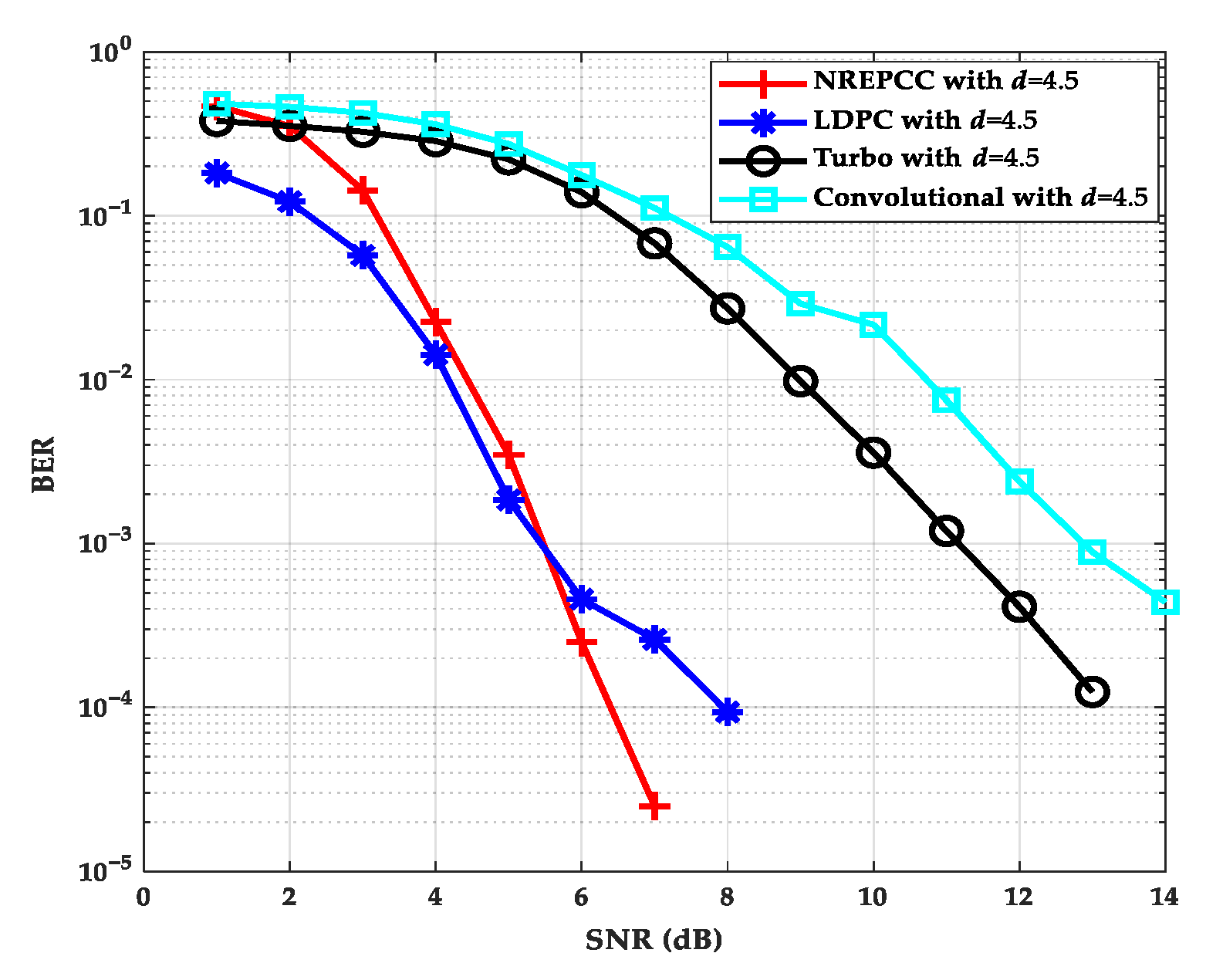
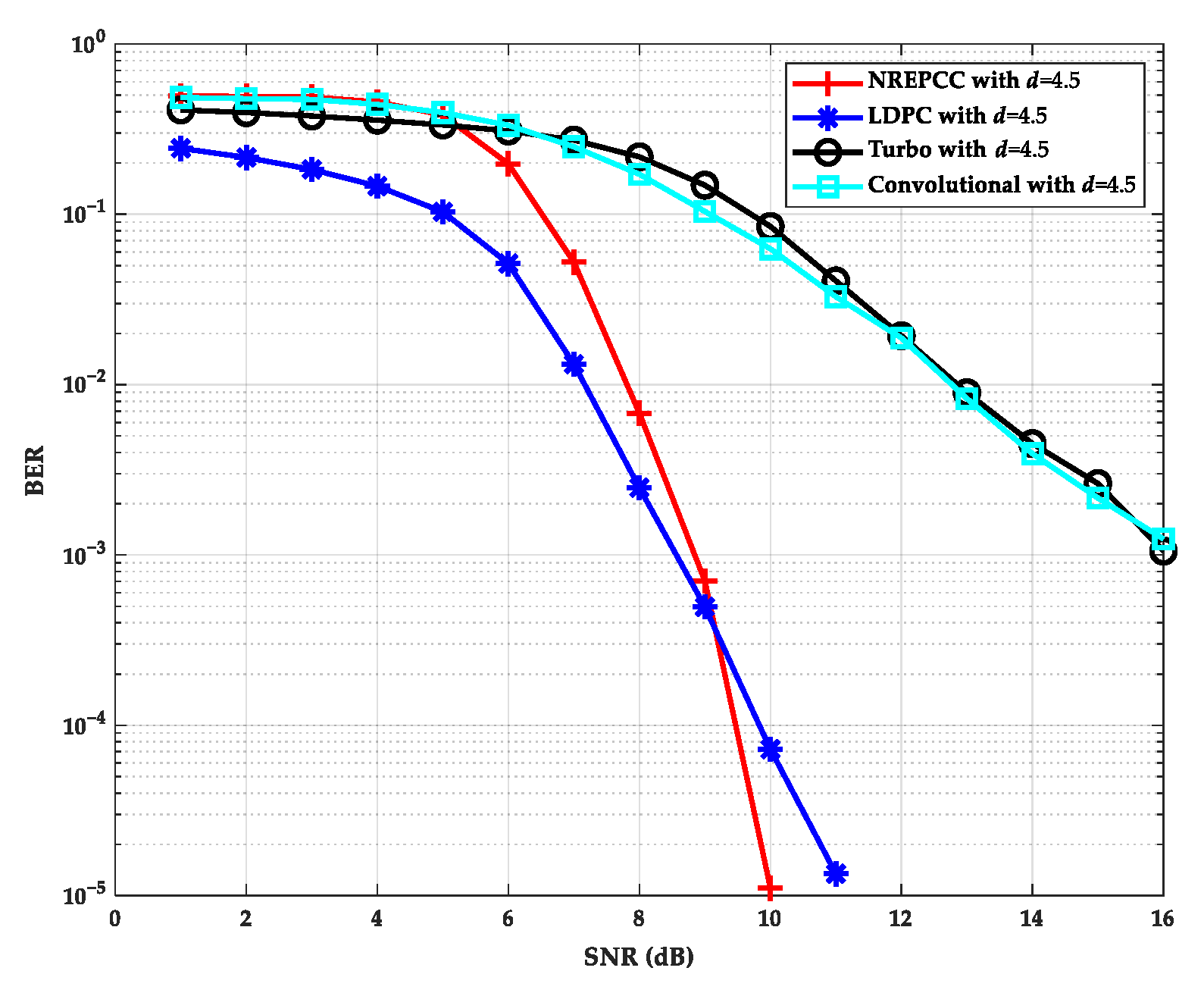
6.3. Performance Comparison of Different Coding Methods
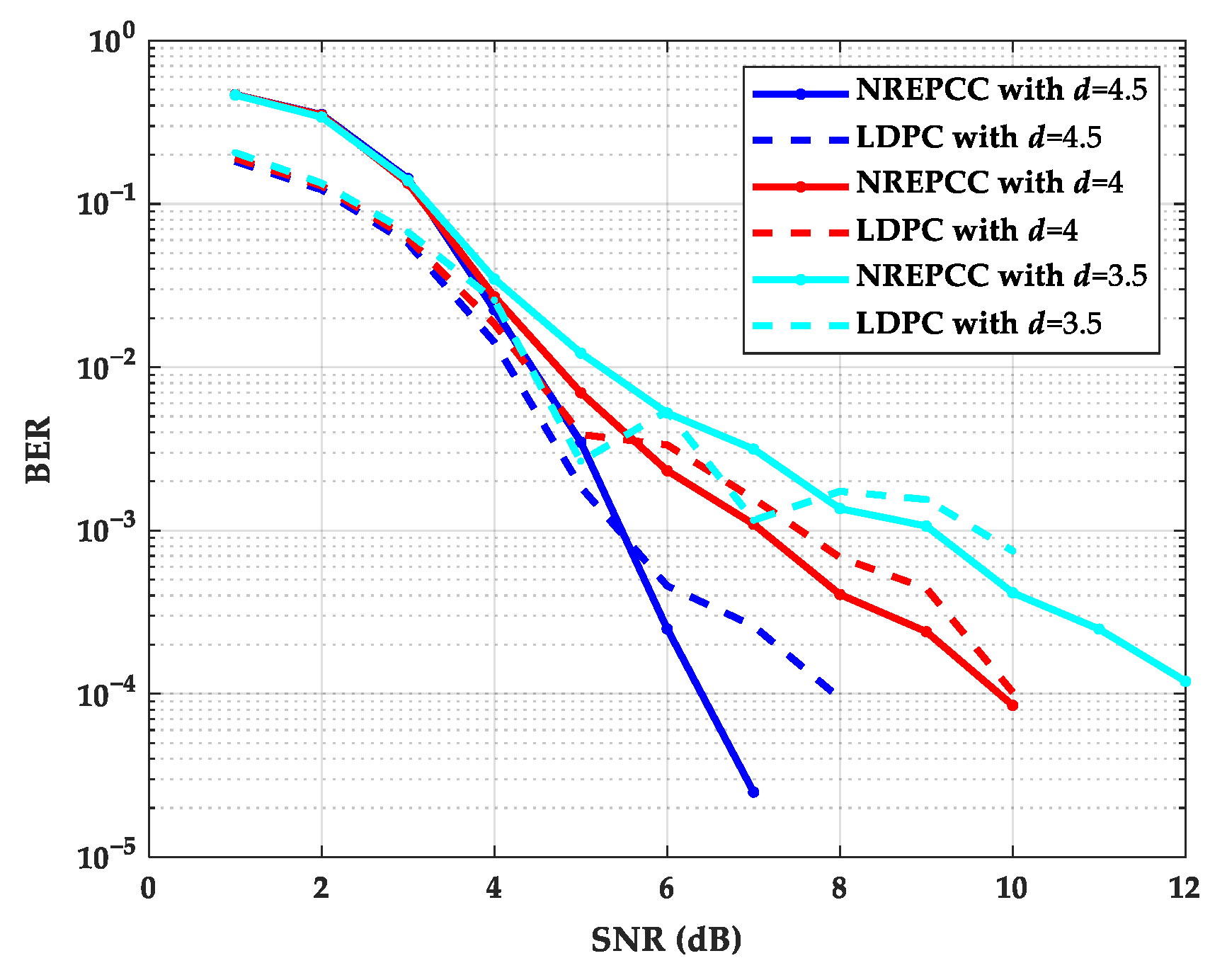
6.4. Impact of Degrees of Freedom d on Coding Performance
6.5. Impact of Code Rates on Coding Performance
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UWAC | underwater acoustic channel |
| NREPCC | novel, robust and efficient polar code construction |
| BPW | base-adversarial polarization weight |
| ISVG | invariable sound velocity gradient |
| NSVG | negative sound velocity gradient |
| PSVG | positive sound velocity gradient |
| OFDM | orthogonal frequency division multiplexing |
| IoT | Internet of things |
| BER | bit error rate |
| UWA | underwater acoustic |
| LDPC | low-density parity-check |
| CRC | cyclic redundancy check |
| SC | successive cancellation |
| SCL | successive cancellation list |
| SSP | sound speed profile |
| BEC | binary erasure channel |
| LR | likelihood ratio |
| PW | polarization weight |
| HPW | higher order polarization weight |
| EPW | extended polarization weight |
| CP | cyclic prefix |
| FFT | fast Fourier transform |
| QPSK | quadrature phase shift keying |
| probability density function | |
| CA-SCL | cyclic redundancy check-aided successive cancellation list |
| MSA | min-sum algorithm |
References
- Zhu, Z.; Zhou, Y.; Wang, R.; Tong, F. Internet of Underwater Things Infrastructure: A Shared Underwater Acoustic Communication Layer Scheme for Real-World Underwater Acoustic Experiments. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6991–7003. [Google Scholar] [CrossRef]
- Mishachandar, B.; Vairamuthu, S. An Underwater Cognitive Acoustic Network Strategy for Efficient Spectrum Utilization. Appl. Acoust. 2021, 175, 107861. [Google Scholar] [CrossRef]
- Jarrot, A.; Gelman, A.; Choi, G.; Speck, A.; Strunk, G.; Croux, A.; Osedach, T.P.; Vannuffelen, S.; Ossia, S.; Vincent, J.; et al. High-Speed Underwater Acoustic Communication for Multi-Agent Supervised Autonomy. In Proceedings of the 2021 Fifth Underwater Communications and Networking Conference (UComms), Lerici, Italy, 31 August–2 September 2021; pp. 1–4. [Google Scholar]
- Beaujean, P.-P.J. High-Speed High-Frequency Acoustic Modem for Image Transmission in Very Shallow Waters. In Proceedings of the OCEANS 2007-Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–6. [Google Scholar]
- Stojanovic, M.; Preisig, J. Underwater Acoustic Communication Channels: Propagation Models and Statistical Characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Yang, T. Properties of Underwater Acoustic Communication Channels in Shallow Water. J. Acoust. Soc. Am. 2012, 131, 129–145. [Google Scholar] [CrossRef]
- Qarabaqi, P.; Stojanovic, M. Statistical Characterization and Computationally Efficient Modeling of a Class of Underwater Acoustic Communication Channels. IEEE J. Ocean. Eng. 2013, 38, 701–717. [Google Scholar] [CrossRef]
- Wang, B.; Wang, Y.; Li, Y.; Guan, X. Underwater Acoustic Communications Based on OCDM for Internet of Underwater Things. IEEE Internet Things J. 2023, 10, 22128–22142. [Google Scholar] [CrossRef]
- Feng, C.; Luo, Y.; Zhang, J.; Li, H. An OFDM-Based Frequency Domain Equalization Algorithm for Underwater Acoustic Communication with a High Channel Utilization Rate. J. Mar. Sci. Eng. 2023, 11, 415. [Google Scholar] [CrossRef]
- Jiang, W.; Tao, Q.; Yao, J.; Tong, F.; Zhang, F. R&D of a Low-Complexity OFDM Acoustic Communication Payload for Micro-AUV in Confined Space. EURASIP J. Adv. Signal Process. 2022, 2022, 64. [Google Scholar]
- Cuji, D.A.; Stojanovic, M. Transmit Beamforming for Underwater Acoustic OFDM Systems. IEEE J. Ocean. Eng. 2023, 49, 145–162. [Google Scholar] [CrossRef]
- Li, B.; Zhou, S.; Stojanovic, M.; Freitag, L.; Willett, P. Multicarrier Communication over Underwater Acoustic Channels with Nonuniform Doppler Shifts. IEEE J. Ocean. Eng. 2008, 33, 198–209. [Google Scholar]
- Berger, C.R.; Zhou, S.; Preisig, J.C.; Willett, P. Sparse Channel Estimation for Multicarrier Underwater Acoustic Communication: From Subspace Methods to Compressed Sensing. IEEE Trans. Signal Process. 2009, 58, 1708–1721. [Google Scholar] [CrossRef]
- Wan, L.; Zhou, H.; Xu, X.; Huang, Y.; Zhou, S.; Shi, Z.; Cui, J.-H. Adaptive Modulation and Coding for Underwater Acoustic OFDM. IEEE J. Ocean. Eng. 2014, 40, 327–336. [Google Scholar] [CrossRef]
- Elias, P. Error-Free Coding. Trans. IRE Prof. Group Inf. Theory 1954, 4, 29–37. [Google Scholar] [CrossRef]
- Pelekanakis, K.; Paglierani, P.; Alvarez, A.; Alves, J. Comparison of Error Correction Codes via Optimal Channel Replay of High North Underwater Acoustic Channels. Comput. Netw. 2024, 242, 110270. [Google Scholar] [CrossRef]
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon Limit Error-Correcting Coding and Decoding: Turbo-Codes. 1. In Proceedings of the ICC’93-IEEE International Conference on Communications, Geneva, Switzerland, 23–26 May 1993; Volume 2, pp. 1064–1070. [Google Scholar]
- Chung, S.-Y.; Forney, G.D.; Richardson, T.J.; Urbanke, R. On the Design of Low-Density Parity-Check Codes within 0.0045 dB of the Shannon Limit. IEEE Commun. Lett. 2001, 5, 58–60. [Google Scholar] [CrossRef]
- Polarization, C. A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels by Erdal Arikan. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar]
- Choi, G.; Lee, N. Deep Polar Codes. IEEE Trans. Commun. 2024, 72, 3842–3855. [Google Scholar] [CrossRef]
- Xing, L.; Li, Z.; Zhang, Z.; Zhao, C. Research on the Application of Polar Codes in Underwater Acoustic Communication. In Proceedings of the 2021 7th International Conference on Computer and Communications (ICCC), Chengdu, China, 10–13 December 2021; pp. 115–119. [Google Scholar]
- Ahmed, M.S.; Shah, N.S.M.; Ghawbar, F.; Jawhar, Y.A.; Almohammedi, A.A. Filtered-OFDM with Channel Coding Based on T-Distribution Noise for Underwater Acoustic Communication. J. Ambient Intell. Humaniz. Comput. 2022, 13, 3379–3392. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Zhang, J.; Guo, Y.; Razzaqi, A.A. A Novel Adaptive Filtering for Cooperative Localization under Compass Failure and Non-Gaussian Noise. IEEE Trans. Veh. Technol. 2022, 71, 3737–3749. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yan, S.; Shi, W.; Yang, X.; Guo, Y.; Gulliver, T.A. A Novel Underwater Acoustic Signal Denoising Algorithm for Gaussian/Non-Gaussian Impulsive Noise. IEEE Trans. Veh. Technol. 2020, 70, 429–445. [Google Scholar] [CrossRef]
- Mori, R.; Tanaka, T. Performance of Polar Codes with the Construction Using Density Evolution. IEEE Commun. Lett. 2009, 13, 519–521. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. How to Construct Polar Codes. IEEE Trans. Inf. Theory 2013, 59, 6562–6582. [Google Scholar] [CrossRef]
- Trifonov, P. Efficient Design and Decoding of Polar Codes. IEEE Trans. Commun. 2012, 60, 3221–3227. [Google Scholar] [CrossRef]
- Zhou, D.; Niu, K.; Dong, C. Construction of Polar Codes in Rayleigh Fading Channel. IEEE Commun. Lett. 2019, 23, 402–405. [Google Scholar] [CrossRef]
- Babar, Z.; Egilmez, Z.B.K.; Xiang, L.; Chandra, D.; Maunder, R.G.; Ng, S.X.; Hanzo, L. Polar Codes and Their Quantum-Domain Counterparts. IEEE Commun. Surv. Tutor. 2019, 22, 123–155. [Google Scholar] [CrossRef]
- Morozs, N.; Gorma, W.; Henson, B.T.; Shen, L.; Mitchell, P.D.; Zakharov, Y.V. Channel Modeling for Underwater Acoustic Network Simulation. IEEE Access 2020, 8, 136151–136175. [Google Scholar] [CrossRef]
- Chen, R.; Wu, W.; Zeng, Q.; Liu, S. Construction and Application of Polar Codes in OFDM Underwater Acoustic Communication. Appl. Acoust. 2023, 211, 109473. [Google Scholar] [CrossRef]
- Zhai, Y.; Li, J.; Feng, H.; Hong, F. Application Research of Polar Coded OFDM Underwater Acoustic Communications. EURASIP J. Wirel. Commun. Netw. 2023, 2023, 26. [Google Scholar] [CrossRef]
- Tian, T.; Yang, K.; Wu, F.-Y.; Zhang, Y. Channel Estimation for Underwater Acoustic Communications in Impulsive Noise Environments: A Sparse, Robust, and Efficient Alternating Direction Method of Multipliers-Based Approach. Remote Sens. 2024, 16, 1380. [Google Scholar] [CrossRef]
- Ma, H.; Sun, S.; Ye, S.; Jiang, Z. Non-Uniform Illumination Underwater Image Enhancement via Minimum Weighted Error Entropy Loss. IEEE Signal Process. Lett. 2023, 30, 1187–1191. [Google Scholar] [CrossRef]
- Banerjee, S.; Agrawal, M. On the Performance of Underwater Communication System in Noise with Gaussian Mixture Statistics. In Proceedings of the 2014 Twentieth National Conference on Communications (NCC), Kanpur, India, 28 February–2 March 2014; pp. 1–6. [Google Scholar]
- Li, D.; Wu, Y.; Zhu, M. Nonbinary LDPC Code for Noncoherent Underwater Acoustic Communication under Non-Gaussian Noise. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–6. [Google Scholar]
- Chitre, M.; Potter, J.; Heng, O.S. Underwater Acoustic Channel Characterisation for Medium-Range Shallow Water Communications. In Proceedings of the Oceans’ 04 MTS/IEEE Techno-Ocean’04 (IEEE Cat. No. 04CH37600), Kobe, Japan, 9–12 November 2004; Volume 1, pp. 40–45. [Google Scholar]
- Yang, C.; Wang, L.; Peng, C.; Zhang, S.; Cui, Y.; Ma, C. A Robust Time-Frequency Synchronization Method for Underwater Acoustic OFDM Communication Systems. IEEE Access 2024, 12, 21908–21920. [Google Scholar] [CrossRef]
- Du, L.; Li, H.; Wang, L.; Lin, X.; Lv, Z. Research on High Robustness Underwater Target Estimation Method Based on Variational Sparse Bayesian Inference. Remote Sens. 2023, 15, 3222. [Google Scholar] [CrossRef]
- Schürch, C. A Partial Order for the Synthesized Channels of a Polar Code. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 220–224. [Google Scholar]
- Xiaomei, X.; Yougan, C.; Lan, Z.; Wei, F. Comparison of the Performance of LDPC Codes over Different Underwater Acoustic Channels. In Proceedings of the 2010 IEEE 12th International Conference on Communication Technology, Nanjing, China, 11–14 November 2010; pp. 155–158. [Google Scholar]
- Yuhui, A.; Junying, H.; Jing, G. A Simulation Study on Correlation Equalization of Underwater Acoustic Channels. Acta Acust. 1999, 24, 589–597. [Google Scholar]
- Chen, Z.; Xu, X.; Chen, Y. Application of Protograph-Based LDPC Codes in Underwater Acoustic Channels. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 5–8 August 2014; pp. 923–927. [Google Scholar]
- Huawei, H. Polar Code Design and Rate Matching. In Proceedings of the 3GPP TSG RAN WG1 Meeting# 86, Gothenburg, Sweden, 22–26 August 2016; pp. 22–26. [Google Scholar]
- Zhou, Y.; Li, R.; Zhang, H.; Luo, H.; Wang, J. Polarization Weight Family Methods for Polar Code Construction. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar]
- NOAA Pacific Islands Fisheries Science Center. Pacific Islands Passive Acoustic Network (PIPAN) 10kHz Data; NOAA National Centers for Environmental Information: Honolulu, HI, USA, 2021. [Google Scholar]
- Lange, K.L.; Little, R.J.; Taylor, J.M. Robust Statistical Modeling Using the t Distribution. J. Am. Stat. Assoc. 1989, 84, 881–896. [Google Scholar] [CrossRef]
- Panaro, J.S.; Lopes, F.R.; Barreira, L.M.; Souza, F.E. Underwater Acoustic Noise Model for Shallow Water Communications. In Proceedings of the Brazilian Telecommunication Symposium, Brasília, Brazil, 13–16 September 2012; Volume 2. [Google Scholar]
- Park, B.; Cheon, H.; Kang, C.; Hong, D. A Novel Timing Estimation Method for OFDM Systems. IEEE Commun. Lett. 2003, 7, 239–241. [Google Scholar] [CrossRef]
- Schmidl, T.M.; Cox, D.C. Robust Frequency and Timing Synchronization for OFDM. IEEE Trans. Commun. 1997, 45, 1613–1621. [Google Scholar] [CrossRef]
- Minn, H.; Zeng, M.; Bhargava, V.K. On Timing Offset Estimation for OFDM Systems. IEEE Commun. Lett. 2000, 4, 242–244. [Google Scholar] [CrossRef]
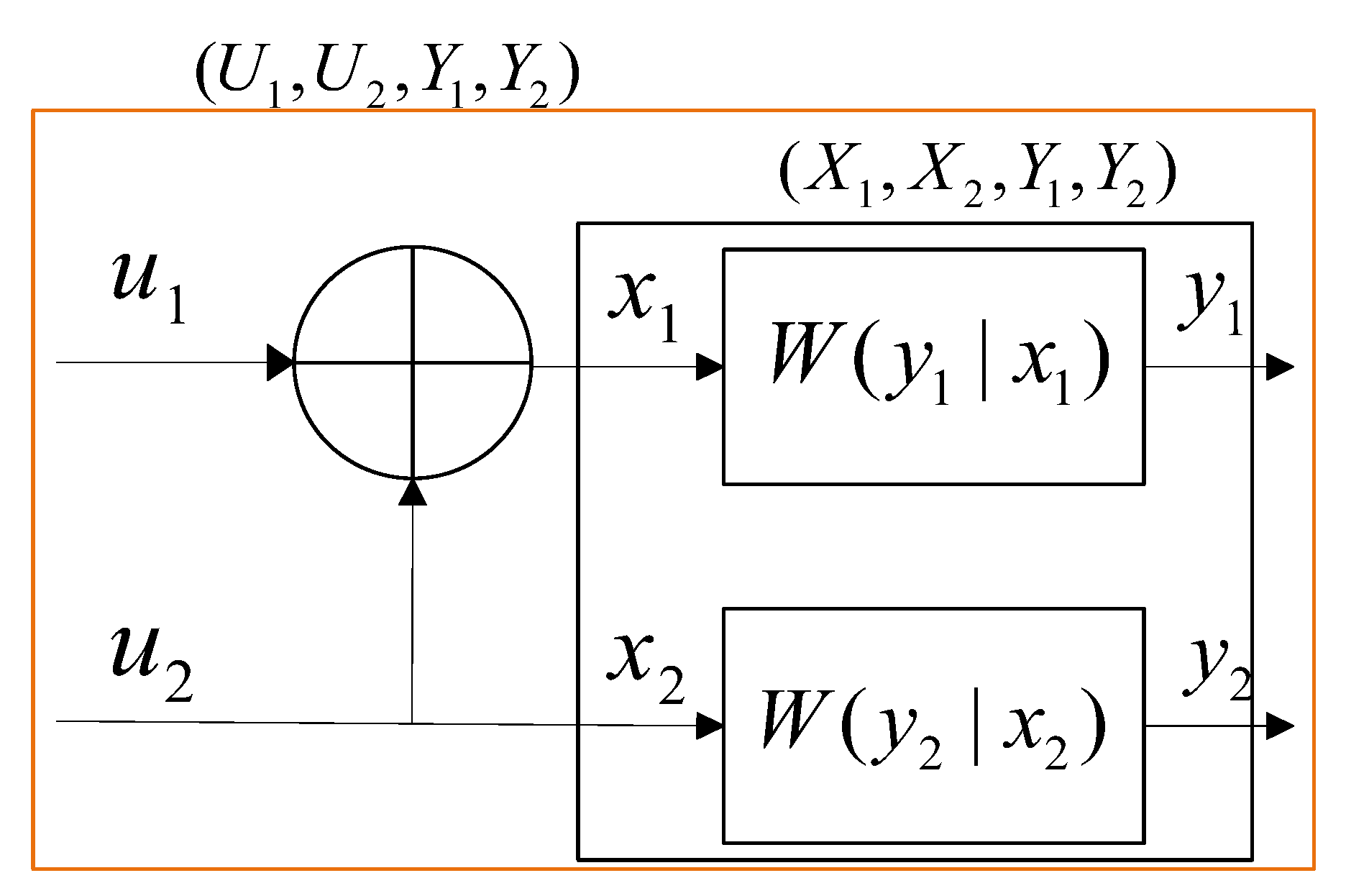

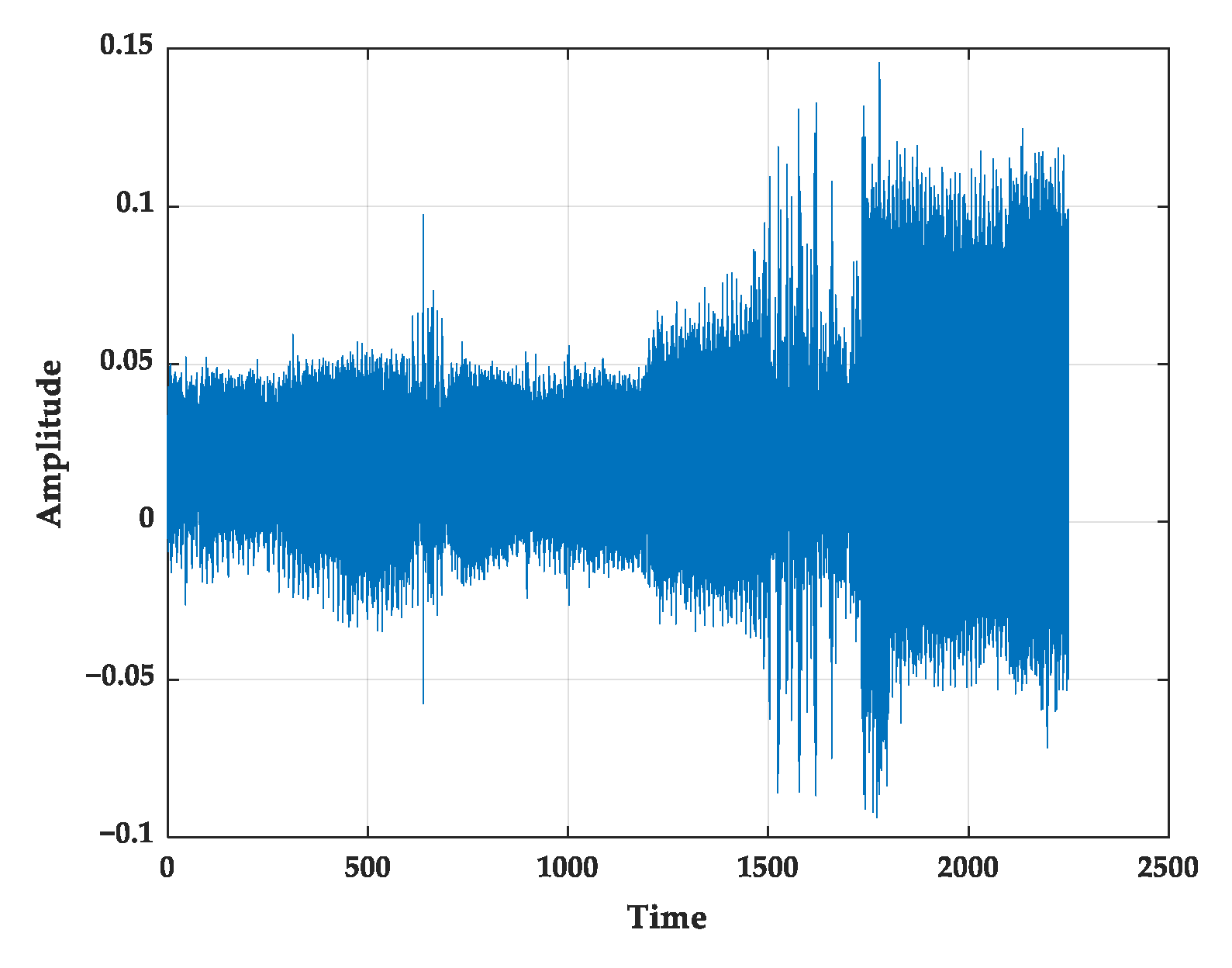


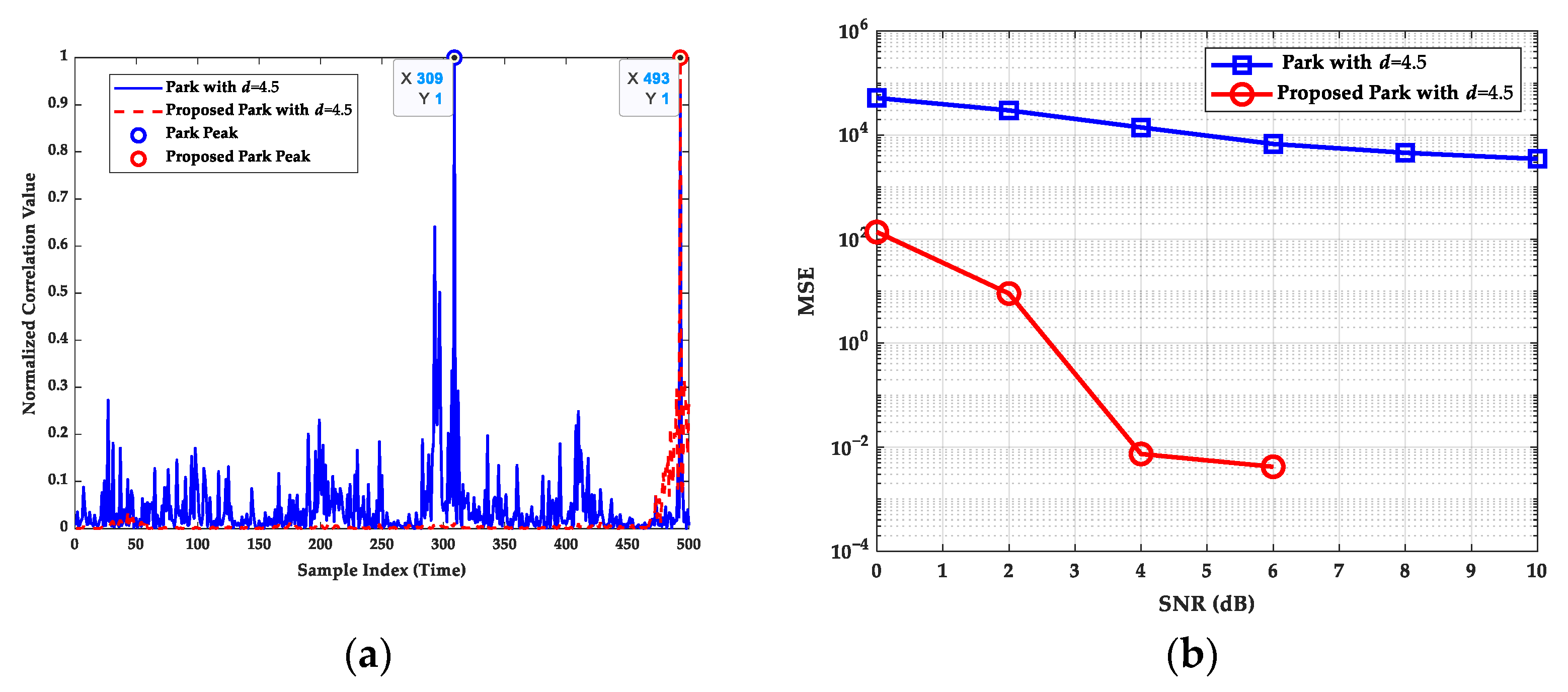
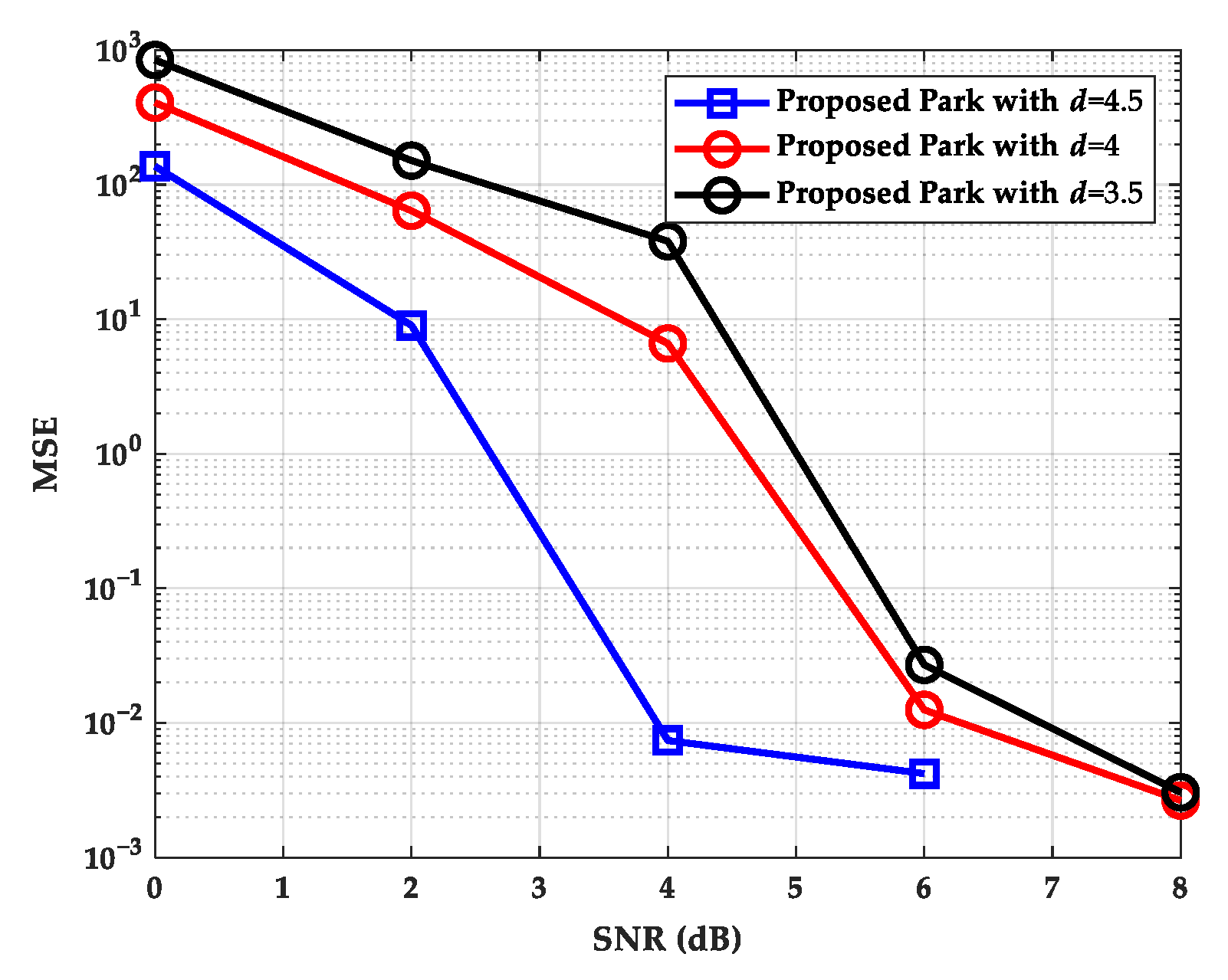
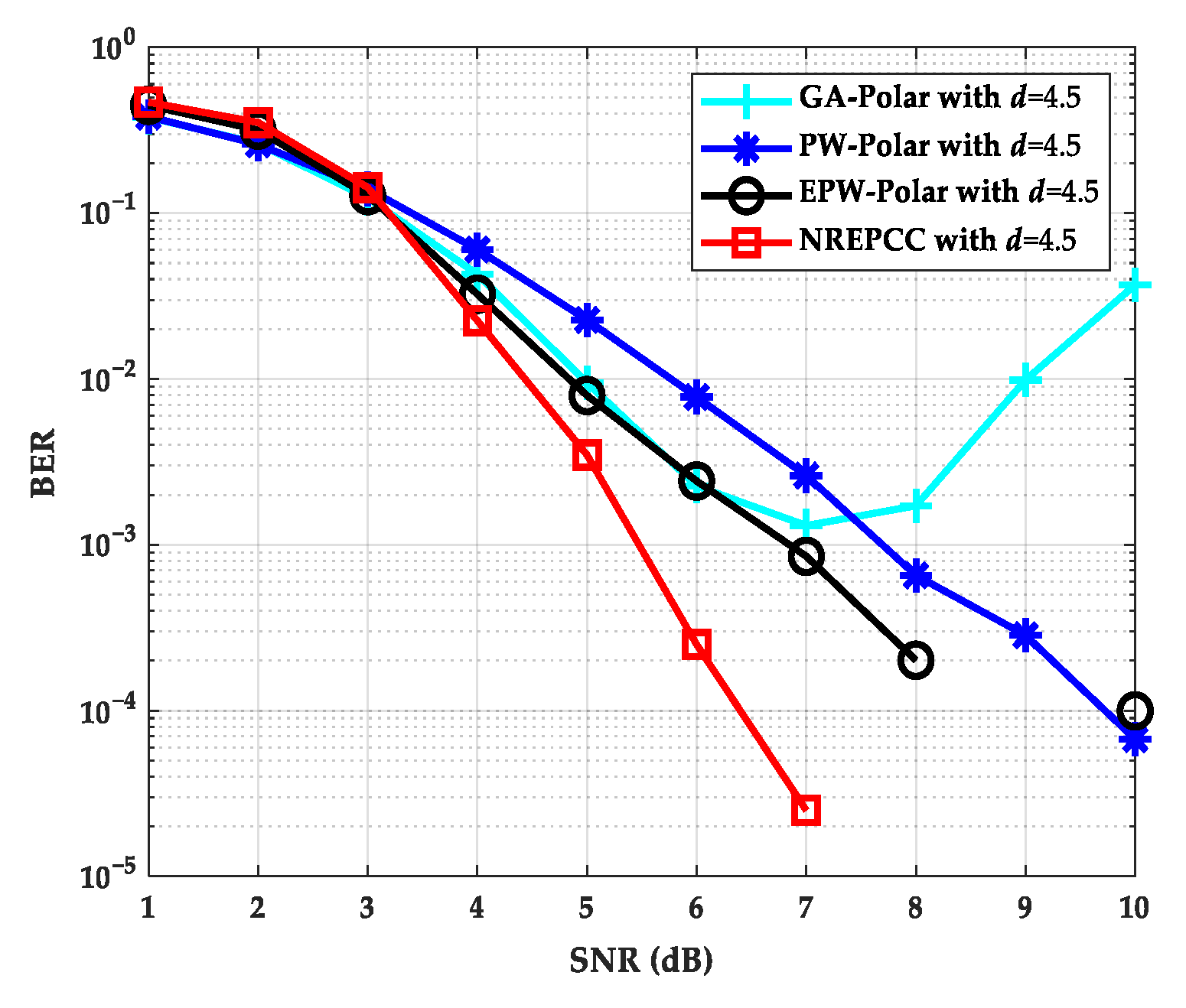


| Noise Model | AIC | BIC |
|---|---|---|
| Gaussian | −107,491,628.6979 | −107,491,598.8399 |
| GMM | −108,780,143.1434 | −108,780,098.3563 |
| -distribution | −108,977,389.7535 | −108,977,315.1084 |
| Hardware | Memory | CPU |
|---|---|---|
| 8 GB | Inter(R) Core(TM) i7-8565U CPU@1.80 GHz | |
| Software | Platform | Operation System |
| Matlab R2023a | Windows 11 |
| Parameter | Value |
|---|---|
| Mapping | QPSK |
| CP Length | 16 |
| Sync Preamble | PN Signal, Length: |
| Channel Estimation | Pilot-Assisted and Training-Based Channel Estimation (802.11a) |
| Correction Coding | Polar; LDPC; Turbo; Convolutional; R: ; ; |
| Number of Subchannels | 64/Symbol |
| Coding Technique | Encoding Complexity | Decoding Complexity |
|---|---|---|
| Polar Codes | ||
| LDPC Codes | ||
| Turbo Codes | ||
| Convolutional Codes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xian, J.; Li, Z.; Wu, H.; Wang, W.; Chen, X.; Mei, X.; Zhang, Y.; Han, B.; Ma, J. Novel Polarization Construction Method and Synchronization Algorithm for Underwater Acoustic Channel Under T-Distribution Noise Environment. J. Mar. Sci. Eng. 2025, 13, 362. https://doi.org/10.3390/jmse13020362
Xian J, Li Z, Wu H, Wang W, Chen X, Mei X, Zhang Y, Han B, Ma J. Novel Polarization Construction Method and Synchronization Algorithm for Underwater Acoustic Channel Under T-Distribution Noise Environment. Journal of Marine Science and Engineering. 2025; 13(2):362. https://doi.org/10.3390/jmse13020362
Chicago/Turabian StyleXian, Jiangfeng, Zhisheng Li, Huafeng Wu, Weijun Wang, Xinqiang Chen, Xiaojun Mei, Yuanyuan Zhang, Bing Han, and Junling Ma. 2025. "Novel Polarization Construction Method and Synchronization Algorithm for Underwater Acoustic Channel Under T-Distribution Noise Environment" Journal of Marine Science and Engineering 13, no. 2: 362. https://doi.org/10.3390/jmse13020362
APA StyleXian, J., Li, Z., Wu, H., Wang, W., Chen, X., Mei, X., Zhang, Y., Han, B., & Ma, J. (2025). Novel Polarization Construction Method and Synchronization Algorithm for Underwater Acoustic Channel Under T-Distribution Noise Environment. Journal of Marine Science and Engineering, 13(2), 362. https://doi.org/10.3390/jmse13020362








