Ship Anomalous Behavior Detection Based on BPEF Mining and Text Similarity
Abstract
1. Introduction
2. Methods
2.1. BPEF Mining Modeling
2.1.1. AIS Data Processing
- MMSI Code Validation: Retain MMSI codes with a length of 9 digits to ensure the uniqueness of maritime mobile communication services.
- Geographic Range Filtering: Retain data with longitude less than 180° and latitude less than 90° to ensure geographic validity.
- Speed and Course Validation: Retain records with speed and course within normal ranges. Specifically, we limit heading values strictly to between 0 and 360 degrees to conform with standard navigational practices, where 0 degrees represents true north and 360 degrees completes the circle, thus ensuring all heading values are within this circular range. Additionally, speeds are ensured not to exceed a reasonable range, relevant to the type of vessel and prevailing conditions.
- Redundant Data Removal: Remove duplicate records from the AIS data. Additionally, if a ship has insufficient trajectory points to reflect its movement characteristics, such data are discarded.
- Drift Point Filtering: Eliminate trajectory drift points in the ship navigation data to improve accuracy.
2.1.2. Behavioral Pattern Characteristics
2.1.3. Behavioral Pattern Association Combinations
2.2. Behavioral Sequence Chain Construction
2.2.1. Behavior Symbolization and Vector Construction
- Time Ratio (T): The time ratio represents the relative position of a specific behavioral pattern within the entire behavioral period. It normalizes the occurrence time of a behavior into the range of [0, 1]. Specifically, Tevent, Tstart, and Tend represent the absolute time of the behavioral event, the time the vessel enters the specified area, and the time it leaves, respectively, all measured in seconds. The time ratio is calculated as shown in Equation (1).
- 2.
- Grid encoding (G): Grid encoding represents the vessel’s geographical location by mapping its latitude and longitude coordinates to predefined grids. The area of interest is divided into fixed-size grids (e.g., 0.01° × 0.01°), and the vessel’s coordinates are assigned to the corresponding grid, producing the grid index G, This index is calculated based on the row (Row) and column (Col) indices of the grid. The specific calculation method is Equations (2)–(4).
- 3.
- Speed Over Ground (S): S represents the rate at which a vessel moves per unit of time and is typically measured in knots (1 knot = 1 nautical mile/h). This value is directly obtained from AIS data.
- 4.
- Sine and cosine values of heading angle(Sin(θ), Cos(θ)): The heading angle θ, measured in degrees and directly obtained from AIS data, is cyclic since 0° and 360° represent the same direction and is transformed into its Sin(θ) and Cos(θ) values to better capture this periodicity. The specific calculation method is outlined in Equations (5) and (6).
2.2.2. Behavioral Sequence Chain
2.3. Anomaly Detection
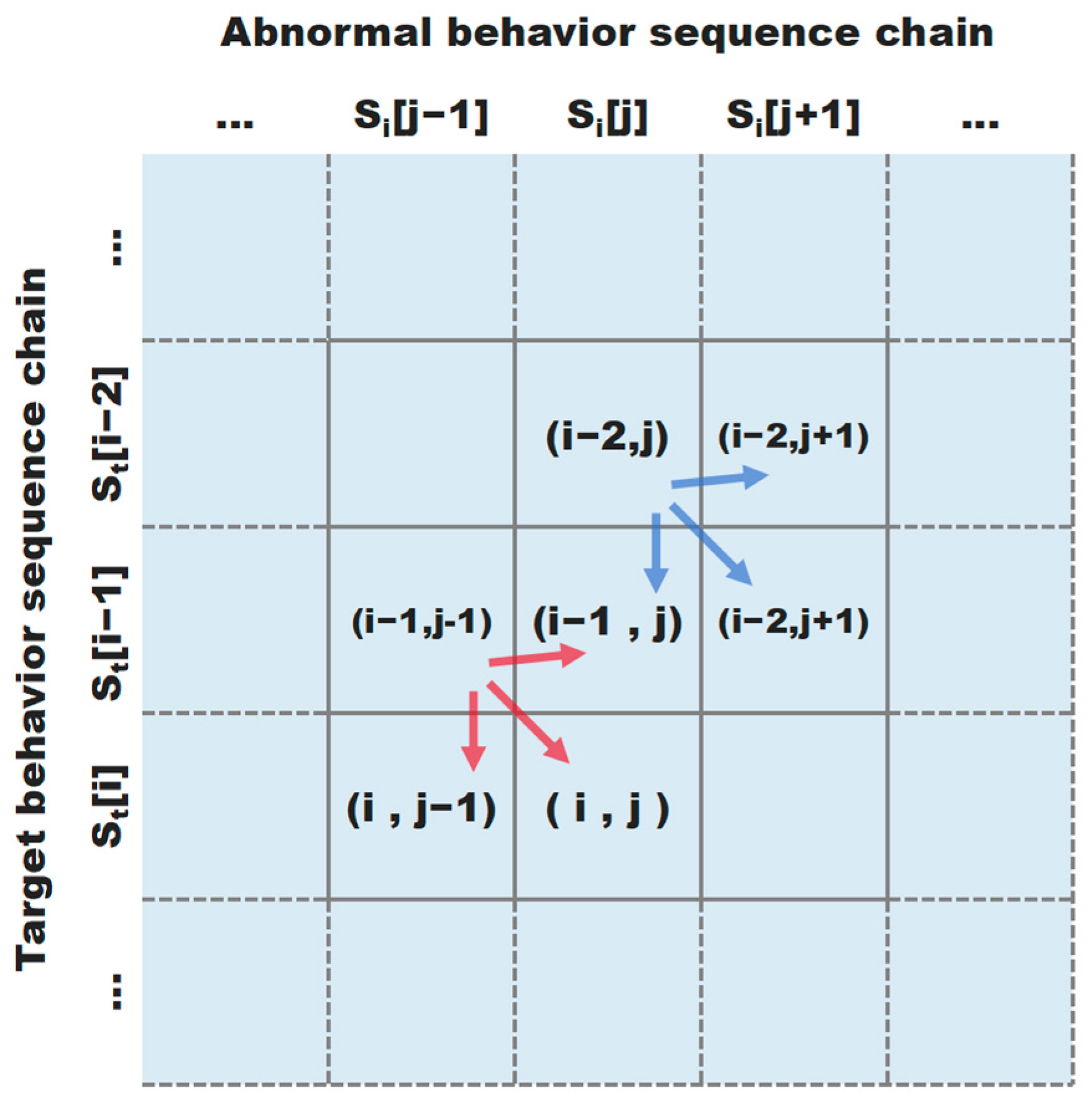
2.3.1. Smith–Waterman Local Alignment
2.3.2. Similarity Calculation
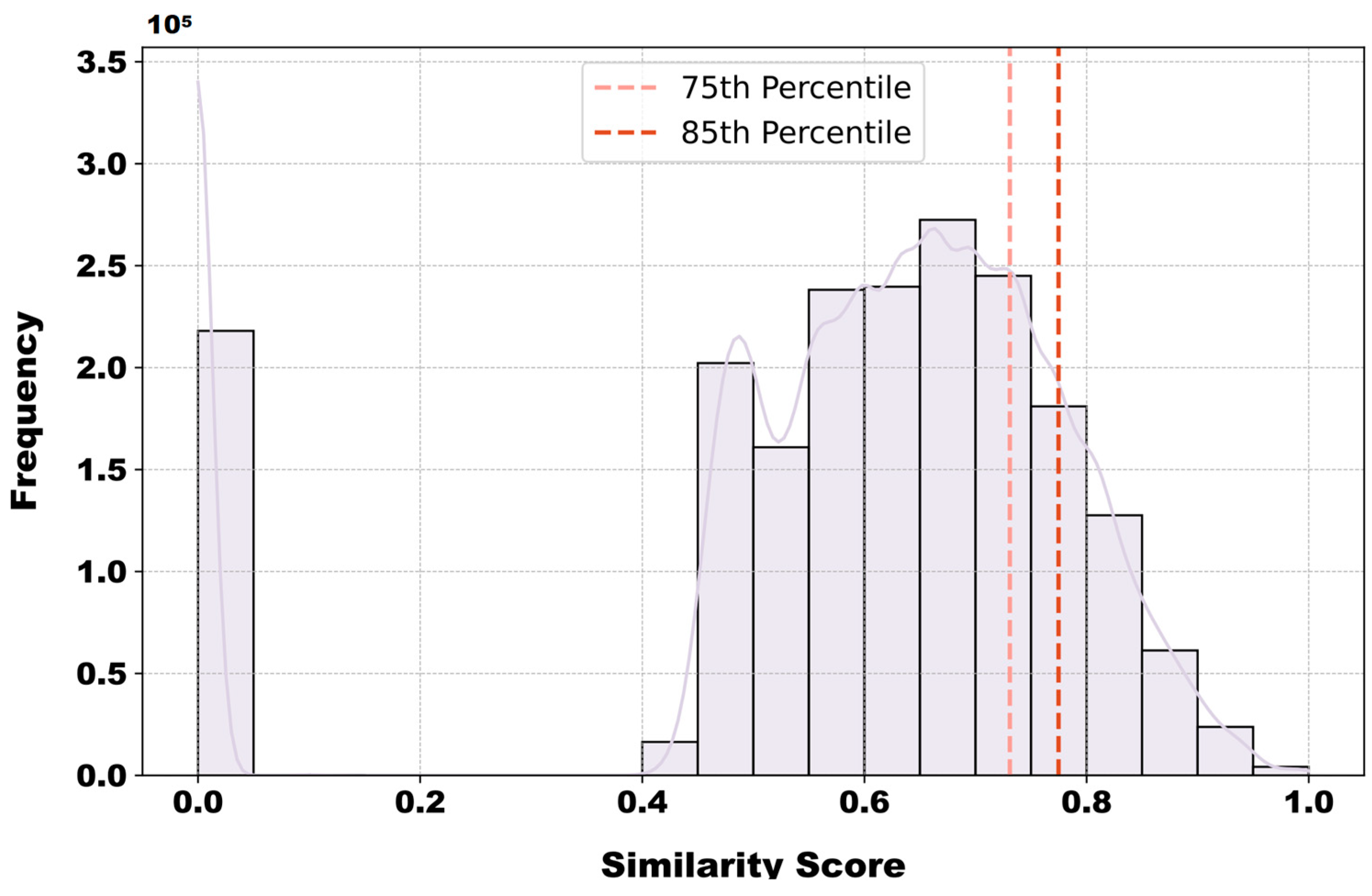
2.3.3. Adaptive Parameter Adjustment
2.4. Mainstream Algorithms for Ship Anomalous Behavior Detection
2.4.1. LSTM
2.4.2. iForest
2.4.3. HDBSCAN
2.5. Evaluation Metrics
3. Experiments and Results
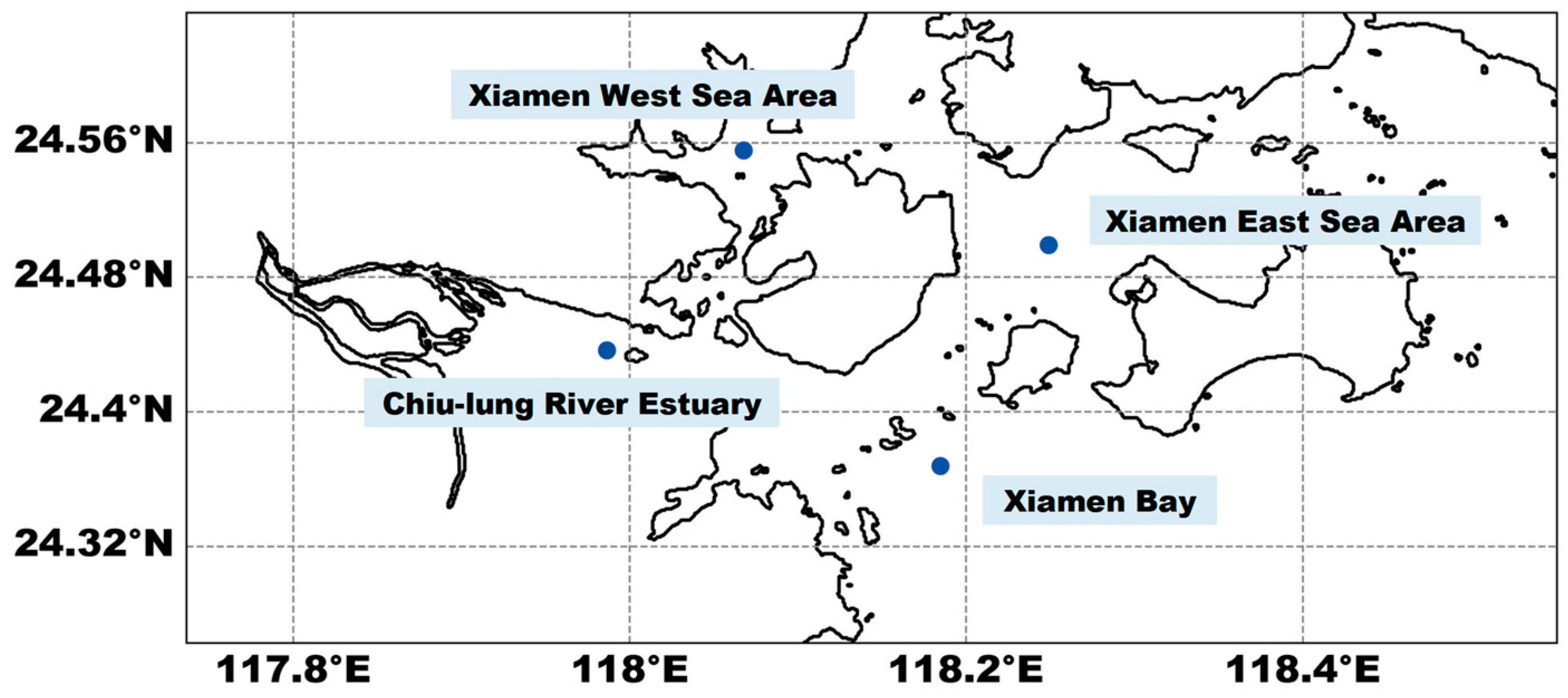
3.1. Study Area and Experimental Setup
3.2. Experimental Results and Analysis
3.2.1. Optimal Model Input Parameters Selection
3.2.2. Dynamic Trends and Validation of Model Performance Indicators
3.2.3. Comparative Experiment with Mainstream Algorithms
4. Discussion
- Over-reliance on AIS data quality: During the experiment, we observed that the BPEF-TSD method is heavily dependent on the quality of AIS data, and its performance is limited by the available anomalous vessel data. AIS data integrity is essential for accurately capturing vessel behavior patterns, but the small number of anomalous data samples restricts model training and validation. To address the lack of real-world anomalous data, we introduced a synthetic data generation method that combines normal and anomalous behaviors, enhancing the dataset and model robustness. However, synthetic data may not fully capture the complexities of real-world anomalies, which could impact detection accuracy in actual maritime environments [40]. In the future, we can employ data augmentation techniques, such as SMOTE, to increase the number of anomalous samples [41,42]. Additionally, data fusion techniques can be used to integrate other data sources, such as radar, satellite imagery, and optical sensors, reducing reliance on a single data source and improving the accuracy and reliability of the detection process [43,44].
- Generalizability of the Xiamen Port data: This study focuses on Xiamen Port, a key coastal and container port in China. However, the methods we developed are designed to be adaptable to other maritime environments. We selected Xiamen Port because it represents typical maritime behaviors, such as navigation, docking, and cargo handling. The BPEF-TSD framework, built on general principles of ship behavior, can be applied to other ports or waterways with similar conditions. By leveraging behavioral patterns, similarity measures, and anomaly detection algorithms, the framework demonstrates broad applicability. In future work, we plan to further test and validate the framework using data from other waterways. This will enable us to evaluate its effectiveness across a wider range of maritime environments, ensuring that the proposed anomaly detection system is not only suitable for Xiamen Port but also adaptable to various maritime contexts.
- Limited applicability to multi-vessel scenarios: The BPEF-TSD method primarily targets the behavior patterns of individual vessels and does not fully account for multi-vessel coexistence scenarios, such as escorting or overtaking. This limitation reduces the method’s effectiveness in areas with frequent vessel interactions [45]. Future research could expand the behavior pattern recognition algorithm to analyze collective vessel behavior, enhancing its ability to recognize complex patterns such as group navigation and strategic avoidance [46,47].
- Challenges in threshold setting: In this study, we used a single threshold for anomaly behavior detection. In practical applications, the complexity of data characteristics and scenarios may render a fixed threshold unsuitable for all cases. Specifically, both excessively high and low thresholds can lead to incorrect anomaly detection. Previous studies have explored this issue, highlighting that the selection of an appropriate threshold should consider both data characteristics and the application scenario [48]. In the future, adaptive threshold techniques could be considered to dynamically adjust thresholds based on real-time data, or machine learning methods could be employed to automatically learn the optimal threshold, potentially improving detection sensitivity and accuracy [49].
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xin, X.; Liu, K.; Loughney, S.; Wang, J.; Yang, Z. Maritime Traffic Clustering to Capture High-Risk Multi-Ship Encounters in Complex Waters. Reliab. Eng. Syst. Saf. 2023, 230, 108936. [Google Scholar] [CrossRef]
- Durlik, I.; Miller, T.; Dorobczyński, L.; Kozlovska, P.; Kostecki, T. Revolutionizing Marine Traffic Management: A Comprehensive Review of Machine Learning Applications in Complex Maritime Systems. Appl. Sci. 2023, 13, 8099. [Google Scholar] [CrossRef]
- Li, B. Multi-Feature Fusion Anomaly Detection Model Based on Ship Behavior Analysis; Dalian Maritime University: Dalian, China, 2022. [Google Scholar]
- Wang, L.; Chen, P.; Chen, L.; Mou, J. Ship Ais Trajectory Clustering: An Hdbscan-Based Approach. J. Mar. Sci. Eng. 2021, 9, 566. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, S.; Suo, Y. Research Progress of Ship Behavior Anomaly Detection. J. Transp. Inf. Saf. 2020, 38, 1–11. [Google Scholar]
- Tang, H.; Yin, Y.; Shen, H. Survey of Abnormal Behavior of Marine Vessels. J. Chongqing Jiaotong Univ. Nat. Sci. 2019, 38, 109–115. [Google Scholar]
- Zhang, B.; Ren, H.; Wang, P.; Wang, D. Research Progress on Ship Anomaly Detection Based on Big Data. In Proceedings of the 2020 IEEE 11th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 16–18 October 2020; pp. 316–320. [Google Scholar]
- Rong, H.; Teixeira, A.P.; Guedes Soares, C. Data Mining Approach to Shipping Route Characterization and Anomaly Detection Based on Ais Data. Ocean Eng. 2020, 198, 106936. [Google Scholar] [CrossRef]
- Yu, S.; Zhou, H.; Ye, C.; Wang, T. Sdfa: Study on Ship Trajectory Clustering Method Based on Multi-Feature Fusion. Comput. Sci. 2022, 49, 250–260. [Google Scholar]
- Wei, H.; Chen, Z.; Zhang, L. Anomaly Detection Framework of System Call Trace Based on Sequence and Frequency Patterns. Comput. Sci. 2022, 49, 350–355. [Google Scholar]
- Zhou, Y.; Damen, W.; Vellinga, T.; Hoogendoorn, S.P. Ship Classification Based on Ship Behavior Clustering from Ais Data. Ocean Eng. 2019, 175, 176–187. [Google Scholar] [CrossRef]
- Sun, S.; Chen, Y.; Zhang, J. Trajectory Outlier Detection Algorithm for Ship Ais Data Based on Dynamic Differential Threshold. J. Phys. Conf. Ser. 2020, 1437, 012013. [Google Scholar]
- Yang, A.; Chang, X.; Zhang, Q.; Zhao, F. Abnormal Behavior Detection of Ships in Sensitive Water Area Based on Ais Data. Command. Inf. Syst. Technol. 2023, 14, 32–37. [Google Scholar]
- Xie, Z.; Bai, X.; Xu, X.; Xiao, Y. An Anomaly Detection Method Based on Ship Behavior Trajectory. Ocean Eng. 2024, 293, 116640. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, S.; Wang, J.; Xiong, N.N. Anomaly Detection Based on Convolutional Recurrent Autoencoder for Iot Time Series. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 112–122. [Google Scholar] [CrossRef]
- Czaplewski, B.; Dzwonkowski, M. A Novel Approach Exploiting Properties of Convolutional Neural Networks for Vessel Movement Anomaly Detection and Classification. ISA Trans. 2022, 119, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhao, K.; Cai, C.; Ding, M.; Wang, P. Analysis of Vessel Abnormal Behavior Based on Dbscan and Iforest Algorithms. Ship Electron. Eng. 2021, 41, 89–94. [Google Scholar]
- Wang, F.; Lei, Y.; Liu, Z.; Wang, X.; Ji, S.; Tung, A.K.H. Fast and Parameter-Light Rare Behavior Detection in Maritime Trajectories. Inf. Process. Manag. 2020, 57, 102268. [Google Scholar] [CrossRef]
- Shi, Y.; Long, C.; Yang, X.; Deng, M. Abnormal Ship Behavior Detection Based on Ais Data. Appl. Sci. 2022, 12, 4635. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Chen, W. Anomaly Detection for Condition Monitoring Data Using Auxiliary Feature Vector and Density-Based Clustering. IET Gener. Transm. Distrib. 2019, 14, 108–118. [Google Scholar] [CrossRef]
- Pallotta, G.; Vespe, M.; Bryan, K. Vessel Pattern Knowledge Discovery from Ais Data: A Framework for Anomaly Detection and Route Prediction. Entropy 2013, 15, 2218–2245. [Google Scholar] [CrossRef]
- Zhao, L.; Shi, G. Maritime Anomaly Detection Using Density-Based Clustering and Recurrent Neural Network. J. Navig. 2019, 72, 894–916. [Google Scholar] [CrossRef]
- Singh, S.K.; Fowdur, J.S.; Gawlikowski, J.; Medina, D. Leveraging Graph and Deep Learning Uncertainties to Detect Anomalous Maritime Trajectories. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23488–23502. [Google Scholar] [CrossRef]
- Karataş, G.B.; Karagoz, P.; Ayran, O. Trajectory Pattern Extraction and Anomaly Detection for Maritime Vessels. Internet Things 2021, 16, 100436. [Google Scholar] [CrossRef]
- Jin, L.; Luo, Z.; Gao, S. Visual Analytics Approach to Vessel Behavior Analysis. J. Navig. 2018, 71, 1195–1209. [Google Scholar] [CrossRef]
- Coleman, J.; Kandah, F.; Huber, B. Behavioral Model Anomaly Detection in Automatic Identification Systems (Ais). In Proceedings of the 2020 10th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 6–8 January 2020; pp. 481–487. [Google Scholar]
- Tang, H.; Wei, L.; Yin, Y.; Shen, H.; Qi, Y. Detection of Abnormal Vessel Behavior Based on Probabilistic Directed Graph Model. J. Navig. 2020, 73, 1014–1035. [Google Scholar] [CrossRef]
- He, F.; He, Z.; Yang, F.; Liu, L. Research on Recognition Method of Abnormal Behavior of Ships Based on Electronic Chart. J. Wuhan Univ. Technol. Transp. Sci. Eng. 2019, 43, 631–636+645. [Google Scholar]
- Bao, L. A Trajectory Data Anomaly Detection Method Based on Trajectory Cluster Distance. Ship Electron. Eng. 2020, 40, 56. [Google Scholar]
- Solano-Carrillo, E.; Carrillo-Perez, B.; Flenker, T.; Steiniger, Y.; Stope, J. Detection and Geo visualization of Abnormal Vessel Behavior from Video. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 2193–2199. [Google Scholar]
- Dorsey, L.T.C.; Wang, B.; Grabowski, M.; Merrick, J.; Harrald, J.R. Self-Healing Databases for Predictive Risk Analytics in Safety-Critical Systems. J. Loss Prev. Process Ind. 2020, 63, 104014. [Google Scholar] [CrossRef]
- Rawson, A.; Brito, M. A Survey of the Opportunities and Challenges of Supervised Machine Learning in Maritime Risk Analysis. Transp. Rev. 2022, 43, 108–130. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, X.; Li, K.X.; Zhou, Y.; Yuen, K.F. Research Topics and Trends in the Maritime Transport: A Structural Topic Model. Transp. Policy 2021, 102, 11–24. [Google Scholar] [CrossRef]
- Amur, Z.H.; Kwang Hooi, Y.; Bhanbhro, H.; Dahri, K.; Soomro, G.M. Short-Text Semantic Similarity (Stss): Techniques, Challenges and Future Perspectives. Appl. Sci. 2023, 13, 3911. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Huang, G.; Guo, Q.; Li, H.; Wei, X. A Short-Text Similarity Model Combining Semantic and Syntactic Information. Electronics 2023, 12, 3126. [Google Scholar] [CrossRef]
- Schopf, T.; Braun, D.; Matthes, F. Semantic Label Representations with lbl2vec: A Similarity-Based Approach for unsupervised Text Classification. In Proceedings of the Web Information Systems and Technologies, Virtual, 26–28 October 2021; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Ismail, S.; Shishtawy, T.E.L.; Alsammak, A.K. A New Alignment Word-Space Approach for Measuring Semantic Similarity for Arabic Text. Int. J. Semant. Web Inf. Syst. 2022, 18, 1–18. [Google Scholar] [CrossRef]
- Deforche, M.; De Vos, I.; Bronselaer, A.; De Tré, G. A Hierarchical Orthographic Similarity Measure for Interconnected Texts Represented by Graphs. Appl. Sci. 2024, 14, 1529. [Google Scholar] [CrossRef]
- Zhang, Z. Ship Behavior Pattern Mining Based on Event Flow; Jimei University: Xiamen, China, 2021. [Google Scholar]
- Du, Y.; Li, L.; Hou, R. Convolutional Neural Network-Based Data Anomaly Detection Considering Class Imbalance with Limited Data. Smart Struct. Syst. 2022, 29, 63–75. [Google Scholar]
- Dablain, D.; Krawczyk, B.; Chawla, N.V. Deepsmote: Fusing Deep Learning and Smote for Imbalanced Data. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 6390–6404. [Google Scholar] [CrossRef]
- Pradipta, G.A.; Wardoyo, R.; Musdholifah, A.; Sanjaya, I.N.H.; Ismail, M. Smote for Handling Imbalanced Data Problem: A Review. In Proceedings of the 2021 Sixth International Conference on Informatics and Computing (ICIC), Virtual, 3–4 November 2021; pp. 1–8. [Google Scholar]
- Zheng, R.; Yu, S.; Wang, J.; Wang, J. Radar-Vision Fusion-Based Object Detection for Abnormal Data. In Proceedings of the Fourth International Conference on Telecommunications, Optics, and Computer Science (TOCS 2023), Xi’an, China, 15–16 December 2023. [Google Scholar]
- Long, J.; Luo, C.; Chen, R. Multivariate Time Series Anomaly Detection with Improved Encoder-Decoder Based Model. In Proceedings of the 2023 IEEE 10th International Conference on Cyber Security and Cloud Computing (CS Cloud)/2023 IEEE 9th International Conference on Edge Computing and Scalable Cloud (Edge Com), Xiangtan, China, 1–3 July 2023; pp. 161–166. [Google Scholar]
- Qiang, H.; Guo, Z.; Peng, X.; Jia, C. Fdbr: Ultra-Fast and Data-Efficient Behavior Recognition of Port Vessels Using a Statistical Framework. Ocean Eng. 2025, 315, 119737. [Google Scholar] [CrossRef]
- Lyu, H.; Ma, X.; Tan, G.; Yin, Y.; Sun, X.; Zhang, L.; Kang, X.; Song, J. Identification of Complex Multi-Vessel Encounter Scenarios and Collision Avoidance Decision Modeling for Mass. J. Mar. Sci. Eng. 2024, 12, 1289. [Google Scholar] [CrossRef]
- Papageorgiou, D.; Hansen, P.N.; Dittmann, K.; Blanke, M. Anticipation of Ship Behaviors in Multi-Vessel Scenarios. Ocean Eng. 2022, 266, 112777. [Google Scholar] [CrossRef]
- Pan, G.; Qian, J.; Ouyang, J.; Luo, Y.; Wang, H. Adaptive Threshold Event Detection Method Based on Standard Deviation. Meas. Sci. Technol. 2023, 34, 075903. [Google Scholar] [CrossRef]
- Yuan, Y.; Huang, Y.; Yuan, Y.; Wang, J. Dynamic Threshold-Based Two-Layer Online Unsupervised Anomaly Detector. arXiv 2024, arXiv:2410.22967. [Google Scholar]


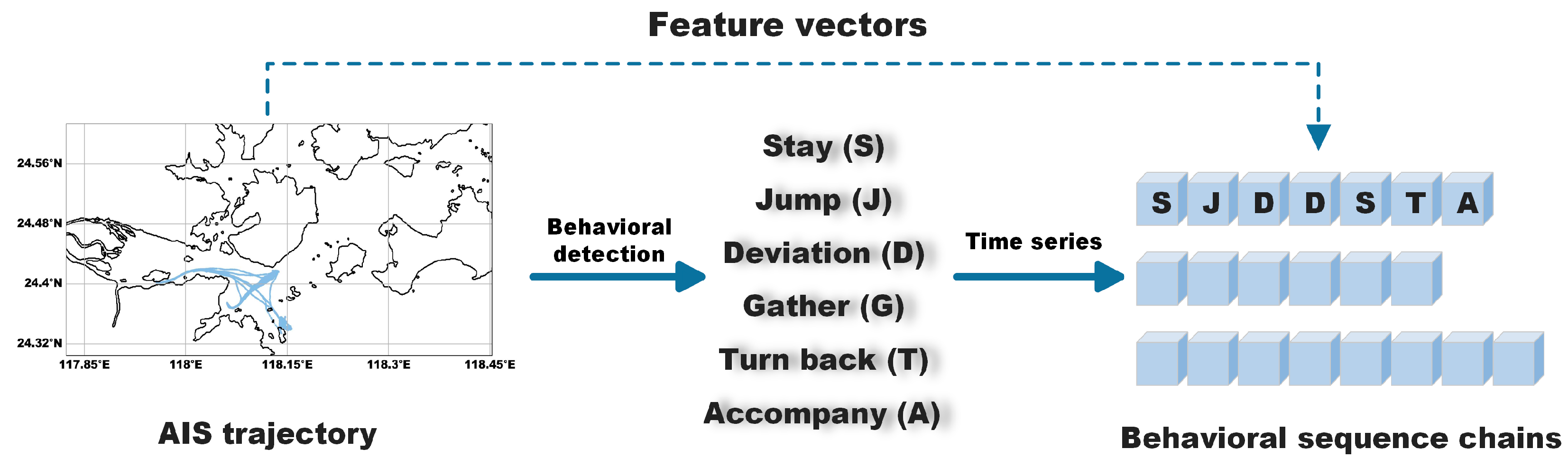






| Behavioral Pattern | Definition and Mathematical Expressions |
|---|---|
| Stay | The vessel maintains a low speed or even a speed of zero over a period of time, typically occurring during berthing or anchoring processes, with trajectory points densely distributed in space. |
| Jump | Due to AIS signal interruption or equipment malfunction, the vessel experiences missing trajectory data over a period of time, resulting in longer time gaps between trajectory points and causing breaks or jumps in the trajectory. |
| Deviation | The vessel deviates from its regular course over a period of time, with the trajectory straying from the main shipping lane, typically accompanied by abnormal changes in speed or heading. |
| Gather | The vessel remains at low speed or in a stationary state over a period of time and comes into close proximity with other vessels within the same spatial range, forming a cluster of vessels. |
| Accompany | Over a period of time, the vessel maintains a similar movement trajectory with one or more other vessels, remaining spatially close and synchronously moving within a similar timeframe. |
| Turn back | Over a period of time, the vessel repeatedly travels back and forth between symmetric starting and destination points, following the same routes or positional points. |
| Vessel Behavior Patterns | Symbolic Representation |
|---|---|
| Stay | “S” |
| Jump | “J” |
| Deviation | “D” |
| Gather | “G” |
| Accompany | “A” |
| Turn back | “T” |
| Model | Precision | Recall | F1-Score | Accuracy |
|---|---|---|---|---|
| BPEF-TSD | 0.964 | 0.928 | 0.945 | 0.910 |
| LSTM | 0.932 | 0.807 | 0.872 | 0.884 |
| iForest | 0.843 | 0.715 | 0.774 | 0.917 |
| HDBSCAN | 0.347 | 0.520 | 0.416 | 0.995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suo, Y.; Wang, Y.; Cui, L. Ship Anomalous Behavior Detection Based on BPEF Mining and Text Similarity. J. Mar. Sci. Eng. 2025, 13, 251. https://doi.org/10.3390/jmse13020251
Suo Y, Wang Y, Cui L. Ship Anomalous Behavior Detection Based on BPEF Mining and Text Similarity. Journal of Marine Science and Engineering. 2025; 13(2):251. https://doi.org/10.3390/jmse13020251
Chicago/Turabian StyleSuo, Yongfeng, Yan Wang, and Lei Cui. 2025. "Ship Anomalous Behavior Detection Based on BPEF Mining and Text Similarity" Journal of Marine Science and Engineering 13, no. 2: 251. https://doi.org/10.3390/jmse13020251
APA StyleSuo, Y., Wang, Y., & Cui, L. (2025). Ship Anomalous Behavior Detection Based on BPEF Mining and Text Similarity. Journal of Marine Science and Engineering, 13(2), 251. https://doi.org/10.3390/jmse13020251






