1. Introduction
Driven by carbon neutrality objectives, the offshore wind industry is advancing rapidly. With nearshore wind resources approaching saturation, deep offshore floating wind technology has become a focal point for future development [
1]. Floating offshore wind turbines rely on seabed anchoring systems for station-keeping, among which suction anchors are widely adopted due to their precise positioning capability, high installation efficiency, and adaptability to varying water depths and diverse seabed soil conditions [
2]. During operation, these anchors experience dynamic soil–structure interactions under mooring loads, posing dual risks of horizontal displacement failure and pull-out failure [
3], thereby compromising the safety of entire floating wind systems. Consequently, assessing the dynamic behaviors of suction anchors when subjected to mooring loads is of paramount importance.
Extensive research has been conducted on the dynamic characteristics exhibited by embedded suction anchors in soil, employing both numerical and experimental methods. Experimental methods primarily include field tests [
4,
5] and model tests [
6,
7,
8]. Ravichandran [
4] conducted field tests on suction anchors with varying diameters and lengths, performing static and cyclic pullout tests to evaluate their extraction behaviors under diverse loading conditions. Chen [
9] employed instrumented model caissons in a centrifuge testing program to assess the behaviors of sealed foundations under different loading conditions. The study, which encompassed normally consolidated, lightly overconsolidated, and sensitive clay deposits, specifically analyzed the changes in uplift capacity and external radial stress during sustained and cyclic loading. However, experimental methods require substantial funding and are time-intensive. Consequently, many researchers employ numerical approaches, predominantly using 3D finite element modeling [
10,
11,
12] to effectively account for soil nonlinearity, soil–structure gaps, and interaction effects through appropriate soil constitutive models and interface properties. While 3D finite element modeling delivers accurate results, its high computational cost and low efficiency have motivated proposals for simplified dynamic response analysis methods.
Simplified dynamic analysis methods designed specifically for suction anchors remain scarce. Nevertheless, as suction anchors constitute a class of embedded rigid foundations, relevant research can be referred to. Gazetas et al. [
13,
14,
15] and Dobry et al. [
16,
17] investigated multi-directional motions of arbitrarily shaped rigid foundations embedded in elastic half-spaces. Gazetas [
18] and Gerolymos [
19] compiled semi-analytical expressions for dynamic stiffness and damping at a foundation base center with a small (0~1) slenderness ratio (depth-to-diameter ratio) using boundary element methods and extensive published data, covering horizontal/vertical translation and rocking. Gadre and Dobry [
20] validated these formulations via centrifuge testing. Zhong [
21] extended applicability to slenderness ratio (1~4) by refining semi-analytical expressions through finite element modeling. However, the semi-analytical expressions compiled by Gazetas et al. [
18] reference the foundation’s base center, whereas mooring forces on suction anchors act at the sidewall padeye—not the base center. To efficiently compute displacements at the padeye (mooring connection point), this study will employ a robust methodology to derive the semi-analytical expressions for dynamic stiffness and damping in reference to the padeye location.
Moreover, in complex marine environments, scour is highly prevalent where seabed soil surrounding foundations erode under combined wave–current actions. Existing research confirms that soil–foundation dynamic characteristics are significantly altered by scour [
22,
23], consequently modifying the dynamic responses of suction anchors under loading [
24]. Hu et al. [
25] investigated local scour around caisson suction anchors under random waves, analyzing scour evolution processes and mechanisms while predicting equilibrium scour depths. Zhang et al. [
26] developed an analytical framework to assess pullout capacity during trench–scour development, revealing pronounced impacts of both trenching and scouring effects on anchor performance.
This study conducts numerical analysis on the mooring load-bearing behaviors of offshore wind suction anchor foundations. To facilitate swift and effective initial design, a streamlined dynamic analysis approach is introduced. Based on the assumption of a linearly elastic, homogeneous soil medium, leveraging dynamic impedance theory and coordinate transformation techniques, stiffness and damping matrices at arbitrary padeye locations are derived. The equations of motion for embedded suction anchors are established, with frequency-domain and time-domain solutions applied to resolve dynamic responses under both harmonic cyclic loading and irregular nonlinear mooring forces. This method achieves a balance between acceptable accuracy and computational speed. The complete framework is outlined in
Section 2. Validation against 3D finite element results in
Section 3 confirms the model’s reliability.
Section 4 presents selected mooring load cases and demonstrates dynamic responses at varying padeye elevations and scour depths. Concluding remarks are synthesized in
Section 5.
2. Mathematical Formulation
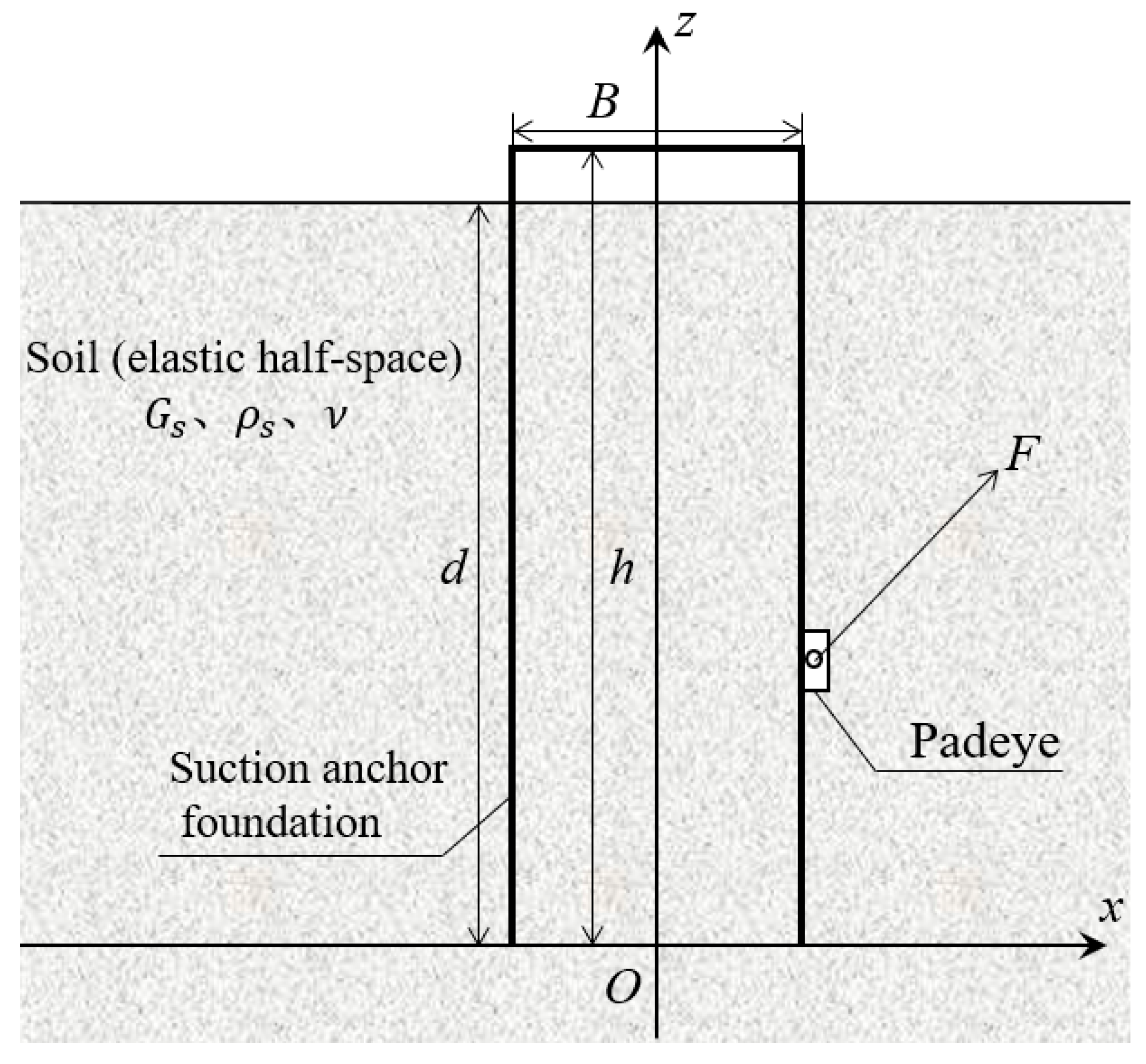
Consider a fully embedded suction anchor foundation interacting with seabed soil under mooring forces. Assuming complete consolidation of the internal soil, the suction anchor and its enclosed soil are simplified and analyzed as an integrated rigid body. For modeling purposes, a 2D Cartesian coordinate system
Oxz is established, as shown in
Figure 1, with its origin at the center of the anchor base. The
x-axis extends horizontally rightward along the base, while the
z-axis extends vertically upward along the central axis. The suction anchor has a height
h, embedment depth
d, and diameter
B. Mooring forces are applied at the padeye on the sidewall. The soil is modeled as a homogeneous, elastic half-space with shear modulus
, Poisson’s ratio
, and density
. Full interfacial contact between the suction anchor and surrounding soil is maintained throughout the analysis.
2.1. Suction Anchor Foundation Motion Equation
Under mooring forces, the motion of a suction anchor foundation primarily comprises three modes: horizontal displacement, vertical displacement, and rotation. Excessive horizontal displacement may trigger soil punching failure, while significant vertical displacement can lead to anchor pull-out. Defining point
as the padeye attachment point, the dynamic response equation for
is expressed as follows:
is the mass matrix,
is the damping matrix and
is the stiffness matrix of the suction anchor foundation. m is the sum of the mass of the suction anchor and the internal soil, with the soil mass accounting for the majority. The specific calculation methods for the damping matrix and stiffness matrix elements are presented in
Section 2.2.
is the displacement at
, which includes horizontal displacement
, vertical displacement
, and rotation angle
. The dots above the variable indicate its time derivative. Therefore,
and
are the velocity and acceleration of the padeye attachment point of the suction anchor
, respectively.
is the mooring force, which includes the horizontal component
, vertical component
and moment
.
and
represent the horizontal and vertical coordinates at the center of mass of the anchor–soil structure, respectively.
approximately represents the moment of inertia of the anchor-soil structure at point
, and it is calculated as follows:
2.2. Suction Anchor Foundation Stiffness and Damping Analysis
2.2.1. Embedded Foundation Impedance Functions
Treat the system composed of the suction anchor foundation and the internal soil as an embedded rigid foundation; the impedance functions for such foundations on a half-space [
18,
19,
21] are utilized to formulate the stiffness matrix
and damping matrix
at the center of the suction anchor’s bottom.
and
contain the following elements:
The horizontal dynamic stiffness
and damping
values [
18,
20] can be calculated as follows:
where
is the horizontal static stiffness of the surface-founded foundation,
is the horizontal embedment coefficient,
is the horizontal dynamic stiffness factor of the embedded foundation,
is the shear wave velocity of soil,
is the ‘Lysmer’s analog’ velocity, and
is the dimensionless frequency.
The vertical dynamic stiffness
and damping
values [
18] can be represented as follows:
where
is the vertical static stiffness of the surface-founded foundation,
is the vertical embedment coefficient, and
is the vertical dynamic stiffness factor of the embedded foundation.
The rocking dynamic stiffness
and damping
values [
18,
19,
21] can be calculated as follows:
where
is the rocking static stiffness of the surface-founded foundation,
and
are intermediate variables,
is the rocking embedment coefficient, and
is the rocking dynamic stiffness factor of the embedded foundation.
The coupled horizontal-rocking dynamic stiffness and damping factors for the center of the embedded suction anchors are determined [
18,
19,
21] by the following relationships:
2.2.2. Dynamic Stiffness and Damping Matrices at the Padeye
During operation, suction anchor foundations are subjected to mooring forces transmitted from the floating wind turbine platform. These forces act at the padeye attachment point on the sidewall rather than at the foundation’s bottom center. Consequently, displacement calculation at the load application point (i.e., the padeye location) under mooring forces constitutes a critical research focus. This study establishes dynamic stiffness and damping matrices at arbitrary surface points (including the padeye) through coordinate transformation of the base–center dynamic stiffness and damping derived in
Section 2.2.1, thus enabling rapid determination of the anchor’s dynamic response. The detailed derivation process is presented as follows.
For the convenience of derivation, the dynamic stiffness matrix at the anchor base center is first expanded to a 6 × 6 matrix and partitioned as follows:
Consequently, the relationship between soil reaction forces, displacements, and the stiffness matrix at the suction anchor base center is formulated as follows:
which is equivalent to
where
and
represent the displacement and rotation angle at the center of the bottom of the suction anchor foundation
, respectively.
and
denote the soil reaction force and moment at
, respectively.
When transforming the coordinate system origin from point
to padeye point
on the suction anchor, the displacements and rotations between these points obey the following kinematic relationships:
where
and
are the displacements and rotations at the point
, respectively.
is a transformation matrix in the following form:
The soil reaction force and moment at
and
obey the following relationship:
where
and
denote the soil reaction force and moment at
, respectively.
Substituting Equations (27)–(30) into Equations (32) and (33), we can obtain the following:
So, the transformed dynamic stiffness matrix
at padeye point
on the suction anchor is given by the following:
Substituting Equation (25) into Equation (36) and reducing to two-dimensional degrees of freedom, the dynamic stiffness matrix
at
is given by the following:
Similarly, the corresponding damping matrix
at padeye point
is as follows:
2.3. Dynamic Response Analysis Method
2.3.1. Calculation Method in the Frequency Domain
For the dynamic response Equation (1) of the suction anchor foundation, when the applied force
F is harmonic, the suction anchor foundation undergoes harmonic motion. Under these conditions, the time-harmonic term can be extracted for frequency-domain analysis as follows:
where
is the circular frequency. Consequently, the dynamic response equation in the frequency domain for the suction anchor under harmonic mooring forces is expressed as follows:
Then the harmonic motion of the suction anchor foundation can be calculated in the frequency domain.
2.3.2. Time Marching Method in the Time Domain
Under the actual operating conditions of suction anchors, the applied load F is typically non-harmonic and manifests as an irregular nonlinear force, necessitating time-domain solutions via time-stepping schemes.
Assume zero initial displacement and velocity of the suction anchor foundation. After determining the values of mass, stiffness, and the damping matrix in Equation (1), the acceleration at the padeye of the suction anchor at the current time step under mooring forces can be obtained. Then a fourth-order Runge–Kutta (RK4) method is employed to derive the displacement and velocity at at the next time step. The specific steps are as follows.
Given the displacement
and velocity
at
at time t, the acceleration
is determined by solving Equation (1). This relationship is formally expressed as follows:
Furthermore, the displacement and velocity at
satisfy Newton’s equations of motion. Thus, these quantities at the subsequent time step (
) are computed via the fourth-order Runge–Kutta (RK4) method:
where
The numerical computation procedure is structured as follows: given the known displacement and velocity at
at time t, the value of
is computed via Equation (43). This acceleration value then drives the iterative update to determine the displacement and velocity at the subsequent time step (
). The recursive integration cycle yields full temporal evolution of the dynamic states. In the end, the displacement and velocity at
at time
are resolved through Equations (44) and (45).
To ensure numerical stability, a time step of
T/100 is adopted (where
T denotes the mooring force period). Additionally, a ramp function applied at simulation initialization enhances stability and accelerates convergence to steady-state conditions. Following Baudic [
27], this ramp function is defined as follows:
3. Validation
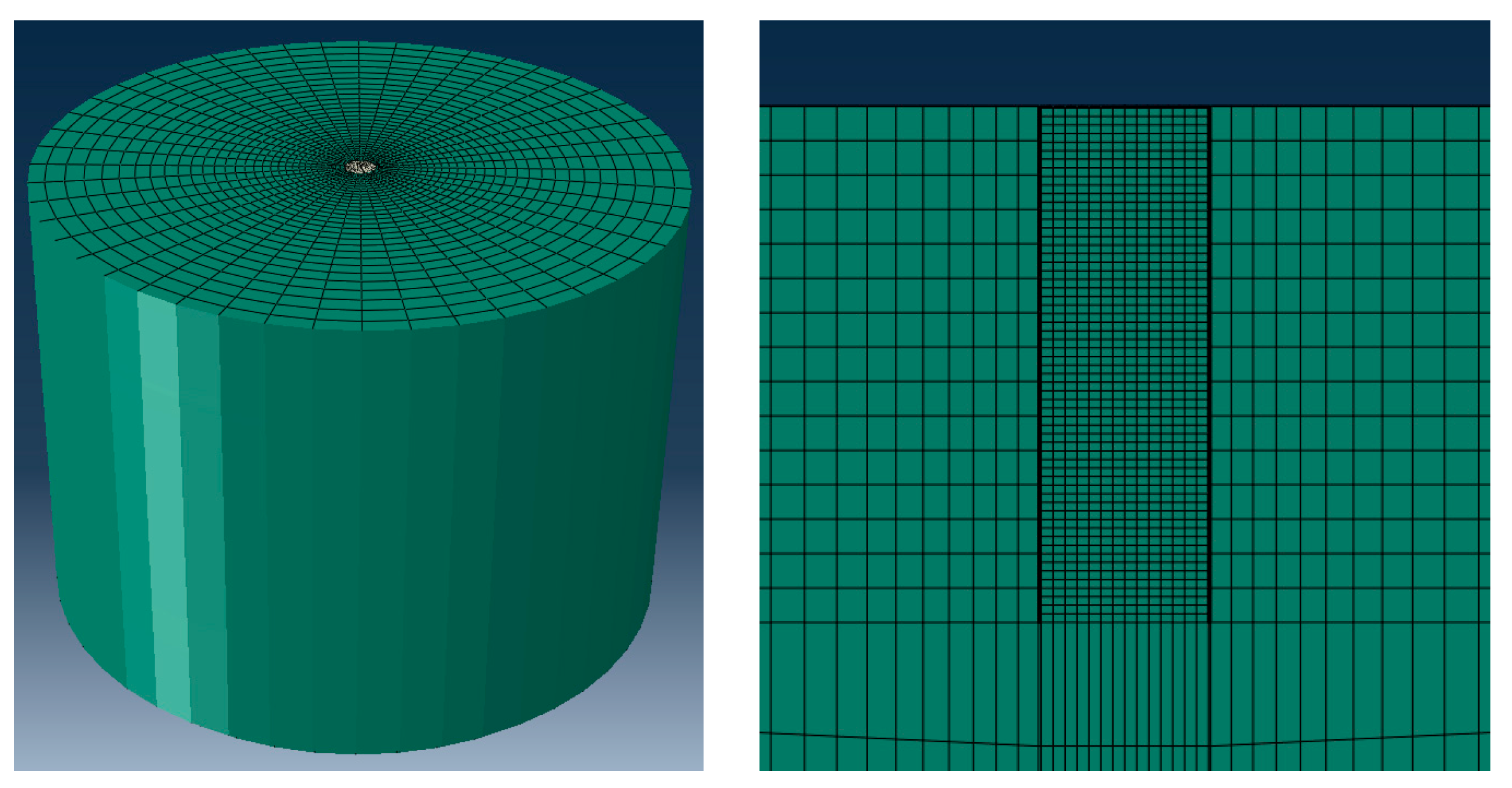
To verify the reliability of our model in simulating the dynamic responses of embedded suction anchors in homogeneous elastic soil, we established a new finite element numerical model for soil–suction anchor interactions using the software Abaqus (Abaqus 2024), as shown in the
Figure 2. The high-fidelity Abaqus model, which explicitly simulates the anchor’s wall thickness, open bottom, and the distinct soil bodies inside and outside the anchor, served as the benchmark. It was compared against the proposed simplified model, which employs the simplification of treating the anchor and interior soil as an integrated rigid body.
In the Abaqus model, the material of soil is homogeneous linear elastic. The suction anchor foundation is idealized as a rigid structure fully embedded at the top center of the soil domain. The suction anchor foundation is open at the bottom and is fully filled with soil. The soil–structure interface maintains fully tied contact without separation. The bottom surface of the soil model is assigned a fully fixed constraint, while its sides are horizontally restrained. Infinite elements are applied to the outer boundaries of the soil model to eliminate wave reflections, thereby simulating an elastic half-space. The model parameters are shown in
Table 1.
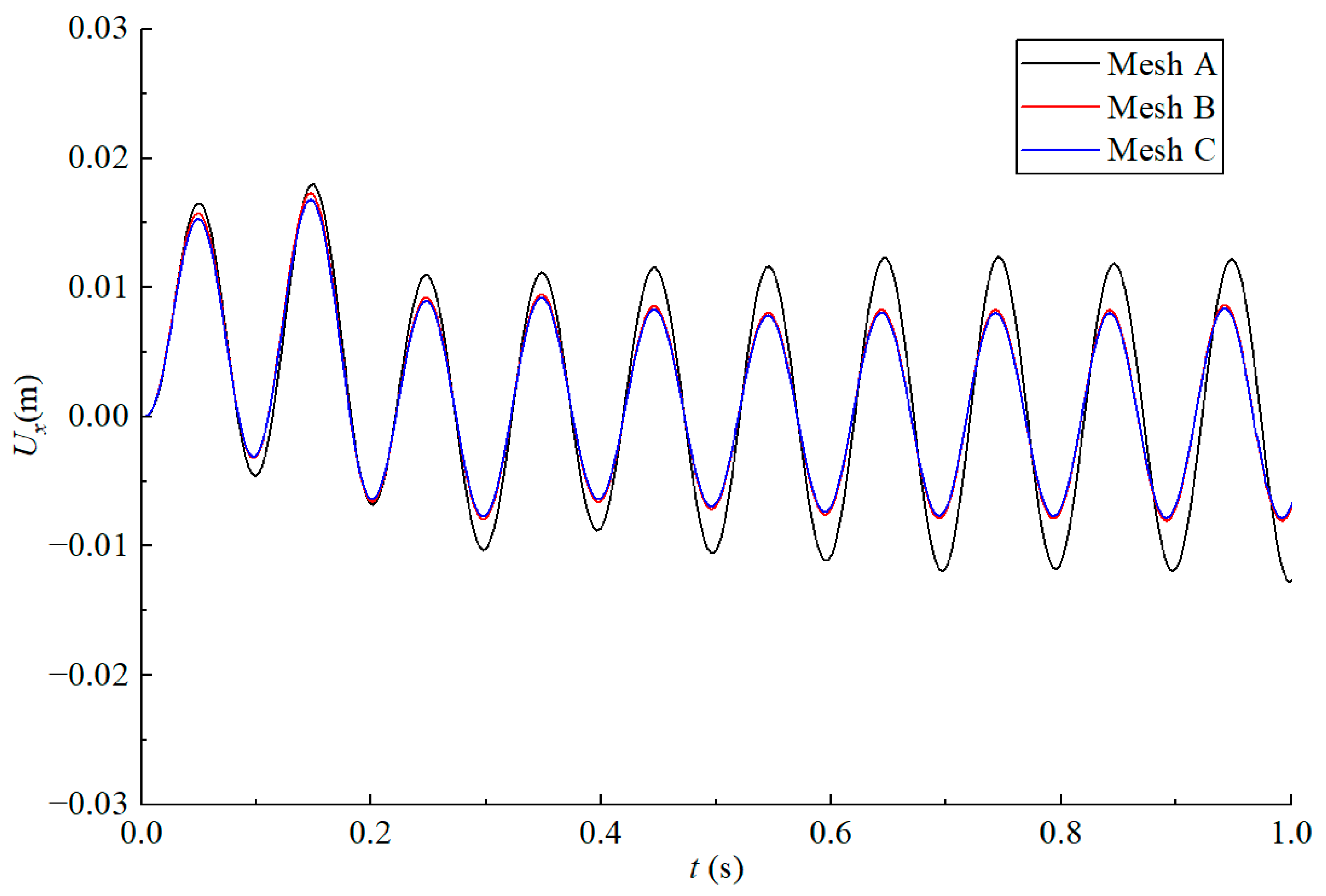
A mesh convergence study was conducted to ensure the accuracy of the numerical results while maintaining computational efficiency. Three mesh configurations with varying levels of refinement (Mesh A, Mesh B, and Mesh C) were generated, with their specific information summarized in
Table 2. The horizontal displacement at the padeye under a 10 Hz dynamic load was selected as the key metric for comparison. As illustrated in
Figure 3, the result from the coarsest mesh (Mesh A) showed a notable deviation. In contrast, the results from the medium and finest meshes (Mesh B and Mesh C) were in close agreement. This indicated that the solution converged with Mesh B. Therefore, Mesh B was adopted for all subsequent simulations in this study, as it provided an optimal balance between numerical accuracy and computational cost. In addition, an explicit dynamics analysis was employed, with the time increment being automatically controlled by the solver to maintain stability.
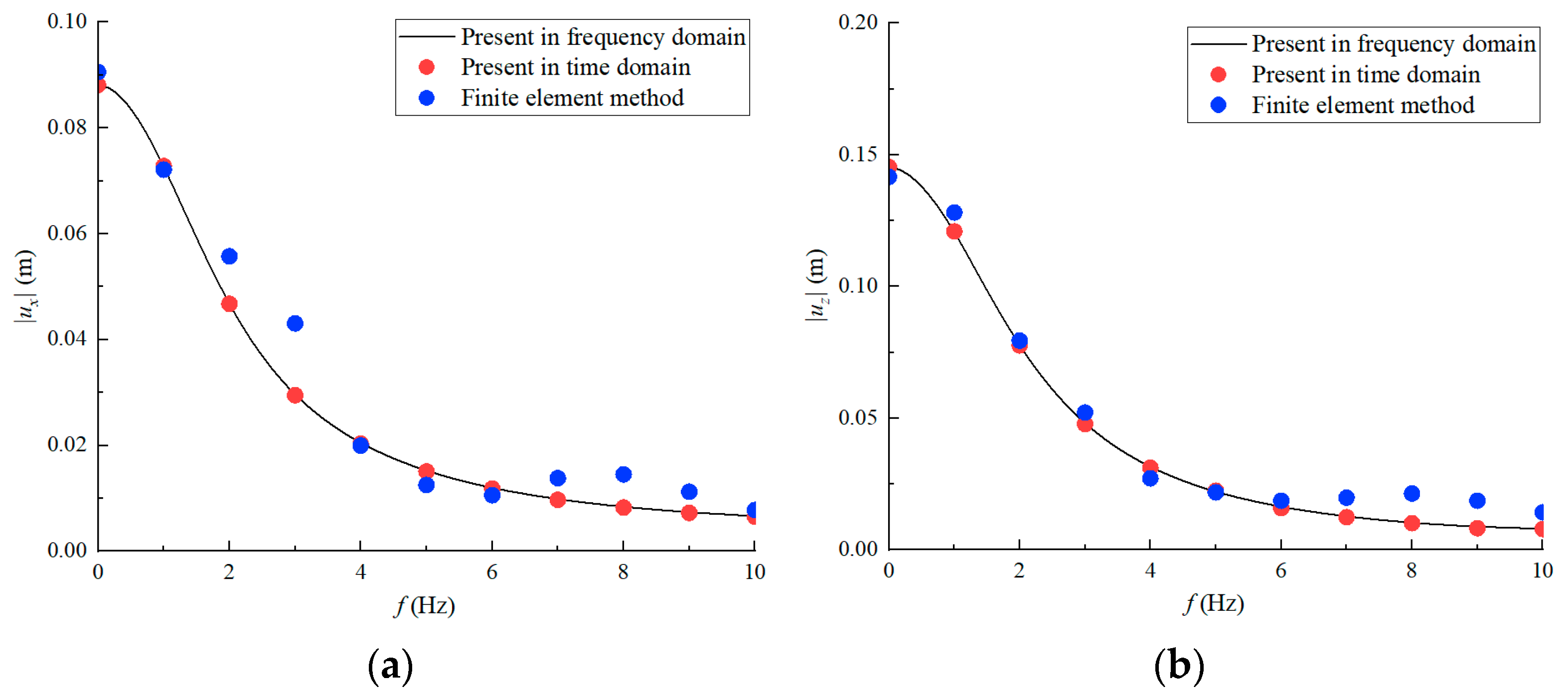
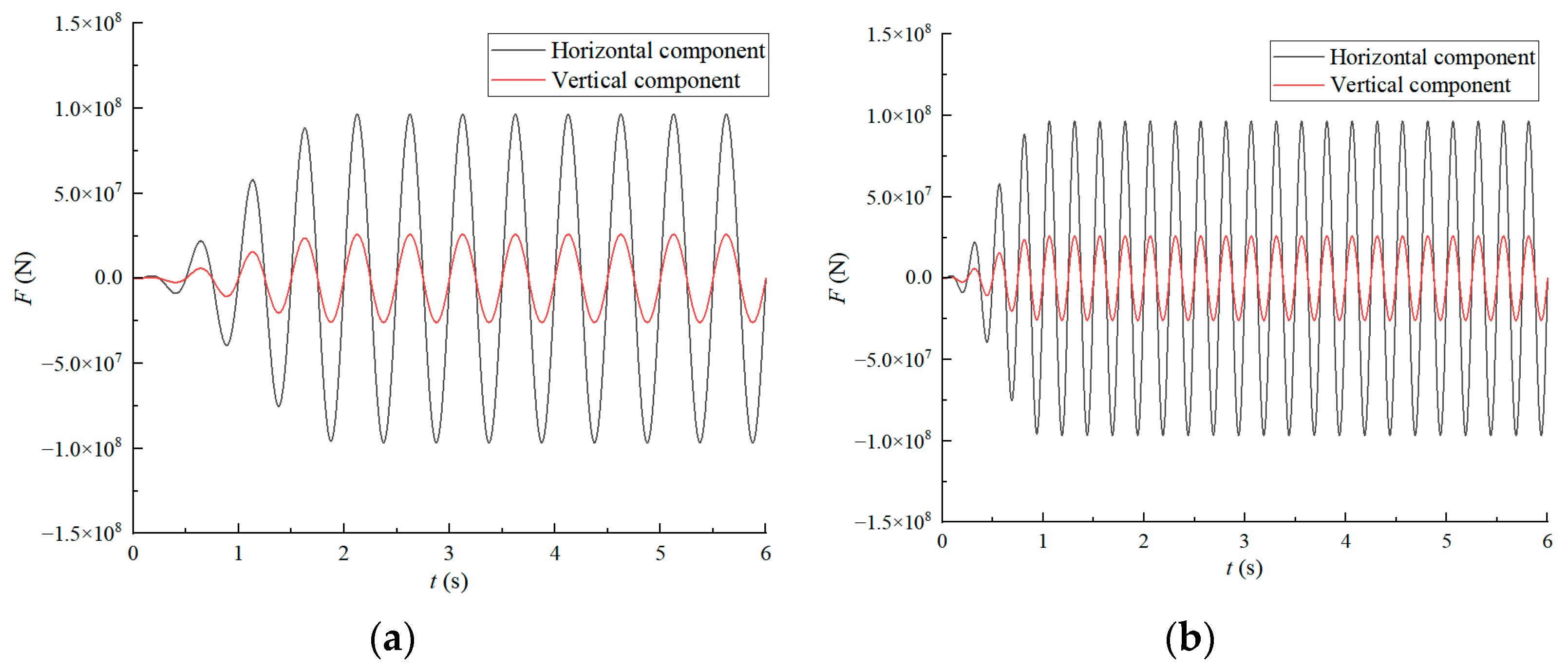
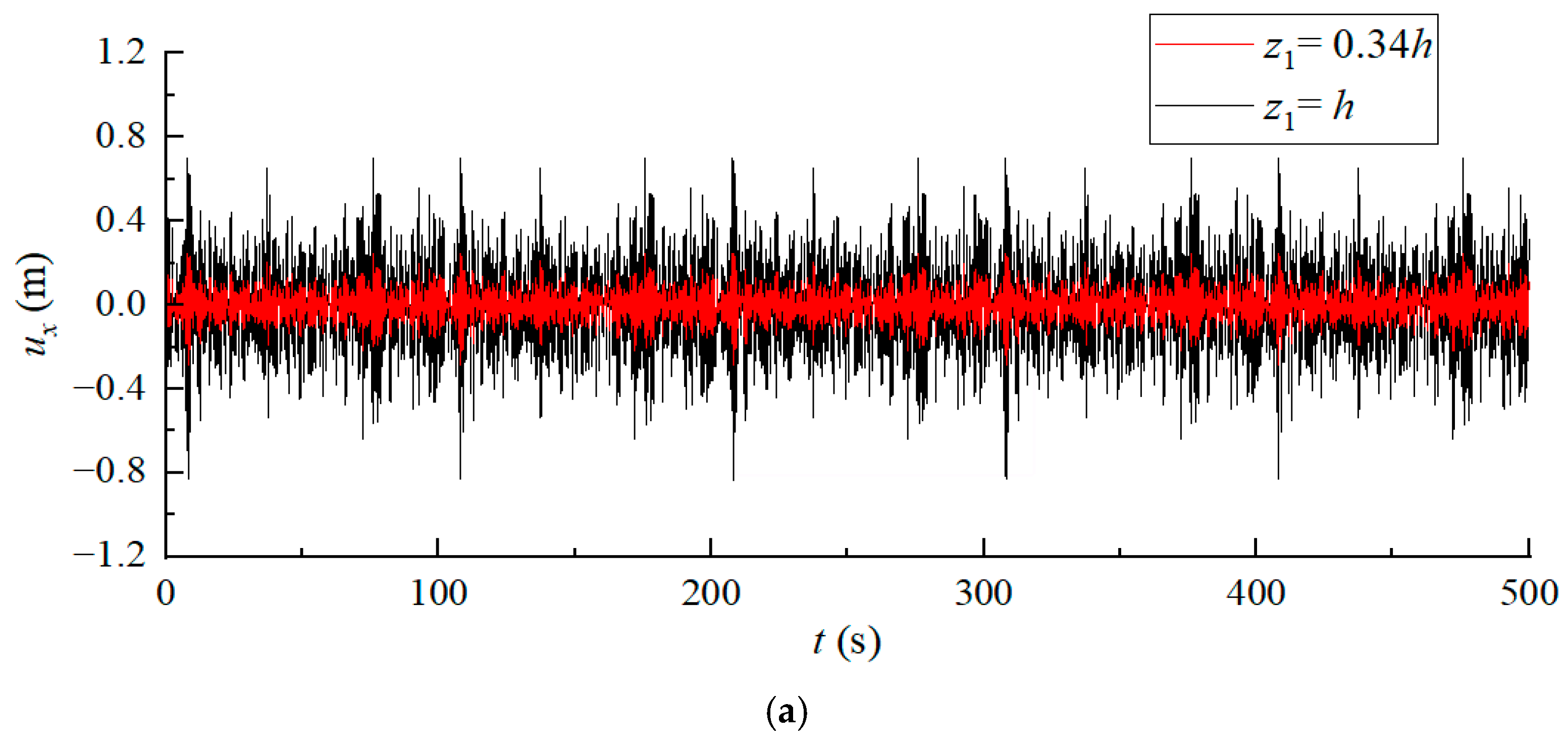
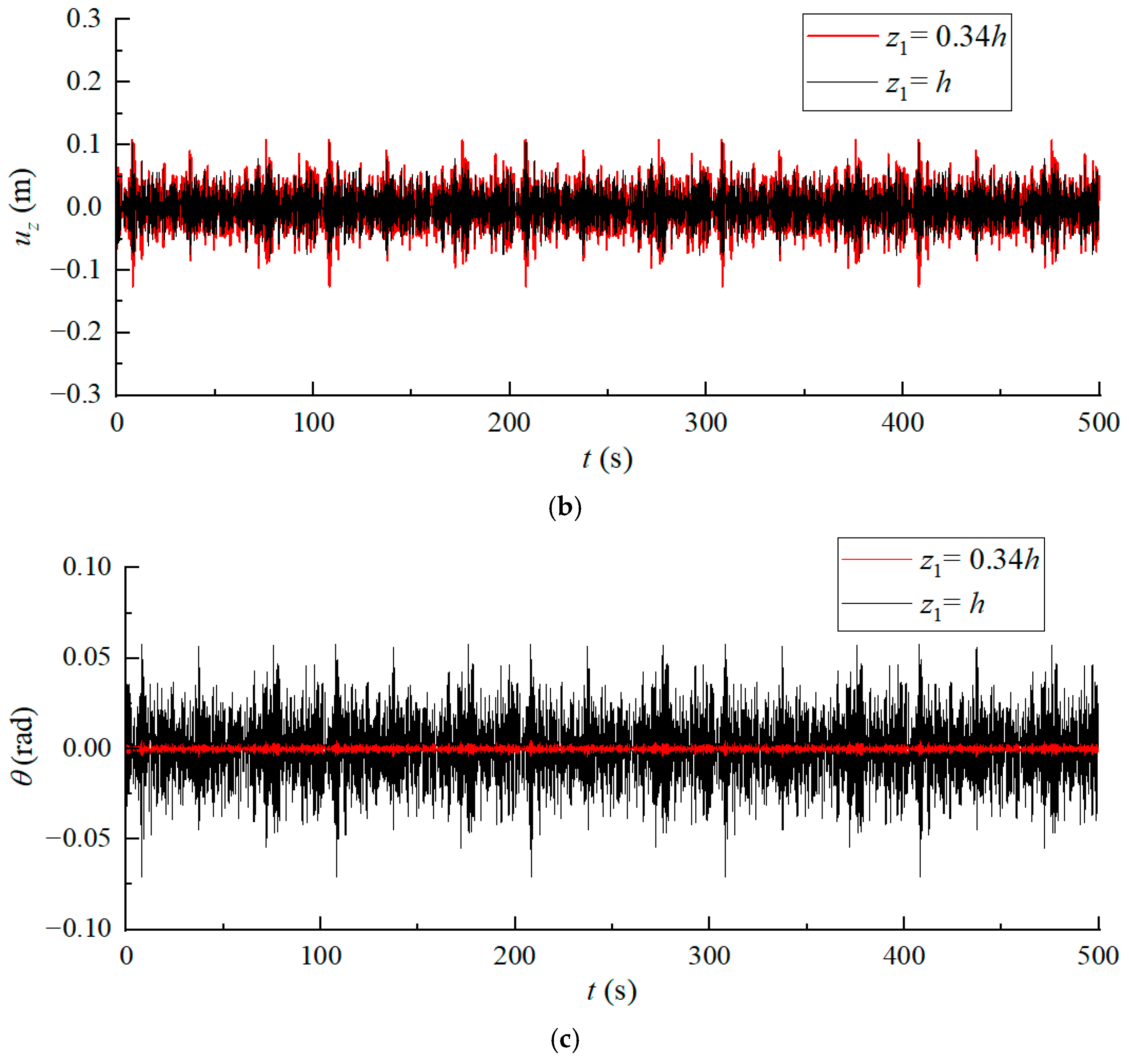
Figure 4 compares horizontal and vertical displacements at the load application point when forces act at the anchor sidewall padeye. The results demonstrate good agreement between the proposed models and finite element simulations. Additionally, computational times are recorded on an Intel(R) Core(TM) i7-14700F processor: the finite element model requires approximately 10 min, the proposed time-domain model completes calculations in under 3 s, and the frequency-domain model requires less than 1 s. This confirms the achievement of a significantly higher computational efficiency while maintaining acceptable accuracy.
5. Conclusions
This study investigates the dynamic response characteristics of embedded suction anchor foundations under mooring forces. Initially, the equations of motion for anchors in soil were established. Subsequently, based on the assumption of a linearly elastic and homogeneous soil medium, dynamic stiffness and damping formulations for embedded foundations were derived, and coordinate transformation techniques were employed to obtain impedance matrices at arbitrary padeye locations. Frequency-domain and time-domain methods were then applied to resolve horizontal, vertical, and rocking motions under both harmonic cyclic loading and irregular nonlinear mooring forces. Parametric analyses examined padeye elevation and scour depth effects on dynamic behavior. The key conclusions were as follows:
- (1)
Validation against a detailed finite element model confirms that the proposed simplified model, based on the integrated rigid body assumption, achieves a favorable balance between predictive accuracy and computational cost. This demonstrates its reliability and practical value for dynamic analysis.
- (2)
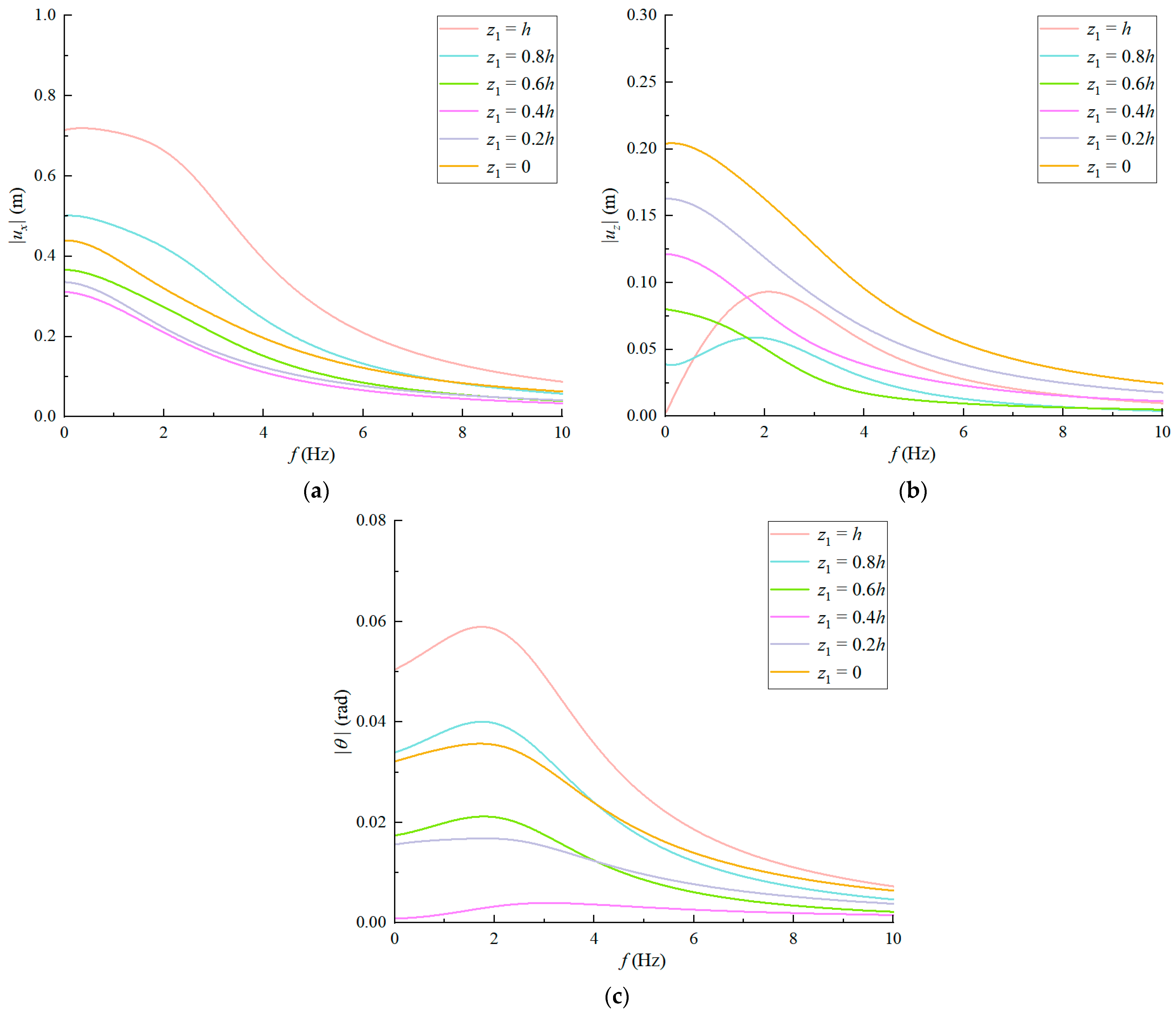
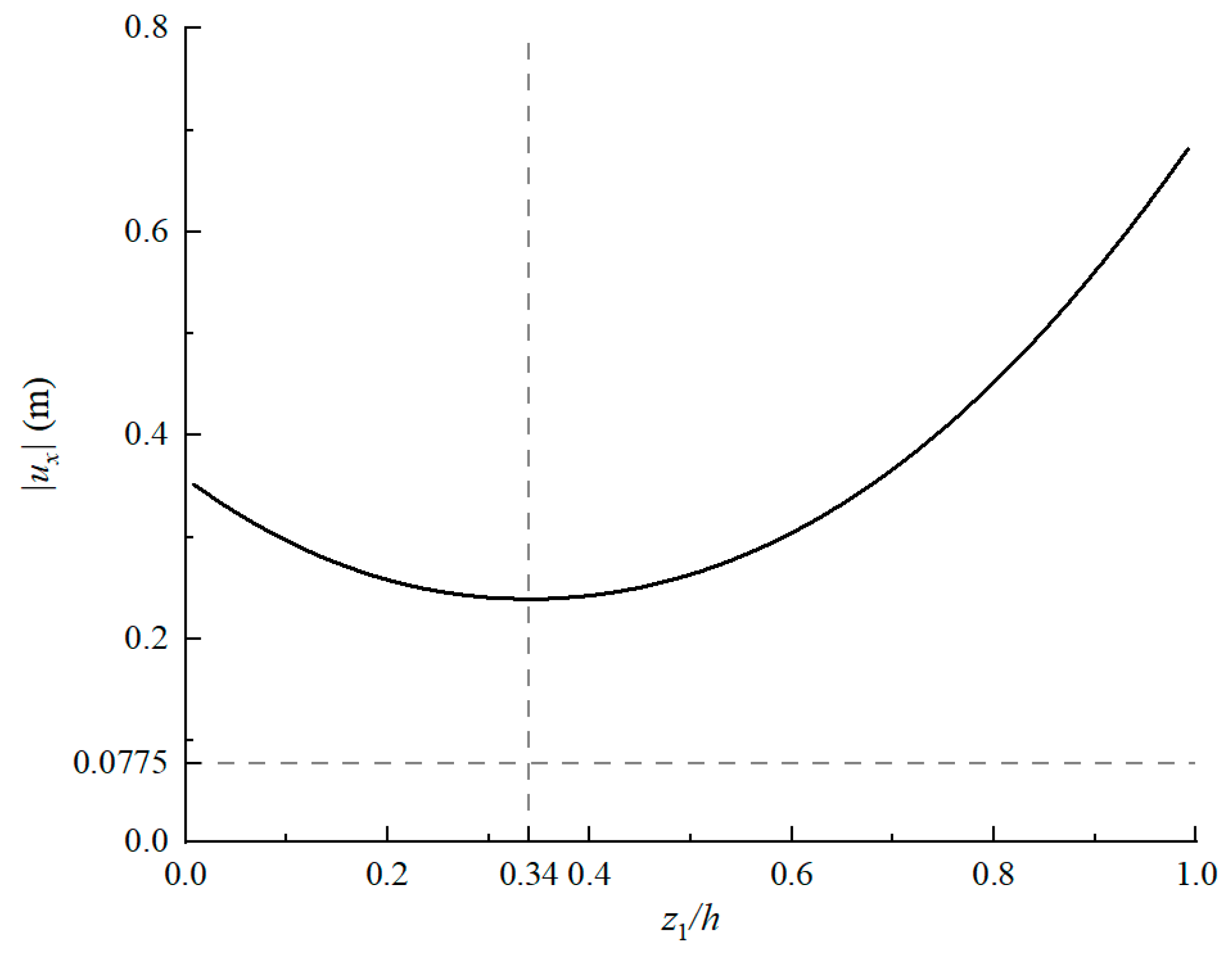
Padeye elevation critically governs dynamic response. The proposed methodology enables rapid optimization of padeye placement to minimize response amplitudes, enhancing design efficiency and structural safety.
- (3)
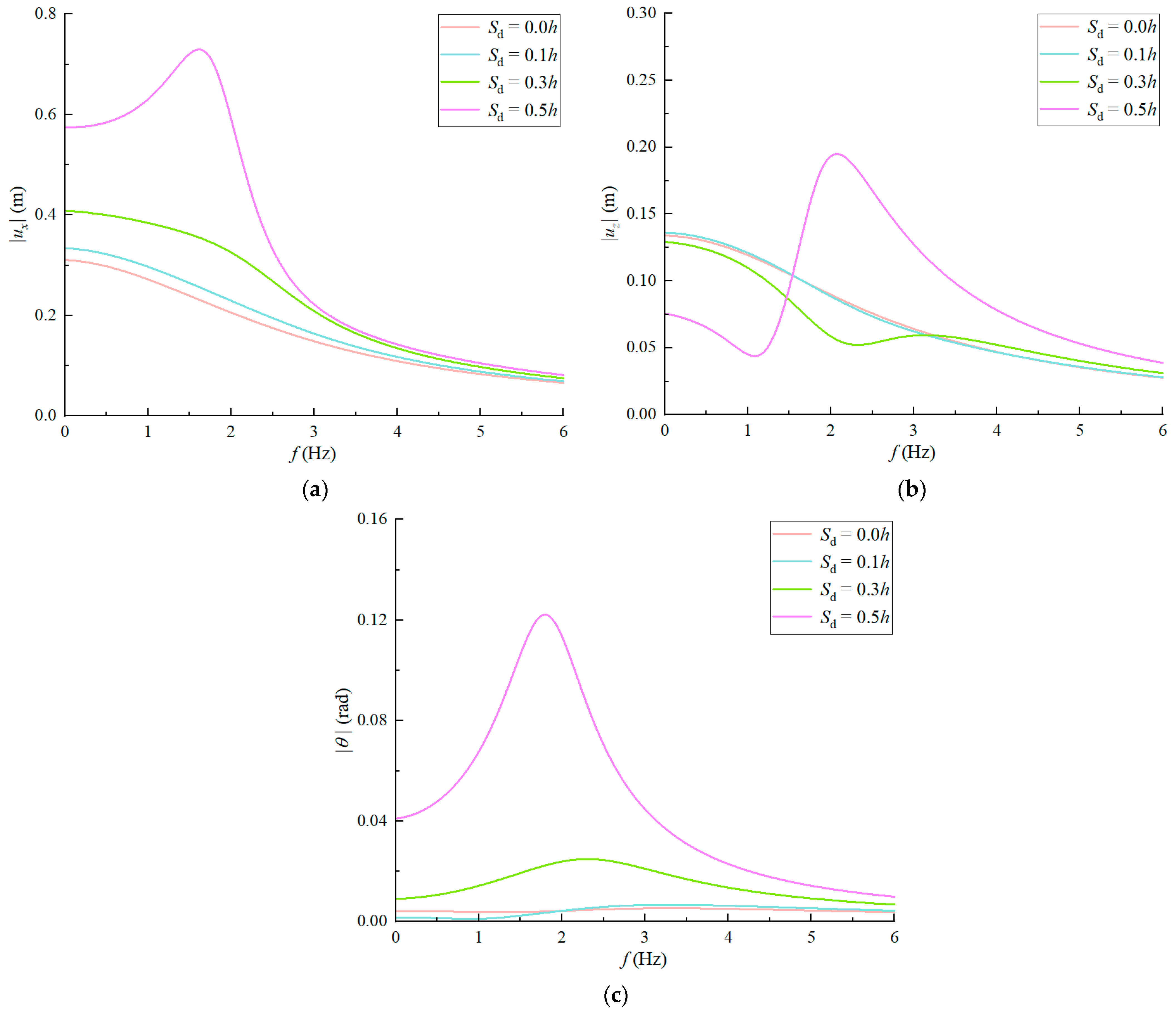
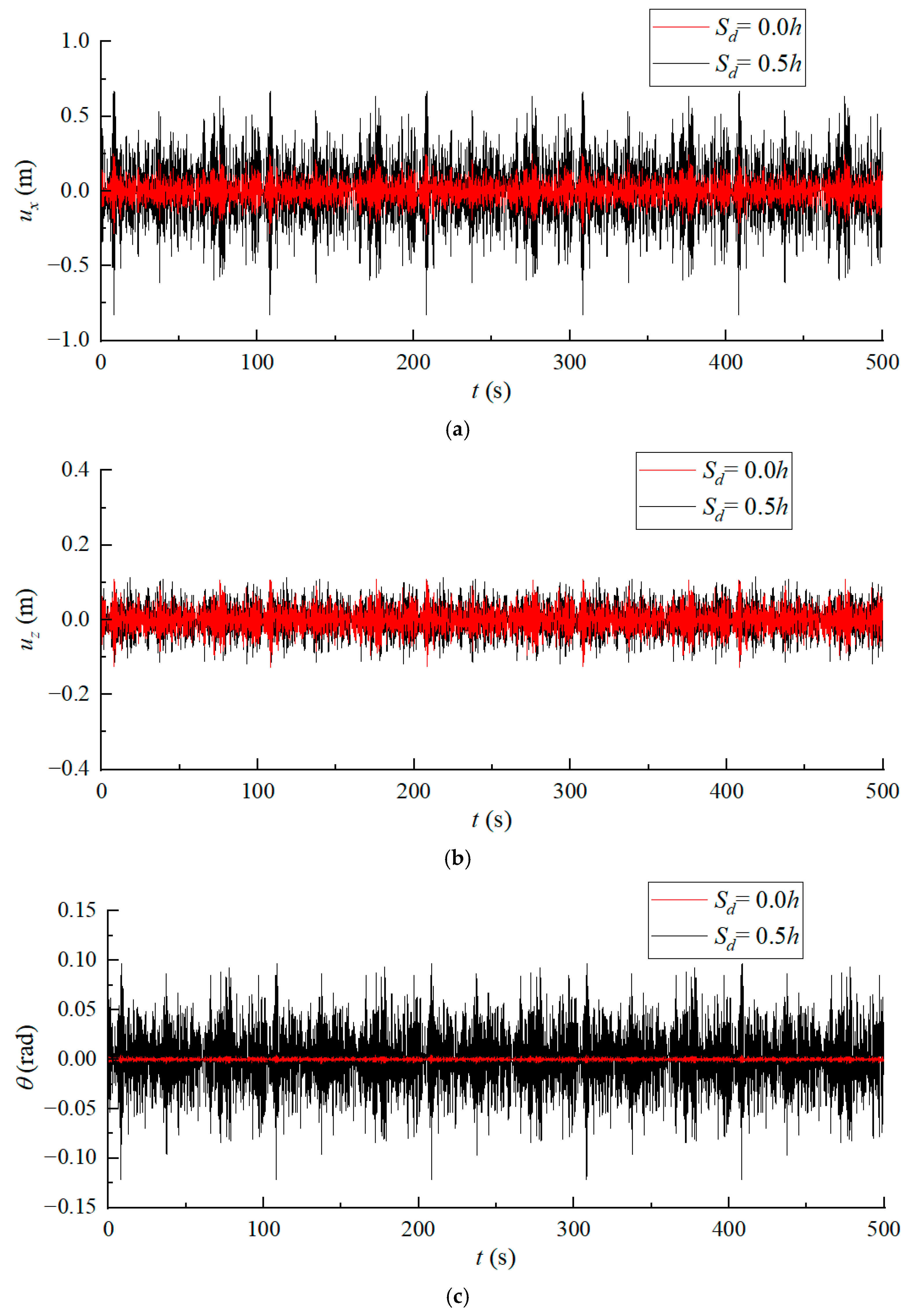
The scouring depth has a significant impact on the dynamic response characteristics of the suction anchor foundation. Severe scour will significantly increase horizontal displacements and rocking rotations, which directly elevates structural failure risks.
Notwithstanding its computational efficiency and value for preliminary design, this study has certain limitations that warrant attention. The adopted linear soil model, while providing satisfactory accuracy under conventional working conditions with small-strain levels, may exhibit lower predictive accuracy under extreme conditions such as earthquakes, as it fails to capture soil nonlinearities, including strain-dependent variations in shear modulus and damping. Future research will focus on enhancing the model’s predictive capability by implementing the Hardin–Drnevich model (Hardin and Drnevich [
29], Tu et al. [
30]) within the time-domain framework to enable real-time updates of the shear modulus and damping ratio based on dynamic strain levels. Experimental validation is also planned to verify and refine the proposed methodology, thereby extending its applicability to a broader range of geotechnical design problems.