A Hybrid Gaussian Process Framework for Rapid Prediction of Umbilical Cable Mechanics in Deep-Sea Mining
Abstract
1. Introduction
2. Theoretical Background
2.1. Three-Dimensional Potential Flow Theory
2.2. Lumped Mass Method
2.3. Time-Domain Coupled Analysis
3. Methodology
3.1. Gaussian Process Regression
3.2. Training Framework
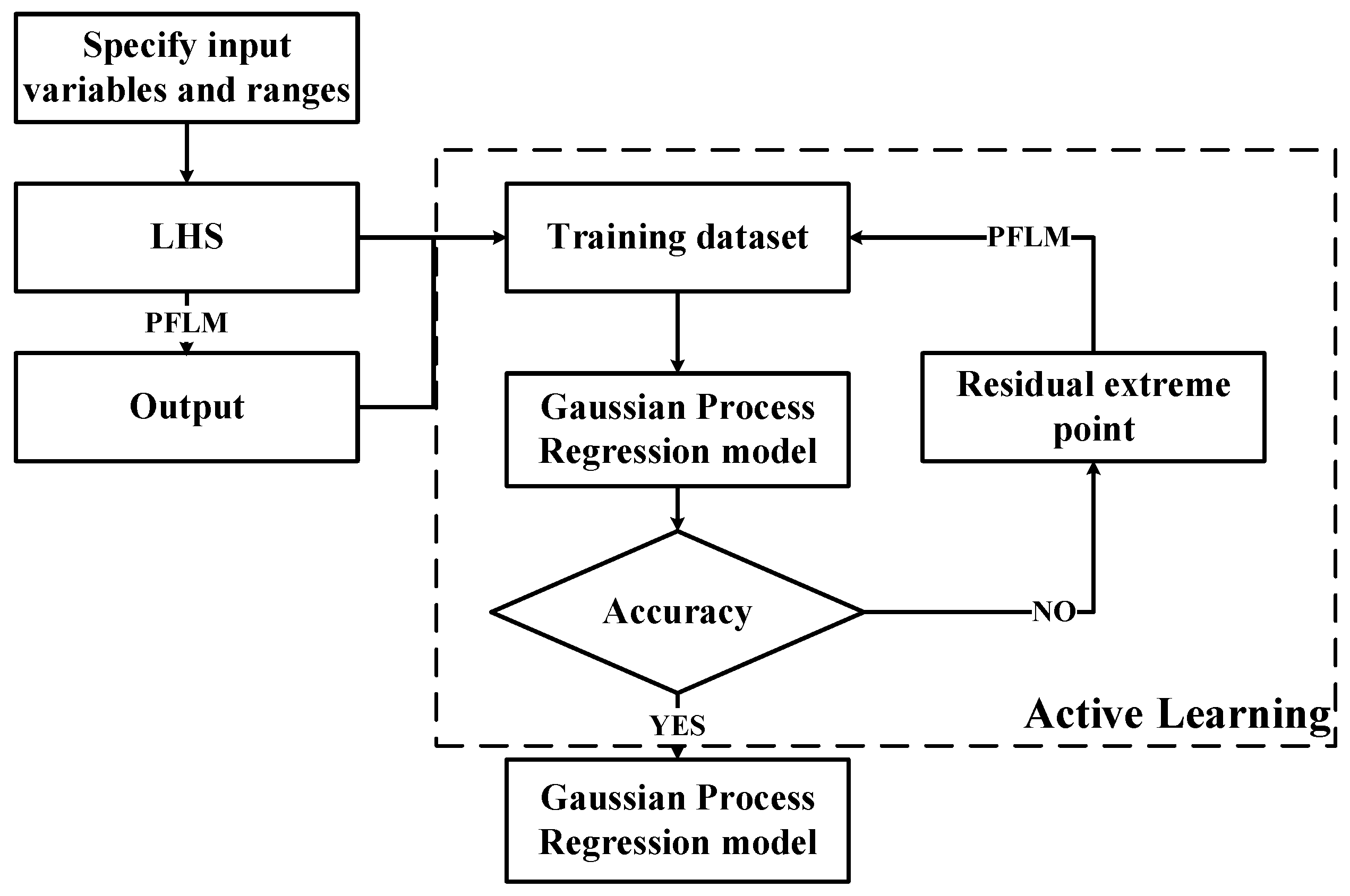
- Data Preparation: Based on the variables affecting the dynamic response of the umbilical cable, the input parameters are determined as wave height (), wave direction (), current velocity (), current direction (), cable length (L), and the relative position of the vehicle and ship (D). The output parameters are determined as the top tension and curvature of the umbilical cable, longitudinal overturning moment and lateral overturning moment of the mining vehicle. Specify the value ranges for the input parameters and generate all possible operating conditions. Use the Latin hypercube sampling method to select samples from all generated conditions and input them into PFLM to obtain the corresponding output responses, thereby forming the initial training dataset.
- Training: A Gaussian process regression model is built based on the dataset, which uses the spectral mixture kernel function to construct the covariance matrix (the spectral mixture kernel function is defined as follows). The kernel function has six Gaussian spectral components, the Adam optimizer is used as the optimizer, and the maximization of the marginal log-likelihood function is used as the objective function.where is the input difference vector. Here, Q denotes the number of mixture components, and in this study ; P is the input dimension, with . The parameter is the weight of the q-th Gaussian component, is the mean frequency of the q-th component in the p-th input dimension, and is the corresponding variance.
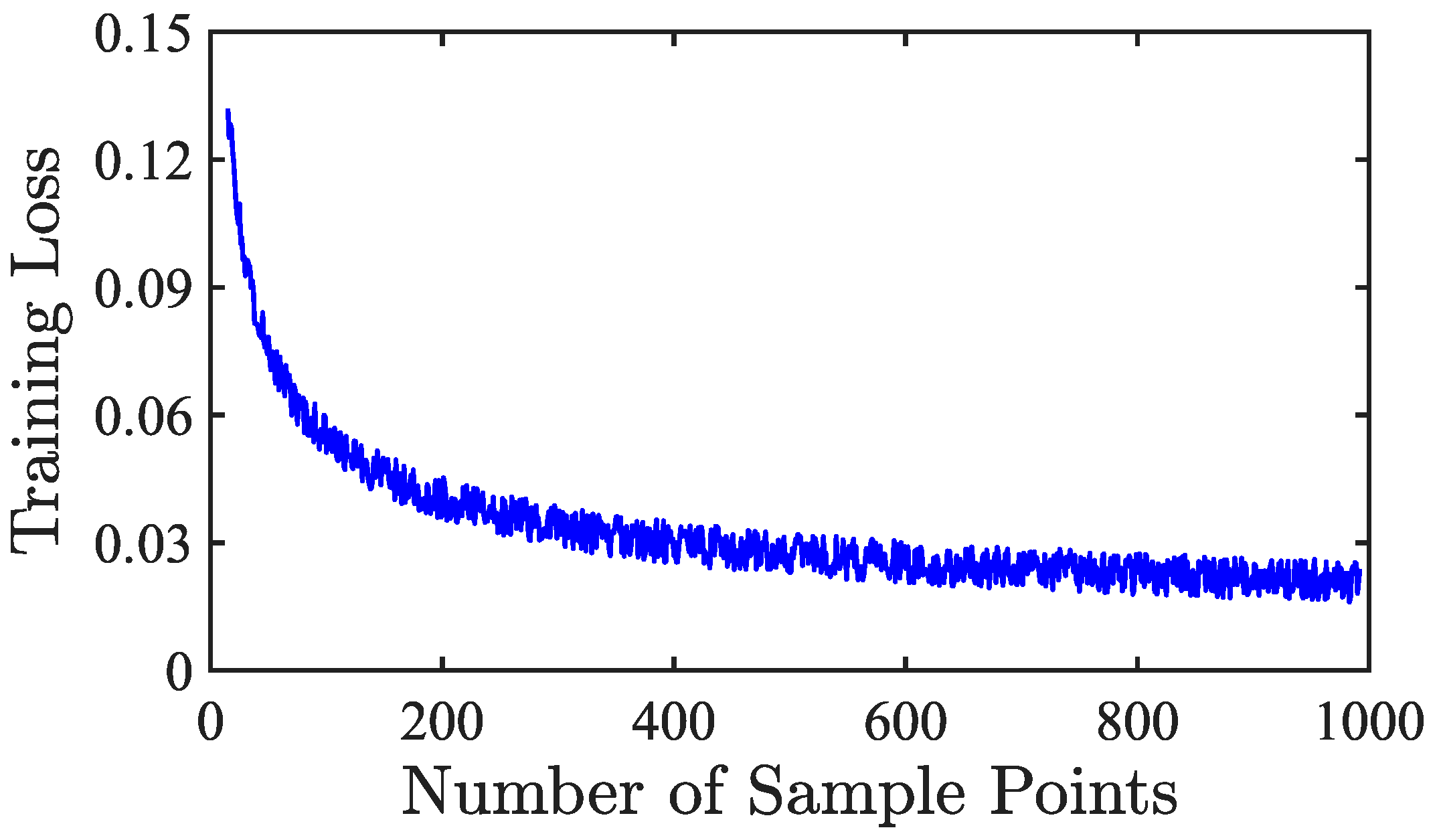
- Iterative Optimization: Randomly select 1000 conditions from all the generated cases, and use the trained Gaussian Process Regression (GPR) model to compute the mean and variance of these 1000 conditions. Extract the residual extreme point and feed the corresponding input parameters back into PFLM to obtain the actual outputs for the point. Add the newly acquired data point to the training dataset and retrain the model. This process continues until the error meets the required accuracy or the number of training samples reaches a specified upper limit. This framework ensures the iterative refinement of the surrogate model, achieving high precision in predicting the dynamic response of the umbilical cable under various operating conditions.
4. Results and Discussion
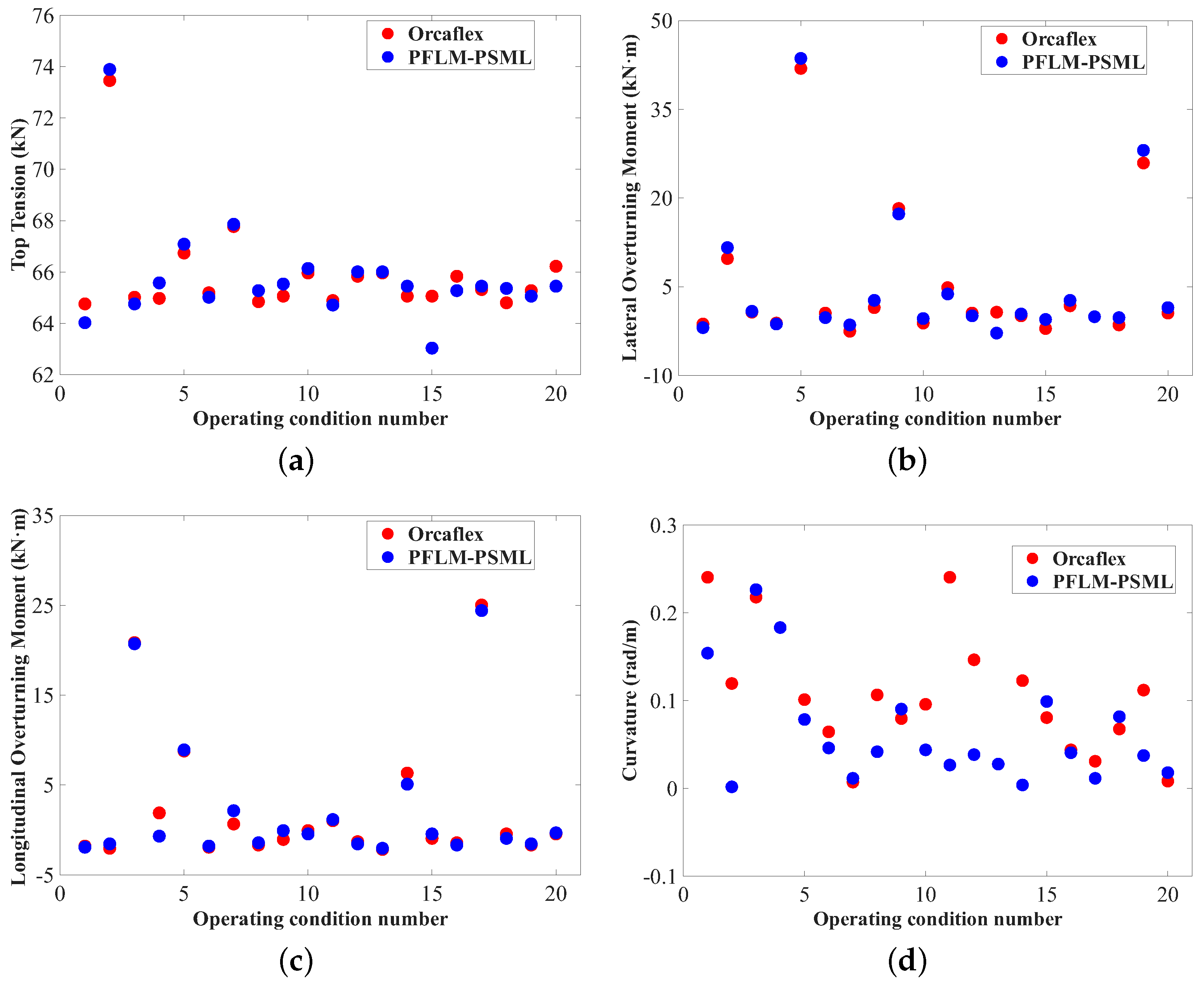
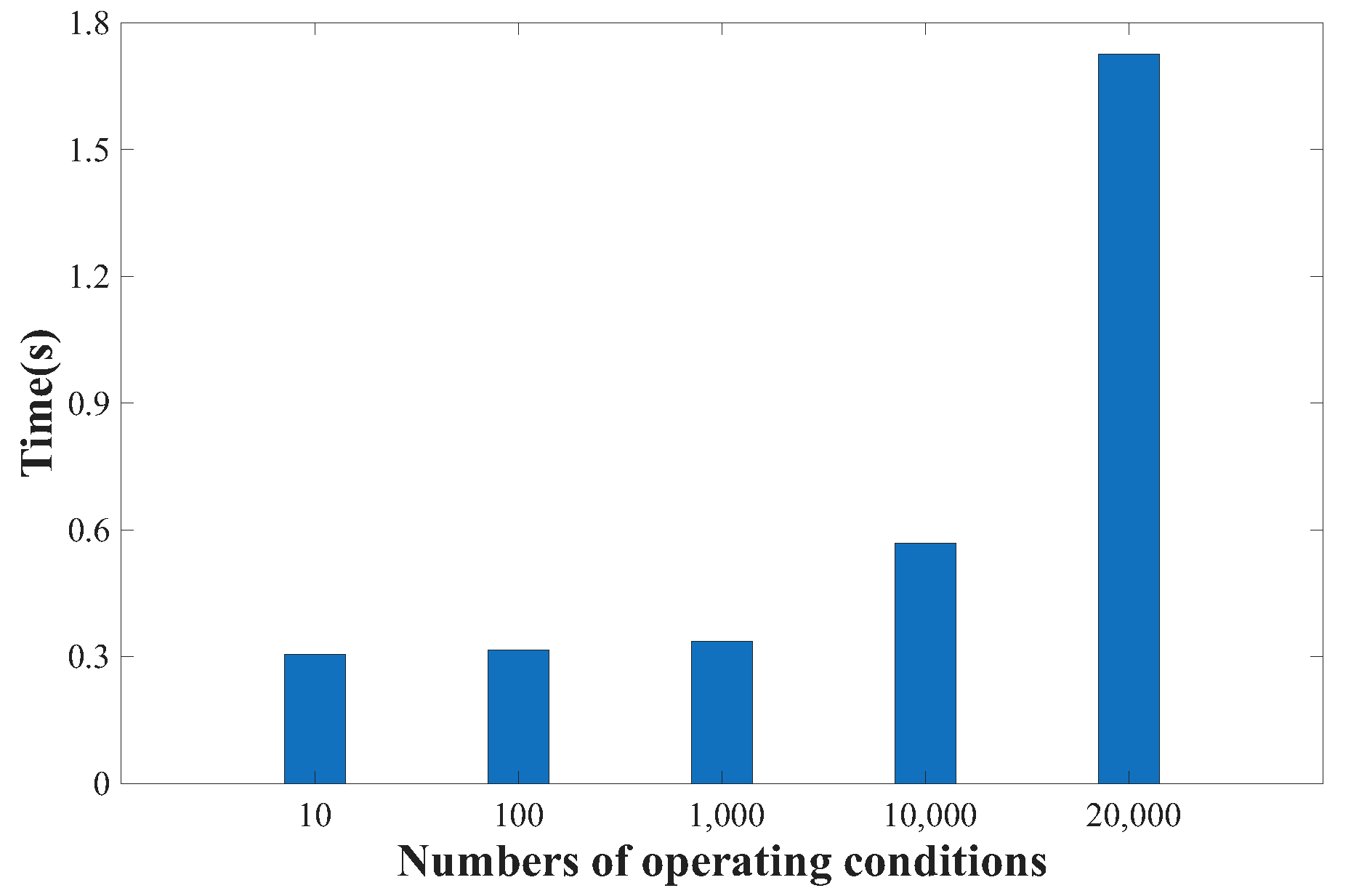
4.1. Numerical Validation
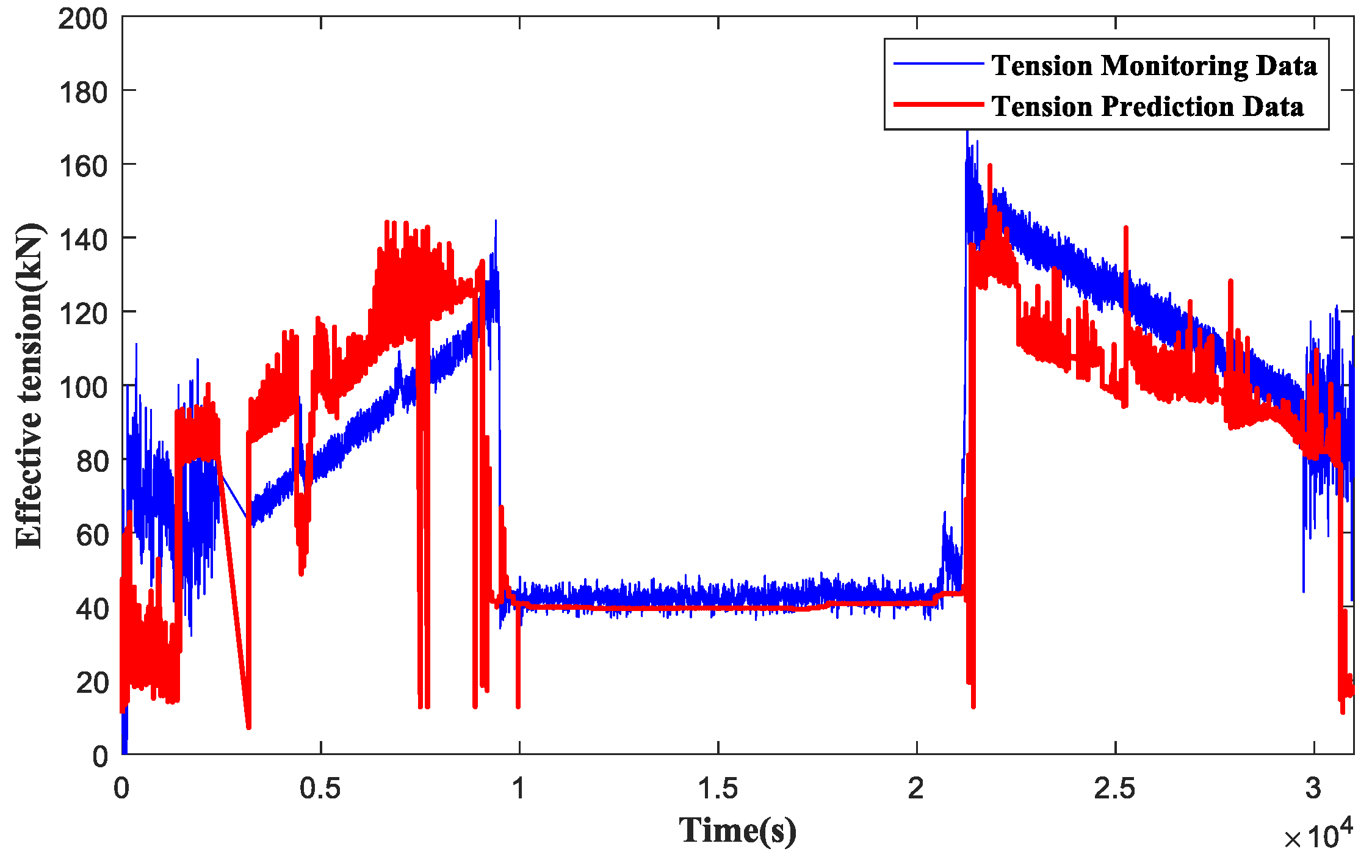
4.2. Sea Trial Validation
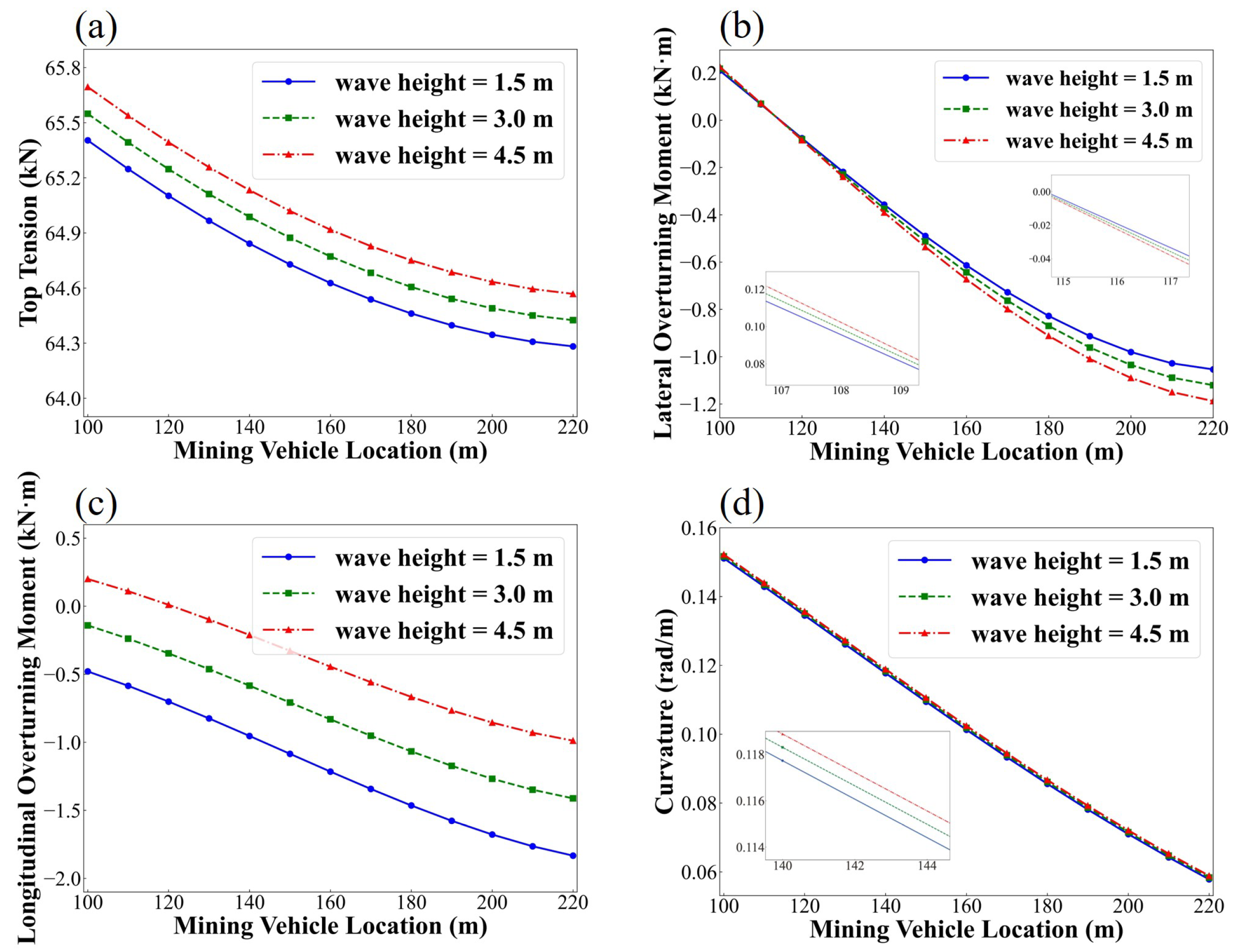
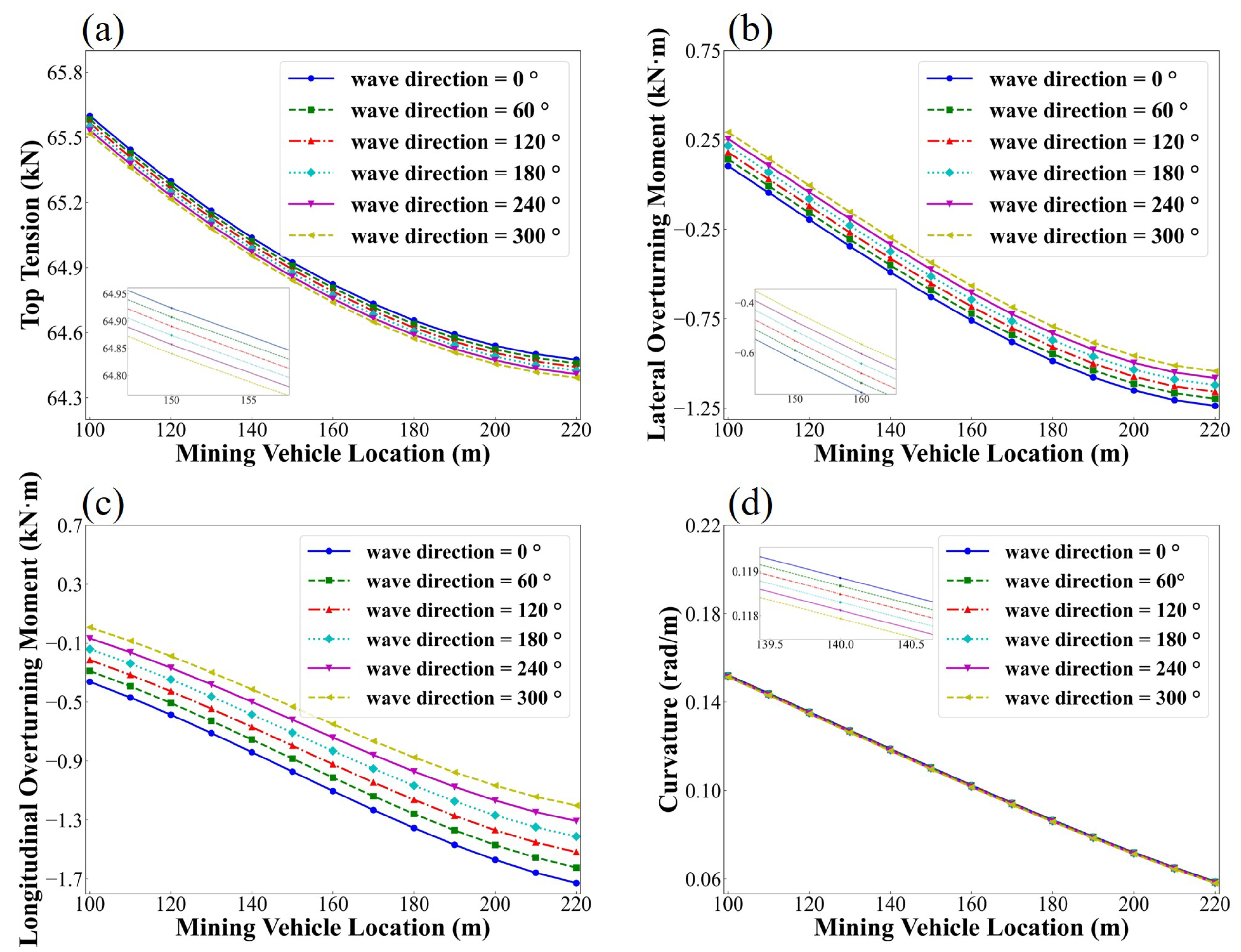
4.3. The Effect of Wave
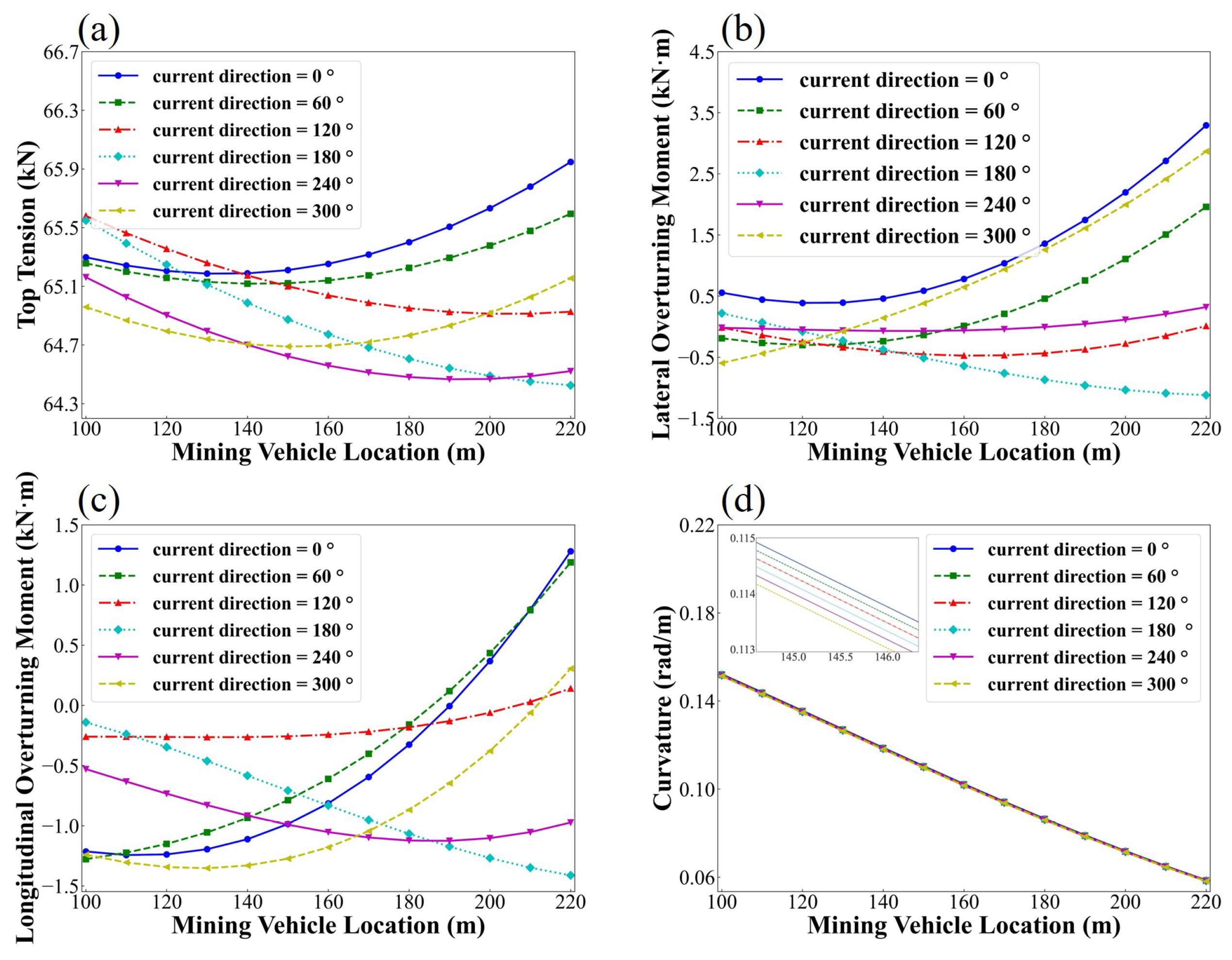
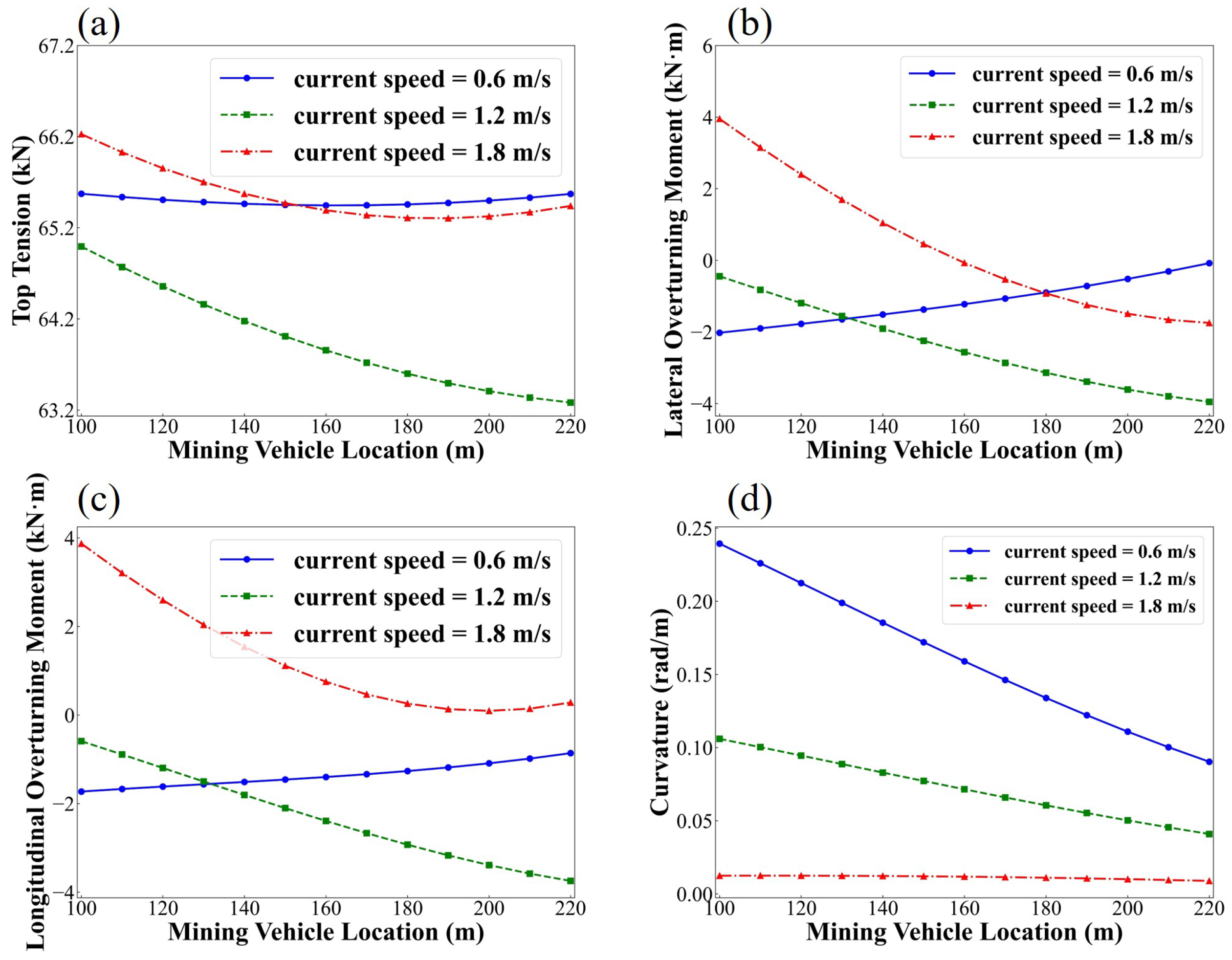
4.4. The Effect of Current
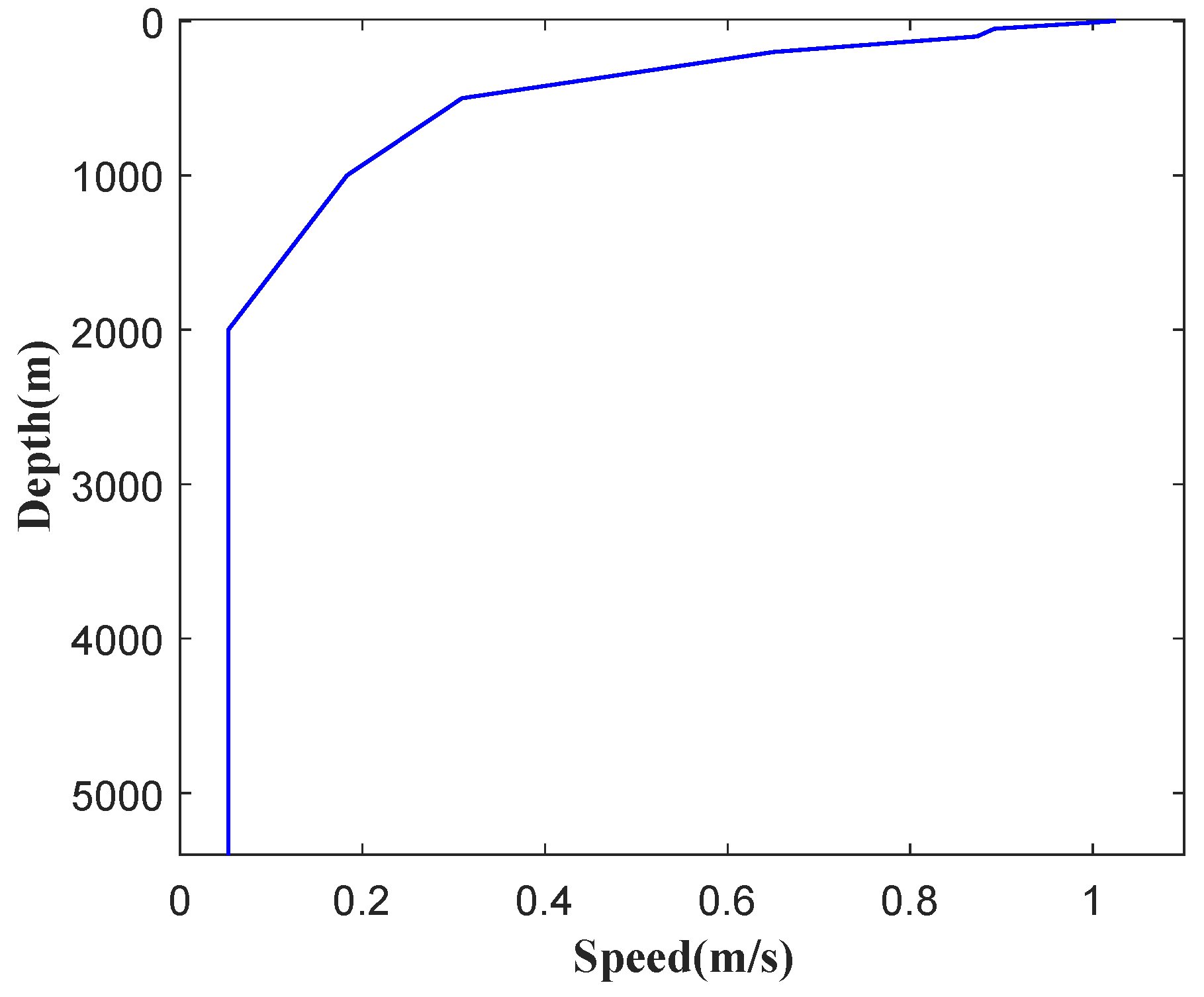
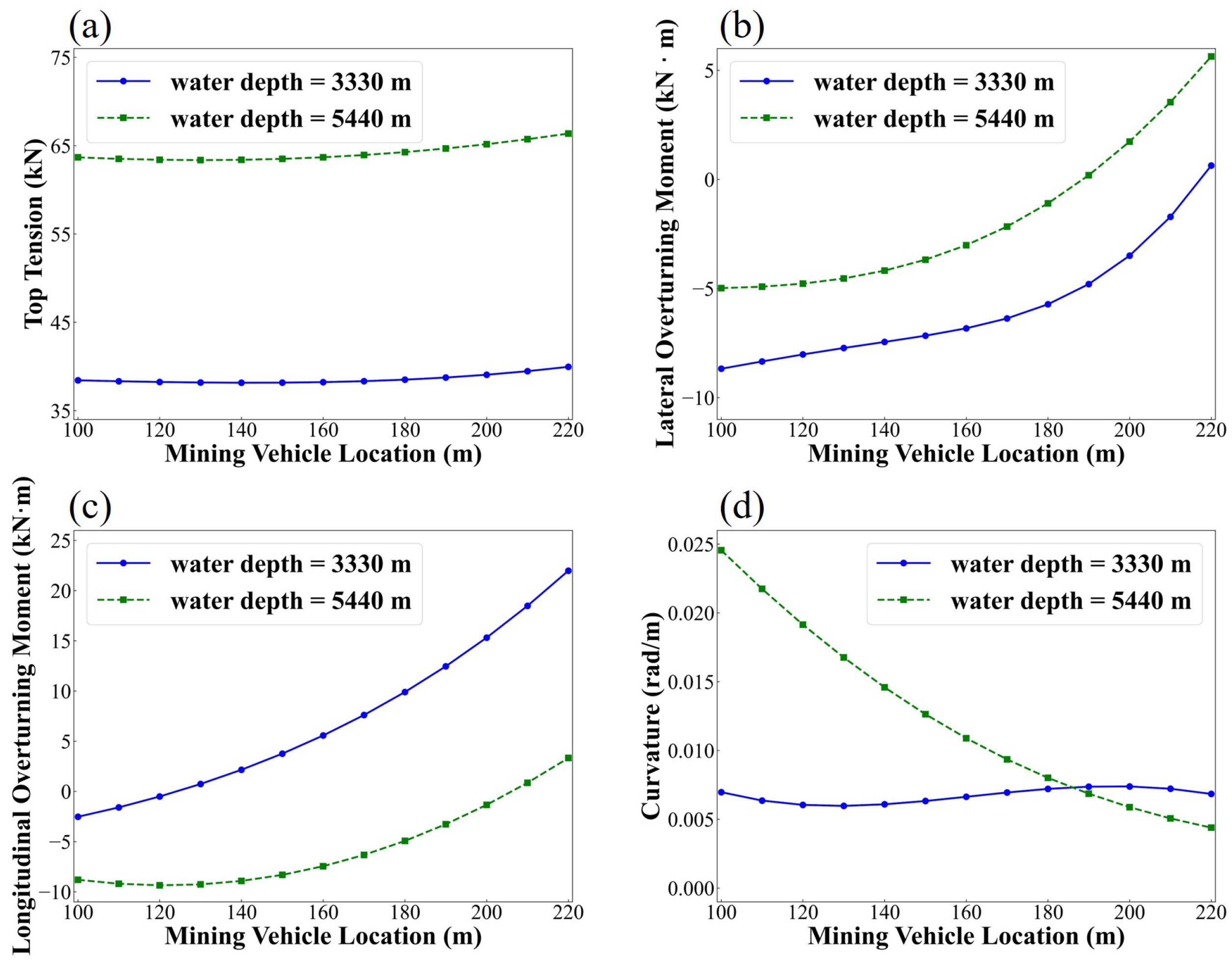
4.5. The Effect of Water Depth
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, N.; Chen, G.G. Status quo and development trendency of deep sea minerals mining technology. Min. Process. Equip. 2010, 38, 4–9. [Google Scholar]
- Mero, J.L. The Mineral Resources of the Sea; Elsevier: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Van Wijk, J.M. Vertical Hydraulic Transport for Deep Sea Mining: A Study into Flow Assurance. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Xiao, Y.X.; Yang, L.B.; Cao, L.; Wang, Z. Distribution of marine mineral resource and advances of deep-sea lifting pump technology. J. Drain. Irrig. Mach. Eng. 2014, 32, 319–326. [Google Scholar]
- Tang, D.S.; Yang, N.; Jin, X. Hydraulic lifting technique with vertical pipe for deep-sea coarse mineral particles. Min. Metall. Eng. 2013, 33, 1–8. [Google Scholar]
- Xiao, L.; Fang, M.; Zhang, W. Advance and present state of the research in oceanic metalliferous nodule mining. Met. Mine 2000, 11–14. [Google Scholar]
- Yang, Z.; Su, Q.; Yan, J.; Wu, S.; Mao, Y.; Lu, Q.; Wang, H. Study on the nonlinear mechanical behaviour of an umbilical under combined loads of tension and torsion. Ocean. Eng. 2021, 238, 109742. [Google Scholar] [CrossRef]
- Garanovic, A. Deep Sea Mining Robot Gets Stuck 4500 Metres Beneath Pacific Ocean’s Surface. 2021. Available online: https://www.offshore-energy.biz/deep-sea-mining-robot-gets-stuck-4500-metres-beneath-pacific-oceans-surface/ (accessed on 17 November 2025).
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Dover Publications: New York, NY, USA, 1944. [Google Scholar]
- McConnell, K.G.; Zemke, W.P. A model to predict the coupled axial torsion properties of ACSR electrical conductors. Exp. Mech. 1982, 22, 237–244. [Google Scholar] [CrossRef]
- Leroy, J.M.; Estrier, P. Calculation of stresses and slips in helical layers of dynamically bent flexible pipes. Oil Gas Sci. Technol. 2001, 56, 545–554. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Cotter, D.C. Motion analysis of articulated tower. J. Waterw. Port Coastal Oceans Div. 1979, 105, 281–292. [Google Scholar] [CrossRef]
- Atalik, T.S.; Utku, S. Stochastic linearization of multi-degree-of-freedom non-linear systems. Earthq. Eng. Struct. Dyn. 1976, 4, 411–420. [Google Scholar] [CrossRef]
- Krolikowski, L.P.; Gay, T.A. An improved linearization technique for frequency domain riser analysis. In Proceedings of the 12th Offshore Technology Conference, Houston, TX, USA, 5–8 May 1980. [Google Scholar]
- Spanos, P.D.; Ghosh, R.; Finn, L.D.; Halkyard, J. Coupled analysis of a spar structure: Monte Carlo and statistical linearization solutions. J. Offshore Mech. Arct. Eng. 2005, 127, 11–16. [Google Scholar] [CrossRef]
- Wu, S.C. The effects of current on dynamic response of offshore platforms. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1976. [Google Scholar]
- Hamilton, J. Three-dimensional Fourier analysis of drag force for compliant offshore structures. Appl. Ocean. Res. 1980, 2, 147–153. [Google Scholar] [CrossRef]
- Langley, R. The linearisation of three dimensional drag force in random seas with current. Appl. Ocean. Res. 1984, 6, 126–131. [Google Scholar] [CrossRef]
- Huang, S.; Vassalos, D. A numerical method for predicting snap loading of marine cables. Appl. Ocean. Res. 1993, 15, 235–242. [Google Scholar] [CrossRef]
- Hahn, G.D. A modified Euler method for dynamic analysis. Int. J. Numer. Methods Eng. 1991, 32, 943–955. [Google Scholar] [CrossRef]
- Huse, E.; Kleiven, G.; Niesien, F. Large scale model testing of deep sea risers. In Proceedings of the Offshore Technology Conference (OTC), Houston, TX, USA, 4–7 May 1998. [Google Scholar]
- Chaplin, J.R.; Bearman, P.W.; Huarte, F.; Pattenden, R.J. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 2005, 21, 3–24. [Google Scholar] [CrossRef]
- Huarte, F.; Bearman, P.W.; Chaplin, J.R. On the force distribution along the axis of a flexible circular cylinder undergoing multi-mode vortex-induced vibrations. J. Fluids Struct. 2006, 22, 897–903. [Google Scholar] [CrossRef]
- Morse, T.I.; Govardhan, R.N.; Williamson, C.H.K. The effect of end conditions on the vortex-induced vibration of cylinders. J. Fluids Struct. 2008, 24, 1227–1239. [Google Scholar] [CrossRef]
- Vandiver, J.K.; Allen, D.; Li, L. The occurrence of lock-in under highly sheared conditions. J. Fluids Struct. 1996, 10, 555–561. [Google Scholar] [CrossRef]
- Costello, G.A.; Phillips, J.W. Effective modulus of twisted wire cables. J. Eng. Mech. Div. 1976, 102, 171–181. [Google Scholar] [CrossRef]
- Monsalve-Giraldo, J.S.; Cortina, J.P.R.; de Sousa, F.J.M.; Videiro, P.M.; Sagrilo, L.V.S. Hybrid parabolic interpolation-artificial neural network method (HPI-ANNM) for long-term extreme response estimation of steel risers. Appl. Ocean. Res. 2018, 76, 221–234. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Dong, S.; Jiang, F.Y. Reliability analysis of mooring lines for floating structures using ANN-BN inference. J. Eng. Marit. Environ. 2021, 235, 236–254. [Google Scholar] [CrossRef]
- Mao, Y.X.; Wang, T.Q.; Duan, M.L. A DNN-based approach to predict dynamic mooring tensions for semisubmersible platform under a mooring line failure condition. Ocean. Eng. 2022, 266, 112767. [Google Scholar] [CrossRef]
- Sivaprasad, H.; Lekkala, M.R.; Latheef, M.; Seo, J.; Yoo, K.; Jin, C.; Kim, D.K. Fatigue damage prediction of top tensioned riser subjected to vortex-induced vibrations using artificial neural networks. Ocean. Eng. 2023, 268, 113393. [Google Scholar] [CrossRef]
- Guarize, R.; Matos, N.A.F.; Sagrilo, L.V.S.; Lima, E.C.P. Neural networks in the dynamic response analysis of slender marine structures. Appl. Ocean. Res. 2007, 29, 191–198. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, T.; Liao, S.J. Predicting future mooring line tension of floating structure by machine learning. Ocean. Eng. 2023, 269, 113470. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, Y.Y.; Su, Q.; Li, R.; Li, H.; Lu, Z.; Lu, H.; Lu, Q. Time series prediction based on LSTM neural network for top tension response of umbilical cables. Mar. Struct. 2023, 91, 103448. [Google Scholar] [CrossRef]
- Xie, Y.J.; Tang, H.S.; Low, Y.M. Deep gated recurrent unit networks for time-domain long-term fatigue analysis of mooring lines considering wave directionality. Ocean. Eng. 2023, 284, 115244. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning, 3rd ed.; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Gao, J.; Ling, H.; Hu, W.; Xing, J. Transfer learning based visual tracking with Gaussian processes regression. In Proceedings of the Computer Vision—ECCV 2014, Part III, Zurich, Switzerland, 6–12 September 2014; pp. 188–203. [Google Scholar]
- Liu, Y.; Pan, Y.; Huang, D.; Wang, Q. Fault prognosis of filamentous sludge bulking using an enhanced multi-output Gaussian processes regression. Control Eng. Pract. 2017, 62, 46–54. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Rezazadeh, N.; De Luca, A.; Perfetto, D.; Salami, M.R.; Lamanna, G. Systematic critical review of structural health monitoring under environmental and operational variability: Approaches for baseline compensation, adaptation, and reference-free techniques. Smart Mater. Struct. 2025, 34, 073001. [Google Scholar] [CrossRef]




| Kernel Type | SM-Q3 | SM-Q6 | SM-Q8 | RBF | Matérn |
|---|---|---|---|---|---|
| Training time (s) | 1.47 | 6.65 | 8.51 | 1.14 | 1.47 |
| Loss | 1.645 | 1.418 | 1.625 | 10.023 | 9.750 |
| Output | Number of Sample Points |
|---|---|
| Top tension | 992 |
| Lateral overturning moment | 1055 |
| Longitudinal overturning moment | 764 |
| Curvature | 1741 |
| Error Sources | Accuracy Level |
|---|---|
| DP3 | ≤0.5 m |
| ADCP | 1% ± 0.5 cm |
| USBL | 1∼5 m |
| LAR | 10% |
| Current Velocity (m/s) | Relative Distance (m) | Wave Height (m) | Top Tension (kN) |
|---|---|---|---|
| 1.50 | 150.0 | 4.0 | 65.9365 |
| 1.48 | 144.5 | 3.6 | 65.7737 |
| 1.48 | 144.5 | 4.4 | 66.0707 |
| 1.48 | 155.5 | 3.6 | 65.7532 |
| 1.48 | 155.5 | 4.4 | 66.0519 |
| 1.52 | 144.5 | 3.6 | 65.8291 |
| 1.52 | 144.5 | 4.4 | 66.1277 |
| 1.52 | 155.5 | 3.6 | 65.8059 |
| 1.52 | 155.5 | 4.4 | 66.1070 |
| 1.52 | 155.5 | 4.4 | 68.5384 |
| Input Parameters | Wave Height | Wave Direction | Current Direction | Current Speed |
|---|---|---|---|---|
| Range | 0∼4.5 m | 0∼360° | 0∼360° | 0∼1.8 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Huang, C.; Wang, S.; Liu, J.; Sun, Y.; Li, L.; Liu, W.; Yu, L.; Li, Y. A Hybrid Gaussian Process Framework for Rapid Prediction of Umbilical Cable Mechanics in Deep-Sea Mining. J. Mar. Sci. Eng. 2025, 13, 2232. https://doi.org/10.3390/jmse13122232
Yu Z, Huang C, Wang S, Liu J, Sun Y, Li L, Liu W, Yu L, Li Y. A Hybrid Gaussian Process Framework for Rapid Prediction of Umbilical Cable Mechanics in Deep-Sea Mining. Journal of Marine Science and Engineering. 2025; 13(12):2232. https://doi.org/10.3390/jmse13122232
Chicago/Turabian StyleYu, Zhihao, Chaojun Huang, Shuqing Wang, Jiancheng Liu, Yuankun Sun, Lei Li, Wencheng Liu, Liwei Yu, and Yuanhe Li. 2025. "A Hybrid Gaussian Process Framework for Rapid Prediction of Umbilical Cable Mechanics in Deep-Sea Mining" Journal of Marine Science and Engineering 13, no. 12: 2232. https://doi.org/10.3390/jmse13122232
APA StyleYu, Z., Huang, C., Wang, S., Liu, J., Sun, Y., Li, L., Liu, W., Yu, L., & Li, Y. (2025). A Hybrid Gaussian Process Framework for Rapid Prediction of Umbilical Cable Mechanics in Deep-Sea Mining. Journal of Marine Science and Engineering, 13(12), 2232. https://doi.org/10.3390/jmse13122232





