A Slow Failure Particle Swarm Optimization Long Short-Term Memory for Significant Wave Height Prediction
Abstract
1. Introduction
2. Materials and Methods
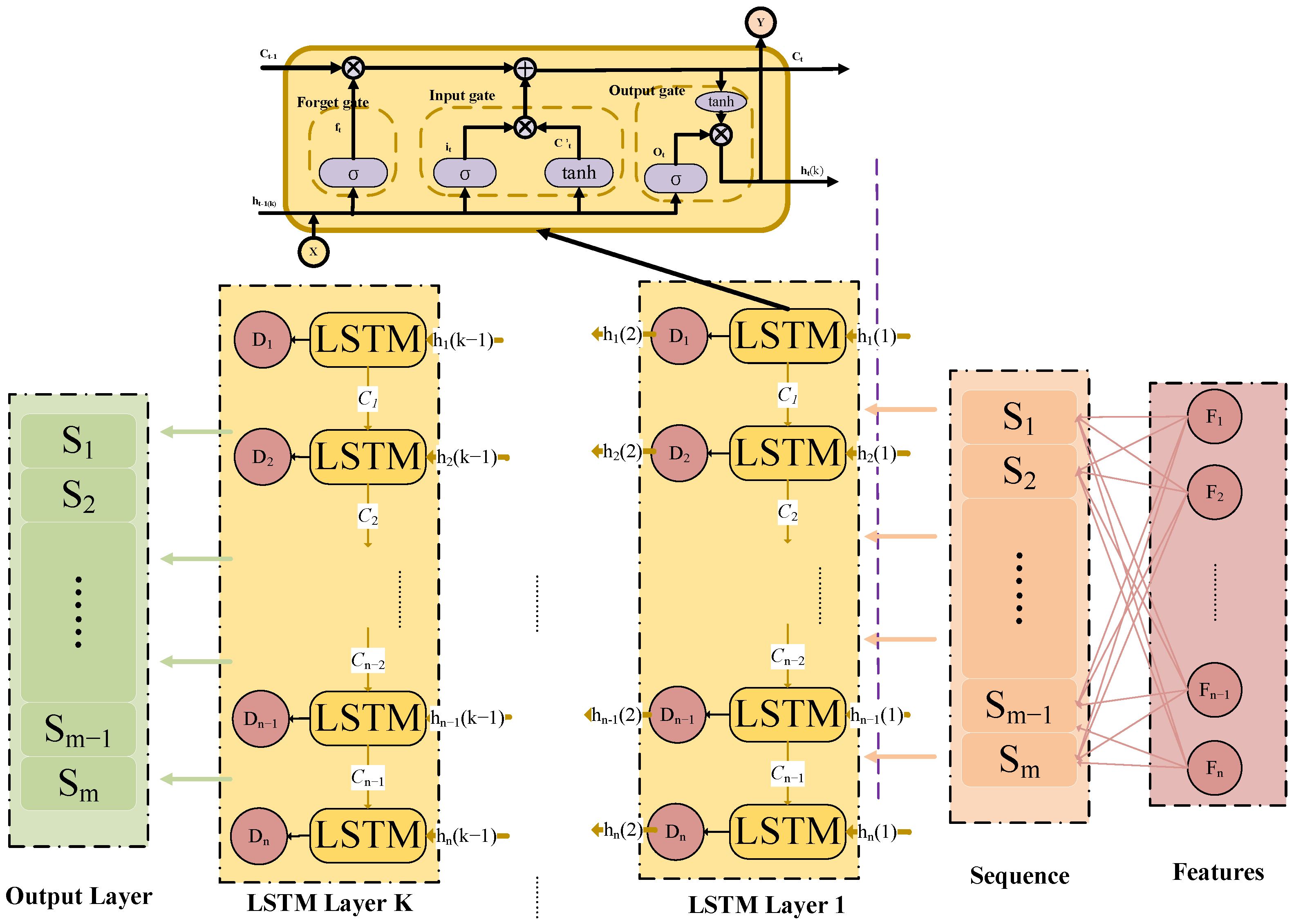
2.1. Long Short-Term Memory
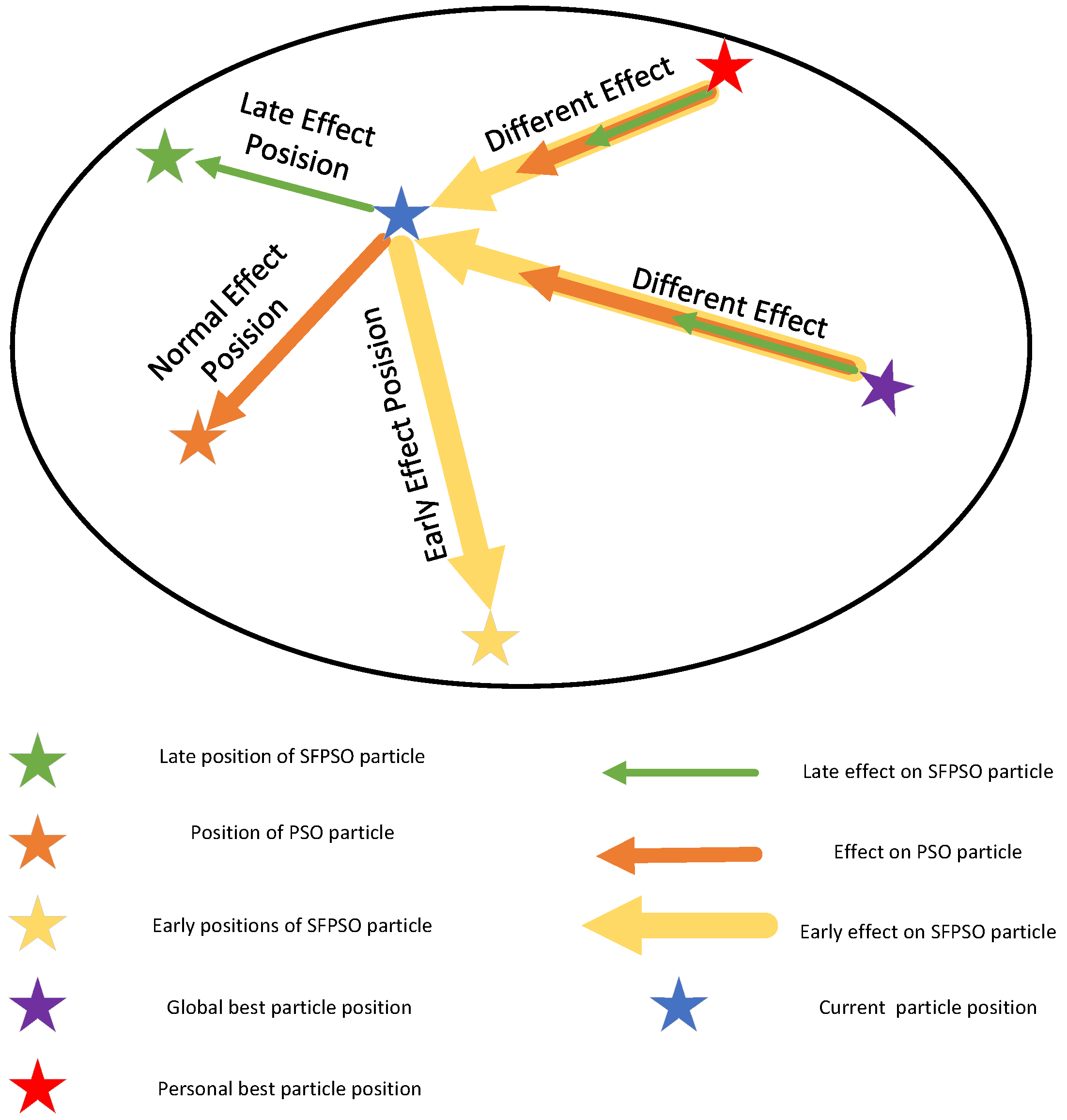
2.2. Slow Failure Particle Swarm Optimization
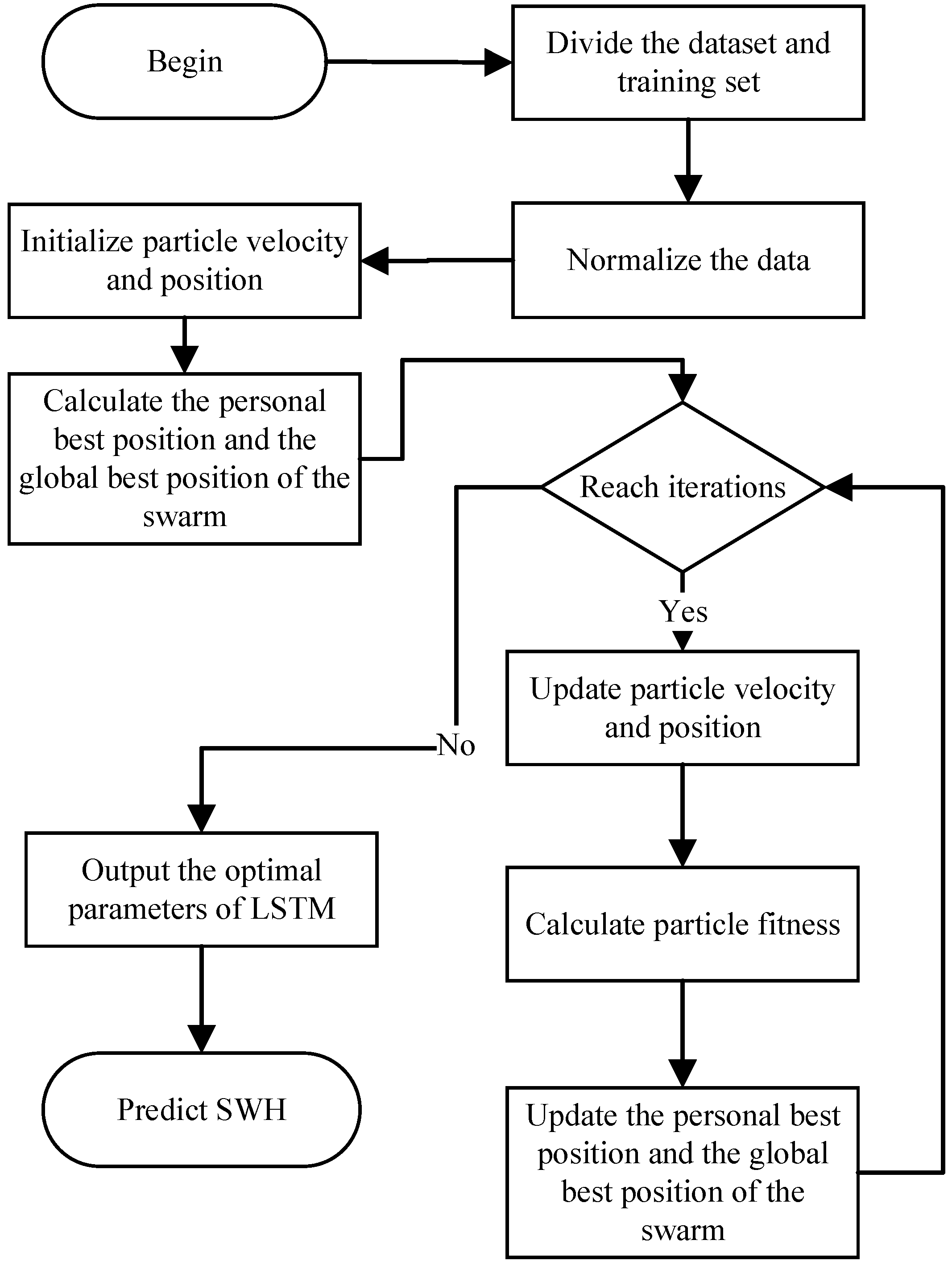
2.3. SFPSO-LSTM
- Step 1: Normalize all the data within the range −1 to 1 by Equation (5). The normalization eliminates the influence of the scale between indicators and increases the speed of calculations.where is the data point after normalization. The X, , and denote the data points for a dimension and the maximum and minimum values for that dimension, respectively.
- Step 2: In the SFPSO process, the mean square error (MSE) is set as the fitness function for SFPSO. All particles continuously update their velocity and position within the range and thus search for the optimal possible combination of parameters. The fitness function of the SFPSO is as follows:where n is the number of samples, and the and present the predicted and the true significant wave heights.
- Step 3: The LSTM model is trained with the parameters searched by SFPSO.
- Step 4: The results are predicted using a trained SFPSO-LSTM.
3. Experiment and Results
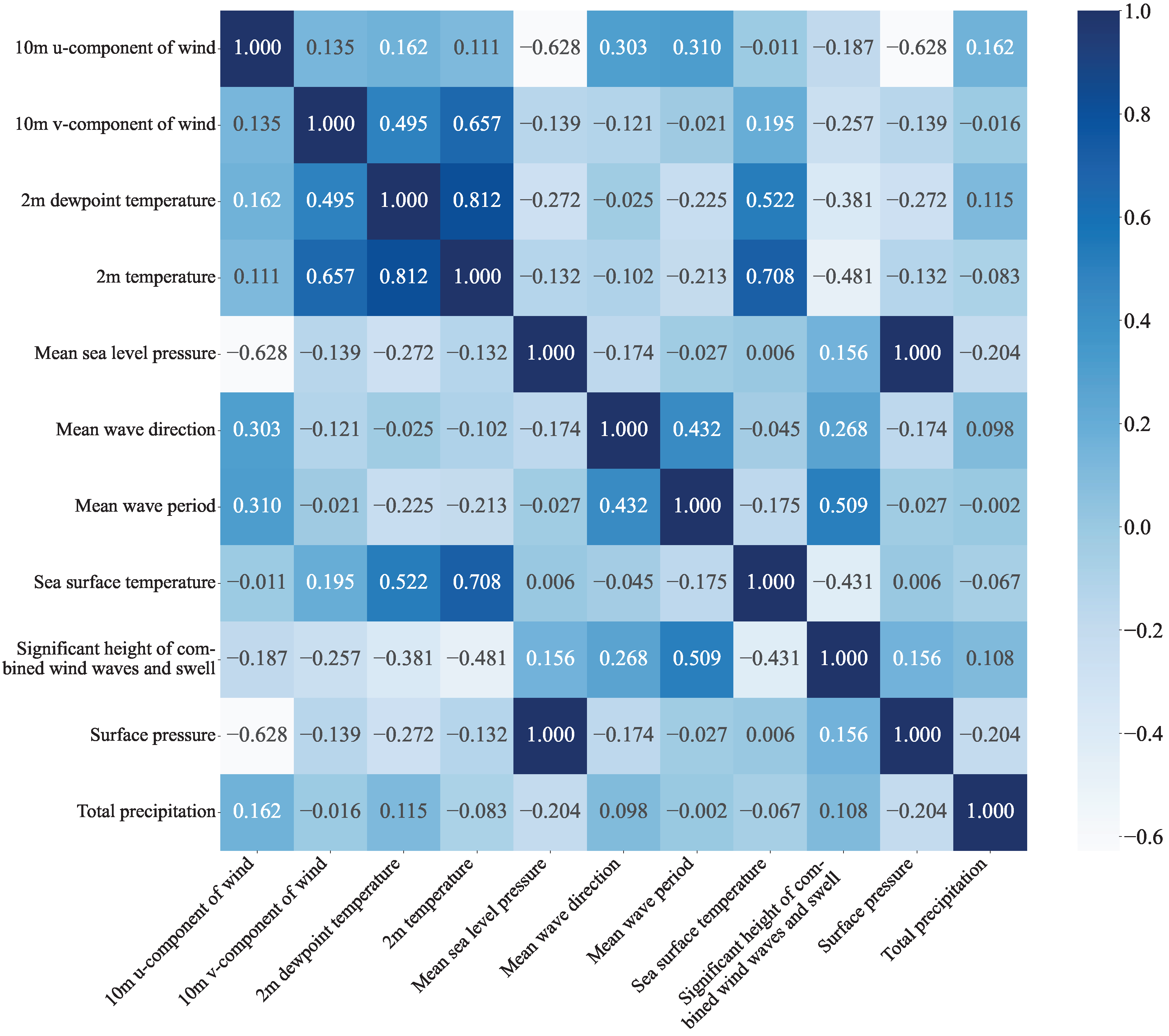
3.1. Data Preparation
- P1, latidude and longitude: 42.0, 29.0, Date: 1 January 2023–31 May 2023, sampling method: hour, 3625 sets of data
- P2, latidude and longitude: 25.0, 165.0, Date: 1 January 2023–31 May 2023, sampling method: hour, 3625 sets of data
- P3, latidude and longitude: −31.0, 74.0, Date: 1 January 2023–31 May 2023, Sampling method: hour, 3625 sets of data
- P4, latidude and longitude: 74.5, 37.5, Date: 1 January 2023–31 May 2023, sampling method: hour, 3625 sets of data
- Diverse Environmental Conditions: The selected points offer a wide range of oceanic environments, from enclosed seas to open oceans, and from temperate to polar regions. This diversity ensures the model’s robustness and adaptability to various maritime conditions.
- Comprehensive Data Representation: By encompassing different latitudinal zones and oceanic conditions, the model can be trained on a comprehensive dataset, enhancing its predictive accuracy and generalizability.
- Enhanced Model Validation: The geographical diversity allows for extensive validation of the model across a range of conditions, ensuring that the model is not overfitted to a specific type of environment.
- Global Applicability: Training the model on data from these varied locations increases the likelihood that it can be effectively applied to wave height prediction in other parts of the world’s oceans, thereby enhancing its global utility.
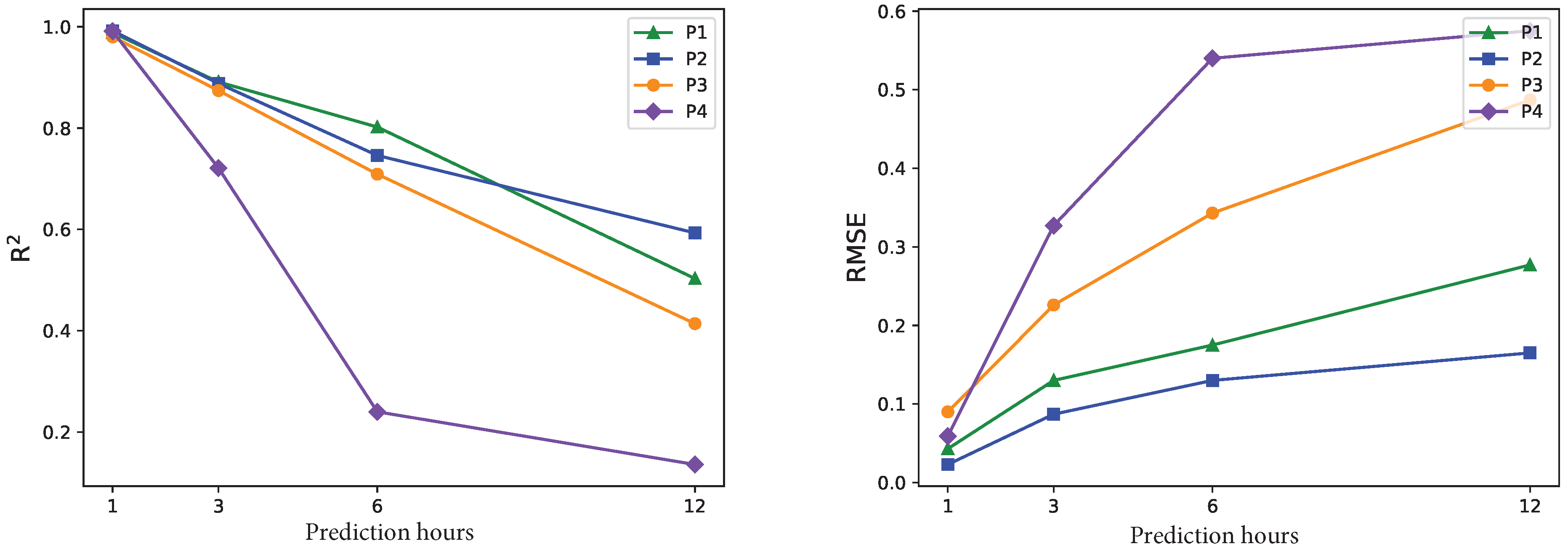
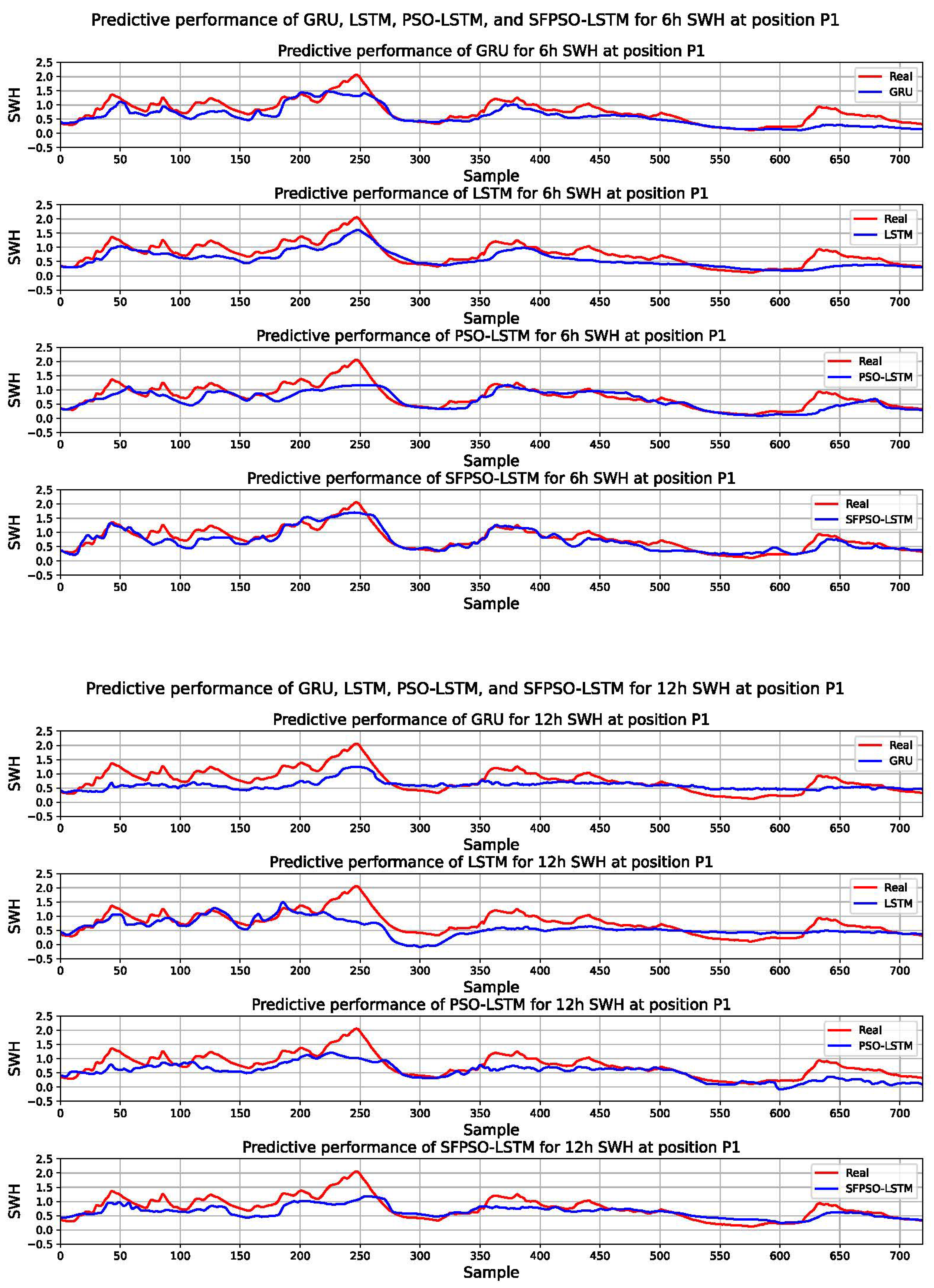
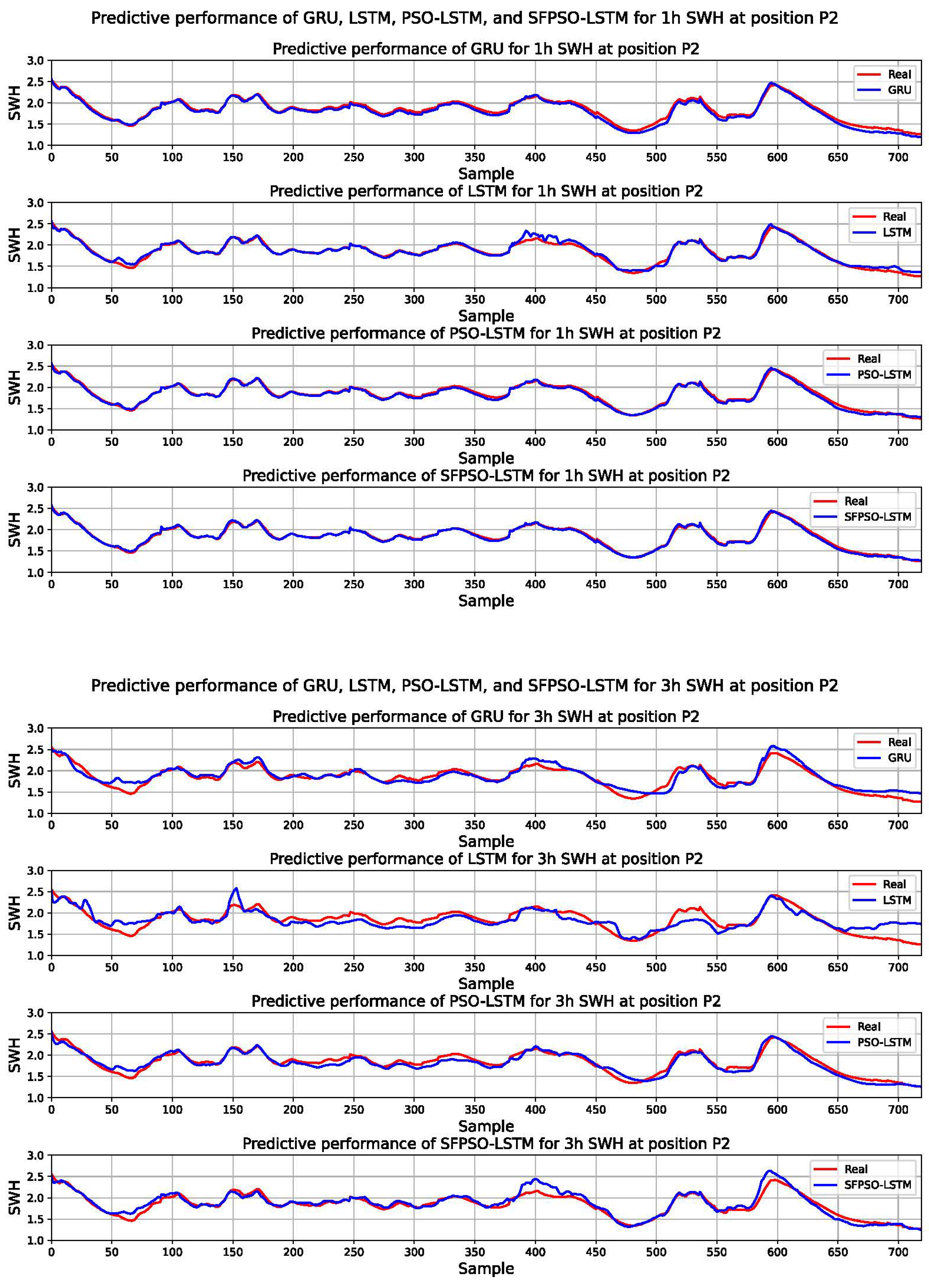
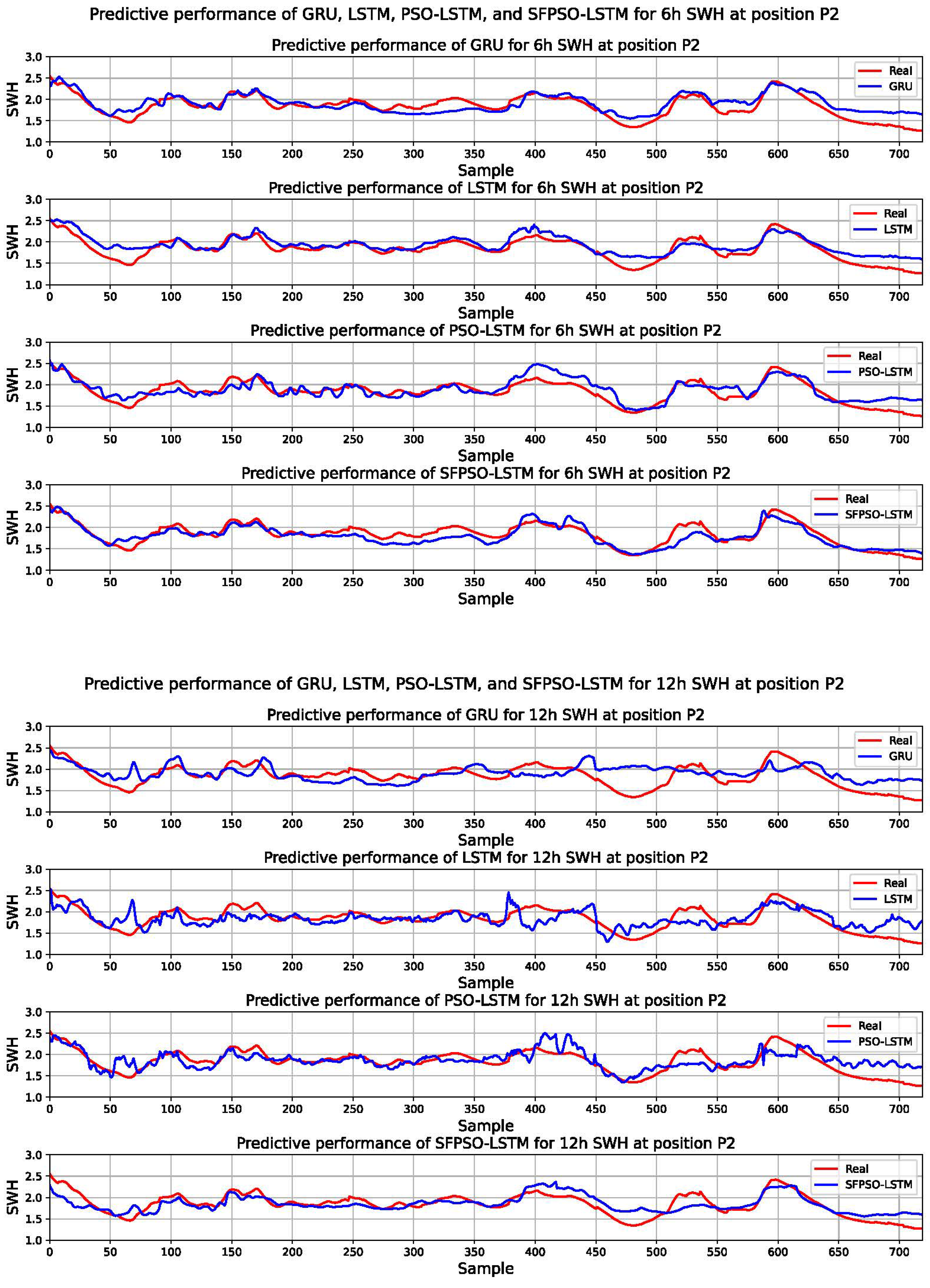
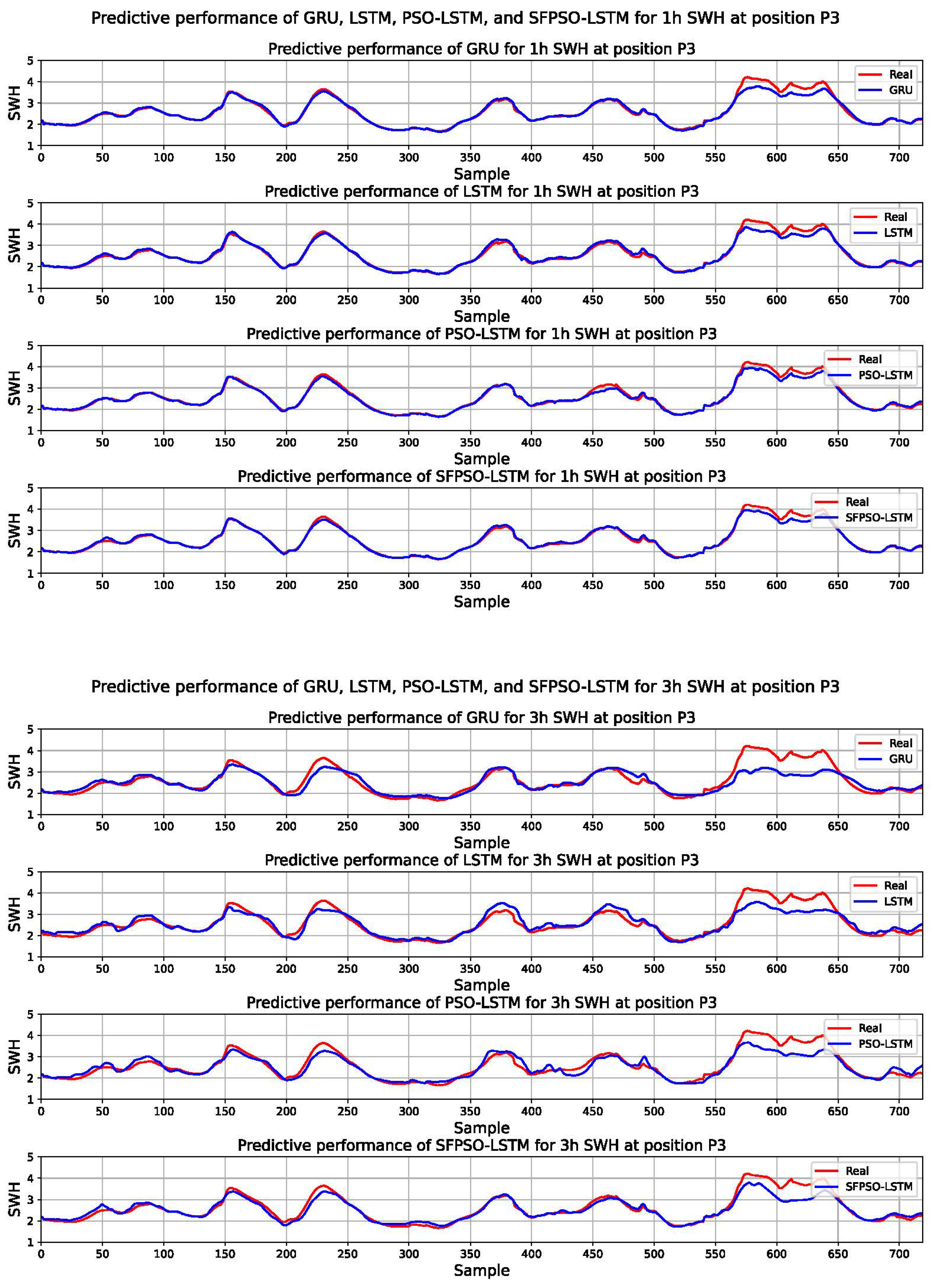
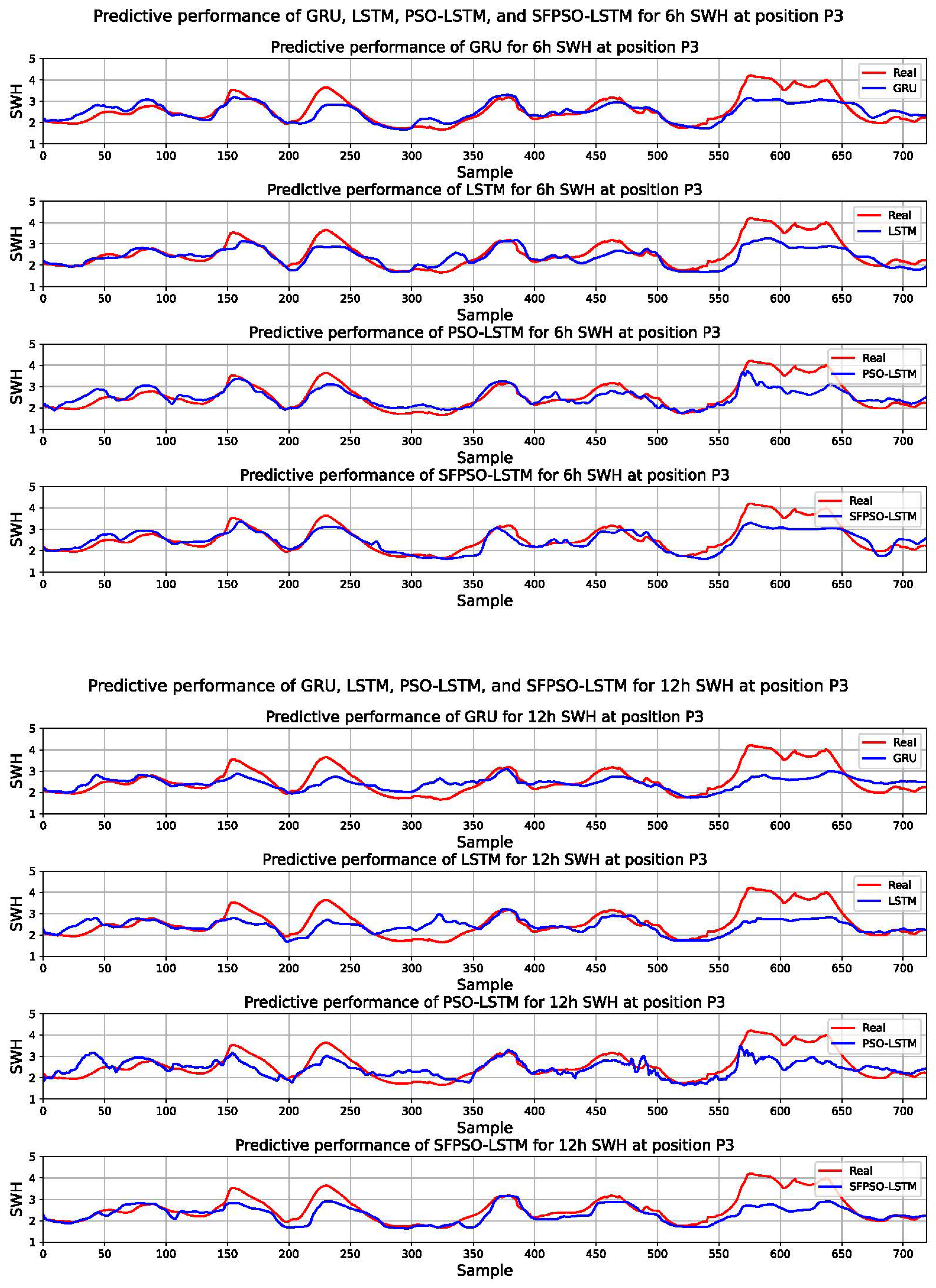
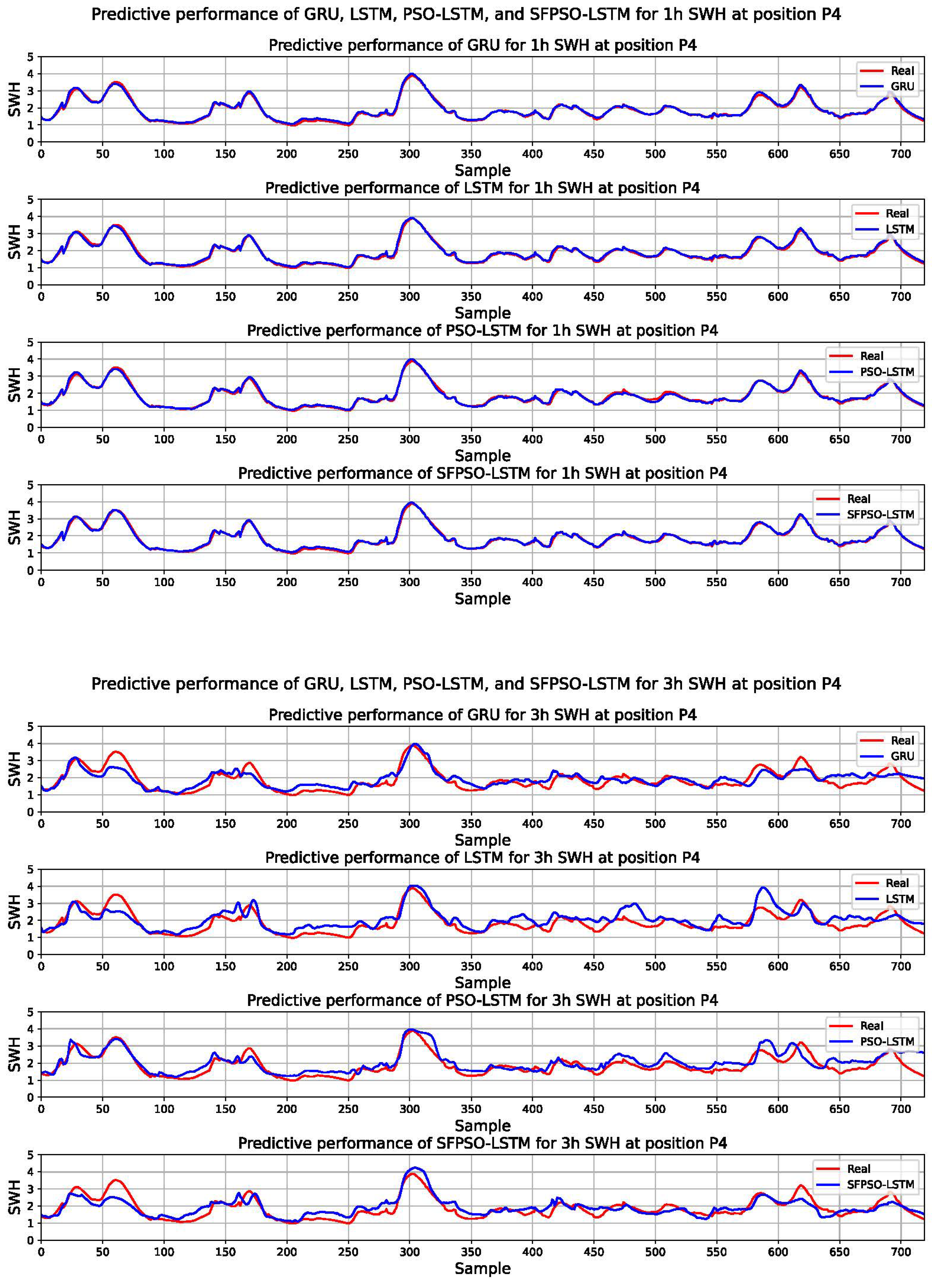
3.2. Results
3.3. Analyses
3.4. Limitations and Future Recommendation
4. Conclusions
- Enhanced Predictive Accuracy: The integration of the slow failure particle swarm optimization (SFPSO) algorithm with the long short-term memory (LSTM) neural network significantly improves the accuracy of significant wave height (SWH) predictions compared to traditional methods.
- Adaptive Algorithm Efficiency: The SFPSO algorithm effectively addresses the limitations of traditional particle swarm optimization (PSO) by adaptively adjusting particle search ranges based on iteration count, reducing premature convergence and improving search precision.
- Robust Model Performance: The LSTM model, optimized with SFPSO, demonstrates robust performance across diverse marine environments, ensuring reliable predictions in various oceanic conditions, including enclosed seas, open oceans, temperate zones, and polar regions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lou, R.; Wang, W.; Li, X.; Zheng, Y.; Lv, Z. Prediction of Ocean Wave Height Suitable for Ship Autopilot. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25557–25566. [Google Scholar] [CrossRef]
- Hlophe, T.; Taylor, P.H.; Kurniawan, A.; Orszaghova, J.; Wolgamot, H. Phase-resolved wave prediction in highly spread seas using optimised arrays of buoys. Appl. Ocean. Res. 2023, 130, 103435. [Google Scholar] [CrossRef]
- Liao, Z.; Sun, T.; Al-Ani, M.; Jordan, L.B.; Li, G.; Wang, Z.; Belmont, M.; Edwards, C.; Zhan, S. Modelling and Control Tank Testing Validation for Attenuator Type Wave Energy Converter—Part II: Linear Noncausal Optimal Control and Deterministic Sea Wave Prediction Tank Testing. IEEE Trans. Sustain. Energy 2023, 14, 1758–1768. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Z.; Zhao, C.; Chen, X.; Wei, Y.; He, J. Deterministic Sea Wave Prediction Based on Least Squares With Regularization Algorithm Using Coherent Microwave Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4209809. [Google Scholar] [CrossRef]
- Al-Ani, M.; Belmont, M.; De Paolo, T. Spectral Algorithm in Waves Profiling and Prediction from Radar Backscatter. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5104711. [Google Scholar] [CrossRef]
- Al-Ani, M.; Belmont, M.; Christmas, J. Sea trial on deterministic sea waves prediction using wave-profiling radar. Ocean Eng. 2020, 207, 107297. [Google Scholar] [CrossRef]
- Fisher, A.; Thomson, J.; Schwendeman, M. Rapid deterministic wave prediction using a sparse array of buoys. Ocean Eng. 2021, 228, 108871. [Google Scholar] [CrossRef]
- Previsic, M.; Karthikeyan, A.; Lyzenga, D. In-Ocean Validation of a Deterministic Sea Wave Prediction (DSWP) System leveraging X-Band Radar to Enable Optimal Control in Wave Energy Conversion Systems. Appl. Ocean. Res. 2021, 114, 102784. [Google Scholar] [CrossRef]
- Simanesew, A.; Trulsen, K.; Krogstad, H.E.; Nieto Borge, J.C. Surface wave predictions in weakly nonlinear directional seas. Appl. Ocean. Res. 2017, 65, 79–89. [Google Scholar] [CrossRef]
- Lu, K.; Wang, J.; Zhang, M. Study on prediction of internal solitary waves propagation in the southern Andaman Sea. J. Oceanogr. 2021, 77, 607–613. [Google Scholar] [CrossRef]
- Demetriou, D.; Michailides, C.; Papanastasiou, G.; Onoufriou, T. Coastal zone significant wave height prediction by supervised machine learning classification algorithms. Ocean Eng. 2021, 221, 108592. [Google Scholar] [CrossRef]
- Huang, W.; Dong, S. Improved short-term prediction of significant wave height by decomposing deterministic and stochastic components. Renew. Energy 2021, 177, 743–758. [Google Scholar] [CrossRef]
- Tang, G.; Lu, P.; Hu, X.; Men, S. Control system research in wave compensation based on particle swarm optimization. Sci. Rep. 2021, 11, 15316. [Google Scholar] [CrossRef] [PubMed]
- Son, B.; Do, K. Optimization of SWAN Wave Model to Improve the Accuracy of Winter Storm Wave Prediction in the East Sea. J. Ocean. Eng. Technol. 2021, 35, 273–286. [Google Scholar] [CrossRef]
- Altunkaynak, A. Prediction of significant wave height using spatial function. Ocean Eng. 2015, 106, 220–226. [Google Scholar] [CrossRef]
- Huchet, M.; Babarit, A.; Ducrozet, G.; Gilloteaux, J.C.; Ferrant, P. Nonlinear deterministic sea wave prediction using instantaneous velocity profiles. Ocean Eng. 2021, 220, 108492. [Google Scholar] [CrossRef]
- Çelik, A. Improving prediction performance of significant wave height via hybrid SVD-Fuzzy model. Ocean Eng. 2022, 266, 113173. [Google Scholar] [CrossRef]
- Yang, H.; Wang, H.; Ma, Y.; Xu, M. Prediction of Wave Energy Flux in the Bohai Sea through Automated Machine Learning. J. Mar. Sci. Eng. 2022, 10, 1025. [Google Scholar] [CrossRef]
- Kim, I.C.; Ducrozet, G.; Bonnefoy, F.; Leroy, V.; Perignon, Y. Real-time phase-resolved ocean wave prediction in directional wave fields: Enhanced algorithm and experimental validation. Ocean Eng. 2023, 276, 114212. [Google Scholar] [CrossRef]
- Son, D.; Jun, K.; Kwon, J.I.; Yoo, J.; Park, S.H. Improvement of wave predictions in marginal seas around Korea through correction of simulated sea winds. Appl. Ocean. Res. 2023, 130, 103433. [Google Scholar] [CrossRef]
- Hlophe, T.; Wolgamot, H.; Taylor, P.H.; Kurniawan, A.; Orszaghova, J.; Draper, S. Wave-by-wave prediction in weakly nonlinear and narrowly spread seas using fixed-point surface-elevation time histories. Appl. Ocean. Res. 2022, 122, 103112. [Google Scholar] [CrossRef]
- Zhan, Y.; Zhang, H.; Li, J.; Li, G. Prediction Method for Ocean Wave Height Based on Stacking Ensemble Learning Model. J. Mar. Sci. Eng. 2022, 10, 1150. [Google Scholar] [CrossRef]
- Sadeghifar, T.; Lama, G.F.; Sihag, P.; Bayram, A.; Kisi, O. Wave height predictions in complex sea flows through soft-computing models: Case study of Persian Gulf. Ocean Eng. 2022, 245, 110467. [Google Scholar] [CrossRef]
- Meng, F.; Song, T.; Xu, D.; Xie, P.; Li, Y. Forecasting tropical cyclones wave height using bidirectional gated recurrent unit. Ocean Eng. 2021, 234, 108795. [Google Scholar] [CrossRef]
- Meng, Z.F.; Chen, Z.; Khoo, B.C.; Zhang, A.M. Long-time prediction of sea wave trains by LSTM machine learning method. Ocean Eng. 2022, 262, 112213. [Google Scholar] [CrossRef]
- Hao, P.; Li, S.; Yu, C.; Wu, G. A Prediction Model of Significant Wave Height in the South China Sea Based on Attention Mechanism. Front. Mar. Sci. 2022, 9, 895212. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Gao, S.; Ren, P. Ocean wave height series prediction with numerical long short-term memory. J. Mar. Sci. Eng. 2021, 9, 514. [Google Scholar] [CrossRef]
- Adytia, D.; Saepudin, D.; Tarwidi, D.; Pudjaprasetya, S.R.; Husrin, S.; Sopaheluwakan, A.; Prasetya, G. Modelling of Deep Learning-Based Downscaling for Wave Forecasting in Coastal Area. Water 2023, 15, 204. [Google Scholar] [CrossRef]
- Wang, H.; Fu, D.; Liu, D.; Xiao, X.; He, X.; Liu, B. Analysis and Prediction of Significant Wave Height in the Beibu Gulf, South China Sea. J. Geophys. Res. Ocean. 2021, 126, e2020JC017144. [Google Scholar] [CrossRef]
- Dakar, E.; Fernández Jaramillo, J.M.; Gertman, I.; Mayerle, R.; Goldman, R. An artificial neural network based system for wave height prediction. Coast. Eng. J. 2023, 65, 309–324. [Google Scholar] [CrossRef]
- Li, S.; Hao, P.; Yu, C.; Wu, G. CLTS-net: A more accurate and universal method for the long-term prediction of significant wave height. J. Mar. Sci. Eng. 2021, 9, 1464. [Google Scholar] [CrossRef]
- Fu, Y.; Ying, F.; Huang, L.; Liu, Y. Multi-step-ahead significant wave height prediction using a hybrid model based on an innovative two-layer decomposition framework and LSTM. Renew. Energy 2023, 203, 455–472. [Google Scholar] [CrossRef]
- Adytia, D.; Saepudin, D.; Pudjaprasetya, S.R.; Husrin, S.; Sopaheluwakan, A. A Deep Learning Approach for Wave Forecasting Based on a Spatially Correlated Wind Feature, with a Case Study in the Java Sea, Indonesia. Fluids 2022, 7, 39. [Google Scholar] [CrossRef]
- Jörges, C.; Berkenbrink, C.; Gottschalk, H.; Stumpe, B. Spatial ocean wave height prediction with CNN mixed-data deep neural networks using random field simulated bathymetry. Ocean Eng. 2023, 271, 113699. [Google Scholar] [CrossRef]
- Ma, J.; Xue, H.; Zeng, Y.; Zhang, Z.; Wang, Q. Significant wave height forecasting using WRF-CLSF model in Taiwan strait. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1400–1419. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, P.; Li, S.; Mo, D. Prediction of Significant Wave Height in Offshore China Based on the Machine Learning Method. J. Mar. Sci. Eng. 2022, 10, 836. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, W.; Lu, Y.; Wang, Y.; Zhou, Y.; Hui, N.; Dong, C. ConvLSTM-Based Wave Forecasts in the South and East China Seas. Front. Mar. Sci. 2021, 8, 680079. [Google Scholar] [CrossRef]
- Song, T.; Han, R.; Meng, F.; Wang, J.; Wei, W.; Peng, S. A significant wave height prediction method based on deep learning combining the correlation between wind and wind waves. Front. Mar. Sci. 2022, 9, 983007. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Çelik, A.; Mandev, M.B. Hourly significant wave height prediction via singular spectrum analysis and wavelet transform based models. Ocean Eng. 2023, 281, 114771. [Google Scholar] [CrossRef]
- Çelik, A.; Altunkaynak, A. Optimal Significant Wave Height Monitoring Network Identification via Empirical Orthogonal Function Analysis with QR Column Pivoting Algorithm. J. Waterw. Port Coastal Ocean. Eng. 2023, 149, 04023018. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, G.; Yan, K.; Shi, B.; Di, Y.; Sato, Y. A novel hermit crab optimization algorithm. Sci. Rep. 2023, 13, 9934. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Shi, B.; Yan, K.; Di, Y.; Tang, J.; Xiao, H.; Sato, Y. A twinning bare bones particle swarm optimization algorithm. PLoS ONE 2022, 17, e0267197. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zhou, G.; Di, Y.; Shi, B.; Yan, K.; Sato, Y. A Bare-bones Particle Swarm Optimization with Crossed Memory for Global Optimization. IEEE Access 2023, 11, 31549–31568. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X.; Jin, S.; Greaves, D. Phase-resolved real-time ocean wave prediction with quantified uncertainty based on variational Bayesian machine learning. Appl. Energy 2022, 324, 119711. [Google Scholar] [CrossRef]

| Parameters | GRU | LSTM | PSO-LSTM | SFPSO-LSTM |
|---|---|---|---|---|
| Number of epochs | 500 | 500 | 500 | 500 |
| Solver | Adam | Adam | Adam | Adam |
| Dropout probability | 0.2 | 0.2 | 0.2 | 0.2 |
| Batch size | 64 | 64 | [16, 128] | [16, 128] |
| Number of hidden layer units | 60 | 60 | [10, 120] | [10, 120] |
| Number of layers | 2 | 2 | [1, 5] | [1, 5] |
| Initial learning rate | 0.001 | 0.001 | [0.0001, 0.005] | [0.0001, 0.005] |
| Popularization | None | None | 5 | 5 |
| Number of iterations | None | None | 20 | 20 |
| Position | Predicted Time | Indicators | GRU | LSTM | PSO-LSTM | SFPSO-LSTM |
|---|---|---|---|---|---|---|
| P1 | 1 h | MAE | 0.074 | 0.050 | 0.043 | 0.035 |
| RMSE | 0.100 | 0.072 | 0.057 | 0.043 | ||
| MAPE | 18.447% | 14.888% | 9.246% | 7.610% | ||
| R2 | 0.936 | 0.966 | 0.979 | 0.988 | ||
| 3 h | MAE | 0.119 | 0.119 | 0.142 | 0.104 | |
| RMSE | 0.168 | 0.024 | 0.182 | 0.130 | ||
| MAPE | 19.587% | 22.905% | 22.721% | 16.496% | ||
| R2 | 0.817 | 0.845 | 0.787 | 0.891 | ||
| 6 h | MAE | 0.197 | 0.210 | 0.168 | 0.131 | |
| RMSE | 0.254 | 0.257 | 0.248 | 0.175 | ||
| MAPE | 25.807% | 28.565% | 20.758% | 20.472% | ||
| R2 | 0.583 | 0.575 | 0.604 | 0.802 | ||
| 12 h | MAE | 0.279 | 0.255 | 0.248 | 0.206 | |
| RMSE | 0.345 | 0.335 | 0.322 | 0.277 | ||
| MAPE | 43.992% | 41.964% | 33.521% | 30.268% | ||
| R2 | 0.229 | 0.274 | 0.330 | 0.503 | ||
| P2 | 1 h | MAE | 0.047 | 0.034 | 0.028 | 0.019 |
| RMSE | 0.053 | 0.049 | 0.034 | 0.023 | ||
| MAPE | 2.701% | 1.973% | 1.574% | 1.060% | ||
| R2 | 0.958 | 0.964 | 0.983 | 0.992 | ||
| 3 h | MAE | 0.075 | 0.116 | 0.064 | 0.061 | |
| RMSE | 0.096 | 0.156 | 0.076 | 0.087 | ||
| MAPE | 4.337% | 6.815% | 3.602% | 3.273% | ||
| R2 | 0.861 | 0.636 | 0.914 | 0.888 | ||
| 6 h | MAE | 0.129 | 0.121 | 0.123 | 0.105 | |
| RMSE | 0.161 | 0.154 | 0.155 | 0.130 | ||
| MAPE | 7.687% | 7.232% | 7.081% | 5.661% | ||
| R2 | 0.611 | 0.644 | 0.639 | 0.746 | ||
| 12 h | MAE | 0.204 | 0.165 | 0.150 | 0.131 | |
| RMSE | 0.256 | 0.211 | 0.194 | 0.165 | ||
| MAPE | 12.058% | 9.449% | 8.615% | 7.399% | ||
| R2 | 0.022 | 0.335 | 0.434 | 0.593 |
| Position | Predicted Time | Indicators | GRU | LSTM | PSO-LSTM | SFPSO-LSTM |
|---|---|---|---|---|---|---|
| P3 | 1 h | MAE | 0.062 | 0.063 | 0.059 | 0.054 |
| RMSE | 0.122 | 0.107 | 0.091 | 0.090 | ||
| MAPE | 1.956% | 2.073% | 1.994% | 1.782% | ||
| R2 | 0.963 | 0.972 | 0.979 | 0.980 | ||
| 3 h | MAE | 0.200 | 0.180 | 0.170 | 0.138 | |
| RMSE | 0.330 | 0.256 | 0.244 | 0.226 | ||
| MAPE | 6.778% | 6.259% | 5.944% | 4.741% | ||
| R2 | 0.731 | 0.838 | 0.853 | 0.874 | ||
| 6 h | MAE | 0.274 | 0.285 | 0.266 | 0.252 | |
| RMSE | 0.381 | 0.404 | 0.376 | 0.343 | ||
| MAPE | 9.853% | 10.163% | 9.657% | 9.079% | ||
| R2 | 0.641 | 0.597 | 0.651 | 0.709 | ||
| 12 h | MAE | 0.374 | 0.376 | 0.365 | 0.318 | |
| RMSE | 0.519 | 0.533 | 0.485 | 0.487 | ||
| MAPE | 13.601% | 13.973% | 13.535% | 10.609% | ||
| R2 | 0.334 | 0.299 | 0.418 | 0.414 | ||
| P4 | 1 h | MAE | 0.055 | 0.060 | 0.054 | 0.045 |
| RMSE | 0.069 | 0.071 | 0.068 | 0.059 | ||
| MAPE | 3.142% | 3.409% | 2.929% | 2.591% | ||
| R2 | 0.988 | 0.987 | 0.988 | 0.991 | ||
| 3 h | MAE | 0.264 | 0.330 | 0.285 | 0.260 | |
| RMSE | 0.330 | 0.416 | 0.361 | 0.327 | ||
| MAPE | 15.007% | 18.993% | 16.686% | 14.560% | ||
| R2 | 0.716 | 0.548 | 0.659 | 0.721 | ||
| 6 h | MAE | 0.463 | 0.472 | 0.440 | 0.449 | |
| RMSE | 0.565 | 0.568 | 0.553 | 0.540 | ||
| MAPE | 27.143% | 27.897% | 26.549% | 26.256% | ||
| R2 | 0.168 | 0.158 | 0.200 | 0.240 | ||
| 12 h | MAE | 0.506 | 0.497 | 0.465 | 0.429 | |
| RMSE | 0.600 | 0.586 | 0.577 | 0.575 | ||
| MAPE | 30.405% | 30.264% | 28.325% | 24.086% | ||
| R2 | 0.060 | 0.103 | 0.132 | 0.136 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Yan, Z.; Shi, B.; Sato, Y. A Slow Failure Particle Swarm Optimization Long Short-Term Memory for Significant Wave Height Prediction. J. Mar. Sci. Eng. 2024, 12, 1359. https://doi.org/10.3390/jmse12081359
Guo J, Yan Z, Shi B, Sato Y. A Slow Failure Particle Swarm Optimization Long Short-Term Memory for Significant Wave Height Prediction. Journal of Marine Science and Engineering. 2024; 12(8):1359. https://doi.org/10.3390/jmse12081359
Chicago/Turabian StyleGuo, Jia, Zhou Yan, Binghua Shi, and Yuji Sato. 2024. "A Slow Failure Particle Swarm Optimization Long Short-Term Memory for Significant Wave Height Prediction" Journal of Marine Science and Engineering 12, no. 8: 1359. https://doi.org/10.3390/jmse12081359
APA StyleGuo, J., Yan, Z., Shi, B., & Sato, Y. (2024). A Slow Failure Particle Swarm Optimization Long Short-Term Memory for Significant Wave Height Prediction. Journal of Marine Science and Engineering, 12(8), 1359. https://doi.org/10.3390/jmse12081359






