Implementation of a Far-Field Water Quality Model for the Simulation of Trace Elements in an Eastern Mediterranean Coastal Embayment Receiving High Anthropogenic Pressure
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Target Compounds

2.2. Model Description and Implementation
2.2.1. Software
2.2.2. Domain and Simulation Period
2.2.3. Modeling Approach
2.2.4. Hydrodynamic Circulation (Delft3D-FLOW)
2.2.5. Process Description and Parameterization (Delft3D-WAQ)
2.2.6. Trace Element Loads
2.2.7. Trace Element Partitioning
- : the partition coefficient of a trace element (mg kg−1/mg L−1);
- : the concentration of a trace element in suspended solids (mg kg−1);
- : the concentration of a trace element in water (mg L−1);
- : the particulate concentration of a trace element (mg L−1);
- : the dissolved concentration of a trace element (mg L−1);
- : the concentration of suspended solids (mgSS L−1).
2.2.8. Trace Element Settling
- Cx: the concentration of a carrier substance (gDM m−3 or gC m−3);
- Fset0: the zero-order settling flux of a carrier substance (gDM m−2 d−1 or gC m−2 d−1);
- s: the settling velocity of a carrier substance (m d−1);
- Δt: the timestep in DELWAQ (d).
- τ: the shear stress (Pa);
- τc: the critical shear stress for the settling of a carrier substance (Pa).
2.2.9. Initial Conditions and Open Boundaries
2.3. Validation Data and Statistics
- : each observation (concentration, field monitoring value);
- : modeled concentration;
- : the number observations/modeled concentrations;
- : the standard deviation of observations;
- : the mean of observations.
3. Results
3.1. Model Evaluation
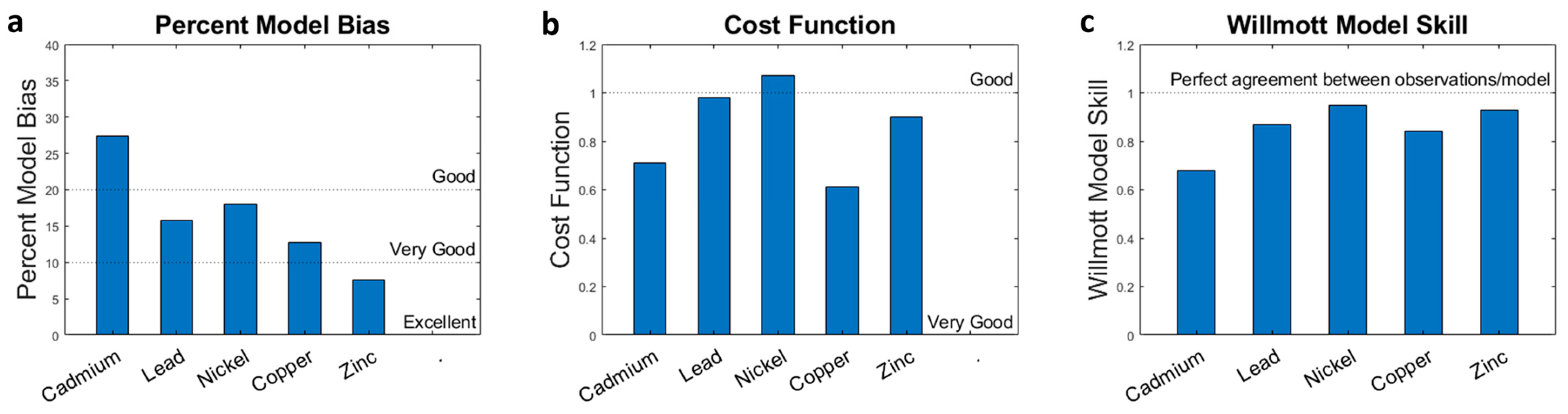
3.1.1. Numerical Error Assessment
3.1.2. Statistical Analysis
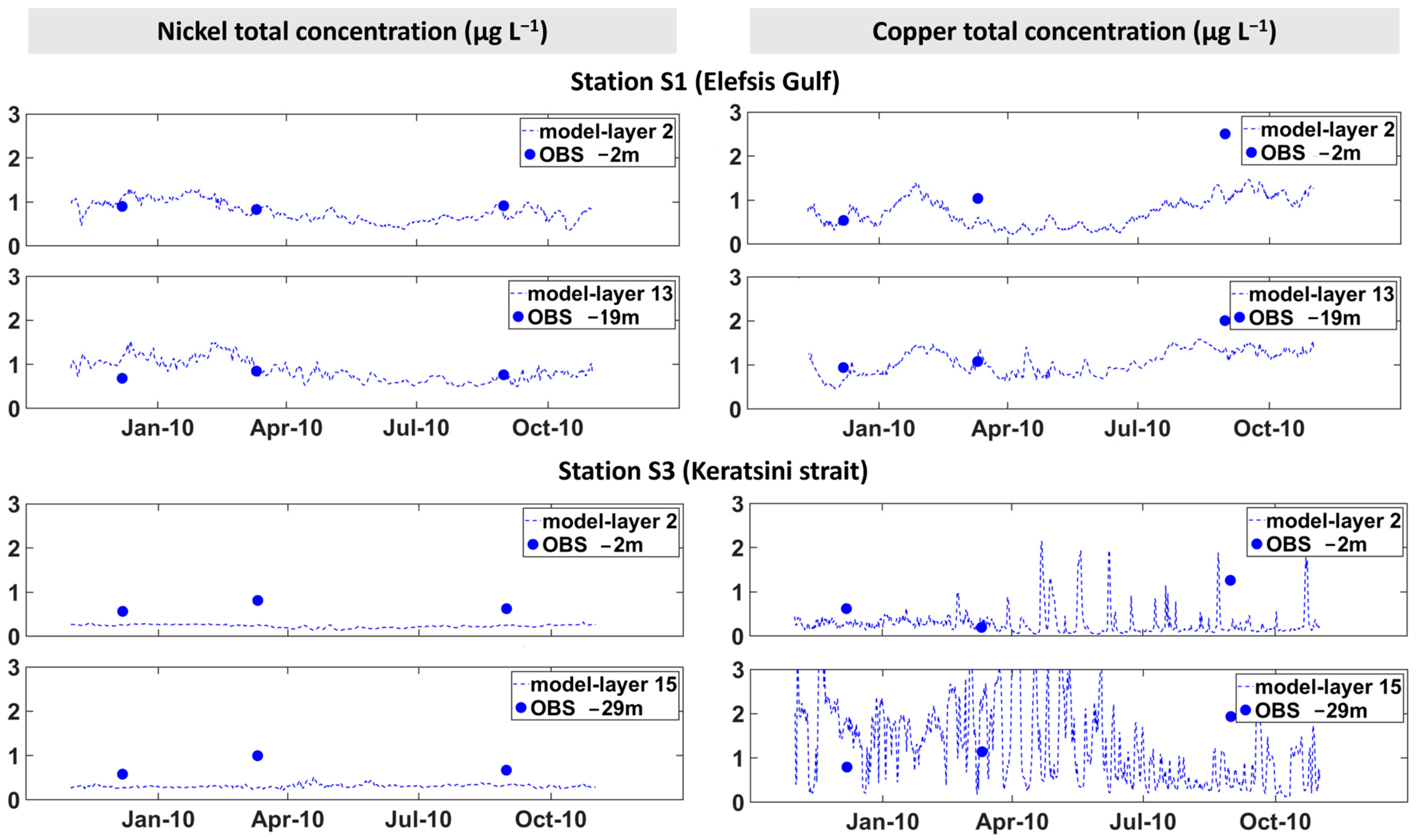
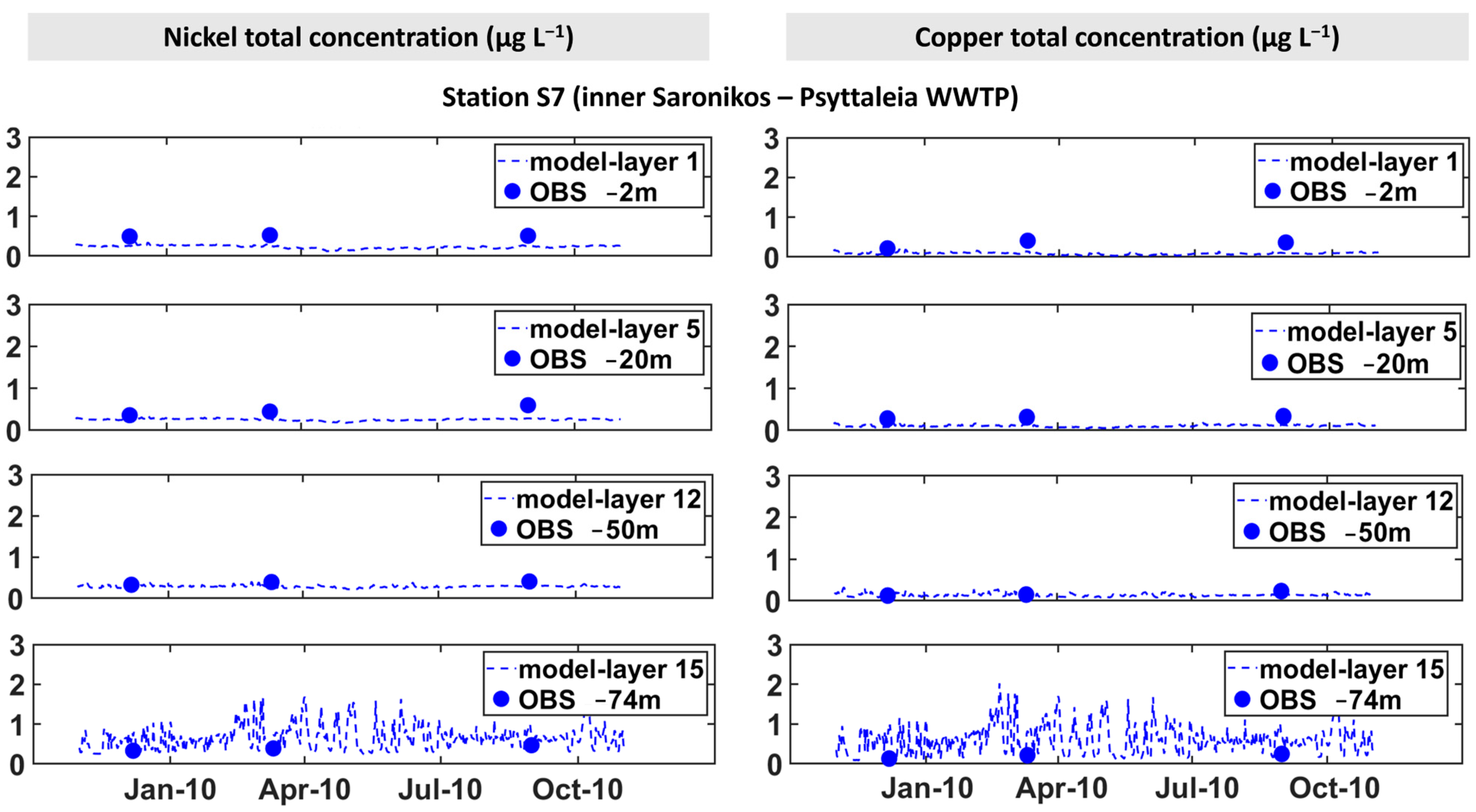
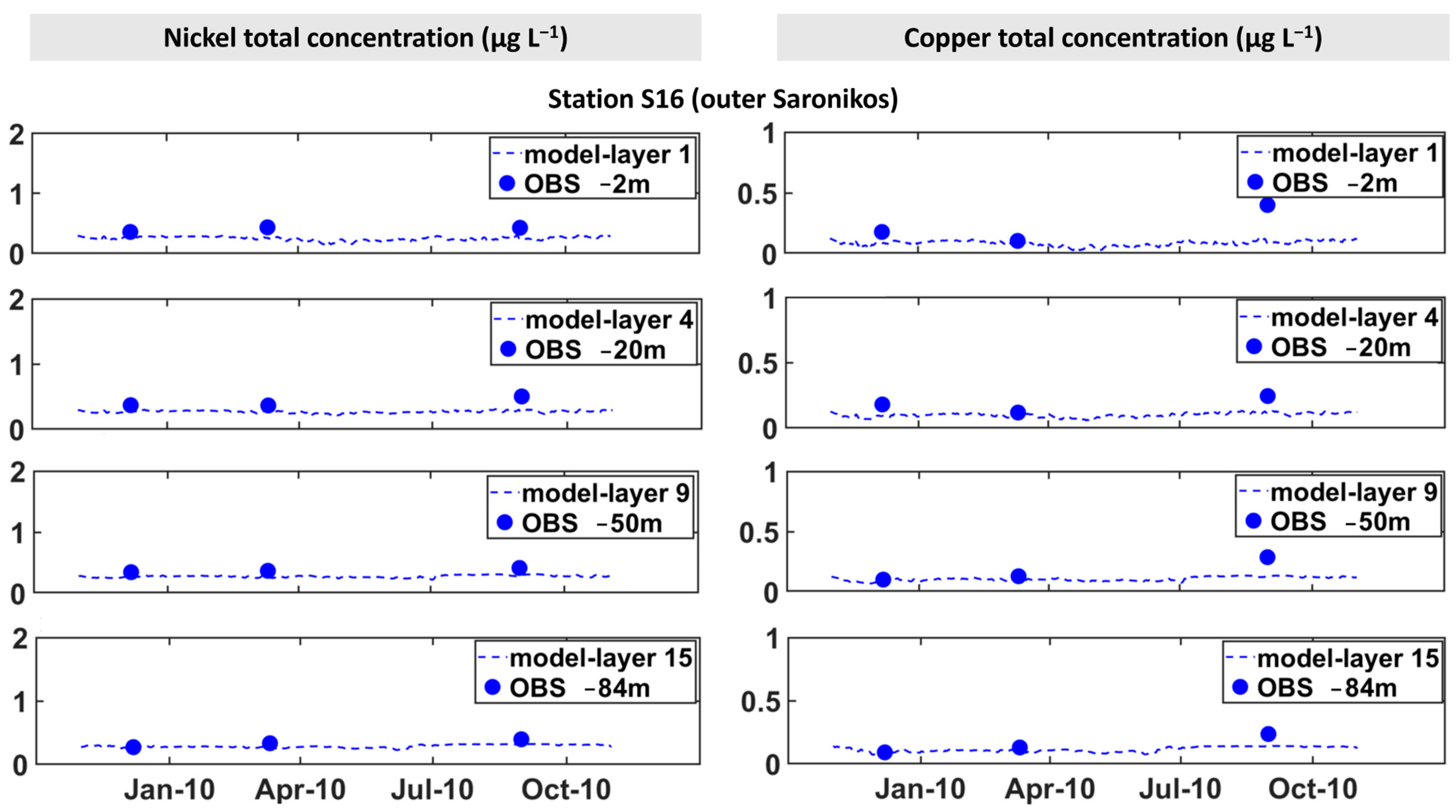
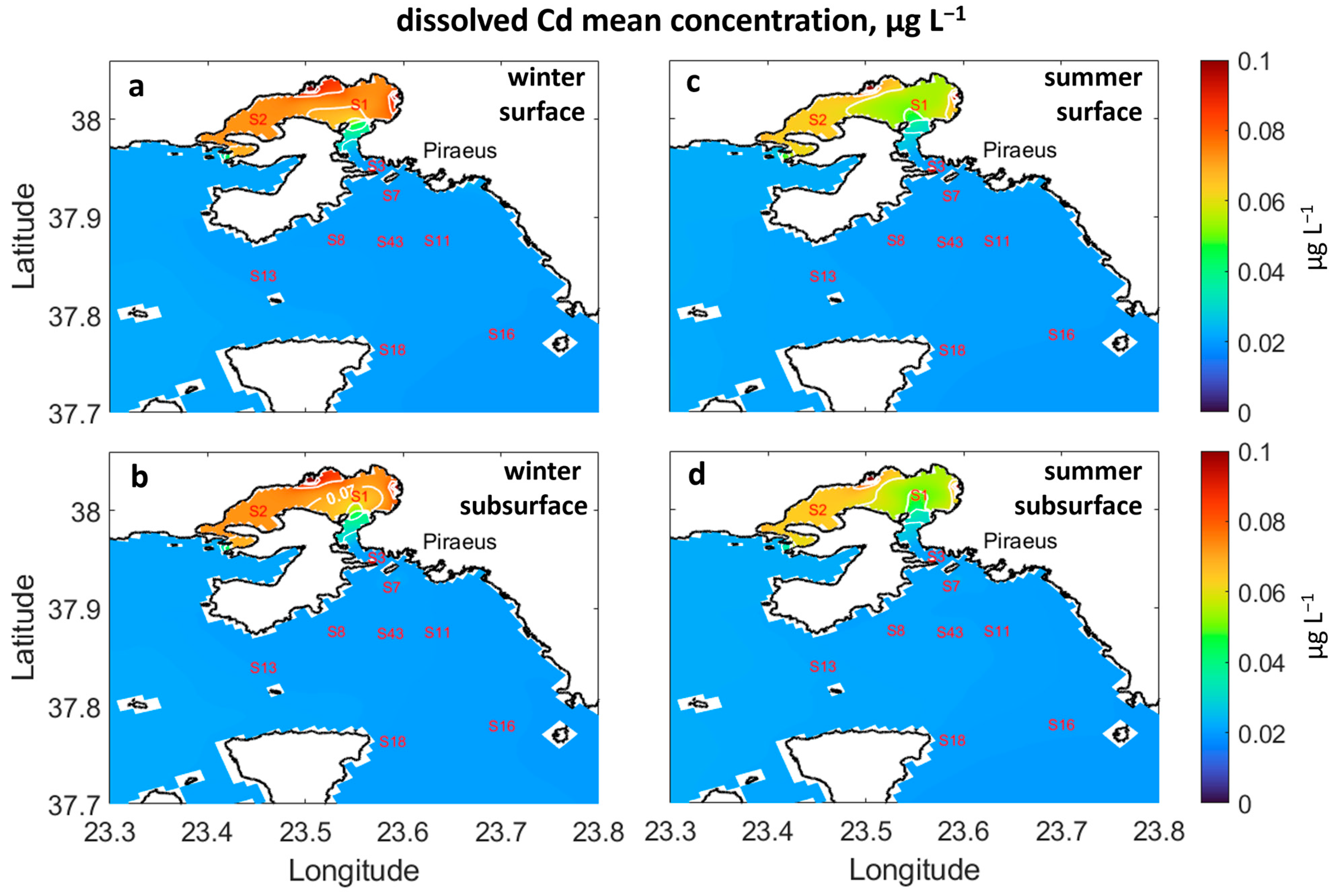
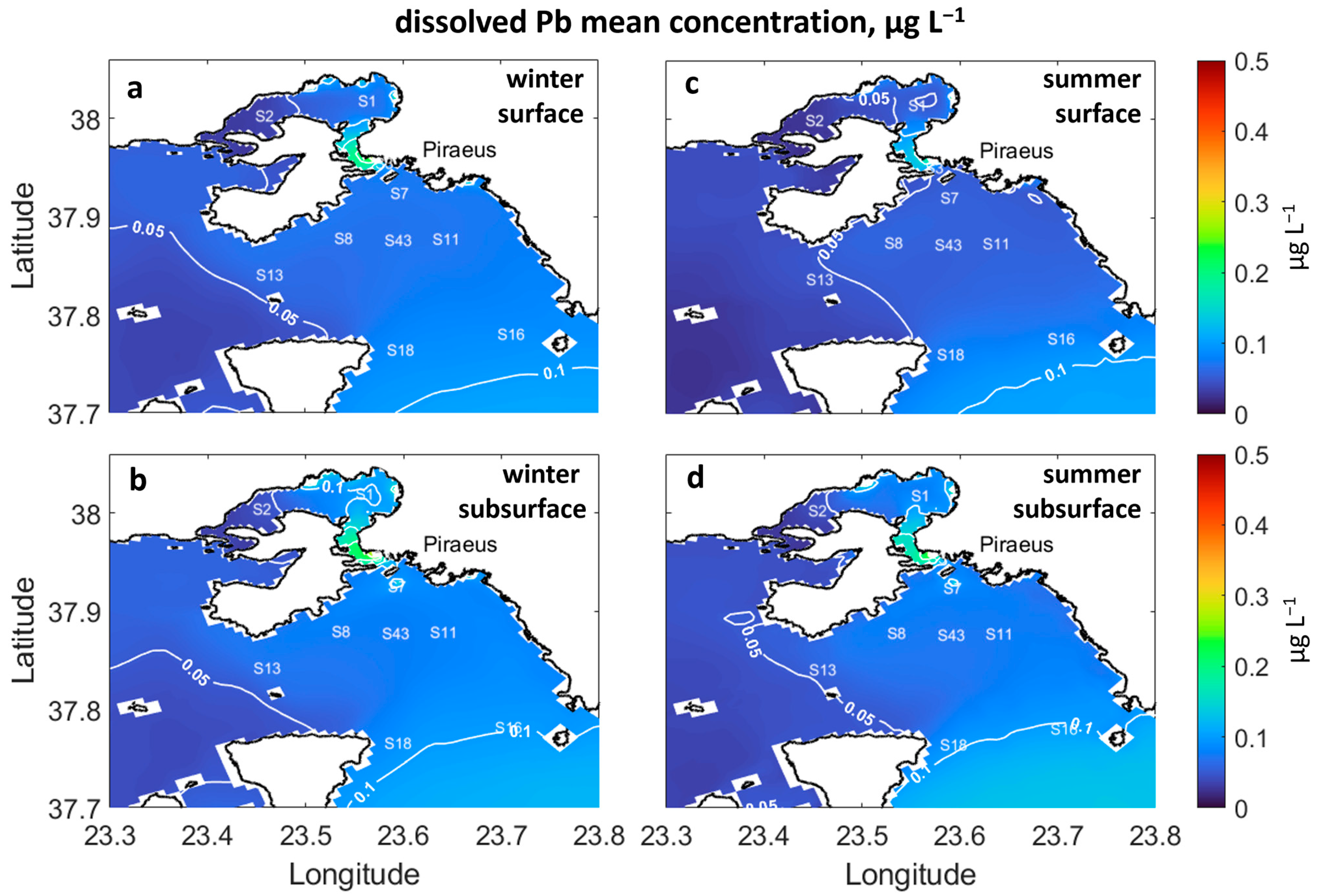
3.2. Spatial Seasonal Distribution of Trace Elements
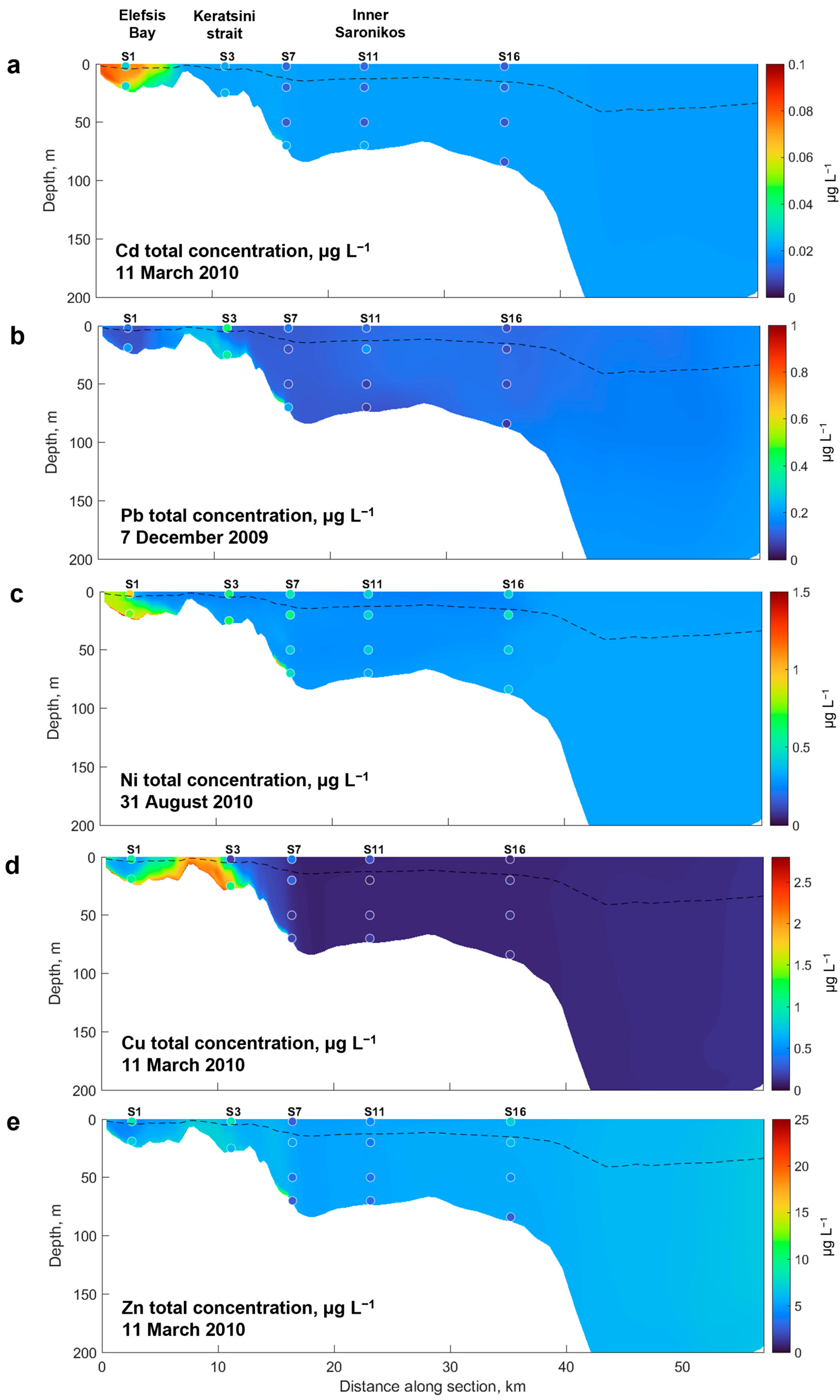
3.3. Vertical Distribution
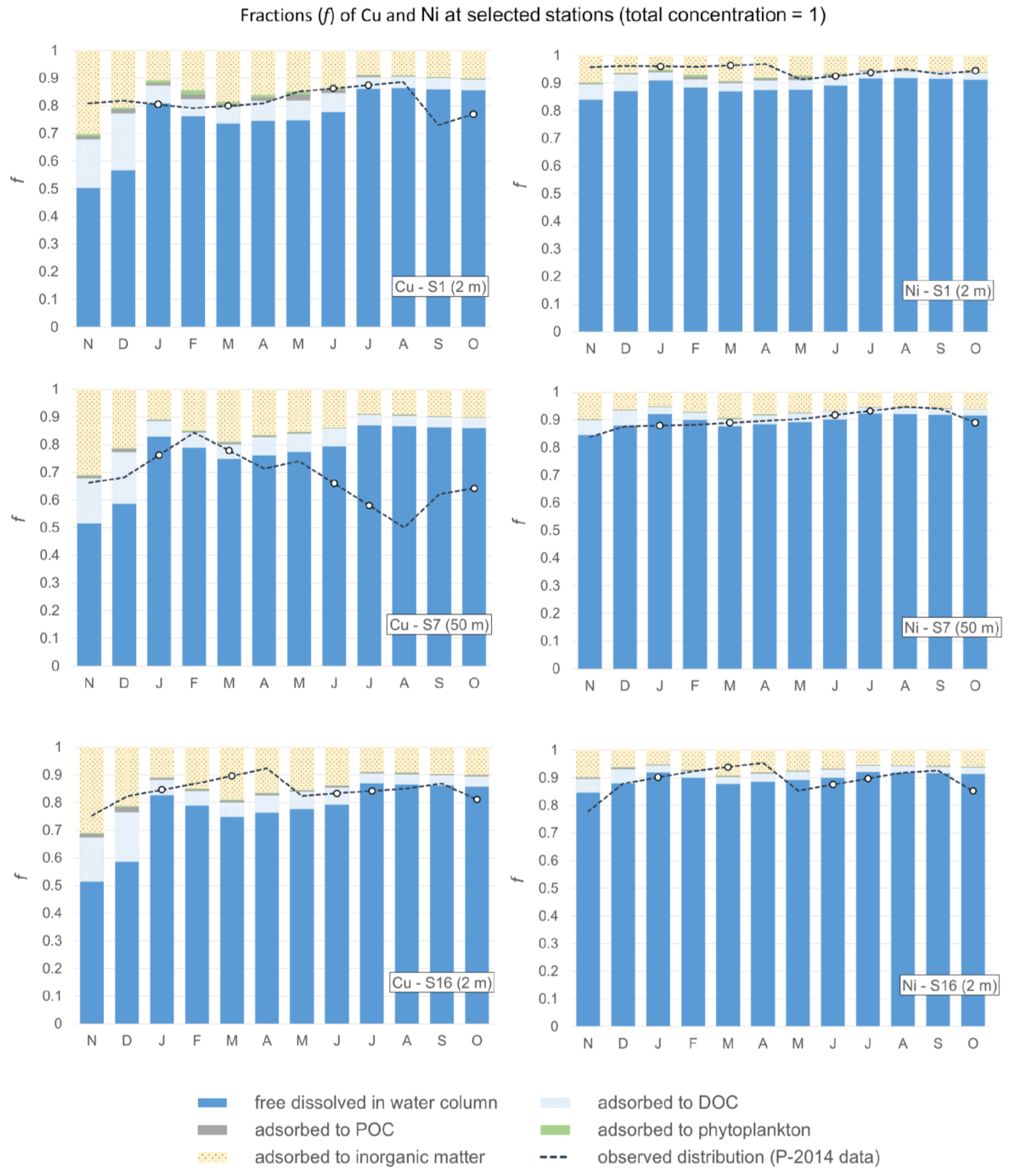
3.4. Partitioning
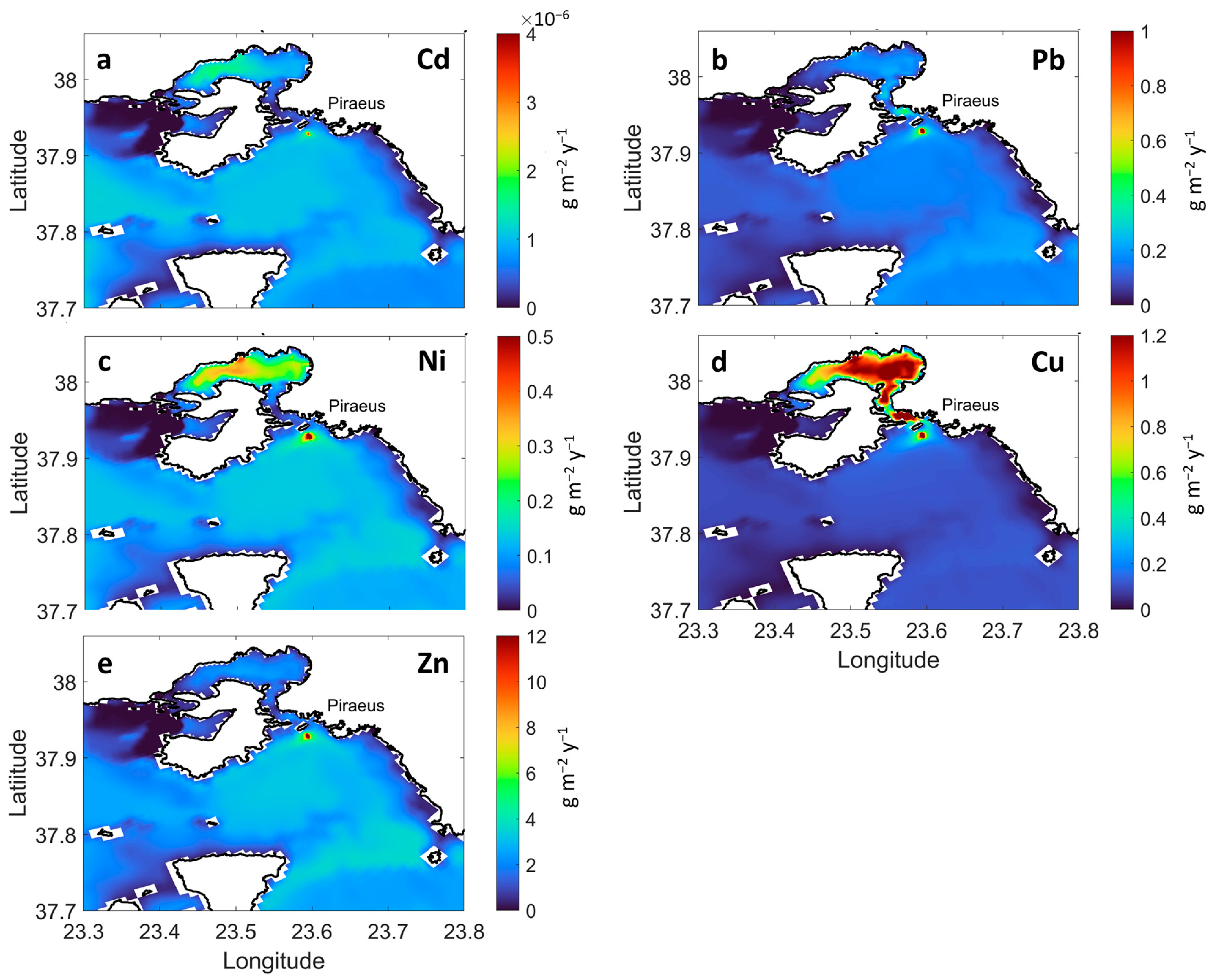
3.5. Sedimentation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mukherjee, P.K.; Das, B.; Bhardwaj, P.K.; Tampha, S.; Singh, H.K.; Chanu, L.D.; Sharma, N.; Devi, S.I. Socio-economic sustainability with circular economy—An alternative approach. Sci. Total Environ. 2023, 904, 166630. [Google Scholar] [CrossRef]
- Simeoni, C.; Furlan, E.; Pham, H.V.; Critto, A.; de Juan, S.; Trégarot, E.; Cornet, C.C.; Meesters, E.; Fonseca, C.; Botelho, A.Z.; et al. Evaluating the combined effect of climate and anthropogenic stressors on marine coastal ecosystems: Insights from a systematic review of cumulative impact assessment approaches. Sci. Total Environ. 2023, 861, 160687. [Google Scholar] [CrossRef]
- Priya, A.K.; Muruganandam, M.; Rajamanickam, S.; Sivarethinamohan, S.; Gaddam, M.K.R.; Velusamy, P.; Gomathi, R.; Ravindiran, G.; Gurugubelli, T.R.; Muniasamy, S.K. Impact of climate change and anthropogenic activities on aquatic ecosystem—A review. Environ. Res. 2023, 238, 117233. [Google Scholar] [CrossRef]
- Ji, Z.G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries, 2nd ed.; Wiley: Hoboken, NJ, USA, 2017; pp. 1–581. [Google Scholar] [CrossRef]
- Talukdar, P.; Kumar, B.; Kulkarni, V.V. A review of water quality models and monitoring methods for capabilities of pollutant source identification, classification, and transport simulation. Rev. Environ. Sci. Biotechnol. 2023, 22, 653–677. [Google Scholar] [CrossRef]
- Ménesguen, A.; Lacroix, G. Modelling the marine eutrophication: A review. Sci. Total Environ. 2018, 636, 339–354. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Wu, F.; Meng, Y.; Byrne, P.; Ghomshei, M.; Abbaspour, K.C. Modeling transport and fate of heavy metals at the watershed scale: State-of-the-art and future directions. Sci. Total Environ. 2023, 878, 163087. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Mohapatra, S.; Zhang, J.; Tran, N.H.; You, L.; He, Y.; Gin, K.Y.-H. Source, fate, transport and modelling of selected emerging contaminants in the aquatic environment: Current status and future perspectives. Water Res. 2022, 217, 118418. [Google Scholar] [CrossRef]
- Addis, T.Z.; Adu, J.T.; Kumarasamy, M.; Demlie, M. Assessment of Existing Fate and Transport Models for Predicting Antibiotic Degradation and Transport in the Aquatic Environment: A Review. Water 2023, 15, 1511. [Google Scholar] [CrossRef]
- Jampani, M.; Mateo-Sagasta, J.; Chandrasekar, A.; Fatta-Kassinos, D.; Graham, D.W.; Gothwal, R.; Moodley, A.; Chadag, V.M.; Wiberg, D.; Langan, S. Fate and transport modelling for evaluating antibiotic resistance in aquatic environments: Current knowledge and research priorities. J. Hazard. Mater. 2024, 461, 132527. [Google Scholar] [CrossRef]
- Jamshidi, S.; Naderi, A. Wetland restoration policies and the sustainability of agricultural productions, lessons learnt from Zrebar Lake, Iran. In Ecorestoration for Sustainability, 1st ed.; Banerjee, A., Jhariya, M.K., Bargali, S.S., Palit, D., Eds.; Wiley: Hoboken, NJ, USA, 2023; pp. 113–166. [Google Scholar] [CrossRef]
- Choukr-Allah, R.; Ragab, R.; Rodriguez-Clemente, R. Integrated Water Resources Management in the Mediterranean region—Dialogue towards New Strategy, 1st ed.; Springer Science & Business Media: Berlin, Germany, 2012; pp. 91–107. [Google Scholar] [CrossRef]
- Hellenic Statistical Authority, Census Results of Population and Housing 2021. Available online: https://www.statistics.gr/news-announcements/-/asset_publisher/oj6VK3PQ0oCe/content/census2022 (accessed on 8 April 2024).
- Papakostidis, G.; Grimanis, A.P.; Zafiropoulos, D.; Griggs, G.B.; Hopkins, T.S. Heavy metals in sediments from the Athens sewage outfall area. Mar. Pollut. Bull. 1975, 6, 136–139. [Google Scholar] [CrossRef]
- Griggs, G.B.; Grimanis, A.P.; Grimani, M.V. Bottom sediments in a polluted marine environment, Upper Saronikos Gulf, Greece. Environ. Geol. 1978, 2, 97–106. [Google Scholar] [CrossRef]
- Scoullos, M.J. Zinc in seawater and sediments of the Gulf of Elefsis, Greece. Water Air Soil Pollut. 1981, 16, 187–207. [Google Scholar] [CrossRef]
- Firfilionis, G.; Paraskevopoulou, V.; Vilioti, G.; Dassenakis, M. The removal of trace metals at the wastewater treatment plant of Psyttalia. Mediterr. Mar. Sci. 2004, 5, 71–82. [Google Scholar] [CrossRef]
- Scoullos, M.J.; Sakellari, A.; Giannopoulou, K.; Paraskevopoulou, V.; Dassenakis, M. Dissolved and particulate trace metal levels in the Saronikos Gulf, Greece, in 2004. The impact of the primary Wastewater Treatment Plant of Psittalia. Desalination 2007, 210, 98–109. [Google Scholar] [CrossRef]
- Pavlidou, A.; Kontoyiannis, H.; Zarokanelos, N.; Hatzianestis, I.; Assimakopoulou, G.; Psyllidou-Giouranovits, R. Seasonal and Spatial Nutrient Dynamics in Saronikos Gulf: The Impact of Sewage Effluents from Athens Sewage Treatment Plant. In Eutrophication: Causes, Consequences and Control, 1st ed.; Ansari, A.A., Gill, S.S., Eds.; Springer Science & Business Media: Berlin, Germany, 2014; pp. 91–107. [Google Scholar] [CrossRef]
- Christoulas, D.G.; Andreadakis, A.D.; Katsiris, N.; Kouzeli-Katsiri, A. Industrial Waste Management in the Athens Area. Water Sci. Technol. 1994, 29, 39–46. [Google Scholar] [CrossRef]
- Paraskevopoulou, V.; Zeri, C.; Kaberi, H.; Chalkiadaki, O.; Krasakopoulou, E.; Dassenakis, M.; Scoullos, M. Trace metal variability, background levels and pollution status assessment in line with the water framework and Marine Strategy Framework EU Directives in the waters of a heavily impacted Mediterranean Gulf. Mar. Pollut. Bull. 2014, 87, 323–337. [Google Scholar] [CrossRef]
- Papantoniou, G.; Zervoudaki, S.; Assimakopoulou, G.; Stoumboudi, M.T.; Tsagarakis, K. Ecosystem-level responses to multiple stressors using a time-dynamic food-web model: The case of a re-oligotrophicated coastal embayment (Saronikos Gulf, E Mediterranean). Sci. Total Environ. 2023, 903, 165882. [Google Scholar] [CrossRef]
- Papantoniou, G.; Giannoulaki, M.; Stoumboudi, M.T.; Lefkaditou, E.; Tsagarakis, K. Food web interactions in a human dominated Mediterranean coastal ecosystem. Mar. Environ. Res. 2021, 172, 105507. [Google Scholar] [CrossRef] [PubMed]
- Christou, E.D.; Stergiou, K.I. Modelling and forecasting the fortnightly cladoceran abundance in the Saronikos Gulf (Aegean Sea). J. Plankton Res. 1998, 20, 1313–1320. [Google Scholar] [CrossRef]
- Kontoyiannis, H. Observations on the circulation of the Saronikos Gulf: A Mediterranean embayment sea border of Athens, Greece. J. Geophys. Res. Ocean. 2010, 115, C06029. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Karathanasi, F.E. Modelling nearshore hydrodynamics and circulation under the impact of high waves at the coast of Varkiza in Saronic-Athens Gulf. Oceanologia 2017, 59, 350–364. [Google Scholar] [CrossRef]
- Tsiaras, K.; Costa, E.; Morgana, S.; Gambardella, C.; Piazza, V.; Faimali, M.; Minetti, R.; Zeri, C.; Thyssen, M.; Ben Ismail, S.; et al. Microplastics in the Mediterranean: Variability from Observations and Model Analysis. Front. Mar. Sci. 2022, 9, 784937. [Google Scholar] [CrossRef]
- Kalaroni, S.; Hatzonikolakis, Y.; Tsiaras, K.; Gkanasos, A.; Triantafyllou, G. Modelling the Marine Microplastic Distribution from Municipal Wastewater in Saronikos Gulf (E. Mediterranean). Fish. Oceanogr. 2019, 9, 555752. [Google Scholar] [CrossRef]
- Makatounis, P.E.Z.; Stamou, A.I.; Ventikos, N.P. Modeling the Agia Zoni II tanker oil spill in Saronic Gulf, Greece. Mar. Pollut. Bull. 2023, 194 Pt B, 115275. [Google Scholar] [CrossRef]
- Fu, Z.Y.; Wu, F.C.; Chen, L.L.; Xu, B.B.; Feng, C.L.; Bai, Y.C.; Liao, H.Q.; Sun, S.Y.; Giesy, J.P.; Guo, W.J. Copper and zinc, but not other priority toxic metals, pose risks to native aquatic species in a large urban lake in Eastern China. Environ. Pollut. 2016, 219, 1069–1076. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.L.; Ding, P.X.; Wang, Z.H.; Yang, S.L. A 2D/3D hydrodynamic and sediment transport model for the Yangtze Estuary, China. J. Mar. Syst. 2009, 77, 114–136. [Google Scholar] [CrossRef]
- Troost, T.A.; Desclaux, T.; Leslie, H.A.; van Der Meulen, M.D.; Vethaak, A.D. Do microplastics affect marine ecosystem productivity? Mar. Pollut. Bull. 2018, 135, 17–29. [Google Scholar] [CrossRef] [PubMed]
- Alosairi, Y.; Alsulaiman, N. Hydro-environmental processes governing the formation of hypoxic parcels in an inverse estuarine water body: Model validation and discussion. Mar. Pollut. Bull. 2019, 144, 92–104. [Google Scholar] [CrossRef] [PubMed]
- Stevens, A.W.; Moritz, H.R.; Elias, E.P.L.; Gelfenbaum, G.R.; Ruggiero, P.R.; Pearson, S.G.; McMillan, J.M.; Kaminsky, G.M. Monitoring and modeling dispersal of a submerged nearshore berm at the mouth of the Columbia River, USA. Coast. Eng. 2023, 181, 104285. [Google Scholar] [CrossRef]
- Kolovoyiannis, V.; Petalas, S.; Mamoutos, I.; Krasakopoulou, E.; Zervakis, V.; Tragou, E.; Kontoyiannis, H. Optimizing the parameterization of a high-resolution numerical simulation of the Saronikos Gulf hydrodynamics. In Proceedings of the 2nd Design and Management of Port, Coastal and Offshore Works (DMPCO), Thessaloniki, Greece, 24–27 May 2023. [Google Scholar]
- Kolovoyiannis, V.; Mazioti, A.A.; Krasakopoulou, E.; Zervakis, V.; Tragou, E.A.; Mamoutos, I.; Potiris, E.; Petalas, S.; Chatzilaou, C.; Mosiou, K.; et al. Implementation of a modelling system for the investigation of the Saronikos Gulf marine ecosystem (Eastern Mediterranean). In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023. EGU23-12514. [Google Scholar] [CrossRef]
- Deltares. D-Water Quality User Manual, Water Quality and Aquatic Ecology Modelling Suite, v5.06, Deltares, P.O. Box 177, 2600 MH Delft, The Netherlands. 2020. Available online: https://content.oss.deltares.nl/delft3d4/D-Water_Quality_User_Manual.pdf (accessed on 25 November 2021).
- Deltares 2020, D-Water Quality User Manual, Sediment Water Interaction, v3.0, Deltares, P.O. Box 177, 2600 MH Delft, The Netherlands. Available online: https://content.oss.deltares.nl/delft3dfm2d3d/D-Water_Quality_Sediment_Water_User_Manual.pdf (accessed on 25 November 2021).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present Copernicus Climate Change Service (C3S) Climate Data Store (CDS). Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.adbb2d47?tab=overview (accessed on 1 March 2024).
- Lindstrom, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the hype (hydrological predictions for the environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Petalas, S.; Tragou, E.; Mamoutos, I.G.; Zervakis, V. Simulating the Interconnected Eastern Mediterranean—Black Sea System on Climatic Timescales: A 30-Year Realistic Hindcast. J. Mar. Sci. Eng. 2022, 10, 1786. [Google Scholar] [CrossRef]
- Krasakopoulou, E.; Karageorgis, A. Spatial and temporal distribution patterns of suspended particulate matter and particulate organic carbon in the Saronikos Gulf (eastern Mediterranean, Greece). Geo-Mar. Lett. 2005, 25, 343–359. [Google Scholar] [CrossRef]
- Special Secretariat for Water, WWTP Monitoring Database. Available online: http://astikalimata.ypeka.gr/Services/Pages/WtpViewApp.aspx# (accessed on 31 May 2023).
- National Legislation, Decision 17823/79, FEK 1132 Β/21-12-79 Regarding the Disposal of Industrial and Municipal Wastewater in Saronikos Gulf. (In Greek). Available online: https://proteas-reach.gr/wp-content/uploads/2014/03/%CE%91%CF%80%CF%8C%CF%86%CE%B1%CF%83%CE%B7-17823_79.pdf (accessed on 31 May 2023).
- Hellenic Integrated Marine Inland Water Observing, Forecasting and Offshore Technology System HIMIOFoTs. Available online: https://system.openhi.net/ (accessed on 31 May 2023).
- Hellenic Petroleum (ELPE). Available online: https://www.helpe.gr/ (accessed on 31 May 2023).
- von Sperling, W. Wastewater Characteristics, Treatment and Disposal, 1st ed.; IWA Publishing: London, UK, 2007; p. 41. [Google Scholar] [CrossRef]
- Motor Oil. Available online: https://www.moh.gr/ (accessed on 31 May 2023).
- OLP (Piraeus Port Authority). Available online: https://www.olp.gr/el/statistika-stoixeia/ (accessed on 31 May 2023).
- National Water Monitoring Network. Available online: http://nmwn.ypeka.gr/?q=surface-stations (accessed on 31 May 2023).
- Environmental, Health, and Safety (EHS) Guidelines—Petroleum Refining (technical Reference Document). IFC. 2016, p. 19. Available online: https://www.ifc.org/content/dam/ifc/doc/2010/2016-annual-crop-production-ehs-guidelines-en.pdf (accessed on 31 May 2023).
- Deltares. D-Water Quality Processes Library Description, Technical Reference Manual. v.5.01. Deltares, P.O. Box 177, 2600 MH Delft, The Netherlands. 2020. Available online: https://content.oss.deltares.nl/delft3d4/D-Water_Quality_Processes_Technical_Reference_Manual.pdf (accessed on 25 November 2021).
- Periáñez, R. Viewpoint on the Integration of Geochemical Processes into Tracer Transport Models for the Marine Environment. Geosciences 2022, 12, 152. [Google Scholar] [CrossRef]
- Periáñez, R.; Brovchenko, I.; Jung, K.T.; Kim, K.O.; Maderich, V. The marine kd and water/sediment interaction problem. J. Environ. Radioact. 2018, 192, 635–647. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.I.; Holt, J.T.; Blackford, J.; Proctor, R. Error quantification of a high-resolution coupled hydrodynamic-ecosystem coastal-ocean model: Part 2. Chlorophyll-a, nutrients and SPM. J. Mar. Syst. 2007, 68, 381–404. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Millward, G.; Turner, A. Metal Pollution. In Encyclopedia of Ocean Sciences, 2nd ed.; Steele, J.H., Thorpe, S.A., Turekian, K.K., Eds.; Academic Press: San Diego, CA, USA, 2001; pp. 768–775. [Google Scholar] [CrossRef]
- Zeri, C.; Hatzianestis, I. Distribution of total dissolved and C18 extractable copper and nickel in relation to dissolved organic matter sources, in the Thermaikos Gulf (eastern Mediterranean). J. Mar. Syst. 2005, 58, 143–152. [Google Scholar] [CrossRef]
- Miranda, L.S.; Ayoko, G.A.; Egodawatta, P.; Goonetilleke, A. Adsorption-desorption behavior of heavy metals in aquatic environments: Influence of sediment, water and metal ionic properties. J. Hazard. Mater. 2022, 421, 126743. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Alayande, A.B.; Lee, J.M.; Jang, J.H.; Jo, S.M.; Jae, M.R.; Yang, E.; Chae, K.J. Emerging marine environmental pollution and ecosystem disturbance in ship hull cleaning for biofouling removal. Sci. Total Environ. 2024, 906, 167459. [Google Scholar] [CrossRef]
- Strogyloudi, E.; Paraskevopoulou, V.; Campillo, J.A.; Zervoudaki, S.; Bouga, V.; Catsiki, V.A.; Dassenakis, E.; Krasakopoulou, E. Metal and metallothionein levels in zooplankton in relation to environmental exposure: Spatial and temporal variability (Saronikos Gulf, Greece). Environ. Sci. Pollut. Res. 2021, 28, 28640–28657. [Google Scholar] [CrossRef]
- Karageorgis, A.P.; Botsou, F.; Kaberi, H.; Iliakis, S. Geochemistry of major and trace elements in surface sediments of the Saronikos Gulf (Greece): Assessment of contamination between 1999 and 2018. Sci. Total Environ. 2020, 717, 137046. [Google Scholar] [CrossRef] [PubMed]
- Prifti, E.; Kaberi, H.; Paraskevopoulou, V.; Michalopoulos, P.; Zeri, C.; Iliakis, S.; Dassenakis, M.; Scoullos, M. Vertical Distribution and Chemical Fractionation of Heavy Metals in Dated Sediment Cores from the Saronikos Gulf, Greece. J. Mar. Sci. Eng. 2022, 10, 376. [Google Scholar] [CrossRef]
- Tzempelikou, E.; Zeri, C.; Iliakis, S.; Paraskevopoulou, V. Cd, Co, Cu, Ni, Pb, Zn in coastal and transitional waters of Greece and assessment of background concentrations: Results from 6 years implementation of the Water Framework Directive. Sci. Total Environ. 2021, 774, 145177. [Google Scholar] [CrossRef]
- Poshtegal, M.K.; Mirbagheri, S.A. Simulation and modelling of heavy metals and water quality parameters in the river. Sci. Rep. 2023, 13, 3020. [Google Scholar] [CrossRef] [PubMed]
- Richir, J.; Bray, S.; McAleese, T.; Watson, G.J. Three decades of trace element sediment contamination: The mining of governmental databases and the need to address hidden sources for clean and healthy seas. Environ. Int. 2021, 149, 106362. [Google Scholar] [CrossRef] [PubMed]
- Lagerström, M.; Ytreberg, E.; Wiklund, A.K.E.; Granhag, L. Antifouling paints leach copper in excess—Study of metal release rates and efficacy along a salinity gradient. Water Res. 2020, 186, 116383. [Google Scholar] [CrossRef] [PubMed]
- Rees, A.B.; Gallagher, A.; Wright, L.A.; Wood, J.; Cathery, T.; Harrison, B.; Down, C.; Comber, S. Leisure craft sacrificial anodes as a source of zinc and cadmium to saline waters. Mar. Pollut. Bull. 2020, 158, 111433. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Zhang, W.; Han, J.; Li, Y. Tracing illegal oil discharges from vessels using SAR and AIS in Bohai Sea of China. Ocean Coast. Manag. 2021, 211, 105783. [Google Scholar] [CrossRef]
- Katsiaras, N.; Simboura, N.; Tsangaris, C.; Hatzianestis, I.; Pavlidou, A.; Kapsimalis, V. Impacts of dredged-material disposal on the coastal soft-bottom macrofauna, Saronikos Gulf, Greece. Sci. Total Environ. 2015, 508, 320–330. [Google Scholar] [CrossRef]
- Chitrakar, P.; Baawain, M.S.; Sana, A.; Al-Mamun, A. Current Status of Marine Pollution and Mitigation Strategies in Arid Region: A Detailed Review. Ocean Sci. J. 2019, 54, 317–348. [Google Scholar] [CrossRef]
- Chatoutsidou, S.E.; Lazaridis, M. Mass concentrations and elemental analysis of PM2.5 and PM10 in a coastal Mediterranean site: A holistic approach to identify contributing sources and varying factors. Sci. Total Environ. 2022, 838 Pt 1, 155980. [Google Scholar] [CrossRef] [PubMed]
- Remoundaki, E.; Bourliva, A.; Kokkalis, P.; Mamouri, R.E.; Papayannis, A.; Grigoratos, T.; Samara, C.; Tsezos, M. PM10 composition during an intense Saharan dust transport event over Athens (Greece). Sci. Total Environ. 2011, 409, 4361–4372. [Google Scholar] [CrossRef]
- Vaz, L.; Frankenbach, S.; Serôdio, J.; Dias, J.M. New insights about the primary production dependence on abiotic factors: Ria de Aveiro case study. Ecol. Indic. 2019, 106, 105555. [Google Scholar] [CrossRef]
- Mendes, J.; Ruela, R.; Picado, A.; Pinheiro, J.P.; Ribeiro, A.S.; Pereira, H.; Dias, J.M. Modeling Dynamic Processes of Mondego Estuary and Óbidos Lagoon Using Delft3D. J. Mar. Sci. Eng. 2021, 9, 91. [Google Scholar] [CrossRef]
- Yao, H.; Ni, T.; You, Z. Characterizing pollutant loading from point sources to the Tongqi River of China based on water quality modeling. Int. J. Environ. Sci. Technol. 2019, 16, 6599–6608. [Google Scholar] [CrossRef]
- Ismanto, A.; Hadibarata, T.; Widada, S.; Atmodjo, W.; Satriadi, A.; Siagian, H.; Safinatunnajah, N. Heavy metal contamination in the marine environment of Pekalongan, Indonesia: Spatial distribution and hydrodynamic modeling. Environ. Qual. Manag. 2023, 1–10. [Google Scholar] [CrossRef]
- Premier, V.; de Souza Machado, A.A.; Mitchell, S.; Zarfl, C.; Spencer, K.; Toffolon, M. Model-Based Analysis of Metal Fate in the Thames Estuary. Estuar. Coast. 2019, 42, 1185–1201. [Google Scholar] [CrossRef]
- Wu, Y.; Falconer, R.A.; Lin, B. Modelling trace metal concentration distributions in estuarine waters. Estuar. Coast. Shelf Sci. 2005, 64, 699–709. [Google Scholar] [CrossRef]
- Falconer, R.A.; Lin, B. Three-dimensional modelling of water quality in the Humber estuary. Water Res. 1997, 31, 1092–1102. [Google Scholar] [CrossRef]
- de Souza Machado, A.A.; Spencer, K.; Kload, W.; Toffolon, M.; Zarfl, C. Metal fate and effects in estuaries: A review and conceptual model for better understanding of toxicity. Sci. Total Environ. 2016, 541, 268–281. [Google Scholar] [CrossRef]
- Liu, W.C.; Chen, W.B.; Chang, Y.P. Modeling the transport and distribution of lead in tidal Keelung River estuary. Environ. Earth Sci. 2012, 65, 39–47. [Google Scholar] [CrossRef]
- Periáñez, R. Environmental modelling in the Gulf of Cadiz: Heavy metal distributions in water and sediments. Sci. Total Environ. 2009, 407, 3392–3406. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.W.; Huang, L.; Wang, J.Y.; He, G.J.; Reible, D. Environmental assessment of heavy metal transport and transformation in the Hangzhou Bay, China. J. Hazard. Mater. 2016, 302, 447–457. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Lin, B.L.; Chen, C.; Horiguchi, F.; Eriguchi, T.; Li, Y.; Wang, X. A 3D-hydrodynamic model for predicting the environmental fate of chemical pollutants in Xiamen Bay, southeast China. Environ. Pollut. 2019, 256, 113000. [Google Scholar] [CrossRef] [PubMed]
- Altenburger, R.; Ait-Aissa, S.; Antczak, P.; Backhaus, T.; Barceló, D.; Seiler, T.B.; Brion, F.; Busch, W.; Chipman, K.; de Alda, M.L.; et al. Future water quality monitoring–adapting tools to deal with mixtures of pollutants in water resource management. Sci. Total Environ. 2015, 512–513, 540–551. [Google Scholar] [CrossRef]
- Zlati, M.L.; Georgescu, L.P.; Iticescu, C.; Ionescu, R.V.; Antohi, V.M. New Approach to Modelling the Impact of Heavy Metals on the European Union’s Water Resources. Int. J. Environ. Res. Public Health 2023, 20, 45. [Google Scholar] [CrossRef]



| Group 1 | Substance (Variable) 1 | Processes |
|---|---|---|
| Dissolved Inorganic Matter | Ammonium (NH4) | Uptake of nutrients by growth of phytoplankton, release, nitrification of ammonium, denitrification in water column |
| Nitrate (NO3) | ||
| Ortho-Phosphate (PO4) | ||
| Dissolved Silicon (Si) | ||
| Organic Matter | Particulate Organic Carbon (POC) | Release, sedimentation of POC, mineralization detritus POC, mineralization DOC |
| Dissolved Organic Carbon (DOC) | ||
| Dissolved Organic Nitrogen (DON) | ||
| Dissolved Organic Phosphorus (DOP) | ||
| Phytoplankton | Diatoms | Net primary production and mortality, limitation, sedimentation |
| Non-Diatoms |
| Name of Discharge | Type | Flow [m3 s−1] | Cadmium [g m−3] | Copper [g m−3] | Nickel [g m−3] | Lead [g m−3] | Zinc [g m−3] | Pollution Data Reference |
|---|---|---|---|---|---|---|---|---|
| Kifisos | River | varying 1 | 0.00013 | 0.01 | 0.005 | 0.002 | 0.03 | 7 |
| Sarantapotamos | Stream | varying 2 | 0.00013 | 0.01 | 0.005 | 0.002 | 0.03 | 8 |
| Mandra | Stream | varying 2 | 0.00013 | 0.01 | 0.005 | 0.002 | 0.03 | 8 |
| Psittalia | WWTP | 7.75 3 | 0.00034 | 0.026 | 0.021 | 0.013 | 0.27 | 9 |
| Thriassion | WWTP | 0.07 3 | 0.00034 | 0.026 | 0.021 | 0.013 | 0.27 | 9 |
| Oil ref. Aspropyrgos | Oil Refinery | 0.06 4 | 0.05 | 1.5 | 1.5 | 0.2 | 1.5 | 10 |
| Oil ref. Elefsina | Oil Refinery | 0.13 4 | 0.05 | 1.5 | 1.5 | 0.2 | 1.5 | 10 |
| Oil ref. Corinthos | Oil Refinery | 0.45 5 | 0.05 | 1.5 | 1.5 | 0.2 | 1.5 | 10 |
| Perama Shipyard | Shipyard | 1.00 6 | 0 | 0.459 | 0 | 0.0597 | 0.459 | 6 |
| Trace Element | A | B [62,63] | A | B [62,63] | ||||
|---|---|---|---|---|---|---|---|---|
| S1 | S1 | S1W | S1E | S7 | S7 | S7W | S7N | |
| Cd | 4.5 × 10−4 | n.a. | n.a. | n.a. | 7.5 × 10−4 | n.a. | n.a. | n.a. |
| Pb | 61 | 134 | 102 | 43 | 214 | 595 | 214 | 884 |
| Ni | 114 | 81 | 62 | 52 | 152 | 408 | 133 | 402 |
| Cu | 389 | 138 | 70 | 30 | 293 | 548 | 99 | 536 |
| Zn | 742 | 368 | 317 | 138 | 2796 | 1397 | 351 | 1747 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazioti, A.A.; Kolovoyiannis, V.; Krasakopoulou, E.; Tragou, E.; Zervakis, V.; Assimakopoulou, G.; Athiniotis, A.; Paraskevopoulou, V.; Pavlidou, A.; Zeri, C. Implementation of a Far-Field Water Quality Model for the Simulation of Trace Elements in an Eastern Mediterranean Coastal Embayment Receiving High Anthropogenic Pressure. J. Mar. Sci. Eng. 2024, 12, 797. https://doi.org/10.3390/jmse12050797
Mazioti AA, Kolovoyiannis V, Krasakopoulou E, Tragou E, Zervakis V, Assimakopoulou G, Athiniotis A, Paraskevopoulou V, Pavlidou A, Zeri C. Implementation of a Far-Field Water Quality Model for the Simulation of Trace Elements in an Eastern Mediterranean Coastal Embayment Receiving High Anthropogenic Pressure. Journal of Marine Science and Engineering. 2024; 12(5):797. https://doi.org/10.3390/jmse12050797
Chicago/Turabian StyleMazioti, Aikaterini Anna, Vassilis Kolovoyiannis, Evangelia Krasakopoulou, Elina Tragou, Vassilis Zervakis, Georgia Assimakopoulou, Alexandros Athiniotis, Vasiliki Paraskevopoulou, Alexandra Pavlidou, and Christina Zeri. 2024. "Implementation of a Far-Field Water Quality Model for the Simulation of Trace Elements in an Eastern Mediterranean Coastal Embayment Receiving High Anthropogenic Pressure" Journal of Marine Science and Engineering 12, no. 5: 797. https://doi.org/10.3390/jmse12050797
APA StyleMazioti, A. A., Kolovoyiannis, V., Krasakopoulou, E., Tragou, E., Zervakis, V., Assimakopoulou, G., Athiniotis, A., Paraskevopoulou, V., Pavlidou, A., & Zeri, C. (2024). Implementation of a Far-Field Water Quality Model for the Simulation of Trace Elements in an Eastern Mediterranean Coastal Embayment Receiving High Anthropogenic Pressure. Journal of Marine Science and Engineering, 12(5), 797. https://doi.org/10.3390/jmse12050797











