A Time-Domain Wavenumber Integration Model for Underwater Acoustics Based on the High-Order Finite Difference Method
Abstract
1. Introduction
2. Time-Domain Wavenumber Integration Model
2.1. Hankel Transform of the Wave Equation
2.2. Wavenumber Discretization
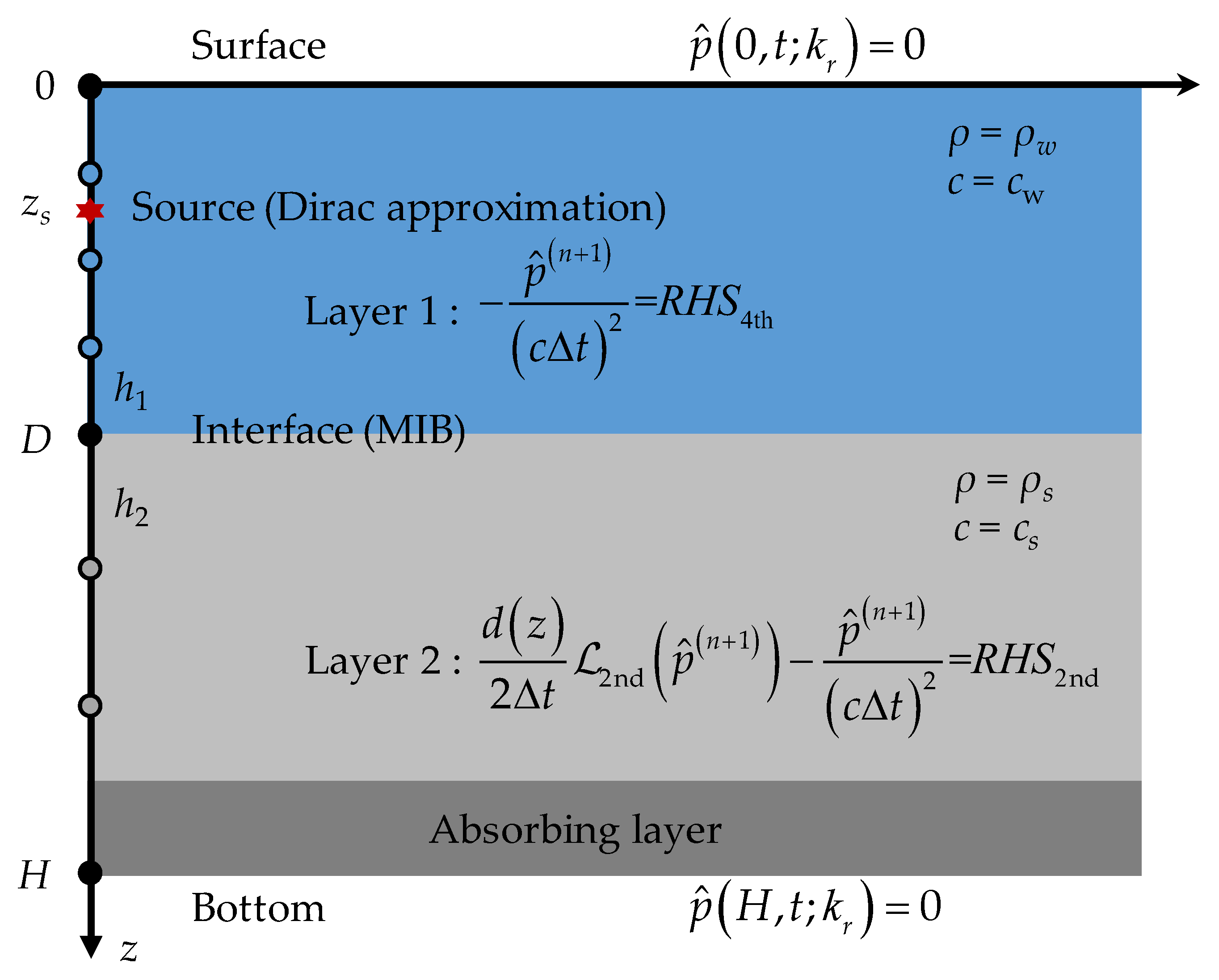
3. The FDM for Solving the Depth Equation
3.1. Temporal Discretization
3.2. Spatial Discretization
3.2.1. Interior Point Schemes
3.2.2. Boundary Schemes
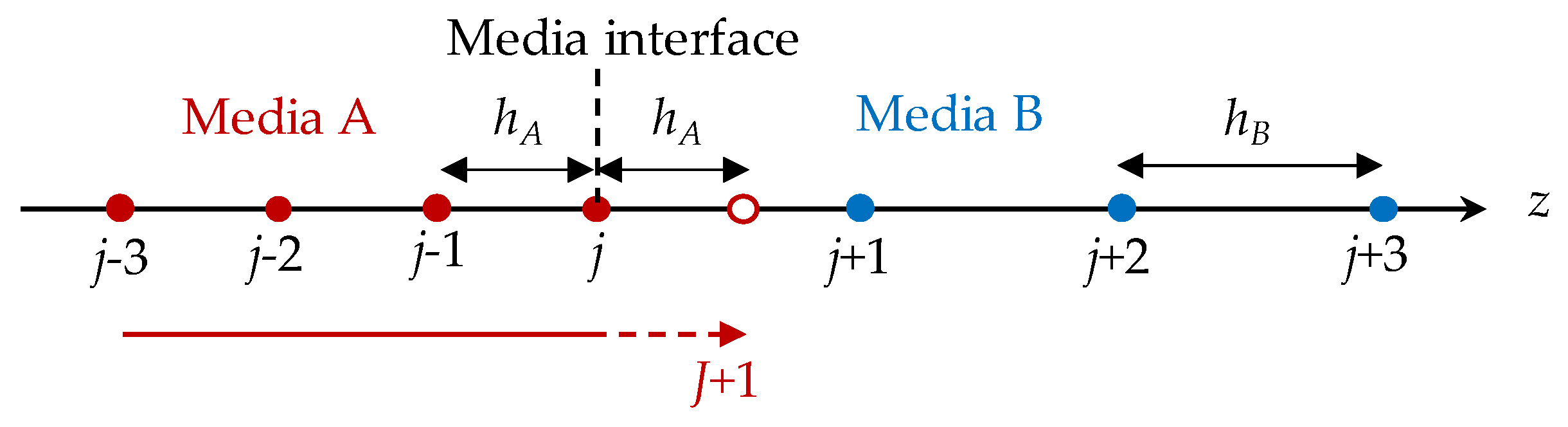
3.2.3. Interface Schemes
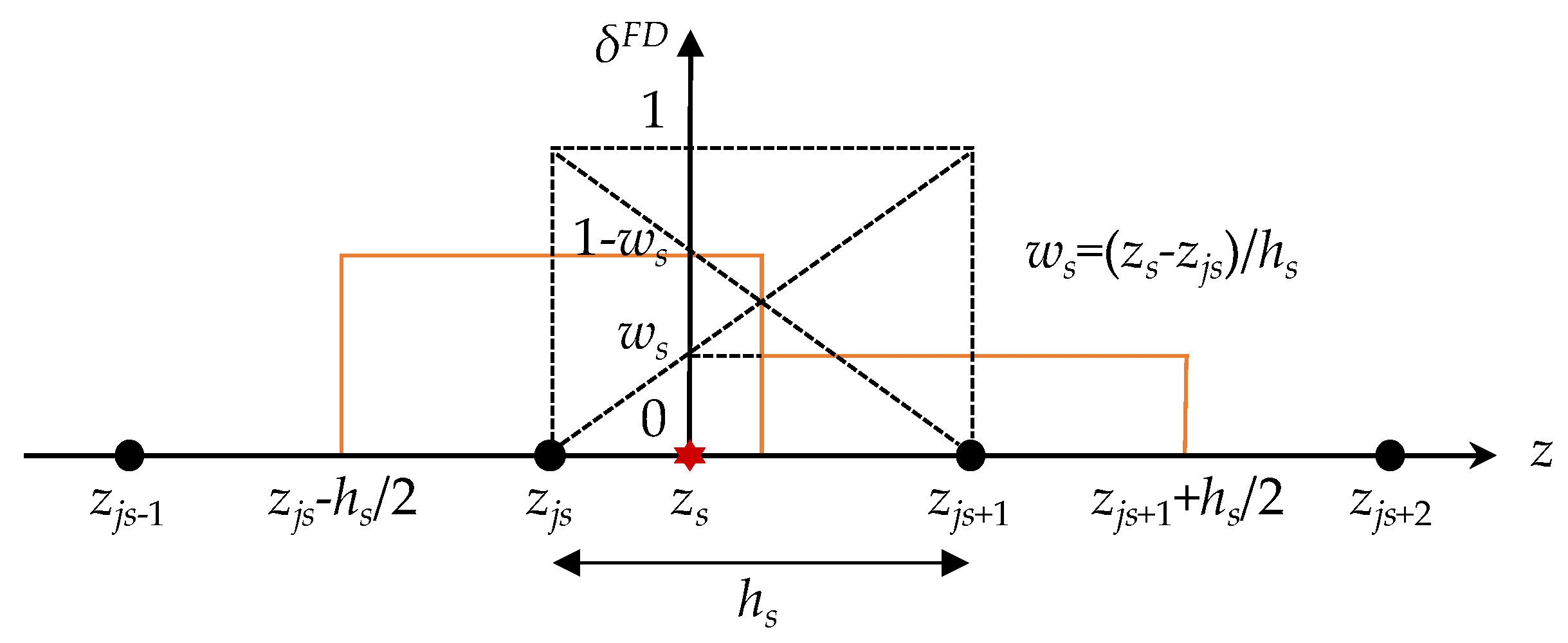
3.3. Source Treatment Method
4. Test Cases
4.1. Lloyd’s Mirror
4.2. Ideal Waveguide
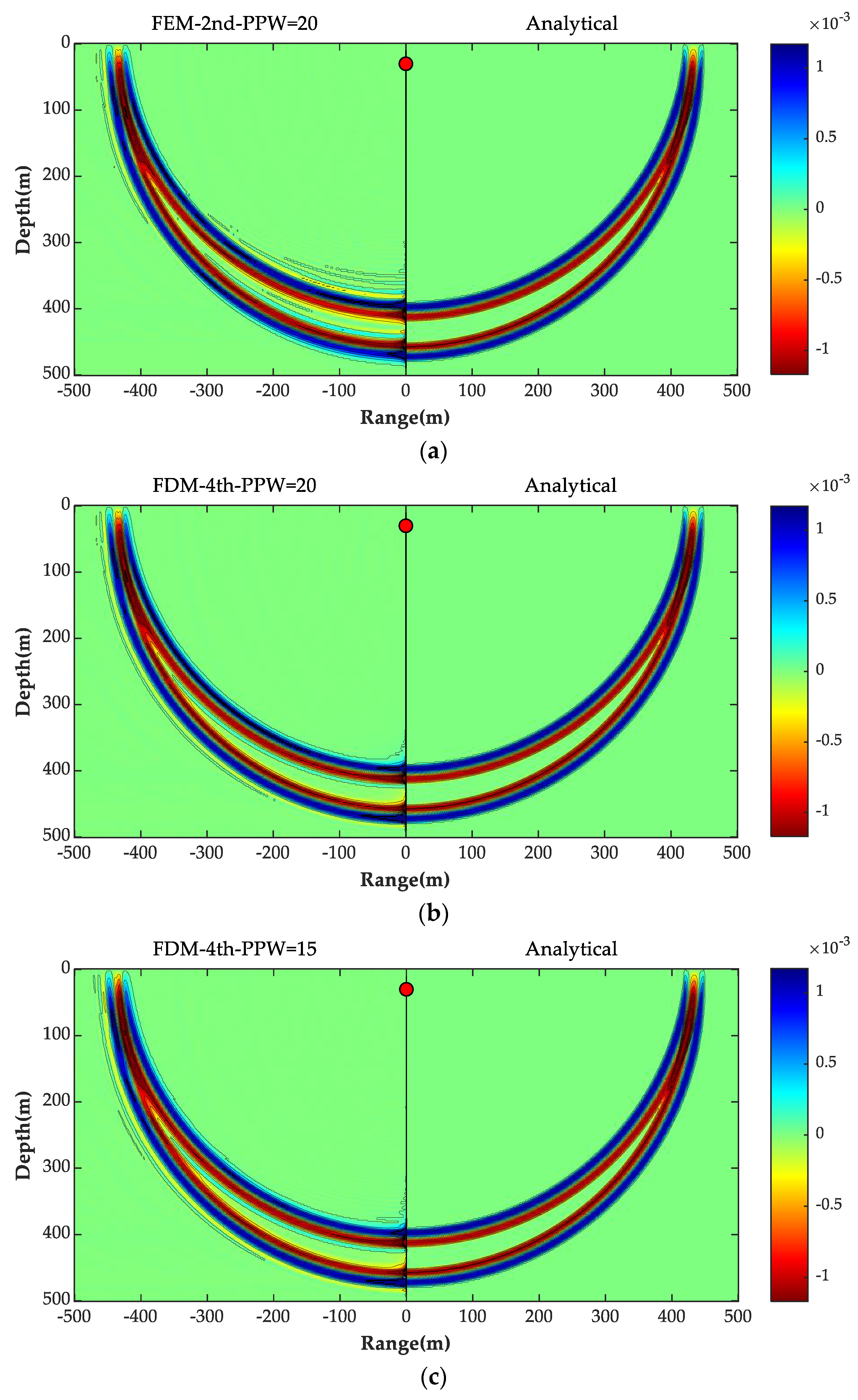
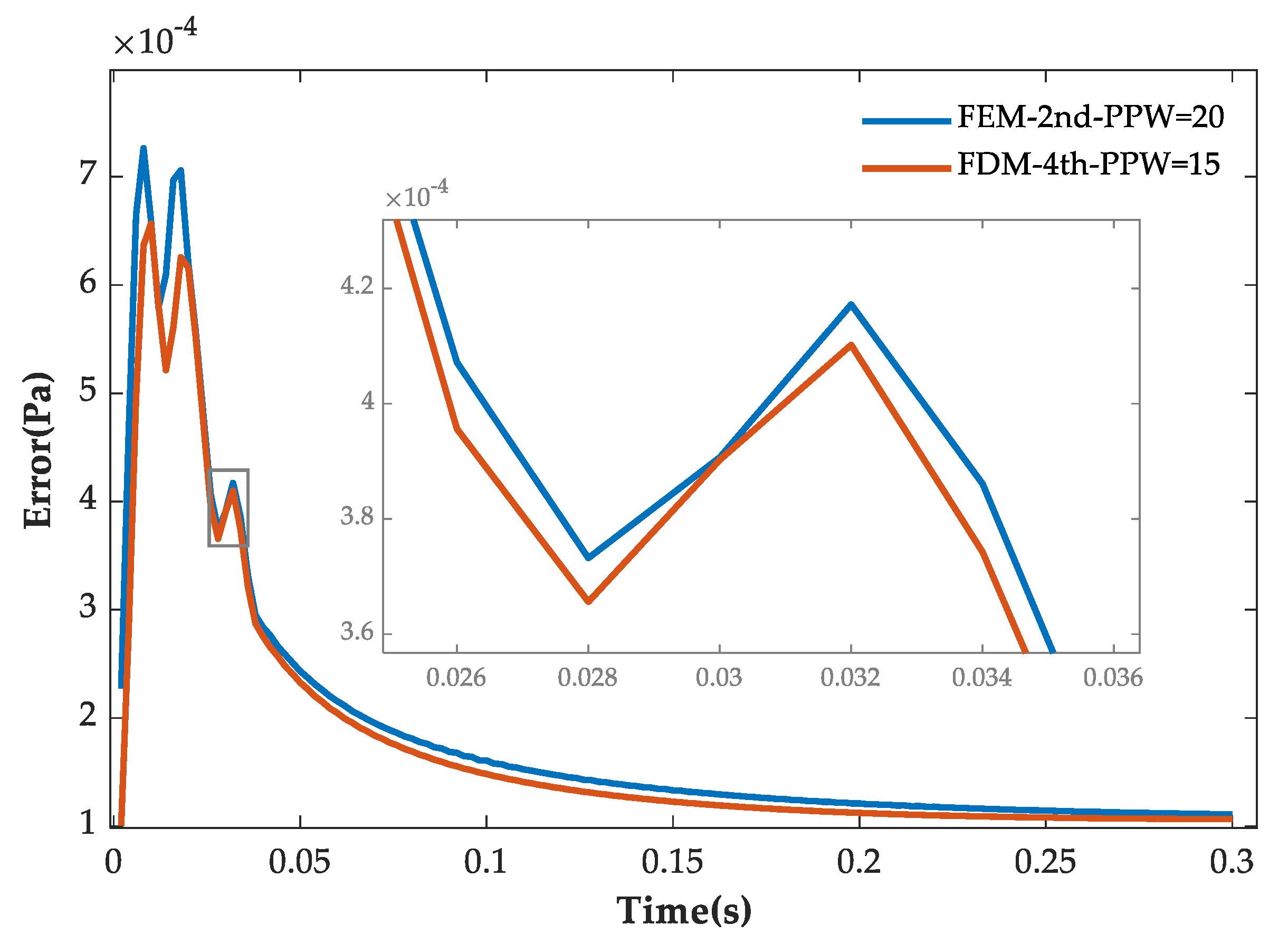
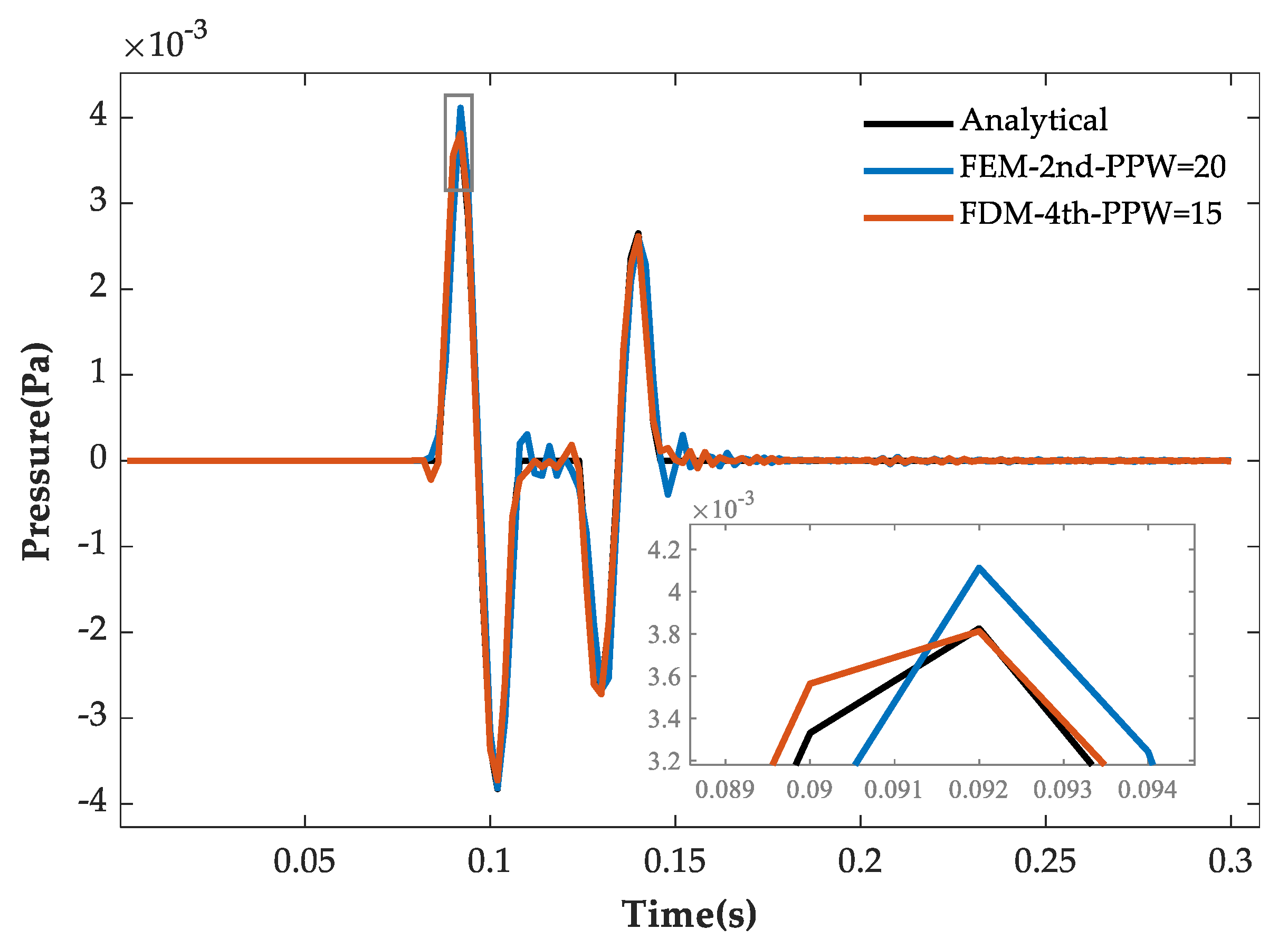
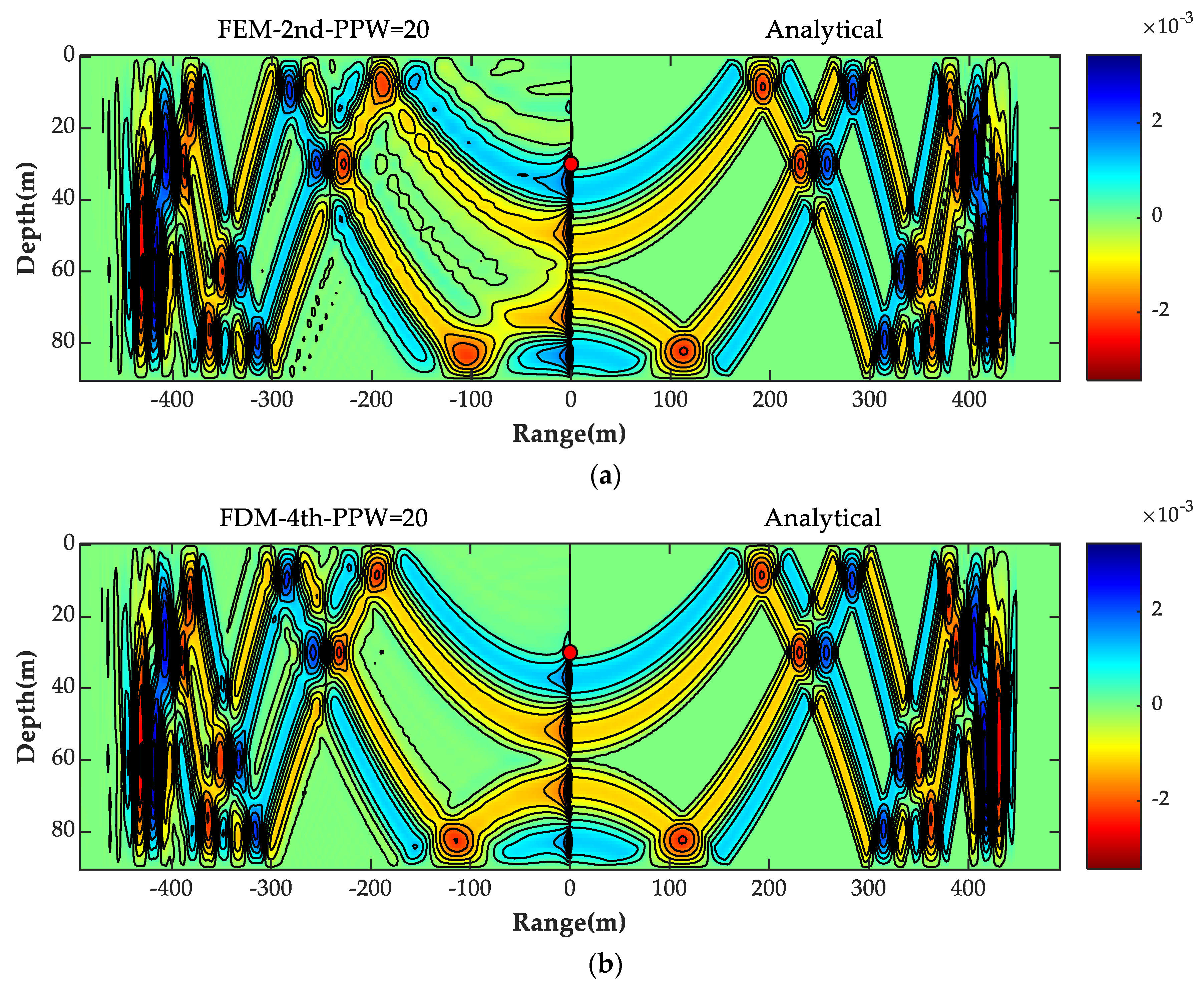
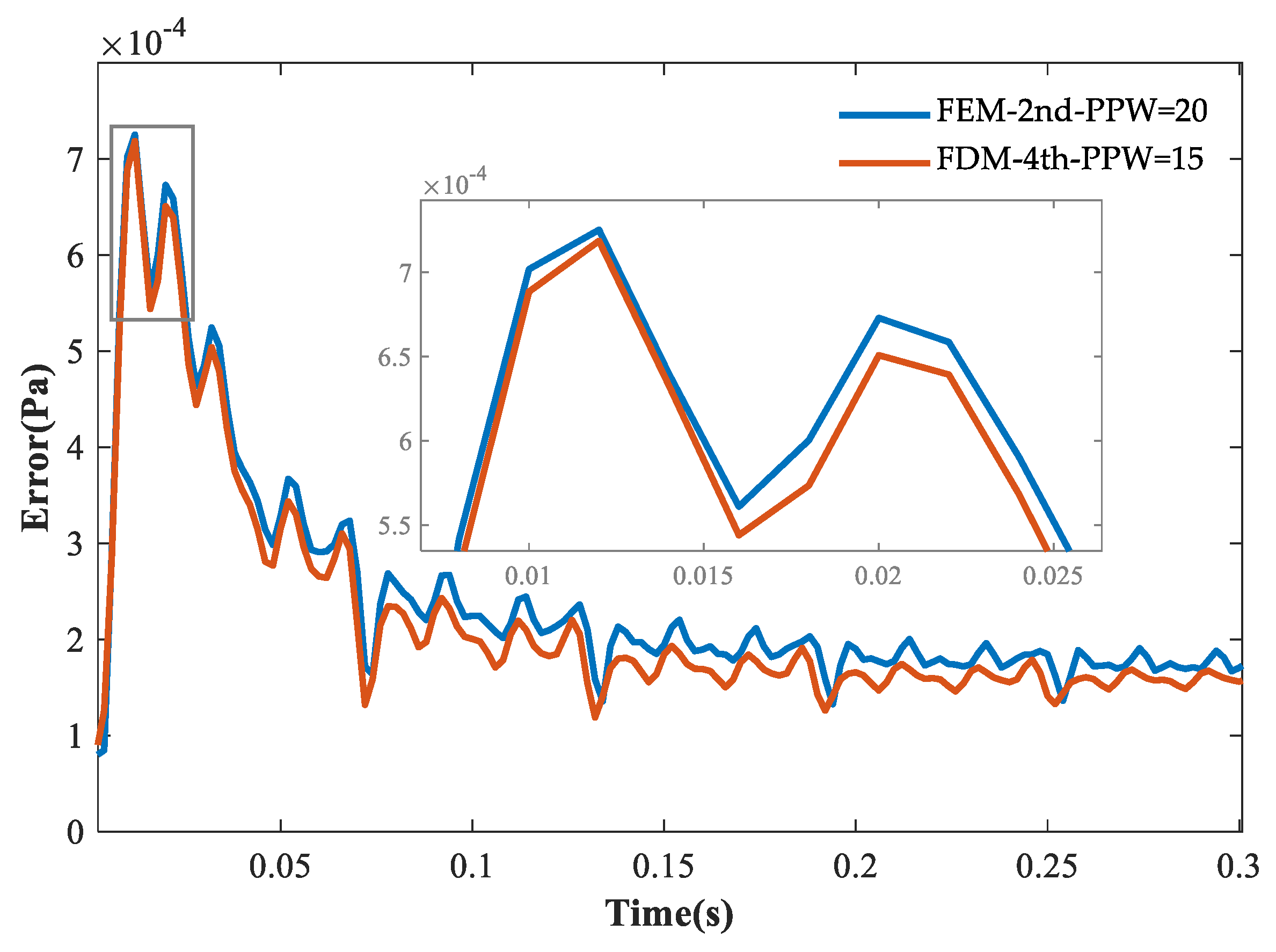
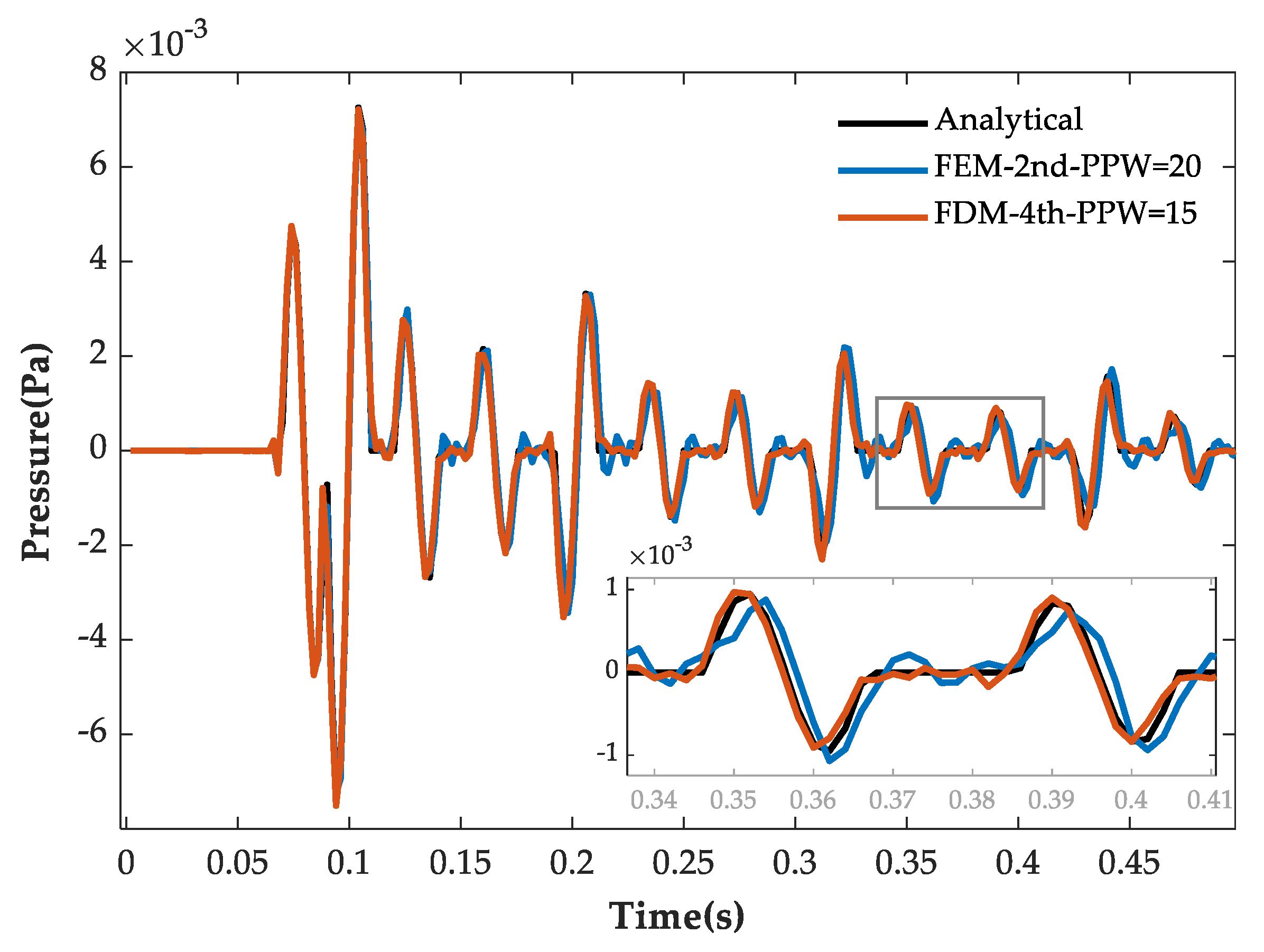
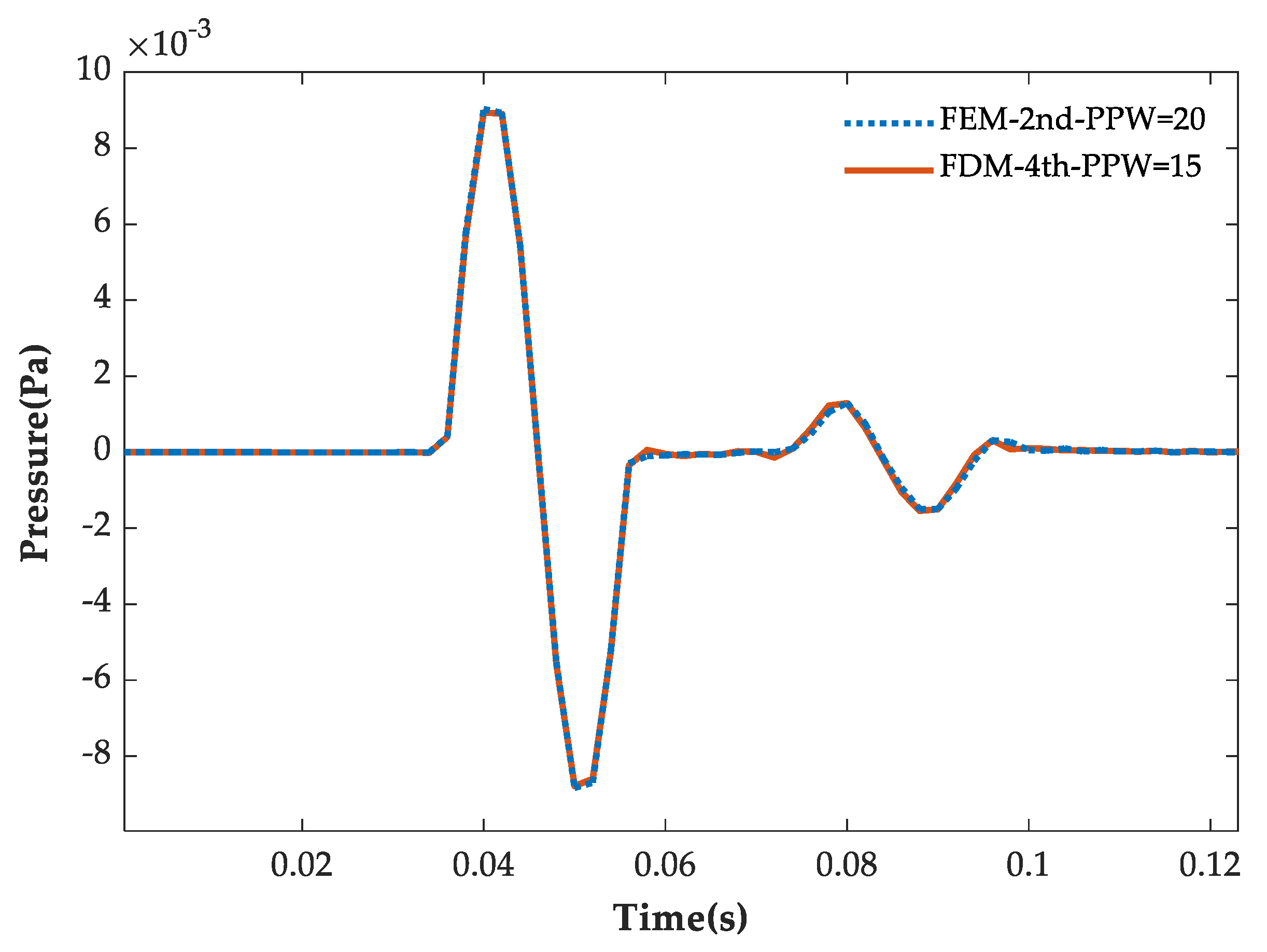
4.3. Head Wave
4.4. Computation Analysis
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jensen, F.B. Wave theory modelling: A convenient approach to CW and pulse propagation modelling in low-frequency acoustics. IEEE J. Ocean. Eng. 1988, 13, 186–197. [Google Scholar] [CrossRef]
- Jensen, F.B.; Ferla, C.M.; Nielsen, P.L.; Martinelli, G. Broadband Signal Simulation in Shallow Water. J. Comput. Acoust. 2003, 11, 577–591. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H.; Tolstoy, A. Computational Ocean Acoustics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 2011. [Google Scholar]
- Sertlek, H.O.; Aksoy, S. Benchmarking of acoustic pulse propagation problems in an isovelocity waveguide by an analytical time domain normal mode method. Proc. Meet. Acoust. 2013, 17, 070103. [Google Scholar] [CrossRef]
- Skarsoulis, E.K. Second-Order Fourier Synthesis of Broadband Acoustic Signals Using Normal Modes. J. Comput. Acoust. 1997, 05, 355–370. [Google Scholar] [CrossRef]
- Porter, M.B. Beam tracing for two- and three-dimensional problems in ocean acoustics. J. Acoust. Soc. Am. 2019, 146, 2016–2029. [Google Scholar] [CrossRef] [PubMed]
- Tu, H.; Wang, Y.; Lan, Q.; Liu, W.; Xiao, W.; Ma, S. A Chebyshev-Tau spectral method for normal modes of underwater sound propagation with a layered marine environment. J. Sound Vib. 2021, 492, 115784. [Google Scholar] [CrossRef]
- Schmidt, H.; Glattetre, J. A fast field model for three-dimensional wave propagation in stratified environments based on the global matrix method. J. Acoust. Soc. Am. 1985, 78, 2105–2114. [Google Scholar] [CrossRef]
- Tu, H.; Wang, Y.; Zhang, Y.; Wang, X.; Liu, W. A spectrally discretized wide-angle parabolic equation model for simulating acoustic propagation in laterally inhomogeneous oceans. J. Acoust. Soc. Am. 2023, 153, 3334. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.M.; Dowling, D.R. Tangent linear approximations for split-step Padé solutions of the parabolic-equation method in two dimensions. J. Acoust. Soc. Am. 2023, 154, A180. [Google Scholar] [CrossRef]
- Zingarelli, R.A.; Chin-Bing, S.A.; Collins, M.D. Optimizations for Fourier synthesized time domain pulse propagation calculations. In Proceedings of the OCEANS 2009, Biloxi, MS, USA, 26–29 October 2009; pp. 1–5. [Google Scholar]
- Deavenport, R.L.; Gilchrest, M.J.; Thomson, D.J. Acoustic modelling of a transient source in shallow water. Appl. Acoust. 2019, 150, 227–235. [Google Scholar] [CrossRef]
- An, L.; Qiu, Y.; Wang, X.; Zhang, L.; Huang, R. Low resolution fourier synthesis modelling for underwater acoustic channel impulse response. Appl. Acoust. 2022, 188, 108596. [Google Scholar] [CrossRef]
- Murphy, J.E. Finite-difference treatment of a time-domain parabolic equation: Theory. J. Acoust. Soc. Am. 1985, 77, 1958–1960. [Google Scholar] [CrossRef]
- Collins, M.D. The time-domain solution of the wide-angle parabolic equation including the effects of sediment dispersion. J. Acoust. Soc. Am. 1988, 84, 2114–2125. [Google Scholar] [CrossRef]
- Özkan Sertlek, H. Time domain normal mode analysis of underwater acoustic wave propagation for a single layered acoustic channel in two dimensional Cartesian coordinates. J. Acoust. Soc. Am. 2009, 126, 3373. [Google Scholar] [CrossRef]
- Cristini, P.; Komatitsch, D. Some illustrative examples of the use of a spectral-element method in ocean acoustics. J. Acoust. Soc. Am. 2012, 131, EL229–EL235. [Google Scholar] [CrossRef] [PubMed]
- Plotnick, D.; Marston, P.L. Modeling and experimental validation of an evanescent wavefield using a wavenumber integration method. J. Acoust. Soc. Am. 2016, 139, 1986. [Google Scholar] [CrossRef]
- Etter, P.C. Underwater Acoustic Modeling and Simulation, 5th ed.; CRC Press: Boca Raton, FL, USA, 2018; p. 608. [Google Scholar]
- Porter, M.B. The time-marched fast-field program (FFP) for modeling acoustic pulse propagation. J. Acoust. Soc. Am. 1990, 87, 2013–2023. [Google Scholar] [CrossRef]
- Isakson, M.J.; Yarbrough, R.A.; Wilson, P.S. Finite-element modeling of long range, range-dependent acoustic propagation in shallow water. J. Acoust. Soc. Am. 2007, 122, 3074. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Wei, G.W. On the fictitious-domain and interpolation formulations of the matched interface and boundary (MIB) method. J. Comput. Phys. 2006, 219, 228–246. [Google Scholar] [CrossRef]
- Pan, K.; Tan, Y.; Hu, H. An interpolation matched interface and boundary method for elliptic interface problems. J. Comput. Appl. Math. 2010, 234, 73–94. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, L.; Wang, Y.; Cheng, X.; Xiao, W. A Vector Wavenumber Integration Model of Underwater Acoustic Propagation Based on the Matched Interface and Boundary Method. J. Mar. Sci. Eng. 2021, 9, 1134. [Google Scholar] [CrossRef]
- Liu, W.; Xu, G.; Cheng, X.; Wang, Y. A Novel Finite Difference Scheme for Normal Mode Models in Underwater Acoustics. J. Mar. Sci. Eng. 2023, 11, 553. [Google Scholar] [CrossRef]
- Porter, M.B. Acoustics Toolbox. 2023. Available online: http://oalib.hlsresearch.com/AcousticsToolbox/ (accessed on 25 April 2024).



| Do j = 2, NTot1 − 1! The number of interior points U2(j) = AD1(j) * U1(j) + AE1(j) * U1(j − 1) + AE1(j + 1) * U1(j + 1) + AD0(j) * U0(j) + AE0(j) * U0(j − 1) + AE0(j + 1) * U0(j + 1) End do ! U0 denotes the kernel function at the previous time step ! U1 denotes the kernel function at the current time step ! U2 denotes the right-hand side ! AD0 denotes the diagonal element of the previous time step coefficient matrix ! AE0 denotes the off-diagonal element of the previous time step coefficient matrix ! AD1 denotes the diagonal element of the current time step coefficient matrix ! AE1 denotes the off-diagonal element of the current time step coefficient matrix |
| Cases | FEM-2nd (PPW = 20) | FDM-4th (PPW = 20) | FDM-4th (PPW = 15) |
|---|---|---|---|
| Lloyd’s mirror | 16.310 s | 19.547 s | 14.120 s |
| Ideal waveguide | 2.712 s | 3.185 s | 2.373 s |
| Head wave | 20.116 s | 24.506 s | 17.336 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Liu, W.; Xu, G. A Time-Domain Wavenumber Integration Model for Underwater Acoustics Based on the High-Order Finite Difference Method. J. Mar. Sci. Eng. 2024, 12, 728. https://doi.org/10.3390/jmse12050728
Xu X, Liu W, Xu G. A Time-Domain Wavenumber Integration Model for Underwater Acoustics Based on the High-Order Finite Difference Method. Journal of Marine Science and Engineering. 2024; 12(5):728. https://doi.org/10.3390/jmse12050728
Chicago/Turabian StyleXu, Xiang, Wei Liu, and Guojun Xu. 2024. "A Time-Domain Wavenumber Integration Model for Underwater Acoustics Based on the High-Order Finite Difference Method" Journal of Marine Science and Engineering 12, no. 5: 728. https://doi.org/10.3390/jmse12050728
APA StyleXu, X., Liu, W., & Xu, G. (2024). A Time-Domain Wavenumber Integration Model for Underwater Acoustics Based on the High-Order Finite Difference Method. Journal of Marine Science and Engineering, 12(5), 728. https://doi.org/10.3390/jmse12050728





