Study on Spatial Scale Selection Problem: Taking Port Spatial Expression as Example
Abstract
1. Introduction
2. Materials and Methods
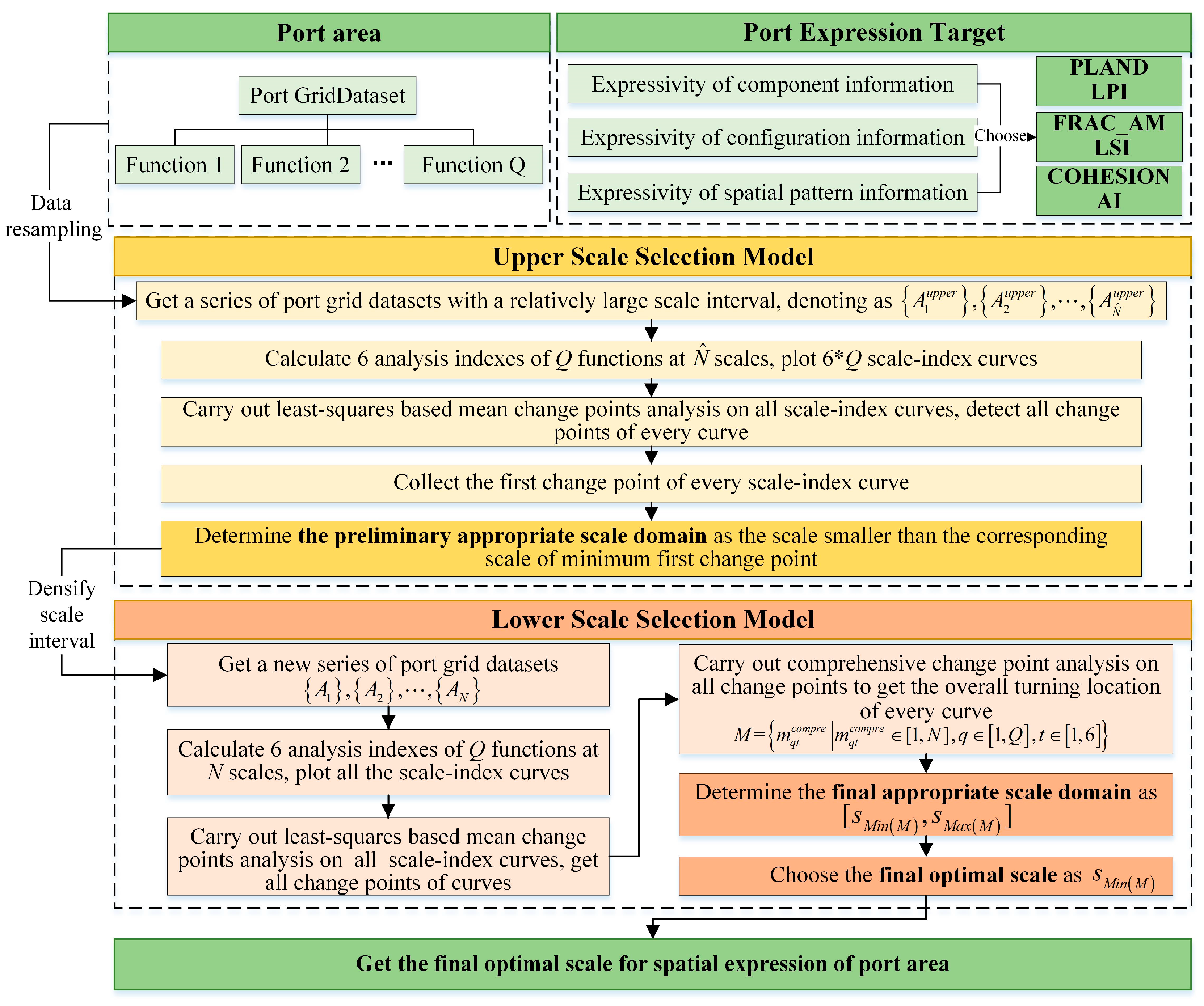
2.1. Two-Layer Scale Selection Framework
2.2. Scale Selection Model for Port Spatial Expression
2.2.1. Data Preprocessing
2.2.2. Scale Selection Analysis Index
2.2.3. Upper Scale Selection Model
2.2.4. Lower Scale Selection Model
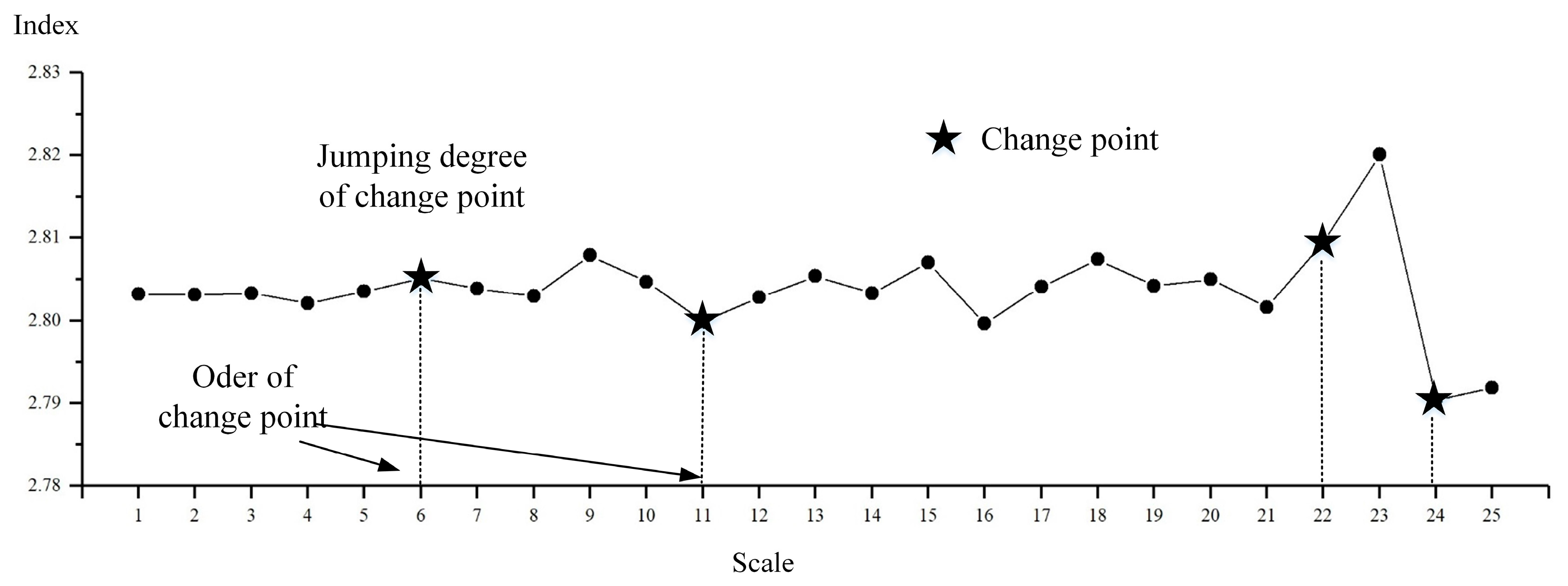
2.2.5. Least-Squares-Based Mean Change Point Analysis
2.2.6. Comprehensive Change Point Analysis and Criterion for Optimal Scale Selection in a Port Area
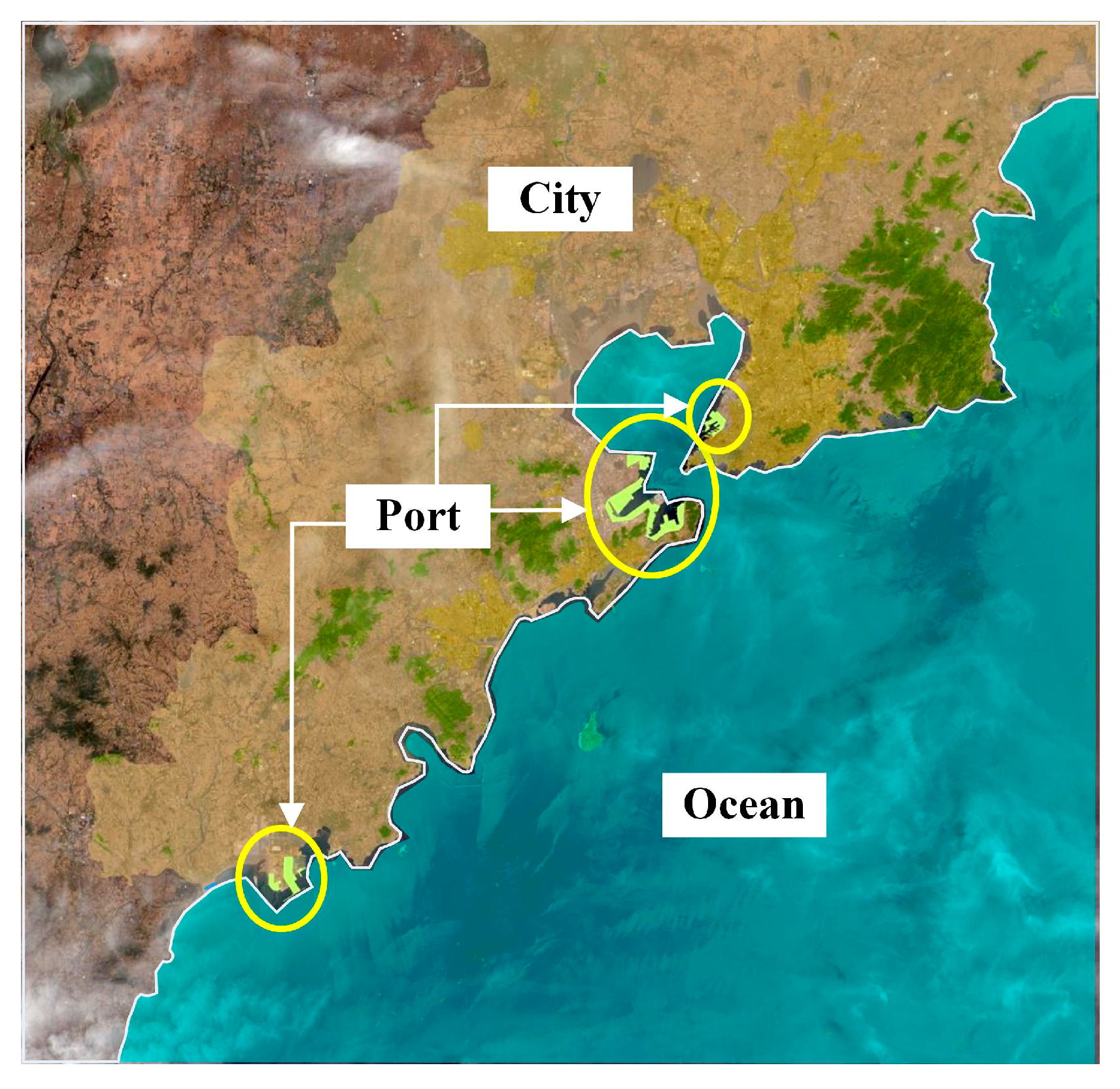
2.3. Research Area and Data
3. Results
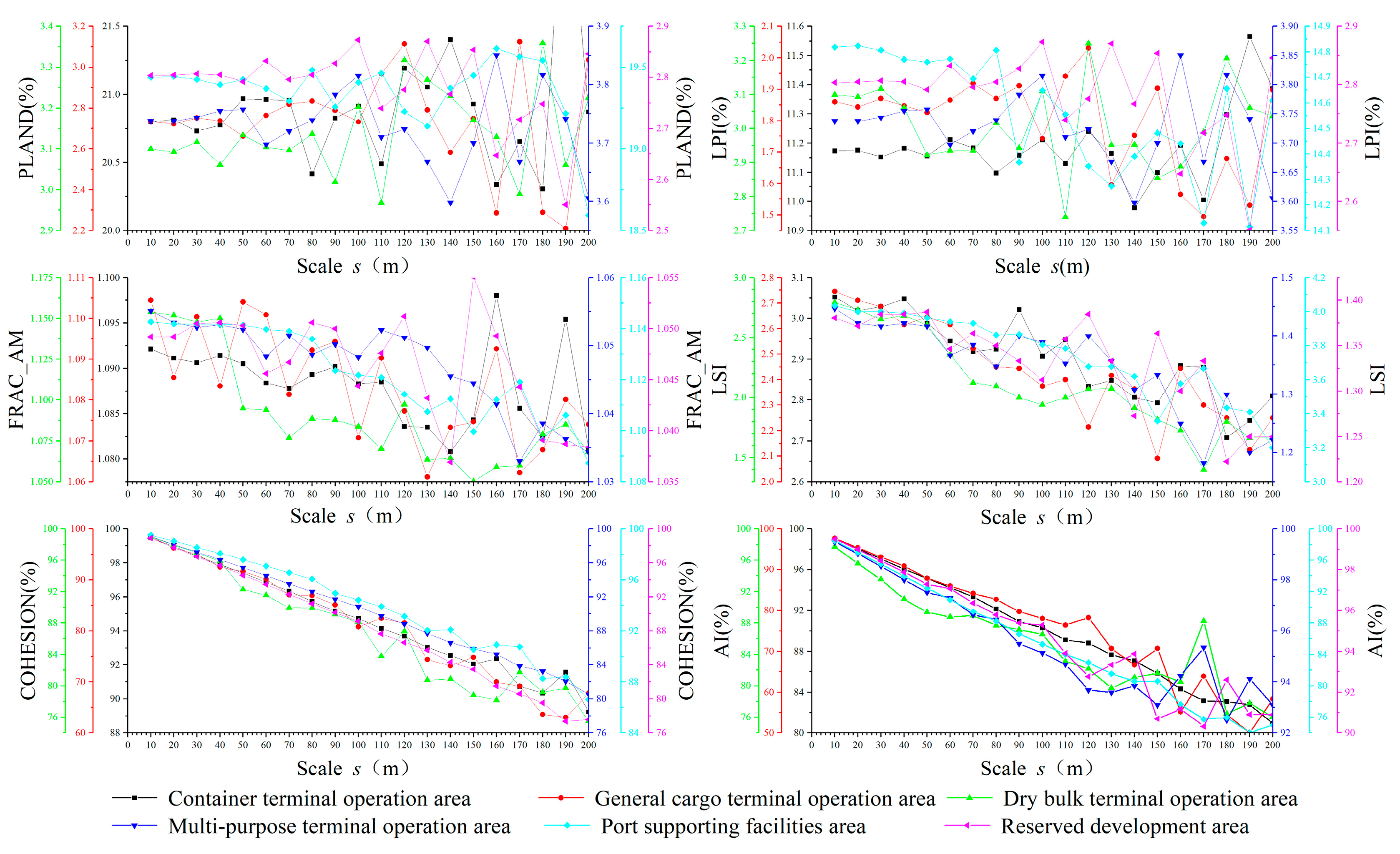
3.1. Analysis of Scale–Index Curves in the Upper Scale Selection Model
3.2. Analysis of Scale–Index Curves in the Lower Scale Selection Model
3.3. Comprehensive Change Point Analysis and Optimal Scale Selection
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Atkinson, P.M.; Tate, N.J. Spatial scale problems and geostatistical solutions: A review. Prof. Geogr. 2000, 52, 607–623. [Google Scholar] [CrossRef]
- Wu, J.G.; Shen, W.J.; Sun, W.Z.; Tueller, P.T. Empirical patterns of the effects of changing scale on landscape metrics. Landsc. Ecol. 2002, 17, 761–782. [Google Scholar] [CrossRef]
- Wu, J.G. Effects of changing scale on landscape pattern analysis: Scaling relations. Landsc. Ecol. 2004, 19, 125–138. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Dragut, L.; Eisank, C.; Strasser, T. Local variance for multi-scale analysis in geomorphometry. Geomorphology 2011, 130, 162–172. [Google Scholar] [CrossRef]
- Yang, D.W.; Herath, S.; Musiake, K. Spatial resolution sensitivity of catchment geomorphologic properties and the effect on hydrological simulation. Hydrol. Process. 2001, 15, 2085–2099. [Google Scholar] [CrossRef]
- Lu, X.Y.; Li, Y.K.; Washington-Allen, R.A.; Li, Y.N.; Li, H.D.; Hu, Q.W. The effect of grid size on the quantification of erosion, deposition, and rill network. Int. Soil Water Conserv. Res. 2017, 5, 241–251. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q.H. Scaling effect on the relationship between landscape pattern and land surface temperature: A case study of Indianapolis, United States. Photogramm. Eng. Remote Sens. 2009, 75, 291–304. [Google Scholar] [CrossRef]
- Wu, Q.; Li, Z.Y.; Yang, C.B.; Li, H.Q.; Gong, L.W.; Guo, F.X. On the scale effect of relationship identification between land surface temperature and 3D landscape pattern: The application of random forest. Remote Sens. 2022, 14, 279. [Google Scholar] [CrossRef]
- Liu, X.L.; Wang, Y.; Li, Y.; Liu, F.; Shen, J.L.; Wang, J.; Xiao, R.L.; Wu, J.S. Multi-scaled response of groundwater nitrate contamination to integrated anthropogenic activities in a rapidly urbanizing agricultural catchment. Environ. Sci. Pollut. Res. 2019, 26, 34931–34942. [Google Scholar] [CrossRef]
- Lü, Y.H.; Feng, X.M.; Chen, L.D.; Fu, B.J. Scaling effects of landscape metrics: A comparison of two methods. Phys. Geogr. 2013, 34, 40–49. [Google Scholar] [CrossRef]
- Tian, P.; Cao, L.D.; Li, J.L.; Pu, R.L.; Shi, X.L.; Wang, L.J.; Liu, R.Q.; Xu, H.; Tong, C.; Zhou, Z.J.; et al. Landscape grain effect in Yancheng Coastal Wetland and its response to landscape changes. Int. J. Environ. Res. Public Health 2019, 16, 2225. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Yang, X.H.; Dong, N.; Cai, H. Evaluating Grid Size Suitability of Population Distribution Data via Improved ALV Method: A Case Study in Anhui Province, China. Sustainability 2017, 10, 41. [Google Scholar] [CrossRef]
- Chen, S.H.; Zhang, R.H.; Su, H.B.; Tian, J.; Xia, J. Scaling-up transformation of multisensor images with multiple resolutions. Sensors 2009, 9, 1370–1381. [Google Scholar] [CrossRef]
- Wang, Q.M.; Shi, W.Z.; Atkinson, P.M.; Zhao, Y.L. Downscaling MODIS images with Area-to-Point Regression Kriging. Remote Sens. Environ. 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Jantz, C.A.; Geotz, S.J. Analysis of scale dependencies in a urban land-use change model. Int. J. Geogr. Inf. Sci. 2005, 19, 217–241. [Google Scholar] [CrossRef]
- Wolock, D.M.; Price, C.V. Effects of digital elevation model map scale and data resolution on a topography-based watershed model. Water Resour. Res. 1994, 30, 3041–3052. [Google Scholar] [CrossRef]
- Yaermaimaiti, A.; Li, X.G.; Ge, X.Y.; Liu, C.J. Analysis of landscape pattern and ecological risk change characteristics in Bosten Lake basin based on optimal scale. Ecol. Indic. 2024, 163, 112120. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Q. Identifying spatial and temporal dynamics and driving factors of cultivated land fragmentation in Shaanxi province. Agric. Syst. 2024, 217, 103948. [Google Scholar] [CrossRef]
- Marceau, D.J.; Gratton, D.J. Remote sensing and the measurement of geographical the entities in a forested environment: 2. The optimal spatial resolution. Remote Sens. Environ. 1994, 49, 105–117. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Curran, P.J. Choosing an appropriate spatial resolution for remote sensing investigations. Photogramm. Eng. Remote Sens. 1997, 63, 1345–1351. [Google Scholar]
- Ming, D.P.; Yang, J.Y.; Li, L.X.; Song, Z.Q. Modified ALV for selecting the optimal spatial resolution and its scale effect on image classification accuracy. Math. Comput. Model. 2011, 54, 1061–1068. [Google Scholar] [CrossRef]
- Li, R.X.; Gao, X.H.; Shi, F.F.; Zhang, H. Scale effect of land cover classification from multi-resolution satellite remote sensing data. Sensors 2023, 23, 6136. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Liu, R.; Men, C.; Wang, Q.; Miao, Y.; Shoaib, M.; Wang, Y.; Jiao, L.; Zhang, Y. Multiscale spatiotemporal characteristics of landscape patterns, hotspots, and influencing factors for soil erosion. Sci. Total Environ. 2021, 779, 146474. [Google Scholar] [CrossRef]
- Scammacca, O.; Sauzet, O.; Michelin, J.; Choquet, P.; Garnier, P.; Gabrielle, B.; Baveye, P.C.; Montagne, D. Effect of spatial scale of soil data on estimates of soil ecosystem services: Case study in 100 km2 area in France. Eur. J. Soil Sci. 2023, 74, e13359. [Google Scholar] [CrossRef]
- Wu, T.; Chen, J.Y.; Li, Y.F.; Yao, Y.; Li, Z.Q.; Xing, S.H.; Zhang, L.M. Resolution effect of soil organic carbon prediction in a large-scale and morphologically complex area. Eurasian Soil Sci. 2023, 56, S260–S275. [Google Scholar] [CrossRef]
- Nouri, H.; Anderson, S.; Sutton, P.; Beecham, S.; Nagler, P.; Jarchow, C.J.; Roberts, D.A. NDVI, scale invariance and the modifiable areal unit problem: An assessment of vegetation in the Adelaide Parklands. Sci. Total Environ. 2017, 584, 11–18. [Google Scholar] [CrossRef]
- Comber, A.; Harris, P. The importance of scale and the MAUP for robust ecosystem service evaluations and landscape decisions. Land 2022, 11, 399. [Google Scholar] [CrossRef]
- Wang, H.C.; Wang, L.; Liu, X.; Wei, B.L. Analysis of landscape pattern vulnerability in Dasi river basin at the optimal scale. Sci. Rep. 2024, 14, 10727. [Google Scholar] [CrossRef]
- Cao, L. Scale effect analysis of urban compactness measurement index based on grid. IOP Conf. Ser. Earth Environ. Sci. 2017, 63, 012049. [Google Scholar] [CrossRef]
- Wang, R.; Feng, Y.J.; Tong, X.H.; Zhao, J.J.; Zhai, S.T. Impacts of spatial scale on the delineation of spatiotemporal urban expansion. Ecol. Indic. 2021, 129, 107896. [Google Scholar] [CrossRef]
- Liu, X.L.; Wang, Y.; Li, Y.; Liu, F.; Shen, J.L.; Wang, J.; Xiao, R.L.; Wu, J.S. Changes in arable land in response to township urbanization in a Chinese low hilly region: Scale effects and spatial interactions. Appl. Geogr. 2017, 88, 24–37. [Google Scholar] [CrossRef]
- Song, L.; Cao, Y.G.; Zhou, W.; Su, R.Q.; Qiu, M. Scale effects and countermeasures of cultivated land changes based on hierarchical linear model. Environ. Monit. Assess. 2020, 192, 346. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.N.; Zhao, W.W.; Zhang, Z.F.; Fang, X.N. Analysis of Multi-Scale Changes in Arable Land and Scale Effects of the Driving Factors in the Loess Areas in Northern Shaanxi, China. Sustainability 2014, 6, 1747. [Google Scholar] [CrossRef]
- Chen, J.Z.; Wang, L.; Ma, L.; Fan, X.Y. Quantifying the scale effect of the relationship between land surface temperature and landscape pattern. Remote Sens. 2023, 15, 2131. [Google Scholar] [CrossRef]
- Meng, Q.Y.; Liu, W.X.; Zhang, L.N.; Allam, M.; Bi, Y.X.; Hu, X.L.; Gao, J.F.; Hu, D.; Jancsó, T. Relationships between land surface temperatures and neighboring environment in highly urbanized areas: Seasonal and scale effects analyses of Beijing, China. Remote Sens. 2022, 14, 4340. [Google Scholar] [CrossRef]
- Ai, J.W.; Yu, K.Y.; Zeng, Z.; Yang, L.Q.; Liu, Y.F.; Liu, J. Assessing the dynamic landscape ecological risk and its driving forces in an island city based on optimal spatial scales: Haitan Island, China. Ecol. Indic. 2022, 137, 108771. [Google Scholar] [CrossRef]
- Wang, Q.X.; Zhang, P.Y.; Chang, Y.H.; Li, G.H.; Chen, Z.; Zhang, X.Y.; Xing, G.R.; Lu, R.; Li, M.F.; Zhou, Z.M. Landscape pattern evolution and ecological risk assessment of the Yellow River Basin based on optimal scale. Ecol. Indic. 2024, 158, 111381. [Google Scholar] [CrossRef]
- Chen, L.; Gao, Y.; Zhu, D.; Yuan, Y.; Liu, Y. Quantifying the scale effect in geospatial big data using semi-variograms. PLoS ONE 2019, 14, e0225139. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Zhang, T.; Chen, L.Q.; Wen, M.X.; Liu, W.Q.; Hu, S. Optimal Grain Size Based Landscape Pattern Analysis for Shanghai Using Landsat Images from 1998 to 2017. Pol. J. Environ. Stud. 2021, 30, 2799–2813. [Google Scholar] [CrossRef]
- Li, Q.X.; Ma, B.; Zhao, L.W.; Mao, Z.X.; Luo, L.; Liu, X.L. Landscape Ecological Risk Evaluation Study under Multi-Scale Grids—A Case Study of Bailong River Basin in Gansu Province, China. Water 2023, 15, 3777. [Google Scholar] [CrossRef]
- Wang, Y.S.; Yan, X.D.; Fang, Q.P.; Wang, L.; Chen, D.B.; Yu, Z.X. Spatiotemporal variation of alpine gorge watershed landscape patterns via multi-scale metrics and optimal granularity analysis: A case study of Lushui City in Yunnan Province, China. Front. Ecol. Evol. 2024, 12, 1448426. [Google Scholar] [CrossRef]
- Jandhyala, V.; Fotopoulos, S.; Macneil, I.; Liu, P. Inference for single and multiple change-points in time series. J. Time Ser. Anal. 2013, 34, 423–446. [Google Scholar] [CrossRef]
- Lavielle, M.; Teyssière, G. Adaptive detection of multiple change-points in asset price volatility. In Long Memory in Economics; Teyssière, G., Kirman, A.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 129–156. [Google Scholar] [CrossRef]
- Reeves, J.; Chen, J.; Wang, X.L.; Lund, R.; Qi, Q.L. A review and comparison of changepoint detection techniques for climate data. J. Appl. Meteorol. Climatol. 2007, 46, 900–915. [Google Scholar] [CrossRef]
- Liu, S.Y.; Huang, S.Z.; Xie, Y.Y.; Wang, H.; Leng, G.Y.; Huang, Q.; Wei, X.T.; Wang, L. Identification of the non-stationarity of floods: Changing patterns, causes, and implications. Water Resour. Manag. 2019, 33, 939–953. [Google Scholar] [CrossRef]
- Chen, X.Q.; Wu, H.; Han, B.; Liu, W.; Montewka, J.; Liu, R.W. Orientation-aware ship detection via a rotation feature decoupling supported deep learning approach. Eng. Appl. Artif. Intell. 2023, 125, 106686. [Google Scholar] [CrossRef]
- Chen, X.Q.; Zheng, J.B.; Li, C.F.; Wu, B.; Wu, H.F.; Montewka, J. Maritime traffic situation awareness analysis via high-fidelity ship imaging trajectory. Multimed. Tools Appl. 2024, 83, 48907–48923. [Google Scholar] [CrossRef]
- Ma, H.L.; Chung, S.H.; Chan, H.K.; Cui, L. An integrated model for berth and yard planning in container terminals with multi-continuous berth layout. Ann. Oper. Res. 2019, 273, 409–431. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, W.Y.; Song, X.Q.; Guo, Z.J. Simulation-based optimization for yard design at mega container terminal under uncertainty. Math. Probl. Eng. 2016, 2016, 7467498. [Google Scholar] [CrossRef]
- Xiao, G.N.; Xu, L. Challenges and opportunities of maritime transport in the post-epidemic era. J. Mar. Sci. Eng. 2024, 12, 1685. [Google Scholar] [CrossRef]
- Xiao, G.N.; Wang, Y.Q.; Wu, R.J.; Li, J.P.; Cai, Z.Y. Sustainable maritime transport: A review of intelligent shipping technology and green port construction applications. J. Mar. Sci. Eng. 2024, 12, 1728. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Design Code of General Layout for Sea Ports: JTS 165-2013; China Communications Press: Beijing, China, 2013. [Google Scholar]
- Masoudi, M.; Tan, P.Y. Multi-year comparison of the effects of spatial pattern of urban green spaces on urban land surface temperature. Landsc. Urban Plan. 2019, 184, 44–58. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Ene, E. FRAGSTATS v4: Spatial Pattern Analysis Program for Categorical Maps. Computer Software Program Produced by the Authors. 2023. Available online: https://www.fragstats.org (accessed on 16 July 2023).
- Zhang, Q.; Chen, C.L.; Wang, J.Z.; Yang, D.Y.; Zhang, Y.; Wang, Z.F.; Gao, M. The spatial granularity effect, changing landscape patterns, and suitable landscape metrics in the three gorges reservoir area 1995–2015. Ecol. Indic. 2020, 114, 106259. [Google Scholar] [CrossRef]



| Landscape Metric | Abbreviation | Description | Equation |
|---|---|---|---|
| Percentage of landscape (%) | PLAND | Quantifies the proportional abundance of a given patch type, used here to reflect the expressivity of component information. | —area (m2) of patch ij —number of patches in the landscape of patch type i A—total landscape area (m2) |
| Largest patch index (%) | LPI | Quantifies the proportion of the largest patch of a given patch type in the total area of the landscape, used here to reflect the expressivity of component information. | |
| Area-weighted mean fractal dimension index | FRAC_AM | Measures the shape complexity of patches, used here to reflect the expressivity of configuration information. | —perimeter (m) of patch ij |
| Landscape shape index | LSI | A modified perimeter–area ratio, a measure of overall shape complexity of patches of a given type, used here to reflect the expressivity of configuration information. | —total length (m) of the edge in the landscape between patch types i and —number of patch types present in the landscape |
| Patch cohesion index (%) | COHESION | Measures the physical connectedness of a given patch type, which is better when the index value is smaller. Used here to reflect the expressivity of spatial distribution information. | —perimeter of patch ij in terms of the number of cell surfaces —area of patch ij in terms of the number of cells Z—total number of cells in the landscape |
| Aggregation index (%) | AI | Measures the level of clumpiness of a given patch type, which is lower when the index value is smaller. Used here to reflect the expressivity of spatial distribution information. | —number of like adjacencies between pixels of patch type i based on the single-count method |
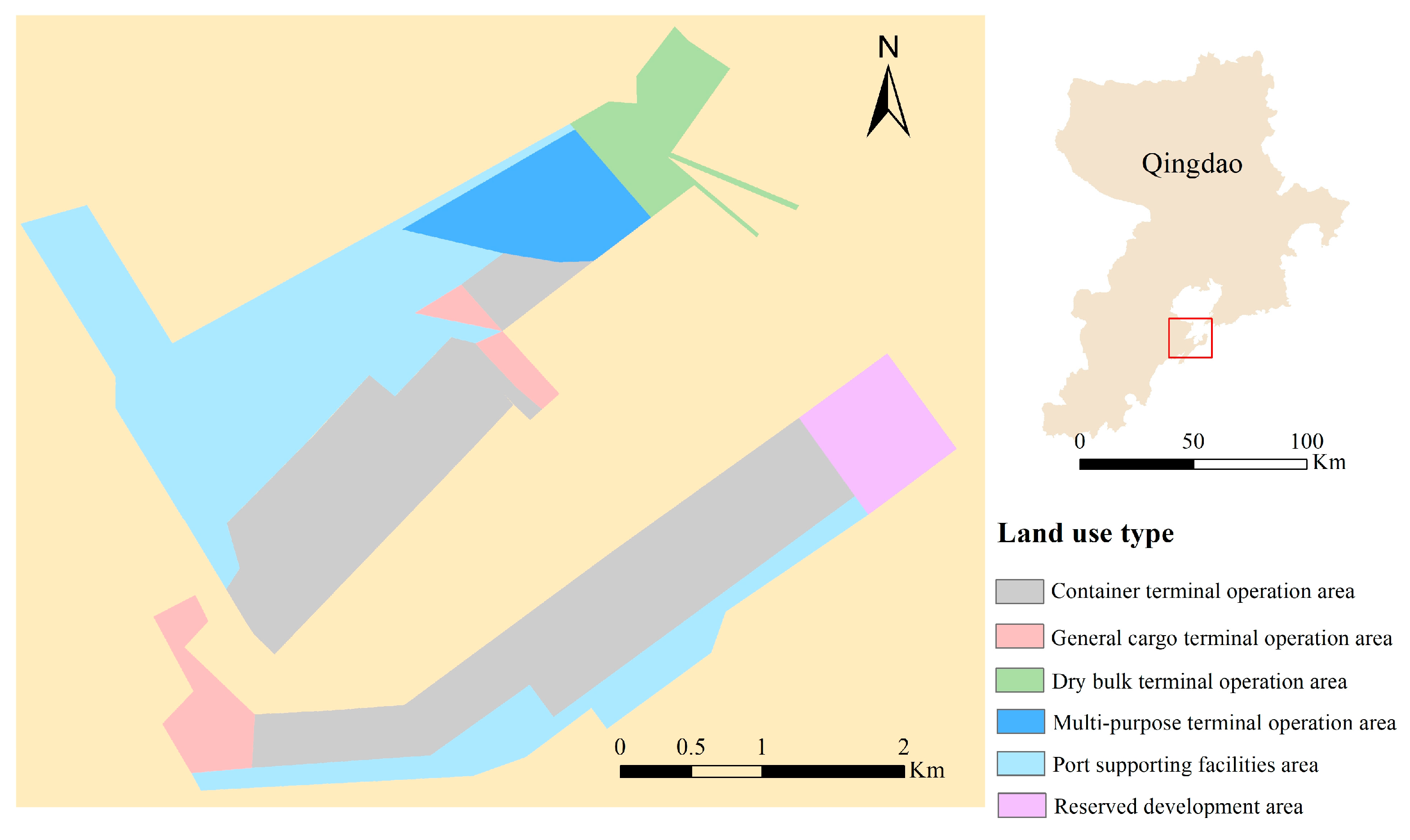
| Land Use Function Types in a Port Area | Description |
|---|---|
| Container terminal operation area | Land use for production and operation of container terminals |
| General cargo terminal operation area | Land use for production and operation of general cargo terminals |
| Dry bulk terminal operation area | Land use for production and operation of dry bulk terminals |
| Multi-purpose terminal operation area | Land use for production and operation of multi-purpose terminals |
| Port supporting facilities area | Land use for other port facilities, which support the daily operation of the port |
| Reserved development area | Land use reserved for future port development |
| Analysis Index | Land Use Function In the Port Area | Change Point | Corresponding Scale of Change Point (m) |
|---|---|---|---|
| PLAND | Container terminal operation area | 5, 8, 9, 12, 15 | 50, 80, 90, 120, 150 |
| General cargo terminal operation area | 6, 11, 14 | 60, 110, 140 | |
| Dry bulk terminal operation area | 5, 12, 14, 15 | 50, 120, 140, 150 | |
| Multi-purpose terminal operation area | 6, 9, 11, 13, 15 | 60, 90, 110, 130, 150 | |
| Port supporting facilities area | 6, 12, 14 | 60, 120, 140 | |
| Reserved development area | 6, 7, 11, 13, 16 | 60, 70, 110, 130, 160 | |
| LPI | Container terminal operation area | 6, 8, 9, 14, 18 | 60, 80, 90, 140, 180 |
| General cargo terminal operation area | 5, 6, 11, 13, 16 | 50, 60, 110, 130, 160 | |
| Dry bulk terminal operation area | 5, 8, 12, 13, 18 | 50, 80, 120, 130, 180 | |
| Multi-purpose terminal operation area | 6, 9, 11, 13, 15 | 60, 90, 110, 130, 150 | |
| Port supporting facilities area | 9, 12 | 90, 120 | |
| Reserved development area | 11, 16 | 110, 160 | |
| FRAC_AM | Container terminal operation area | 5, 6, 12, 14, 16 | 50, 60, 120, 140, 160 |
| General cargo terminal operation area | 5, 10, 12, 17 | 50, 100, 120, 170 | |
| Dry bulk terminal operation area | 5, 7, 10, 13, 18 | 50, 70, 100, 130, 180 | |
| Multi-purpose terminal operation area | 6, 11, 14, 17 | 60, 110, 140, 170 | |
| Port supporting facilities area | 6, 9, 12, 18 | 60, 90, 120, 180 | |
| Reserved development area | 6, 8, 10, 13, 18 | 60, 80, 100, 130, 180 | |
| LSI | Container terminal operation area | 5, 10, 12, 18 | 50, 100, 120, 180 |
| General cargo terminal operation area | 7, 10, 15, 19 | 70, 100, 150, 190 | |
| Dry bulk terminal operation area | 6, 7, 14, 17 | 60, 70, 140, 170 | |
| Multi-purpose terminal operation area | 6, 9, 14, 16 | 60, 90, 140, 160 | |
| Port supporting facilities area | 5, 8, 12, 15, 18 | 50, 80, 120, 150, 180 | |
| Reserved development area | 6, 8, 14, 18 | 60, 80, 140, 180 | |
| COHESION | Container terminal operation area | 5, 9, 13, 17 | 50, 90, 130, 170 |
| General cargo terminal operation area | 5, 9, 13, 17 | 50, 90, 130, 170 | |
| Dry bulk terminal operation area | 5, 10, 13, 20 | 50, 100, 130, 200 | |
| Multi-purpose terminal operation area | 5, 9, 13, 17 | 50, 90, 130, 170 | |
| Port supporting facilities area | 5, 9, 13, 18 | 50, 90, 130, 180 | |
| Reserved development area | 5, 9, 13, 17 | 50, 90, 130, 170 | |
| AI | Container terminal operation area | 5, 9, 13, 16 | 50, 90, 130, 160 |
| General cargo terminal operation area | 5, 9, 13, 16 | 50, 90, 130, 160 | |
| Dry bulk terminal operation area | 5, 8, 9, 11, 18 | 50, 80, 90, 110, 180 | |
| Multi-purpose terminal operation area | 5, 9, 12, 16 | 50, 90, 120, 160 | |
| Port supporting facilities area | 5, 9, 13, 17 | 50, 90, 130, 170 | |
| Reserved development area | 5, 11, 15, 18 | 50, 110, 150, 180 |
| Analysis Index | Land Use Function in the Port Area | Change Point | Corresponding Scale of Change Point (m) | Comprehensive Change Point | Corresponding Scale of Comprehensive Change Point (m) |
|---|---|---|---|---|---|
| PLAND | Container terminal operation area | 5, 15, 18 | 10, 30, 36 | 16 | 32 |
| General cargo terminal operation area | 11, 14, 15, 22 | 22, 28, 30, 44 | 14 | 28 | |
| Dry bulk terminal operation area | 9, 14, 16 | 18, 28, 32 | 16 | 32 | |
| Multi-purpose terminal operation area | 8, 16, 18 | 16, 32, 36 | 16 | 32 | |
| Port supporting facilities area | 5, 11, 18 | 10, 22, 36 | 14 | 28 | |
| Reserved development area | 6, 11, 22, 24 | 12, 22, 44, 48 | 20 | 40 | |
| LPI | Container terminal operation area | 11, 18, 19 | 22, 36, 38 | 18 | 36 |
| General cargo terminal operation area | 10, 15 | 20, 30 | 12 | 24 | |
| Dry bulk terminal operation area | 9, 14, 16, 23 | 18, 28, 32, 46 | 20 | 40 | |
| Multi-purpose terminal operation area | 8, 16, 18 | 16, 32, 36 | 16 | 32 | |
| Port supporting facilities area | 7, 10, 17, 18, 22 | 14, 20, 34, 36, 44 | 16 | 32 | |
| Reserved development area | 5, 9, 10, 13, 23, 24 | 10, 18, 20, 26, 46, 48 | 17 | 34 | |
| FRAC_AM | Container terminal operation area | 3, 5, 7, 13, 15, 18 | 6, 10, 14, 26, 30, 36 | 7 | 14 |
| General cargo terminal operation area | 3, 7, 8, 10, 13, 19 | 6, 14, 16, 20, 26, 38 | 9 | 18 | |
| Dry bulk terminal operation area | 7, 10, 14, 22, 23 | 14, 20, 28, 44, 46 | 20 | 40 | |
| Multi-purpose terminal operation area | 3, 6, 9, 13, 14, 22 | 6, 12, 18, 26, 28, 44 | 11 | 22 | |
| Port supporting facilities area | 4, 8, 10, 13, 19, 22 | 8, 16, 20, 26, 38, 44 | 11 | 22 | |
| Reserved development area | 10, 12, 13, 20, 21 | 10, 24, 26, 40, 42 | 14 | 28 | |
| LSI | Container terminal operation area | 4, 10, 12, 16, 21 | 8, 20, 24, 32, 42 | 9 | 18 |
| General cargo terminal operation area | 4, 7, 9, 12, 15, 19 | 8, 14, 18, 24, 30, 38 | 10 | 20 | |
| Dry bulk terminal operation area | 4, 10, 14, 20, 23 | 8, 20, 28, 40, 46 | 12 | 24 | |
| Multi-purpose terminal operation area | 5, 9, 15, 16, 22 | 10, 18, 30, 32, 44 | 11 | 22 | |
| Port supporting facilities area | 5, 8, 10, 13, 14, 21, 22 | 10, 16, 20, 26, 28, 42, 44 | 12 | 24 | |
| Reserved development area | 5, 10, 13, 21 | 10, 20, 26, 42 | 10 | 20 | |
| COHESION | Container terminal operation area | 5, 15, 18 | 10, 30, 36 | 16 | 32 |
| General cargo terminal operation area | 11, 14, 15, 22 | 22, 28, 30, 44 | 14 | 28 | |
| Dry bulk terminal operation area | 9, 14, 16 | 18, 28, 32 | 16 | 32 | |
| Multi-purpose terminal operation area | 8, 16, 18 | 16, 32, 36 | 16 | 32 | |
| Port supporting facilities area | 5, 11, 18 | 10, 22, 36 | 14 | 28 | |
| Reserved development area | 6, 11, 22, 24 | 12, 22, 44, 48 | 20 | 40 | |
| AI | Container terminal operation area | 11, 18, 19 | 22, 36, 38 | 18 | 36 |
| General cargo terminal operation area | 10, 15 | 20, 30 | 12 | 24 | |
| Dry bulk terminal operation area | 9, 14, 16, 23 | 18, 28, 32, 46 | 20 | 40 | |
| Multi-purpose terminal operation area | 8, 16, 18 | 16, 32, 36 | 16 | 32 | |
| Port supporting facilities area | 7, 10, 17, 18, 22 | 14, 20, 34, 36, 44 | 16 | 32 | |
| Reserved development area | 5, 9, 10, 13, 23, 24 | 10, 18, 20, 26, 46, 48 | 17 | 34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Xu, X.; Wang, W.; Guo, Z. Study on Spatial Scale Selection Problem: Taking Port Spatial Expression as Example. J. Mar. Sci. Eng. 2024, 12, 2057. https://doi.org/10.3390/jmse12112057
Xu Y, Xu X, Wang W, Guo Z. Study on Spatial Scale Selection Problem: Taking Port Spatial Expression as Example. Journal of Marine Science and Engineering. 2024; 12(11):2057. https://doi.org/10.3390/jmse12112057
Chicago/Turabian StyleXu, Yunzhuo, Xinglu Xu, Wenyuan Wang, and Zijian Guo. 2024. "Study on Spatial Scale Selection Problem: Taking Port Spatial Expression as Example" Journal of Marine Science and Engineering 12, no. 11: 2057. https://doi.org/10.3390/jmse12112057
APA StyleXu, Y., Xu, X., Wang, W., & Guo, Z. (2024). Study on Spatial Scale Selection Problem: Taking Port Spatial Expression as Example. Journal of Marine Science and Engineering, 12(11), 2057. https://doi.org/10.3390/jmse12112057







