Analysis of Impact of Control Strategies on Integrated Electric Propulsion System Performance During Icebreaking Process
Abstract
1. Introduction
- A DP-MPC energy management strategy is suggested to optimize the power distribution for the integrated electric propulsion system of an icebreaker to improve the adaptability to strong fluctuation loads.
- The parameter uncertainties of battery and supercapacitor have been introduced in the DP-MPC strategy to emphasize the impact on system performance during the icebreaking process.
- A hybrid energy storage system with battery degradation is introduced to reduce the battery energy losses.
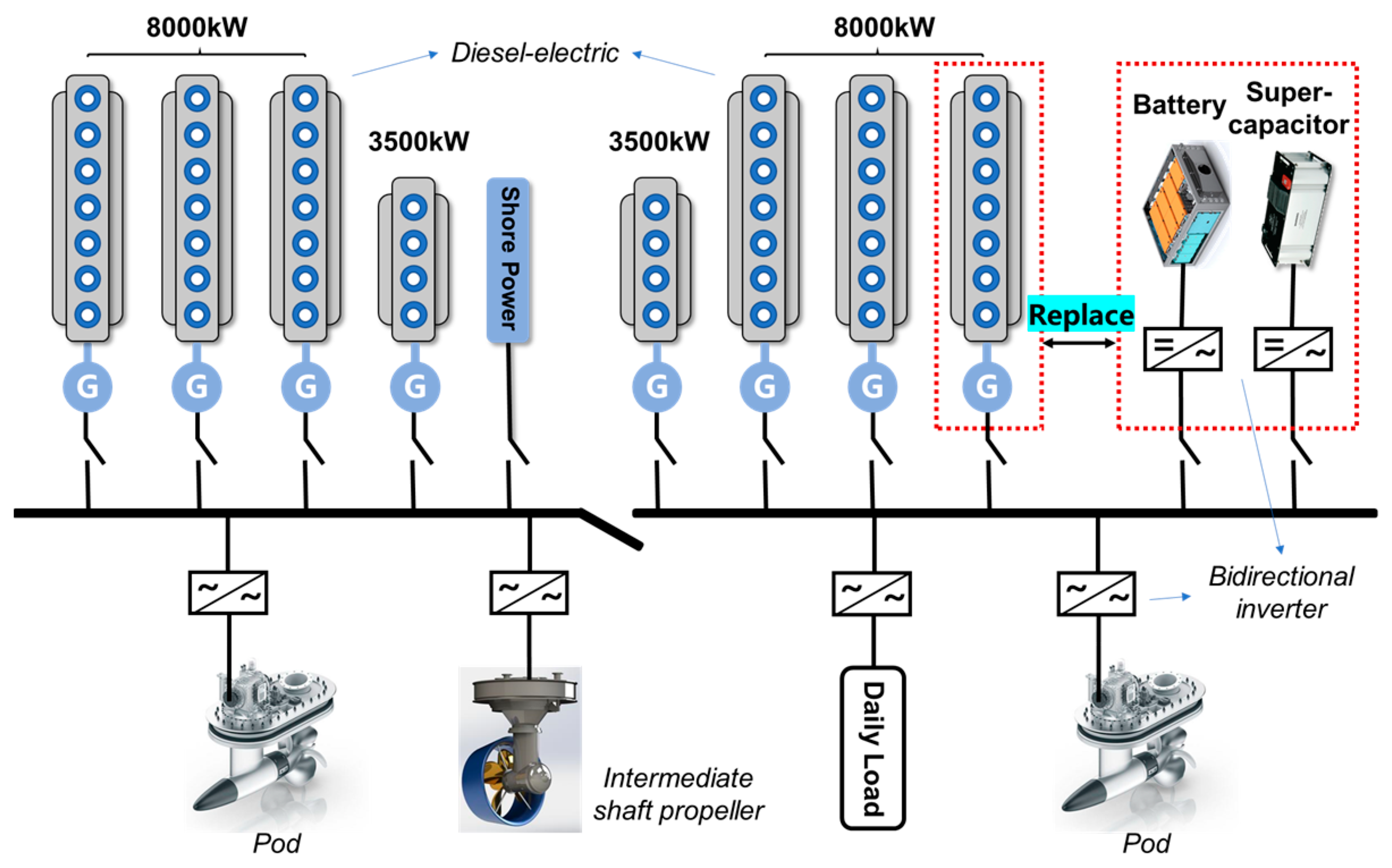
2. Structure and Modeling of Integrated Electric Propulsion System
2.1. Model of Diesel–Electric Unit
2.2. Model of ESS/HESS Element
2.3. Model of Bidirectional Inverter
2.4. Model of Propulsion Power
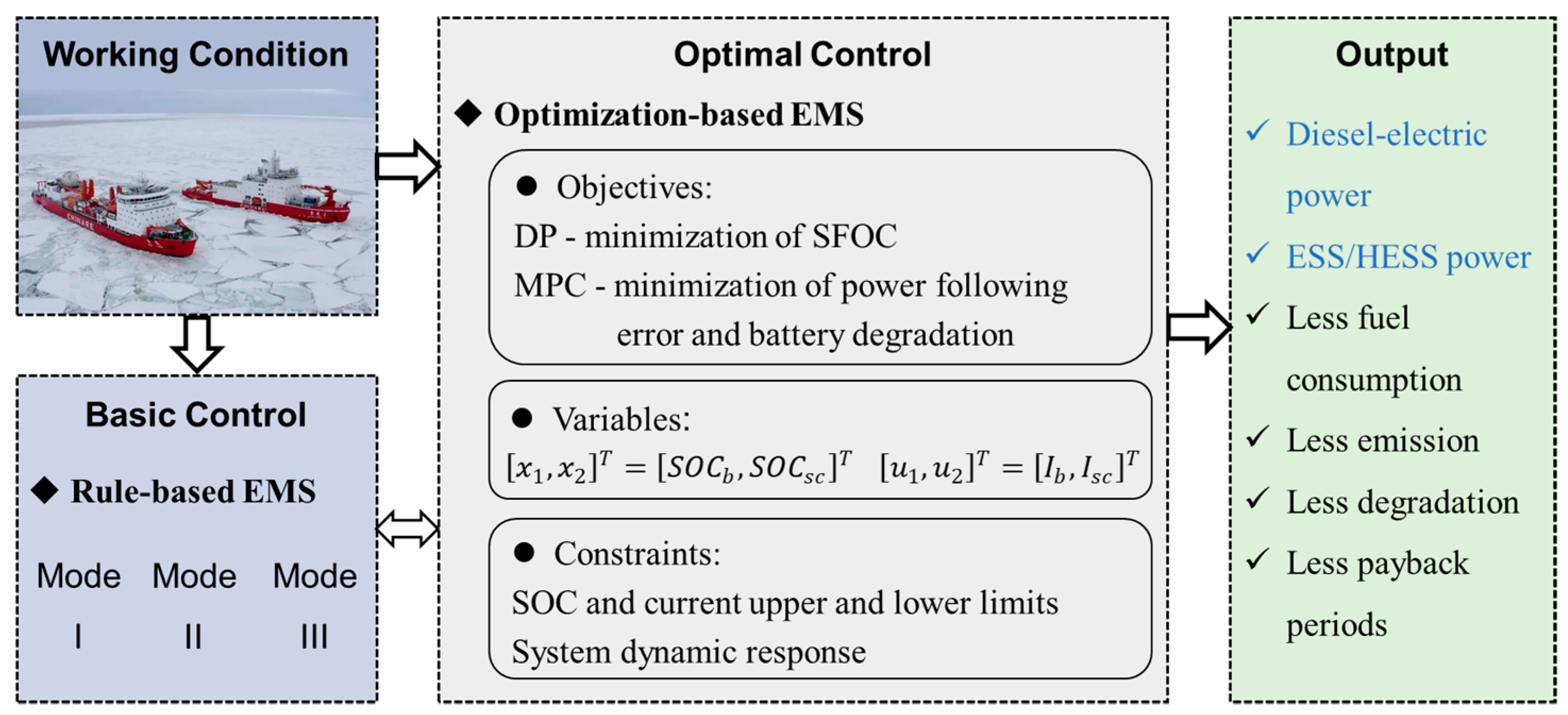
3. Control and Optimization
3.1. Rule-Based EMS
- Mode I: As the load power is lower than the minimum power of the diesel–electric sets, the diesel–electric sets operate at the minimum power, i.e., 75% load, and the excess energy is absorbed by the ESS. As the SOC of the ESS is higher than the threshold (90%), the diesel–electric sets operate at load reduction.
- Mode II: As the load power is in the optimal operating range of the diesel–electric sets, i.e., 75–90% load, the power demand is fully provided by the diesel–electric sets.
- Mode III: As the load power is higher than the maximum power of the operating diesel–electric sets, the diesel–electric sets operate at the maximum power, i.e., 90% load, and the shortfall power is provided by the ESS. When the SOC of the ESS is below the threshold (20%), the standby diesel–electric set is turned on to take up the power difference and charge the ESS.
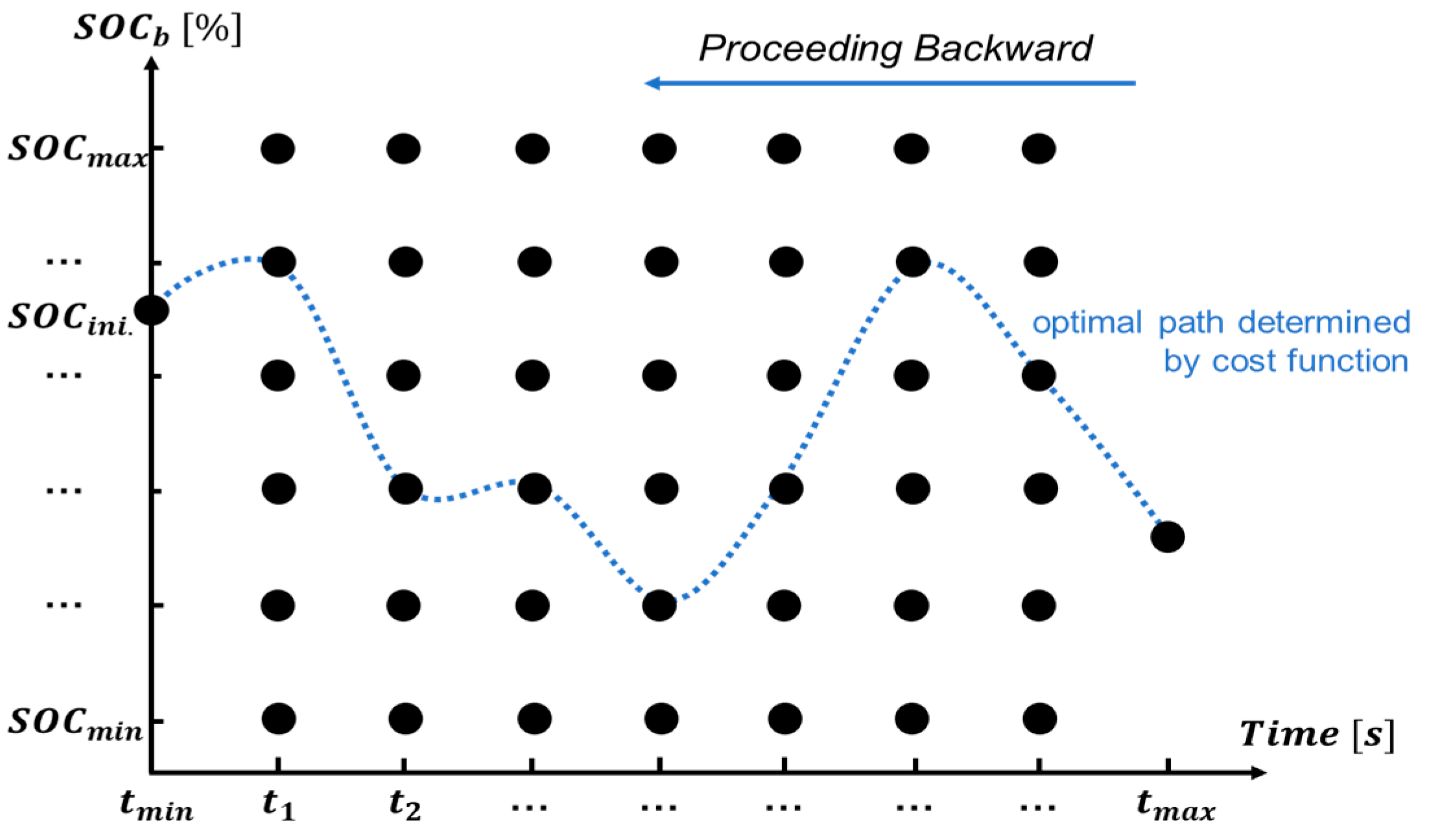
3.2. DP-Based EMS
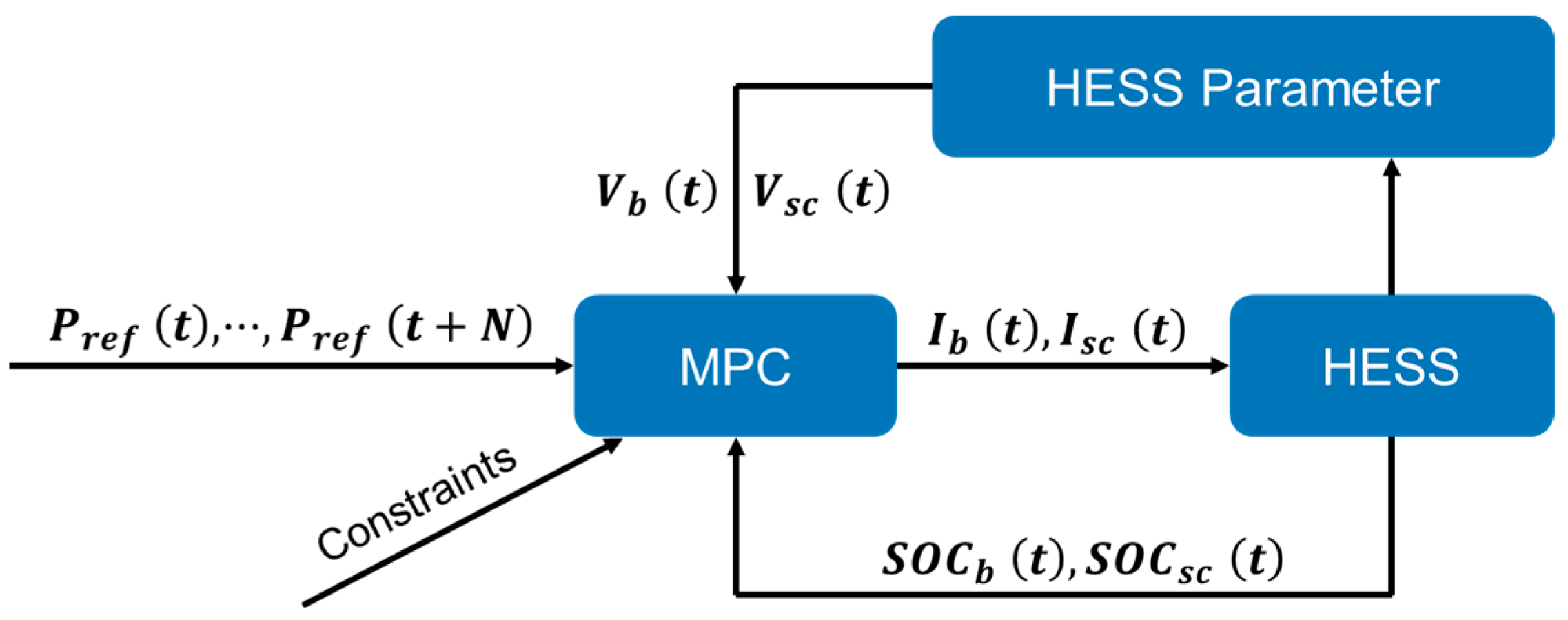
3.3. Model Predictive Control
4. Case Study
4.1. Specific Fuel Oil Consumptions
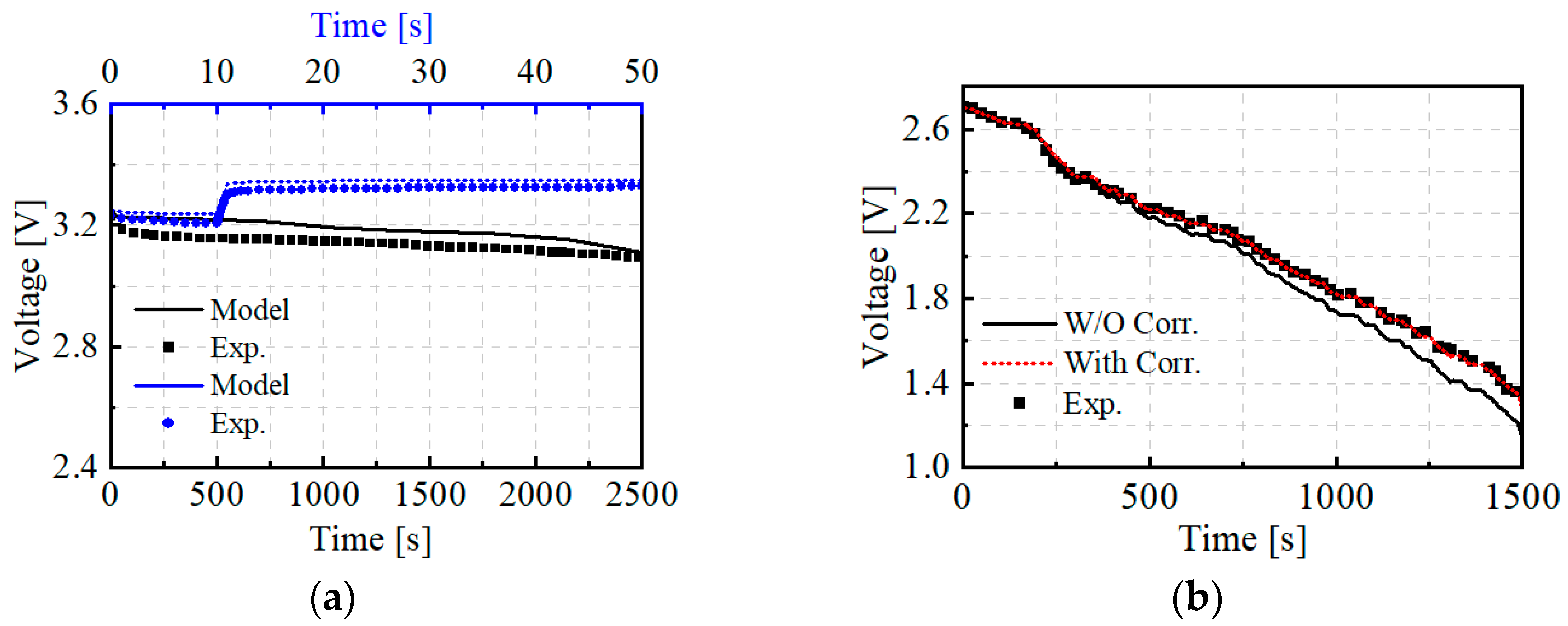
4.2. HESS Model Validation
5. Results and Discussions
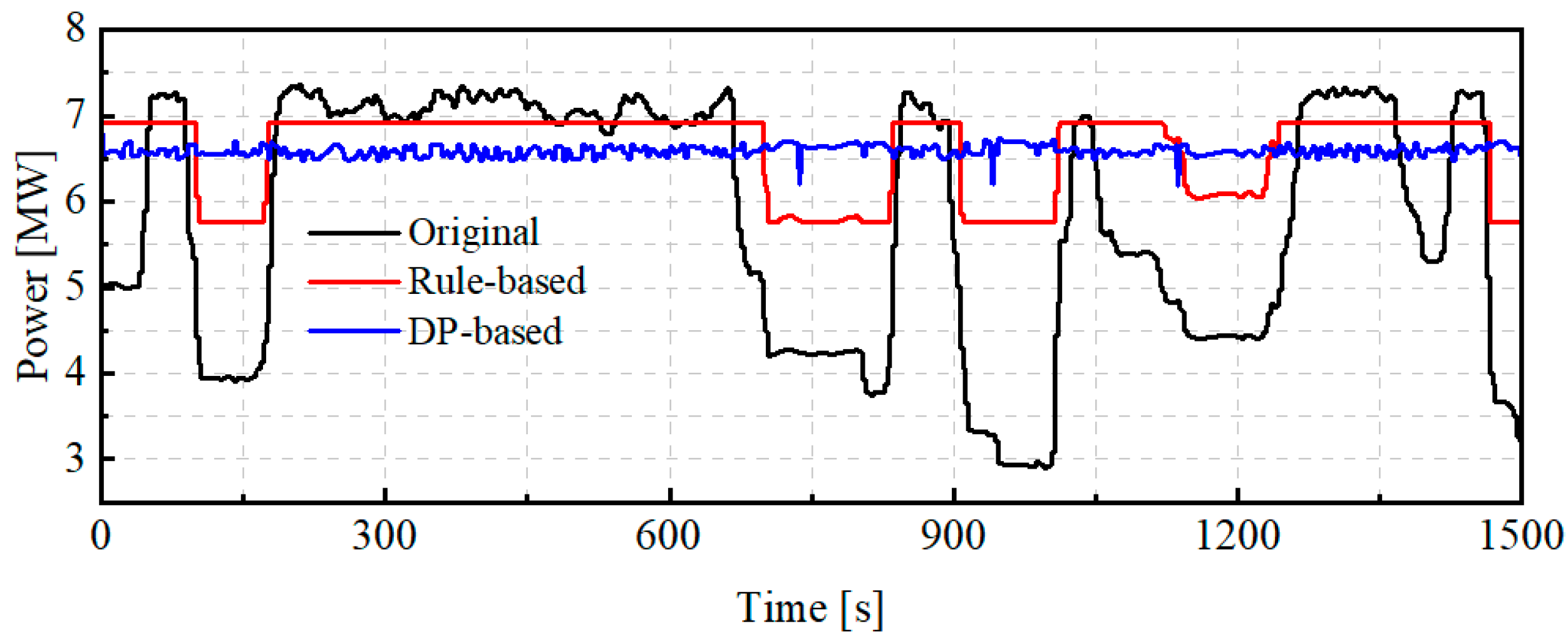
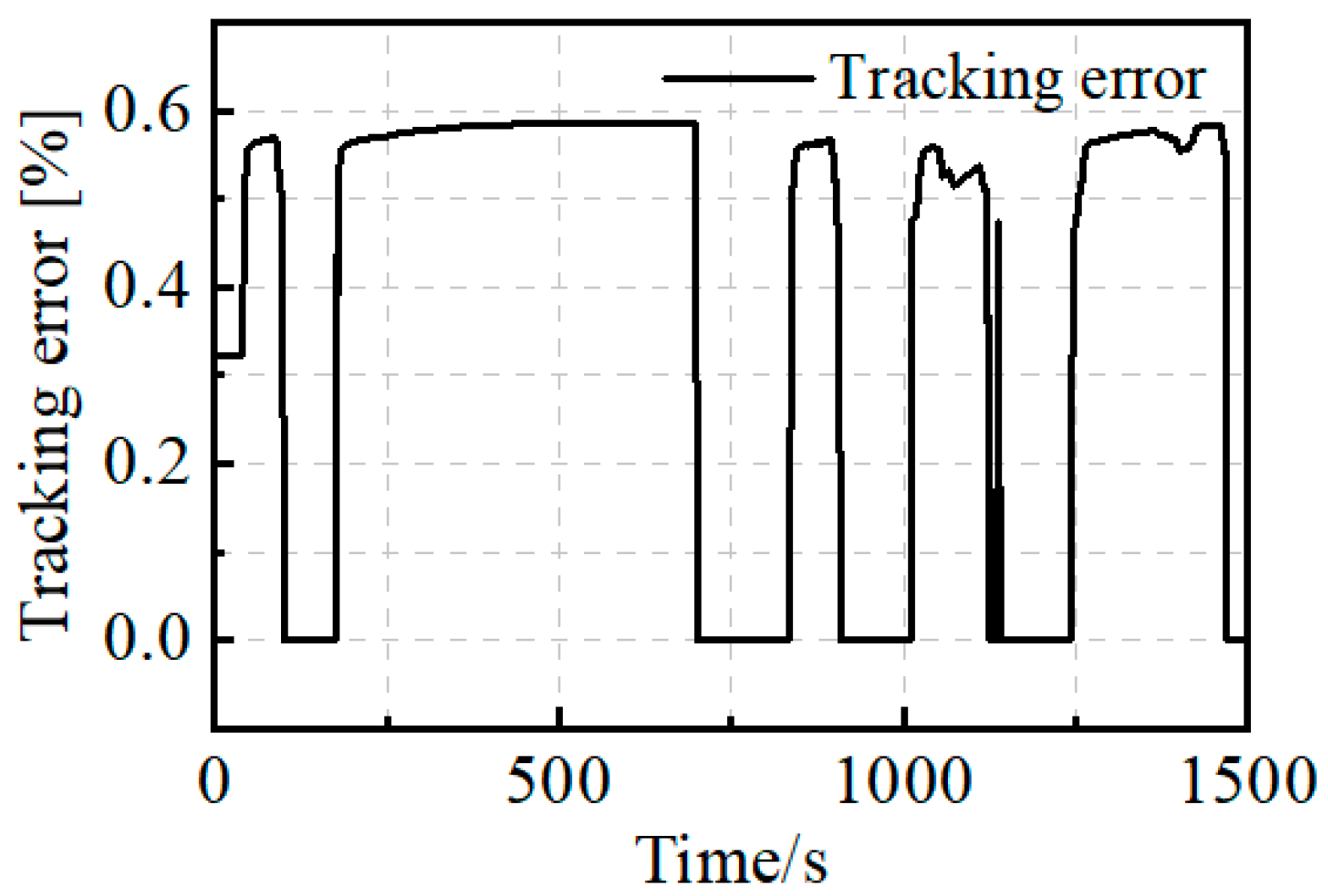
5.1. System Dynamic Performance
5.2. Battery Degradation Rate
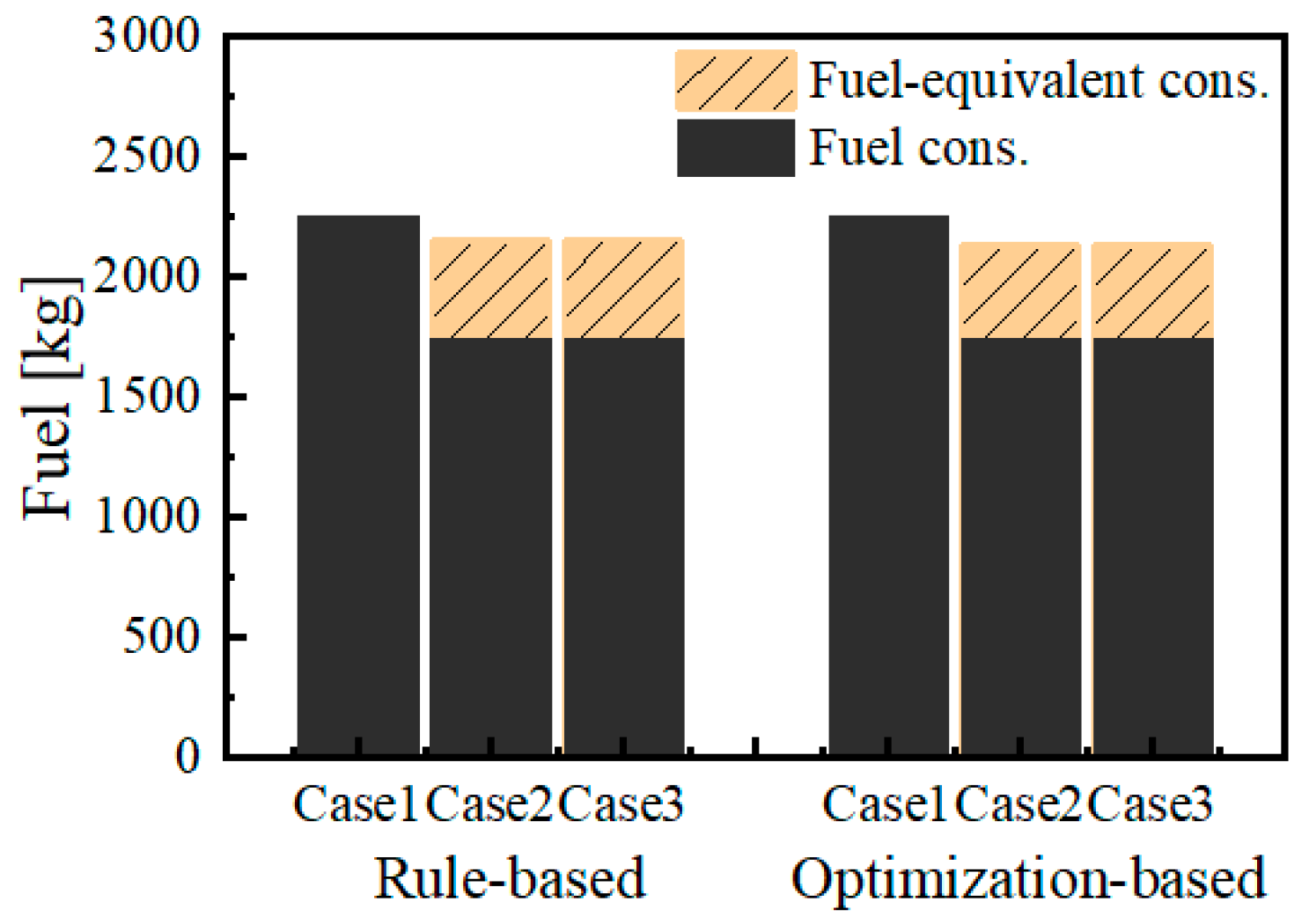
5.3. Fuel Oil Consumption and Emission
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| IMO | International Maritime Organization |
| ESS | Energy storage system |
| HESS | Hybrid energy storage system |
| SC | Supercapacitor |
| EMS | Energy management strategy |
| DP | Dynamic programming |
| MPC | Model predictive control |
| SOC | State of charge |
| ECM | Equivalent circuit model |
| RC | Resistor–capacitor |
| SFOC | Specific fuel oil consumption |
References
- Theocharis, D.; Pettit, S.; Rodrigues, V.S.; Haider, J. Arctic shipping: A systematic literature review of comparative studies. J. Transp. Geogr. 2018, 69, 112–128. [Google Scholar] [CrossRef]
- Progress of China’s Polar Science and Technology Innovation Work. Available online: https://aoc.ouc.edu.cn/2021/1012/c9821a352702/page.htm (accessed on 12 December 2023).
- Bjørnø, J.; Berg, M.V.D.; Lu, W.J.; Skjetne, R.; Lubbad, R.; Løset, S. Performance quantification of icebreaker operations in ice management by numerical simulations. Cold Reg. Sci. Technol. 2022, 194, 103435. [Google Scholar] [CrossRef]
- Zambon, A.; Moro, L.; Oldford, D. Impact of different characteristics of the ice–propeller interaction torque on the torsional vibration response of a Polar-Class shaftline. Ocean Eng. 2022, 266, 112630. [Google Scholar] [CrossRef]
- Long, F.; Fang, B.; Yang, C. State-of-the-Art of polar icebreaker pod propulsion system. Ship Boat 2023, 34, 154–160. [Google Scholar]
- Lindstad, H.G.; Psaraftis, H.N.; Sandaas, I.; Strømman, A.H. Maritime shipping and emissions: A three-layered, damage-based approach. Ocean Eng. 2015, 110, 94–101. [Google Scholar] [CrossRef]
- IMO Revises Strategy to Achieve Net-Zero Emissions from Global Shipping by 2050. Available online: https://news.un.org/zh/story/2023/07/1119527 (accessed on 9 January 2024).
- Georgescu, I.; Godjevac, M.; Visser, K. Efficiency constraints of energy storage for on-board power systems. Ocean Eng. 2018, 162, 239–247. [Google Scholar] [CrossRef]
- Pang, B.; Liu, S.; Zhu, H.; Feng, Y.; Dong, Z. Real-Time Optimal Control of an LNG-Fueled Hybrid Electric Ship Considering Battery Degradations. Energy 2024, 296, 131170. [Google Scholar] [CrossRef]
- Ghimire, P.; Zadeh, M.; Thapa, S.; Thorstensen, J.; Pedersen, E. Operational Efficiency and Emissions Assessment of Ship Hybrid Power Systems with Battery; Effect of Control Strategies. IEEE Trans. Transp. Electrif. 2024, 1. Available online: https://ieeexplore.ieee.org/document/10433233 (accessed on 27 June 2024). [CrossRef]
- Huang, J.; An, Q.; Zhou, M.; Tang, R.; Dong, Z.; Lai, J.; Li, X.; Yang, X.G. A self-adaptive joint optimization framework for marine hybrid energy storage system design considering load fluctuation characteristics. Appl. Energy 2024, 361, 122973. [Google Scholar] [CrossRef]
- Ostadi, A.; Kazerani, M. A comparative analysis of optimal sizing of battery-only, ultracapacitor-only, and battery-ultracapacitor hybrid energy storage systems for a city bus. IEEE Trans. Veh. Technol. 2014, 64, 4449–4460. [Google Scholar] [CrossRef]
- Inal, O.B.; Charpentier, J.F.; Deniz, C. Hybrid power and propulsion systems for ships: Current status and future challenges. Renew. Sustain. Energy Rev. 2022, 156, 111965. [Google Scholar] [CrossRef]
- Hou, J.; Sun, J.; Hofmann, H. Adaptive model predictive control with propulsion load estimation and prediction for all-electric ship energy management. Energy 2018, 150, 877–889. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Deng, J.; Dorrell, D.G. Multi-objective optimal sizing of hybrid energy storage system for electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 1027–1035. [Google Scholar] [CrossRef]
- Yan, D.; Lu, L.; Li, Z.; Feng, X.; Ouyang, M.; Jiang, F. Durability comparison of four different types of high-power batteries in HEV and their degradation mechanism analysis. Appl. Energy 2016, 179, 1123–1130. [Google Scholar] [CrossRef]
- Zou, C.F.; Zhang, L.; Hu, X.S.; Wang, Z.P.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Acanfora, M.; Balsamo, F.; Fantauzzi, M.; Lauria, D.; Proto, D. Design of an electrical energy storage system for hybrid diesel electric ship propulsion aimed at load levelling in irregular wave conditions. Appl. Energy 2023, 350, 121728. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Diao, L.J.; Pei, H.Y.; Ma, X.N.; Liu, S.Y.; Zhang, S.H.; Du, H.Q.; Xu, C.M. A GRNN informed ECMS-ALPF operational management strategy for reducing fuel consumption of diesel/battery/supercapacitor hybrid vehicles. Ocean Coast. Manag. 2023, 245, 106838. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Zhang, J.K.; Zhou, M.; Wang, T.; Tan, X.; Lai, J.; Yang, X.G. An adaptive multi-objective joint optimization framework for marine hybrid energy storage system design considering energy management strategy. J. Energy Storage 2023, 68, 107689. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Wang, B. Tri-Objective optimal design of a hybrid electric propulsion system for a polar mini-cruise ship. Ocean Eng. 2024, 300, 117355. [Google Scholar] [CrossRef]
- Tona, G.L.; Luna, M.; Piazza, M.C.; Pietra, A. Energy management system for efficiency increase in cruise ship microgrids. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Geertsma, R.D.; Negenborn, R.R.; Visser, K.; Hopman, J.J. Design and control of hybrid power and propulsion systems for smart ships: A review of development. Appl. Energy 2017, 194, 30–54. [Google Scholar] [CrossRef]
- Antonopoulos, S.; Visser, K.; Kalikatzarakis, M.; Reppa, V. MPC framework for the energy management of hybrid ships with an energy storage system. J. Mar. Sci. Eng. 2021, 9, 993. [Google Scholar] [CrossRef]
- Wang, C.; He, H.; Zhang, Y.; Mu, H. A comparative study on the applicability of ultracapacitor models for electric vehicles under different temperatures. Appl. Energy 2017, 196, 268–278. [Google Scholar] [CrossRef]
- Hou, J.; Song, Z.; Hofmann, H.; Sun, J. Adaptive model predictive control for hybrid energy storage energy management in all-electric ship microgrids. Energy Conver. Manag. 2019, 198, 111929. [Google Scholar] [CrossRef]
- Lu, W.; Zhi, L. On Power Grid Architecture of Heavy Icebreakers. Ship Boat 2023, 34, 129–136. [Google Scholar]
- Zhai, Y. Optimal Configuration and Simulation Research on Management Strategy of Hybrid Power System. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Belyaev, M.E.; Gerasimov, D.N.; Rymalis, M.R.; Semenov, S.A. Design of diesel engine mathematical model oriented to speed control. J. Comput. Syst. Sci. Int. 2018, 57, 626–639. [Google Scholar] [CrossRef]
- IMO. Third IMO Greenhouse Gas Study 2014. Executive Summary and Final Report; International Maritime Organization: London, UK, 2015; pp. 176–178. Available online: https://greenvoyage2050.imo.org/wp-content/uploads/2021/01/third-imo-ghg-study-2014-executive-summary-and-final-report.pdf (accessed on 12 November 2023).
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Zhu, T.; Wills, R.G.; Lot, R.; Kong, X.D.; Yan, X.D. Optimal sizing and sensitivity analysis of a battery-supercapacitor energy storage system for electric vehicles. Energy 2021, 221, 119851. [Google Scholar] [CrossRef]
- Lagnoni, M.; Scarpelli, C.; Lutzemberger, G.; Bertei, A. Critical comparison of equivalent circuit and physics-based models for lithium-ion batteries: A graphite/lithium-iron-phosphate case study. J. Energy Storage 2024, 94, 112326. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.C.; Dorrell, D.G. A Review of Supercapacitor Modelling, Estimation, and Applications: A Control/Management Perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.J.; Chen, Z.H.; Ling, Q. A variable capacitance-based modeling and power capability predicting method for ultracapacitor. J. Power Sources 2018, 374, 121–133. [Google Scholar] [CrossRef]
- Ovrum, E.; Bergh, T.F. Modelling lithium-ion battery hybrid ship crane operation. Appl. Energy 2015, 152, 162–172. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Q.; Gao, D.; Shi, W.; Yu, W. Two-level model predictive control energy management strategy for hybrid power ships with hybrid energy storage system. J. Energy Storage 2022, 52, 104763. [Google Scholar] [CrossRef]
- Liu, Y.S.; Ee, F.; Feng, H.; Li, Y. Optimization of energy storage capacity of electric propulsion system for icebreaker. J. Shanghai Ship Shipp. Res. Ins. 2016, 39, 47–51. [Google Scholar]
- General-purpose Technology Specification for Energy Storage Cabinet. Available online: https://www.ces.org.cn/res/ces/2307/e7c3fa4d9b82e95caa1916c37da4e866.pdf (accessed on 20 December 2023).
- Santucci, A.; Sorniotti, A.; Lekakou, C. Power split strategies for hybrid energy storage systems for vehicular applications. J. Power Sources 2014, 258, 395–407. [Google Scholar] [CrossRef]
- Nuchturee, C.; Li, T.; Xia, H. Design of cost-effective and emission-aware power plant system for integrated electric propulsion ships. Mar. Sci. Eng. 2021, 9, 684. [Google Scholar] [CrossRef]
- Zhao, J.M. Modeling and Simulation of Soc Estimation for Lithium-Ion Battery Based on Second-Order EKF. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2018. [Google Scholar]






| Types | Formula |
|---|---|
| ESOx = SFOC × 2 × 0.97753 × S% × P × ∆t | |
| ENOx = 44 × n−0.23 × P × ∆t | |
| EPM = [0.23 + SFOC × 7 × 0.02247 × (S% − 0.0024)] × P × ∆t | |
| ECO2 = 3.114 × SFOC × P × ∆t |
| Parameters | Battery | Supercapacitor |
|---|---|---|
| Rated capacity | 1350 mAh | F |
| Rated voltage | 3.20 V | 2.70 V |
| Maximum continuous current | 2.7 A (2C) | 130 A |
| Internal resistance | 84.69 mΩ | 0.29 mΩ |
| SOC | 20%~90% | 20%~90% |
| Case | Overall Configuration | Diesel Generator | Battery | Supercapacitor |
|---|---|---|---|---|
| Case1 | 6 × 8 MW, 2 × 3.5 MW | 5 × 8 MW | − | − |
| Case2 | 5 × 8 MW, 2 × 3.5 MW, battery | 3 × 8 MW, 1 × 3.5 MW | 8000 kWh | − |
| Case3 | 5 × 8 MW, 2 × 3.5 MW, battery and supercapacitor | 3 × 8 MW, 1 × 3.5 MW | 5315 kWh | 46.17 kWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Yi, P.; Wu, S.; Huang, S.; Li, T. Analysis of Impact of Control Strategies on Integrated Electric Propulsion System Performance During Icebreaking Process. J. Mar. Sci. Eng. 2024, 12, 1888. https://doi.org/10.3390/jmse12101888
Li L, Yi P, Wu S, Huang S, Li T. Analysis of Impact of Control Strategies on Integrated Electric Propulsion System Performance During Icebreaking Process. Journal of Marine Science and Engineering. 2024; 12(10):1888. https://doi.org/10.3390/jmse12101888
Chicago/Turabian StyleLi, Liang, Ping Yi, Shen Wu, Shuai Huang, and Tie Li. 2024. "Analysis of Impact of Control Strategies on Integrated Electric Propulsion System Performance During Icebreaking Process" Journal of Marine Science and Engineering 12, no. 10: 1888. https://doi.org/10.3390/jmse12101888
APA StyleLi, L., Yi, P., Wu, S., Huang, S., & Li, T. (2024). Analysis of Impact of Control Strategies on Integrated Electric Propulsion System Performance During Icebreaking Process. Journal of Marine Science and Engineering, 12(10), 1888. https://doi.org/10.3390/jmse12101888







