TG-PGAT: An AIS Data-Driven Dynamic Spatiotemporal Prediction Model for Ship Traffic Flow in the Port
Abstract
1. Introduction
- Aiming at the cyclical patterns and dynamic spatiotemporal dependence features of ship traffic flow in the port, a multidimensional spatiotemporal feature fusion model is constructed to tap the spatiotemporal dynamic influence and interdependence of ship traffic flow. The model can accurately capture the spatiotemporal dependencies of different nodes in the port, enabling precise predictions of traffic flow with significant spatiotemporal changes in complex navigational environments.
- The TCN and BiGRU models are employed to extract temporal features from ship traffic flow, significantly enhancing the performance of the model in the time learning module. Based on GAT, spatial features in ship traffic flow are extracted by utilizing the spatial correlation coefficient matrix and traffic flow matrix, enhancing the model’s capability to model node relationships and features.
- Based on the historical AIS data from the port, the performance of the constructed model is evaluated comparatively. The results show that the TG-PGAT model has higher accuracy, robustness, and anti-interference capability, enabling the prediction and analysis of ship traffic flow dynamics in the port.
2. Materials and Methods
2.1. Problem Description
2.1.1. Construction of Ship Traffic Map in the Port
2.1.2. Analysis of Spatiotemporal Features of Ship Traffic Flow in the Port
- Temporal Feature Analysis
- Spatial Feature Analysis
2.2. Model Construction
2.2.1. Model Input
2.2.2. Spatial Feature Extraction Module
- The Calculation of Spatial Attention Coefficient of Ship Traffic Flow in the Port
- Node Correlation Calculation of Ship Traffic Flow in the Port
- Fusion of Local Spatial Attention Features and Global Node Correlation Features
2.2.3. Temporal Feature Extraction Module
- Local Time-series Feature Extraction of Ship Traffic Flow in the Port
- Global Time-domain Feature Extraction of Ship Traffic Flow in the Port
2.2.4. Feature Fusion Module
3. Experiment
3.1. Experimental Data
3.2. Experimental Setup
3.2.1. Evaluation Indicator Setting
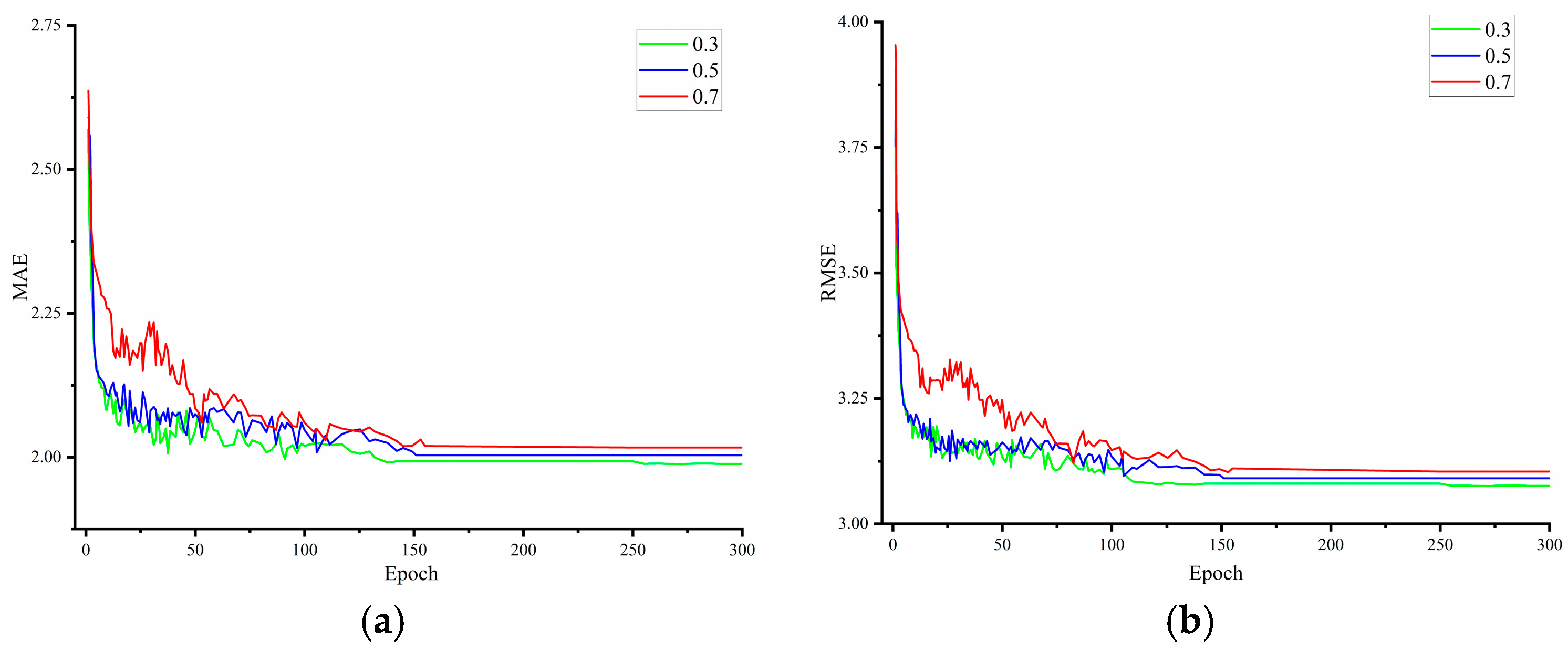
3.2.2. Model Optimization and Parameter Setting
3.3. Model Performance Experiment
3.3.1. Overall Prediction Effect of the Model
3.3.2. Comparative Analysis of Model Performance
3.4. Ablation Experiment
3.5. Robustness Experiment
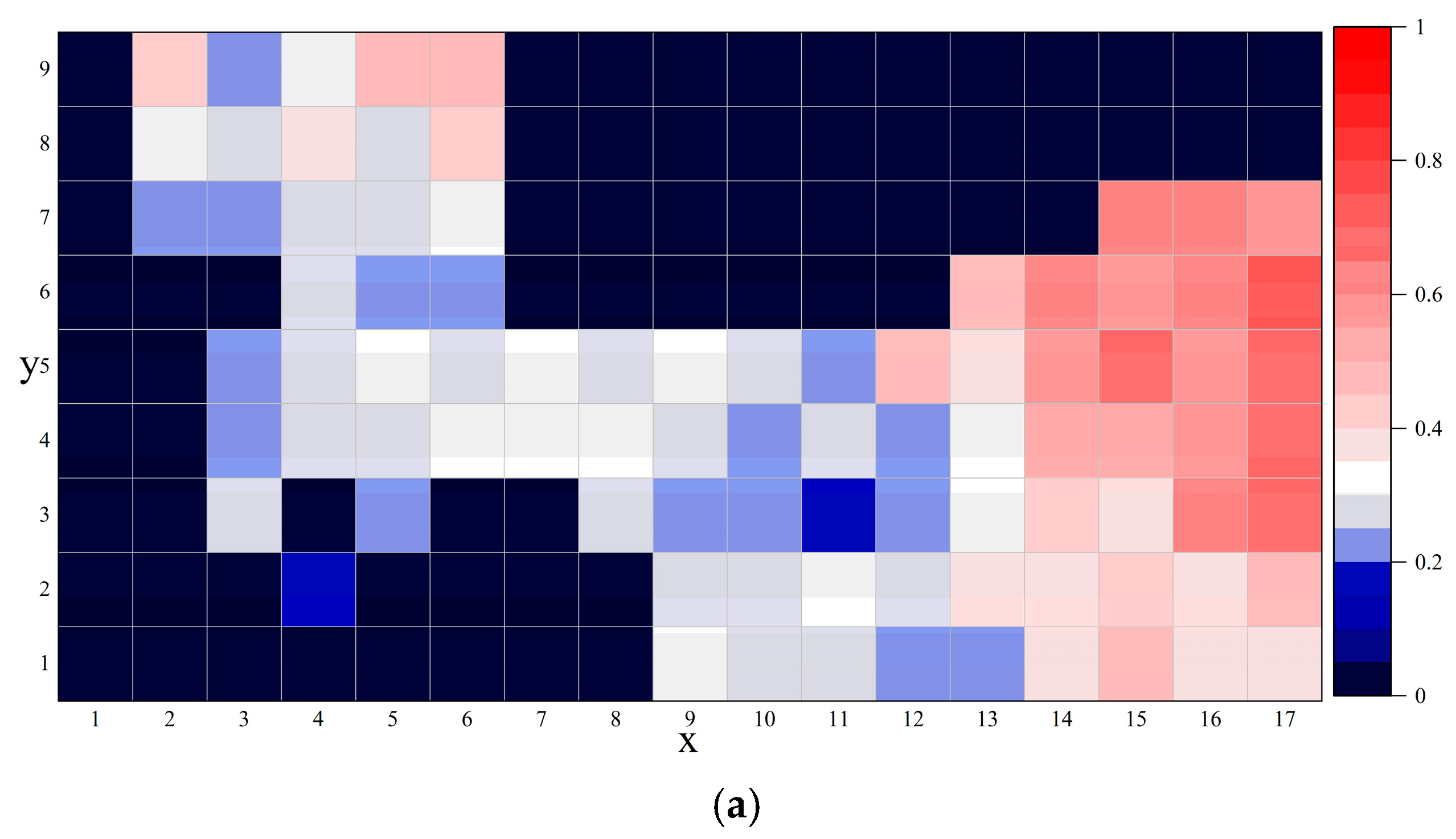
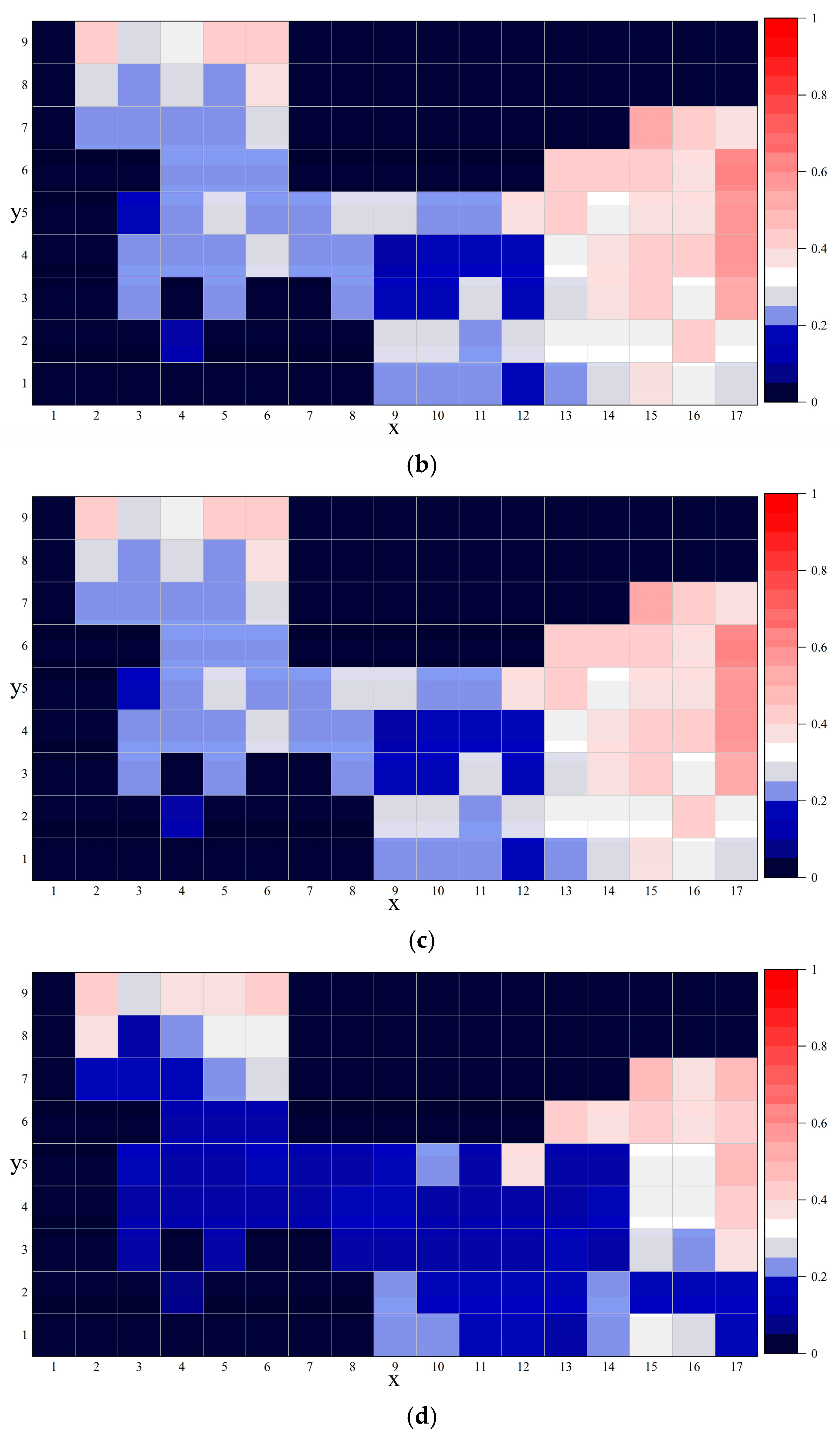
3.6. Visualization Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, W.; Zhong, C.; Sotelo, M.A.; Chu, X.; Liu, X.; Li, Z. Short-term vessel traffic flow forecasting by using an improved Kalman model. Clust. Comput. 2019, 22, 7907–7916. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.; Yang, Y.; Wu, H.; Zhang, W.; Zhao, J.; Xiong, Y. Traffic flow prediction by an ensemble framework with data denoising and deep learning model. Phys. A 2021, 565, 125574. [Google Scholar] [CrossRef]
- Harrou, F.; Dairi, A.; Zeroual, A.; Sun, Y. Forecasting of bicycle and pedestrian traffic using flexible and efficient hybrid deep learning approach. Appl. Sci. 2022, 12, 4482. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, H.; Guo, D.; Lin, Y. Improving airport arrival flow prediction considering heterogeneous and dynamic network dependencies. Inf. Fusion 2023, 100, 101924. [Google Scholar] [CrossRef]
- Yan, X.; Gan, X.; Tang, J.; Zhang, D.; Wang, R. ProSTformer: Progressive space-time self-attention model for short-term traffic flow forecasting. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1–15. [Google Scholar] [CrossRef]
- Zhao, L.; Chang, D.; Zhu, Z.; Gao, Y. Port traffic volume forecast with SARIMA-BP model. Navig. China 2020, 43, 50–55. [Google Scholar]
- Wan, J.; Li, J.; Zhang, S. Prediction model for ship traffic flow considering periodic fluctuation factors. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 1506–1510. [Google Scholar]
- Zissis, D.; Xidias, E.K.; Lekkas, D. Real-time vessel behavior prediction. Evol. Syst. 2016, 7, 29–40. [Google Scholar] [CrossRef]
- Yang, L.; Yang, Q.; Li, Y.; Feng, Y. K-nearest neighbor model based short-term traffic flow prediction method. In Proceedings of the 2019 18th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Wuhan, China, 8–10 November 2019; pp. 27–30. [Google Scholar]
- Chen, E.Y.; Chen, R. Modeling dynamic transport network with matrix factor models: An application to international trade flow. J. Data Sci. 2023, 21, 490–507. [Google Scholar] [CrossRef]
- Zeng, X. Ship traffic flow prediction method based on support vector machine. Ship Sci. Technol. 2023, 45, 160–163. [Google Scholar]
- Han, X.; Liu, C.; Wang, J. Ship traffic flow prediction based on fractional order gradient descent with momentum for RBF neural network. J. Ship. Res. 2021, 65, 100–107. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.; Zhou, Z.; Zhao, J.; Wang, S.; Chen, X. Extracting vessel speed based on machine learning and drone images during ship traffic flow prediction. J. Adv. Transp. 2022, 2022, 3048611. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, M.; Song, K.; Wang, T. Prediction of ship traffic flow and congestion based on extreme learning machine with whale optimization algorithm and fuzzy c-Means clustering. J. Adv. Transp. 2023, 2023, 7175863. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Y.; Qi, Y.; Shu, F.; Wang, Y. Short-term traffic flow prediction based on spatio-temporal analysis and CNN deep learning. Transp. A Transp. Sci. 2019, 15, 1688–1711. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, X.; Ding, Z.; Zhao, J. An approach to ship behavior prediction based on AIS and RNN optimization model. Int. J. Transp. Eng. Technol. 2020, 6, 16. [Google Scholar]
- Lee, E.; Khan, J.; Son, W.-J.; Kim, K. An efficient feature augmentation and LSTM-based method to predict maritime traffic conditions. Appl. Sci. 2023, 13, 2556. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, Q. Ship traffic flow prediction in wind farms water area based on spatiotemporal dependence. J. Mar. Sci. Eng. 2022, 10, 295. [Google Scholar] [CrossRef]
- Li, Y.; Liang, M.; Li, H.; Yang, Z.; Du, L.; Chen, Z. Deep learning-powered vessel traffic flow prediction with spatial-temporal attributes and similarity grouping. Eng. Appl. Artif. Intell. 2023, 126, 107012. [Google Scholar] [CrossRef]
- El Mekkaoui, S.; Benabbou, L.; Caron, S.; Berrado, A. Deep learning-based ship speed prediction for intelligent maritime traffic management. J. Mar. Sci. Eng. 2023, 11, 191. [Google Scholar] [CrossRef]
- Ding, R.; Xie, H.; Dai, C.; Qiao, G. Research on ship traffic flow prediction based on GTO-CNN-LSTM. In Proceedings of the Seventh International Conference on Traffic Engineering and Transportation System (ICTETS 2023), Dalian, China, 22–24 September 2023; pp. 62–69. [Google Scholar]
- Ma, Q.; Du, X.; Liu, C.; Jiang, Y.; Liu, Z.; Xiao, Z.; Zhang, M. A hybrid deep learning method for the prediction of ship time headway using automatic identification system data. Eng. Appl. Artif. Intell. 2024, 133, 108172. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Mei, Q.; Wang, P.; Hu, W.; Wang, Z.; Xie, W.; Yang, Y.; Chen, Y. Research on multi-port ship traffic prediction method based on spatiotemporal graph neural networks. J. Mar. Sci. Eng. 2023, 11, 1379. [Google Scholar] [CrossRef]
- Li, L.; Pan, M.; Liu, Z.; Sun, H.; Zhang, R. Semi-dynamic spatial–temporal graph neural network for traffic state prediction in waterways. Ocean Eng. 2024, 293, 116685. [Google Scholar] [CrossRef]
- Man, J.; Chen, D.; Wu, B.; Wan, C.; Yan, X. An effective approach for Yangtze river vessel traffic flow forecasting: A case study of Wuhan area. Ocean Eng. 2024, 296, 116899. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Okwonu, F.Z.; Asaju, B.L.; Arunaye, F.I. Breakdown analysis of pearson correlation coefficient and robust correlation methods. In Proceedings of the International Conference on Technology, Engineering and Sciences (ICTES), Penang, Malaysia, 17–18 April 2020; p. 012065. [Google Scholar]
- Li, H.; Xing, W.; Jiao, H.; Yang, Z.; Li, Y. Deep bi-directional information-empowered ship trajectory prediction for maritime autonomous surface ships. Transp. Res. Part E Logist. Transp. Rev. 2024, 181, 103367. [Google Scholar] [CrossRef]
- Zhang, D.; Li, X.; Wan, C.; Man, J. A novel hybrid deep-learning framework for medium-term container throughput forecasting: An application to China’s Guangzhou, Qingdao and Shanghai hub ports. Marit. Econ. Logist. 2024, 26, 44–73. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 3 May 2018; pp. 1–12. [Google Scholar]
- Lea, C.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal convolutional networks: A unified approach to action segmentation. In Proceedings of the Computer Vision–ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10 October 2016; pp. 47–54. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, X.; Hu, Y.; Duan, F.; Guo, K.; Wang, B.; Gao, J.; Yin, B. Dual dynamic spatial-temporal graph convolution network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23680–23693. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, S.; Deng, L.; Jia, M.; Xu, J. Ship motion attitude prediction model based on IWOA-TCN-Attention. Ocean Eng. 2023, 272, 113911. [Google Scholar] [CrossRef]
- Luo, P.; Wang, B.; Tian, J. TTSAD: TCN-Transformer-SVDD Model for Anomaly Detection in air traffic ADS-B data. Comput. Secur. 2024, 141, 103840. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, S.; Yan, L.; Feng, J.; Xia, Y. A hybrid-convolution spatial–temporal recurrent network for traffic flow prediction. J. Comput. 2024, 67, 236–252. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Chen, H.; Zhao, Y.; Wang, H. A TDV attention-based BiGRU network for AIS-based vessel trajectory prediction. iScience 2023, 26, 106383. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, T.; Peng, X.; Ren, J.; Liang, S. An AIS-based deep learning model for multi-task in the marine industry. Ocean Eng. 2024, 293, 116694. [Google Scholar] [CrossRef]
- Allen, D.M. Mean square error of prediction as a criterion for selecting variables. Technometrics 1971, 13, 469–475. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Meyer, G.P. An alternative probabilistic interpretation of the huber loss. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 5261–5269. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the 19th International Conference on Computational Statistics (COMPSTAT), Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012. [Google Scholar] [CrossRef]
- Zhao, W.; Gao, Y.; Ji, T.; Wan, X.; Ye, F.; Bai, G. Deep temporal convolutional networks for short-term traffic flow forecasting. IEEE Access 2019, 7, 114496–114507. [Google Scholar] [CrossRef]



















| Module | Model | Parameter | Value |
|---|---|---|---|
| Feature Decomposition | VMD | K | 5 |
| Temporal Feature Extraction | TCN | L | 4 |
| k | 5 | ||
| d | 1, 2, 4, 8, 16 | ||
| BiGRU | Hidden Layer Neurons | 64 | |
| Spatial Feature Extraction | GAT | Number of Layers | 3 |
| Number of Attention Heads | 4 |
| Prediction Methods | Characteristics | Literature | |
|---|---|---|---|
| Traditional Statistical Models | ARIMA | It has a good effect on predicting long-term traffic flow with obvious trends and seasonality but cannot handle the nonlinear characteristics of traffic flow. | [6] |
| KF | It can effectively address the nonstationary characteristics of traffic flow time series and has good performance in short-term traffic flow prediction. | [1] | |
| Classical Machine Learning Methods | SVM | It can capture the complex nonlinear relationships in traffic flow data, but the parameter settings significantly impact the prediction results. | [11] |
| KNN | As a nonparametric learning method, it cannot uncover the periodic characteristics of traffic flow. | [9] | |
| Deep Learning Models | CNN | It can capture spatial correlations by using multiple layers of convolution and nonlinear activation functions. | [15] |
| TCN | It captures local temporal dependencies in time-series data through convolution operations and is sensitive to hyperparameters and data noise. | [45] | |
| GRU | It effectively solves the gradient vanishing or explosion problem that traditional RNNs encounter when processing long sequences, thereby being able to capture long-term dependencies in traffic flow data. | [18] | |
| Data-Driven Spatiotemporal Fusion Models | CNN-LSTM | It can simultaneously extract the spatial and temporal features of traffic flow data, achieving a deep integration of spatiotemporal features. | [21] |
| Semi-Dynamic Spatial–Temporal GNN (SDSTGNN) | It can effectively extract the spatiotemporal features of channel traffic flow by integrating GNN, LSTM, and Transformer. | [24] | |
| Spatial-Temporal Attention Bidirectional LSTM (STA-BiLSTM) | It can achieve spatiotemporal traffic flow prediction in inland waters by combining GAT and BiLSTM models. | [25] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Zhou, Y.; Chang, Y.; Zhu, Z.; Liu, G.; Chen, Z. TG-PGAT: An AIS Data-Driven Dynamic Spatiotemporal Prediction Model for Ship Traffic Flow in the Port. J. Mar. Sci. Eng. 2024, 12, 1875. https://doi.org/10.3390/jmse12101875
Ma J, Zhou Y, Chang Y, Zhu Z, Liu G, Chen Z. TG-PGAT: An AIS Data-Driven Dynamic Spatiotemporal Prediction Model for Ship Traffic Flow in the Port. Journal of Marine Science and Engineering. 2024; 12(10):1875. https://doi.org/10.3390/jmse12101875
Chicago/Turabian StyleMa, Jianwen, Yue Zhou, Yumiao Chang, Zhaoxin Zhu, Guoxin Liu, and Zhaojun Chen. 2024. "TG-PGAT: An AIS Data-Driven Dynamic Spatiotemporal Prediction Model for Ship Traffic Flow in the Port" Journal of Marine Science and Engineering 12, no. 10: 1875. https://doi.org/10.3390/jmse12101875
APA StyleMa, J., Zhou, Y., Chang, Y., Zhu, Z., Liu, G., & Chen, Z. (2024). TG-PGAT: An AIS Data-Driven Dynamic Spatiotemporal Prediction Model for Ship Traffic Flow in the Port. Journal of Marine Science and Engineering, 12(10), 1875. https://doi.org/10.3390/jmse12101875







