Abstract
An approach combining the stochastic resonance, the harmonic wavelet packet transforms and the probability density function was proposed to obtain the early fault signal of a rolling bearing. Firstly, an adaptive variable-scale stochastic resonance was employed to detect the frequency range of the rolling bearing’s fault signal based on the improved signal-to-noise ratio, and then the harmonic wavelet packet transforms and the probability density function were utilized to extract and identify the fault signal of the rolling bearings from the detected signals. The case studies show that the proposed method can effectively obtain the early fault signals of the outer race, inner race and rolling element in the rolling bearings despite not knowing the frequency band distribution, and that the early fault diagnosis of the rolling bearings can be achieved.
1. Introduction
The rolling bearing stands as a pivotal component across a broad spectrum of machinery, exerting a direct impact on the operational safety within industrial settings. Statistical data reveal that rolling bearing failures account for approximately 20% of gearbox malfunctions, 30% of rotating machinery breakdowns and 40% of motor failures [1]. Consequently, ensuring the safe and reliable functioning of mechanical systems necessitates the implementation of fault diagnosis and condition monitoring for rolling bearings.
In the course of rolling bearing operation, if a working surface of a bearing element is damaged, the impact response will be evoked. Research shows that the impact response carries important information for bearing fault diagnosis and the faults of inner races, outer races, rolling elements and cages in a rolling bearing can be identified by the impact response [2]. However, due to the low energy of an early weak impact and the frequency instability caused by variable operating conditions, it is still a great challenge to extract the impact response from the collected signals. Despite the great number of methods proposed for extracting the impact response with a certain specific frequency bandwidth [3], there is a notable lack of studies that present a clearly optimal analysis method for identifying early bearing faults under variable speed conditions. Therefore, how to obtain the early fault signals of rolling bearings from the collected signals without knowing its exact frequency distribution remains a problem that requires further study.
Over the past few years, a multitude of signal processing techniques have been incorporated into the field of fault diagnosis for rolling element bearings, aiming to mitigate the noise embedded within signals and thereby facilitate the extraction of fault-related features [4]. These methodologies encompass a range of approaches, including wavelet decomposition (WD) [5], singular value decomposition (SVD) [6], spectral kurtosis (SK) [7], morphological filtering (MF) [8] and minimum entropy deconvolution (MED) [9], among others. Compared with these methods, stochastic resonance (SR) has attracted more attention for its applicability for weak signal detection. Zhao et al. [10] combined SR with a demodulation method to extract feature signals. Liu et al. [11] employed monostable SR to enhance the fault features of underwater robot thrusters. While the aforementioned SR method effectively optimizes individual parameters, it notably neglects the interactions between different parameters. This approach, although useful in certain contexts, may potentially limit the comprehensive understanding and optimization of the overall system. Researchers used optimization algorithms to synchronize multiple parameters in the SR system for better output performance. Wang et al. applied the adaptive monostable SR method to realize the weak signal detection of the time grid sensor [12]. Liang et al. proposed a new SR method based on the fast artificial fish swarm algorithm to solve the problem of a slow convergence speed of adaptive parameter-induced SR weak signal detection [13]. Although the evaluation indicators like signal-to-noise ratio (SNR) [14], the spectral amplification factor (SAF) [15] and weighted power spectral kurtosis (WPSK) [16] provide valuable metrics for assessing adaptive SR methods, they share a notable drawback. Specifically, these indicators rely on prior knowledge of the fault feature frequency, which can be a significant obstacle to their broad application and overall efficacy. This prerequisite can potentially hinder the widespread application and effectiveness of these evaluation indicators, especially in scenarios where such prior knowledge is not available or reliable. To address this issue, in this study, an adaptive SR based on the improved signal-to-noise ratio (ISNR) was employed to detect the frequency range of the rolling bearings fault characteristic signal, which does not require prior knowledge of specific frequencies and only needs to search within a known frequency range to detect the fault characteristic signals [17].
Although SR is favored in weak signal detection, the identification of fault characteristic signals is challenging when relying solely on SR. As the damage point traverses the surface of the bearing element, a sudden impact pulse force is generated. This broadband signal invariably encompasses the natural vibration frequency and resonance of the mechanical system. It can be seen that the feature frequencies detected by the adaptive SR may be both the fault feature signals and the inherent vibration and resonance signals of the system. Therefore, it is necessary to extract the detected signal and analyze its properties. Harmonic wavelet packet transforms (HWPT) can decompose vibration signals into equal and independent frequency bands without redundancy, refine the frequency band of the target signal and then extract signals within a certain frequency range. Qin et al. [18] employed an enhanced version of the continuous HWPT method to derive energy values indicative of diverse fault characteristics from the decomposed frequency subbands. Chen et al. [19] used the improved continuous HWPT decomposition method to decompose and reconstruct the composite fault signal to obtain the corresponding single-point fault signal. After extracting the detected periodic signal, it is necessary to identify whether the frequency component is a fault signal. Given that both harmonic responses and natural frequency responses exhibit periodic characteristics, differentiating between them based solely on time-domain waveforms and spectral analysis presents a significant challenge. To overcome this limitation, the statistical attributes inherent in harmonic responses and natural frequencies are leveraged [20]. More specifically, through the application of the probability density function (PDF), it becomes feasible to differentiate between natural frequencies and signals indicative of faults within the extracted periodic signal.
In summary, a fault diagnosis approach for a roller bearing based on the SR, the HWPT and the PDF is put forward in this study. First, adaptive SR based on the ISNR was employed to detect the frequency range of the rolling bearings fault signal, also based on the ISNR. Then, the HWPT and the PDF were utilized to extract and identify the fault signal of the rolling bearings from the detected signals. In order to verify the effectiveness of the proposed method, taking the rolling bearings of the motor as an example, its faults from inner races, outer races and rolling elements were discussed.
2. Proposed Method
As illustrated in Figure 1, the workflow proposed in this study comprises three primary methodologies: detection, extraction and identification processes.
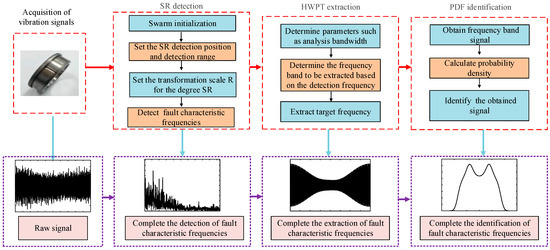
Figure 1.
Overall workflow diagram.
2.1. Detection of Fault Signals
SR is a phenomenon wherein weak fault signals and noise signals interact under specific nonlinear conditions, leading to the transfer of noise energy to fault signals and thereby enhancing the fault signals. The following are the commonly employed SR models:
where x represents the system output. U(x) is a nonlinear bistable potential function, U(x) = −(ax2/2) + (bx4/4), where a and b are the system parameters. s(t) denotes a weak periodic signal, whereas n(t) signifies Gaussian white noise.
The SNR of the SR output is influenced by the system parameters a and b in Equation (1) and the noise intensity, which subsequently impact the detection performance of the weak periodic signal. Adjusting the system parameters and noise intensity can achieve the optimal SNR. In the fault detection of rolling bearings, the noise intensity is typically fixed. To ensure the maximum SNR, the optimal solution for the system parameters a and b is frequently employed. Utilizing the global optimization capability of the particle swarm optimization algorithm [21], the system parameters a and b of SR are optimized to achieve the most efficient SR. Figure 2 displays the specific steps of the particle swarm optimization algorithm.
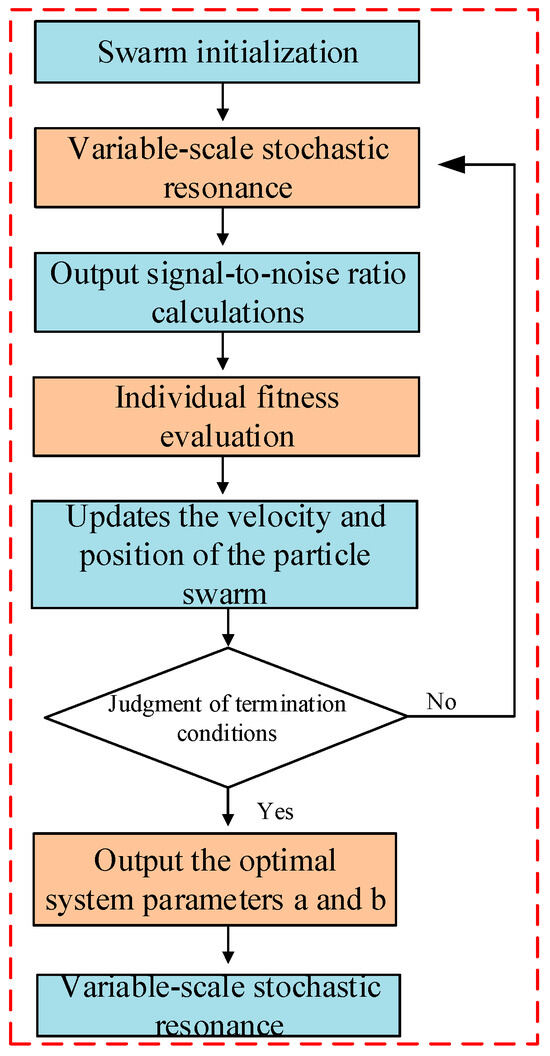
Figure 2.
Process diagram of variable-scale SR optimized by particle swarm optimization.
Step 1: The particle positions x and velocities v are initialized, where each particle position x corresponds to a specific set of SR system parameters a and b and the velocity v represents the update step for the position x.
Step 2: Secondary sampling pretreatment is performed on the vibration signal; the frequency transformation scale R is set and the large parameter signal is converted into a low-frequency signal that satisfies the small parameter requirements of the SR system.
Step 3: The position x and the preprocessed vibration signal are introduced into the SR system. The SNR of the system output serves as the fitness function. The fitness value for each particle is determined through the application of Equation (2). The particle with the highest fitness value within its own set is designated as the individual optimal value (pbest), while the particle with the highest fitness value across the entire population is designated as the population optimal value (gbest).
where S(f0) is the fault signal power of the rolling bearing; N(f0) is the background noise power of rolling bearing fault signal.
Step 4: The velocities and positions of all of the particles are updated in accordance with Equations (3) and (4).
where w is inertia weight; c1 and c2 are learning factors; r1 and r2 are random numbers on [0, 1]; d is the maximum evolution algebra; i = 1, 2, ⋯, n; and n is the population number.
Step 5: The fitness value of each particle is calculated following the update. The individual and population optimal values are updated by comparing them with the respective optimal values of the previous generation of particles. Subsequently, it is determined whether the current iteration number has reached the maximum evolution algebra. If the end conditions are met, the optimal system parameters a and b are directly outputted. If not, the process returns to the previous step.
Step 6: Once the vibration signal has been converted into a small parameter signal via the frequency transformation scale R, the optimal system parameters a and b, along with the vibration signal, are introduced into the SR system to facilitate the detection of the rolling bearing fault signal.
The fitness function SNR, as mentioned in the particle swarm optimization algorithm, is commonly employed to evaluate the SR output. Nevertheless, this indicator poses a significant challenge, requiring prior knowledge of the rolling bearings’ fault frequency. In practical scenarios, determining the accurate fault frequency beforehand is challenging due to unstable and variable operating conditions, rendering the traditional SNR unusable. Consequently, the ISNR indicator is employed to detect unknown fault frequencies. The representation of ISNR is
where ft is the theoretical fault frequency, kt is the digital index corresponding to ft, |X(∙)| represents the amplitude value after the Fourier transform and S(ft) represents the total energy in the interval [ft − lΔf, ft + lΔf] centered at ft. The value of l is determined based on the sampling frequency fs and the number of sampling points N. Δf is the frequency resolution of the output signal and S(ft) is the total energy within a neighborhood of the theoretical fault frequency. N(ft) represents the total noise energy excluding S(ft), where N represents the number of sampling points.
According to Equation (5), prior knowledge of the accurate fault frequency is not required. It suffices to employ SR to search within a known frequency range for detecting the accurate fault frequency. To assess the feasibility of the aforementioned method, a set of simulated input signals u(t) was generated, expressed as follows:
The simulated signal comprises Gaussian white noise and a sinusoidal signal with an amplitude of A0 = 0.3, a frequency of f0 = 40 Hz and a noise intensity of D = 9.1. The simulated data acquisition parameters include a sampling frequency of fs = 2000 Hz and a total of N = 4000 sampling points. Figure 3 presents both the time-domain waveform and the corresponding spectrum of the simulated signal. As depicted in Figure 3a, the time-domain waveform of the simulated signal lacks periodic characteristics and the detected periodic signal is not evident. Figure 3b indicates that the frequency components of the simulated signal are complex, with varying amplitudes, making it challenging to identify the detected periodic signal.
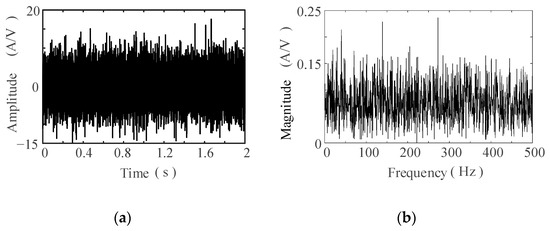
Figure 3.
Simulation signals: (a) waveform; (b) spectrum.
Subsequently, the SR technique was employed to process the simulated signal. To attain the optimal performance of the PSO algorithm, its parameters were empirically configured as detailed below: the swarm consisted of 50 particles, with a maximum iteration count set at 150. The particles’ maximum search velocity was capped at 20% of the maximum adjustment step size. The parameter l was assigned a value of 4, corresponding to a frequency search interval spanning 38 Hz to 42 Hz. Both parameters a and b were confined to a search range of [0.1, 10] while the solution precision was set to 1 × 10−5; the frequency transformation scale R was established at 250. Figure 4 displays the output of the variable-scale SR system. Notably, Figure 4b reveals a pronounced detected frequency component.
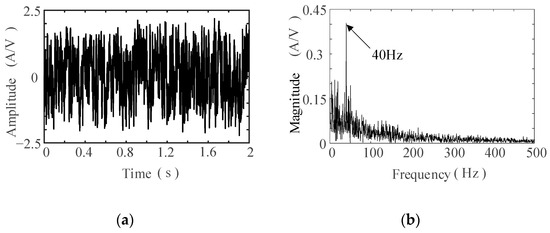
Figure 4.
SR output signals: (a) waveform; (b) spectrum.
2.2. Extraction of Fault Signals
To extract the detected frequency component, the HWPT is utilized. The frequency domain decomposition diagram of the HWPT is presented in Figure 5.
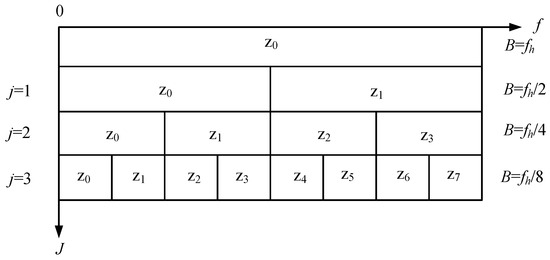
Figure 5.
Frequency domain decomposition of HWPT.
Firstly, the HWPT’s decomposition layer numbers j (j = 0, 1, 2, 3, …) are ascertained. Following this, the bandwidth B corresponding to each layer j can be expressed as
where fh represents the highest frequency component to be analyzed within the signal. The variables m and n are utilized to denote the higher and lower boundaries of the frequency band, respectively.
Using the number of frequency band S and further determining the frequency range of interest (m, n), the harmonic wavelet’s frequency domain expression can be obtained.
Subsequently, the acquired signal x(t) undergoes Fourier transformation to derive its discrete counterparts in the frequency domain. A discrete HWPT’s frequency expression is presented as follows:
where represents the complex conjugate of .
After performing the inverse Fourier transform on Equation (8), in the time domain, the HWPT’s equivalent expression can be obtained.
In this formulation, k serves as the translation parameter, while the ratio k/(m − n) defines the translation step size of the harmonic wavelet. The harmonic wavelet’s general expression in the time domain is denoted by ψm,n and m,n corresponds to the complex conjugate of the harmonic wavelet’s time-domain expression.
Ultimately, through the application of the HWPT, the time-domain signal, denoted as W(m,n,k), corresponds to the interested frequency band (m,n) and can be extracted.
2.3. Identification of Fault Signals
Despite the periodic signals detected by SR, these signals may be the natural frequency components or the harmonic frequency components (fault signals). Therefore, it is very necessary to determine whether the extracted frequency component is a fault signal. Based on the distinctions in the statistical properties observed between natural frequency components and harmonic frequency components, the PDF serves as a means to differentiate the extracted frequency components. The detailed methodology is outlined below:
The response at natural frequencies is represented as a linear combination of responses resulting from various random excitations. The corresponding PDF, designated as P1(x), exhibits an approximate adherence to a Gaussian distribution. This can be formulated as follows:
where μ denotes the average value of the stochastic variable x, whereas σ signifies the standard deviation of the stochastic variable x.
The fault-related frequency component in rolling bearings manifests as a harmonic signal characterized by periodic fluctuations. The associated factor, denoted as P2(x), deviates from a Gaussian distribution and can be articulated as follows:
According to Equations (12) and (13), the PDFs of the resonance response excited by random excitation and the harmonic response due to harmonic excitation are plotted as shown in Figure 6. An inspection of Figure 6 reveals notable distinctions in the shapes of the PDFs for random and harmonic responses. Specifically, the PDF for the random response exhibits a single peak, as depicted in Figure 6a, whereas the PDF for the harmonic response displays two peaks, as displayed in Figure 6b. Consequently, through an analysis of the shape of the PDF of the extracted periodic response signal, it is feasible to identify the fault frequency component and distinguish it from the natural frequency component.
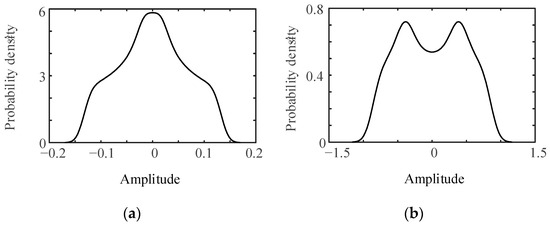
Figure 6.
Probability density curve: (a) random responses; (b) harmonic response.
3. Instance Validation
3.1. Example Introduction
The rolling bearing, as a pivotal element, exerts a profound influence on the motor’s operational performance. In this study, the motor bearing of the injection water pump unit in the offshore platform in Jinzhou City, Liaoning Province, China was taken as an example; as shown in Figure 7, a motor is applied to drive the injection water pump through the coupling. The drive end of the motor is sustained by a combination of a deep-groove ball bearing, specifically model 6219 and a cylindrical roller bearing, model NU219. Conversely, the non-drive end of the motor is supported solely by a cylindrical roller bearing, also model NU219. The principal structural parameters pertaining to these rolling bearings are detailed in Table 1. To monitor the running state of the motor, a vibration monitoring system is used to evaluate the performance of rolling bearings. The vibration measuring points are arranged on both the driving and non-driving end bearing housings. An alarm is triggered by the vibration monitoring system if the measured vibration exceeds a threshold of 5 mm/s.
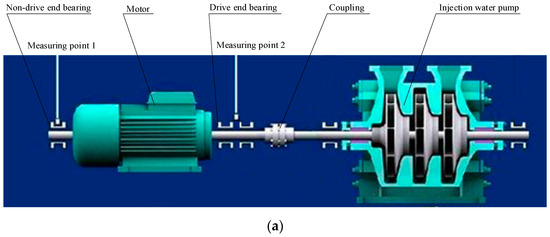

Figure 7.
Injection water pump unit in the offshore platform: (a) schematic diagram; (b) physical layout images.

Table 1.
Main structure parameters of rolling bearing.
After 180 days of continuous operation, the vibration amplitude of the motor drive end increased significantly and approached the warning value of 5 mm/s, which means that the drive-end bearing may begin to fail. To ascertain the underlying reason for the heightened vibration levels, the fault of the rolling bearing was detected utilizing the proposed methodology. For capturing the vibration signals, a triaxial acceleration sensor, specifically the model 356A24 ICP from PCB Piezotronics Company located in New York, NY, USA, was employed. This type of the sensor boasts a sensitivity of 100 mv/g and an operational range of ±50 g. It was positioned to monitor the vibrations of the bearing at the drive end. Additionally, a data acquisition system, the PXIe-1071 model from NI Company located in Austin, TX, USA, was utilized for data collection purposes. In the course of testing, a sampling rate of 2560 Hz was chosen, and a signal consisting of 10,240 data points was recorded at intervals of 60 s. Concurrently, the motor’s operational speed was around 900 r/min, translating to an actual frequency (fr) of approximately 15 Hz. For the ensuing data analysis, the data gathered along the z-axis (vertical direction) were utilized. The vibration signal is processed based on MATLAB R2023b.
The driving end of the motor under test is equipped with NU219 and 6219 bearings, and their structural attributes are outlined in Table 1. Simultaneously, the motor operates at a speed of approximately 900 r/min, which translates to an actual frequency (fr) of roughly 15 Hz. By utilizing the computational formula presented in Table 2, the fault-related characteristic frequency of the bearings was derived and is displayed in Table 3.

Table 2.
Calculation formula of fault characteristic frequency for rolling bearing.

Table 3.
Characteristic frequency of bearing failures.
3.2. Results and Discussion
Under rated operational conditions, the vibration signal’s time-domain waveform and frequency spectrum, captured at the motor drive-end bearing, are depicted in Figure 8 and Figure 9, respectively. Upon inspection, the time-domain waveforms of the vibration signals emanating from the NU219 and 6219 bearings do not exhibit discernible periodic characteristics. Moreover, the frequency components of these vibration signals diverge, with notable disparities in their amplitudes. The signal amplitude proximal to the theoretical characteristic frequency is feeble, rendering it challenging to detect amidst intense background noise. Consequently, identifying the fault frequency of rolling bearings directly from the measured vibration signals is arduous, and ascertaining the faulty bearing, as well as pinpointing its fault location, remains impracticable.
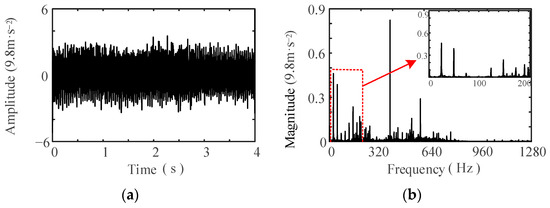
Figure 8.
Vibration signal of NU219 bearing: (a) waveform; (b) spectrum.
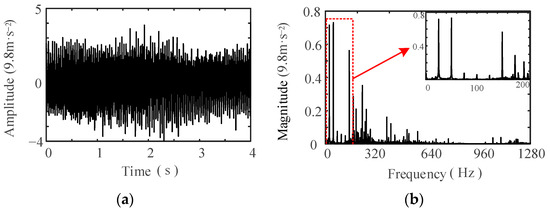
Figure 9.
Vibration signal of 6219 bearing: (a) waveform; (b) spectrum.
3.2.1. Fault Detection of Rolling Element
Utilizing the distinct distribution patterns of rolling element fault frequencies, a particle swarm optimization-based variable-scale SR technique was employed to analyze the vibration signals measured from NU219 and 6219 bearings. This analysis was conducted to identify periodic components within specific frequency ranges: 23.1–25.1 Hz for the NU219 bearings and 39.2–41.2 Hz for the 6219 bearings, respectively. To achieve good optimization results for the PSO algorithm, the PSO algorithm parameters and SR parameters are empirically set as shown in Table 4. Following processing by the SR system, the corresponding time-domain waveforms and their associated frequency spectra of the output signals are able to be depicted; see Figure 10 and Figure 11, respectively. An examination of the time-domain waveforms, presented in Figure 10a and Figure 11a, reveals a notable reduction in noise components within the vibration signals after SR processing. Furthermore, the analysis of the spectrograms in Figure 10b and Figure 11b indicates that, for both the NU219 and 6219 bearings, a distinct frequency component consistently appears in proximity to their respective fault characteristic frequencies, specifically 23.25 Hz and 39 Hz. Therefore, there may be rolling element faults in the NU219 and 6219 bearings.

Table 4.
Parameter setting of particle swarm optimization algorithm.
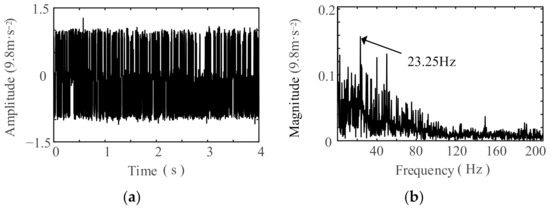
Figure 10.
Output signals from SR systems near the fault frequencies of NU219 rolling elements: (a) waveform; (b) spectrum.
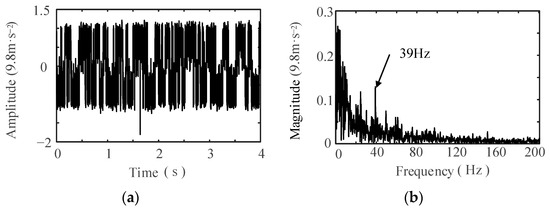
Figure 11.
Output signals from SR systems near the fault frequencies of 6219 rolling elements: (a) waveform; (b) spectrum.
To determine whether the detected frequency components belong to the fault-related frequency of the rolling element within the bearings, HWPT is applied to extract the detected characteristic vibration signals. The specific method is to decompose the vibration signal into 2048 frequency bands using 11 layers, with each band having a bandwidth of 0.625 Hz; for the frequency range of the characteristic signals of NU219 and 6219 bearings, the 37th and 62nd frequency bands were extracted, respectively, and the results are illustrated in Figure 12 and Figure 13. Upon examining Figure 12 and Figure 13, it becomes evident that HWPT is adept at mitigating the interference from extraneous frequency components, thereby enabling the successful isolation of distinct bearing characteristic signals. Nonetheless, the extracted feature signals exhibit periodic characteristics and present as line spectra in the frequency domain, rendering it challenging to differentiate between harmonic signals and natural frequency components.
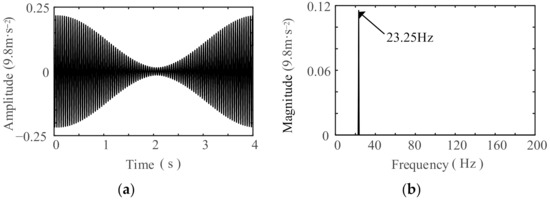
Figure 12.
Signals of NU219 rolling element extracted by HWPT: (a) waveform; (b) spectrum.
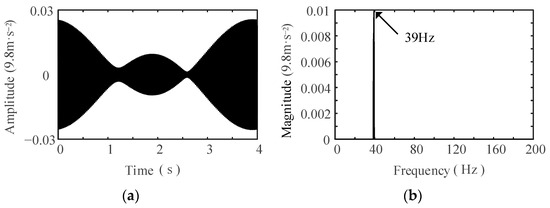
Figure 13.
Signals of 6219 rolling element extracted by HWPT: (a) waveform; (b) spectrum.
To differentiate between the natural frequency and harmonic response within the extracted periodic signal, the PDFs of the extracted periodic signal were computed, as depicted in Figure 14. The results reveal that the PDF of the 23.25 Hz characteristic signal for the NU219 bearing exhibits a bimodal pattern, whereas the probability density curve for the 39 Hz characteristic signal of the 6219 bearing is unimodal. Based on the definition of the PDF provided in Section 2.3, the extracted 23.25 Hz periodic signal represents a harmonic response. Conversely, the 39 Hz periodic signal displays a linear superposition response, suggesting that 39 Hz corresponds to the natural frequency response. This indicates that the periodic response of the NU219 bearing detected by SR is a characteristic signal of its rolling element failure; that is, the rolling elements of the NU219 bearing have faults, while the rolling elements of the 6219 bearing do not exhibit fault characteristics. In addition, there is a certain difference between the fault frequency detected by the rolling bearings and the characteristic frequency of the theoretical faults, mainly due to speed fluctuations under actual working conditions.
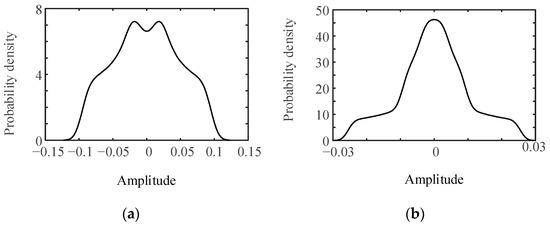
Figure 14.
PDF of periodic frequency extracted from vibration signal of different rolling bearings: (a) NU219 rolling element PDF recognition; (b) 6219 rolling element PDF recognition.
3.2.2. Fault Detection of Outer Ring
The variable-scale SR method based on particle swarm optimization was applied to detect the vibration signals of NU219 and 6219 bearings, according to the distribution characteristics of the fault frequency of the outer ring of the bearing. The periodic components in the frequency range of 84.7–86.7 Hz for the NU219 bearing and 60.5–62.5 Hz for the 6219 bearing were searched for. The parameter selection for SR is based on Table 4.
The time-domain waveform and the frequency spectrum of the signals processed by the SR system are illustrated in Figure 15 and Figure 16, respectively. Upon examining these figures, it is evident that the SR processing effectively attenuated the noise components present in the vibration signals. However, no corresponding frequency components were detected near the outer ring fault-related characteristic frequency of the NU219 and 6219 bearings. Therefore, there are no faults in the outer rings of the NU219 and 6219 bearings.
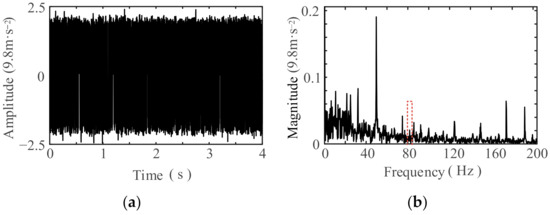
Figure 15.
Output signals of the SR system near the fault frequency of the NU219 outer rings: (a) waveform; (b) spectrum.
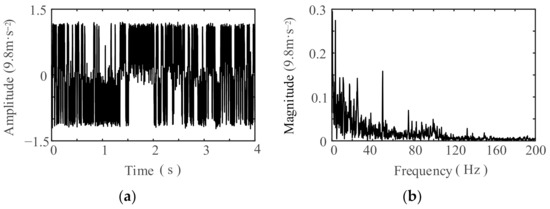
Figure 16.
Output signals of the SR system near the fault frequency of the 6219 outer rings: (a) waveform; (b) spectrum.
3.2.3. Fault Detection of Inner Ring
Based on the distribution characteristics of the inner ring fault frequency, a variable-scale SR method based on particle swarm optimization was used to detect the vibration signals of NU219 and 6219 bearings, searching for periodic components in the frequency range of 153.3–155.3 Hz for NU219 bearings and 87.5–89.5 Hz for 6219 bearings, respectively. Table 4 can be consulted for the selected parameters of the SR method. Following processing by the SR system, the resultant time-domain waveform and frequency spectrum of the signal are depicted in Figure 17 and Figure 18, respectively. Upon the examination of these figures, it becomes apparent that the amplitude near the inner ring fault frequency is not prominent in the entire spectrum, indicating that the fault-related characteristic frequency cannot be detected from the vibration signals of the NU219 and 6219 bearings. Therefore, there are no faults in the inner rings of the NU219 and 6219 bearings.
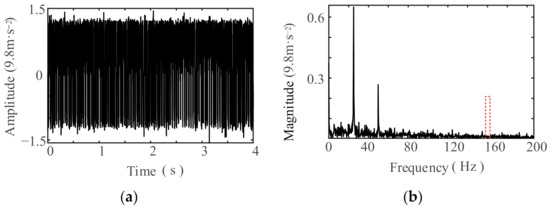
Figure 17.
Output signal of the SR system near the fault frequency of the NU219 inner rings: (a) waveform; (b) spectrum.
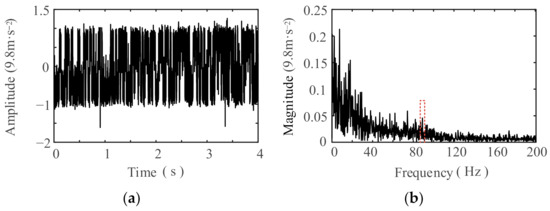
Figure 18.
Output signal of the SR system near the fault frequency of the 6219 inner rings: (a) waveform; (b) spectrum.
The above analysis indicates that adaptive SR based on ISNR can detect fault signals under low SNR conditions; when the characteristic frequency of rolling bearing faults fluctuates, adaptive SR based on ISNR can still detect fault signals within its detection range. Extracting and identifying detected periodic signals using HWPT and PDF can avoid interference from natural frequencies. Finally, it was determined that the single fault of the NU219 bearing rolling element was the main cause of the excessive vibration of the drive-end bearing.
4. Conclusions
In this study, a methodology integrating SR, HWPT and PDF is utilized to identify the characteristic signals of weak faults in rolling bearings. A case analysis is conducted on the fault detection for rolling bearings in the motor of a water injection pump unit on an offshore platform. Based on the analysis conducted, the subsequent conclusions have been derived:
- (1)
- Actual failure cases of rolling bearings in the drive motors of offshore platform water injection pumps reveal a significant discrepancy between the failure frequencies observed under real operating conditions and those theoretically derived under rated conditions. Consequently, relying exclusively on failure frequency values derived from theoretical calculations is inadequate for accurately identifying and extracting bearing fault characteristic signals from measured vibration signals.
- (2)
- When employing SR for the detection of fault frequencies within a specified range, it is crucial to recognize that the detected periodic components may not invariably correspond to the fault characteristic frequencies of rolling bearings. Consequently, it is of utmost importance to carry out a verification of the frequencies detected through SR in order to validate their authenticity as representative of fault characteristic frequencies.
- (3)
- Without knowing the exact failure characteristic frequency of rolling bearing, the weak fault signal can be detected, extracted and identified by using a hybrid approach combining SR, HWPT and PDF.
In future research, it is planned to further investigate the SR algorithm, with the objective of enhancing its capability to detect weak periodic signals, thereby facilitating the early warning of rolling bearing faults. Simultaneously, methods to integrate the processing outcomes of the SR for bearing vibration signals with intelligent algorithms, such as deep learning, will be explored, aiming to ensure that the diagnosis process becomes more intelligent [22,23]. This integration is expected to overcome the limitations associated with manual signal screening and enhance the overall efficiency and accuracy of the diagnosis process.
Author Contributions
Conceptualization, P.X., Z.F. and G.L.; methodology, Z.F. and G.L.; software, P.X., Z.F. and L.Z.; validation, P.X., Z.F. and G.L.; formal analysis, P.X., Z.F. and L.L.; investigation, P.X. and Z.F.; resources, P.X. and Z.F.; data curation, Z.F.; writing—original draft preparation, Z.F. and G.L.; writing—review and editing, P.X., Z.F. and G.L.; visualization, P.X. and Z.F.; supervision, G.L.; project administration, P.X.; funding acquisition, P.X., G.L., X.H. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Doctoral Start-up Foundation of Liaoning Province, grant number 2024-BS-023, the China Postdoctoral Science Foundation, grant number 2024M750298, the National Natural Science Foundation of China, grant number 52471311 and the Fundamental Research Funds for the Central Universities, grant numbers 3132024215 and 3132023522.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to acknowledge the funders and extend their appreciation to each of the anonymous reviewers for their valuable comments and suggestions for improving the quality of this paper.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Yuchen, W.; Le, X.; Jiahui, L.; Du, Y. Fault mechanism and diagnostic analysis method of rolling bearings. Plant Maint. Eng. 2021, 23, 149–150. [Google Scholar] [CrossRef]
- Chen, X.; Shu, G.; Zhang, K.; Duan, M.; Li, L. A fault characteristics extraction method for rolling bearing with variable rotational speed using adaptive time-varying comb filtering and order tracking. J. Mech. Sci. Technol. 2022, 36, 1171–1182. [Google Scholar] [CrossRef]
- Ding, J.; Huang, L.; Xiao, D.; Li, X. GMPSO-VMD Algorithm and Its Application to Rolling Bearing Fault Feature Extraction. Sensors 2020, 20, 1946. [Google Scholar] [CrossRef]
- Xiang, Q.; Wang, Y.-W. Research on stochastic Resonation-Hilbert Transform method for fault diagnosis of rolling Bearings. In Proceedings of the 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 4–6 December 2020; pp. 703–706. [Google Scholar]
- Qin, B.; Hou, P.; Yi, X.; Dong, H. Research on feature extraction method for fault diagnosis of rolling bearings based on wavelet packet decomposition. In Proceedings of the IEEE International Conference on Prognostics and Health Management (ICPHM), Seattle, WA, USA, 11–13 June 2018. [Google Scholar]
- Yang, M.; Xu, Y.; Zhang, K.; Zhang, X. Singular component decomposition and its application in rolling bearing fault diagnosis. Meas. Sci. Technol. 2024, 35, 015120. [Google Scholar] [CrossRef]
- Huang, X.; Qu, H.; Lv, M.; Yang, J. Fault Diagnosis of Rolling Bearings Based on Spectral Kurtosis Graph and LFMB Network. Russ. J. Nondestruct. Test. 2023, 59, 886–901. [Google Scholar] [CrossRef]
- Cui, L.; Wang, J.; Ma, J. Early fault detection method for rolling bearing based on multiscale morphological filtering of information-entropy threshold. J. Mech. Sci. Technol. 2019, 33, 1513–1522. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, N.; Zhang, W.; Wang, Z. Application of an improved minimum entropy deconvolution method for railway rolling element bearing fault diagnosis. J. Sound Vib. 2018, 425, 53–69. [Google Scholar] [CrossRef]
- Jun, Z.; Xinhuan, L.; Ming, K.; Tiantai, G. Weak feature extraction of gear fault based on stochastic resonance denoising. In Proceedings of the Eighth International Symposium on Precision Engineering Measurement and Instrumentation, Chengdu, China, 8–11 August 2012; Volume 8759, pp. 725–732. [Google Scholar]
- Liu, W.-x.; Wang, Y.-j.; Liu, X.; Zhang, M.-j. Weak thruster fault detection for AUV based on stochastic resonance and wavelet reconstruction. J. Cent. South Univ. 2016, 23, 2883–2895. [Google Scholar] [CrossRef]
- Hui, W.; Fei, W.; Hongxia, L.; Yanqiu, X.; Guoning, S. Research on the Weak Signal Extraction Method with Adaptive Stochastic Resonance Based on the Time Grid Sensor for PMSM. Math. Probl. Eng. 2022, 2022, 5013997. [Google Scholar]
- Chenxi, L.; Zheng, D.; Lihao, L.; Xingyang, W. An adaptive stochastic resonance detection method based on a fast artificial fish swarm algorithm. J. Phys. Conf. Ser. 2023, 2517, 012013. [Google Scholar]
- He, B.; Huang, Y.; Wang, D.; Yan, B.; Dong, D. A parameter-adaptive stochastic resonance based on whale optimization algorithm for weak signal detection for rotating machinery. Measurement 2019, 136, 658–667. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E. Stochastic resonance:: The role of α-stable noises. Acta Phys. Pol. B 2006, 37, 1479–1490. [Google Scholar]
- Kangping, G.; Xinxin, X.; Jiabo, L.; Shengjie, J.; Ning, S. Weak fault feature extraction for polycrystalline diamond compact bit based on ensemble empirical mode decomposition and adaptive stochastic resonance. Measurement 2021, 178, 109304. [Google Scholar]
- Zhang, J.; Yang, J.; Liu, H.; Zhou, D. Improved SNR to detect the unknown characteristic frequency by SR. IET Sci. Meas. Technol. 2018, 12, 795–801. [Google Scholar] [CrossRef]
- Qin, Q.; Fuping, Z.; Fangyan, Y.; Yin, L. Fault Feature Extraction of Rolling Bearings Based on Full Vector Improved Continuous Harmonic Wavelet Packet. Mech. Sci. Technol. Aerosp. Eng. 2023, 42, 2040–2046. [Google Scholar] [CrossRef]
- Chen, L.; Tan, A.; Yang, L.; Pang, X.; Qiu, M. Defect Size Evaluation of Cylindrical Roller Bearings with Compound Faults on the Inner and Outer Races. Math. Probl. Eng. 2022, 2022, 6070822. [Google Scholar] [CrossRef]
- Yimin, Z.; Shouyuan, Z.; He, L.; Wen, B. models in operational modal analysis. J. Vib. Shock 2009, 28, 64–67+196. [Google Scholar] [CrossRef]
- Meng, Z.; He, J.; Liu, J.; Jin, Y.; Li, J.; Fan, F. Fault Diagnosis of Rolling Bearings Based on Optimal Noise and Optimal Step Length Superimposed Segmental Bistable Stochastic Resonance. J. Vib. Eng. Technol. 2023, 11, 3521–3534. [Google Scholar] [CrossRef]
- Nasir, V.; Sassani, F. A review on deep learning in machining and tool monitoring: Methods, opportunities, and challenges. Int. J. Adv. Manuf. Technol. 2021, 115, 2683–2709. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; da Silva, L.R.; Ercetin, A.; Der, O.; Mikolajczyk, T.; Giasin, K. State-of-the-art review of applications of image processing techniques for tool condition monitoring on conventional machining processes. Int. J. Adv. Manuf. Technol. 2024, 130, 57–85. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).