Abstract
The article discusses the problem of adaptive system synthesis to provide the detection, estimation, and elimination of the negative consequences of faults in the thrusters of underwater robots and deviations of their parameters. For this purpose, an approach consisting of three stages is proposed. At the first stage, based on a bank of diagnostic observers, deviations of the thruster parameters from their nominal values or the occurrence of errors in the readings of its sensors are detected. At the second stage, the magnitudes of the detected deviations and errors are estimated using sliding mode observers. To estimate not only single but also multiple faults, the additional sliding mode observers are used. At the third stage, a control signal is generated to retain the basic dynamic properties of the thruster based on the estimated magnitudes of deviations and errors. Thus, the main contribution of this paper is designing the systems compensating for the consequences of faults occurring in the thrusters of the UR and errors in the readings of the angular velocity sensors. This avoids reducing the accuracy of movement along specified trajectories, as well as preventing accidents that could lead to the loss of the vehicle. The operability and efficiency of the proposed systems were tested using computer simulations and experimental studies on an electro-mechanical stand.
1. Introduction
Currently, the areas of use for underwater robots (URs) and the complexity of their operations are significantly expanding [1,2,3]. The occurrence of faults that result in the deviation of the UR thrusters’ parameters from their nominal values can lead to a significant decrease in the quality of the underwater missions and operations and to various emergency situations, as well as to the loss of the expensive robots.
A general idea of ways to improve the reliability of robotic systems is suggested in [4,5,6]. One promising approach to solve this problem is the use of fault diagnosis methods for rapid fault detection and estimation followed by the generation of special control allowing the automatic preservation of the most important characteristics of the UR during its operation.
The traditional way to increase the survivability of technical systems is to increase the reliability of individual elements of these systems [7,8]. However, the use of this method applied to modern systems, operating for a long time in an aggressive marine environment, does not always give the required positive effect. In addition, the reason for failures and accidents in UR operation is often the human factor, as they are caused by personnel errors.
These errors can be identified by conducting various pre-launch tests. However, these tests provide only the most general verification of the operability of individual elements and subsystems of the UR before diving and do not identify faults that occur during the operation of the UR.
Another traditional approach to improve the reliability and survivability of responsible systems is the use of hardware redundancy when the additional elements are included in the technical systems. Such elements perform the same functions as the main elements and allow the maintenance of normal operation in case of failure. In [9], an approach to adaptive systems design that neutralizes the negative effects of faults in the thrusters of the UR is considered. It involves the shutdown of a faulty thruster with the subsequent distribution of its thrust among other additional thrusters. The disadvantage of this approach is the need to use an excessive number of thrusters in the UR. Furthermore, the addition of backup elements is limited by the maximum permissible design and operational (weight, size, energy, etc.) characteristics of the device.
An alternative approach that does not require complicating the control system is the use of diagnostic systems that allow the timely detection of emerging malfunctions in the process of the direct execution of the prescribed missions and technological operations performed by robots. Currently, the URs are equipped by control and emergency systems to assess the technical condition and identify possible malfunctions of on-board equipment. But these systems, as a rule, provide only general monitoring of the operability of the UR subsystems and when a malfunction is detected, they assume an emergency stop of the missions being performed and an ascent to the surface. In addition, these systems do not guarantee the verification of the correct functioning of individual elements of the control system, and therefore cannot detect errors in sensor readings and deviations in the parameters of robot thrusters.
To overcome these drawbacks, different fault diagnosis methods can be used which can detect the facts of the improper operation of individual elements of the UR when the faults occur. The process of fault diagnosis contains two stages: the generation of a residual and decision making. The residual is the difference between the transformed output of the actual object and the output of the diagnostic system.
There exist two main methods to generate a residual: Kalman filters [10,11,12] and asymptotically stable observers (Luenberger observers) [13,14,15]. In [16,17]. The methods of fault diagnosis in various robotic systems using extended Kalman filters are described. They are mainly focused on detecting and estimating single slowly changing faults or errors in sensor readings. In [18,19], Kalman filters are used for fault diagnosis in dynamic systems described by nonlinear differential equations. These methods use a preliminary local linearization as well as an approximate solution of the covariance equation to determine the covariance matrix of errors and the feedback matrix. For these reasons, they cannot guarantee not only the optimality, but also the stability of the filter.
In addition to Kalman filters, diagnostic observers (DOs) based on Luenberger observers [13,14,15] have been widely used in the last decades. Their main advantage is that they design the DO for systems described by nonlinear differential equations. There are methods of designing the DO for nonlinear systems; these include differential geometry [20,21,22,23] and the algebra of functions [23]. These methods make it possible to obtain an optimal solution to the diagnostic problem and minimize the dimension of the DO. However, they require rather complex analytical transformations which makes it difficult to apply them in practice.
In contrast, there exists the so-called logic-dynamic approach suggested in [24] which does not guarantee the minimum dimension of the DO but produces a simple procedure based on the methods of linear algebra.
To solve the problem of fault isolation, a bank of the DO should be used. In this situation, the determination of a malfunction is achieved through the use of a matrix of symptoms [24]. Columns of this matrix correspond to possible faults and the rows correspond to the residuals generated by the observers.
Currently, a common approach to fault estimation is the use of neural networks [25,26,27,28], including adaptive networks and networks with fuzzy logic [29,30,31]. These methods make it possible to determine the parameters of nonlinear dynamic systems in the presence of faults, as well as to compensate the detected changes. The disadvantage of these approaches is the need for preliminary complex and long-term training of neural networks, as well as the use of special test modes of their movement [32], which are not always acceptable.
Another approach for estimating the faults is the use of sliding mode observers (SMOs) [33,34,35]. These SMOs are effectively used in practice to estimate faults, as well as to design fault-tolerant systems [36,37,38]. Their disadvantage is that a number of restrictions are imposed on the mathematical model of the object of diagnosis. In particular, it is required that the so-called matching condition be fulfilled that assumes that all phase coordinates of the object must be measured by appropriate sensors, and this is not always possible in the modern UR. In addition, it is necessary that the systems under diagnosis be minimal phase.
Furthermore, SMOs in the known papers are designed on the basis of the full models of the objects under diagnosis. Therefore, SMOs have a dimension no less than the dimension of these objects, which makes it difficult to implement them in practice on on-board computers. Known approaches to determining the magnitude of errors in sensor readings using SMOs provide only an approximate solution or require observers of an increased dimension for their implementation.
The well-known least squares method [39,40,41] and algorithms based on simplified linearized models of the UR motion can be used to estimate the values of the parameters of the UR thrusters but they are effective only for linear models.
The analysis shows that the methods to design control systems for the UR can be combined into two groups. The methods of the first group ensure insensitivity to emerging faults without measuring the deviations of parameters caused by them. But the systems designed by these methods have a complex practical implementation. In addition, they are applicable and effective only for a small number of faults.
The methods of the second group are based on generating special control signals. These indicators guarantee their continued functioning and maintain the stability of the critical features of these systems even in the face of faults. These methods are often quite applicable and effective for many faults that can occur in the UR.
To compensate for the consequences of faults arising in the UR, several types of robust control systems are used. The first type includes self-adjusting systems with a reference model. The main feature of these systems is the presence of a model that has specified the dynamic properties of a faulty system. Such systems are used in both terrestrial and underwater robotics, providing high-quality control of robots using fairly simple means without identifying faulty parameters. The disadvantage of such systems is the presence of high-frequency oscillations in the self-tuning circuit that often significantly reduces the quality of compensation. In addition, during the operation of such systems, deviations in parameters from their nominal values are not evaluated, which does not allow the timely termination of the UR mission when critical faults appear. These systems do not take into account the errors that occur in the readings of the sensors.
The second type includes optimally robust adaptive systems, the advantage of which is their sufficiently high robustness to uncertain parameters of the control objects. But to design such systems, linearized models should be used, which limits their application in the spatial movement of objects.
The third type of fault-tolerant control systems includes systems with a variable structure [37,38]. The disadvantage of these systems is that, in order to ensure the operability of systems with a variable structure over the entire range of changes in the parameters, they are designed taking into account the “worst case” when their parameters reduce the system performance. As a result, even in the absence of faults, additional control signals are generated, increasing the amplitude of the control signals and energy consumption and reducing the battery life of the device.
To stabilize the dynamic properties of thrusters when their parameters change, the well-known method of the synthesis of adaptive control systems can be used [24]. However, the current control systems that employ this approach do not account for potential malfunctions in the thrusters or inaccuracies in the readings of the angular velocity sensors.
As a result, the analysis shows that due to the high complexity of the implementation of the obtained control laws or low speed, most of the considered methods cannot be used to design the systems compensating for the consequences of faults occurring in the thrusters and sensors.
The main contribution of this paper is designing the systems compensating for the consequences of faults occurring in the thrusters of the UR and errors in the readings of the angular velocity sensors. The components of such systems are diagnostic and sliding mode observers for detecting, isolating, and estimating the faults and errors followed by compensating for the consequences of their appearance. These observers are of minimal dimension, which allows them to be used in on-boat computers.
The article will be organized as follows. In Section 2.1, a mathematical model of the propulsion system is described, taking into account possible faults. Section 2.2 provides a method for creating a DO bank to isolate faults. Section 2.3 describes a method for constructing SMOs to identify the values of previously isolated faults. In Section 2.4, the construction of additional observers is described, which makes it possible to simultaneously identify the values of two faults that have occurred. In Section 2.5, a synthesis of the compensation system for previously isolated and identified faults is presented, as well as the verification of its operation using computer modeling. In Section 3, the results of an experimental study of the developed systems on a special electromechanical stand is presented. Section 4 concludes the paper.
2. Methods
2.1. Mathematical Model of the UR Thruster and Its Faults
The operation of the URs shows that the occurrence of faults in their thrusters as well as errors in the angular velocity sensors, can lead to a significant decrease in UR movement accuracy along spatial trajectories or emergency situations (in exceptional cases, to a loss of the expensive robots). To develop a method of fault diagnosis, it is firstly necessary to create adequate mathematical models of thrusters, taking into account all frequently occurring faults.
UR thrusters usually use DC electric motors or motors with permanent magnets which are equipped with angular velocity sensors for their output shafts and armature circuit current sensors [24]. A full mathematical model of the underwater vehicle’s dynamics is described in [42]. It is known [24] that each individual thruster with possible faults can be described by a system of differential equations of the form
with the measurements
where is the angular velocity for their output shafts and is the armature circuit current; is the input voltage; and are the inductance and electrical resistance the of the armature circuit, respectively; is back-emf coefficient; is the power amplifier gain; is the torque coefficient; is the coefficient of viscous friction; is the moment on the propeller shaft from the interaction of the propeller with a viscous environment; and , and are auxiliary variables.
is the speed of the movement of the surrounding fluid along the propeller axis relative to the UR; and are hydrodynamic and geometric pitches of the propeller; is the hydrodynamic correction for propeller pitch; is the generalized torque coefficient; and are coefficients of lift and propeller torque at ; is the coefficient characterizing the decrease in lift and propeller torque at ; is the propeller profile loss coefficient; is a density of the surrounding liquid; is the area of the propeller disk; is the moment of the inertia of the rotating parts of the thruster taking into account the added moment of the inertia of the liquid; and is the absolute slip of the propeller.
The following typical faults can occur in the thruster:
- (1)
- Errors in readings of angular velocity sensors resulting in the errors ;
- (2)
- A deviation of the active resistance of the motor armature circuit from its nominal value due to the excessive heating of the motor or a short circuit of the winding turns;
- (3)
- The unknown external moment on the output shafts of the propellers.
The block diagram of the thruster described by the system of Equations (1) and (2) is shown in Figure 1.
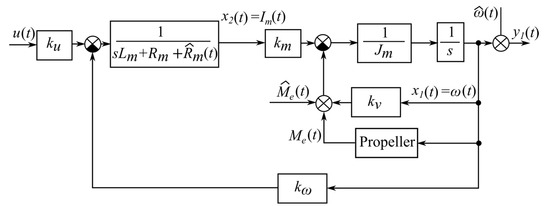
Figure 1.
Block diagram of the UR thruster.
To develop the method to design DOs, rewrite (1) in the matrix form as follows:
where is the matrix of dynamic properties of the thruster; is the state vector; is the matrix-column of gain coefficients; are state variables measured by sensors; is the faults matrix indicating the location of faults; is a vector characterizing faults (in the absence of faults, all elements of the vector are equal to zero, and when they appear, a specific element becomes non-zero); is the output matrix; is the vector function that takes into account the nonlinearities of the electric drive; and is the vector of faults in sensors of the thruster, indicating the sensor in which the fault occurred.
Recorded in (3), the matrices and vectors have the following form:
where .
The model (3) will be used to synthesize a bank of DOs and to solve the problem of fault diagnosis. Each observer of the bank must be synthesized in such a way that the generated residuals are sensitive to the occurrence of various combinations of non-zero functions , and .
2.2. Bank of DO Design for Fault Isolation in Thrusters
To isolate faults in thrusters described by nonlinear differential Equation (3), the bank of DOs should be used. To design DOs in such a bank, we will use the logical-dynamic approach [24], which allows the study of nonlinear systems only by linear methods. In contrast to the typical logical-dynamic approach that provides the sensitivity of the DO to strictly specified faults only, a new algorithm is developed which enables the design of observers sensitive to various sets of faults.
The logical-dynamic approach consists of the following three stages:
- (1)
- The transformation of the original nonlinear dynamic model (3) into a linear one by discarding the nonlinear term ;
- (2)
- Solving (using a special algorithm) the problem of designing a bank of linear DOs, which should ensure the rapid detection of the appearance in (3) of the specific non-zero functions , , and ;
- (3)
- The calculation of the additional nonlinear components by algebraic methods and their addition to the linear DO designed at the second stage.
After discarding the component , the system (3) takes the form
At the second stage, the linear DO are designed. Every DO is described as follows:
where is the state vector; is the output signal; , , , and are matrices to be determined; is the matrix of the observer’s feedback coefficients; is the residual generated by the DO; and is the dimension of the DO.
The residual should be sensitive to one or more non-zero functions , , and . If all of these functions are equal to zero, , otherwise . The residual is determined as follows:
with the matrix to be determined.
Introduce the matrix satisfying the condition
when , , and . It is known that the matrices describing the system and the DO satisfy the conditions
According to the proposed method, each specific DO should be constructed in such a way that the appropriate residual is sensitive to the appearance of non-zero functions , , and . That is, the obtained relations must be supplemented with the conditions of the sensitivity and insensitivity of the DO to these functions. To do this, rewrite expression (6) taking into account (3), (5), (7), and (8):
Differentiating (9) with respect to time and taking into account (3), (5), and (8), one obtains
where
From (10) and (11), one obtains the conditions of the sensitivity and insensitivity of the residual as follows:
- The residual is sensitive to if
- It is insensitive to if
- It is sensitive to if
- It is insensitive to if
The decision on the appearance of a specific fault is made on the basis of the matrix of syndromes . If the -th DO is sensitive to the -th fault, then , otherwise . If columns of the matrix are different, the faults can be isolated.
It is known [24] that the linear DO (5) design is performed easily if these observers are specified in the canonical form when
In this case, Equation (8) can be represented as a set of equations as follows:
where and are the th rows of the matrices and , respectively. It is known that these equations can be transformed into the single one as follows:
To determine the elements of the vector , the Equation (10) can be written taking into account (8) under , , and as follows:
It follows from (19) that to obtain a stabile linear DO, the matrix must have eigenvalues with negative real parts. Let be the components of the feedback matrix , then
The coefficients related to the prescribed eigenvalues are given by
To solve Equation (18), the following new algorithm is proposed (Algorithm 1).
| Algorithm 1: New algorithm To solve Equation (18) | |
| 1: | . |
| 2: | If (18) has a solution, find the matrices and . Otherwise, go to step 3. If the number of equations in (18) is smaller than the number of variables of the matrices and , then some of these elements can be taken as free variables, and the rest of the elements express through them; go to step 4. |
| 3: | Take and go to step 2. |
| 4: | Find the rows of the matrix according to the following relations obtained from (8) and (16): |
| The elements of may depend on previously accepted free variables. | |
| 5: | Check the obtained matrices , , and for sensitivity or insensitivity to various combinations of non-zero functions , , and using criteria (12)–(15). The values of all free variables should be selected in such a way that the vector is non-zero. If it is not possible to fulfill these criteria, return to step 3. |
| 6: | Calculate the matrix using (8). |
As a result, the linear DO (5) sensitive to the combinations of non-zero functions , , and has been constructed.
At the third stage of the proposed approach, the nonlinear component is added to the designed linear DO which is calculated using expression [24]
The final description of each DO has the following form:
If = 0, the elements of the feedback matrix are calculated using (20). Otherwise, the matrix can be found based on [43].
Based on the algorithm, one can construct a bank of DOs which are sensitive only to a certain set of functions , and . The implementation of the above procedure to design a bank for isolating faults in thrusters provides the following results.
DO-1 of the first order is sensitive to the non-zero functions and , but insensitive to as follows:
DO-2 of the first order is sensitive to and , but is insensitive to as follows:
DO-3 of the second order is sensitive to and , but is insensitive to as follows:
It can be shown that the matrix for DO-3 is given by
The bank of DOs (23)–(25) makes it possible to determine the fact of the appearance of non-zero functions , (or the functions and dependent on them), and caused by the occurrence of the corresponding faults in the thrusters of the UR. For this bank, the matrix of syndromes S is given by
DOs (24)–(25) allow the timely detection and isolation of single faults appearing in the UR thrusters. However, they do not identify the magnitude of faults, which is necessary for further compensation of the negative consequences of their occurrence.
2.3. Bank of SMO Design for Fault Estimation
To solve the problem of fault estimation, SMOs are traditionally used. The theory for such observer design is described in many works [44]. SMOs in these papers, as a rule, are designed on the basis of full models of the object under diagnosis which makes their practical implementation difficult when using standard onboard computers of underwater robots.
Using the DOs obtained in the previous section, it is possible to modify them in order to design the SMOs. In particular, one can see from (23) and (24) that the synthesized DO-1 and DO-2 are described by simple first-order differential equations, and the generated residuals are sensitive to different functions , , or .
Since the functions and correspond to and by the relations , it is possible to obtain the values for the external torque and the deviation of the active resistance from its nominal value.
To design the SMO, supplement (5) with the nonlinear term and fault:
Unlike DO (23), the SMO contains the discontinuous function :
where is a discontinuous function, and and are constant coefficients.
Using (28) and (29) for , , and , one obtains
where . Since the maximum value of the torque on the propeller shaft from the interaction of the screw with a viscous medium is bounded (), then the functions and are also bounded and the function is bounded as well: . The elements of the vector associated with the values and are assumed to be also bounded: .
Introduce into consideration the Lyapunov function . As is known, the equilibrium position will be stable if the condition is met. Differentiating the function with respect to time and taking into account (30), one obtains
Obviously, when the inequalities for , , and are satisfied
the inequality will always be satisfied. Really, if , then due to (31); if , then and as well.
If conditions (31) are met, the relations and will be fulfilled for the first-order SMOs in a finite amount of time. Thus, the expression is valid, and therefore . In this case, (31) can be written as , where is a signal passed through a low-pass filter.
Taking into account (23)–(25) and (29) for the UR thrusters, one obtains the following:
SMO-1, used to obtain an estimate of the function is described by the following equations:
SMO-2, used to obtain an estimate of the function , has the following form:
SMO-3, to obtain an estimate of the function , is given by the following:
Thus, SMOs (32)–(34) make it possible to estimate single faults in the UR thrusters. However, if two faults occur simultaneously, then their estimation using the considered SMOs is impossible. A solution to this problem is discussed below.
2.4. Additional SMO Design for the Multiple Fault Estimation
To solve the problem of the multiple fault estimation, the DOs (23)–(25) and SMOs (32)–(34) should be modified. This can be done by using the additional SMO-4 and SMO-5 described below. SMO-4 is given by
SMO-5 is described as
To explain these SMOs, note that they are based on DO-3 (25) being insensitive to ; remember that the matrix for DO-3 is
and
This relation allows an estimation of the variable . Based on the SMO-4, one obtains
by analogy, SMO-5 yields
Due to the discontinuous function in (35), the estimate is independent of , and by construction it is independent of . By analogy, the estimate is independent of , and .
Since , to modify the Dos (23) and (24), one should replace the variable in (23) and (24) by estimates and , respectively. As a result, the matrix of syndromes (27) becomes


Really, since is independent of and , and it is used instead of in (23), then is insensitive to and . The rest of the errors can be explained by analogy.
Equation (37) can reveal which pair of faults occurred. Consider four cases.
- (1)
- If and attain a value other than zero, and continues to be zero, the values of and can be estimated with the help of the previously built SMO-1 (32) and SMO-2 (33), respectively.
- (2)
- If and but , then can be found using the modified version of SMO-1 (32). Namely, the variable in (32) distorted by should be replaced by . The value is estimated as .
- (3)
- If and and , then can be estimated using the modified version of SMO-2 (33) where the variable is replaced by . The value is estimated as .
- (4)
- If all functions , , and attain a non-zero value., the estimation of their values is impossible.
2.5. Design of Systems to Compensate the Negative Consequences of Identified Faults in the Thrusters of Underwater Robots
The motion of the UR in three-dimensional space is achieved through the application of force generated by its propulsion systems. There are in place efficient control systems [45,46] that guarantee the precise movement of the UR along predetermined smooth trajectories. In these systems, the dynamic characteristics of the UR thrusters are assumed to be represented by linear differential equations with constant parameters [46]
where is the thrust of the UR thruster, (t) is the desired thrust, and is the time constant.
Nevertheless, as demonstrated in [46], the dynamic characteristics of the UR thrusters are defined by nonlinear equations with fluctuating parameters, rendering the application of conventional high-performance control systems impractical. To solve this problem, it is essential to simplify the intricate nonlinear representation of the propulsion systems into the form (38). To achieve this, one can employ the approach outlined in [46]. However, this method does not consider the possible changes of the thruster parameters due to the faults. Therefore, it is suggested to develop a new adaptive control system based on the approach outlined in [46], which incorporates the consideration of faults resulting in the non-zero functions , , and .
To develop a new adaptive UR thruster control system, one has to perform the following steps:
- (1)
- Consider the initial differential equation that governs the relationship between the thrust of the thruster and its control ;
- (2)
- Synthesize the control law for the implementation of the adaptive nonlinear controller by solving the system of the original equation and Equation (38).
According to [46], to derive a differential equation that captures the relationship between thrust and signal, , one should supplement (1) and (2) with
where is the coefficient of thruster force. Then Equations (1), (2), and (39) should be transformed into a single equation. To do this, differentiate (39) with respect to time as follows:
Since according to [46]
expression (40) can be rewritten as
Substituting in (41) by the right-hand side of the first equation in (1) and taking into account the replacement of functions and with their identified values and , one obtains
where
In contemporary DC motors, the inductance of the armature windings is negligible, so it can be disregarded. Consequently, the armature current of the electric motor, as calculated from the second equation in (1), is determined by
Similar to [46], it is assumed that the expression for the moment in (2) can be simplified by removing the second addend; as a result,
The final description of the dynamics of the thruster is reduced to a single first-order differential equation where possible faults are taken into account as follows:
To stabilize the dynamic properties of UR thrusters under the faults, it is necessary to change the control signal . For this, it is necessary to find the control from (45), and replace from (45) by the expressed in (38). As a result, the final form of the desired control that ensures the creation of a given thrust by the thruster is given by
Obviously, (46) takes into account the errors and ; the error is accounted for according to .
A schematic representation of the system for compensating for the consequences of single faults is depicted in Figure 2. Residual signals , , and are generated by a bank of three DOs (23)–(25) and then the fault is isolated. Then, the values of , , or are estimated by the corresponding SMO, (32), (33), or (34). Finally, these values are used for generating the control signals (46) for UR thrusters, as described by (1).
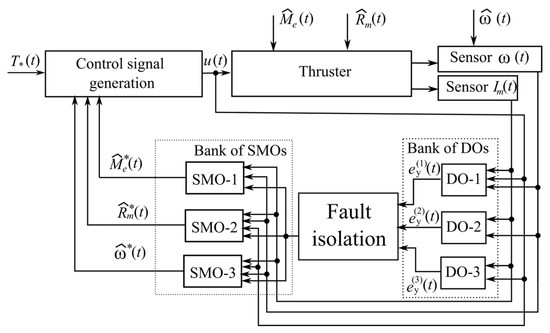
Figure 2.
Block diagram of a system compensating for the consequences of a single fault in the UR thrusters.
When the paired faults are detected and isolated, the appropriate compensating system shown in Figure 3 is used. Here, instead of SMO-3 (34), SMO-4 (35) and SMO-5 (36) are used. In addition, unlike Figure 2, the signals and are employed instead of the readings from the angular velocity sensor in DO-1 (23), DO-2 (24), SMO-1 (32), and SMO-2 (33).
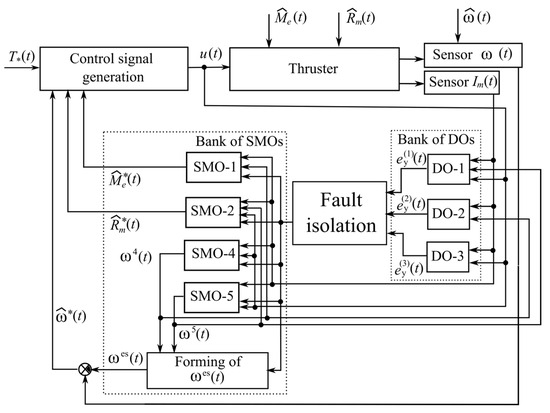
Figure 3.
Block diagram of the system compensating for the consequences of paired faults in the UR thrusters.
To check the effectiveness of the compensating system shown in Figure 2, computational simulating is carried out. For simulation, the UR with six thrusters (Figure 4) moving along the program trajectory m, m, m (see Figure 5) is considered. The beginning of the trajectory is indicated by the number 1 and the end by 2. Faults occur in the UR thruster creating the thrust . The parameters of the UR are consistent with those outlined in [45].
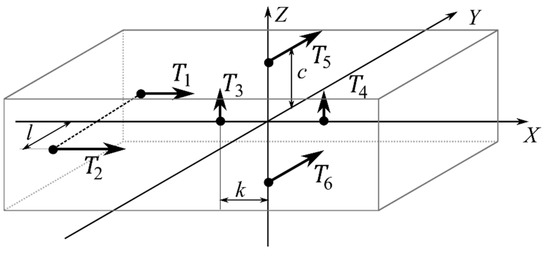
Figure 4.
Layout of UR thrusters.
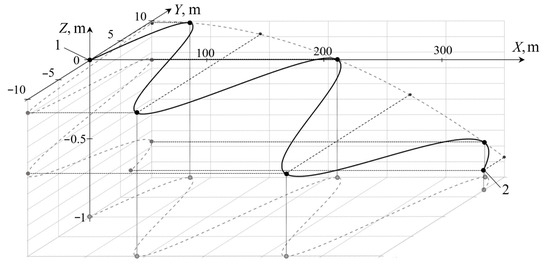
Figure 5.
Programmed trajectory of the UR movement.
Simulation results in the form of the tracking errors of the UR with and without the compensating systems are shown in Figure 6. If there are no faults, the tracking error of the UR does not exceed 0.3 m (see the curve 1 in Figure 6). But when the faults occur and the compensating system is not used, the accuracy of the UR movement decreases significantly.
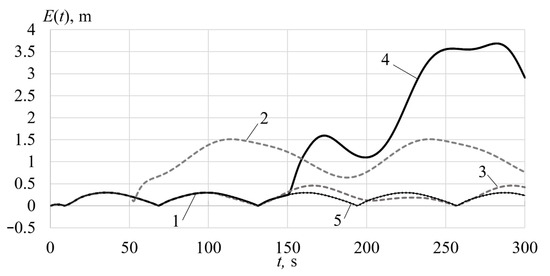
Figure 6.
The UR tracking errors in the program trajectory with and without paired faults.
Curve 2 in Figure 6 represents the graph of the tracking error when the error rad/s occurs at s, which is about 30% of the average rotational speed of the propeller shaft. The tracking error grows to 1.51 m (in 5.03 times).
Curve 3 shows the tracking error where the active resistance of the propulsion armature increases by 30% ( Ω) at s. The error increases to 0.46 m (by 53.3%).
Curve 4 indicates the error when an additional external torque appears on the shaft of the specified thruster at s. This fault leads to an increase in the tracking error to 3.68 m (in 12.27 times).
Curve 5 shows the tracking error with any single faults where the proposed compensating system is used. In this case, the maximum deviation of the UR from the specified trajectory does not exceed 0.302 m. It should be added that the information about the non-zero function can serve as an indicator for the overheating of the thruster and for a possible change in the mode (speed) of UR movement or for the complete termination of its mission.
The results of computational simulation to verify the effectiveness of the system designed to compensate for the consequences of paired faults (see Figure 3) are shown in Figure 7. The magnitudes and time of appearance of faults are chosen to be the same as in the case with the single faults.
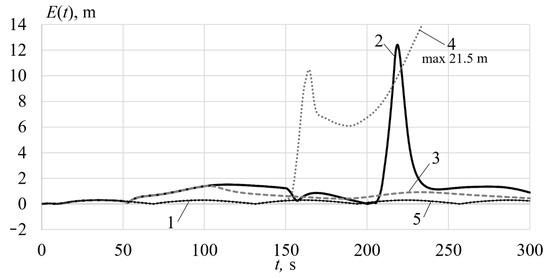
Figure 7.
The UR tracking errors with and without paired faults.
Curve 1 in Figure 7 shows the tracking error without any faults. Curve 2 shows the tracking errors when the errors and appear without compensating. In this situation, the tracking inaccuracy increases to 12.3 m (in 41.6 times). Curve 3 shows the graph of the tracking error when functions and appear. Here, the tracking error increases to 1.4 m (in 4.66 times). Curve 4 indicates the tracking error exceeds 21 m (in more than 70 times) when non-zero functions and appear. Curve 5 indicates the error when any combinations of the paired faults occur but the compensating system shown on Figure 3 is used. Obviously, this system stabilizes the tracking error at the nominal value for any set of the paired faults.
Thus, the simulation results show that the use of the compensating systems shown in Figure 2 and Figure 3 maintains the initial accuracy of the UR trajectory movement with the occurrence of single and paired faults. Similar results are obtained when the faults occur in the other thrusters of the UR.
3. Experimental Research
To verify the functionality of the proposed compensating system, in addition to computational simulation, a series of full-scale experiments were carried out using an electromechanical stand shown in Figure 8. It contains two DC electric motors with toothed pulleys on their output shafts (see Figure 8, numbers 1 and 2), connected by a belt drive (Figure 8, number 3). The sensors in the stand are a tachogenerator for measuring the speed of the rotation of the motor shafts and current sensors installed on both electric motors. A PC with Matlab 2021b software (Figure 8, number 4) was used to control the stand and display the appropriate information (Figure 8, number 5). The digital control of the stand was carried out using the ESP-32 microcontroller (Figure 8, number 6).

Figure 8.
General view of the laboratory electromechanical stand.
The appearance of an external load torque is modeled by applying a constant V or alternating V voltage to the second electric drive of the stand preventing the rotation of the first electric motor. The appearance of the error in the angular velocity sensor is modeled by software adding constant (5 rad/s) or variable ( rad/s) signals to the real sensor readings.
During the experiment, the compensating system (see Figure 2 and Figure 3) ensures the rotation of the first electric motor with the angular velocity rad/s. It is assumed, for simplicity, that the error . This results in reducing the complex control law (51), and the simplified law compensating the influence of the load torque is as follows:
where is the control signal generated by a standard PID controller.
In Figure 9 and Figure 10, the errors of the angular velocity of the electric motor when constant fault and variable errors, respectively, occur at time s are shown. In these figures, curves 1 and 2 show the error when only a standard PID controller and the compensating system are used, respectively.
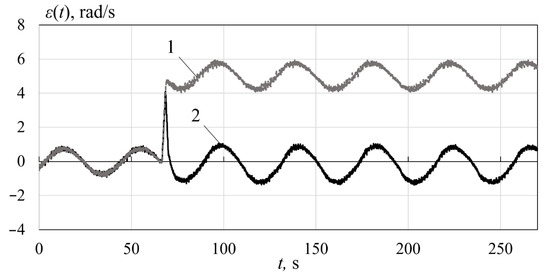
Figure 9.
The errors under the constant error
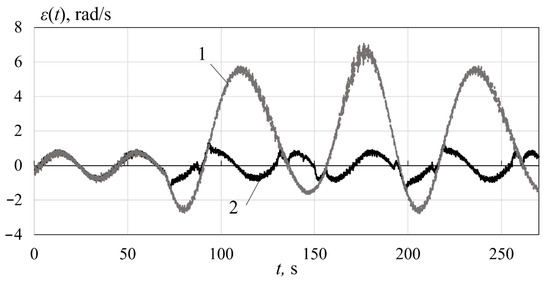
Figure 10.
The errors under the variable error .
As it follows from Figure 9, the appearance of the constant error increases the maximum errors from 0.8 rad/s to 5.8 rad/s, i.e., 7.25 times. However, when the compensating system is used, the error is only 1.1 rad/s, i.e., it is decreased 5.27 times.
If a variable error appears in the angular velocity sensor readings (see Figure 10), the maximum error increases from 0.8 rad/s to 7.1 rad/s (8.87 times). The use of the compensating system reduces this error to 1.3 rad/s (6.82 times).
The errors of the angular velocity of the first electric motor when the constant or variable load torque is applied to its output shaft are shown in Figure 11 and Figure 12, respectively. One can see from these figures that under the constant load the maximum error increases to 1.1 rad/s (by 37.5%) and under the variable load it increases to 3.2 rad/s (4 times). When the compensating system is used, the maximum errors are 1 rad/s and 1.3 rad/s for the constant and variable load torque, respectively. Thus, the use of the compensating system reduces the errors by 9% in the first case and 2.4 times in the second.
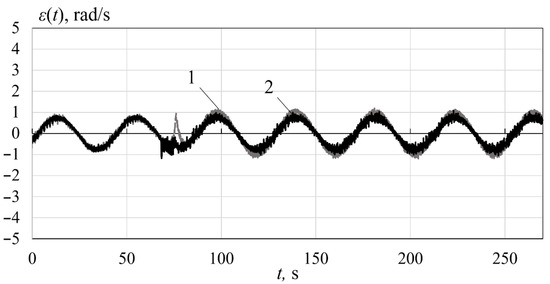
Figure 11.
The errors under the constant load torque .
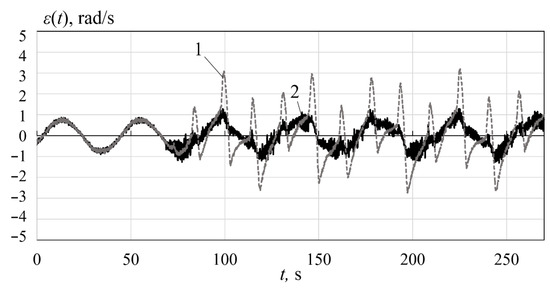
Figure 12.
The errors under the variable load torque
In Figure 13 and Figure 14, the error under the paired fault is shown. Figure 13 shows the graph of this error when the variable load moment and the constant error occur at and , respectively. On the other hand, in Figure 14, the variable error is used. From these figures it is clear that the indicated paired fault leads to an increase in the maximum error to 7.5 rad/s (9.37 times) in the first case and to 6.9 rad/s (8.62 times) in the second. The compensating system shown in Figure 3 reduces this error to 1.6 rad/s (4.68 times) and to 1.7 rad/s (4.05 times), respectively.
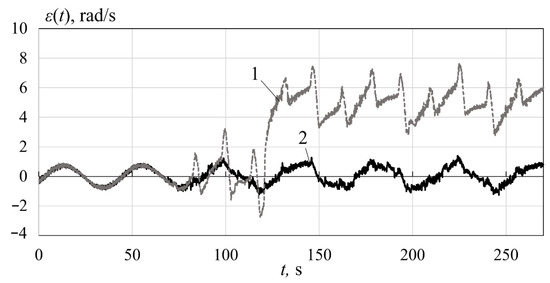
Figure 13.
The errors under the constant and the variable
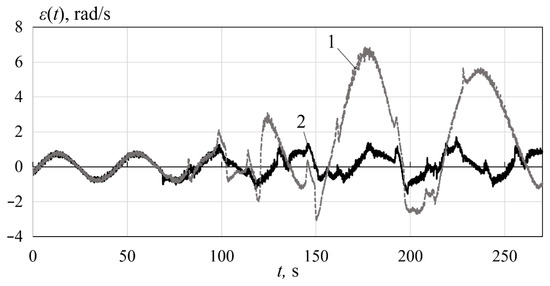
Figure 14.
The errors under the variable and the variable
Thus, the results of full-scale experiments fully confirm the high efficiency of the suggested compensating system when various single and paired faults occur.
4. Conclusions
This article has developed a method of designing the systems for detecting, estimating, and compensating for the consequences of faults. These systems provide an accurate estimation of the values of single and paired changes for all parameters in the UR thrusters from their nominal values and inaccuracies in the readings of their angular velocity sensors. Based on the well-known method of nonlinear controller design, these systems have been developed to compensate for the effects of single and paired faults. These systems enable the continued functioning and stabilization of the critical parameters of these propulsion systems in the event of unforeseen faults. The performance and operability of the proposed system was verified through computational simulation and full-scale experiments using the electromechanical stand.
Author Contributions
C.L.: Conceptualization, Methodology, Writing—original draft, Formal analysis, Data curation, and Supervision; V.F. Filaretov: Project administration, Funding acquisition, Writing—original draft, Methodology, and Software; A.Z. (Alexander Zuev): Writing—review and editing, Investigation, and Resources; A.P.: Visualization, Validation, and Writing—review and editing; A.Z. (Alexey Zhirabok): Data curation, Software, and Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Russian Scientific Foundation (grant 22-19-00392).
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declared no potential conflicts of interest with respect to the research, author-ship, and/or publication of this article.
References
- Ayob, A.F.; Arshad, M.R.; Jamaludin, S.; Ahmad, S.Z.A.S. A Brief Review of Unmanned Underwater Vehicle Human-Machine Interaction. In Proceedings of the 2022 IEEE 9th International Conference on Underwater System Technology: Theory and Applications (USYS), Kuala Lumpur, Malaysia, 5–6 December 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, R.; Wang, S.; Wang, Y.; Cheng, L.; Tan, M. Development and Motion Control of Biomimetic Underwater Robots: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 833–844. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Yu, J. A Survey of Underwater Multi-Robot Systems. IEEE/CAA J. Autom. Sin. 2022, 9, 1–18. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Ouyang, L. A survey of fault tolerance hardware architecture. In Proceedings of the 2021 International Conference on Advanced Computing and Endogenous Security, Nanjing, China, 21–22 April 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Safari, S.; Ansari, M.; Khdr, H.; Gohari-Nazari, P.; Yari-Karin, S.; Yeganeh-Khaksar, A.; Hessabi, S.; Ejlali, A.; Henkel, J. A Survey of Fault-Tolerance Techniques for Embedded Systems from the Perspective of Power, Energy, and Thermal Issues. IEEE Access 2022, 10, 12229–12251. [Google Scholar] [CrossRef]
- Nedeljković, J.N.; Đošić, S.M.; Nikolić, G.S. A Survey of Hardware Fault Tolerance Techniques. In Proceedings of the 2023 58th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Nis, Serbia, 29 June–1 July 2023; pp. 223–226. [Google Scholar] [CrossRef]
- Cong, C.; Lu, W.; Zhang, Z.; Fan, L. Reliability assessment analysis of a cruise ship electric propulsion system pods. In Proceedings of the 2022 2nd International Conference on Electrical Engineering and Control Science (IC2ECS), Nanjing, China, 16–18 December 2022; pp. 812–816. [Google Scholar] [CrossRef]
- Fatema, A.; Kuriakose, I.; Devendra, D.; Hussain, A.M. Investigation of the Mechanical Reliability of a Velostat-based Flexible Pressure Sensor. In Proceedings of the 2022 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Vienna, Austria, 10–13 July 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Yin, Z.; Gan, W.; Ou, J.; Wang, Z. Fault-Tolerant Control of Remotely Operated Vehicle Thrusters Based on the Dung Beetle Optimizer. In Proceedings of the 2024 7th International Conference on Advanced Algorithms and Control Engineering (ICAACE), Shanghai, China, 1–3 March 2024; pp. 1186–1189. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, H.; Wang, R. An Improved Unscented Kalman Filter for Interrupted and Drift Sensor Faults of Aircrafts. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Zemali, Z.; Hadroug, N.; Cherroun, L.; Hafaifa, A.; Nadour, M. Fault Diagnosis via Kalman Filters and ANFIS Classifiers for a Wind Turbine. In Proceedings of the 2023 2nd International Conference on Electronics, Energy and Measurement (IC2EM), Medea, Algeria, 28–29 November 2023; Volume 1, pp. 1–6. [Google Scholar] [CrossRef]
- Zexue, Y.; Zhiguo, H.; Ting, W. An Online Fault Location Method for DC Distribution Networks Using Adaptive Kalman Filter. In Proceedings of the 2023 IEEE International Conference on Advanced Power System Automation and Protection (APAP), Xuchang, China, 8–12 October 2023; pp. 301–305. [Google Scholar] [CrossRef]
- Kumara, P.A.; Cahyadi, A.I.; Wahyunggoro, O. Fault Detection Algorithm on Lithium-Polymer (Li-Po) Battery based on Luenberger Observer. In Proceedings of the 2021 International Seminar on Machine Learning, Optimization, and Data Science (ISMODE), Jakarta, Indonesia, 29–30 January 2022; pp. 108–113. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Jlassi, I.; Cardoso, A.J.M.; Yahia, K.; Sahraoui, M. Inter-Turn Short-Circuit Faults Diagnosis in Synchronous Reluctance Machines, Using the Luenberger State Observer and Current’s Second-Order Harmonic. IEEE Trans. Ind. Electron. 2022, 69, 8420–8429. [Google Scholar] [CrossRef]
- Zhao, K.; Gao, S.; Si, W. Time-varying Threshold Design for Intermittent Fault Detection of Dynamic Systems with Luenberger Observer. In Proceedings of the 2024 7th International Symposium on Autonomous Systems (ISAS), Chongqing, China, 7–9 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Kim, T.; Kim, Y.; Kim, S.; Suk, J. Thrust Fault Diagnosis Using Extended Kalman Filter Considering Dynamics of Lift-Cruise UAV. In Proceedings of the 2024 International Conference on Control, Automation and Diagnosis (ICCAD), Paris, France, 15–17 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Larik, N.A.; Li, M.S.; Wu, Q.H. Enhanced Fault Detection and Localization Strategy for High-Speed Protection in Medium-Voltage DC Distribution Networks Using Extended Kalman Filtering Algorithm. IEEE Access 2024, 12, 30329–30344. [Google Scholar] [CrossRef]
- Qian, H.; Yan, S.; Ding, P.; Chu, S. Actuator Fault Diagnosis of Nonlinear Systems Based on Unknown Input Root-Mean-Square Cubature Kalman Filter. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Vouliagmeni, Greece, 28 June–1 July 2022; pp. 767–772. [Google Scholar] [CrossRef]
- Ge, Q.; Ma, Z.; Lu, Z.; Feng, X. Fault-Tolerant Cubature Kalman Filter for Engineering Estimation Control Systems. IEEE Trans. Cybern. 2024, 54, 3943–3953. [Google Scholar] [CrossRef]
- Hu, X.; Luo, S.; Xu, D.; Wan, B. A Quantitative Method for the Fault Diagnosability of Affine Nonlinear System. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 5974–5979. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X. Geometric Approach Based Fault Detection and Isolation: A Review. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 4136–4141. [Google Scholar] [CrossRef]
- Guo, T.; Guo, H.; Tu, L.; Huang, L.; Lu, Y. Nonlinear Optimal Control Method for DC/DC Converters in DC Microgrid Based on the Differential Geometry Theory. In Proceedings of the 2023 IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 15–17 September 2023; Volume 7, pp. 1036–1040. [Google Scholar] [CrossRef]
- Shumsky, A.Y.; Zhirabok, A.N. Nonlinear diagnostic filter design: Algebraic and geometric points of view. Int. J. Appl. Math. Comput. Sci. 2006, 16, 115–127. [Google Scholar]
- Filaretov, V.; Zuev, A.; Zhirabok, A.; Protsenko, A. Development of fault accommodation system for thrusters of underwater robots. In Proceedings of the International Conference “Nonlinearity, Information and Robotics”, Innopolis, Russia, 26–29 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zabihifar, S.H.; Yushchenko, A.S.; Navvabi, H. Robust control based on adaptive neural network for Rotary inverted pendulum with oscillation compensation. Neural Comput. Appl. 2020, 32, 14667–14679. [Google Scholar] [CrossRef]
- Chopdar, S.M.; Koshti, A.K. Fault Detection and Classification in Power System Using Artificial Neural Network. In Proceedings of the 2022 2nd International Conference on Intelligent Technologies (CONIT), Hubli, India, 24–26 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chu, K.; Chew, K.; Chang, Y. Fault Diagnosis System of Hall Sensor in Brushless DC Motor based on Neural Networks Approach. In Proceedings of the 2022 IEEE 18th International Colloquium on Signal Processing & Applications (CSPA), Selangor, Malaysia, 12 May 2022; pp. 35–40. [Google Scholar] [CrossRef]
- Dai, Y.; Ren, S.; Si, F. A Novel Fault Diagnosis Method Integrating Reconstruction-based Principal Component Analysis with Probabilistic Neural Network on Condenser. In Proceedings of the 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 22–24 April 2022; pp. 496–501. [Google Scholar] [CrossRef]
- Ammar, A.; Bellakhal, M.; Hamza, T.; Belaroussi, O.; Benakcha, M. Open-Switch Fault Detection of Five-Phase PMSM Drive Using TS-Fuzzy Logic Strategy. In Proceedings of the 2024 2nd International Conference on Electrical Engineering and Automatic Control (ICEEAC), Setif, Algeria, 12–14 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Rana, S.G.; Talati, S.; Desai, M.J. Fuzzy Logic Technique based Fault Diagnosis for Electrical Distribution Network. In Proceedings of the 2024 3rd International Conference for Innovation in Technology (INOCON), Bangalore, India, 1–3 March 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Shen, Q.; Shi, P.; Lim, C.P. Fuzzy Adaptive Fault-Tolerant Stability Control Against Novel Actuator Faults and Its Application to Mechanical Systems. IEEE Trans. Fuzzy Syst. 2024, 32, 2331–2340. [Google Scholar] [CrossRef]
- Yan, Y.; Wei, X.; Li, X.; Li, S. Fault diagnosis method of launch vehicle based on sequential neural network. In Proceedings of the 2023 2nd International Symposium on Aerospace Engineering and Systems (ISAES), Nanjing, China, 19–21 May 2023; pp. 208–212. [Google Scholar] [CrossRef]
- Cheng, R.; Li, L.; Li, H.; Cheng, S.; Fang, X.; Fan, Y. Fixed-Time Fault-Tolerant Sliding Mode Control for Robot Manipulator. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 581–586. [Google Scholar] [CrossRef]
- Lee, J.; Oh, K.; Yoon, Y.; Song, T.; Lee, T.; Yi, K. Adaptive Fault Detection and Emergency Control of Autonomous Vehicles for Fail-Safe Systems Using a Sliding Mode Approach. IEEE Access 2022, 10, 27863–27880. [Google Scholar] [CrossRef]
- Zeghlache, A.; Mekki, H.; Djerioui, A.; Benkhoris, M.F.; Dahmane, N. Fault-tolerant control of PMSM based on second-order sliding mode. In Proceedings of the 2022 IEEE International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 26–28 October 2022; Volume 4, pp. 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Fang, Y.-M.; Li, J.-X.; Li, K.-D. Fixed-Time Sliding Mode Fault-Tolerant Consensus Control for Second-Order Multi-Agent System with Actuator Fault. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 4153–4158. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, C.; Zhao, J. Adaptive Sliding Mode-based Fault-tolerant Tracking Control of Multi-USV Systems. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 5980–5985. [Google Scholar] [CrossRef]
- Elghoul, K.; Dehri, K.; Abdennour, R.B. A Fault Tolerant Second Order Sliding Mode Control. In Proceedings of the 2023 IEEE 11th International Conference on Systems and Control (ICSC), Sousse, Tunisia, 18–20 December 2023; pp. 811–816. [Google Scholar] [CrossRef]
- Cheng, C.; Ge, C.; Fu, Z.; Liu, Y.; Chen, H. Fault Detection Based on Least Squares with Limited Samples. In Proceedings of the 2022 5th International Conference on Robotics, Control and Automation Engineering (RCAE), Changchun, China, 28–30 October 2022; pp. 65–69. [Google Scholar] [CrossRef]
- Gajula, K.; Marepalli, L.K.; Yao, X.; Herrera, L. Recursive Least Squares and Adaptive Kalman Filter-Based State and Parameter Estimation for Series Arc Fault Detection on DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4715–4724. [Google Scholar] [CrossRef]
- Elshenawy, L.M.; Gafar, A.A.; Awad, H. Fault detection and diagnosis strategy for wind turbine system using partial least square technique. In Proceedings of the 2023 3rd International Conference on Electronic Engineering (ICEEM), Menouf, Egypt, 7–8 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley & Sons: New York, NY, USA, 1999; 494p. [Google Scholar]
- Zhirabok, A.; Zuev, A.; Filaretov, V.; Shumsky, A. Fault identification in nonlinear dynamic systems not satisfying matching, minimum phase, and detectability conditions. Int. J. Syst. Sci. 2022, 53, 1390–1400. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K.; Patton, R.J. Sliding mode observers for fault detection and isolation. Automatica 2000, 36, 541–553. [Google Scholar] [CrossRef]
- Filaretov, V.; Yukhimets, D. Control system with reference model for spatial motion of a cargo AUV. In Proceedings of the 2020 International Conference on Control, Automation and Diagnosis (ICCAD), Paris, France, 7–9 October 2020; IEEE: Paris, France, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Filaretov, V.; Yukhimets, D. Synthesis Method of Control System for Spatial Motion of Autonomous Underwater Vehicle. Int. J. Ind. Eng. Manag. 2012, 3, 133–141. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).