Life Cycle Assessment of a Coastal Concrete Bridge Aided by Non-Destructive Damage Detection Methods
Abstract
1. Introduction
2. Materials and Methods
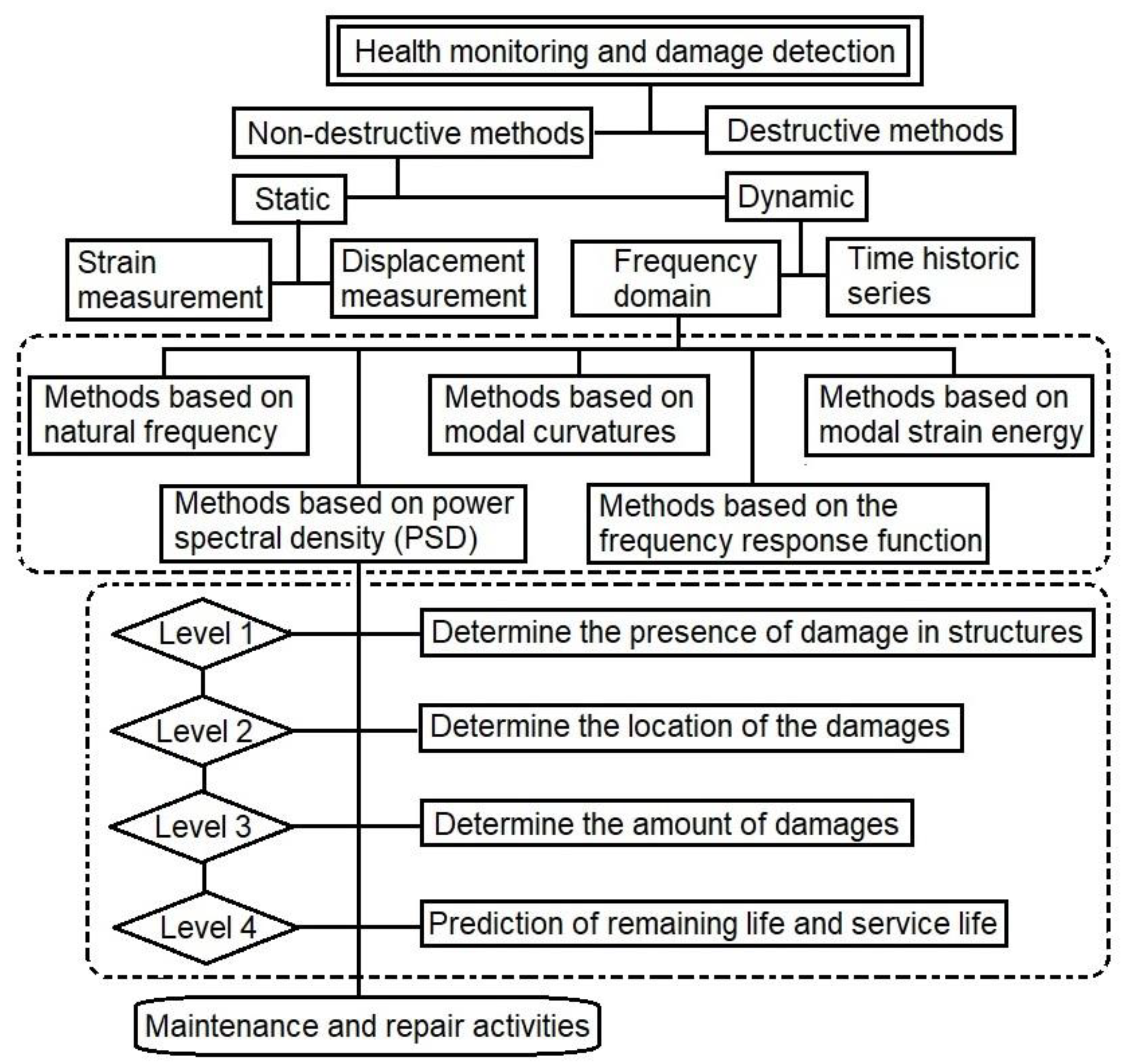
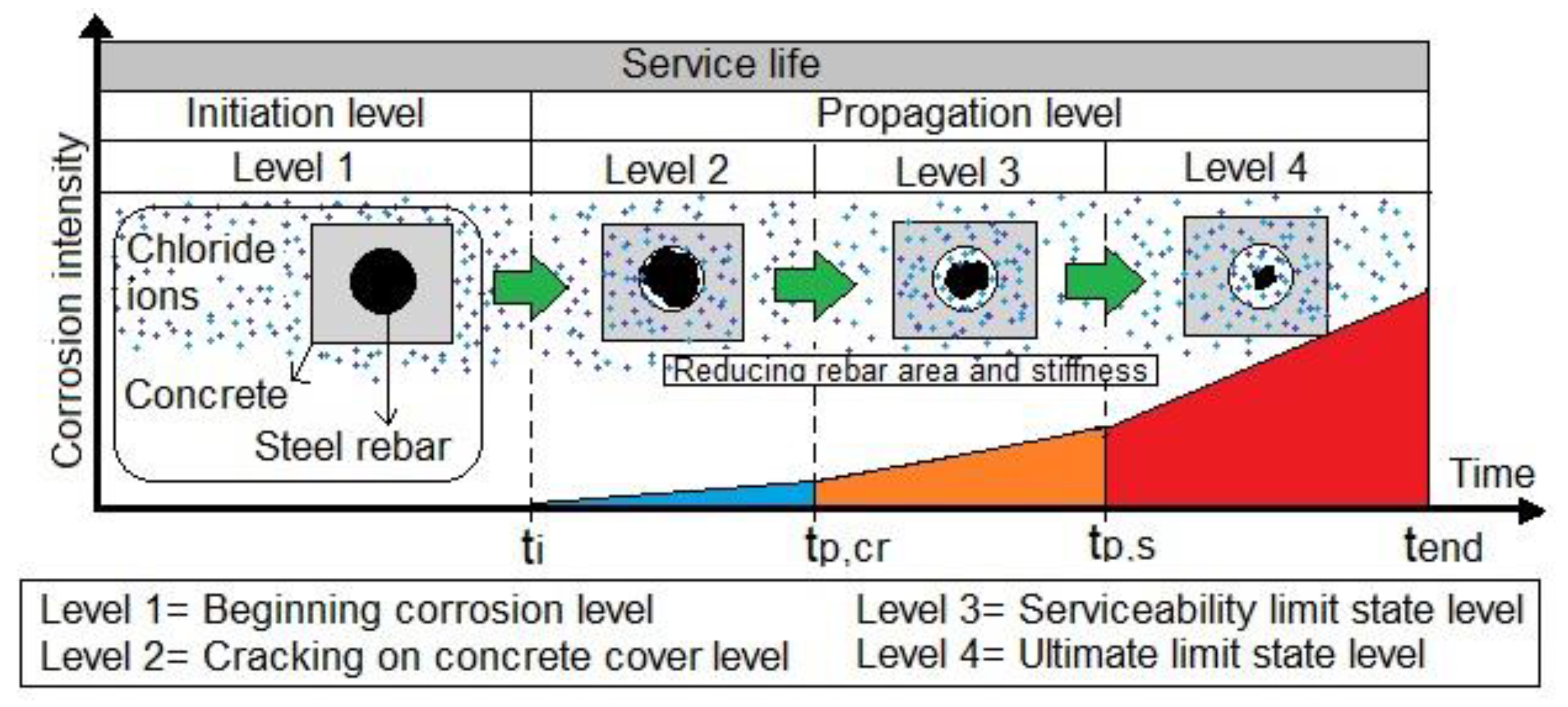
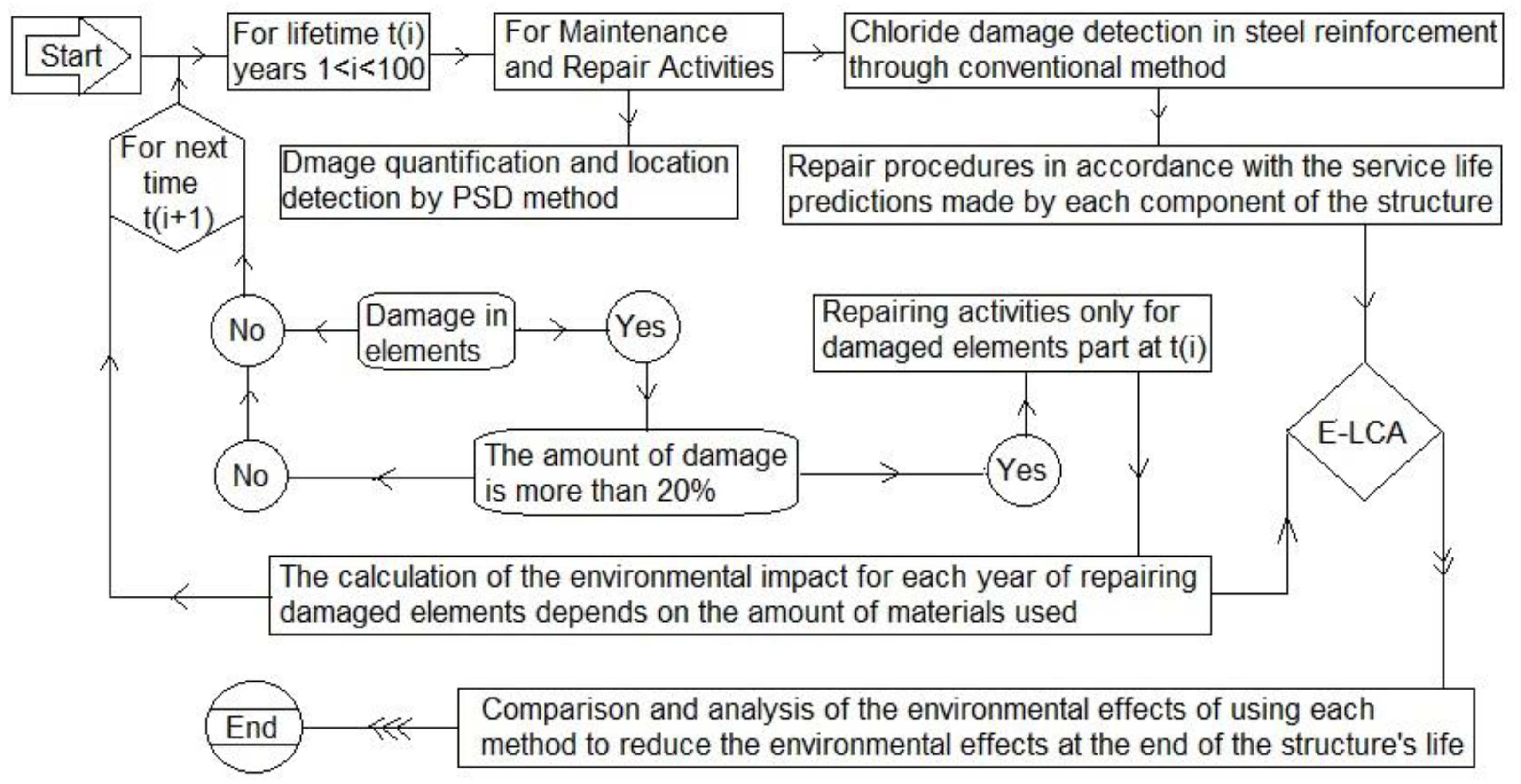
2.1. Service Life and Damage Prediction Methods
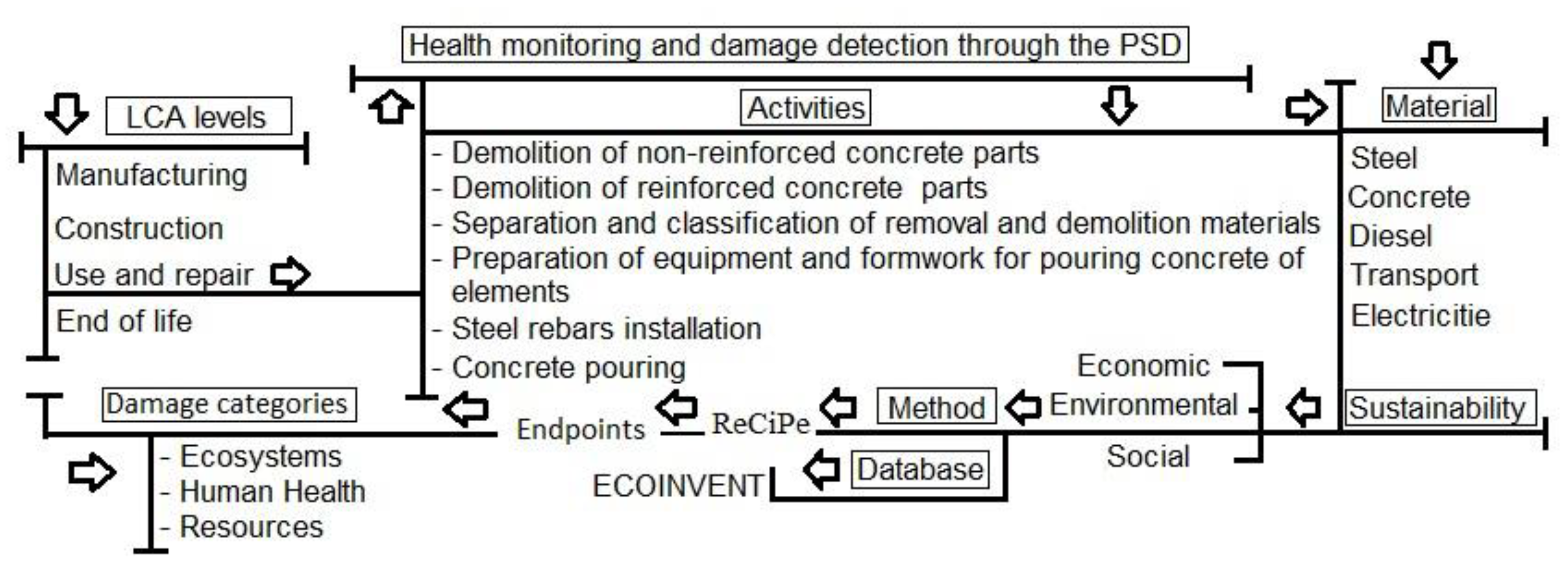
2.2. Life Cycle Assessment
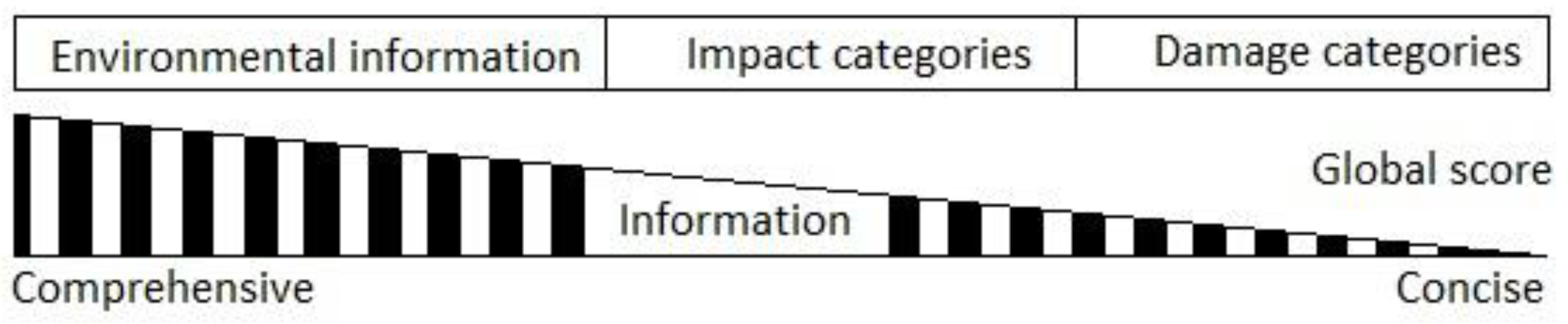
Environmental Impact Assessment
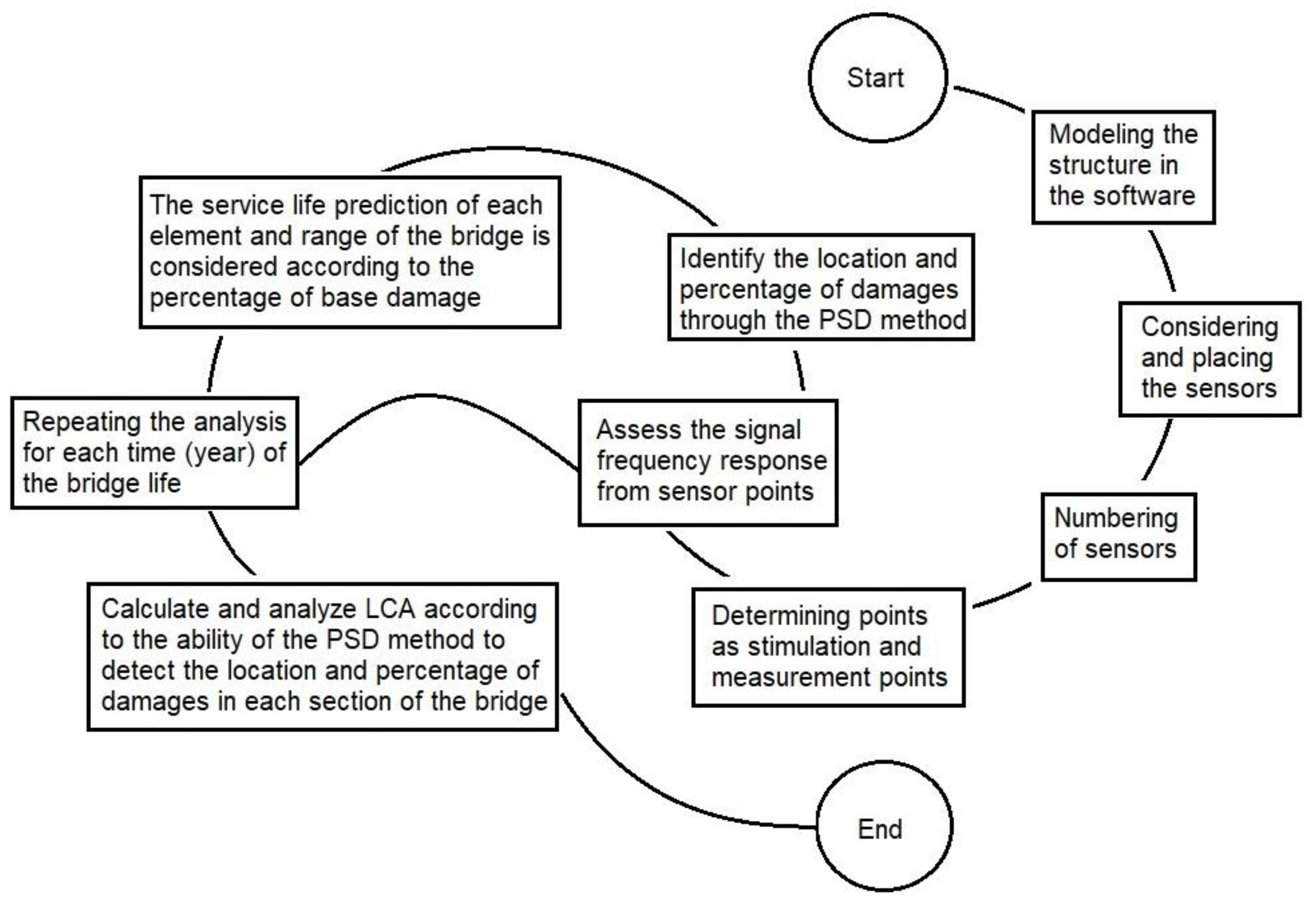
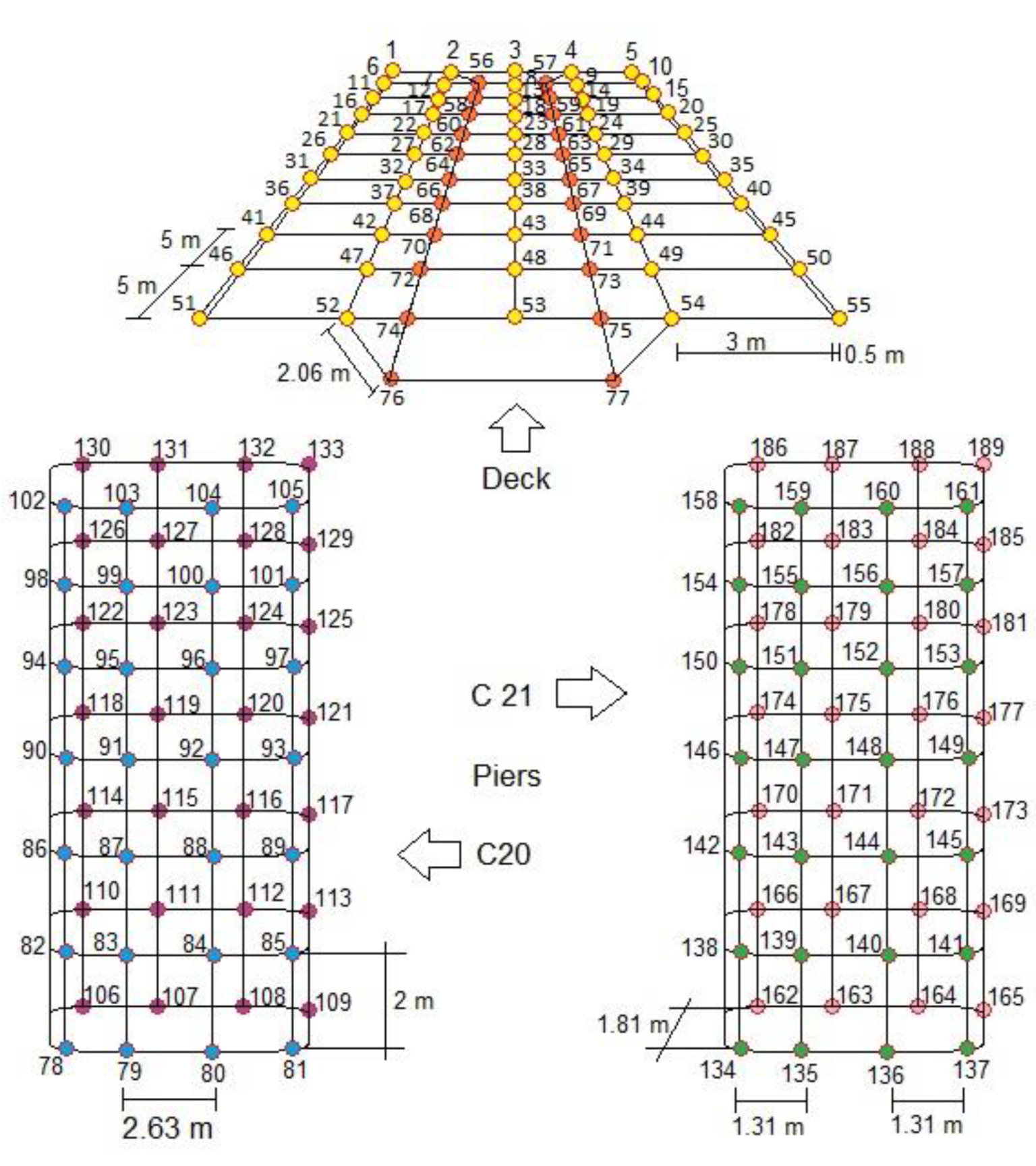
3. Model Description
The Numerical Model Analyses
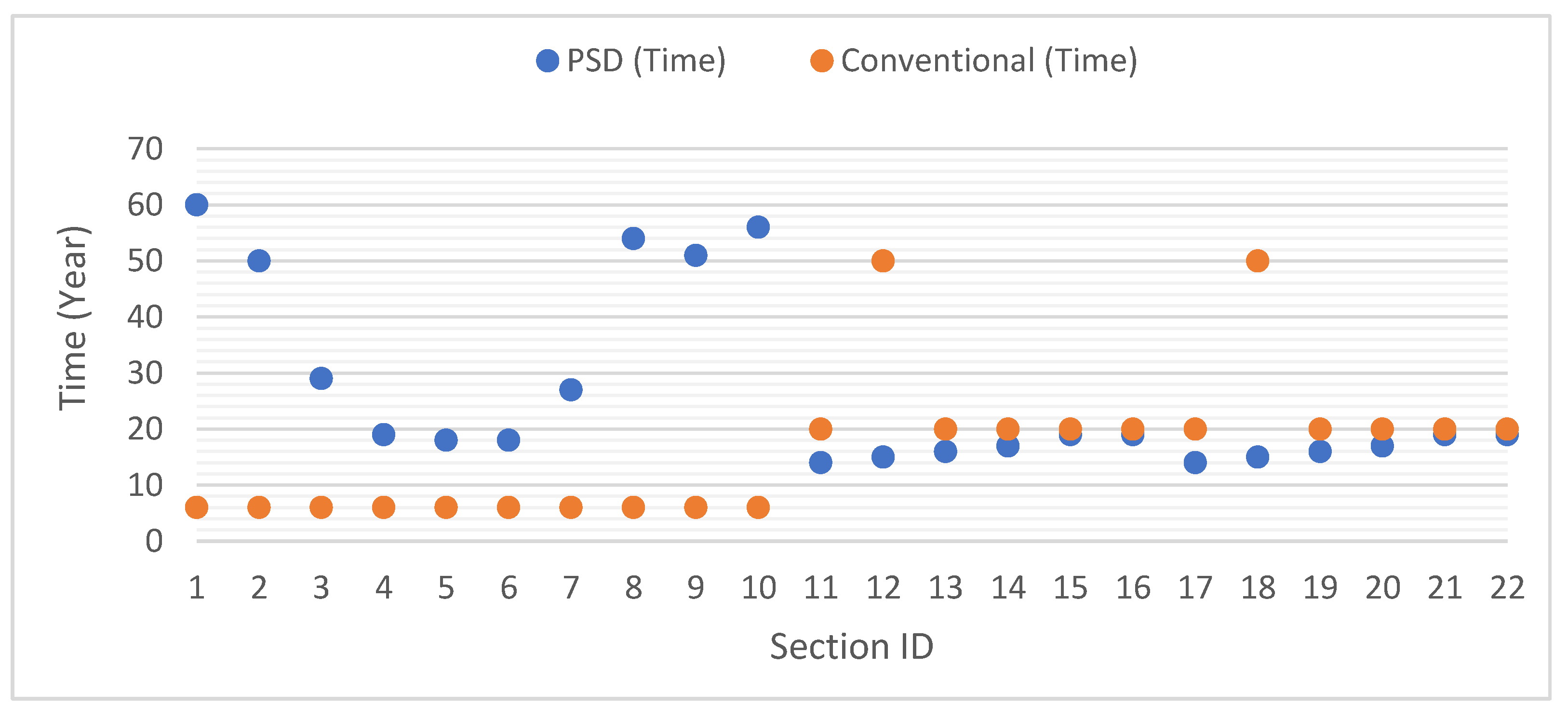
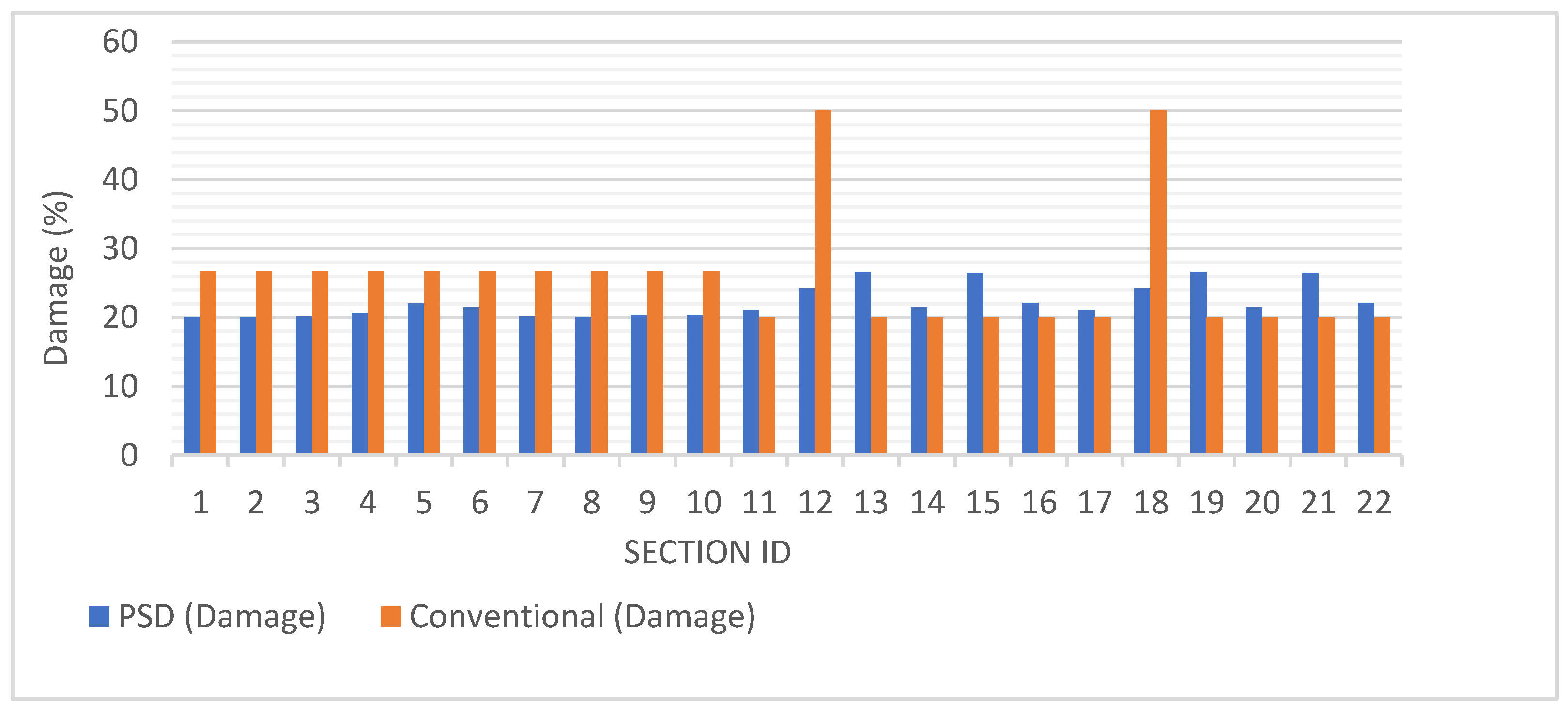
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Keeble, B.R. The Brundtland report: Our common future. Med. Confl. Surviv. 1988, 4, 17–25. [Google Scholar] [CrossRef]
- Liljenström, C.; Björklund, A.; Toller, S. Including maintenance in life cycle assessment of road and rail infrastructure—A literature review. Int. J. Life Cycle Assess. 2022, 27, 316–341. [Google Scholar] [CrossRef]
- Renne, N.; Kara De Maeijer, P.; Craeye, B.; Buyle, M.; Audenaert, A. Sustainable Assessment of Concrete Repairs through Life Cycle Assessment (LCA) and Life Cycle Cost Analysis (LCCA). Infrastructures 2022, 7, 128. [Google Scholar] [CrossRef]
- Caruso, M.; Pinho, R.; Bianchi, F.; Cavalieri, F.; Lemmo, M.T. A Life Cycle Framework for the Identification of Optimal Building Renovation Strategies Considering Economic and Environmental Impacts. Sustainability 2020, 12, 10221. [Google Scholar] [CrossRef]
- Kazemeini, A.; Swei, O. Identifying environmentally sustainable pavement management strategies via deep reinforcement learning. J. Clean. Prod. 2023, 390, 136124. [Google Scholar] [CrossRef]
- Celauro, C.; Cardella, A.; Guerrieri, M. LCA of Different Construction Choices for a Double-Track Railway Line for Sustainability Evaluations. Sustainability 2023, 15, 5066. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Z.; Hu, M.; Li, J.; Wang, Y.; Lu, Z.; Chen, S.; Xia, B. Environmental performances and energy efficiencies of various urban green infrastructures: A life-cycle assessment. J. Clean. Prod. 2020, 248, 119244. [Google Scholar] [CrossRef]
- Balogun, T.B.; Tomor, A.; Lamond, J.; Gouda, H.; Booth, C.A. Life-cycle assessment environmental sustainability in bridge design and maintenance. Proc. ICE Eng. Sustain. 2020, 173, 365–375. [Google Scholar] [CrossRef]
- Pons, J.J.; Penadés-Plà, V.; Yepes, V.; Martí, J.V. Life cycle assessment of earth-retaining walls: An environmental comparison. J. Clean. Prod. 2018, 192, 411–420. [Google Scholar] [CrossRef]
- Navarro, I.J.; Penadés-Plà, V.; Martínez-Muñoz, D.; Rempling, R.; Yepes, V. Life cycle sustainability assessment for multi-criteria decision making in bridge design: A review. J. Civ. Eng. Manag. 2020, 26, 690–704. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. A Review of Multicriteria Assessment Techniques Applied to Sustainable Infrastructure Design. Adv. Civ. Eng. 2019, 2019, 6134803. [Google Scholar] [CrossRef]
- Niu, Y.; Fink, G. Life Cycle Assessment on modern timber bridges. Wood Mater. Sci. Eng. 2019, 14, 212–225. [Google Scholar] [CrossRef]
- Navarro, I.J.; Martí, J.V.; Yepes, V. Reliability-based maintenance optimization of corrosion preventive designs under a life cycle perspective. Environ. Impact Assess. Rev. 2019, 74, 23–34. [Google Scholar] [CrossRef]
- Longarini, N.; Crespi, P.; Zucca, M.; Giordano, N.; Silvestro, G. The advantages of fly ash use in concrete structures. Inz. Miner. 2014, 15, 141–145. [Google Scholar]
- Orozco, C.; Babel, S.; Tangtermsirikul, S.; Sugiyama, T. Understanding the environmental, economic, and social impact of fly ash utilization on early-age high-strength mass concrete using life cycle analysis. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Cheng, B.; Lu, K.; Li, J.; Chen, H.; Luo, X.; Shafique, M. Comprehensive assessment of embodied environmental impacts of buildings using normalized environmental impact factors. J. Clean. Prod. 2021, 334, 130083. [Google Scholar] [CrossRef]
- Khorgade, P.; Rettinger, M.; Burghartz, A.; Schlaich, M. A Comparative Cradle-to-Gate Life Cycle Assessment of Carbon Fiber-Reinforced Polymer and Steel-Reinforced Bridges. Struct. Concr. 2022, 24, 1737–1750. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V.; González-Vidosa, F. Life cycle impact assessment of corrosion preventive designs applied to prestressed concrete bridge decks. J. Clean. Prod. 2018, 196, 698–713. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Social life cycle assessment of concrete bridge decks exposed to aggressive environments. Environ. Impact Assess. Rev. 2018, 72, 50–63. [Google Scholar] [CrossRef]
- Peng, J.X.; Yang, Y.M.; Bian, H.B.; Zhang, J.R.; Wang, L. Optimisation of maintenance strategy of deteriorating bridges considering sustainability criteria. Struct. Infrastruct. Eng. 2022, 18, 395–411. [Google Scholar] [CrossRef]
- Rathod, H.; Gupta, R. Sub-surface simulated damage detection using Non-Destructive Testing Techniques in reinforced-concrete slabs. Constr. Build. Mater. 2019, 215, 754–764. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Tan, X. Review on Vibration-Based Structural Health Monitoring Techniques and Technical Codes. Symmetry 2021, 13, 1998. [Google Scholar] [CrossRef]
- Baybordi, S.; Esfandiari, A. Model updating and damage detection of jacket type platform using explicit and exact time domain sensitivity equation. Ocean Eng. 2023, 269, 113551. [Google Scholar] [CrossRef]
- Yao, J.; Zeng, B.; Zhou, Z.; Zhang, Q. Damage identification analysis of Cable-stayed arch-truss based on multi-node time-domain data fusion. Lat. Am. J. Solids Struct. 2023, 20. [Google Scholar] [CrossRef]
- Li, Z.; Lan, Y.; Lin, W. Investigation of Frequency-Domain Dimension Reduction for A2M-Based Bridge Damage Detection Using Accelerations of Moving Vehicles. Materials 2023, 16, 1872. [Google Scholar] [CrossRef]
- Chen, M.J.; Sivakumar, K.; Banyay, G.A.; Golchert, B.M.; Walsh, T.F.; Zavlanos, M.M.; Aquino, W. Bayesian Optimal Sensor Placement for Damage Detection in Frequency-Domain Dynamics. J. Eng. Mech. 2022, 148, 04022078. [Google Scholar] [CrossRef]
- Liu, N.; Schumacher, T.; Li, Y.; Xu, L.; Wang, B. Damage Detection in Reinforced Concrete Member Using Local Time-Frequency Transform Applied to Vibration Measurements. Buildings 2023, 13, 148. [Google Scholar] [CrossRef]
- Yang, Y.B.; Li, Z.; Wang, Z.L.; Liu, Z.; Mo, X.Q.; Qiu, F.Q. Closely spaced modes of bridges estimated by a hybrid time–frequency method using a multi-sensor scanning vehicle: Theory and practice. Mech. Syst. Signal Process. 2023, 192, 110236. [Google Scholar] [CrossRef]
- Khan, M.W.; Akmal Din, N.; Ul Haq, R. Damage detection in a fixed-fixed beam using natural frequency changes. J. Vibroengineering 2020, 30, 38–43. [Google Scholar] [CrossRef][Green Version]
- Wang, Y. Adaptive Finite Element Algorithm for Damage Detection of Non-Uniform Euler-Bernoulli Beams with Multiple Cracks Based on Natural Frequencies. In Adaptive Analysis of Damage and Fracture in Rock with Multiphysical Fields Coupling; Springer: Singapore, 2021; pp. 73–103. [Google Scholar] [CrossRef]
- Ciambella, J.; Pau, A.; Vestroni, F. Modal curvature-based damage localization in weakly damaged continuous beams. Mech Syst Signal Process. 2019, 121, 171–182. [Google Scholar] [CrossRef]
- Ganguli, R. Modal Curvature Based Damage Detection. In Structural Health Monitoring; Springer: Singapore, 2020; pp. 37–78. [Google Scholar] [CrossRef]
- Alavinezhad, M.; Hassanabad, M.G.; Ketabdari, M.J.; Nekooei, M. Numerical and experimental structural damage detection in an offshore flare bridge using a proposed modal strain energy method. Ocean Eng. 2022, 252, 111055. [Google Scholar] [CrossRef]
- Le, T.C.; Ho, D.D. Structural damage identification of plates using two-stage approach combining modal strain energy method and genetic algorithm. In Modern Mechanics and Applications: Select, Proceedings of the International Conference on Modern Mechanics and Applications, Ho Minh City, Vietnam, 2–4 December 2020; Springer: Singapore, 2022; pp. 1004–1017. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, J.; An, X.; Jankowski, Ł.; Duan, Z.; Hu, X. Vehicle parameter identification based on vehicle frequency response function. J. Sound Vib. 2023, 542, 117375. [Google Scholar] [CrossRef]
- Kurent, B.; Brank, B.; Ao, W.K. Model updating of seven-storey cross-laminated timber building designed on frequency-response-functions-based modal testing. Struct. Infrastruct. Eng. 2023, 19, 178–196. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, X.; Xing, J.; Li, Z.; Zhang, Y. Substructure damage identification based on sensitivity of Power Spectral Density. J. Sound Vib. 2023, 545, 117451. [Google Scholar] [CrossRef]
- Hadizadeh-Bazaz, M.; Navarro, I.J.; Yepes, V. Performance comparison of structural damage detection methods based on Frequency Response Function and Power Spectral Density. Dyna 2022, 97, 493–500. [Google Scholar] [CrossRef]
- Nilsson, A.; Liu, B. Frequency domain. In Vibro-Acoustics; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1, pp. 31–66. [Google Scholar] [CrossRef]
- Hadizadeh-Bazaz, M.; Navarro, I.J.; Yepes, V. Power Spectral Density method performance in detecting damages by chloride attack on coastal RC bridge. Struct. Eng. Mech. 2023, 85, 197–206. [Google Scholar] [CrossRef]
- Bayat1a, M.; Ahmadi, H.R.; Mahdavi, N. Application of power spectral density function for damage diagnosis of bridge piers. Struct. Eng. Mech. 2019, 71, 57–63. [Google Scholar] [CrossRef]
- Gunawan, F.E. Reliability of the power spectral density method in predicting structural integrity. Int. J. Innov. Comput. Inf. Control 2019, 15, 1717–1727. [Google Scholar] [CrossRef]
- Hadizadeh-Bazaz, M.; Navarro, I.J.; Yepes, V. Life-Cycle Cost Assessment Using the Power Spectral Density Function in a Coastal Concrete Bridge. J. Mar. Sci. Eng. 2023, 11, 433. [Google Scholar] [CrossRef]
- ISO 14040:2006; Environmental Management—Life Cycle Assessment—Principles and Framework. International Standards Organization: Geneva, Switzerland, 2006.
- ISO 14044:2006; Environmental Management—Life Cycle Assessment—Requirements and Guidelines. International Standards Organization: Geneva, Switzerland, 2006.
- Soust-Verdaguer, B.; Galeana, I.B.; Llatas, C.; Montes, M.; Hoxha, E.; Passer, A. How to conduct consistent environmental, economic, and social assessment during the building design process. A BIM-based Life Cycle Sustainability Assessment method. J. Build. Eng. 2021, 45, 103516. [Google Scholar] [CrossRef]
- Zheng, Z.D.; Lu, Z.R.; Chen, W.H.; Liu, J.K. Structural damage identification based on power spectral density sensitivity analysis of dynamic responses. Comput. Struct. 2015, 146, 176–184. [Google Scholar] [CrossRef]
- Pedram, M.; Esfandiari, A.; Khedmati, M.R. Damage detection by a FE model updating method using power spectral density: Numerical and experimental investigation. J. Sound Vib. 2017, 397, 51–76. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete; Report. Cement-och Betonginst 1982, 4, 468. [Google Scholar]
- Zhang, D.; Zeng, Y.; Fang, M.; Jin, W. Service life prediction of precast concrete structures exposed to chloride environment. Adv. Civ. Eng. 2019, 2019, 3216328. [Google Scholar] [CrossRef]
- Spanish Ministry of Public Works. EHE-08 Instrucción del Hormigón Estructural; Spanish Ministry of Public Works: Madrid, Spain, 2008; ISBN 978-84-498-0899-9. [Google Scholar]
- FIB. Model Code for Service Life Design; Federation Internationale du Beton, fib. Bulletin: Lausanne, Switzerland, 2006; No. 34. [Google Scholar]
- Esfandiari, A.; Bakhtiari-Nejad, F.; Rahai, A.; Sanayei, M. Structural model updating using frequency response function and quasi-linear sensitivity equation. J. Sound Vib. 2009, 326, 557–573. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Martínez-Muñoz, D.; García-Segura, T.; Navarro, I.J.; Yepes, V. Environmental and Social Impact Assessment of Optimized Post-Tensioned Concrete Road Bridges. Sustainability 2020, 12, 4265. [Google Scholar] [CrossRef]
- Barahmand, Z.; Eikeland, M.S. Life Cycle Assessment under Uncertainty: A Scoping Review. World 2022, 3, 692–717. [Google Scholar] [CrossRef]
- Goedkoop, M.; Heijungs, R.; Huijbregts, M.; De Schryver, A.; Struijs, J.; Van Zelm, R. ReCiPe 2008 a Life Cycle Impact Assessment Method Which Comprises Harmonised Category Indicators at the Midpoint and the Endpoint Level; Ministerie van VROM: Hague, The Netherlands, 2009.
- Huijbregts, M.A.J.; Steinmann, Z.J.N.; Elshout, P.M.F.; Stam, G.; Verones, F.; Vieira, M.D.M.; Hollander, A.; Zijp, M.; Zelm, R. ReCiPe 2016 a Harmonized Life Cycle Impact Assessment Method at Midpoint and Endpoint Level Report I: Characterization; Rijksinstituut voor Volksgezondheid en Milieu RIVM: De Bilt, The Netherlands, 2016.
- Association, E. Ecoinvent Datebase. Ecoinvent 3.3. 2016. Available online: https://ecoinvent.org/the-ecoinvent-database (accessed on 20 May 2023).
- León, J.; Prieto, F.; Rodríguez, F. Proyecto de rehabilitación del puente de la Isla de Arosa. Hormig. Acero 2013, 270, 75–89. [Google Scholar]
- Pérez-Fadón Martínez, S. Puente a la Isla de Arosa. Hormig. Acero 1985, 36, 157. [Google Scholar]
- Pérez-Fadón Martínez, S. Puente sobre la Ría de Arosa. Rev. Obras Publicas 1986, 3243, 1–16. [Google Scholar]



| Marine Exposure Classification | Cs (% of Concrete Weight) | Vcorr (μm/Year) | D0 (×10−12 m2/s) |
|---|---|---|---|
| Aerial (IIIa) | 0.14 | 20 | 10.0 |
| Submerged (IIIb) | 0.72 | 4 | |
| In tide zone (IIIc) | 0.50 | 50 |
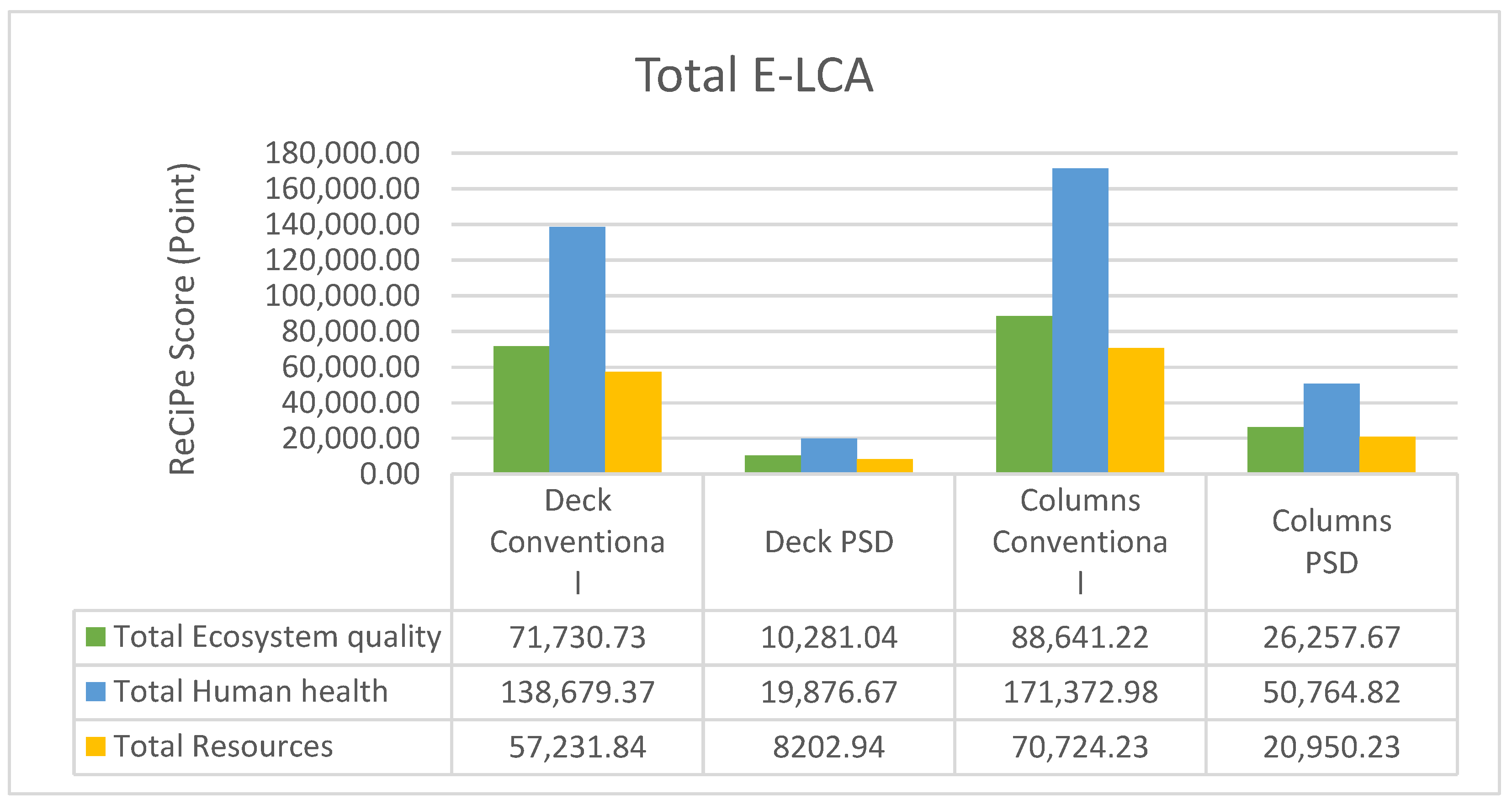
| Impact Category | Environmental Impact (Points) | |||
|---|---|---|---|---|
| Desk | Columns | |||
| Conventional | PSD | Conventional | PSD | |
| Ecosystem quality | ||||
| Agricultural land occupation | 1872.4 | 268.3 | 2313.8 | 685.4 |
| Climate change, ecosystems | 46,192.7 | 6620.7 | 57,082.6 | 16,909.2 |
| Freshwater ecotoxicity | 5.9 | 0.8 | 7.3 | 2.1 |
| Freshwater eutrophication | 23.4 | 3.3 | 29.0 | 8.5 |
| Marine ecotoxicity | 129.2 | 18.5 | 159.6 | 47.2 |
| Natural land transformation | 22,668.7 | 3249.0 | 28,012.8 | 8298.0 |
| Terrestrial acidification | 151.4 | 21.7 | 187.1 | 55.4 |
| Terrestrial ecotoxicity | 512.9 | 73.5 | 633.8 | 187.7 |
| Urban land occupation | 444.1 | 63.6 | 548.8 | 162.5 |
| Human health | ||||
| Climate change, human health | 58,117.0 | 8329.8 | 71,818.1 | 21,274.2 |
| Human toxicity | 72,315.3 | 10,364.8 | 89,363.6 | 26,471.6 |
| Ionizing radiation | 60.7 | 8.7 | 75.0 | 22.2 |
| Ozone depletion | 3.7 | 0.5 | 4.6 | 1.3 |
| Particulate matter formation | 7975.7 | 1143.1 | 9855.9 | 2919.5 |
| Photochemical oxidant formation | 206.7 | 29.6 | 255.5 | 75.6 |
| Resources | ||||
| Fossil depletion | 49,089.4 | 7035.9 | 60,662.3 | 17,969.6 |
| Metal depletion | 8142.3 | 1167.0 | 10,061.9 | 2980.5 |
| Impact Category | Difference | Impact Category | Difference |
|---|---|---|---|
| Ecosystem Quality | Human Health | ||
| Agricultural land occupation | 3232.5 | Climate change, human health | 100,331 |
| Climate change, ecosystems | 79,745.4 | Human toxicity | 124,842.5 |
| Freshwater ecotoxicity | 10.3 | Ionizing radiation | 104.7 |
| Freshwater eutrophication | 40.5 | Ozone depletion | 6.54 |
| Marine ecotoxicity | 223 | Particulate matter formation | 13,768.9 |
| Natural land transformation | 39,134.4 | Photochemical oxidant formation | 356.9 |
| Terrestrial acidification | 261.4 | Resources | |
| Terrestrial ecotoxicity | 885.5 | Fossil depletion | 84,746.2 |
| Urban land occupation | 766.71 | Metal depletion | 14,056.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadizadeh-Bazaz, M.; Navarro, I.J.; Yepes, V. Life Cycle Assessment of a Coastal Concrete Bridge Aided by Non-Destructive Damage Detection Methods. J. Mar. Sci. Eng. 2023, 11, 1656. https://doi.org/10.3390/jmse11091656
Hadizadeh-Bazaz M, Navarro IJ, Yepes V. Life Cycle Assessment of a Coastal Concrete Bridge Aided by Non-Destructive Damage Detection Methods. Journal of Marine Science and Engineering. 2023; 11(9):1656. https://doi.org/10.3390/jmse11091656
Chicago/Turabian StyleHadizadeh-Bazaz, Mehrdad, Ignacio J. Navarro, and Víctor Yepes. 2023. "Life Cycle Assessment of a Coastal Concrete Bridge Aided by Non-Destructive Damage Detection Methods" Journal of Marine Science and Engineering 11, no. 9: 1656. https://doi.org/10.3390/jmse11091656
APA StyleHadizadeh-Bazaz, M., Navarro, I. J., & Yepes, V. (2023). Life Cycle Assessment of a Coastal Concrete Bridge Aided by Non-Destructive Damage Detection Methods. Journal of Marine Science and Engineering, 11(9), 1656. https://doi.org/10.3390/jmse11091656








