Bi-Objective Integrated Scheduling of Quay Cranes and Automated Guided Vehicles
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Related Work
1.2.1. QCSP
1.2.2. Integrated Scheduling Related to QCs
- (1)
- Integrated scheduling of QCs and horizontal transport equipment
- (2)
- Integrated Scheduling Problem of other types of equipment
1.3. Contributions and Structure
- (1)
- The majority of the existing literature on integrated scheduling focuses on optimizing a single objective, with less consideration of the efficiency of AGVs. Considering the pooling strategy of AGVs, this research constructs a MOMIP model with the objectives of minimizing vessels’ makespan and AGVs’ unladen time.
- (2)
- An NSGA-II algorithm embedded with a heuristic method is designed to solve the proposed mathematical model, in which the heuristic method consists of two steps: a QC allocation strategy based on bays and a QC-AGV scheduling strategy based on containers. The heuristic method can quickly complete the allocation and scheduling of the QCs and AGVs.
- (3)
- The effectiveness of the proposed model and the NSGA-II algorithm are tested based on differently sized computational experiments, and the results of the sensitivity analysis in this research can provide some references for terminal operators.
2. Problem Description and Formulation
2.1. Problem Description
- Import containers and export containers are stored in different blocks.
- The stowage plan is already provided. In practice, the stowage plan is usually drawn up by liner companies, and terminals will draw up a handling plan based on it. Thus, this assumption is in line with the real situation.
- There are precedence relationships between containers. For example, the discharging containers are required to be handled before the loading ones when they are both in the same bay. Moreover, tasks on the deck must be performed before those in the hold.
- QCs are not allowed to cross each other. This is because QCs move on the same track while working.
- Two adjacent QCs must be at least one bay apart to perform their tasks without interference.
- Preemption on a task is not allowed, which means that a QC will not stop its operation on a task until it completes it.
- There is enough space to stack containers in the yard, and the AGVs will not wait for the operation of YCs.
2.2. Mathematical Model
3. Solution Development
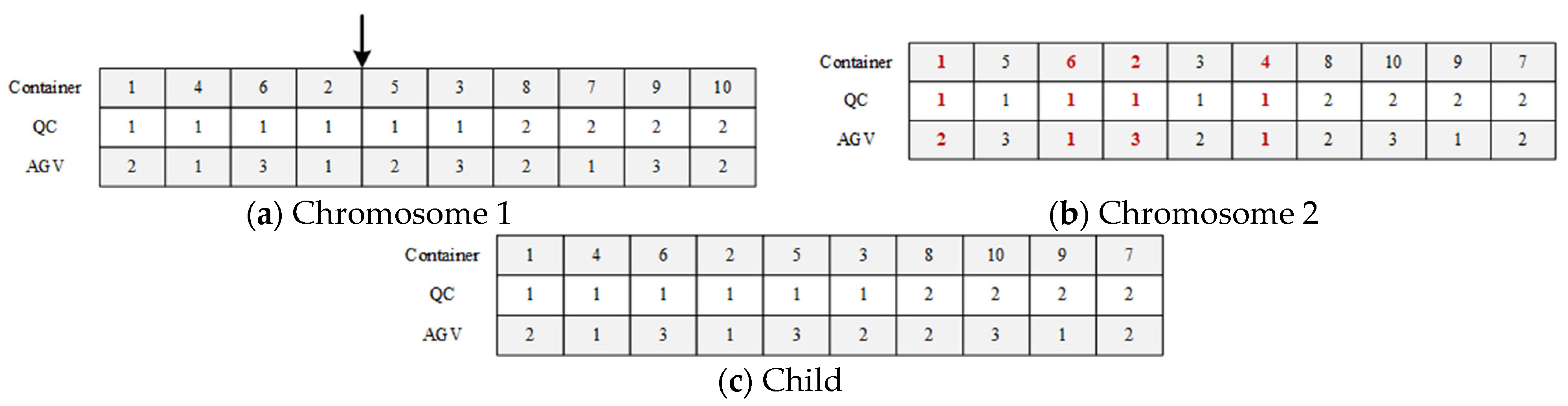
3.1. Chromosome Encoding
- (1)
- Take QC 1 as an example; it will serve container 1 first, and then sequentially serve containers 4, 6, 2, 5 and 3.
- (2)
- Now look at AGV 2. It will deliver container 1 first and then deliver containers 5, 8 and finally 10.
- (3)
- Explanations for other QCs and AGVs follow the above steps.
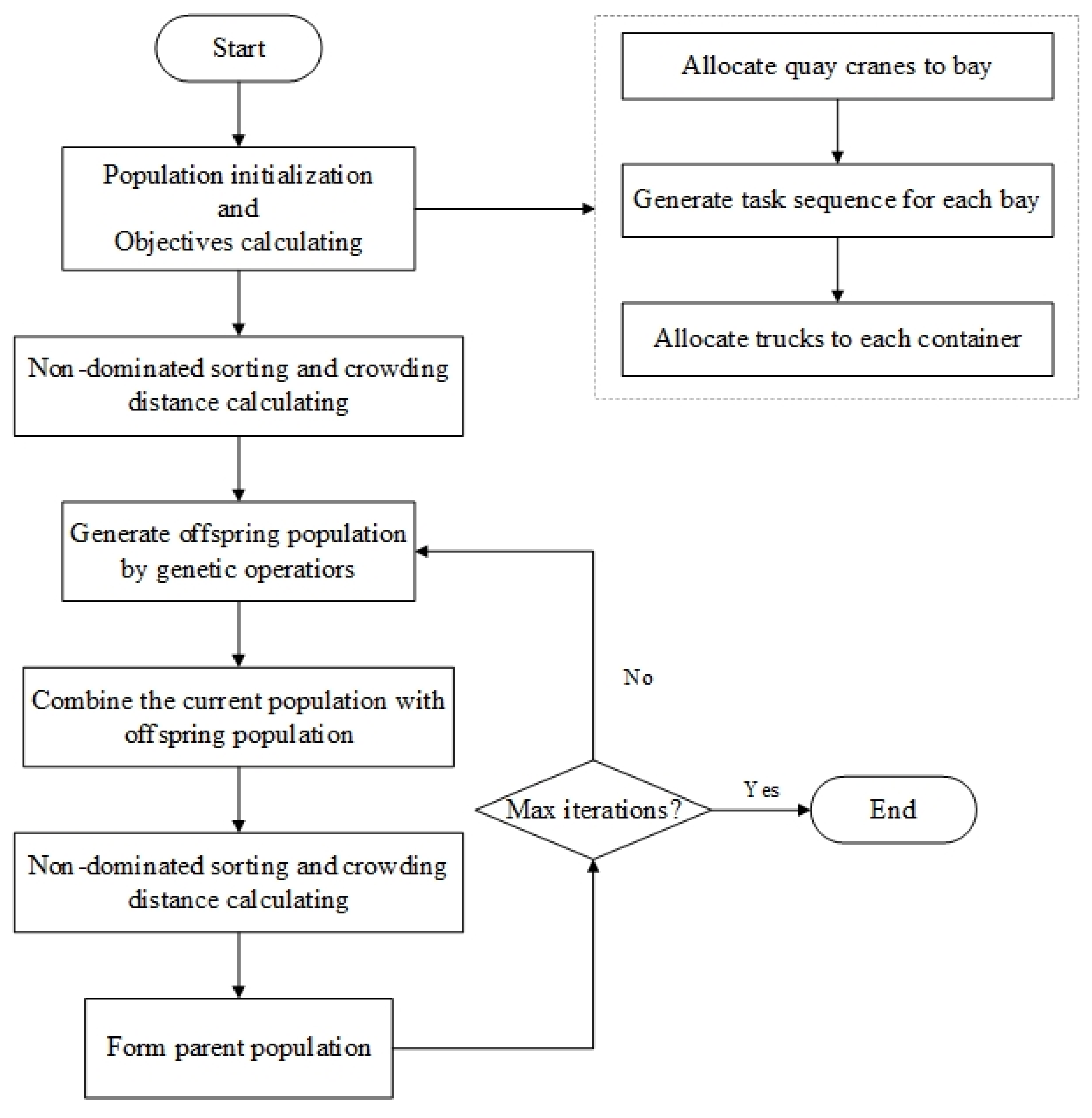
3.2. Population Initialization
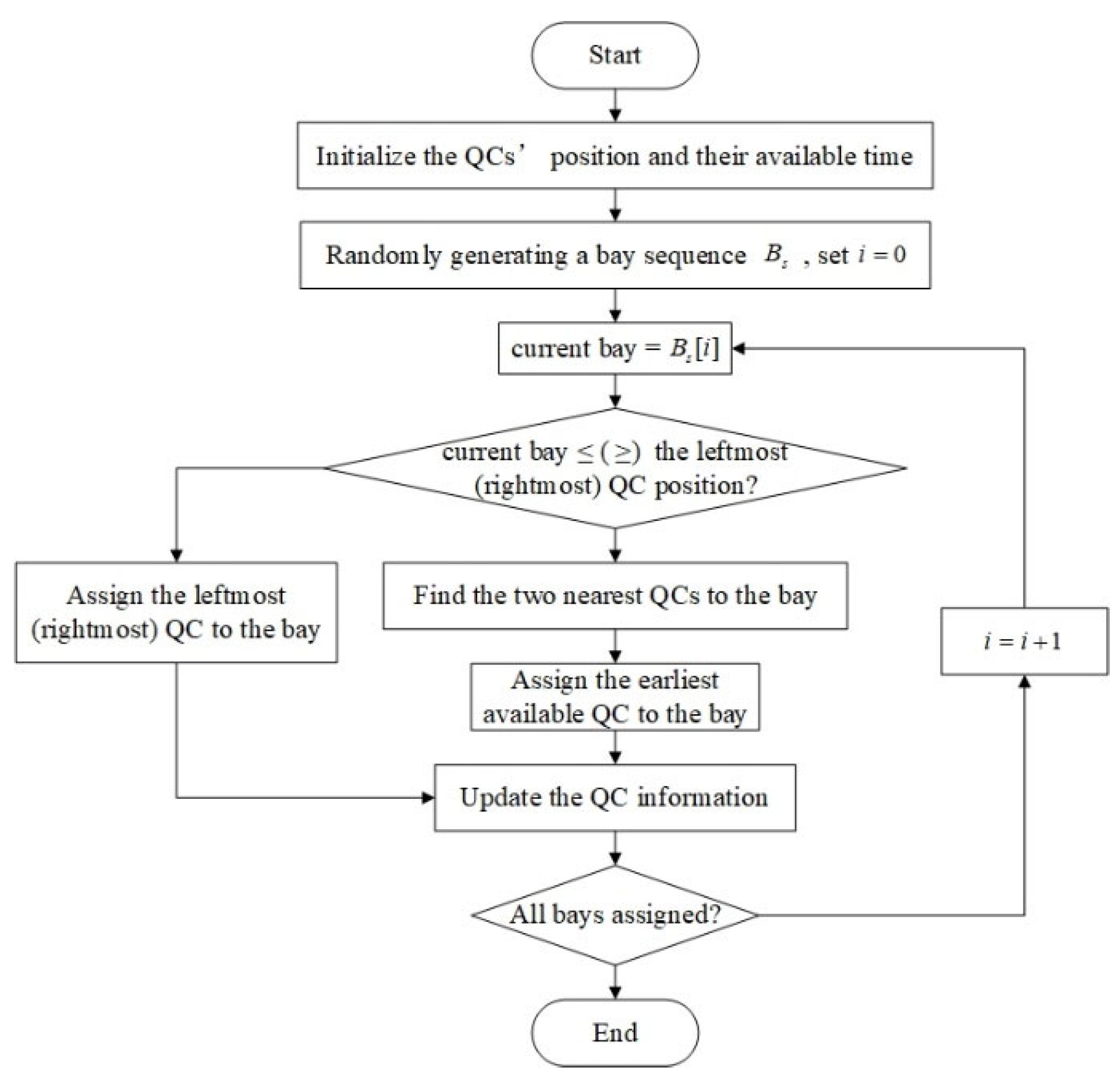
- QCs are assigned to bays based on the position and available time, and the process of this part is shown in Figure 4. The strategy specifically includes the following steps: (1) initialize the position and available time of all QCs. (2) Allocate QCs to each bay according to the position and available time. There are mainly two situations while allocating QCs. The first is that only one side of the current bay has QCs. Then, the nearest QC on this side is assigned to the bay. The second is that there are QCs on both sides of the current bay. In this case, the one with the earlier available time among the two QCs closest to the current bay will be assigned. (3) Update the information of the QC and allocate the quay crane for the next bay until all bays are allocated.
- 2.
- The sequence of operations for all tasks in each berth is randomly generated and corrected based on the precedence relationships.
- 3.
- Allocate the AGVs to containers in terms of the quay crane scheduling sequence. Algorithm 1 indicates the strategy for AGV allocation. The specific process is as follows: (1) firstly, calculate the QC operation time of each container according to the QC allocation results. (2) Secondly, assign the AGV with the earliest available time to the current task. (3) Since the allocation of AGVs may require the corresponding QC to wait or wait for QC operations, it is necessary to update the scheduling information of the task according to the type of task (import/export container), available AGV time and the original planned QC operation time. (4) Finally, update the information of AGVs. Do step 2 to 4 until all tasks are scheduled and completed.
| Algorithm 1 AGV Assignment |
| 1: Arrange all tasks in ascending order according to the completion time of QCs’ operations |
| 2: Set , |
| 3. while , do: |
| 4. Assign task i to AGV k with the earliest available time |
| 5. Add the AGV k to |
| 6. Update the information of AGV k, set |
| 7. end while |
| 8. return |
3.3. Genetic Operators Design
3.4. Stop Criterion
4. Experimental Results
4.1. Performance Indicators
- (1)
- Inverted generational distance (IGD): this metric was developed by Czyzzak et al. [41] and was used to represent the average distance from PF to the non-dominated solution set obtained by the algorithm. So, the smaller the IGD, the better the performance of the algorithm. The specific calculation process is as follows:
- (2)
- Hypervolume (HV) ratio: Zitzler et al. [42] proposed HV to evaluate the performance of a multi-objective evolutionary algorithm. It has excellent theoretical support and is widely used. The calculation formula is
- (3)
- Number of Pareto solutions (NOP): NOP indicates the number of solutions in PF, and a larger NOP implies that the algorithm is better.
4.2. Problem Generation
- (1)
- The time of unloading or loading a container for a QC is generated following the Gaussian distribution, i.e., .
- (2)
- The speed of the AGV is 210 m/min when loaded and 350 m/min while empty.
- (3)
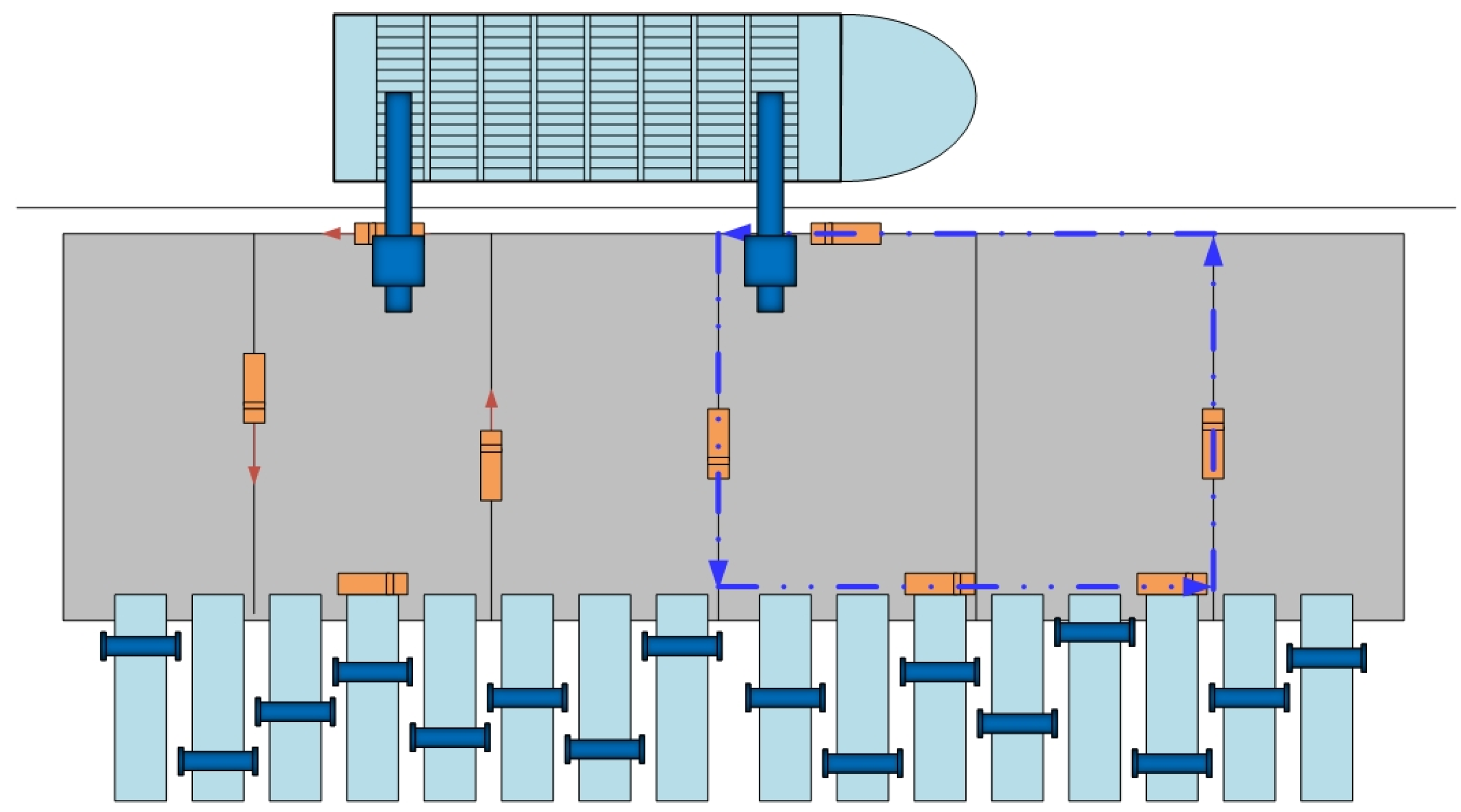
- The layout of the container terminal is shown in Figure 1, where the length of the quay shoreline is 900 m and the horizontal distance from the quay front to the junction of the yard is 200 m. Let the point (0,0) be the intersection point between the left edge of the shoreline and the yard. So, the y coordinates of all the yards are 0, and the x coordinates of each yard area are shown in Table 4.
- (4)
- The position of import and export containers and their precedence relationship in the experiments are randomly generated according to the layout of the container terminal.
4.3. Experimental Results and Analysis
4.3.1. Parameter Setting
4.3.2. Experimental Results
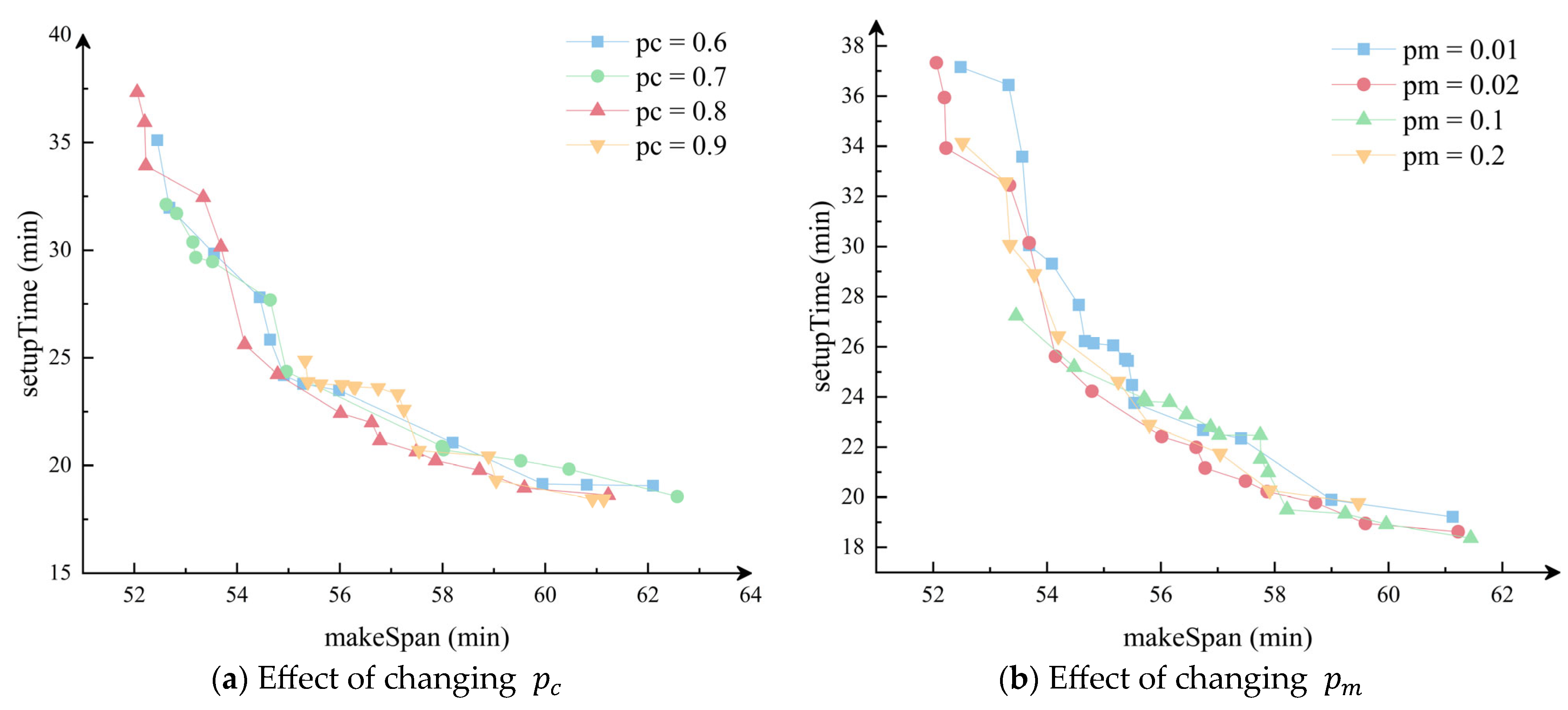
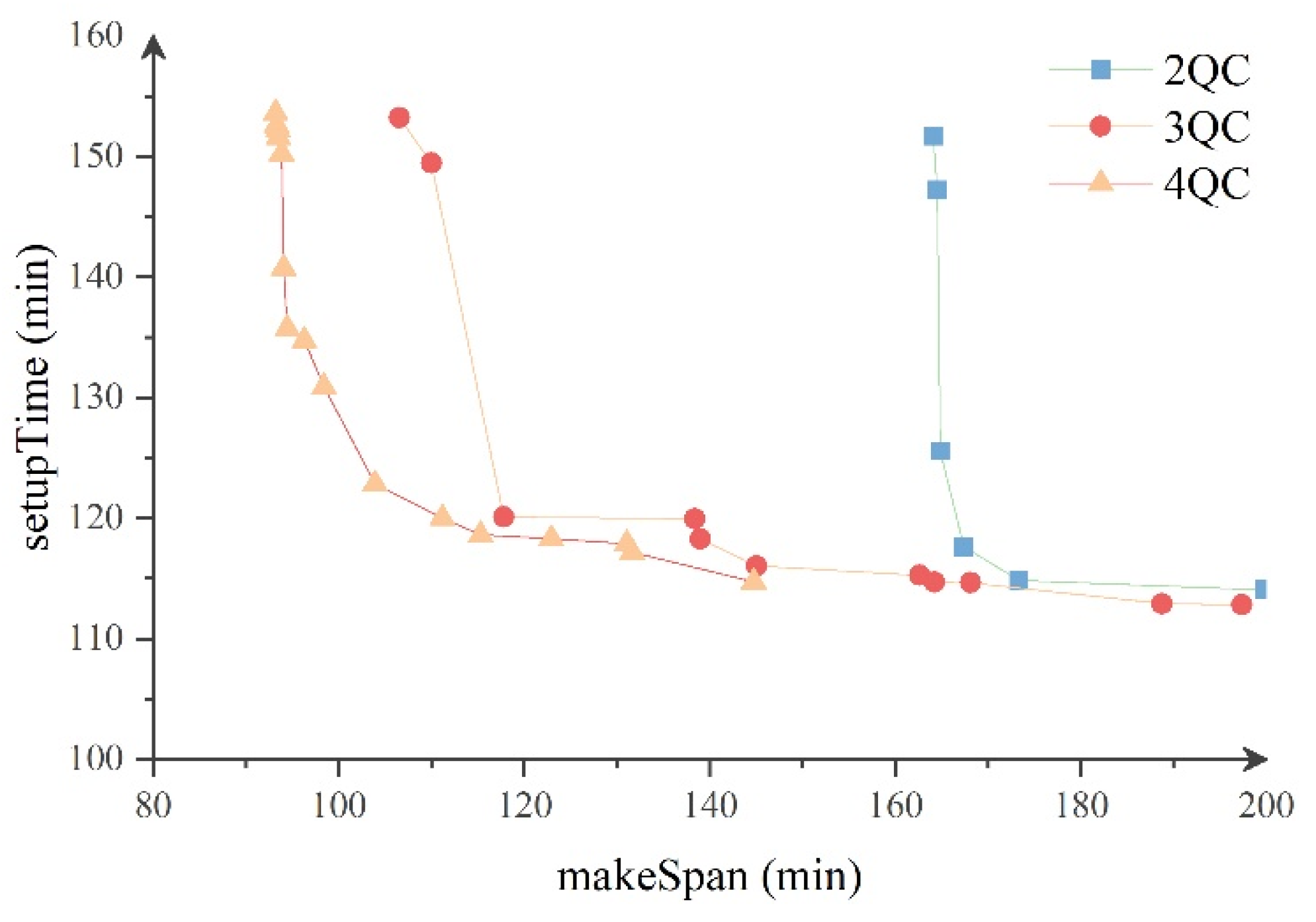
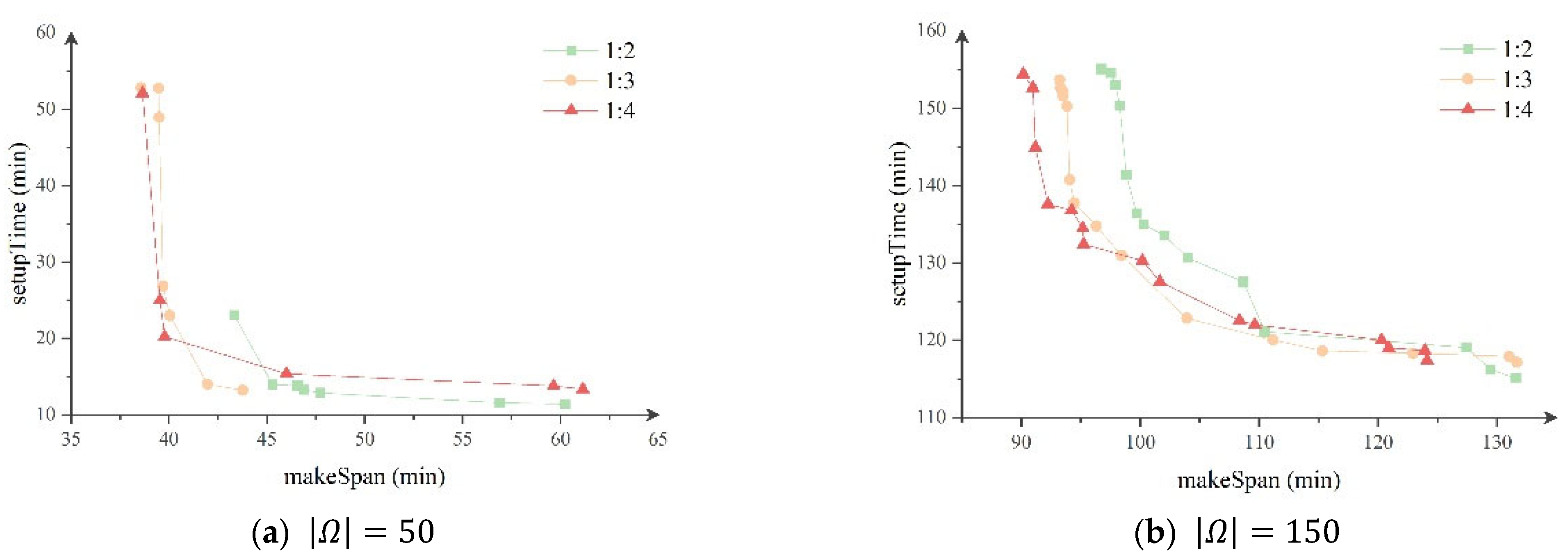
4.3.3. Sensitivity Analysis
5. Conclusions
- The number of QCs has a high influence on the efficiency of terminal operations. The makespan of vessels and the efficiency of AGVs are optimized with the increase in the QCs, but in contrast, the marginal benefit decreases as the number of QCs increases.
- The ratio of QCs and AGVs also affects the efficiency of the terminal. If the vessel has a high volume of containers and needs to leave the port quickly, an average of four AGVs can be assigned to each QC. Otherwise, given the efficiency of the AGVs, an average of three AGVs per bridge should be used.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Peng, J.; Wang, X.; Wan, J. Integrated Resource Assignment and Scheduling Optimization with Limited Critical Equipment Constraints at an Automated Container Terminal. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7607–7618. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Abbasy, M.S.; Zayed, T.; Alfalah, G.; Alkass, S. Synchronized scheduling model for container terminals using simulated double-cycling strategy. Comput. Ind. Eng. 2021, 154, 107118. [Google Scholar] [CrossRef]
- UNCTAD. Review of Maritime Transport; United Nations: San Francisco, CA, USA, 2021. [CrossRef]
- He, J.; Zhang, W.; Huang, Y.; Yan, W. A simulation optimization method for internal trucks sharing assignment among multiple container terminals. Adv. Eng. Inform. 2013, 27, 598–614. [Google Scholar] [CrossRef]
- Daganzo, C.F. The crane scheduling problem. Transp. Res. Part B Methodol. 1989, 238, 159–175. [Google Scholar] [CrossRef]
- Peterkofsky, R.I.; Daganzo, C.F. A branch and bound solution method for the crane scheduling problem. Transp. Res. Part B Methodol. 1990, 24, 159–172. [Google Scholar] [CrossRef]
- Zhu, Y.; Lim, A. Crane scheduling with non-crossing constraint. J. Oper. Res. Soc. 2006, 57, 1464–1471. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, Y.-M. A crane scheduling method for port container terminals. Eur. J. Oper. Res. 2004, 156, 752–768. [Google Scholar] [CrossRef]
- Moccia, L.; Cordeau, J.-F.; Gaudioso, M.; Laporte, G. A branch-and-cut algorithm for the quay crane scheduling problem in a container terminal. Nav. Res. Logist. (NRL) 2005, 53, 45–59. [Google Scholar] [CrossRef]
- Sammarra, M.; Cordeau, J.-F.; Laporte, G.; Monaco, M.F. A tabu search heuristic for the quay crane scheduling problem. J. Sched. 2007, 10, 327–336. [Google Scholar] [CrossRef]
- Al-Dhaheri, N.; Jebali, A.; Diabat, A. The quay crane scheduling problem with nonzero crane repositioning time and vessel stability constraints. Comput. Ind. Eng. 2016, 94, 230–244. [Google Scholar] [CrossRef]
- Al-Dhaheri, N.; Diabat, A. The Quay Crane Scheduling Problem. J. Manuf. Syst. 2015, 36, 87–94. [Google Scholar] [CrossRef]
- Chen, J.H.; Bierlaire, M. The study of the unidirectional quay crane scheduling problem: Complexity and risk-aversion. Eur. J. Oper. Res. 2017, 260, 613–624. [Google Scholar] [CrossRef]
- Msakni, M.K.; Diabat, A.; Rabadi, G.; Al-Salem, M.; Kotachi, M. Exact methods for the quay crane scheduling problem when tasks are modeled at the single container level. Comput. Oper. Res. 2018, 99, 218–233. [Google Scholar] [CrossRef]
- Rouky, N.; Abourraja, M.N.; Boukachour, J.; Boudebous, D.; Alaoui, A.E.H.; El Khoukhi, F. Simulation optimization based ant colony algorithm for the uncertain quay crane scheduling problem. Int. J. Ind. Eng. Comput. 2019, 10, 111–132. [Google Scholar] [CrossRef]
- Kizilay, D.; Van Hentenryck, P.; Eliiyi, D.T. Constraint programming models for integrated container terminal operations. Eur. J. Oper. Res. 2020, 286, 945–962. [Google Scholar] [CrossRef]
- Homayouni, S.; Tang, S.; Ismail, N.; Ariffin, M.; Samin, R. A hybrid genetic-heuristic algorithm for scheduling of automated guided vehicles and quay cranes in automated container terminals. In Proceedings of the 2009 International Conference on Computers & Industrial Engineering, Troyes, France, 6–9 July 2009; pp. 96–101. [Google Scholar] [CrossRef]
- Homayouni, M.; Hong, T.S.; Ismail, N.; Khairol, M. A Genetic Algorithm for Optimization of Simultaneous Scheduling of AGVs and QCs in Container Terminals. In Proceedings of the 11th Asia Pacific Industrial Engineering and Management Systems Conference, Melaka, Malaysia, 7–10 December 2010. [Google Scholar]
- Cao, J.; Shi, Q.; Lee, D.-H. Integrated quay crane and yard truck schedule problem in container terminals. Tsinghua Sci. Technol. 2010, 15, 467–474. [Google Scholar] [CrossRef]
- Tang, L.; Zhao, J.; Liu, J. Modeling and solution of the joint quay crane and truck scheduling problem. Eur. J. Oper. Res. 2014, 236, 978–990. [Google Scholar] [CrossRef]
- Kaveshgar, N.; Huynh, N. Integrated quay crane and yard truck scheduling for unloading inbound containers. Int. J. Prod. Econ. 2015, 159, 168–177. [Google Scholar] [CrossRef]
- Vahdani, B.; Mansour, F.; Soltani, M.; Veysmoradi, D. Bi-objective optimization for integrating quay crane and internal truck assignment with challenges of trucks sharing. Knowl.-Based Syst. 2018, 163, 675–692. [Google Scholar] [CrossRef]
- Zhen, L.; Yu, S.; Wang, S.; Sun, Z. Scheduling quay cranes and yard trucks for unloading operations in container ports. Ann. Oper. Res. 2016, 273, 455–478. [Google Scholar] [CrossRef]
- Chen, J.; Du, W.; Wang, H.; Guo, D. Research on Integrated Scheduling Optimization of Double-trolley Quay Crane and AGV in Automated Terminal. IOP Conf. Ser. Mater. Sci. Eng. 2020, 790, 012071. [Google Scholar] [CrossRef]
- Castilla-Rodríguez, I.; Expósito-Izquierdo, C.; Melián-Batista, B.; Aguilar, R.M.; Moreno-Vega, J.M. Simulation-optimization for the management of the transshipment operations at maritime container terminals. Expert Syst. Appl. 2019, 139, 112852. [Google Scholar] [CrossRef]
- Hop, D.C.; Van Hop, N.; Anh, T.T.M. Adaptive particle swarm optimization for integrated quay crane and yard truck scheduling problem. Comput. Ind. Eng. 2020, 153, 107075. [Google Scholar] [CrossRef]
- Chen, L.; Bostel, N.; Dejax, P.; Cai, J.; Xi, L. A tabu search algorithm for the integrated scheduling problem of container handling systems in a maritime terminal. Eur. J. Oper. Res. 2007, 181, 40–58. [Google Scholar] [CrossRef]
- Lau, H.Y.K.; Zhao, Y. Integrated scheduling of handling equipment at automated container terminals. Ann. Oper. Res. 2007, 159, 373–394. [Google Scholar] [CrossRef]
- Chen, L.; Langevin, A.; Lu, Z. Integrated scheduling of crane handling and truck transportation in a maritime container terminal. Eur. J. Oper. Res. 2013, 225, 142–152. [Google Scholar] [CrossRef]
- He, J.; Huang, Y.; Yan, W.; Wang, S. Integrated internal truck, yard crane and quay crane scheduling in a container terminal considering energy consumption. Expert Syst. Appl. 2015, 42, 2464–2487. [Google Scholar] [CrossRef]
- Jonker, T.; Duinkerken, M.B.; Yorke-Smith, N.; de Waal, A.; Negenborn, R.R. Coordinated optimization of equipment operations in a container terminal. Flex. Serv. Manuf. J. 2019, 33, 281–311. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y. Scheduling of container-handling equipment during the loading process at an automated container terminal. Comput. Ind. Eng. 2020, 149, 106848. [Google Scholar] [CrossRef]
- Qin, T.; Du, Y.; Chen, J.H.; Sha, M. Combining mixed integer programming and constraint programming to solve the integrated scheduling problem of container handling operations of a single vessel. Eur. J. Oper. Res. 2020, 285, 884–901. [Google Scholar] [CrossRef]
- Niu, B.; Liu, Q.; Wang, Z.; Tan, L.; Li, L. Multi-objective bacterial colony optimization algorithm for integrated container terminal scheduling problem. Nat. Comput. 2020, 20, 89–104. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A. Functional integration approach for the berth allocation, quay crane assignment and specific quay crane assignment problems. Comput. Ind. Eng. 2016, 102, 458–466. [Google Scholar] [CrossRef]
- Iris, C.; Christensen, J.; Pacino, D.; Ropke, S. Flexible ship loading problem with transfer vehicle assignment and scheduling. Transp. Res. Part B Methodol. 2018, 111, 113–134. [Google Scholar] [CrossRef]
- Naeem, D.; Eltawil, A.; Iijima, J.; Gheith, M. Integrated Scheduling of Automated Yard Cranes and Automated Guided Vehicles with Limited Buffer Capacity of Dual-Trolley Quay Cranes in Automated Container Terminals. Logistics 2022, 6, 82. [Google Scholar] [CrossRef]
- Kizilay, D.; Eliiyi, D.T. A comprehensive review of quay crane scheduling, yard operations and integrations thereof in container terminals. Flex. Serv. Manuf. J. 2020, 33, 1–42. [Google Scholar] [CrossRef]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for Optimizing Machining Process Parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y. Modelling of dual-cycle strategy for container storage and vehicle scheduling problems at automated container terminals. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 49–64. [Google Scholar] [CrossRef]
- Czyzżak, P.; Jaszkiewicz, A. Pareto simulated annealing—A metaheuristic technique for multiple-objective combinatorial optimization. J. Multi-Criteria Decis. Anal. 1998, 7, 34–47. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Tang, L.; Li, Y.; Bai, D.; Liu, T.; Coelho, L.C. Bi-objective optimization for a multi-period COVID-19 vaccination planning problem. Omega 2022, 110, 102617. [Google Scholar] [CrossRef]



| Research | Method | Objectives | ||||
|---|---|---|---|---|---|---|
| GA/NSGA-II | PSO/MOPSO | Others | Makespan | Cost-Related | Others | |
| Homayouni [17] | √ | √ | ||||
| Homayouni [18] | √ | √ | ||||
| Cao [19] | √ | √ | √ | |||
| Tang [20] | √ | √ | ||||
| Kaveshgar [21] | √ | √ | ||||
| Vahdani [22] | √ | √ | √ | √ | ||
| Zhen [23] | √ | √ | √ | |||
| Chen [24] | √ | √ | ||||
| Castilla-Rodríguez [25] | √ | √ | √ | |||
| HOP [26] | √ | √ | ||||
| Notation | Description |
|---|---|
| The set of dummy tasks 0 for all quay cranes | |
| The set of dummy tasks F for all quay cranes | |
| The set of tasks to be unloaded from the ship | |
| The set of tasks to be loaded onto the ship | |
| The set of all tasks, | |
| The set of quay cranes | |
| The set of AGVs | |
| The set of all bays | |
| The set of task pairs between which there is a precedence relationship means task must precede task j | |
| The set of tasks in bay h | |
| The completion time of task i handled by a QC | |
| The start time of AGV operations for task i | |
| The quay crane time needed to serve task i | |
| The time for an AGV to transport container i from the initial position to its destination | |
| The completion time of container i handled by an AGV | |
| Set-up time of container i | |
| The start time of bay h | |
| The completion time of bay h | |
| The bay in which container i is located |
| Variable | Description |
|---|---|
| Equal to 1 if container i is handled immediately before container j by QC q, and 0 otherwise. When container j is the first task of QC q, . Also, when container j is the last task of QC q, . | |
| Equal to 1 if container i is performed immediately before container j by AGV u, and 0 otherwise. | |
| Equal to 1, if container i is handled by QC q and 0 otherwise. | |
| Equal to 1, if container i is handled by AGV u and 0 otherwise. | |
| Equal to 1, if bay h is handled by QC q and 0, otherwise. | |
| Equal to 1, if bay h is finished no later than bay h′ starts; 0 otherwise. |
| Yard | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 |
| X coordinate | 25 | 75 | 125 | 175 | 225 | 275 | 325 | 375 |
| Yard | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 |
| X coordinate | 525 | 575 | 625 | 675 | 725 | 775 | 825 | 875 |
| Instance | Ω/Q/T | Weighted-Sum | MOPSO | NSGA-II | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IGD | HV Ratio | NOP | IGD | HV Ratio | NOP | IGD | HV Ratio | NOP | ||
| 1 | 5/2/2 | 1.115 | 0.785 | 3 | 0.379 | 0.836 | 3 | 0.124 | 0.795 | 3 |
| 2 | 5/2/3 | 1.31 | 0.95 | 5 | 0.588 | 0.942 | 5 | 0.095 | 0.975 | 5 |
| 3 | 7/2/2 | 1.988 | 0.862 | 5 | 0.536 | 0.888 | 7 | 0.235 | 0.965 | 8 |
| 4 | 7/2/3 | 1.886 | 0.961 | 3 | 0.701 | 0.838 | 5 | 0.244 | 0.999 | 4 |
| 5 | 10/2/2 | 2.567 | 0.761 | 4 | 1.104 | 0.987 | 4 | 0.533 | 0.96 | 7 |
| 6 | 10/2/3 | 2.238 | 0.856 | 5 | 0.861 | 0.915 | 5 | 0.488 | 0.929 | 7 |
| 7 | 15/2/2 | 2.568 | 0.879 | 6 | 2.719 | 0.841 | 5 | 0.261 | 0.941 | 5 |
| 8 | 15/2/3 | 2.953 | 0.845 | 5 | 1.221 | 0.913 | 5 | 0.124 | 0.928 | 6 |
| 9 | 20/2/2 | 1.917 | 0.827 | 5 | 1.617 | 0.829 | 5 | 0.124 | 0.977 | 5 |
| 10 | 20/2/3 | 1.11 | 0.832 | 5 | 2.113 | 0.892 | 7 | 0.115 | 0.973 | 9 |
| 11 | 50/2/4 | 8.632 | 0.834 | 7 | 2.957 | 0.959 | 7 | 2.38 | 0.977 | 9 |
| 12 | 50/2/6 | 1.991 | 0.735 | 3 | 1.327 | 0.813 | 6 | 0.691 | 0.799 | 7 |
| 13 | 50/2/8 | 1.38 | 0.745 | 7 | 1.446 | 0.98 | 6 | 0.375 | 0.959 | 9 |
| 14 | 50/3/6 | 1.533 | 0.899 | 6 | 2.411 | 0.925 | 8 | 1.154 | 0.966 | 7 |
| 15 | 50/3/9 | 2.504 | 0.817 | 5 | 1.037 | 0.904 | 7 | 0.791 | 0.967 | 7 |
| 16 | 50/3/12 | 2.892 | 0.735 | 4 | 1.749 | 0.825 | 6 | 1.137 | 0.834 | 6 |
| Min | 1.11 | 0.735 | 3 | 0.379 | 0.813 | 3 | 0.095 | 0.795 | 3 | |
| Max | 8.632 | 0.961 | 7 | 2.957 | 0.987 | 8 | 2.38 | 0.999 | 9 | |
| Average | 2.411 | 0.833 | 4.875 | 1.423 | 0.893 | 5.688 | 0.554 | 0.934 | 6.5 | |
| Std. Dev | 3.107 | 4.85 × 10−3 | 1.583 | 0.623 | 3.29 × 10−3 | 1.696 | 0.359 | 4.21 × 10−3 | 3.2 | |
| NOP | Number of Best | Number of Suboptimal | Number of Worst |
|---|---|---|---|
| NSGA-II | 13 | 3 | 0 |
| MOPSO | 7 | 8 | 1 |
| Weighted-sum | 4 | 7 | 5 |
| IGD | Number of Best | Number of Suboptimal | Number of Worst |
|---|---|---|---|
| NSGA-II | 16 | 0 | 0 |
| MOPSO | 0 | 12 | 4 |
| Weighted-sum | 0 | 4 | 12 |
| HV Ratio | Number of Best | Number of Suboptimal | Number of Worst |
|---|---|---|---|
| NSGA-II | 12 | 4 | 0 |
| MOPSO | 4 | 9 | 3 |
| Weighted-sum | 0 | 3 | 13 |
| Instance | Ω/Q/T | Weighted-Sum | MOPSO | NSGA-II | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IGD | HV Ratio | NOP | IGD | HV Ratio | NOP | IGD | HV Ratio | NOP | ||
| 17 | 70/2/4 | 9.917 | 0.855 | 4 | 8.041 | 0.78 | 7 | 1.086 | 0.911 | 14 |
| 18 | 70/2/6 | 6.939 | 0.804 | 6 | 7.31 | 0.87 | 9 | 0.598 | 0.841 | 11 |
| 19 | 70/2/8 | 9.685 | 0.806 | 7 | 9.529 | 0.873 | 8 | 1.252 | 0.975 | 13 |
| 20 | 70/3/6 | 9.971 | 0.792 | 3 | 10.555 | 0.88 | 10 | 1.333 | 0.941 | 12 |
| 21 | 70/3/9 | 2.503 | 0.86 | 4 | 8.481 | 0.93 | 10 | 1.086 | 0.931 | 17 |
| 22 | 70/3/12 | 10.788 | 0.832 | 8 | 9.216 | 0.946 | 9 | 1.137 | 0.974 | 16 |
| 23 | 100/2/4 | 10.808 | 0.879 | 5 | 9.514 | 0.886 | 8 | 1.217 | 0.987 | 12 |
| 24 | 100/2/6 | 10.244 | 0.844 | 6 | 10.981 | 0.825 | 10 | 1.486 | 0.935 | 17 |
| 25 | 100/2/8 | 9.892 | 0.726 | 5 | 8.611 | 0.878 | 9 | 1.167 | 0.898 | 19 |
| 26 | 100/3/6 | 11.065 | 0.857 | 9 | 11.827 | 0.897 | 8 | 1.318 | 0.934 | 11 |
| 27 | 100/3/9 | 11.856 | 0.822 | 5 | 10.046 | 0.927 | 9 | 0.426 | 0.966 | 14 |
| 28 | 100/3/12 | 11.442 | 0.868 | 3 | 11.747 | 0.899 | 9 | 0.827 | 0.965 | 11 |
| 29 | 150/2/6 | 11.334 | 0.848 | 4 | 11.181 | 0.953 | 9 | 1.672 | 0.956 | 6 |
| 30 | 150/2/8 | 9.501 | 0.899 | 3 | 9.391 | 0.879 | 9 | 0.499 | 0.998 | 15 |
| 31 | 150/3/9 | 9.319 | 0.743 | 4 | 8.308 | 0.835 | 10 | 0.897 | 0.975 | 11 |
| 32 | 150/3/12 | 12.703 | 0.839 | 7 | 9.158 | 0.91 | 10 | 0.755 | 0.921 | 8 |
| 33 | 150/4/10 | 10.303 | 0.831 | 8 | 9.735 | 0.936 | 10 | 0.644 | 0.97 | 14 |
| 34 | 150/4/12 | 11.985 | 0.827 | 7 | 15.056 | 0.884 | 9 | 1.164 | 0.994 | 16 |
| 35 | 150/4/16 | 12.354 | 0.821 | 5 | 14.083 | 0.818 | 9 | 1.281 | 0.961 | 15 |
| 36 | 200/2/6 | 12.369 | 0.738 | 6 | 12.864 | 0.879 | 9 | 2.695 | 0.934 | 19 |
| 37 | 200/3/9 | 13.607 | 0.822 | 9 | 12.915 | 0.916 | 11 | 2.709 | 0.998 | 24 |
| 38 | 200/3/12 | 12.277 | 0.825 | 4 | 11.134 | 0.951 | 10 | 1.941 | 0.998 | 12 |
| 39 | 200/4/10 | 17.679 | 0.829 | 3 | 10.286 | 0.877 | 10 | 0.727 | 0.966 | 12 |
| 40 | 200/4/12 | 11.842 | 0.876 | 14 | 11.941 | 0.939 | 11 | 3.626 | 0.941 | 22 |
| 41 | 200/4/16 | 13.517 | 0.822 | 11 | 12.341 | 0.875 | 7 | 1.614 | 0.999 | 11 |
| Min | 2.503 | 0.726 | 3 | 7.31 | 0.78 | 7 | 0.426 | 0.841 | 6 | |
| Max | 17.679 | 0.899 | 14 | 15.056 | 0.953 | 11 | 3.626 | 0.999 | 24 | |
| Average | 10.956 | 0.827 | 6 | 10.570 | 0.890 | 9.2 | 1.326 | 0.955 | 14.08 | |
| Std. Dev | 7.031 | 1.80 × 10−3 | 7.417 | 3.787 | 1.90 × 10−3 | 1.083 | 0.563 | 1.39 × 10−3 | 16.827 | |
| NOP | Number of Best | Number of Suboptimal | Number of Worst |
|---|---|---|---|
| NSGA-II | 23 | 2 | 0 |
| MOPSO | 2 | 20 | 3 |
| Weighted-sum | 1 | 2 | 22 |
| IGD | Number of Best | Number of Suboptimal | Number of Worst |
|---|---|---|---|
| NSGA-II | 24 | 1 | 0 |
| MOPSO | 1 | 20 | 4 |
| Weighted-sum | 0 | 4 | 20 |
| HV Ratio | Number of Best | Number of Suboptimal | Number of Worst |
|---|---|---|---|
| NSGA-II | 23 | 2 | 0 |
| MOPSO | 2 | 20 | 3 |
| Weighted-sum | 1 | 2 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Y.; Ren, H.; Xu, F.; Yang, X.; Meng, Y. Bi-Objective Integrated Scheduling of Quay Cranes and Automated Guided Vehicles. J. Mar. Sci. Eng. 2023, 11, 1492. https://doi.org/10.3390/jmse11081492
Duan Y, Ren H, Xu F, Yang X, Meng Y. Bi-Objective Integrated Scheduling of Quay Cranes and Automated Guided Vehicles. Journal of Marine Science and Engineering. 2023; 11(8):1492. https://doi.org/10.3390/jmse11081492
Chicago/Turabian StyleDuan, Yating, Hongxiang Ren, Fuquan Xu, Xiao Yang, and Yao Meng. 2023. "Bi-Objective Integrated Scheduling of Quay Cranes and Automated Guided Vehicles" Journal of Marine Science and Engineering 11, no. 8: 1492. https://doi.org/10.3390/jmse11081492
APA StyleDuan, Y., Ren, H., Xu, F., Yang, X., & Meng, Y. (2023). Bi-Objective Integrated Scheduling of Quay Cranes and Automated Guided Vehicles. Journal of Marine Science and Engineering, 11(8), 1492. https://doi.org/10.3390/jmse11081492






