An Emergency Port Decision-Making Method for Maritime Accidents in Arctic Waters
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Data Collection
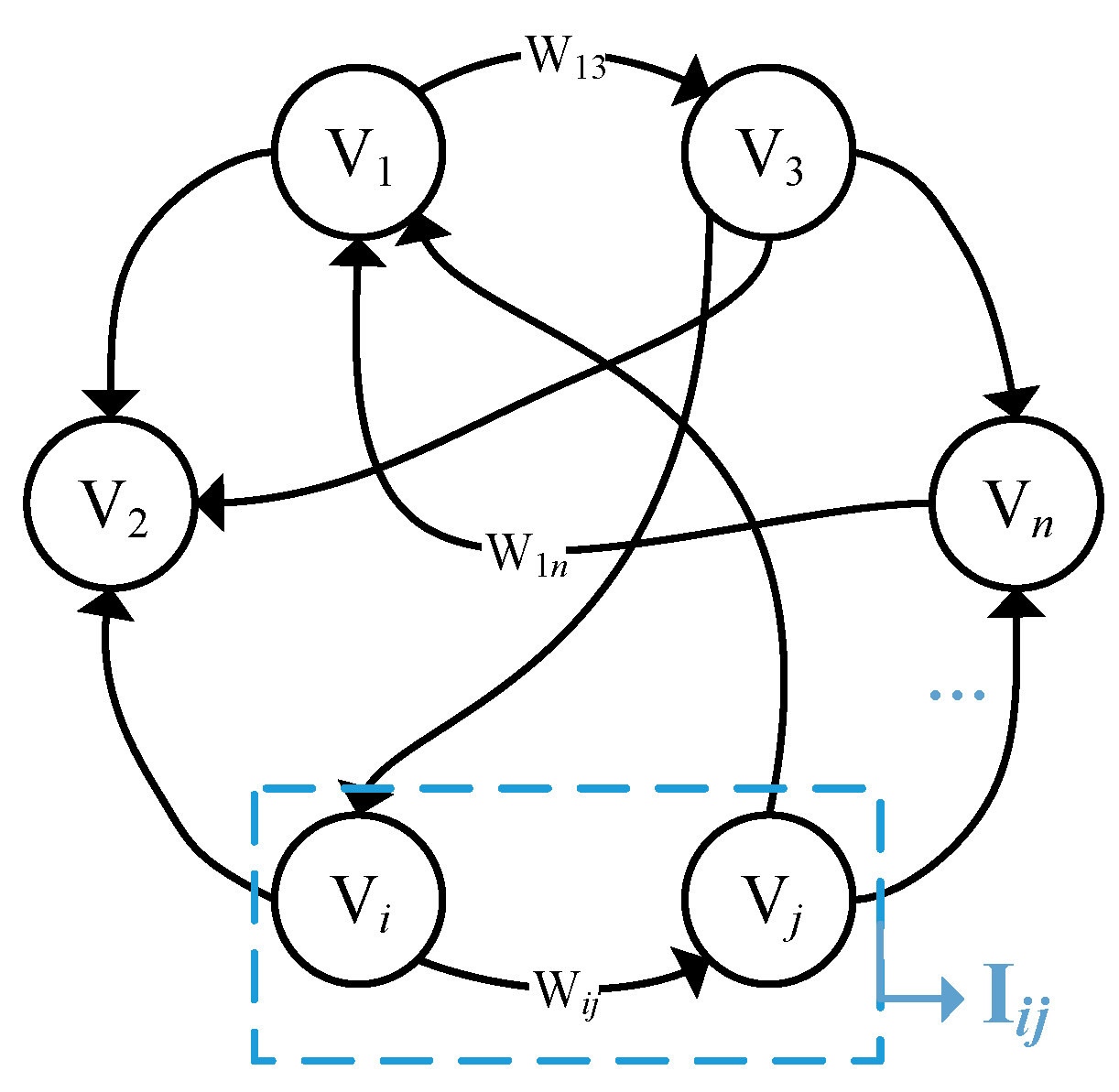
3.2. Complex Network
3.3. K-Means Clustering Algorithm
3.4. Entropy-Weighted TOPSIS
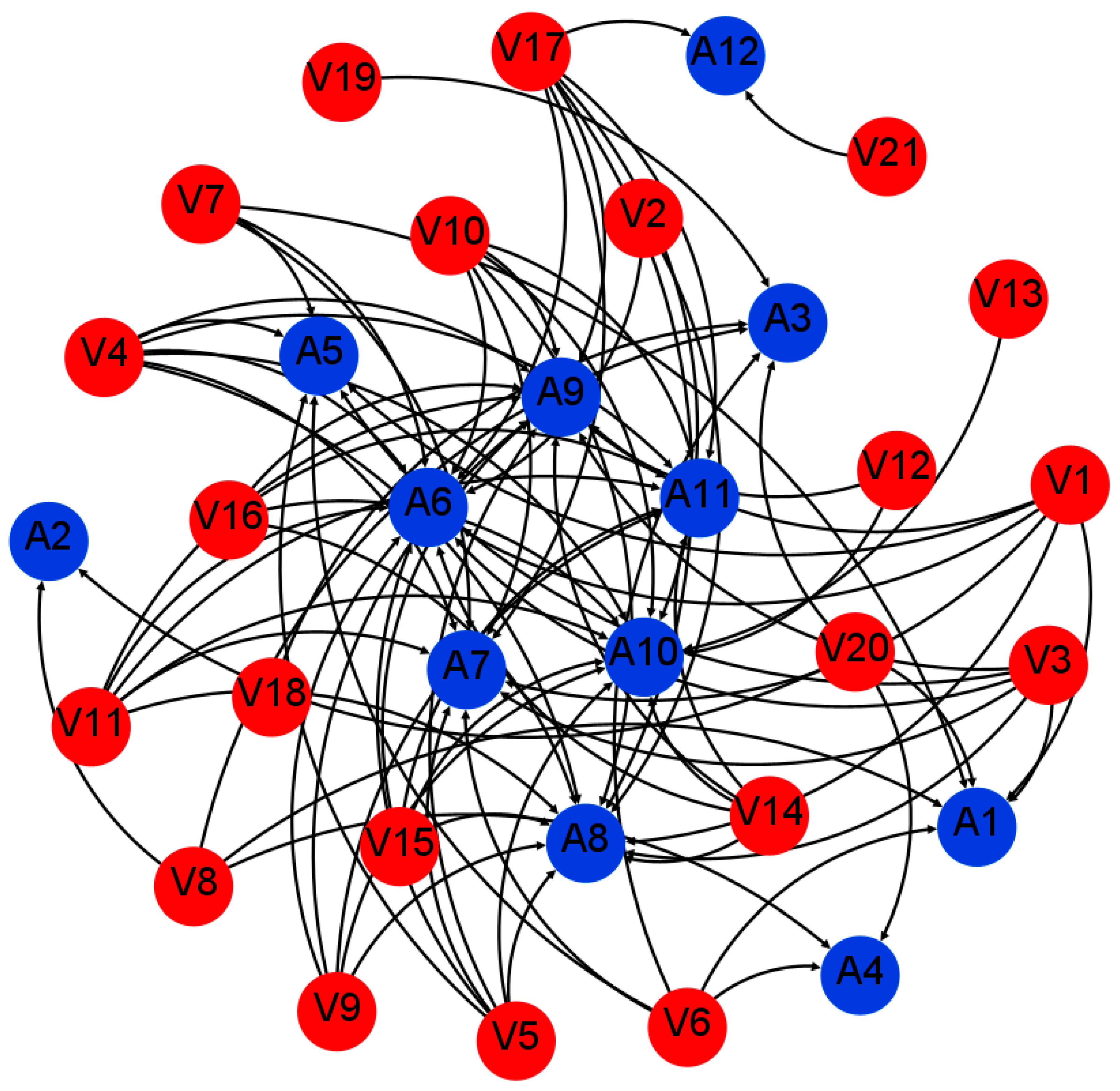
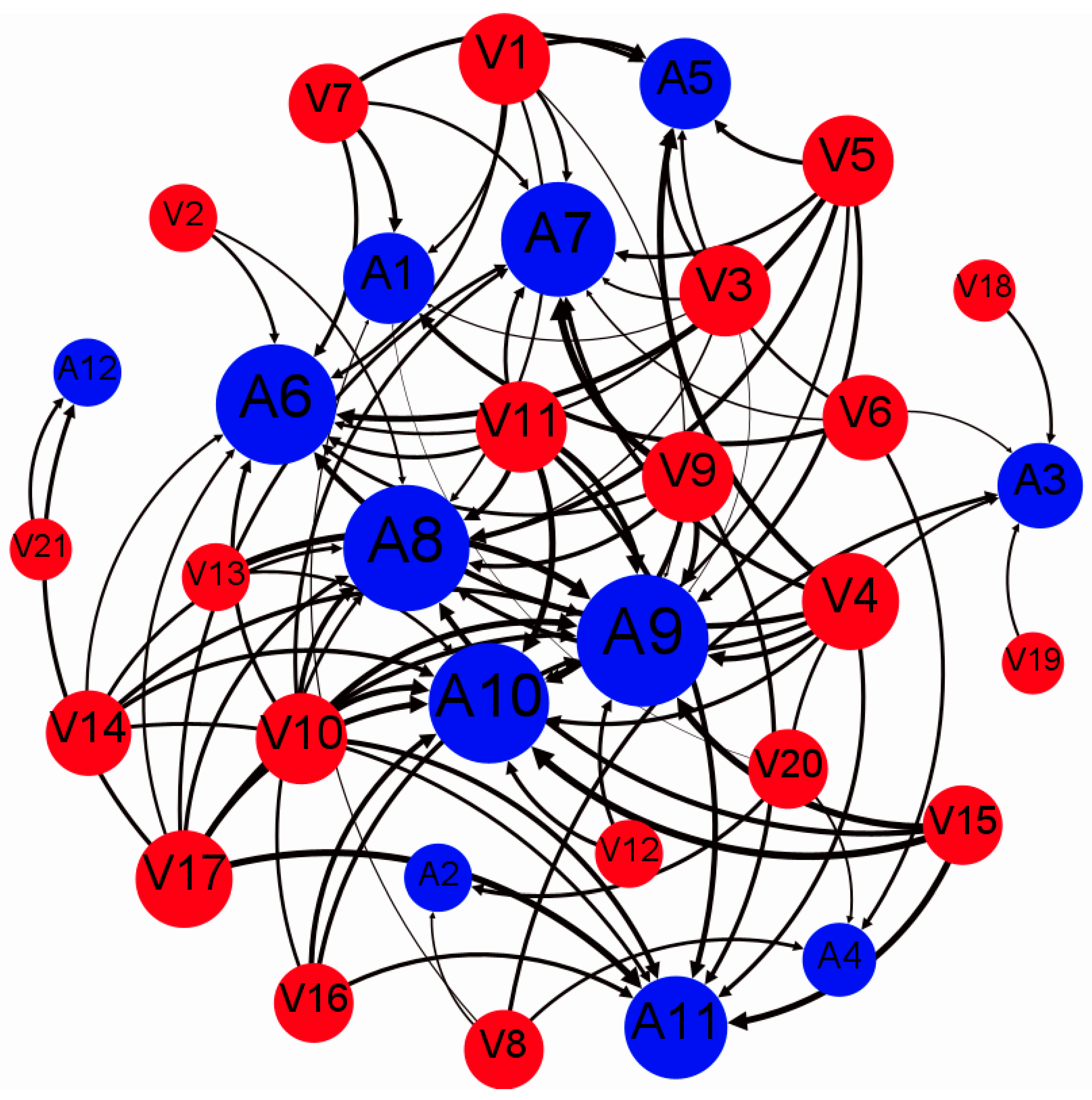
4. Construction of the Emergency Port Network in Arctic Waters
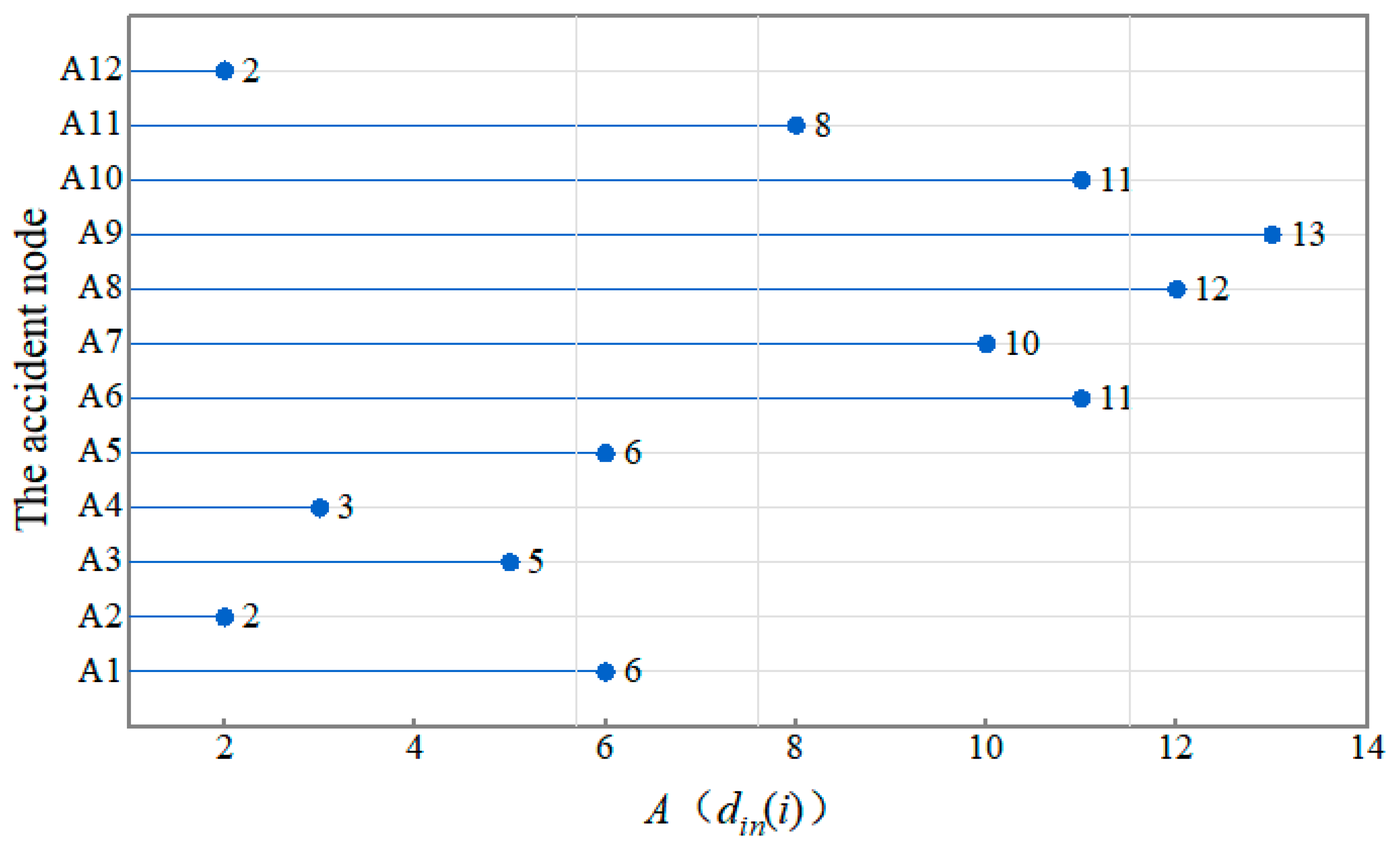
4.1. Determination of the Accident Nodes
4.2. Determination of the Port Nodes
4.3. Determination of the Edges between Nodes
4.3.1. Determination of the Edges
4.3.2. Determination of the Weights for Edges
4.4. Establishment of the Emergency Port Network
5. Results and Discussions
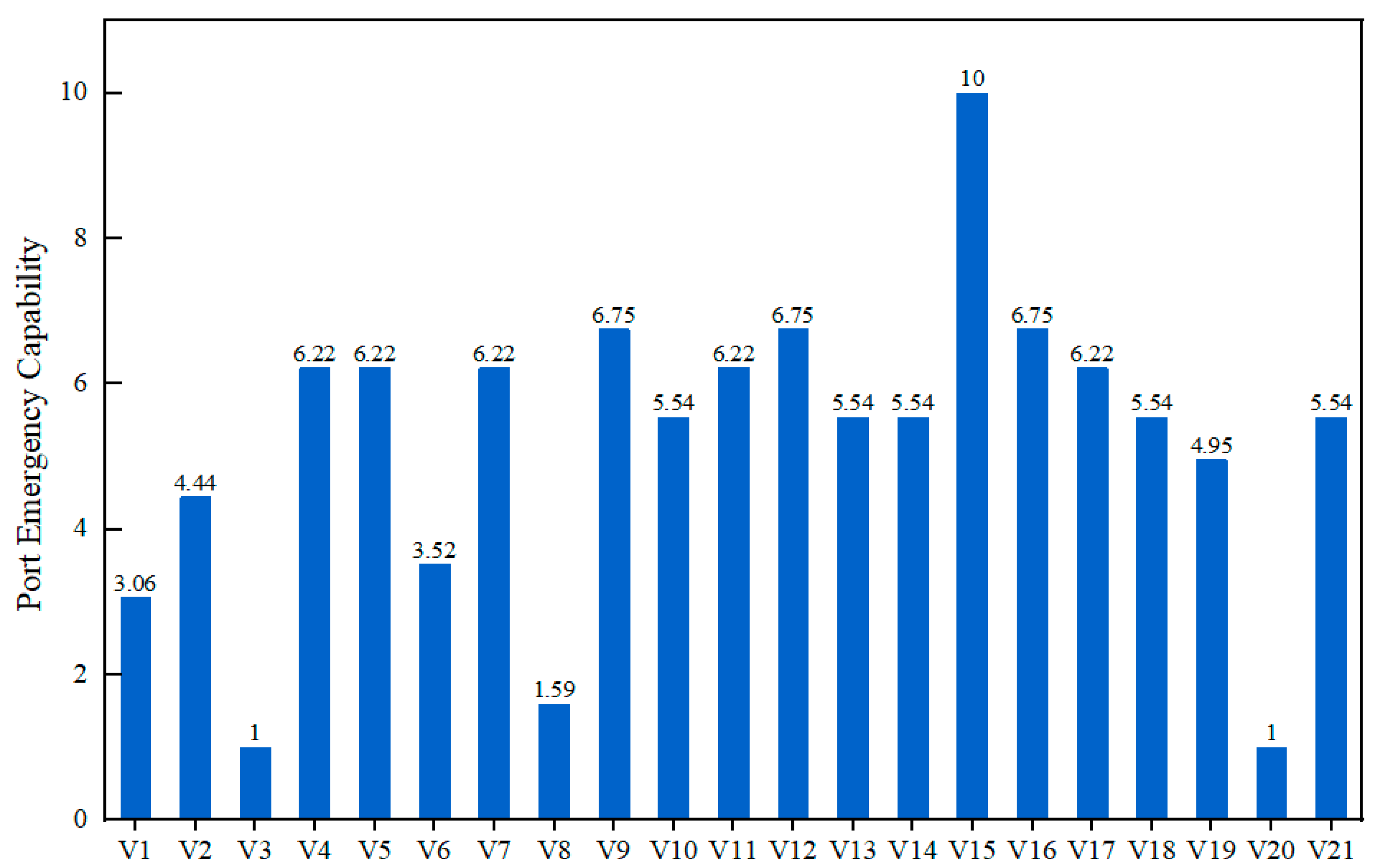
5.1. Emergency Port Ranking for Accident Prone Areas in Arctic Waters
5.2. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Aj | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vi | |||||||||||||
| V1 | 3.16 | 0.72 | 2.32 | 2.65 | 3.40 | 4.90 | |||||||
| V2 | 3.55 | 4.55 | |||||||||||
| V3 | 3.85 | 0.98 | 1.84 | 2.72 | 3.12 | 4.56 | |||||||
| V4 | 0.98 | 1.84 | 2.72 | 3.12 | 2.02 | 3.60 | 3.70 | ||||||
| V5 | 3.44 | 1.56 | 3.50 | 2.27 | 3.05 | 4.58 | |||||||
| V6 | 1.02 | 4.87 | 2.71 | 3.18 | 4.56 | ||||||||
| V7 | 3.00 | 2.65 | 3.71 | 4.56 | |||||||||
| V8 | 4.24 | 3.55 | 1.01 | 1.99 | |||||||||
| V9 | 4.45 | 3.56 | 2.39 | 2.71 | 3.72 | ||||||||
| V10 | 3.40 | 3.67 | 2.20 | 0.74 | 1.24 | 2.03 | |||||||
| V11 | 3.76 | 4.11 | 2.59 | 1.18 | 1.19 | 2.17 | |||||||
| V12 | 4.37 | 3.88 | |||||||||||
| V13 | 4.34 | ||||||||||||
| V14 | 4.76 | 3.84 | 2.59 | 2.69 | 3.77 | ||||||||
| V15 | 4.21 | 2.71 | 2.03 | 3.16 | |||||||||
| V16 | 4.83 | 3.33 | 2.66 | 3.79 | |||||||||
| V17 | 4.99 | 4.08 | 3.53 | 2.51 | 1.47 | 0.66 | 3.50 | ||||||
| V18 | 4.43 | ||||||||||||
| V19 | 4.68 | ||||||||||||
| V20 | 4.90 | 1.02 | 1.75 | 2.81 | |||||||||
| V21 | 4.07 | ||||||||||||
Appendix B
| Indicators for PEC | Weight | |
|---|---|---|
| Port size | 1 | |
| Communication facilities | Emergency telephone | 0.3214 |
| Radio | 0.0967 | |
| Telegraph | 0.2606 | |
| Radio-Tel | 0.3214 | |
| Medical equipment | 1 | |
| Port tug | Rescue | 0.1074 |
| Salvage | 0.8926 | |
Appendix C
| Port | Port Size | Communication Facilities | Medical Equipment | Port Tug |
|---|---|---|---|---|
| V1 | 0 | 0.3140 | 0 | 1 |
| V2 | 0.6667 | 0.5057 | 0 | 1 |
| V3 | 0.3333 | 0 | 0 | 0 |
| V4 | 0.6667 | 1 | 0.2576 | 1 |
| V5 | 0.6667 | 1 | 0.2576 | 1 |
| V6 | 0.3333 | 0.3140 | 0 | 1 |
| V7 | 0.6667 | 0.6016 | 0.2576 | 1 |
| V8 | 0 | 0.1957 | 0.2576 | 0 |
| V9 | 1 | 1 | 0.2576 | 1 |
| V10 | 0.3333 | 1 | 0.2576 | 1 |
| V11 | 0.6667 | 1 | 0.2576 | 1 |
| V12 | 1 | 1 | 0.2576 | 1 |
| V13 | 0.3333 | 1 | 0.2576 | 1 |
| V14 | 0.3333 | 1 | 0.2576 | 1 |
| V15 | 0.6667 | 1 | 1 | 1 |
| V16 | 1 | 1 | 0.2576 | 1 |
| V17 | 0.6667 | 0.6016 | 0.2576 | 1 |
| V18 | 0.3333 | 1 | 0.2576 | 1 |
| V19 | 0 | 0.6016 | 0.2576 | 1 |
| V20 | 0.3333 | 0 | 0 | 0 |
| V21 | 0.3333 | 1 | 0.2576 | 1 |
Appendix D
| The Accident Node | Name of Sea Area | The Port Node | Edge Weight | Total (Number) |
|---|---|---|---|---|
| A1 (70.0583 N,126.3500 E) | Laplacev Sea | V6 (Tiksi) | 5.8 | 5 |
| V7 (Igarka) | 5.4 | |||
| V1 (Dikson) | 3.7 | |||
| V8 (Providenija) | 3.71 | |||
| V3 (Sabetta) | 3.64 | |||
| A2 (64.5467 N, 122.8136 W) | Beaufort Sea | V20 (PrudhoeBay) | 4.6 | 2 |
| V8 (Providenija) | 2.6 | |||
| A3 (60.5057 N, 169.4958 W) | Chukchi Sea | V8 (Providenija) | 4.9 | 5 |
| V20 (PrudhoeBay) | 3.9 | |||
| V18 (Anchorage) | 3.8 | |||
| V19 (Valdez) | 3.3 | |||
| V6 (Tiksi) | 2.4 | |||
| A4 (65.6333 N, 172.3833 E) | East Siberian Sea | V6 (Tiksi) | 4.3 | 3 |
| V8 (Providenija) | 4.0 | |||
| V20 (PrudhoeBay) | 3.0 | |||
| A5 (71.1102 N, 76.9400 E) | Kara Sea | V4 (Murmansk) | 7.2 | 6 |
| V1 (Dikson) | 5.9 | |||
| V7 (Igarka) | 5.7 | |||
| V5 (Arkhangelsk) | 5.0 | |||
| V3 (Sabetta) | 4.6 | |||
| V6 (Tiksi) | 3.9 | |||
| A6 (68.8734 N, 41.2654 E) | Barents Sea | V5 (Arkhangelsk) | 6.7 | 11 |
| V4 (Murmansk) | 6.4 | |||
| V7 (Igarka) | 4.8 | |||
| V10 (Grenland) | 4.7 | |||
| V11 (Bergen) | 4.7 | |||
| V9 (Goteborg) | 4.4 | |||
| V1 (Dikson) | 4.4 | |||
| V2 (Petropavlovsk) | 4.0 | |||
| V3 (Sabetta) | 3.8 | |||
| V17 (Reykjavik) | 3.6 | |||
| V14 (Aalborg) | 3.5 | |||
| A7 (79.7167 N, 26.6975 E) | Barents Sea | V9 (Goteborg) | 8.4 | 10 |
| V4 (Murmansk) | 5.7 | |||
| V5 (Arkhangelsk) | 4.9 | |||
| V10(Grenland) | 4.5 | |||
| V11(Bergen) | 4.4 | |||
| V17 (Reykjavik) | 4.4 | |||
| V1 (Dickson) | 4.1 | |||
| V7 (Igarka) | 4.0 | |||
| V3 (Sabetta) | 3.0 | |||
| V6 (Tiksi) | 2.7 | |||
| A8 (68.7003 N, 16.1478 E) | Norwegian Sea | V15 (Aarhus) | 6.2 | 12 |
| V5 (Arkhangelsk) | 6.1 | |||
| V10(Grenland) | 5.8 | |||
| V11(Bergen) | 5.8 | |||
| V4 (Murmansk) | 5.3 | |||
| V9 (Goteborg) | 5.2 | |||
| V17 (Reykjavik) | 4.9 | |||
| V14 (Aalborg) | 4.3 | |||
| V16 (Copenhagen) | 4.0 | |||
| V1 (Dickson) | 3.5 | |||
| V2 (Petropavlovsk) | 3.1 | |||
| V3 (Sabetta) | 2.7 | |||
| A9 (61.4108 N,6.1256 E) | Norwegian Sea | V13 (Kokkola) | 7.8 | 13 |
| V15 (Aarhus) | 7.6 | |||
| V11(Bergen) | 7.1 | |||
| V10(Grenland) | 7.1 | |||
| V4 (Murmansk) | 6.3 | |||
| V9 (Goteborg) | 6.2 | |||
| V17 (Reykjavik) | 5.8 | |||
| V14 (Aalborg) | 5.4 | |||
| V16 (Copenhagen) | 5.4 | |||
| V5 (Arkhangelsk) | 5.4 | |||
| V12(Helsinki) | 4.4 | |||
| V1 (Dickson) | 2.1 | |||
| V3 (Sabetta) | 1.4 | |||
| A10 (61.5567 N, 6.8985 W) | Greenland Sea | V15 (Aarhus) | 8.2 | 11 |
| V11(Bergen) | 7.0 | |||
| V17 (Reykjavik) | 6.8 | |||
| V10(Grenland) | 6.7 | |||
| V16 (Copenhagen) | 6.0 | |||
| V9 (Goteborg) | 5.9 | |||
| V14 (Aalborg) | 5.3 | |||
| V4 (Murmansk) | 4.9 | |||
| V12(Helsinki) | 4.9 | |||
| V5 (Arkhangelsk) | 4.0 | |||
| V13(Kokkola) | 3.9 | |||
| A11 (63.7347 N, 15.9265 W) | Greenland Sea | V17 (Reykjavik) | 7.5 | 8 |
| V15 (Aarhus) | 7.2 | |||
| V11(Bergen) | 6.2 | |||
| V10(Grenland) | 5.9 | |||
| V9 (Goteborg) | 5.0 | |||
| V16 (Copenhagen) | 5.0 | |||
| V4 (Murmansk) | 4.8 | |||
| V14 (Aalborg) | 4.4 | |||
| A12 (65.4355 N, 55.6285 W) | Davis Strait | V17 (Reykjavik) | 4.9 | 2 |
| V21 (Churchill) | 4.1 |
References
- Cao, Y.F.; Liang, S.L.; Sun, L.X.; Liu, J.P.; Cheng, X.; Wang, D.D.; Feng, K.S. Trans-Arctic shipping routes expanding faster than the model projections. Glob. Environ. Chang. 2022, 73, 102488. [Google Scholar] [CrossRef]
- Melia, N.; Haines, K.; Hawkins, E. Sea ice decline and 21st century trans-arctic shipping routes. Geophys. Res. Lett. 2016, 43, 9720–9728. [Google Scholar] [CrossRef]
- Agreement on Cooperation on Aeronautical and Maritime Search and Rescue in the Arctic. Available online: http://library.arcticportal.org/1474/#:~:text=Agreement%20on%20Cooperation%20on%20Aeronautical%20and%20Maritime%20Search,2011%20in%20the%20Arctic%20Council%20Nuuk%20Ministerial%20Meeting (accessed on 12 May 2011).
- Safety and Shipping Review 2020. Available online: https://www.agcs.allianz.com/news-and-insights/reports.result.html/2.html (accessed on 15 July 2020).
- Liu, Y.; Ma, X.X.; Qiao, W.L.; Han, B. On the determination and rank for the environmental risk aspects for ship navigating in the Arctic based on big Earth data. Risk Anal. 2022. [Google Scholar] [CrossRef]
- Qian, H.; Zhang, R.; Zhang, Y.J. Dynamic risk assessment of natural environment based on Dynamic Bayesian Network for key nodes of the arctic Northwest Passage. Ocean Eng. 2020, 203, 107205. [Google Scholar] [CrossRef]
- Cheaitou, A.; Faury, O.; Cariou, P.; Hamdan, S.; Fabbri, G. Economic and environmental impacts of Arctic shipping: A probabilistic approach. Transp. Res. Part D Transp. Environ. 2020, 89, 102606. [Google Scholar] [CrossRef]
- Browne, T.; Taylor, R.; Veitch, B.; Kujala, P.; Khan, F.; Smith, D. A framework for integrating life-safety and environmental consequences into conventional arctic shipping risk models. Appl. Sci. 2020, 10, 2937. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Zhang, D.; Goerlandt, F.; Yan, X.P.; Kujala, P. Use of HFACS and fault tree model for collision risk factors analysis of icebreaker assistance in ice-covered waters. Saf. Sci. 2019, 111, 128–143. [Google Scholar] [CrossRef]
- Li, Z.; Hu, S.P.; Gao, G.P.; Yao, C.Y.; Fu, S.S.; Xi, Y.T. Decision-making on process risk of arctic route for LNG carrier via dynamic bayesian network modeling. J. Loss Prev. Process Ind. 2021, 71, 104473. [Google Scholar] [CrossRef]
- Fu, S.S.; Zhang, D.; Montewka, J.; Yan, X.P.; Zio, E. Towards a probabilistic model for predicting ship besetting in ice in arctic waters. Reliab. Eng. Syst. Saf. 2016, 155, 124–136. [Google Scholar] [CrossRef]
- Fu, S.S.; Zhang, D.; Montewka, J.; Zio, E.; Yan, X.P. A quantitative approach for risk assessment of a ship stuck in ice in Arctic waters. Saf. Sci. 2018, 107, 145–154. [Google Scholar] [CrossRef]
- Vanhatalo, J.; Huuhtanen, J.; Bergström, M.; Helle, I.; Mäkinen, J.; Kujala, P. Probability of a ship becoming beset in ice along the northern sea route a bayesian analysis of real-life data. Cold Reg. Sci. Technol. 2021, 184, 103238. [Google Scholar]
- Xu, S.; Kim, E.; Haugen, S.; Zhang, M.Y. A Bayesian network risk model for predicting ship besetting in ice during convoy operations along the Northern Sea Route. Reliab. Eng. Syst. Saf. 2022, 223, 108475. [Google Scholar]
- Gupta, M. The Arctic sea-ice navigability index. Curr. Sci. 2021, 121, 567–570. [Google Scholar] [CrossRef]
- Khan, B.; Khan, F.; Veitch, B.; Yang, M. An operational risk analysis tool to analyze marine transportation in arctic waters. Reliab. Eng. Syst. Saf. 2018, 169, 485–502. [Google Scholar] [CrossRef]
- Khan, B.; Khan, F.; Veitch, B. A Dynamic Bayesian Network model for ship-ice collision risk in the Arctic waters. Saf. Sci. 2020, 130, 104858. [Google Scholar] [CrossRef]
- Fedi, L.; Faury, O.; Etienne, L. Mapping and analysis of maritime accidents in the Russian Arctic through the lens of the Polar Code and POLARIS system. Mark. Policy 2020, 118, 103984. [Google Scholar] [CrossRef]
- Browne, T.; Veitch, B.; Taylor, R.; Smith, J.; Smith, D.; Khan, F. Consequence modelling for arctic ship evacuations using expert knowledge. Mark. Policy 2021, 130, 104582. [Google Scholar] [CrossRef]
- Fu, S.S.; Yu, Y.R.; Chen, J.H.; Xi, Y.T.; Zhang, M.Y. A framework for quantitative analysis of the causation of grounding accidents in arctic shipping. Reliab. Eng. Syst. Saf. 2022, 226, 108706. [Google Scholar] [CrossRef]
- Marchenko, N.A.; Andreassen, N.; Borch, O.J.; Kuznetsova, S.Y.; Ingimundarson, V.; Jakobsen, U. Arctic shipping and risks: Emergency categories and response capacities. TransNav-Int. J. Mar. Navig. Saf. Sea Transp. 2018, 12, 107–114. [Google Scholar] [CrossRef]
- Ford, J.; Clark, D. Preparing for the impacts of climate change along Canada’s Arctic coast: The importance of search and rescue. Mark. Policy 2019, 108, 103662. [Google Scholar] [CrossRef]
- Kruke, B.I.; Auestad, A.C. Emergency preparedness and rescue in Arctic waters. Saf. Sci. 2021, 136, 105163. [Google Scholar] [CrossRef]
- Benz, L.; Münch, C.; Hartmann, E. Development of a search and rescue framework for maritime freight shipping in the Arctic. Transp. Res. Part A Policy Pract. 2021, 152, 54–69. [Google Scholar] [CrossRef]
- VanderBerg, J.D. Optimal Arctic Port locations: A quantitative composite multiplier analysis of potential sites. Polar Geogr. 2018, 41, 55–74. [Google Scholar] [CrossRef]
- Shan, Y.L.; Zhang, R. Study on the allocation of a rescue base in the Arctic. Symmetry 2019, 11, 1073. [Google Scholar] [CrossRef]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. Proc. Symp. Math. Statist. Prob. 1967, 1967, 281–297. [Google Scholar]
- Hwang, C.; Yoon, K. Multiple attribute decision making. Lect. Notes Econ. Math. Syst. 1981, 404, 287–288. [Google Scholar]
- Chen, P.Y. Effects of the entropy weight on topsis. Expert Syst. Appl. 2020, 168, 114186. [Google Scholar] [CrossRef]
- Wu, H.W.; Li, E.Q.; Sun, Y.Y.; Dong, B.T. Research on the operation safety evaluation of urban rail stations based on the improved TOPSIS method and entropy weight method. J. Rail Transp. Plan. Manag. 2021, 20, 100262. [Google Scholar] [CrossRef]
- Ma, X.Y.; Shao, J.A.; Xu, X.L. Rural transportation accessibility in mountainous areas based on the entropy-weight TOPSIS method: A case study of Shizhu County, Chongqing Municipality. Prog. Geogr. 2016, 35, 1144–1154. [Google Scholar]
- An, Y.; Tan, X.; Gu, B.; Zhu, K.; Shi, L.; Ding, Z. An assessment of renewable energy development in Belt and Road Initiative countries: An entropy and TOPSIS approach. Energy Rep. 2023, 9, 166–181. [Google Scholar]
- Chen, C.H. A hybrid multi-criteria decision-making approach based on ANP-Entropy TOPSIS for building materials supplier selection. Entropy 2021, 23, 1597. [Google Scholar] [CrossRef] [PubMed]
- National Geospatial-Intelligence Agency. World Port Index 2019. Available online: https://data.humdata.org/dataset/world-port-index (accessed on 1 December 2019).
- Solberg, K.E.; Jensen, J.E.; Barane, E.; Hagen, S.; Kjøl, A.; Johansen, G.; Gudmestad, O.T. Time to Rescue for Different Paths to Survival Following a Marine Incident. J. Mar. Sci. Eng. 2020, 8, 997. [Google Scholar] [CrossRef]
- Zhang, W.B.; Zou, Z.Y.; Goerlandt, F.; Qi, Y.; Kujala, P. A multi-ship following model for icebreaker convoy operations in ice-covered waters. Ocean Eng. 2019, 180, 238–253. [Google Scholar] [CrossRef]
- Woldaregay, A.Z.; Walderhaug, S.; Hartvigsen, G. Telemedicine services for the arctic: A systematic review. JMIR Med. Inform. 2017, 5, 2–16. [Google Scholar] [CrossRef] [PubMed]



| Category | Variable | Meaning | Computing Technology | |
|---|---|---|---|---|
| Network nodes | n | The network nodes | The number of elements in V | |
| Network edges | M | The number of links between the nodes | The number of elements in E | |
| Adjacency matrix | The structure of the network | |||
| Point centrality | In-degree | Total number of edges that directly connect and point to | ||
| Out-degree | Total number of edges that are directly connected but do not point to |
| Algorithm: K-means clustering algorithm |
| Require: Dataset: , cluster number: k Ensure: k cluster centroids, cluster belongings of all data 1: Initialize k centroids randomly. 2: while Convergence condition is not satisfied do 3: for i ← 1 to N do 4: Calculate k distances between data and k centroids . 5: belongs to a cluster of centroid based on the minimum distance . 6: end for 7: Calculate k centroids 8: end while |
| The Accident Node | Location | Name of the Sea Located |
|---|---|---|
| A1 | 70.0583 N,126.3500 E | Laptev Sea |
| A2 | 64.5467 N, 122.8136 W | Beaufort Sea |
| A3 | 60.5057 N, 169.4958 W | Chukchi Sea |
| A4 | 65.6333 N, 172.3833 E | East Siberian Sea |
| A5 | 71.1102 N, 76.9400 E | Kara Sea |
| A6 | 68.8734 N, 41.2654 E | Barents Sea |
| A7 | 79.7167 N, 26.6975 E | Barents Sea |
| A8 | 68.7003 N, 16.1478 E | Norwegian Sea |
| A9 | 61.4108 N, 6.1256 E | Norwegian Sea |
| A10 | 61.5567 N, 6.8985 W | Greenland Sea |
| A11 | 63.7347 N, 15.9265 W | Greenland Sea |
| A12 | 65.4355 N, 55.6285 W | Davis Strait |
| Nation | Vi | Location | |
|---|---|---|---|
| Russia | V1 | Dickson | N 73°30′24.49″, E 80°30′36.14″ |
| V2 | Petropavlovsk | N 57°60′11″, E 49°12′19″ | |
| V3 | Sabetta | N 71°16′43.76″, E 72°03′36.04″ | |
| V4 | Murmansk | N 68°59′02.84″, E 33°03′39.58″ | |
| V5 | Arkhangelsk | N 64°32′16.23″, E 40°32′02.60″ | |
| V6 | Tiksi | N 71.64,757°, E 128.8989° | |
| V7 | Igarka | N 67°31′, E 86°33′ | |
| V8 | Providenija | N 64°41′98″, W 173°22′63″ | |
| Sweden | V9 | Goteborg | N 57°41′58.20″, E 11°52′58.79″ |
| Norway | V10 | Grenland | N 59°3′6″, E 9°41′57″ |
| V11 | Bergen | N 60°23′27.06″, E 5°19′20.82″ | |
| Finland | V12 | Helsinki | N 60°10′06.61″, E 24°56′40.19″ |
| V13 | Kokkola | N 63°51′02.02″, E 23°01′51.03″ | |
| Denmark | V14 | Aalborg | N 57°04′10.19″, E 9°59′09.60″ |
| V15 | Aarhus | N 56°09′14.39″, E 10°13′46.19″ | |
| V16 | Copenhagen | N 55°42′03.60″, E 12°36′32.39″ | |
| Iceland | V17 | Reykjavik | N 64°14′97″, W 21°87′11″ |
| USA | V18 | Anchorage | N 61°14′8″, W 149°53′25″ |
| V19 | Valdez | N 61°6′13″, W 146°21′40″ | |
| V20 | PrudhoeBay | N 70°23′38″, W 148°31′24″ | |
| Canada | V21 | Churchill | N 58°46′33″, W 94°11′38″ |
| Aj | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vi | |||||||||||||
| V1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| V2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | |
| V3 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| V4 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| V5 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| V6 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| V7 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| V8 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| V9 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| V10 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| V11 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| V12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |
| V13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| V14 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| V15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |
| V16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |
| V17 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| V18 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| V19 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| V20 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| V21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| Aj | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vi | |||||||||||||
| V1 | 4.31 | 8.70 | 5.83 | 5.22 | 3.88 | 1.18 | |||||||
| V2 | 3.60 | 1.80 | |||||||||||
| V3 | 3.06 | 8.23 | 6.69 | 5.09 | 4.38 | 1.78 | |||||||
| V4 | 8.23 | 6.69 | 5.09 | 4.38 | 6.37 | 3.51 | 3.34 | ||||||
| V5 | 3.79 | 7.19 | 3.69 | 5.91 | 4.51 | 1.74 | |||||||
| V6 | 8.16 | 1.22 | 5.11 | 4.27 | 1.78 | ||||||||
| V7 | 4.59 | 5.22 | 3.32 | 1.78 | |||||||||
| V8 | 2.37 | 3.60 | 8.18 | 6.41 | |||||||||
| V9 | 1.98 | 10.00 | 3.58 | 5.69 | 5.11 | 3.29 | |||||||
| V10 | 3.88 | 3.38 | 6.04 | 8.66 | 7.77 | 6.35 | |||||||
| V11 | 3.23 | 2.59 | 5.33 | 7.88 | 7.85 | 6.10 | |||||||
| V12 | 2.12 | 3.01 | |||||||||||
| V13 | 10.00 | 2.18 | |||||||||||
| V14 | 1.42 | 3.07 | 5.34 | 5.15 | 3.20 | ||||||||
| V15 | 2.42 | 5.12 | 6.34 | 4.30 | |||||||||
| V16 | 1.29 | 3.99 | 5.21 | 3.17 | |||||||||
| V17 | 1.00 | 2.65 | 3.64 | 5.47 | 7.35 | 8.82 | 3.69 | ||||||
| V18 | 2.02 | ||||||||||||
| V19 | 1.56 | ||||||||||||
| V20 | 1.18 | 8.16 | 6.85 | 4.94 | |||||||||
| V21 | 2.67 | ||||||||||||
| Country | Vi | Port Size | Communication Facilities (Exist: 1; Non-Exist: 0) | Medical Equipment (Exist: 1; Non-Exist: 0) | Port Tug (Exist: 1; Non-Exist: 0) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Emergency Telephone | Radio | Telegraph | Radio-Tel | Rescue | Salvage | ||||
| Russia | V1 | V | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| V2 | M | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| V3 | S | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| V4 | M | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| V5 | M | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| V6 | S | 0 | 1 | 0 | 0 | 1 | 0 | 0 | |
| V7 | M | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| V8 | V | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| Sweden | V9 | L | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Norway | V10 | S | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| V11 | M | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| Finland | V12 | L | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| V13 | S | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| Denmark | V14 | S | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| V15 | M | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| V16 | L | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| Iceland | V17 | M | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| USA | V18 | S | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| V19 | V | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| V20 | S | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Canada | V21 | S | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Aj | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vi | |||||||||||||
| V1 | 3.69 | 5.88 | 4.44 | 4.14 | 3.47 | 2.12 | |||||||
| V2 | 4.02 | 3.12 | |||||||||||
| V3 | 2.03 | 4.61 | 3.85 | 3.05 | 2.69 | 1.39 | |||||||
| V4 | 7.22 | 6.45 | 5.65 | 5.30 | 6.29 | 4.87 | 4.78 | ||||||
| V5 | 5.01 | 6.70 | 4.95 | 6.07 | 5.36 | 3.98 | |||||||
| V6 | 5.84 | 2.37 | 4.32 | 3.89 | 2.65 | ||||||||
| V7 | 5.41 | 5.72 | 4.77 | 4.00 | |||||||||
| V8 | 1.98 | 2.60 | 4.89 | 4.00 | |||||||||
| V9 | 4.37 | 8.38 | 5.17 | 6.22 | 5.93 | 5.02 | |||||||
| V10 | 4.71 | 4.46 | 5.79 | 7.10 | 6.66 | 5.94 | |||||||
| V11 | 4.72 | 4.40 | 5.78 | 7.05 | 7.03 | 6.16 | |||||||
| V12 | 4.44 | 4.88 | |||||||||||
| V13 | 7.77 | 3.86 | |||||||||||
| V14 | 3.48 | 4.31 | 5.44 | 5.35 | 4.37 | ||||||||
| V15 | 6.21 | 7.56 | 8.17 | 7.15 | |||||||||
| V16 | 4.02 | 5.37 | 5.98 | 4.96 | |||||||||
| V17 | 3.61 | 4.43 | 4.93 | 5.84 | 6.78 | 7.52 | 4.95 | ||||||
| V18 | 3.78 | ||||||||||||
| V19 | 3.25 | ||||||||||||
| V20 | 1.09 | 4.58 | 3.93 | 2.97 | |||||||||
| V21 | 4.11 | ||||||||||||
| The Accident Node | Name of Sea Area | The Port Node | Edge Weight | Ranking |
|---|---|---|---|---|
| A1 (70.0583 N,126.3500 E) | Laplacev Sea | V6 (Tiksi) | 5.8 | 1 |
| V7 (Igarka) | 5.4 | 2 | ||
| V1 (Dikson) | 3.7 | 3 | ||
| A2 (73.2167 N, 134.567 W) | Beaufort Sea | V20 (PrudhoeBay) | 4.6 | 1 |
| V8 (Providenija) | 2.6 | 2 | ||
| - | - | - | ||
| A3 (64.4167 N, 165.333 W) | Chukchi Sea | V8 (Providenija) | 4.9 | 1 |
| V20 (PrudhoeBay) | 3.9 | 2 | ||
| V18 (Anchorage) | 3.8 | 3 | ||
| A4 (69.7167 N, 170.3 E) | East Siberian Sea | V6 (Tiksi) | 4.3 | 1 |
| V8 (Providenija) | 4.0 | 2 | ||
| V20 (PrudhoeBay) | 3.0 | 3 | ||
| A5 (76.15 N, 71.9333 E) | Kara Sea | V4 (Murmansk) | 7.2 | 1 |
| V1 (Dikson) | 5.9 | 2 | ||
| V7 (Igarka) | 5.7 | 3 | ||
| A6 (70.2833 N, 44.3167 E) | Barents Sea | V5 (Arkhangelsk) | 6.7 | 1 |
| V4 (Murmansk) | 6.4 | 2 | ||
| V7 (Igarka) | 4.8 | 3 | ||
| A7 (79.7167 N, 26.65 E) | Barents Sea | V9 (Goteborg) | 8.4 | 1 |
| V4 (Murmansk) | 5.7 | 2 | ||
| V5 (Arkhangelsk) | 4.9 | 3 | ||
| A8 (71.3 N, 22.3 E) | Norwegian Sea | V15 (Aarhus) | 6.2 | 1 |
| V5 (Arkhangelsk) | 6.1 | 2 | ||
| V10(Grenland) | 5.8 | 3 | ||
| A9 (66.033 N, 8.0833 E) | Norwegian Sea | V13(Kokkola) | 7.8 | 1 |
| V15 (Aarhus) | 7.6 | 2 | ||
| V11(Bergen) | 7.1 | 3 | ||
| A10 (61.55 N, 6.8 W) | Greenland Sea | V15 (Aarhus) | 8.2 | 1 |
| V11(Bergen) | 7.0 | 2 | ||
| V17 (Reykjavik) | 6.8 | 3 | ||
| A11 (66.2 N, 15.333 W) | Greenland Sea | V17 (Reykjavik) | 7.5 | 1 |
| V15 (Aarhus) | 7.2 | 2 | ||
| V11(Bergen) | 6.2 | 3 | ||
| A12 (65.4355 N, 55.6285 W) | Davis Strait | V17 (Reykjavik) | 4.9 | 1 |
| V21 (Churchill) | 4.1 | 2 | ||
| - | - | - |
| The Accident Node | The Port Node | |
|---|---|---|
| Considering ERT Only | Considering ERT and PEC | |
| A1 | V6 | V6 |
| A2 | V20 | V20 |
| A3 | V8 | V8 |
| A4 | V8 | V6 |
| A5 | V1 | V4 |
| A6 | V5 | V5 |
| A7 | V9 | V9 |
| A8 | V10 | V15 |
| A9 | V13 | V13 |
| A10 | V11 | V15 |
| A11 | V17 | V17 |
| A12 | V17 | V17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Ma, X.; Ma, L.; Zhao, Y. An Emergency Port Decision-Making Method for Maritime Accidents in Arctic Waters. J. Mar. Sci. Eng. 2023, 11, 1330. https://doi.org/10.3390/jmse11071330
Wang T, Ma X, Ma L, Zhao Y. An Emergency Port Decision-Making Method for Maritime Accidents in Arctic Waters. Journal of Marine Science and Engineering. 2023; 11(7):1330. https://doi.org/10.3390/jmse11071330
Chicago/Turabian StyleWang, Ting, Xiaoxue Ma, Laihao Ma, and Yulan Zhao. 2023. "An Emergency Port Decision-Making Method for Maritime Accidents in Arctic Waters" Journal of Marine Science and Engineering 11, no. 7: 1330. https://doi.org/10.3390/jmse11071330
APA StyleWang, T., Ma, X., Ma, L., & Zhao, Y. (2023). An Emergency Port Decision-Making Method for Maritime Accidents in Arctic Waters. Journal of Marine Science and Engineering, 11(7), 1330. https://doi.org/10.3390/jmse11071330





