The Practice and Development of T-Bar Penetrometer Tests in Offshore Engineering Investigation: A Comprehensive Review
Abstract
1. Introduction
2. Development of Marine Penetrometer Deployment Technology and T-Bar Penetrometer
- The high pore water pressure during penetration testing in a high-pressure environment on the seabed and the low strength of the soft soils on the seabed compared to the soft soils on the seabed has a greater impact on the sensitivity of the penetration resistance during testing.
- There is a significant correction for unequal area effect and uncertainty in the overburden stress correction on penetration resistance.
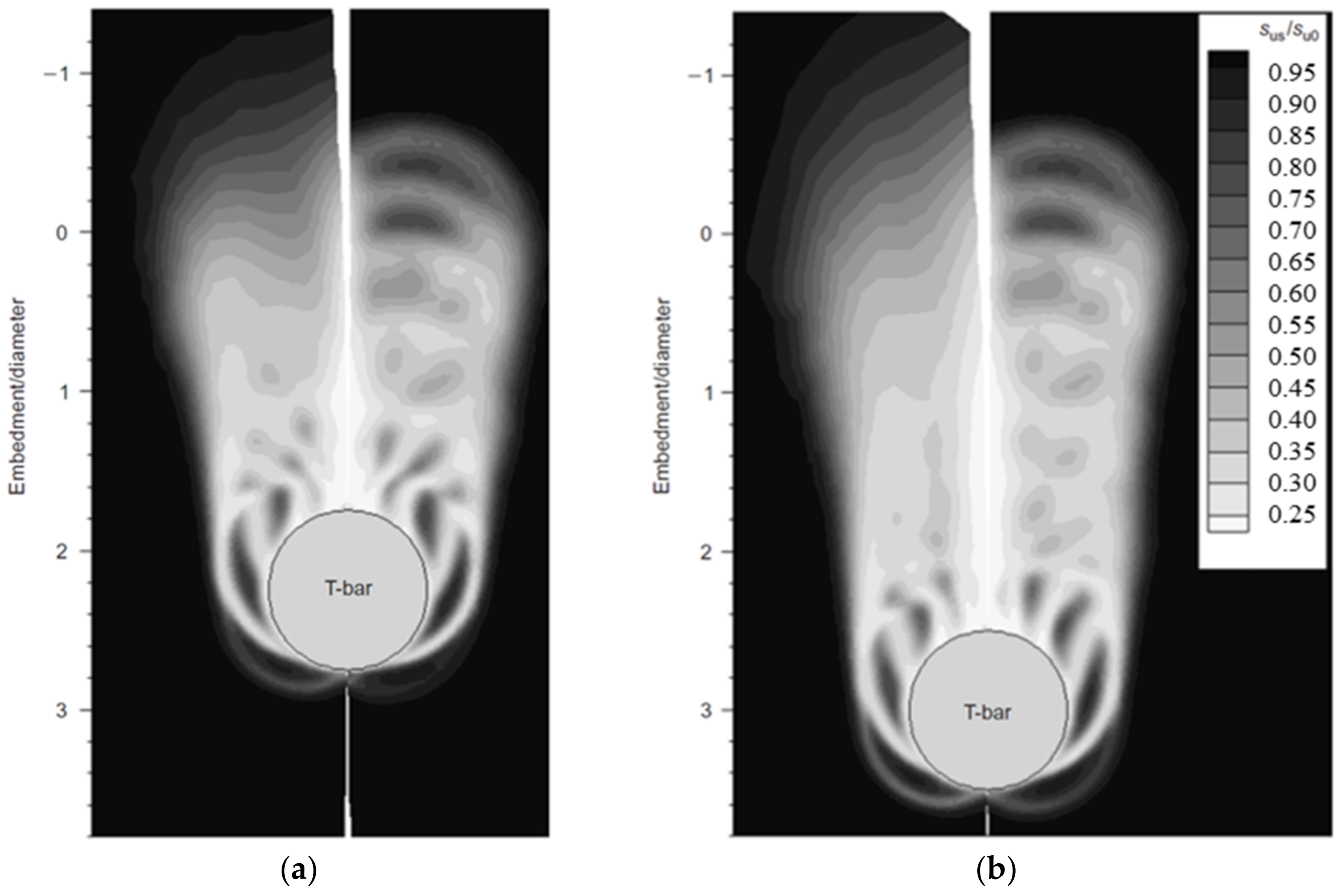
3. Analysis of T-Bar Full-Flow Penetration Test Results
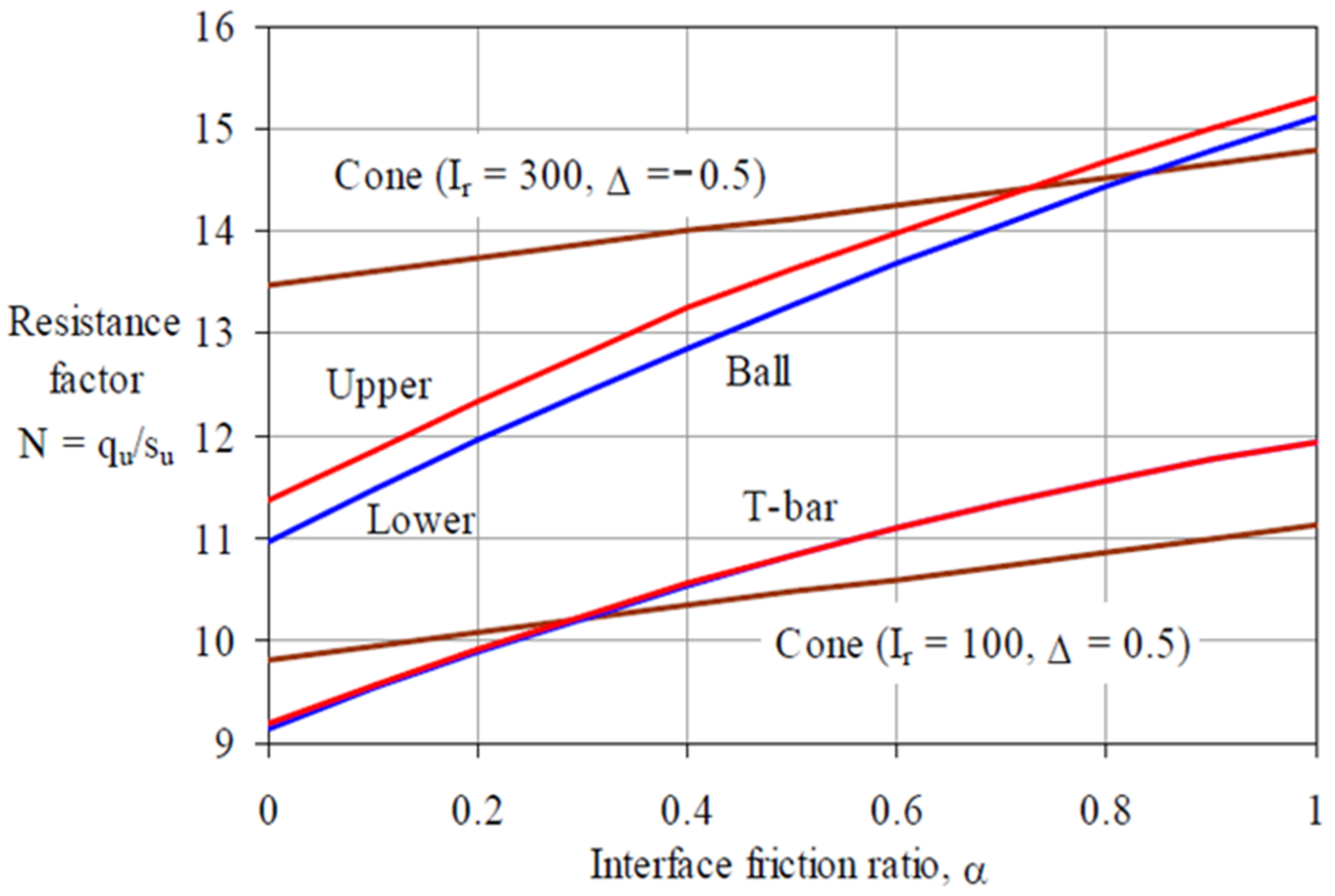
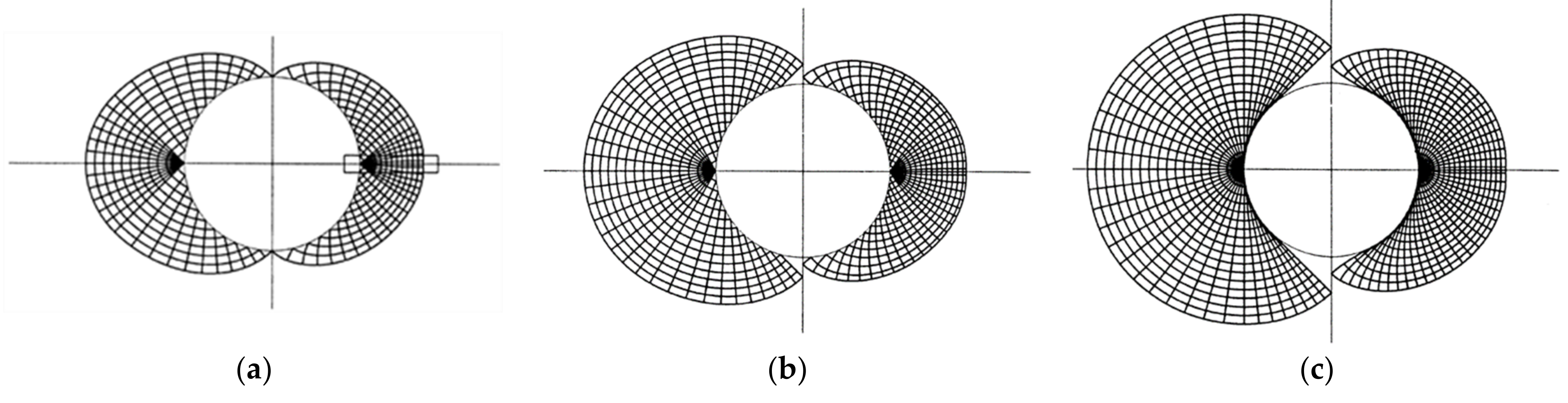
3.1. Analytical Solution of the Resistance Factor
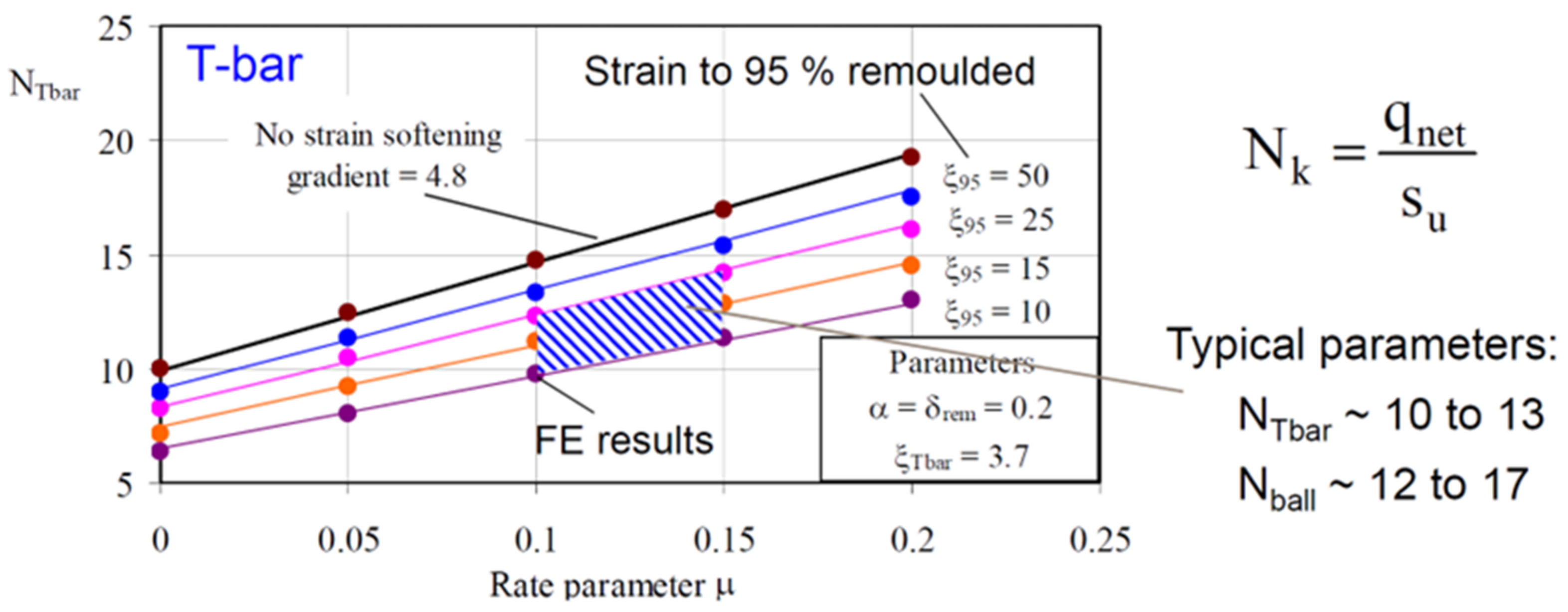
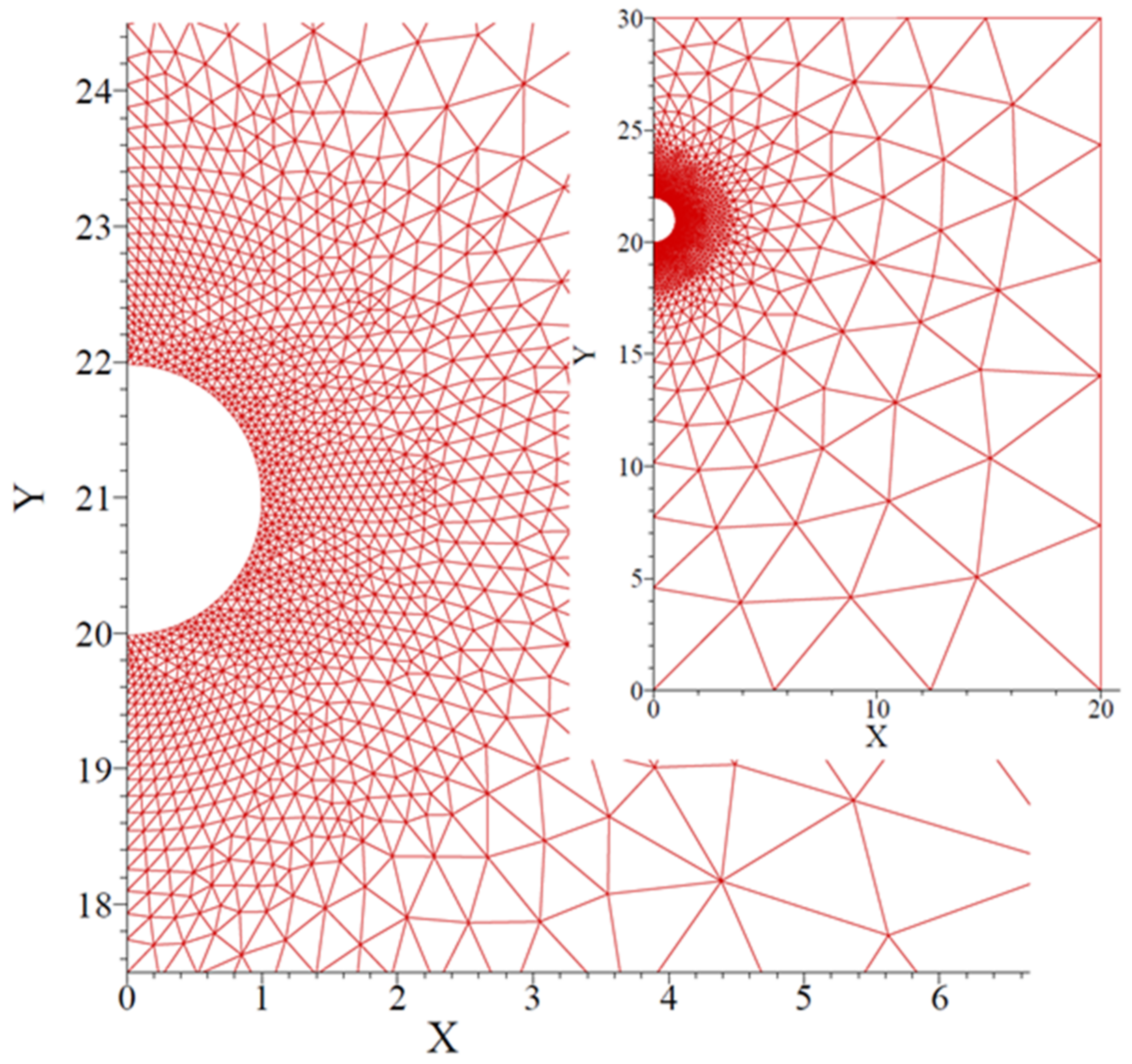
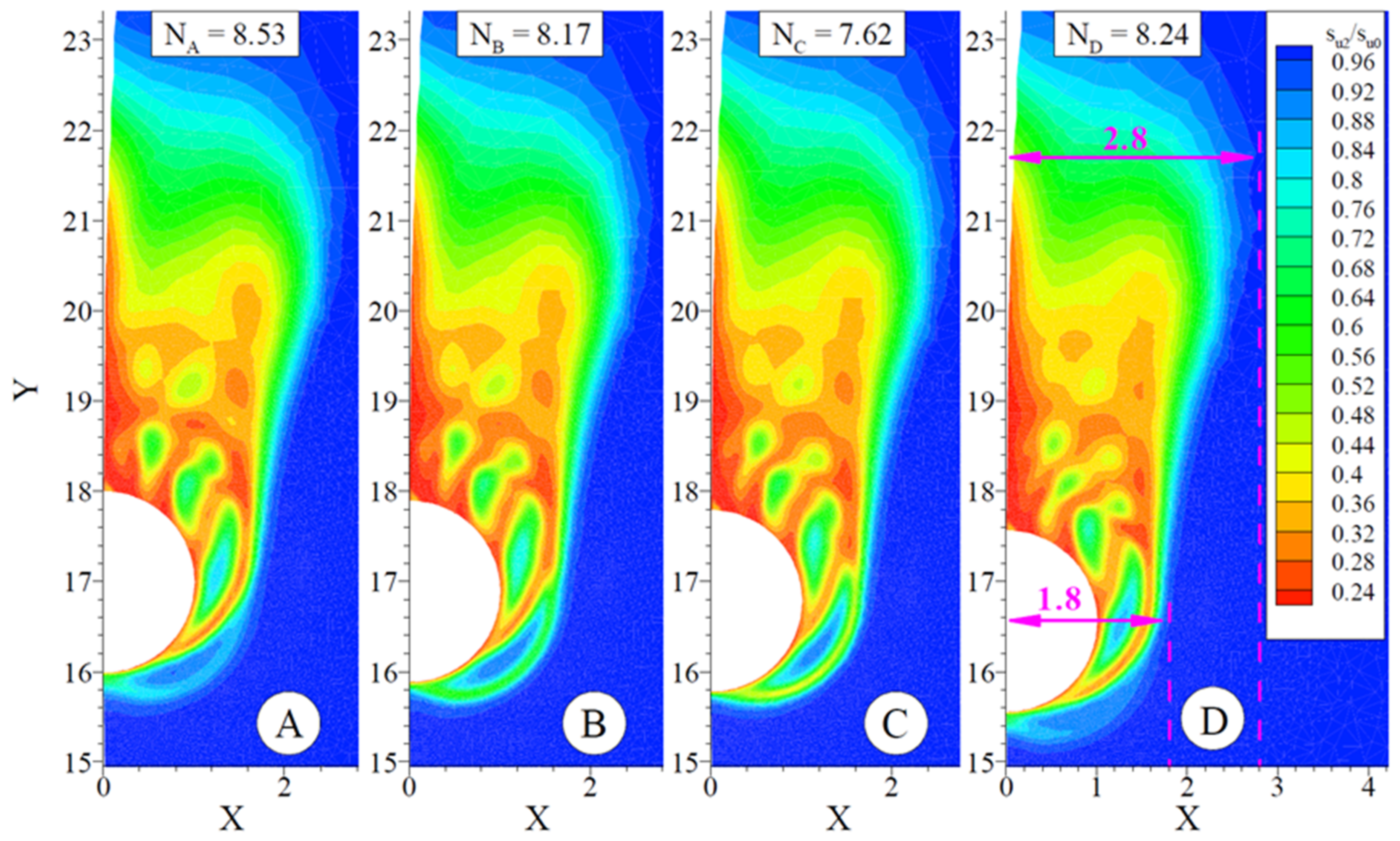
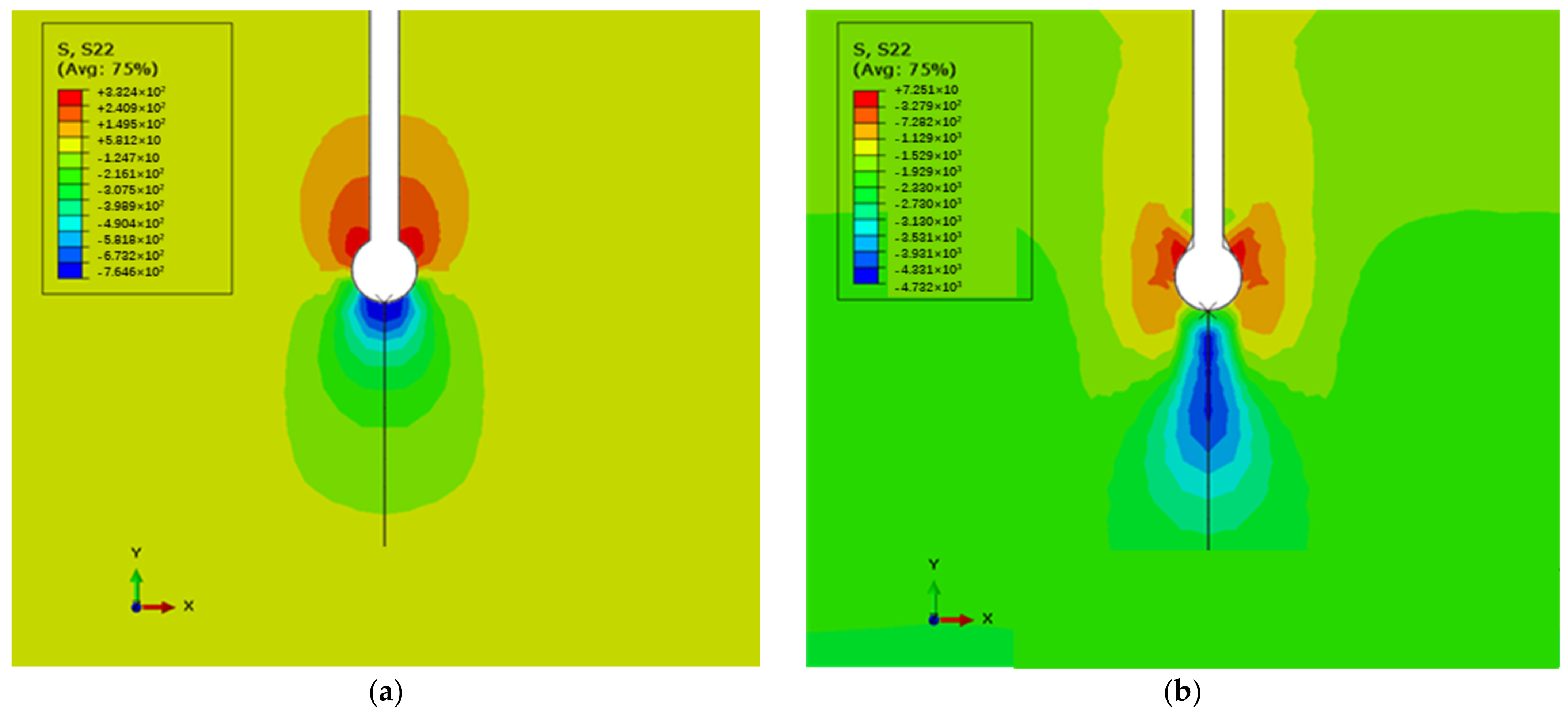
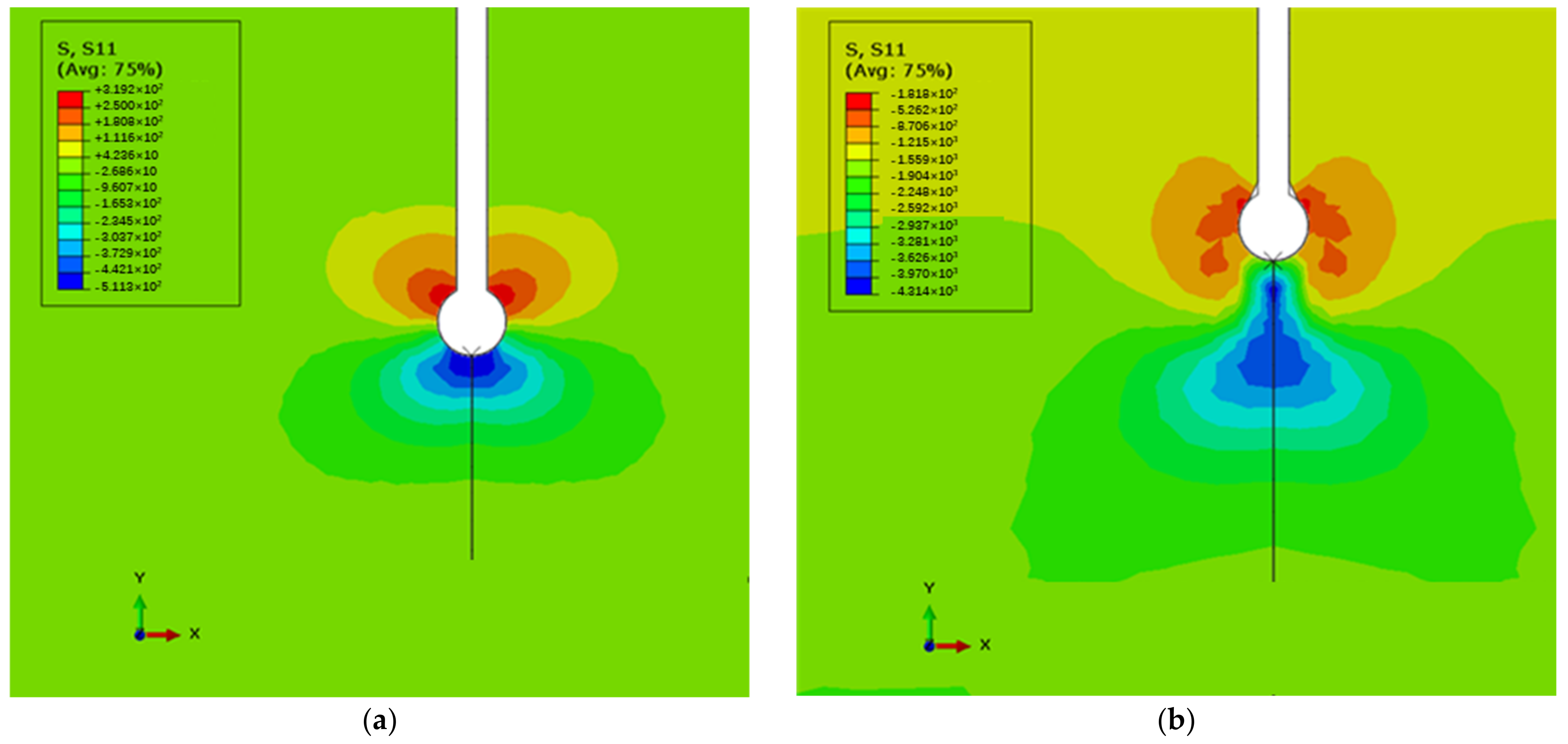
3.2. Numerical Simulation
3.3. Laboratory Model Test
- 1.
- Development of the calibration laboratory model tank test
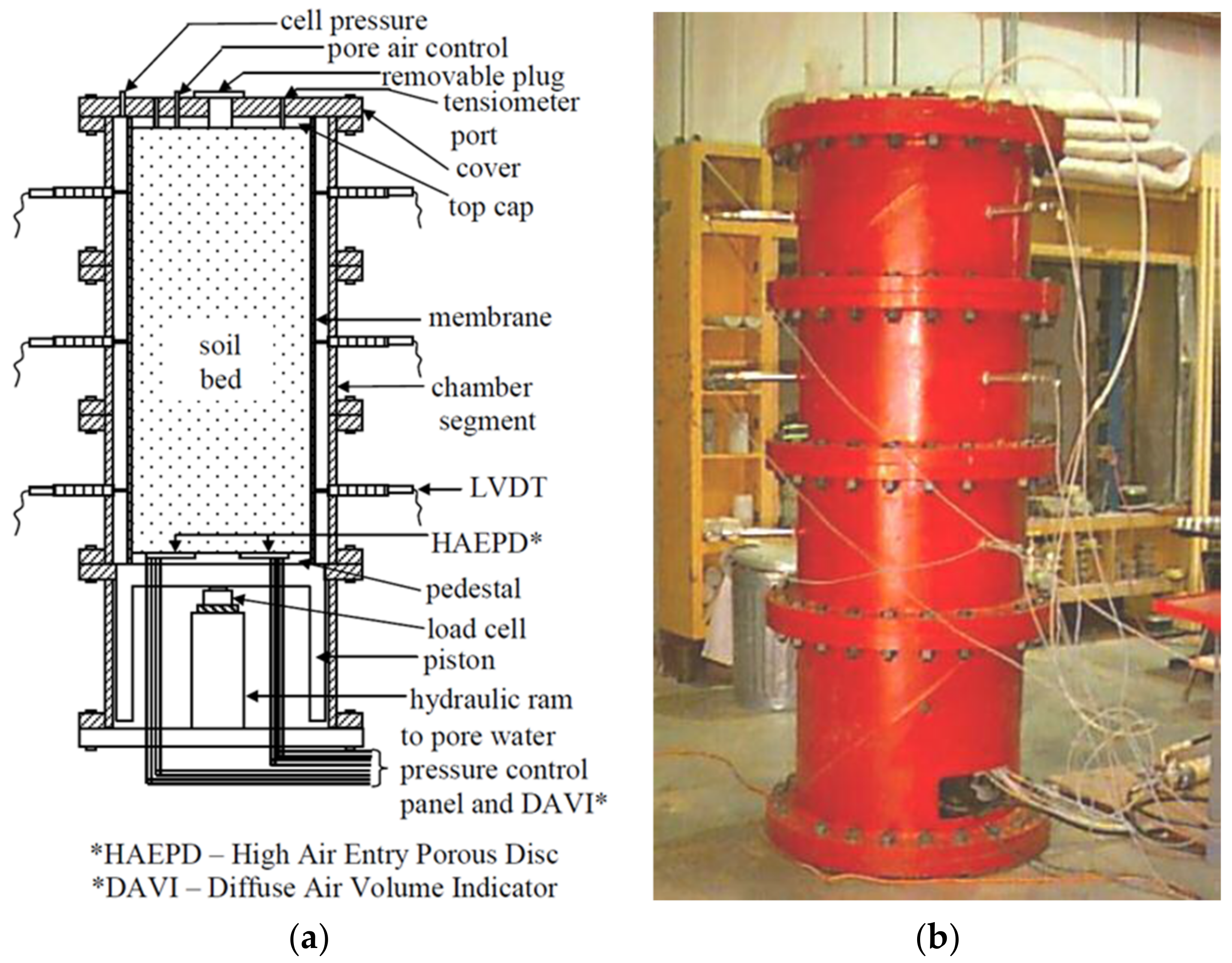
- 2.
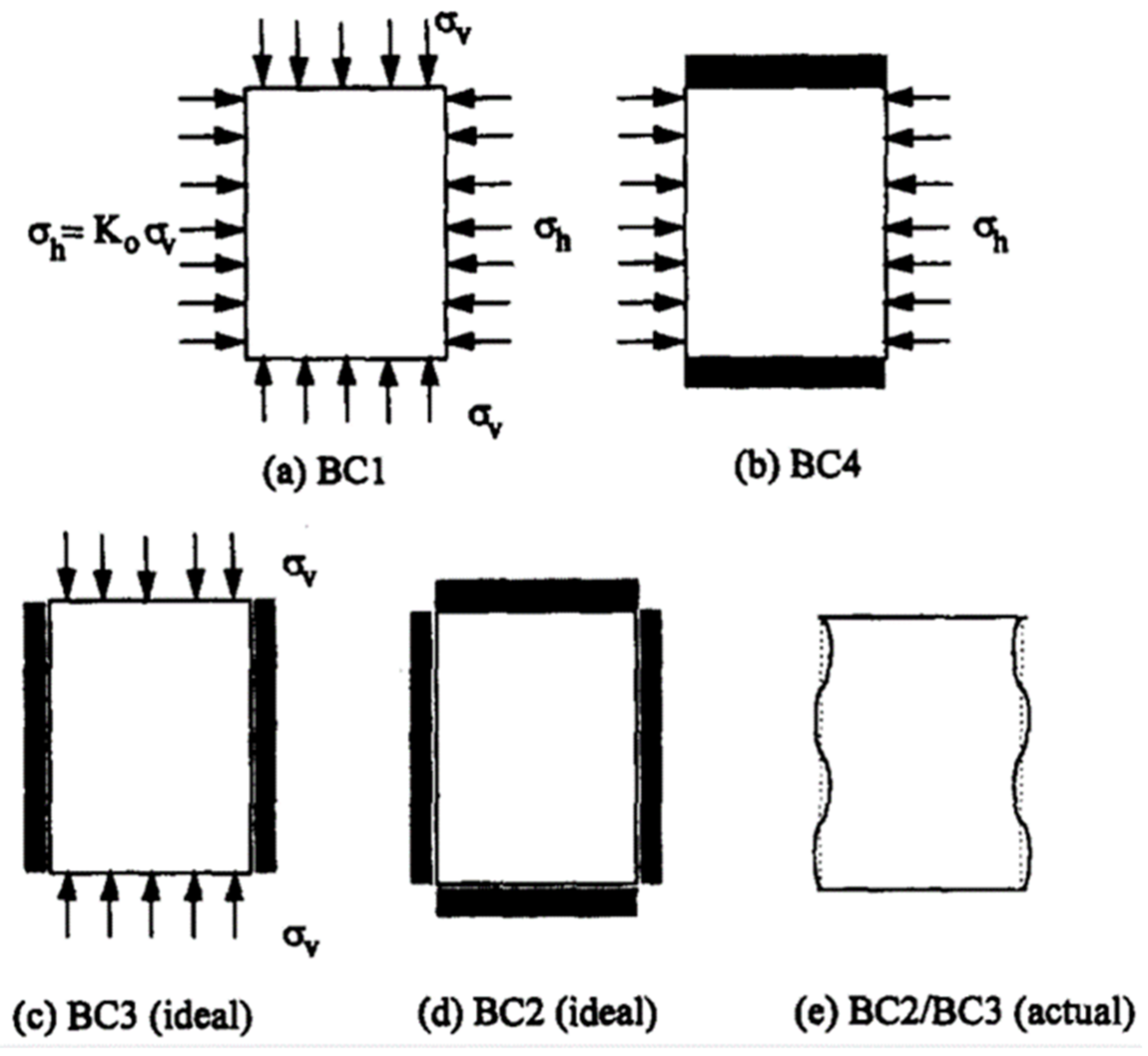
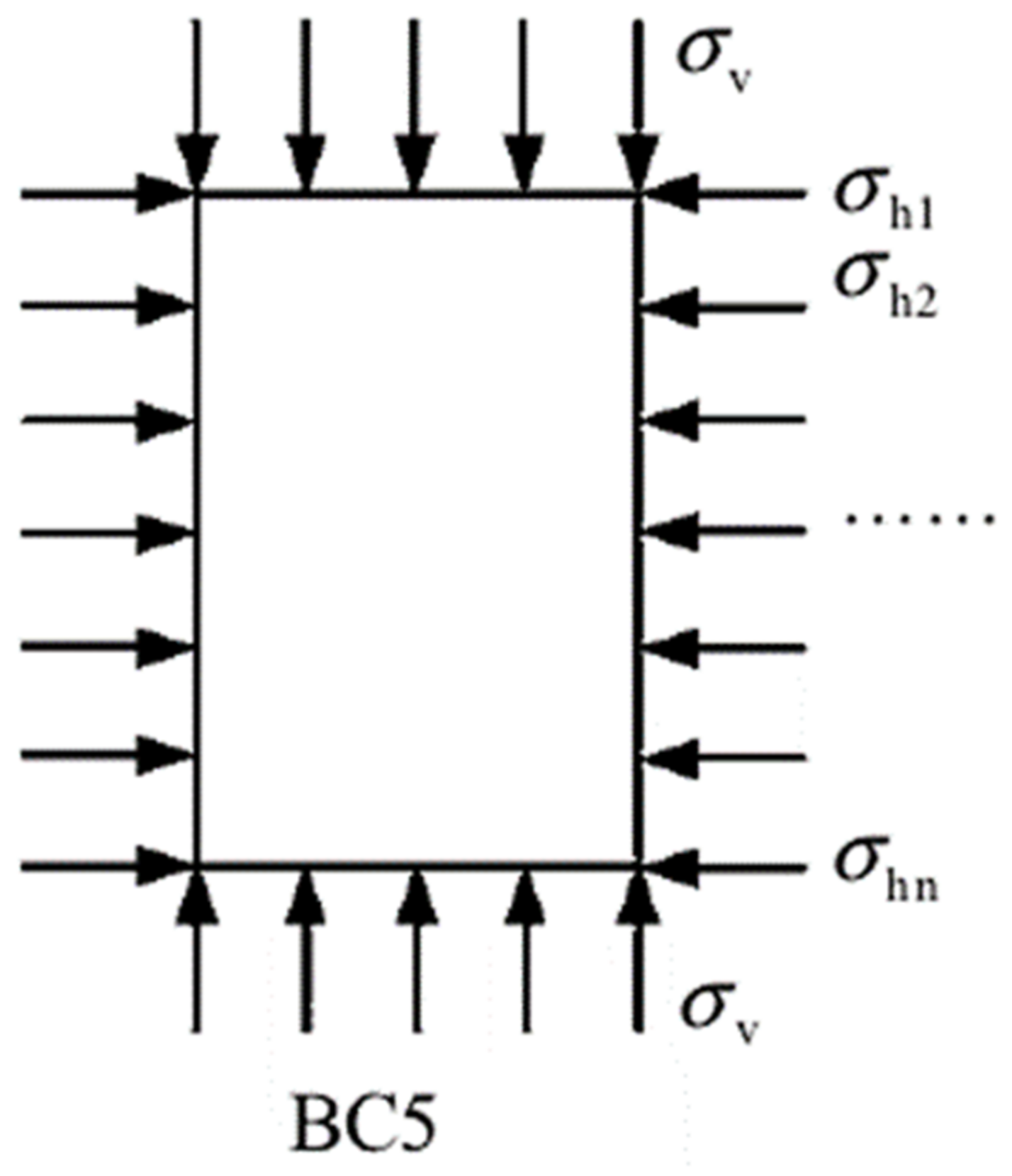
- Boundary state control for calibration tank tests
- 3.
- Factors influencing the calibration tank test
- Boundary effects
- Size effect
3.4. In Situ Test
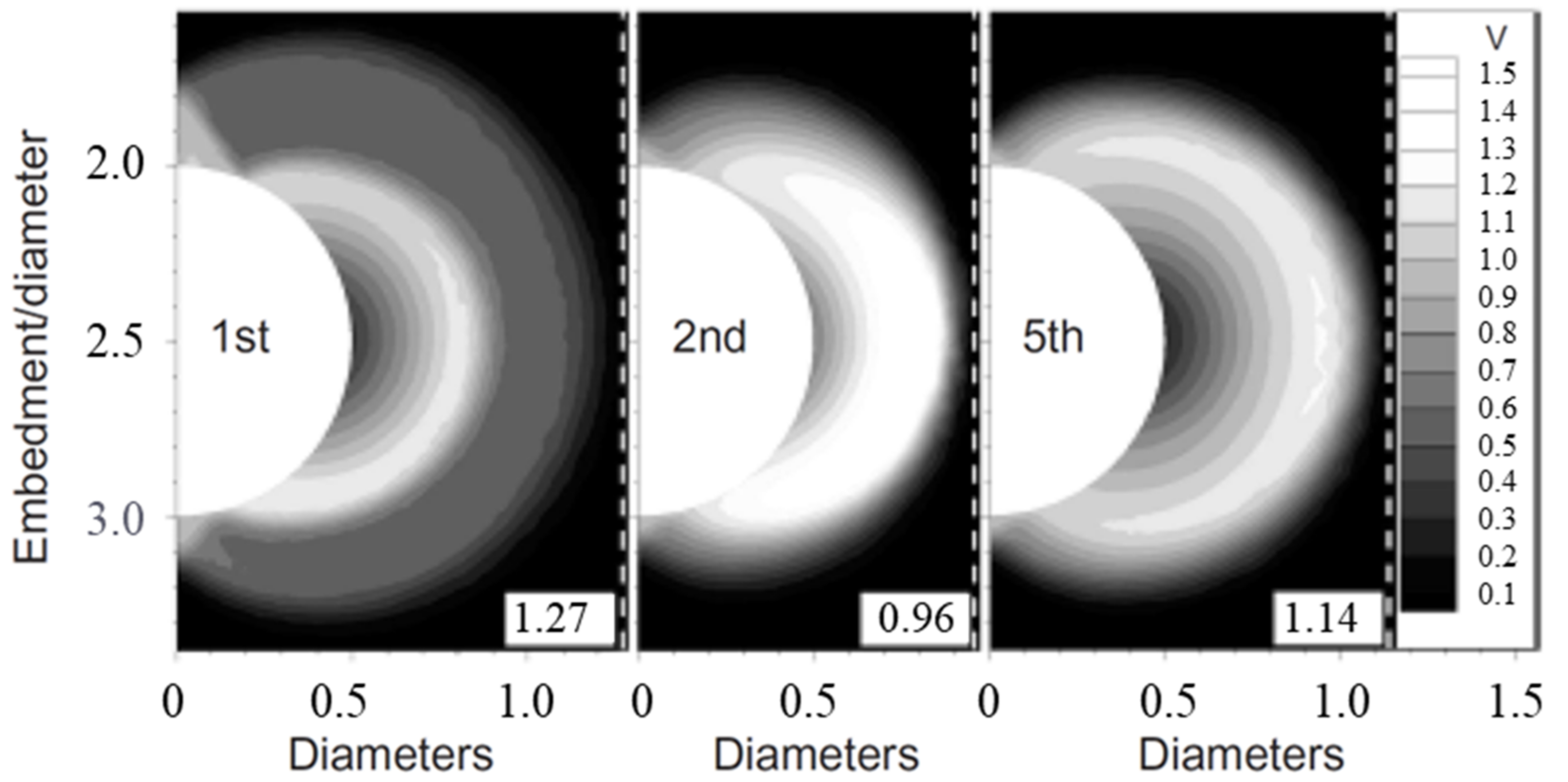
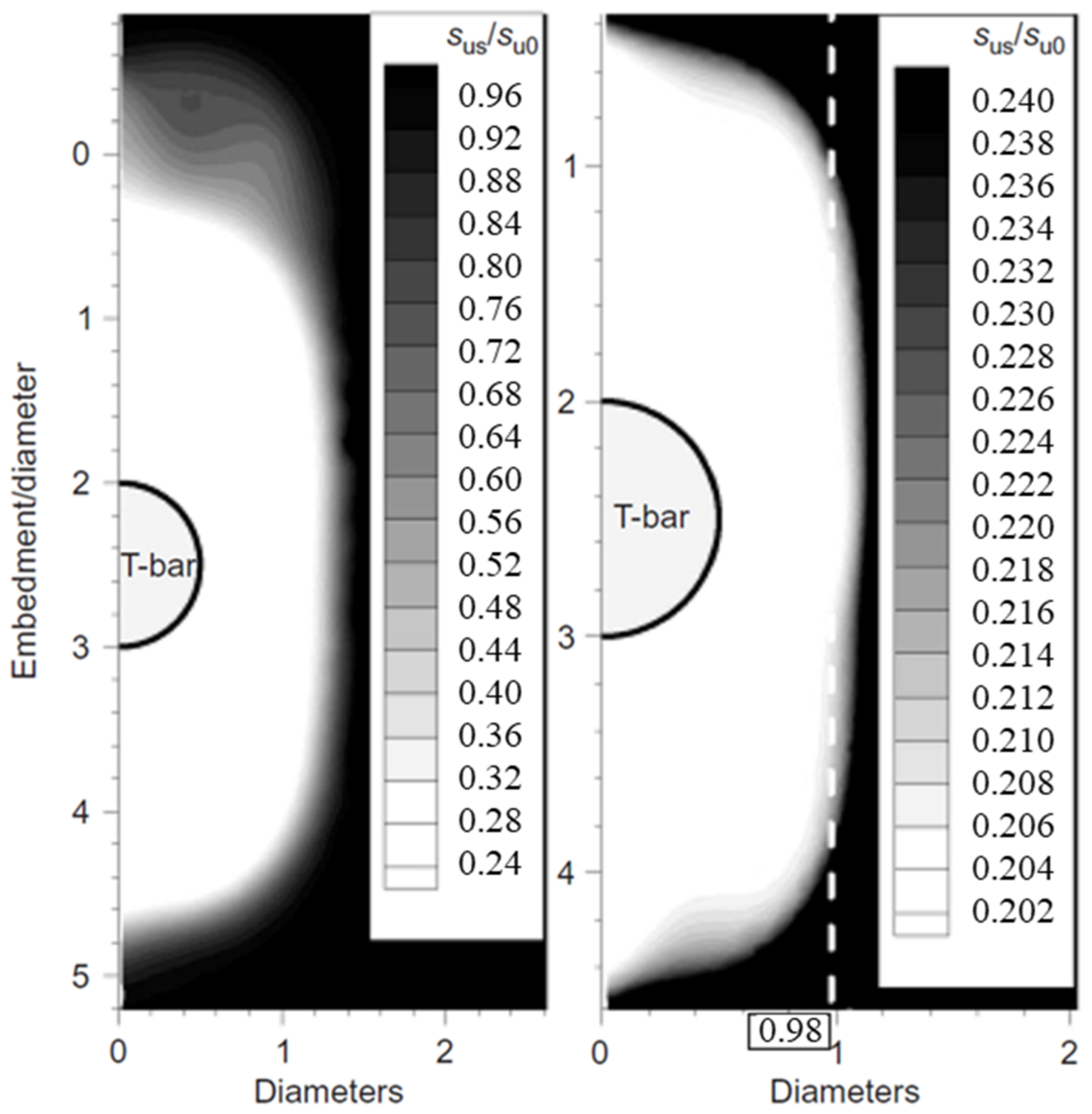
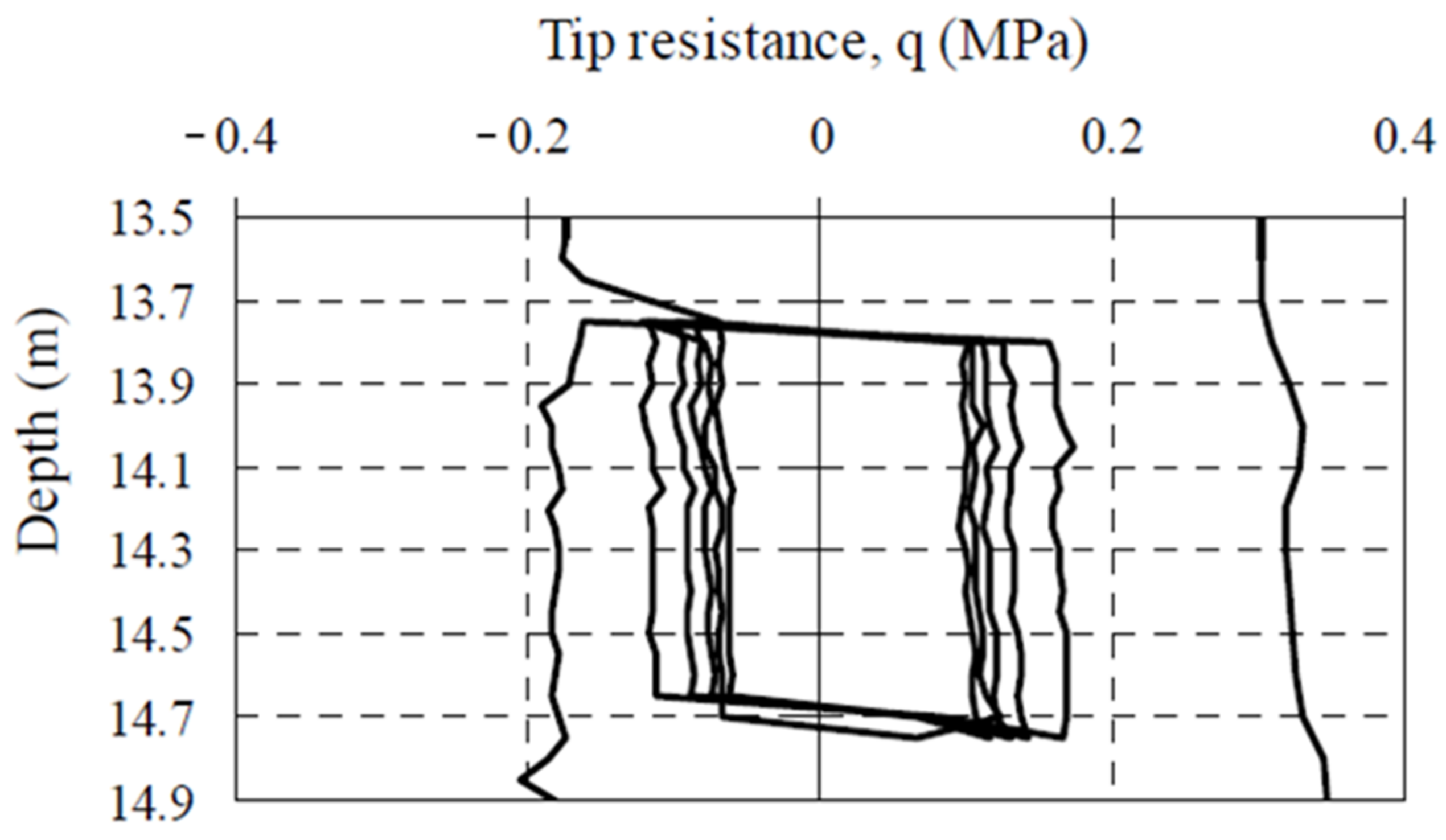
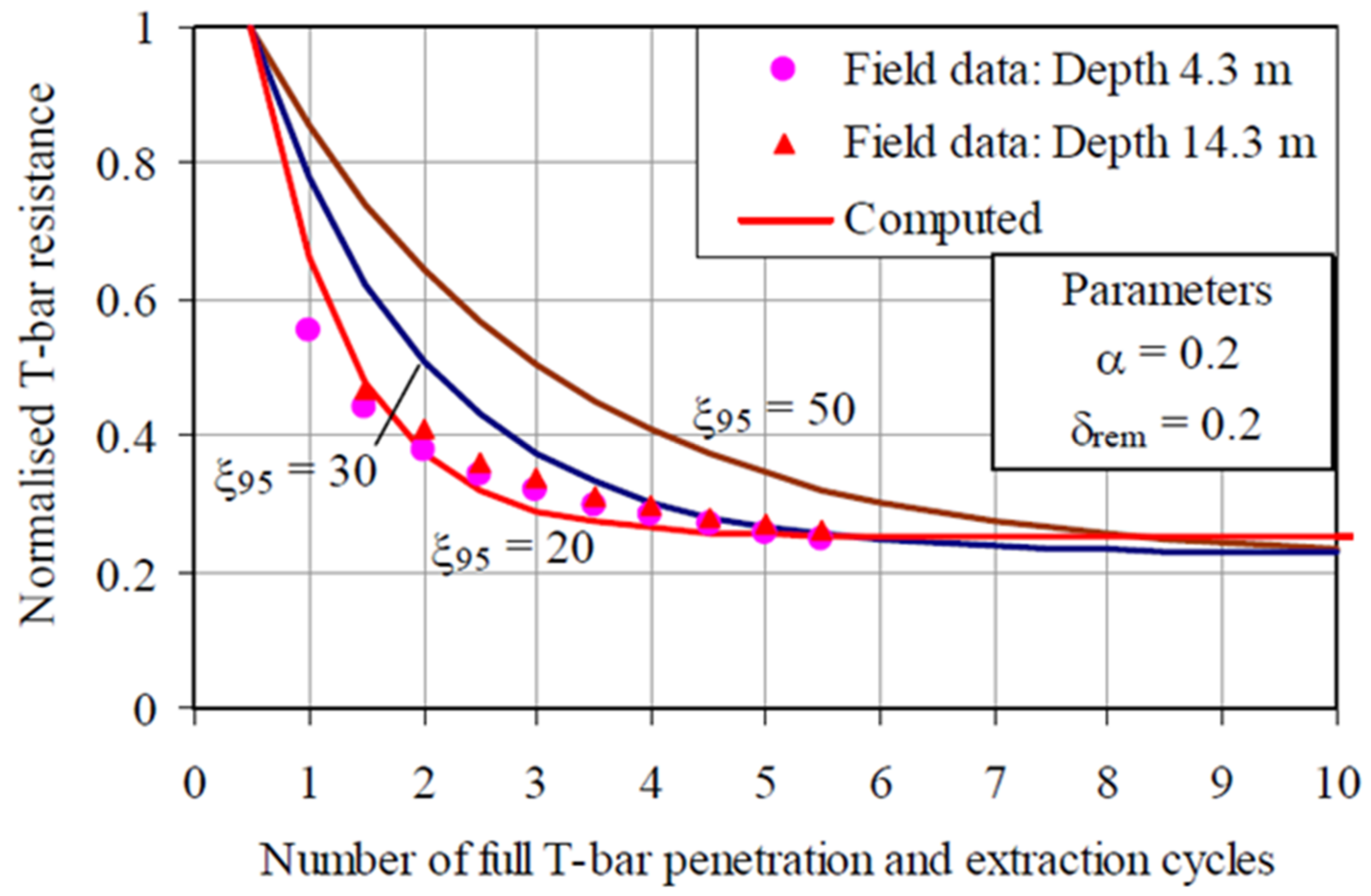
3.4.1. Cyclic Penetration Tests
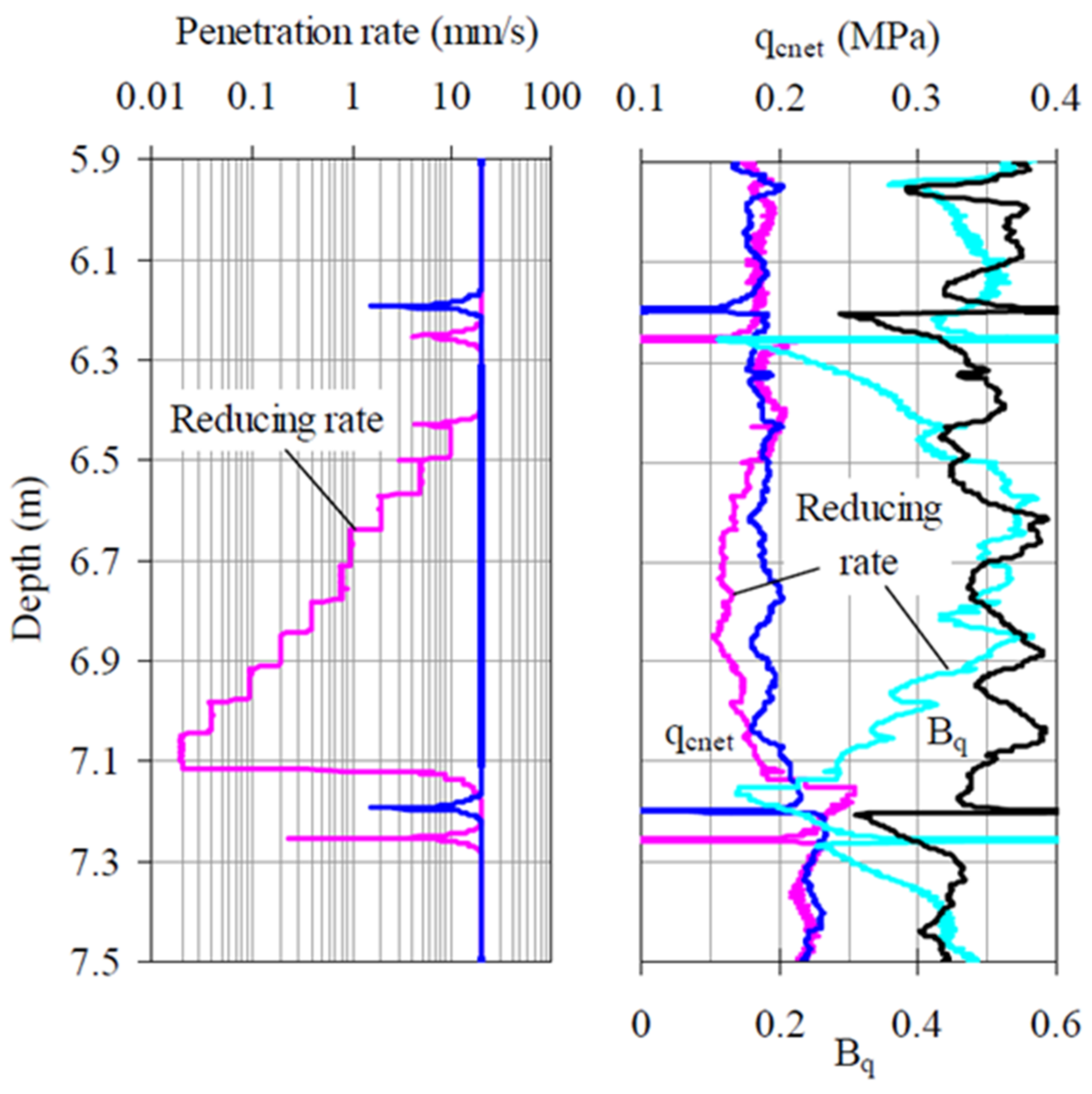
3.4.2. Variable Rate Penetration Experiments
4. Application of the T-Bar Penetrometer for Marine Soft Soil Engineering
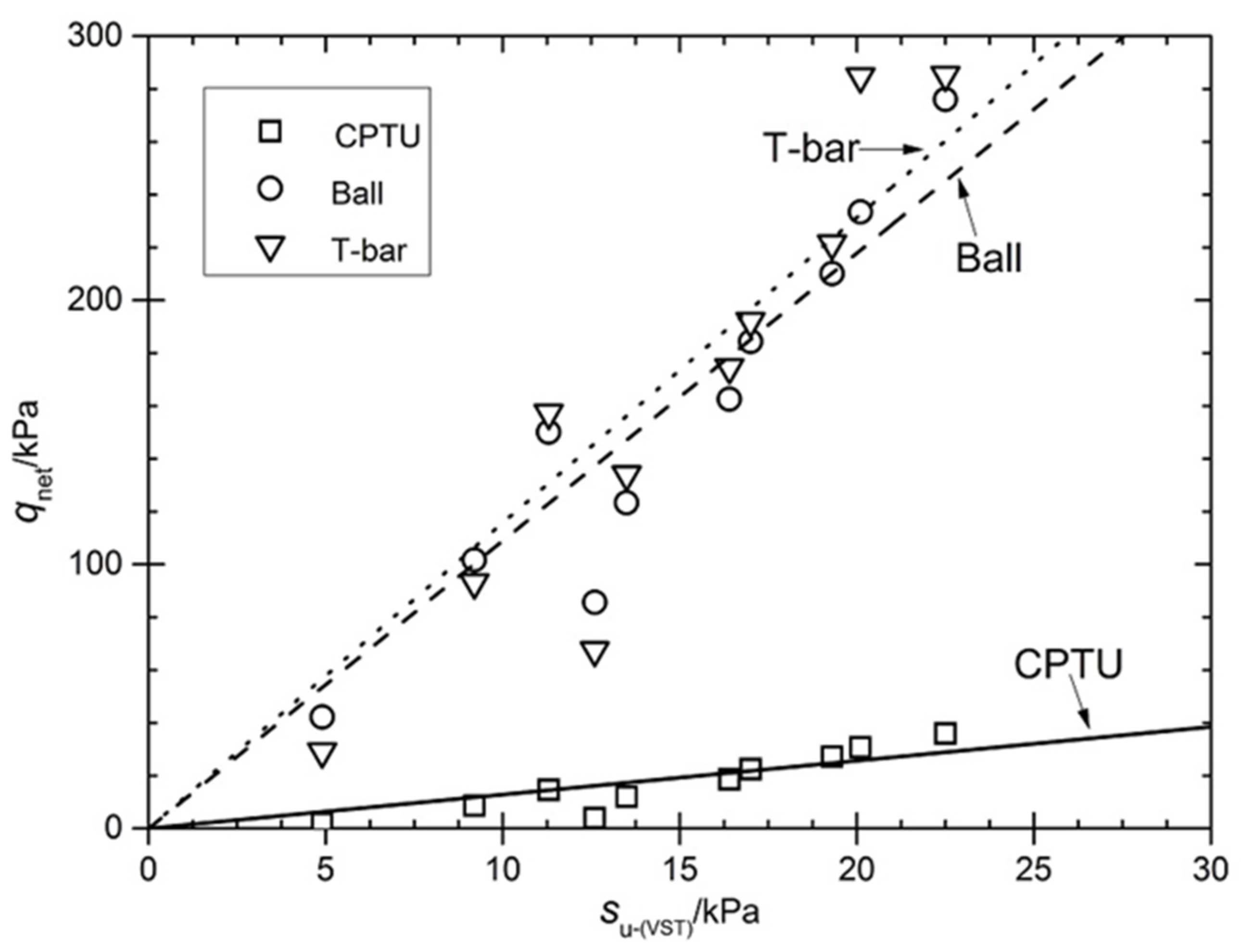
4.1. Evaluation of the Undrained Shear Strength of Soft Marine Soils
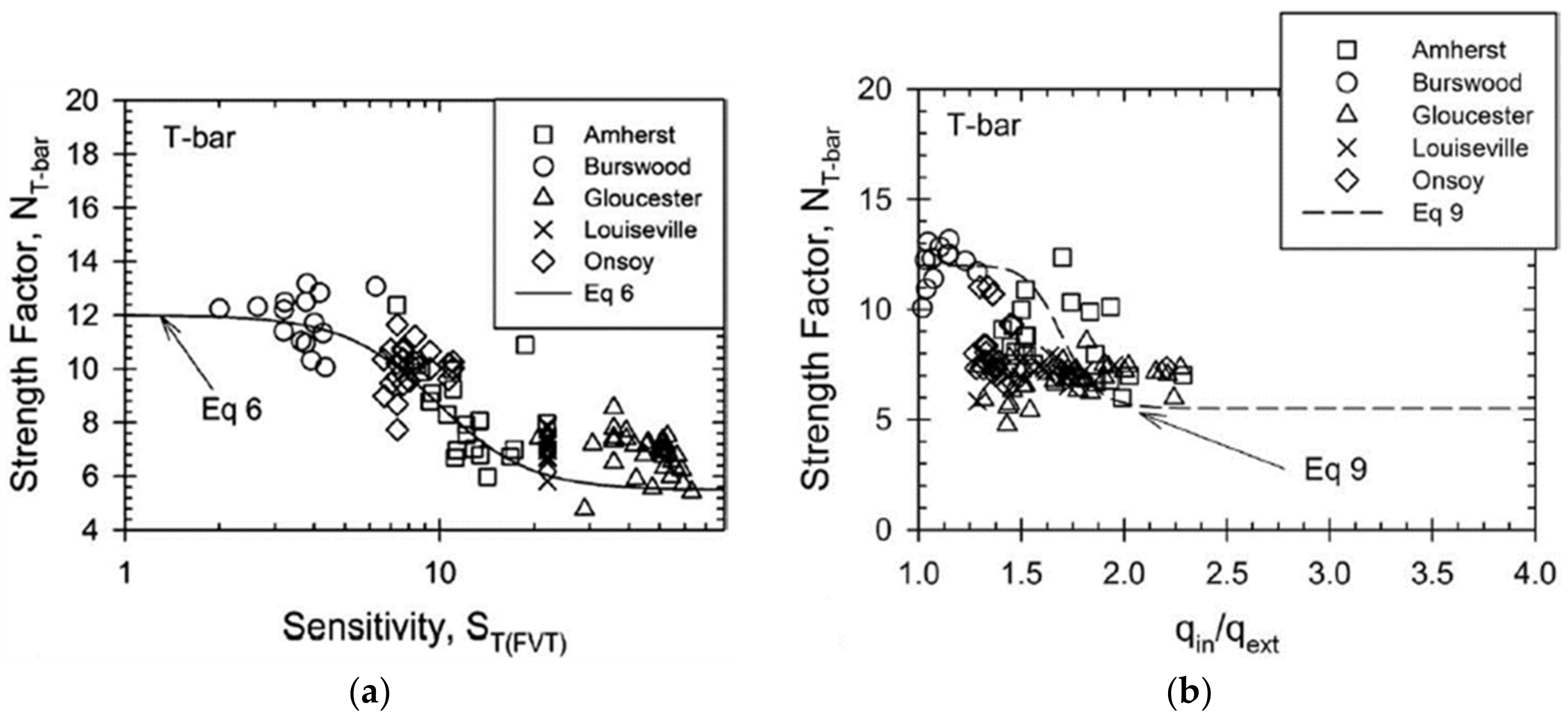
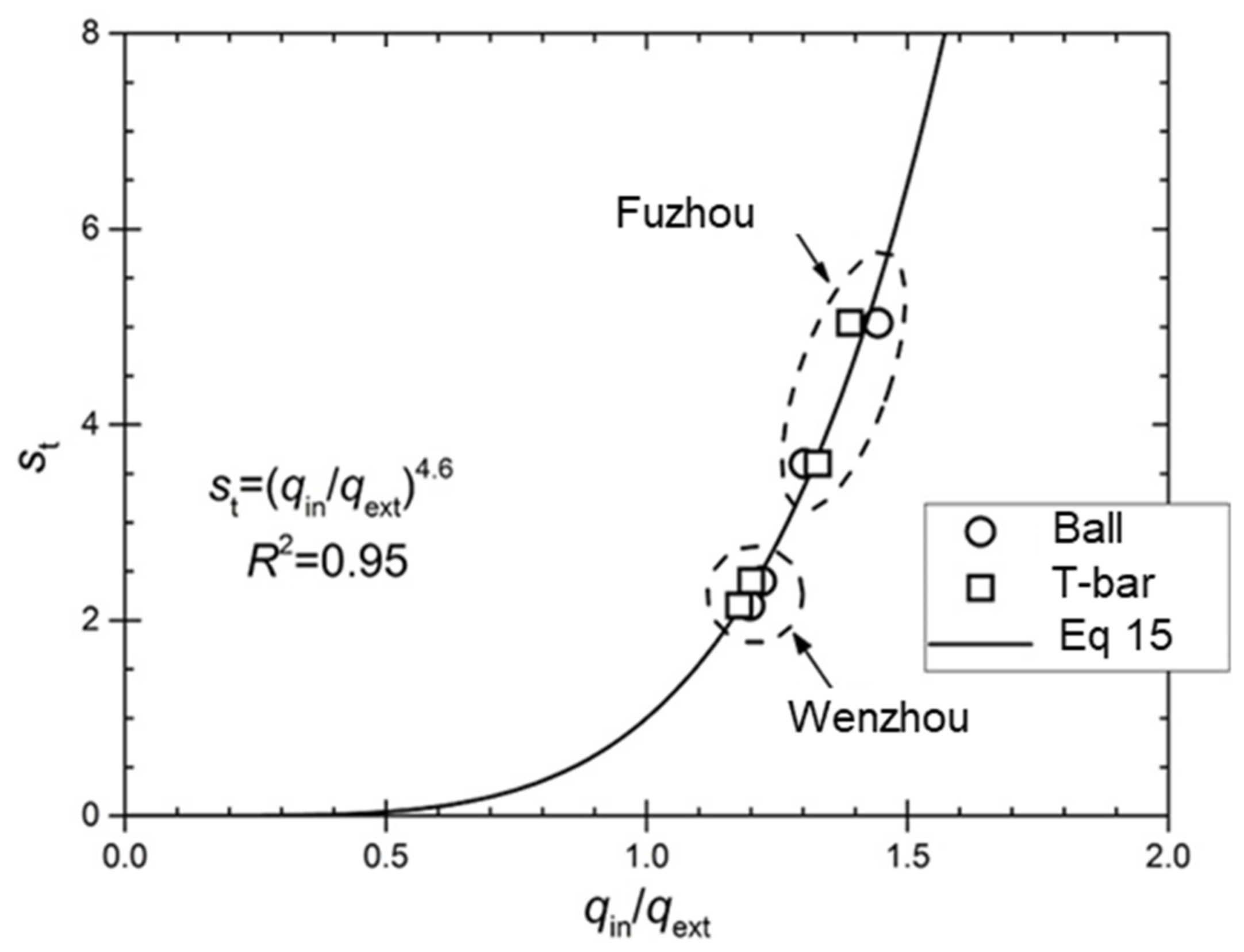
4.2. Sensitivity Evaluation of Marine Soft Soils
4.3. Discussion and Conclusions
| Geotechnical Problem | Depth Below Seabed (m) | Comment | Applicability–Reliability | |||
|---|---|---|---|---|---|---|
| CPTU | T-bar, ball (Fitted with Pore Water Pressure Sensors) | |||||
| Soil Profiling | Soil Parameters Interpreted | Soil Profiling | Soil Parameters Interpreted | |||
| Backfilled trenches: upheaval buckling | 0–1 | Extremely soft material may be encountered | Soil profile 1,2 | γ 2, u 2, OCR 3, K0 4,5, su 2,3, sru 5, St 2,3, c’ 3,4, φ’ 3,4, Gmax 4, E 5, G 5, M 5, k 2–4, ch 2,3 | Soil profile 3 | u 2, OCR 3, su 1,2, sru 1,2, St 1,2, k 2−4, ch 2,3 |
| Pipeline–riser soil interaction | 0–3 | Very soft material may be encountered | Soil profile 1,2 Classification 2 | γ 2, u 2, OCR 3, K0 4,5, su 2,3, sru 5, St 2,3, c’ 3,4, φ’ 3,4, Gmax 4, E 5, G 5, M 5, k 2−4, ch 2,3 | Soil profile 3 | u 2, OCR 3, su 1,2, sru 1,2, St 1,2, k 2−4, ch 2,3 |
| Seabed templates, penetration, stability, settlements | 0–10 | - | Soil profile 1,2 Classification 2 | γ 2, u 2, OCR 3, K0 4,5, su 2,3, sru 5, St 2,3, c’ 3,4, φ’ 3,4, Gmax 4, E 5, G 5, M 5, k 2−4, ch 2,3 | Soil profile 3 | u 2, OCR 3, su 1,2, sru 1,2, St 1,2, k 2−4, ch 2,3 |
| Geohazards; slope stability | 0–10/100 | Use of T-bar, ball, and vane may be limited to 40 m depth | Soil profile 1,2 Classification 2 | γ 2, u 2, OCR 3, K0 4,5, su 2,3, sru 5, St 2,3, c’ 3,4, φ’ 3,4, Gmax 4, E 5, G 5, M 5, k 2−4, ch 2,3 | Soil profile 3 | u 2, OCR 3, su 1,2, sru 1,2, St 1,2, k 2−4, ch 2,3 |
5. Summary and Outlook
- 1.
- An analysis of the theoretical solution of the T-bar penetrometer data. In practical applications, the interpretation of the T-bar penetrometer test data to predict the undrained shear strength and sensitivity of soft soils mainly relies on empirical formulas. However, the evaluated parameters of soft soils through the empirical relationship method lack reliability due to the absence of a large amount of reliable test data. This problem can be solved by gaining a deeper understanding of the mechanism of the T-bar full-flow test evaluation system and the derivation of a more accurate theoretical analytical solution.
- 2.
- The numerical simulation of the T-bar full-flow penetrometer. Recently, the numerical simulation of the T-bar penetrometer is proposed by researchers, which considers the effects of the strain rate, strain softening, and strength anisotropy. However, it is difficult to restore the soil material and the penetration process in the simulation process nowadays, and further development of numerical techniques is needed.
- 3.
- The laboratory model experiment of the T-bar penetrometer. Most of the present research on laboratory model experiments is focused on the traditional CPTU testing of sandy soils, while the research on the penetration mechanism of the T-bar full-flow penetrometer of soft soil is still insufficient.
- 4.
- The T-bar penetrometer field experimental research. The good performance of the T-bar penetrometer technology depends on the large number of accurate field test data, which are used for repeated verification and calibration. In recent years, the T-bar penetrometer technology has mainly been used in Europe and the United States, and the test results are usually available for these areas. However, in many Asian countries, such as China, the research and application of the T-bar penetrometer technology is still in its infancy. Therefore, a large number of field tests still need to be conducted to verify the applicability of the T-bar penetrometer in soft coastal soils in Asian countries.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baumert, H.Z.; Simpson, J.; Simpson, J.H.; Sündermann, J. Marine Turbulence: Theories, Observations, and Models; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Guo, Z.; Jeng, D.-S.; Guo, W.; Wang, L. Failure mode and capacity of suction caisson under inclined short-term static and one-way cyclic loadings. Mar. Georesources Geotechnol. 2018, 36, 52–63. [Google Scholar]
- Guo, Z.; Zhou, W.; Zhu, C.; Yuan, F.; Rui, S. Numerical simulations of wave-induced soil erosion in silty sand seabeds. Engineering 2019, 7, 52. [Google Scholar]
- Lei, H.; Lu, H.; Wang, X.; Ren, Q.; Li, B. Changes in soil micro-structure for natural soft clay under accelerated creep condition. Geotechnology 2016, 34, 365–375. [Google Scholar] [CrossRef]
- Lei, H.; Xu, Y.; Jiang, M.; Jiang, Y. Deformation and fabric of soft marine clay at various cyclic load stages. Ocean Eng. 2020, 195, 106757. [Google Scholar] [CrossRef]
- Randolph, M.; Cassidy, M.; Gourvenec, S.; Erbrich, C. Challenges of offshore geotechnical engineering. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Lahore, Pakistan, 7–8 December 2022; p. 123. [Google Scholar]
- Shan, Y.; Meng, Q.; Yu, S.; Mo, H.; Li, Y. Energy based cyclic strength for the influence of mineral composition on artificial marine clay. Eng. Geol. 2020, 274, 105713. [Google Scholar] [CrossRef]
- Yang, Y. Research on Penetration Mechanism and Application of Ball Penetrometer in Offshore Engineering. Master’s Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]
- Guo, Z.; Yu, L.; Wang, L.; Bhattacharya, S.; Nikitas, G.; Xing, Y. Model tests on the long-term dynamic performance of offshore wind turbines founded on monopiles in sand. J. Offshore Mech. Arct. Eng. 2015, 137, 041902. [Google Scholar] [CrossRef]
- Guo, Z.; Hong, Y.; Jeng, D.-S. Structure–Seabed Interactions in Marine Environments. J. Mar. Sci. Eng. 2021, 9, 972. [Google Scholar] [CrossRef]
- Jewell, R.A. The mechanics of reinforcede bankments on soft soils. Geotext. Geomembr. 1988, 7, 237–273. [Google Scholar]
- Lunne, T.; Andersen, K.H.; Low, H.E.; Randolph, M.F.; Sjursen, M. Guidelines for offshore in situ testing and interpretation in deepwater soft clays. Can. Geotech. J. 2011, 48, 543–556. [Google Scholar]
- Lei, H.; Lu, H.; Liu, J.; Zheng, G. Experimental study of the clogging of dredger fills under vacuum preloading. Int. J. Geomech. 2017, 17, 04017117. [Google Scholar] [CrossRef]
- Lei, H.; Liu, X.; Wang, P.; Liu, J.; Hu, Y. Experimental investigation of influence of air-boost pressure and duration on air-boost vacuum preloading consolidation. Int. J. Geomech. 2021, 21, 04021088. [Google Scholar] [CrossRef]
- Duan, W.; Cai, G.; Liu, S.; Puppala, A.J.; Chen, R. In-situ evaluation of undrained shear strength from seismic piezocone penetration tests for soft marine clay in Jiangsu, China. Transp. Geotech. 2019, 20, 100253. [Google Scholar] [CrossRef]
- Dejong, J.; Yafrate, N.; Degroot, D.; Low, H.E.; Randolph, M. Recommended practice for full-flow penetrometer testing and analysis. ASTM Geotech. Test. J. 2010, 33, 137–149. [Google Scholar]
- Randolph, M. Characterization of soft sediments for offshore applications. Proc. ISC-2 Geotech. Geophys. Site Charact. 2004, 2004, 10017599903. [Google Scholar]
- Lunne, T.; Powell, J.J.; Robertson, P.K. Cone Penetration Testing in Geotechnical Practice; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Duan, W.; Congress, S.S.C.; Cai, G.; Liu, S.; Dong, X.; Chen, R.; Liu, X. A hybrid GMDH neural network and logistic regression framework for state parameter–based liquefaction evaluation. Can. Geotech. J. 2021, 99, 1801–1811. [Google Scholar] [CrossRef]
- Duan, W.; Congress, S.S.C.; Cai, G.; Zhao, Z.; Liu, S.; Dong, X.; Chen, R.; Qiao, H. Prediction of in situ state parameter of sandy deposits from CPT measurements using optimized GMDH-type neural networks. Acta Geotech. 2022, 17, 4515–4535. [Google Scholar] [CrossRef]
- Cai, G.; Liu, S.; Peng, P.; Yang, Y. Theory and Engineering Application of Marine In Situ Testing Technology, 1st ed.; Science Press: Beijing, China, 2021. [Google Scholar]
- Liu, X.; Shen, J.; Yang, M.; Cai, G.; Liu, S. Subsurface characterization of a construction site in Nanjing, China using ERT and CPTU methods. Eng. Geol. 2022, 299, 106563. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, K.; Wang, D.; Zheng, J. Coefficient of consolidation measured by cone penetration tests in overconsolidated cohesive soils. Ocean Eng. 2023, 276, 114301. [Google Scholar] [CrossRef]
- Lin, J.; Hou, X.; Cai, G.; Liu, S. Uncertainty analysis of axial pile capacity in layered soils by the piezocone penetration test. Front. Earth Sci. 2022, 10, 443. [Google Scholar] [CrossRef]
- Zhou, H.; Randolph, M.F. Resistance of full-flow penetrometers in rate-dependent and strain-softening clay. Géotechnique 2009, 59, 79–86. [Google Scholar] [CrossRef]
- Liu, K.; Wang, D.; Zheng, J. Numerical study of piezoball dissipation test with penetration under partially drained conditions. Comput. Geotech. 2023, 159, 105469. [Google Scholar] [CrossRef]
- Guo, X.; Nian, T.; Gu, Z. A fluid mechanics approach to evaluating marine soft clay strength by a ball full-flow penetrometer. Appl. Ocean Res. 2021, 116, 102865. [Google Scholar] [CrossRef]
- Li, C.; Yu, L.; Kong, X.; Zhang, H. Estimation of undrained shear strength in rate-dependent and strain-softening surficial marine clay using ball penetrometer. Comput. Geotech. 2023, 153, 105084. [Google Scholar] [CrossRef]
- Yu, L.; Yang, Q.; Zhang, J. Undrained bearing capacity of irregular T-bar by the lower bound method in clay. Appl. Ocean Res. 2020, 105, 102409. [Google Scholar] [CrossRef]
- Guo, X.; Nian, T.; Zhao, W.; Gu, Z.; Liu, C.; Liu, X.; Jia, Y. Centrifuge experiment on the penetration test for evaluating undrained strength of deep-sea surface soils. Int. J. Min. Sci. Technol. 2022, 32, 363–373. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, X.; Zhou, M.; Zhang, X. The behavior of ball penetrometer in soft-over-stiff soil deposits. Ocean Eng. 2023, 273, 114011. [Google Scholar] [CrossRef]
- Lunne, T. The CPT in offshore soil investigations-a historic perspective. Proc. CPT 2010, 10, 71–113. [Google Scholar]
- Cai, G.; Liu, S.; Puppala, A.J. Comparative performance of the international piezocone and China CPT in Jiangsu Quaternary clays of China. Transp. Geotech. 2015, 3, 1–14. [Google Scholar] [CrossRef]
- Hanzawa, H.; Tanaka, H. Normalized undrained strength of clay in the normally consolidated state and in the field. Soils Found. 1992, 32, 132–148. [Google Scholar] [CrossRef]
- Li, S.M. Research on the Mechanical Structures of CPT System on Seabed of Shallow Ocean Area. Ph.D. Thesis, Jilin University, Changchun, China, 2005. [Google Scholar]
- Shi, Y.H. Key Technology Research of the Cone Penetration Test (CPT) on Seabottom. Master’s Thesis, Ocean University of China, Qingdao, China, 2005. [Google Scholar]
- Chung, S.F.; Randolph, M.F.; Schneider, J.A. Effect of penetration rate on penetrometer resistance in clay. J. Geotech. Geoenviron. Eng. 2006, 132, 1188–1196. [Google Scholar] [CrossRef]
- Kelly, R.; O’Loughlin, C.; Bates, L.; Gourvenec, S.; Colreavy, C.; White, D.; Gaone, F.; Doherty, J.; Randolph, M.F. In situ testing at the national soft soil field testing facility, Ballina, New South Wales. Aust. Geomech. J. 2014, 49, 15–28. [Google Scholar]
- Randolph, M.; Hefer, P.; Geise, J.; Watson, P. Improved seabed strenght profiling using T-bar penetrometer. In Proceedings of the Offshore Site Investigation and Foundation Behaviour: New Frontiers—Proceedings of an International Conference, London, UK, 22–24 September 1998. [Google Scholar]
- Kelleher, P.; Randolph, M. Seabed geotechnical characterisation with a ball penetrometer deployed from the portable remotely operated drill. In Proceedings of the 1st International Symposium on Frontiers in Offshore Geotechnics, Lisse, Switzerland, 15 August 2005; pp. 365–371. [Google Scholar]
- Randolph, M. Analytical contributions to offshore geotechnical engineering. 2nd McClelland Lecture. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013. [Google Scholar]
- Weemees, I.; Howie, J.; Woeller, D.; Sharp, J.; Cargill, E.; Greig, J. Improved techniques for the in-situ determination of undrained shear strength of soft clays. In Proceedings of the Sea to Sky Geotechnics, 59th Canadian Geotechnical Conference, Vancouver, BC, Canada, 1–4 October 2006; pp. 1–4. [Google Scholar]
- Yafrate, N.J.; DeJong, J.T.; DeGroot, D.J. The influence of full-flow penetrometer area ratio on penetration resistance and undrained and remoulded shear strength. In Proceedings of the Offshore Site Investigation and Geotechnics: Confronting New Challenges and Sharing Knowledge, London, UK, 11–13 September 2007. [Google Scholar]
- Low, H.E.; Lunne, T.; Andersen, K.H.; Sjursen, M.A.; Li, X.; Randolph, M.F. Estimation of intact and remoulded undrained shear strengths from penetration tests in soft clays. Géotechnique 2010, 60, 843–859. [Google Scholar] [CrossRef]
- Yafrate, N.; Dejong, J.; Degroot, D.; Randolph, M. Evaluation of Remolded Shear Strength and Sensitivity of Soft Clay Using Full-Flow Penetrometers. J. Geotech. Geoenviron. Eng. 2009, 135, 1179–1189. [Google Scholar] [CrossRef]
- Martin, C.M.; Randolph, M.F. Upper-bound analysis of lateral pile capacity in cohesive soil. Géotechnique 2006, 56, 141–145. [Google Scholar] [CrossRef]
- Randolph, M.F.; Houlsby, G.T. The limiting pressure on a circular pile loaded laterally in cohesive soil. Geotechnique 1984, 34, 613–623. [Google Scholar] [CrossRef]
- Randolph, M.; Martin, C.; Hu, Y.J.G. Limiting resistance of a spherical penetrometer in cohesive material. Geotechnique 2000, 50, 573–582. [Google Scholar] [CrossRef]
- Einav, I.; Randolph, M.F. Combining upper bound and strain path methods for evaluating penetration resistance. Int. J. Numer. Methods Eng. 2005, 63, 1991–2016. [Google Scholar] [CrossRef]
- Zhou, H.; Randolph, M.F. Numerical investigations into cycling of full-flow penetrometers in soft clay. Géotechnique 2009, 59, 801–812. [Google Scholar] [CrossRef]
- Klar, A.; Pinkert, S. Steady-state solution for cylindrical penetrometers. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 645–659. [Google Scholar] [CrossRef]
- Zhou, H.; Randolph, M. Effect of shaft on resistance of a ball penetrometer. Géotechnique 2011, 61, 973–981. [Google Scholar] [CrossRef]
- Randolph, M.F.; Andersen, K.H. Numerical analysis of T-bar penetration in soft clay. Int. J. Geomech. 2006, 6, 411–420. [Google Scholar] [CrossRef]
- Fan, Q.; Luan, M.; Liu, Z. Numerical simulation of penetration resistance of T-bar penetrometer in soft clay. Rock Soil Mech. 2009, 30, 2850–2854. [Google Scholar]
- Parkin, A. The calibration of cone penetrometers. In Proceedings of the International Symposium on Penetration Testing (ISOPT-1. 1), Orlando, FL, USA, 20–24 March 1988; pp. 221–243. [Google Scholar]
- Ghionna, V.; Jamiolkowski, M. A critical appraisal of calibration chamber testing of sands. In Proceedings of the 1st International Symposium on Calibration Chamber Testing, New York, NY, USA, 28–29 June 1991; pp. 13–39. [Google Scholar]
- Holden, J. The calibration of electrical penetrometers in sand. Nor. Geotech. Inst. Intern. Rep. 1976, 55, 345–354. [Google Scholar]
- Tcheng, Y. Fondations profonds en milieu pulverulent a diverses compacities. Ann. De I’Institut Tech. Du Batim. Et Des Trav. Publics Sols Et Fond. 1966, 54, 219–220. [Google Scholar]
- Villet, W.C.; Mitchell, J.K. Cone resistance, relative density and friction angle. In Proceedings of the Cone Penetration Testing and Experience, St. Louis, MO, USA, 26–30 October 1981; pp. 178–208. [Google Scholar]
- Pournaghiazar, M.; Russell, A.; Khalili, N. CPT in unsaturated soils using a new calibration chamber. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010. [Google Scholar]
- Tan, N.K. Pressuremeter and Cone Penetrometer Testing in a Calibration Chamber with Unsaturated Minco Silt; The University of Oklahoma: Norman, OK, USA, 2005. [Google Scholar]
- Huang, A.-B.; Hsu, H.-H. Cone penetration tests under simulated field conditions. Geotechnique 2005, 55, 345–354. [Google Scholar] [CrossRef]
- Parkin, A.; Lunne, T. Boundary Effects in the Laboratory Calibration of a Cone Penetrometer for Sand. Presented at the 2nd (European Symposium on Penetration Testing (ESOPT II); Amsterdam, The Netherlands, 24–27 May 1982; pp. 1–7. [Google Scholar]
- Salgado, R.; Mitchell, J.; Jamiolkowski, M. Cavity expansion and penetration resistance in sand. J. Geotech. Geoenviron. Eng. 1997, 123, 344–354. [Google Scholar] [CrossRef]
- Schnaid, F.; Houlsby, G.T. An assessment of chamber size effects in the calibration of in situ tests in sand. Geotechnique 1991, 41, 437–445. [Google Scholar] [CrossRef]
- Wesley, L.D. Interpretation of calibration chamber tests involving cone penetrometers in sands. Geotechnique 2002, 52, 289–293. [Google Scholar] [CrossRef]
- House, A.; Oliveira, J.; Randolph, M.F. Evaluating the coefficient of consolidation using penetration tests. Int. J. Phys. Model. Geotech. 2001, 1, 17–26. [Google Scholar] [CrossRef]
- DeJong, J.T.; Yafrate, N.J.; DeGroot, D. Evaluation of undrained shear strength using full-flow penetrometers. J. Geotech. Geoenviron. Eng. 2011, 137, 14–26. [Google Scholar] [CrossRef]
- Lunne, T.; Randolph, M.; Chung, S.; Andersen, K.; Sjursen, M. Comparison of cone and T-bar factors in two onshore and one offshore clay sediments. In Frontiers in Offshore Geotechnics (Proc. ISFOG-1, Perth); Taylor & Francis Group: London, UK, 2005; pp. 981–989. [Google Scholar]
- Jorat, M.; Mörz, T.; Schunn, W.; Kreiter, S.; Moon, V.; de Lange, W. Geotechnical Offshore Seabed Tool (GOST): A new cone penetrometer. In Proceedings of the 3rd International Symposium on Cone Penetration Testing, Las Vegas, NV, USA, 12–14 May 2014; pp. 207–215. [Google Scholar]
- Tand, K.; Funegard, E.; Warden, P. Predicted/measured bearing capacity of shallow footings on sand. In Proceedings of the International Symposium on Cone Penetration Testing (CPT’95), Linköping, Sweden, 4–5 October 1995; pp. 589–594. [Google Scholar]
- Oliveira, J.; Almeida, M. Pore-pressure generation in cyclic T-bar tests on clayey soil. Int. J. Phys. Model. Geotech. 2010, 10, 19–24. [Google Scholar] [CrossRef]
- Watson, P. Performance of Skirted Foundations for Offshore Structures. Ph.D. Thesis, The University of Western Australia, Crawley, Australia, 1999. [Google Scholar]
- Colreavy, C. Use of Piezoball Penetrometers for Measuring Shear Strength and Consolidation Characteristics of Soft Soil. Ph.D. Thesis, University of Western Australia, Perth, Australia, 2017. [Google Scholar]
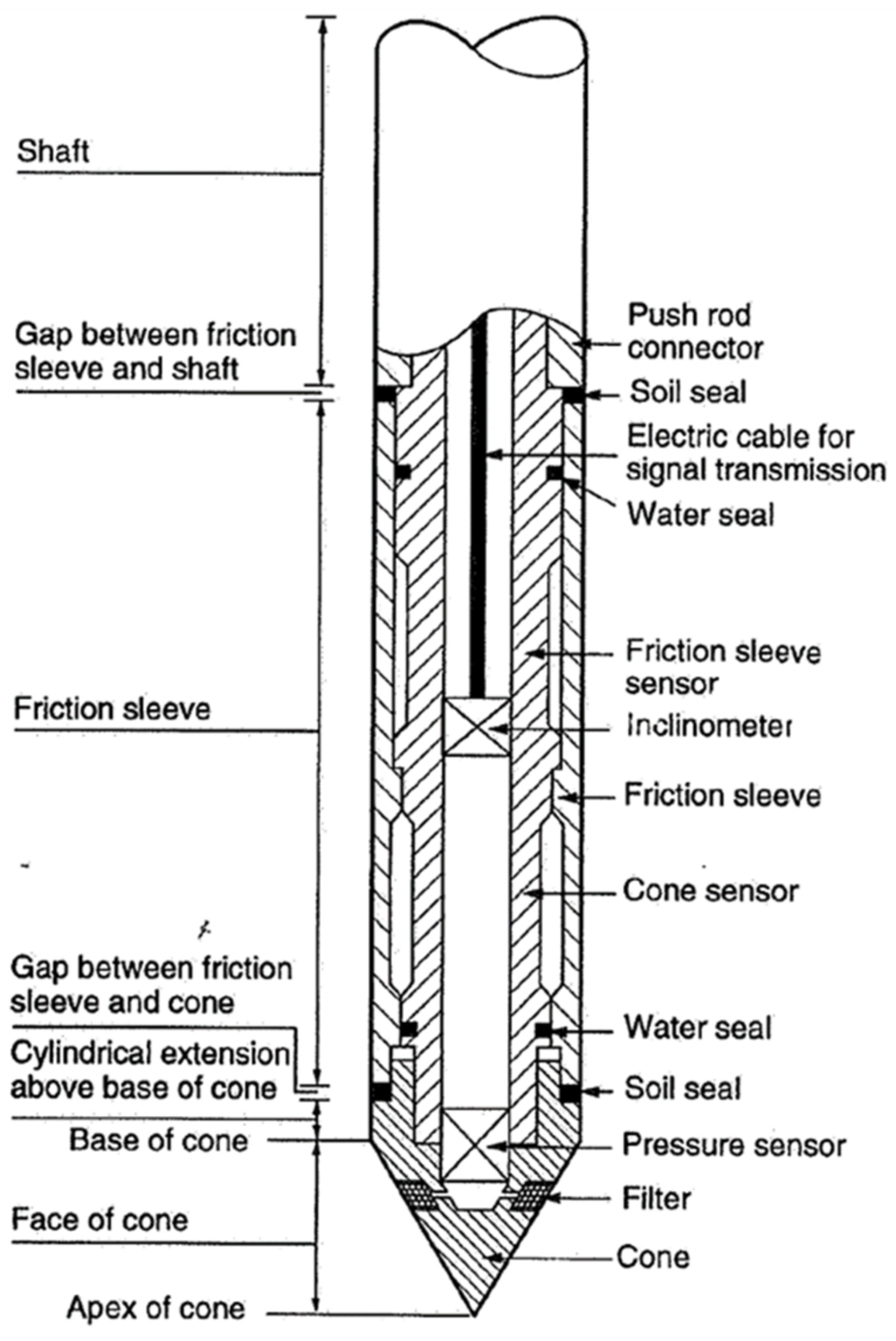

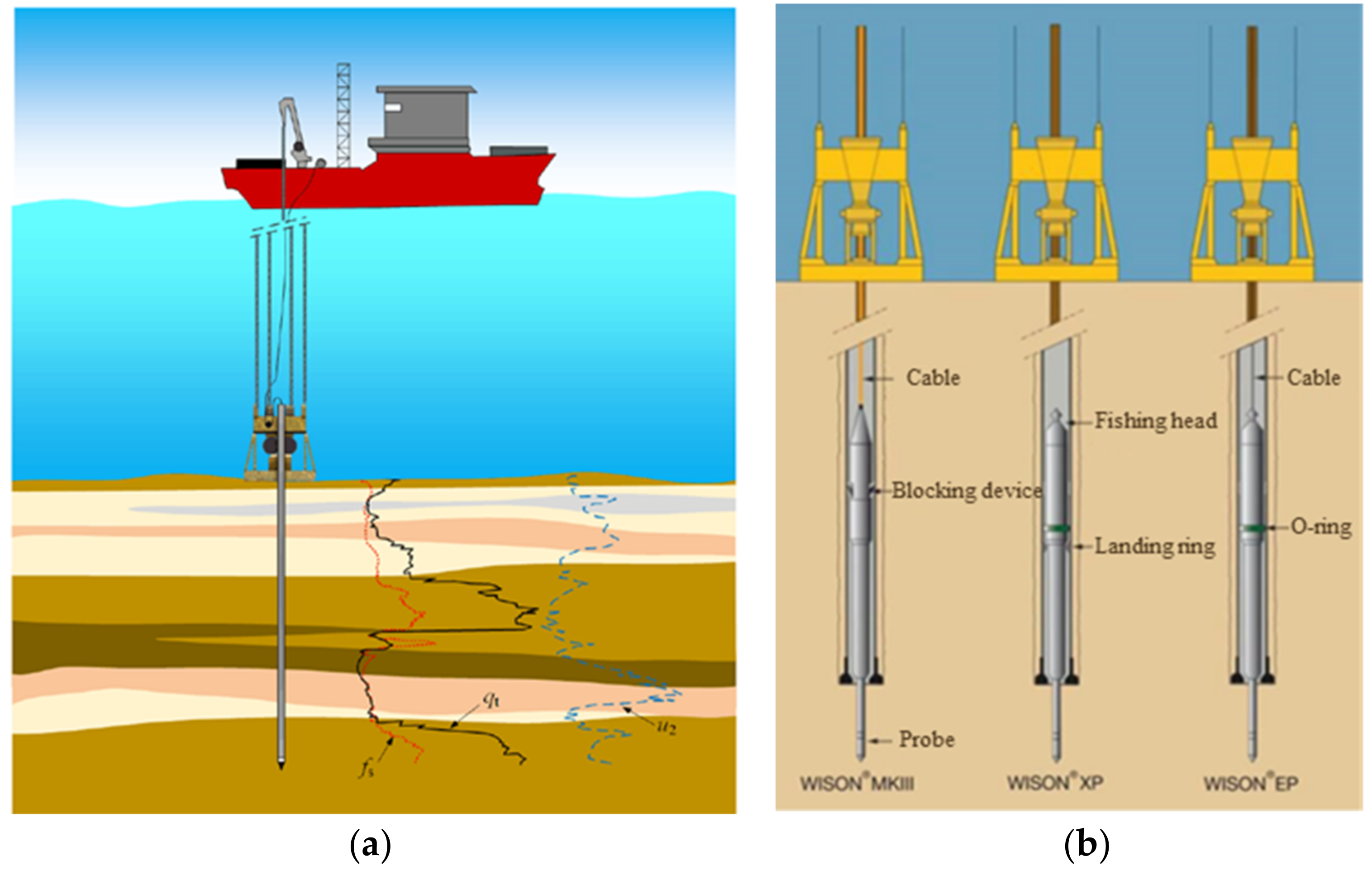






| Penetration Mechanism/ Main Penetration Equipment | Date | Equipment | Company | Notes |
|---|---|---|---|---|
| Discontinuous push Hydraulic cylinder | 1972.3 | Dead weight operated from platform | NGI, Norway/McClelland, Houston, Texas, USA | Max 4 m penetration reached in dense sand |
| 1972.3 | Seacalf | Fugro, The Netherlands | 25 m penetration reached in 130 m water depth | |
| 1974 | Stingray | McClelland, Houston, Texas, USA | Push on drill pipe, not on cone rod | |
| 1976 | Diving bell | Delf Soil Mechanics Laboratory (Deltares) | 600 kN reaction force, 60 m penetration achieved | |
| 1991 | SCOPE | Geo, Denmark | Self-leveling | |
| Continuous push | 1983 | ROSON | APvandenBerg/ D’Appolonia | Roller wheels |
| 1984 | Modified BORROS rig | McClelland, Houston, Texas, USA | Synopticated hydraulic cylinders | |
| 1984 | Wheel drive Seacalf | Fugro, Netherlands | Roller wheels | |
| 2010 | DeepCPT | Gregg Drilling & Testing Inc., California, USA | Suction anchor; 200 kN thrust capacity, 10 and 15 cm2 cones | |
| Coiled rod (on full size rods) | 2000 | Penfeld | IFREMER, France | Self-powered by lead batteries. Can penetrate to 30 m |
| Seabed drilling Test and sampling rigs | 2001 | PROD | Benthic, Australia | Rods stored in carousel on sea bottom |
| Combined rig | 1997 | Searobin | Fugro, The Netherlands | Can take sample to 1 m and perform 10 cm2 CPT to 2 m in one deployment |
| 2001 | Geoceptor | Geo, Denmark | Can take sample to 6 m and perform 10 cm2 CPT to 10 m in one deployment | |
| Minirigs | 1992 | Seascout | Fugro, The Netherlands | Coiled rod, wt < 1 ton, 1 cm2 cone penetrometer |
| 1999 | MiniCPT | Gregg Drilling & Testing Inc., California, USA | Coiled rod; 2 cm2 cones up to 12 m penetration | |
| 2000 | Neptune | DATEM, UK | Coiled rod, 5 and 10 cm2 cones; up to 20 m penetration | |
| ROV mounted | 1983 | Mini Wison | Fugro, The Netherlands | 1 m stroke, 5 cm2 cone penetrometer |
| Production Companies | Type of Touch | Equipment Model | Max Penetration Reached Depth (m) |
|---|---|---|---|
| A.P. van den Berg Corp., Heerenveen, The Netherlands | Downhole CPT | Wison-APB downhole mode deep-sea CPT system | 3000 |
| A.P. van den Berg Corp., Heerenveen, The Netherlands | Seabed CPT | Roson seabed mode deep-sea CPT system for the seabed | 4000 |
| Geomil Corp., Moordrecht, The Netherlands | Seabed CPT | MANTA seabed mode CPT system | 2000 |
| Datem Corp., Sleaford, UK | Seabed CPT | Neptune 5000 Standard Marine CPT | 3000 |
| Fugro Corp., Leidschendam, The Netherlands | Seabed CPT | SEACALF seabed mode CPT system | 4000 |
| Calibration Tank (Inventor or Unit) | Design Time | Calibration Tank Type | Soil Sample Size | Boundary Conditions | |||
|---|---|---|---|---|---|---|---|
| Diameter (m) | Height (m) | Radial Boundaries | Bottom | Top | |||
| National Roads Australia | 1969 | Double wall | 0.76 | 0.91 | Flexibility | Bedding | Rigid |
| University of Florida, USA | 1971 | Double wall | 1.20 | 1.20 | Flexibility | Bedding | Rigid |
| Monash University, Australia | 1974 | Double wall | 1.20 | 1.80 | Flexibility | Bedding | Rigid |
| Norwegian Institute of Geotechnical Engineering | 1979 | Double wall | 1.20 | 1.50 | Flexibility | Bedding | Just |
| Italian Electricity Commission | 1982 | Double wall | 1.20 | 1.50 | Flexibility | Bedding | Rigid |
| 1982 | Double wall | 0.60 | 1.00 | Flexibility | Bedding | Rigid | |
| ISMES Laboratory, Italy | 1986 | Double wall | 1.20 | 1.50 | Flexibility | Bedding | Rigid |
| University of California, USA | 1975 | Single wall | 0.76 | 0.80 | Flexibility | Rigid | Rigid |
| University of Texas, USA | 1984 | Single wall | Square: 2.1 × 2.1 × 2.1 | Flexibility | Flexibility | Flexibility | |
| 1993 | Single wall | 0.60 | 1.20 | Flexibility | Bedding | Rigid | |
| 2008 | Single wall | 1.37 | 2.13 | Flexibility | Bedding | Rigid | |
| University of Houston, USA | 1991 | Single wall | 0.76 | 2.54 | Flexibility | Bedding | Bedding |
| North Carolina State University, USA | 1991 | Single wall | 0.94 | 1.00 | Flexibility | Rigid | Rigid |
| University of Louisiana, USA | 1992 | Double wall | 0.55 | 0.80 | Flexibility | Flexibility | Rigid |
| Gouda Group Canada | 1991 | Single wall | 1.40 | 1.00 | Flexibility | Rigid | Bedding |
| Virginia Tech, USA | 1987 | Single wall | 1.50 | 1.50 | Flexibility | Rigid | Rigid |
| University of Grenoble, France | 1991 | Single wall | 1.20 | 1.50 | Flexibility | Bedding | Bedding |
| University of Oxford, UK | 1988 | Single wall | 0.90 | 1.10 | Flexibility | Bedding | Rigid |
| University of Tokyo, Japan | 1988 | Single wall | 0.90 | 1.10 | Flexibility | Rigid | Rigid |
| Clarkson University, USA | 2006 | Single wall | 0.51 | 0.76 | Flexibility | Rigid | Rigid |
| University of Sheffield, UK | 1991 | Single wall | 0.79 | 1.00 | Flexibility | Rigid | Flexibility |
| 2003 | Single wall | 0.40 | 0.42 | Flexibility | Bedding | Rigid | |
| Cornell University, USA | 1991 | Single wall | 2.10 | 2.90 | Flexibility | Rigid | Rigid |
| American Waterways Experiment Station | 1991 | Single wall | 0.80–3.00 | 0.6 × X | Flexibility | Rigid | Rigid |
| National Chiao Tung University, Taiwan | 1991 | Double wall | 0.51 | 0.76 | Flexibility | Rigid | Rigid |
| 1998 | Single wall | 0.79 | 1.60 | Flexibility | Rigid | Bedding | |
| 1988 | Double wall | 0.20 | 0.36 | Flexibility | Bedding | Rigid | |
| Osaka University, Japan | 2008 | Double wall | 1.40 | 1.45 | Flexibility | Rigid | Bedding |
| Technical University of Gdansk, Poland | 2006 | Double wall | 0.53 | 1.00 | Flexibility | Bedding | Rigid |
| University of Oklahoma, USA | 2002 | Single wall | 0.61 | 0.45–1.42 | Flexibility | Bedding | Rigid |
| University of New South Wales, Australia | 2010 | Single wall | 0.46 | 0.80 | Flexibility | Bedding | Rigid |
| Boundary Conditions | Vertical | Horizontal | ||
|---|---|---|---|---|
| Stress/σv | Strain/εv | Stress/σh | Strain/εh | |
| BC1 | Constant | -- | Constant | -- |
| BC2 | -- | 0 | -- | 0 |
| BC3 | Constant | -- | -- | 0 |
| BC4 | -- | 0 | Constant | -- |
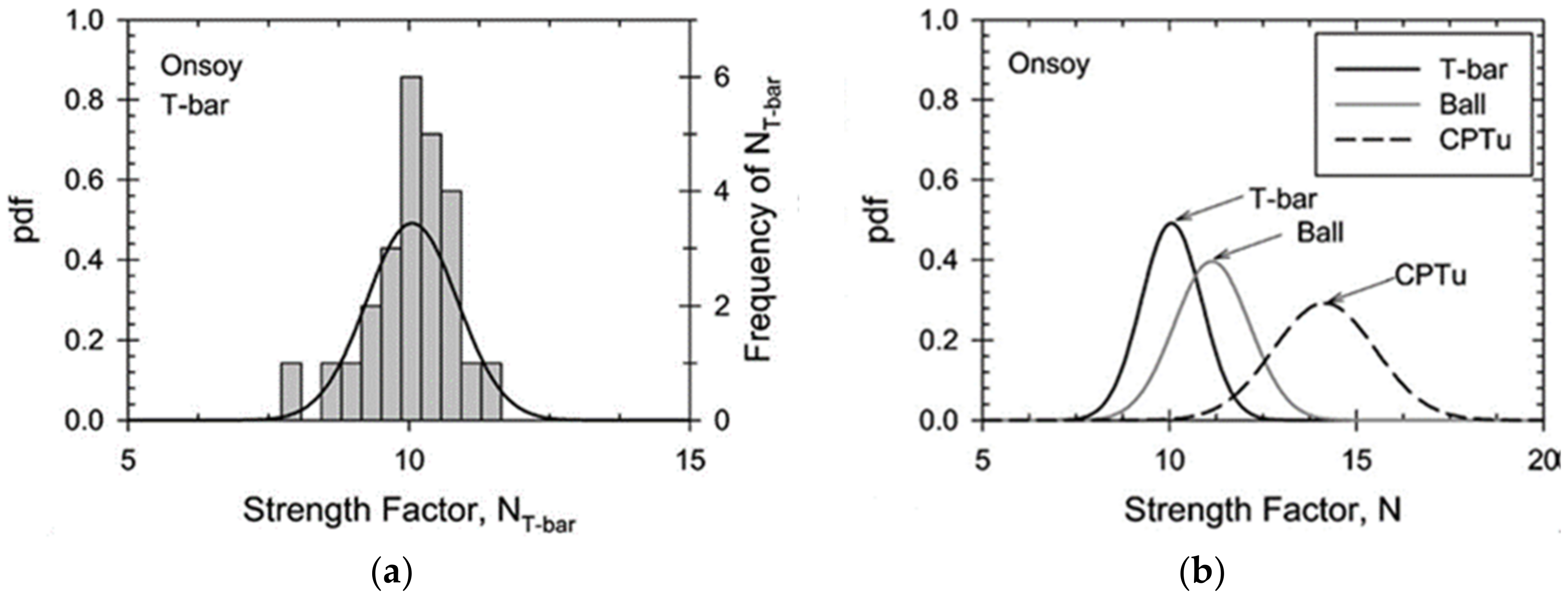
| Location | NT-bar-DSS, Average | NT-bar-DSS, Rang | NT-bar-FVT, Average |
|---|---|---|---|
| Burswood, Australia | 11.9 b | - | 10.9 b |
| Onsoy, Norway | 11.9 a, 12.5 b | 11.0–13.4 a | 11.6 b |
| Coastal Australia | 12.4 b | - | 11.3 b |
| West African Coastal Region | 12.2 b | - | 12.7 b |
| Watchet Bay, Canada | 13.0 a | - | - |
| Wenzhou, China (this paper) | - | - | 12.0 c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, H.; Liu, L.; He, H.; Liu, X.; Liu, X.; Peng, P. The Practice and Development of T-Bar Penetrometer Tests in Offshore Engineering Investigation: A Comprehensive Review. J. Mar. Sci. Eng. 2023, 11, 1160. https://doi.org/10.3390/jmse11061160
Qiao H, Liu L, He H, Liu X, Liu X, Peng P. The Practice and Development of T-Bar Penetrometer Tests in Offshore Engineering Investigation: A Comprehensive Review. Journal of Marine Science and Engineering. 2023; 11(6):1160. https://doi.org/10.3390/jmse11061160
Chicago/Turabian StyleQiao, Huanhuan, Lulu Liu, Huan He, Xiaoyan Liu, Xuening Liu, and Peng Peng. 2023. "The Practice and Development of T-Bar Penetrometer Tests in Offshore Engineering Investigation: A Comprehensive Review" Journal of Marine Science and Engineering 11, no. 6: 1160. https://doi.org/10.3390/jmse11061160
APA StyleQiao, H., Liu, L., He, H., Liu, X., Liu, X., & Peng, P. (2023). The Practice and Development of T-Bar Penetrometer Tests in Offshore Engineering Investigation: A Comprehensive Review. Journal of Marine Science and Engineering, 11(6), 1160. https://doi.org/10.3390/jmse11061160






