Abstract
In this paper, an adaptive control scheme with disturbance estimation is proposed for the station keeping and trajectory tracking of an underwater vehicle-manipulator system (UVMS) in a task space. The control of UVMSs encounters time-varying and lumped disturbances introduced by the motion of the manipulator and currents. The proposed control scheme includes an observer to identify disturbances without introducing additional sensors. Using state-of-the-art UVMS control technologies, it alleviates the restriction of the feedforward control applied to the UVMS. In addition, the proposed control scheme is not designed based on the worst case. In other words, the robustness of the controller is not achieved at the price of performance, and the performance of the controller can be recovered in the absence of disturbance. Meanwhile, the controller can also realize quick responses to attenuating disturbance and closed-loop stability when encountering an unexpected disturbance. The effectiveness of the proposed control scheme was demonstrated by a series of spatial trajectory tracking experiments under various disturbances. A limitation of this study is that the proposed control scheme is specialized for the underwater manipulation of UVMSs.
1. Introduction
The ocean is a main resource for food and economic revenue, as well as a potential source of alternative and sustainable energies in future [1]. It is not suitable for humans to carry out long-term operations offshore and in deep oceans that are subject to high pressures and low temperatures related to harsh environments. Compared with the risk and cost of a human occupied vehicle (HOV), which has humans on board, unmanned underwater vehicles (UUVs) have been routinely used for the investigation, observation, sampling, and persistent monitoring of the ocean, enhancing our capability to explore and exploit the marine environment [2]. A UUV is composed of an autonomous underwater vehicle (AUV) and a remotely operated underwater vehicle (ROV).
The ROV obtains the power and control commands though the umbilical tethered to the host ship, where the pilot can remotely operate the ship for days without energy constraints. ROVs are routinely equipped with manipulators and powerful propellers to provide complex operation ability and large volume capacity. Hence, ROVs are widely used for marine rescue, marine science, and offshore industry applications. Offshore industry applications of ROVs include the maintenance of permanent observatories, submerged oil wells, cabled sensor networks, the deployment/recovery of benthic stations etc. The breakthroughs in ROV technology are often driven by the requirements of the deep ocean scientific domain. There are many famous 6000 m depth-rated work-class ROVs for deep ocean scientific investigation, for example, the Jason ROV [3] from the Woods Hole Oceanographic Institution (WHOI), the Isis ROV [4] from the National Oceanography Centre (NOC), and the Haixing-6000 ROV [5] from the Shenyang Institute of Automation, Chinese Academy of Science (SIA). Nevertheless, the working radius of ROVs is limited by the umbilical cable tethered to the supporting ship; in addition, the ROV also needs an expensive support ship that is equipped with a heavy crane, a tether management system (TMS), and a dynamic position system (DP) [6].
AUVs are untethered, battery-powered vehicles that can be operated independently to carry out pre-programmed survey missions. The life of AUVs typically ranges from hours to days depending on the capability of the batteries, while the operational depth ranges from hundred meters to 6000 m, and even full ocean depth. AUVs are categorized as cruising or hovering types based on their propeller configuration [7]. Cruising AUVs are generally torpedo-shaped and driven by a single propeller, which allow them to cover large distances along the programmed trajectory. Cruising AUVs are the main type of AUVs used in commercial and scientific domains, including the Remus [8], Bluefin [9], and Gavia [10] series. Considering cruise safety in a hazardous environment, hovering AUVs are equipped with several propellers. This configuration provides the capability for station keeping, maintaining a constant height above the seafloor, and slow precise motions in three-dimensional space. Some famous hovering AUVs have carried out investigations of hydrothermal vents and coral reefs, for example, Sentry [11] and Mesobot [12] from WHOI, TriMARES [13] from the University of Porto, and Tansuo 4500 [14] from SIA. Although AUVs can carry a variety of acoustic, optical, hydrological, and chemical sensors, they are more suitable for survey missions along pre-programmed routes considering their limited energy and acoustic communication. In contrast, ROVs are optimal for high-resolution and highly interactive operations, including optical investigations, seabed sampling, and oceanographic interventions.
The underwater vehicle-manipulator system (UVMS) is a hybrid vehicle composed of an ROV and AUV, which coordinates the vehicle/manipulator using an optical fiber tether instead of an umbilical tether [15]. The optical fiber is used not as a power supply link but as an interactive data transfer link when the ROV is in operation mode. Meanwhile, the fiber can also be detached in AUV cruise mode. In addition, a UVMS can be operated from surface support vessels to perform intervention tasks and close-seabed optical investigations without the need for expensive TMS and DP. However, UVMSs usually only allow for light intervention tasks due to their self-powered limitations. The key element of UVMS technology is its ability to improve autonomy for underwater manipulation.
The coordinated control of a UVMS includes the control of the vehicle, the control of the manipulator, and control allocation. The objective of coordinated control is navigating the end effector precisely to the desirable position in the task space. However, UVMSs are kinematically redundant because their manipulators usually have more degrees than the required dimensions of the task space. Such a configuration also leads to infinite joint space solutions corresponding to a specific task space vector. The solving of the inverse kinematic problem requires sophisticated optimization techniques and substantial computational time. The joint space control scheme assumes that the set-point capability of the vehicle can isolate the disturbance of the manipulator, and its objective is to improve the dynamic tracking precision of the manipulator joints. In contrast, the task space scheme regards the manipulator and the vehicle as a whole object and aims at navigating the end effector to the goal precisely. Compared with the joint space control scheme, the task space control scheme is more suitable for multiple task constraints or online motion modification, especially for floating-base UVMS manipulation tasks.
Considering the dynamic couplings of the vehicle and manipulator, a sliding mode control (SMC) is used for UVMS motion control [16,17] to overcome the disturbance of uncertain parameters, such as errors in the estimation of the center of gravity caused by manipulation. However, one major drawback of SMC is chattering control action, which may be strengthened by high-order dynamic uncertainties in UVMS motion. To ensure tracking quality against disturbance, the fuzzy logic control (FLC) scheme [18,19] is also employed to handle the highly nonlinear nature of the vehicle-manipulator system by heuristics fuzzy control rules and the appropriate choice of membership functions for the input/output signals. However, FLC requires substantially more computational time due to its complex decision-making process. The decision-making process of FLC involves fuzzification, rule-base storage, an inference mechanism, and defuzzification operations. To improve the robustness to various motions of the manipulator, FLC requires more complex fuzzy rules and a longer time for parameter tuning. The adaptive control scheme dynamically adjusts control gains to suppress the hydrodynamic disturbance caused by underwater manipulation [20,21]. Compared to FLC, adaptive control is simpler and has higher computational efficiency. However, adaptive control is sensitive to sensor noise and responds slowly to disturbance attenuations.
In this paper, a new adaptive control scheme is proposed for the end effector trajectory tracking of UVMSs. The control scheme is constituted of a feedforward term and an adaptive control law. The first part is designed to enhance the control capacity of perturbed isolation by means of desired acceleration and estimated perturbed vectors. In other words, the first part is seen as a patch to compensate for the externally stochastic disturbance and internally dynamic model deviation. The second part is used to achieve closed-loop control through an adaptive feedback portion. The proposed scheme adopts a disturbance observer-based feedforward compensation and an adaptive feedback control law to navigate the end effector of the UVMS precisely to the set-point position/orientation under various disturbances, including external and internal disturbances. External disturbances include environmental currents and payload variations, while internal disturbances refer to time-varying hydrodynamic effects, parametric uncertainties, and interactive vehicle-manipulator forces. The effectiveness of the scheme was verified through a series of trajectory tracking experiments.
Using the state-of-the-art control technology of UVMSs, the proposed scheme provides an effective approach to alleviate the application restriction of floating-base UVMS when it encounters a disturbance due to underwater manipulator motion. The main contributions of the paper are the design of a disturbance estimation and an adaptive disturbance observer-based feedback controller for UVMS. Firstly, the proposed disturbance estimation is based on feedback state errors and feedback control input, which do not introduce additional sensors. Traditional disturbance estimation directly measures disturbances via additional sensors, which may be impossible for underwater vehicles. Compared with traditional disturbance estimation, the proposed estimation is less sensitive to system noise and more robust for ocean applications. Secondly, the proposed estimation alleviates the restrictions faced by the feedforward control, which is regarded as an effective disturbance attenuation approach. Thirdly, the robustness of the proposed disturbance observer-based feedback controller is not at the price of degraded nominal performance. In other words, the performance of proposed control algorithm can be recovered in the absence of disturbance.
The proposed algorithm is different from sliding mode control (SMC) in that it does not require previous knowledge of the upper bound of disturbance. Different from adaptive control, which suppresses disturbances by scheduling gains and may introduce a slow response, the proposed algorithm is based on disturbance observer, which has a quick response in attenuating disturbance. Finally, the proposed algorithm differs from fuzzy logic control (FLC), which suppresses disturbances by complex heuristic rules and requires substantial tuning time, in that it adopts an adaptive feedback item which has high computational efficiency.
2. Dynamic Modeling
The north-east-down (NED) coordinate frame was chosen as the inertial-fixed frame, which defines the axis pointing north, axis pointing east, and axis pointing downward, normal to the location on the Earth’s surface. The body-fixed reference frame assigns as the longitudinal axis directed fore, as the transversal axis directed from port side to starboard, and as the normal axis directed from top to bottom. The dynamic equation in the body-fixed frame is expressed as follows:
where:
Here, represents the vector of absolute positions (north, east, and down) in the inertial-fixed frame, Euler angles, and joint values in the inertial frame. represents a position vector and denotes an attitude vector of Euler angles (roll, pitch, yaw), which describe the rotation between the inertial-fixed frame and the body-fixed frame. is the vector of the underwater manipulator joint position variables while is the number of joints. is the vehicle-manipulator inertial matrix, including an added mass matrix; is the Coriolis and centripetal matrix of the vehicle manipulator; is the damping matrix of the vehicle manipulator; is the restoring forces and moments of the vehicle manipulator; and is the vector of the coupling dynamic effects between the vehicle and the manipulator. is the control input vector of thrusters and joints. and are the inertial matrix of the vehicle and manipulator, respectively. and are the centripetal matrix of the vehicle and manipulator, respectively. and are the damping matrix of vehicle and manipulator, respectively. is an interaction effect force/moment acted on the vehicle due to the motion of the manipulator. is a coupling interaction acted on the manipulator due to vehicle motion (including inertial effects). and represent the restoring forces and moments matrix of vehicle and manipulator, respectively. represents the total control input vector in the body-fixed frame, where and are the control vector of the thrusters and torque of the joints, respectively. is the lumped vector of disturbance, including external disturbance due to ocean current and payload and internal disturbance introduced by parametric uncertainties in the model. and represent the internal and external disturbance in the body-fixed frame, respectively. represents the vehicle-manipulator velocity vector in terms of the body-fixed frame. and denote the linear velocity and angular velocity of the body origin, respectively, while represents the joint position derivative of the individual origin. The body-fixed velocity in the inertial-fixed frame can be decomposed as follows:
where is the Jacobian matrix that maps the body-fixed velocity to the derivative of the position in the inertial-fixed frame.
To simplify the trajectory control design, the dynamic motion can be projected with respect to the body-fixed frame in Equation (1) to the task space frame through the velocity Jacobian matrix in Equation (3). The dynamic model of the UVMS in the task space can be expressed as follows:
where:
Here, represent the inertial matrix, the centripetal matrix, the damping matrix, the interactive force matrix, and the restoring force matrix in the task space, respectively. and represent the control input vector and the lumped disturbance vector in the task space.
3. Control Scheme
3.1. Disturbance Estimation
Disturbance consists of external disturbance and internal disturbance. External disturbance is due to external forces, including environmental currents, reaction forces, etc. Internal disturbance is mainly due to the parametric uncertainty.
3.1.1. External Disturbance Model
External disturbance involves reaction forces, payload variations, and the influence of currents. Reaction force and payload variation are classified as hydrostatic disturbances, which are usually described with a linearization function. Among the above disturbances, current influence is the dominant factor for submerged vehicles. The current not only generates an additional drag force and moment imposed on the vehicle, but also affects the drag and drift coefficients of the damping matrix due to the variation in the projected frontal area and cross-flow around the vehicle. The kinematics of currents are assumed to vary slowly and follow a Markov process. The effect of the currents imposed on the vehicle is usually modelled as a first-order Gauss–Markov process.
The current vector can be defined in the flow axes where is the magnitude of the current speed in the x-direction and is the flow angle vector. and represent the flow attack and sideslip angle describing the transformation between the NED frame and the flow frame, respectively. We can assume that the kinematic model of the current in the flow frame is as follows:
where:
Here, is the process noise vector of the current speed that follows a Gaussian white distribution, and is the covariance matrix of . is a small negative constant gain vector.
The current vector can be defined in the body reference frame, where , , and represent the surge, sideway, and heave motions, respectively. The current velocity can be projected to the body reference frame as follows:
where:
Here, is the Jacobin matrix in terms of Euler angles between the flow reference frame and the body reference frame; and represent the rotation about the z and y axis, respectively; is the rotation matrix from NED coordinates to flow coordinates; and is the rotation matrix from the body coordinates to the NED coordinates.
Considering that the acceleration of current motion is very small, the external disturbance due to currents in the task space can be simplified as follows:
Here, is the Jacobian matrix that maps the body-fixed velocity to the derivative of the position in the inertial-fixed frame.
3.1.2. Internal Disturbance Model
Internal distance mainly originates from uncertainties in hydrodynamic coefficient variation. The motion of the manipulator modifies the geometry of the vehicle. The oscillation excitation of the current not only modifies vortex shedding around the vehicle, but also introduces radiation potential energy imposed on the vehicle. In consequence, the parameter uncertainties are not constant but time-varying. The internal disturbance model can be stated as follows:
Here, represents the internal disturbance in the task space. , , , , and are the parameter estimation errors for the inertia matrixes, centripetal matrixes, damping matrixes, restoring force/moment matrixes, and interactive force matrixes due to the manipulator motion, respectively. Compared with the disturbance induced by errors in the estimation of hydrodynamic terms, estimation errors in hydrostatic terms can be negligible, for example, and .
The hydrodynamic coefficient matrix includes an inertia matrix, Coriolis centripetal matrix, and damping matrix, while the major parameter uncertainties arise from damping matrix terms. Although the inertia matrix (including added mass) varies with the joint rotation of the manipulator, it can be theoretically calculated with high accuracy. The inertia matrix is usually designed as a feedforward control term, and it is not regarded as a main source of parameter uncertainty. Although the Coriolis and centripetal matrices (including added mass) are a function of the inertia matrix and velocity vectors, their model error is negligible.
Hydrodynamic damping consists of potential damping, skin friction, interference drag, and lift. Hydrodynamic damping is sensitive to the oscillation excitation/orientation of currents, surface skin roughness, and hull geometry. The motion of the manipulator modifies the vehicle geometry, which affects interference drag due to the shedding of vortex sheets. The current forces the vehicle to oscillate with turbulent boundary layers, which introduces radiation potential damping and nonlinear skin friction. The current orientations change the attack and sideslip angles that are relevant to the lift and drag acting on the UVMS. An increase in attack angles enlarges the cross-flow area of the vehicle and accelerates water circulation around the vehicle. Obviously, an increase in attack angles promotes an increase in the lift damping force upon the vehicle. In the same way, an increase in sideslip angles acts to expand the front-projected cross-sectional area parallel to the flow and enhance vortex shedding friction in viscous fluid. In other words, an increase in sideslip angle results in an increase in drag damping on the vehicle. However, considering the nonlinear coupling interaction between the current and the vehicle, it is difficult to model individual damping terms with accurate functions according to time-varying currents and various manipulator attitudes.
On the other hand, damping coefficients are usually evaluated using offline FEM (finite element method) computation with CFD (computational fluid dynamics) tools or derived from experimental data with various combinations of attack and sideslip angles. The identification of damping coefficients may introduce a high computational payload that opposes the constraint of real-time performance. Consequently, it is impossible to update the whole damping coefficients online according to various manipulator attitudes and currents. For the purpose of numerical iterations, it is convenient to lump various damping terms into linear and quadratic terms.
3.1.3. Observer Design
Under the assumption that the rotation of the manipulator is very slow, the basic idea is to adjust the gradients of the estimation errors according to the difference between predicted states and feedback states. This idea aims to asymptotically achieve the equilibrium point of disturbance estimation. Recalling the nature of hydrodynamic and hydrostatic effects, it is a basic strategy that lumps all unknown internal and external disturbance forces into one observer. The observer adopts a linear approximation strategy with the negligence of quadratic and higher-order hydrodynamic terms. The disturbance estimator is proposed as follows:
where:
Here, is the estimation vector of the disturbances, represents the auxiliary estimation vector, and refers to the positive gain vector of estimation.
The estimation error vector can be defined as follows:
Here, is the real disturbance vector, while represents the error vector of disturbance estimation.
For a simple description, the NED coordinated frame is chosen as the task space, where the task space error and the augmented space error are designed as follows:
The space error of the end effector trajectory can be defined as follows:
where is the derivative of the space error, and and are the desired and actual position vectors, respectively. and are designed as positive gain matrixes. The purpose of the augmented space error is to guarantee the control precision of the closed-loop system. Obviously, the space error goes to zero when the augmented space error goes to zero asymptotically.
From Equations (1) and (10)–(12), the derivative of the disturbance estimation error is obtained as follows:
Here, represents the derivative of the disturbance estimation error.
Substituting with based on Equation (12) and adjusting Equation (15), we obtain the following:
Here, represents the derivative of .
Under the assumption that model uncertainty varies slowly, Equation (18) can be simplified as follows:
3.2. Control Scheme
We propose an adaptive control law along with a feedforward term and disturbance estimation term. The control formula can be expressed as follows:
where:
In the controller scheme, and are the closed-loop feedback gains and is a feedforward term based on the prior dynamic model to resist the known interactive force and moment. is a lumped disturbance estimation item, which is a function of model uncertainties and internal and external disturbance.
The disturbance observer alleviates the precision restriction of the previous model parameters. Although the proposed controller demands a set of dynamic motion model parameters for the feedforward control design, it does not require high-precision dynamic models. Apart from the dynamic model, it also requires state variables and desired variables. The state variables consist of displacement and the derivative of task space trajectory. Displacement is obtained from the calculation of velocity and attitude measurements. The derivatives of task space displacement are transformed from direct body-fixed velocity measurements. The desired displacement, velocity, and acceleration in the task space are obtained from the trajectory planner. Obviously, augmented task space errors, task space errors, and derivatives of task space errors are middle variables. Such middle variables are obtained from the state variables and desired variables. Some external disturbances are hard to measure explicitly, such as the current, manipulator reaction force, payload variations, etc. Moreover, the internal disturbance that originates from model uncertainties makes it difficult to extract the exact values. In terms of this issue, the disturbance observer lumps various external and internal disturbances to one approximate term. The disturbance observer is updated depending on the feedback from augment task errors and state measurements. Such a strategy makes the observer immune to the precision and noise of the dynamic model. The observer alleviates the restriction of the feedforward term, which is regarded as a patch to compensate known disturbance, unmodeled disturbance, model uncertainties, etc. Similarly, the feedback control aims to enhance the closed-loop stability and performance of the system, where the control variables are calculated according to the desired acceleration and actual state errors. Therefore, the proposed control law can exponentially converge to the desired position under bounded disturbance and model uncertainties.
3.3. Stability Analysis
A Lyapunov-like candidate function can be defined as follows:
Here, represents the Lyapunov-like candidate function.
If represents the derivative of , Equation (22) can be differentiated with respect to time as follows:
Substituting the disturbance item with the disturbance estimation and disturbance error from Equation (12), the dynamic motion equation in Equation (4) can be rewritten as follows:
Substituting the control input term based on Equation (17), the acceleration of UVMS in the task space can be derived from Equation (20) as follows:
Differentiating the augmented space error from Equation (15) and substituting with Equation (4), Equation (15) can be expressed as:
Substituting Equations (19) and (26) in Equation (23) and adjusting leads to the following:
The derivative function is equal to zero only if and are zero. Otherwise, is less than zero when and are not equal to zero. Since the candidate Lyapunov-like function is lower bounded and , the augmented space error and disturbance estimation error asymptotically converge to zero as based on Barbalat’s Lemma. Thus, the task space tracking error also asymptotically converges to zero with the augmented space error as .
4. Experiments and Discussion
The performance of the proposed control scheme was verified using the variable structure robot (VSR) platform. The VSR is a new kind of UVMS that can switch from AUV mode (Figure 1a) to ROV mode (Figure 1b) by lifting the upper hull and spreading the manipulator outside the streamlined hull. The VSR is equipped with an electric seven-DOF manipulator (including a grasper). In addition, the VSR is actuated by eight thrusters; such a mechanism provides the vehicle with six-DOF control ability. In other words, the VSR can individually perform control surge, sway, heave, roll, pitch, and yaw motions.

Figure 1.
Multiple work modes of the VSR: (a) AUV mode for cruising; (b) ROV mode for manipulation work.
The experiments were conducted in a 3.5 m depth-rated pool. To simulate the influence of current on the UVMS, a first-order Gauss–Markov process was added to the velocity measurement in the task space, where the mean value of the simulation current was 10 cm/s.
For underwater manipulation tasks, the attitude of the vehicle and the trajectory of the end effector are the most important issue, especially under the disturbance of manipulator motion and currents.
To verify the attitude control effectiveness of the proposed scheme, the vehicle was guided to rotate from heading 0 degrees to 90 degrees. To simulate the manipulator disturbance, the end twist joint of the manipulator was set to follow an angle curve of 2×sin (0.4t). Figure 2 shows the attitude control results of the vehicle in station keeping mode between the proposed scheme and SMC. Figure 2a shows the heading control results for the vehicle. The heading control response of the SMC was quicker than the response of the proposed scheme. However, the heading control stability of the proposed scheme was much better than that of the SMC under time-varying disturbance. Figure 2b shows the pitch control results for the vehicle. Compared with the control of the horizon plane, the control of the vertical plane was more sensitive to disturbance due to manipulator motion. In Figure 2b, it can be seen that the pitch control of the proposed scheme attenuated time-varying disturbance more promptly and achieved better stability than that of SMC. Once the proposed scheme compensated the disturbance in the vertical plane, the nominal performance of the proposed scheme was recovered. Hence, the attitude control effectiveness of the proposed scheme was higher than that of SMC, especially under time-varying disturbance from manipulator motion.
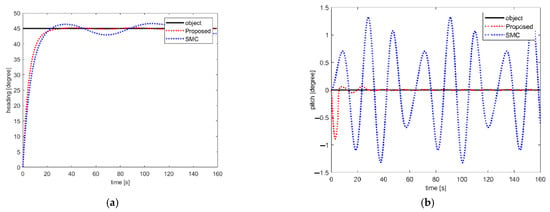
Figure 2.
Attitude change in the vehicle under disturbance caused by manipulator motion: (a) heading curve of the vehicle in station keeping control mode; (b) pitch curve of the vehicle in station keeping control mode.
To verify the trajectory tracking performance of the proposed scheme, the end effector was guided from [0,0,0] to [180,120,0] in the task space. Figure 3 shows the trajectory results for the end effector between the proposed scheme and SMC. Figure 3a,b show the end effector position in X-direction and Y-direction, respectively. The position curves in Figure 3 are divided into two stages. The motion of the end effector was determined by the rotation of manipulator joints and the displacement of the vehicle. In the first stage of Figure 3, the speed of the trajectory was mainly determined by vehicle displacement because the objective position was far beyond the reachable space of the manipulator. The trajectory speeds of SMC and the proposed scheme were very close. However, the trajectory of the proposed scheme was smoother than that of SMC when the position was closed to the objective position. In the second stage of Figure 3, the speed of trajectory was mainly determined by the rotation of the manipulator joints when the position error was less than 20 cm. In other words, the trajectory control encounters more complex interactive forces between the vehicle and the manipulator. From the position error curves in the Figure 3a,b, the trajectory of the proposed scheme was smoother than that of SMC, and the proposed scheme could asymptotically converge to zero even under time-varying disturbance. Therefore, the trajectory control performance of the proposed scheme was also verified, even under the complex disturbance of interactive forces between the vehicle and the manipulator.
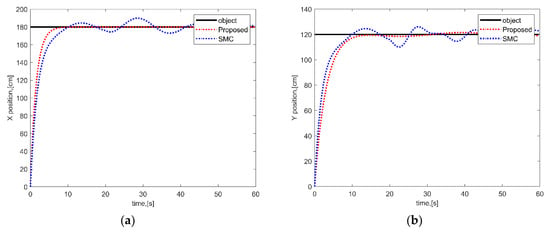
Figure 3.
The trajectory tracking of the end effector under the coordinated control of the vehicle and the manipulator: (a) trajectory in x-axis motion; (b) trajectory in y-axis motion.
5. Conclusions
In this paper, an adaptive control scheme with disturbance estimation was proposed for the end effector trajectory tracking control of UVMSs. The main contributions of the paper are the design of a disturbance estimation and adaptive disturbance observer-based feedback controller for UVMS. Firstly, the disturbance estimation alleviates the restriction faced by the feedforward control for UVMS. Compared with traditional estimation, the proposed disturbance estimation is based on feedback state errors, which does not introduce additional sensors. Meanwhile, the proposed estimation is less sensitive to system noise than traditional estimation. Secondly, the effectiveness of the proposed control scheme was verified through a series of attitude and trajectory control experiments in a pool. The proposed control scheme is not a conservative design. The attitude curve of the horizontal plane shows that performance can be recovered when the influence of the manipulator is weakened. In other words, the robustness is not at the price of degraded nominal performance. Compared with other control schemes, the position error curve of the proposed scheme also can asymptotically converge to zero even under time-varying disturbance. This shows that the proposed estimation observer is effective in identifying complex disturbances in interactive forces between the vehicle and the manipulator. The position control curve also shows that the proposed adaptive controller can promptly achieve high-precision control with attenuating disturbance. A limitation of the study is that the proposed control scheme is specialized for the underwater manipulation of UVMSs.
Author Contributions
Conceptualization, Y.L. and Y.W.; methodology, Y.W.; investigation, Y.Z.; data curation, H.S.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W.; project administration, S.L.; funding acquisition, Q.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by Priority Research Program of the Chinese Academy of Sciences (XDA22040106) and Youth Innovation Promotion Association, Chinese Academy of Sciences (2023208). This research was also partly funded by the Research Fund of State Key Laboratory of Robotics (Grant No. 2020-Z04, No. 2021-Z11L02).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the VSR robot design team, including Xueshan Zhou, Jingang Bai, Xinbao Zhai, and Daosong Yang.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zereik, E.; Bibuli, M.; Mišković, N.; Ridao, P.; Pascoal, A. Challenges and future trends in marine robotics. Annu. Rev. Control 2018, 46, 350–368. [Google Scholar] [CrossRef]
- Rigaud, V. Innovation and operation with robotized underwater systems. J. Field Robot. 2007, 24, 449–459. [Google Scholar] [CrossRef]
- Yoerger, D.R.; Kelley, D.S.; Delaney, J.R. Fine-Scale Three-Dimensional Mapping of a Deep-Sea Hydrothermal Vent Site Using the Jason ROV System. Int. J. Robot. Res. 2000, 19, 1000–1014. [Google Scholar] [CrossRef]
- Marsh, L.; Copley, J.T.; Huvenne, V.A.I.; Tyler, P.A.; the Isis ROV Facility. Getting the bigger picture: Using precision Remotely Operated Vehicle (ROV) videography to acquire high-definition mosaic images of newly discovered hydrothermal vents in the Southern Ocean. Deep Sea Res. Part II Top. Stud. Oceanogr. 2013, 92, 124–135. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Li, B.; Cui, S.; Zhao, Y.; Zhu, P.; Sun, B.; Zhang, Z.; Li, Z.; Li, S. Development and Sea Trials of a 6000m Class ROV for Marine Scientific Research. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Ludvigsen, M.; Sorensen, A.J. Towards integrated autonomous underwater operations for ocean mapping and monitoring. Annu. Rev. Control 2016, 42, 145–157. [Google Scholar] [CrossRef]
- Wynn, R.B.; Huvenne, V.A.I.; Bas, T.L.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Jaffré, F.M.; Littlefield, R.H.; Grund, M.; Purcell, M. Development of a New Version of the REMUS 6000 Autonomous Underwater Vehicle. In Proceedings of the OCEANS 2019-Marseille, Marseille, France, 17–20 June 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Wolek, A.; McMahon, J.; Dzikowicz, B.R. Tracking Multiple Surface Vessels with an Autonomous Underwater Vehicle: Field Results. IEEE J. Ocean. Eng. 2022, 47, 32–45. [Google Scholar] [CrossRef]
- Singh, W.; Örnólfsdóttir, E.B.; Stefansson, G. A Small-Scale Comparison of Iceland Scallop Size Distributions Obtained from a Camera Based Autonomous Underwater Vehicle and Dredge Survey. PLoS ONE 2014, 9, e109369. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, C.L.; Yoerger, D.R.; Kinsey, J.C.; Kelley, S.; Billings, A.; Fujii, J.; Suman, S.; Jakuba, M.; Berkowitz, Z.; German, C.R.; et al. The design and 200 day per year operation of the Autonomous Underwater Vehicle Sentry. In Proceedings of the 2016 IEEE/OES Autonomous Underwater Vehicles (AUV), Tokyo, Japan, 6–9 November 2016; pp. 251–260. [Google Scholar] [CrossRef]
- Yoerger, D.R.; Curran, M.; Fujii, J.; German, C.R.; Gomez-Ibanez, D.; Govindarajan, A.F.; Howland, J.C.; Llopiz, J.K.; Wiebe, P.H.; Hobson, B.W.; et al. Mesobot: An Autonomous Underwater Vehicle for Tracking and Sampling Midwater Targets. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Cruz, N.A.; Matos, A.C.; Ferreira, B.M. Modular building blocks for the development of AUVs—From MARES to TriMARES. In Proceedings of the 2013 IEEE International Underwater Technology Symposium (UT), Tokyo, Japan, 5–8 March 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Xu, H.; Zhao, H.; Wang, Y. Research status of autonomous underwater vehicles in China. Sci. Sin. Inf. 2018, 48, 1152–1164. [Google Scholar] [CrossRef]
- Simetti, E.; Campos, R.; Vito, D.D.; Quintana, J.; Antonelli, G.; Garcia, R.; Turetta, A. Sea Mining Exploration With an UVMS: Experimental Validation of the Control and Perception Framework. IEEE/ASME Trans. Mechatron. 2021, 26, 1635–1645. [Google Scholar] [CrossRef]
- Borlaug, I.-L.G.; Pettersen, K.Y.; Gravdahl, J.T. Comparison of two second-order sliding mode control algorithms for an articulated intervention AUV: Theory and experimental results. Ocean Eng. 2021, 222, 108480. [Google Scholar] [CrossRef]
- Cui, R.; Zhang, X.; Cui, D. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities. Ocean Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]
- Wei, Y.; Hou, Y.; Luo, S.; Li, Q.; Xie, J. Combined dynamics and kinematics networked fuzzy task priority motion planning for underwater vehicle-manipulator systems. Int. J. Adv. Robot. Syst. 2021, 18, 1–15. [Google Scholar] [CrossRef]
- Antonelli, G.; Chiaverini, S. Fuzzy redundancy resolution and motion coordination for underwater vehicle-manipulator systems. IEEE Trans. Fuzzy Syst. 2003, 11, 109–120. [Google Scholar] [CrossRef]
- Zhou, S.; Shen, C.; Xia, Y.; Chen, Z.; Zhu, S. Adaptive robust control design for underwater multi-DoF hydraulic manipulator. Ocean Eng. 2022, 248, 110822. [Google Scholar] [CrossRef]
- Antonelli, G.; Caccavale, F.; Chiaverini, S. Adaptive tracking control of underwater vehicle-manipulator systems based on the virtual decomposition approach. IEEE Trans. Robot. Autom. 2004, 20, 594–602. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).