An Improved NSGA-II Based on Multi-Task Optimization for Multi-UAV Maritime Search and Rescue under Severe Weather

Abstract

The international trade heavily relies on maritime transportation. Due to the vastness of the ocean, once an accident happens, fast maritime search and rescue (MSR) is a must, as it is of life-and-death matter. Using unmanned air vehicles (UAVs) is an effective approach to completing complex MSR tasks, especially when the environment is dangerous and changeable. However, how to effectively plan paths for multi-UAVs under severe weather, e.g., to rescue the most urgent targets in the shortest time, is a challenging task. In this study, an improved NSGA-II based on multi-task optimization (INSGA-II-MTO) is proposed to plan paths for multi-UAVs in the MSR tasks. In the INSGA-II-MTO, a novel population initialization method is proposed to improve the diversity of an initial population. Further, two tasks are introduced during the execution of the search algorithm. Namely, one assistant task, which solves a simplified MSR problem through multi-task optimization, is implemented to provide necessary evolutional knowledge to a main task that solves an original MSR problem. The performance of the proposed INSGA-II-MTO is compared with other competitors in three MSR scenarios. Experimental results indicate that the proposed algorithm performs best among the compared ones. It is observed that the INSGA-II-MTO can find a set of shorter total paths and handle the most urgent task in the shortest possible time. Therefore, the proposed method is an effective and promising approach to solving multi-UAVs MSR problems to reduce human causalities and property losses.

1. Introduction

With the rapid development of the global economy and trade, the throughput and scale of cargo transportation between countries have sharply increased in recent years. Due to the low freight, large transport capacity, and strong adaptability, maritime transportation is playing an increasingly important role in cargo transportation [1,2]. However, because of the rough and unpredictable marine environment due to the ever-change weather, maritime accidents occur frequently [3], which has caused many human causalities [4], huge property losses [5], and terrible damages to the marine ecological environment [6].

To carry out the MSR tasks in complex marine environments, assigning manual driving ships is a traditional way, which has many limitations, such as high cost, low efficiency, and poor applicability. In comparison, using UAVs is a much more promising and effective method to solve MSR problems due to high mobility, wide view field, and no risk of injury or death [7,8]. More importantly, UAVs can adapt to various challenging marine environments. Until now, a large number of related studies have been proposed. For example, Raap et al. [9] proposed a novel model to achieve search-trajectory planning for a single dynamic target. Kilic and Mostarda [10] proposed a new framework for path planning by optimizing the charging station grid to use a single UAV to reach multiple static ships. To further make the planned path more suitable and realistic for MSR tasks, a weight related to the path based on the time of accident is introduced into the Ant Colony Optimization (ACO) [11]. It is worth noting that the best path obtained by the improved ACO may not be the shortest. However, a single UAV can only complete a limited number of tasks, and its efficiency is often low. Therefore, some research has focused on implementing a group of UAVs. For example, Yang et al. [12] proposed a cognitive mobile computing network composed of UAVs and unmanned surface vehicles (USVs) for collaborative MSR tasks. An iteration of the Markov decision process (MDP) is used in sub-areas to find the paths with the highest reward for multiple pieces of equipment. The experimental results show that this method can successfully avoid obstacles and find an optimal path. Subsequently, some studies pointed out that there should be priorities according to urgency level or high-value tasks among different MSR tasks [13,14]. Furthermore, Huang et al. [15] proposed a multi-objective maritime patrolling problem, in which the vessels that need to be visited are regarded as circular areas. Then, a novel method inspired by the immune-endocrine short feedback system is proposed to solve the problem. Compared with other algorithms, the proposed algorithm showed good global and local search abilities for a given instance.

Although the existing studies can effectively solve MSR problems, they considered a relatively simple marine environment model with relatively few MSR targets. Generally, the solution complexity of multi-objective MSR problems increases exponentially with the increased number of tasks. Additionally, the previous study [16] pointed out that severe weather is a key factor causing marine accidents. Therefore, the present study aims to propose an advanced algorithm to solve complex multi-objective MSR problems under severe weather conditions.

To implement the above objective, the path planning problems of multi-objective MSR under severe weather are proposed in the present study. Moreover, an improved NSGA-II based on multi-task optimization (INSGA-II-MTO) is proposed. In the INSGA-II-MTO, a novel population initialization method is proposed to improve population diversity. Additionally, a multi-task optimization method, which can share knowledge among different tasks, is incorporated into the improved NSGA-II. Specifically, the original MSR problem is considered the main task, and a simplified MSR problem is used as the assistant task. The performance of the proposed INSGA-II-MTO is compared with the other two competitors in three test scenarios. The simulation results demonstrate that the INSGA-II-MTO is superior to the compared algorithms in three MSR scenarios. Therefore, the proposed algorithm is an effective and competitive approach to solving complex multi-objective MSR problems under severe weather.

The main contributions of this study are as follows: (1) the complex multi-objective MSR problems under severe weather are proposed. Different from previous studies, the number of tasks is more; (2) an improved NSGA-II based on multi-task optimization (INSGA-II-MTO) is proposed, where the multi-task optimization method is used to share knowledge among different tasks to speed up the convergence of the algorithm.

The rest of this paper is organized as follows. Section 2 introduces some preliminary knowledge of multi-objective optimization problems. Section 3 reviews the related literature on MSR. The problem definition and mathematical model of the multi-objective MSR are given in Section 4. Section 5 describes the proposed INSGA-II-MTO. Section 6 demonstrates the effectiveness of this proposed algorithm in solving multi-objective MSR through comparison with other algorithms on three testing examples. Conclusions are shown in Section 7.

2. Preliminary Knowledge

2.1. Multi-Objective Optimization Problem

A multi-objective optimization problem (MOP) involves multiple conflicting objectives that need to be optimized concurrently. Moreover, these objectives cannot be achieved optimally at the same time [17].

Without loss of generality, the minimization MOP can be mathematically described as:

$$\min \mathit{f}(\mathit{x})={(f_1(\mathit{x}),f_2(\mathit{x}),\dots ,f_M(\mathit{x}))}^T$$

(1)

where x = (x₁, x₂, …, x_D) ∈Ω is a D-dimensional decision variable; $\Omega \subset {ℝ}^D$ is the decision space; f(x) is an objective vector with M objective functions; $f(\mathit{x})\subset {ℝ}^M$ is the objective vector.

Some basic concepts of MOP are described as follows [18,19,20]:

Definition 1. 

Dominant relationship. Suppose two variables u = (u₁, u₂, …, u_D), v= (v₁, v₂, …, v_D), u is called to dominate v (denoted as $\mathit{u}\succ \mathit{v}$) if and only if u is no more than v, that is:

$$\mathit{u} \succ \mathit{v} \iff \forall d\in \mathit{\Phi },{\mathit{u}}_k\le {\mathit{v}}_k\wedge \exists b\in \mathit{\Phi },{\mathit{u}}_h<{\mathit{v}}_h$$

(2)

where  $\mathit{\Phi }=(1,2,\dots ,D)$

Definition 2. 

Pareto optimal solution set. Assuming a solution x*∈Ω, x* is called to be a Pareto optimal solution if and only if there are not any x satisfy $\mathit{f}(\mathit{x})\succ \mathit{f}(\mathit{x}*)$. All of Pareto optimal solutions compose a Pareto optimal set (PS), marked as X^∗.

Definition 3. 

Pareto front. The objective vector corresponding to the PS in the object space is called the Pareto frontier (PF), represented as $\mathrm{PF}=\{\mathit{f}({\mathit{x}}^{\ast }) |{\mathit{x}}^{\ast }\in {\mathit{X}}^{\ast }\}$.

To evaluate the performance of multi-objective evolutionary algorithms (MOEAs), various performance indicators have been proposed [21,22]. Two commonly used performance metrics are applied in the current study, i.e., the Hypervolume (HV) and the Non-dominance ratio (NR). The HV proposed by Zitzler and Thiele [23] is a comprehensive performance metric, which can evaluate the convergence and diversity of the PF approximation at the same time. A larger HV value means that the algorithm performance is better. Moreover, the NR proposed by Goh and Tan [24] is used to evaluate which MOEA can find more Pareto solutions. A larger NR means that the algorithm performance is better.

2.2. Non-Dominated Sorting Genetic Algorithm-II

The Non-dominated Sorting Genetic Algorithm (NSGA-II) [25] is one of the most popular MOEAs, and has been successfully used to solve MOPs in various fields [26,27]. The main steps of the NSGA-II are as follows [28]:

First, generate the initial population P randomly and calculate the fitness value of each individual. Then, the offspring population OP is generated by the binary tournament selection [25], crossover and mutation strategies. For the integer-coded NSGA-II, the two-point crossover and multi-point mutation operator [29] are commonly adopted to generate offspring individuals. For the real-coded NSGA-II, the Simulated Binary Crossover (SBX) and polynomial mutation (PM) [30] operator are commonly used to produce offspring individuals. Note that the SBX is an operator simulating single-point binary crossover. Assuming that $x^1=(x_1^1,x_2^1,\dots ,x_D^1)$ and ${\mathrm{x}}^2=(x_1^2,x_2^2,\dots ,x_D^2)$ are two parent individuals, two offspring individuals $c^1=(c_1^1,c_2^1,\dots ,c_D^1)$ and $c^2=(c_1^2,c_2^2,\dots ,c_D^2)$ can be obtained by the SBX:

$$\begin{array}{l}\left\{\begin{array}{l}{c}_k^1=0.5\times \left[(1+\beta )\cdot x_k^1+(1-\beta )\cdot x_k^2\right]\\ c_k^2=0.5\times \left[(1-\beta )\cdot x_k^1+(1+\beta )\cdot x_k^2\right]\end{array}\right.\\ \beta =\left\{\begin{array}{l}{\left(2\times rand\right)}^{\frac{1}{1+{\eta }_c}},rand\le 0.5\\ {\left(\frac{1}{2(1-rand)}\right)}^{\frac{1}{1+{\eta }_c}},otherwise\end{array}\right.\end{array}$$

(3)

where rand is a random number between 0 and 1; k is an integer between 1 and D; ${\eta }_c$ is a customization parameter.

The mathematical formula of the PM is as follows:

$$\begin{array}{l}{x}_k^1=x_k^1+\Delta t\\ \mathrm{\Delta }t=\left\{\begin{array}{l}{(2\times rand)}^{\frac{1}{1+{\eta }_u}}-1,rand<0.5\\ 1-{[2\times (1-rand)]}^{\frac{1}{1+{\eta }_u}},otherwise\end{array}\right.\end{array}$$

(4)

where ${\eta }_u$ is a customization parameter.

Next, the parent and offspring populations are merged to form P_all, which is sized 2NP. Subsequently, the non-dominated sorting and crowding distance method [25] are used to select NP individuals from P_all to obtain a new parent population. Repeat these steps until the termination conditions are met. The pseudocode of NSGA-II is given in Algorithm 1.

Algorithm 1: NSGA-II

Input: Population size: NP; maximum generation: G

1: Generate and evaluate the initial population P

2: Set G = 1

3: while termination criterion not satisfied do

4: OP ← Generate offspring by crossover and mutation strategies

5: Pall ← OP ∪ P

6: P ← Select NP individuals from Pall based on the non-dominated sorting and crowding distance

7: G = G + 1

8: end while

Output: The PS and PF

3. Literature Review

To reduce the damages caused by maritime accidents and complete the MSR tasks, a large number of methods have been proposed in previous studies. As MSR stations are often set up on coastal lands and far from the accident scenes, determining their locations is an optimization problem. Namely, selecting appropriate MSR stations can improve the MSR capability and reduce potential losses. Zhou et al. [31] proposed a new framework to plan the locations of the MSR stations. First, the response time of candidate islands, which are determined according to potential demands, can be calculated. Then, the best islands are selected as the MSR stations by solving the maximal covering location problem (MCLP). Experimental results indicate that this method can improve the primary coverage and reduce rescue time. Peng et al. [32] proposed a hybrid algorithm, in which the tabu search algorithm is incorporated into the ACO to solve a bi-level programming model of the location-routing problem. The proposed hybrid algorithm performs better than the ACO.

Apart from the location optimization of MSR stations, a number of methods have been proposed to support the planning of search areas. For example, Otote et al. [33] proposed a decision-making model to implement an MSR plan based on the support of optimal search theory. Specifically, they introduced the concept of density ratio and a random detection function to improve the accuracy of probability of containment (POC) and probability of detection (POD), respectively. Experiments confirm that the values of POC and POD are obviously improved and can support MSR tasks. Based on the above studies, Xiong et al. [34] proposed a time domain-based iterative planning (TIP) method to plan the search areas. In the TIP, the probability map is updated based on the mean drift direction in each iteration. Subsequently, an iterative search method is used to determine the optimal search areas based on the grid with the highest POC in the map. It was concluded that the probability of success (POS) of the search areas obtained by the TIP is higher than other methods. However, the TIP may easily fall into local optima, especially when the potential search area is large. To alleviate this issue, a method based on the minimum bounding rectangle and K-means clustering (MBRK) is proposed [35]. In the MBRK, the K-means clustering method is used to divide the potential locations of survivors into multiple regions. Moreover, the minimum bounding rectangle is used to generate probability maps for each region. Finally, the optimal search areas can be further optimized by adding or subtracting multiple cells. Simulation experiments confirm that MBRK can further improve the POS values of the search areas.

Apart from the above studies in the MSR, task allocation and path planning are also two key tasks. For task allocation, Ai et al. [36] proposed a regional task allocation algorithm to quickly respond to maritime accidents. The proposed method considers both the temporal and spatial characteristics of task assignment. Based on experimental tests, the proposed algorithm can avoid repeated searches and improve MSR efficiency. For path planning, Cho et al. [37] proposed a two-stage coverage path planning (CPP) method for multiple UAVs to minimize the completion time. In the first stage, a grid-based decomposition method is used to decompose the search area into squares. In the second stage, a three-phases randomized search heuristic (RSH) algorithm is proposed to find optimal paths in large-scale instances. Extensive numerical experiments show that the RSH has a faster convergence speed than other methods. To make the moving direction more diverse, Cho et al. [38] proposed a mixed-integer linear programming (MILP) model based on a hexagonal grid-based decomposition method. According to the results, the proposed model can obtain high-quality paths. However, Ho et al. [39] established new MSR route models, which consider path length and people information in distress simultaneously. Moreover, the grey relational analysis is used to quantify the people’s information and then convert them into distance weight, which is combined with the distance matrix of the Floyd–Warshall algorithm. The experiment shows that the model can be applied to the actual decision-making situation to provide reasonable schemes. In addition, it should be noted that task allocation and path planning are coupled in most cases. Therefore, Yan et al. [40] proposed an improved particle swarm optimization combined with a genetic algorithm (GA-PSO) to solve task allocation and path planning problems. Namely, the partial matching crossover and second transposition mutation are introduced to improve the performance. The simulation results show that this algorithm can improve the efficiency of task allocation and path planning when compared with competitors. Except for the application scenarios of MSR, some researchers have proposed search and rescue strategies for other scenarios, which can be used as references for MSR. Yazdani et al. [41] proposed using public transportation systems to improve evacuation capability in extreme weather disasters. Gharib et al. [42] developed a comprehensive model to plan the delivery of construction materials to post disaster reconstruction projects.

4. Multi-Objective Maritime Search and Rescue Problem under Severe Weather

Maritime accidents can cause huge damage and often occur under severe weather, such as storms. Therefore, how to carry out MSR tasks efficiently in a complex environment is important. However, the cost and time consumption of a task are usually conflicting goals in a rescue operation. Additionally, people or vessels in a high-risk area need to be visited as soon as possible. Therefore, a multi-objective MSR problem under severe weather is considered in the current study.

4.1. Description of Multi-Objective MSR Problem under Severe Weather

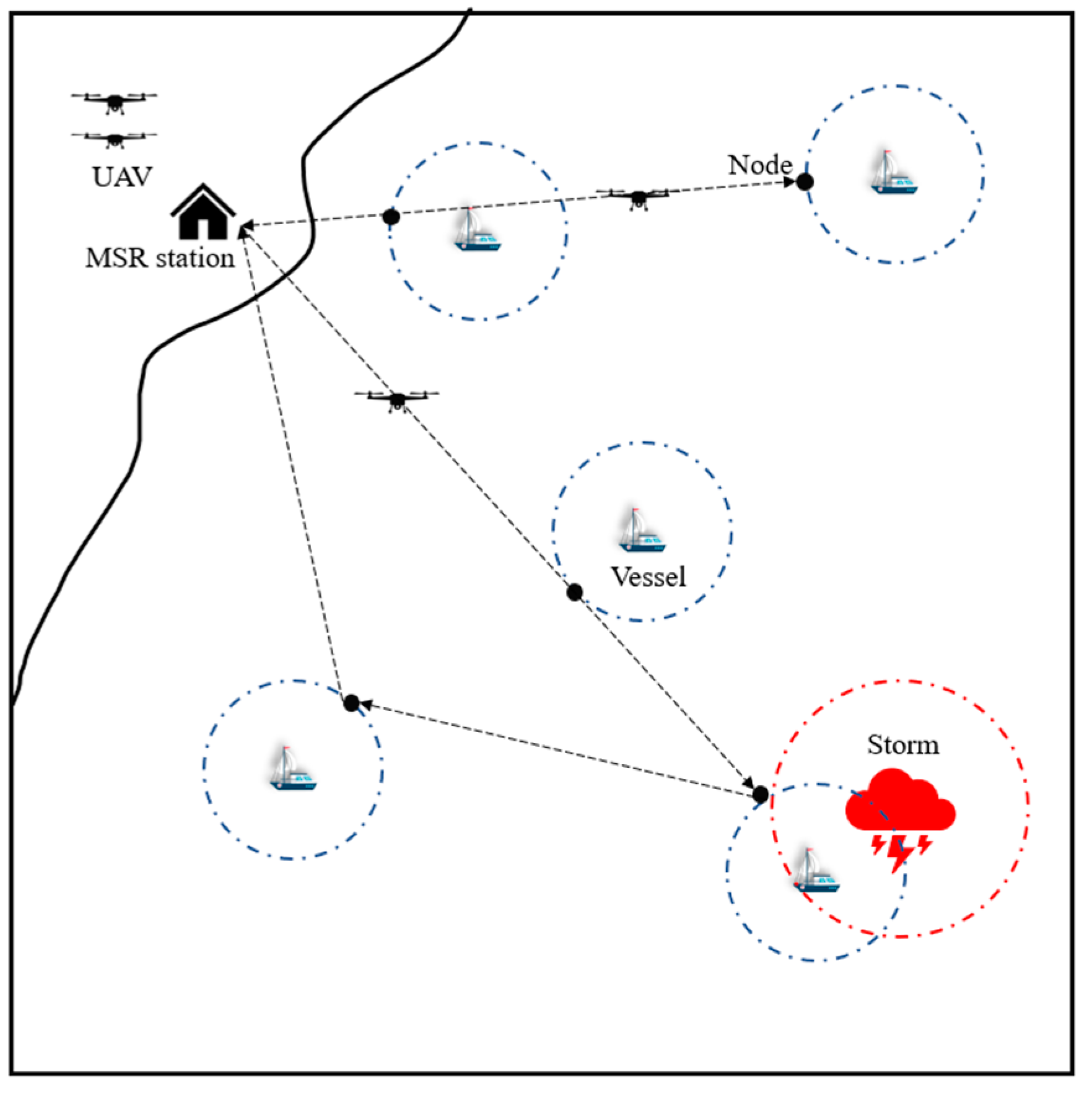
In the current study, a scenario of one MSR station equipped with a group of UAVs is used. If the MSR station receives signals for help from a vessel in danger, it will dispatch UAVs to provide various necessary assistance as well as to collect real-time information about the troubled vessel. This can help decision-makers develop the next rescue plans to reduce damages and save time. After completing the MSR tasks, the UAVs return to the MSR station. It should be noted that the UAV does not have to reach the exact position of the vessel. However, the position where the UAV actually arrives must be within the contact range of the vessel. Assuming that this position between the UAV and the vessel is called a node, and then a task is considered successfully completed when the UAV reaches a node. Additionally, a storm is considered in the current study. Therefore, the UAV should prioritize the vessels which are in the high-risk area affected by the storm. An example of the problem is illustrated in Figure 1. As shown in Figure 1, two UAVs are dispatched to accomplish the MSR tasks. One will visit two vessels, and another will visit three vessels. Moreover, the red circle represents the high-risk area affected by the storm.

4.2. Mathematical Model of Multi-Objective MSR Problem under Severe Weather

Supposing that the position of an MSR station P is (x_P, y_P) and the number of UAVs is n. Moreover, there are q vessels in distress. The coordinate and contact range of the i-th vessel is represented as (x_i, y_i) and r_i, respectively. The center position of the storm S is (x_s, y_s) and its influencing radius is r_S. The j-th UAV is assigned to visit a set of vessels. Moreover, the nodes corresponding to these vessels are denoted as T(j), in which N_i is denoted as the corresponding node of the i-th vessel. Therefore, all the targets visited by the j-th UAV is W(j) = {P, T(j), P}.

Furthermore, E_i is used to determine whether the i-th vessel is within the influencing scope of the storm. It is calculated by the following formula:

$$\begin{array}{l}{E}_i=\left\{\begin{array}{l}1,d_{iS}<r_S\\ 0,oherwise\end{array}\right.,\\ d_{iS}=\sqrt{{(x_i-x_S)}^2+{(y_i-y_S)}^2}\end{array}$$

(5)

where d_iS denotes the Euclidean distance between the i-th vessel and the center position of the storm. If E_i = 1, the i-th vessel is within the influencing scope of the storm and should be visited as soon as possible. Otherwise, the i-th vessel is relatively safe.

If the j-th UAV is assigned to visit the vessels which should be visited as soon as possible, ${\gamma }_{j\max }$ is represented as the order number of the last urgent vessel in the visiting sequence. Therefore, the MSR station and the nodes of vessels whose order numbers are before ${\gamma }_{j\max }$ in j-th path compose a set G(j). Moreover, ${\delta }_{uv}\in \left\{0,1\right\}$ is a binary variable, which denotes the movement between the node u and v. If ${\delta }_{uv}$ = 1, it means that UAV moves from node u to v. If ${\delta }_{uv}$ = 0, it means that there is no path between the two nodes. Additionally, the d_uv stands for the Euclidean distance between the two nodes.

Based on the research of Huang et al. [15], the objectives of the model of multi-objective MSR problem under severe weather can be defined as follows:

$$\begin{array}{c}\min F=(f_1,f_2,f_3)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_1={\displaystyle \sum _{j=1}^n{d}_{uv}}{\delta }_{uv},u,v\in W(j)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_2=\underset{1\le j\le n}{\max }{d}_{uv}{\delta }_{uv},u,v\in W(j)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_3=\underset{1\le j\le n}{\max }{d}_{uv}{\delta }_{uv},u,v\in G(j)\end{array}$$

(6)

The f₁ is to minimize the total path length of multi-UAVs. The shorter the total path length of UAVs, the less energy they consume. The f₂ aims at minimizing the total task completion time, which is equivalent to minimizing the longest single path length. The f₃ aims at minimizing the completion time of urgent tasks. That is, UAVs are required to visit the vessels within the affected area of the storm as early as possible. Concretely, it is represented to minimize the path length from the MSR station to the vessels which need priority.

5. The Proposed Method

Solving multi-objective MSR problems is a difficult task, thus it is important to develop advanced MOEAs. It is worth mentioning that multi-task optimization is considered an effective method to solve various complex optimization problems [43,44]. To effectively solve multi-objective MSR problems, an improved NSGA-II based on multi-task optimization (INSGA-II-MTO) is proposed in this study.

5.1. Encoding and Decoding Method

In this subsection, the encoding and decoding methods of the main and assistant tasks are introduced. Moreover, a boundary-based encoding approach [45] is adopted since it can reduce the size of the search space. The polar coordinate is used to represent the node position.

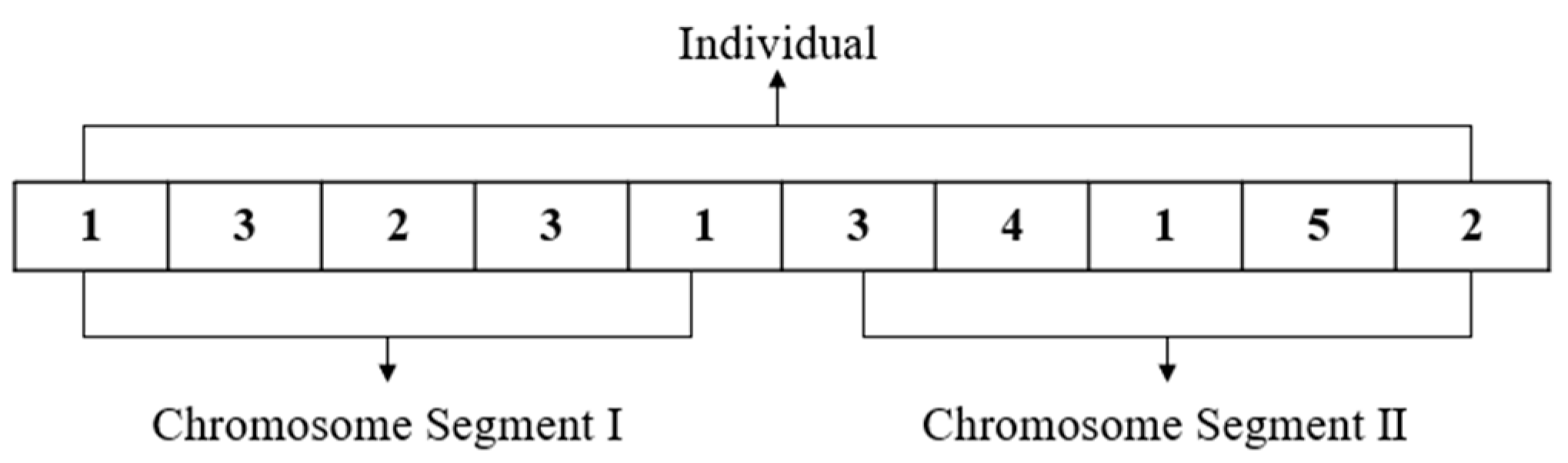
Individual encoding of the main task: The individuals in the main task are all encoded by real numbers, where each individual is 3 × q. Moreover, the individual is divided into three segments in the current study. The first segment (i.e., Chromosome Segment I) represents the task allocation of UAVs. It consists of q integer numbers within the range of [1, n]. The second segment (Chromosome Segment II) contains a series of vessel numbers, whose order will be mapped to the visiting sequence in the UAV paths. It also consists of q integer numbers within the range of [1, q]. To ensure that the UAVs traverse all vessels without repetition and omission, all genes in Chromosome Segment II are different from each other. The locations of nodes are indicated in the third segment (Chromosome Segment III), in which genes are represented as angles between the vessels and nodes. The Chromosome Segment III is composed of q floating-point numbers within the range of [0, 360]. An example of a main task containing 5 vessels and 3 UAVs is shown in Figure 2.

Individual encoding of the assistant task: Unlike the encoding of the main task, a new encoding for the simplified MSR problem (i.e., the target is regarded as an ideal point) is used. Therefore, the length of each individual in the assistant task is 2 × q. All the individuals are encoded by integer numbers. Moreover, the individual is divided into two segments. The first segment (i.e., Chromosome Segment I) represents the task allocation of UAVs, and the second segment (i.e., Chromosome Segment II) denotes the visiting sequence of each UAV. An example of an assistant task containing 5 vessels and 3 UAVs is shown in Figure 3.

Since the encoding method of the assistant task is the same as that of part of the main task, the decoding methods of three chromosome segments in the main task are given as follows:

Chromosome Segment I: Each gene represents the number of a UAV, i.e., which UAV will visit the matching vessel. The same genes mean that these vessels are assigned to the same UAV.

Chromosome Segment II: Each gene represents the number of a vessel. For a given UAV, its visiting sequence is determined by the corresponding order in the Chromosome Segment II.

Chromosome Segment III: Each node location is computed by the following formulas:

$$\begin{array}{l}{x}_{N_i}=x_i+r_i\cos {\theta }_i\\ y_{N_i}=y_i+r_i\sin {\theta }_i\end{array}$$

(7)

where ${\theta }_i$ is represented as the angle between the i-th vessel and its corresponding node; $x_{N_i}$ and $y_{N_i}$ are the abscissa and ordinate of the node, respectively.

To further illustrate the decoding method of Chromosome Segments I and II, an example is given in Figure 4. It can be seen from Figure 4a that, for the Chromosome Segment I, UAV “2” visits one vessel, and UAVs “1” and “3” visit two vessels, respectively. It should be noted that the MSR station does not necessarily dispatch all UAVs for MSR tasks. For the Chromosome Segment II, the visiting sequence of UAV “2” is “0→1→0”; the visiting sequences of the UAVs “1” and “3” are “0→3→2→0” and “0→4→5→0”, respectively. All paths are shown in Figure 4b, where “0” is denoted as an MSR station.

5.2. Population Initialization Method

A good initial population can accelerate the convergence of the algorithm and improve the quality of final solutions. Therefore, how to generate a high-quality initial population is vital. Although a randomly generated population can enhance the exploration ability of algorithms in the early stage, it has some limitations in solving MSR problems. Specifically, the probability of generating Chromosome Segment I with identical genes via random initializing is extremely small. Namely, it is hard to generate individuals that dispatch one UAV to accomplish the MSR tasks. In addition, this probability will be further reduced with the expansion of search space.

To alleviate the above problem, a two-stage population initialization method is proposed, which is described as follows:

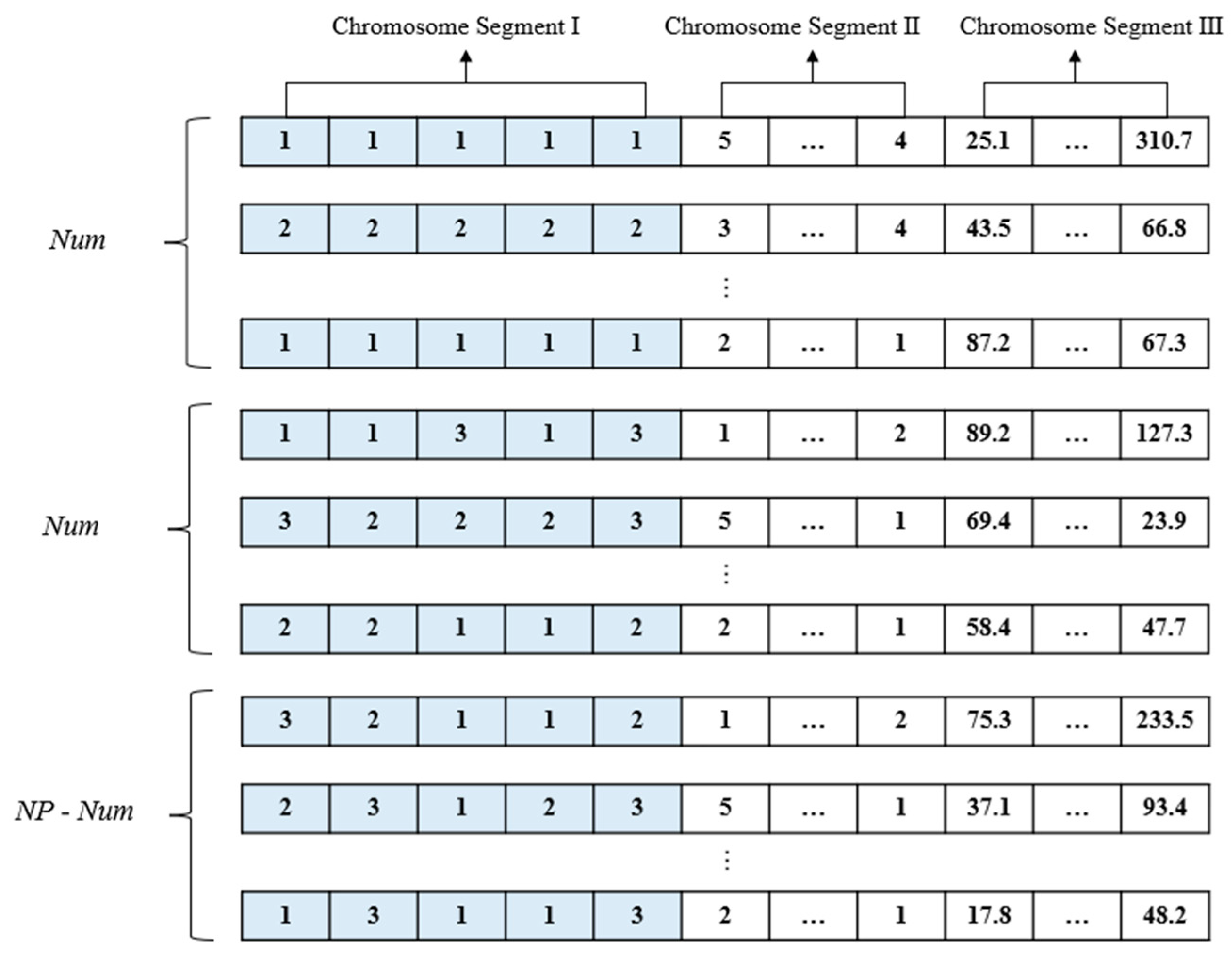
Step 1: The total number of UAVs and population size is set to n and NP, respectively. Generally, NP is much greater than n. The number of individuals of each particular type is defined as Num = [NP/n]. Then Num individuals that dispatch one UAV and Num individuals that dispatch two UAVs are generated, respectively.

Step 2: For the remaining individuals in the initial population, they are generated randomly.

Figure 5 shows an example of the proposed initialization method containing 5 vessels and 3 UAVs. It can be observed from Figure 5 that the first Num individuals are generated to dispatch one UAV to complete the MSR tasks. The next Num individuals are generated to dispatch two UAVs. Moreover, there is a wide variety of individuals among the rest of the population.

5.3. Knowledge Transfer in the Multi-Task Optimization

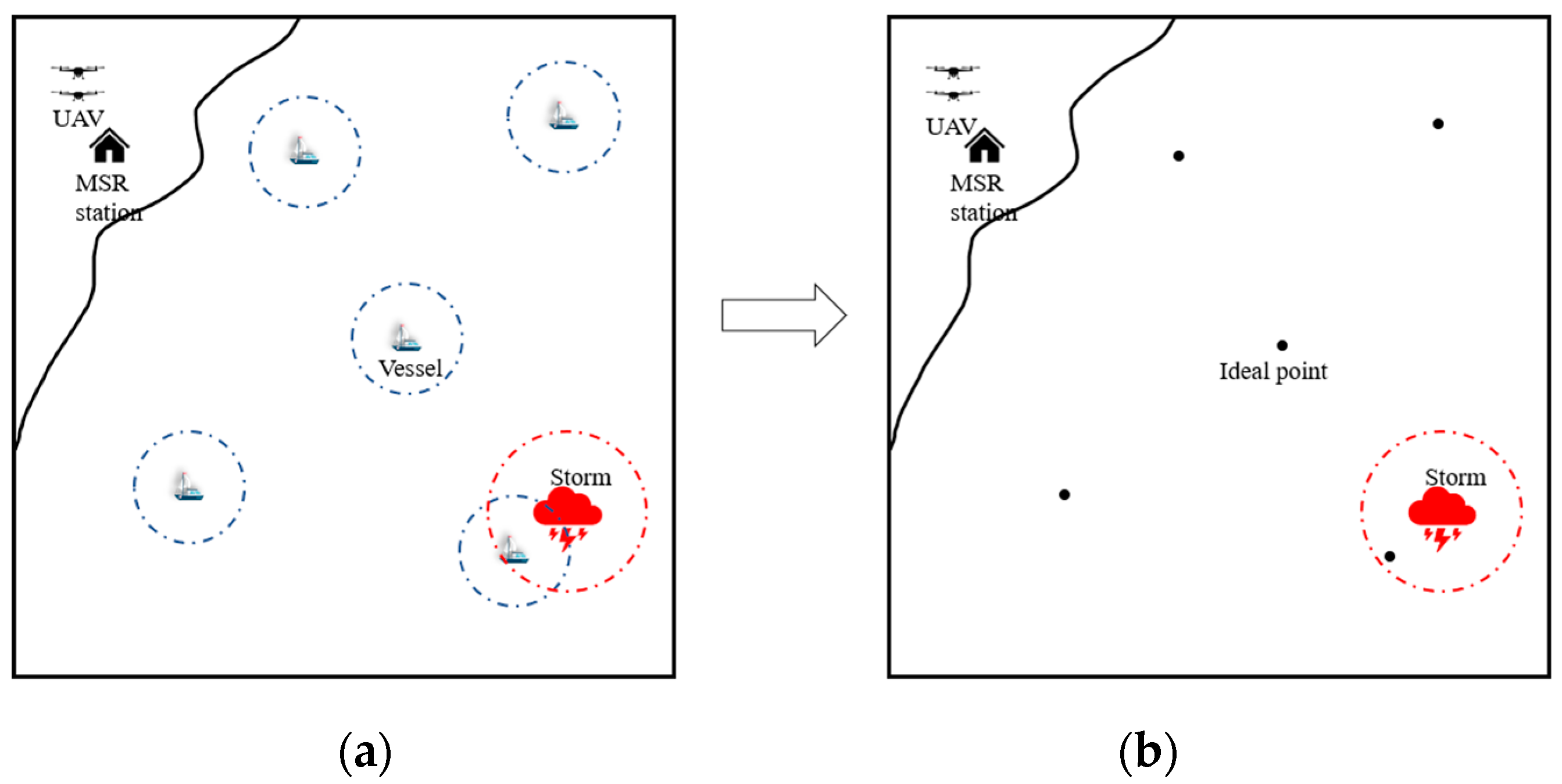
The multi-task optimization is an effective method to solve complex problems, thus it is incorporated into the proposed algorithm to improve the performance in solving multi-objective MSR problems. A main task and an assistant task are used in the INSGA-II-MTO. The schematic diagrams of the original and simplified MSR tasks are shown in Figure 6. It can be seen from Figure 6a that the main task focuses on solving the original MSR problems. Figure 6b shows that the visiting target can be considered as an ideal point by ignoring the contact range, thus the assistant task can focus on solving the simplified MSR problem.

According to Section 5.1, the encoding methods of these two tasks are not identical. Therefore, the knowledge between the main task and the assistant task cannot be transferred directly. To illustrate the transfer process, an example is given in Figure 7.

Knowledge transfer from main task to assistant task: As mentioned in Section 5.1, the individual in the main task has three parts (i.e., Chromosome Segments I, II, and III), while there are two components of the individual in the assistant task. Therefore, if the knowledge of the main task is transferred to the assistant task, then the third part (i.e., Chromosome Segment III) should be deleted. It can be observed from Figure 7 that, to achieve knowledge transfer from the main task to the assistant task, the Chromosome Segment III of the individual in the main task is deleted to obtain a transferred individual, which can help the assistant task.

Knowledge transfer from assistant task to main task: The first two parts of individuals between two tasks are versatile. However, individuals in the assistant task do not contain the third part. Therefore, if the knowledge of the assistant task is transferred to the main task, the third part of the individual in the main task can be added to the transferred individual. It can be observed from Figure 7 that a Chromosome Segment III is randomly selected as a reference from the PS of the main task, which can provide high-quality node information. Then, combine this Chromosome Segment III with the assistant task individual to form a transferred individual.

5.4. The Overall Process of the INSGA-II-MTO

In the INSGA-II-MTO, the main task and the assistant task are incorporated to improve the NSGA-II. It optimizes the main task and the assistant task independently and simultaneously, and the two tasks are expected to assist each other during the search process through a knowledge transfer process in multi-task optimization. Its pseudocode is described in Algorithm 2.

In line 1, generate the initial populations P₁ and P₂ with NP individuals according to the proposed initialization method. In line 2, all individuals in P₁ are evaluated via the original multi-objective MSR problem; in line 3, all individuals in P₂ are evaluated via the simplified multi-objective MSR problem.

Next, the main loop begins. In lines 5–6, select NP/2 individuals from P₁ and P₂ via the binary tournament method, which are denoted as MP₁ and MP₂. Then, the SBX and PM are adopted to generate an offspring population OP₁ sized NP/2 in line 7; the two-point crossover and multi-point mutation operator are adopted to generate an offspring population OP₂ sized NP/2 in line 8. After generating two offspring populations, in lines 9–10, OP₁ and OP₂ are evaluated via the original multi-objective and simplified multi-objective MSR problem, respectively. Subsequently, knowledge sharing between two tasks is achieved by transferring individuals. In line 11, generate OP_1new as a transferred population by deleting the Chromosome Segment III in OP₁; in line 12, generate OP_2new as another transferred population by randomly adding the Chromosome Segment III to the individual in OP₂. In lines 13–14, P₁, OP₁ and OP_2new are combined as P_1all; P₂, OP₂ and OP_1new are combined as P_2all. Next, in lines 15–16, NP individuals are selected from P_1all and P_2all for the next iteration according to the non-dominated sorting and crowding distance, respectively. Finally, the PS and PF of the main task is output when the termination condition is satisfied.

Algorithm 2: INSGA-II-MTO

Input: Population size: NP; maximum generation: Gmax; population of the main task: P1; population of the assistant task: P2

1: Initialize P1 and P2 of size NP via the proposed initialization method in Section 5.2

2: Evaluate P1 on the original multi-objective MSR

3: Evaluate P2 on the simplified multi-objective MSR

4: while termination criterion not satisfied do

5:  MP1 ← Select NP/2 individuals from P1 using binary tournament selection method

6:  MP2 ← Select NP/2 individuals from P2 using binary tournament selection method

7:  OP1 ← Generate NP/2 offspring by MP1 according to SBX and PM

8:  OP2 ← Generate NP/2 offspring by MP2 according to two-point crossover and multi-point mutation operator

9:  Evaluate OP1 on the original multi-objective MSR problem

10:  Evaluate OP2 on the simplified multi-objective MSR problem

11:  OP1new ← OP1 delete the Chromosome Segment III to generate a transferred population according to;

12:  OP2new ← OP2 randomly add the Chromosome Segment III to generate a transferred population according to Section 5.3;

13:  P1all ←P1 ∪ OP1 ∪ OP2new;

14:  P2all ←P2 ∪ OP2 ∪ OP1new;

15:  P1 ← Select NP individuals from P1all based on the non-dominated sorting and crowding distance

16:  P2 ← Select NP individuals from P2all based on the non-dominated sorting and crowding distance

17: end while

Output: The PS and PF of the main task

6. Experimental Results and Analysis

In this section, the performance of the INSGA-II-MTO is verified via comparing with the other excellent multi-objective optimization algorithms in three scenarios. All of the following experiments are tested via MATLAB R2021.

Three task scenarios are used and set to be 1000 × 1000 km, which are shown in Figure 8. Although the three scenarios are the same, the number of vessels is different. It can be seen from Figure 8a that 5 vessels should be visited. Figure 8b,c show that UAVs should visit 10 and 15 vessels. Clearly, the solution difficulty of the three scenarios is different. Moreover, the number of UAVs is set to be 4 in the MSR station in all scenarios. In addition, the radius of the affected range of the storm and the contact range of each vessel are set to 120 km and 60 km, respectively.

To ensure the fairness of comparisons, for all compared algorithms, the total number of fitness evaluations in each scenario is the same, i.e., 20,000 is set in scenario 1 (see Figure 8a), 40,000 is set in scenario 2, and 60,000 is set in scenario 3. Each comparison algorithm runs 20 times independently in each scenario. Moreover, the performance metrics HV and NR are selected in the following experiments. The same reference point is set for three algorithms in each MSR scenario. Additionally, parameter settings of all compared algorithms are shown in

Table 1. Parameter settings of three compared algorithms.

Name	Value	Algorithms
pc1	0.9	INSGA-II-MTO, NSGA-II, NSGA-II-GLS
pm1	0.6	INSGA-II-MTO, NSGA-II, NSGA-II-GLS
pc1	0.8	INSGA-II-MTO
pm1	1	INSGA-II-MTO
NP	100	INSGA-II-MTO, NSGA-II, NSGA-II-GLS

.

6.1. Comparison Results with Other Algorithms

To verify the performance of the proposed algorithm, it is compared with the NSGA-II [25] and the NSGA-II-GLS [46] in three scenarios. The NSGA-II is a classical algorithm for solving MOPs, and the NSGA-II-GLS is an improved version of the NSGA-II.

The average and standard values of HV of the three algorithms are provided in

Table 2. HV results of all comparison algorithms in three scenarios.

	Test Scenario 1	Test Scenario 2	Test Scenario 3
INSGA-II-MTO	0.1929 (2.46 × 10−4)	0.2846 (1.1 × 10−2)	0.2567 (1.2 × 10−2)
NSGA-II	0.1923 (5.8 × 10−4) +	0.2099 (2.5 × 10−2) +	0.1571 (4.1 × 10−2) +
NSGA-II-GLS	0.1924 (5.98 × 10−4) +	0.2211 (3.6 × 10−2) +	0.1774 (3.9 × 10−2) +

. The best results are marked in bold, and Wilcoxon’s rank sum test is employed to analyze the results from the statistical perspective. Specifically, the symbols “+”, “−”, and “=” represent that the compared algorithms are better than, worse than, and similar to the INSGA-II-MTO, respectively. From the results shown in Table 2, it can be observed that the performance of the proposed algorithm is superior to that of the two compared algorithms. Due to the relative simplicity of scenario 1, HV obtained by the three algorithms are similar. However, Table 2 shows that the INSGA-II-MTO significantly outperforms the NSGA-II and the NSGA-II-GLS in scenarios 2 and 3 in terms of HV. The main reason may be that the initialization method can improve the diversity of the solutions and the performance of an algorithm. In addition, the knowledge transfer in multi-task optimization can enhance the search capability and save computational resources.

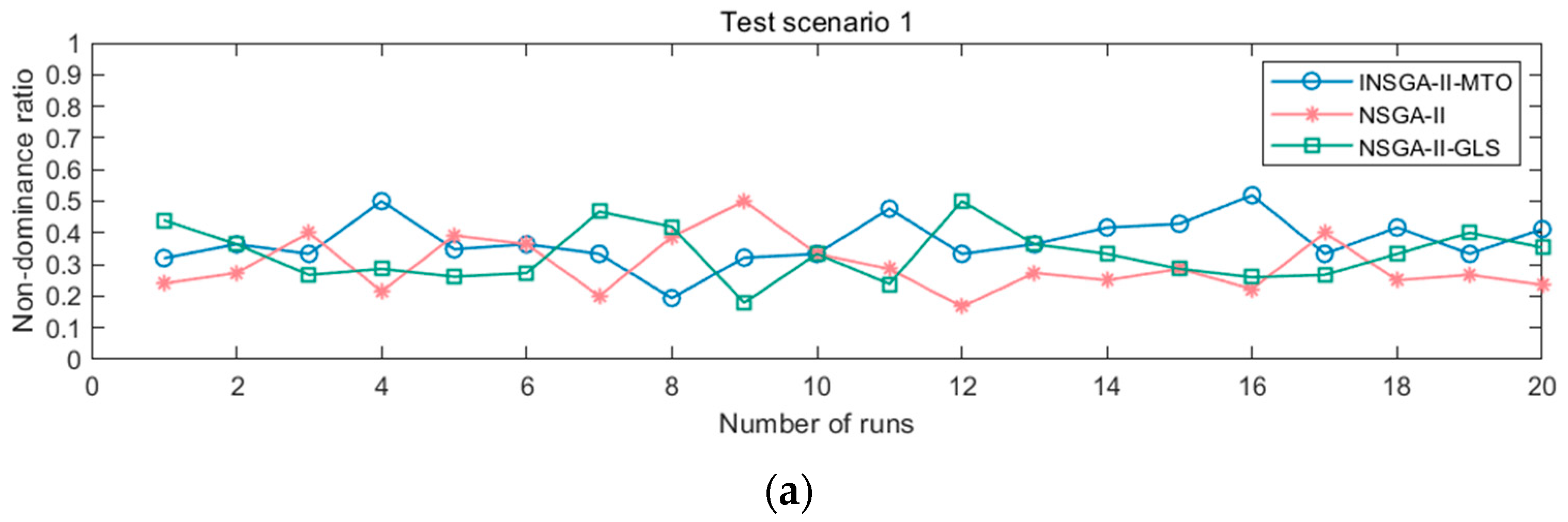
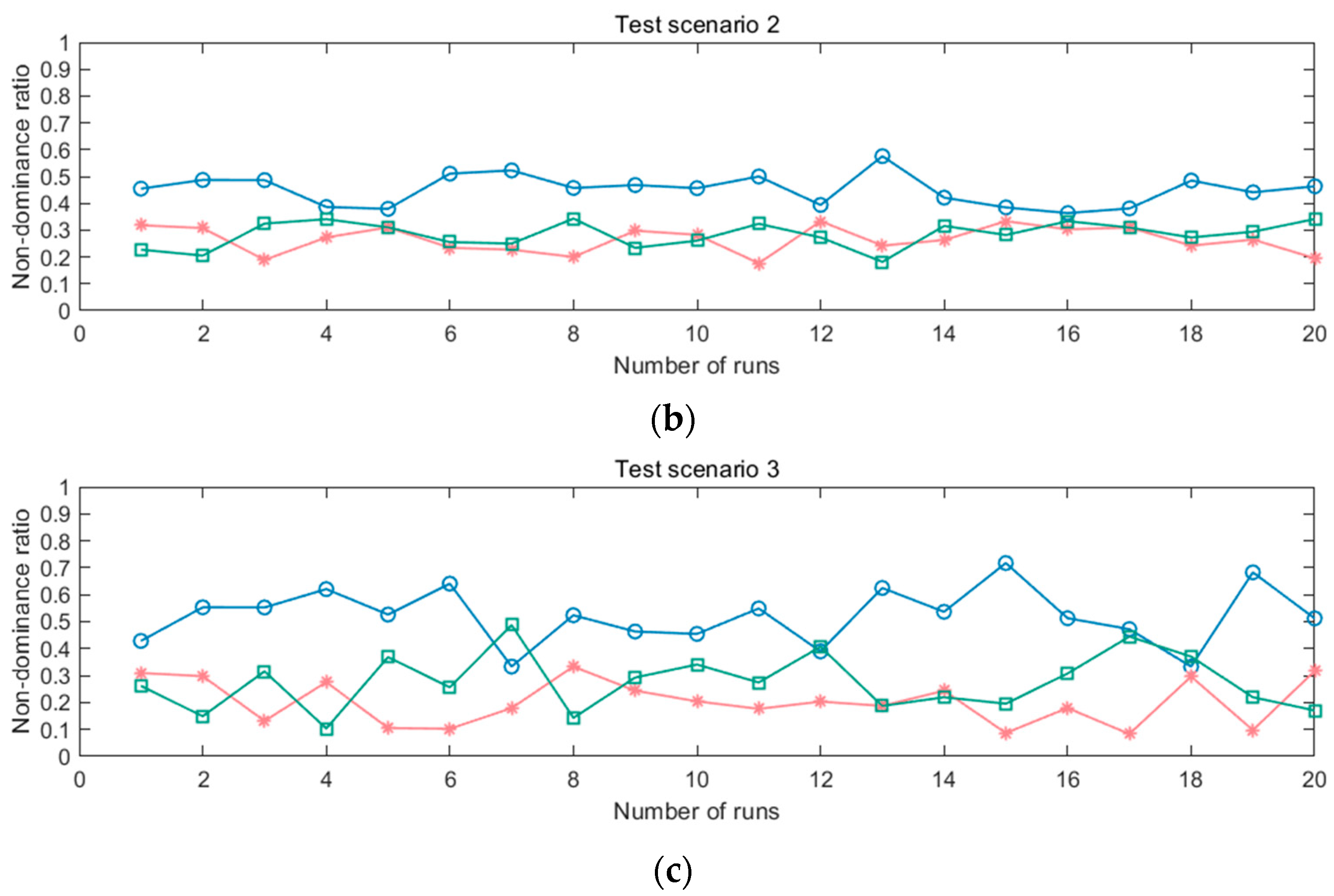
Besides the above comparisons, the other performance indicator NR is employed to assess the performance of three algorithms. Specifically, NR is used to explore the dominant relationship between the optimal solutions obtained by three algorithms. The NR values in three scenarios are plotted in Figure 9. From Figure 9a, the NR values obtained by the three algorithms are similar, while Figure 9b,c show that the NR values of the INSGA-II-MTO are larger than that of the other two algorithms during twenty experiments. This means that the INSGA-II-MTO can find more high-quality solutions which can dominate the most of non-dominated solutions obtained by the other two algorithms. Same as the above experiment, this is mainly because using the initialization method and multi-task optimization method is effective. It is worth noting that this advantage will be more evident in relatively complex scenarios.

Based on the above analyses, it can be concluded that the INSGA-II-MTO is an effective and efficient approach to solving complex multi-objective MSR problems.

6.2. Experimental Analysis

As mentioned above, the population initialization method and the multi-task optimization method are used to improve the performance of the proposed algorithm. In this subsection, their effectiveness is verified by the following experiments.

(1)

The effectiveness of the population initialization method

To illustrate the effectiveness of the initialization method, the INSGA-II-MTO and INSGA-II-MTO without the proposed initialization method (denoted as INSGA-II-MTO-R) are applied to solve three multi-objective MSR problems.

The average and standard values of HV achieved by the two algorithms are provided in

Table 3. HV results of the INSGA-II-MTO and INSGA-II-MTO-R.

	Test Scenario 1	Test Scenario 2	Test Scenario 3
INSGA-II-MTO	0.1929 (2.46 × 10−4)	0.2846 (1.1 × 10−2)	0.2567 (1.2 × 10−2)
INSGA-II-MTO-R	0.1926 (3.7 × 10−4) +	0.2465 (3.0 × 10−2) +	0.1908 (3.1 × 10−2) +

. As shown in Table 3, the HV of the INSGA-II-MTO is better than that of the INSGA-II-MTO-R in all three scenarios. Therefore, the population initialization method can help the proposed algorithm improve the search performance and provide a high-quality initial population.

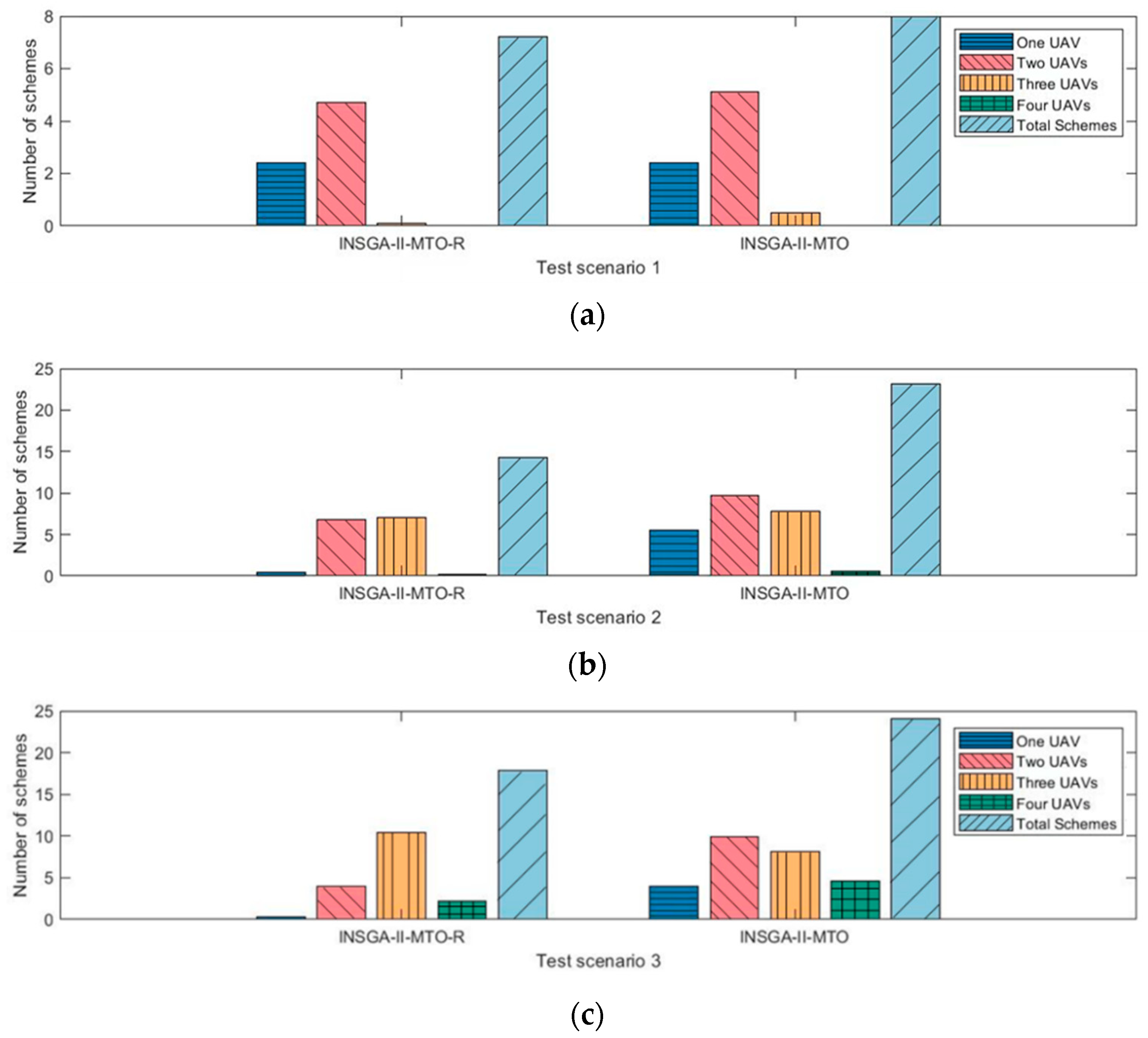
Furthermore, the average number of various schemes obtained by two algorithms in twenty experiments is shown in Figure 10. “One UAV” means that the station dispatches one UAV to complete MSR tasks; “Two UAVs” represents two UAVs dispatched to complete tasks. “Three UAVs” and “Four UAVs” refer to schemes that dispatch three UAVs and four UAVs, respectively. The average number of schemes that can be obtained in experiments by each algorithm is denoted as “Total Schemes”. From Figure 10a, except for the “Four UAVs”, the INSGA-II-MTO and INSGA-II-MTO-R can find three other schemes. It can be seen from Figure 10b,c, the number of “One UAVs” and “Four UAVs” obtained by the INSGA-II-MTO is larger than the INSGA-II-MTO-R. Moreover, the results show that the total number of schemes obtained by the INSGA-II-MTO is always more than the INSGA-II-MTO-R in all three scenarios. Therefore, the proposed population initialization method can assist the proposed algorithm in finding more different schemes.

Based on the above analyses, it can be inferred that the proposed population initialization method is effective and can help the proposed algorithm find more diverse and high-quality schemes.

(2)

The effectiveness of the multi-task optimization

To verify the effectiveness of the multi-task optimization, the INSGA-II-MTO without assistant task (called INSGA-II-MTO-I) and the INSGA-II-MTO are used to solve three multi-objective MSR problems.

Table 4. HV results of the INSGA-II-MTO and INSGA-II-MTO-I.

	Test Scenario 1	Test Scenario 2	Test Scenario 3
INSGA-II-MTO	0.1929 (2.46 × 10−4)	0.2846 (1.1 × 10−2)	0.2567 (1.2 × 10−2)
INSGA-II-MTO-I	0.1926 (2.8 × 10−4) +	0.2593 (1.2 × 10−2) +	0.2272 (1.8 × 10−2) +

lists the HV values of two algorithms in three scenarios. It can be seen from Table 4 that the performance of the INSGA-II-MTO-I and the INSGA-II-MTO is similar in scenario 1. The main reason may be that scenario 1 is relatively simple, and the multi-task cannot play an important role. However, Table 4 shows that the INSGA-II-MTO outperforms the INSGA-II-MTO-I in the remaining two scenarios. Compared with the first scenario, these two cases are more complex. Therefore, it can be concluded that multi-task optimization can help the proposed algorithm improve its performance in solving complex scenarios. This may mainly be because the computational resources of the INSGA-II-MTO-I are evenly distributed in a huge search space, which will lead to a large amount of wasted computational resources. However, the INSGA-II-MTO can allocate more resources in a specific search space due to the existence of an assistant task, which can contribute greatly to the performance.

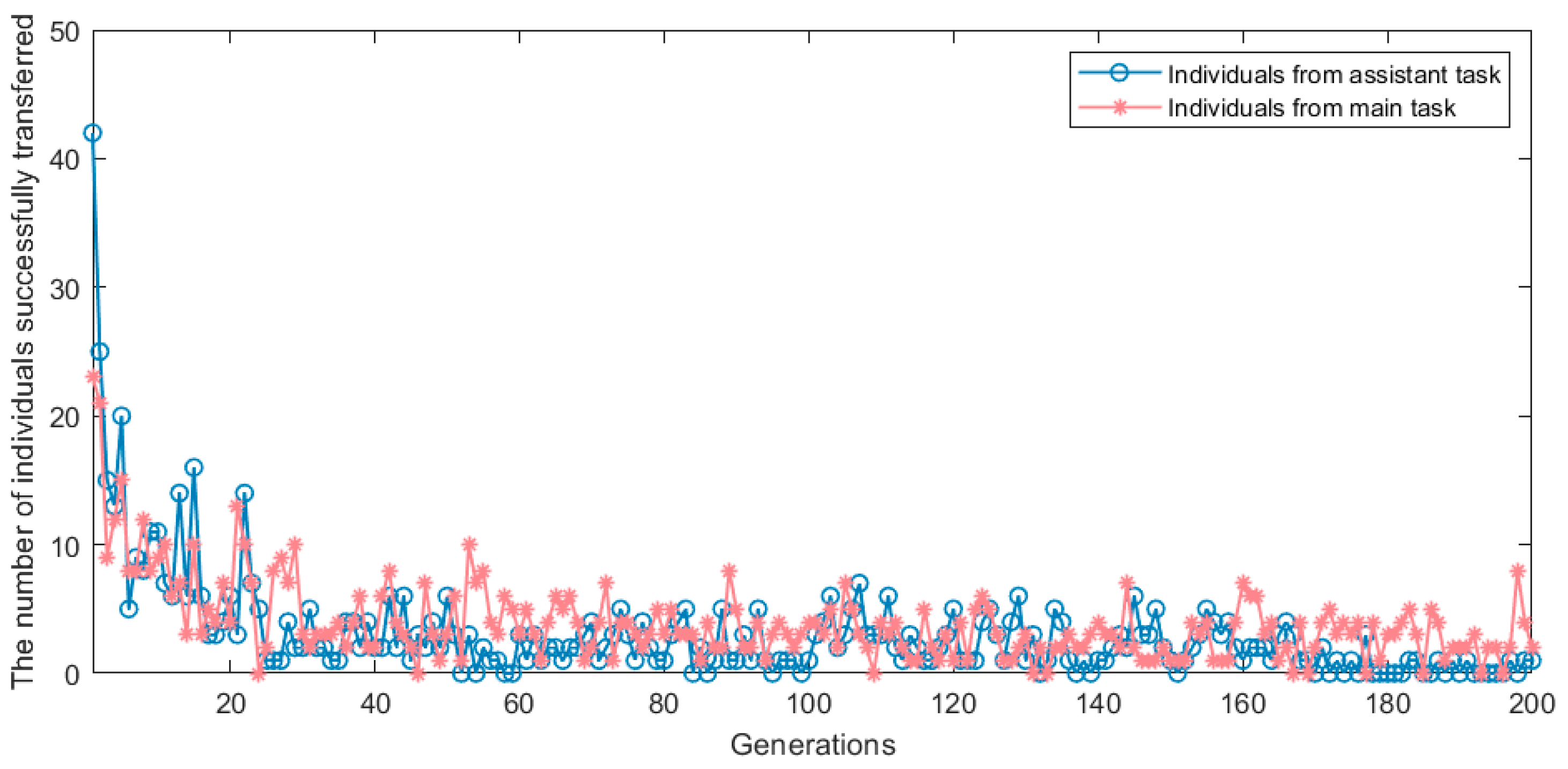
To further test the effectiveness of the multi-task optimization method, the proposed algorithm is used to solve the MSR task in scenario 2. Moreover, the successfully transferred individuals in each generation between two tasks are illustrated in Figure 11. “Individuals from assistant task” represents the number of individuals successfully transferred from the assistant task to the main task. “Individuals from main task” means the number of individuals successfully transferred from the main task to the assistant task. It can be observed from Figure 11 that the knowledge can be effectively transferred between the two tasks. This means that the multi-task optimization method can greatly improve search efficiency. Figure 11 also shows that the assistant task can provide a lot of useful knowledge to the main task in the early and middle stages. Especially, the number of individuals from the assistant task is extraordinary more than 4/5 at the first generation. As the assistant task may contain more useful knowledge when compared with the main task in the beginning, this result is as expected. In addition, the problem that the genetic algorithm is easy to fall into the local optimization can be alleviated by the multi-task optimization in the subsequent generations.

Based on the above experimental analyses, for complex multi-objective MSR problems, multi-task optimization is an effective approach for improving the performance of the proposed algorithm.

6.3. Diversity of the Solutions

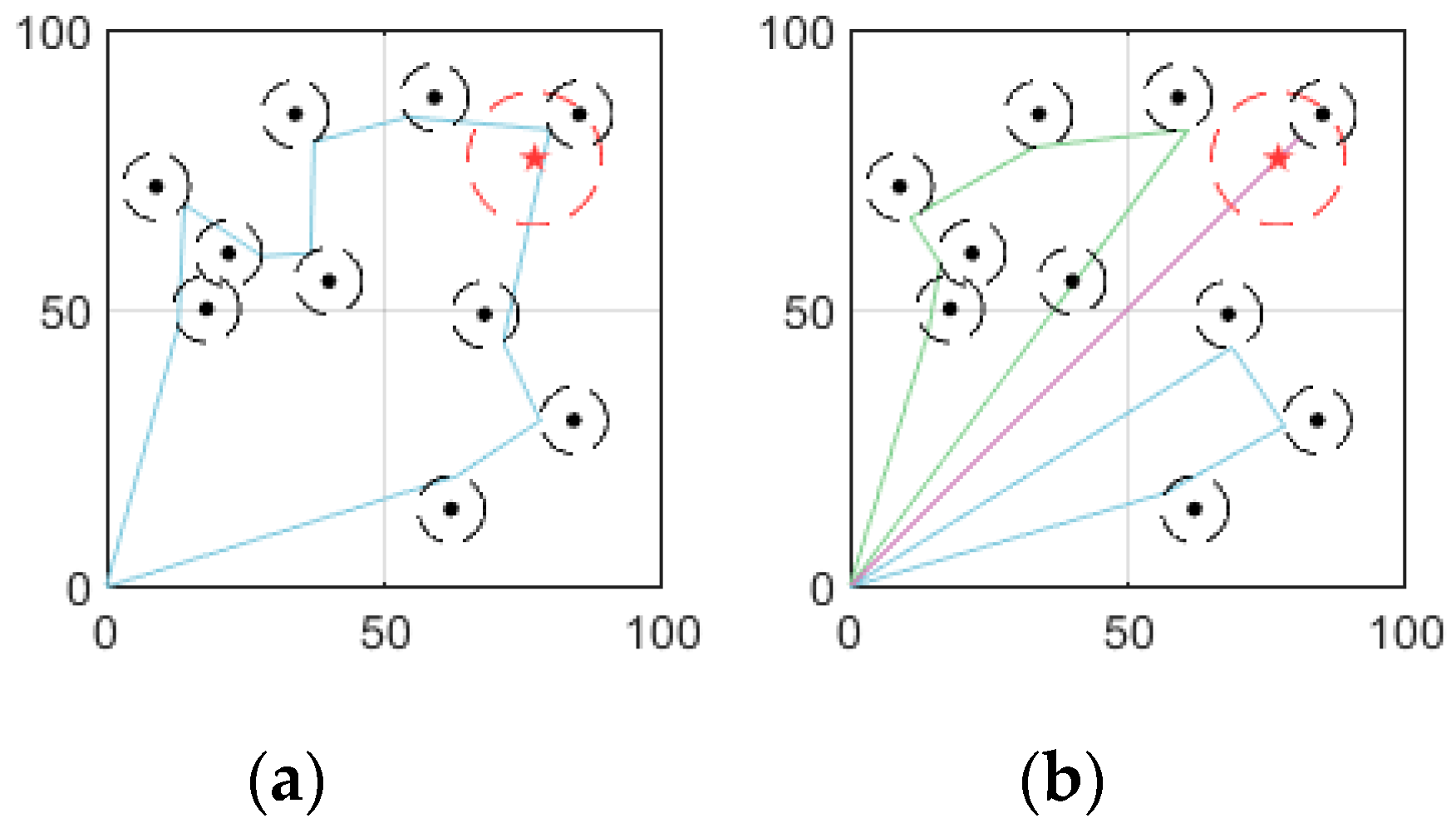
To demonstrate the performance of the INSGA-II-MTO, scenario 2 is used in this experiment. Moreover, two typical solutions are illustrated in Figure 12 and their objective values are shown in

Table 5. The typical objective values.

	Objective 1	Objective 2	Objective 3
(a)	297.876	297.876	138.7735
(b)	636.1917	228.4096	114.2048

.

From Table 5 and Figure 12, we can see that the total path length in the first row of Table 5 is the shortest. However, the total completion time of all tasks and urgent tasks is the longest. Moreover, Figure 12a shows that the MSR station dispatched one UAV to complete the tasks. Clearly, using one UAV can save cost, but it will reduce the efficiency of MSR. It is suitable for situations where decision-makers pursue low cost. It can be observed from Figure 12b that the MSR station dispatches three UAVs to visit vessels. Moreover, Table 5 indicates that the total path length of the second scheme is the longest, while the completion time is the shortest and the vessels in the risk region can be visited in the shortest possible time. This scheme pays more attention to the urgency of the tasks. Therefore, the MSR cost and the MSR efficiency are conflicting. Decision-makers can flexibly select different schemes to adapt to different MSR environments based on the obtained solution set.

7. Conclusions

Severe weather is the main factor leading to marine accidents, thus solving MSR problems under unpredictable weather conditions is an urgent problem. Using UAVs is an effective method to complete MSR tasks facing a harsh environment. In the present study, an improved NSGA-II based on multi-task optimization (INSGA-II-MTO) is proposed to solve the multi-objective MSR problem under severe weather. A main task aims to solve the original MSR problem, and an assistant task aims to solve the simplified MSR problem. Moreover, the knowledge can be transferred between the two tasks. Additionally, a novel population initialization method is proposed to improve population diversity. The experimental results show that the INSGA-II-MTO obtained maximum values in terms of HV and NR in three testing cases, that is, the proposed algorithm outperforms the other two competitors. In addition, the effectiveness of the multi-task optimization and the population initialization method is verified. Namely, the INSGA-II-MTO can find shorter total paths and handle the most urgent task in the shortest possible time. Therefore, the proposed algorithm is a competitive method to solve complex MSR problems under severe weather for providing decision-makers with effective MSR schemes when a marine accident occurs.

For future work, the energy consumption constraints of UAVs and the time window of tasks will be considered in the MSR tasks. Further, UAV-Ship collaborative systems can also be studied for the MSR tasks. Moreover, it is promising to extend this work to other application scenarios such as data collection.