A Numerical Simulation of Internal Wave Propagation on a Continental Slope and Its Influence on Sediment Transport
Abstract
1. Introduction
2. Numerical Model of Internal Waves
2.1. Governing Equations
2.2. Turbulence Model
2.2.1. Vertical Eddy Viscosity Coefficient
2.2.2. Horizontal Eddy Viscosity Coefficient
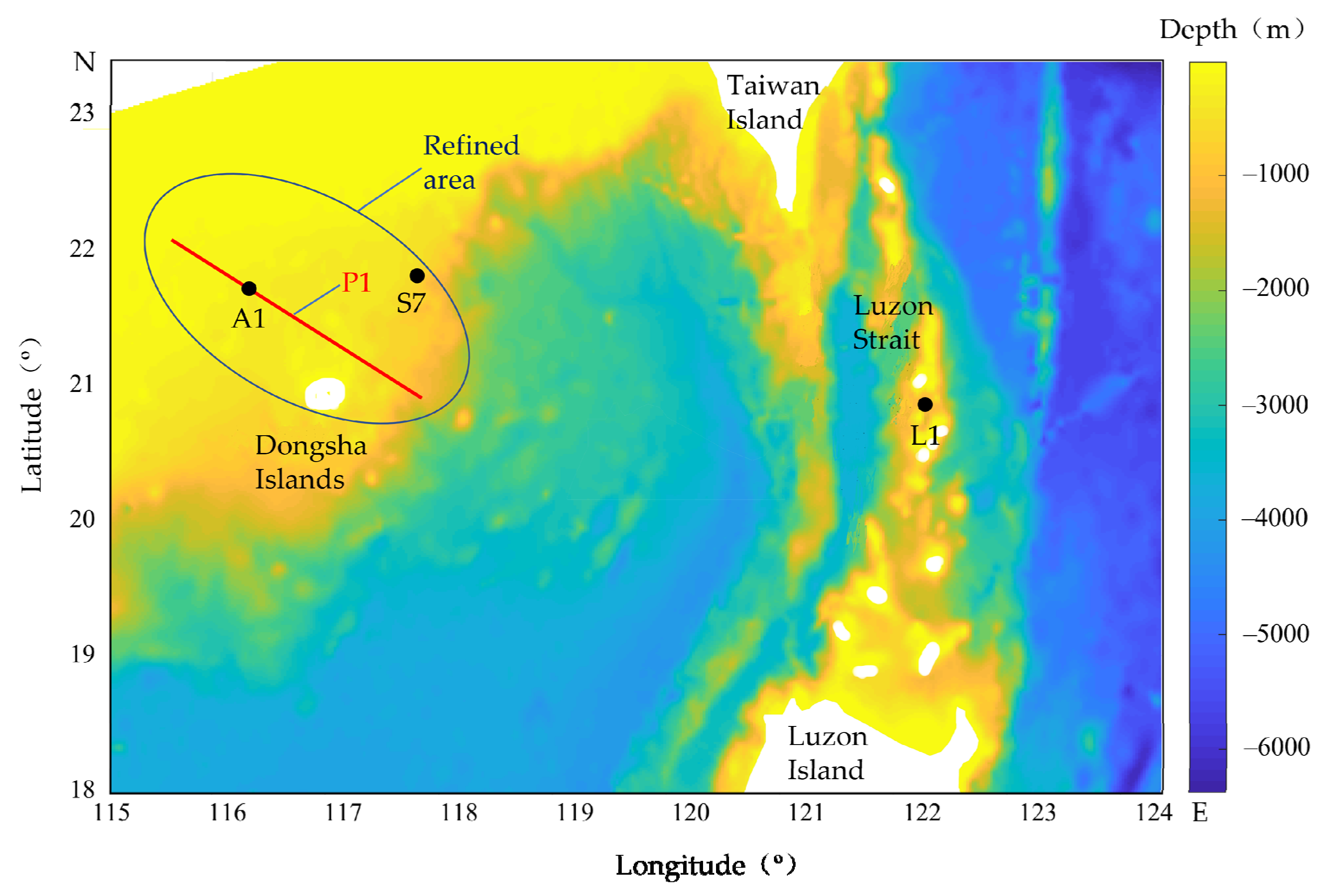
2.3. Model Setup
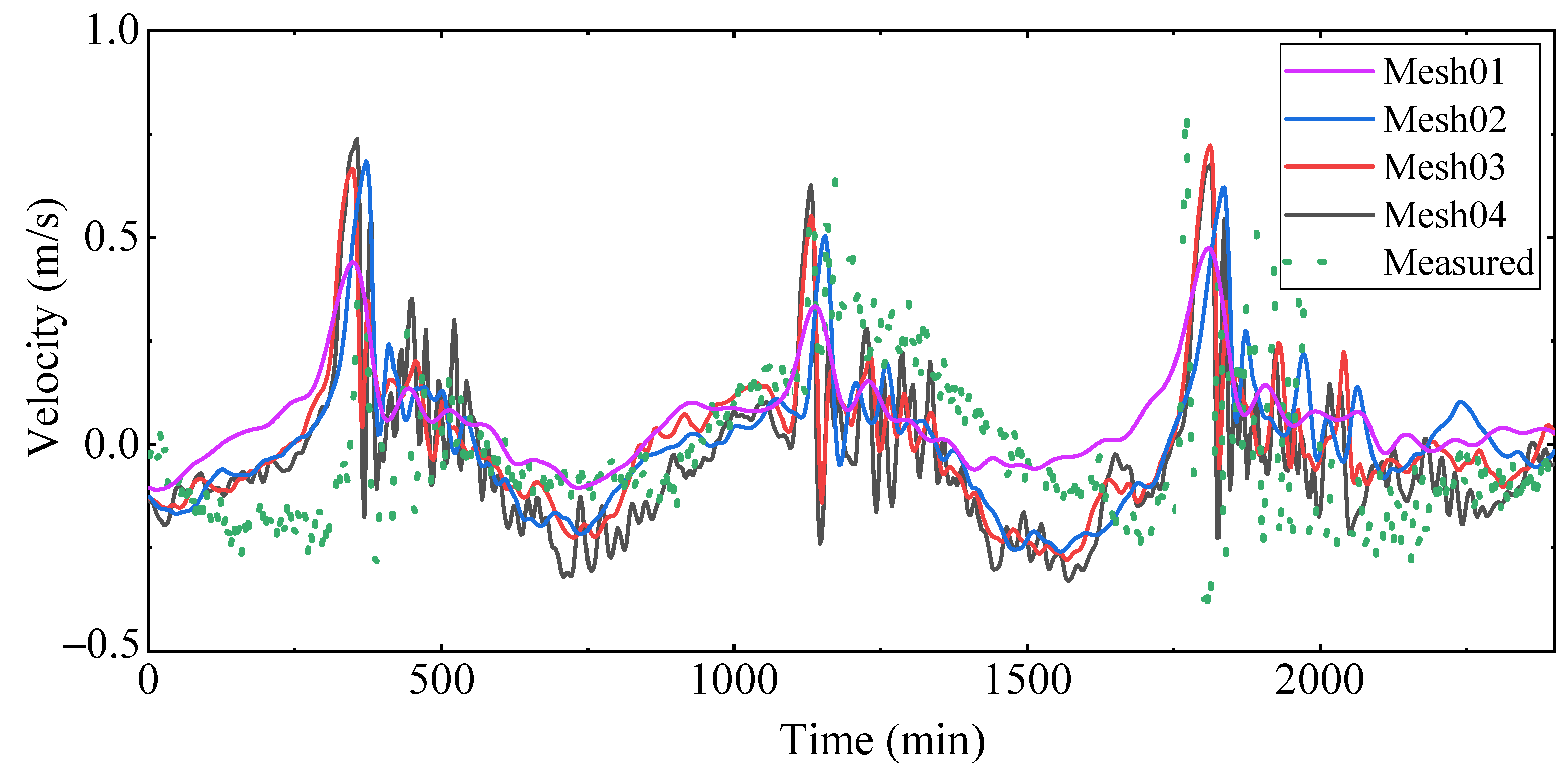
2.4. Mesh Sensitivity Analysis
3. Model Validation
3.1. Barotropic Tide Simulation
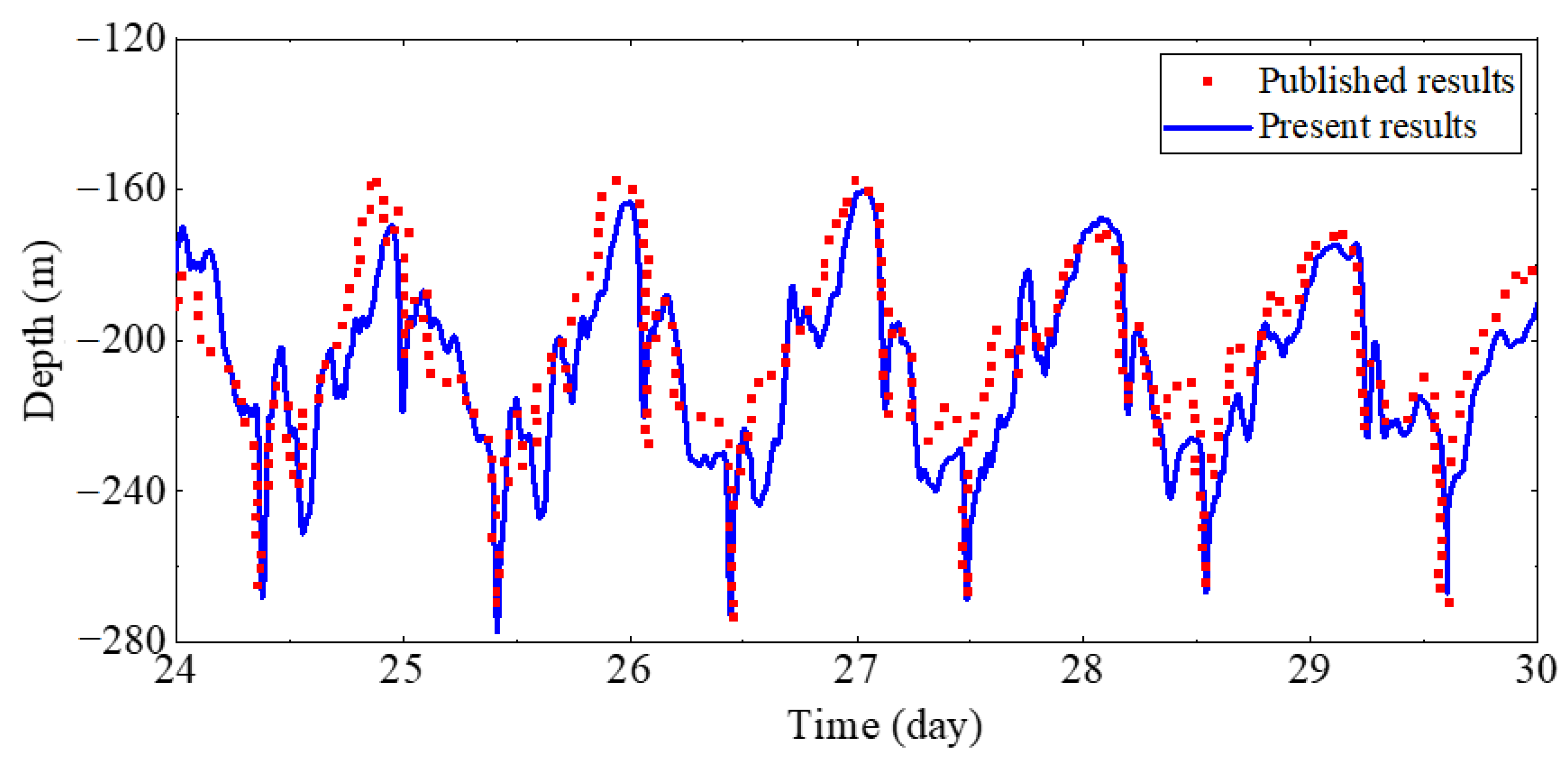
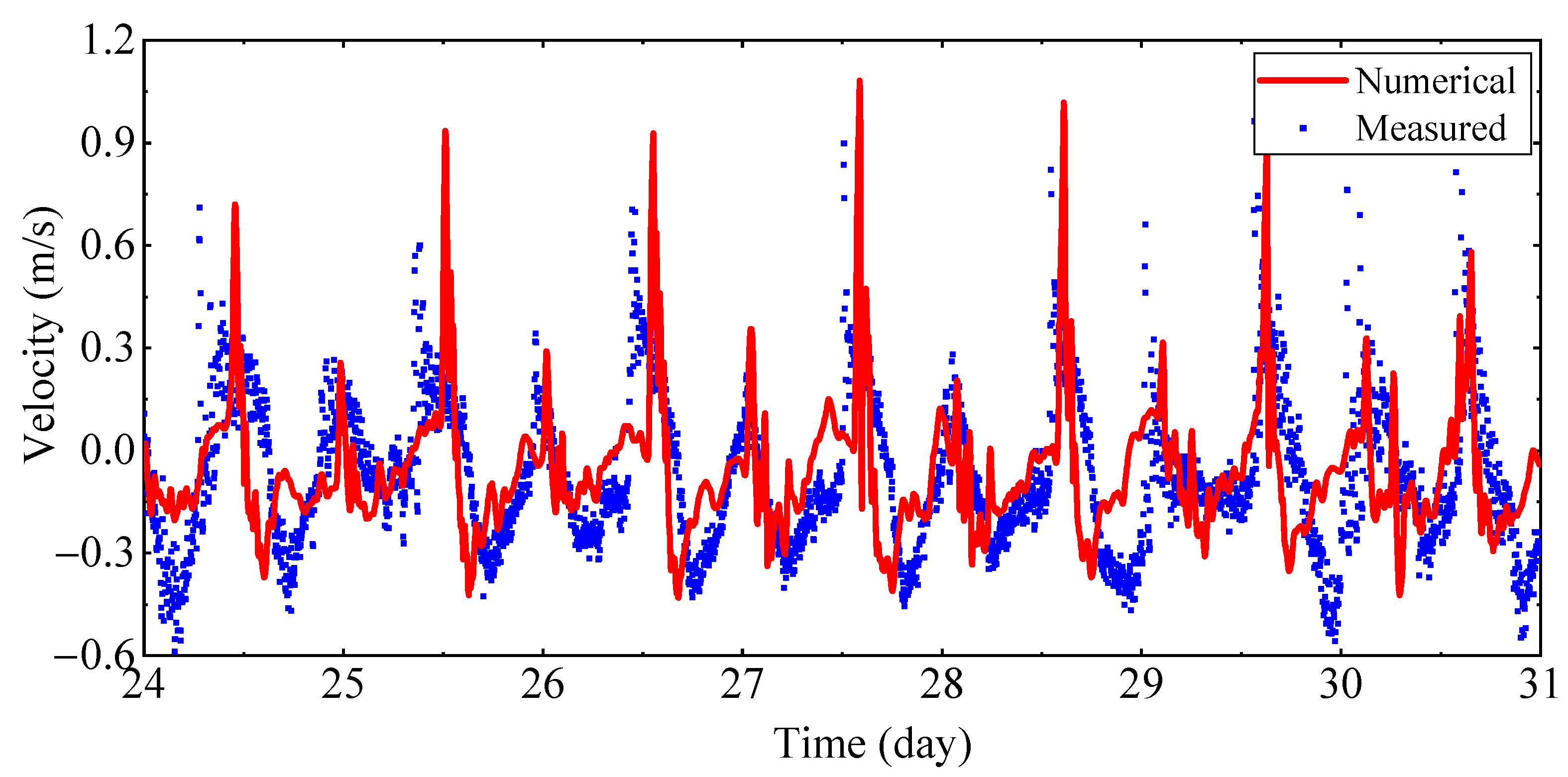
3.2. Internal Wave Simulation
4. Flow Characteristics of Internal Waves on the Continental Slope
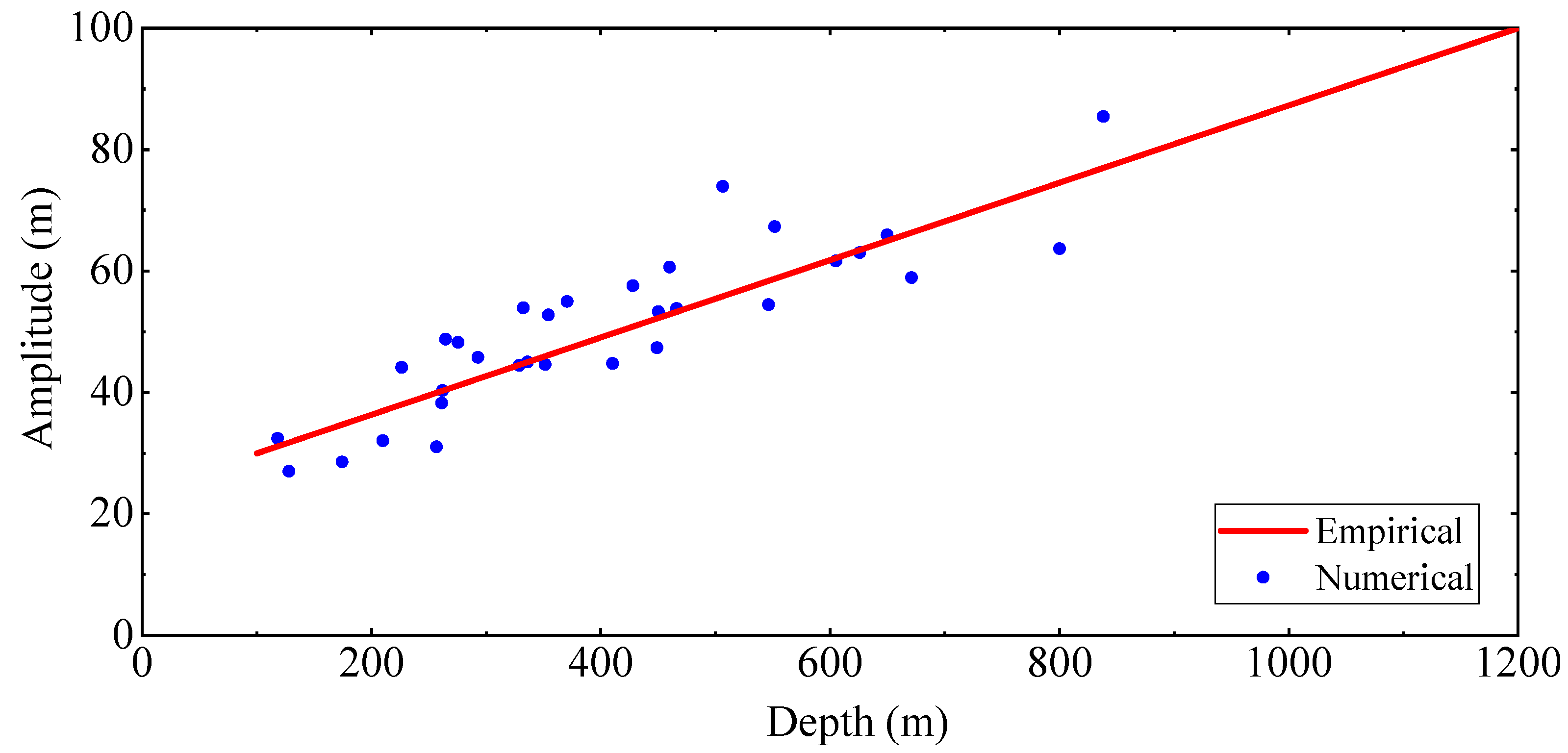
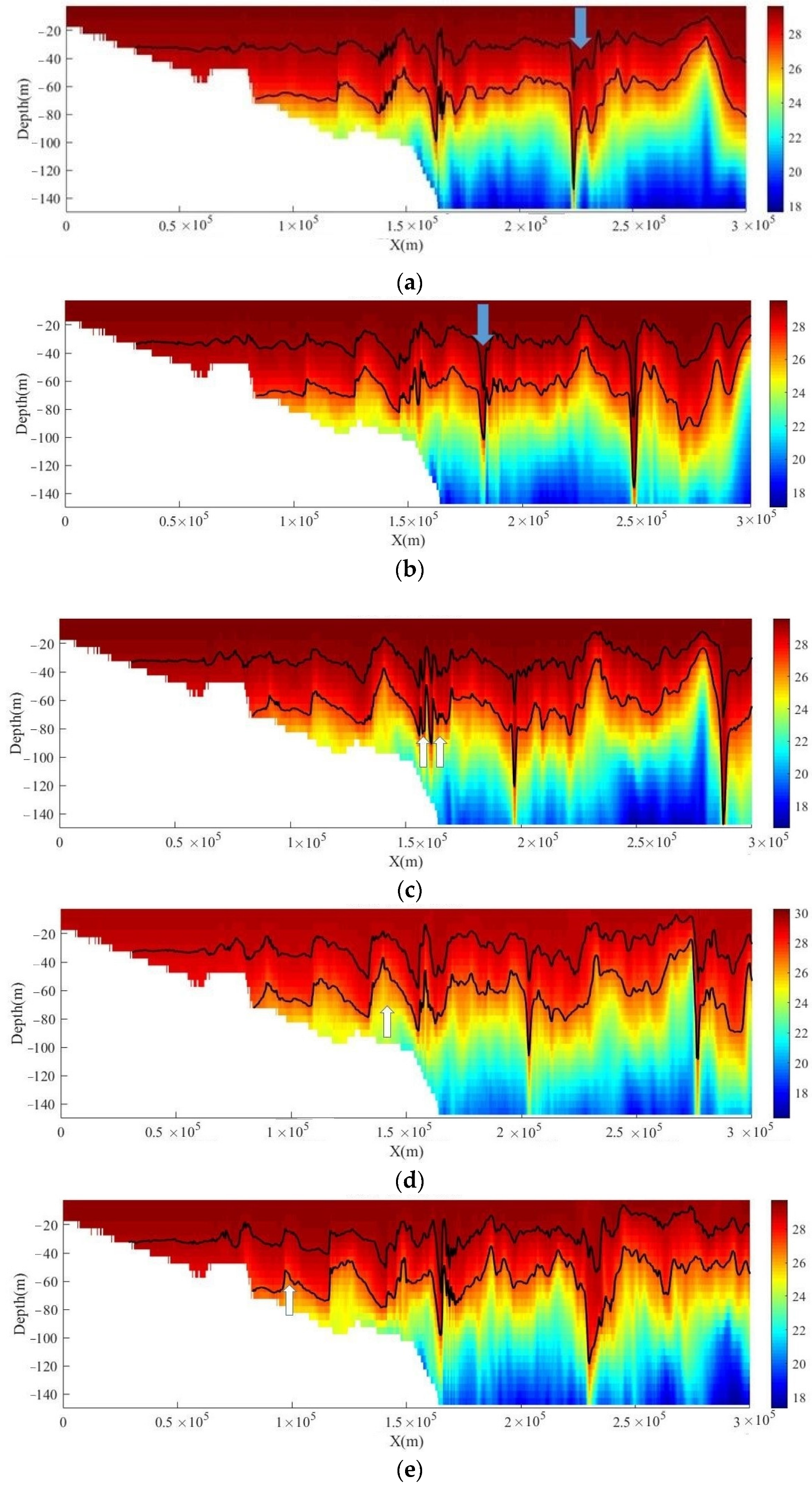
4.1. Polarity Conversion of Internal Waves Due to Shoaling
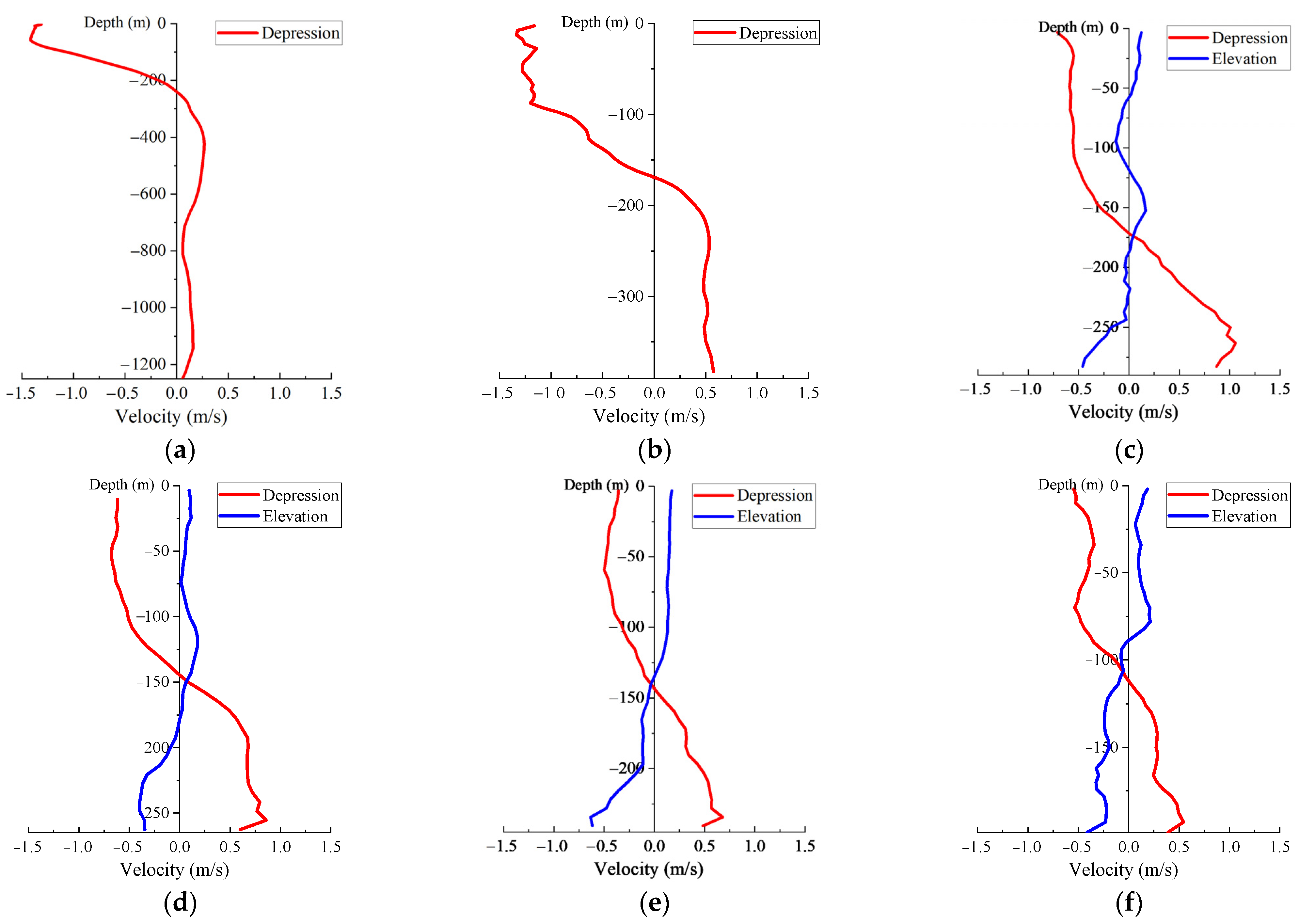
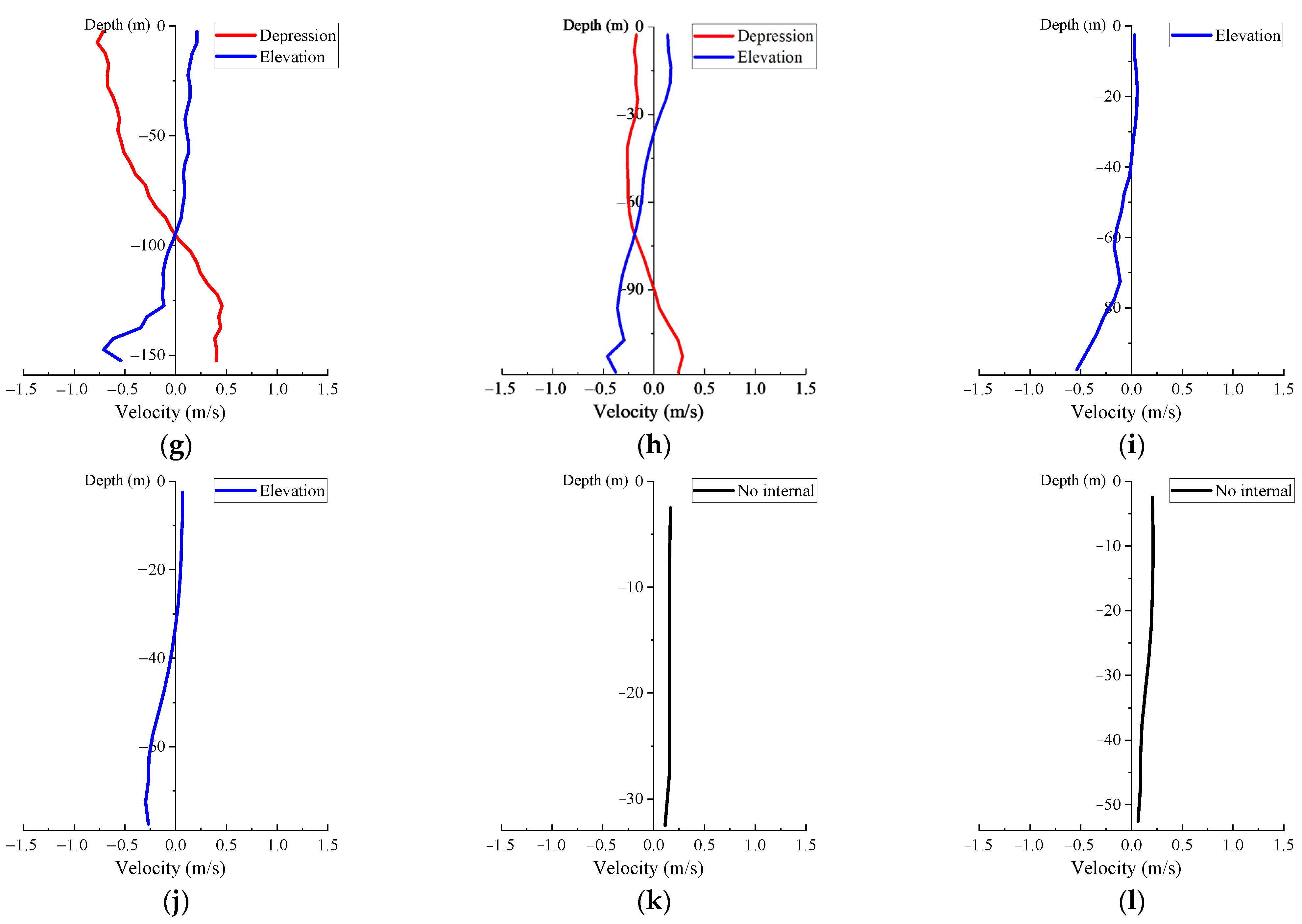
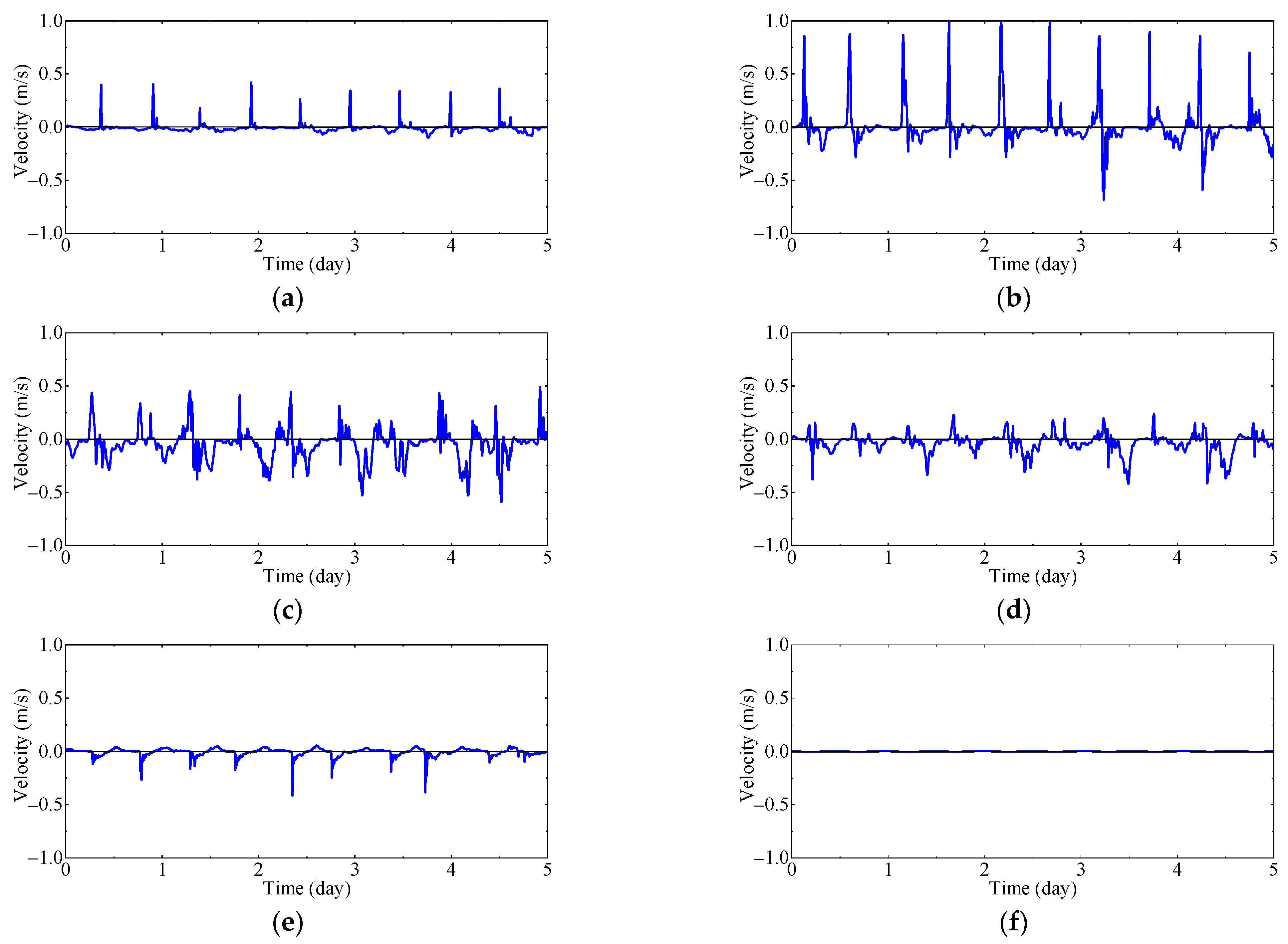
4.2. Current Induced by the Internal Waves
5. Sediment Transport on the Continental Slope Induced by Internal Waves
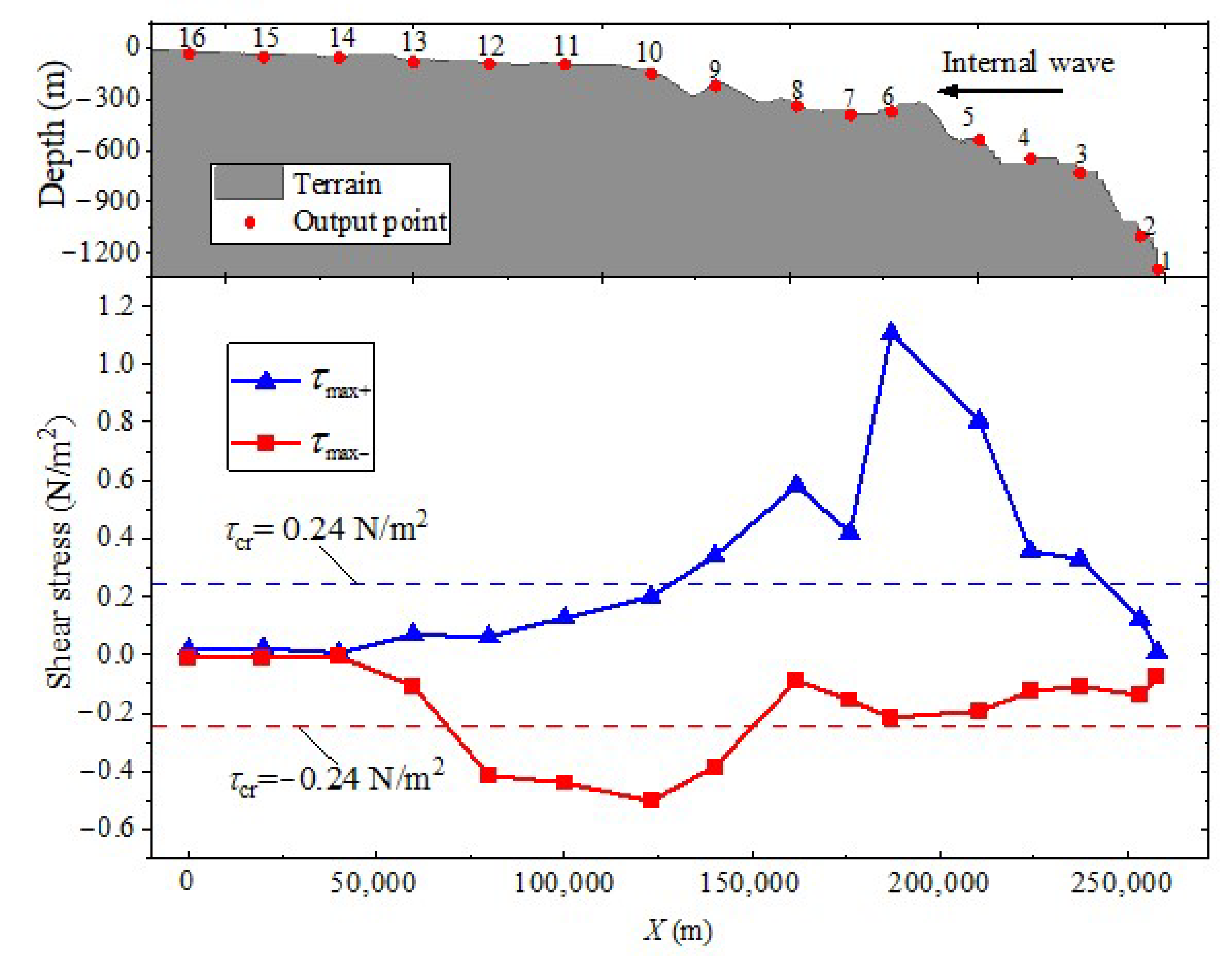
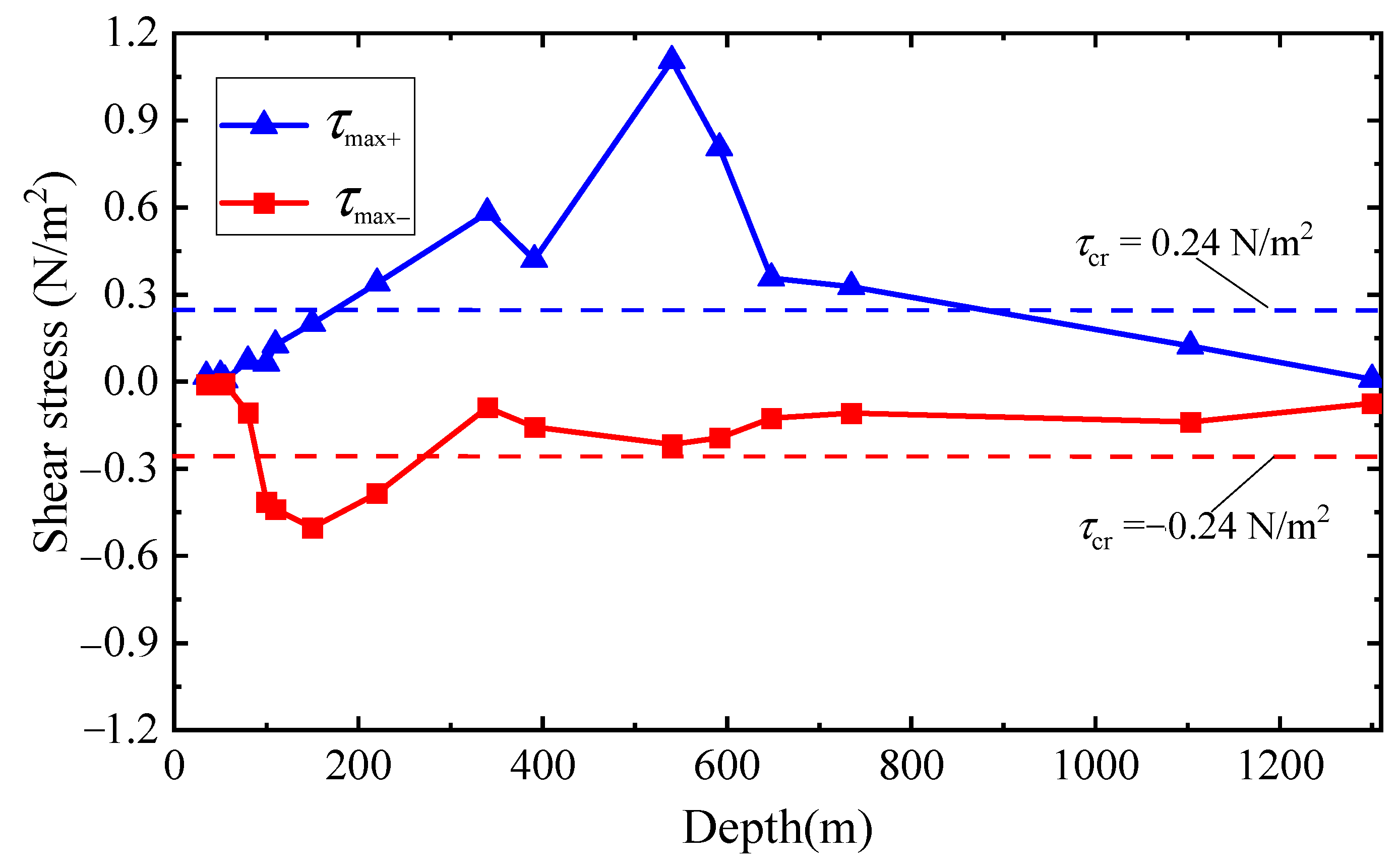
5.1. Bed Shear Stress
5.2. Bedload Transport
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lamb, K.G. Internal Wave Breaking and Dissipation Mechanisms on the Continental Slope/Shelf. Annul. Rev. Fluid Mech. 2014, 46, 231–254. [Google Scholar] [CrossRef]
- Lou, M.; Yu, C.; Chen, P. Dynamic Response of a Riser Under Excitation of Internal Waves. J. Ocean Univ. China (Ocean. Coast. Sea Res. 2015, 14, 982–988. [Google Scholar] [CrossRef]
- Zhang, Y.; Zang, Z.; Yi, Q.; Liang, D.; Liu, Z.; Li, G. Simulation of migration of sand waves under current induced by internal waves. In Proceedings of the 10th International Conference on Asian and Pacific Coasts (APAC 2019), Hanoi, Vietnam, 25–28 September 2019; pp. 457–462. [Google Scholar]
- Zhang, H.; Ma, X.; Zhuang, L.; Yan, J. Sand waves near the shelf break of the northern South China Sea: Morphology and recent mobility. Geo-Mar. Lett. 2019, 39, 19–36. [Google Scholar] [CrossRef]
- Chen, T. Numerical Investigation of the Internal Solitary Wave in the Northeastern South China Sea Based on Nonhydrostatic Model. Doctoral Thesis, Tianjin University, Tianjin, China, 2012. [Google Scholar]
- Shaw, P.T.; Kodong, S.; Chao, S.Y. Internal solitary waves induced by flow over a ridge: With applications to the northern South China Sea. J. Geophys. Res. Oceans 2009, 114, C02019–C02029. [Google Scholar] [CrossRef]
- Warn-Varnas, A.; Hawkins, J.; Lamb, K.G.; Piacsek, S.; Burgos, G. Solitary wave generation dynamics at Luzon strait. Ocean Model. 2010, 31, 9–27. [Google Scholar] [CrossRef]
- Qiang, L.; Farmer, D.M. The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea. J Phys. Oceanogr. 2011, 41, 1345–1363. [Google Scholar]
- Fang, W.; Chen, R.; Mao, Q. Abrupt strong currents over continental slope of Northern South China Sea. Tropic. Oceanol. 2000, 1, 70–75. [Google Scholar]
- Reeder, D.B.; Ma, B.B.; Yang, Y.J. Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves. Mar. Geol. 2011, 279, 12–18. [Google Scholar] [CrossRef]
- Hsu, M.K.; Liu, A.K. Nonlinear internal waves in the South China Sea. Can. J. Remote Sens. 2000, 26, 72–81. [Google Scholar] [CrossRef]
- Zhao, Z.; Klemas, V.; Zheng, Q.; Yan, X.H. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea. Geophys. Res. Lett. 2004, 31, 14. [Google Scholar] [CrossRef]
- Liu, A.K.; Chang, Y.S.; Hsu, M.K.; Liang, N.K. Evolution of nonlinear internal waves in the eastern South China Seas. J. Geophys. Res. Oceans 1998, 103, 7995–8008. [Google Scholar] [CrossRef]
- Orr, M.H.; Mignerey, P.C. Nonlinear internal waves in the South China Sea: Observation of the conversion of depression internal waves to elevation internal waves. J. Geophys. Res. Oceans 2003, 108, 1–16. [Google Scholar] [CrossRef]
- Xu, S.; Xu, H.; Geng, M.; Guan, Y. Study on the form of internal solitary wave in Dongsha area of the South China Sea. J. Mar. Sci. 2016, 34, 1–9. [Google Scholar]
- Carr, M.; Stastna, M.; Davies, P.A. Internal solitary wave-induced flow over a corrugated bed. Ocean Dynam. 2010, 60, 1007–1025. [Google Scholar] [CrossRef]
- Faraci, C.; Musumeci, R.E.; Marino, M.; Ruggeri, A.; Carlo, L.; Jensen, B.; Foti, E.; Barbaro, G.; Elsaßer, B. Wave- and current dominated combined orthogonal flows over fixed rough beds. Cont. Shelf Res. 2021, 220, 104403. [Google Scholar] [CrossRef]
- Olsthoorn, J.; Stastna, M. Numerical investigation of internal wave-induced sediment motion: Resuspension versus entrainment. Geophys. Res. Lett. 2014, 41, 2876–2882. [Google Scholar] [CrossRef]
- Aghsaee, P.; Boegman, L. Experimental investigation of sediment resuspension beneath internal solitary waves of depression. J. Geophys. Res. Oceans 2015, 120, 3301–3314. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, S.; Guo, X.; Yu, L.; Jia, Y. Experimental investigation of sediment dynamics in response to breaking high-frequency internal solitary wave packets over a steep slope. J. Mar. Syst. 2019, 199, 103191. [Google Scholar] [CrossRef]
- Jia, Y.; Tian, Z.; Shi, X.; Liu, J.P.; Chen, J.; Liu, X.; Ye, R.; Ren, Z.; Tian, J. Deep-sea sediment resuspension by internal solitary waves in the northern South China Sea. Sci. Rep. 2019, 9, 12137. [Google Scholar] [CrossRef]
- Afzal, M.S.; Holmedal, L.E.; Myrhaug, D. Three-dimensional streaming in the seabed boundary layer beneath propagating waves with an angle of attack on the current. J. Geophys. Res. Oceans 2015, 120, 4370–4391. [Google Scholar] [CrossRef]
- Marino, M.; Faraci, C.; Musumeci, R.E. Shoaling Waves Interacting with an Orthogonal Current. J. Mar. Sci. Eng. 2020, 8, 281. [Google Scholar] [CrossRef]
- la Forgia, G.; Tokyay, T.; Adduce, C.; Constantinescu, G. Bed shear stress and sediment entrainment potential for breaking of internal solitary waves. Adv. Water Resour. 2020, 135, 103475. [Google Scholar] [CrossRef]
- Fringer, O.B.; Gerritsen, M.; Street, R.L. An unstructured-grid, finite-volume, nonhydrostatic, parallel coastal ocean simulator. Ocean Model. 2006, 14, 139–173. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Galperin, B.; Kantha, L.H.; Hassid, S. A quasi-equilibrium turbulent energy model for geophysical flows. J. Atmos. Sci. 1988, 45, 55–62. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. Etopo1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; National Geophysical Data Center, NOAA: Boulder, CO, USA, 2008. [Google Scholar]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Zhang, Z.; Fringer, O.B.; Ramp, S.R. Three-dimensional, nonhydrostatic numerical simulation of nonlinear internal wave generation and propagation in the South China Sea. J. Geophys. Res. Oceans 2011, 116, 1–26. [Google Scholar] [CrossRef]
- Ning, J.; Wang, J.; Zhang, M.; Cui, H.; Lu, K. Amplitude Inversion Model and Application of Internal Solitary Waves of the Northern South China Sea Based on Optical Remote-sensing Images. Acta Photonica Sinica 2019, 48, 1228003. [Google Scholar] [CrossRef]
- Afzal, M.S.; Kumar, L. Propagation of waves over a rugged topography. J. Ocean Eng. Sci. 2022, 7, 14–28. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Whitehouse, R.J.S.W. Threshold of sediment motion in coastal environments. In Pacific Coasts and Ports'97. Proceedings; University of Canterbury: Christchurch, New Zealand, 1997; Volume 1, pp. 149–154. [Google Scholar]
- Soulsby, R. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford: London, UK, 1997. [Google Scholar]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In IAHSR 2nd Meeting, Stockholm, Appendix 2; IAHR: Stokholm, Sweeden, 1948; pp. 39–62. [Google Scholar]
- Kumar, L.; Afzal, M.S.; Afzal, M.M. Mapping shoreline change using machine learning: A case study from the eastern Indian coast. Acta Geophys. 2020, 68, 1127–1143. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, Z.; Zhang, Y.; Chen, T.; Xie, B.; Zou, X.; Li, Z. A Numerical Simulation of Internal Wave Propagation on a Continental Slope and Its Influence on Sediment Transport. J. Mar. Sci. Eng. 2023, 11, 517. https://doi.org/10.3390/jmse11030517
Zang Z, Zhang Y, Chen T, Xie B, Zou X, Li Z. A Numerical Simulation of Internal Wave Propagation on a Continental Slope and Its Influence on Sediment Transport. Journal of Marine Science and Engineering. 2023; 11(3):517. https://doi.org/10.3390/jmse11030517
Chicago/Turabian StyleZang, Zhipeng, Yiping Zhang, Tongqing Chen, Botao Xie, Xing Zou, and Zhichuan Li. 2023. "A Numerical Simulation of Internal Wave Propagation on a Continental Slope and Its Influence on Sediment Transport" Journal of Marine Science and Engineering 11, no. 3: 517. https://doi.org/10.3390/jmse11030517
APA StyleZang, Z., Zhang, Y., Chen, T., Xie, B., Zou, X., & Li, Z. (2023). A Numerical Simulation of Internal Wave Propagation on a Continental Slope and Its Influence on Sediment Transport. Journal of Marine Science and Engineering, 11(3), 517. https://doi.org/10.3390/jmse11030517






