Abstract
Recently, the repair and maintenance of structures has been necessary to prevent these structures’ sudden collapse and to prevent human and financial damage. A natural factor in marine environments that destroys structures and reduces their life is the presence of chloride ions. So regular health monitoring of concrete coastal buildings for on-time repair is essential. This study investigates the performance of the power spectral density (PSD) method as a non-destructive damage-detection method to monitor the location and amount of damage caused by chloride ions during a structure’s life using different approaches according to life-cycle assessment (LCA) and life-cycle cost assessment (LCCA). In this regard, chloride corrosion damage dependent on zone distance from seawater was first calculated to obtain the service life of each part of a coastal concrete bridge according to the conventional method. Based on rebar corrosion each year, the next stage forecasted the bridge’s concrete deterioration. The PSD method monitored the annual loss of reinforcement cross-sectional area, changes in dynamic characteristics such as stiffness and mass, and the bridge structure’s life using sensitivity equations and the linear-least-squares algorithm. Finally, according to the location and quality of damage in each year of bridge life until the end of life, LCC and maintenance and repair costs of the PSD method were compared with the conventional method. The results showed that this strategy was very effective at lowering and optimizing the costs of maintenance and repair caused by chloride corrosion.
1. Introduction
For many years, discussion about costs during the lifetime of structures has been one of the most important discussions among researchers and engineers. In general, the costs of any civil structure activity include the costs of design and construction, repair and maintenance, and finally the destruction of the structure at the end of its life. In particular, for bridges, the costs associated with maintenance and repair are an important portion of the costs resulting from their life cycle. Many factors are effective in reducing the maintenance costs of structures over time. A factor that can reduce the costs of repair and maintenance in structures such as bridges is accurate health monitoring and damage-detection methods to predict the time and location of damage to structural elements during the structure’s life cycle.
Damage-identification methods in structures are carried out using destructive or non-destructive techniques. Destructive approaches depend on models which often include the removal of structural samples to assess damage. On the other hand, non-destructive techniques are independent models that may identify damage with a numerical software model without causing harm to the structure []. Non-destructive damage-detection techniques may be monitored utilizing technologies based on signals. The employment of modern, high-tech computers and sensors has increased the popularity of signal-based methodologies in structural health monitoring []. There are many different signal-based techniques, some of which include the time domain [,], the frequency domain [,], and the time–frequency domain [,]. These methodologies are used in order to examine the dynamic properties of structures []. Stochastic processes are standard in time-domain methodologies []. Frequency-domain techniques may create many responses and data points by configuring model-update equations []. Mode shape [,], modal curvatures [,,], natural frequency [,], modal strain energy [,], the frequency response function [,], and the power spectral density function [,,] are some methods of dynamic frequency-domain approaches. Lastly, required data and information in the time–frequency domain are obtained by changing the recorded signal frequency over time []. Empirical mode decomposition (EMD) [], the wavelet transform (WT) [], and blind source separation (BSS) [] are some examples of time–frequency approaches that may be utilized for modal identification.
As a frequency-domain approach, power spectral density (PSD) employs the frequency response of a periodic or random signal, which defines the mean power distribution. In order to construct a second-order transfer function, this technique uses a sensitive nonlinear function of structural parameters []. In recent years, researchers in different fields have investigated the reliability of the PSD method for identifying various damage types. Bayati et al. [] tested a novel technique based on the PSD function and the least-squares distance approach to identify deterioration in concrete bridge piers. Gunawan [] assessed the reliability of the PSD method for seven 1 kg lumped masses connected by eight similar linear elastic springs. Hadizadeh-Bazaz et al. [] compared the performance of power spectral density (PSD) with the frequency response function for a steel bridge structure.
On the other hand, investigating the performance of non-destructive damage-detection methods for life-cycle assessment (LCA) and life-cycle cost analysis (LCCA) is necessary for finding suitable and affordable methods of repair and maintenance for essential and costly structures. Life-cycle cost analysis (LCCA) can obtain costs during a structure’s life. This approach can reduce and optimize total costs at each level of the structure’s life cycle, including initial cost, maintenance cost, repair and replacement, personnel casualties or loss of goods during operation, road-use cost, and indirect loss of socio-economic benefits [,,]. Studies have carried out LCCA for structures during their life cycles. Frangopol et al. [], using analysis, prediction, optimization, and decision-making, investigated a bridge’s life-cycle performance and cost assessment. Goh et al. [] developed an integration model to leverage the fuzzy analytical hierarchy process (fuzzy AHP) and life-cycle cost analysis (LCCA) in evaluating highway infrastructure investments using their proposed model which assessed the quantitative factors of cost components. Heidari et al. [] developed a probabilistic and uncertain model to evaluate the life-cycle costs and environmental effects of pavements by considering managerial flexibilities.
Researchers have previously studied and assessed LCCA using non-destructive damage-detection methods for health monitoring in different structures [,,]. Some studies have investigated LCC through the PSD method as a non-destructive damage-detection technique. Micheli et al. [] evaluated a performance-based design with life-cycle costs for damping systems built into a 39-storey structure in a time-domain frequency technique for wind load and a multivariate stochastic process to optimize a damping system design under different wind conditions using the PSD method. In addition, Chu et al. [] looked at the life-cycle wind-resistant performance of a long-span suspension bridge built in the coastal region of China. They used the Bayesian spectral density approach to quantify multisource time-varying effects and uncertainties and to provide a reference for future designs of long-span bridges. Root-mean-square (RMS) tests were used to investigate responses to buffeting and were thought to be time-independent.
This research evaluated the performance of the non-destructive damage-prediction PSD method for a coastal concrete structure and, as well, the importance of using this method in LCCA to reduce overall costs of the maintenance and repair phase of the structure due to chloride ions in marine and coastal environments by a different approach during the lifetime of this structure. In this regard, LCCA of the repair and maintenance of a coastal concrete bridge in northwest Spain exposed to damage by chloride ion attack was investigated with PSD as a frequency-domain technique using sensitivity equations, and the linear least-squares methodology was monitored during its lifetime. Health monitoring of this structure was analyzed annually using a variety of approaches and also according to changes in dynamic components, including stiffness and mass of the rebars and other elements of the bridge’s structure.
2. Materials and Methods
Life-cycle analysis (LCA) is a widely used approach that has recently established a strong foothold in the international environment, and which has been standardized [,]. The LCA approach involves modeling a process, product, or service and evaluating the impact of each activity on several factors, including cost, the environment, and society as a whole, amongst other considerations [,]. Regarding durability, a life-cycle cost analysis (LCCA) can be used to determine the most cost-effective and sustainable solution []. LCCA of the repair and maintenance techniques for different structures based on a variety of structural-element damage-diagnosis and prediction methods has differing costs and performances. So, consideration of the various factors that cause damage, such as corrosion by the attack of chloride ions on the metal parts of a structure in coastal environments, can help to determine the relative cost-effectiveness of non-destructive and frequency-based methods and more traditional approaches to damage identification.
2.1. Goal and Scope Definition
This research pursues several essential goals. The first goal is to investigate the performance of a non-destructive damage-detection method in detecting the quantity, location, and amount of damage caused by chloride ion corrosion of the steel sections and the whole parts and elements of a coastal structure during its lifetime. The second goal is economic comparison of the PSD method for repair and maintenance costs and a general check of the performance of this method in LCA and LCCA along with other conventional methods in service-life predictions and identifying damage. This study aims to improve the early phases of design by providing additional information about the effects of corrosion-prevention designs on concrete buildings and structures. For this purpose, these comparisons and tests have been carried out on a coastal concrete bridge with pillars in seawater undergoing corrosion and erosion.
2.1.1. Model Description
The concrete bridge is called the Arosa bridge and is located in Galicia, Spain (see Figure 1). This bridge is 1980 m long and has 40 spans (the first and end spans are 40 m, and the other 38 intermediate spans are 50 m). This construction’s geometry and durability parameters were based on data from the literature [,,].
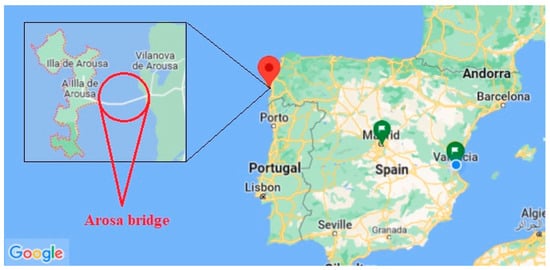
Figure 1.
The location map of the Arosa bridge in Spain.
The concrete bridge deck is a single box girder. As indicated in Figure 2, the bridge deck is 13 m wide and 2.30 m high. There are two walkways on the sides of the deck with widths of 1.5 m. The columns are 5.26 m wide and 1.80 m thick. Under normal circumstances, the bridge deck is about 12 m above sea level and 9.6 m during high tide.
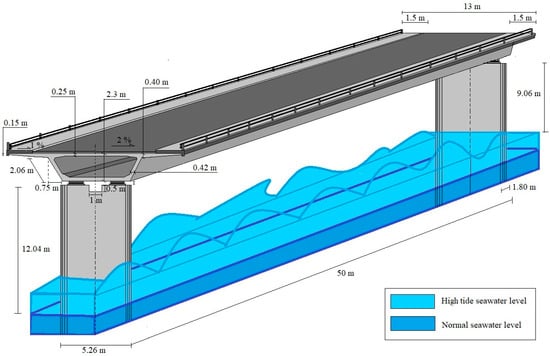
Figure 2.
Dimensions of a span of the Arosa bridge.
The concrete cover on the deck reinforcements was considered to be 35 mm, and for the columns, 45 mm. The reinforcing steel quantity is 100 kg/m3 of concrete [].
2.1.2. Functional Unit
Both the conventional and the PSD-based methods for LCCA were performed on the same functional unit consisting of construction, maintenance, and repair activities for the service life of the bridge. The dimensions of the span of the bridge include a concrete deck measuring 50 m in length and 13 m wide, with two piers standing in seawater. The material’s manufacturing techniques may vary. Table 1 shows the assumed mechanical characteristics and concrete mixtures of the bridge.

Table 1.
The Arosa structure’s concrete mixtures and mechanical parameters.
According to Table 1, the reference design has a characteristic compressive strength fcm equal to 40 MPa, and a modulus of elasticity Ec equal to 29 GPa. The concrete mix for the bridge has a water-to-cement ratio (w/c) of 0.45 and contains 485.6 kg/m3 of cement.
2.2. Service Life Prediction
The service life of the RC bridge, which is damaged by chloride corrosion to its steel reinforcements, was analyzed over the structure’s lifetime using damage detection and prediction techniques. The initial step was to determine the steel components’ service life using Fick’s second chloride-diffusion equation. Then, in the second step, the existence, quantity, and location of chloride damage to the concrete caused by corrosion of the steel reinforcements were investigated using the PSD method, by measuring the frequency response function and monitoring changes in the dynamic parameters. The service life prediction description for the bridge using different methods and materials of the reinforced concrete bridge is as follows:
2.2.1. Prediction Techniques for Chloride Degradation in RC Rebars
Most steel is fragile and easily damaged by natural and manufactured factors, especially in coastal regions where chloride ions, which cause corrosion, are in high concentrations. Reinforced concrete structures, such as bridges and concrete coastal constructions, are regularly susceptible to corrosion. According to the deterioration model proposed by Tuutti [], corrosion and damage caused by chloride in the rebars of a concrete structure have certain service-life levels [].
As demonstrated in Figure 3, chloride corrosion commences in an initiation phase. There are chlorides present in the initiation phase, but they are fewer than the chloride threshold (which means there are not enough to start the corrosion process). The propagation phase of chloride ion activity comprises stages such as starting corrosion, cracking in the concrete cover, the serviceability limit state, and the final limit state [].
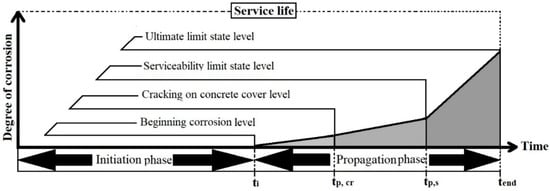
Figure 3.
The service life of rebars in an RC structure according to the model by Tuutti [].
According to the following Equation, the total time of chloride corrosion () is the service life of the bridge structure’s reinforcements, obtained by summing the initiation and propagation phases together [].
The corrosion initiation period () is the time it takes for chlorides to build up to a concentration that causes corrosion to begin on the rebars (the chloride threshold, dependent on the steel properties and, to some extent, on the concrete properties). Additionally, is the time it takes for corrosion to permeate throughout a structural part before it starts to fail substantially [].
In order to calculate the initiation time, a physical model must obtain the movement of chloride ions within the concrete cover. Existing models for predicting the time required to commence corrosion are based mainly on the assumption of a Fickian process. This assumes that the porous concrete cover is a homogeneous material in which ions move via a diffusion process in sufficient humidity. This diffusive mechanism depends on chloride between the surface and the cover of the concrete structure. This analysis will use a deterministic solution according to Fick’s equation for chloride diffusion in concrete cover. This analysis will use the equation given in Fib Bulletin 34 [], which assumes a constant, time-independent surface chloride concentration. So, the expected level of chloride in the concrete cover with depth x and at a particular time t can be written as:
where denotes the chloride content (weight percent/binder) at concrete cover depth (mm) and time (years). At the concrete cover surface, represents the surface chloride concentration (wt%/binder). The Gauss error function is denoted by . According to the Spanish concrete design code, the age factor () equals 0.5. When using as a reference point, 28 days are converted to years ( = 0.0767), and is the non-steady-state chloride-diffusion coefficient at time (mm2/years). However, the chloride transport time () can be calculated using the inverse of Equation (2), as given in Equation (3) [,].
In this case, is the chloride-diffusion coefficient, which changes with the age of the concrete (). Additionally, if and when reaches its threshold concentration , the initiation period of chloride diffusion () is calculated using Equation (4) as follows [,].
From Alonso et al. [], the chloride threshold obtained from natural experiments includes a broad range of values, from more than 0.4 to 4 percent. In this study, and also other research [,,], and according to the Spanish concrete design code [], the critical chloride concentration () must be determined by the designer in line with the structure’s unique concerns, where under normal conditions a value of 0.6% of the cement weight could be used to assess the limit state in relation to passive reinforcement corrosion. Therefore, the mean value of critical chloride concentration under normal conditions could be considered to be 0.6% of the cement weight. The initiation time is said to be reached when the chloride concentration at the rebars reaches the critical chloride threshold . This means that corrosion and damage to the rebars begins at this time. On the other hand, if it is less than this value, damage to the reinforcements has not begun [].
The propagation chloride-corrosion phase (), which begins when chloride ions on the surface of the inner rebars start to erode steel reinforcements, starts after the chloride-diffusion initiation stage. Over time, chloride corrosion reduces the steel bars’ stiffness and cross-sectional areas. The following calculation is provided to determine this time according to the Spanish concrete design code []:
In Equation (5), is the propagation time in years. Additionally, is the thickness of the concrete cover, is the diameter of the reinforcement, and is the corrosion rate. According to the Spanish Ministry of Public Works [], durability parameters depend on the elements’ distance to the seawater for the Arosa bridge, which can be obtained as follows in Table 2.

Table 2.
Durability parameters for the Arosa bridge.
Damage over time caused by corrosion can be predicted as a percentage using the following formula, which considers the initiation and propagation levels for chloride corrosion of the reinforcements of an RC marine or coastal construction.
In Equation (6), represents the percentage of reinforcements damaged by chloride corrosion for each year () that has passed from the beginning of the propagation .
Different scenarios and marine exposure classifications, including aerial, submerged, and tidal zones, were considered to determine the percentage of damage to the RC bridge’s deck and columns. In addition, the percentage of chloride corrosion damage to the concrete of the RC structure was acquired, along with results of the changes in stiffness and loss of cross-sectional area of the reinforcements for damage identification.
2.2.2. Damage Detection using the PSD Method
The PSD technique was applied in this research to evaluate damage to the concrete components. The percentage damage of chloride-corroded rebars was utilized to determine which strategy to apply. This study accounted for differences in dynamic characteristics across years and situations due to changes in cross-sectional area and rebar stiffness. Given that PSD relies on vibration and signals, this was derived from the frequency response (FRF) using the following equations [,,,].
The transfer function is defined in Equation (7):
, , and denote the stiffness, mass, and damping matrices; they denote the frequency, and = −1 is the identity matrix. The equation of structural response using power spectral density is written in Equation (8).
The complex conjugate of a transfer function is denoted as , and SFF is the PSD input matrix at all of the active Degrees Of Freedom (DOF). Equation (8) demonstrates that the power spectral density is a second-order function of the FRF, which may be a highly nonlinear response to structural features.
The model updating base on the sensitivity equation and by considering () and (), where is the frequency response function from the structure damaged by chloride corrosion, is the impedance matrix, and the transfer function is inverse. Therefore, the power spectral density function equation for damaged elements can be written as Equation (9).
is the complex conjugate of the damaged RC structure transfer function during reinforcement chloride corrosion, according to the conventional chloride damage-prediction method.
An expression of the exact presented by Esfandiari et al. [] is given in Equation (10):
Equation (9) can be rewritten using Equations (8) and (10) as follows:
To determine corrosion damage of the reinforcing bars and its influence on the system’s structural behavior, the stiffness of each RC element is varied in proportion to the corrosion damage of the rebars over time. The structural stiffness equation is:
In Equation (12), is the level of stiffness matrices of the structural elements of a structure. indicates that structural parameter changes are between −1 and 1.
The sensitivity matrices allocated to the n th parameter of the structure for determining the passive stiffness ratios and for RC bridges damaged by chloride corrosion throught to Equation (11) are as follows:
A final equation of PSD for estimating changes in dynamic characteristic parameters during damage each year may be predicted using Equation (14):
illustrate the changes in structural stiffness due to chloride corrosion and deterioration over time according to the equations for chloride corrosion deterioration of reinforcements, using the power spectral density method to monitor the health of the changes in the stiffness and loss of cross-sectional areas in the RC marine bridge elements during their lifetime by the frequency response function of the bridge elements and using the least-squares technique.
2.3. Calculation Procedure for LCCA
Life-cycle cost assessment is an essential criteria to consider when assessing the performance of a bridge. The LCCA for the bridge in this study was assessed according to location and percentage of yearly damage predicted using damage-detection methods. The life-cycle and life-cycle cost in each stage of a structure’s life usually includes manufacturing, construction, use and maintenance, and, finally, the end of the structure’s life. Therefore, the following formulae can be used to represent the expected total cost throughout the bridge’s life cycle: [,].
In Equation (15), the initial cost is shown as ; is the maintenance cost; is the cost of inspections; is the total repair cost; is the expected damage cost. The total cost for the repair activity of the concrete bridge can be calculated according to the following items:
where , is the interval time investigated; is the cost of demolition of non-reinforced concrete parts such as the structure’s cover, is the cost of demolition of reinforced concrete parts of the structural parts of the bridge, is the cost of separation and classification of materials resulting from demolition, is the cost of preparing equipment for repairing the concrete and rebars of the columns and deck of the bridge, is the overall cost of buying and replacing damaged steel reinforcements, is the total cost of the concrete parts of the bridge damaged over the time period. Due to various damage factors, such as corrosion and damage caused by the presence of chloride ions in coastal structures, as well as other factors, such as floods and earthquakes following a Poisson process, the total life-cycle damages in each structural part and elements of a bridge can be computed within the time interval [,]:
In Equation (17), is the number and amount of damage factors on a structure during the time interval. D is the percentage of annual damage at time , which in this study referred to yearly damage caused by chloride corrosion predicted by the PSD method; is the discount rate in this study ( = 5%). According to the Poisson model, at a mean rate λf, time tk follows a uniform interval distribution throughout [0, ]. The estimated annual percentage of the damage of bridge elements under hazard effects can be written as () [,].
In Equation (18), is the value of damaged and corroded bridge elements.
In this study, the LCCA related to the repair and maintenance stage of a chloride-corroded concrete bridge was analyzed using the power spectral density method at different stages of the bridge’s life for each section and span location (see Figure 4).
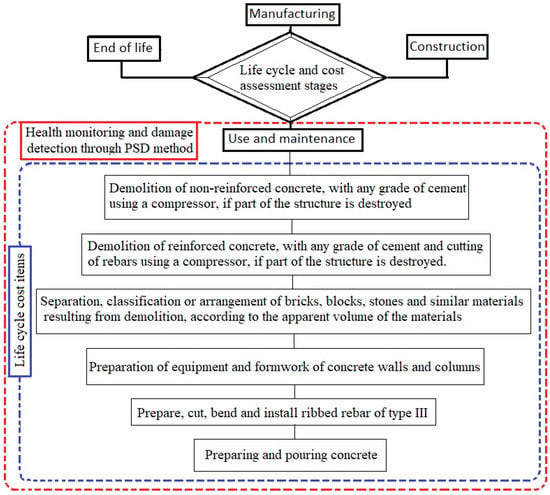
Figure 4.
The LCCA using the PSD for maintenance and repair of the concrete bridge.
According to the above figure, this study analyzes the monitoring of the repair and maintenance costs of the Arosa bridge, demolition of damaged parts, separation and classification of damaged material, preparation and installation of new reinforcements, and concrete activity costs and materials during the bridge life evaluated. In this study, the damage that chloride ions can cause to the foundations and deck of the bridge has been specifically addressed. In this regard, we investigated the accuracy and performance of the PSD to reduce the bridge’s repair and maintenance costs. Table 3 shows the costs of repairing the concrete and coastal Arosa bridge according to national construction-related databases of Spain [].

Table 3.
Repair activity cost (EUR) according to Spain data code (2022) [] for the concrete and coastal Arosa bridge.
Finally, for LCCA, the total bridge repair and maintenance costs according to the percentage of damage predicted for the whole bridge is obtained from the following Equation [].
The LCCA cost for overall maintenance and repair properties is given by over the lifetime of the bridge structure. , , , and are the total costs of demolishing the unreinforced concrete parts; the demolition, management, and separation of the reinforced concrete parts; and categorization of debris resulting from the destruction, installation, and subsequent removal of each concrete repair activity; repair and replacement of damaged bar steel with corrugated bar steel with improved ductility characteristics; and costs of preparing and pouring concrete during and until the end of bridge life, respectively.
Overall, in the calculation and analysis for this research, the life cycle of coastal concrete bridge elements was investigated according to the location of structural elements in respect to seawater. Then, using the PSD method, the extent and location of the damage caused during the bridge’s life was predicted and calculated for different years. Finally, the costs of maintenance and repair of the concrete bridge were investigated according to the type of damage that can be caused by chloride corrosion. In addition, the performance and accuracy of this method was evaluated for detecting the location, extent, and time of failure and how much the use of this method could reduce the maintenance and repair costs of a structure.
3. Description of the Numerical Model
The use of non-destructive and independent models based on numerical models of structures to detect damage is appealing to engineers and researchers as computers and sensors develop in speed and capability. The PSD approach, a vibration and signal-based method, investigated damage induced by chloride ions on a numerical model of a coastal concrete bridge. The numerical model of the bridge considered certain locations and sensors at specific distances from each other for health monitoring of the bridge structure each year from the start to the end of the concrete bridge reinforcement’s corrosion period. The deck and column numbers of these particular spans were renumbered from 1 to 167, as seen in Figure 5. One of the bridge’s forty spans was selected as the most vulnerable to chloride attack because it is located in the deepest part of the seawater. In addition, its columns are at the highest point above sea level, and the bridge is more exposed to tides and seawater here than at the beginning or end spans, which are shorter and some are out of the seawater.
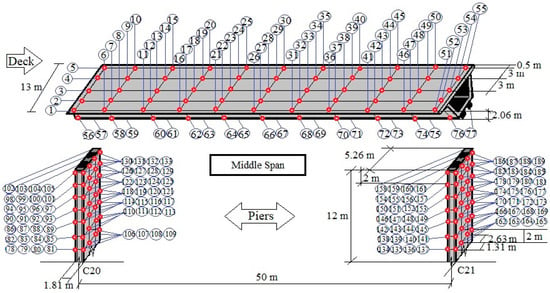
Figure 5.
Numbering and division of sensor points in 1 of 40 spans of the Arosa bridge.
Figure 5 demonstrates the numbering of the sensor points for analysis. Numbers 1 to 77 correspond to bridge deck points, which are spaced 5 m from each other in length and 3 m apart in the width of the bridge. The point numbers in one pier start at 78 and continue to 189 in the other. The points on the lengths of the piers are 2.63 m in width and 2 m in height from each other. The points on the widths of the piers are approximately 1.80 m apart.
To monitor the amount of damage at each bridge location during each year of chloride attack, we considered some points as simulation points and others as measurement points. The position and situation of these simulation and measurement points for annual test monitoring and analysis were assumed to be fixed for each year analyzed.
In this respect, some sites within a variety of sections and components were chosen to serve as simulation points, and others were chosen as measurement points. The distance between the simulation points and the measurement points varied widely. Thus, on the bridge deck span, points 3, 18, 33, 48, 58, 59, 64, 65, 70, 71, 76, and 77 were selected as simulation points; and between piers, points 86, 89, 98, 101, 115, 116, 127, 128, 135, 136, 147, 148, 159, 160, 162, 165, 174, 177, 186, and 189 were considered. These points were analyzed for each year of bridge life with constant location. The locations of these simulation and measurement points were assumed to be fixed until the end of the analysis as well as until the end of the structure’s life for each year of its life. This assumption was critical to the investigation because it allowed the researchers to determine how the locations of these points changed over time. In this analysis, the number and locations of sensors on the bridge span were determined by trial and error, as most techniques using software comparing sensor distances and frequency responses to calculate the distances between these sensors point to each other. On the other hand, the number and location of these sensors determines the distance between them. So, reducing the number of sensors causes an increase in the distance between the sensors, which can cause a decrease in the received signals from simulation points; even if considering a long distance, this creates a problem for receiving frequencies at measurement points, which can affect the results.
Moreover, the effect of the chloride ions in destroying any component of the concrete coastal bridge was estimated to be subject to 10% noise and error within the scope of this numerical analysis. The PSD method’s ability to detect damage caused by the presence and activity of chloride ions was analyzed using MATLAB software, and the finite-element-based software Open Sees was utilized. Figure 6 depicts a summary of the studies conducted to assess the PSD and a conventional methods approach, its efficacy in predicting the location and quantification of structure failure, and its influence on decreasing the maintenance and repair expenses of concrete and coastal structures.
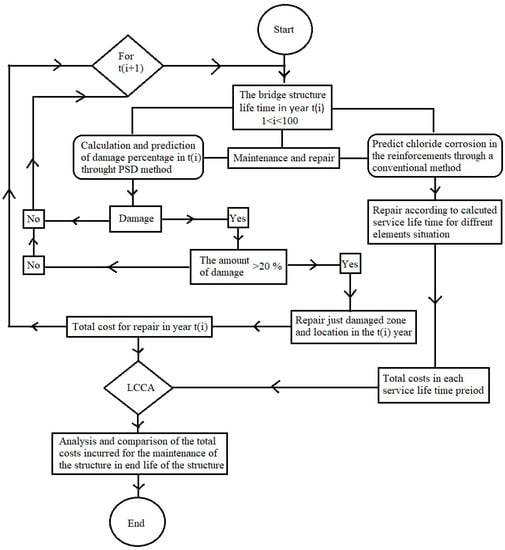
Figure 6.
The summary of analysis and calculation processes performed on the numerical model of the Arosa bridge.
As shown in the flowchart in Figure 6, the cost of repair and maintenance of a bridge structure is considered while assuming 100 years to be end of life. The amount and location of predicted damage to the bridge for each year of the structure’s life was analyzed. Then, the repair operation in the event of damage to the structure and more than 20% damage to the elements and regions was considered. Selection of the percentage damage to represent the start of damage could vary according to the importance for monitoring the time to repair and carry out maintenance to the structure. In this study bridge model, 20% damage was considered to be noticeable, and this was viewed as the beginning of damage for the software analysis. Then, we added up the annual expenses of repairing and maintaining the bridge, as well as the cost of the techniques that calculated the service-life interval and repair costs based on 20% damage to components (obtained using the PSD method and another technique). These approaches have been used to compare and contrast the bridge’s various parts every few years.
4. Results
Results were evaluated of examining the ability of a non-destructive method to detect damage and analyze the state of repair and maintenance costs of a span of the Arosa bridge located in the marine environment, with the lower part of the bridge piers immersed in seawater and exposed to corrosion and damage by chloride ions. Table 4 shows the repair time for each area between the measurement and simulation points in the Arosa bridge span. These times were obtained according to damages equal to or greater than 20% as the percentage of base damage for bridge repair using the PSD method and according to the service life of the conventional method in calculating the appropriate period and interval for the repair and maintenance of reinforced concrete structures exposed to corrosion and proximity to chloride ions.

Table 4.
Identified location, time, and amount of damage, and conventional service life of the Arosa bridge.
As mentioned in Table 4, for a more effective evaluation of the deck of the bridge span, it was divided into ten sections with distances of 5 m. In addition, each bridge column was divided into six sections with a distance of 2 m. Each deck section was divided into seven area ranges between the measurement points. In this division, the first four ranges of each section in Table 4 represent the upper part of the bridge deck box, and the following three peaks are related to the area of the sides and bottom of the deck in one section of the bridge. Each section of the piers is divided into three adjacent parts of equal volume.
The results of the PSD approach to damage detection and the performance of this method in reducing repair and maintenance costs are compared to the conventional method using the Spanish concrete code EHE-08 [] to determine service life according to chloride corrosion deterioration to decrease the total cost of maintenance and repair. Analysis is carried out in the same conditions until the end lifetime of this structure. Conventional methods predicted regular service life and repair periods for damage by corrosion caused by chloride ions. The total estimated costs for repairs for the life (100 years) of the Arosa bridge, which is subject to damage by chloride ions, using PSD and conventional methods, are shown in Figure 7.
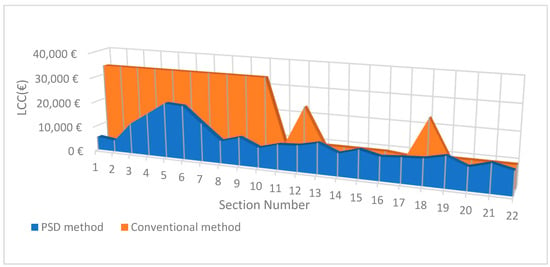
Figure 7.
The life-cycle cost assessment for the Arosa bridge until the end of bridge life.
The total LCC for one span of the Arosa bridge through PSD and conventional methods was calculated at about EUR 248,001.19 and EUR 470,113.12, respectively. The LCC for the columns using the PSD method was approximately EUR 122,688.59, and the cost using the conventional method was EUR 135,707.47. Furthermore, for a 50 m length of one span of the bridge, the costs using the PSD method and the conventional method in diagnosing and predicting the location and amount of damage were EUR 125,312.60 and EUR 334,405.64, respectively. Overall, using the PSD method for maintenance and repair of the bridge could save approximately EUR 222,111.92. These costs relate to all costs incurred for regular and continuous repair and maintenance of the Arosa coastal bridge for 100 years. Therefore, to more accurately examine the accuracy of the PSD method in reducing costs compared with the conventional methods of predicting structural damage, the LCC of total expenses for bridge repair and maintenance was investigated and analyzed according to a discount rate of 5 percent.
5. Conclusions
The results show that the use of the PSD method as a non-destructive and dynamic damage-detection method has acceptable performance in detecting the presence, location, and amount of damage due to chloride ion attack on coastal structures such as the concrete Arosa bridge. In addition, according to the LCC results during the life of the bridge structure, which is assumed to be 100 years, the use of this method along with an alternative approach significantly reduces the costs of repair and maintenance, especially in the deck section.
In conclusion, PSD, as a non-destructive method of identifying structural damage, has acceptable performance in identifying damage caused by chloride corrosion in different locations, including the concrete and internal rebars of the RC bridge that had damage which was not visible to the eye. In addition, this research on PSD as a non-destructive method has shown that chloride corrosion damage had a minor influence on the analysis through the PSD method performance. Furthermore, this method was used in various analyses to determine the time and quantification of damage in each location of the coastal bridge structure based on the distance of each element from the seawater. These areas include submerged and tidal-zone columns and dry sections such as the top of the columns and the deck. Moreover, using this method for LCCA of this bridge will play an essential role in reducing approximately 40% of the total LCC and maintenance and repair during the bridge life because of accurate prediction of location and amount and time of damage caused by corrosion. So, the PSD method can significantly optimize costs through on-time maintenance and repair of structures. In general, it is clear that non-destructive damage-detection has more advantages compared to destructive methods in the LCA discussion, especially in the maintenance and repair phase. However, the ability and accuracy of each non-destructive damage-detection method to detect the presence, location, and amount of damage in each part of structures, considering that each is suitable for different conditions and types of construction and environment, determin advantageous each method by other methods.
However, after ruling out other causes of damage, such as during bridge inspection, this study uses the PSD method to identify only structural deterioration caused by reinforcement corrosion where chloride ions are the cause. On the other hand, electrochemical methods, e.g., linear polarization resistance (LPR), galvanostatic pulse (GP), or electrochemical impedance spectroscopy (EIS), were not used to determine the corrosion rate due to the technical nature of the tests and the undesirable extension of the entire testing process. For this reason, the approach to identifying the corrosion process has been simplified, while being aware of a certain probability of damage.
Author Contributions
Conceptualization, M.H.-B.; methodology, M.H.-B. and I.J.N.; formal analysis, M.H.-B.; data curation, M.H.-B.; investigation, M.H.-B.; writing—original draft preparation, M.H.-B.; supervision, V.Y. and I.J.N.; resources, M.H.-B. and I.J.N.; visualization, I.J.N.; project administration, I.J.N. and V.Y.; funding acquisition, V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
Grant PID2020-117056RB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rathod, H.; Gupta, R. Sub-surface simulated damage detection using Non-Destructive Testing Techniques in reinforced-concrete slabs. Constr. Build. Mater. 2019, 215, 754–764. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Tan, X. Review on Vibration-Based Structural Health Monitoring Techniques and Technical Codes. Symmetry 2021, 13, 1998. [Google Scholar] [CrossRef]
- Aloisio, A.; Alaggio, R.; Fragiacomo, M. Time-domain identification of the elastic modulus of simply supported box girders under moving loads: Method and full-scale validation. Eng. Struct. 2020, 215, 110619. [Google Scholar] [CrossRef]
- Yu, H.; Wang, B.; Xia, C.; Gao, Z.; Li, Y. Efficient non-stationary random vibration analysis of vehicle-bridge system based on an improved explicit time-domain method. Eng. Struct. 2021, 231, 111786. [Google Scholar] [CrossRef]
- Pérez, M.A.; Font-Moré, J.; Fernández-Esmerats, J. Structural damage assessment in lattice towers based on a novel frequency domain-based correlation approach. Eng. Struct. 2021, 226, 111329. [Google Scholar] [CrossRef]
- Ronchei, C.; Vantadori, S.; Carpinteri, A.; Iturrioz, I.; Rodrigues, R.I.; Scorza, D.; Zanichelli, A. A frequency-domain approach for damage detection in welded structures. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 1134–1148. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Z.; Wu, J.; Liang, J.; Ge, J.; Liu, X.; Fang, G. A new time-frequency domain simulation method for damage accumulation and life prediction of composite thin-wall structures under random cyclic loadings. Compos. Struct. 2022, 281, 114999. [Google Scholar] [CrossRef]
- Tran, K.T.; Nguyen, T.D.; Hiltunen, D.R.; Stokoe, K.; Menq, F. 3D full-waveform inversion in time-frequency domain: Field data application. Appl. Geophys. 2020, 178, 104078. [Google Scholar] [CrossRef]
- Najafabadi, A.A.; Daneshjoo, F.; Bayat, M. A novel index for damage detection of the deck and dynamic behavior of horizontally curved bridges under moving load. J. Vibroeng. 2017, 19, 5421–5433. [Google Scholar] [CrossRef]
- Seyedpoor, S.M.; Ahmadi, A.; Pahnabi, N. Structural damage detection using time-domain responses and an optimization method. Inverse Probl. Sci. Eng. 2019, 27, 669–688. [Google Scholar] [CrossRef]
- Arora, V. Comparative study of finite element model updating methods. J. Vib. Control 2011, 17, 2023–2039. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y.; Zhou, X. Structural damage detection based on l1 regularization using natural frequencies and mode shapes. Struct. Control Health Monit. 2018, 25, e2107. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, W.; Cao, M.; Wu, H.; Zhu, R. A novel damage index for damage detection and localization of plate-type structures using twist derivatives of laser-measured mode shapes. JSV 2020, 481, 115448. [Google Scholar] [CrossRef]
- Dessi, D.; Camerlengo, G. Damage identification techniques via modal curvature analysis: Overview and comparison. Mech. Syst. Signal. Process. 2015, 52, 181–205. [Google Scholar] [CrossRef]
- Ganguli, R. Modal Curvature Based Damage Detection. In Structural Health Monitoring; Springer: Singapore, 2020; pp. 37–78. [Google Scholar] [CrossRef]
- Pooya, S.M.; Massumi, A. A novel and efficient method for damage detection in beam-like structures solely based on damaged structure data and using mode shape curvature estimation. Appl. Math. Model. 2021, 91, 670–694. [Google Scholar] [CrossRef]
- Wang, Y. Adaptive Finite Element Algorithm for Damage Detection of Non-Uniform Euler-Bernoulli Beams with Multiple Cracks Based on Natural Frequencies. In Adaptive Analysis of Damage and Fracture in Rock with Multiphysical Fields Coupling; Springer: Singapore, 2021; pp. 73–103. [Google Scholar] [CrossRef]
- Khan, M.W.; Akmal Din, N.; Ul Haq, R. Damage detection in a fixed-fixed beam using natural frequency changes. Vibroeng. Procedia 2020, 30, 38–43. [Google Scholar] [CrossRef]
- Arefi, S.L.; Gholizad, A. Damage identification of structures by reduction of dynamic matrices using the modified modal strain energy method. Struct. Monit. Maint. 2020, 7, 125–147. [Google Scholar] [CrossRef]
- Khosravan, A.; Asgarian, B.; Shokrgozar, H.R. Improved Modal Strain Energy Decomposition Method for damage detection of offshore platforms using data of sensors above the water level. Ocean Eng. 2021, 219, 108337. [Google Scholar] [CrossRef]
- Rahmatalla, S.; Eun, H.C.; Lee, E.T. Damage detection from the variation of parameter matrices estimated by incomplete FRF data. Smart. Struct. Syst. 2012, 9, 55–70. [Google Scholar] [CrossRef]
- Niu, Z. Frequency response-based structural damage detection using Gibbs sampler. JSV 2020, 470, 115160. [Google Scholar] [CrossRef]
- Zheng, Z.D.; Lu, Z.R.; Chen, W.H.; Liu, J.K. Structural damage identification based on power spectral density sensitivity analysis of dynamic responses. Comput. Struct. 2015, 146, 176–184. [Google Scholar] [CrossRef]
- Pedram, M.; Esfandiari, A.; Khedmati, M.R. Damage detection by a FE model updating method using power spectral density: Numerical and experimental investigation. JSV 2017, 397, 51–76. [Google Scholar] [CrossRef]
- Gao, D.Y.; Yao, W.X.; Wen, W.D.; Huang, J. Equivalent Spectral Method to Estimate the Fatigue Life of Composite Laminates Under Random Vibration Loadings. Mech. Compos. Mater. 2021, 57, 101–114. [Google Scholar] [CrossRef]
- Aquino, R.E.; Barbosh, M.; Sadhu, A. Comparison of Time-Domain and Time-Frequency-Domain System Identification Methods on Tall Building Data with Noise. In Dynamics of Civil Structures; Springer: Berlin/Heidelberg, Germany, 2021; Volume 2, pp. 179–184. [Google Scholar] [CrossRef]
- Barbosh, M.; Singh, P.; Sadhu, A. Empirical mode decomposition and its variants: A review with applications in structural health monitoring. SMS 2020, 29, 093001. [Google Scholar] [CrossRef]
- Silik, A.; Noori, M.; Altabey, W.A.; Ghiasi, R.; Wu, Z. Analytic Wavelet Selection for Time-Analysis of Big Data Form Civil Structure Monitoring. In Proceedings of the International Workshop on Civil Structural Health Monitoring, Naples, Italy, 31 March–2 April 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 431–455. [Google Scholar] [CrossRef]
- Li, J.T.; Zhu, X.Q.; Samali, B. Bridge operational modal identification using sparse blind source separation. In ACMSM25; Springer: Singapore, 2020; pp. 911–920. [Google Scholar] [CrossRef]
- Nilsson, A.; Liu, B. Frequency domain. In Vibro-Acoustics; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1, pp. 31–66. [Google Scholar] [CrossRef]
- Bayat1a, M.; Ahmadi, H.R.; Mahdavi3b, N. Application of power spectral density function for damage diagnosis of bridge piers. Struct. Eng. Mech. 2019, 71, 57–63. [Google Scholar] [CrossRef]
- Gunawan, F.E. Reliability of the power spectral density method in predicting structural integrity. Int. J. Innov. Comput. Inf. Control 2019, 15, 1717–1727. [Google Scholar] [CrossRef]
- Hadizadeh-Bazaz, M.; Navarro, I.J.; Yepes, V. Performance comparison of structural damage detection methods based on Frequency Response Function and Power Spectral Density. DYNA 2022, 97, 493–500. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. An optimization-LCA of a prestressed concrete precast bridge. Sustainability 2018, 10, 685. [Google Scholar] [CrossRef]
- Navarro, I.J.; Penadés-Plà, V.; Martínez-Muñoz, D.; Rempling, R.; Yepes, V. Life cycle sustainability assessment for multi-criteria decision making in bridge design: A review. J. Civil. Eng. Manag. 2020, 26, 690–704. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Dong, Y.; Sabatino, S. Bridge life-cycle performance and cost: Analysis, prediction, optimization, and decision-making. Struct. Infrastruct. Eng. 2017, 13, 1239–1257. [Google Scholar] [CrossRef]
- Goh, K.C.; Goh, H.H.; Chong, H.Y. Integration model of fuzzy AHP and life-cycle cost analysis for evaluating highway infrastructure investments. J. Infrastruct. Syst. 2019, 25, 04018045. [Google Scholar] [CrossRef]
- Heidari, M.R.; Heravi, G.; Esmaeeli, A.N. Integrating life-cycle assessment and life-cycle cost analysis to select sustainable pavement: A probabilistic model using managerial flexibilities. J. Clean. Prod. 2020, 254, 120046. [Google Scholar] [CrossRef]
- Kleingesinds, S.; Lavan, O.; Venanzi, I. Life-cycle cost-based optimization of MTMDs for tall buildings under multiple hazards. Struct. Infrastruct. Eng. 2021, 17, 921–940. [Google Scholar] [CrossRef]
- Kamariotis, A.; Chatzi, E.; Straub, D. Value of information from vibration-based structural health monitoring extracted via Bayesian model updating. Mech. Syst. Signal Process. 2022, 166, 108465. [Google Scholar] [CrossRef]
- Mitseas, I.P.; Kougioumtzoglou, I.A.; Beer, M. Nonlinear stochastic dynamic analysis for performance based multi-objective optimum design considering life cycle seismic loss estimation. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP), Vancouver, BC, Canada, 12–15 July 2015; Available online: https://open.library.ubc.ca/cIRcle/collections/53032/items/1.0076149 (accessed on 21 May 2015).
- Micheli, L.; Alipour, A.; Laflamme, S.; Sarkar, P. Performance-based design with life-cycle cost assessment for damping systems integrated in wind excited tall buildings. Eng. Struct. 2019, 195, 438–451. [Google Scholar] [CrossRef]
- Chu, X.; Cui, W.; Zhao, L.; Ge, Y. Life-Cycle Assessment of Long-Span Bridge’s Wind Resistant Performance Considering Multisource Time-Variant Effects and Uncertainties. J. Struct. Eng. 2022, 148, 04022092. [Google Scholar] [CrossRef]
- ISO 14040:2006; Environmental Management—Life Cycle Assessment—Principles and Framework. International Standards Organization: Geneva, Switzerland, 2006.
- ISO 14044:2006; Environmental Management—Life Cycle Assessment—Requirements and Guidelines. International Standards Organization: Geneva, Switzerland, 2006.
- Navarro, I.J.; Yepes, V.; Martí, J.V. Social life cycle assessment of concrete bridge decks exposed to aggressive environments. Environ. Impact Assess. Rev. 2018, 72, 50–63. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V.; González-Vidosa, F. Life cycle impact assessment of corrosion preventive designs applied to prestressed concrete bridge decks. J. Clean. Prod. 2018, 196, 698–713. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Martí, J.V.; García-Segura, T.; Yepes, V. Life-cycle assessment: A comparison between two optimal post-tensioned concrete box-girder road bridges. Sustainability 2017, 9, 1864. [Google Scholar] [CrossRef]
- León, J.; Prieto, F.; Rodríguez, F. Proyecto de rehabilitación del puente de la Isla de Arosa. Hormig Acero 2013, 270, 75–89. [Google Scholar]
- Pérez-Fadón Martínez, S. Puente a la Isla de Arosa. Hormigón y Acero 1985, 36, 157. [Google Scholar]
- Pérez-Fadón Martínez, S. Puente sobre la Ría de Arosa. Rev. Obras Publicas 1986, 3243, 1–16. [Google Scholar]
- Tuutti, K. Corrosion of Steel in Concrete; Report. Cement-och Betonginst 1982, 4, 468. [Google Scholar]
- Hájková, K.; Šmilauer, V.; Jendele, L.; Červenka, J. Prediction of reinforcement corrosion due to chloride ingress and its effects on serviceability. Eng. Struct. 2018, 174, 768–777. [Google Scholar] [CrossRef]
- Zhang, D.; Zeng, Y.; Fang, M.; Jin, W. Service life prediction of precast concrete structures exposed to chloride environment. Adv. Civ. Eng. 2019, 2019, 3216328. [Google Scholar] [CrossRef]
- Spanish Ministry of Public Works. EHE-08 Instrucción del Hormigón Estructural; Spanish Ministry of Public Works: Madrid, Spain, 2008; ISBN 978-84-498-0899-9. [Google Scholar]
- FIB. Model Code for Service Life Design; Federation Internationale du Beton, fib. Bulletin: Lausanne, Switzerland, 2006; No. 34. [Google Scholar]
- Khan, M.U.; Ahmad, S.; Al-Gahtani, H.J. Chloride-induced corrosion of steel in concrete: An overview on chloride diffusion and prediction of corrosion initiation time. Int. J. Corros. 2017, 2017, 5819202. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion—Appendix A Solution of Fick’s Second Law, 2nd ed.; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Alonso, M.C.; Sanchez, M. Analysis of the variability of chloride threshold values in the literature. Corros. Mater. 2009, 60, 631–637. [Google Scholar] [CrossRef]
- Navarro, I.J.; Marti, J.V.; Yepes, V. Reliability-based maintenance optimization of corrosion preventive designs under a life cycle perspective. Environ. Impact Assess. Rev. 2019, 74, 23–34. [Google Scholar] [CrossRef]
- Bru, D.; González, A.; Baeza, F.J.; Ivorra, S. Seismic behavior of 1960’s RC buildings exposed to marine environment. Eng. Fail. Anal. 2018, 90, 324–340. [Google Scholar] [CrossRef]
- Frontera, A.; Cladera, A. Long-term shear strength of RC beams based on a mechanical model that consid-ers reinforcing steel corrosion. Struct. Concr. 2022, 1–16. [Google Scholar] [CrossRef]
- Hadizadeh-Bazaz, M.; Navarro, I.J.; Yepes, V. Power Spectral Density method performance in detecting damages by chloride attack on coastal RC bridge. Struct. Eng. Mech. 2023, 85, 197–206. [Google Scholar] [CrossRef]
- Esfandiari, A.; Bakhtiari-Nejad, F.; Rahai, A.; Sanayei, M. Structural model updating using frequency response function and quasi-linear sensitivity equation. JSV 2009, 326, 557–573. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Lin, K.Y.; Estes, A.C. Life-cycle cost design of deteriorating structure. J. Struct. Eng. 1997, 123, 1390. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Probabilistic time-dependent multihazard life-cycle assessment and resilience of bridges considering climate change. J. Perform. Constr. Facil. 2016, 30, 04016034. [Google Scholar] [CrossRef]
- Yeo, G.L. Stochastic Characterization and Decision Bases under Time-Dependent Aftershock Risk in Performance-Based Earthquake Engineering; Stanford University: Stanford, CA, USA, 2005. [Google Scholar]
- MITMA. Reference Price Base of the General Directorate of Highways; Ministry of Transport, Mobility and Urban Agenda: Madrid, Spain, 2022. [Google Scholar]
- Lee, K.M.; Cho, H.N.; Cha, C.J. Life-cycle cost-effective optimum design of steel bridges considering environmental stressors. Eng. Struct. 2006, 28, 1252–1265. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).