A Bi-Level Programming Approach to Optimize Ship Fouling Cleaning
Abstract
:1. Introduction
2. Literature Review
- This study provides a quantitative approach to optimize the fouling cleaning process, which is a unique contribution compared to the existing literature. By applying mathematical techniques and optimization methods, the present research offers a systematic framework for achieving efficient and effective foul cleaning.
- The present research introduces a bi-level model that incorporates both service providers and demanders. In this model, the upper-level decision makers, who are the service providers, determine the optimal deployment of cleaning equipment, including location, quantity, and timing, in order to maximize total profits. On the other hand, the lower-level decision makers, which are the ships, decide when and where to clean fouling to minimize the total cost. It is important to note that the upper-level deployment decision influences the cleaning decisions of the lower-level ships, while the lower-level decisions also impact the upper-level deployment. This bi-level model allows for the simultaneous optimization of equipment deployment and service purchase decisions. By considering the interactions between these two groups, the study offers comprehensive solutions that address the needs and objectives of both service providers and demanders.
- To enhance computational efficiency, the present research transforms the complex bi-level non-linear problem into a single-level linear problem through the big-M method, which converts the formulation of the lower-level problem into constraints for the upper-level problem. By doing so, the two problems are effectively merged into a single-level optimization problem, which can be solved using linear programming techniques. This transformation simplifies the optimization process and reduces the computational complexity, resulting in faster solution times.
3. Problem Description and Formulation
3.1. Bi-Level Decisions
3.2. Model Formulation
4. Solution Method
5. Numerical Experiments
5.1. Parameter Setting
5.2. Computational Performance
| Algorithm 1. The heuristic for solving bi-level problems | |
| 1 | Initialization: Regard all in Problem (1), denoted by , as the input of P3 |
| 2 | Repeat until stays unchanged: |
| 3 | Solve P3 with and obtain |
| 4 | Solve P2 with and obtain |
| 5 | Return and |
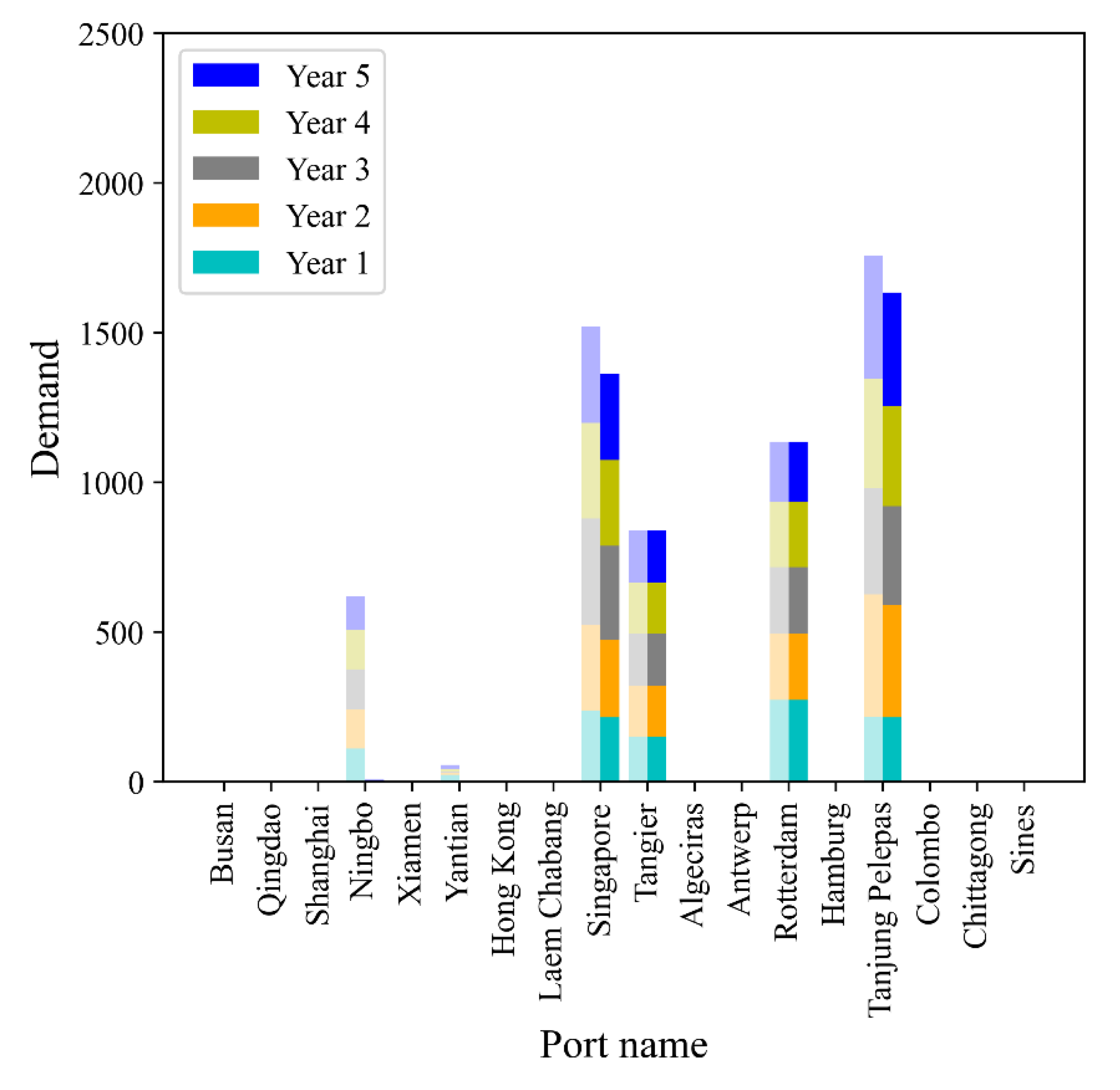
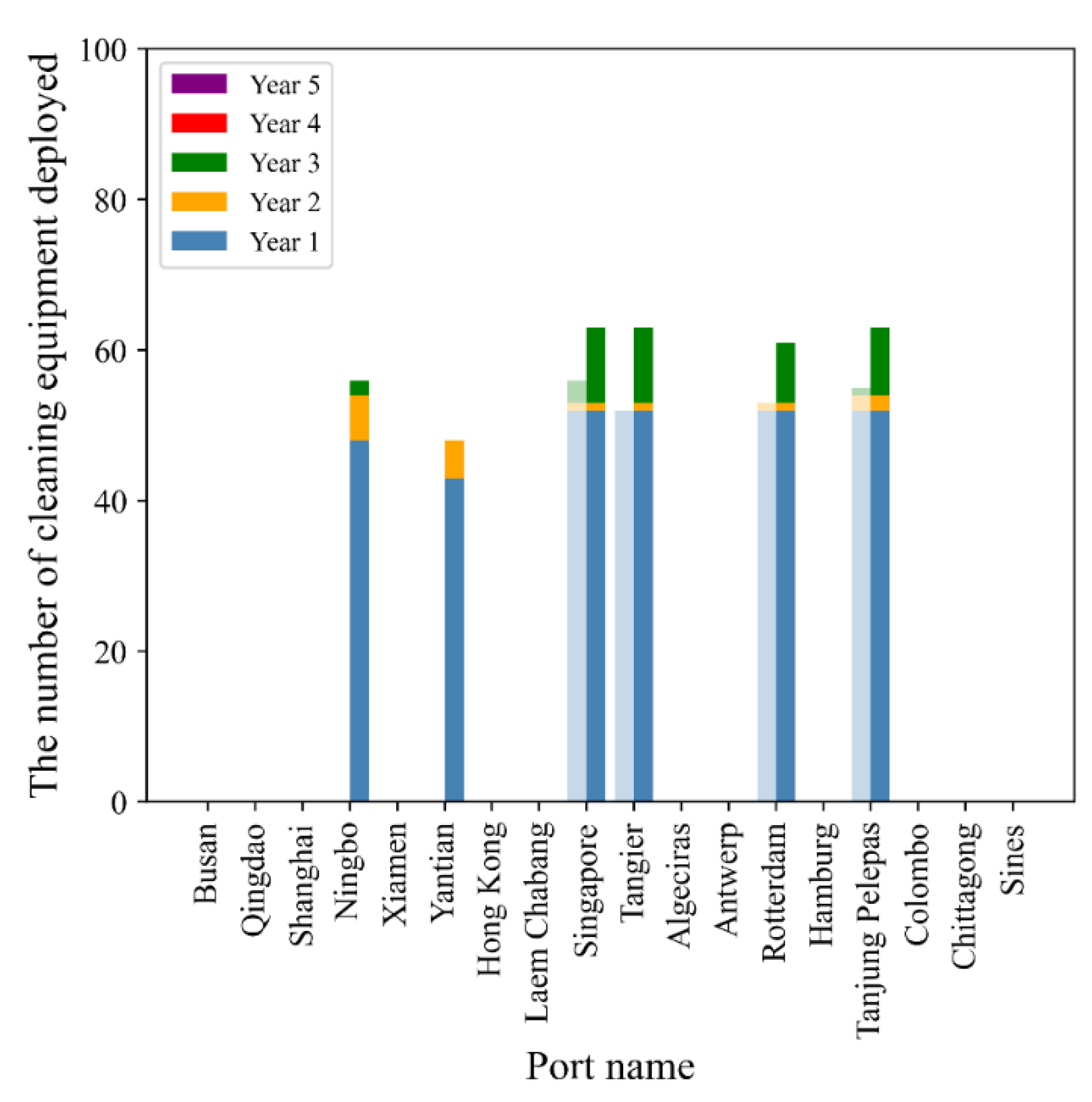
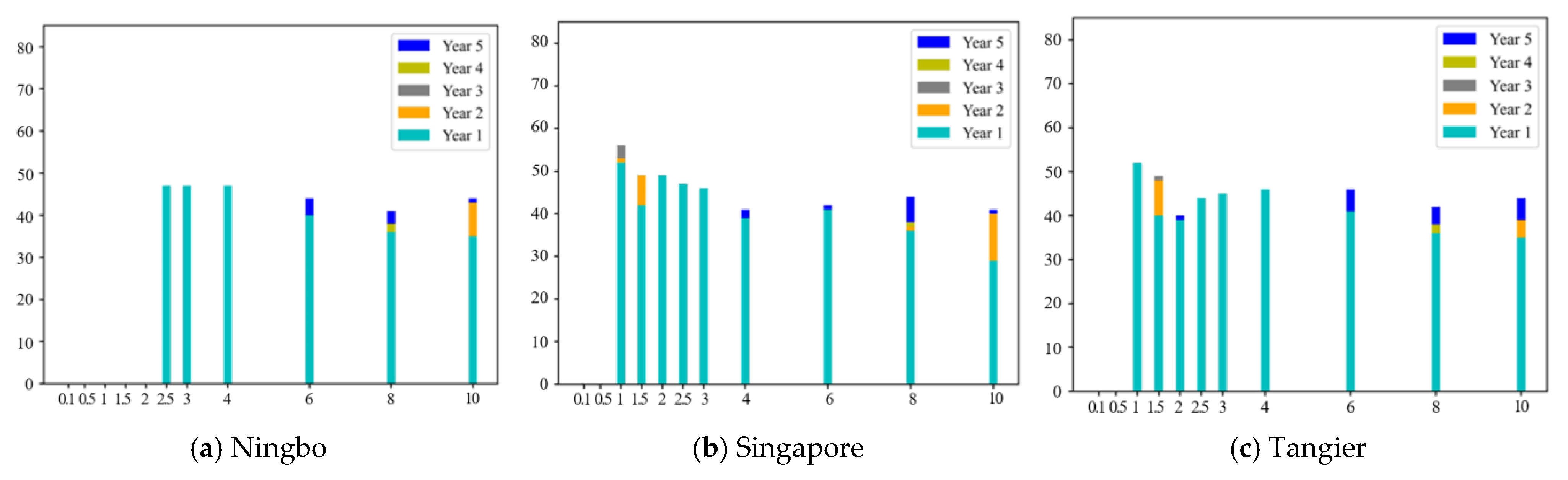
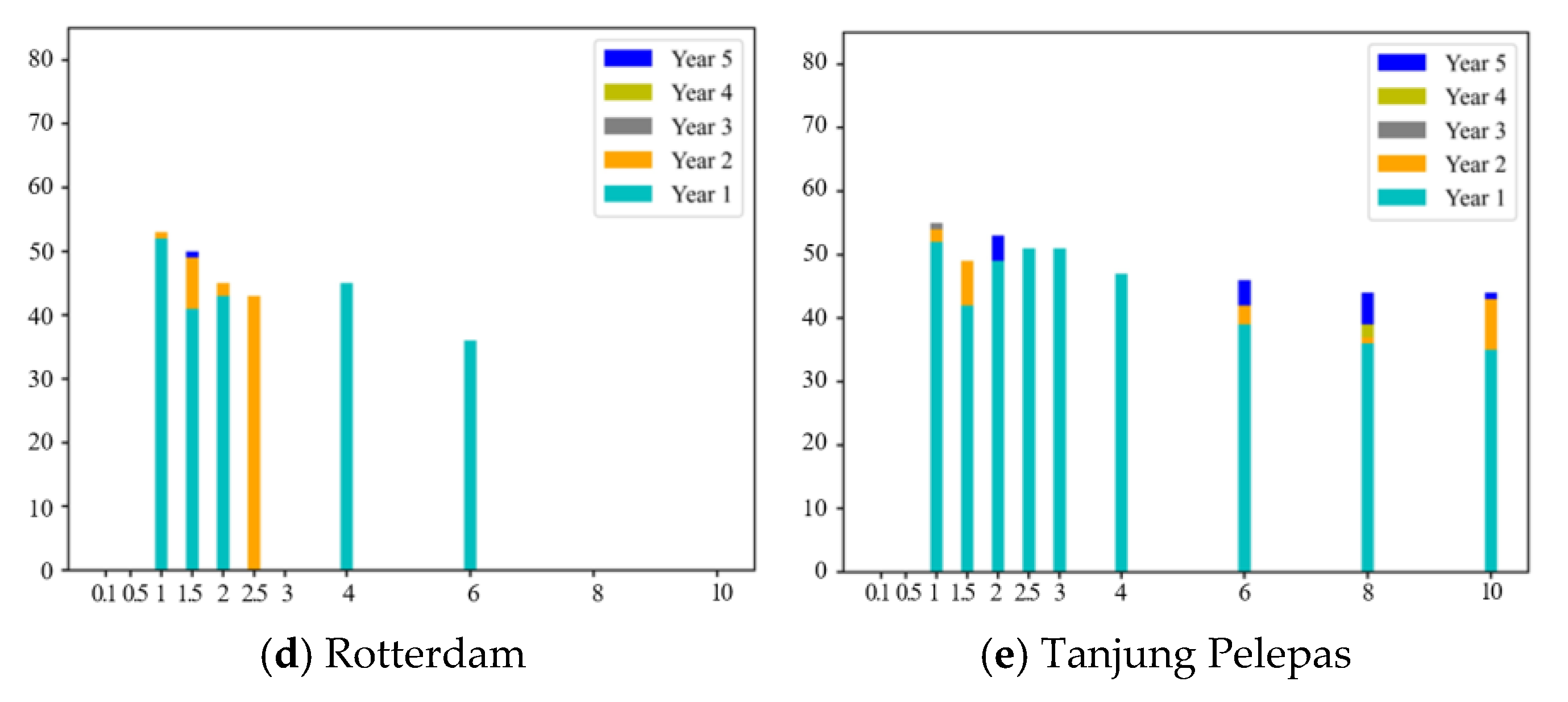
5.3. Sensitivity Analysis
6. Discussions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | This regulation can be found on the following links: https://www.mpi.govt.nz/import/border-clearance/ships-and-boats-border-clearance/biofouling/biofouling-management/; https://www.amsa.gov.au/about/regulations-and-standards/112022-biofouling-and-water-cleaning (accessed on 15 October 2023). |
References
- Utama IK, A.P.; Nugroho, B. Biofouling, ship drag, and fuel consumption: A brief overview. J. Ocean Technol. 2018, 13, 42–48. [Google Scholar]
- Hakim, M.L.; Utama, I.K.A.P.; Nugroho, B.; Yusim, A.K.; Baithal, M.S.; Suastika, I.K. Review of correlation between marine fouling and fuel consumption on a ship. In Proceedings of the SENTA: 17th Conference on Marine Technology, Surabaya, Indonesia, 6–7 December 2017; pp. 122–129. [Google Scholar]
- Fitridge, I.; Dempster, T.; Guenther, J.; De Nys, R. The impact and control of biofouling in marine aquaculture: A review. Biofouling 2012, 28, 649–669. [Google Scholar] [CrossRef] [PubMed]
- Farkas, A.; Degiuli, N.; Martić, I.; Vujanović, M. Greenhouse gas emissions reduction potential by using antifouling coatings in a maritime transport industry. J. Clean. Prod. 2021, 295, 126428. [Google Scholar] [CrossRef]
- Dinariyana AA, B.; Deva, P.P.; Ariana, I.; Handani, D.W. Development of model-driven decision support system to schedule underwater hull cleaning. Brodogradnja 2022, 73, 21–37. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Ančić, I. Energy savings potential of hull cleaning in a shipping industry. J. Clean. Prod. 2022, 374, 134000. [Google Scholar] [CrossRef]
- Yebra, D.M.; Kiil, S.; Dam-Johansen, K. Antifouling technology—Past, present and future steps towards efficient and environmentally friendly antifouling coatings. Prog. Org. Coat. 2004, 50, 75–104. [Google Scholar] [CrossRef]
- Maan, A.M.; Hofman, A.H.; de Vos, W.M.; Kamperman, M. Recent developments and practical feasibility of polymer-based antifouling coatings. Adv. Funct. Mater. 2020, 30, 2000936. [Google Scholar] [CrossRef]
- Evans, L.V. Marine algae and fouling: A review, with particular reference to ship-fouling. Bot. Mar. 1981, 24, 167–171. [Google Scholar] [CrossRef]
- Callow, M. Ship fouling: Problems and solutions. Chem. Ind. 1990, 5, 123–127. [Google Scholar]
- Townsin, R.L. The ship hull fouling penalty. Biofouling 2003, 19 (Suppl. S1), 9–15. [Google Scholar] [CrossRef]
- Monty, J.P.; Dogan, E.; Hanson, R.; Scardino, A.J.; Ganapathisubramani, B.; Hutchins, N. An assessment of the ship drag penalty arising from light calcareous tubeworm fouling. Biofouling 2016, 32, 451–464. [Google Scholar] [CrossRef] [PubMed]
- Demirel, Y.K.; Uzun, D.; Zhang, Y.; Fang, H.C.; Day, A.H.; Turan, O. Effect of barnacle fouling on ship resistance and powering. Biofouling 2017, 33, 819–834. [Google Scholar] [CrossRef] [PubMed]
- Coraddu, A.; Oneto, L.; Baldi, F.; Cipollini, F.; Atlar, M.; Savio, S. Data-driven ship digital twin for estimating the speed loss caused by the marine fouling. Ocean Eng. 2019, 186, 106063. [Google Scholar] [CrossRef]
- Demirel, Y.K.; Song, S.; Turan, O.; Incecik, A. Practical added resistance diagrams to predict fouling impact on ship performance. Ocean Eng. 2019, 186, 106112. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Dejhalla, R. Impact of hard fouling on the ship performance of different ship forms. J. Mar. Sci. Eng. 2020, 8, 748. [Google Scholar] [CrossRef]
- Song, S.; Demirel, Y.K.; Muscat-Fenech CD, M.; Tezdogan, T.; Atlar, M. Fouling effect on the resistance of different ship types. Ocean Eng. 2020, 216, 107736. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I. An investigation into the effect of hard fouling on the ship resistance using CFD. Appl. Ocean Res. 2020, 100, 102205. [Google Scholar] [CrossRef]
- Erol, E.; Cansoy, C.E.; Aybar, O.Ö. Assessment of the impact of fouling on vessel energy efficiency by analyzing ship automation data. Appl. Ocean Res. 2020, 105, 102418. [Google Scholar] [CrossRef]
- Tribou, M.; Swain, G. Grooming using rotating brushes as a proactive method to control ship hull fouling. Biofouling 2015, 31, 309–319. [Google Scholar] [CrossRef]
- Oliveira, D.R.; Granhag, L. Ship hull in-water cleaning and its effects on fouling-control coatings. Biofouling 2020, 36, 332–350. [Google Scholar] [CrossRef]
- Zhong, X.; Dong, J.; Liu, M.; Meng, R.; Li, S.; Pan, X. Experimental study on ship fouling cleaning by ultrasonic-enhanced submerged cavitation jet: A preliminary study. Ocean Eng. 2022, 258, 111844. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I. The impact of biofouling on the propeller performance. Ocean Eng. 2021, 219, 108376. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I. Assessment of the effect of biofilm on the ship hydrodynamic performance by performance prediction method. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 102–114. [Google Scholar] [CrossRef]
- Georgiev, P.; Garbatov, Y. Multipurpose vessel fleet for short black sea shipping through multimodal transport corridors. Brodogradnja 2021, 72, 79–101. [Google Scholar] [CrossRef]
- Degiuli, N.; Farkas, A.; Martić, I.; Grlj, C.G. Optimization of maintenance schedule for containerships sailing in the Adriatic Sea. J. Mar. Sci. Eng. 2023, 11, 201. [Google Scholar] [CrossRef]
- Chang, J.S.; Mackett, R.L. A bi-level model of the relationship between transport and residential location. Transp. Res. Part B Methodol. 2006, 40, 123–146. [Google Scholar] [CrossRef]
- Stoilova, K.; Stoilov, T. Model predictive traffic control by bi-level optimization. Appl. Sci. 2022, 12, 4147. [Google Scholar] [CrossRef]
- Gang, J.; Tu, Y.; Lev, B.; Xu, J.; Shen, W.; Yao, L. A multi-objective bi-level location planning problem for stone industrial parks. Comput. Oper. Res. 2015, 56, 8–21. [Google Scholar] [CrossRef]
- Abareshi, M.; Zaferanieh, M. A bi-level capacitated P-median facility location problem with the most likely allocation solution. Transp. Res. Part B Methodol. 2019, 123, 1–20. [Google Scholar] [CrossRef]
- Casas-Ramírez, M.S.; Camacho-Vallejo, J.F.; Díaz, J.A.; Luna, D.E. A bi-level maximal covering location problem. Oper. Res. 2020, 20, 827–855. [Google Scholar] [CrossRef]
- Camacho-Vallejo, J.F.; González-Rodríguez, E.; Almaguer, F.J.; González-Ramírez, R.G. A bi-level optimization model for aid distribution after the occurrence of a disaster. J. Clean. Prod. 2015, 105, 134–145. [Google Scholar] [CrossRef]
- Lee, M.C.; Wee, H.M.; Wu, S.; Wang, C.E.; Chung, R.L. A bi-level inventory replenishment strategy using clustering genetic algorithm. Eur. J. Ind. Eng. 2015, 9, 774–793. [Google Scholar] [CrossRef]
- Qi, J.; Wang, S.; Psaraftis, H. Bi-level optimization model applications in managing air emissions from ships: A review. Commun. Transp. Res. 2021, 1, 100020. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Yan, X.; Huang, L.; Jiang, X.; Yuan, Y.; Negenborn, R.R. A novel bi-level distributed dynamic optimization method of ship fleets energy consumption. Ocean Eng. 2020, 197, 106802. [Google Scholar] [CrossRef]
- Zhu, M.; Shen, S.; Shi, W. Carbon emission allowance allocation based on a bi-level multi-objective model in maritime shipping. Ocean Coast. Manag. 2023, 241, 106665. [Google Scholar] [CrossRef]
- Yang, D.; Pan, K.; Wang, S. On service network improvement for shipping lines under the one belt one road initiative of China. Transp. Res. Part E Logist. Transp. Rev. 2018, 117, 82–95. [Google Scholar] [CrossRef]
- Zhuge, D.; Wang, S.; Zhen, L.; Laporte, G. Subsidy design in a vessel speed reduction incentive program under government policies. Nav. Res. Logist. 2021, 68, 344–358. [Google Scholar] [CrossRef]
- Ziar, E.; Seifbarghy, M.; Bashiri, M.; Tjahjono, B. An efficient environmentally friendly transportation network design via dry ports: A bi-level programming approach. Ann. Oper. Res. 2023, 322, 1143–1166. [Google Scholar] [CrossRef]
- Wang, W.; Wang, S.; Zhen, L. Optimal subsidy design for energy generation in ship berthing. Marit. Policy Manag. 2023, 1–14. [Google Scholar] [CrossRef]
- Cai, L.; Wu, Y.; Zhu, S.; Tan, Z.; Yi, W. Bi-level programming enabled design of an intelligent maritime search and rescue system. Adv. Eng. Inform. 2020, 46, 101194. [Google Scholar] [CrossRef]
- Meng, Q.; Du, Y.; Wang, Y. Shipping log data based container ship fuel efficiency modeling. Transp. Res. Part B Methodol. 2016, 83, 207–229. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, Y.; Wang, H.; Zhen, L. Nonlinear programming for fleet deployment, voyage planning and speed optimization in sustainable liner shipping. Electron. Res. Arch. 2023, 31, 147–168. [Google Scholar] [CrossRef]
- Schultz, M.P.; Bendick, J.A.; Holm, E.R.; Hertel, W.M. Economic impact of biofouling on a naval surface ship. Biofouling 2011, 27, 87–98. [Google Scholar] [CrossRef]
- Bryers, J.; Characklis, W. Early fouling biofilm formation in a turbulent flow system: Overall kinetics. Water Res. 1981, 15, 483–491. [Google Scholar] [CrossRef]


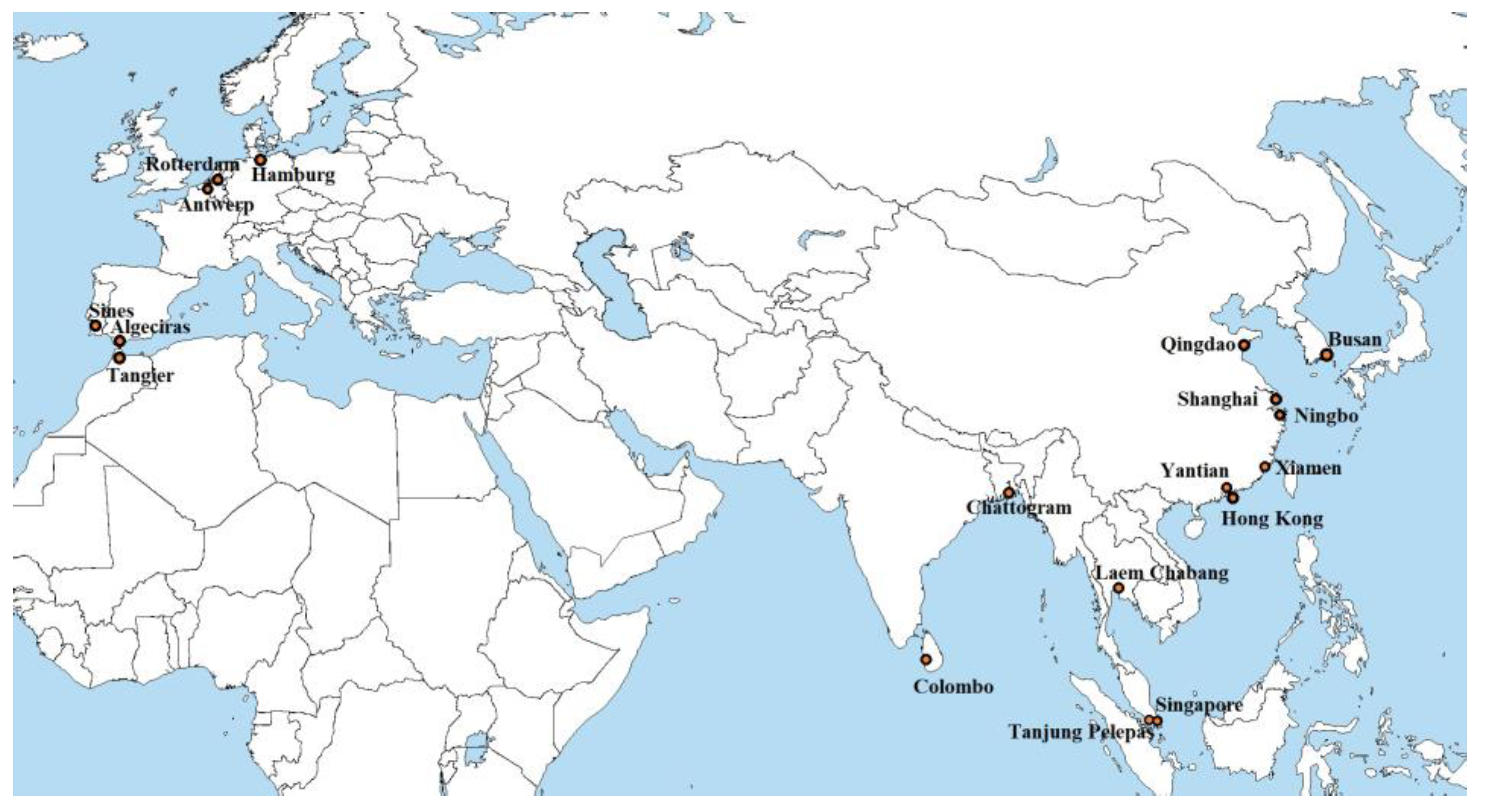

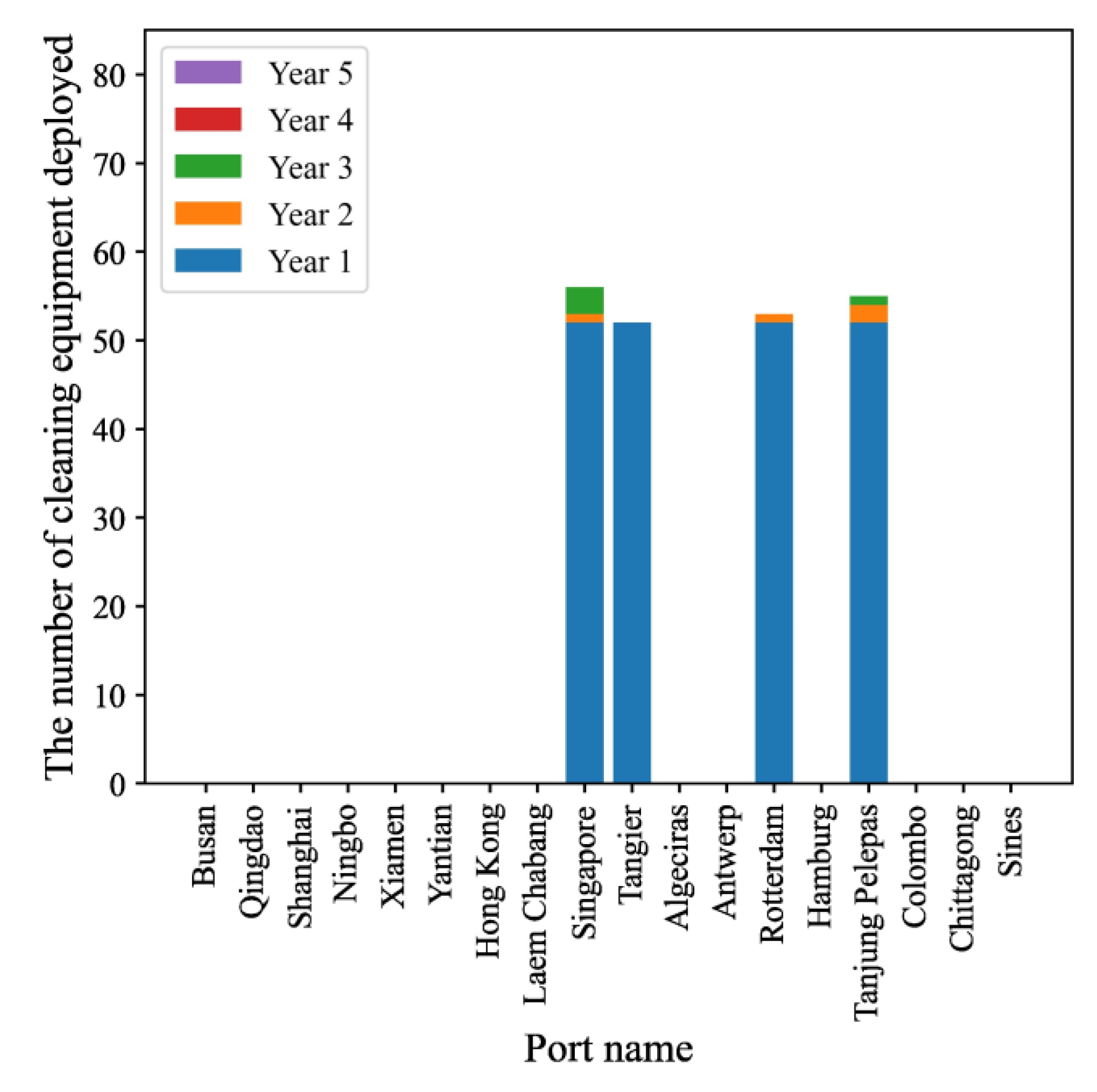
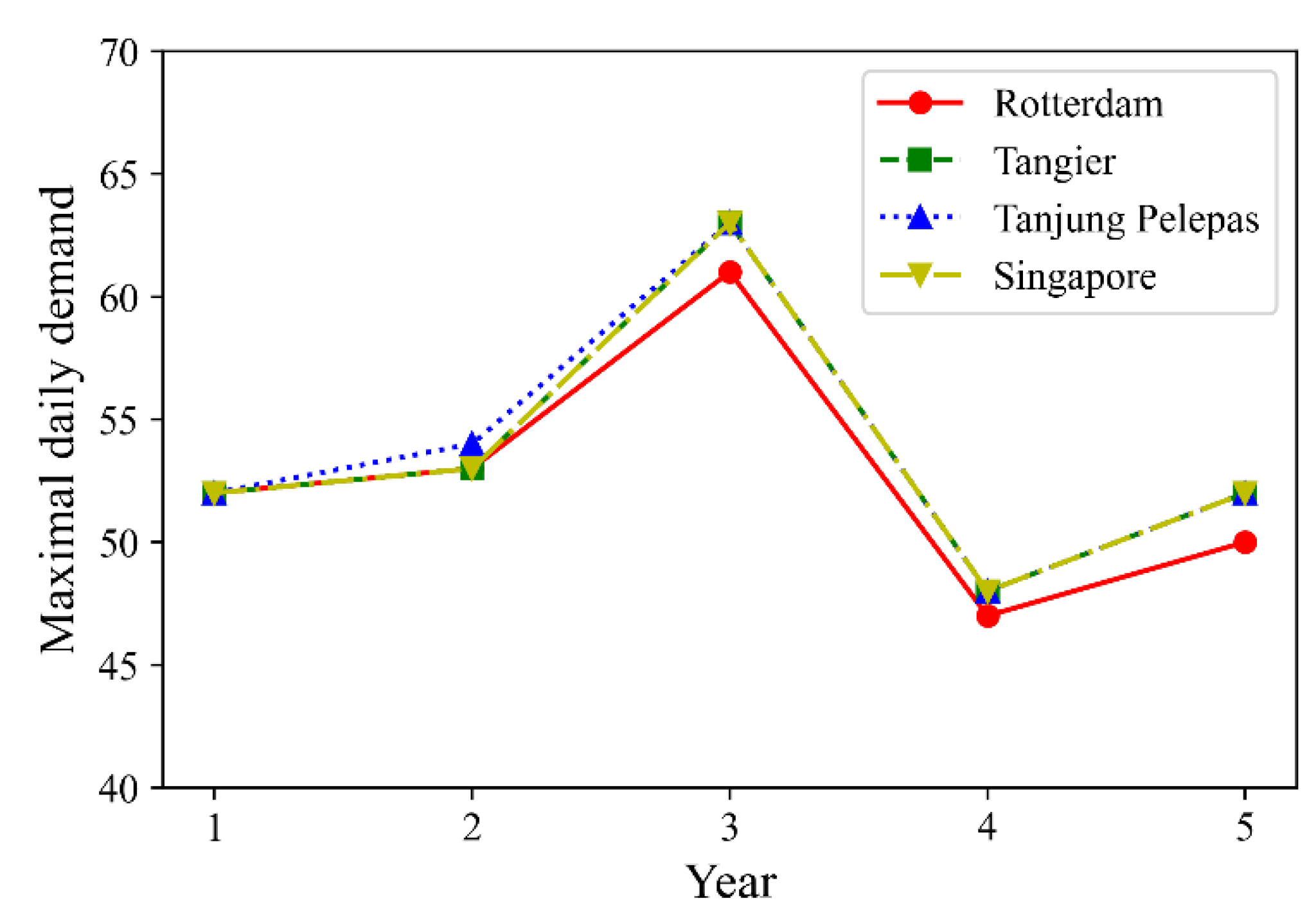


| Sets | |
| Set of container shipping routes, indexed by , | |
| Set of all ports on shipping routes, indexed by , | |
| Set of homogenous ships, indexed by , | |
| Planning period, indexed by , | |
| An ordered set of port–time pairs of ship | |
| Set of all port–time pairs of ship at the th year | |
| Set of all port–time pairs of ship that have | |
| Set of all port–time pairs of ship that have and | |
| Set of ships that are in service at port when ship arrives at this port at the port–time pair | |
| Set of non-negative integers | |
| Parameters | |
| The unit fuel cost (USD/nautical mile) | |
| The cleaning price (USD) at port | |
| The amortized purchasing cost (USD/year) of cleaning equipment | |
| The distance (nautical mile) of the next leg for ship after visiting port | |
| The dwell time (days) of ship at port | |
| The increase in the rate of fouling (kg/m2·day) | |
| The coefficient between fuel consumption growth rate and ship fouling level | |
| The position of port–time pair at set | |
| The position of port–time pair at set | |
| Decision variables | |
| The amount of equipment to be deployed at port at the beginning of the th year | |
| Binary variable which equals 1 if the ship cleans fouling at the port–time pair or 0 otherwise | |
| The fouling accumulation (kg) on a ship at port–time pair | |
| Index | Route |
|---|---|
| 1 | Ningbo → Xiamen → Yantian → Tanjung Pelepas → Rotterdam → Port Tanger Med → Hong Kong → Ningbo |
| 2 | Shanghai → Yantian → Tanjung Pelepas → Colombo → Port Tanger Med → Hamburg → Antwerp → Port Tanger Med → Singapore → Laem Chabang → Ningbo → Shanghai |
| 3 | Antwerp → Rotterdam → Algeciras → Singapore → Hong Kong → Shanghai → Qingdao → Busan → Ningbo → Shanghai→ Yantian → Tanjung Pelepas → Sines → Antwerp |
| 4 | Busan → Ningbo → Tanjung Pelepas→ Rotterdam → Tanjung Pelepas → Shanghai → Qingdao → Ningbo → Busan |
| 5 | Shanghai → Tanjung Pelepas → Chittagong → Tanjung Pelepas → Singapore → Laem Chabang → Ningbo → Shanghai |
| Planning Period | Computation Time | |
|---|---|---|
| Single Level | Algorithm | |
| 5 | 17.1 | 390.8 |
| 10 | 19.7 | 430.8 |
| 20 | 20.3 | 480.5 |
| Revenue (USD, Millions) | Cost (USD, Millions) | Profit (USD, Millions) | |
|---|---|---|---|
| Partial satisfaction | 153 | 107 | 46 |
| Full satisfaction | 187 | 168 | 19 |
| Change | 34 | 61 | −27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Guo, H.; Li, F.; Zhen, L.; Wang, S. A Bi-Level Programming Approach to Optimize Ship Fouling Cleaning. J. Mar. Sci. Eng. 2023, 11, 2324. https://doi.org/10.3390/jmse11122324
Wang W, Guo H, Li F, Zhen L, Wang S. A Bi-Level Programming Approach to Optimize Ship Fouling Cleaning. Journal of Marine Science and Engineering. 2023; 11(12):2324. https://doi.org/10.3390/jmse11122324
Chicago/Turabian StyleWang, Wei, Haoran Guo, Fei Li, Lu Zhen, and Shuaian Wang. 2023. "A Bi-Level Programming Approach to Optimize Ship Fouling Cleaning" Journal of Marine Science and Engineering 11, no. 12: 2324. https://doi.org/10.3390/jmse11122324
APA StyleWang, W., Guo, H., Li, F., Zhen, L., & Wang, S. (2023). A Bi-Level Programming Approach to Optimize Ship Fouling Cleaning. Journal of Marine Science and Engineering, 11(12), 2324. https://doi.org/10.3390/jmse11122324







