Machine Learning-Based Approach to Wind Turbine Wake Prediction under Yawed Conditions

Abstract

As wind energy continues to be a crucial part of sustainable power generation, the need for precise and efficient modeling of wind turbines, especially under yawed conditions, becomes increasingly significant. Addressing this, the current study introduces a machine learning-based symbolic regression approach for elucidating wake dynamics. Utilizing WindSE’s actuator line method (ALM) and Large Eddy Simulation (LES), we model an NREL 5-MW wind turbine under yaw conditions ranging from no yaw to 40 degrees. Leveraging a hold-out validation strategy, the model achieves robust hyper-parameter optimization, resulting in high predictive accuracy. While the model demonstrates remarkable precision in predicting wake deflection and velocity deficit at both the wake center and hub height, it shows a slight deviation at low downstream distances, which is less critical to our focus on large wind farm design. Nonetheless, our approach sets the stage for advancements in academic research and practical applications in the wind energy sector by providing an accurate and computationally efficient tool for wind farm optimization. This study establishes a new standard, filling a significant gap in the literature on the application of machine learning-based wake models for wind turbine yaw wake prediction.

1. Introduction

Background

As global energy consumption continues to rise in the face of dwindling fossil fuel reserves and escalating climate change concerns, the search for sustainable and clean energy sources has become a pressing imperative. One such source, wind energy, has rapidly become prominent in the global energy landscape. Recognized for its renewable nature and significant potential for reducing carbon emissions, wind energy has positioned itself as a viable and critical solution to the energy conundrum [1].

The translation of this potential into practical energy production at scale has been realized through wind farms, which are large arrays of wind turbines designed to convert the kinetic energy of wind into electricity. Scattered across both land and sea, these towering structures have become symbols of our pursuit of renewable energy, embodying our commitment to a sustainable future [2].

However, despite the apparent simplicity of their operation, wind turbines are governed by complex dynamics that pose considerable challenges to their efficiency and longevity. A central element in these dynamics is the ’wake’ that each turbine generates as it extracts energy from the wind [3]. These wakes—areas of turbulent airflow and reduced wind speed, or ’velocity deficit’, behind the turbines—pose significant challenges to harnessing wind energy effectively. The turbulence within the wake not only leads to efficiency losses but also results in increased fatigue loads, which can reduce the operational lifespan of turbines [4,5].

The intricacies of wake effects are magnified within wind farms, where the close positioning of turbines creates an interplay of wakes that can lead to a cascading effect of power loss across the installation. When multiple wakes intersect, the downstream turbines face lower wind speeds and increased turbulence, leading to a substantial drop in energy production and heightened structural stresses [6]. Moreover, when turbines are not aligned directly with the incoming wind—a condition known as ’yaw’—the wake characteristics become even more complex. Yawed conditions induce changes in wake structure, which complicate the prediction and management of wakes and introduce additional efficiency and load challenges [7].

Given these challenges, modeling wind turbine wakes is of paramount importance in the pursuit of efficient wind energy harvesting. Traditional methods of wake modeling often employ Computational Fluid Dynamics (CFD) simulations. Techniques such as Large Eddy Simulation (LES) and Reynolds-Averaged Navier–Stokes (RANS) equations have been widely used to simulate and study the dynamics of wakes. While these methods provide valuable insights, they are computationally intensive and require significant time to complete, rendering them impractical for large-scale or real-time applications [8].

Additionally, the wake dynamics of yawed turbines present unique challenges that current analytical models do not fully address. Despite the crucial role of yaw in real-world wind turbine operation, the body of research on yaw-induced wake behavior is notably sparse. Existing models often fall short in accurately representing wake behavior under yawed conditions, leading to significant gaps in our understanding and prediction of wake dynamics in these scenarios [9]. A comprehensive understanding of yawed wake dynamics is critical not only for improving individual turbine performance but also for optimizing the design and control strategies of wind farms. It can provide pathways for increasing overall energy yield and reducing mechanical loading on turbines, thus enhancing the durability and efficiency of wind farms [10].

With its ability to recognize patterns and learn from data, machine learning offers a promising alternative to traditional wake modeling. Leveraging machine learning techniques, such as symbolic regression, allows for the generation of models that can accurately predict wake behavior under various operating conditions, including yaw misalignment [11]. Particularly, symbolic regression provides the added advantage of producing transparent and interpretable models, a significant departure from the ’black-box’ nature of many conventional machine learning methods [12]. Consequently, the development and refinement of machine learning-based symbolic regression models for predicting yawed wind turbine wakes represent a promising and emerging field of research. This approach holds significant potential for enhancing wind energy production and shaping the future of the wind energy sector.

2. Literature Review

2.1. Wind Turbine Wake Aerodynamics

Understanding the intricacies of wind turbine aerodynamics, specifically wake phenomena, plays a critical role in enhancing turbine performance and, consequently, the overall efficiency of wind energy systems [3,13]. Wind turbines, by their very nature, interact with wind flow, causing disruptions and giving rise to a wake—a region characterized by reduced wind speed and increased turbulence.

The fundamental principles underpinning wake aerodynamics in wind turbines are firmly grounded in the broader discipline of fluid dynamics and, specifically, the study of turbulence and vorticity [14,15]. As wind interacts with the turbine’s rotor, a momentum deficit ensues in the immediate downstream region. This deficit translates into a change in velocity, often marked by a velocity deficit in the wake compared to the free stream wind speed [16].

The formation and propagation of wind turbine wakes are contingent upon many factors. From a meteorological perspective, atmospheric stability, wind speed, and turbulence intensity are major influencing factors [5,17]. Meanwhile, parameters related to turbine design and operation, such as rotor diameter, tower height, blade pitch, and turbine control strategies, can significantly modulate wake characteristics [18,19]. Understanding these factors is paramount for predicting wake behavior and optimizing wind farm performance.

Wake effects have a significant bearing on both individual turbine performance and the overall efficiency of wind farms. Owing to wake interference, downstream turbines (i.e., turbines located behind other turbines relative to the prevailing wind direction) often face reduced wind speeds, leading to lower power output [4,5,19,20,21]. Furthermore, the wake’s turbulent nature increases the wind load’s variability on the turbine structures, potentially resulting in increased structural fatigue and reduced component life [22,23].

To mitigate these detrimental wake effects, various strategies have been proposed and implemented. Wind farm layout optimization, for example, seeks to arrange turbines to minimize wake interference and maximize overall power production [24,25]. Similarly, active wake control strategies such as deliberate yaw misalignment and adaptive blade pitch control can redirect wakes away from downstream turbines [26,27].

Empirical research and computational modeling have been invaluable in extending our understanding of wind turbine wake aerodynamics. Real-world measurements of wake effects using advanced technologies such as LIDAR and SODAR provide critical insights into wake behavior under varying operational and environmental conditions [6,19,28,29,30]. Concurrently, computational studies utilizing methods such as Computational Fluid Dynamics (CFD) and Large Eddy Simulation (LES) have provided a platform to simulate and study wake dynamics in controlled conditions, enabling researchers to isolate and understand the influence of specific factors [8,31,32]. It is worth noting that Large Eddy Simulation (LES) is a computational technique frequently used for turbulence modeling and is often deemed advantageous for capturing a wide range of turbulent flow scales. However, it has its limitations. One of the primary constraints is computational expense, as LES demands significant computational resources and time, especially for high Reynolds number flows [33,34]. Additionally, the accuracy of LES is highly dependent on the quality of subgrid-scale models employed to represent unresolved scales, and inadequate modeling can lead to erroneous results.

The understanding and characterization of wake aerodynamics continue to evolve as researchers harness new technologies, adopt innovative modeling techniques, and continue to collect and analyze field data from wind farms operating worldwide. Through continued research and development, the wind energy sector hopes to overcome the challenges posed by wake effects and move closer to realizing the full potential of wind power.

The analysis of wind turbine wakes under normal operating conditions is a pivotal component in designing and optimizing wind farms. Over the years, various analytical wake velocity models have been proposed, each bearing unique assumptions and simplifications derived from flow-governing equations.

Popular models for wind turbine wakes under axial inflow conditions from the existing literature include the Jensen model [35], the Katic Model [35,36], the Larsen Model [37], the Frandsen Model [38], the B-P (EPFL) Model [39,40], the Tian Model [41], and the Gao Model [42]. However, the modeling of wakes under yawed wind turbine conditions is not extensively covered in the existing literature, and this represents an area requiring further investigation [43].

2.2. Wake in Yawed Wind Turbines

Yaw in wind turbines pertains to the rotation of a turbine around its vertical axis in relation to the wind’s oncoming direction [44,45]. This ability to adjust and control yaw angles ensures the optimal operation of wind turbines, balancing the maximization of power output against the minimization of structural loads [46,47]. The mechanical systems enabling yaw adjustments are central to the functional design of modern wind turbines, ensuring that they can respond adaptively to fluctuating wind directions [48,49].

When wind turbines operate under yawed conditions, as shown in Figure 1, distinct changes occur in the downstream wake characteristics. The misalignment introduced by yawing the turbine causes a deflection and skewness of the wake, effectively steering it away from its normal trajectory [50,51]. Additionally, this yaw misalignment increases turbulence within the wake, leading to a more chaotic and diffuse wake structure [52].

The phenomena involved in yaw-induced wake redirection have broad implications for wind farm operations. While the altered wake can influence the performance of downstream turbines, potentially leading to power losses and increased turbulence loads [44,52], strategic yaw misalignment can also be beneficial. By actively controlling the yaw angle of turbines, operators can effectively steer the wake away from downstream turbines. This active wake control method can potentially increase the overall power output of wind farms [53,54].

Comprehensive research has to be conducted to further characterize wind turbine wakes under different yaw conditions. Planned future studies, which will involve comparative analyses of wake features under various yaw angles, are anticipated to illuminate the complex dynamics of yaw-induced wakes [7,52,55,56,57].

2.3. Analytical Models for Yawed Wind Turbines

In 2016, Micallef and Sant [44] noted in their study on wind turbine yaw aerodynamics that, regrettably, no empirical models had been put forth to characterize the wake deformation in yaw. A handful of analytical models for predicting the wake characteristics of yawed turbines have been put forward in recent years [43]. These models and their limitations are discussed below.

2.3.1. Jiménez et al. [52] Wake Model for Yawed Conditions, 2010

Introduced in 2010, the wake model by Jiménez et al. [52] adopts a “hat-shaped” approach to predict the wake characteristics in yawed conditions. The model is particularly known for its straightforward computational architecture but has several limitations that need to be addressed.

• Limitations

  -

  The model has a tendency to exaggerate the deflection of the wake [9,43,58,59,60,61].

  -

  Additionally, this model has a tendency to underestimate the maximum velocity deficit [61].

2.3.2. Bastankhah and Porté-Agel [58] Wake Model for Yawed Conditions, 2016

Developed in 2016, the wake model by Bastankhah and Porté-Agel utilizes Gaussian functions to better capture the characteristics of wakes in yawed conditions. The model excels in its computational efficiency but also presents challenges with respect to empirical parameter estimation.

• Advantages

  -

  A cost-effective analytical approach for computational prediction of wake characteristics in the far wake [62].

• Limitations

  -

  The estimation of two empirical parameters is necessary to figure out the initiation of the far wake zone. However, obtaining universal values for these parameters is challenging, as their forecasts heavily rely on computer simulations or experiments. Consequently, the practicality of the wake model is significantly constrained [61].

  -

  Wake is significantly impacted by turbulence intensity, which is not sufficiently taken into consideration in this model [62].

2.3.3. Qian and Ishihara [9] Wake Model for Yawed Conditions, 2018

The wake model by Qian and Ishihara, formulated in 2018, also employs Gaussian functions but with distinct improvements over the Bastankhah and Porté-Agel model. Specifically, this model accommodates varying conditions of ambient turbulence and thrust, enhancing its practical utility.

• Advantages

  -

  In contrast to the Bastankhah and Porté-Agel model, this model incorporates input parameters that are expressed as functions of ambient turbulence intensity and thrust coefficient. This consideration is believed to improve the practicality of the model [61].

• Limitations

  -

  The model has a tendency to underestimate the maximum velocity deficit in scenarios involving yaw angles of 10${}^{\circ }$ and 20${}^{\circ }$ [63].

  -

  The underestimation of maximum velocity deficit is especially evident in the instances of yaw angles $\gamma ={20}^{\circ }$ and $\gamma ={30}^{\circ }$ [61].

  -

  More validation studies are necessary to support the efficacy of this model [61].

2.3.4. General Limitations of Existing Analytical Models for Yawed Wind Turbines

There are several disparities included within the wake models pertaining to yawed turbines. In their study, Dou et al. [43] extensively elucidated the variations in the concept of wake center across various models. In general, experts regard the wake center as the spot where the foremost velocity deficit occurs at each subsequent downstream position. Therefore, in this study, the maximum velocity deficit is considered to be the wake center. Another crucial assumption is that the suggested models for downstream velocity distribution are based on a presumption of symmetry in the streamwise velocity distribution around the center of the wake. However, this assumption is seldom validated by experimental findings. The presence of asymmetry in the flow conditions may significantly impact the operation of the downstream turbine, perhaps resulting in inaccurate predictions of the wake [43].

2.4. Role of Machine Learning in Wind Turbine Wake Modeling

Machine learning (ML) has recently emerged as a transformative paradigm across multiple domains, bringing innovative solutions and improved efficiency to long-standing challenges. Wind energy, specifically in the context of wake modeling, stands as a conspicuous beneficiary of this technological influx. Although conventional approaches like the Blade Element Momentum (BEM) method and Computational Fluid Dynamics (CFD) provide valuable insights, their limitations in accurately capturing complex aerodynamic behaviors or high computational cost have led researchers to consider data-driven approaches [12].

It is salient to note that machine learning’s active application in modeling yawed wake characteristics such as deflection or velocity deficit has been relatively minimal. Nevertheless, its potent influence in related areas of wind turbine wake modeling is irrefutable. For instance, machine learning algorithms like Support Vector Regression (SVR), Artificial Neural Networks (ANNs), and Extreme Gradient Boosting (XGBoost) have been applied to accurately predict wake velocity and wake turbulence intensity [11]. These algorithms have demonstrated their ability to be commensurate with CFD simulations while operating at speeds akin to those of low-fidelity wake models.

Similarly, Genetic Programming (GP), another machine learning technique, has been used to formulate new analytical models for predicting wake velocities and turbulence intensities [64]. This highlights machine learning’s adaptability in generating models that accommodate the complex and non-linear nature of wake effects, including the Atmospheric Boundary Layer (ABL) impacts.

Moreover, machine learning algorithms have been integrated with physics-based models to yield hybrid methodologies that strive for increased generalization. The focus on the generalizability of these models has been a noteworthy avenue of investigation, aiming to ensure that machine learning-based wake models can predict properties across multiple turbines and varying operating conditions [65].

Data-driven approaches have proven effective not only in static models but also in dynamic wind farm wake modeling, utilizing sophisticated deep learning techniques like Long Short-Term Memory networks (LSTMs) [66]. In addition, reinforcement learning has been employed for optimizing the power output of wind farms through yaw-based wake steering, showcasing machine learning’s potential in real-time applications [67].

Nevertheless, while machine learning brings forth numerous advantages, it is crucial to exercise prudence. The limitations in machine learning approaches, particularly in the context of training data and the need for advanced regularization techniques, still present challenges that warrant further research [65].

Although machine learning has yet to be actively applied in creating data-driven models for yawed wake characteristics, it has played a significant role in advancing wind turbine wake modeling. Not only has it improved the accuracy and efficiency of existing models, but it has also opened avenues for real-time optimization and control. The synergy of machine learning with traditional computational methods presents an exciting frontier for the wind energy sector, promising more robust and versatile wake models in the future.

2.5. Original Contributions and Objectives of the Study

The present study endeavors to make contributions to existing knowledge through the following carefully articulated objectives:

• To develop a data-driven symbolic regression model aimed at accurately capturing vital aerodynamic parameters, including velocity deficit at hub height, velocity deficit for a yawed wake center, and wake deflection.
• To move beyond traditional modeling assumptions, such as actuator disc models and Gaussian velocity deficit estimates, in an effort to achieve a more faithful representation of the intricate physics involved in wind turbine operations.
• To employ the actuator line method as the computational foundation of this research, recognizing its merits in better representing complex flow dynamics compared to traditional actuator disc models.
• To make use of symbolic regression’s natural ability for interpretability, with the aspiration of revealing not just empirical relationships but also the underlying physical principles that govern aerodynamic behaviors.
• To conduct a thorough parametric study, covering a meaningful range of yaw angles and thrust coefficients, with the intent of validating the model’s efficacy and broadening its range of applicability.

3. Methodology

3.1. WindSE

This investigation utilizes the WindSE (FY23Q3 Release) software package, a Navier–Stokes solver developed at the National Renewable Energy Laboratory (NREL) [68,69]. WindSE is uniquely equipped with an actuator line methodology, providing superior fidelity in capturing complex flow dynamics, especially in wake studies [70]. The software is built on the FEniCS framework, an open-source platform for the automated finite-element solution for partial differential equations [71].

3.1.1. Unsteady Solver in WindSE

To accurately capture the wake characteristics under yawed conditions, a time-resolved solution for the flow field is essential. The underlying physics are governed by the filtered Navier-Stokes and continuity equations as follows [70]:

$$\rho \left(\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}·\nabla \mathbf{u}\right)=-\nabla P+\mu {\nabla }^2\mathbf{u}-\nabla ·\tau +\mathit{F}\nabla ·\mathbf{u}=0.$$

(1)

The solver employs first-order continuous piecewise finite elements for spatial discretization. The benefit lies in computational efficiency while maintaining acceptable fidelity.

Temporal discretization is realized via a fractional-step method. A predicted fluid velocity field at the next time step, ${\mathit{u}}^{*}$, is first computed, followed by a pressure-correction step to enforce the divergence-free constraint.

The total viscosity, $\nu$, in the model includes subgrid-scale eddy viscosity, formulated as:

$${\nu }_T={(C\Delta )}^2\left|\mathit{S}\right|\mathit{S}=\frac{1}{2}\left(\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T\right).$$

(2)

In this formulation, C denotes the Smagorinsky constant, presently set at $0.17$. The symbol $\Delta$ signifies the representative length scale for each computational cell. The strain rate tensor, $\mathbf{S}$, is the resolved strain within the fluid domain.

3.1.2. Actuator Line Method in WindSE

The implementation of blade geometry and rotor induction effects in WindSE utilizes the external forcing term, $\mathit{F}$, described in Equation (1). This is accomplished through the actuator line method, which spatially distributes time-dependent blade forces. Specifically, the actuator line method employs a summation of discrete forces, each modeled by Gaussian-distributed point forces [70]. The mathematical representation of this forcing term is:

$$\mathit{F}(x,y,z,t)=-\sum _{j=1}^N{\mathit{f}}_j\left(x_j,y_j,z_j,t\right)\frac{1}{{\epsilon }^3{\pi }^{3/2}}exp\left(-\frac{{\left|{\mathit{d}}_j\right|}^2}{{\epsilon }^2}\right).$$

Here, N represents the count of blade discretization segments, and $\epsilon$ governs the Gaussian width. The distance vector ${\mathit{d}}_j$ indicates the separation between any fluid point and the jth actuator point.

The actuator force, ${\mathit{f}}_j$, constitutes the vector sum of lift and drag forces, whose magnitudes are represented as:

$$\begin{array}{cc}& \mathcal{L}(x,y,z,t)=\beta \frac{1}{2}{C}_l\left(\alpha \right)\rho cw{\left|u_{rel}(x,y,z,t)\right|}^2\hfill \\ & \mathcal{D}(x,y,z,t)=\beta \frac{1}{2}{C}_d\left(\alpha \right)\rho cw{\left|u_{rel}(x,y,z,t)\right|}^2.\hfill \end{array}$$

The local angle of attack, $\alpha$, is functionally dependent on the relative velocity and the blade twist. The tip-loss factor, $\beta$, is included to moderate the force near the blade tip and is expressed as:

$$\beta =\frac{2}{\pi }{cos}^{-1}\left[exp\left(\frac{3}{2}\frac{(R-r)}{rsin\left({\alpha }_{rp}\right)}\right)\right].$$

Finally, the rotor power W is formulated as:

$$W=\omega \sum _{j=1}^N{r}_j\left({\mathit{f}}_j·{\widehat{\mathbf{n}}}_j\right).$$

This mathematical framework provides a comprehensive yet computationally efficient method to emulate the complex physics involved in rotor-blade interactions within the fluid domain.

3.2. Symbolic Regression

In an era where artificial intelligence (AI) has found applications ranging from mundane household utilities to advanced medical diagnostic systems [72,73,74,75], a plethora of analytical methodologies have emerged to tackle complex, data-driven challenges. One such method, critical to the discourse of this study, is regression analysis. This statistical approach is pivotal for discerning and quantifying the intricate relationships among variables [76,77].

Among the diverse array of regression techniques, symbolic regression distinguishes itself. Unlike conventional regression methods, which necessitate an initial hypothesis regarding the model’s form, symbolic regression is uniquely capable of both identifying the optimal model structure and fine-tuning the associated parameters [78].

Symbolic regression excels at approximating mathematical functions through a rigorous exploration of the formulaic space, while also ensuring that the derived models are readily interpretable [79,80]. Two prevailing optimization techniques used in symbolic regression are Genetic Programming (GP) [81] and Simulated Annealing (SA) [82,83]. While both employ tree-structured representations to encapsulate mathematical expressions, they diverge substantially in their optimization mechanisms.

In this study, we have opted for Simulated Annealing as our optimization technique. SA is proficient at initiating its algorithmic search with a broad scope, subsequently refining its focus based on the iterative adjustment of parameters and probabilistic acceptance or rejection of proximal solutions. The primary goal of our symbolic regression implementation is to strike an optimal balance between the complexity of the model and the fidelity with which it represents the data. To realize this objective, we employed Pareto Simulated Annealing, a Multi-Objective Combinatorial Optimization (MOCO) method, which refines solutions based on multiple objectives rather than a single metric.

The implementation was executed on an AMD Ryzen™ 9 5900 CPU with 24 threads using the TuringBot Python library and consumed approximately 3000 CPU hours in total.

3.3. Data Generation

3.3.1. NREL 5-MW Wind Turbine

The National Renewable Energy Laboratory’s (NREL) 5-MW offshore wind turbine serves as a benchmark in the analysis of wind turbine wakes under yawed conditions. This standardized model is characterized by a rotor diameter of 126 m and a hub height of 90 m, and it is specifically designed for offshore applications. With a rated power of 5 MW, it has been instrumental in providing a consistent framework for understanding wake behavior when the rotor is misaligned with the incoming wind direction [84].

The aerodynamic attributes of this particular model are conducive for studying wake deflection and recovery under yaw misalignment. Given the large rotor diameter and high hub height, the turbine provides an ideal scale for scrutinizing the subtleties of wake flow properties during yawed conditions. Consequently, the NREL 5-MW turbine becomes a pivotal tool in investigating how yaw adjustments impact the downwind energy capture and turbulence intensity [85].

Often employed in Computational Fluid Dynamics (CFD) studies, the NREL 5-MW turbine enables high-fidelity simulations that illuminate the complex interactions occurring in the wake when the turbine operates under yawed states [86]. Due to its widespread adoption and well-documented specifications, the NREL 5-MW wind turbine serves as an invaluable reference model for wake studies under yawed conditions, aiding in both the calibration of computational models and the validation of empirical findings [59].

3.3.2. Case Setup

The aim of this computational study is to investigate the aerodynamic behavior and wake dynamics of the NREL 5-MW wind turbine under different yaw conditions. A series of five simulations are conducted, including a baseline scenario with no yaw, as well as cases with yaw angles of ${10}^{\circ }$, ${20}^{\circ }$, ${30}^{\circ }$, and ${40}^{\circ }$.

For these simulations, the actuator line method (ALM) is employed to represent the turbine. The rotor operates at a speed of 9.155 RPM, and blade aerodynamic features are configured using chord and Gaussian weighting factors set to $1.0$ and $2.0$, respectively.

The computational domain is box-shaped and discretized based on the rotor diameter D of 130 m. The domain spans from $-2D$ to $20D$ in the streamwise direction, $-2D$ to $2D$ in the spanwise direction, and approximately 0 to $4D$ in the vertical direction. The grid consists of 190 nodes in the streamwise direction, 35 nodes in the spanwise direction, and 35 nodes in the vertical direction.

Mesh refinement is implemented via a split-type strategy that modifies $83.33\%$ of the cells below a height of 260 m. Additional custom refinements are also applied in the streamwise direction to capture the wake dynamics more accurately. Linear finite elements are utilized for both pressure and velocity field calculations.

The inlet features a uniform velocity profile with a hub-height velocity of 10 m/s. Boundary conditions include inflow conditions at the upwind boundary, stress-free conditions at the downwind boundary, free-slip conditions at the lateral and top boundaries, and no-slip conditions at the bottom surface.

This setup offers a robust framework for scrutinizing the aerodynamic performance and wake behavior of wind turbines under varying yaw conditions, while maintaining a reasonable computational expense.

3.4. Procedure: Yawed Wake Model Development through Symbolic Regression

3.4.1. Objective

The primary objective of this research is to construct a symbolic regression model optimized for a rigorous analysis of pivotal aerodynamic parameters related to wind turbines. The parameters in focus are: wake deflection $y/D$, velocity deficit $\Delta U$ at the hub height in the absence of yaw effects, and $\Delta U$ when exposed to yawed wake conditions. By deeply understanding these parameters, we aim to facilitate optimized wind turbine operations across a spectrum of yaw angles.

3.4.2. Input Parameters

To capture the intricacies of the aerodynamic behaviors associated with wind turbines, our model integrates the following salient input parameters:

• Yaw angle, $\gamma$, measured in radians;
• Downstream distance normalized to the rotor diameter, represented as $x/D$;
• Yaw-specific thrust coefficient, defined as $C_{T_{\gamma }}=C_{T_{\gamma =0}}\times cos\left(\gamma \right)$;
• Ambient turbulence intensity, $I_a$, capturing the environmental dynamics the turbine operates within.

The strategic selection of input parameters is intrinsically aligned with the primary objective of this research: to construct a symbolic regression model designed for an in-depth analysis of crucial aerodynamic parameters affecting wind turbines. Specifically, the yaw angle $\gamma$ serves as a foundational input that directly influences wake deflection $y/D$ and velocity deficit $\Delta U$, thus offering insight into the turbine’s performance across a range of yaw conditions. This is particularly relevant for our focus on optimizing operations over diverse yaw angles. The downstream distance normalized to the rotor diameter, $x/D$, adds a spatial dimension to the model, enabling a granular understanding of how wake deflection and velocity deficit evolve at varying distances from the turbine. Such understanding is paramount for optimizing the spatial configuration of wind farms. Furthermore, the yaw-specific thrust coefficient $C_{T_{\gamma }}$ enhances our ability to precisely quantify the nuanced aerodynamic behavior under yawed conditions. Finally, the inclusion of the ambient turbulence intensity $I_a$ permits the model to capture the interplay between the wind turbine’s operational parameters and the environmental conditions it faces. Therefore, each chosen input parameter serves as a sophisticated tool in dissecting the aerodynamic phenomena under study, directly contributing to our objective of achieving optimized wind turbine operations. This meticulous parameterization forms the crux of our symbolic regression model, ensuring it is well-suited for the rigorous analytical tasks set forth by our research aims.

3.4.3. Symbolic Regression

Our approach hinges on a sophisticated symbolic regression algorithm, tailored for precision and efficiency.

• Automated Input Selection: The algorithm autonomously sifts through potential input variables, zeroing in on those of paramount importance for creating mathematical representations of $y/D$, $\Delta U$ at hub height, and $\Delta U$ of yawed wake.
• Optimization Technique: The optimization leverages the prowess of Simulated Annealing (SA). SA is prized in computational research for its unparalleled ability to perform exhaustive searches within vast solution spaces, ensuring that the optimal solution is approached.
• Balancing Complexity and Accuracy: To strike the delicate balance between a model’s complexity and its representational accuracy, we have intertwined Pareto Simulated Annealing within our approach. This method is a specialized variant of Multi-Objective Combinatorial Optimization (MOCO) and ensures our model remains both versatile and true to the data it represents.

3.4.4. Mathematical Operators in Symbolic Regression

To ensure our model’s adaptability and resilience, we have incorporated a diverse set of mathematical operators:

• Multiplication;
• Division;
• Exponentiation;
• Square root function;
• Trigonometric functions.

The selection of mathematical operators for incorporation into the symbolic regression model has been carried out with calculated intention, aligning closely with our research objective of facilitating a nuanced analysis of key aerodynamic parameters affecting wind turbines. Multiplication and division serve as fundamental building blocks, permitting the model to establish basic proportional relationships among the variables, which constitute an essential feature for understanding linear and inverse dependencies. The inclusion of exponentiation and the square root function adds a layer of complexity, enabling the model to capture nonlinear relationships that are often inherent in aerodynamic phenomena. These functions thereby enhance the model’s ability to represent more intricate patterns in the data, thus aligning closely with the objective of a rigorous analytical framework. Trigonometric functions, on the other hand, are particularly relevant for our focus on yaw angles and their corresponding effects. Given that trigonometric functions naturally describe oscillatory behavior and angular relationships, their inclusion is strategically poised to yield valuable insights into the aerodynamic parameters that are inherently angle-dependent, such as yaw-specific thrust coefficients. Collectively, the chosen operators ensure that the symbolic regression model is not only adaptable and resilient but also adequately equipped for the detailed and multifaceted examination mandated by our research aims.

3.4.5. Model Training and Validation

Integral to the development of a robust symbolic regression model is the manner in which the data are managed and the model is trained, validated, and tested. We carefully curated our approach to guarantee a model that is both predictive and interpretable.

Data Management: A stratified sampling approach was used to segment the dataset, ensuring that the training, validation, and testing datasets represent the entire spectrum of yaw angles and other aerodynamic behaviors. Specifically, 70% of the data was used for training, 15% for hyperparameter tuning (validation), and the remaining 15% for testing.

Hyperparameter Tuning: To further refine our model, we employed a grid search coupled with hold-out validation. This iterative process fine-tuned the model’s key hyperparameters, such as the coefficient $c_1$ in Equation (5), coefficient $c_2$ in Equation (8) and coefficients $c_3$ and $c_4$ in Equation (11).

Prevention of Overfitting: In the current investigation, we judiciously segmented the dataset into separate partitions for rigorous model development and performance assessment: 70% was allocated for training, 15% for hold-out validation, and the remaining 15% for testing. Utilizing symbolic regression, we endeavored to derive functional forms that encapsulate the intrinsic physical principles governing the system. To that end, we incorporated a Multi-Objective Combinatorial Optimization (MOCO) technique. This approach was crucial for traversing the intricate solution space with the dual aims of simplicity and accuracy in the resulting functional forms. By adopting this strategy, we effectively mitigated the propensity for overfitting, a prevalent issue in black-box machine learning frameworks [87,88]. The resulting Equations (5) and (8) serve as tangible evidence supporting the model’s robustness; their structural simplicity, in conjunction with high predictive efficacy, strongly indicates that our model is not over-optimized to the training data. It is worth noting that the integration of MOCO with symbolic regression introduces considerable computational complexity to the training process. Furthermore, due to the model’s focus on determining precise functional forms, a k-fold validation strategy was eschewed to avoid potential model instability, making the hold-out method a more suitable choice for this particular study.

Model Evaluation Metrics: Two primary metrics were used to assess the model’s performance:

• $R^2$ (Coefficient of Determination): A measure that illustrates how well the model predictions approximate the real data points. An $R^2$ value of 1 indicates perfect predictions, while values closer to 0 indicate a model that fails to capture the underlying data trend.
• RMSE (Root Mean Square Error): It provides a quantifiable measure of how far off our model predictions are from the actual values. Lower RMSE values signify that the model predictions are close to the true values, while higher values suggest potential issues with the model or underlying data.

Post-training, the model was rigorously validated using the validation dataset, and hyperparameters were adjusted to achieve the best balance between precision and generalizability. The final model, post-tuning, was then tested on the reserved test dataset to ensure its performance in predicting unseen data.

The combination of strategic data management, meticulous hyperparameter tuning, and rigorous evaluation has resulted in a symbolic regression model tailored for analyzing pivotal aerodynamic parameters related to wind turbines.

4. Results and Discussion

Wind turbines, due to their imposing structures and intricate engineering, are consistently exposed to myriad aerodynamic forces. These forces play a pivotal role in determining the performance, longevity, and efficiency of the turbines. Hence, the demand for accurate modeling of these forces and understanding their interplay is incessant. This section demystifies the key aerodynamic parameters associated with wind turbines and elucidates the new models proposed in this work to capture their behaviors.

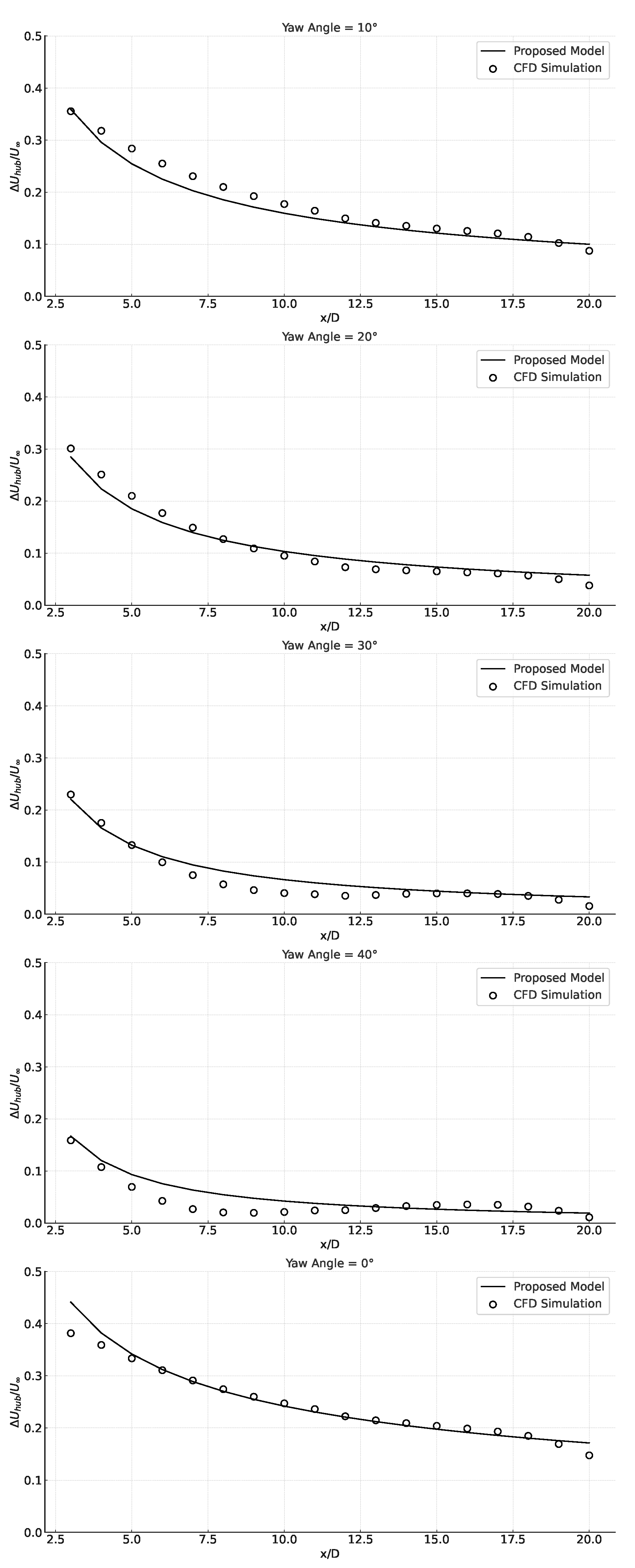
4.1. Velocity Deficit at Hub Height ($\Delta U_{\mathit{hub}}/U_{\infty }$)

Velocity deficit at the hub height, denoted as $\Delta U_{\mathrm{hub}}/U_{\infty }$, is a critical parameter that sheds light on the reduction in wind speed as it interacts with the turbine blades at the hub height. Mathematically, it is expressed as:

$$\Delta U_{\mathrm{hub}}/U_{\infty }=\frac{U_{\infty }-U_{\mathrm{hub}}}{U_{\infty }},$$

(3)

where $U_{\infty }$ represents the undisturbed wind speed, and $U_{\mathrm{hub}}$ is the wind speed at the hub height after the wind interacts with the turbine. Computational Fluid Dynamics (CFD) simulations, especially those with yaw considerations, are pivotal in deriving $U_{\mathrm{hub}}$. Grasping this parameter is paramount for optimizing turbine placements in wind farms, given its implications for downstream turbine performances. This relationship is given by:

$$\Delta U_{\mathrm{hub}}/U_{\infty }=f(\gamma ,X/D,C_{T_{\gamma }},I_a).$$

(4)

Our new model for this relationship is:

$$\Delta U_{\mathrm{hub}}/U_{\infty }=\frac{c_1\times C_{t,\gamma }}{\sqrt{{\left(\frac{x}{D}\right)}^{2sin\left(\gamma \right)+1}\times I_a}},$$

(5)

with $c_1=0.11$.

The discussion surrounding the velocity deficit at the hub height, $\Delta U_{\mathrm{hub}}/U_{\infty }$, serves as a robust validation of our symbolic regression model, notably when compared to Computational Fluid Dynamics (CFD) simulations. Our model, described by Equation (5), introduces a nuanced understanding of the relationship between velocity deficit and several key aerodynamic parameters, including yaw-specific thrust coefficient $C_{t,\gamma }$, downstream distance normalized by rotor diameter $\frac{x}{D}$, and ambient turbulence intensity $I_a$. This relationship is critical for understanding wind–turbine interactions and wake characteristics, with direct implications for optimized wind farm operations.

The equation includes the variable $C_{t,\gamma }$ in the numerator, emphasizing its importance in affecting the velocity deficit at the hub height. Higher values of this yaw-dependent thrust coefficient would lead to a greater velocity deficit, in line with the physical intuition that a larger thrust coefficient entails stronger wind–turbine interactions.

On the other hand, the denominator includes a term ${\left(\frac{x}{D}\right)}^{2sin\left(\gamma \right)+1}\times I_a$ under a square root. This term combines the downstream distance $\frac{x}{D}$ with yaw angle $\gamma$ and ambient turbulence intensity $I_a$. It indicates that the velocity deficit is more sensitive to downstream distance as the yaw angle increases, reflecting the yawed flow’s propensity to spread the wake. In addition, higher ambient turbulence levels would help recover the wind speed downstream, thus reducing the velocity deficit.

The term $sin\left(\gamma \right)$ in the equation further emphasizes the yaw angle’s critical role in the velocity deficit. Hence, the model provides wind farm operators with the ability to predict wind speed at hub heights more accurately for varying yaw angles and downstream distances. Such predictive prowess allows for more optimized spacing and placement of turbines to minimize wake interference, fulfilling the overarching aim of wind farm optimization.

The model’s reliability is further corroborated by Figure 2, which presents a compelling alignment between our symbolic regression predictions and the CFD simulations. Despite the highly nonlinear nature of the aerodynamic phenomena being studied, the consistency between these datasets underlines the model’s utility and applicability in real-world scenarios.

It is worth noting the slight mismatch between the model and CFD simulations at a yaw angle of zero and $x/D<5$. While this warrants acknowledgment, these discrepancies do not significantly detract from the model’s utility in the context of our specific research objective. Given that our primary focus is on wake characteristics at higher $x/D$ values—which are more pertinent for wind farm studies—the model’s minor inconsistencies at lower $x/D$ values and zero yaw angle can be considered acceptable limitations.

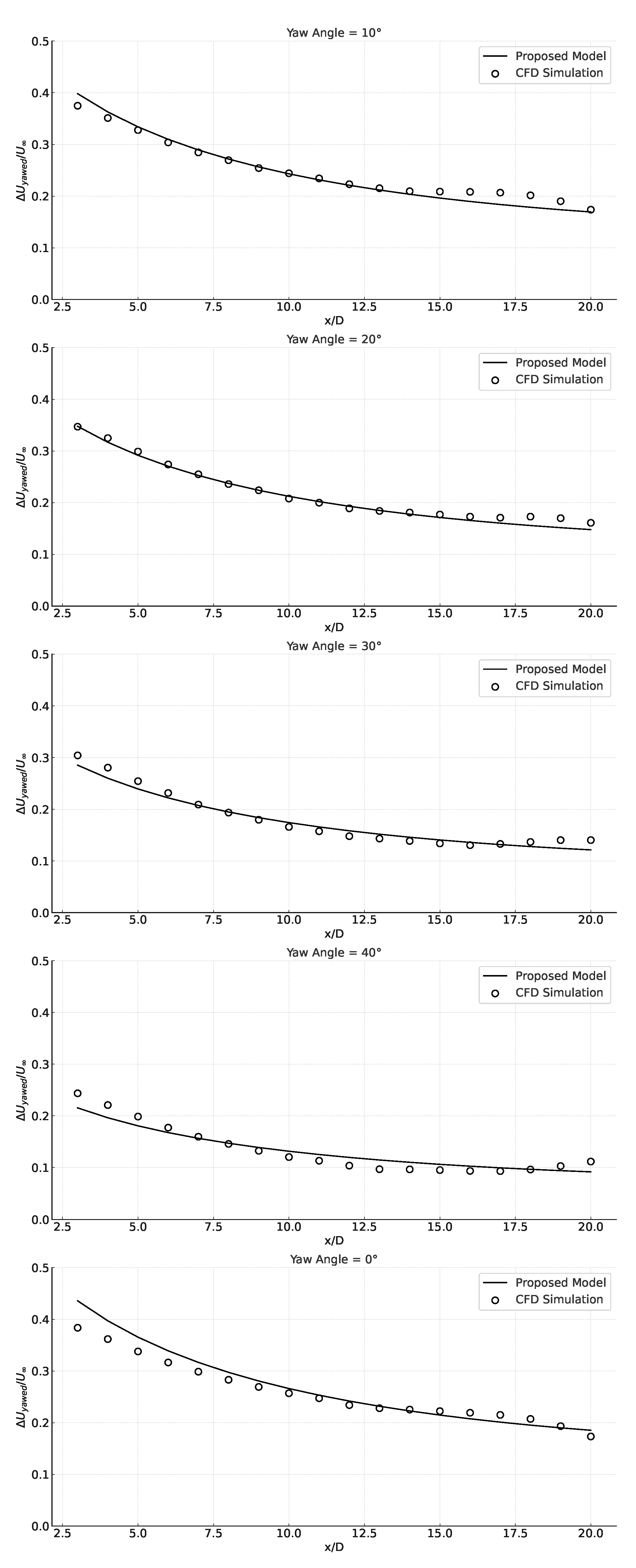
4.2. Maximum Velocity Deficit of Yawed Wake ($\Delta U_{\mathit{yawed}}/U_{\infty }$)

Yaw-induced maximum velocity deficits, represented by $\Delta U_{\mathrm{yawed}}/U_{\infty }$, are pivotal in understanding the turbine’s wake behavior under varying yaw conditions. It is described as:

$$\Delta U_{\mathrm{yawed}}/U_{\infty }=\frac{U_{\infty }-U_{\mathrm{yawed}}}{U_{\infty }}.$$

(6)

This modeling becomes indispensable when devising strategies like “wake steering”, where turbines are intentionally misaligned with the wind direction to deflect the wake and optimize performance of downstream turbines. Furthermore, understanding the yaw-induced maximum velocity deficit is also essential for analyzing fatigue loads due to yaw misalignments. The underlying relationship is:

$$\Delta U_{\mathrm{yawed}}/U_{\infty }=f(\gamma ,X/D,C_{T_{\gamma }},D,I_a).$$

(7)

In this work, we propose:

$$\Delta U_{\mathrm{yawed}}/U_{\infty }=C_{t,\gamma }^{sin\left(\gamma \right)+1}\times {\left(I_a\times {\left(\frac{x}{D}\right)}^2\right)}^{c_2\times \frac{x}{D}},$$

(8)

with $c_2=0.0197$.

The yawed wake velocity deficit, as captured by this equation, encapsulates the complex interplay of yaw angle with other influential parameters. The equation suggests a non-linear relationship, emphasizing the significant role of yaw misalignment in shaping the wake profile. The exponent $sin\left(\gamma \right)+1$ applied to $C_{t,\gamma }$ accentuates the yaw angle’s substantive role, implying that even a small deviation in yaw angle could lead to considerable changes in the velocity deficit. The term $I_a\times {\left(\frac{x}{D}\right)}^2$ illustrates the combined effects of turbulence and downstream distance, which are further modulated by $c_2\times \frac{x}{D}$, an empirical constant tailored to align the model with observed data. Such insights can be invaluable for strategies like wake steering, guiding operators on the degree of yaw misalignment for desired wake deflections, and reduced turbine fatigue.

The efficacy of the proposed model in predicting yaw-induced maximum velocity deficits is visually portrayed in Figure 3. This figure juxtaposes the symbolic regression’s outcomes with the findings from the CFD simulations. The CFD results are vividly illustrated using scatter plots, while the proposed model’s predictions are rendered through line plots. A notable alignment between the two datasets is clearly discernible, underpinning the model’s ability to accurately replicate CFD results across varied conditions.

The discussion of yaw-induced maximum velocity deficits, denoted as $\Delta U_{\mathrm{yawed}}/U_{\infty }$, merits particular attention in evaluating the robustness of our symbolic regression model against Computational Fluid Dynamics (CFD) simulations, as depicted in Figure 3. Our model, succinctly represented by Equation (8), exhibits substantial congruence with the CFD data, particularly at higher $x/D$ values. This level of agreement serves as a testament to the model’s suitability for practical applications, particularly in the realm of wake steering strategies aimed at optimizing the performance of downstream turbines. Nonetheless, it is imperative to acknowledge a marginal divergence between the model and CFD simulations at lower $x/D$ values across nearly all yaw angles. While this might initially appear to be a limitation, it is worth emphasizing that our principal research objective is focused on wake characteristics at higher $x/D$ ranges, where the model demonstrates considerable accuracy. In this light, the slight discrepancies at lower $x/D$ values can be deemed tolerable given the broader context of our study aims. These minor deviations do not significantly undermine the model’s overarching efficacy in furnishing a nuanced, quantitative understanding of yaw-induced maximum velocity deficits, thereby aligning well with our end goal of optimized wind farm operations.

4.3. Wake Deflection $y/D$

Wake deflection, denoted as $y/D$, is a pivotal metric for understanding the sideways drift of turbine wakes. It can be described as:

$$y/D=\frac{\mathrm{Wake}\mathrm{deflection}}{\mathrm{Diameter}\mathrm{of}\mathrm{the}\mathrm{wind}\mathrm{turbine}}.$$

(9)

An accurate model for $y/D$ becomes essential in wind farms in order to comprehend how wakes from one turbine might affect adjacent turbines, potentially influencing their efficiency and causing wear. The derived relationship is:

$$y/D=f(\gamma ,X/D,C_{T_{\gamma }},D,I_a).$$

(10)

Our new equation for this is:

$$y/D={\left(\frac{c_3\times C_{t,\gamma }}{{\left(c_4\times \frac{x}{D}\right)}^{\sqrt{sin\left(\gamma \right)}}}\times {\left(\frac{x}{D}\right)}^2\times I_a\right)}^{\frac{1}{2}},$$

(11)

where $c_3=5.56$ and $c_4=0.00089$.

The proposed equation for wake deflection $y/D$ serves as a comprehensive analytical tool that captures the complex interrelationships among key aerodynamic variables. Central to this equation is the yaw-specific thrust coefficient $C_{t,\gamma }$, whose presence in the numerator underlines its pivotal role in dictating the wake’s lateral behavior. Further sophistication is introduced by the $sin\left(\gamma \right)$ term, enclosed within a square root function. This mathematical nuance accentuates the heightened sensitivity of wake deflection to changes in yaw angles. When coupled with the exemplary predictive fidelity demonstrated in Figure 4, where a compelling alignment between the symbolic regression outcomes and CFD data is evident, the equation gains substantial empirical validation. The robustness of the model is corroborated by an impressive $R^2$ value of 0.98, substantiating its accuracy. Therefore, this equation serves not merely as a theoretical construct but also as a pragmatic instrument. Wind farm designers can judiciously leverage its predictive power to anticipate the lateral displacements of wakes, thereby optimizing turbine placement to both minimize detrimental wake interactions and maximize overall farm efficiency.

5. Conclusions and Future Work

5.1. Summary of Findings

In the specialized domain of wind energy engineering, a critical research challenge is optimizing the aerodynamic properties of wind turbines, which is crucial for enhancing both power extraction efficiency and structural longevity. The present research advances this line of inquiry by employing a hybrid methodology, integrating symbolic regression algorithms and the actuator line method (ALM) for a comprehensive aerodynamic evaluation. Symbolic regression was specifically deployed for data-driven quantification and modeling of imperative aerodynamic parameters, notably velocity deficit and wake deflection, which have a direct impact on turbine power extraction and downstream wake interaction. Simultaneously, ALM acted as the underpinning computational platform, facilitating high-fidelity Computational Fluid Dynamics (CFD) simulations that capture complex flow structures, including tip vortices and blade–boundary layer interactions.

This integrated approach has distinct advantages over traditional actuator disc models and Gaussian wake formulations, by providing a multi-faceted, physically consistent, and empirically validated representation of the underlying aerodynamic phenomena.

The primary findings of this research work are:

• The symbolic regression model demonstrated the ability to characterize aerodynamic parameters, notably velocity deficit and wake deflection.
• By moving beyond actuator disc models and Gaussian velocity deficit assumptions, the study approached a more nuanced depiction of the physics involved in wind turbine operations.
• The actuator line model served as the computational foundation, highlighting its potential in representing complex flow dynamics.
• Symbolic regression’s inherent interpretability facilitated insights into the underlying physical principles that govern wind turbine aerodynamics.
• The extensive parametric study encompassed a diverse range of yaw angles and thrust coefficients, reinforcing the model’s adaptability and potential applicability.

In summary, this study integrates symbolic regression techniques with high-fidelity Computational Fluid Dynamics (CFD) simulations via the actuator line method (ALM) for wind turbine aerodynamic analysis. The practical implications of this research focus on the optimization of wind turbine design and operational planning. Specifically, the model effectively quantifies key aerodynamic parameters such as yaw-induced maximum velocity deficits and wake deflections. These parameters are critical for engineering decisions concerning turbine placement and layout to optimize energy yield. Given the range of yaw angles and thrust coefficients tested in this study, the model offers broad applicability for wind farm design considerations.

5.2. Future Directions

Given the advancements and findings of this research, it is evident that a vast expanse of exploration lies ahead. The potential demonstrated by the models developed, combined with the evolving landscape of computational techniques and wind energy practices, lays the groundwork for future endeavors. The authors, in their work, have developed a non-symmetrical analytical model for velocity profile distribution in uniform inflow. This model addresses the maximum velocity deficit and the velocity deficit at the wake center. In future studies, the authors plan to develop a model for yawed input. In climatic conditions marked by highly variable or turbulent winds, additional research may be needed to fine-tune the model for those specific scenarios. In conclusion, this study serves as a testament to the advancements in understanding wind turbine aerodynamics, setting the stage for future studies focused on further refinement and exploration.