A Deep-Sea Broadband Sound Source Depth Estimation Method Based on the Interference Structure of the Compensated Beam Output
Abstract
:1. Introduction
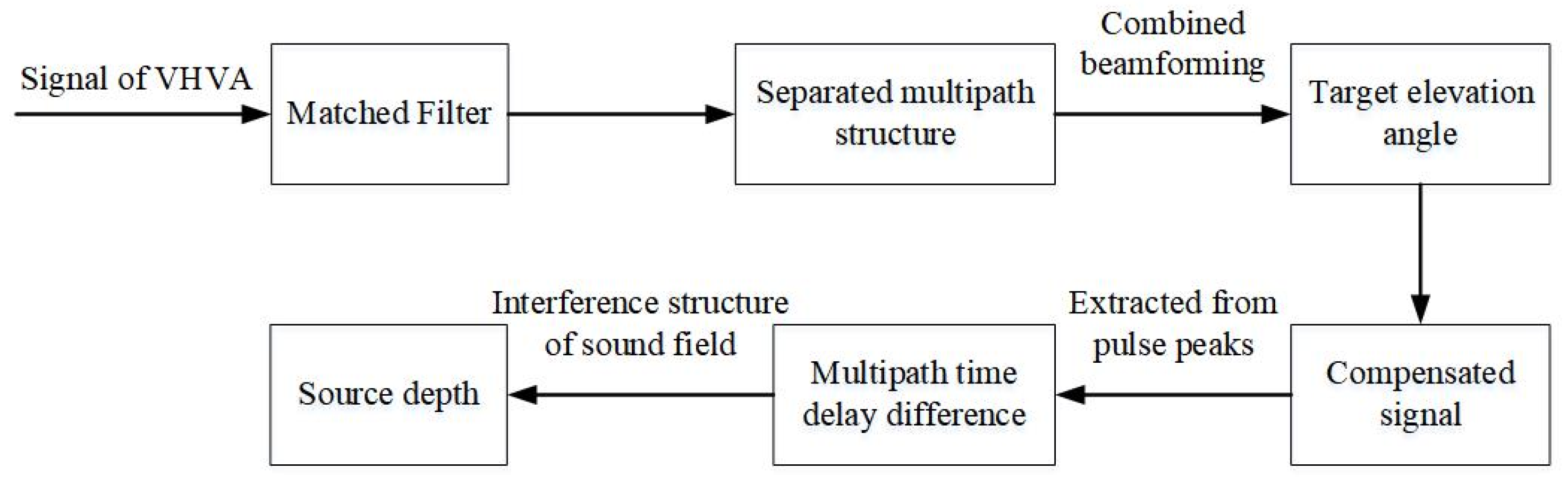
2. Methods
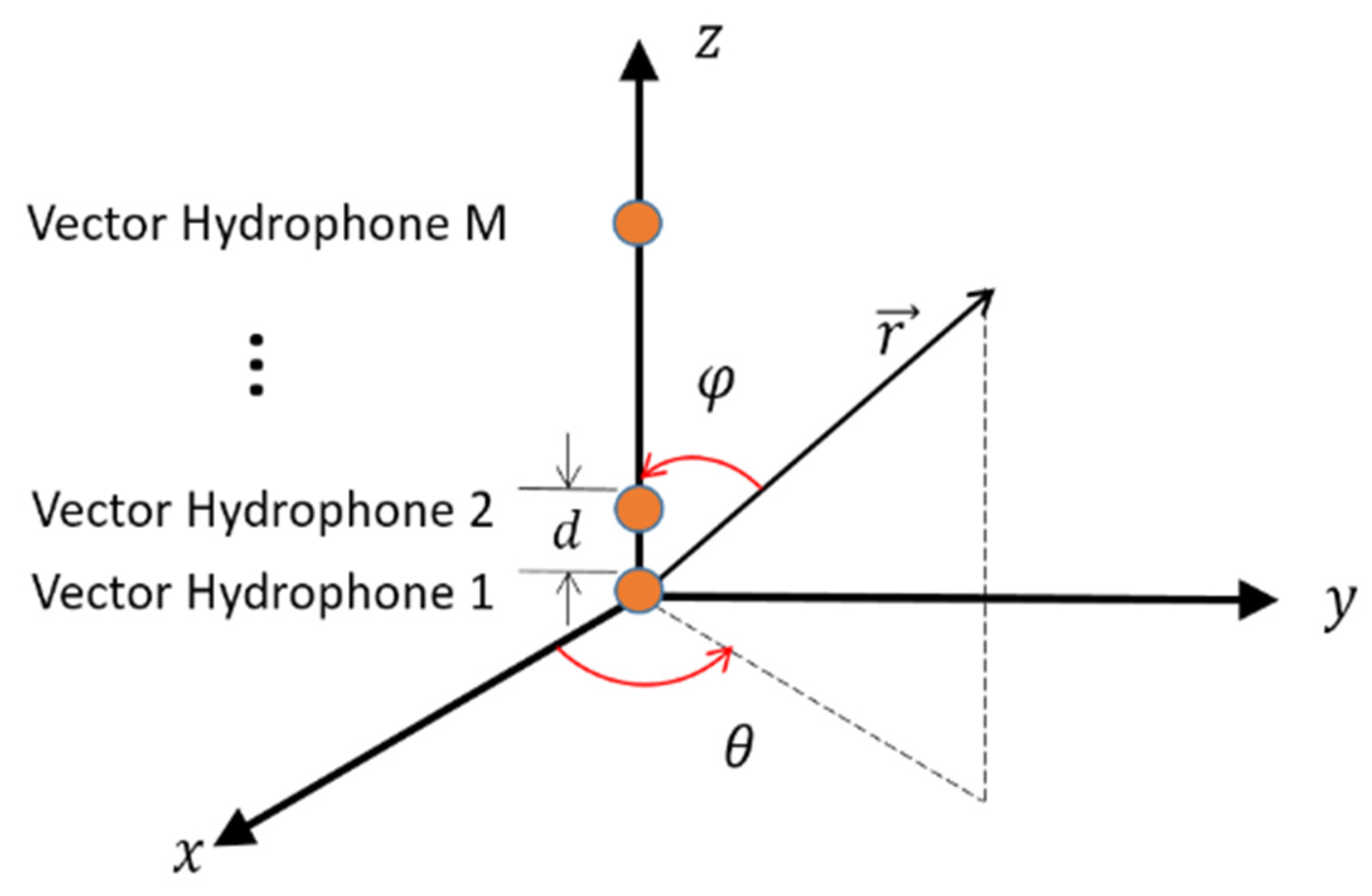
2.1. Elevation Angle Estimation
2.2. Depth Estimation
2.2.1. In the Direct Wave Zone
2.2.2. Outside the Direct Wave Zone
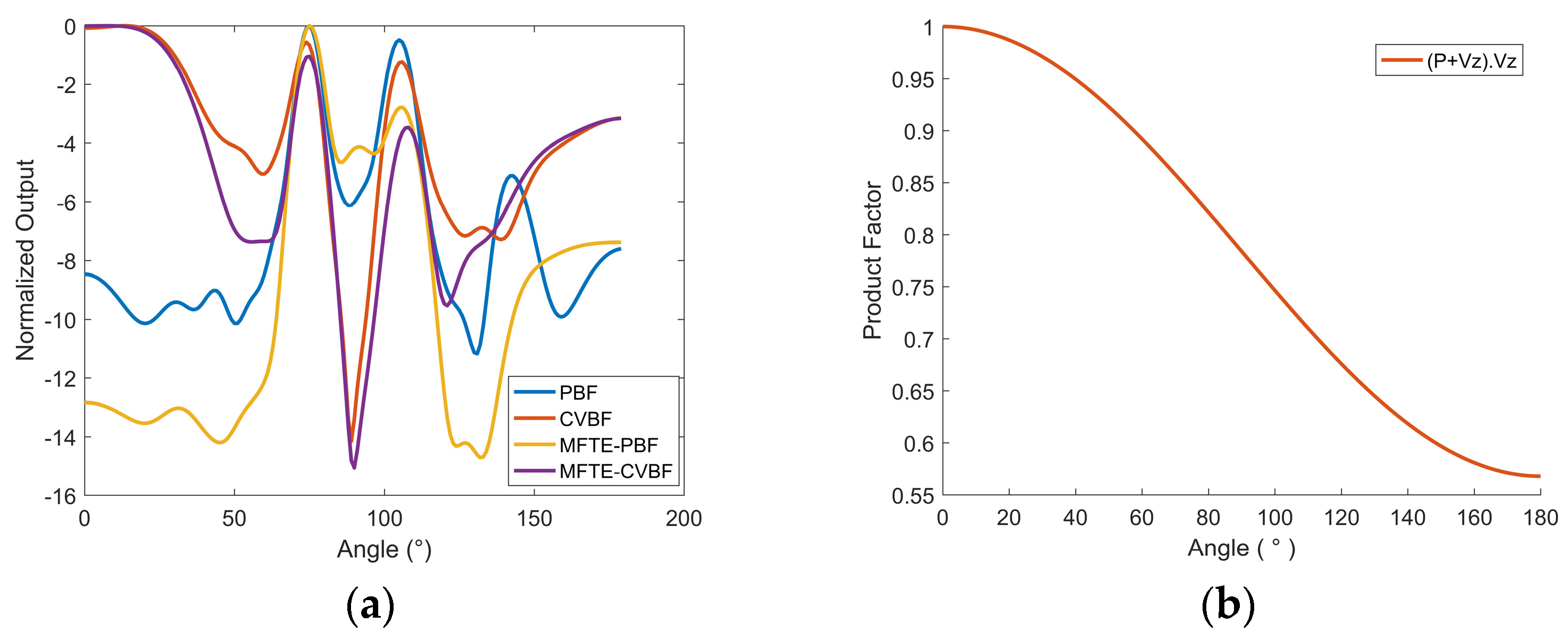
3. Simulation
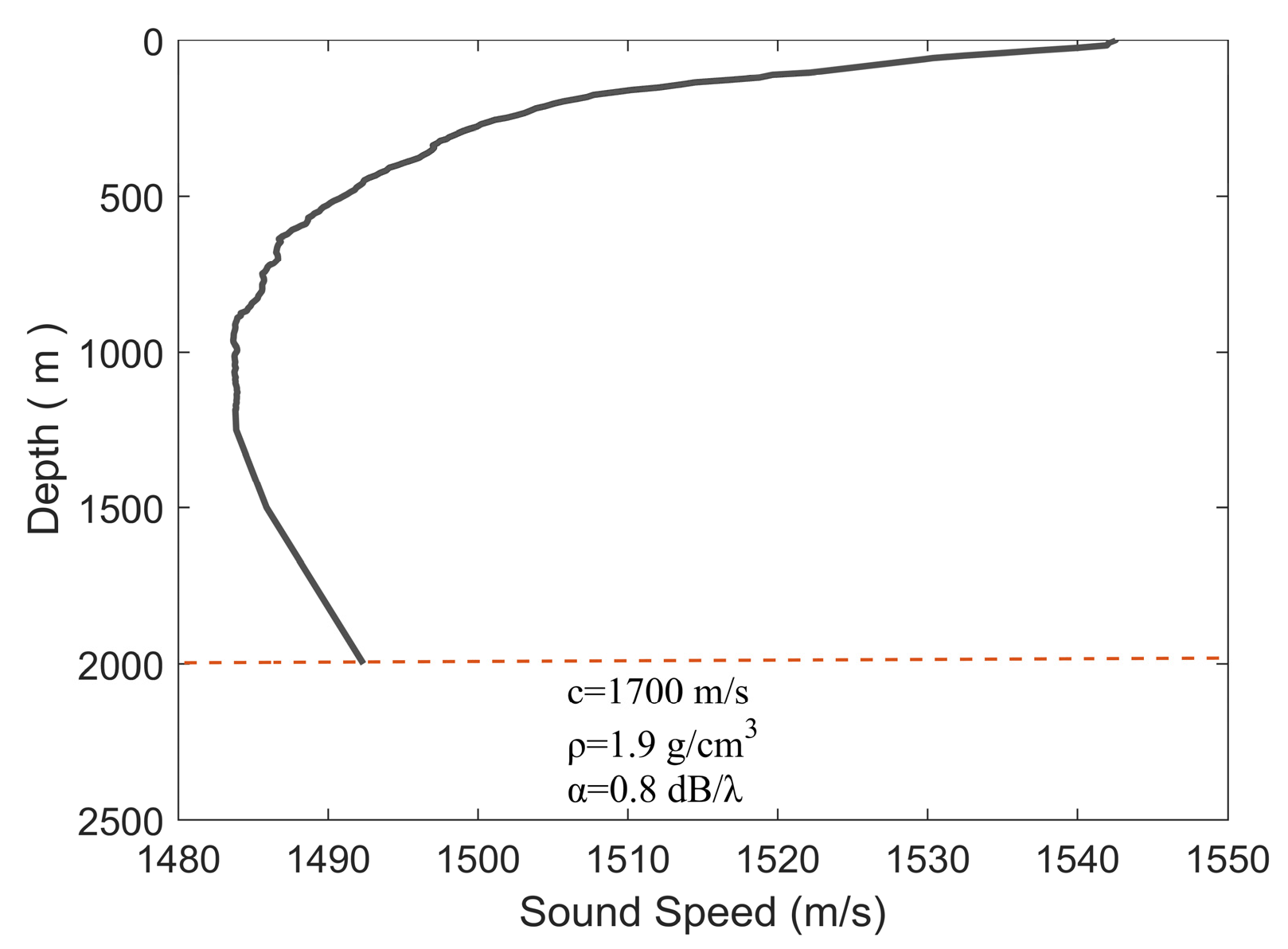
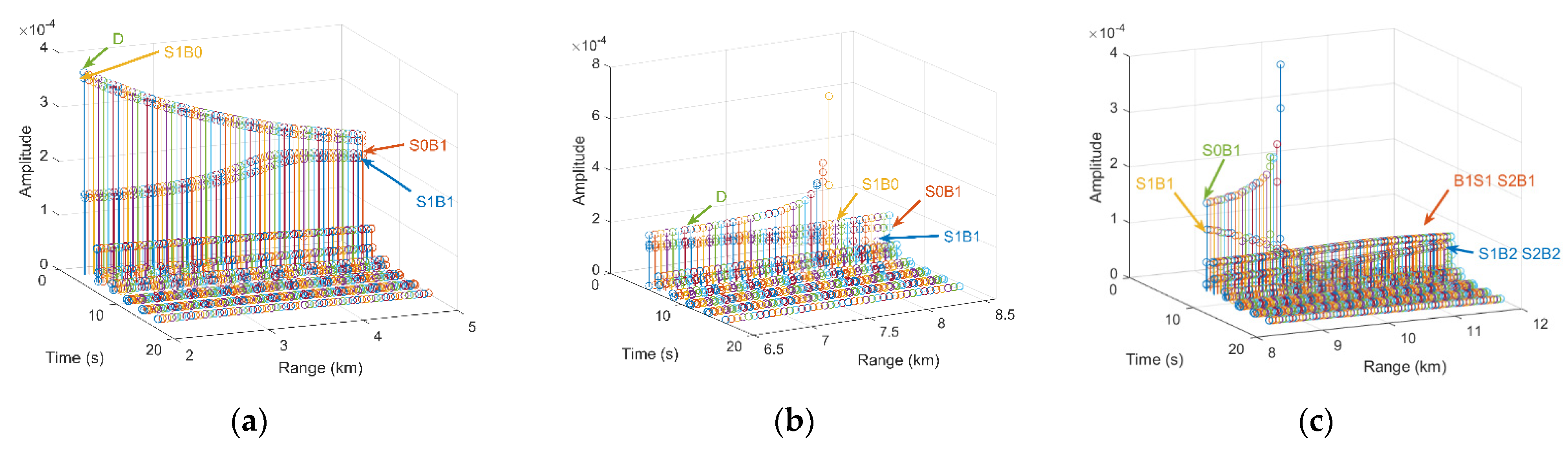
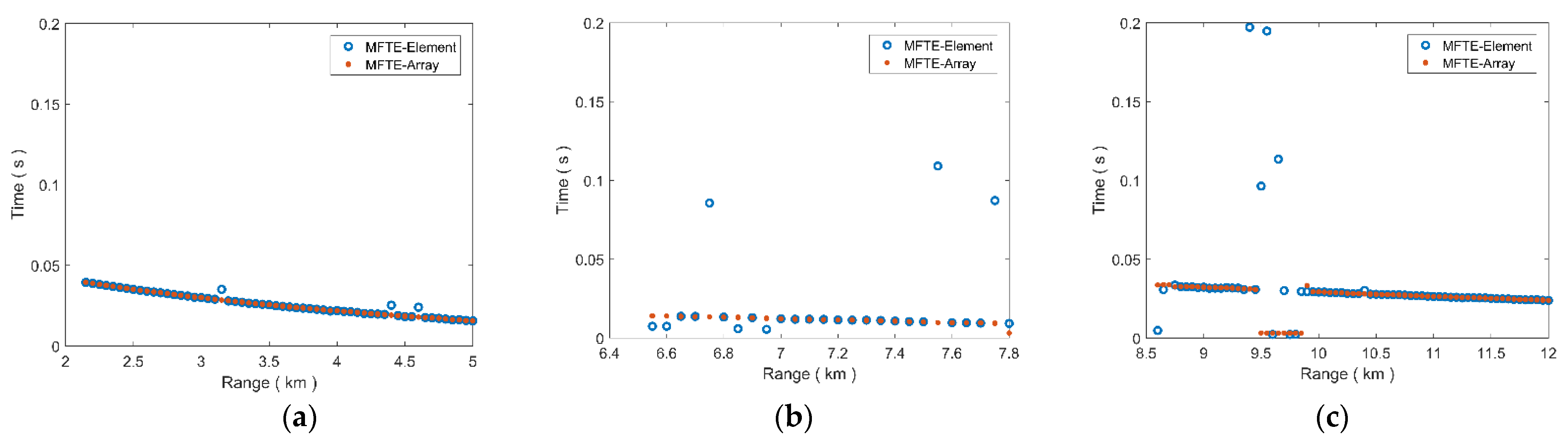
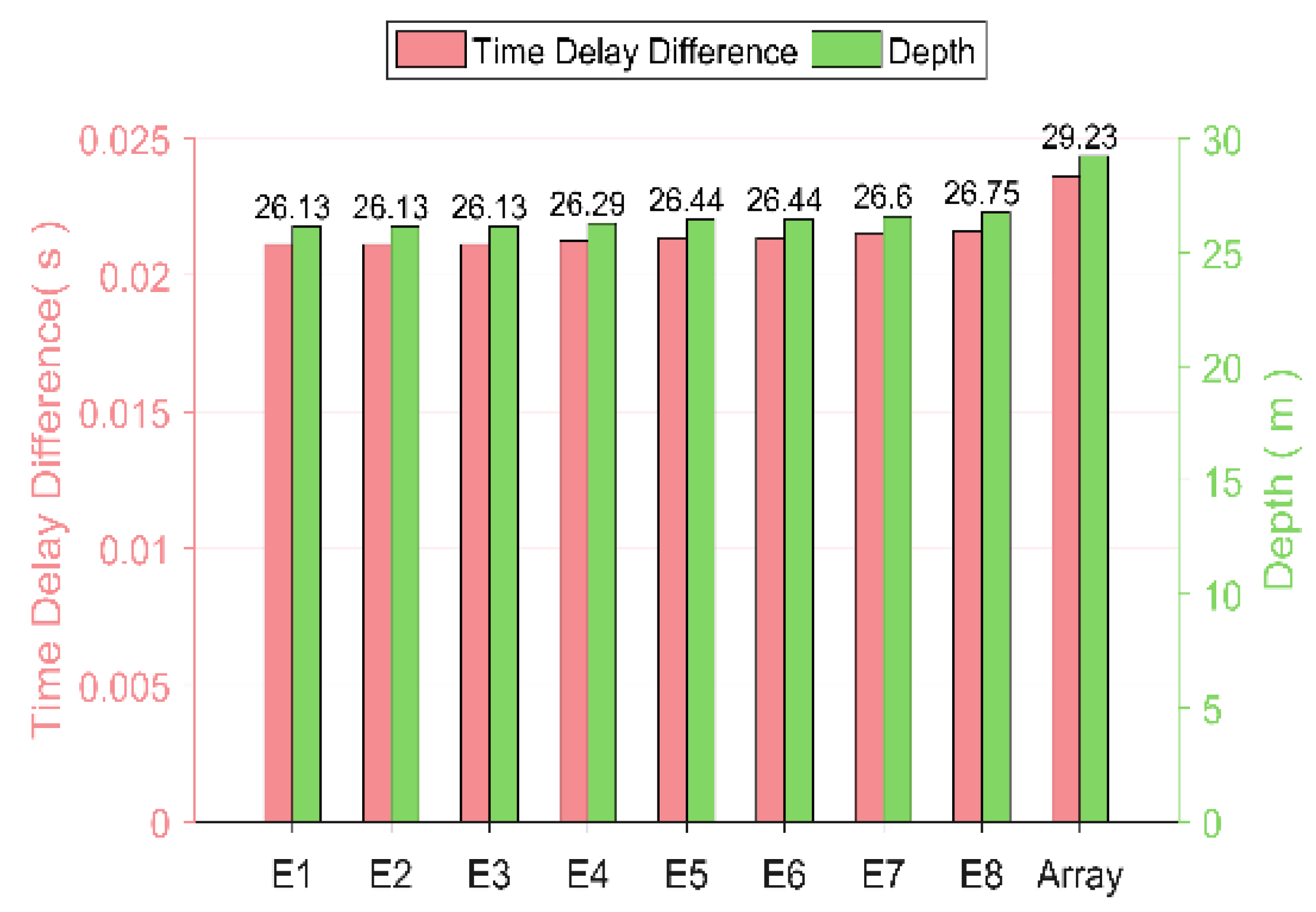
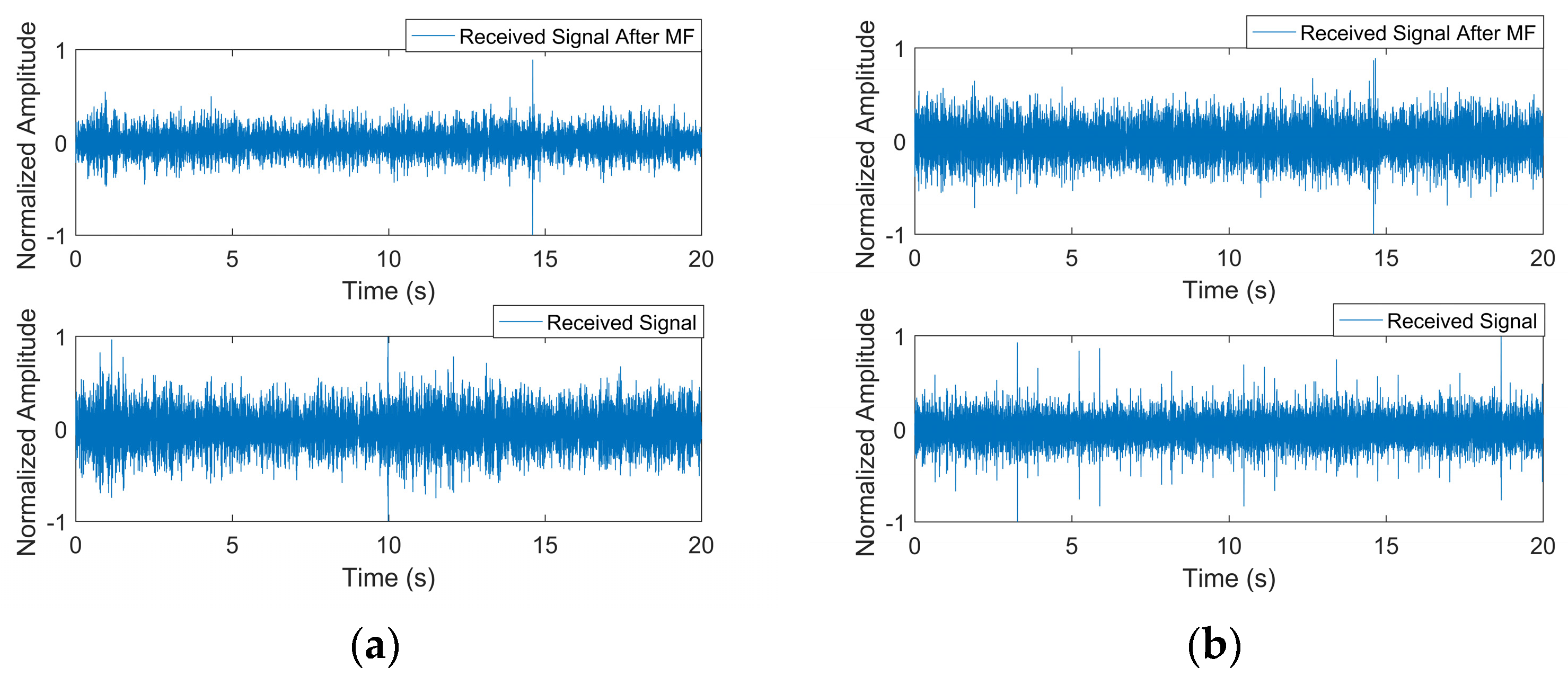
4. Experimental Analysis
4.1. Experimental Setup
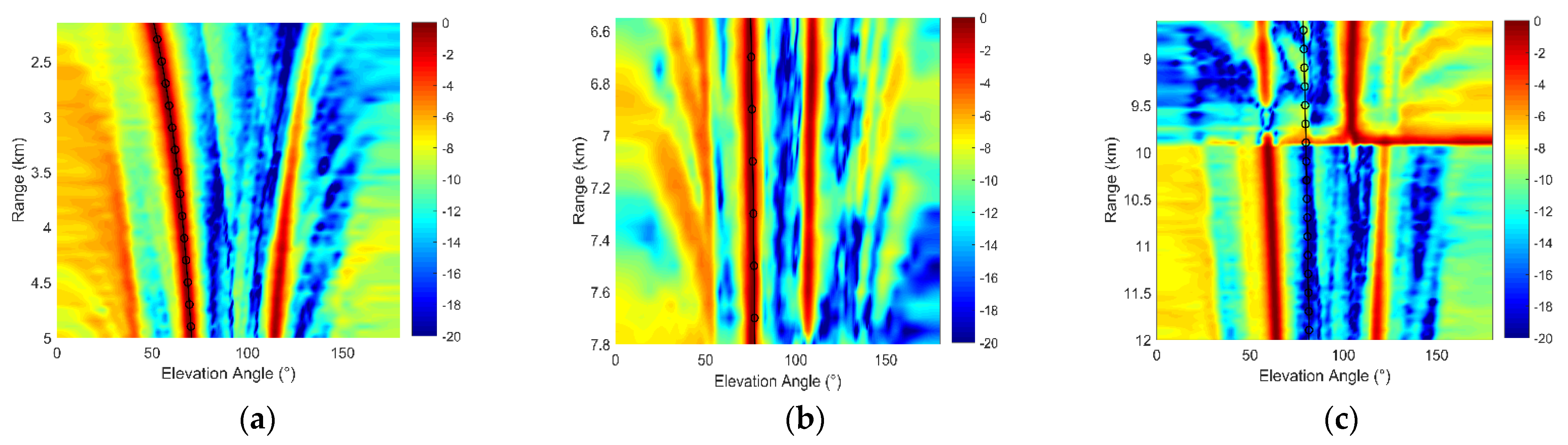
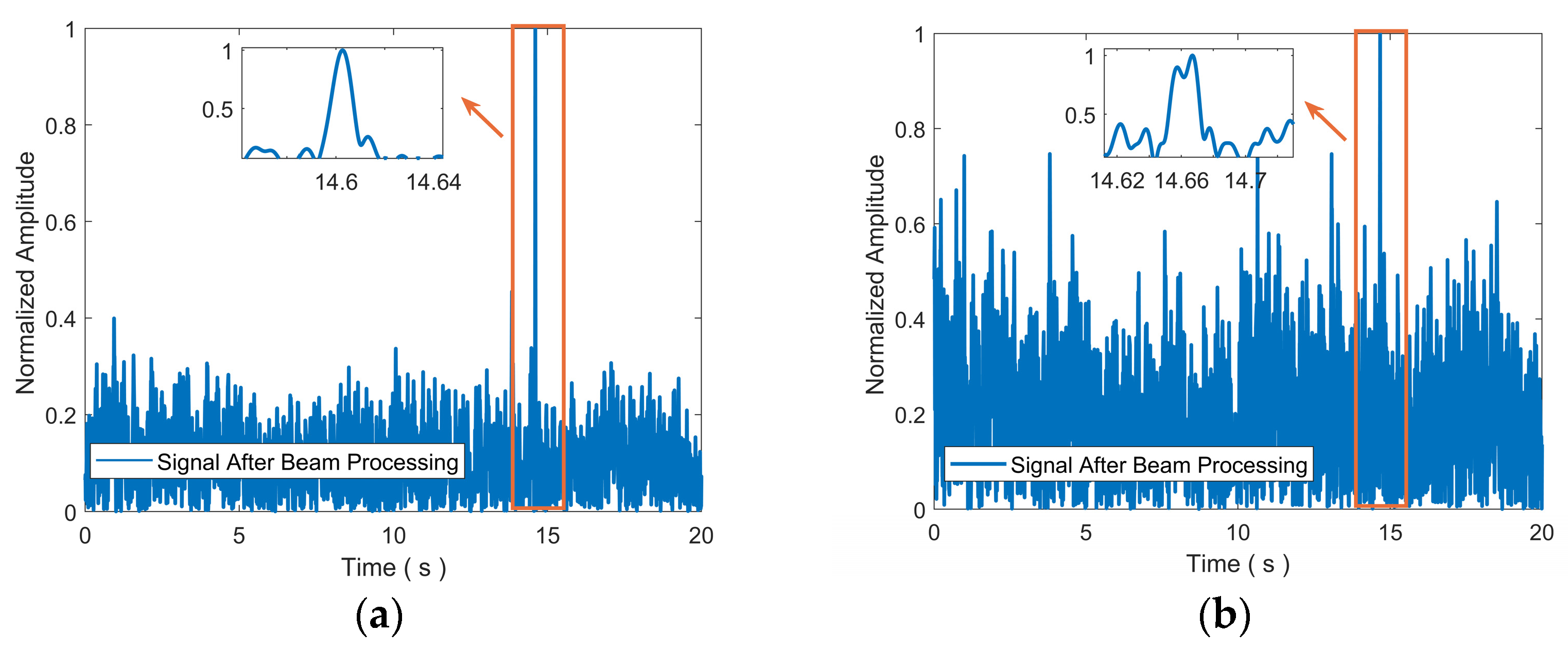
4.2. Processing Results
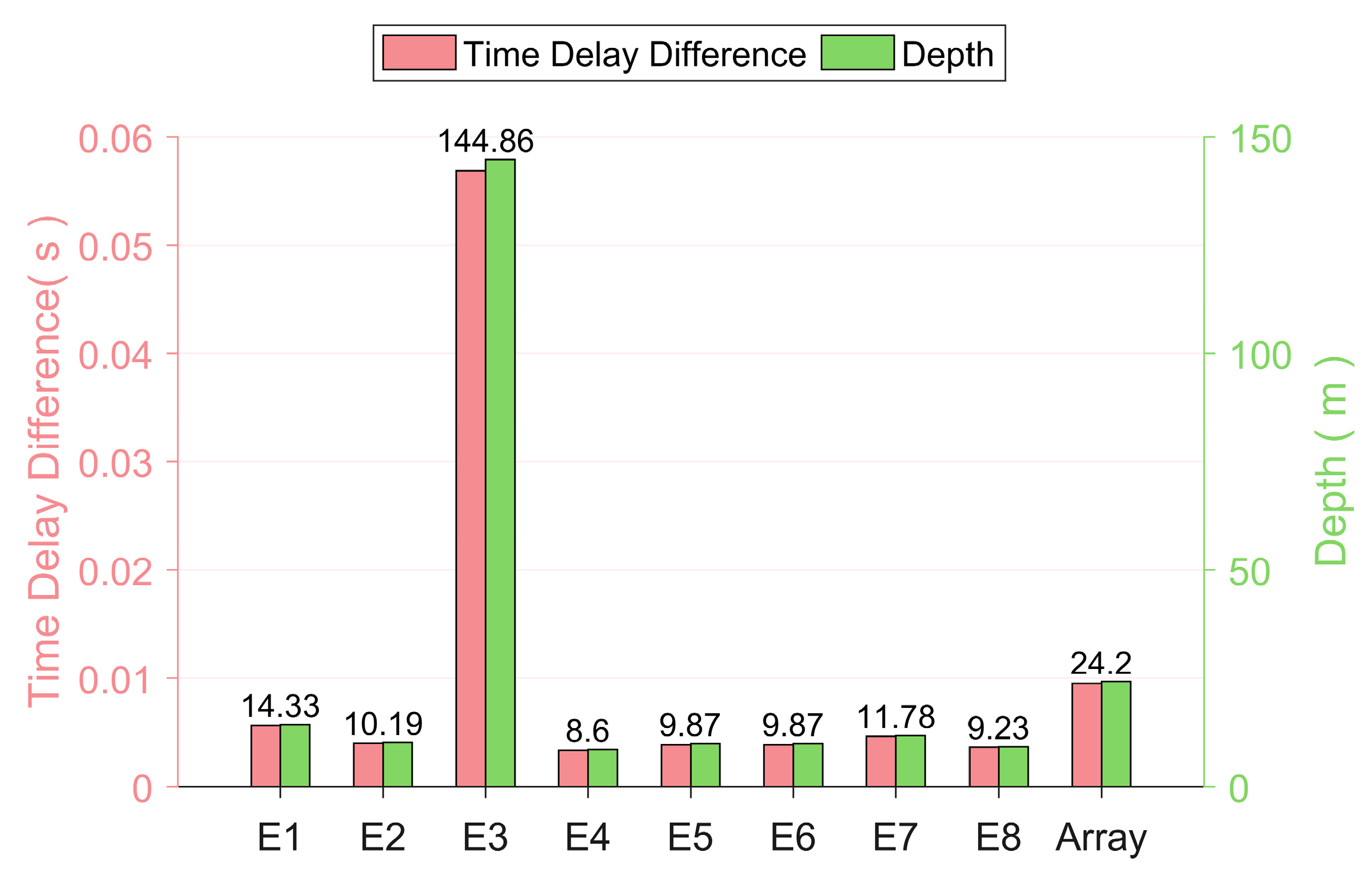
4.3. Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baggeroer, A.B.; Kuperman, W.A. Matched field processing: Source localization in correlated noise as an optimum parameter estimation problem. J. Acoust. Soc. Am. 1988, 83, 571–587. [Google Scholar] [CrossRef]
- Baggeroer, B.; Kuperman, W.A.; Mikhalevsky, P.N. An overview of matched field methods in ocean acoustics. IEEE J. Ocean. Eng. 1993, 18, 401–424. [Google Scholar]
- Tollefsen, D.; Dosso, S.E. Matched-field source localization with multiple small-aperture arrays. J. Acoust. Soc. Am. 2015, 138, 1754. [Google Scholar] [CrossRef]
- Tollefsen, D.; Dosso, S.E. Source localization with multiple hydrophone arrays via matched-field processing. IEEE J. Ocean. Eng. 2016, 42, 654–662. [Google Scholar] [CrossRef]
- Cao, R.; Yang, K.D.; Ma, Y.L.; Yang, Q.L.; Yang, S. Passive broadband source localization based on a Riemannian distance with a short vertical array in the deep ocean. J. Acoust. Soc. Am. 2019, 145, 567–573. [Google Scholar] [CrossRef]
- Zhu, F.W.; Zheng, G.Y.; Liu, F.C. Matched arrival pattern-based method for estimating source depth in deep sea bottom bounce areas. J. Harbin Eng. Univ. 2021, 42, 1510–1517. [Google Scholar]
- Lopatka, M.; Grégoire, L.T.; Nicolas, B.; Cristol, X.; Jérôme, I.M.; Fattaccioli, D. Underwater broadband source localization based on modal filtering and features extraction. EURASIP J. Adv. Signal Process. 2010, 2010, 304103. [Google Scholar] [CrossRef]
- Conan, E.; Bonnel, J.; Chonavel, T.; Nicolas, B. Source depth discrimination with a vertical line array. J. Acoust. Soc. Am. 2016, 140, 434–440. [Google Scholar] [CrossRef]
- Xu, G.J.; Zhang, W.H.; Zhu, M.; Guo, J.Z.; Wu, Y.Q.; Zhu, J.H. Research on Underwater Acoustic Target Depth Classification Based on Modal Filtering Characteristics of Long Horizontal Line Array. Int. J. Acoust. Vib. 2022, 27, 3–9. [Google Scholar] [CrossRef]
- Duan, R.; Yang, K.D.; Ma, Y.L.; Yang, Q.L.; Li, H. Moving source localization with a single hydrophone using multipath time delays in the deep ocean. J. Acoust. Soc. Am. 2014, 136, 159–165. [Google Scholar] [CrossRef]
- An, L.; Chen, L.J. Underwater acoustic passive localization base on multipath arrival structure. In Proceedings of the 43rd International Congress on Noise Control Engineering, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Yang, K.D.; Yang, Q.L.; Guo, X.L.; Cao, R. A simple method for source depth estimation with multi-path time delay in deep ocean. Chin. Phys. Lett. 2016, 33, 124302. [Google Scholar] [CrossRef]
- Urick, R.J. Priciples of Underwater Sound, 3rd ed.; MaGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- McCargar, R.; Zurk, L.M. Depth-based signal separation with vertical line arrays in the deep ocean. J. Acoust. Soc. Am. 2013, 13, 320–325. [Google Scholar] [CrossRef] [PubMed]
- Kniffin, G.P.; Boyle, J.K.; Zurk, L.M.; Siderius, M. Performance metrics for depth-based signal separation using deep vertical line arrays. J. Acoust. Soc. Am. 2016, 139, 418–425. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.D.; Xu, L.Y.; Yang, Q.L.; Duan, R. Striation-based source depth estimation with a vertical line array in the deep ocean. J. Acoust. Soc. Am. 2018, 143, 8–12. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.D.; Li, H.; Duan, R.; Yang, Q.L. Analysis on the characteristic of cross-correlated field and its potential application on source localization in deep water. J. Comput. Acoust. 2017, 25, 1750001. [Google Scholar] [CrossRef]
- Duan, R.; Yang, K.D.; Li, H.; Ma, Y.L. Acoustic-intensity striations below the critical depth: Interpretation and modeling. J. Acoust. Soc. Am. 2017, 142, 245–250. [Google Scholar]
- Duan, R.; Yang, K.D.; Li, H.; Yang, Q.L.; Wu, F.Y.; Ma, Y.L. A performance study of acoustic interference structure applications on source depth estimation in deep water. J. Acoust. Soc. Am. 2019, 145, 903–916. [Google Scholar] [CrossRef]
- Li, H.; Yang, K.D.; Duan, R.; Lei, Z. Joint Estimation of Source Range and Depth Using a Bottom-Deployed Vertical Line Array in Deep Water. Sensors 2017, 17, 1315. [Google Scholar] [CrossRef]
- Reeder, B.D. Clutter depth discrimination using the wavenumber spectrum. J. Acoust. Soc. Am. 2013, 135, 1–7. [Google Scholar] [CrossRef]
- Qi, Y.B.; Zhou, S.H.; Liang, Y.Q.; Du, S.Y.; Liu, C.P. Passive broadband source depth estimation in the deep ocean using a single vector sensor. J. Acoust. Soc. Am. 2020, 148, 88–92. [Google Scholar] [CrossRef]
- Li, H.; Wang, T.; Su, L.; Wang, W.B.; Guo, X.Y.; Wang, C.; Ma, L. A multi-step method for passive broadband source localisation using a single vector sensor. IET Radar Sonar Navig. 2022, 16, 1656–1669. [Google Scholar] [CrossRef]
- Yang, S.G.; Li, Y.; Zhang, K.H.; Liu, J.S. A Signal Processing Algorithm Based on 2D Matched Filtering for SSAR. Math. Probl. Eng. 2017, 12, 4047983. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhao, A.; Hui, J.; Hou, B.; Sotudeh, R.; Niu, F. A Frequency-Domain Adaptive Matched Filter for Active Sonar Detection. Sensors 2017, 17, 897. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer: New York, NY, USA, 2011. [Google Scholar]







| Parameter | Value |
|---|---|
| Source depth | 50 m |
| Source form | 30–500 Hz LFM |
| SNR | 0 dB |
| Signal duration | 1 s |
| Sampling rate | 16 kHz |
| Element number | 8 |
| Element interval | 7.5 m |
| Array depth | 1750–1802.5 m |
| Parameter | Value | |
|---|---|---|
| Array | Theoretical element interval | 7.5 m |
| Element number | 8 | |
| Array depth | 1750–1802.5 m | |
| Signal | Type | emission from fixed point |
| Frequency | 50–200 Hz LFM | |
| Duration | 5 s | |
| Sampling rate | 8 kHz | |
| Others | Sea condition | sea state 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Chen, Y.; Meng, Z.; Zhou, X.; Zhang, Y. A Deep-Sea Broadband Sound Source Depth Estimation Method Based on the Interference Structure of the Compensated Beam Output. J. Mar. Sci. Eng. 2023, 11, 2059. https://doi.org/10.3390/jmse11112059
Liang Y, Chen Y, Meng Z, Zhou X, Zhang Y. A Deep-Sea Broadband Sound Source Depth Estimation Method Based on the Interference Structure of the Compensated Beam Output. Journal of Marine Science and Engineering. 2023; 11(11):2059. https://doi.org/10.3390/jmse11112059
Chicago/Turabian StyleLiang, Yan, Yu Chen, Zhou Meng, Xin Zhou, and Yichi Zhang. 2023. "A Deep-Sea Broadband Sound Source Depth Estimation Method Based on the Interference Structure of the Compensated Beam Output" Journal of Marine Science and Engineering 11, no. 11: 2059. https://doi.org/10.3390/jmse11112059
APA StyleLiang, Y., Chen, Y., Meng, Z., Zhou, X., & Zhang, Y. (2023). A Deep-Sea Broadband Sound Source Depth Estimation Method Based on the Interference Structure of the Compensated Beam Output. Journal of Marine Science and Engineering, 11(11), 2059. https://doi.org/10.3390/jmse11112059







