Regime Shifts in the Damage Caused by Tropical Cyclones in the Guangdong–Hong Kong–Macao Greater Bay Area of China
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
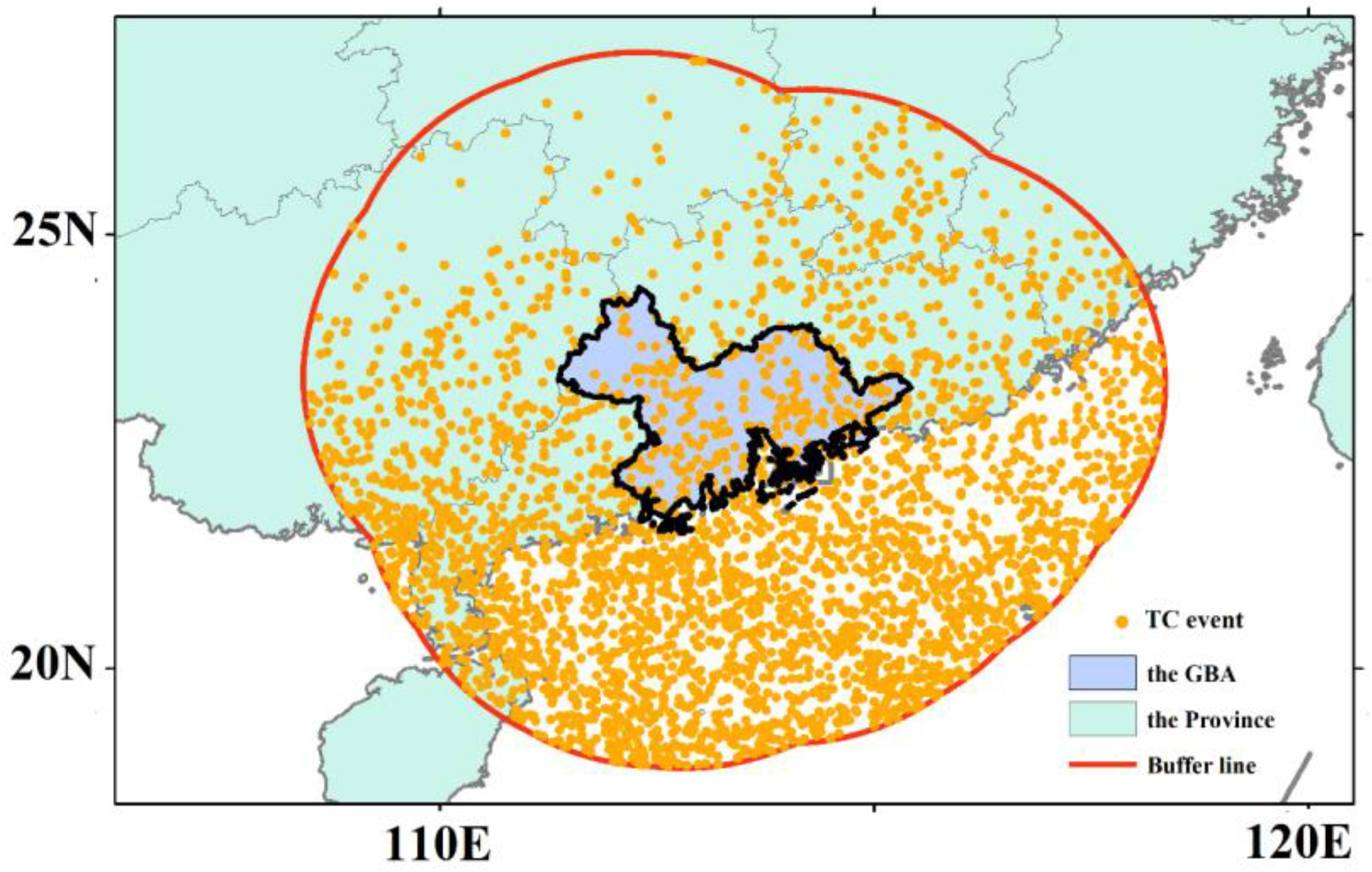
2.2. TC Information Extraction
2.3. Damage Assessment Index
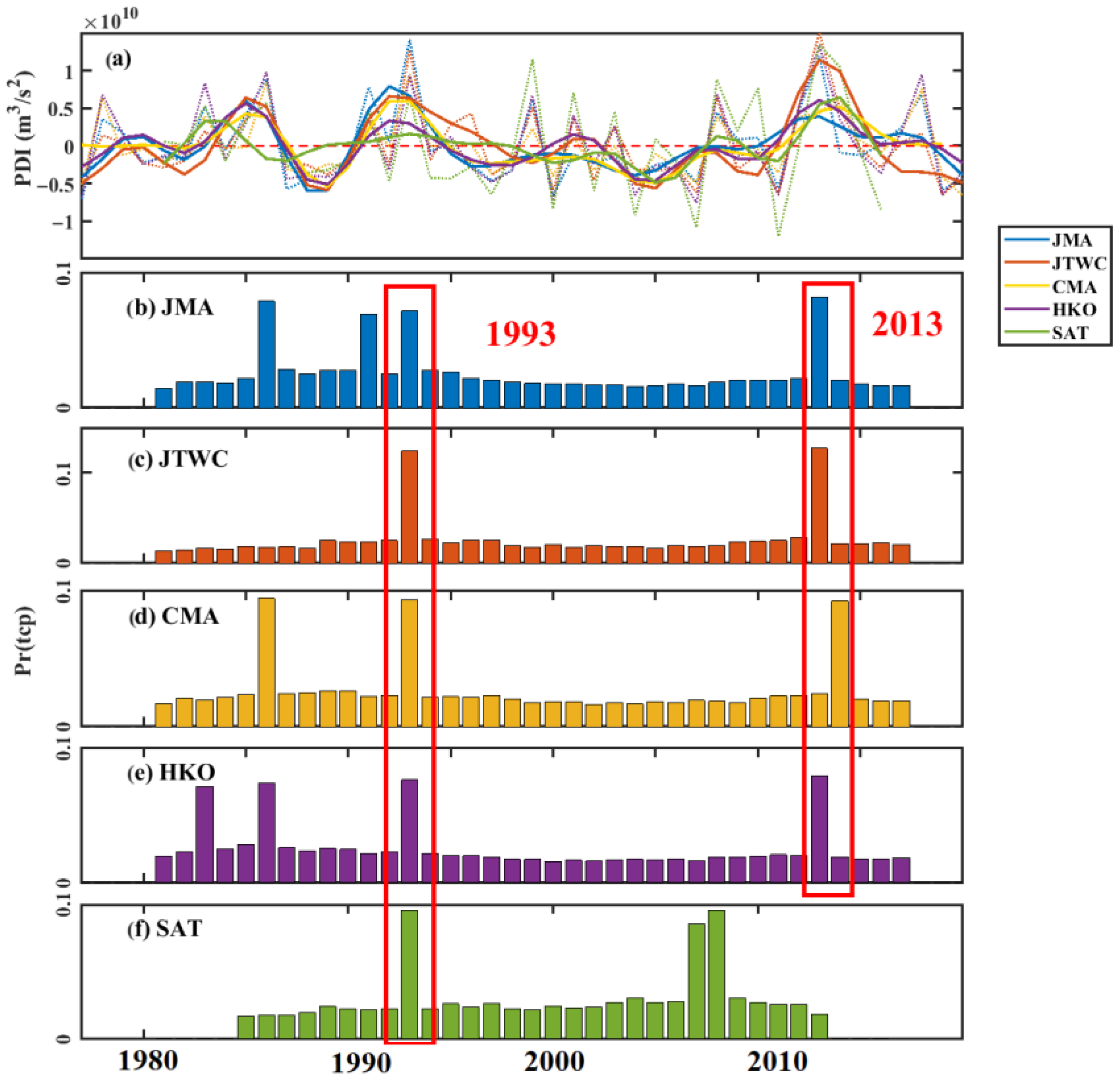
2.4. Bayesian Changepoint Method for Interdecadal Changes
2.5. Mann–Whitney U Test
3. Results
3.1. Interdecadal Variations in TC Damage
3.1.1. Interdecadal Variations in PDI and SDP
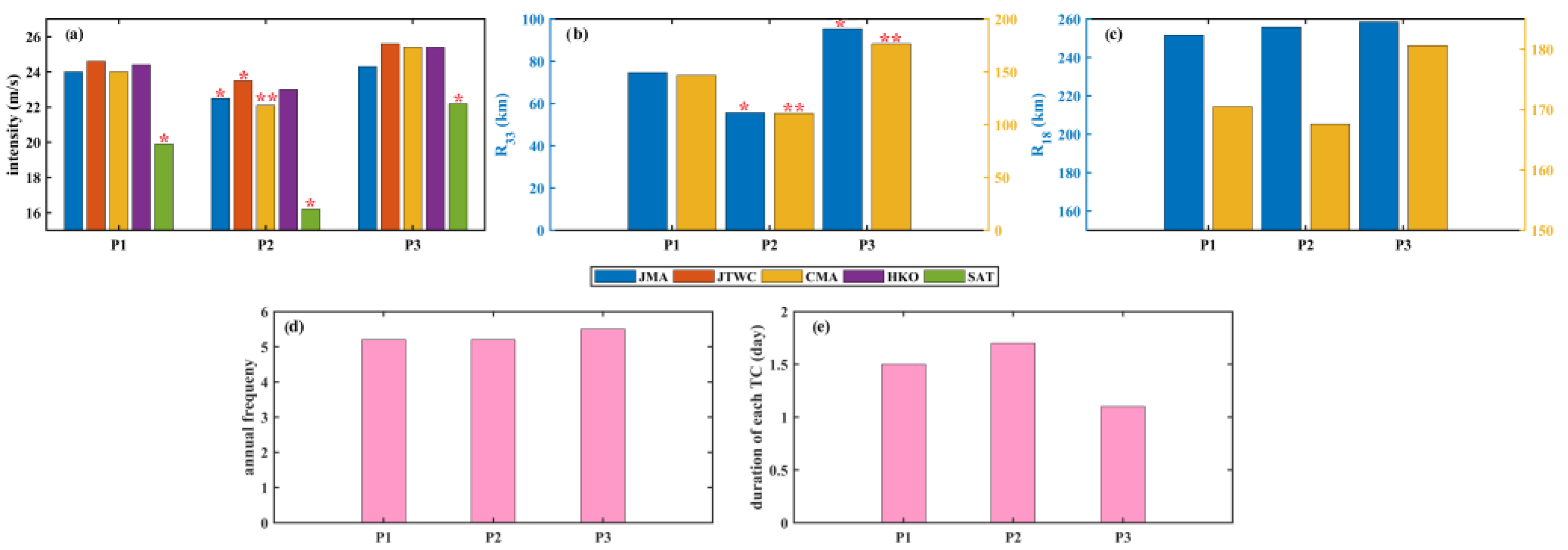
3.1.2. The Performance of Different Incorporated Parameters in Three Epochs
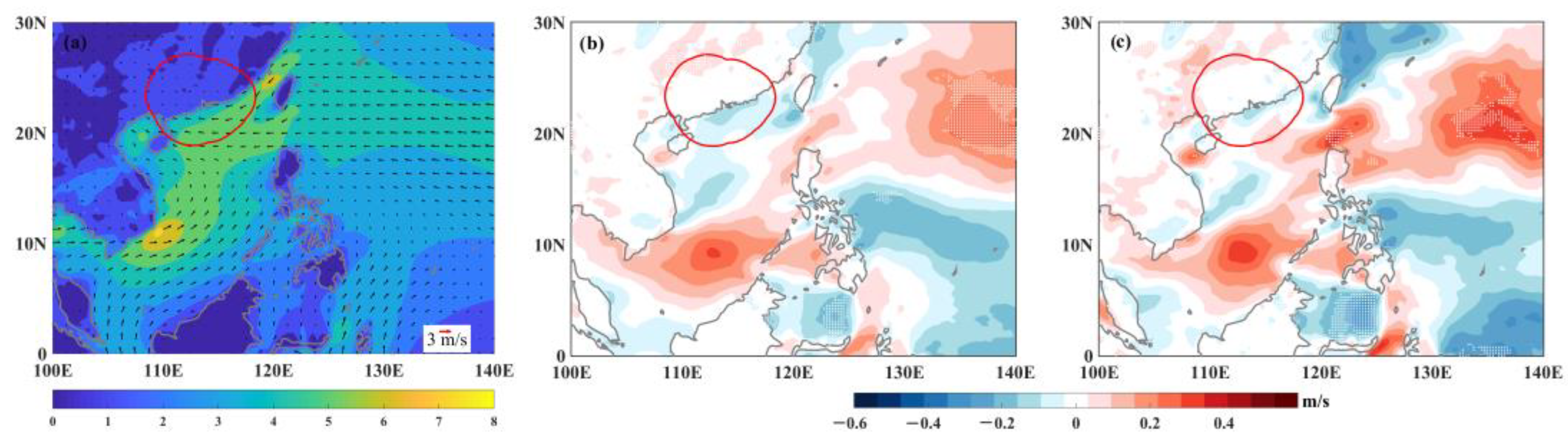
3.2. Possible Mechanisms
3.2.1. Environmental Factor
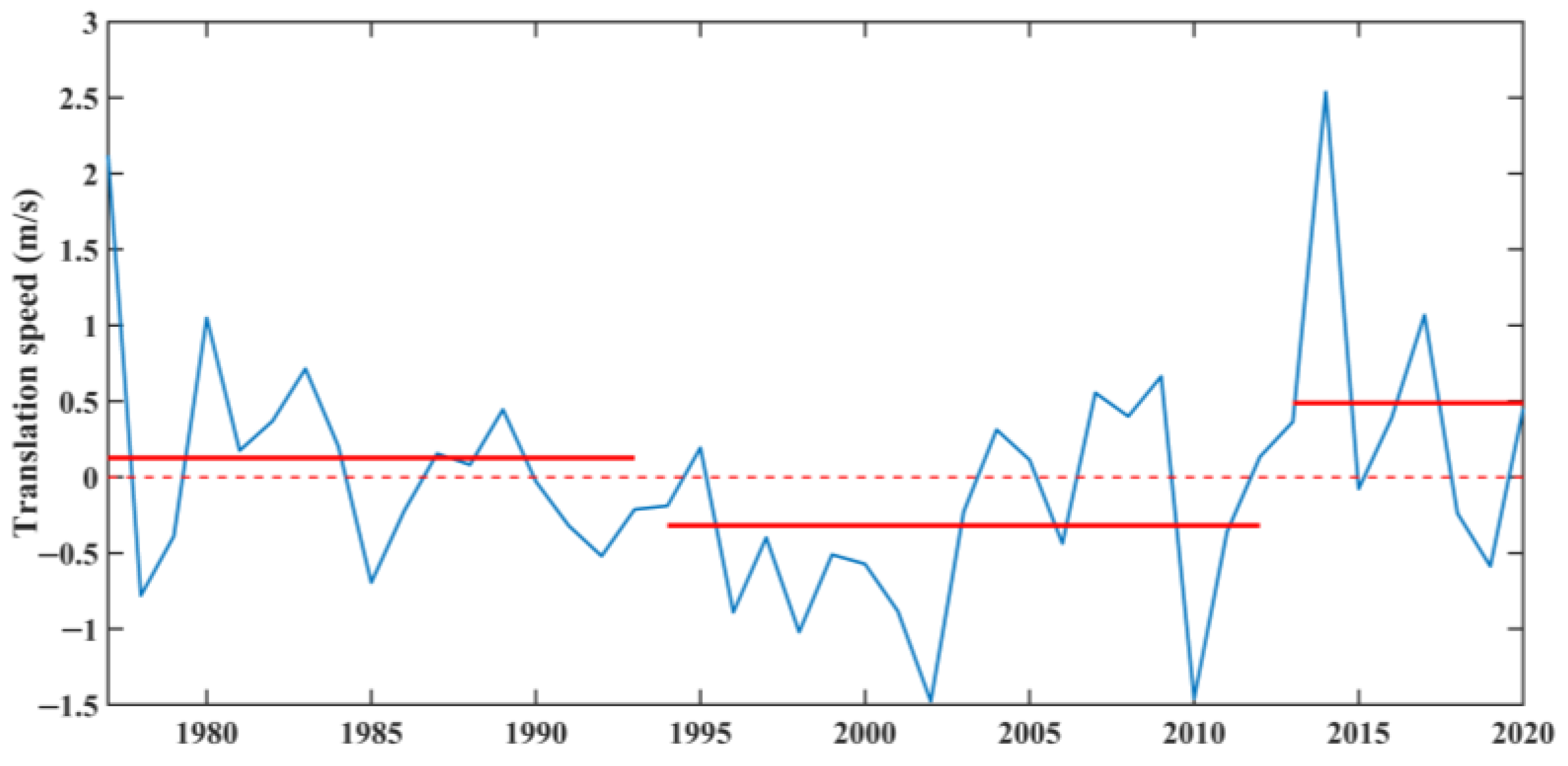
3.2.2. TC Translation Speed
4. Discussion
4.1. The Relationship between the NSCS SST and Luzon Strait Transport
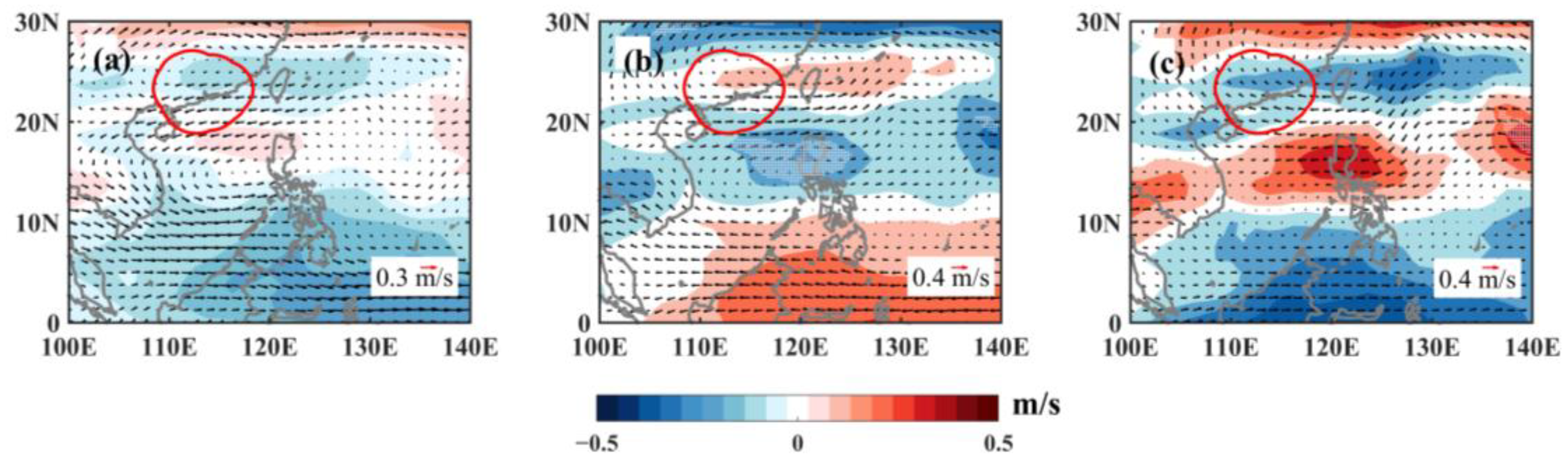
4.2. TC Translation Speed Modulated by Steering Flow in the SCS
4.3. Significance and Innovation of This Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Emanuel, K. Environmental factors affecting tropical cyclone power dissipation. J. Clim. 2007, 20, 5497–5509. [Google Scholar] [CrossRef]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Du, Y.; Xie, S.; Wang, D. An interdecadal change of tropical cyclone activity in the South China Sea in the early 1990s. Chin. J. Oceanol. Limnol. 2012, 30, 953–959. [Google Scholar] [CrossRef]
- Ha, Y.; Zhong, Z.; Sun, Y.; Lu, W. Decadal change of South China Sea tropical cyclone activity in mid-1990s and its possible linkage with intraseasonal variability. J. Geophys. Res.-Atmos. 2014, 119, 5331–5344. [Google Scholar] [CrossRef]
- Zhou, W.; Li, R.C.Y. Interdecadal change in South China Sea tropical cyclone frequency in association with zonal sea surface temperature gradient. J. Clim. 2014, 27, 5468–5480. [Google Scholar] [CrossRef]
- Ha, Y.; Zhong, Z. Decadal change in tropical cyclone activity over the South China Sea around 2002/03. J. Clim. 2015, 28, 5935–5951. [Google Scholar] [CrossRef]
- Li, H.; Xu, F.; Sun, J.; Lin, Y.; Wright, J.S. Subtropical high affects interdecadal variability of tropical cyclone genesis in the South China Sea. J. Geophys. Res.-Atmos. 2019, 124, 6379–6392. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C.L. Recent increase in extreme intensity of tropical cyclones making landfall in South China. Clim. Dynam. 2020, 55, 1059–1074. [Google Scholar] [CrossRef]
- Zheng, M.; Wang, C. Interdecadal changes of tropical cyclone intensity in the South China Sea. Clim. Dynam. 2023, 60, 409–425. [Google Scholar] [CrossRef]
- Mok, D.K.H.; Chan, J.C.L.; Chan, K.T.F. A 31-year climatology of tropical cyclone size from the NCEP Climate Forecast System Reanalysis. Int. J. Climatol. 2018, 38, e796–e806. [Google Scholar] [CrossRef]
- Weng, H.; Wu, G.; Liu, Y.; Behera, S.K.; Yamagata, T. Anomalous summer climate in China influenced by the tropical Indo-Pacific Oceans. Clim. Dynam. 2009, 36, 769–782. [Google Scholar] [CrossRef][Green Version]
- Chen, W.; Yang, S.; Wu, Z.; Cai, F. Large-scale atmospheric features favoring the tropical cyclone activity affecting the Guangdong–Hong Kong–Macao Greater Bay Area of China. Environ. Res. Lett. 2022, 17, 104057. [Google Scholar] [CrossRef]
- Wu, L.; Zhao, H.; Wang, C.; Cao, J.; Liang, J. Understanding of the effect of climate change on tropical cyclone intensity: A review. Adv. Atmos. Sci. 2022, 39, 205–221. [Google Scholar] [CrossRef]
- Moon, I.J.; Kim, S.H.; Chan, J.C.L. Climate change and tropical cyclone trend. Nature 2019, 570, E3–E5. [Google Scholar] [CrossRef]
- Quiring, S.; Schumacher, A.; Labosier, C.; Zhu, L. Variations in mean annual tropical cyclone size in the Atlantic. J. Geophys. Res. 2011, 116, D9. [Google Scholar] [CrossRef]
- Cao, X.; Wu, R.; Zhan, Y. Re-examining the decadal change of tropical cyclogenesis over the South China Sea around the mid-1990s. Int. J. Climatol. 2019, 39, 3188–3200. [Google Scholar] [CrossRef]
- Dong, W.; Feng, Y.; Chen, C.; Wu, Z.; Xu, D.; Li, S.; Xu, Q.; Wang, L.; Beardsley, R.C.; Lin, H.; et al. Observational and modeling studies of oceanic responses and feedbacks to typhoons Hato and Mangkhut over the northern shelf of the South China Sea. Prog. Oceanogr. 2021, 191, 102507. [Google Scholar] [CrossRef]
- Shan, K.; Chu, P.-S.; Yu, X. Interdecadal change of tropical cyclone translation speed during peak season in South China Sea: Observed evidence, model results, and possible mechanism. J. Clim. 2023, 36, 4531–4541. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C.L. Variations in the power dissipation index in the East Asia region. Clim. Dynam. 2016, 48, 1963–1985. [Google Scholar] [CrossRef]
- Li, R.C.Y.; Zhou, W.; Shun, C.M.; Lee, T.C. Change in destructiveness of landfalling tropical cyclones over China in recent decades. J. Clim. 2017, 30, 3367–3379. [Google Scholar] [CrossRef]
- Luo, X.; Yang, L.; Chen, S.; Liang, D.; Chan, J.C.L.; Wang, D. The decadal variation of eastward-moving tropical cyclones in the South China Sea during 1980–2020. Geophys. Res. Lett. 2022, 49, e2021GL096640. [Google Scholar] [CrossRef]
- Xuan, J.; Ding, R.; Zhou, F. Storm surge risk under various strengths and translation speeds of landfalling tropical cyclones. Environ. Res. Lett. 2021, 16, 124055. [Google Scholar] [CrossRef]
- Leung, H.-S. Storm Surge Hazard in Hong Kong under Global Climate Changes. HKU Theses Online (HKUTO). 2011. Available online: https://www.airitilibrary.com/Publication/alDetailedMesh1?DocID=U0029-1812201200019956 (accessed on 6 September 2023).
- Ji, T.; Li, G.; Liu, Y.; Liu, R.; Zhu, Y. Spatiotemporal features of storm surge activity and its response to climate change in the southeastern coastal area of China in the past 60 years. J. Geophys. Res.-Atmos. 2021, 126, e2020JD033234. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C.L.; Kubota, H. Meridional oscillation of tropical cyclone activity in the western North Pacific during the past 110 years. Clim. Chang. 2021, 164, 23. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; Zhan, R.; Xu, J.; Duan, Y. Increasing destructive potential of landfalling tropical cyclones over China. J. Clim. 2020, 33, 3731–3743. [Google Scholar] [CrossRef]
- Yin, Y. Analysis on the characteristics of typhoon affecting Shenzhen City from 1961 to 2018. Adv. Meteor. Sci. Technol. 2022, 12, 50–54. [Google Scholar]
- Mingjie, W.; Xiaoli, Z.; Xiaoya, Z.; Yuanzhao, C. Changes in disastrous weather climate events in Shenzhen of Guangdong Province during 1953–2005. Adv. Clim. Chang. Res. 2007, 3, 350–355. (In Chinese) [Google Scholar]
- Zhuo, J.; Tan, Z. Physics-augmented deep learning to improve tropical cyclone intensity and size estimation from satellite imagery. Mon. Weather Rev. 2021, 149, 2097–2113. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C. Quantifying Interagency differences in tropical cyclone best-track wind speed estimates. Mon. Weather Rev. 2010, 138, 1459–1473. [Google Scholar] [CrossRef]
- Yan, Z.; Ping, Z. Comparison of tropical cyclone datasets and a data-correction scheme for data from TC yearly book. J. Trop. Meteorol. 2009, 25, 295–299. [Google Scholar]
- Park, D.-S.R.; Ho, C.-H.; Kim, J.-H.; Kim, H.-S. Strong landfall typhoons in Korea and Japan in a recent decade. J. Geophys. Res. 2011, 116, D7. [Google Scholar] [CrossRef]
- Von Storch, H.; Feser, F.; Barcikowska, M. Usability of best track data in climate statistics in the Western North Pacific. Mon. Weather Rev. 2012, 140, 2818–2830. [Google Scholar] [CrossRef]
- Xiang, B.; Dong, X.; Li, Y. Climate change trend and causes of tropical cyclones affecting the South China Sea during the past 50 years. Atmos. Ocean. Sci. Lett. 2020, 13, 301–307. [Google Scholar] [CrossRef]
- Imaoka, K.; Spencer, R.W. Diurnal variation of precipitation over the tropical oceans observed by TRMM/TMI combined with SSM/I. J. Clim. 2000, 13, 4149–4158. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Yang, X.; Li, X. Estimating tropical cyclone size in the Northwestern Pacific from geostationary satellite infrared images. Remote Sens. 2017, 9, 728. [Google Scholar] [CrossRef]
- Kossin, J.P.; Knapp, K.R.; Vimont, D.J.; Murnane, R.J.; Harper, B.A. A globally consistent reanalysis of hurricane variability and trends. Geophys. Res. Lett. 2007, 34, L04815. [Google Scholar] [CrossRef]
- Ansari, S.; Knapp, K.R.; Bain, C.L.; Bourassa, M.A.; Dickinson, M.J.; Funk, C.; Helms, C.N.; Hennon, C.C.; Holmes, C.D.; Huffman, G.J.; et al. Globally gridded satellite observations for climate studies. Bull. Am. Meteorol. Soc. 2011, 92, 893–907. [Google Scholar] [CrossRef]
- Knapp, K.R. Calibration Assessment of ISCCP geostationary infrared observations using HIRS. J. Atmos. Ocean. Technol. 2008, 25, 183–195. [Google Scholar] [CrossRef]
- Knapp, K. Scientific data stewardship of international satellite cloud climatology project B1 global geostationary observations. J. Appl. Remote Sens. 2008, 2, 023548. [Google Scholar] [CrossRef]
- Kossin, J.P.; Olander, T.L.; Knapp, K.R. Trend analysis with a new global record of tropical cyclone intensity. J. Clim. 2013, 26, 9960–9976. [Google Scholar] [CrossRef]
- Kossin, J.P.; Emanuel, K.A.; Vecchi, G.A. The poleward migration of the location of tropical cyclone maximum intensity. Nature 2014, 509, 349–352. [Google Scholar] [CrossRef]
- Liang, M.; Xu, J.; Chan, J.C.L.; Liu, C.; Xu, H. How does the onset time of El Niño events affect tropical cyclone genesis and intensity over the western North Pacific? Int. J. Climatol. 2021, 42, 1–16. [Google Scholar] [CrossRef]
- Chen, L.; Ding, Y. Introduction to Typhoons in the Western Pacific; Science Press: Beijing, China, 1979. (In Chinese) [Google Scholar]
- Powell, M.D.; Reinhold, T.A. Tropical Cyclone Destructive potential by integrated kinetic energy. Bull. Am. Meteorol. Soc. 2007, 88, 513–526. [Google Scholar] [CrossRef]
- Irish, J.L.; Resio, D.T. A hydrodynamics-based surge scale for hurricanes. Ocean Eng. 2010, 37, 69–81. [Google Scholar] [CrossRef]
- Jiang, Z.; Hua, F.; Qu, P. A new scheme for adjusting the tropical cyclone parameters. Adv. Mar. Sci. 2008, 26, 1. (In Chinese) [Google Scholar]
- Zhao, X.; Chu, P.-S. Bayesian changepoint analysis for extreme events (typhoons, heavy rainfall, and heat waves): An RJMCMC approach. J. Clim. 2010, 23, 1034–1046. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Chu, P.-S.; Murakami, H.; Zhao, X. An abrupt decrease in the late-sseason typhoon activity over the Western North Pacific. J. Clim. 2014, 27, 4296–4312. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Wilks, D. Statistical Methods in the atmospheric sciences. Int. Geophys. Ser. 2006, 59, xi. [Google Scholar] [CrossRef]
- Gómez, S.I.; Jaramillo, L.M.; Moreno, G.C.; Roa, N.S.; Rodríguez, A. Differential reactivity of salivary IgA and IgG against Streptococcus mutans proteins in humans with different caries experience. Acta Odontol. Latinoam. 2015, 28, 3–12. [Google Scholar]
- Yuan, J.; Wang, D.; Wan, Q.; Liu, C. A 28-year climatological analysis of size parameters for Northwestern Pacific tropical cyclones. Adv. Atmos. Sci. 2007, 24, 24–34. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C.L. Size of tropical cyclones as inferred from ERS-1 and ERS-2 Data. Mon. Weather Rev. 1999, 127, 2992–3001. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, S.; Li, X.; Shen, X. Key environmental factors for rapid intensification of the South China Sea tropical cyclones. Front. Earth Sci. 2021, 8, 609727. [Google Scholar] [CrossRef]
- Hill, K.A.; Lackmann, G.M. Influence of environmental humidity on tropical cyclone size. Mon. Weather Rev. 2009, 137, 3294–3315. [Google Scholar] [CrossRef]
- Chan, K.T.F.; Chan, J.C.L. Angular momentum transports and synoptic flow patterns associated with tropical cyclone size change. Mon. Weather Rev. 2013, 141, 3985–4007. [Google Scholar] [CrossRef]
- Li, M.; Chu, K.; Gu, J.-F.; Tan, Z.-M. On the relationship between tropical cyclone size and environmental helicity in the South China Sea. Atmos. Ocean. Sci. Lett. 2022, 15, 100205. [Google Scholar] [CrossRef]
- Lin, N.; Chavas, D.R.; Dong, W.; Lin, Y. Observedtropical cyclone size revisited. J. Clim. 2016, 29, 2923–2939. [Google Scholar] [CrossRef]
- Chen, K.; Chen, G.; Shi, D. Reexamination of the relationship between tropical cyclone size and intensity over the Western North Pacific. Adv. Atmos. Sci. 2022, 39, 1956–1968. [Google Scholar] [CrossRef]
- Chang, Y.-T.; Lin, I.I.; Huang, H.-C.; Liao, Y.-C.; Lien, C.-C. The association of typhoon intensity increase with translation speed increase in the South China Sea. Sustainability 2020, 12, 939. [Google Scholar] [CrossRef]
- Lin, I.-I.; Liu, W.T.; Wu, C.-C.; Chiang, J.C.H.; Sui, C.-H. Satellite observations of modulation of surface winds by typhoon-induced upper ocean cooling. Geophys. Res. Lett. 2003, 30, 1131. [Google Scholar] [CrossRef]
- Chiang, T.; Hsin, Y.; Wu, C. Multidecadal Changes of Upper-Ocean Thermal Conditions in the Tropical Northwest Pacific Ocean versus South China Sea during 1960–2015. J. Clim. 2018, 31, 3999–4016. [Google Scholar] [CrossRef]
- Lee, M.A.; Kuo, Y.C.; Chan, J.W.; Chen, Y.K.; Teng, S.Y. Long-term (1982–2012) summertime sea surface temperature variability in the Taiwan Strait. Terr. Atmos. Ocean. Sci. 2015, 26, 183–192. [Google Scholar] [CrossRef]
- Qu, T.; Du, Y.; Sasaki, H. South China Sea throughflow: A heat and freshwater conveyor. Geophys. Res. Lett. 2006, 33, L23617. [Google Scholar] [CrossRef]
- Thompson, B.; Tkalich, P.; Malanotte-Rizzoli, P. Regime shift of the South China Sea SST in the late 1990s. Clim. Dynam. 2016, 48, 1873–1882. [Google Scholar] [CrossRef]
- Yu, K.; Qu, T. Imprint of the Pacific decadal oscillation on the South China Sea throughflow variability. J. Clim. 2013, 26, 9797–9805. [Google Scholar] [CrossRef]
- Nan, F.; Xue, H.; Yu, F. Kuroshio intrusion into the South China Sea: A review. Prog. Oceanogr. 2015, 137, 314–333. [Google Scholar] [CrossRef]
- Liu, Q.-Y.; Wang, D.; Wang, X.; Shu, Y.; Xie, Q.; Chen, J. Thermal variations in the South China Sea associated with the eastern and central Pacific El Niño events and their mechanisms. J. Geophys. Res.-Ocean. 2014, 119, 8955–8972. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, W.; Lu, X.; Chen, Y.D. Landfalling tropical cyclones activities in the south China: Intensifying or weakening? Int. J. Climatol. 2012, 32, 1815–1824. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C. Growing threat of rapidly-intensifying tropical cyclones in East Asia. Adv. Atmos. Sci. 2022, 39, 222–234. [Google Scholar] [CrossRef]





| 1977–1993 | 1994–2012 | 2013–2020 | |
|---|---|---|---|
| JMA | 1.0 | 0.8 * | 1.0 |
| JTWC | 1.1 | 1.0 | 1.2 |
| CMA | 1.0 ** | 0.7 ** | 1.2 ** |
| HKO | 1.0 | 0.9 ** | 1.2 * |
| SAT | 0.6 | 0.5 ** | 0.9 * |
| 1977–1993 | 1994–2012 | 2013–2020 | |
|---|---|---|---|
| CMA | 23.9 | 18.6 ** | 27.7 |
| JMA | 22.3 | 12.9 ** | 35.3 ** |
| 1977–1993 | 1994–2012 | 2013–2020 | |
|---|---|---|---|
| SST (°C) | 28.6 | 28.5 | 28.7 |
| SLHF (negative is upward, W/m2) | −118.3 | −117.3 | −119.0 |
| RH (%) | 55.3 | 54.8 | 55.7 |
| TC movement (m/s) | 5.1 | 4.6 | 5.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, M.; Mu, L.; Li, W.; Wang, F.; Li, Y. Regime Shifts in the Damage Caused by Tropical Cyclones in the Guangdong–Hong Kong–Macao Greater Bay Area of China. J. Mar. Sci. Eng. 2023, 11, 1889. https://doi.org/10.3390/jmse11101889
Zheng M, Mu L, Li W, Wang F, Li Y. Regime Shifts in the Damage Caused by Tropical Cyclones in the Guangdong–Hong Kong–Macao Greater Bay Area of China. Journal of Marine Science and Engineering. 2023; 11(10):1889. https://doi.org/10.3390/jmse11101889
Chicago/Turabian StyleZheng, Manli, Lin Mu, Wenjuan Li, Fei Wang, and Yan Li. 2023. "Regime Shifts in the Damage Caused by Tropical Cyclones in the Guangdong–Hong Kong–Macao Greater Bay Area of China" Journal of Marine Science and Engineering 11, no. 10: 1889. https://doi.org/10.3390/jmse11101889
APA StyleZheng, M., Mu, L., Li, W., Wang, F., & Li, Y. (2023). Regime Shifts in the Damage Caused by Tropical Cyclones in the Guangdong–Hong Kong–Macao Greater Bay Area of China. Journal of Marine Science and Engineering, 11(10), 1889. https://doi.org/10.3390/jmse11101889








