Dynamics Modeling and Hydrodynamic Coefficients Identification of the Wave Glider
Abstract
:1. Introduction
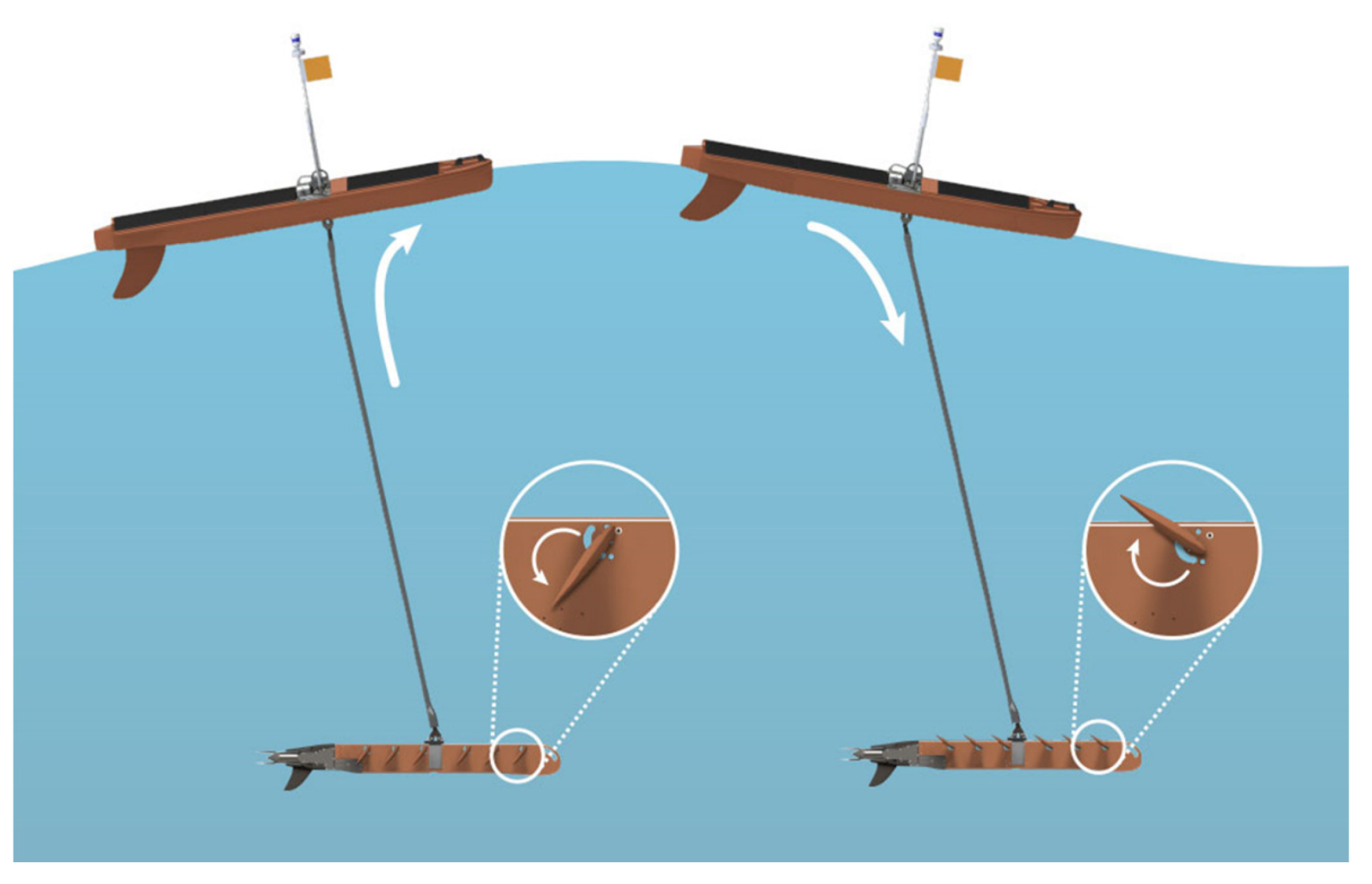
2. Dynamic Models of the “Black Pearl” Wave Glider
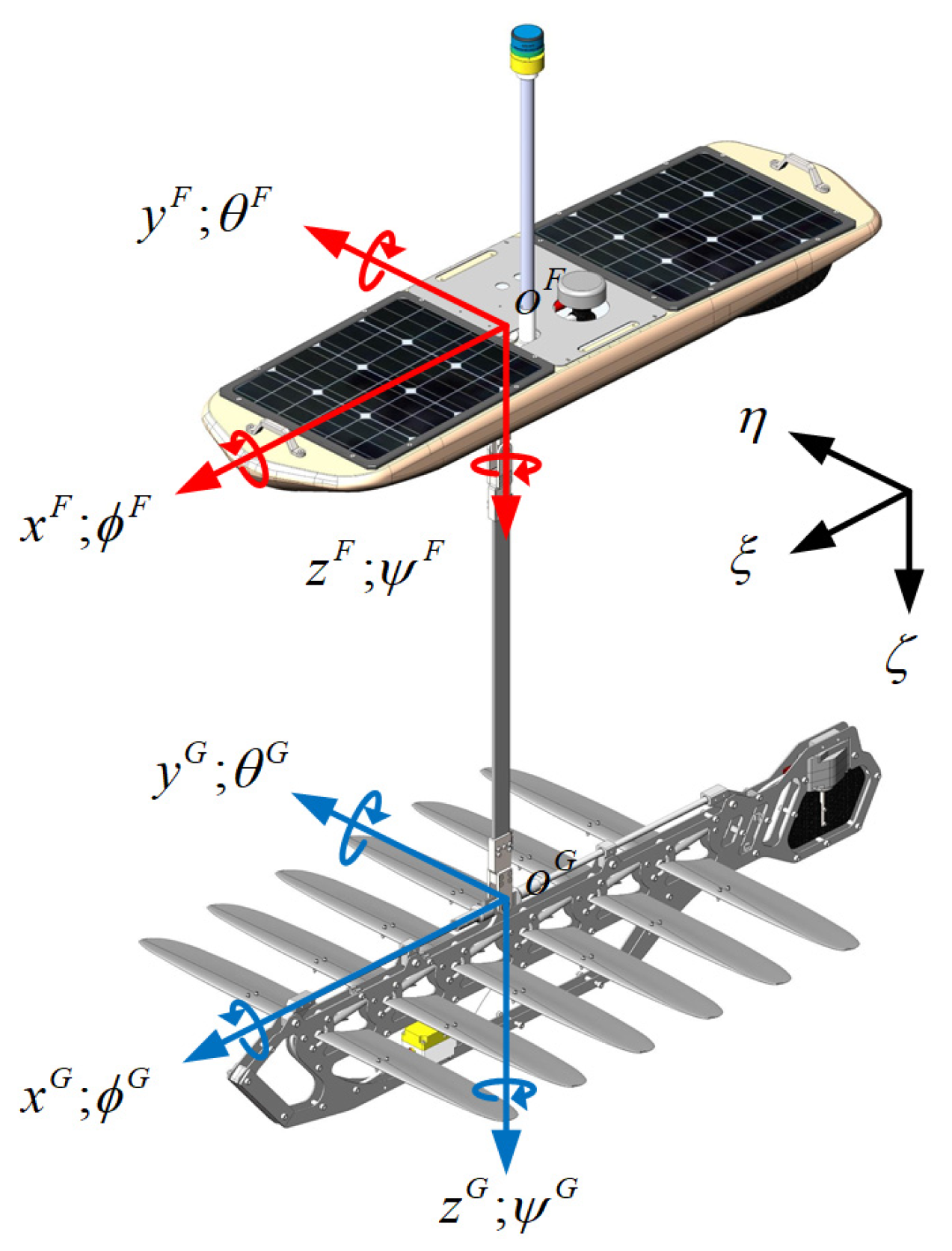
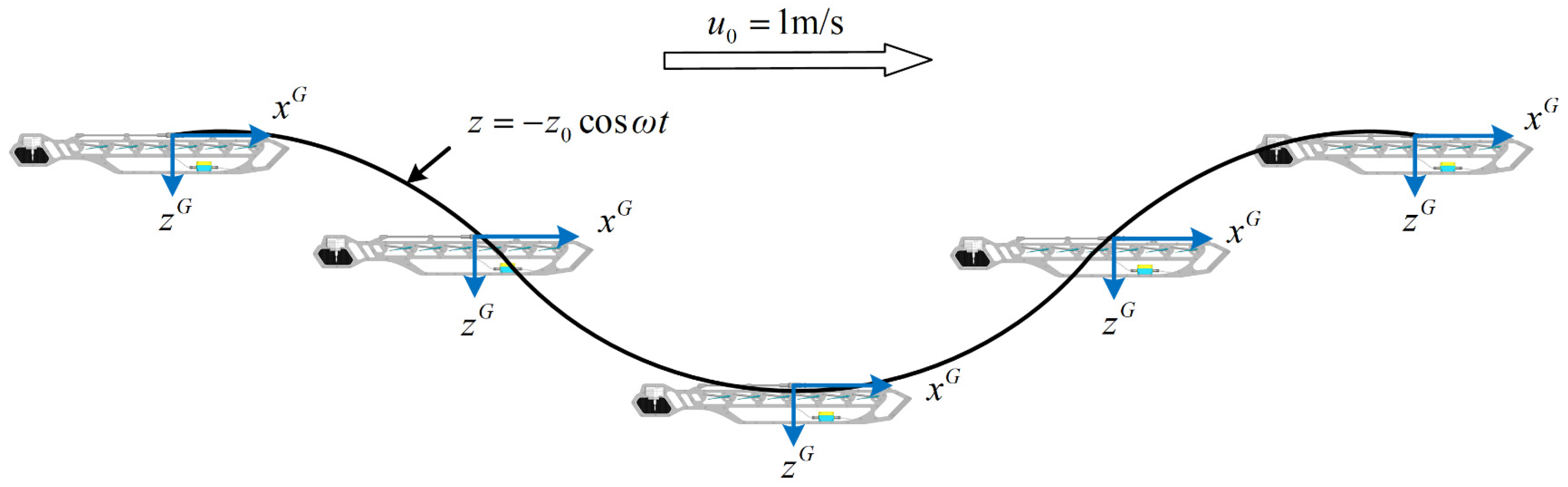
2.1. The Reference Frames
- (1)
- Float frame (with the right-superscript F): the hinge point between the surface float and the umbilical is as the origin of the coordinate frame. , and are positive toward the bow, the starboard and the bottom of the surface float, respectively;
- (2)
- Glider frame (with the right-superscript G): the hinge point between the submerged glider and the umbilical is as the origin of the glider frame. , and positive toward the bow, the starboard and the bottom of the submerged glider, respectively;
- (3)
- Inertial reference frame (): , and ζ point toward north, east and downwards, respectively.
2.2. Dynamic Model of the Surface Float
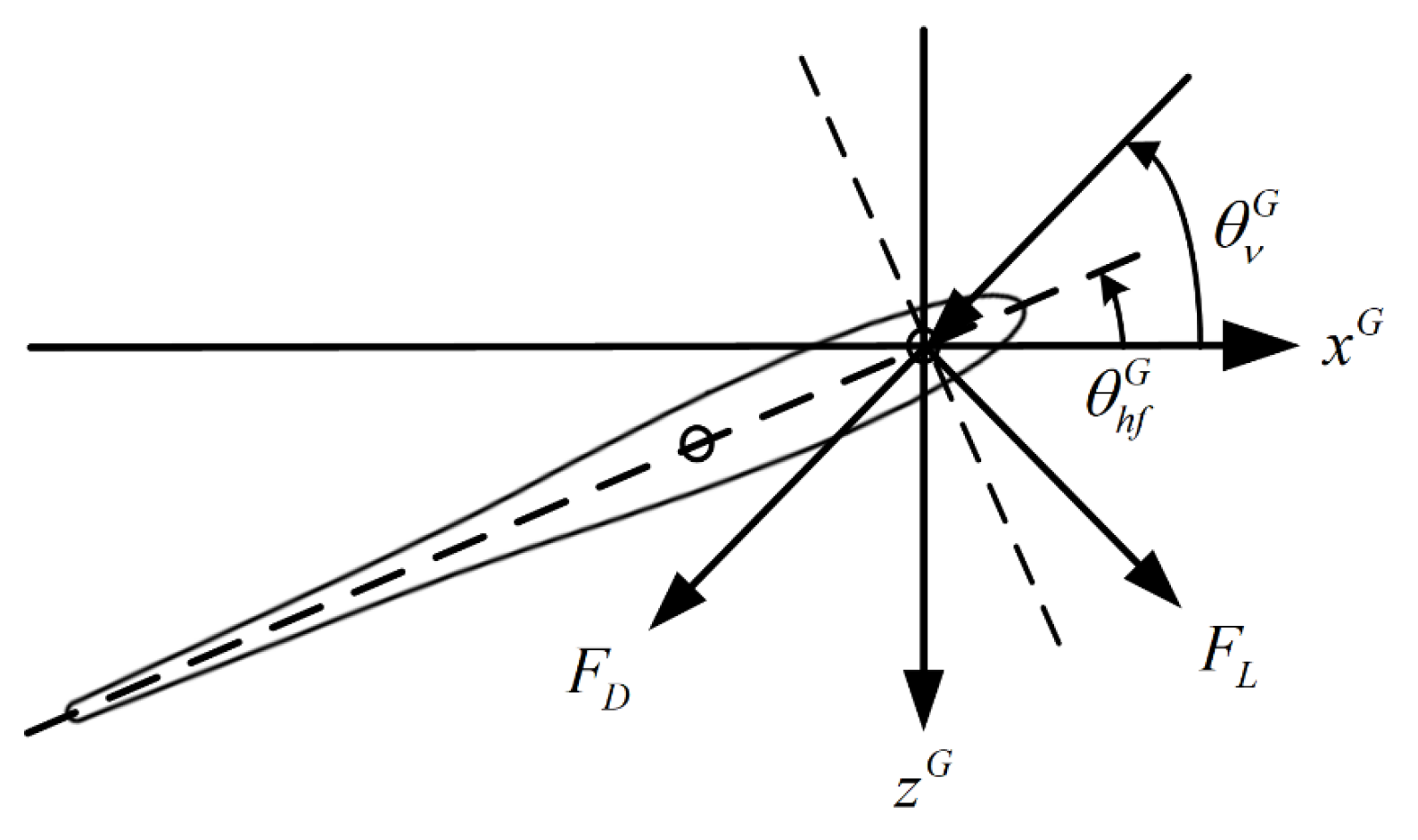
2.3. Dynamic Model of the Submerged Glider
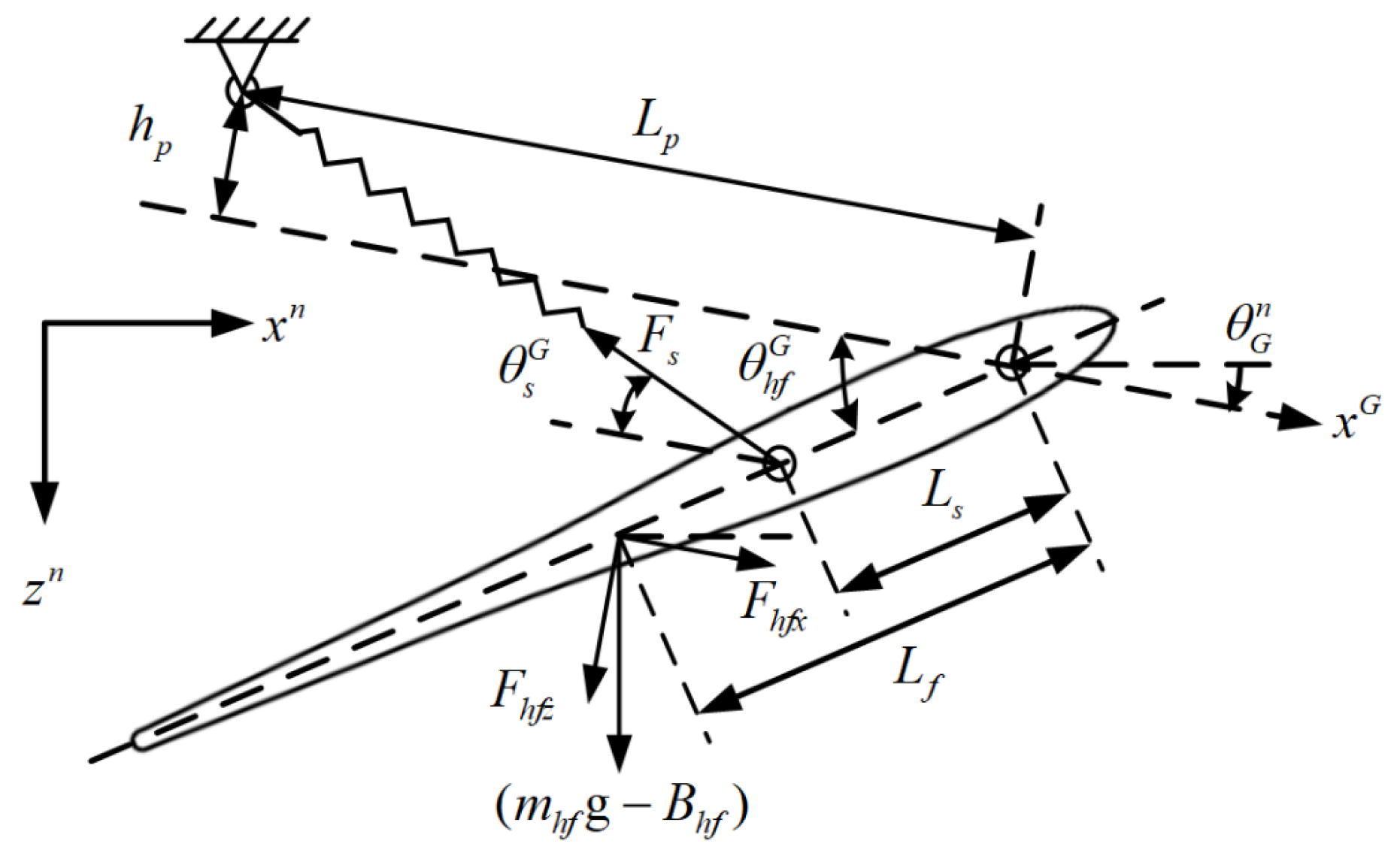
2.4. Umbilical Model
3. Simulation for Hydrodynamic Coefficients
3.1. Simulation Details
3.1.1. Turbulent Model
3.1.2. Computational Domain Decomposition and Mesh Generation
3.1.3. Boundary Conditions
3.1.4. Grid Convergence
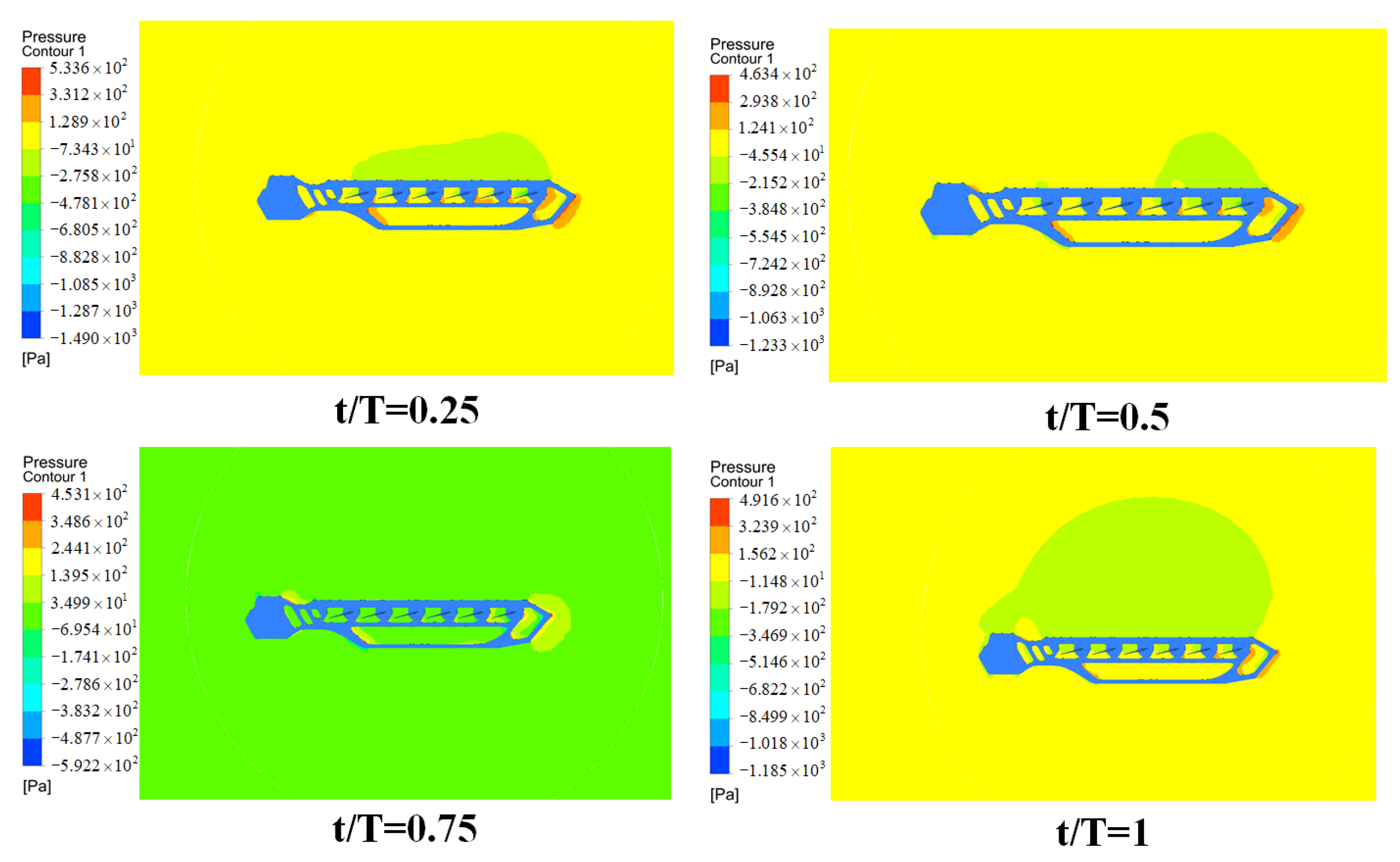
3.2. Static Test Simulations
3.3. Simulation of the VPMM Test
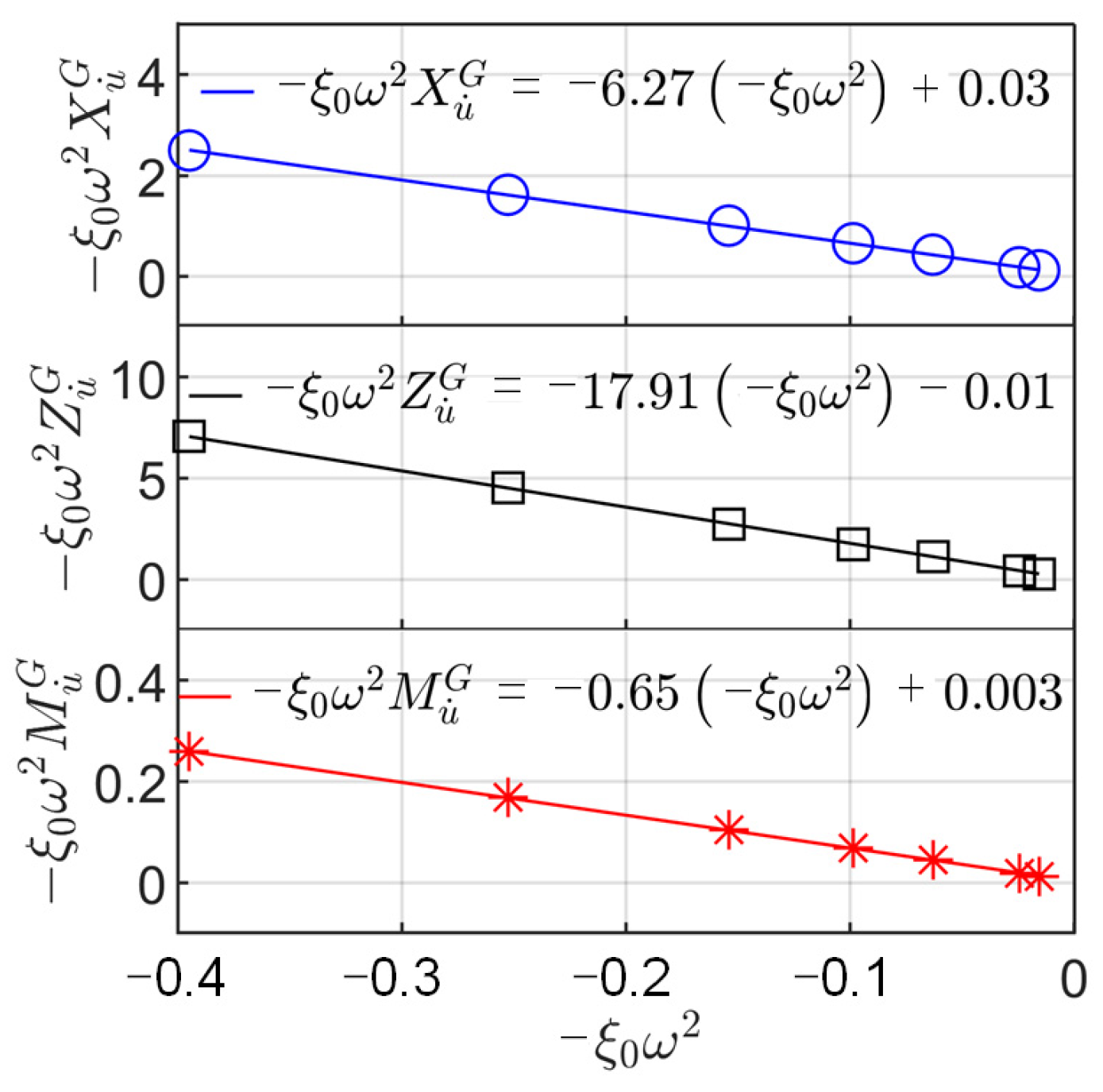
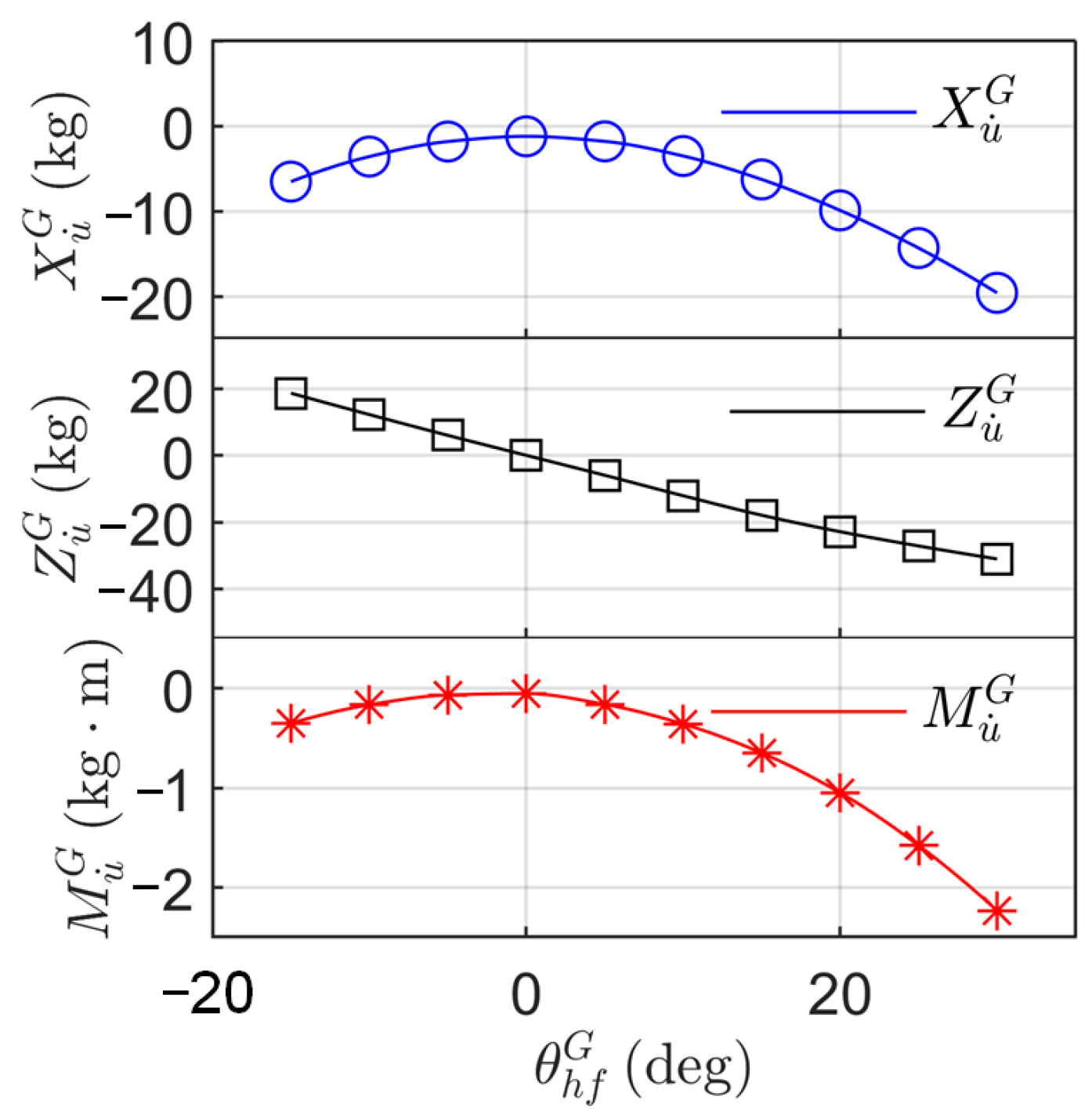
3.3.1. Pure Surge Simulation
3.3.2. Pure Heave Simulation
3.3.3. Pure Pitch Simulation
4. Numerical Simulation Validation and Analysis
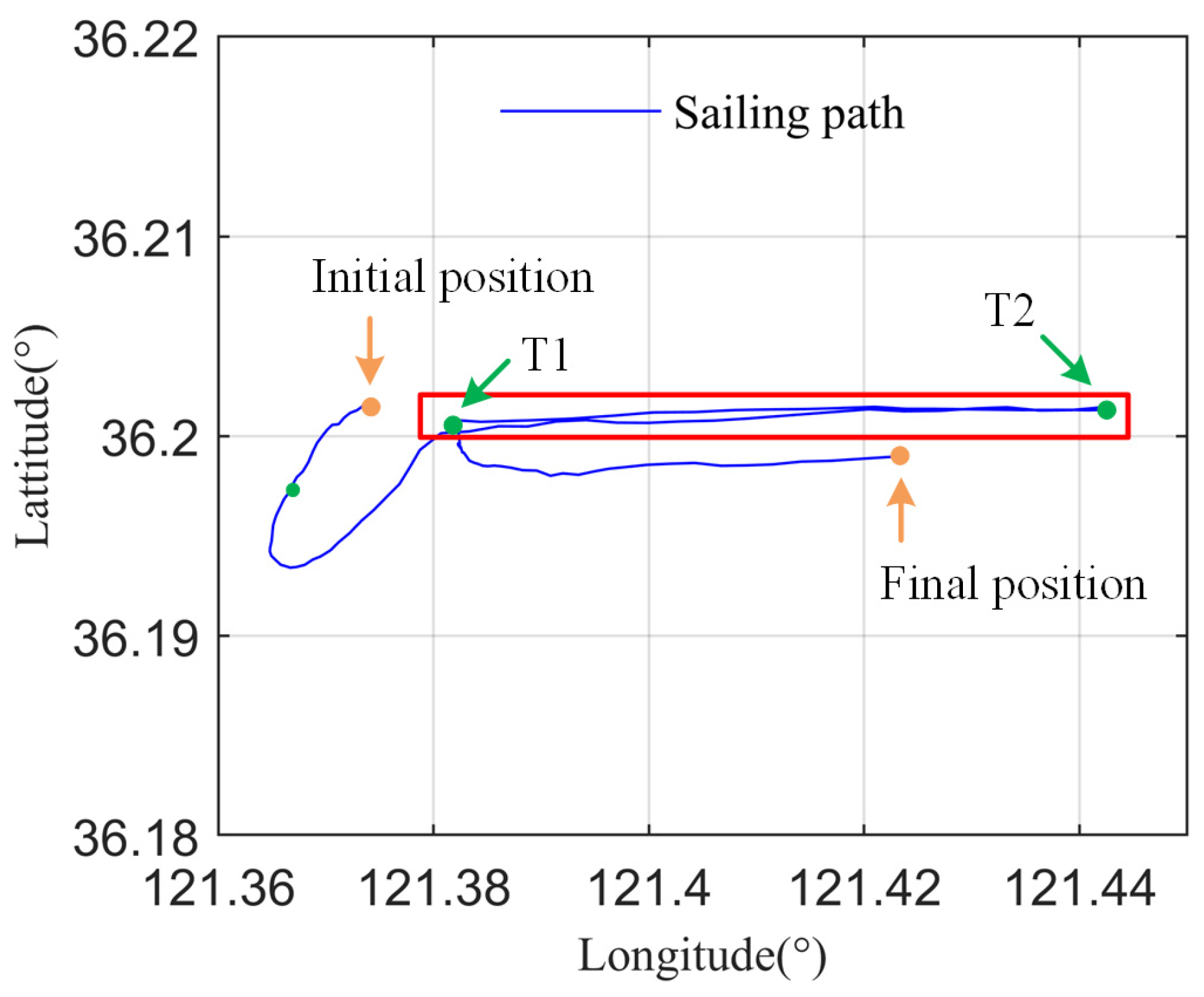
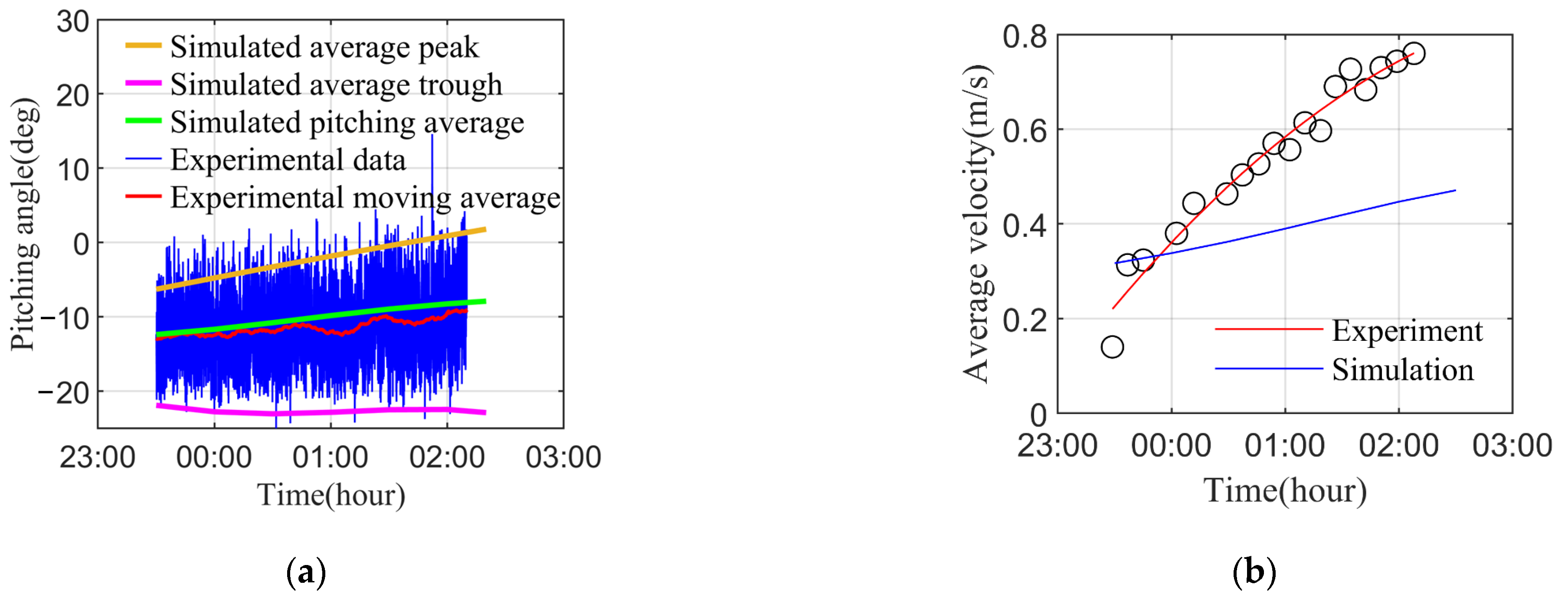
4.1. Sea Trial
4.2. Numerical Simulation
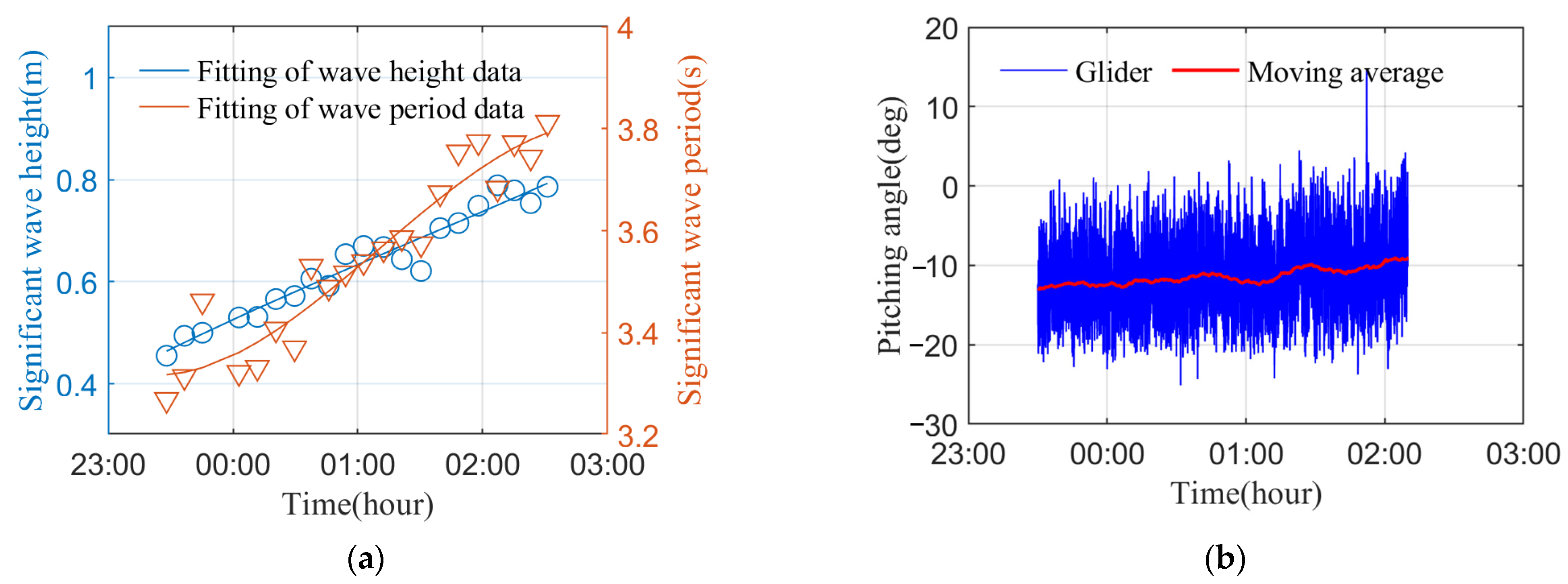
4.2.1. Numerical Simulation with the Specific Sea State
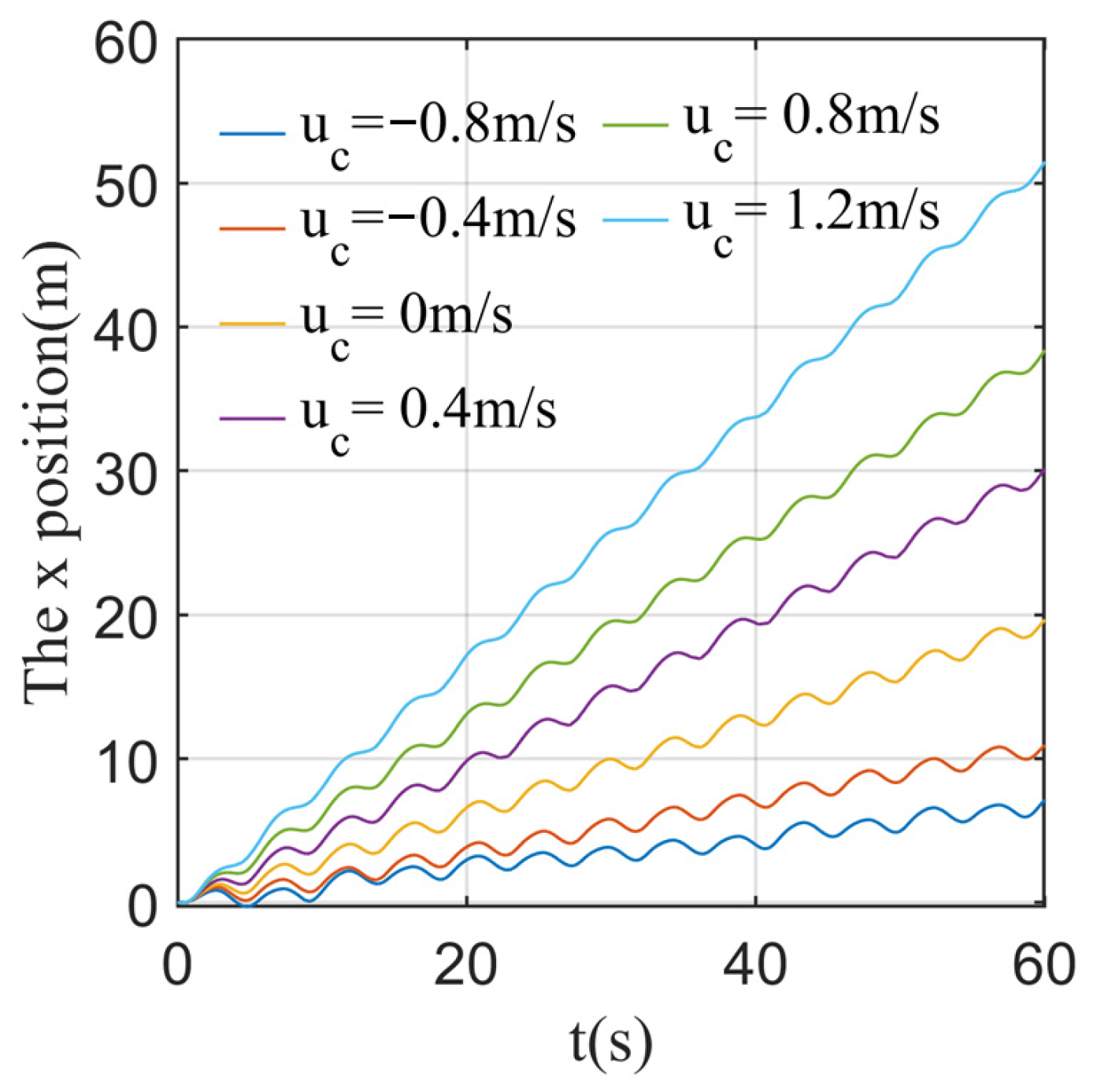
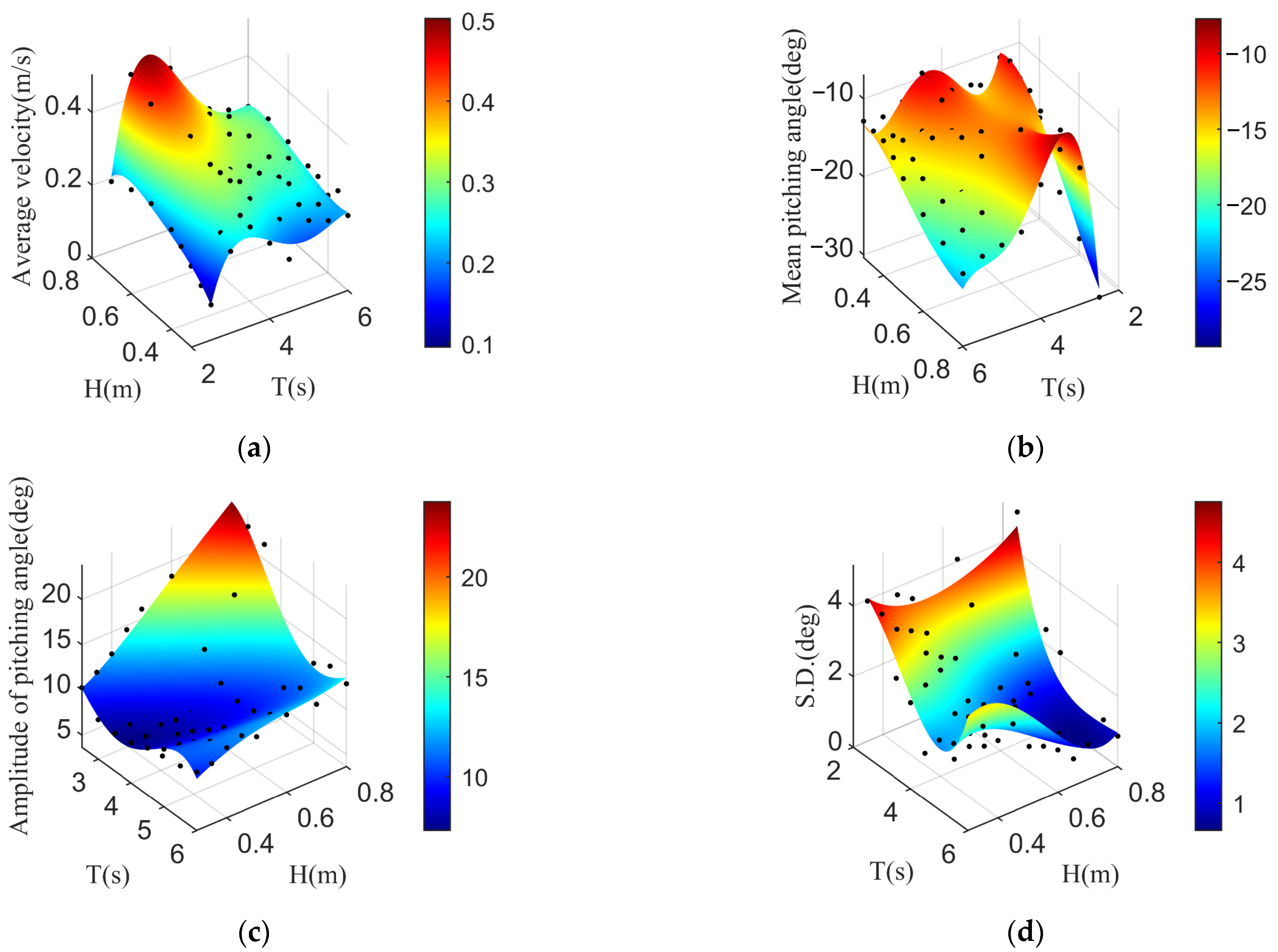
4.2.2. Numerical Simulation Results with Different Current Velocities
4.2.3. Numerical Simulation Results with the Different Sea States
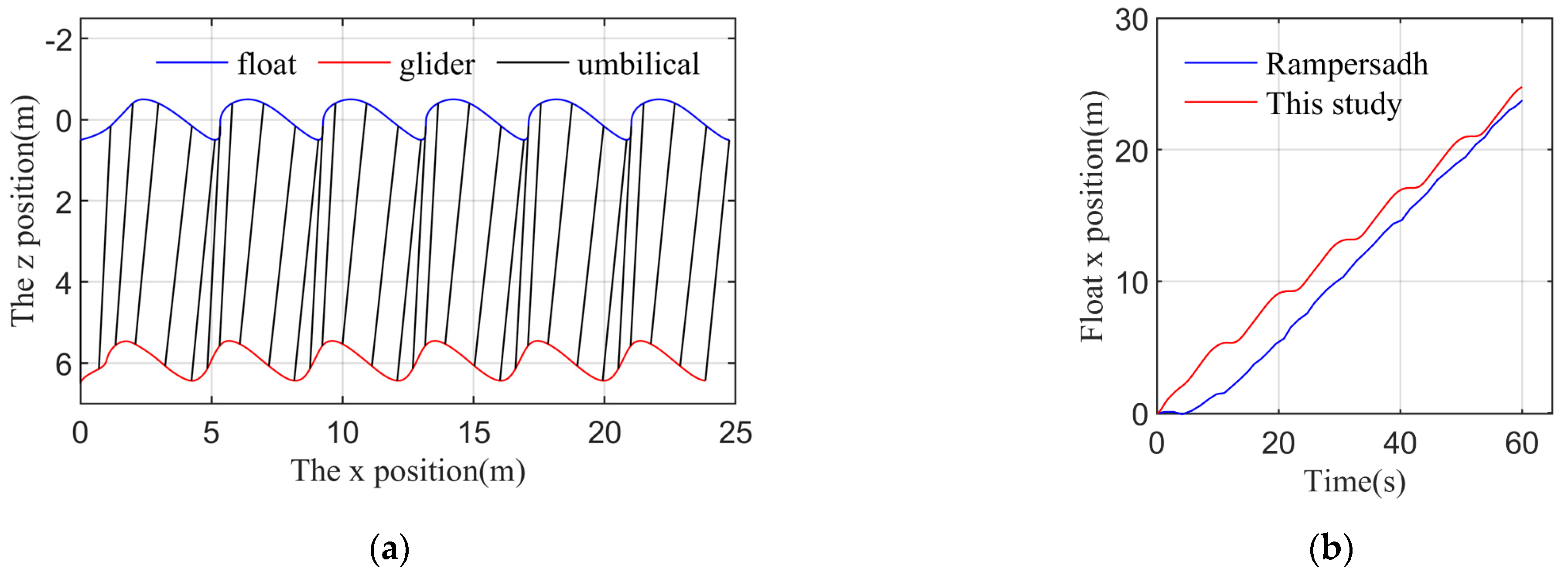
4.3. Numerical Simulation Validation
5. Conclusions
- (1)
- The proposed model and the numerical simulation using those hydrodynamic coefficients are found to be reasonable and acceptable in practice by comparison with the experimental data;
- (2)
- The numerical simulation can predict the longitudinal velocity of the wave glider and the pitching angle of the submerged glider and analyze the stability of the submerged glider from the mean value, the amplitude and the standard deviation of the pitching angle;
- (3)
- Under the same sea state, the positive current velocity is conducive to improving the navigation velocity of the wave glider, but the negative current velocity will reduce the navigation performance of the wave glider, reflecting the bigger hydrodynamic damping. In addition, the greater the positive or negative current velocity, the greater the favorable or hindering effect on the navigation performance of the wave glider;
- (4)
- The wave height and the wave period are the main factors affecting the straight-line sailing performance of the wave glider. Furthermore, the pitching stability of the submerged glider is also crucial for the wave glider to converse the energy obtained from ocean waves into the forward thrust.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hine, R.; Willcox, S.; Hine, G.; Richardson, T. The Wave Glider: A Wave-Powered autonomous marine vehicle. In Proceedings of the OCEANS 2009, Biloxi, MS, USA, 26–29 October 2009; IEEE: New York, NY, USA, 2010; pp. 1–6. [Google Scholar]
- Liu, P.; Su, Y.M.; Liao, Y.L. Numerical and experimental studies on the propulsion performance of a Wave Glide propulsor. China Ocean Eng. 2016, 30, 393–406. [Google Scholar] [CrossRef]
- Qi, Z.; Zou, B.; Lu, H.; Shi, J.; Li, G.; Qin, Y.; Zhai, J. Numerical investigation of the semi-active flapping foil of the wave glider. J. Mar. Sci. Eng. 2020, 8, 13. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Shi, W.; Wang, D. Systematic study on propulsive performance of tandem hydrofoils for a wave glider. Ocean Eng. 2019, 179, 361–370. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Shi, W.; Zhou, X.; Guo, B.; Wang, D. Numerical investigation of a wave glider in head seas. Ocean Eng. 2018, 164, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Kraus, N.; Bingham, B. Estimation of wave glider dynamics for precise positioning. In Proceedings of the OCEANS’11 MTS/IEEE KONA, Waikoloa, HI, USA, 19–22 September 2011; IEEE: New York, NY, USA, 2011; pp. 1–9. [Google Scholar]
- Kraus, N.D. Wave Glider Dynamic Modeling, Parameter Identification and Simulation. Master’s Thesis, University of Hawaii, Honolulu, HI, USA, 2012. [Google Scholar]
- Qi, Z.F.; Liu, W.X.; Jia, L.J.; Qin, Y.F.; Sun, X.J. Dynamic modeling and motion simulation for wave glider. Appl. Mech. Mater. 2013, 397–400, 285–290. [Google Scholar] [CrossRef]
- Li, X.T.; Liu, F.; Wang, L.; She, H.Q. Motion analysis of wave glider based on multibody dynamic theory. In Proceedings of the 10th International Conference on Intelligent Robotics and Applications, ICIRA, Wuhan, China, 16–18 August 2017; Springer: Cham, Switzerland; pp. 721–734. [Google Scholar]
- Rampersadh, G. Sea-State Interaction Based Dynamic Model of the Liquid Robotics’ Wave Glider: Modelling and Control of a Hybrid Multi-Body Vessel. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2018. [Google Scholar]
- Wang, P.; Tian, X.L.; Lu, W.Y.; Hu, Z.H.; Luo, Y. Dynamic modeling and simulations of the wave glider. Appl. Math. Model. 2019, 66, 77–96. [Google Scholar] [CrossRef]
- Chen, J.; Ge, Y.; Yao, C.; Zheng, B. Dynamics Modeling of a Wave Glider with Optimal Wing Structure. IEEE Access 2018, 6, 71555–71565. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Liao, Y.; Pan, K.; Zhang, W. Dynamics modeling of an unmanned wave glider with flexible umbilical. Ocean Eng. 2019, 180, 267–278. [Google Scholar] [CrossRef]
- Slone, A.K.; Pericleous, K.; Bailey, C.; Cross, M. Dynamic fluid–structure interaction using finite volume unstructured mesh procedures. Comput. Struct. 2002, 80, 371–390. [Google Scholar] [CrossRef]
- Westphalen, J.; Greaves, D.M.; Raby, A.; Hu, Z.Z.; Causon, D.M.; Mingham, C.G.; Omidvar, P.; Stansby, P.K.; Rogers, B.D. Investigation of Wave-Structure Interaction Using State of the Art CFD Techniques. Open J. Fluid Dyn. 2014, 4, 18–43. [Google Scholar] [CrossRef] [Green Version]
- Ren, B.; Jin, Z.; Gao, R.; Wang, Y.X.; Xu, Z.L. SPH-DEM modeling of the hydraulic stability of 2D blocks on a slope. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 04014022. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami Loads on a Representative Coastal Bridge Deck: Experimental Study and Validation of Design Equations. J. Waterw. Port Coast. Ocean. Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Y.R.; Cai, H.P. Using CFD software to calculate hydrodynamic coefficients. J. Mar. Sci. Appl. 2010, 9, 149–155. [Google Scholar] [CrossRef]
- Malik, S.A.; Guang, P. Transient numerical simulations for hydrodynamic derivatives predictions of an axisymmetric submersible vehicle. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 5003–5011. [Google Scholar] [CrossRef]
- Can, M. Numerical Simulation of Hydrodynamic Planar Motion Mechanism Test for Underwater Vehicles. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2014. [Google Scholar]
- Singh, Y.; Bhattacharyya, S.K.; Idichandy, V.G. CFD approach to modelling, hydrodynamic analysis and motion characteristics of a laboratory underwater glider with experimental results. J. Ocean Eng. Sci. 2017, 2, 90–119. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Rudmana, M.; Cleary, P.W. Oblique impact of rogue waves on a floating platform. In Proceedings of the International Ocean and Polar Engineering Conference 2009, Osaka, Japan, 21–26 June 2009; The International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2009; pp. 572–579. [Google Scholar]
- Peregrine, D.H.; Bredmose, H.; Bullock, G.; Obrhai, C.; Muller, G.; Wolters, G. Water wave impact on walls and the role of air. In Proceedings of the Coastal Engineering 2004, Lisbon, Portugal, 19–24 September 2004; World Scientific: Hackensack, NJ, USA, 2005; pp. 4005–4017. [Google Scholar]
- Ghosh, S.; Reins, G.; Koo, B.; Wang, Z.; Yang, J.; Stern, F. Plunging wave breaking: EFD and CFD. In Proceedings of the International Conference on Violent Flows, Fukuoka, Japan, 20–22 November 2007; National University: Fukuoka, Japan, 2007. [Google Scholar]
- Istrati, D. Large-Scale Experiments of Tsunami Inundation of Bridges including Fluid-Structure-Interaction. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2017. [Google Scholar]
- Leschka, S.; Oumeraci, H. Solitary waves and bores passing three cylinders-effect of distance and arrangement. Coast. Eng. 2014, 1, 39. [Google Scholar] [CrossRef] [Green Version]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef] [Green Version]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control, 1st ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2011. [Google Scholar]
- Jakuba, M.V. Modeling and Control of an Autonomous Underwater Vehicle with Combined Foil/Thruster Actuators. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries Inc.: La Canada, CA, USA, 2006. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluid Eng. Trans. ASME 2008, 130, 078001–078004. [Google Scholar]
- Park, J.Y.; Kim, N.; Shin, Y.K. Experimental study on hydrodynamic coefficients for high-incidence-angle maneuver of a submarine. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 100–113. [Google Scholar] [CrossRef] [Green Version]
- Watt, G.D. Modelling and Simulating Unsteady Six Degrees-of-Freedom Submarine Rising Maneuvers; DRDC Atlantic TR 2007-008; Defence Research and Development Canada: Ottawa, ON, Canada, 2007. [Google Scholar]
- Coe, R.G.; Neu, W.L. Amplitude effects on virtual PMM tests. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 26–29 October 2012; IEEE: New York, NY, USA, 2013; pp. 1–5. [Google Scholar]
- Li, C. Dynamics Analysis and Performance Optimization of the Wave Glider. Master’s Thesis, Tiangong University, Tianjin, China, 2018. (In Chinese). [Google Scholar]

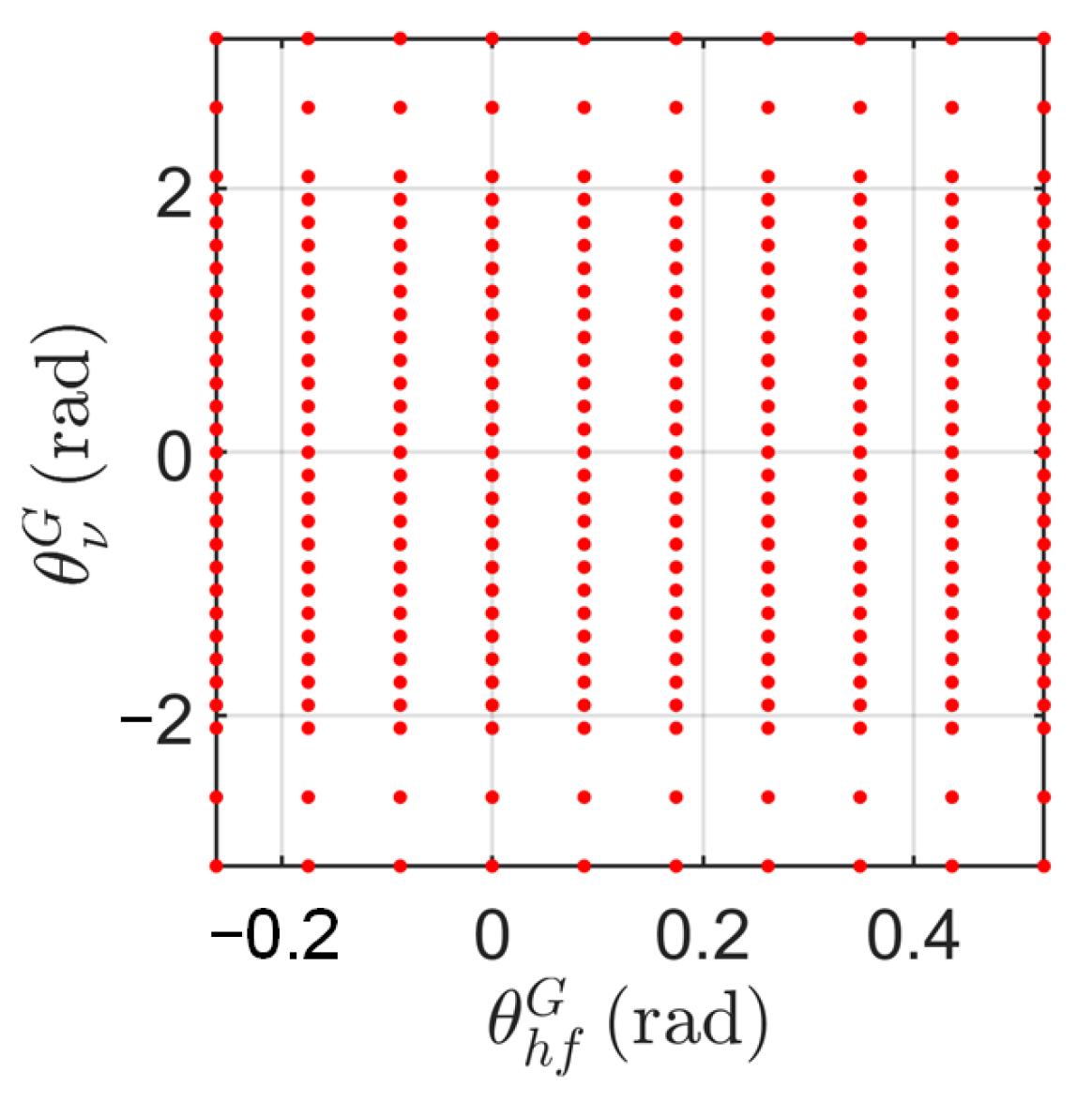
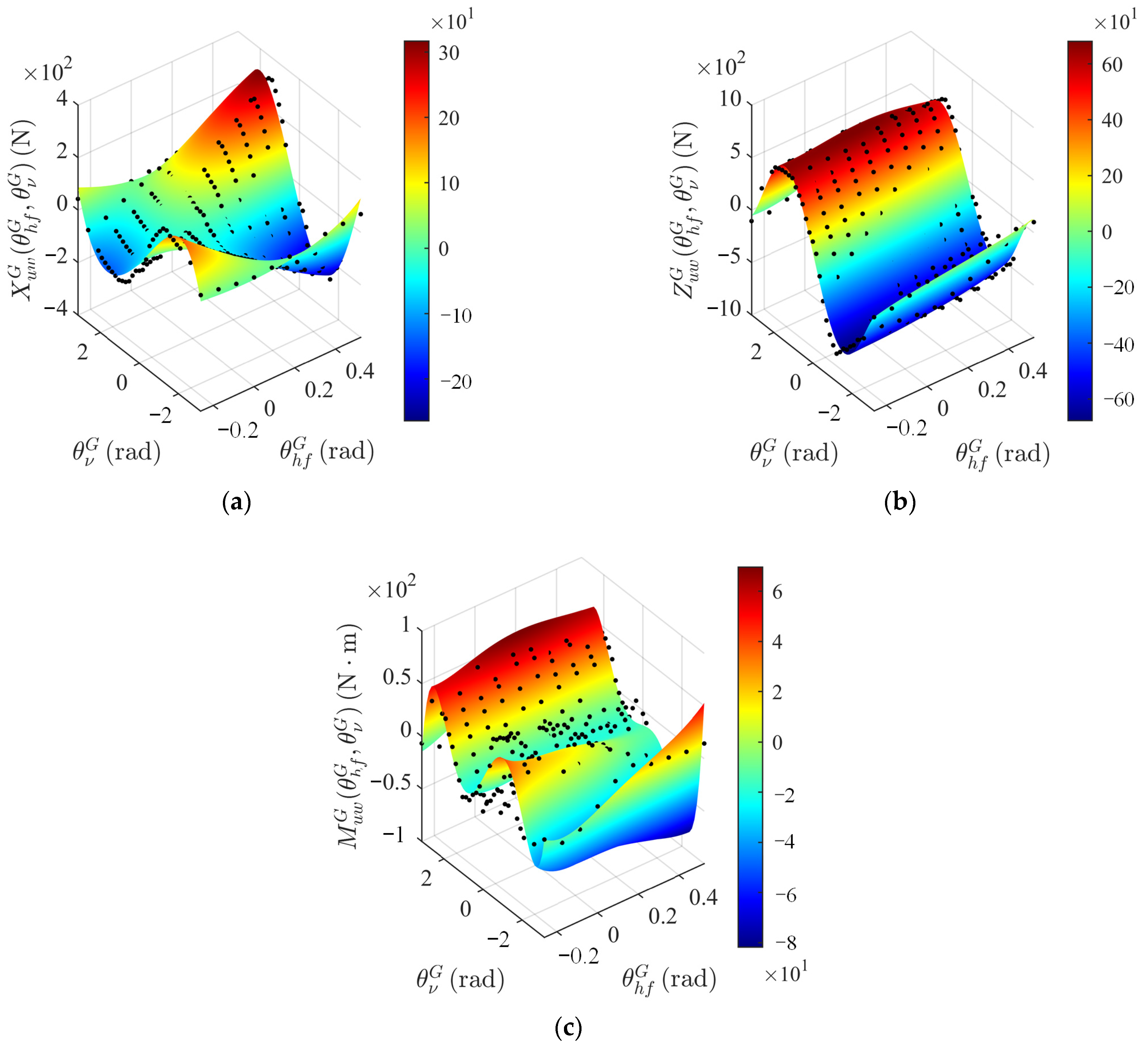
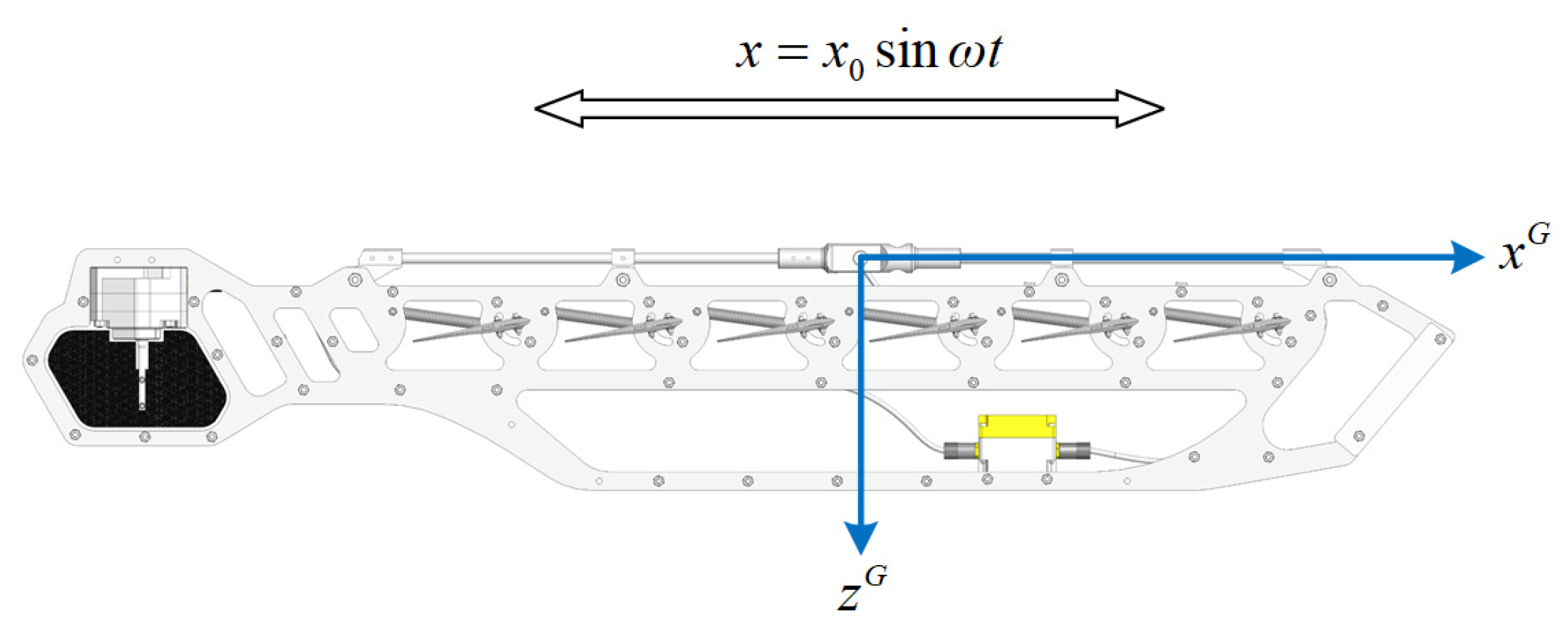
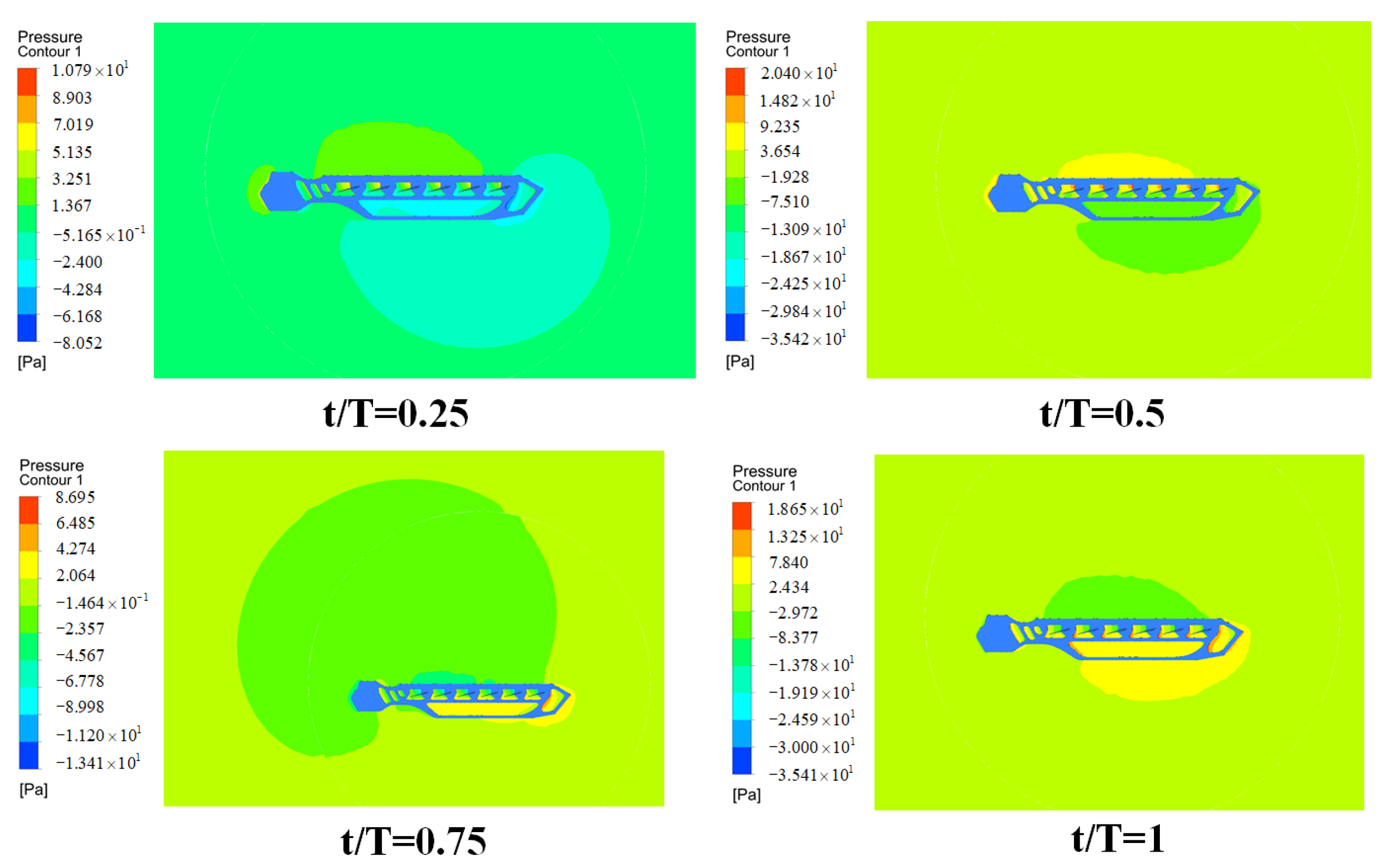
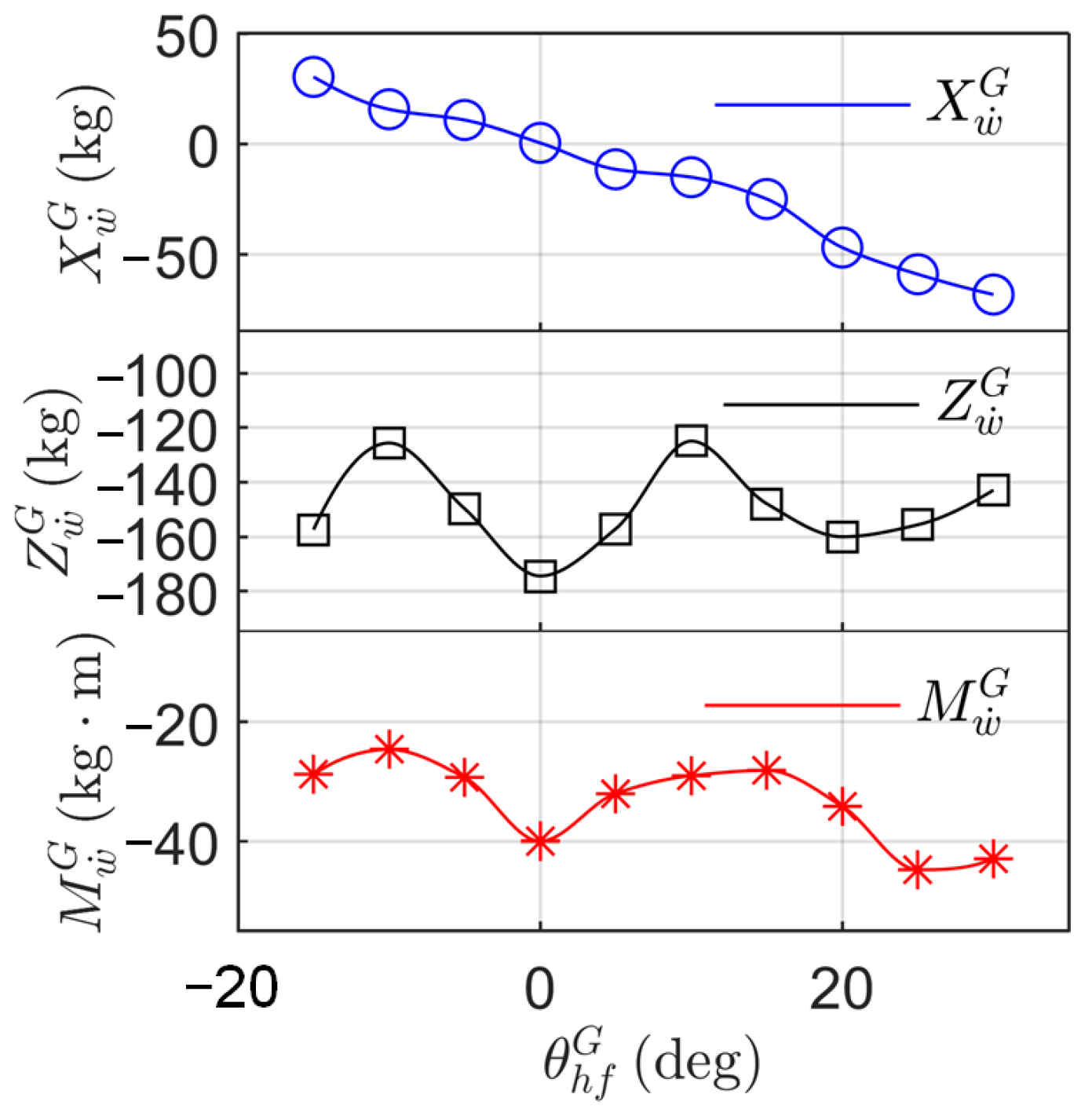
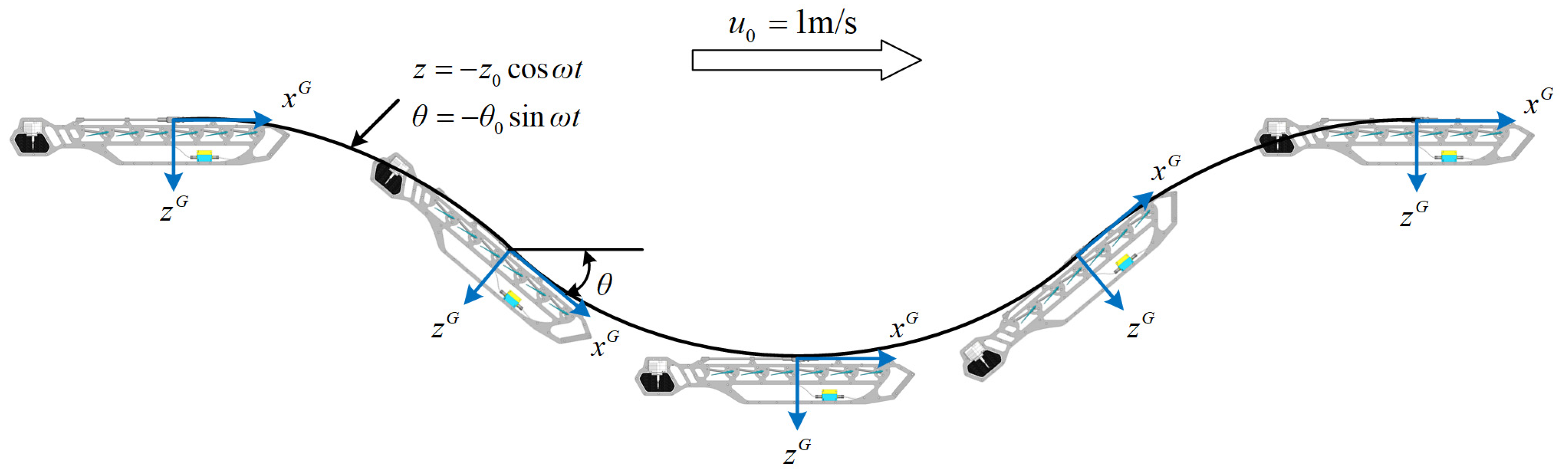
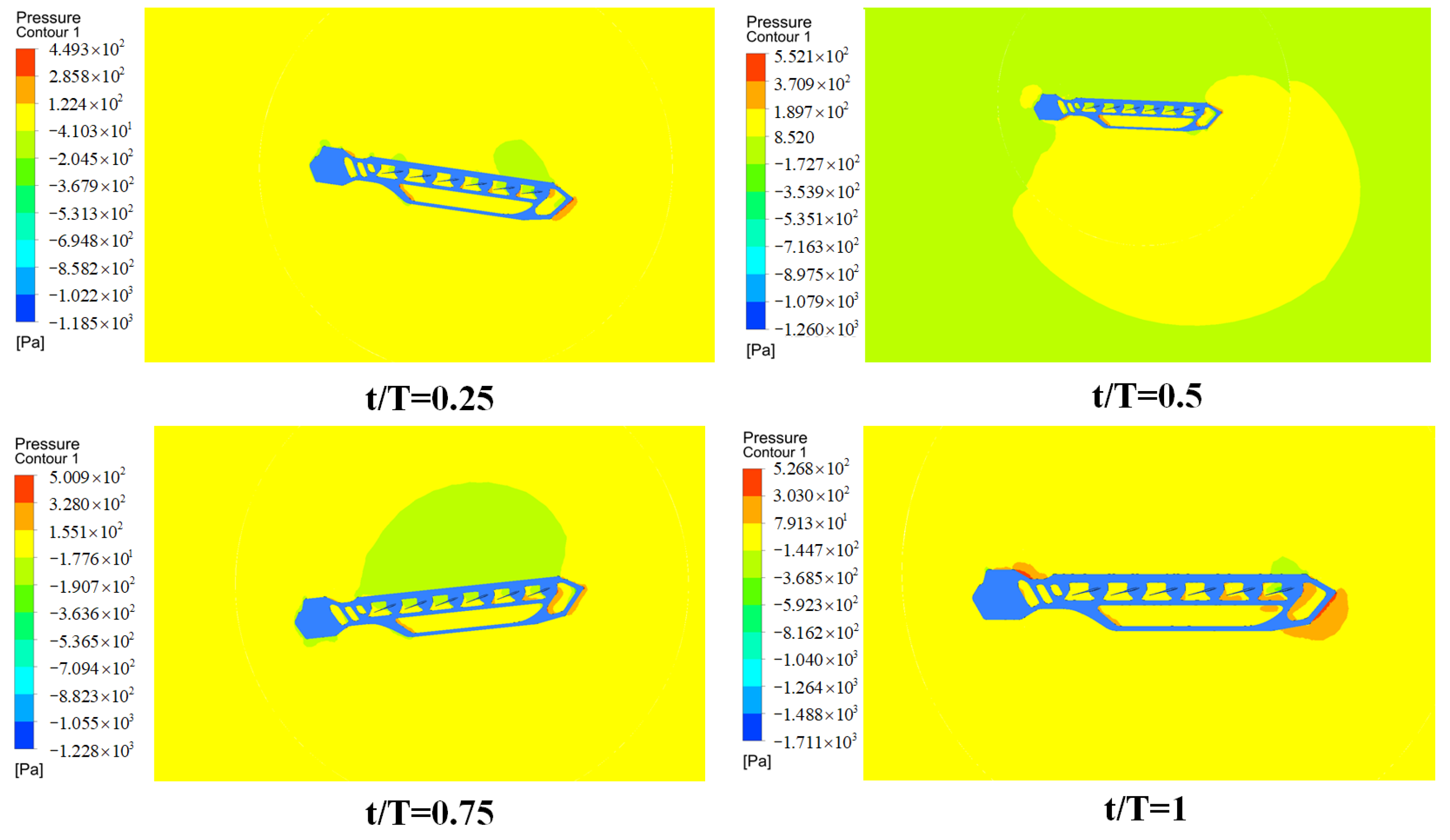
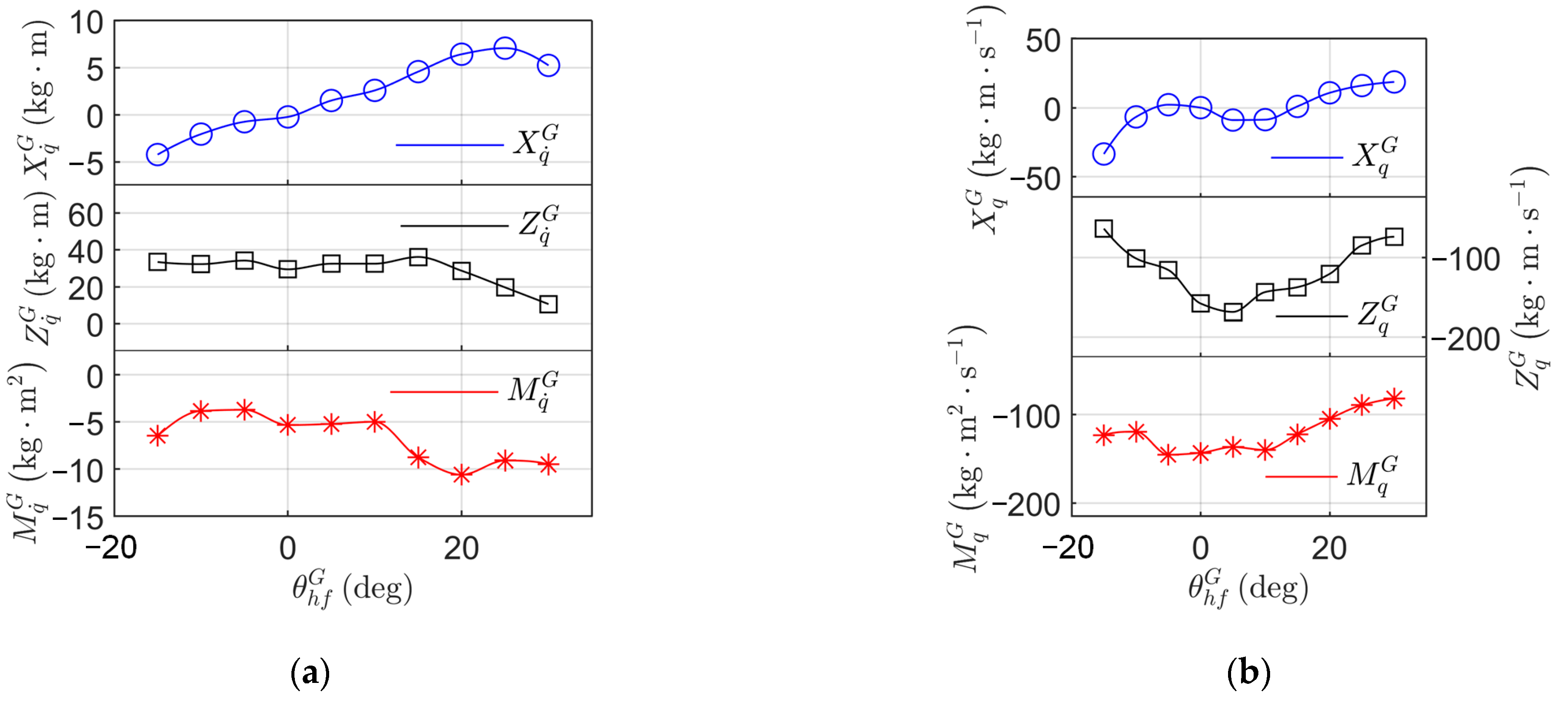

| Value | Unit | |
|---|---|---|
| Inner zone | m3 | |
| Middle zone | m3 | |
| Outer zone | m3 |
| Axial Force | Vertical Force | Pitch Moment | ||
|---|---|---|---|---|
| Output values | −34.094 | 116.552 | 21.503 | |
| −34.116 | 116.484 | 21.602 | ||
| −34.142 | 116.513 | 21.681 | ||
| Refinement ratio | 1.342 | |||
| 1.358 | ||||
| Order of accuracy | 0.4227 | 2.9829 | 0.9229 | |
| GCI | 0.0061 | 0.00052 | 0.018 | |
| 0.0069 | 0.00021 | 0.014 | ||
| Parameter | Description | Value | Unit |
|---|---|---|---|
| Mass of the surface float | 27.5 | kg | |
| Mass of the submerged glider | 30 | kg | |
| Mass of a pair of tandem hydrofoils | 2.137 | kg | |
| Pitching added mass of a pair of tandem hydrofoils | 0.3734 | kg∙m2 | |
| Buoyancy of a pair of tandem hydrofoils | 11.065 | N | |
| Surface float dimension | 1.8 × 0.5 × 0.2 | m3 | |
| Submerged glider dimension | 1.9 × 1.1 × 0.3 | m3 | |
| Initial length of the umbilical | 6 | m | |
| Gravity constant | 9.81 | m/s2 |
| Wave Height (m) | Wave Period (s) |
|---|---|
| 0.3 | 2.5 |
| 0.35 | 3 |
| 0.4 | 3.5 |
| 0.45 | 4 |
| 0.5 | 4.5 |
| 0.6 | 5 |
| 0.7 | 5.5 |
| 0.8 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Sun, C.; Sang, H.; Li, C. Dynamics Modeling and Hydrodynamic Coefficients Identification of the Wave Glider. J. Mar. Sci. Eng. 2022, 10, 520. https://doi.org/10.3390/jmse10040520
Sun X, Sun C, Sang H, Li C. Dynamics Modeling and Hydrodynamic Coefficients Identification of the Wave Glider. Journal of Marine Science and Engineering. 2022; 10(4):520. https://doi.org/10.3390/jmse10040520
Chicago/Turabian StyleSun, Xiujun, Chenyu Sun, Hongqiang Sang, and Can Li. 2022. "Dynamics Modeling and Hydrodynamic Coefficients Identification of the Wave Glider" Journal of Marine Science and Engineering 10, no. 4: 520. https://doi.org/10.3390/jmse10040520
APA StyleSun, X., Sun, C., Sang, H., & Li, C. (2022). Dynamics Modeling and Hydrodynamic Coefficients Identification of the Wave Glider. Journal of Marine Science and Engineering, 10(4), 520. https://doi.org/10.3390/jmse10040520





