Numerical and Experimental Analysis of the Velocity Field Inside an Artificial Reef. Application to the Ares-Betanzos Estuary
Abstract
1. Introduction
- Determining the characteristics of the current velocity against the depth through a 3D hydrodynamic model.
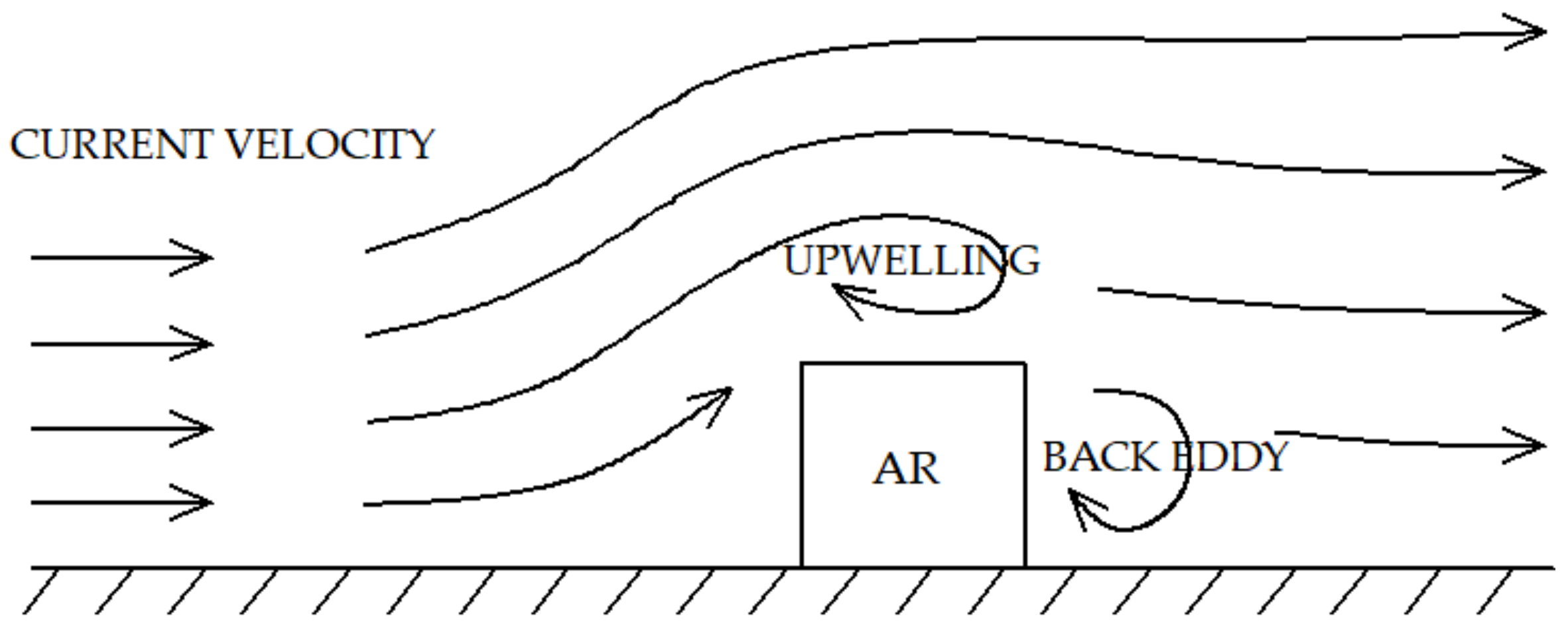
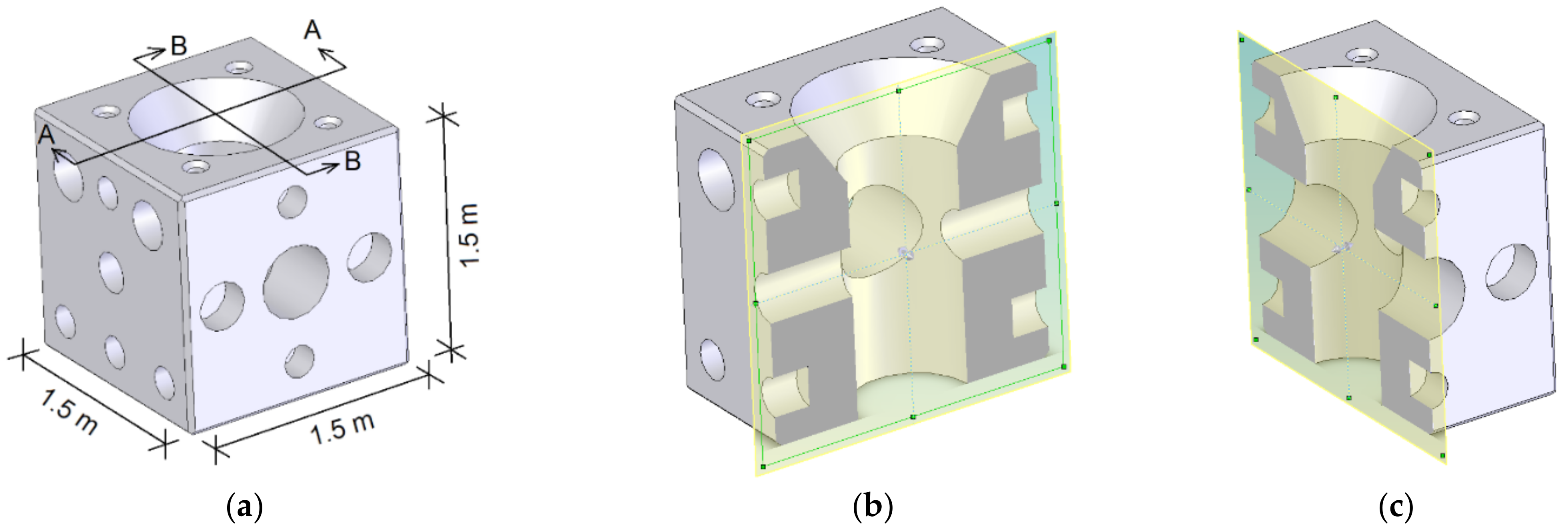
- Determining the hydrodynamics around the AR through a CFD model. Two different configurations of the AR are analyzed in order to see which favors the most circulation for the specific area based on the value of the velocity inside the AR module.
- Validating the CFD results through towing tank tests.
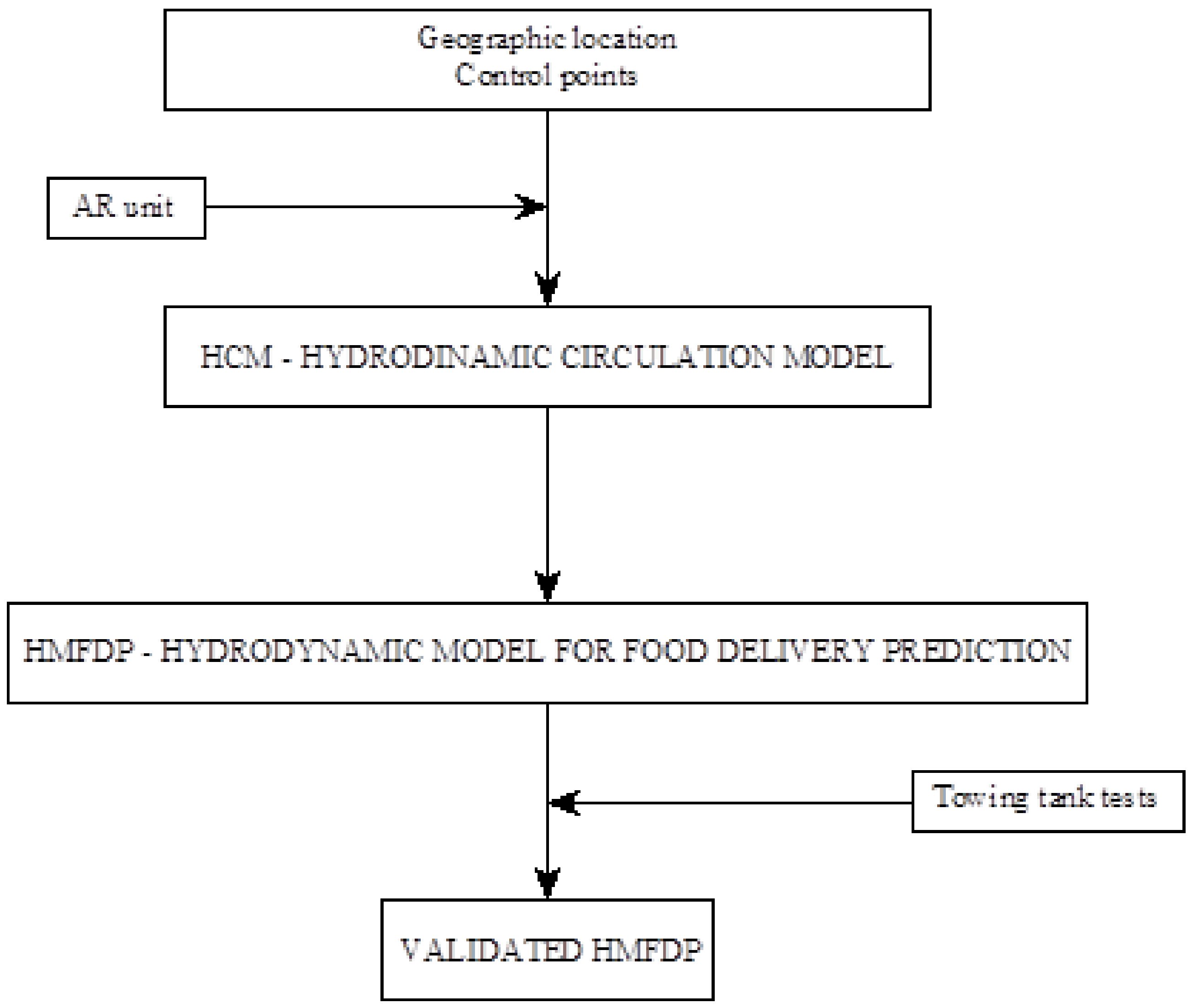
2. Materials and Methods
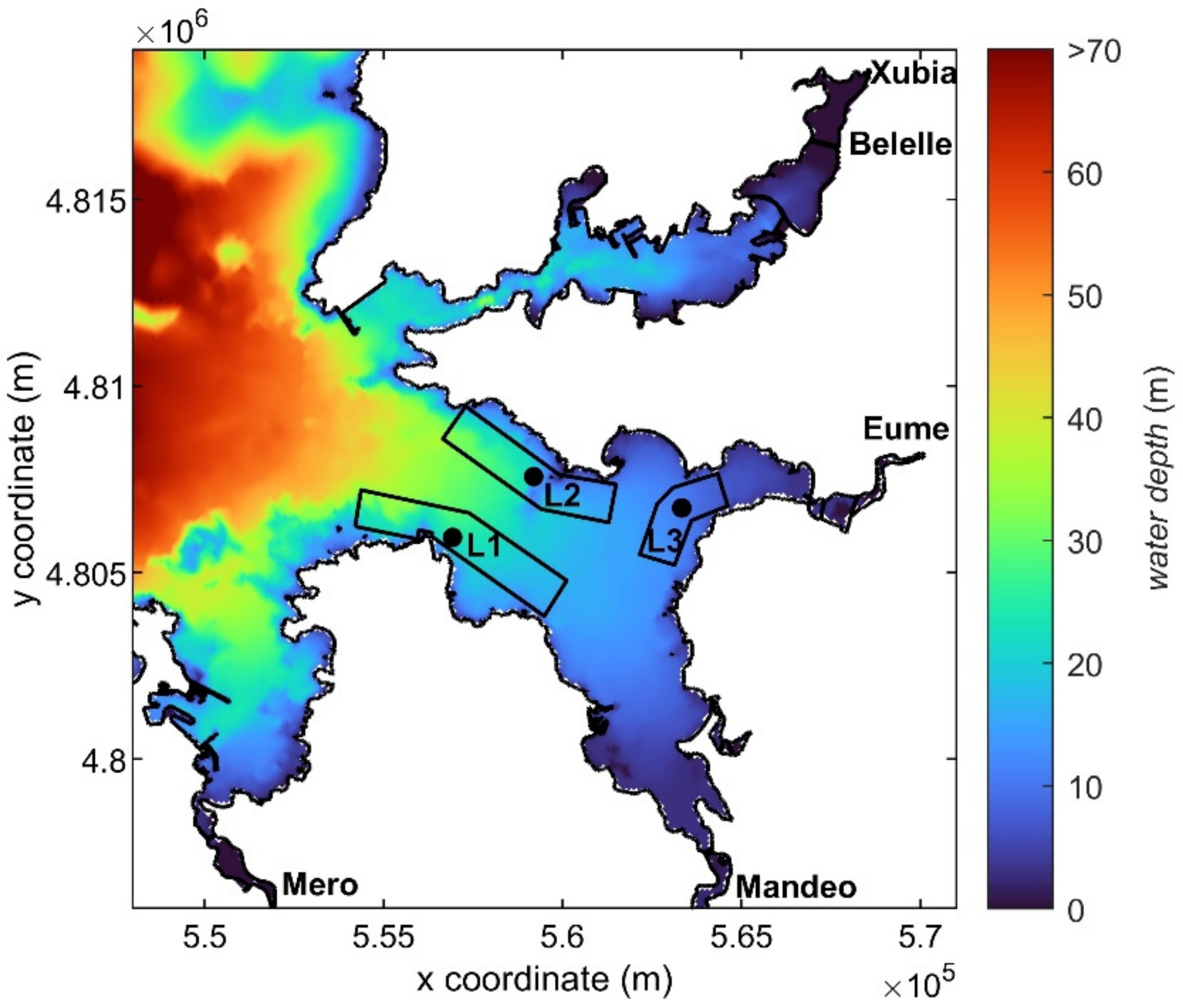
2.1. Hydrodynamic Circulation Model (HCM)
2.2. Hydrodynamic Model for Food Delivery Prediction (HMFDP)
- -
- Orientation A: 0.25 m diameter hole parallel to the current velocity.
- -
- Orientation B: 0.45 m diameter hole parallel to the current velocity.
2.3. Towing Tank Tests
3. Results
3.1. Hydrodynamic Circulation Model results
3.2. Hydrodynamic Model for Food Delivery Prediction Results
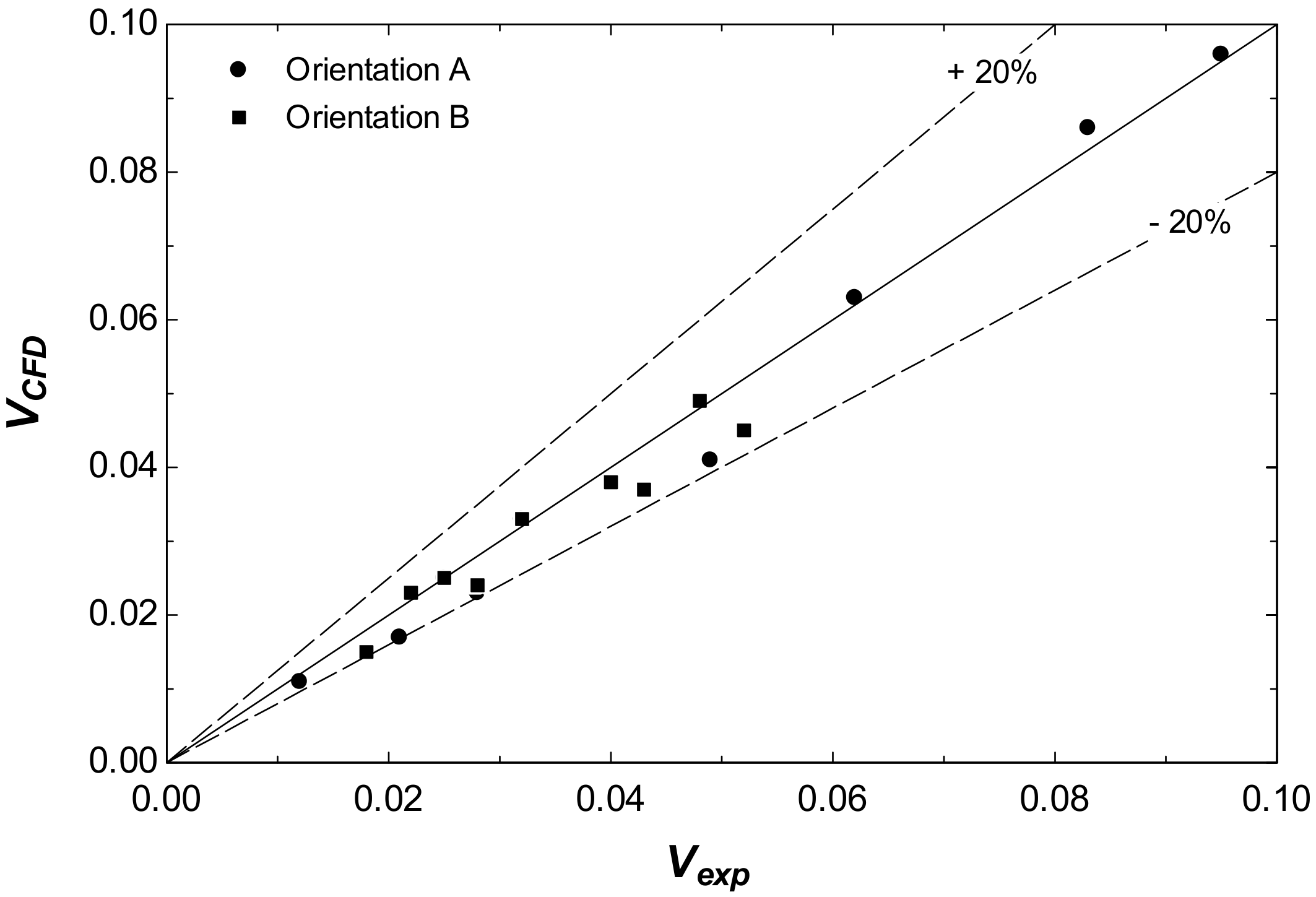
3.3. Towing Tank Tests
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ADCP | Acoustic doppler current profiler |
| ADI | Alternating-direction implicit |
| AR | Artificial reef |
| CAR | Conventional artificial reef |
| CFD | Computational fluid dynamics |
| GAR | Green artificial reef |
| HCM | Hydrodynamic circulation model |
| HMFDP | Hydrodynamic model for food delivery prediction |
| NE | North East |
| OG-GAR | One generation–green artificial reef |
| PIV | Particle image velocity |
| W | West |
References
- Rashid Sumaila, U.; Bellmann, C.; Tipping, A. Fishing for the Future: An Overview of Challenges and Opportunities. Mar. Policy 2016, 69, 173–180. [Google Scholar] [CrossRef]
- Visbeck, M.; Kronfeld-Goharani, U.; Neuman, B.; Rickels, W.; Shmidt, J.; Van Doorn, E.; Matz-Lück, N.; Ott, K.; Quas, M.F. Securing Blue Wealth: The Need for a Special Sustainable Development Goal for the Ocean and Coasts. Mar. Policy 2014, 48, 184–191. [Google Scholar] [CrossRef]
- Rickels, W.; Dovern, J.; Quaas, M. Beyond Fisheries: Common-Pool Resource Problems in Oceanic Resources and Services. Glob. Environ. Chang. 2016, 40, 37–49. [Google Scholar] [CrossRef]
- Bacher, C.; Grant, J.; Hawkins, A.J.S.; Fang, J.; Zhu, M.; Besnard, M. Modelling the Effect of Food Depletion on Scallop Growth in Sungo Bay (China). Aquat. Living Resour. 2003, 16, 10–24. [Google Scholar] [CrossRef]
- Carral, L.; Rodriguez-Guerreiro, M.; Tarrio-Saavedra, J.; Alvarez-Feal, J.C.; Fraguela Formoso, J. Social Interest in Developing a Green Modular Artificial Reef Structure in Concrete for the Ecosystems of the Galician Rías. J. Clean. Prod. 2018, 172, 1881–1898. [Google Scholar] [CrossRef]
- Carral, L.; Lamas-Galdo, M.I.; Rodríguez-Guerreiro, M.J.; Vargas, A.; Álvarez-Feal, C.; Carballo, R. Configuration Methodology for a Green Variety Reef System (AR Group) Based on Hydrodynamic Criteria—Application to the Ría de Ares-Betanzos. Estuar. Coast. Shelf Sci. 2021, 252, 107301. [Google Scholar] [CrossRef]
- Carral, L.; Cartelle Barros, J.J.; Carro Fidalgo, H.; Camba Fabal, C.; Munín Doce, A. Greenhouse Gas Emissions and Energy Consumption of Coastal Ecosystem Enhancement Programme through Sustainable Artificial Reefs in Galicia. Int. J. Environ. Res. Public Health 2021, 18, 1909. [Google Scholar] [CrossRef]
- Caballero Miguez, G.; Garza Gil, M.D.; Varela Lafuente, M.M. Institutions and Management of Fishing Resources: The Governance of the Galician Model. Ocean Coast. Manag. 2008, 51, 625–631. [Google Scholar] [CrossRef]
- Nogueira, C. Galicia En La Unión Europea. Una Economía Emergente. Rev. Galega Econ. 2008, 17, 1–14. [Google Scholar]
- Kim, D.; Woo, J.; Na, W. Intensively Stacked Placement Models of Artificial Reef Sets Characterized by Wake and Upwelling Regions. Mar. Technol. Soc. J. 2017, 51, 60–70. [Google Scholar] [CrossRef]
- Klaoudatos, D.; Anastasopoulou, A.; Papaconstantinou, C.; Conides, A. The Greek Experience of Artificial Reef Construction and Management. J. Environ. Prot. Ecol. 2012, 13, 1647–1655. [Google Scholar]
- Techera, E.J.; Chandler, J. Offshore Installations, Decommissioning and Artificial Reefs: Do Current Legal Frameworks Best Serve the Marine Environment? Mar. Policy 2015, 59, 53–60. [Google Scholar] [CrossRef]
- Yun, D.-H.; Kim, Y.-T. Experimental Study on Settlement and Scour Characteristics of Artificial Reef with Different Reinforcement Type and Soil Type. Geotext. Geomembr. 2018, 46, 448–454. [Google Scholar] [CrossRef]
- Kim, D.; Jung, S.; Kim, J.; Na, W.-B. Efficiency and Unit Propagation Indices to Characterize Wake Volumes of Marine Forest Artificial Reefs Established by Flatly Distributed Placement Models. Ocean Eng. 2019, 175, 138–148. [Google Scholar] [CrossRef]
- Camba, C.; Mier, J.L.; Carral, L.; Lamas, M.I.; Álvarez, J.D.; Díaz-Díaz, A.M.; Tarrío-Saavedra, J. Erosive Degradation Study of Concrete Augmented by Mussel Shells for Marine Construction. J. Clean. Prod. 2021, 9, 1087. [Google Scholar] [CrossRef]
- Carral, L.; Camba Fabal, C.; Lamas Galdo, M.I.; Rodríguez-Guerreiro, M.J.; Cartelle Barros, J.J. Assessment of the Materials Employed in Green Artificial Reefs for the Galician Estuaries in Terms of Circular Economy. Int. J. Environ. Res. Public Health 2020, 17, 8850. [Google Scholar] [CrossRef] [PubMed]
- Mo, K.H.; Alengaram, U.J.; Jumaat, M.Z.; Yap, S.P.; Lee, S.C. Green Concrete Partially Comprised of Farming Waste Residues: A Review. J. Clean. Prod. 2016, 117, 122–138. [Google Scholar] [CrossRef]
- Carral, L.; Lamas, M.I.; Mier, J.L.; Cartelle Barros, J.J.; Naya, S.; Tarrio-Saavedra, J. Application of Residuals from Purification of Bivalve Molluscs in Galicia to Facilitate Marine Ecosystem Resiliency through Artificial Reefs with Shells—One Generation. Sci. Total Environ. 2023, 856, 159095. [Google Scholar] [CrossRef]
- Wang, G.; Wan, R.; Wang, X.; Zhao, F.; Lan, X.; Cheng, H.; Tang, W.; Guan, Q. Study on the Influence of Cut-Opening Ratio, Cut-Opening Shape, and Cut-Opening Number on the Flow Field of a Cubic Artificial Reef. Ocean Eng. 2018, 162, 341–352. [Google Scholar] [CrossRef]
- He, D.R.; Shi, Y.M. Attractive Effect of Fish Reef Model on Black Porgy (Sparus Macrocephalus). J. Xiamen Univ. (Nat. Sci) 1995, 34, 653–658. [Google Scholar]
- Baine, M. Artificial Reefs: A Review of Their Design, Application, Management and Performance. Ocean Coast. Manag. 2001, 44, 241–259. [Google Scholar] [CrossRef]
- Haro, A.; Castro-Santos, T.; Noreika, J.; Odeh, M. Swimming Performance of Upstream Migrant Fishes in Open-Channel Flow: A New Approach to Predicting Passage through Velocity Barriers. Can. J. Fish. Aquat. Sci. 2004, 61, 1590–1601. [Google Scholar] [CrossRef]
- Lan, C.H.; Chen, C.C.; Hsui, C.Y. An Approach to Design Spatial Configuration of Artificial Reef Ecosystem. Ecol. Eng. 2004, 22, 217–226. [Google Scholar] [CrossRef]
- Bohnsack, J.A.; Sutherland, D.L. Artificial Reef Research: A Review with Recommendations for Future Priorities. Bull. Mar. Sci. 1985, 37, 11–39. [Google Scholar]
- Collins, K.J.; Jensen, A.C.; Lockwood, A.P.M. Fishery Enhancement Reef Building Exercise. J. Chem. Ecol. 1990, 4, 179–187. [Google Scholar] [CrossRef]
- Godoy, E.; Almeida, T.; Zalmon, I. Fish Assemblages and Environmental Variables on an Artificial Reef North of Rio de Janeiro, Brazil. ICES J. Mar. Sci. 2002, 59, S138–S143. [Google Scholar] [CrossRef][Green Version]
- Pickering, H.; Withmarsh, D.; Jensen, A. Artificial Reefs as a Tool to Aid Rehabilitation of Coastal Ecosystems: Investigating the Potential. Mar. Pollut. Bull. 1999, 37, 505–514. [Google Scholar] [CrossRef]
- Tang, Y.L.; Wang, L.; Liang, Z.L.; Jiang, Z.Y.; Shi, H.W. Test of the Hydrodynamic Performance of Square Artificial Reefs. Period. Ocean Univ. China 2007, 37, 713–716. [Google Scholar]
- Liu, Y.; Guan, C.T.; Zhao, Y.P.; Cui, Y.; Dong, G.H. Numerical Simulation and PIV Study of Unsteady Flow around Hollow Cube Artificial Reef with Free Water Surface. Eng. Appl. Comput. Fluid Mech. 2012, 6, 527–540. [Google Scholar] [CrossRef]
- Liu, T.L.; Su, D.T. Numerical Analysis of the Influence of Reef Arrangements on Artificial Reef Flow Fields. Ocean Eng. 2013, 75, 81–89. [Google Scholar] [CrossRef]
- Fu, D.W.; Luan, S.G.; Zhang, R.J.; Chen, Y. Two-Way Analysis of Variance of Effects of Cut-Opening Ratio and Surface Shape Facing Flowing in Artificial Fish Reefs on the Flowing Field. J. Dalian Ocean Univ. 2012, 27, 274–278. [Google Scholar]
- Nie, Z.; Zhu, L.; Xie, W.; Zhang, J.; Wang, J.; Jiang, Z.; Liang, Z. Research on the Influence of Cut-Opening Factors on Flow Field Effect of Artificial Reef. Ocean Eng. 2022, 249, 110890. [Google Scholar] [CrossRef]
- Woo, J.; Kim, D.; Yoon, H.S.; Na, W.B. Characterizing Korean General Artificial Reefs by Drag Coefficients. Ocean Eng. 2014, 82, 105–114. [Google Scholar] [CrossRef]
- Kim, D.; Woo, J.; Yoon, H.-S.; Na, W.-B. Wake Lengths and Structural Responses of Korean General Artificial Reefs. Ocean Eng. 2014, 92, 83–91. [Google Scholar] [CrossRef]
- Sherman, R.L.; Gilliam, D.S.; Spieler, R.E. Artificial Reef Design: Void Space, Complexity, and Attractants. ICES J. Mar. Sci. 2002, 59, 196–200. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Tang, Y.; Zhao, F.; Luo, Y. Numerical Analysis of the Flow Effect of the Menger-Type Artificial Reefs with Different Void Space Complexity Indices. Symmetry 2021, 13, 1040. [Google Scholar] [CrossRef]
- Carral, L.; Alvarez-Feal, C.; Rodríguez-Guerreiro, M.J.; Vargas, A.; Arean, N.; Carballo, R. Methodology for Positioning a Group of Green Artificial Reef Based on a Database Management System, Applied in the Estuary of Ares-Betanzos (Nw Iberian Peninsula). J. Clean. Prod. 2019, 233, 1047–1060. [Google Scholar] [CrossRef]
- Carral, L.; Lamas, M.I.; Cartelle Barros, J.J.; López, I.; Carballo, R. Proposed Conceptual Framework to Design Artificial Reefs Based on Particular Ecosystem Ecology Traits. Biology 2022, 11, 680. [Google Scholar] [CrossRef]
- Gómez-Gesteira, M.; de Castro, M.; Prego, R.; Martins, F. Influence of the Barrie de La Maza Dock on the Circulation Patterns of the Ría of A Coruña (NW-Spain). Sci. Mar. 2002, 66, 337–346. [Google Scholar] [CrossRef]
- Carballo, R.; Iglesias, G.; Castro, A. Residual Circulation in the Ría de Muros (NW Spain): A 3D Numerical Model Study. J. Mar. Syst. 2009, 75, 116–130. [Google Scholar] [CrossRef]
- Duarte, P.; Álvarez-Salgado, X.A.; Fernández-Reiriz, M.J.; Piedracoba, S.; Labarta, U. A Modeling Study on the Hydrodynamics of a Coastal Embayment Occupied by Mussel Farms (Ria de Ares-Betanzos, NW Iberian Peninsula). Estuar. Coast. Shelf Sci. 2014, 147, 42–55. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Effects of High Winds on the Circulation of the Using a Mixed Open Boundary Condition: The Ría de Muros, Spain. Environ. Model. Softw. 2010, 25, 455–466. [Google Scholar] [CrossRef]
- Deltares. Delft3D-FLOW. User Manual; Delft: Deltares, The Netherlands, 2010; Available online: https://content.oss.deltares.nl/delft3d/manuals/Delft3D-FLOW_User_Manual.pdf (accessed on 3 October 2022).
- Lamas Galdo, M.I.; Guerreiro, M.J.R.; Lamas Vigo, J.; Ameneiros Rodriguez, I.; Veira Lorenzo, R.; Carral Couce, J.C.; Carral Couce, L. Definition of an Artificial Reef Unit through Hydrodynamic and Structural (CFD and FEM) Models. Application to the Ares-Betanzos Estuary. J. Mar. Sci. Eng. 2022, 10, 230. [Google Scholar] [CrossRef]
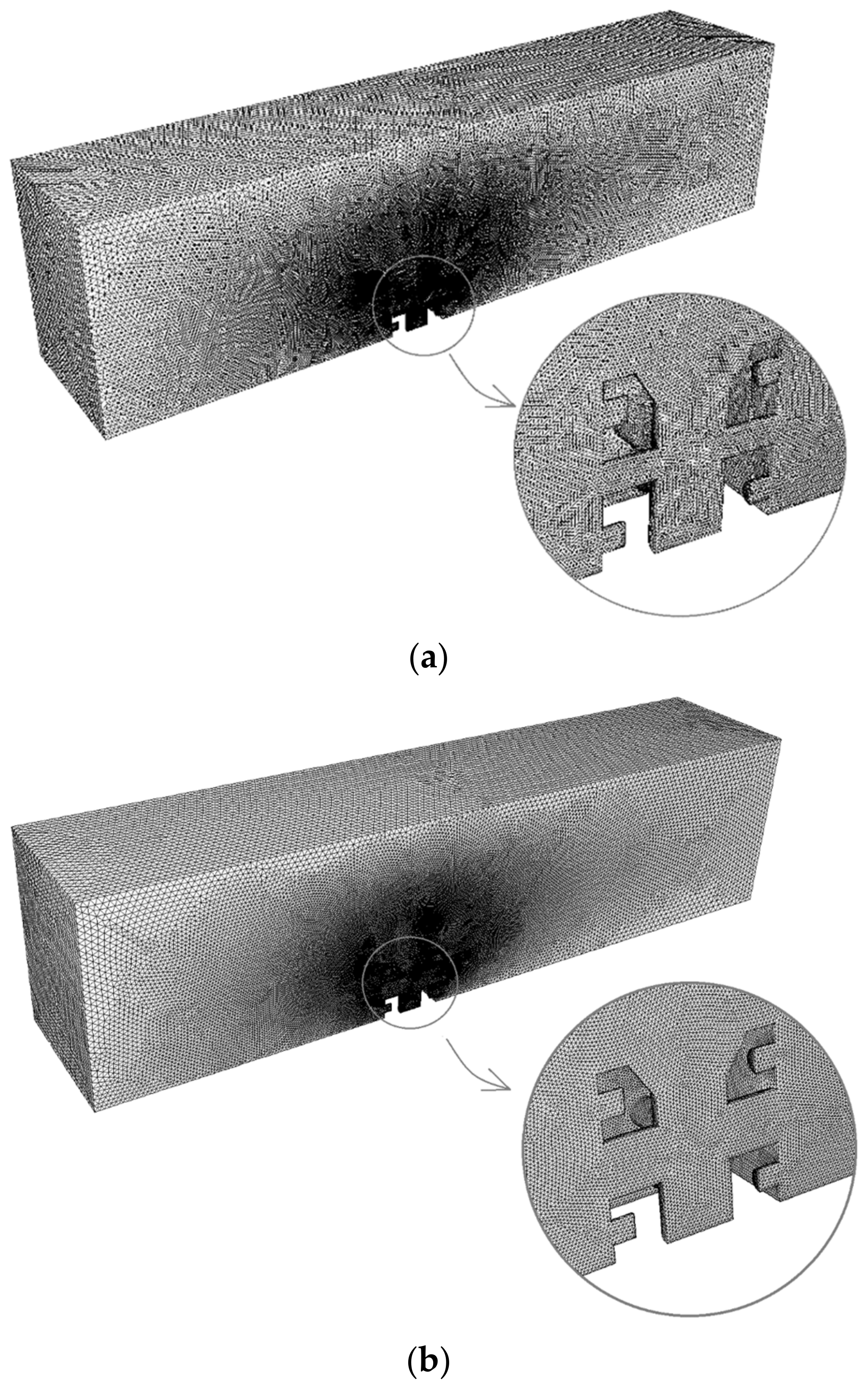



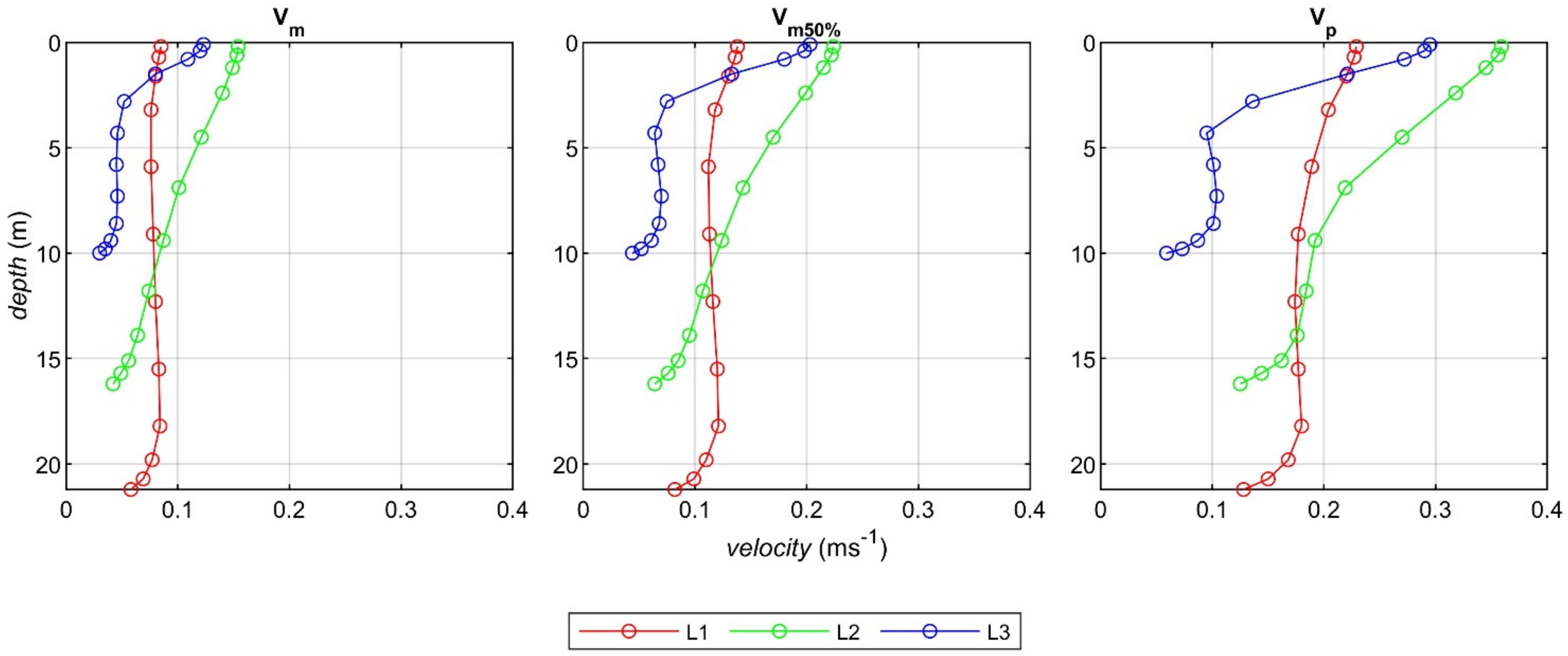
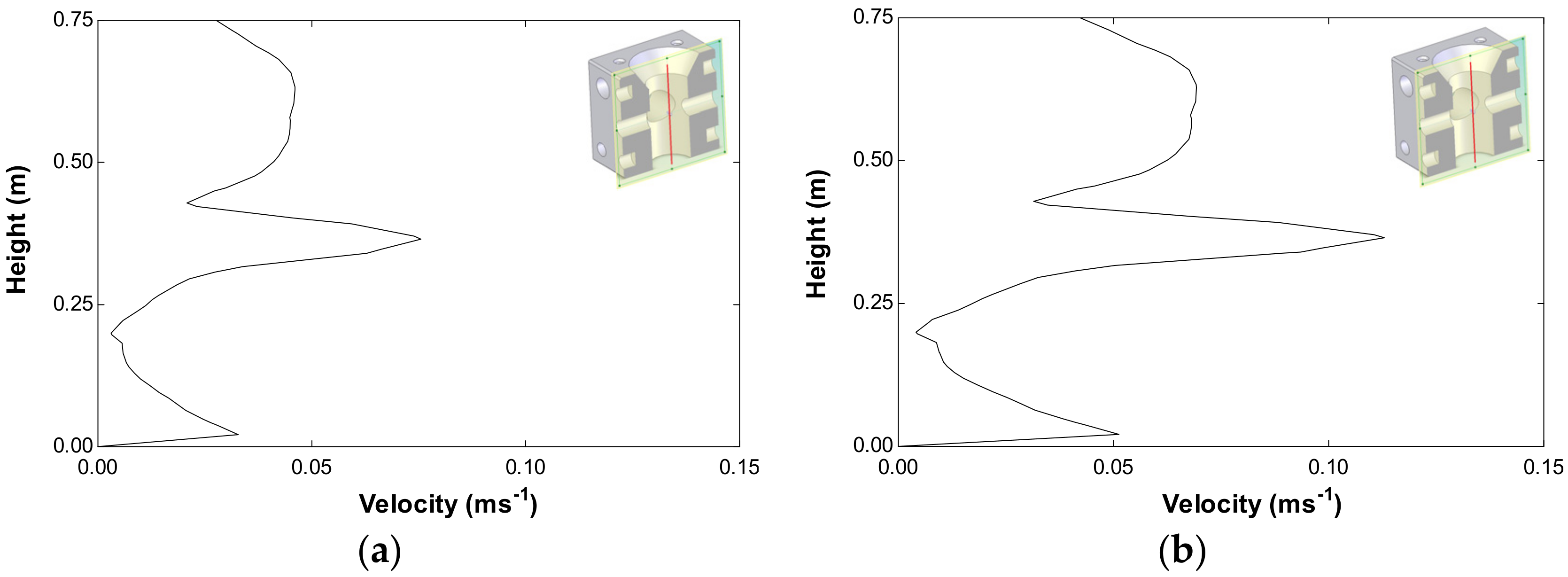
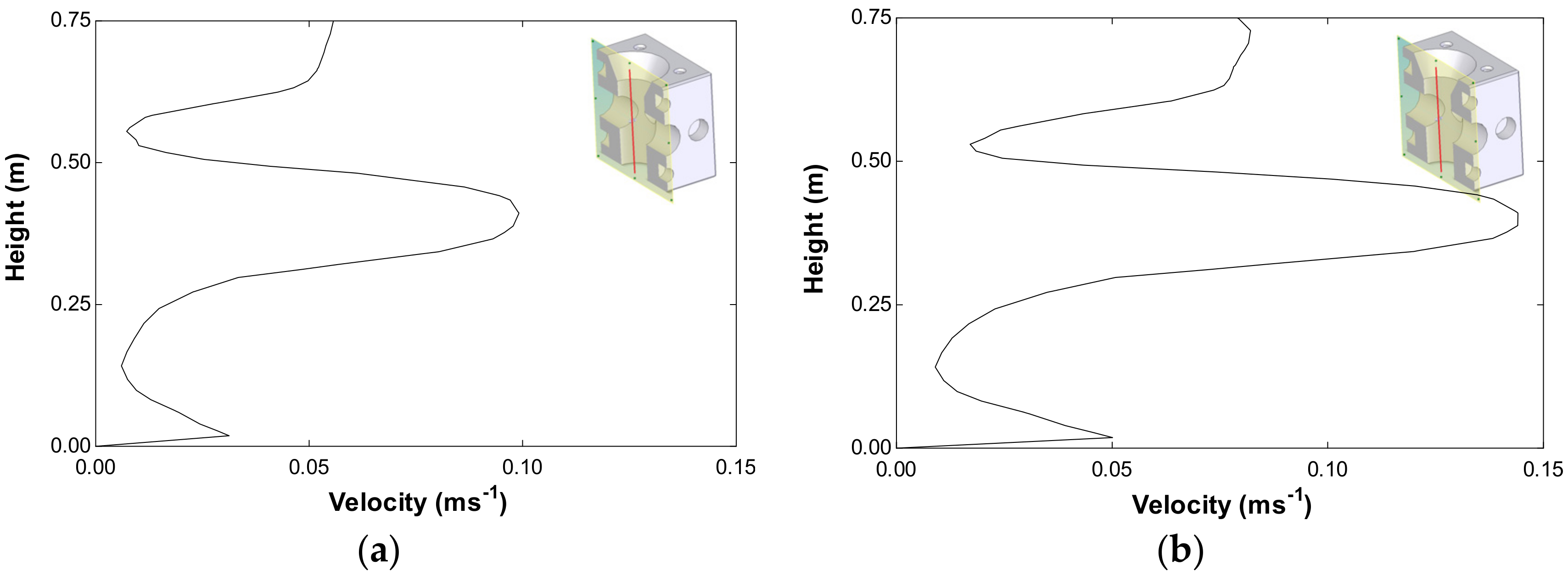
| Location | Vm (ms−1) | Vm50% (ms−1) |
|---|---|---|
| L1 | 0.071 | 0.101 |
| L2 | 0.051 | 0.078 |
| L3 | 0.037 | 0.055 |
| Scaled Current Velocity (ms−1) | Corresponding Real Current Velocity (ms−1) |
|---|---|
| 0.074 | 0.037 |
| 0.110 | 0.055 |
| 0.142 | 0.071 |
| 0.156 | 0.078 |
| 0.202 | 0.101 |
| Orientation A | Orientation B | ||||
|---|---|---|---|---|---|
| 0.25 m Height (S1) | 0.50 m Height (S2) | 0.25 m Height (S1) | 0.50 m Height (S2) | ||
| L1 | Vm = 0.142 ms−1 | 0.023 | 0.086 | 0.033 | 0.039 |
| Vm50% = 0.202 ms−1 | 0.033 | 0.125 | 0.049 | 0.045 | |
| L2 | Vm = 0.110 ms−1 | 0.017 | 0.063 | 0.023 | 0.024 |
| Vm50% = 0.156 ms−1 | 0.025 | 0.096 | 0.037 | 0.038 | |
| L3 | Vm = 0.074 ms−1 | 0.011 | 0.041 | 0.015 | 0.025 |
| Vm50% = 0.110 ms−1 | 0.017 | 0.063 | 0.023 | 0.024 | |
| Orientation A | Orientation B | ||||
|---|---|---|---|---|---|
| 0.25 m Height (S1) | 0.50 m Height (S2) | 0.25 m Height (S1) | 0.50 m Height (S2) | ||
| L1 | Vm = 0.142 ms−1 | 0.028 | 0.083 | 0.032 | 0.104 |
| Vm50% = 0.202 ms−1 | 0.032 | 0.103 | 0.048 | 0.052 | |
| L2 | Vm = 0.110 ms−1 | 0.026 | 0.062 | 0.022 | 0.028 |
| Vm50% = 0.156 ms−1 | 0.025 | 0.095 | 0.043 | 0.040 | |
| L3 | Vm = 0.074 ms−1 | 0.012 | 0.049 | 0.020 | 0.025 |
| Vm50% = 0.110 ms−1 | 0.026 | 0.062 | 0.022 | 0.028 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santiago Caamaño, L.; Lamas Galdo, M.I.; Carballo, R.; López, I.; Cartelle Barros, J.J.; Carral, L. Numerical and Experimental Analysis of the Velocity Field Inside an Artificial Reef. Application to the Ares-Betanzos Estuary. J. Mar. Sci. Eng. 2022, 10, 1827. https://doi.org/10.3390/jmse10121827
Santiago Caamaño L, Lamas Galdo MI, Carballo R, López I, Cartelle Barros JJ, Carral L. Numerical and Experimental Analysis of the Velocity Field Inside an Artificial Reef. Application to the Ares-Betanzos Estuary. Journal of Marine Science and Engineering. 2022; 10(12):1827. https://doi.org/10.3390/jmse10121827
Chicago/Turabian StyleSantiago Caamaño, Lucía, María Isabel Lamas Galdo, Rodrigo Carballo, Iván López, Juan José Cartelle Barros, and Luis Carral. 2022. "Numerical and Experimental Analysis of the Velocity Field Inside an Artificial Reef. Application to the Ares-Betanzos Estuary" Journal of Marine Science and Engineering 10, no. 12: 1827. https://doi.org/10.3390/jmse10121827
APA StyleSantiago Caamaño, L., Lamas Galdo, M. I., Carballo, R., López, I., Cartelle Barros, J. J., & Carral, L. (2022). Numerical and Experimental Analysis of the Velocity Field Inside an Artificial Reef. Application to the Ares-Betanzos Estuary. Journal of Marine Science and Engineering, 10(12), 1827. https://doi.org/10.3390/jmse10121827










