Forecasting Liquefied Natural Gas Bunker Prices Using Artificial Neural Network for Procurement Management
Abstract
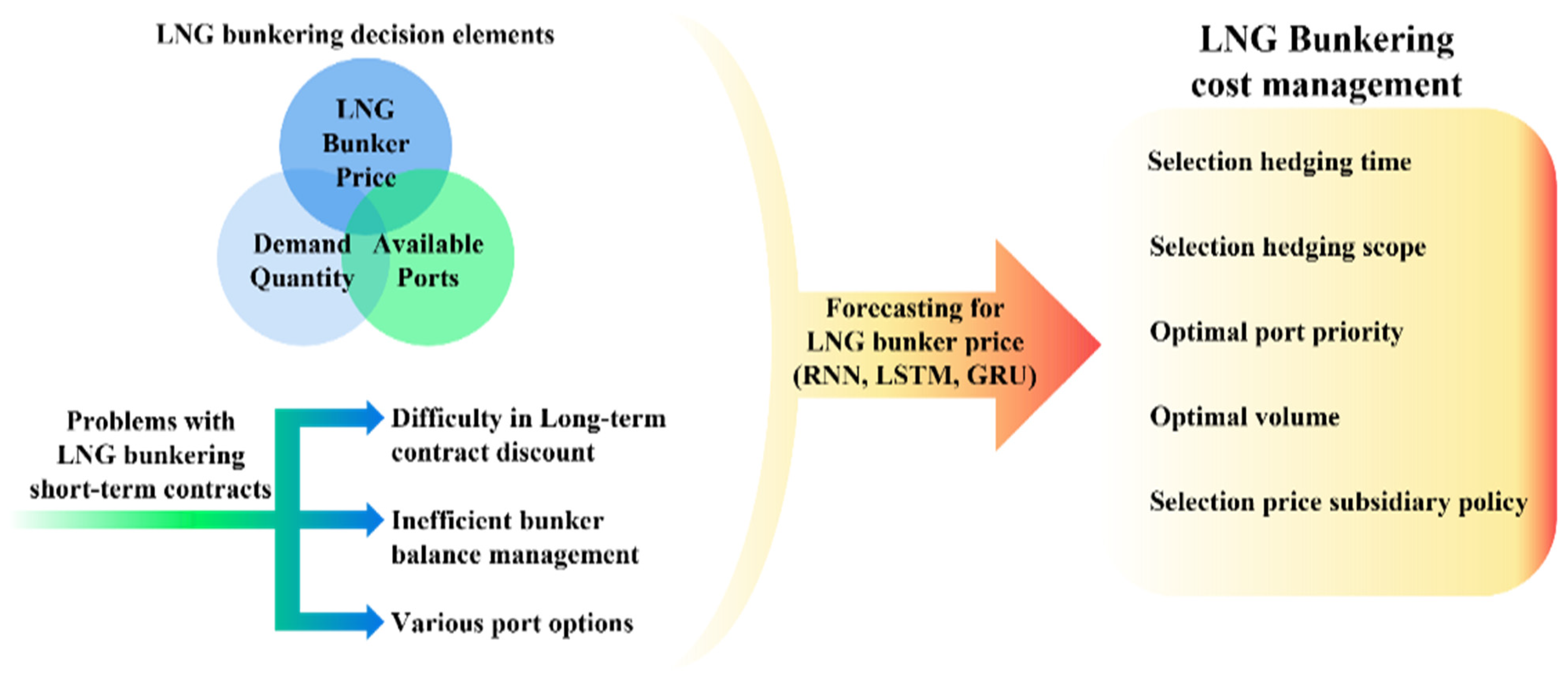
1. Introduction
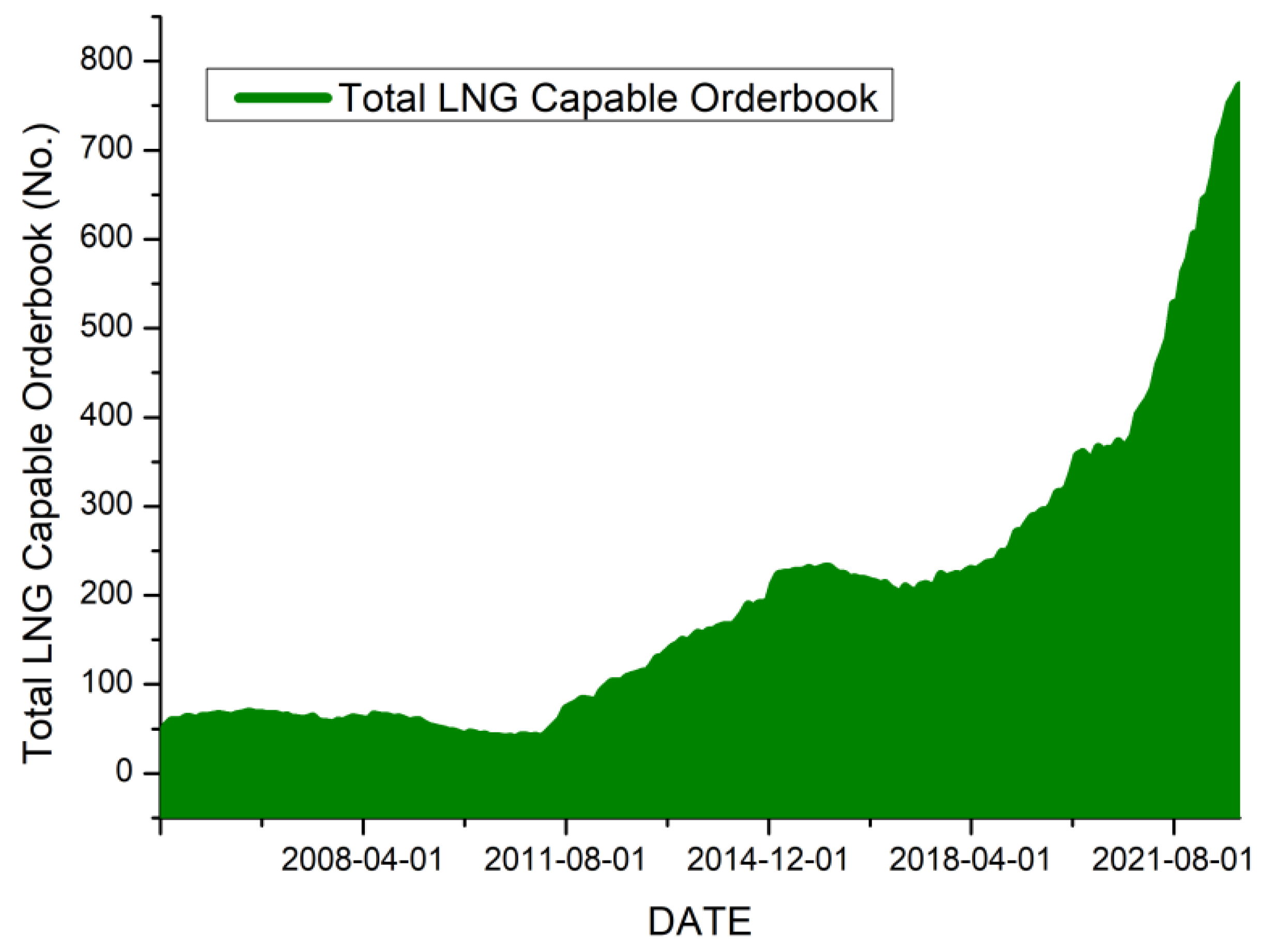
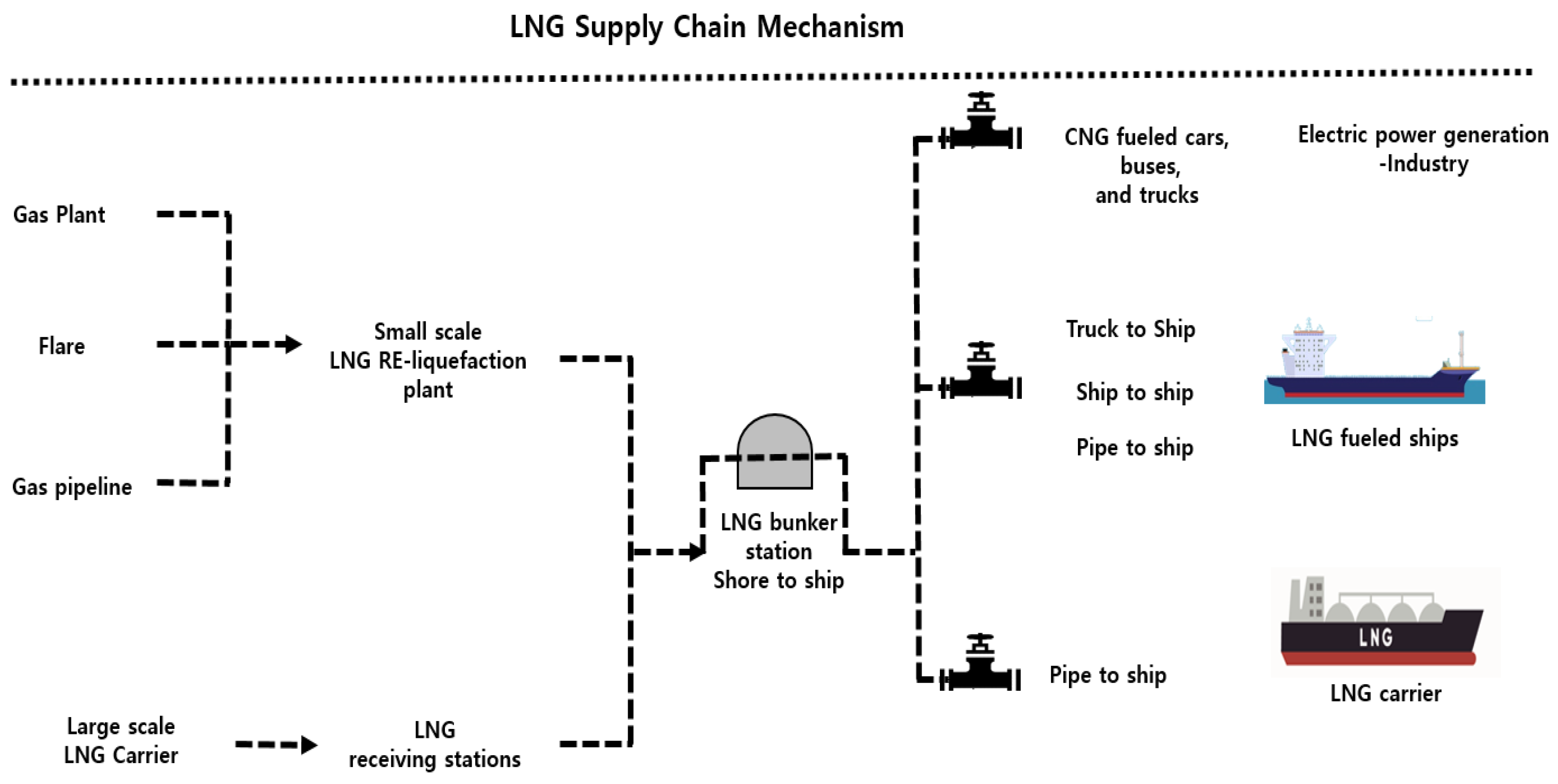
1.1. Background
1.2. Purpose
1.3. Literature Review
2. Materials and Methods
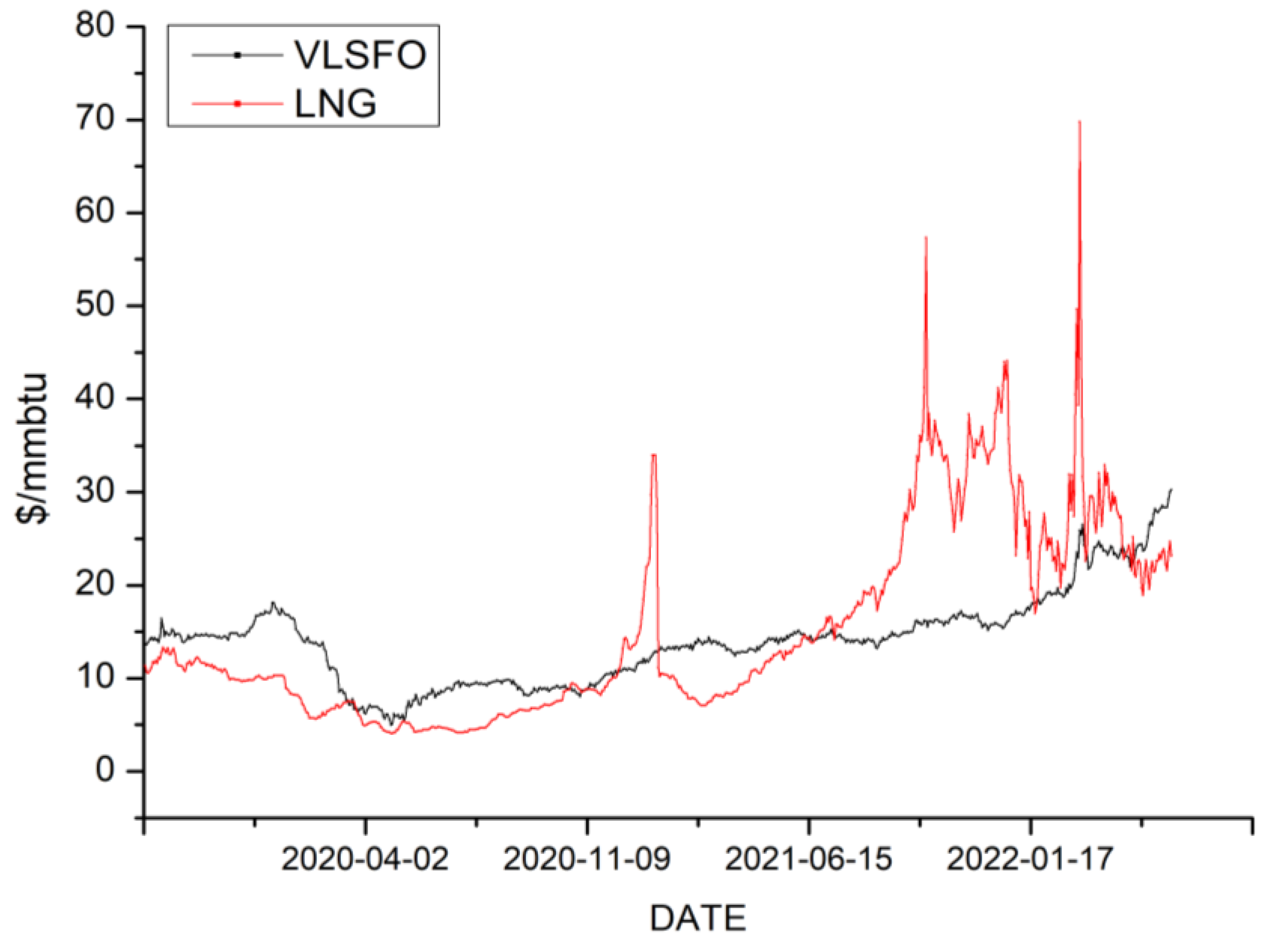
2.1. Data
2.2. Research Modeling
2.2.1. Simple RNN
2.2.2. LSTM
2.2.3. GRU
2.2.4. Hyper Parameter Modelling
2.3. Performance Indicators
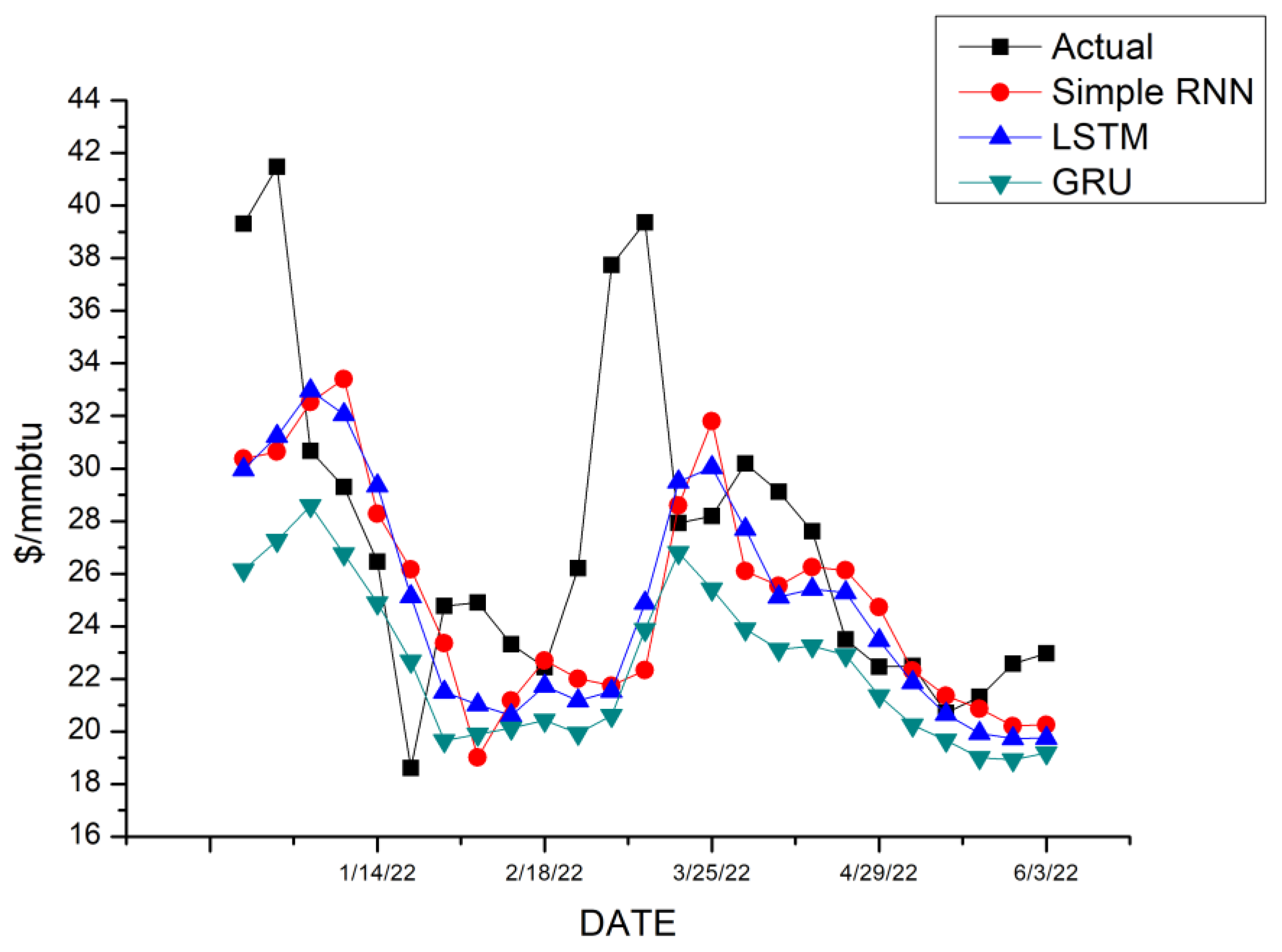
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Meng, Q.; Liu, Z. Bunker consumption optimization methods in shipping: A critical review and extensions. Transp. Res. Part E Logist. Transp. Rev. 2013, 53, 49–62. [Google Scholar] [CrossRef]
- Stopford, M. Maritime Economics 3e; Routledge: London, UK, 2009. [Google Scholar]
- Notteboom, T.E.; Vernimmen, B. The effect of high fuel costs on liner service configuration in container shipping. J. Transp. Geogr. 2009, 17, 325–337. [Google Scholar] [CrossRef]
- Alizadeh, A.H.; Nomikos, N.K. Shipping Derivatives and Risk Management; Palgrave Macmillan: London, UK, 2009; ISBN 978-0-230-21591-7. [Google Scholar]
- Clarkson Research Shipping Intelligence Network. Available online: https://sin.clarksons.net/ (accessed on 19 March 2022).
- Platts bunkerwire. Available online: https://www.spglobal.com/commodityinsights/en/products-services/shipping/bunkerwire (accessed on 28 September 2022).
- Available online: https://www.jpmorgan.com/insights/research/oil-gas-energy-prices (accessed on 28 September 2022).
- Ronen, D. The effect of oil price on containership speed and fleet size. J. Oper. Res. Soc. 2011, 62, 211–216. [Google Scholar] [CrossRef]
- Alizadeh, A.H.; Kavussanos, M.G.; Menachof, D.A. Hedging against bunker price fluctuations using petroleum futures contracts: Constant versus time-varying hedge ratios. Appl. Econ. 2004, 36, 1337–1353. [Google Scholar] [CrossRef]
- Qi, J.; Wang, H.; Zheng, J. Promoting liquefied natural gas (LNG) bunkering for maritime transportation: Should ports or ships be subsidized? Sustainability 2022, 14, 6647. [Google Scholar] [CrossRef]
- Livaniou, S.; Chatzistelios, G.; Lyridis, D.V.; Bellos, E. LNG vs. MDO in marine fuel emissions tracking. Sustainability 2022, 14, 3860. [Google Scholar] [CrossRef]
- Lloyd’s Register Advisory Service Korea LNG Bunkering Review (Busan, Incheon, and Ulsan Ports). 2022.
- Stefanakos, C.N.; Schinas, O. Forecasting bunker prices; A nonstationary, multivariate methodology. Transp. Res. Part C Emerg. Technol. 2014, 38, 177–194. [Google Scholar] [CrossRef]
- Stefanakos, C.; Schinas, O. Fuzzy time series forecasting of bunker prices: Nonstationary considerations. WMU J. Marit. Aff. 2015, 14, 177–199. [Google Scholar] [CrossRef]
- Choi, J. Forecasting Bunker Price Using System Dynamics. J. Korea Port Econ. Assoc. 2017, 33, 75–87. [Google Scholar] [CrossRef]
- Kim, K. A Study on the Forecasting of Bunker Price Using Recurrent Neural Network. J. Korea Soc. Comput. Inf. 2021, 26, 179–184. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. Forecasting crude oil price with an EMD-based neural network ensemble learning paradigm. Energy Econ. 2008, 30, 2623–2635. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, X.; Wang, S. Assessing potentiality of support vector machine method in crude oil price forecasting. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 7893–7904. [Google Scholar] [CrossRef]
- Jammazi, R.; Aloui, C. Crude oil price forecasting: Experimental evidence from wavelet decomposition and neural network modeling. Energy Econ. 2012, 34, 828–841. [Google Scholar] [CrossRef]
- Salvi, H. Long short-term model for brent oil price forecasting. Int. J. Res. Appl. Sci. Eng. Technol. 2019, 7, 315–319. [Google Scholar] [CrossRef]
- Güleryüz, D.; Özden, E. The prediction of Brent crude oil trend using LSTM and Facebook prophet. Avrupa Bilim Ve Teknol. Derg. 2020, 1–9. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Q.; Zhu, J. Improved EEMD-based crude oil price forecasting using LSTM networks. Physica A 2019, 516, 114–124. [Google Scholar] [CrossRef]
- Manowska, A.; Bluszcz, A. Forecasting Crude Oil Consumption in Poland Based on LSTM Recurrent Neural Network. Energies 2022, 15, 4885. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. 2014. Available online: https://arxiv.org/abs/1406.1078 (accessed on 28 September 2022).
- Kim, D.; Kim, H.; Sim, S.; Choi, Y.; Bae, H.; Yun, H. Prediction of dry bulk freight index using deep learning. J. Korean Inst. Ind. Eng. 2019, 45, 111–116. [Google Scholar] [CrossRef]
- Han, M.; Yu, S. Prediction of Baltic Dry Index by Applications of Long Short-Term Memory. J. Korean Soc. Qual. Manag. 2019, 47, 497–508. [Google Scholar]
- Lim, S.; Yun, H. Forecasting bulk market indices with recurrent neural network models. J. Marit. Bus. 2018, 40, 159–180. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Wallach, D.; Goffinet, B. Mean squared error of prediction as a criterion for evaluating and comparing system models. Ecol. Model. 1989, 44, 299–306. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- de Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Lin, H.; Sun, Q. Crude oil prices forecasting: An approach of using ceemdan-based multi-layer gated recurrent unit networks. Energies 2020, 13, 1543. [Google Scholar] [CrossRef]
| Period | Prediction |
|---|---|
| Early 2020s | Gradual ramp up of deliveries of LNG-fueled ships |
| 2024–2030 | LNG-fueled ship deliveries begin to surpass those of conventional oil-fueled ships |
| 2030s | LNG-fueled ships shares begin to fall as zero-carbon technologies develop |
| 2040s | Zero-carbon vessels account for the major share of shipyard output |
| Statistics | Weekly LNG Bunker Price | |
|---|---|---|
| Observations | 144 | |
| Mean | 15.04 | |
| Std. error | 0.83 | |
| Median | 11.09 | |
| Std. dev. | 10.00 | |
| ADF test | t-stat. | −1.85 |
| Prob | 0.353 | |
| Model | MAE | MSE | MAPE | RMSE | |
|---|---|---|---|---|---|
| Simple RNN | Tr | 1.17 | 6 | 11.81 | 2.45 |
| Te | 4.26 | 38.13 | 14.14 | 6.18 | |
| LSTM | Tr | 1.23 | 5.75 | 12.19 | 2.4 |
| Te | 4.14 | 33.81 | 13.77 | 5.82 | |
| GRU | Tr | 1.15 | 5.26 | 12.1 | 2.29 |
| Te | 5.09 | 47.52 | 16.81 | 6.89 | |
| Benchmark | Squared Error | Absolute Error | Squared Proportional Error | |||
|---|---|---|---|---|---|---|
| Simple RNN | GRU | Simple RNN | GRU | Simple RNN | GRU | |
| LSTM | −1.254 (0.105) | −2.623 (0.004) | −0.577 (0.282) | −3.159 (0.001) | −1.029 (0.152) | −3.289 (0.001) |
| Simple RNN | −1.576 (0.058) | −2.160 (0.015) | −1.702 (0.044) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Lim, S.; Lee, C.-h.; Lee, W.-J.; Jeon, H.; Jung, J.; Jung, D. Forecasting Liquefied Natural Gas Bunker Prices Using Artificial Neural Network for Procurement Management. J. Mar. Sci. Eng. 2022, 10, 1814. https://doi.org/10.3390/jmse10121814
Kim K, Lim S, Lee C-h, Lee W-J, Jeon H, Jung J, Jung D. Forecasting Liquefied Natural Gas Bunker Prices Using Artificial Neural Network for Procurement Management. Journal of Marine Science and Engineering. 2022; 10(12):1814. https://doi.org/10.3390/jmse10121814
Chicago/Turabian StyleKim, Kyunghwan, Sangseop Lim, Chang-hee Lee, Won-Ju Lee, Hyeonmin Jeon, Jinwon Jung, and Dongho Jung. 2022. "Forecasting Liquefied Natural Gas Bunker Prices Using Artificial Neural Network for Procurement Management" Journal of Marine Science and Engineering 10, no. 12: 1814. https://doi.org/10.3390/jmse10121814
APA StyleKim, K., Lim, S., Lee, C.-h., Lee, W.-J., Jeon, H., Jung, J., & Jung, D. (2022). Forecasting Liquefied Natural Gas Bunker Prices Using Artificial Neural Network for Procurement Management. Journal of Marine Science and Engineering, 10(12), 1814. https://doi.org/10.3390/jmse10121814







