Hydrodynamic and Particle Drift Modeling as a Support System for Maritime Search and Rescue (SAR) Emergencies: Application to the C-212 Aircraft Accident on 2 September, 2011, in the Juan Fernández Archipelago, Chile
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and SAR Emergency
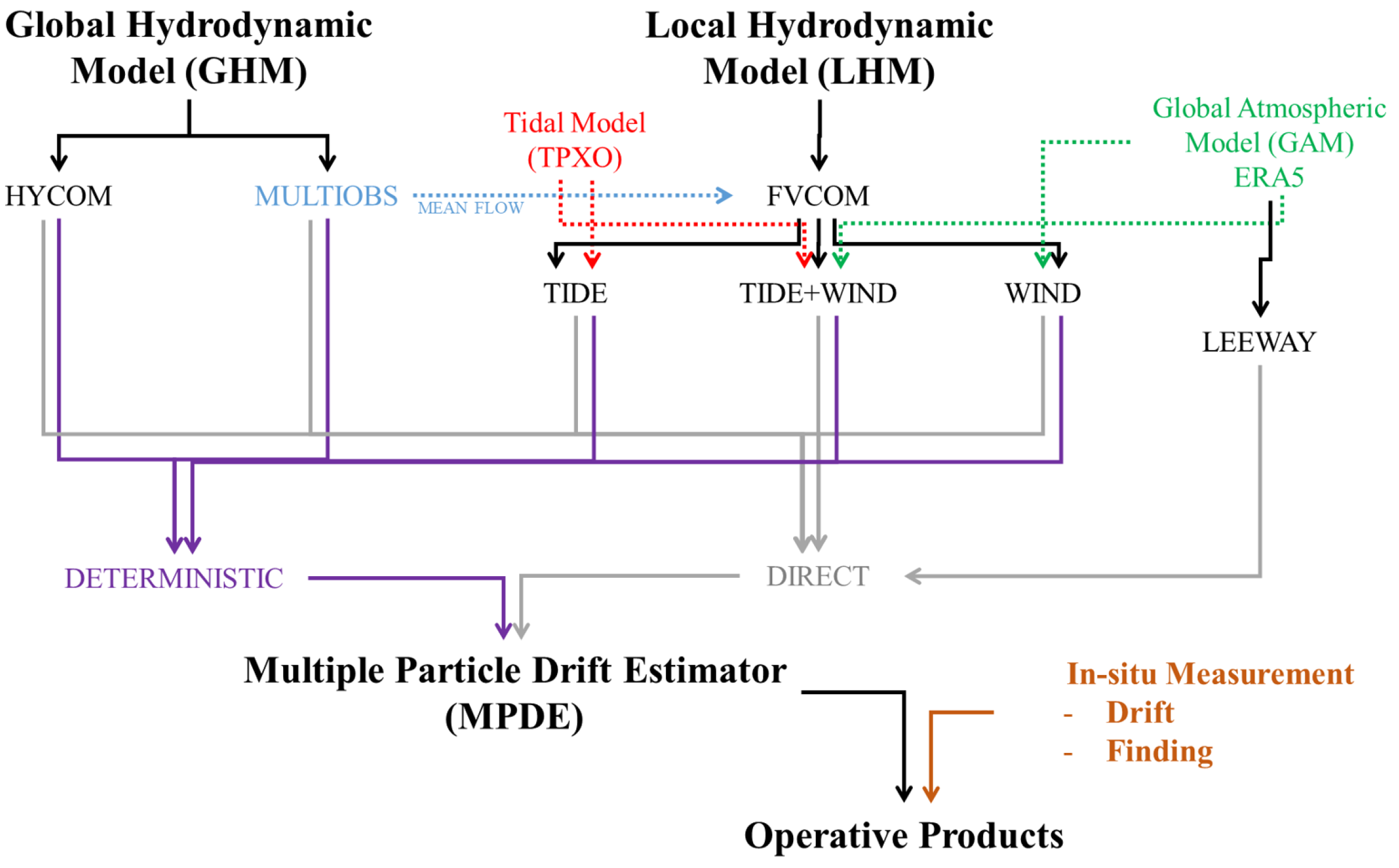
2.2. Model Components and Data Sources
2.2.1. Global Hydrodynamic and Atmospheric Models (GHM and GAM)
2.2.2. Local Hydrodynamic Model (LHM)
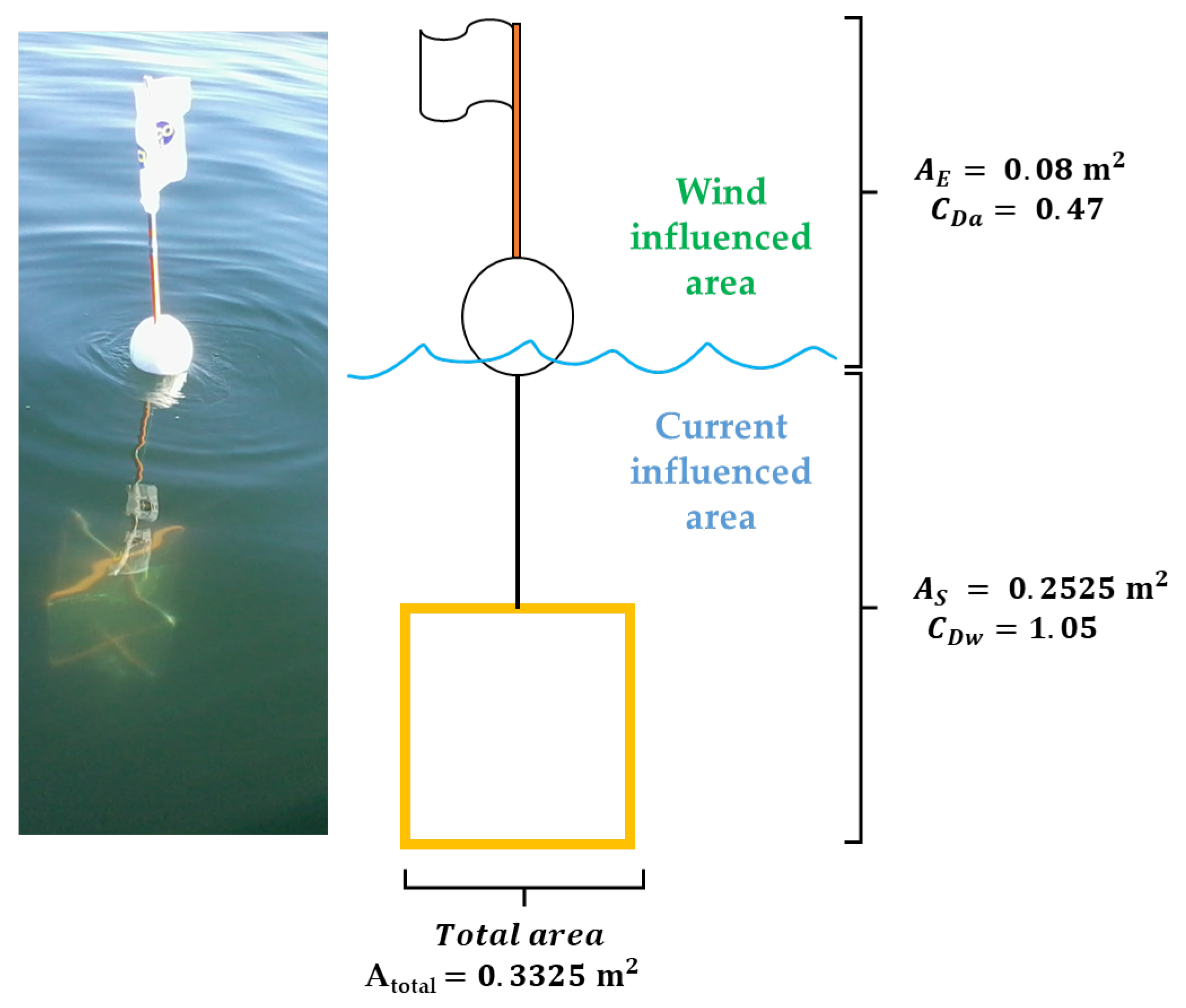
2.2.3. Multiple Particle Drift Estimator (MPDE)
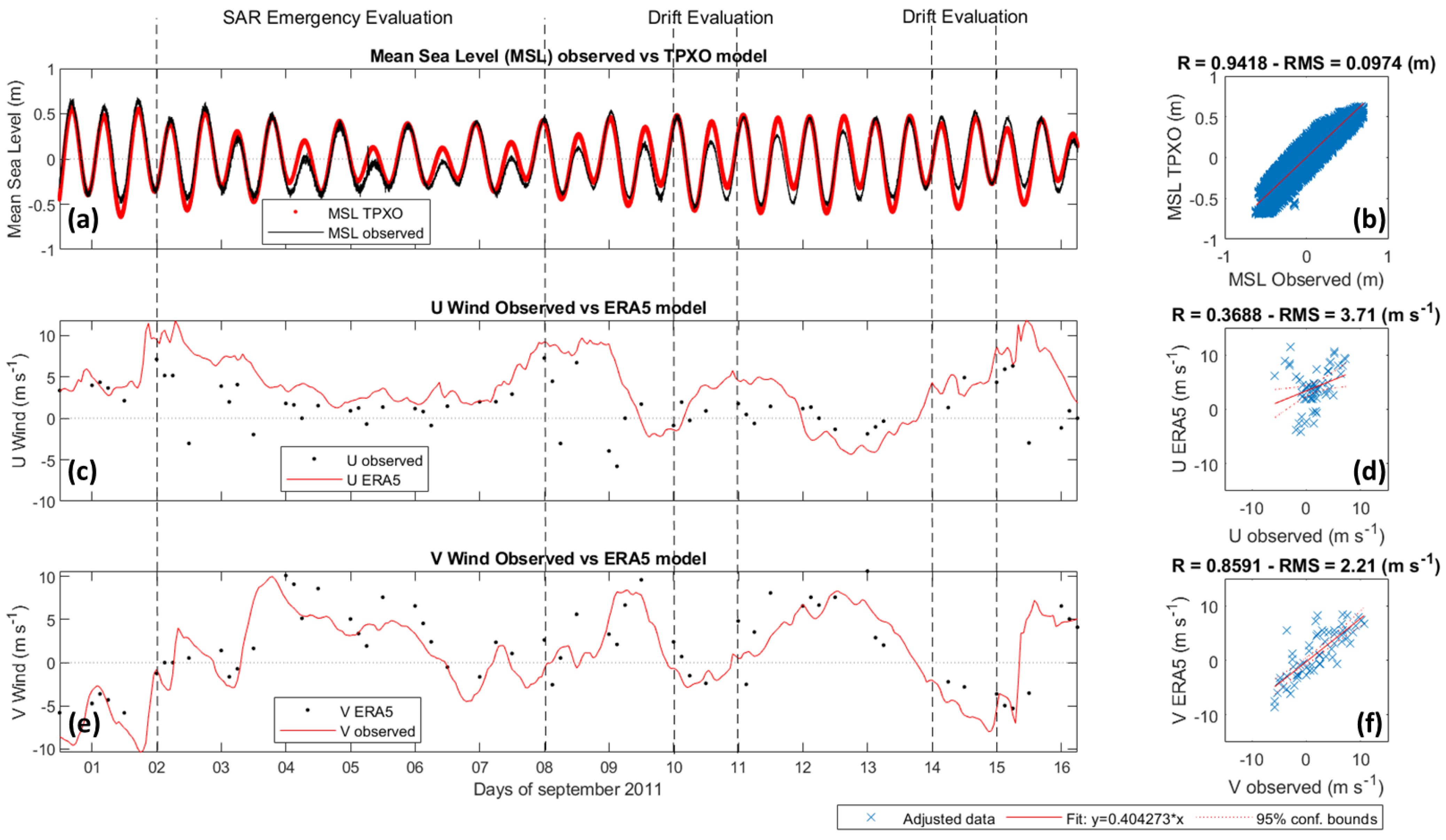
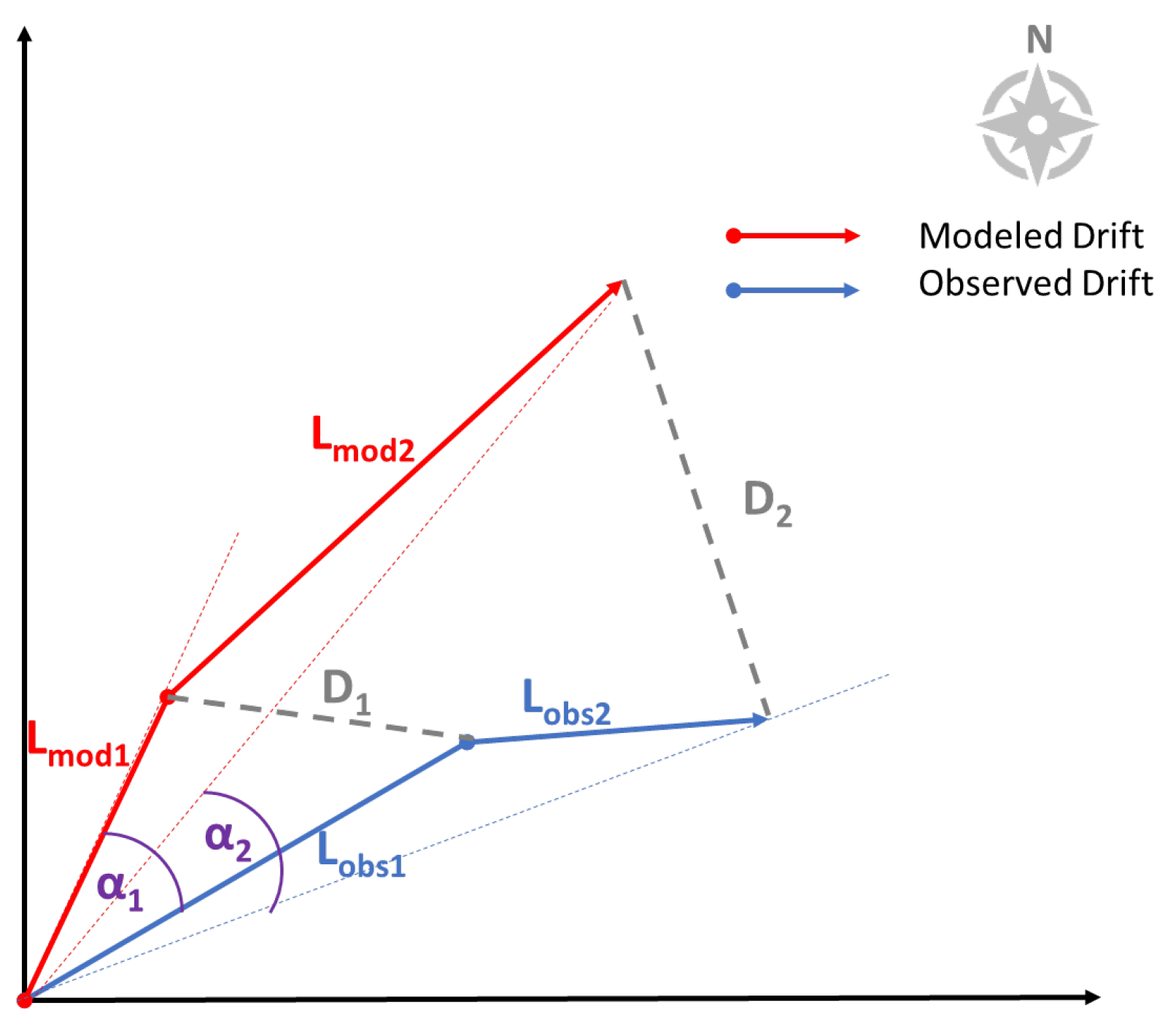
2.2.4. Performance Analysis
3. Results
3.1. Model Validation and Trajectory Calibrations
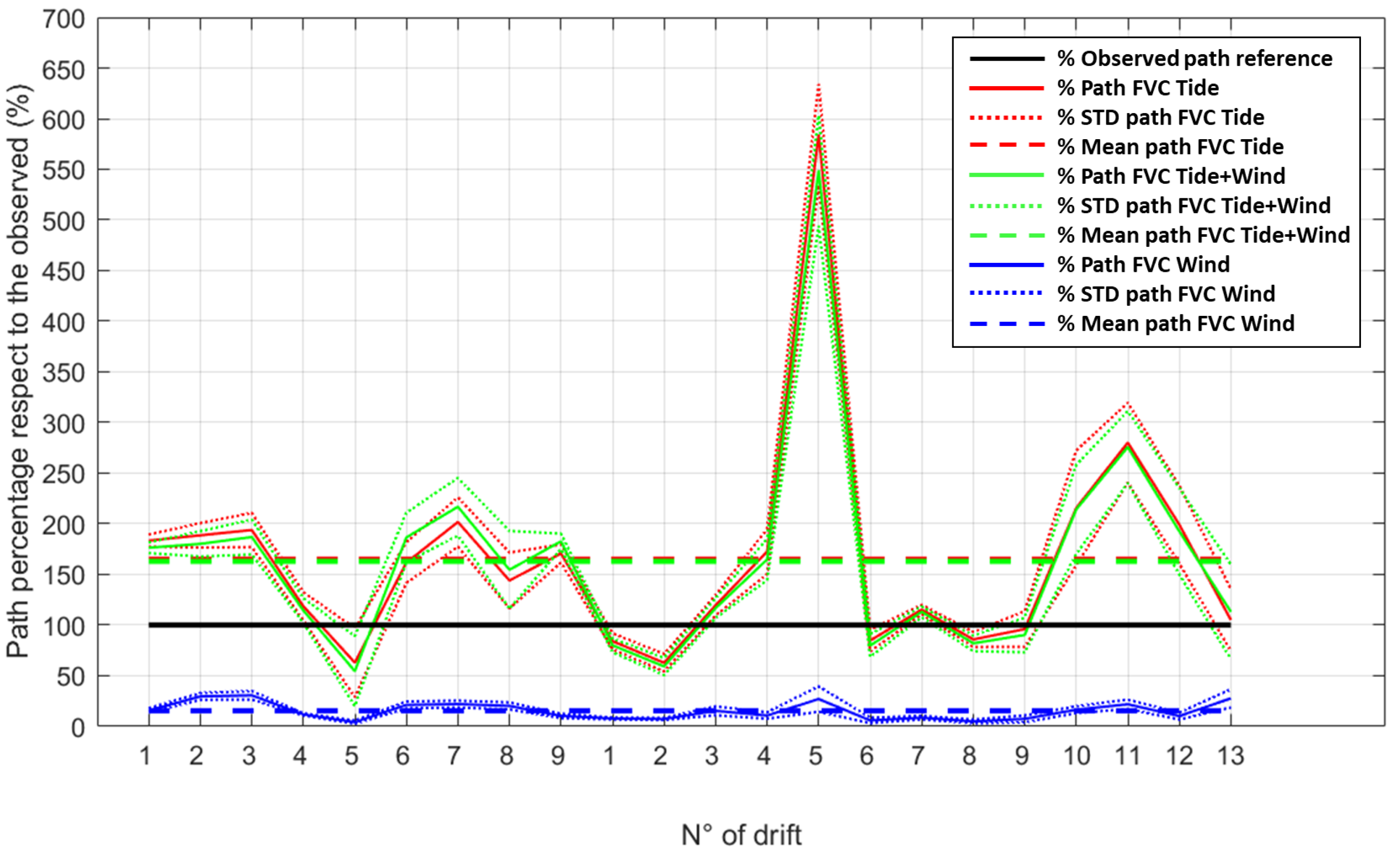
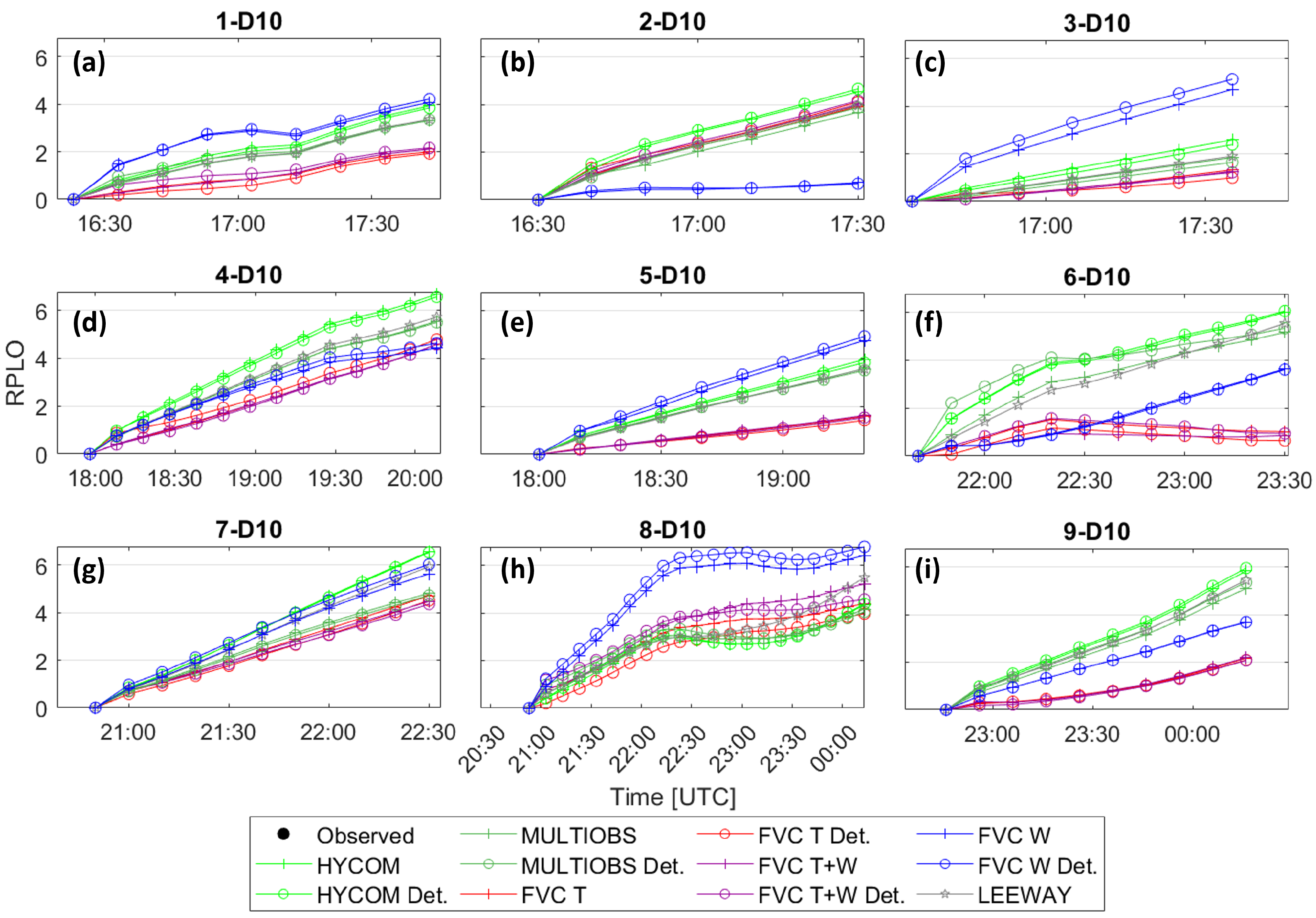
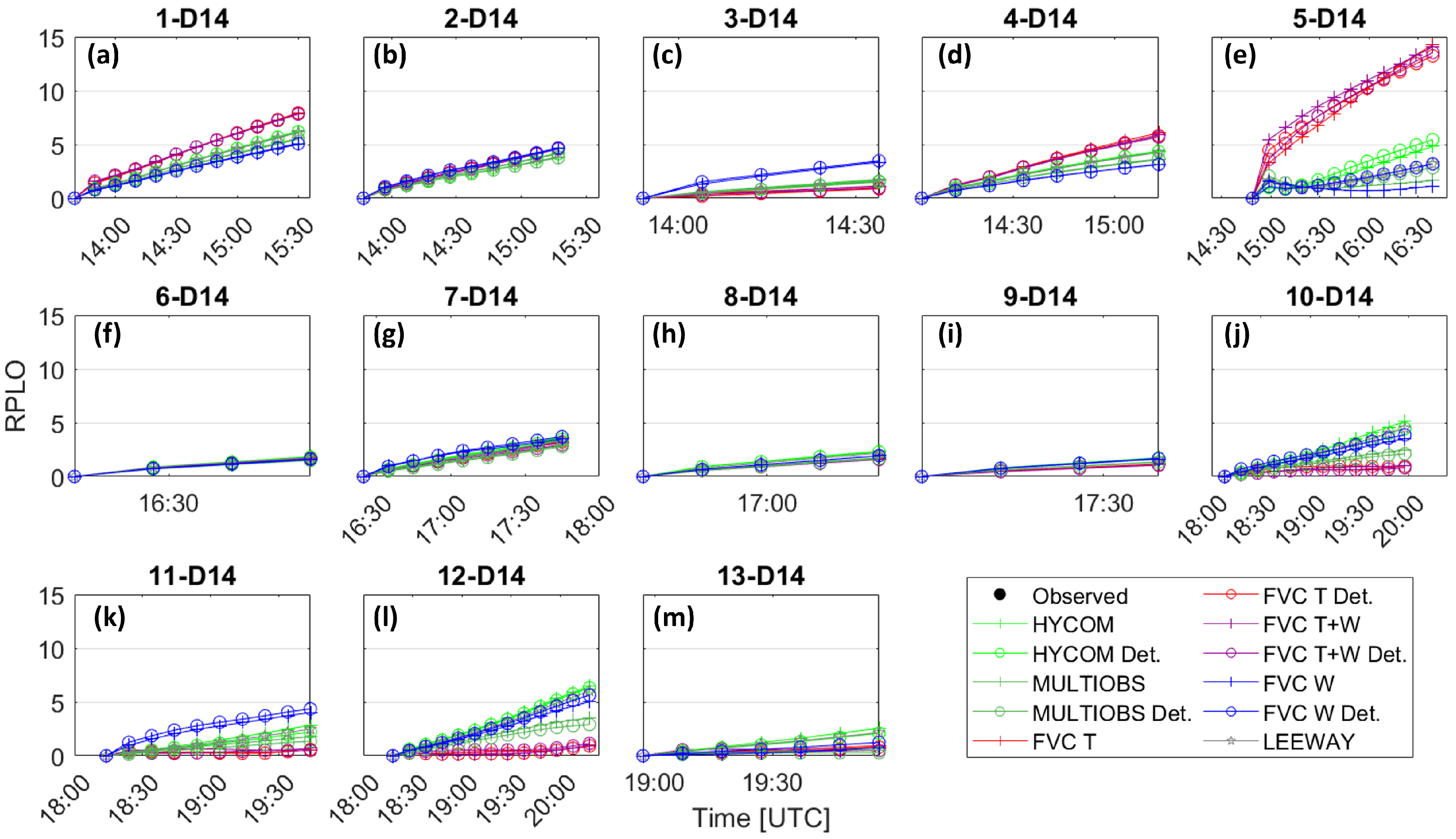
3.2. Quantitative Performance Analysis
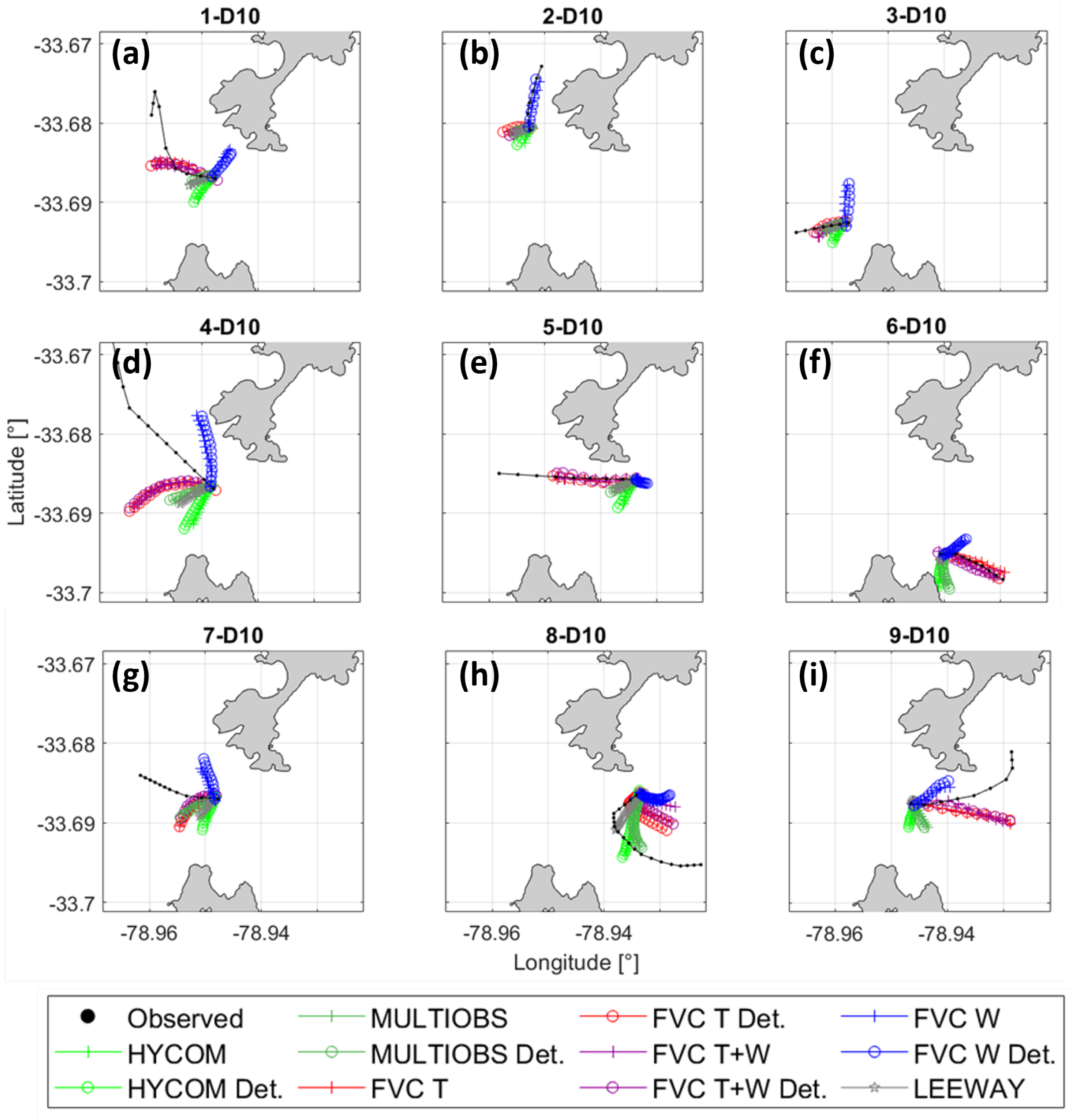
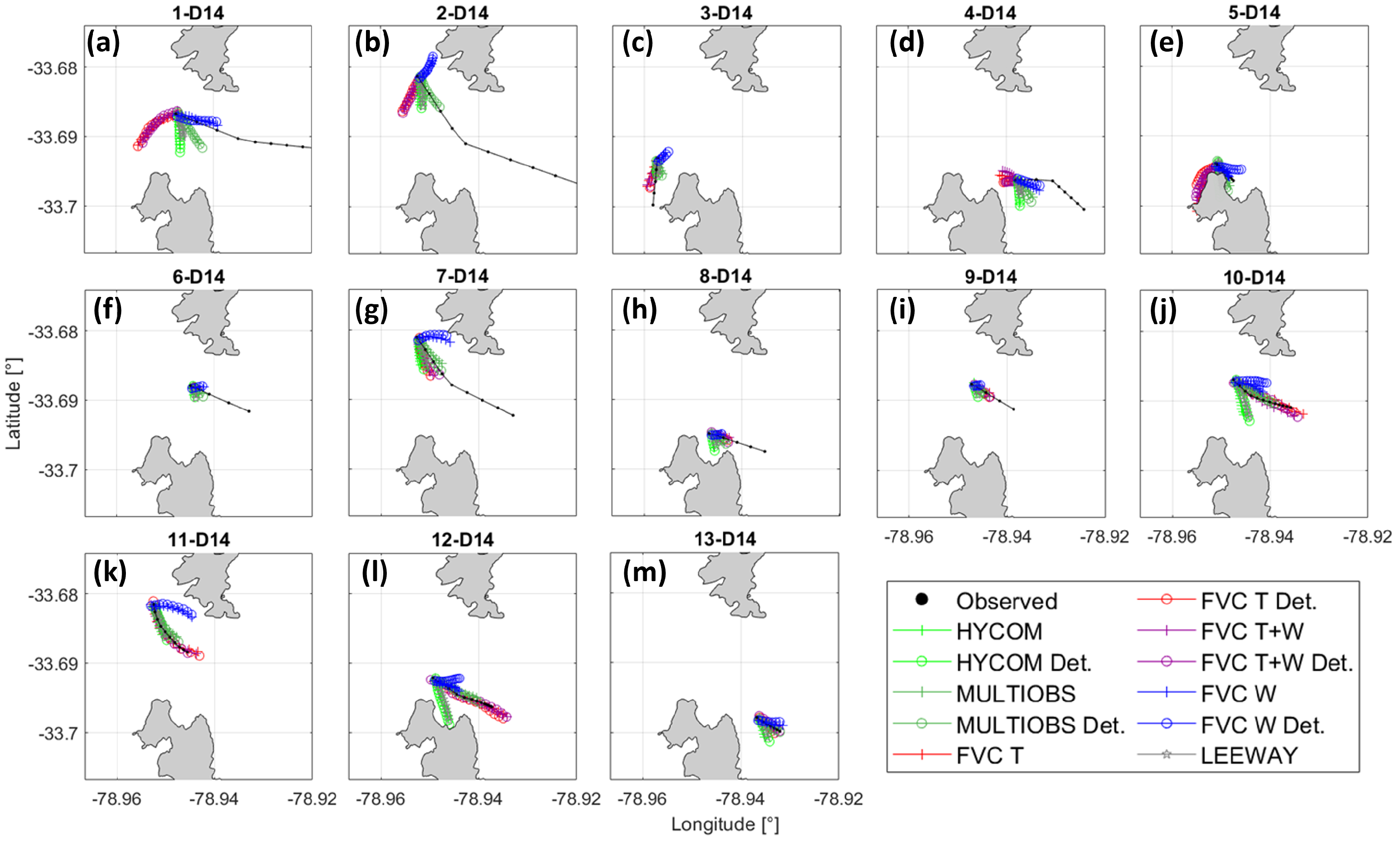
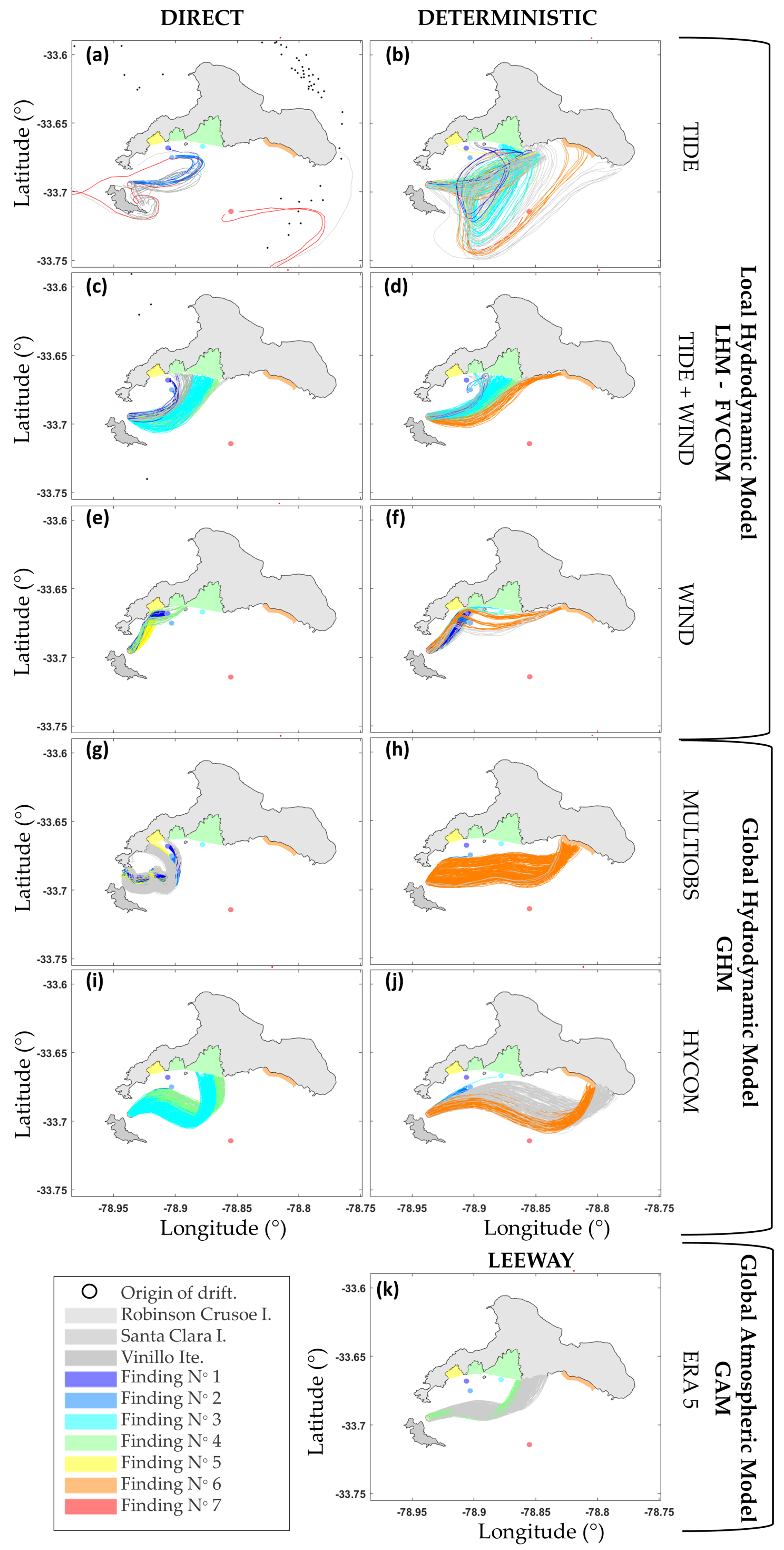
3.3. Qualitative Performance
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Test of NCLS and NCLS mod Indices

Appendix B. Statistic Performance Result of Quantitative Analyses of Trajectories
| Best NCLS Trajectory | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | NCLS | Angle [°] | Path | NCLS | ||||
| Final | Mean | STD | Final | Mean | STD | Difference (m) | [46] | |
| FVC T | 2.850 | 1.708 | 0.825 | 33.3 | 23.3 | 9.4 | 602.4 | 2.713 |
| FVC T Det. | 2.714 | 1.599 | 0.783 | 32.5 | 23.1 | 8.9 | 562.4 | 2.582 |
| FVC T + W | 2.921 | 1.721 | 0.837 | 35.2 | 23.9 | 10.5 | 674.4 | 2.779 |
| FVC T + W Det | 2.841 | 1.758 | 0.801 | 32.5 | 24.0 | 9.9 | 605.1 | 2.697 |
| FVC W | 4.405 | 2.854 | 1.182 | 58.1 | 58.6 | 12.9 | 999.6 | 4.072 |
| FVC W Det. | 4.225 | 2.698 | 1.149 | 52.3 | 49.7 | 15.2 | 1029.1 | 3.946 |
| HYCOM | 4.932 | 3.003 | 1.333 | 87.3 | 67.4 | 19.7 | 1122.2 | 4.534 |
| HYCOM Det. | 4.908 | 2.988 | 1.315 | 84.0 | 65.7 | 16.8 | 1046.4 | 4.516 |
| MULTIOBS | 4.130 | 2.507 | 1.138 | 54.0 | 38.2 | 15.0 | 1101.5 | 3.893 |
| MULTIOBS Det. | 4.143 | 2.625 | 1.067 | 51.6 | 41.4 | 12.3 | 1049.5 | 3.886 |
| LEEWAY | 4.542 | 2.655 | 1.266 | 69.6 | 42.8 | 19.3 | 1199.8 | 4.267 |
| Mean of All Trajectories | ||||||||
| Model | NCLS | Angle [°] | Path | NCLS | ||||
| Final | Mean | STD | Final | Mean | STD | Difference (m) | [46] | |
| FVC T | 5.238 | 3.488 | 1.736 | 71.6 | 69.1 | 34.9 | 661.5 | 4.795 |
| FVC T Det. | 5.223 | 3.475 | 1.750 | 71.6 | 68.9 | 34.6 | 639.6 | 4.781 |
| FVC T + W | 5.302 | 3.532 | 1.740 | 71.8 | 69.8 | 34.7 | 663.8 | 4.855 |
| FVC T + W Det | 5.290 | 3.518 | 1.748 | 71.7 | 69.5 | 34.3 | 642.4 | 4.844 |
| FVC W | 6.133 | 4.239 | 1.588 | 106.4 | 113.7 | 33.9 | 1108.2 | 5.467 |
| FVC W Det. | 6.079 | 4.194 | 1.595 | 106.3 | 112.8 | 35.9 | 1129.2 | 5.415 |
| HYCOM | 5.538 | 3.671 | 1.287 | 99.8 | 91.9 | 21.9 | 1131.2 | 4.995 |
| HYCOM Det. | 5.531 | 3.642 | 1.283 | 97.8 | 89.2 | 20.8 | 1080.2 | 5.001 |
| MULTIOBS | 5.631 | 3.724 | 1.404 | 94.7 | 90.8 | 38.8 | 1159.6 | 5.078 |
| MULTIOBS Det. | 5.620 | 3.692 | 1.393 | 94.0 | 88.6 | 35.9 | 1119.1 | 5.078 |
| LEEWAY | 5.316 | 3.483 | 1.273 | 88.0 | 78.7 | 26.0 | 1254.0 | 4.833 |
| Best NCLS Trajectory | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | NCLS | Angle [°] | Path | NCLS | ||||
| Final | Mean | STD | Final | Mean | STD | Difference (m) | [46] | |
| FVC T | 3.481 | 2.161 | 0.929 | 42.0 | 39.4 | 6.3 | 934.2 | 3.183 |
| FVC T Det. | 3.341 | 2.152 | 0.860 | 42.6 | 40.5 | 6.3 | 888.8 | 3.010 |
| FVC T + W | 3.405 | 2.214 | 0.852 | 42.0 | 39.8 | 5.9 | 909.9 | 3.097 |
| FVC T + W Det | 3.294 | 2.134 | 0.846 | 39.3 | 39.1 | 6.4 | 892.8 | 2.992 |
| FVC W | 3.357 | 2.101 | 0.902 | 32.8 | 31.1 | 6.6 | 1012.2 | 3.158 |
| FVC W Det. | 3.013 | 1.908 | 0.821 | 25.0 | 25.6 | 6.6 | 1006.0 | 2.878 |
| HYCOM | 3.677 | 2.148 | 1.058 | 42.7 | 33.2 | 9.2 | 1069.2 | 3.455 |
| HYCOM Det. | 3.531 | 2.066 | 1.016 | 41.5 | 32.7 | 8.5 | 994.1 | 3.310 |
| MULTIOBS | 2.479 | 1.554 | 0.684 | 12.5 | 10.4 | 4.3 | 947.9 | 2.411 |
| MULTIOBS Det. | 2.403 | 1.493 | 0.669 | 14.6 | 11.6 | 4.4 | 898.1 | 2.320 |
| LEEWAY | 3.337 | 1.961 | 0.950 | 36.6 | 27.2 | 8.4 | 1046.0 | 3.158 |
| Mean of All Trajectories | ||||||||
| Model | NCLS | Angle [°] | Path | NCLS | ||||
| Final | Mean | STD | Final | Mean | STD | Difference (m) | [46] | |
| FVC T | 6.318 | 4.091 | 1.917 | 112.0 | 112.5 | 36.7 | 870.6 | 5.572 |
| FVC T Det. | 6.129 | 3.965 | 1.880 | 107.7 | 108.1 | 36.2 | 849.9 | 5.417 |
| FVC T + W | 6.147 | 3.981 | 1.894 | 108.6 | 109.0 | 37.4 | 876.9 | 5.425 |
| FVC T + W Det | 5.984 | 3.869 | 1.856 | 104.7 | 104.9 | 36.7 | 855.1 | 5.293 |
| FVC W | 4.894 | 3.233 | 1.265 | 68.5 | 75.1 | 28.8 | 1103.4 | 4.382 |
| FVC W Det. | 4.547 | 3.027 | 1.195 | 58.2 | 66.5 | 29.6 | 1124.7 | 4.115 |
| HYCOM | 4.534 | 2.883 | 1.160 | 60.8 | 60.2 | 22.6 | 1113.4 | 4.119 |
| HYCOM Det. | 4.507 | 2.845 | 1.154 | 59.4 | 58.2 | 19.4 | 1055.4 | 4.107 |
| MULTIOBS | 3.673 | 2.444 | 1.050 | 39.1 | 42.9 | 30.7 | 1090.7 | 3.387 |
| MULTIOBS Det. | 3.608 | 2.386 | 1.021 | 40.2 | 42.7 | 27.3 | 1043.9 | 3.329 |
| LEEWAY | 4.220 | 2.691 | 1.089 | 52.4 | 51.9 | 21.5 | 1095.6 | 3.865 |
References
- National Search and Rescue Manual; Technical Report; Australian Maritime Safety Authority: Canberra, Australia, 2022.
- COSPAS-SARSAT. Technical Report Nº47; Technical Report; Secretariat of the International Cospas-Sarsat Programme: Monteréal, QC, Canada, 2021. [Google Scholar]
- International Aeronautical and Maritime Rescue Manual; International Maritime Organization: London, UK; International Civil Aviation Organization: Montreal, QC, Canada, 2019.
- Chen, C.; Limeburner, R.; Gao, G.; Xu, Q.; Qi, J.; Xue, P.; Lai, Z.; Lin, H.; Beardsley, R.; Owens, B.; et al. FVCOM model estimate of the location of Air France 447. Ocean Dyn. 2012, 62, 943–952. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3. NCAR Technical Note-475+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Cho, K.H.; Li, Y.; Wang, H.; Park, K.S.; Choi, J.Y.; Shin, K.I.; Kwon, J.I. Development and validation of an operational search and rescue modeling system for the Yellow Sea and the East and South China Seas. J. Atmos. Ocean. Technol. 2014, 31, 197–215. [Google Scholar] [CrossRef]
- Campuzano, F.; Brito, D.; Juliano, M.; Fernandes, R.; de Pablo, H.; Neves, R. Coupling watersheds, estuaries and regional ocean through numerical modelling for Western Iberia: A novel methodology. Ocean Dyn. 2016, 66, 1745–1756. [Google Scholar] [CrossRef]
- Révelard, A.; Reyes, E.; Mourre, B.; Hernández-Carrasco, I.; Rubio, A.; Lorente, P.; Fernández, C.D.L.; Mader, J.; Álvarez-Fanjul, E.; Tintoré, J. Sensitivity of Skill Score Metric to Validate Lagrangian Simulations in Coastal Areas: Recommendations for Search and Rescue Applications. Front. Mar. Sci. 2021, 8, 630388. [Google Scholar] [CrossRef]
- Artale, V.; Boffetta, G.; Celani, A.; Cencini, M.; Vulpiani, A. Dispersion of passive tracers in closed basins: Beyond the diffusion coefficient. Phys. Fluids 1997, 9, 3162–3171. [Google Scholar] [CrossRef]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in the large: An extension of the concept of Lyapunov exponent. J. Phys. A Math. Gen. 1997, 30, 1–26. [Google Scholar] [CrossRef]
- Haza, A.C.; Griffa, A.; Martin, P.; Molcard, A.; Özgökmen, T.M.; Poje, A.C.; Barbanti, R.; Book, J.W.; Poulain, P.M.; Rixen, M.; et al. Model-based directed drifter launches in the Adriatic Sea: Results from the DART experiment. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Haza, A.C.; Poje, A.C.; Özgökmen, T.M.; Martin, P. Relative dispersion from a high-resolution coastal model of the Adriatic Sea. Ocean Model. 2008, 22, 48–65. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Phys. D Nonlinear Phenom. 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Serra, M.; Sathe, P.; Rypina, I.; Kirincich, A.; Ross, S.D.; Lermusiaux, P.; Allen, A.; Peacock, T.; Haller, G. Search and rescue at sea aided by hidden flow structures. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Muller-Karger, F.; Roffer, M.; Walker, N.; Oliver, M.; Schofield, O.; Abbott, M.; Graber, H.; Leben, R.; Goni, G. Satellite remote sensing in support of an integrated ocean observing system. IEEE Geosci. Remote Sens. Mag. 2013, 1, 8–18. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Reppucci, A.; Alvarez Fanjul, E.; Aouf, L.; Behrens, A.; Belmonte, M.; Bentamy, A.; Bertino, L.; Brando, V.E.; Kreiner, M.B.; et al. From observation to information and users: The Copernicus Marine Service perspective. Front. Mar. Sci. 2019, 6, 234. [Google Scholar] [CrossRef]
- Sotillo, M.G. Ocean Modelling in Support of Operational Ocean and Coastal Services. J. Mar. Sci. Eng. 2022, 10, 1482. [Google Scholar] [CrossRef]
- Hufford, G.; Broida, S. Estimation of the leeway drift of small craft. Ocean Eng. 1976, 3, 123–132. [Google Scholar] [CrossRef]
- Di Maio, A.; Martin, M.V.; Sorgente, R. Evaluation of the search and rescue LEEWAY model in the Tyrrhenian Sea: A new point of view. Nat. Hazards Earth Syst. Sci. 2016, 16, 1979–1997. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Metzger, E.J.; Smedstad, O.M.; Cummings, J.A.; Halliwell, G.R.; Bleck, R.; Baraille, R.; Wallcraft, A.J.; Lozano, C.; et al. US GODAE: Global ocean prediction with the HYbrid Coordinate Ocean Model (HYCOM). Oceanography 2009, 22, 64–75. [Google Scholar] [CrossRef]
- Rio, M.H.; Mulet, S.; Picot, N. Beyond GOCE for the ocean circulation estimate: Synergetic use of altimetry, gravimetry, and in situ data provides new insight into geostrophic and Ekman currents. Geophys. Res. Lett. 2014, 41, 8918–8925. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Derrotero de la Costa de Chile. Volumen I. De Arica a Canal Chacao; Technical Report; Hydrographic and Oceanographic Service of the Chilean Navy: Valparaíso, Chile, 2013.
- Gracia, L. Links for a successful investigation: C-212 Robinson Crusoe Island Accident Case. Airbus Def. Space. Mil. Aircr. 2017, 1–12. Available online: https://www.isasi.org/Documents/library/technical-papers/2016/Thurs/Gracia_C212RobisonCrusoe.pdf (accessed on 15 September 2022).
- Hunke, E.; Lipscomb, W. The Los Alamos Sea Ice Model Documentation and Software User’s Manual, Version 4.1; National Center for Atmospheric Research: Boulder, CO, USA, 2010. Available online: https://csdms.colorado.edu/w/images/CICE_documentation_and_software_user’s_manual.pdf (accessed on 15 September 2022).
- Cowles, G.W. Parallelization of the FVCOM coastal ocean model. Int. J. High Perform. Comput. Appl. 2008, 22, 177–193. [Google Scholar] [CrossRef]
- Shore, J.A. Modelling the circulation and exchange of Kingston Basin and Lake Ontario with FVCOM. Ocean Model. 2009, 30, 106–114. [Google Scholar] [CrossRef]
- Qu, K.; Tang, H.; Agrawal, A.; Jiang, C.; Deng, B. Evaluation of SIFOM-FVCOM system for high-fidelity simulation of small-scale coastal ocean flows. J. Hydrodyn. 2016, 28, 994–1002. [Google Scholar] [CrossRef]
- Guerra, M.; Cienfuegos, R.; Thomson, J.; Suarez, L. Tidal energy resource characterization in Chacao Channel, Chile. Int. J. Mar. Energy 2017, 20, 1–16. [Google Scholar] [CrossRef]
- Olson, C.J.; Becker, J.J.; Sandwell, D.T. A new global bathymetry map at 15 arcsecond resolution for resolving seafloor fabric: SRTM15_PLUS. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2014; Volume 2014, p. OS34A-03. [Google Scholar]
- Engwirda, D. Locally Optimal Delaunay-Refinement and Optimisation-Based Mesh Generation. Ph.D. Thesis, The University of Sydney, Sydney, Australia, 2014. [Google Scholar]
- Chen, C.; Beardsley, R.; Cowles, G.; Qi, J.; Lai, Z.; Gao, G.; Stuebe, D.; Xu, Q.; Xue, P.; Ge, J.; et al. An Unstructured-Grid, Finite-Volume Community Ocean Model: FVCOM User Manual; Sea Grant College Program; Massachusetts Institute of Technology: Cambridge, MA, USA, 2012. [Google Scholar]
- Atlas Oceanográfico de Chile (18°21′ S a 50°00′ S) Volumen 1; Technical Report; Hydrographic and Oceanographic Service of the Chilean Navy: Valparaíso, Chile, 1996.
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Instrucciones Oceanográficas Nº 2: Método Oficial Para el Cálculo de los Valores No Armónicos de la Marea; Technical Report; Hydrographic and Oceanographic Service of the Chilean Navy: Valparaíso, Chile, 1999.
- Lai, Z. A Non-Hydrostatic Unstructured-Grid Finite-Volume Coastal Ocean Model System (fvcom-nh): Development, Validation and Application: A Dissertation in Marine Science and Technology. Ph.D. Thesis, University of Massachusetts, North Dartmouth, MA, USA, 2009. [Google Scholar]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Grant, W.; Madsen, O. Combined Wave and Current Interaction with a Rough Bottom. J. Geophys. Res. Atmos. 1979, 84, 1797–1808. [Google Scholar] [CrossRef]
- Celia, M.A.; Gray, W.G. Numerical Methods for Differential Equations: Fundamental Concepts for Scientific and Engineering Applications; Pearson College Division: Engelwood Cliffs, NJ, USA, 1992. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R. Fluid Mechanics; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Allen, A.A. Leeway Divergence; Technical Report; U.S. Coast Guard Research and Development Center: Groton, CT, USA, 2005. [Google Scholar]
- Sayol, J.; Orfila, A.; Simarro, G.; Conti, D.; Renault, L.; Molcard, A. A Lagrangian model for tracking surface spills and SaR operations in the ocean. Environ. Model. Softw. 2014, 52, 74–82. [Google Scholar] [CrossRef]
- Allen, A.A.; Plourde, J.V. Review of Leeway: Field Experiments and Implementation; Technical Report; U.S. Coast Guard Research and Development Center: Groton, CT, USA, 1999. [Google Scholar]
- Ohlmann, J.; Romero, L.; Pallàs-Sanz, E.; Perez-Brunius, P. Anisotropy in coastal ocean relative dispersion observations. Geophys. Res. Lett. 2019, 46, 879–888. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid-Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance; Hoerner Fluid Dynamics: Brick Town, NJ, USA, 1965. [Google Scholar]
- Liu, Y.; Weisberg, R.H. Evaluation of trajectory modeling in different dynamic regions using normalized cumulative Lagrangian separation. J. Geophys. Res. Ocean. 2011, 116, C09013. [Google Scholar] [CrossRef]
- Sperrevik, A.K.; Röhrs, J.; Christensen, K.H. Impact of data assimilation on E ulerian versus L agrangian estimates of upper ocean transport. J. Geophys. Res. Ocean. 2017, 122, 5445–5457. [Google Scholar] [CrossRef]
- Mourre, B.; Aguiar, E.; Juza, M.; Hernandez-Lasheras, J.; Reyes, E.; Heslop, E.; Escudier, R.; Cutolo, E.; Ruiz, S.; Mason, E.; et al. Assessment of high-resolution regional ocean prediction systems using multi-platform observations: Illustrations in the western Mediterranean Sea. New Front. Oper. Oceanogr. 2018, 663–694. [Google Scholar] [CrossRef]
- Aguiar, E.; Mourre, B.; Juza, M.; Reyes, E.; Hernández-Lasheras, J.; Cutolo, E.; Mason, E.; Tintoré, J. Multi-platform model assessment in the Western Mediterranean Sea: Impact of downscaling on the surface circulation and mesoscale activity. Ocean Dyn. 2020, 70, 273–288. [Google Scholar] [CrossRef]
- Döös, K.; Rupolo, V.; Brodeau, L. Dispersion of surface drifters and model-simulated trajectories. Ocean Model. 2011, 39, 301–310. [Google Scholar] [CrossRef]
- Brushett, B.A.; Allen, A.A.; King, B.A.; Lemckert, C.J. Application of leeway drift data to predict the drift of panga skiffs: Case study of maritime search and rescue in the tropical pacific. Appl. Ocean Res. 2017, 67, 109–124. [Google Scholar] [CrossRef]
- Dagestad, K.F.; Röhrs, J. Prediction of ocean surface trajectories using satellite derived vs. modeled ocean currents. Remote Sens. Environ. 2019, 223, 130–142. [Google Scholar] [CrossRef]
- Tang, C.L.; Perrie, W.; Jenkins, A.D.; DeTracey, B.M.; Hu, Y.; Toulany, B.; Smith, P.C. Observation and modeling of surface currents on the Grand Banks: A study of the wave effects on surface currents. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Zhang, J.; Teixeira, Â.P.; Soares, C.G.; Yan, X. Probabilistic modelling of the drifting trajectory of an object under the effect of wind and current for maritime search and rescue. Ocean Eng. 2017, 129, 253–264. [Google Scholar] [CrossRef]
- Breivik, Ø.; Allen, A.A. An operational search and rescue model for the Norwegian Sea and the North Sea. J. Mar. Syst. 2008, 69, 99–113. [Google Scholar] [CrossRef]
- Minola, L.; Zhang, F.; Azorin-Molina, C.; Pirooz, A.; Flay, R.; Hersbach, H.; Chen, D. Near-surface mean and gust wind speeds in ERA5 across Sweden: Towards an improved gust parametrization. Clim. Dyn. 2020, 55, 887–907. [Google Scholar] [CrossRef]
- Aksamit, N.O.; Sapsis, T.; Haller, G. Machine-Learning Mesoscale and Submesoscale Surface Dynamics from Lagrangian Ocean Drifter Trajectories. J. Phys. Oceanogr. 2020, 50, 1179–1196. [Google Scholar] [CrossRef]
- Jiang, Y.; Han, S.; Shi, C.; Gao, T.; Zhen, H.; Liu, X. Evaluation of HRCLDAS and ERA5 datasets for near-surface wind over hainan island and south China sea. Atmosphere 2021, 12, 766. [Google Scholar] [CrossRef]
- Li, S.; Chen, C. Air-sea interaction processes during hurricane Sandy: Coupled WRF-FVCOM model simulations. Prog. Oceanogr. 2022, 206, 102855. [Google Scholar] [CrossRef]
- Edwards, K.; Werner, F.; Blanton, B. Comparison of observed and modeled drifter trajectories in coastal regions: An improvement through adjustments for observed drifter slip and errors in wind fields. J. Atmos. Ocean. Technol. 2006, 23, 1614–1620. [Google Scholar] [CrossRef]
- Bellafiore, D.; Umgiesser, G. Hydrodynamic coastal processes in the North Adriatic investigated with a 3D finite element model. Ocean Dyn. 2010, 60, 255–273. [Google Scholar] [CrossRef]
- Amemou, H.; Koné, V.; Aman, A.; Lett, C. Assessment of a Lagrangian model using trajectories of oceanographic drifters and fishing devices in the Tropical Atlantic Ocean. Prog. Oceanogr. 2020, 188, 102426. [Google Scholar] [CrossRef]
- Austin, J.A.; Lentz, S.J. The inner shelf response to wind-driven upwelling and downwelling. J. Phys. Oceanogr. 2002, 32, 2171–2193. [Google Scholar] [CrossRef]
- Fewings, M.; Lentz, S.J.; Fredericks, J. Observations of cross-shelf flow driven by cross-shelf winds on the inner continental shelf. J. Phys. Oceanogr. 2008, 38, 2358–2378. [Google Scholar] [CrossRef]
- Battjes, J.A.; Sobey, R.J.; Stive, M. Nearshore circulation. In Manuscript for “The Sea” The Sea, Volume 9: Ocean Engineering Science; Harvard University Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Lentz, S.; Fewings, M. The wind-and wave-driven inner-shelf circulation. Annu. Rev. Mar. Sci. 2012, 4, 317–343. [Google Scholar] [CrossRef]
- Carniel, S.; Warner, J.C.; Chiggiato, J.; Sclavo, M. Investigating the impact of surface wave breaking on modeling the trajectories of drifters in the northern Adriatic Sea during a wind-storm event. Ocean Model. 2009, 30, 225–239. [Google Scholar] [CrossRef]
- Thornton, E.B.; Guza, R. Surf zone longshore currents and random waves: Field data and models. J. Phys. Oceanogr. 1986, 16, 1165–1178. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Q.; Wu, Y.; Ji, C.; Yang, J.; Liu, G. Development of a wave-current model through coupling of FVCOM and SWAN. Ocean Eng. 2018, 164, 443–454. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Córdova, P.; Flores, R.P. Hydrodynamic and Particle Drift Modeling as a Support System for Maritime Search and Rescue (SAR) Emergencies: Application to the C-212 Aircraft Accident on 2 September, 2011, in the Juan Fernández Archipelago, Chile. J. Mar. Sci. Eng. 2022, 10, 1649. https://doi.org/10.3390/jmse10111649
Córdova P, Flores RP. Hydrodynamic and Particle Drift Modeling as a Support System for Maritime Search and Rescue (SAR) Emergencies: Application to the C-212 Aircraft Accident on 2 September, 2011, in the Juan Fernández Archipelago, Chile. Journal of Marine Science and Engineering. 2022; 10(11):1649. https://doi.org/10.3390/jmse10111649
Chicago/Turabian StyleCórdova, Pablo, and Raúl P. Flores. 2022. "Hydrodynamic and Particle Drift Modeling as a Support System for Maritime Search and Rescue (SAR) Emergencies: Application to the C-212 Aircraft Accident on 2 September, 2011, in the Juan Fernández Archipelago, Chile" Journal of Marine Science and Engineering 10, no. 11: 1649. https://doi.org/10.3390/jmse10111649
APA StyleCórdova, P., & Flores, R. P. (2022). Hydrodynamic and Particle Drift Modeling as a Support System for Maritime Search and Rescue (SAR) Emergencies: Application to the C-212 Aircraft Accident on 2 September, 2011, in the Juan Fernández Archipelago, Chile. Journal of Marine Science and Engineering, 10(11), 1649. https://doi.org/10.3390/jmse10111649






