Accelerating Predictions of Morphological Bed Evolution by Combining Numerical Modelling and Artificial Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Aspects
2.2. Methodology Outline
- Three idealized alongshore uniform bathymetries were set up, each characterized by a different value of the bed slope tanβ, namely 1:5, 1:25, and 1:50.
- Determination of a number of combinations of the Input Parameters (IP) of to be inserted in the numerical modelling simulations.
- 3.
- For each set of IP, nearshore wave propagation simulations were carried out utilizing a spectral version of a nonlinear parabolic mild slope wave model and the resulting radiation stresses were then inserted as forcing input to a flow model based on the depth-averaged Shallow Water Equations, providing the current speed and current direction.
- 4.
- Subsequently calculations of the value of over a wave cycle were carried out for a cross-section in the middle of the domain in the alongshore direction through a post-processing algorithm. The value of is taken as the average value computed shoreward the maximum depth where initiation of breaking occurs, according to the criterion of [27], out of all the 3200 distinct wave records. The set of IP are consequently linked to a unique value of the Output Parameter (OP) . The corresponding values of IP and OP are provided for the training and validation of an ANN, which will predict for any values within the ranges defined in Table 1.
- 5.
- Through Equations (8) and (9) estimation of follows. Each wave record that satisfies the condition is eliminated, since it is considered unable to initiate sediment motion and thus produce significant morphological changes. Each eliminated wave record is considered to contribute to the “calm conditions” (i.e., waves from directions exiting the numerical domain) hence it retains its individual frequency of occurrence . After elimination, a reduced dataset containing only the sea-states satisfying the Shield’s criterion of incipient sediment motion is obtained.
- 6.
- Utilizing the reduced dataset as input and implementing Equations (12) and (13) a set of annual “equivalent” wave characteristics are defined. The equivalent wave characteristics are used to force the coastal area model and obtain predictions of the coastal bed evolution. In our implementations, we used a combination of a parabolic mild slope wave model (PMS) a hydrodynamic model (HYD), and an initial sedimentation/erosion and morphological model (SDT).
2.3. Overview of the Numerical Models
2.3.1. The Parabolic Mild Slope Wave Model (PMS)
2.3.2. The Hydrodynamic Model (HYD)
2.3.3. The Sediment Transport and Morphological Model (SDT)
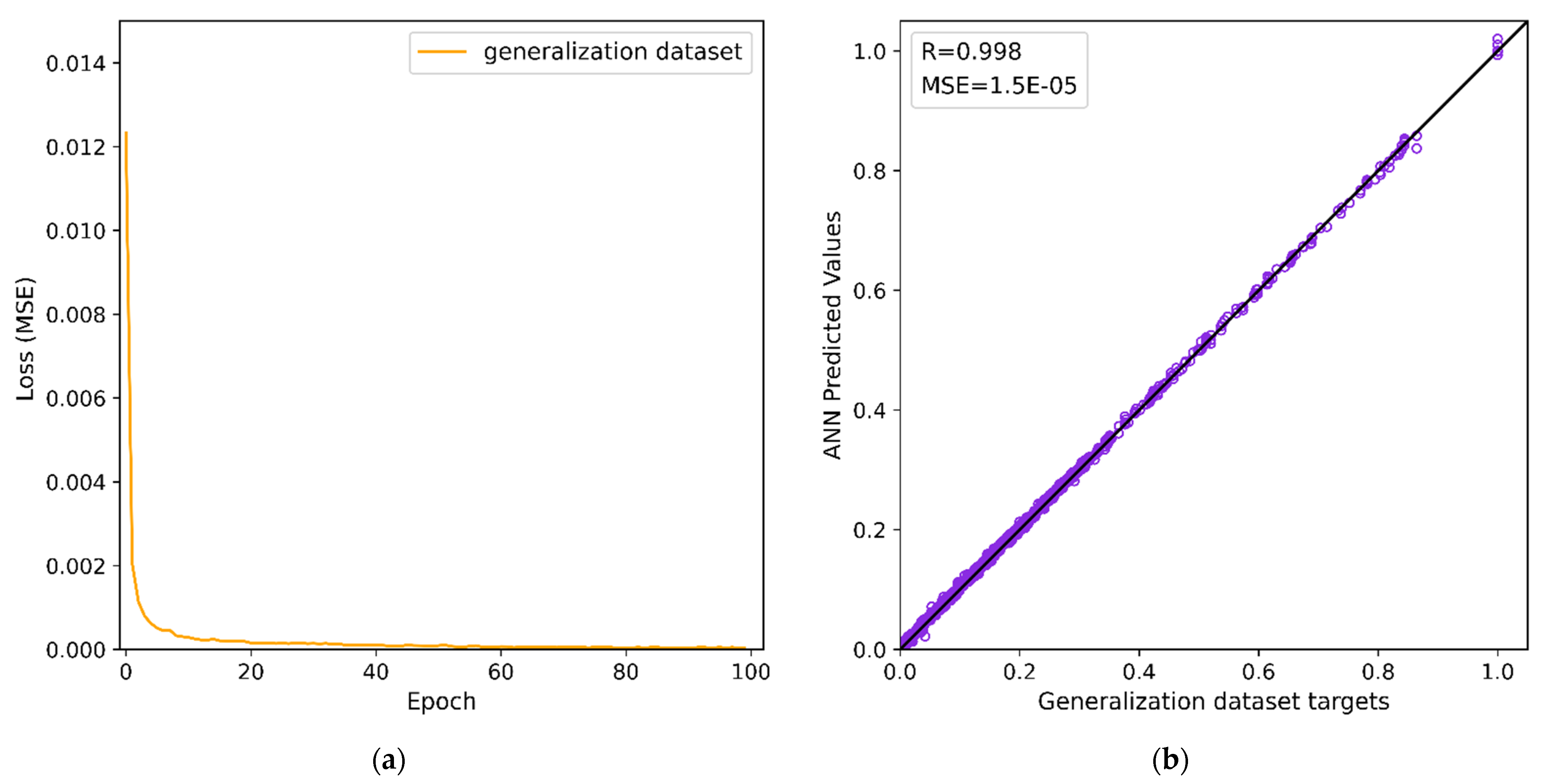
2.4. ANN Parametrization and Training
- An input layer sending input data to the network
- A hidden layer composed of 32 units and a rectified linear unit (relu) activation function
- A hidden layer composed of 64 units using also a reLU activation function
- An output layer with an identity function
3. Methodology Implementation
3.1. Idealized Test Case Validation
- A “brute force” simulation set (BF) containing a detailed representation of the wave climate composed of 36 sea-states propagating from the dominant wave directions.
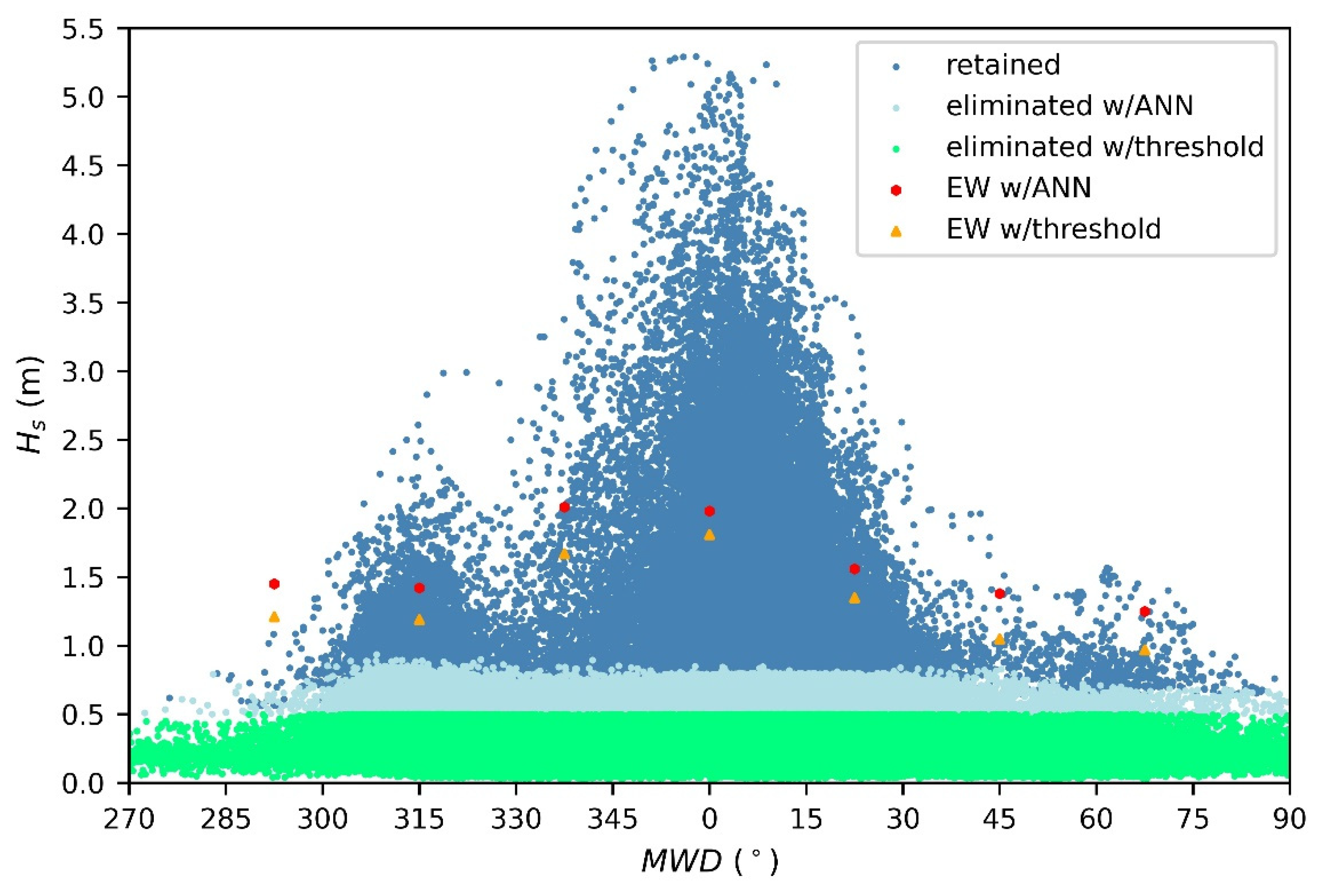
- A simulation set with the elimination of sea-states considered unable to initiate sediment motion by implementing the developed ANN to reduce the input dataset. Thereafter seven “annual equivalent” wave representatives are obtained from the reduced dataset, one for each dominant wave direction and are used to force the integrated models. This simulation will be thereafter denoted as “EW w/ANN”
- A simulation set with the forcing conditions being the seven “annual equivalent” wave representatives considering the full wave climate. This simulation will be thereafter denoted as “EW”
3.2. Real-Field Test Case
- A “brute force” simulation set (BF) containing a robust representation of the wave climate composed of 78 sea-states.
- A simulation set with the elimination of sea-states considered unable to initiate sediment motion by implementing the developed ANN to reduce the input dataset. This simulation set will be thereafter denoted as “EW w/ANN” and contains a representative sea-state for each dominant wave direction.
- A simulation set with the forcing conditions being the seven “annual equivalent” wave representatives after the elimination of wave records by employing an arbitrary threshold of < 0.5. This simulation will be thereafter denoted as “EW w/threshold”.
4. Results and Discussion
4.1. Idealized Test Case
4.1.1. Obtained Representative Wave Conditions
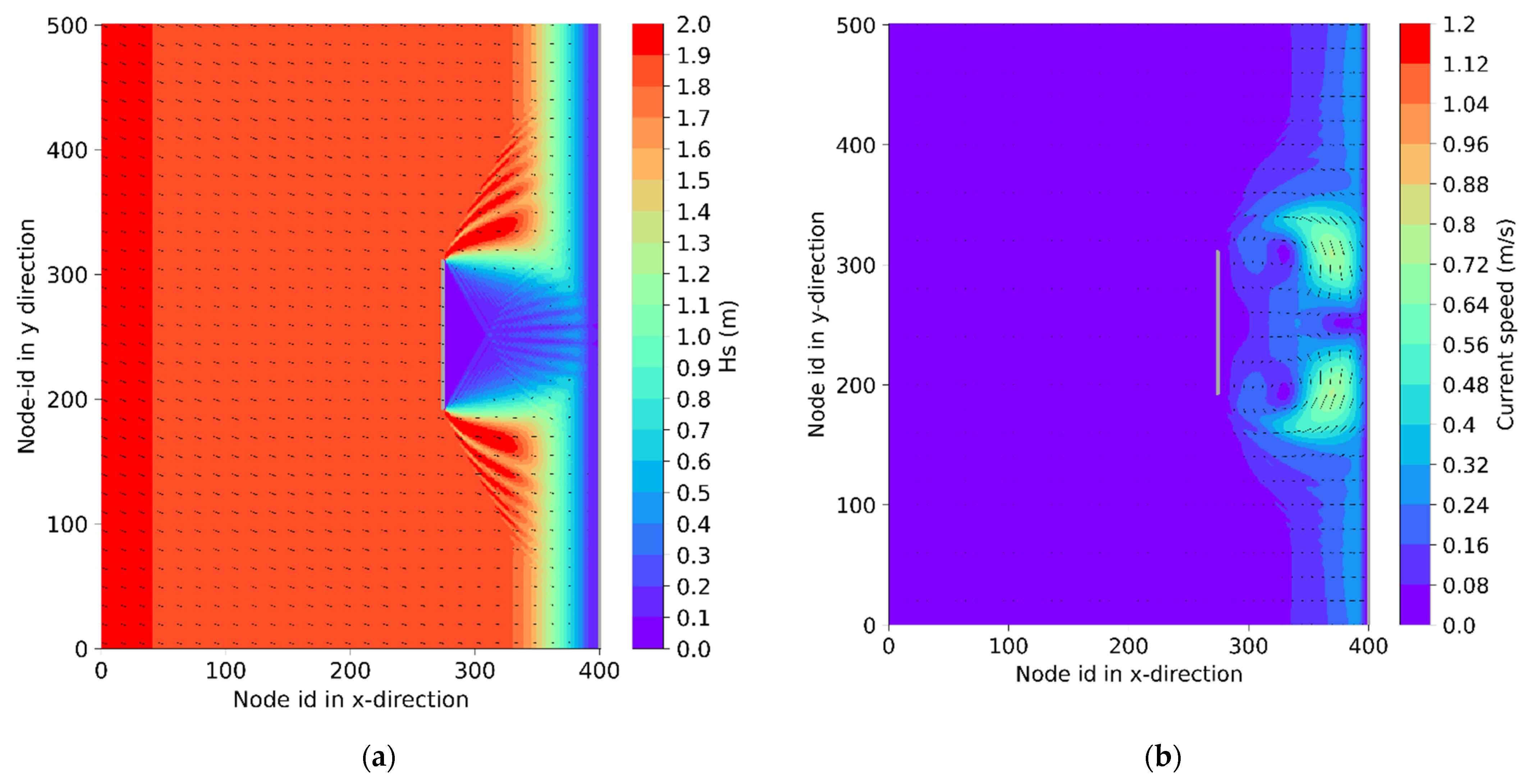
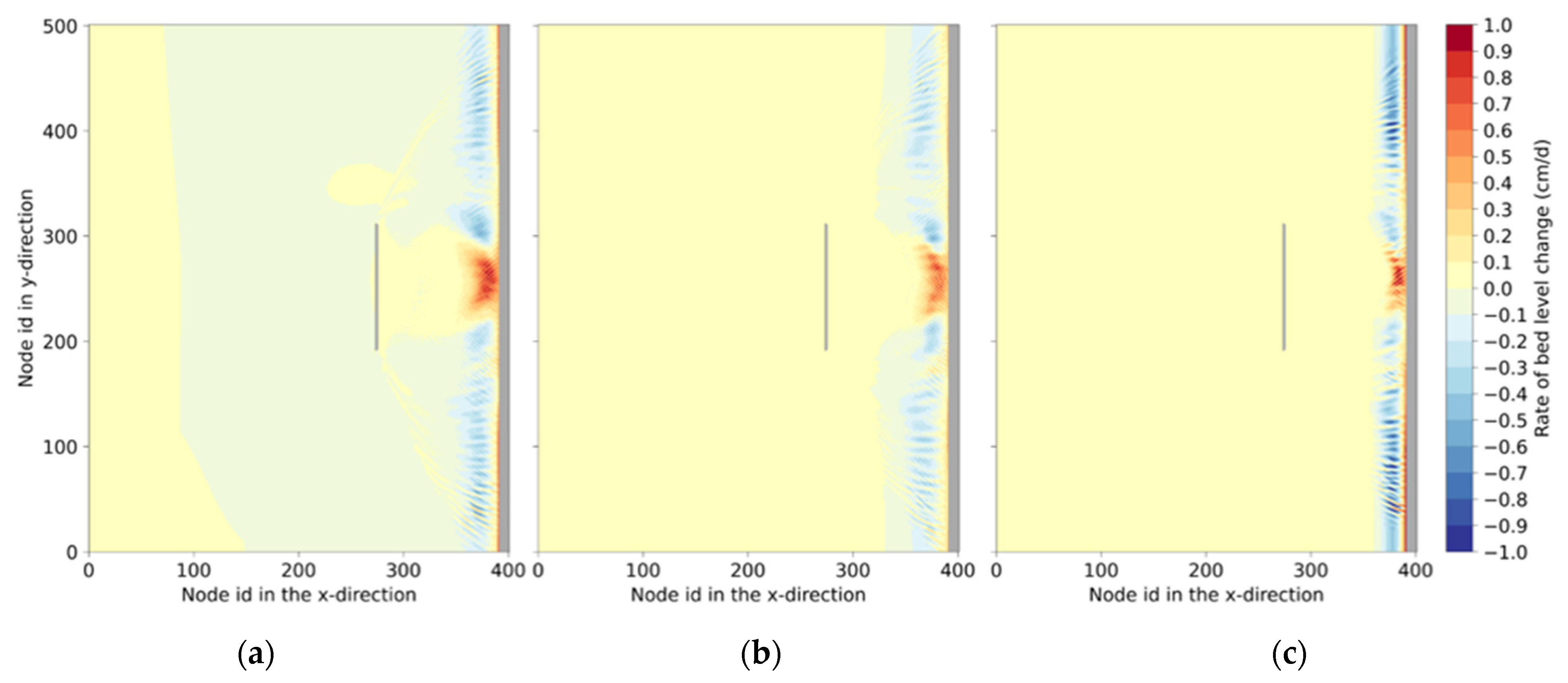
4.1.2. Morphological Modelling Results and Evaluation
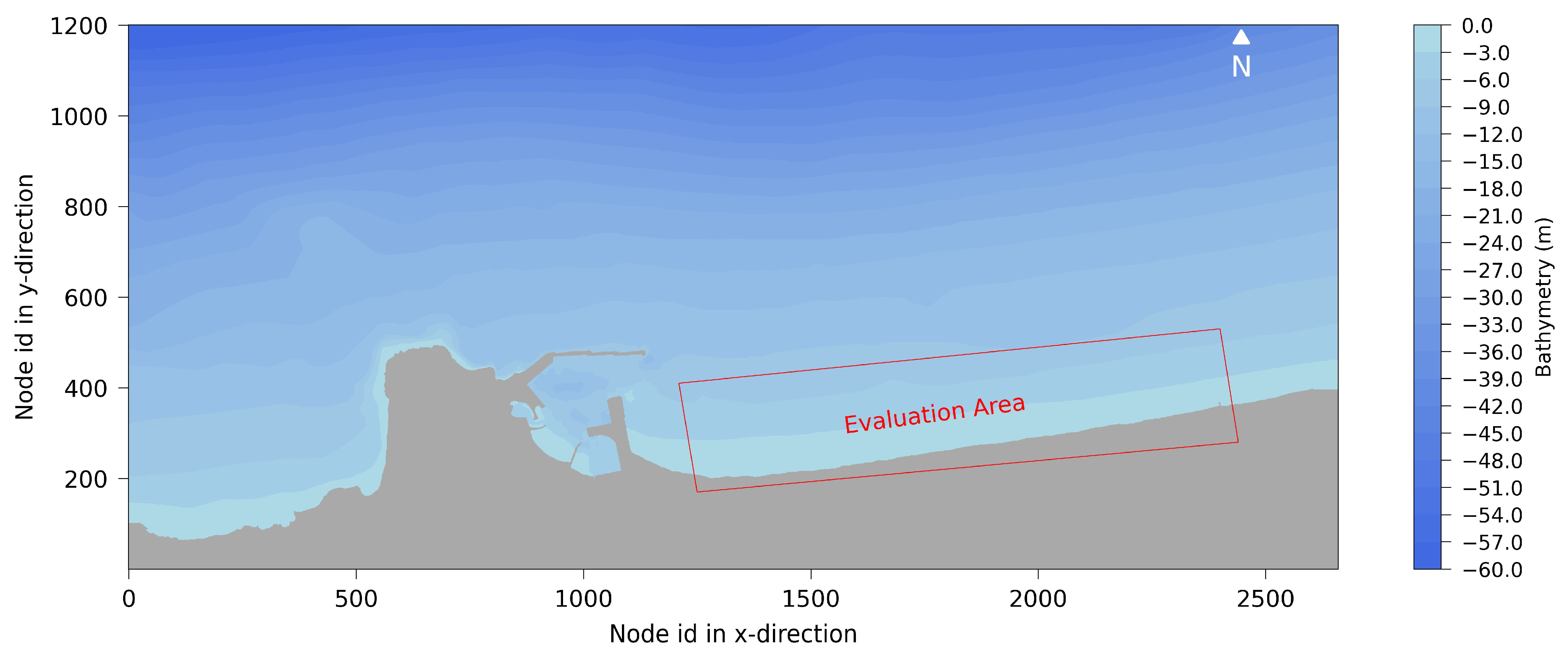
4.2. Real-Field Case Study
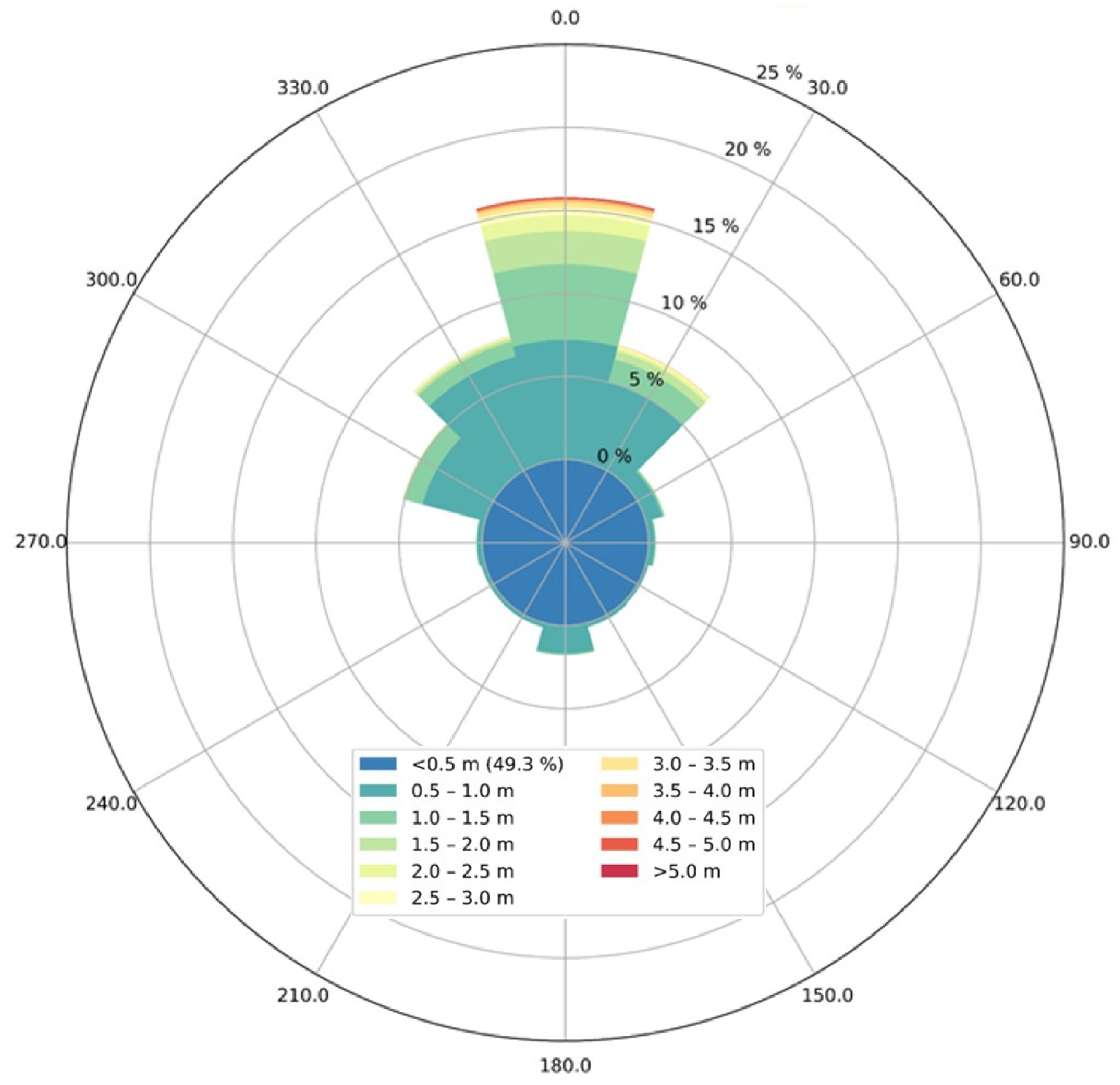
4.2.1. Obtained Representative Wave Conditions
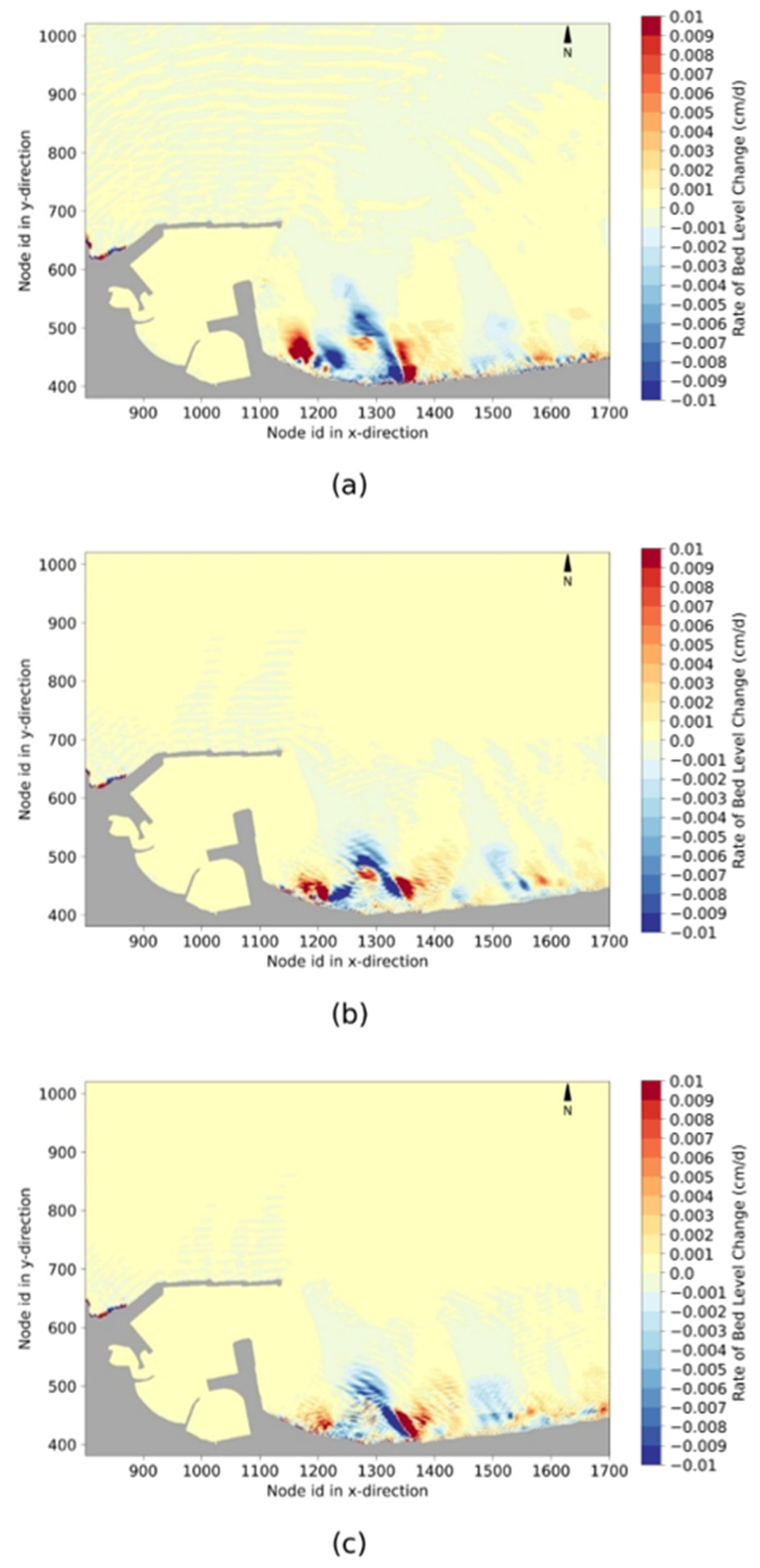
4.2.2. Morphological Modelling Results and Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Roelvink, D.; Reniers, A. A Guide to Modeling Coastal Morphology, 1st ed.; Word Scientific: Singapore, 2012; p. 292. [Google Scholar]
- de Vriend, H.J.; Zyserman, J.; Nicholson, J.; Roelvink, J.A.; Péchon, P.; Southgate, H.N. Medium-term 2DH coastal area modelling. Coast. Eng. 1993, 21, 193–224. [Google Scholar] [CrossRef]
- Roelvink, J.A. Coastal Morphodynamic Evolution Techniques. Coast. Eng. 2006, 53, 277–287. [Google Scholar] [CrossRef]
- Lesser, G.R. An Approach to Medium-Term Coastal Morphological Modelling. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 4 June 2009. [Google Scholar]
- Borah, D.K.; Balloffet, A. Beach Evolution Caused by Littoral Drift Barrier. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 645–660. [Google Scholar] [CrossRef]
- Brown, J.M.; Davies, A.G. Methods for Medium-Term Prediction of the Net Sediment Transport by Waves and Currents in Complex Coastal Regions. Cont. Shelf Res. 2009, 29, 1502–1514. [Google Scholar] [CrossRef]
- Walstra, D.J.R.; Hoekstra, R.; Tonnon, P.K.; Ruessink, B.G. Input Reduction for Long-Term Morphodynamic Simulations in Wave-Dominated Coastal Settings. Coast. Eng. 2013, 77, 57–70. [Google Scholar] [CrossRef]
- Benedet, L.; Dobrochinski, J.P.F.; Walstra, D.J.R.; Klein, A.H.F.; Ranasinghe, R. A morphological modeling study to compare different methods of wave climate schematization and evaluate strategies to reduce erosion losses from a beach nourishment project. Coast. Eng. 2016, 112, 69–86. [Google Scholar] [CrossRef]
- de Queiroz, B.; Scheel, F.; Caires, S.; Walstra, D.J.; Olij, D.; Yoo, J.; Reniers, A.; de Boer, W. Performance Evaluation of Wave Input Reduction Techniques for Modeling Inter-Annual Sandbar Dynamics. J. Mar. Sci. Eng. 2019, 7, 148. [Google Scholar] [CrossRef]
- Chonwattana, S.; Weesakul, S.; Vongvisessomjai, S. 3D Modeling of Morphological Changes Using Representative Waves. Coast. Eng. J. 2005, 47, 205–229. [Google Scholar] [CrossRef]
- Karambas, T.V.; Koutandos, E.V.; Kampanis, N.A. Numerical Simulation of Wave-Induced Morphology Evolution. Marit. Eng. 2013, 166, 113–124. [Google Scholar] [CrossRef]
- Papadimitriou, A.; Tsoukala, V. Performance Evaluation of the K-Means Clustering Algorithm for the Prediction of Annual Bed Morphological Evolution. In Proceedings of the 7th IAHR Europe Congress, Athens, Greece, 7–9 September 2022; pp. 161–162. [Google Scholar]
- Pletcha, S.; Sancho, F.; Silva, P.; Dias, J.M. Representative Waves for Morphological Simulations. J. Coast. Res. 2007, SI 50, 995–999. [Google Scholar]
- Papadimitriou, A.; Panagopoulos, L.; Chondros, M.; Tsoukala, V. A Wave Input-Reduction Method Incorporating Initiation of Sediment Motion. J. Mar. Sci. Eng. 2020, 8, 597. [Google Scholar] [CrossRef]
- Bosboom, J.; Stive, M.J.F. Coastal Dynamics; TU Delft Open Textbooks: Delft, The Netherlands, 2022; p. 579. [Google Scholar]
- Soulsby, R.L. Dynamics of Marine Sands: A Manual for Practical Applications, 1st ed.; Thomas Telford: London, UK, 1997; p. 249. [Google Scholar]
- Shields, I.A. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; U.S. Soil Conservation Service Cooperative Laboratory; Ott, W.P.; van Uchelen, J.C., Translators; Hydrodynamics Laboratory Publication, California Institute of Technology: Pasadena, CA, USA, 1936; Volume 167. [Google Scholar]
- Grant, W.D.; Madsen, O.S. Combined Wave and Current Interaction with a Rough Bottom. J. Geophys. Res. Ocean. 1979, 84, 1797–1808. [Google Scholar] [CrossRef]
- Fredsøe, J. Turbulent Boundary Layer in Wavecurrent Motion. J. Hydraul. Eng. 1984, 110, 1103–1120. [Google Scholar] [CrossRef]
- Davies, A.G.; Soulsby, R.L.; King, H.L. A Numerical Model of the Combined Wave and Current Bottom Boundary Layer. J. Geophys. Res. Ocean. 1988, 93, 491–508. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Hamm, L.; Klopman, G.; Myrhaug, D.; Simons, R.R.; Thomas, G.P. Wave-Current Interaction within and Outside the Bottom Boundary Layer. Coast. Eng. 1993, 21, 41–69. [Google Scholar] [CrossRef]
- Swart, D.H. Offshore Sediment Transport and Equilibrium Beach Profiles. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 18 December 1974. [Google Scholar]
- Soulsby, R.L.; Whitehouse, R.J. Threshold of sediment motion in coastal environments. In Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Canterbury, UK, 28–30 September 1997. [Google Scholar]
- Chondros, M.K.; Metallinos, A.S.; Memos, C.D.; Karambas, T.V.; Papadimitriou, A.G. Concerted Nonlinear Mild-Slope Wave Models for Enhanced Simulation of Coastal Processes. Appl. Math. Model. 2021, 91, 508–529. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef] [PubMed]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 1 January 1967. [Google Scholar]
- Miche, M. Le Pouvoir Réfléchissant des Ouvrages Maritimes Exposés à l’action de La Houle; Technical Report; Annales de Ponts et Chaussées, École nationale des Ponts et Chaussées: Paris, France, 1951. [Google Scholar]
- Berkhoff, J.C.W. Computation of Combined Refraction-Diffraction. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972. [Google Scholar]
- Kirby, J.T.; Dalrymple, R.A. A parabolic equation for the combined refraction diffraction of Stokes waves by mildly varying topography. J. Fluid Mech. 1983, 136, 453–466. [Google Scholar] [CrossRef]
- Kirby, J.T. Higher-Order Approximations in the Parabolic Equation Method for Water Waves. J. Geophys. Res. 1986, 91, 933–952. [Google Scholar] [CrossRef]
- Kirby, J.T. Rational approximations in the parabolic equation method for water waves. Coast. Eng. 1986, 10, 355–378. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due To Breaking of Random Waves. In Proceedings of the Coastal Engineering Conference, Hamburg, Germany, 27 August–3 September 1979. [Google Scholar]
- Putnam, J.A.; Johson, J.W. The dissipation of wave energy by bottom friction. Eos Trans. Am. Geophys. Union 1949, 30, 67–74. [Google Scholar] [CrossRef]
- Kirby, J.T.; Dalrymple, R.A. An approximate model for nonlinear dispersion in monochromatic wave propagation models. Coast. Eng. 1986, 9, 545–561. [Google Scholar] [CrossRef]
- Xia, M.; Mao, M.; Niu, Q. Implementation and comparison of the recent three-dimensional radiation stress theory and vortex-force formalism in an unstructured-grid coastal circulation model. Estuar. Coast. Shelf Sci. 2020, 240, 106771. [Google Scholar] [CrossRef]
- Moghimi, S.; Klingbeil, K.; Gräwe, U.; Burchard, H. A direct comparison of a depth-dependent Radiation stress formulation and a Vortex force formulation with a three-dimensional coastal ocean model. Ocean Model. 2013, 70, 132–144. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. I: Initiation of Motion, Bed Roughness, and Bed-Load Transport. J. Hydraul. Eng. 2007, 133, 649–667. [Google Scholar] [CrossRef]
- van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. II: Suspended Transport. J. Hydraul. Eng. 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Niu, Q.; Xia, M.; Ludsin, S.; Chu, P.; Mason, D.; Rutherford, E. High-turbidity events in Western Lake Erie during ice-free cycles: Contributions of river-loaded vs. resuspended sediments. Limnol. Oceanogr. 2018, 63, 2545–2562. [Google Scholar] [CrossRef]
- Chou, Y.-J.; Nelson, K.; Holleman, R.; Fringer, O.; Stacey, M.; Lacy, J.; Monismith, S.; Koseff, J. Three-Dimensional Modeling of Fine Sediment Transport by Waves and Currents in a Shallow Estuary. J. Geophys. Res. Ocean. 2018, 123, 4177–4199. [Google Scholar] [CrossRef]
- Long, W.; Kirby, J.T.; Shao, Z. A Numerical Scheme for Morphological Bed Level Calculations. Coast. Eng. 2008, 55, 167–180. [Google Scholar] [CrossRef]
- Keras: The Python Deep Learning API. Available online: https://keras.io/ (accessed on 18 September 2022).
- Coppernicus Marine Environment Monitoring Service CMEMS. Available online: http://marine.copernicus.eu/ (accessed on 18 September 2022).
- Korres, G.; Ravdas, M.; Zacharioudaki, A. [Dataset] Mediterranean Sea Waves Hindcast (CMEMS MED-Waves). Available online: https://resources.marine.copernicus.eu/?option=com_csw&view=details&product_id=MEDSEA_MULTIYEAR_WAV_006_012 (accessed on 18 September 2022).
- Sutherland, J.; Peet, A.H.; Soulsby, R.L. Evaluating the performance of morphological models. Coast. Eng. 2004, 51, 917–939. [Google Scholar] [CrossRef]
- Tsoukala, V.K.; Chondros, M.; Kapelonis, Z.G.; Martzikos, N.; Lykou, A.; Belibassakis, K.; Makropoulos, C. An Integrated Wave Modelling Framework for Extreme and Rare Events for Climate Change in Coastal Areas—The Case of Rethymno, Crete. Oceanologia 2016, 58, 71–89. [Google Scholar] [CrossRef]
- Chondros, M.; Tsoukala, V.; Metallinos, A.; Papadimitriou, A.; Memos, C. A Coastal Flood Early-Warning System Based on Offshore Sea State Forecasts and Artificial Neural Networks. J. Mar. Sci. Eng. 2021, 9, 1272. [Google Scholar] [CrossRef]
- NAVIONICS: A Garmin Company. Available online: https://webapp.navionics.com/ (accessed on 11 September 2022).
- Copeland, G.J.M. A Practical Alternative to the “Mild-Slope” Wave Equation. Coast. Eng. 1985, 9, 125–149. [Google Scholar] [CrossRef]
- Yu, Y.X.; Liu, S.X.; Li, L. Numerical simulation of multi-directional waves. In Proceedings of the International Society of Offshore and Polar Engineers Conference, Edinburgh, UK, 11–16 August 1991. [Google Scholar]



| minimum | 0 | 0 | −90 | 0.06 | 1:50 |
| maximum | 7 | 15 | 90 | 2.0 | 1:5 |
| Test ID | ||
|---|---|---|
| IC1 | 0.1 | 1:50 |
| IC2 | 1.0 | 1:50 |
| IC3 | 2.0 | 1:50 |
| IC4 | 0.1 | 1:20 |
| IC5 | 1.0 | 1:20 |
| IC6 | 2.0 | 1:20 |
| BSS | |
|---|---|
| Excellent (E) | 1.0–0.5 |
| Good (G) | 0.5–0.2 |
| Reasonable/Fair (R/F) | 0.2–0.1 |
| Poor (P) | 0.1–0.0 |
| Bad (B) | <0.0 |
| Sector | EW w/ANN | EW | ||||||
|---|---|---|---|---|---|---|---|---|
| He (m) | Te (s) | MWD (°) | f (%) | He (m) | Te (s) | MWD (°) | f (%) | |
| SSW | 0.96 | 7.94 | 202.5 | 0.9765 | 0.62 | 6.04 | 202.5 | 13.30 |
| SW | 1.04 | 8.35 | 225.0 | 1.6568 | 0.60 | 6.07 | 225.0 | 20.46 |
| WSW | 0.98 | 7.87 | 247.5 | 0.2747 | 0.52 | 5.55 | 247.5 | 5.78 |
| W | 1.02 | 7.08 | 270.0 | 0.2447 | 0.53 | 5.18 | 270.0 | 5.93 |
| WNW | 1.15 | 6.72 | 292.5 | 2.5289 | 0.72 | 5.10 | 292.5 | 27.86 |
| NW | 0.99 | 6.75 | 315.0 | 0.7542 | 0.51 | 4.58 | 315.0 | 24.93 |
| NNW | 0.81 | 7.36 | 337.5 | 0.0034 | 0.46 | 5.89 | 337.5 | 0.50 |
| Test ID | EW w/ANN | EW |
|---|---|---|
| IC1 | 0.92 (E) | 0.65 (E) |
| IC2 | 0.77 (E) | 0.24 (G) |
| IC3 | 0.65 (E) | 0.22 (G) |
| IC4 | 0.86 (E) | 0.45 (G) |
| IC5 | 0.86 (E) | 0.19 (R/F) |
| IC6 | 0.72 (E) | 0.04 (P) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadimitriou, A.; Chondros, M.; Metallinos, A.; Tsoukala, V. Accelerating Predictions of Morphological Bed Evolution by Combining Numerical Modelling and Artificial Neural Networks. J. Mar. Sci. Eng. 2022, 10, 1621. https://doi.org/10.3390/jmse10111621
Papadimitriou A, Chondros M, Metallinos A, Tsoukala V. Accelerating Predictions of Morphological Bed Evolution by Combining Numerical Modelling and Artificial Neural Networks. Journal of Marine Science and Engineering. 2022; 10(11):1621. https://doi.org/10.3390/jmse10111621
Chicago/Turabian StylePapadimitriou, Andreas, Michalis Chondros, Anastasios Metallinos, and Vasiliki Tsoukala. 2022. "Accelerating Predictions of Morphological Bed Evolution by Combining Numerical Modelling and Artificial Neural Networks" Journal of Marine Science and Engineering 10, no. 11: 1621. https://doi.org/10.3390/jmse10111621
APA StylePapadimitriou, A., Chondros, M., Metallinos, A., & Tsoukala, V. (2022). Accelerating Predictions of Morphological Bed Evolution by Combining Numerical Modelling and Artificial Neural Networks. Journal of Marine Science and Engineering, 10(11), 1621. https://doi.org/10.3390/jmse10111621










