Optimal Level of Woody Biomass Co-Firing with Coal Power Plant Considering Advanced Feedstock Logistics System
Abstract
:1. Introduction
1.1. Background and Research Objectives
- We incorporate the torrefaction processing option in the estimation of optimized biomass co-firing ratio.
- We compare the conventional and advanced logistics to verify the most appropriate logistics system for biomass co-firing.
- We evaluate the proposed model through a case study for the Great Lakes States considering actual seasonal variations of biomass feedstock in study area.
- We compare the impacts of (1) the tax credit as a governmental incentive, and (2) selecting torrefaction process on the preferred level of biomass co-firing.
1.2. Literature Review
2. Materials and Methods
2.1. Advanced Woody Biomass Logistics System
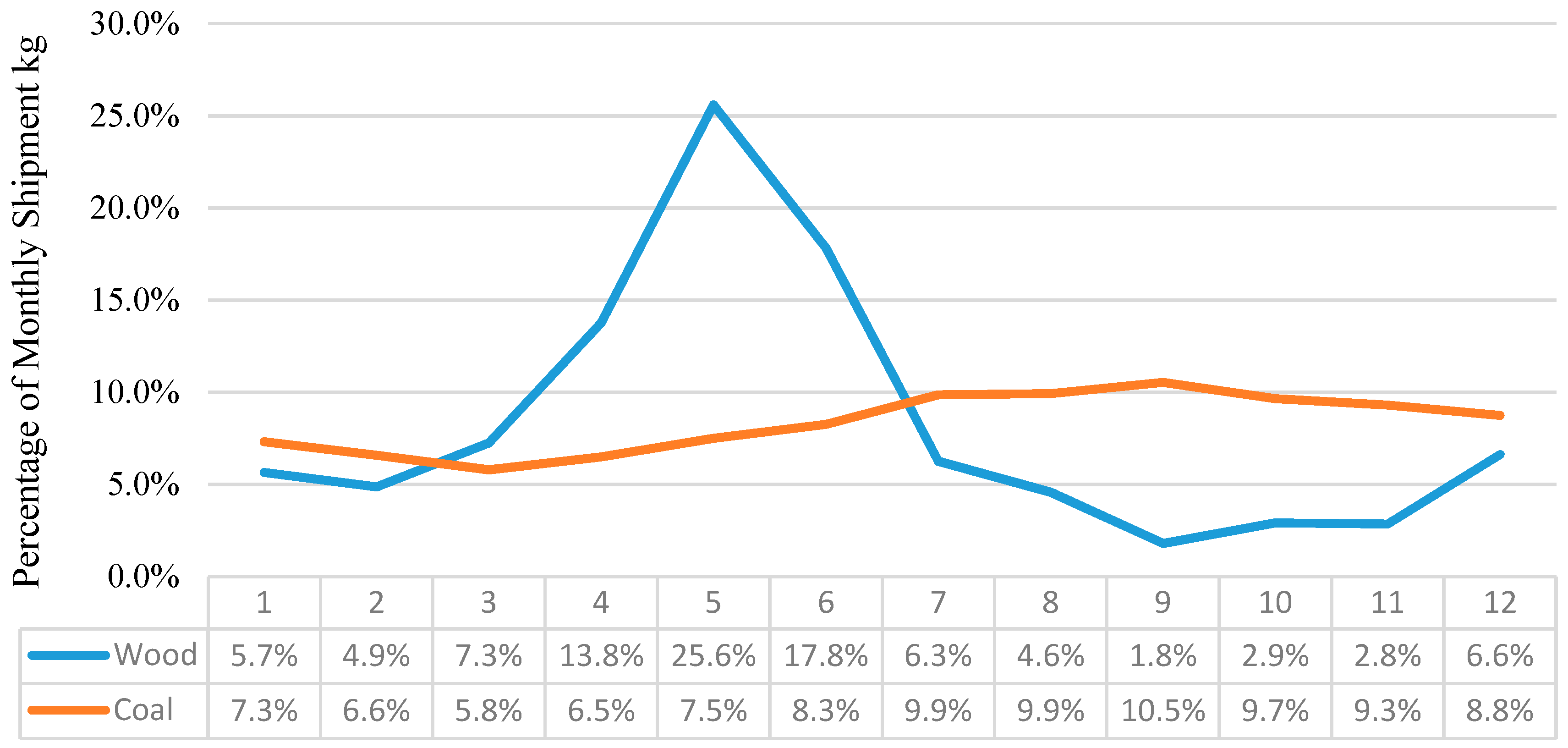
2.2. Seasonality
2.3. Economic Incentives and Mandates for Renewable Energy
2.4. Loss of Boiler Efficiency and Maximum Co-Firing Ratio
2.5. Mathematical Model
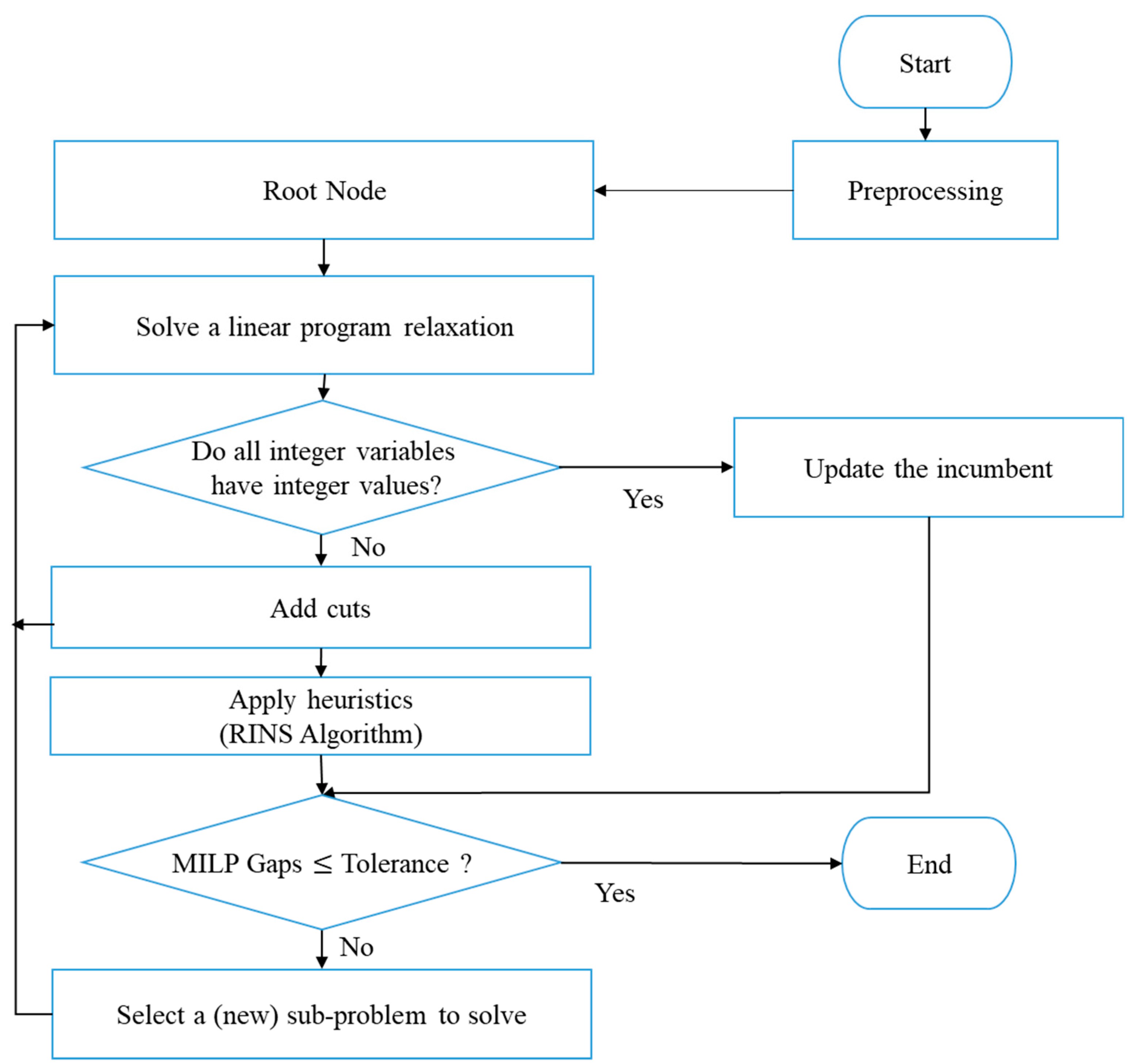
2.6. The Solution Approaches
3. Results and Discussions: Case Study of Optimal Level of Woody Biomass for Co-Firing in Existing Coal Power Plants in the Great Lakes States of the US
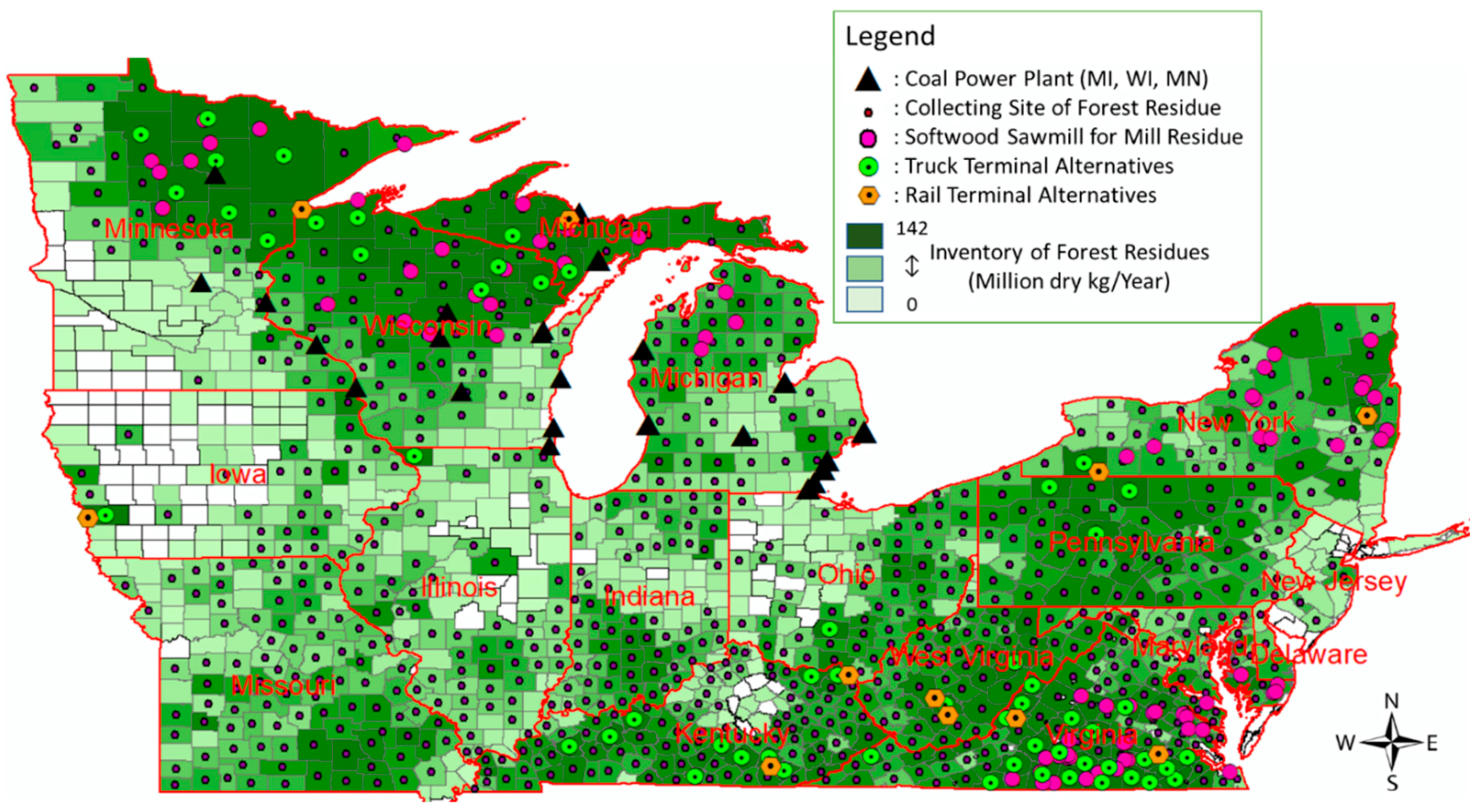
3.1. Data Collection and Pre-Processing
- -
- Feedstock availability
- -
- Alternative locations for truck and rail terminals
- -
- Purchase cost of woody biomass feedstock
- -
- Transportation cost for truck and rail
- -
- Capital and operation cost occurred at both terminal/depot and power plant locations
3.1.1. Data for Coal Power Plants
3.1.2. Data for Seasonal Variations of Feedstocks
3.2. Experimental Results
- -
- Scenario 1: Conventional logistics with no tax credit
- -
- Scenario 2: Conventional logistics with tax credit
- -
- Scenario 3: Advanced logistics with no tax credit
- -
- Scenario 4: Advanced logistics with tax credit
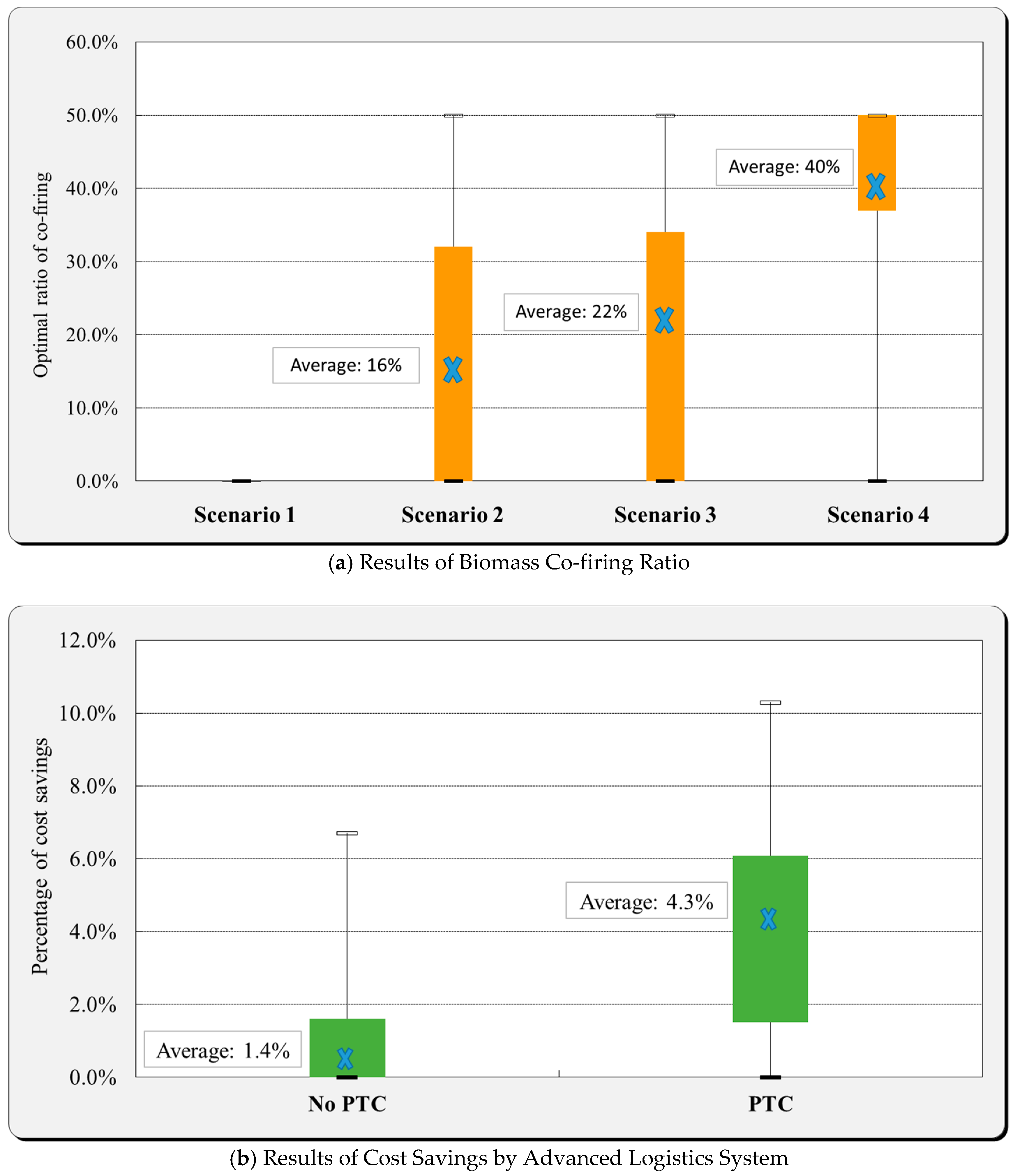
3.2.1. Biomass Co-Firing Ratio and Cost Savings
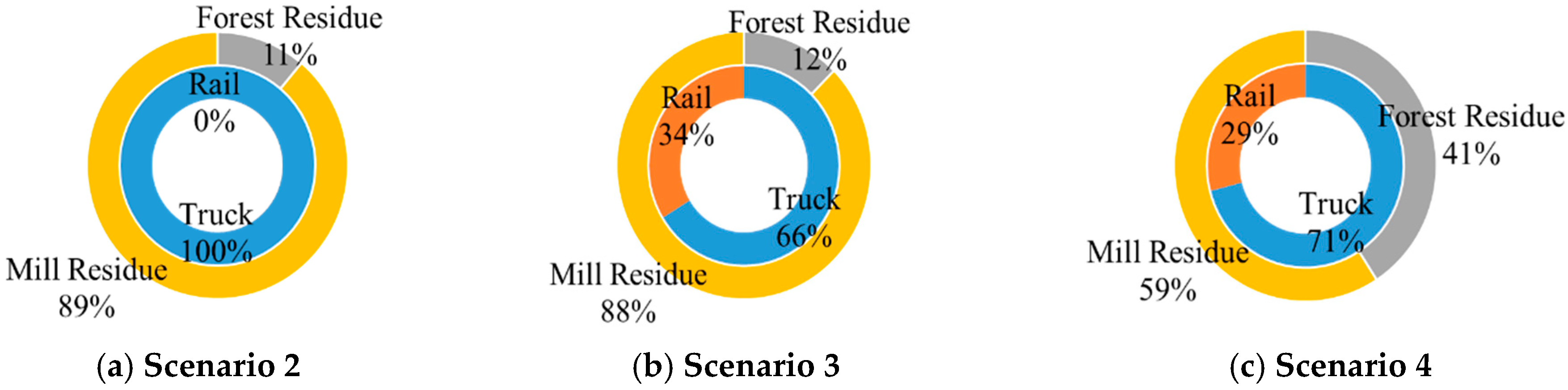
3.2.2. Biomass Feedstock Types and Transportation Mode
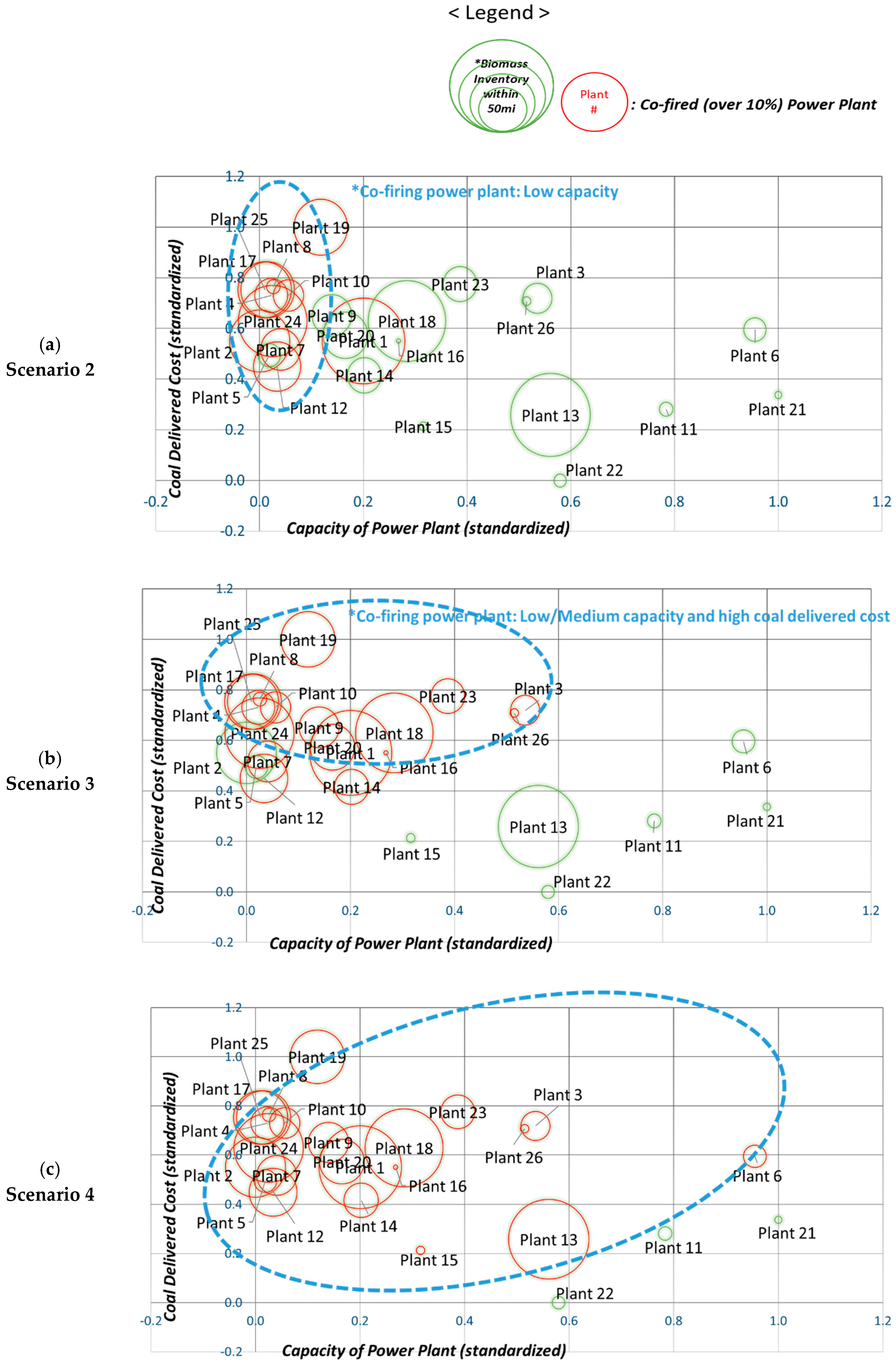
3.2.3. Relationship between Logistics Conditions and Co-Firing Ratio
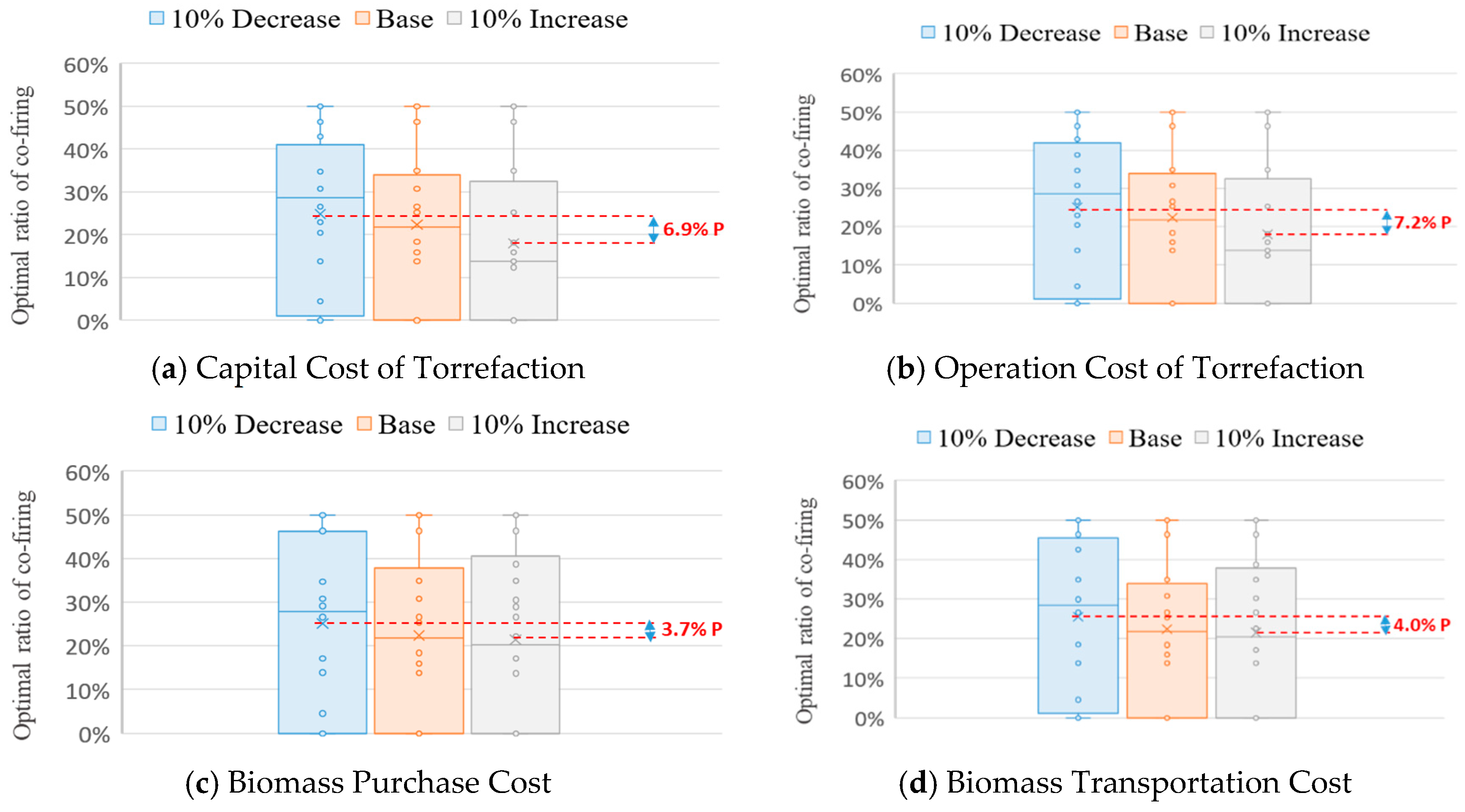
3.3. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Data | Value | Reference | |
|---|---|---|---|
| Feedstock Availability | Forest Residue | Kilograms for 845 potential collecting sites in 16 States | US Department of Agriculture (USDA) [40] |
| Mill Residue | Kilograms for 74 Softwood Sawmills in 16 States | USDA Forest Service [41] | |
| Feedstock Purchasing Cost | Forest Residue | $0.017/kg | US Department of Energy [26] |
| Mill Residue | $0.024/kg | ||
| Transport Rate | Truck Rate ($/Thousand kg) | Before Terminal: After Terminal: | Interview with Local Forest Company [36] |
| Rail Rate ($/Carload) | CN Rail: NS Rail: | Official Tariffs [42,43]; Interview with Local Forest Company [36] | |
| Energy Contents (Before & After torrefaction) | Forest Residue | 0.011 GJ/kg & 0.015 GJ/kg | US EPA [44]; Van der Stelt et al. [11] |
| Mill Residue | 0.019 GJ/kg & 0.025 GJ/kg | ||
| Coal | 0.029 GJ/kg | ||
| Mass conversion factor after torrefaction ( | 1.43 | Dutta and Leon [12] | |
| Storage Cost of Biomass Feedstock ( | $0.639/Thousand kg | Zhang et al. [45] | |
| Capital Cost/Operation Cost (2016 US $ Per Dry Thousand kg) | Processes in Terminal or Depot | Processes in Power Plant | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Receiving/Handling | Dryer | Torre-Faction | Densifi-Cation | Storage | Surge Bin | Sum | In-Plant Handling | In-Plant Drying | In-Plant Storage | Sum | ||
| Conventional Logistics | (1) Supply area ↓ Power Plant | n/a | n/a | n/a | n/a | n/a | n/a | 0.0/0.0 | 19.75/4.72 | 39.14/12.68 | 3.63/1.17 | 62.52/18.56 |
| (2) Supply area ↓ Terminal ↓ Power Plant | 12.04/2.71 | n/a | n/a | n/a | 3.59/1.14 | 0.86/0.08 | 16.49/3.92 | 19.75/4.72 | 39.14/12.68 | 3.63/1.17 | 62.52/18.56 | |
| Advanced Logistics | (3) Supply area ↓ Terminal + Depot ↓ Power Plant | 12.04/2.71 | 45.83/17.34 | 75.73/11.18 | 3.16/6.16 | 3.59/1.14 | 0.86/0.08 | 141.2/38.6 | 0.67/0.2 | n/a | 3.63/1.17 | 4.3/1.37 |
Appendix B
| Level of Biomass Co-Firing (Mass Base) | Cost Savings by Changing Logistics System | |||||
|---|---|---|---|---|---|---|
| Scenario 1 CL + No PTC | Scenario 2 CL + PTC | Scenario 3 AL + No PTC | Scenario 4 AL + PTC | No PTC | PTC | |
| Plant 1 | 0% | 16% | 27% | 50% | 1.5% | 5.6% |
| Plant 2 | 0% | 50% | 0% | 50% | 0.0% | 0.0% |
| Plant 3 | 0% | 0% | 14% | 35% | 0.4% | 2.7% |
| Plant 4 | 0% | 47% | 50% | 50% | 4.6% | 8.1% |
| Plant 5 | 0% | 0% | 0% | 50% | 0.0% | 4.7% |
| Plant 6 | 0% | 0% | 0% | 19% | 0.0% | 1.1% |
| Plant 7 | 0% | 16% | 31% | 50% | 0.1% | 4.6% |
| Plant 8 | 0% | 33% | 35% | 50% | 2.6% | 6.7% |
| Plant 9 | 0% | 0% | 27% | 50% | 0.7% | 6.5% |
| Plant 10 | 0% | 29% | 46% | 50% | 2.9% | 8.0% |
| Plant 11 | 0% | 0% | 0% | 5% | 0.0% | 0.0% |
| Plant 12 | 0% | 16% | 31% | 50% | 0.5% | 4.8% |
| Plant 13 | 0% | 0% | 0% | 14% | 0.0% | 0.7% |
| Plant 14 | 0% | 0% | 14% | 43% | 0.2% | 3.5% |
| Plant 15 | 0% | 0% | 0% | 18% | 0.0% | 0.9% |
| Plant 16 | 0% | 0% | 16% | 50% | 0.6% | 4.6% |
| Plant 17 | 0% | 50% | 50% | 50% | 3.9% | 5.9% |
| Plant 18 | 0% | 6% | 18% | 50% | 1.2% | 5.6% |
| Plant 19 | 0% | 47% | 50% | 50% | 6.7% | 10.3% |
| Plant 20 | 0% | 6% | 25% | 46% | 1.4% | 6.1% |
| Plant 21 | 0% | 0% | 0% | 9% | 0.0% | 0.4% |
| Plant 22 | 0% | 0% | 0% | 0% | 0.0% | 0.0% |
| Plant 23 | 0% | 6% | 31% | 50% | 1.6% | 6.0% |
| Plant 24 | 0% | 47% | 50% | 50% | 5.5% | 9.5% |
| Plant 25 | 0% | 50% | 50% | 50% | 1.6% | 3.3% |
| Plant 26 | 0% | 0% | 17% | 47% | 0.6% | 3.3% |
| Average, % | 0% | 16% | 22% | 40% | 1.4% | 4.3% |
References
- U.S. EIA. Annual Energy Outlook; U.S. EIA: Washington, WA, USA, 2014.
- Basu, P.; Butler, J.; Leon, M.A. Biomass co-firing options on the emission reduction and electricity generation costs in coal-fired power plants. Renew. Energy 2011, 36, 282–288. [Google Scholar] [CrossRef]
- Tillman, D.A. Biomass cofiring: The technology, the experience, the combustion consequences. Biomass Bioenergy 2000, 19, 365–384. [Google Scholar] [CrossRef]
- Roni, M.S.; Eksioglu, S.D.; Searcy, E.; Jha, K. A supply chain network design model for biomass co-firing in coal-fired power plants. Transp. Res. Part E Logist. Transp. Rev. 2014, 61, 115–134. [Google Scholar] [CrossRef]
- Sondreal, E.A.; Benson, S.A.; Hurley, J.P.; Mann, M.D.; Pavlish, J.H.; Swanson, M.L.; Weber, G.F.; Zygarlicke, C.J. Review of advances in combustion technology and biomass cofiring. Fuel Process. Technol. 2001, 71, 7–38. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Biomass Cofiring in Coal-Fired Boilers. In Federal Energy Management Program; NREL: Golden, CO, USA, 2004. [Google Scholar]
- Fernando, R. Cofiring High Ratios of Biomass with Coal; IEA Clean Coal Centre: London, UK, 2012; Volume 300, p. 194. [Google Scholar]
- Mendell, C.B.; Haber, J.A.; Sydor, T. Evaluating the potential for shared log truck resources in middle Georgia. South. J. Appl. For. 2006, 30, 86–91. [Google Scholar]
- Carlsson, D.; Rönnqvist, M. Backhauling in forest transportation: Models, methods, and practical usage. Can. J. For. Res. 2007, 37, 2612–2623. [Google Scholar] [CrossRef]
- Rentizelas, A.A.; Li, J. Techno-economic and carbon emissions analysis of biomass torrefaction downstream in international bioenergy supply chains for co-firing. Energy 2016, 114, 129–142. [Google Scholar] [CrossRef]
- Van der Stelt, M.J.C.; Gerhauser, H.; Kiel, J.H.A.; Ptasinski, K.J. Biomass upgrading by torrefaction for the production of biofuels: A review. Biomass Bioenergy 2011, 35, 3748–3762. [Google Scholar] [CrossRef]
- Dutta, A.; Leon, M.A. Pros and Cons of Torrefaction of Woody Biomass; University of Guelph, Joint eco ETI & CEF projects workshop Turfgrass Institute: Guelph, ON, Canada, 2011. [Google Scholar]
- Ghenai, C.; Janajreh, I. CFD analysis of the effects of co-firing biomass with coal. Energy Convers. Manag. 2010, 51, 1694–1701. [Google Scholar] [CrossRef]
- Levendis, Y.A.; Joshi, K.; Khatami, R.; Sarofim, A.F. Combustion behavior in air of single particles from three different coal ranks and from sugarcane bagasse. Combust. Flame 2011, 158, 452–465. [Google Scholar] [CrossRef]
- Gubba, S.; Ingham, D.B.; Larsen, K.J.; Ma, L.; Pourkashanian, M.; Tan, H.Z.; Williams, A.; Zhou, H. Numerical modelling of the co-firing of pulverised coal and straw in a 300 MWe tangentially fired boiler. Fuel Process. Technol. 2012, 104, 181–188. [Google Scholar] [CrossRef]
- Álvarez, L.; Yin, C.; Riaza, J.; Pevida, C.; Pis, J.J.; Rubiera, F. Biomass co-firing under oxy-fuel conditions: A computational fluid dynamics modelling study and experimental validation. Fuel Process. Technol. 2014, 120, 22–33. [Google Scholar] [CrossRef]
- Berggren, M.; Ljunggren, E.; Johnsson, F. Biomass co-firing potentials for electricity generation in Poland—Matching supply and co-firing opportunities. Biomass Bioenergy 2008, 32, 865–879. [Google Scholar] [CrossRef]
- Ekşioğlu, S.D.; Karimi, H.; Ekşioğlu, B. Optimization models to integrate production and transportation planning for biomass co-firing in coal-fired power plants. IIE Trans. 2016, 48, 901–920. [Google Scholar] [CrossRef]
- Bergman, P.C.A.; Prins, M.J.; Boersma, A.R.; Ptasinski, K.J.; Kiel, J.H.A.; Janssen, F.J.J.G. Torrefaction for Entrained-Flow Gasification of Biomass; ECN: Petten, The Netherlands, 2005. [Google Scholar]
- Nikolopoulos, N.; Isemin, R.; Atsonios, K.; Kourkoumpas, D.; Kuzmin, S.; Mikhalev, A.; Nikolopoulos, A.; Agraniotis, M.; Grammelis, P.; Kakaras, E. Modeling of wheat straw torrefaction as a preliminary tool for process design. Waste Biomass Valoriz. 2013, 4, 409–420. [Google Scholar] [CrossRef]
- Arteaga-Pérez, L.E.; Segura, C.; Espinoza, D.; Radovic, L.R.; Jiménez, R. Torrefaction of Pinus radiata and Eucalyptus globulus: A combined experimental and modeling approach to process synthesis. Energy Sustain. Dev. 2015, 29, 13–23. [Google Scholar] [CrossRef]
- Bach, Q.-V.; Skreiberg, Ø.; Lee, C.-J. Process modeling and optimization for torrefaction of forest residues. Energy 2017, 138, 348–354. [Google Scholar] [CrossRef]
- Svanberg, M.; Olofsson, I.; Flodén, J.; Nordin, A. Analysing biomass torrefaction supply chain costs. Bioresour. Technol. 2013, 142, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Batidzirai, B.; van der Hilst, F.; Meerman, H.; Junginger, M.H. Optimization potential of biomass supply chains with torrefaction technology. Biofuels Bioprod. Biorefin. 2014, 8, 253–282. [Google Scholar] [CrossRef]
- Boardman, R.D.; Cafferty, K.G.; Nichol, C.; Searcy, E.M.; Westover, T.; Wood, R.; Bearden, M.D.; Cabe, J.E.; Drennan, C.; Jones, S.B.; et al. Logistics, Costs, and GHG Impacts of Utility Scale Cofiring with 20% Biomass; Idaho National Laboratory (INL): Idaho Falls, ID, USA; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2014.
- Office of Energy Efficiency & Renewable Energy. 2016 Billion-Ton Report: Advancing Domestic Resources for a Thriving Bioeconomy, Volume 1: Economic Availability of Feedstocks; Langholtz, M.H., Stokes, B.J., Eaton, L.M., Eds.; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2016; p. 448.
- Beck, R. Review of Biomass Fuels and Technologies; Yakima County Public Works Solid Waste Division: Yakima, WA, USA, 2003. [Google Scholar]
- Durkay, J. State Renewable Portfolio Standards and Goals. 2017. Available online: http://www.ncsl.org/research/energy/renewable-portfolio-standards.aspx (accessed on 20 December 2017).
- Bracmort, K. Biomass: Comparison of Definitions in Legislation, Congressional Research Service Report 7-5700, R40529; University of North Texas: Denton, TX, USA, 2015. [Google Scholar]
- Pronobis, M.; Wojnar, W. The impact of biomass co-combustion on the erosion of boiler convection surfaces. Energy Convers. Manag. 2013, 74, 462–470. [Google Scholar]
- Miedema, J.H.; Benders, R.M.J.; Moll, H.C.; Pierie, F. Renew, reduce or become more efficient? The climate contribution of biomass co-combustion in a coal-fired power plant. Appl. Energy 2017, 187, 873–885. [Google Scholar]
- IBM. Branch & Cut or Dynamic Search? IBM Knowledge Center 2017. Available online: https://www.ibm.com/support/knowledgecenter/pl/SSSA5P_12.7.1/ilog.odms.cplex.help/CPLEX/UsrMan/topics/discr_optim/mip/performance/13_br_cut_dyn_srch.html (accessed on 15 December 2017).
- Danna, E.; Rothberg, E.; le Pape, C. Exploring relaxation induced neighborhoods to improve MIP solutions. Math. Program. 2005, 102, 71–90. [Google Scholar] [CrossRef]
- IBM. CPLEX User’s Manual, Version 12 Release 7; IBM ILOG CPLEX Optimization; IBM Corp.: New York, NY, USA, 2016. [Google Scholar]
- Lima, R. IBM ILOG CPLEX-What is inside of the box? In EWO Seminar; Carnegie Mellon University: Pittsburgh, PA, USA, 2010. [Google Scholar]
- Ko, S.; Lautala, P. Advanced Woody Biomass Logistics for Cofiring in Existing Coal Power Plant: A Case Study of the Great Lakes States. Transp. Res. Record 2018, in press. [Google Scholar]
- Bureau of Transportation Statistics. Transportation Networks, National Transportation Atlas Database 2015; Bureau of Transportation Statistics: Washington, WA, USA, 2016.
- U.S. EIA. Form 906/920/923: Utility, Non-Utility, and Combined Heat and Power Plant Database; Monthly Time Series; U.S. Energy Information Administration: Washington, WA, USA, 2017.
- U.S. EIA. Form EIA 923 Power Plant Operations Report Instructions; U.S. Energy Information Administration: Washington, WA, USA, 2015.
- The United States Department of Agriculture (USDA). Timber Product Output (TPO) Reports; USDA Forest Service, Southern Research Station: Knoxville, TN, USA, 2012.
- Spelter, H.; McKeever, D.; Toth, D. Profile 2009: Softwood Sawmills in the United States and Canada; U.S. Department of Agriculture Forest Service, Forest Products Laboratory: Madison, WI, USA, 2009; p. 55.
- CN. Canadian National Railway: Prices, Tariffs & Transit Times. 2016. Available online: https://www.cn.ca/en/customer-centre/prices-tariffs-transit-times (accessed on 25 June 2016).
- NS. Norfolk Southern Railway: Public Price Publications. 2016. Available online: http://www.nscorp.com/mktgpublic/publicprices/ (accessed on 25 June 2016).
- U.S. EPA. Biomass Combined Heat and Power Catalog of Technologies; U.S. EPA: Washington, WA, USA, 2007.
- Zhang, L.F.; Johnson, D.M.; Wang, J.J. Integrating multimodal transport into forest-delivered biofuel supply chain design. Renew. Energy 2016, 93, 58–67. [Google Scholar] [CrossRef]

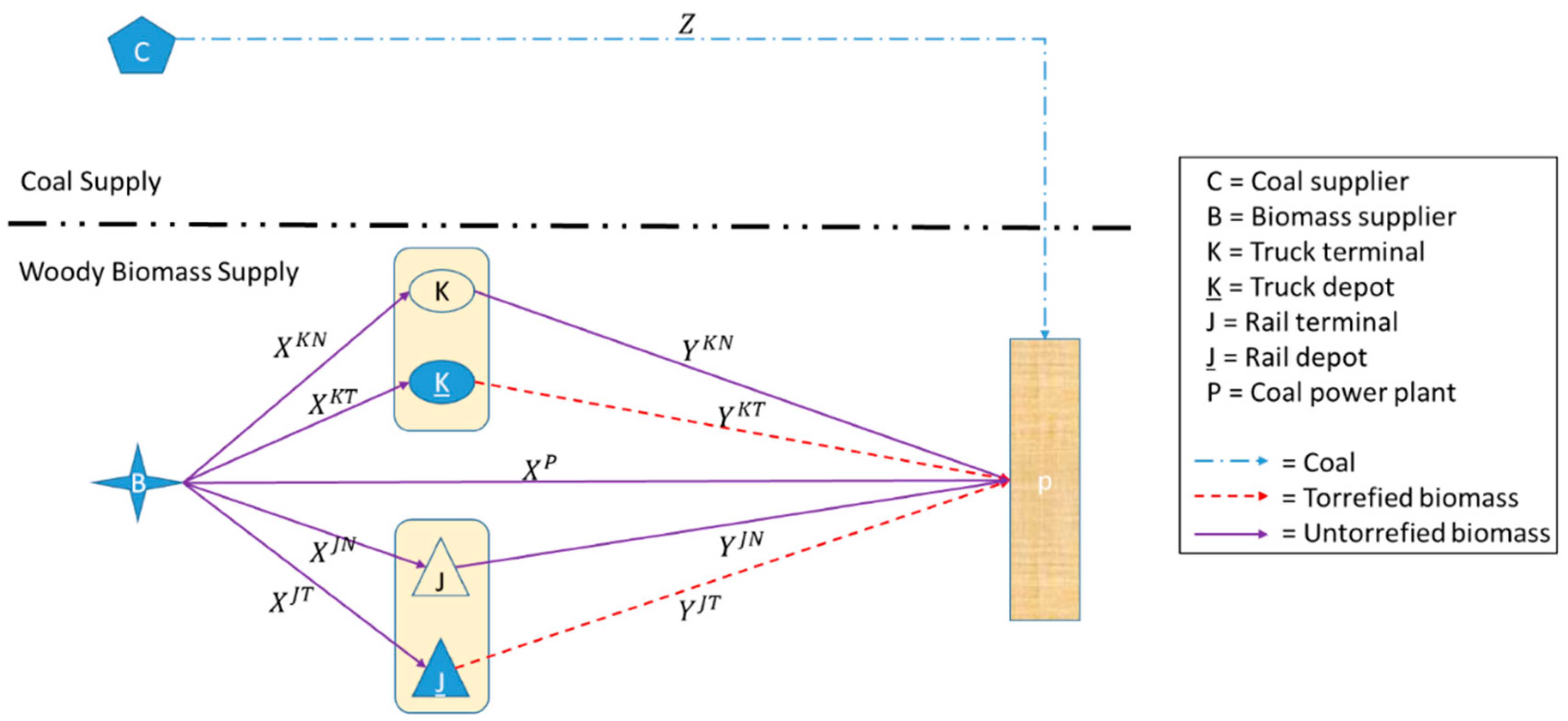
| Set |
| ▪ B = Set of biomass feedstock, |
| ▪ I = Set of biomass feedstock supplier, |
| ▪ J = Set of rail intermediate facility (terminal or depot), |
| ▪ K = Set of truck intermediate facility (terminal or depot), |
| ▪ T = Set of successive time periods, |
| ▪ L = Set of capacity level of intermediate facility (terminal or depot), |
| Parameter |
| ▪ = Fixed transport cost of biomass feedstock b by truck and rail, respectively ($/kg) |
| ▪ = Variable transport cost of biomass feedstock b by truck and rail, respectively ($/kg-km) |
| ▪ = Trans-loading cost of biomass feedstock b ($/kg) |
| ▪ = Purchasing cost of biomass feedstock b ($/kg) |
| ▪ = Capital cost of truck and rail terminal with capacity l, respectively ($/kg) |
| ▪ = Capital cost of truck and rail depot with capacity l, respectively ($/kg) |
| ▪ = Operations cost in terminal and depot for biomass feedstock b, respectively ($/kg) |
| ▪ = Capital cost at the plant for untorrefied and torrefied biomass b, respectively ($/kg) |
| ▪ = Operation cost at the plant for untorrefied and torrefied biomass b, respectively ($/kg) |
| ▪ = Storage cost of biomass feedstock b ($/kg) |
| ▪ = Delivered cost of coal at period t ($/kg) |
| ▪ = Distance between supplier i and truck intermediate facility j, and between supplier i and rail intermediate facility k, respectively (km) |
| ▪ = Distance between supplier i and plant (km) |
| ▪ = Distance between truck intermediate facility k and plant, and between rail intermediate facility j and plant, respectively (km) |
| ▪ = Capacity level of intermediate facility (terminal or depot) (kg) |
| ▪ = Heating value of untorrefied and torrefied biomass b, respectively (Gigajoules/kg) |
| ▪ = Heating value of coal (Gigajoules/kg) |
| ▪ = Maximum quantity of biomass b available from supplier i during period t (kg) |
| ▪ = Current demand quantity of coal shipped to plant during period t (kg) |
| ▪ = Energy conversion factor from Gigajoules to kWh |
| ▪ = Mass conversion factor of biomass feedstock b after torrefaction process (%) |
| ▪ = Production tax credit ($/kWh) |
| ▪ M = Big number |
| Decision Variable |
| ▪ = Flow of biomass b shipped from supplier i to truck terminal k or truck depot k at period t, respectively |
| ▪ = Flow of biomass b shipped from supplier i to rail terminal j or rail depot j at period t, respectively |
| ▪ = Flow of biomass b transported directly from supplier i to plant during period t |
| ▪ = Flow of untorrefied biomass b transported from truck terminal k to plant, and from rail terminal j to plant during period t, respectively |
| ▪ , = Flow of torrefied biomass b transported from truck depot k to plant, and from rail depot j to plant during period t, respectively |
| ▪ = 1 if truck terminal k with capacity level l is used during period t, 0 otherwise |
| ▪ = 1 if truck depot with capacity level l is built at truck terminal k during period t, 0 otherwise |
| ▪ = 1 if rail terminal j with capacity level l is used during period t, 0 otherwise |
| ▪ = 1 if rail depot with capacity level l is built at rail terminal j during period t, 0 otherwise |
| ▪ = Untorrefied biomass b stored at truck terminal k, and at rail terminal j during period t, respectively |
| ▪ , = Torrefied biomass b stored at truck terminal k, and at rail terminal j during period t, respectively |
| ▪ = Flow of coal shipped to plant during period t |
| ▪ = Random variable |
| ▪ = Binary variable |
| Number | Plant Name | State | Average Delivered Costs of Coal ($/kg) | Average Input Energy Required by Month (MMBTU) |
|---|---|---|---|---|
| 1 | Presque Isle | MI | 0.249 | 2,125,153 |
| 2 | Escanaba Mill | MI | 0.249 | 25,315 |
| 3 | J H Campbell | MI | 0.266 | 5,533,214 |
| 4 | J C Weadock | MI | 0.267 | 253,890 |
| 5 | J R Whiting | MI | 0.244 | 211,879 |
| 6 | Monroe (MI) | MI | 0.254 | 10,732,869 |
| 7 | River Rouge | MI | 0.246 | 434,755 |
| 8 | St Clair | MI | 0.270 | 418,851 |
| 9 | Trenton Channel | MI | 0.259 | 1,567,210 |
| 10 | Eckert Station | MI | 0.267 | 595,575 |
| 11 | BRSC Shared Storage | MI | 0.223 | 8,571,533 |
| 12 | TES Filer City Station | MI | 0.239 | 466,748 |
| 13 | Clay Boswell | MN | 0.220 | 5,907,394 |
| 14 | Allen S King | MN | 0.236 | 2,103,891 |
| 15 | South Oak Creek | WI | 0.216 | 3,228,271 |
| 16 | Edgewater | WI | 0.249 | 2,752,947 |
| 17 | Pulliam | WI | 0.269 | 177,931 |
| 18 | Weston | WI | 0.257 | 2,941,119 |
| 19 | Genoa | WI | 0.293 | 1,242,263 |
| 20 | John P Madgett | WI | 0.251 | 1,714,462 |
| 21 | Sherburne County | MN | 0.228 | 10,074,508 |
| 22 | Pleasant Prairie | WI | 0.195 | 5,668,994 |
| 23 | Columbia (WI) | WI | 0.271 | 3,923,054 |
| 24 | Biron Mill | WI | 0.257 | 284,699 |
| 25 | Green Bay West Mill | WI | 0.269 | 151,019 |
| 26 | Elm Road Generating Station | WI | 0.265 | 5,920,150 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, S.; Lautala, P. Optimal Level of Woody Biomass Co-Firing with Coal Power Plant Considering Advanced Feedstock Logistics System. Agriculture 2018, 8, 74. https://doi.org/10.3390/agriculture8060074
Ko S, Lautala P. Optimal Level of Woody Biomass Co-Firing with Coal Power Plant Considering Advanced Feedstock Logistics System. Agriculture. 2018; 8(6):74. https://doi.org/10.3390/agriculture8060074
Chicago/Turabian StyleKo, Sangpil, and Pasi Lautala. 2018. "Optimal Level of Woody Biomass Co-Firing with Coal Power Plant Considering Advanced Feedstock Logistics System" Agriculture 8, no. 6: 74. https://doi.org/10.3390/agriculture8060074
APA StyleKo, S., & Lautala, P. (2018). Optimal Level of Woody Biomass Co-Firing with Coal Power Plant Considering Advanced Feedstock Logistics System. Agriculture, 8(6), 74. https://doi.org/10.3390/agriculture8060074





