2.3. Methodology
The methodology of the study is summarized in six steps, as follows:
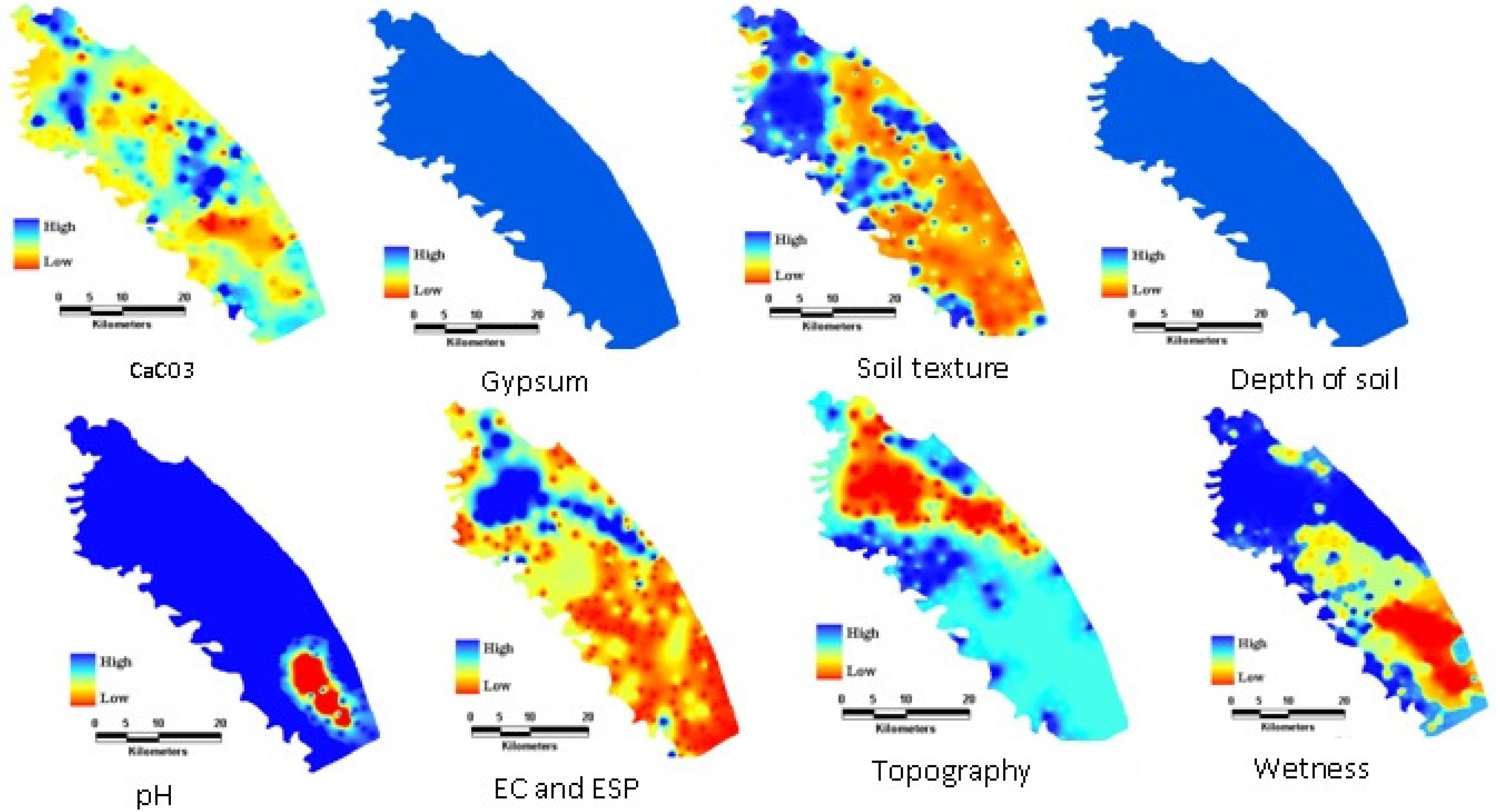
Step 1: Geospatial maps of each parameter presented in
Table 1 were constructed. For this we used the geostatistical analysis and the Ordinary Kriging model was applied to the 256 sampled points.
Step 2: Based on a previous study [
28,
29,
30,
31], the following functions (Equations (1) and (2)) were determined as the best fuzzy membership functions for each parameter, and these were used to prepare fuzzy maps for all parameters. Function 1 was used for soil depth and wetness, and function 2 was used for soil texture, EC, ESP, gypsum (%), CaCO
3 (%), topography, and pH values.
Supposing that
X = {
x is a finite set of points, a fuzzy subset,
A subset
A of
X, is defined by a function,
μA(
X), in the ordered pairs:
A = {
x,
μA(
X)} for each
x,
x belongs to
X. where
μA(
X) is membership function that defines the grade of membership of
x in A fuzzy set. The
μA(
X) takes values between 0 and 1, inclusive. The value of 1 means that
x belongs completely to
A, and 0 means that
x absolutely does not belong to the subset
A.
A value between 0 and 1 indicates that, to some degree,
x belongs to the subset
A. The values
a,
b are the lower and upper limit values according to Sys’s table [
34].
Step 3: The AHP method was employed in order to determine the weights of assessment parameters for land suitability classification. This method is based on a pair wise comparison matrix [
43,
44]. To derive the pair wise comparison matrix, the relative importance of input parameters (
Table 1) was defined by using the published reports by the Khuzestan Soil and Water Research Institute [
42]. This report shows that soil salinity and alkalinity, soil wetness, CaCO
3, gypsum, pH, soil texture, soil depth and topography are the most important parameters (restriction) for the cultivation of barley in the study area, respectively. The relative importance of these parameters were assigned based on Saaty’s scale (
Table 2) and the pair-wise comparison matrix and the final weights for each parameter were derive (
Table 3).
Step 4: Finally, to compute the land suitability map of the study area, the convex combination of the raster values containing the different fuzzy parameters were calculated using the linear additive combination models [
12] as in Equation (3):
where the value of
SI is the land suitability index,
k is the number of parameters (
Table 1),
Wj is the weight of parameter
j, which is computed by using AHP (
Table 3), and
μj (X) is the membership grade for factor
j. The value of
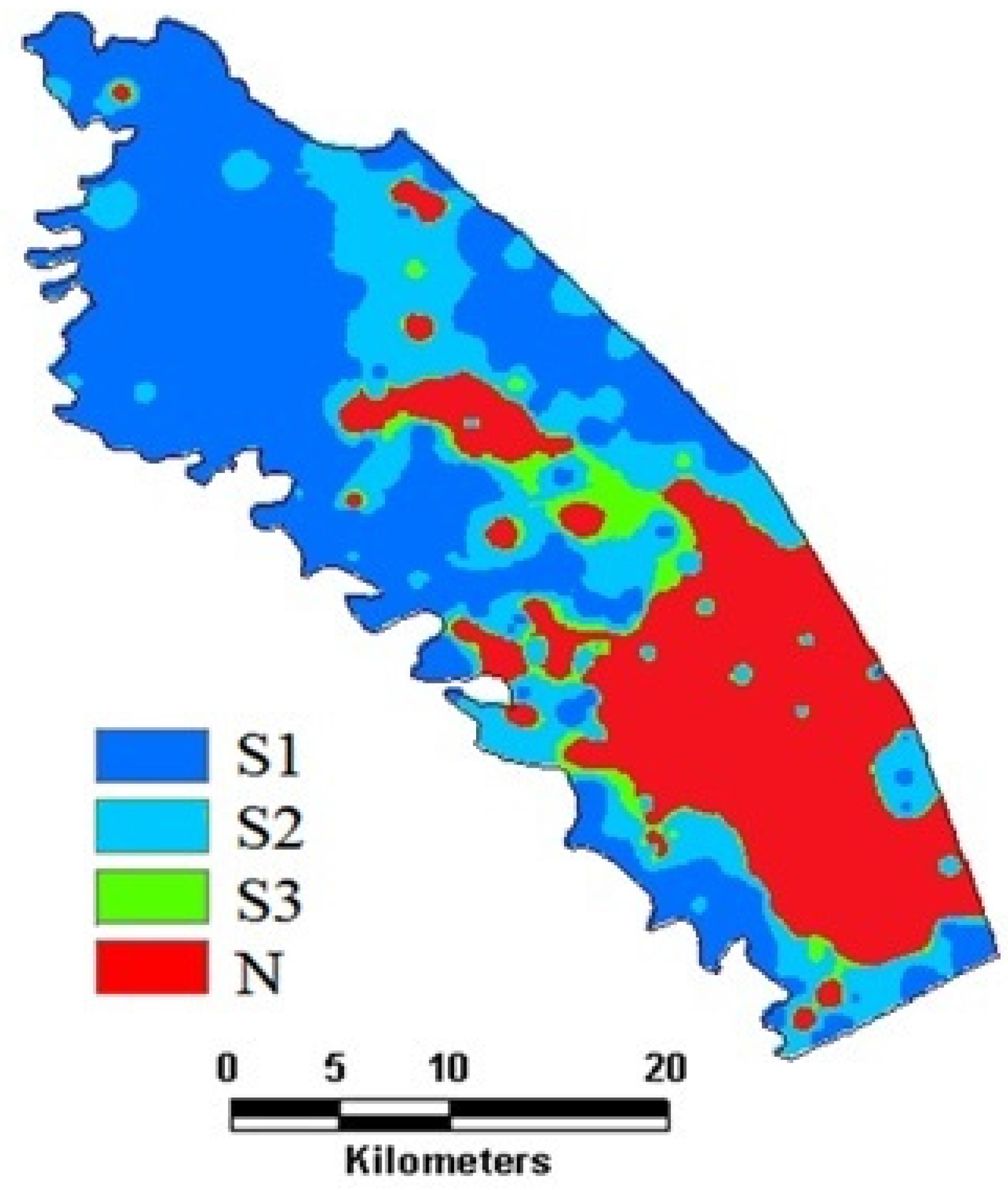
SI is between 0 and 1, where a value of 0 represents totally unsuitability and 1 indicates 100% suitability. The suitability classification was assigned as presented in
Table 4, based on the FAO framework [
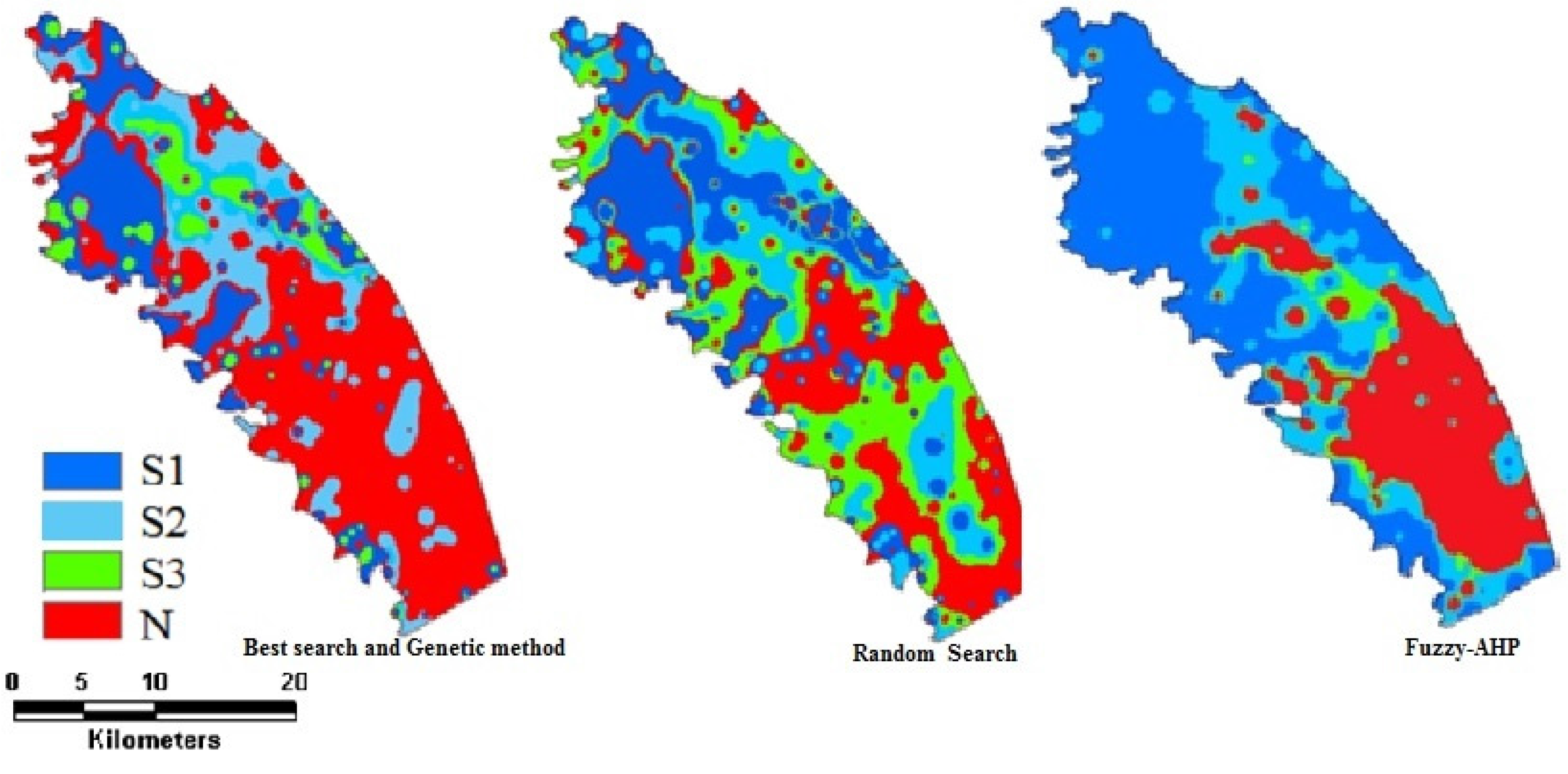
1], and modified slightly in this study. Thus S1 represents that the land unit is highly suitable to barely crop production with no limitations; S2 represents that the land unit is moderately suitable with some limitations; S3 represents that the land unit is marginally suitable with severe limitations; and N represents that the land unit is unsuitable for barely growth.
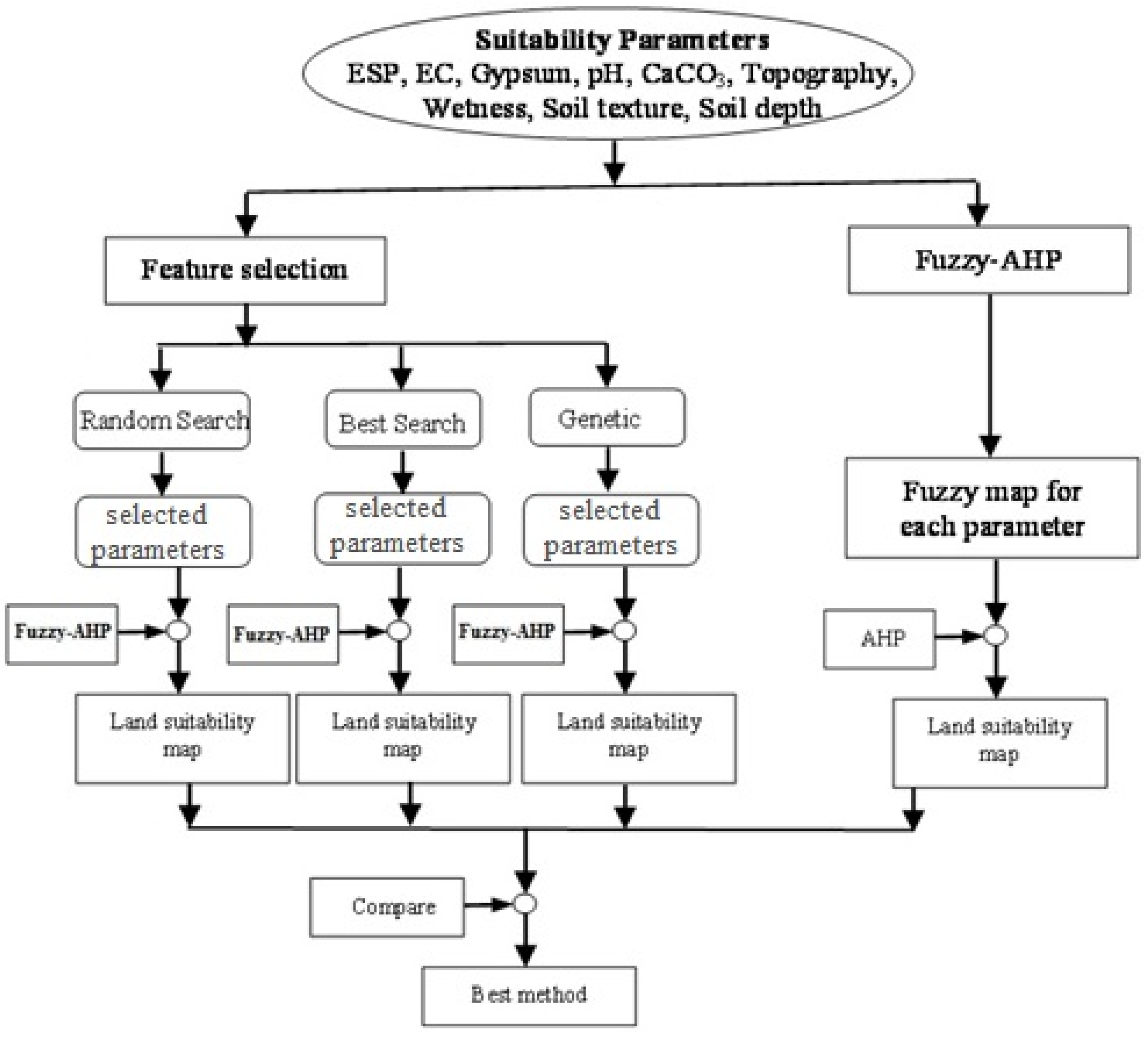
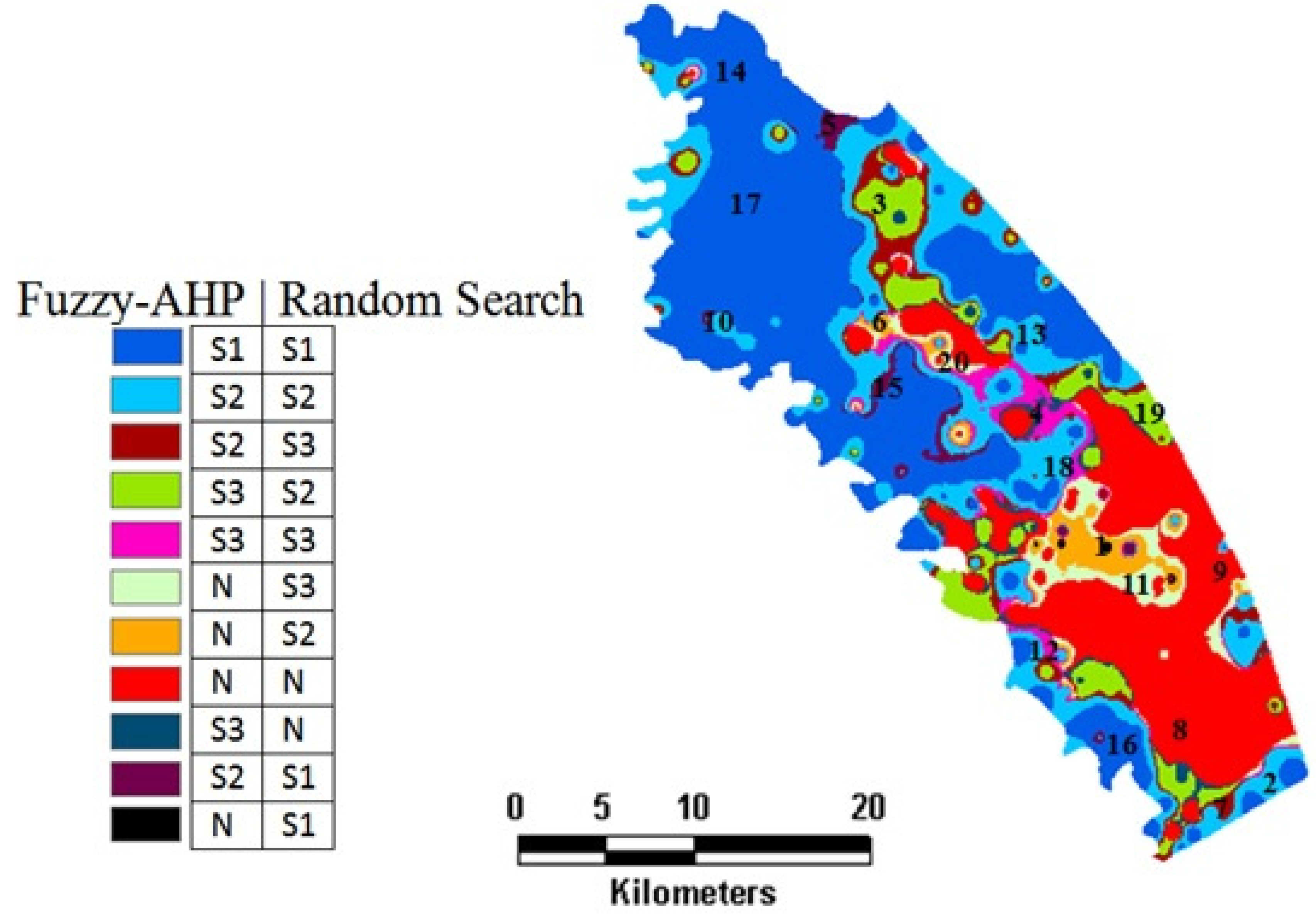
Step 5: The previous approach needs a large number of land and soil parameters for land evaluation, therefore in this study three different feature selection algorithms which are most common and used methods—random search, best search and genetic methods—were used to determine the most effective parameters for land suitability classification. For each feature selection method, the most effective parameters were selected, and then weights for each parameter were re-calculated according to the AHP. Land suitability classes were calculated for all methods (datasets) using a fuzzy-AHP approach. The details of feature selection methodology are explained in the next section.
Step 6: The Kappa coefficient developed by Cohen [
46], was used to assess the agreement between the standard fuzzy-AHP map and the maps obtained from the different feature selection methods. The Kappa coefficient is a measurement of the degree of agreement between two observations (maps). A Kappa value of 0 indicates that there is a poor agreement between two maps and a value of 1 indicates an almost perfect agreement. The methodology of this study is summarized in
Figure 2.
Feature Selection Method
The main idea of feature selection is to choose a subset of input variables by eliminating features with little or no predictive information. Feature selection can significantly improve the comprehensibility of the resulting classifier models, and it often builds a model that better generalizes to unseen points. Feature selection has been developed for decades in statistical pattern recognition [
47], machine learning [
48], data mining [
49] and statistics [
50].
Ideally, feature selection methods search through the subsets of features, and try to find the best one among the competing 2N (size) candidate subsets according to some evaluation function. This procedure is exhaustive as it tries to find only the best one. There are four basic steps in a typical feature selection method, as follows:
- (a)
The generation procedure: this is basically a search procedure, which generates subsets of features for evaluation.
- (b)
The evaluation function: An evaluation function measures the goodness of a subset produced by some generation procedure, and this value is compared with the previous best. If it is found to be better, then it replaces the previous best subset.
- (c)
The stopping condition: Without a suitable stopping criterion, the feature selection process may run exhaustively or forever through the space of subsets. Generation procedures and evaluation functions can influence the choice of a stopping criterion. A Stopping criteria based on a generation procedure include: (i) whether a predefined number of features are selected; and (ii) whether a predefined number of iterations is reached. Stopping criteria based on an evaluation function can be: (i) whether addition (or deletion) of any feature does not produce a better subset; and (ii) whether an optimal subset according to some evaluation function is obtained. The loop continues until the stopping criterion is satisfied.
- (d)
The validation procedure: the validation procedure is not a part of the feature selection process itself, but a feature selection method (in practice) must be validated. It tries to test the validity of the selected subset by carrying out different tests, and comparing the results with previously established results, or with the results of competing feature selection methods, using artificial datasets, real-world datasets, or both [
51].
In this research, the different feature selection methods applied were best search, genetic search and random search. A short description of each method is given in the following boxes:
1. Begin with the OPEN list containing the start state, the CLOSED list empty, and BEST start state.
2. Let s = arg max e(x) (get the state from OPEN with the highest evaluation).
3. Remove s from OPEN and add to CLOSED.
4. If e(s) ≥ e(BEST), then BEST←s.
5. For each child t of s that is not in the OPEN or CLOSED list, evaluate and add to OPEN.
6. If BEST changed in the last set of expansions, go to 2.
7. Return BEST.
1. Begin by randomly generating an initial population P.
2. Calculate e(x) for each member x ϵ P.
3. Define a probability distribution p over the members of P where p(x) α e(x).
4. Select two population members x and y with respect to p.
5. Apply crossover to x and y to produce new population members x′ and y′.
6. Apply mutation to x′ and y′.
7. Insert x′ and y′ into P′ (the next generation).
8. If |P′| < |P|, go to 4.
9. Let P←P′.
10. If there are more generations to process, go to 2.
11. Return x ϵ P for which e(x) is highest.
Input: F = {f1, f2, …, fn}
Output: A subset of F
Step 1: Initial r0 = r = Q, s = ∅, Gbest = F, k = 0, C, K are specified
Step 2: Partition r0,
Step 3: Find the most promising index:
σ = {η|η∈children(r)|}, m =|σ|, σm+1 = s, Index = 0;
For i = 1: m + 1
Randomly sample N subsets in σi, find the best
End;
Index = arg ,
If index then
If || = 1 then go to Step 5
Step 4: If 1 ≤ index ≤ m then , s = r0\r else r = sup(r); k = k + 1;
If k > K then go to Step 5 else go to Step 3
Step 5: Output the Gbest