Optimizing the Genomic Evaluation Model in Crossbred Cattle for Smallholder Production Systems in India
Abstract
1. Introduction
2. Materials and Methods
2.1. Source of Data
2.2. Type of Data
2.2.1. Phenotypic Data
2.2.2. Genotypic Data and Quality Control
2.3. Statistical Analysis
2.4. Estimation of (Co)variance Components
2.5. Breeding Value Prediction Models
2.5.1. Pedigree-Based Prediction of Breeding Values
2.5.2. Genomic BLUP (GBLUP)
2.5.3. Single-Step GBLUP (ssGBLUP)
2.5.4. Genomic Evaluation Using the Bayesian Alphabets
2.5.5. Single Step Bayesian Regression (SSBR)
2.6. Estimated Accuracy
2.7. LR (Linear Regression) Method
- Bias (∆p): The estimator of the bias is obtained from the difference between the mean of GEBVp and the mean of GEBVw, ∆p = up − uw. In the absence of bias, the expected value of this estimator is 0.
- Dispersion (bp): The estimator of dispersion of GEBV is the slope of the regression of GEBVw on GEBVp, . If over- or under-dispersion does not exist, the expected value of the estimator is 1; values of bp < 1 indicate over-dispersion; and values of bp > 1 indicate under-dispersion.
- Ratio of accuracies (ρw,p): This estimator estimates the inverse of the relative gain in accuracy from GEBVp to GEBVw. It is the correlation between GEBVp and GEBVw, , and the expected value is accp/accw. A high value of this estimator means a small increase in accuracy, whereas a low value means a large increase in accuracy when we add phenotypic information to genetic evaluations. This can be seen also as the relative increase in accuracy brought by phenotypes is − 1.
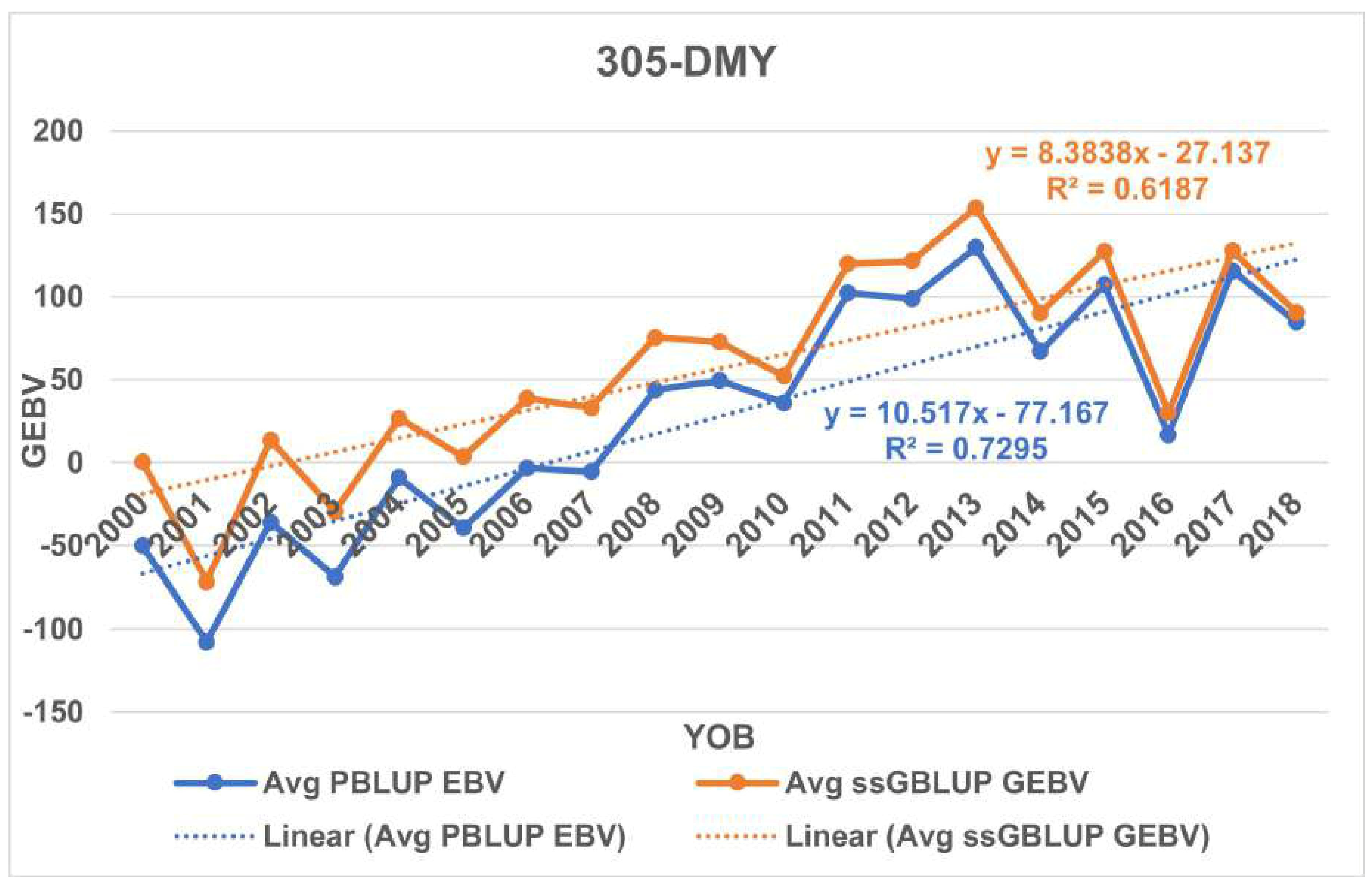
2.8. Genetic Trend for 305-DMY in Crossbred Cattle
3. Results
3.1. Descriptive Statistics
3.2. Generation of Genotypic Data
3.3. Least Squares Analysis for 305-Day Milk Yield (305-DMY) in Crossbred Cattle
3.4. Genetic Parameter Estimation
3.5. Prediction of Breeding Value
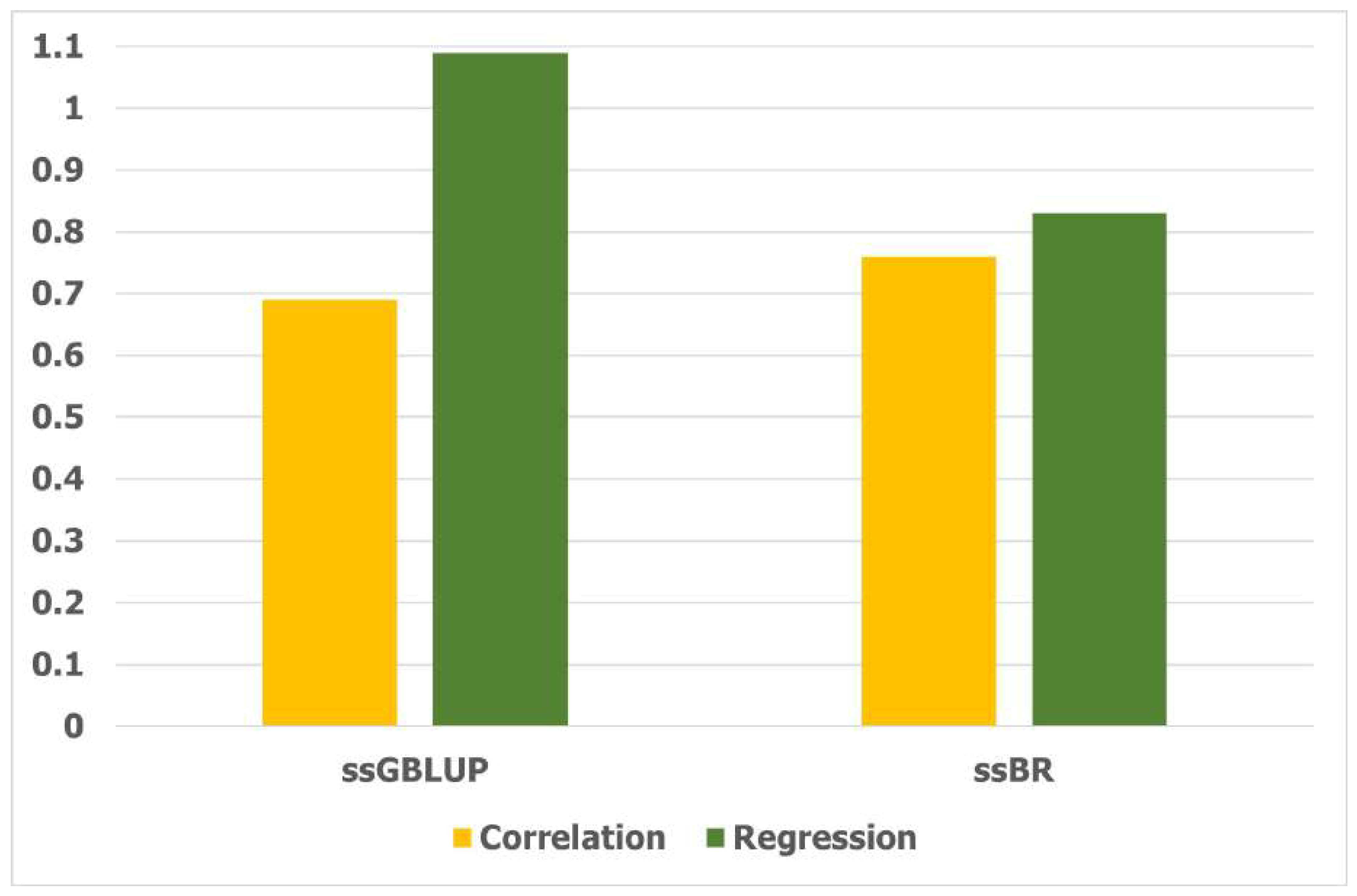
3.6. LR Method for Accuracy of Prediction for GEBV
3.7. Genetic Trend
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basic Animal Husbandry Statistics of India 2023–2024; Department of Animal Husbandry and Dairying, Ministry of Fisheries, Animal Husbandry and Dairying, Government of India: New Delhi, India, 2024.
- 20th Livestock Census Report of India; Department of Animal Husbandry, Dairying and Fisheries, Ministry of Fisheries, Animal Husbandry & Dairying, Government of India: New Delhi, India, 2019.
- Breed Wise Report of Livestock and Poultry 2022; Department of Animal Husbandry and Dairying, Ministry of Fisheries, Animal Husbandry and Dairying, Government of India: New Delhi, India, 2022.
- Henderson, C.R. Best linear unbiased estimation and prediction under a selection model. Biometrics 1975, 31, 423–447. [Google Scholar] [CrossRef] [PubMed]
- Sorensen, D.A.; Kennedy, B.W. Estimation of response to selection using least-squares and mixed model methodology. J. Anim. Sci. 1984, 58, 1097–1106. [Google Scholar] [CrossRef]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef]
- Fernando, R.L.; Dekkers, J.C.; Garrick, D.J. A class of Bayesian methods to combine large numbers of genotyped and non-genotyped animals for whole-genome analyses. Genet. Sel. Evol. 2014, 46, 50. [Google Scholar] [CrossRef]
- Ojango, J.M.; Mrode, R.; Rege JE, O.; Mujibi, D.; Strucken, E.M.; Gibson, J.; Mwai, O. Genetic evaluation of test-day milk yields from smallholder dairy production systems in Kenya using genomic relationships. J. Dairy Sci. 2019, 102, 5266–5278. [Google Scholar] [CrossRef]
- Powell, O.; Mrode, R.; Gaynor, R.C.; Johnsson, M.; Gorjanc, G.; Hickey, J.M. Genomic evaluations using data recorded on smallholder dairy farms in low-to middle-income countries. JDS Commun. 2021, 2, 366–370. [Google Scholar] [CrossRef]
- Al Kalaldeh, M.; Swaminathan, M.; Gaundare, Y.; Joshi, S.; Aliloo, H.; Strucken, E.M.; Ducrocq, V.; Gibson, J.P. Genomic evaluation of milk yield in a smallholder crossbred dairy production system in India. Genet. Sel. Evol. 2021, 53, 73. [Google Scholar] [CrossRef]
- Gowane, G.R.; Alex, R.; Mukherjee, A.; Vohra, V. Impact and utility of shallow pedigree using single-step genomic BLUP for prediction of unbiased genomic breeding values. Trop. Anim. Health Prod. 2022, 54, 339. [Google Scholar] [CrossRef]
- Gowane, G.R.; Alex, R.; Worku, D.; Chhotaray SMukherjee, A.; Vohra, V. Optimizing multi-breed joint genomic prediction issues in numerically small breeds for sex-limited trait in a loosely structured dairy cattle breeding system. Trop. Anim. Health Prod. 2025, 57, 149. [Google Scholar] [CrossRef]
- VanRaden, P.M.; Tassell, C.P.; Wiggans, G.R.; Sonstegard, T.S.; Schnabel, R.D.; Taylor, J.F. Invited Review: Reliability of genomic predictions for North American dairy bulls. J. Dairy Sci. 2009, 92, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Gowane, G.R.; Lee, S.H.; Clark, S.; Moghaddar, N.; Al-Mamun, H.A.; van der Werf, J.H. Effect of selection and selective genotyping for creation of reference on bias and accuracy of genomic prediction. J. Anim. Breed. Genet. 2019, 136, 390–407. [Google Scholar] [CrossRef] [PubMed]
- Nayee, N.; Su, G.; Gajjar, S.G.; Sahana, G.; Saha, S.; Trivedi, K.R.; Sudhakar, A.; Guldbrandtsen, B.; Lund, M.S. Genomic prediction by single-step genomic BLUP using cow reference population in Holstein crossbred cattle in India. In Proceedings of the 11th World Congress on Genetics Applied to Livestock Production, Auckland, New Zealand, 11–16 February 2018. [Google Scholar]
- Patry, C.; Ducrocq, V. Accounting for genomic pre-selection in national BLUP evaluations in dairy cattle. Genet. Sel. Evol. 2011, 43, 30. [Google Scholar] [CrossRef] [PubMed]
- Vitezica, Z.G.; Aguilar, I.; Misztal, I.; Legarra, A. Bias in genomic predictions for populations under selection. Genet. Res. 2011, 93, 357–366. [Google Scholar] [CrossRef]
- VanRaden, P.M.; Wright, J.R. Measuring genomic pre-selection in theory and in practice. Interbull Bull. 2013, 47, 147–150. [Google Scholar]
- Legarra, A.; Christensen, O.F.; Aguilar, I.; Misztal, I. Single Step, a general approach for genomic selection. Livest. Sci. 2014, 166, 54–65. [Google Scholar] [CrossRef]
- Gowane, G.R.; Kumar, A.; Nimbkar, C. Challenges and opportunities to livestock breeding programmes in India. J. Anim. Breed. Genet. 2019, 136, 329–338. [Google Scholar] [CrossRef]
- Ducrocq, V.; Laloe, D.; Swaminathan, M.; Rognon, X.; Tixier-Boichard, M.; Zerjal, T. Genomics for ruminants in developing countries: From principles to practice. Front. Genet. 2018, 9, 251. [Google Scholar] [CrossRef]
- Rao, C.K.; Bachhman, F.; Sharma, V.; Venkataramaiah, P.; Panda, J.; Rathinam, R. Smallholder Dairy Value Chain Development in India and Selected States (Assam and Bihar): Situation Analysis and Trends; ILRI Project Report; International Livestock Research Institute: Nairobi, Kenya, 2014. [Google Scholar]
- Trivedi, K.R.; Nayee, N.G.; Saha, S.; Gajjar, S.G.; Kishore, G.; Namjoshi, M.; Sudhakar, A.; Gupta, R.O. Genetic improvement of cattle and buffaloes in smallholder production systems in India. Indian J. Anim. Sci. 2020, 90, 1270–1278. [Google Scholar] [CrossRef]
- Costilla, R.; Zeng, J.; Al Kalaldeh, M.; Swaminathan, M.; Gibson, J.P.; Ducrocq, V.; Hayes, B.J. Developing flexible models for genetic evaluations in smallholder crossbred dairy farms. J. Dairy Sci. 2023, 106, 9125–9135. [Google Scholar] [CrossRef]
- Chang, C.C.; Chow, C.C.; Tellier, L.C.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-generation PLINK: Rising to the challenge of larger and richer datasets. Gigascience 2015, 4, s13742-015. [Google Scholar] [CrossRef] [PubMed]
- Lenth, R.V. Least-squares means: The R package lsmeans. J. Stat. Softw. 2016, 69, 1–33. [Google Scholar] [CrossRef]
- Misztal, I.; Tsuruta, D.; Lourenco, D.; Masuda, Y.; Aguilar, I.; Legarra, A.; Vitezica, Z. Manual for BLUPF90 Family of Programs; Animal and Dairy Science; University of Georgia: Athens, GA, USA, 2014. [Google Scholar]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- Christensen, O.F.; Lund, M.S. Genomic prediction when some animals are not genotyped. Genet. Sel. Evol. 2010, 42, 1–8. [Google Scholar] [CrossRef]
- Gianola, D.; De Los Campos, G.; Hill, W.G.; Manfredi, E.; Fernando, R. Additive genetic variability and the Bayesian alphabet. Genetics 2009, 183, 347–363. [Google Scholar] [CrossRef]
- Rosa, G.J.M.; Padovani, C.R.; Gianola, D. Robust linear mixed models with normal/independent distributions and Bayesian MCMC implementation. J. Math. Methods Biosci. 2003, 45, 573–590. [Google Scholar] [CrossRef]
- Yin, L.L.; Zhang, H.H.; Li, X.Y.; Zhao, S.H.; Liu, X.L. Hibayes: An R Package to Fit Individual-Level, Summary-Level and Single-Step Bayesian Regression Models for Genomic Prediction and Genome-Wide Association Studies. bioRxiv 2022. [Google Scholar] [CrossRef]
- Mrode, R. Linear Models for the Prediction of Animal Breeding Values, 3rd ed.; CABI: Oxfordshire, UK, 2014. [Google Scholar]
- Legarra, A.; Reverter, A. Semi-parametric estimates of population accuracy and bias of predictions of breeding values and future phenotypes using the LR method. Genet. Sel. Evol. 2018, 50, 53. [Google Scholar] [CrossRef]
- Bulmer, M. The effect of selection on genetic variability. Am. Nat. 1971, 105, 201–211. [Google Scholar] [CrossRef]
- Legarra, A. Comparing estimates of genetic variance across different relationship models. Theor. Popul. Biol. 2016, 107, 26–30. [Google Scholar] [CrossRef]
- Henderson, C.R. Applications of Linear Models in Animal Breeding; University of Guelph: Guelph, Italy, 1984; Volume 462. [Google Scholar]
- Mrode, R.; Ojango, J.; Ekine-Dzivenu, C.; Aliloo, H.; Gibson, J.; Okeyo, M.A. Genomic prediction of crossbred dairy cattle in Tanzania: A route to productivity gains in smallholder dairy systems. J. Dairy Sci. 2021, 104, 11779–11789. [Google Scholar] [CrossRef] [PubMed]
- López-Correa, R.D.; Legarra, A.; Aguilar, I. Modelling missing pedigree with metafounders and validating single-step genomic predictions in a small dairy cattle population with a great influence of foreign genetics. J. Dairy Sci. 2024, 107, 4685–4692. [Google Scholar] [CrossRef] [PubMed]
- Falconer, D.S. Introduction to Quantitative Genetics; Pearson Education: Zamin, India, 1996. [Google Scholar]
- Haile-Mariam, M.; Nieuwhof, G.J.; Beard, K.T.; Konstatinov, K.V.; Hayes, B.J. Comparison of heritabilities of dairy traits in Australian Holstein-Friesian cattle from genomic and pedigree data and implications for genomic evaluations. J. Anim. Breed. Genet. 2013, 130, 20–31. [Google Scholar] [CrossRef]
- Loberg, A.; Dürr, J.W.; Fikse, W.F.; Jorjani, H.; Crooks, L. Estimates of genetic variance and variance of predicted genetic merits using pedigree or genomic relationship matrices in six Brown Swiss cattle populations for different traits. J. Anim. Breed. Genet. 2015, 132, 376–385. [Google Scholar] [CrossRef]
- Misztal, I.; Aguilar, I.; Lourenco, D.; Ma, L.; Steibel, J.P.; Toro, M. Emerging issues in genomic selection. J. Anim. Sci. 2021, 99, skab092. [Google Scholar] [CrossRef]
- Jensen, J.; Su, G.; Madsen, P. Partitioning additive genetic variance into genomic and remaining polygenic components for complex traits in dairy cattle. BMC Genet. 2012, 13, 44. [Google Scholar] [CrossRef]
- Veerkamp, R.F.; Mulder, H.A.; Thompson, R.; Calus, M.P.L. Genomic and pedigree-based genetic parameters for scarcely recorded traits when some animals are genotyped. J. Dairy Sci. 2011, 94, 4189–4197. [Google Scholar] [CrossRef]
- Peters, S.O.; Kızılkaya, K.; Ibeagha-Awemu, E.M.; Sinecen, M.; Zhao, X. Comparative accuracies of genetic values predicted for economically important milk traits, genome-wide association, and linkage disequilibrium patterns of Canadian Holstein cows. J. Dairy Sci. 2021, 104, 1900–1916. [Google Scholar] [CrossRef]
- Buitenhuis, A.J.; Sundekilde, U.K.; Poulsen, N.A.; Bertram, H.C.; Larsen, L.B.; Sørensen, P. Estimation of genetic parameters and detection of quantitative trait loci for metabolites in Danish Holstein milk. J. Dairy Sci. 2013, 96, 3285–3295. [Google Scholar] [CrossRef]
- Poulsen, N.A.; Buitenhuis, A.J.; Larsen, L.B. Phenotypic and genetic associations of milk traits with milk coagulation properties. J. Dairy Sci. 2015, 98, 2079–2087. [Google Scholar] [CrossRef]
- Karimi, Z.; Sargolzaei, M.; Robinson, J.A.B.; Schenkel, F. Assessing haplotype-based models for genomic evaluation in Holstein cattle. Can. J. Anim. Sci. 2018, 98, 750–759. [Google Scholar] [CrossRef]
- Daetwyler, H.D.; Kemper, K.E.; Van Der Werf, J.H.J.; Hayes, B.J. Components of the accuracy of genomic prediction in a multi-breed sheep population. J. Anim. Sci. 2012, 90, 3375–3384. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.A.; Hickey, J.M.; Daetwyler, H.D.; van der Werf, J.H. The importance of information on relatives for the prediction of genomic breeding values and the implications for the makeup of reference data sets in livestock breeding schemes. Genet. Sel. Evol. 2012, 44, 4. [Google Scholar] [CrossRef] [PubMed]
- Hayes, B.J.; Bowman, P.J.; Chamberlain, A.J.; Goddard, M.E. Invited review: Genomic selection in dairy cattle: Progress and challenges. J. Dairy Sci. 2009, 92, 433–443. [Google Scholar] [CrossRef]
- Brown, A.; Ojango, J.; Gibson, J.; Coffey, M.; Okeyo, M.; Mrode, R. Genomic selection in a crossbred cattle population using data from the dairy genetics East Africa project. J. Dairy Sci. 2016, 99, 7308–7312. [Google Scholar] [CrossRef]
- Nayee, N. GS appeared promising in bull selection for HFCB for 1st lactation Milk Yield. In Proceedings of the World Congress on Genetics Applied to Livestock Production, Auckland, New Zealand, 11–16 February 2018; Volume 825. [Google Scholar]
- Thompson, R. Statistical validation of genetic models. Livest. Prod. Sci. 2001, 72, 129–134. [Google Scholar] [CrossRef]
- Reverter, A.; Golden, B.L.; Bourdon, R.M.; Brinks, J.S. Detection of bias in genetic predictions. J. Anim. Sci. 1994, 72, 34–37. [Google Scholar] [CrossRef]
- Boichard, D.; Bonaiti, B.; Barbat, A.; Mattalia, S. Three methods to validate the estimation of genetic trend for dairy cattle. J. Dairy Sci. 1995, 78, 431–437. [Google Scholar] [CrossRef]
- Spelman, R.J.; Arias, J.; Keehan, M.D.; Obolonkin, V.; Winkelman, A.M.; Johnson, D.L.; Harris, B.L. Application of genomic selection in the New Zealand dairy cattle industry. In Proceedings of the 9th World Congress on Genetics Applied to Livestock Production, Leipzig, Germany, 1–6 August 2010; pp. 1–6. [Google Scholar]
- Sargolzaei, M.; Chesnais, J.; Schenkel, F. Assessing the bias in top GPA bulls. Can. Dairy Netw. Open Ind. Sess. 2012, 30, 1–9. [Google Scholar]
- Reverter, A.; Golden, B.L.; Bourdon, R.M.; Brinks, J.S. Method R variance components procedure: Application on the simple breeding value model. J. Anim. Sci. 1994, 72, 2247–2253. [Google Scholar] [CrossRef]
- Misztal, I.; Lourenco, D. Potential negative effects of genomic selection. J. Anim. Sci. 2024, 102, skae155. [Google Scholar] [CrossRef]
- Misztal, I.; Gowane, G. Estimation of heritabilities and genetic correlations by time slices using predictivity in large genomic models. Genetics 2025, iyaf066. [Google Scholar] [CrossRef]

| Particulars | 305-Day Milk Yield (305-DMY) |
|---|---|
| Number of records | 17,650 |
| Total number of sires | 764 |
| Total number of dams | 2998 |
| Maximum paternal family size | 127 |
| Maximum maternal family size | 6 |
| Total number of individuals | 21,407 |
| Mean ± SE | 3130.49 ± 7.05 kg |
| Phenotypic standard deviation | 936.88 kg |
| Coefficient of variation | 29.93% |
| Factors | 305-DMY | |
|---|---|---|
| Classification | LS Mean (µ) 2875 ± 123.54 | |
| Age at first calving *** (AFC) | ≤816 | 3149.16 a |
| 817–933 | 3092.25 a | |
| 934–1050 | 3093.33 a | |
| 1051–1167 | 3106.85 a | |
| 1168–1284 | 3154.25 a | |
| 1285–1401 | 3106.36 a | |
| ≥1402 | 3330.48 b | |
| Period of calving *** (POC) | 2004–2007 | 2729.48 a |
| 2008–2011 | 2868.40 b | |
| 2012–2015 | 3144.40 c | |
| 2016–2019 | 3334.86 d | |
| 2020–2022 | 3459.50 e | |
| Season of calving *** (SOC) | Jan–Feb (Winter season) | 3171.07 b |
| March–May (Hot season) | 3060.30 a | |
| June–Sept (S–W monsoon) | 3141.00 b | |
| Oct–Dec (N–E monsoon) | 3157.04 b | |
| Period of birth *** (POB) | ≤2006 | 2808.77 b |
| 2007–2010 | 3006.96 c | |
| 2011–2014 | 3294.56 d | |
| 2015–2018 | 3380.44 e | |
| 2019–2021 | 2671.94 a | |
| Geography *** | Highland | 3748.75 c |
| Midland | 3050.94 b | |
| Lowland | 2957.44 a | |
| Units *** | Kanjirappally | 2987.70 cde |
| Kannur | 2905.97 cd | |
| Kattappana | 4005.57 g | |
| Kottayam | 3090.33 de | |
| Kozikhode | 2599.78 b | |
| Mavellikkara | 2950.30 cde | |
| Vaikom | 2825.08 c | |
| Wayanad | 3167.76 ef | |
| Kulathupuzha | 2274.89 a | |
| Mattuppatty | 2987.08 cde | |
| Peerumed | 3303.59 f | |
| Model | No. of Animals | Vg ± S. E | Ve ± S. E | h2 ± S. E |
|---|---|---|---|---|
| NRM-based | 18,858 | 240,310 ± 23,377 | 518,820 ± 19,217 | 0.32 ± 0.03 |
| GREML | 2273 | 181,300 ± 56,904 | 533,220 ± 54,094 | 0.25 ± 0.08 |
| ssGREML | 18,858 | 308,610 ± 26,109 | 463,150 ± 20,703 | 0.40 ± 0.08 |
| Bayes A | 2273 | 342,353.42 ± 20,675.49 | 531,114.77 ± 35,345.17 | 0.26 ± 0.02 |
| Bayes B | 2273 | 258,336.79 ± 22,878.80 | 596,264.24 ± 37,406.55 | 0.20 ± 0.02 |
| Bayes C | 2273 | 301,447.29 ± 60,795.20 | 565,125.75 ± 56,612.60 | 0.23 ± 0.05 |
| Bayes Cπ | 2273 | 310,940.72 ± 57,625.16 | 556,776.70 ± 55,074.72 | 0.24 ± 0.04 |
| ssBR Bayes A | 18,858 | 326,225.72 ± 27,231.98 | 439,324.73 ± 28,051.43 | 0.43 ± 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, K.D.; Alex, R.; Yadav, A.; Sahana, V.N.; Upadhyay, A.; Mani, R.V.; Kumar, T.S.; Pillai, R.R.; Vohra, V.; Gowane, G.R. Optimizing the Genomic Evaluation Model in Crossbred Cattle for Smallholder Production Systems in India. Agriculture 2025, 15, 945. https://doi.org/10.3390/agriculture15090945
Khan KD, Alex R, Yadav A, Sahana VN, Upadhyay A, Mani RV, Kumar TS, Pillai RR, Vohra V, Gowane GR. Optimizing the Genomic Evaluation Model in Crossbred Cattle for Smallholder Production Systems in India. Agriculture. 2025; 15(9):945. https://doi.org/10.3390/agriculture15090945
Chicago/Turabian StyleKhan, Kashif Dawood, Rani Alex, Ashish Yadav, Varadanayakanahalli N. Sahana, Amritanshu Upadhyay, Rajesh V. Mani, Thankappan Sajeev Kumar, Rajeev Raghavan Pillai, Vikas Vohra, and Gopal Ramdasji Gowane. 2025. "Optimizing the Genomic Evaluation Model in Crossbred Cattle for Smallholder Production Systems in India" Agriculture 15, no. 9: 945. https://doi.org/10.3390/agriculture15090945
APA StyleKhan, K. D., Alex, R., Yadav, A., Sahana, V. N., Upadhyay, A., Mani, R. V., Kumar, T. S., Pillai, R. R., Vohra, V., & Gowane, G. R. (2025). Optimizing the Genomic Evaluation Model in Crossbred Cattle for Smallholder Production Systems in India. Agriculture, 15(9), 945. https://doi.org/10.3390/agriculture15090945






