Abstract
Global climate change poses a serious threat to Torreya grandis, a rare and economically important tree species, making the accurate mapping of its spatial distribution essential for forest resource management. However, extracting forest-growing areas remains challenging due to the limited spatial and temporal resolution of remote sensing data and the insufficient classification capability of traditional algorithms for complex land cover types. This study utilized monthly Sentinel-2 imagery from 2023 to extract multitemporal spectral bands, vegetation indices, and texture features. Following minimum redundancy maximum relevance (mRMR) feature selection, a spatial–spectral fused attention network (SSFAN) was developed to extract the distribution of T. grandis in the Kuaiji Mountain area and to analyze the influence of topographic factors. Compared with traditional deep learning models such as 2D-CNN, 3D-CNN, and HybridSN, the SSFAN model achieved superior performance, with an overall accuracy of 99.1% and a Kappa coefficient of 0.961. The results indicate that T. grandis is primarily distributed on the western, southern, and southwestern slopes, with higher occurrence at elevations above 500–600 m and on slopes steeper than 20°. The SSFAN model effectively integrates spectral–spatial information and leverages a self-attention mechanism to enhance classification accuracy. Furthermore, this study highlights the joint influence of natural factors and human land-use decisions on the distribution pattern of T. grandis. These findings aid precision planting and resource management while advancing methods for identifying tree species.
1. Introduction
Global climate change has led to increases in temperature and changes in precipitation patterns, significantly impacting the distribution and ecosystems of forest resources [1,2]. As a rare tree species with important economic value endemic to China [3,4], Torreya grandis has also been affected by climate change. The increased frequency of extreme weather events, such as low temperatures, droughts [5], soil loss [6], and pest infestations [7], poses a serious threat to the survival of T. grandis trees. Additionally, ecological and environmental problems have become increasingly prominent, leading to a reduction in the ecological and economic benefits associated with T. grandis. The lack of comprehensive distribution data for T. grandis has hindered the government’s ability to implement effective forestry policies and management strategies. Furthermore, the extraction accuracy of T. grandis distributions based solely on object-oriented or machine learning methods still needs improvement [8,9,10,11]. Therefore, the accurate identification of the spatial distribution of T. grandis has become an urgent problem.
Traditional tree species identification methods rely mainly on ground surveys, which usually require considerable manpower and material resources. With advancements in remote sensing technology and machine learning methods, researchers have carried out numerous studies on tree species classification using remote sensing data. Various machine learning algorithms, such as the maximum likelihood method [12], decision trees [13], random forests [14,15,16] and support vector machines [17,18,19,20], have been applied. While these methods offer advantages such as fast training speeds and a high degree of automation, they struggle to fully utilize the complex feature structures of high-dimensional remote sensing data. Deep learning has emerged as a powerful approach, capable of automatically extracting more abstract and deeper feature information [21] and are well-suited for processing large-scale remote sensing datasets. Among deep learning models, convolutional neural networks (CNNs) are most commonly used for classifying tree species in remote sensing images [22,23,24]. Based on the dimensionality of the input remote sensing data, deep learning methods for tree species classification can be categorized into one-dimensional CNNs (1D-CNNs), two-dimensional CNNs (2D-CNNs), and three-dimensional CNNs (3D-CNNs). In remote sensing tree species classification, 1D-CNNs mainly focus on spectral features and offer certain advantages [25,26]. However, they only consider spectral information and do not consider spatial information. In contrast, 2D-CNNs have demonstrated strong performance in tree species classification by reducing the dimensionality of the original 3D remote sensing image data and extracting the spatial information around each pixel [27,28]. Meanwhile, 3D-CNNs utilize convolution kernels to process input data in spatial and spectral dimensions simultaneously to extract spectral and spatial features. Despite their ability to capture richer joint features, 3D-CNNs often come with high computational costs and a large number of parameters, making them prone to overfitting. Researchers frequently construct self-designed models for tree species classification based on hyperspectral data and light detection and ranging (LiDAR) data [29,30,31,32,33]. Furthermore, some researchers have used different networks to separately extract spectral and spatial features and then combined them, providing an approach that takes both dimensions of spatial and spectral information into account for remote sensing data [34,35,36]. The dual-branch network can independently process spectral and spatial features, effectively preserving the integrity of each feature and fully leveraging their respective advantages [37]. In this study, drawing inspiration from the dual-attention network (DANet) with an adaptive self-attention mechanism [38] and a dual-branch dual-attention (DBDA) mechanism network [39] for hyperspectral image classification, this paper introduces a spatial–spectral fused attention network (SSFAN) to mine spectral and spatial information more efficiently for accurate identification of tree species such as T. grandis.
As remote sensing technology continues to mature, the spectral resolution and spatiotemporal resolution of satellite images have also greatly improved [40]. This progress has facilitated the acquisition of multitemporal and multiscale remote sensing data, providing a more reliable source. Various types of remote sensing data have been used for tree species identification, including multispectral data, hyperspectral data, and LiDAR data [12,16,17,18,19,33,41,42,43]. However, traditional multispectral imagery typically has limited spatial resolution and relatively few spectral bands, which restricts its capacity to capture subtle spectral differences among tree species. As a result, challenges such as “same spectrum for different objects” and “different spectrum for the same object” frequently arise. Moreover, although hyperspectral and LiDAR data offer greater detail, their high cost and limited accessibility constrain their use in large-scale applications. The multispectral instruments onboard the Sentinel-2 series satellites, launched by the European Space Agency (ESA), offer high spatial, spectral, and temporal resolution, providing detailed information at a relatively small scale. Importantly, Sentinel-2 imagery is freely and publicly available through the ESA Copernicus program, making it highly accessible for research use. In addition, multitemporal remote sensing images enable the extraction and analysis of vegetation phenology information, which can accurately reflect seasonal periodic changes in the vegetation growth process [15,44]. Therefore, the application of high-resolution Sentinel-2 multitemporal remote sensing imagery presents significant potential for advancing tree species identification methods.
At present, despite advancements in deep learning networks for tree species classification, several challenges remain. On the one hand, existing CNN-based methods are applied primarily to uncrewed aerial vehicle (UAV) hyperspectral remote sensing images, which contain hundreds of spectral bands. However, when applied to satellite multispectral images with fewer bands, classification accuracy decreases because of insufficient band information. On the other hand, many studies are based only on single-temporal imagery and fail to make full use of the differences in different surface objects in the temporal dimension. To address these problems, in this study, based on the spectral information, vegetation index, and texture features of 12 multitemporal Sentinel-2 images that were synthesized monthly in 2023, a structure similar to that of hyperspectral data was constructed, and after applying minimum redundancy maximum relevance (mRMR) feature optimization, the spatial–spectral fused attention network (SSFAN) was constructed. The SSFAN was used to extract the T. grandis growing areas in the Kuaiji Mountain region. Then, the distribution characteristics of T. grandis were analyzed under different topographic factors. The SSFAN was compared with other deep learning models to explore its advantages, and factors affecting the distribution of T. grandis were analyzed. The proposed model provides a new extraction method for T. grandis, has high research and application value, and provides a scientific basis for the management and protection of T. grandis resources in the Kuaiji Mountain region.
2. Data and Methods
2.1. Study Area
Kuaiji Mountain (Figure 1) is located in Shaoxing City, Zhejiang Province, China (120°44′–120°50′ E, 29°18′–29°59′ N), at the junction of the hilly areas of Eastern Zhejiang and the plains of Northern Zhejiang. The region’s average elevation is approximately 500 m, with Dongbai Mountain reaching the highest point at 1187 m above sea level. The Kuaiji Mountain area experiences a typical subtropical monsoon climate, with an annual average sunshine duration of approximately 1900 h, an annual average temperature of 16 °C, and an annual average precipitation of approximately 1200 mm. These climatic conditions are highly favorable for the growth of T. grandis. The area also holds the best-preserved group of ancient T. grandis trees in China, with more than 70,000 trees over 100 years old and several thousand over 1000 years old, making it a valuable site for research on T. grandis cultivation and conservation. Given its typical southern hilly terrain and representative climate, Kuaiji Mountain serves as a suitable case study area for T. grandis, reflecting the characteristics of other major T. grandis distribution regions in Southern China.
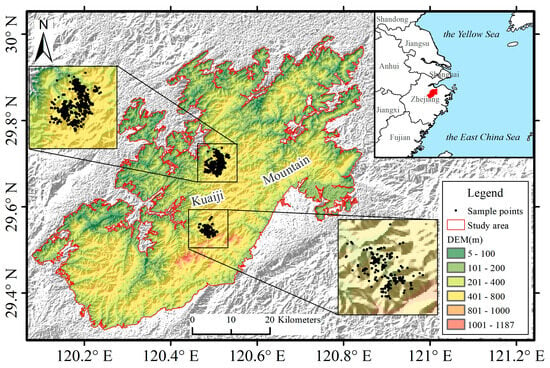
Figure 1.
Overview of the Kuaiji Mountain study area in Shaoxing City, Zhejiang Province, China.
2.2. Data
2.2.1. Sentinel-2 Data
The remote sensing data used in this study were obtained from Sentinel-2 imagery available from the ESA Copernicus Data Centre. The Sentinel-2 satellites consist of two multispectral imaging satellites, Sentinel-2A and Sentinel-2B, launched by the ESA. These satellites have slight differences in their launch dates and orbital positions, but both are equipped with the same multispectral imager (MSI). With a revisit period of up to 5 days, these two satellites capture images of vegetation, soil and water cover, inland waterways and coastal areas. They are widely utilized for applications such as land cover detection, forestry and water monitoring, and natural disaster assessment [45,46,47,48]. In addition, the freely available Sentinel-2 data offer a favorable balance between cost-effectiveness and classification accuracy, making them highly suitable for large-scale vegetation mapping applications. Each Sentinel-2 image comprises 13 spectral bands, covering visible, near-infrared, and shortwave infrared wavelengths, with widths of up to 290 km and spatial resolutions of 10, 20, and 60 m, respectively, as shown in Table 1.

Table 1.
Specifications of spectral bands for Sentinel-2 remote sensing images.
2.2.2. T. grandis Sample Data
Field survey data on T. grandis were collected from two representative zones with dense T. grandis populations in the Kuaiji Mountain area. These zones were selected to capture spatial heterogeneity, encompassing diverse topographic conditions such as variations in elevation, slope gradients, and slope aspects. In addition, the sampling areas contained various non-target land cover types, including buildings, farmland, shrubs, and broadleaf forests. The recorded attributes included geographic coordinates (latitude and longitude), elevation, tree height, east–west crown width, and north–south crown width, which were all obtained using a handheld GPS device with a typical position accuracy of approximately less than 1 m. After data cleaning and abnormal sample removal, a total of 1348 valid sample points for T. grandis were retained. The spatial distribution of the sample points is shown in Figure 1.
2.2.3. Supplementary Data
Additional data used for analyzing the distribution characteristics of T. grandis included a digital elevation model (DEM) provided by the National Aeronautics and Space Administration (NASA) Shuttle Radar Topography Mission (SRTM), with a spatial resolution of 30 m. Other supplementary data included vector diagrams of the study area and high-resolution Google Earth images. High-resolution Google Earth images were used to train labels for the deep learning model, and the prediction results of different models were compared to ensure the accuracy and reliability of the study results.
2.3. Methods
2.3.1. Data Preprocessing
In this work, a total of 159 Sentinel-2 Level-1C images acquired throughout 2023 were selected, each with less than 30% cloud cover, covering the entire Kuaiji Mountain study area using four scenes. These images were downloaded from the ESA Copernicus Data Centre and underwent orthorectification and geometric refinement. Atmospheric correction and band resampling to a 10 m resolution were performed using Sen2Cor [49] and SNAP software [50], respectively, for the L1C-level multispectral data. Sen2Cor is an open-source atmospheric correction processor developed by the ESA, while SNAP is an open-source platform provided by ESA for remote sensing image preprocessing tasks such as resampling. Both tools were freely downloaded from the ESA website. During resampling, the 20 m and 60 m bands of Sentinel-2 were unified to a 10 m resolution using the nearest neighbor interpolation method in SNAP. This method preserves the original spectral information, thereby minimizing the introduction of additional spectral noise during downscaling, and offers a simple and efficient solution [51]. Subsequently, the ENVI software (version 5.3) was employed to mosaic the Sentinel-2 imagery into a seamless dataset covering the entire study area. ENVI is a commercial remote sensing image processing and analysis software used here for image mosaicking, cropping, and other related operations. The vector files defining the study area boundaries were generated by calculating the slope from the DEM and extracting areas with a slope greater than 3 degrees [52] to delineate the mountainous region of Kuaiji Mountain. These vector files were then used to clip the mosaicked imagery. Following the mosaicking and clipping processes, a monthly synthesis was conducted using ENVI to generate a multitemporal remote sensing image set consisting of 12 synthesized monthly average images, where all available Sentinel-2 images within each calendar month were combined through pixel-wise averaging to produce one representative image per month. The clipped DEM was further used to derive aspect and slope datasets, and all resulting datasets, including elevation, aspect, and slope, were resampled to a 10 m resolution.
For each synthesized monthly average Sentinel-2 image, all 13 spectral bands were selected as the original input spectral features. On this basis, six vegetation indices were calculated pixel-wise using the corresponding spectral bands according to their standard formulas, including the normalized difference vegetation index (NDVI), green normalized difference vegetation index (GNDVI), soil-adjusted vegetation index (SAVI), enhanced vegetation index (EVI), Sentinel-2 red-edge position index (S2REP), and normalized difference red-edge index (NDREI), with all computations performed in ENVI. The calculation formulas for these vegetation indices are provided in Table 2.

Table 2.
Vegetation index and calculation formulas.
Texture features play an important role in tree species identification. They effectively capture the spatial heterogeneity caused by variations in crown morphology and stand structure, which cannot be fully represented by spectral features alone [59]. As a valuable complement to spectral information, texture features not only enrich the description of tree species but also significantly enhance the separability between different species, thereby improving the accuracy and stability of classification results. In particular, T. grandis plantations typically exhibit large crown sizes and are planted at high densities with regular spacing, resulting in distinctive and consistent spatial structures compared to the surrounding vegetation. To capture these spatial patterns, texture features were extracted using the gray-level co-occurrence matrix (GLCM) method with a 3 × 3 moving window in ENVI. GLCM characterizes the spatial distribution and structural relationships of pixel intensity values by analyzing gray-level spatial correlations [60]. Based on the texture features of T. grandis and a comprehensive consideration of the correlations, differences and redundancies among texture parameters, six key texture features were selected in this study: information entropy (ENT), correlation (CORR), contrast (CON), an-gular second moment (ASM), dissimilarity (DISS) and variance (VAR).
Ultimately, the 13 spectral bands, six vegetation indices, and six texture features for each synthesized monthly average Sentinel-2 image were combined. The bands of all 12 monthly images were merged to construct a raw feature set consisting of multitemporal spectral features, vegetation indices, texture features, and temporal information, resulting in a dataset with a structure similar to that of a hyperspectral image and comprising a total of 300 bands (Figure 2).
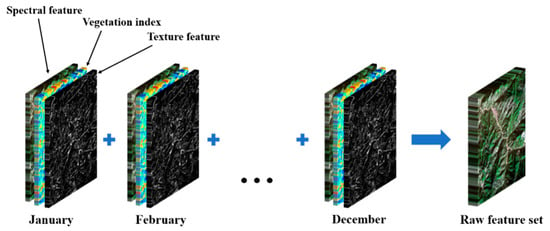
Figure 2.
The construction process of the raw feature set.
Based on existing sample point data for T. grandis, buffer zones were created using ArcGIS 10.8 software by incorporating east–west and north–south crown width information obtained from field surveys. These were then overlaid on contemporaneous high-resolution Google Earth imagery for visual interpretation, allowing for the correction of T. grandis distribution boundaries. The resulting vector data were subsequently rasterized into pixel-level labels for training the deep learning model (Figure 3). Non-T. grandis samples were similarly generated through visual interpretation of the same imagery to obtain vector labels, which were then converted into pixel-level classification labels, resulting in a complete labeled dataset.
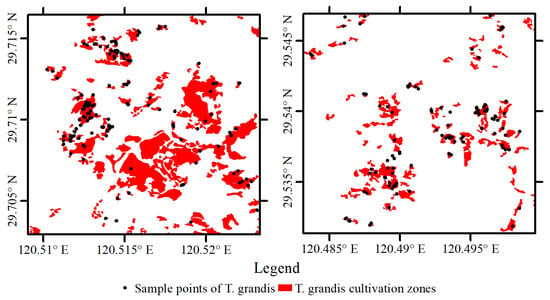
Figure 3.
Example of partial T. grandis labels generated from sample points.
A total of 215,640 pixels from the study areas were selected as the sample set, including 29,104 T. grandis pixels and 186,536 non-T. grandis pixels. After feature optimization, the input band data were normalized, and a 3D patch was generated for each pixel. The label of each patch was determined by the class of the central pixel. The sample data were then randomly divided into training, validation, and test sets in a 60%, 20%, and 20% ratio, respectively. The training set was used to train the deep learning model, the validation set was used to select the optimal model parameters, and the test set was used to evaluate the classification accuracy of the model [61].
2.3.2. Feature Selection via the mRMR Algorithm
The comprehensive use of various features for tree species identification can effectively increase the amount of information, thereby improving classification accuracy. However, as the number of features increases, weakly correlated or highly redundant features are often introduced [62]. Feature optimization helps eliminate redundant bands and prevent classification errors caused by poor separation between target and background objects. The mRMR algorithm is a widely used feature selection method originally proposed by Peng et al. [63]. Compared with PCA and random forest-based methods, mRMR retains the interpretability of original features and improves model generalization by reducing redundancy with lower computational cost. Its principle is based on information theory, which measures feature relevance through mutual information with the target variable and quantifies redundancy as the average mutual information among features. The goal of mRMR is to select a subset of features that are highly relevant to the target variable while minimizing redundancy among them.
In the mRMR algorithm, the maximum correlation criterion is used to select the features with high correlation with class c, whereas the minimum redundancy criterion is used to remove redundant features in the feature set. The formulas are as follows:
where is the number of features selected in feature subset S, is the mutual information between characteristic and class c, and the mutual information between characteristic and characteristic . The selection of the final feature subset is based on the following comprehensive evaluation indicator:
In this study, the mRMR algorithm was used to select 300 bands from the raw feature set, the redundant bands were excluded, and several optimal bands were selected. These bands were input into the deep learning network for subsequent analysis.
2.3.3. SSFAN
To fully utilize the spectral and spatial features of multispectral imagery, the SSFAN was introduced in this paper. The overall network architecture is shown in Figure 4 and consists of two main branches, namely, the spectral branch and the spatial branch. The spectral branch employs a 3D-CNN to extract spectral features from pixels, and the spatial branch uses a 2D-CNN to extract spatial features from pixels. After the original data are input into the two branches, the spectral feature map and spatial feature map can be obtained. To enhance the characterization ability of the model and improve the performance of object detection, the spectral attention module and spatial attention module are embedded in the spectral branch and spatial branch, respectively. Finally, after the feature maps of the two branches are fused, the prediction result is obtained through the pooling and fully connected layers.
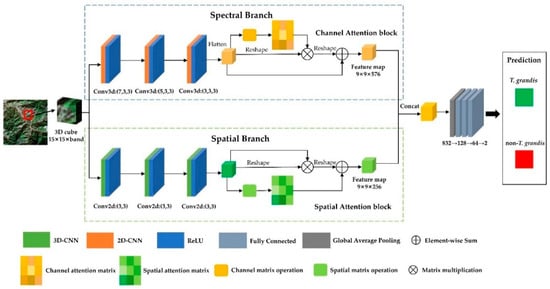
Figure 4.
Structure of the SSFAN model.
- 1.
- Spectral branch and spectral attention
The 3D-CNN can simultaneously extract the spatial and spectral features of remote sensing imagery. Therefore, in this study, a 3D-CNN is employed as the basic structure of the spectral branch. The 3D convolution kernels across the height, width, and channel dimensions to compute the activation value for each pixel at the spatial position (x, y, z) in the j-th feature map of the i-th layer, which is denoted as . The specific calculation formula is as follows:
where is the activation function, is the bias term, , , and are the sizes of the convolution kernels, is the weight of the m-th feature map connected to the position of , is the activation value of the pixel in the m-th feature map of the layer at .
The spectral branch employs multiple 3D convolution layers in conjunction with a channel attention mechanism to fully extract spectral features. The input data is formatted as (1, 15, 15, band), representing a 15 × 15 spatial neighborhood centered on the target pixel. Three consecutive 3D convolutional layers are applied with kernel sizes of 3 × 3 × 7, 3 × 3 × 5, and 3 × 3 × 3, respectively, and the number of filters in these layers is set to 8, 16, and 32. All layers use a stride of (1, 1, 1) and are followed by the rectified linear unit (ReLU) activation function to introduce nonlinearity. Following the convolution operations, the channel and spectral dimensions of the output are fused, and the channel attention mechanism is applied to obtain the spectral feature map.
The channel attention module is designed to capture the dependency between different channels through a self-attention mechanism. The main process is as follows. First, the input feature map is reconstructed as , and the channel attention map is calculated. The formula is as follows:
where denotes the effect of the i-th channel on the j-th channel. Then, the channel attention map is used to weight the original feature map , and the spectral feature map is obtained by combining with a learnable scaling factor , as shown in Equation (6):
- 2.
- Spatial branch and spatial attention
In the spatial branch, the model uses a 2D-CNN as the fundamental structure to extract the spatial features from remote sensing imagery. The 2D convolution kernel slides along the height and width dimensions, applying nonlinear transformations through an activation function. The activation value of the pixel at the spatial position (x, y) in the j-th feature map of the i-th layer is denoted as , and the calculation formula is as follows:
The parameters in Equation (7) are the same as those in Equation (4).
The spatial branch incorporates multiple 2D convolution layers combined with a spatial attention mechanism to capture spatial semantic information. The input data patch has the shape (15, 15, band), centered on the target pixel. Specifically, the spatial branch consists of three sequential 2D convolutional layers, each with a kernel size of 3 × 3 and a stride of 1. The number of filters in these layers is set to 64, 128, and 256, respectively. Each layer is followed by a ReLU activation function. After feature extraction, the spatial attention mechanism is applied to generate the final spatial feature map.
The spatial attention module incorporates a self-attention mechanism to capture the long-range dependencies between spatial locations, and the specific process is as follows. The original feature map is processed by two convolutional layers and then reshaped to obtain two new feature maps . Then, the spatial attention feature map is computed, as shown in Equation (8):
where denotes the effect of the i-th position on the j-th position. Next, the initial feature map passes through a convolutional layer, is reshaped to obtain a new feature map and combined with the scaling factor . Then, the spatial feature map is obtained, as shown in Equation (9).
- 3.
- Feature fusion
After the input data pass through the spectral and spatial branches, the spectral and spatial feature maps are obtained, respectively. These two feature maps are concatenated along the channel dimension to preserve the independence and integrity of both spectral and spatial information. The fused feature map is then passed through an adaptive average pooling layer with an output size of 1 × 1, which reduces the spatial dimensions while retaining global contextual information. The resulting feature vector is fed into a fully connected classifier consisting of three sequential linear layers. The first layer projects the feature vector from 832 to 128 dimensions, followed by a ReLU activation and a dropout layer with a dropout rate of 0.4. The second layer further reduces the dimensionality from 128 to 64, also followed by a ReLU activation and dropout (rate = 0.4). The final linear layer maps the 64-dimensional vector to two output neurons corresponding to the classification categories (T. grandis and non-T. grandis). The output is directly used for pixel-wise classification.
2.3.4. Evaluation Methods
The extraction of T. grandis growing areas is essentially a binary classification task. To evaluate the prediction performance of the modem in determining the spatial distribution of T. grandis in the Kuaiji Mountain area, a confusion matrix was introduced based on the test set to evaluate the accuracy of the classification results of the different methods. The confusion matrix is the most basic and intuitive method for measuring the accuracy of a classification model. For each class, the number of samples predicted correctly and incorrectly by the classification model can be calculated. On this basis, the user accuracy (UA), producer accuracy (PA), overall accuracy (OA), and Kappa coefficient are chosen as the evaluation indicators. UA represents the proportion of correctly classified pixels for a specific class. PA measures the proportion of actual class pixels that were correctly identified. OA denotes the proportion of correctly classified pixels relative to the total number of pixels. The Kappa coefficient is a statistical measure used to assess the agreement between classified data and reference data, quantifying the reduction in classification errors compared to what would be expected by chance. The specific formulas are as follows:
In Equations (10)–(14), where represents the number of correctly classified pixels of T. grandis, represents the number of incorrectly classified pixels of T. grandis, represents the number of correctly classified pixels of other surface objects, and represents the number of incorrectly classified pixels of other surface objects.
To better analyze the distribution characteristics of T. grandis in the study area, a distribution index [64] was introduced in this study. The relationships between the spatial distribution of T. grandis and topographic factors (including aspect, slope and elevation) are described below:
In Equation (15), is the distribution index, is the total area of the study area, is the area of a specific grade of topographic factor in the study area, is the area of a topographic factor within class at that specific grade, and is the total area of class in the study area.
3. Result Analysis
3.1. Extraction of T. grandis Growing Areas Using the SSFAN
3.1.1. Feature Optimization
The original band features used as input for the deep learning model were first selected through the mRMR algorithm. The number of optimized features plays a critical role in the model performance. To evaluate the effects of different numbers of features, while keeping other experimental conditions unchanged, the top 10 to 50 features (with a step of 10) were selected as model input for classification, and the results are shown in Figure 4.
As shown in Figure 5, an increase in the number of selected features leads to continuous improvements in the model’s classification performance. However, when the feature count exceeds 30, the rate of improvement becomes more gradual. This trend occurs because too few features may reduce the model’s ability to distinguish between different classes. Conversely, too many features can introduce redundancy and noise, which may increase the training cost and slow convergence. Based on a comprehensive consideration of the speed and performance of the model, the top 30 optimal features were selected as the model input. Table 3 provides a detailed ranking and description of these 30 optimal features.
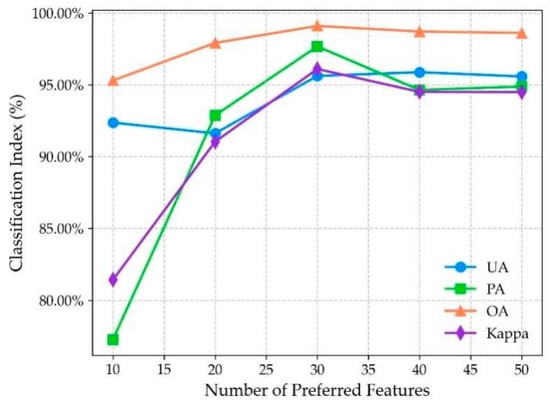
Figure 5.
Classification indices under different numbers of features.

Table 3.
Bands obtained from feature optimization.
After feature selection, we selected sample points of T. grandis and other typical non-T. grandis land cover types (coniferous forest, broadleaf forest, buildings, and shrubs) to compare their spectral features, vegetation indices, and texture features. As shown in Figure 6, T. grandis exhibits significant differences from other categories in the selected features—specifically, it shows generally lower spectral reflectance and relatively higher vegetation index values. Due to its large canopy and concentrated distribution, T. grandis also presents distinct texture patterns compared to natural vegetation. In addition, the selected temporal features are mainly concentrated in March and May. March marks a critical transition period from dormancy to active growth for T. grandis, during which the canopy structure changes significantly, making it more distinguishable from other vegetation still in early spring conditions. May represents the peak of canopy development, with increased spectral reflectance and vegetation indices, and T. grandis exhibits notable spectral differences from coniferous forests, shrubs, and other land cover types during this period. These differences indicate that the selected features have strong discriminative power for identifying T. grandis.
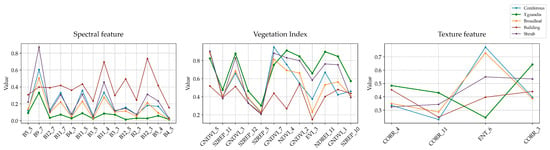
Figure 6.
Comparison of spectral, vegetation index, and texture features among Torreya grandis and other land cover types.
3.1.2. Deep Learning Environment Settings
In this study, a cloud-based deep learning server was utilized for model training. Specifically, the system ran Ubuntu 20.04, equipped with 80 GB of RAM. The computational resources included a 16 vCPU Intel(R) Xeon(R) Platinum 8481C CPU and an NVIDIA RTX 4090D GPU with 24 GB of memory. The deep learning model was implemented using the PyTorch 2.0.0 framework with Python 3.8 as the programming language. During model training, the image bands were first normalized and then segmented into 15 × 15 patches before being fed into the deep learning model. The initial learning rate was set to 0.01, the batch size to 64, and the number of epochs to 200. The cross-entropy loss function was employed, and the Adam optimizer was used to adaptively adjust the learning rate based on historical gradient information. Using a larger learning rate in the early stages of training facilitates rapid convergence, while a smaller learning rate in later stages helps achieve more precise identification of the minimum loss function value. The specific hyperparameter settings before training are shown in Table 4.

Table 4.
Hyperparameter settings for the experiments.
3.1.3. Model Validation and Extraction Results for T. grandis
The test set was used to assess the model’s performance. The OA of the proposed model was 99.1%, the Kappa coefficient was 0.961, the UA was 95.2%, and the PA was 97.67% (Table 5). The trained model was applied to identify the spatial distribution of T. grandis in the Kuaiji Mountain area. Owing to the large size of the study area, the system memory cannot process the entire image at one time. Therefore, the image of the study area was divided into several small blocks, which were then input to the model block by block for prediction. The prediction results were stitched based on geographic location information to obtain a distribution map of T. grandis in the Kuaiji Mountain area (Figure 7).

Table 5.
Comparison of classification accuracy of different models across train, validation, and test sets.
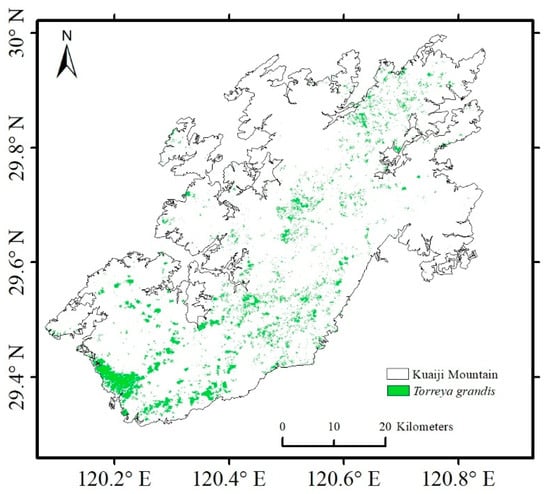
Figure 7.
Distribution of T. grandis predicted by the SSFAN model.
3.2. Analysis of the Distribution Characteristics of T. grandis
To analyze the distribution characteristics of T. grandis in the Kuaiji Mountain area, DEM data were used to analyze the extracted T. grandis data. The distribution characteristics of T. grandis were investigated from three aspects: elevation, aspect and slope. The distribution index could be used to describe the distribution characteristics of T. grandis under different slopes, aspects and elevations. The aspect was divided into eight directions, and the elevation and slope were graded at steps of 100 m and 5°, respectively. Figure 8a shows that the distribution indices of T. grandis are different at different aspects, with the highest distribution index occurring on the western slope and high distribution indices occurring on the southern and southwestern slopes, which may be attributed to more suitable sunshine and climatic conditions on these slopes. As shown in Figure 8b, as the slope increases, the distribution index of T. grandis generally tends to increase, and the distribution index is high on steep slopes > 20°, indicating that a steep slope environment is more conducive to the growth of T. grandis. Figure 8c shows that the distribution index at 500–600 m is the highest, and the distribution indices in other high-elevation areas are also relatively high, indicating that T. grandis has a clear distribution advantage at relatively high elevations.
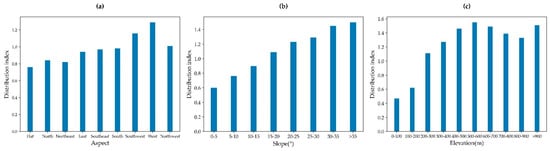
Figure 8.
Distribution indices of T. grandis: (a) distribution index along aspect, (b) distribution index along slope, and (c) distribution index along elevation.
3.3. Comparison of Different Models
To evaluate the effectiveness of the SSFAN model proposed in this paper, it was compared with other deep learning-based classifiers of 2D-CNN, 3D-CNN and HybridSN. In addition, to explore the effects of the channel attention and spatial attention modules on model performance, comparisons with the attention mechanism removed were also performed. All the experiments were implemented in PyTorch on the same platform with the same data. These methods are briefly described below:
- 2D-CNN: Makantasis et al. described the specific network architecture [65]. This model is mainly based on the 2D-CNN.
- 3D-CNN: Zhang et al. described the specific network architecture [33]. This model is mainly based on the 3D-CNN.
- HybridSN: This hybrid model combines the 3D-CNN and 2D-CNN in a series. Roy et al. described the specific network architecture [66].
- SSFN: The attention mechanism is removed from the original SSFAN model, while the remainder of the structure remains unchanged.
A confusion matrix was introduced to the test set, and various evaluation indicators were calculated accordingly. The confusion matrix of each model is shown in Figure 9, and the corresponding evaluation indicators are shown in Table 5.
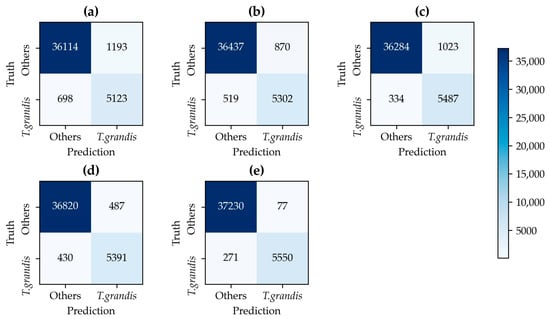
Figure 9.
Confusion matrices of different models on the test set: (a) 2D-CNN, (b) 3D-CNN, (c) HybridSN, (d) SSFN, (e) SSFAN.
Table 5 presents the classification performance of different models across the training, validation, and testing datasets. All models adopted a consistent data split strategy and training configuration, with sufficient training epochs to ensure model convergence. Except for the 2D-CNN, the other four models (3D-CNN, HybridSN, SSFN, and SSFAN) achieved over 99% OA on the training set, with less than 1% fluctuation across performance metrics, indicating a stable and fully converged training process. This setup provides a reliable foundation for evaluating the models’ generalization ability on testing sets. The proposed SSFAN model achieved the best classification performance, with an OA of 99.11% and a Kappa coefficient of 0.961 on the testing set. This indicates that SSFAN not only has strong fitting ability but also excellent generalization capacity, effectively identifying key features in unseen samples. In contrast, the 2D-CNN model exhibited lower performance due to its relatively simple architecture and limited feature extraction capability. The 3D-CNN outperformed 2D-CNN on the testing set as it can extract both spectral and spatial features simultaneously rather than relying solely on spatial convolution, thus enhancing its representational power. The HybridSN model further integrated the 2D-CNN and 3D-CNN architectures in series, aiming to capture both spectral and spatial abstractions. However, its testing performance did not surpass that of SSFN or SSFAN. The SSFN model maintained good consistency between the training and validation phases, showing strong stability and generalizability. Nevertheless, its UA and PA for both classes were slightly lower than those of SSFAN, especially in edge cases or small fragmented patches. Compared with SSFN, which lacks attention mechanisms, SSFAN incorporates both channel and spatial attention modules into its architecture. These allow the model to focus more effectively on critical bands and spatially informative regions, resulting in an additional improvement in classification accuracy.
In addition, to more intuitively represent the prediction effect of each model, the prediction results of different models can be visualized. Since the resolution of Sentinel-2 images is 10 m, it is difficult to distinguish T. grandis ground objects from non-T. grandis ground objects directly with the naked eye. Therefore, in this study, a high-resolution Google Earth image of the corresponding area was selected as a control to aid in evaluation.
As shown in Figure 10, the extraction results of the T. grandis growing areas by the 2D-CNN and 3D-CNN models exhibit some degree of misclassification and omission. In addition, the distribution areas of T. grandis extracted by these two networks and HybridSN are continuous; however, there is still a serious lack of edge information. In general, the extraction results of the SSFAN model are the most consistent with the ground truth. To enhance the model’s ability to capture feature information from T. grandis blocks and reduce the interference of complex background information, an attention mechanism was introduced in the network to highlight the key features of T. grandis identification and reduce the influence of the complex environment on the extraction accuracy of the T. grandis blocks. However, all the model results inevitably differ from actual conditions. These errors are mainly concentrated in small or more scattered T. grandis blocks, which is partly due to the insufficient resolution of the remote sensing images and partly due to the more severe mixing between T. grandis and other ground objects.

Figure 10.
Prediction maps of different models and ground truths of high-resolution remote sensing images.
4. Discussion
The extraction results of T. grandis growing areas (Figure 10) and the evaluation indicators based on the test set (Table 5) between the SSFAN constructed in this paper and other deep learning networks, such as 2D-CNN, 3D-CNN, and HybridSN, were compared. The results showed the superiority of the SSFAN. Studies have shown that methods using only 2D-CNNs or 3D-CNNs, which are based solely on spatial or spectral features, may result in the loss of critical information, thereby limiting the ability to fully exploit the comprehensive characteristics of remote sensing images [37]. In contrast, approaches that simultaneously consider both spectral and spatial information tend to be more robust and yield improved classification performance [34]. The dual-branch network architecture allows the design of different spectral and spatial networks for feature extraction, offering greater flexibility and advantages. Therefore, in this study, 3D-CNN and 2D-CNN models were selected as the main structures of the spectral and spatial branches, respectively. Considering that the spectral and spatial features are in uncorrelated domains, compared with the 3D-2D tandem structure used in HybridSN, the dual-branch structure that first extracts spectral and spatial features in parallel, followed by series fusion in the later stage, can better retain the independence between the two branches [39]. Moreover, this study introduced a self-attention mechanism in both the spectral and spatial dimensions, and the effectiveness of this mechanism was verified by comparing the results of models with and without the spectral and spatial attention mechanisms. The self-attention mechanism can adaptively integrate local semantic features and global dependencies [38], thus effectively capturing long-range contextual information. The spectral attention module focuses on information-rich bands, whereas the spatial attention module emphasizes pixels with significant spatial features. In summary, the SSFAN introduced in this study can effectively extract T. grandis growing areas and fully demonstrate the effectiveness and superiority of fused space-spectral features and a self-attention mechanism.
This study also presented an analysis of the distribution characteristics of T. grandis (Figure 8). The results revealed that topographic factors were the key factors affecting the distribution of T. grandis in the Kuaiji Mountain area. The higher distribution indices on the west and southwest slopes are related to the warm growth habit of T. grandis [67]; these two slopes have relatively warm climatic conditions and long sunshine hours. Slope also has a significant effect on the distribution of T. grandis. Large slopes provide sufficient sunlight, which makes the distribution of T. grandis more concentrated on steep slopes. T. grandis is also suitable for planting on mountainous or hilly terrain [68]. Due to human land-use preferences, residential areas are generally concentrated on flat land or gentle slopes on the west side of Kuaiji Mountain. Low-elevation and relatively flat areas near residential zones are therefore often prioritized for cultivating staple crops such as rice and corn. To avoid occupying arable land, T. grandis is typically planted on steep slopes in the west and southwest near residential areas. Elevation is also an important factor affecting the planting of T. grandis, which exhibits strong adaptability to high-elevation environments. In contrast, land-use decisions in low-elevation areas have limited the distribution of T. grandis, which has a long growth cycle, bearing fruit in five to six years. Therefore, residents often choose to plant T. grandis on relatively barren mountains at relatively high elevations. In addition, elevation has a significant effect on the quality of T. grandis fruit, which is best in high-elevation areas [69] and result in greater economic benefits. Therefore, the distribution of T. grandis is the result of the combined influence of natural and human factors.
In this study, a spatial–spectral fused attention network (SSFAN) was constructed to extract Torreya grandis growing areas based on multitemporal Sentinel-2 imagery. Compared with traditional machine learning methods previously used for T. grandis extraction [11], the overall accuracy was significantly improved from 78% to 99.1%. Although deep learning methods have primarily been applied in tree species identification based on hyperspectral imagery, this study successfully adapted SSFAN to multispectral data by constructing a multitemporal band combination that mimics a hyperspectral structure. However, this study still has certain limitations. The sample data were collected from two typical T. grandis distribution areas in the Kuaiji Mountain region. While these areas are representative within the study region and the model performed well, its generalizability to regions with different geographical and climatic conditions requires further validation. In addition, although most T. grandis individuals have large canopies and are densely distributed, the 10 m spatial resolution of Sentinel-2 imagery still presents challenges in edge areas or scattered distributions, where mixed pixels may lead to local misclassification. To address this issue, future studies could consider incorporating higher spatial resolution remote sensing data to further improve extraction accuracy and model performance.
5. Conclusions
In this study, on the basis of multitemporal Sentinel-2 images and the SSFAN model, the T. grandis growing areas in the Kuaiji Mountain area were identified, and the distribution characteristics of T. grandis under different aspects, slopes, and elevations were analyzed. In addition, the extraction results obtained using SSFAN were compared with those of other deep learning models, and the superiority of the proposed model and the factors affecting the distribution of T. grandis were discussed. The following conclusions were reached:
- On the basis of the spectral bands, vegetation indices, and texture features of 12 synthesized monthly average Sentinel-2 images from 2023, a hyperspectral image-like band structure was formed. After the mRMR feature selection, the SSFAN was constructed. The T. grandis growing areas in the Kuaiji Mountain area were extracted. The model’s accuracy was validated. The model achieved an OA of 99.1% and a Kappa coefficient of 0.961, with the UA and PA of T. grandis reaching 95.2% and 97.67%, respectively, indicating good extraction results.
- Elevation, aspect, and slope have significant impacts on the distribution of T. grandis. The distribution index of T. grandis is the most concentrated on the western, southern, and southwestern slopes, where light and heat conditions are more suitable. As slope steepness increased, the T. grandis distribution index exhibited an upward trend, with a particular preference for steep slopes (>20°). Additionally, regions at 500–600 m or greater elevation exhibited a relatively high distribution index.
- The test set was used to assess the evaluation indicators for each model. The performance ranking from highest to lowest was as follows: SSFAN > SSFN > HybridSN > 3D-CNN > 2D-CNN. The proposed model performed best and had an advantage in the extraction of T. grandis growing areas.
- In the extraction of T. grandis growing areas, the SSFAN, which fuses spectral and spatial features and introduces a self-attention mechanism, exhibited notable effectiveness and superiority. Additionally, the distribution of T. grandis is influenced by a combination of natural and human factors, providing a valuable scientific basis for the planting and management of T. grandis.
In future research, this method could be extended to other economic tree species or different regions and integrated with higher-resolution remote sensing data and multi-source environmental factors to further improve the model’s generalization ability and classification accuracy.
Author Contributions
Conceptualization, Y.L. and Y.W.; methodology, Y.L.; software, Y.L.; validation, Y.L., Y.W. and X.S.; formal analysis, Y.L.; investigation, Y.W.; resources, Y.W. and X.S.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, Y.W.; visualization, Y.L.; supervision, Y.W.; project administration, Y.W. and X.S.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the NUIST Students’ Platform for Innovation and Entrepreneurship Training Program, grant number XJDC202410300172; the Jiangsu Students’ Platform for Innovation and Entrepreneurship Training Program, grant number 202410300169Y; and the National Key R&D Program of China, grant number 2019YFB2102003.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to the privacy policy of the authors’ institution.
Acknowledgments
We would like to thank the NUIST Students’ Platform for Innovation and Entrepreneurship Training Program, the Jiangsu Students’ Platform for Innovation and Entrepreneurship Training Program, and the National Key R&D Program of China for their financial support of this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Milad, M.; Schaich, H.; Bürgi, M.; Konold, W. Climate change and nature conservation in Central European forests: A review of consequences, concepts and challenges. For. Ecol. Manag. 2011, 261, 829–843. [Google Scholar] [CrossRef]
- Nunes, L.J.R.; Meireles, C.I.R.; Gomes, C.J.P.; Ribeiro, N.M.C.A. The Impact of Climate Change on Forest Development: A Sustainable Approach to Management Models Applied to Mediterranean-Type Climate Regions. Plants 2021, 11, 69. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Jin, H. A Case Study of Enhancing Sustainable Intensification of Chinese Torreya Forest in Zhuji of China. Environ. Nat. Resour. Res. 2019, 9, 53–60. [Google Scholar] [CrossRef]
- Chen, X.; Jin, H. Review of cultivation and development of Chinese torreya in China. For. Trees Livelihoods 2018, 28, 68–78. [Google Scholar] [CrossRef]
- Cook, B.I.; Mankin, J.S.; Anchukaitis, K.J. Climate Change and Drought: From Past to Future. Curr. Clim. Chang. Rep. 2018, 4, 164–179. [Google Scholar] [CrossRef]
- Ramos, M.C.; Martínez-Casasnovas, J.A. Climate change influence on runoff and soil losses in a rainfed basin with Mediterranean climate. Nat. Hazards 2015, 78, 1065–1089. [Google Scholar] [CrossRef]
- Skendzic, S.; Zovko, M.; Zivkovic, I.P.; Lesic, V.; Lemic, D. The Impact of Climate Change on Agricultural Insect Pests. Insects 2021, 12, 440. [Google Scholar] [CrossRef]
- Han, N.; Zhang, X.; Wang, X.; Wang, K. Extraction of Torreya grandis Merrillii based on object-oriented method from IKONOS imagery. J. Zhejiang Univ. (Agric. Life Sci.) 2009, 35, 670–676. [Google Scholar] [CrossRef]
- Han, N.; Zhang, X.; Wang, X.; Chen, L.; Wang, K. Identification of distributional information Torreya Grandis Merrlllii using high resolution imagery. J. Zhejiang Univ. (Eng. Sci.) 2010, 44, 420–425. [Google Scholar]
- Wang, Y. Distribution Information Extraction and Dynamic Change Monitoring of Torreya Grandis Based on Multi-Source Data. Master’s Thesis, Zhejiang A&F University, Hangzhou, China, 2017. [Google Scholar]
- Ji, J.; Yu, X.; Yu, C.; Zhang, Y.; Li, D. The Spatial Distribution Extraction of Torreya grandis Forest Based on Remote Sensing and Random Forest. South China Agric. 2018, 12, 93–95. [Google Scholar] [CrossRef]
- Axelsson, A.; Lindberg, E.; Reese, H.; Olsson, H. Tree species classification using Sentinel-2 imagery and Bayesian inference. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102318. [Google Scholar] [CrossRef]
- Franklin, S.E.; Ahmed, O.S. Deciduous tree species classification using object-based analysis and machine learning with unmanned aerial vehicle multispectral data. Int. J. Remote Sens. 2017, 39, 5236–5245. [Google Scholar] [CrossRef]
- Bjerreskov, K.S.; Nord-Larsen, T.; Fensholt, R. Forest type and tree species classification of nemoral forests with Sentinel-1 and 2 Time Series data. Preprints 2021. [Google Scholar] [CrossRef]
- Ghorbanian, A.; Zaghian, S.; Asiyabi, R.M.; Amani, M.; Mohammadzadeh, A.; Jamali, S. Mangrove Ecosystem Mapping Using Sentinel-1 and Sentinel-2 Satellite Images and Random Forest Algorithm in Google Earth Engine. Remote Sens. 2021, 13, 2565. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, J.; Guo, S.; Ye, Z.; Deng, H.; Hou, X.; Zhang, H. Urban Tree Classification Based on Object-Oriented Approach and Random Forest Algorithm Using Unmanned Aerial Vehicle (UAV) Multispectral Imagery. Remote Sens. 2022, 14, 3885. [Google Scholar] [CrossRef]
- Modzelewska, A.; Fassnacht, F.E.; Sterenczak, K. Tree species identification within an extensive forest area with diverse management regimes using airborne hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101960. [Google Scholar] [CrossRef]
- Nasiri, V.; Beloiu, M.; Darvishsefat, A.A.; Griess, V.C.; Maftei, C.; Waser, L.T. Mapping tree species composition in a Caspian temperate mixed forest based on spectral-temporal metrics and machine learning. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103154. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Demir, B.; Dalponte, M. Weighted support vector machines for tree species classification using lidar data. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6740–6743. [Google Scholar]
- Yang, G.; Zhao, Y.; Li, B.; Ma, Y.; Li, R.; Jing, J.; Dian, Y. Tree Species Classification by Employing Multiple Features Acquired from Integrated Sensors. J. Sens. 2019, 2019, 3247946. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- La Rosa, L.E.C.; Sothe, C.; Feitosa, R.Q.; de Almeida, C.M.; Schimalski, M.B.; Oliveira, D.A.B. Multi-task fully convolutional network for tree species mapping in dense forests using small training hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2021, 179, 35–49. [Google Scholar] [CrossRef]
- Li, Q.; Wong, F.K.K.; Fung, T. Mapping multi-layered mangroves from multispectral, hyperspectral, and LiDAR data. Remote Sens. Environ. 2021, 258, 112403. [Google Scholar] [CrossRef]
- Zhao, H.; Zhong, Y.; Wang, X.; Hu, X.; Luo, C.; Boitt, M.; Piiroinen, R.; Zhang, L.; Heiskanen, J.; Pellikka, P. Mapping the distribution of invasive tree species using deep one-class classification in the tropical montane landscape of Kenya. ISPRS J. Photogramm. Remote Sens. 2022, 187, 328–344. [Google Scholar] [CrossRef]
- Wei, X.; Yu, X.; Liu, B.; Zhi, L. Convolutional neural networks and local binary patterns for hyperspectral image classification. Eur. J. Remote Sens. 2019, 52, 448–462. [Google Scholar] [CrossRef]
- Xi, Y.; Ren, C.; Wang, Z.; Wei, S.; Bai, J.; Zhang, B.; Xiang, H.; Chen, L. Mapping Tree Species Composition Using OHS-1 Hyperspectral Data and Deep Learning Algorithms in Changbai Mountains, Northeast China. Forests 2019, 10, 818. [Google Scholar] [CrossRef]
- Fricker, G.A.; Ventura, J.D.; Wolf, J.A.; North, M.P.; Davis, F.W.; Franklin, J. A Convolutional Neural Network Classifier Identifies Tree Species in Mixed-Conifer Forest from Hyperspectral Imagery. Remote Sens. 2019, 11, 2326. [Google Scholar] [CrossRef]
- Sothe, C.; De Almeida, C.M.; Schimalski, M.B.; La Rosa, L.E.C.; Castro, J.D.B.; Feitosa, R.Q.; Dalponte, M.; Lima, C.L.; Liesenberg, V.; Miyoshi, G.T.; et al. Comparative performance of convolutional neural network, weighted and conventional support vector machine and random forest for classifying tree species using hyperspectral and photogrammetric data. GIScience Remote Sens. 2020, 57, 369–394. [Google Scholar] [CrossRef]
- Guan, H.; Yu, Y.; Yan, W.; Li, D.; Li, J. 3D-Cnn Based Tree species classification using mobile lidar data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 989–993. [Google Scholar] [CrossRef]
- Liu, M.H.; Han, Z.W.; Chen, Y.M.; Liu, Z.; Han, Y.S. Tree species classification of LiDAR data based on 3D deep learning. Measurement 2021, 177, 109301. [Google Scholar] [CrossRef]
- Mäyrä, J.; Keski-Saari, S.; Kivinen, S.; Tanhuanpää, T.; Hurskainen, P.; Kullberg, P.; Poikolainen, L.; Viinikka, A.; Tuominen, S.; Kumpula, T.; et al. Tree species classification from airborne hyperspectral and LiDAR data using 3D convolutional neural networks. Remote Sens. Environ. 2021, 256, 112322. [Google Scholar] [CrossRef]
- Nezami, S.; Khoramshahi, E.; Nevalainen, O.; Pölönen, I.; Honkavaara, E. Tree species classification of drone hyperspectral and RGB imagery with deep learning convolutional neural networks. Remote Sens. 2020, 12, 1070. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, L.; Zhang, X. Three-dimensional convolutional neural network model for tree species classification using airborne hyperspectral images. Remote Sens. Environ. 2020, 247, 111938. [Google Scholar] [CrossRef]
- Liang, J.; Li, P.; Zhao, H.; Han, L.; Qu, M. Forest species classification of UAV hyperspectral image using deep learning. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 7126–7130. [Google Scholar]
- Shi, C.; Liao, D.; Xiong, Y.; Zhang, T.; Wang, L. Hyperspectral Image Classification Based on Dual-Branch Spectral Multiscale Attention Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10450–10467. [Google Scholar] [CrossRef]
- Xu, J.; Li, K.; Li, Z.; Chong, Q.; Xing, H.; Xing, Q.; Ni, M. Fuzzy graph convolutional network for hyperspectral image classification. Eng. Appl. Artif. Intell. 2024, 127, 107280. [Google Scholar] [CrossRef]
- Hou, C.; Liu, Z.; Chen, Y.; Wang, S.; Liu, A. Tree Species Classification from Airborne Hyperspectral Images Using Spatial–Spectral Network. Remote Sens. 2023, 15, 5679. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of Hyperspectral Image Based on Double-Branch Dual-Attention Mechanism Network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef]
- Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 126–134. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Wagner, F.H.; Aragao, L.; Shimabukuro, Y.E.; de Souza, C.R. Tree species classification in tropical forests using visible to shortwave infrared WorldView-3 images and texture analysis. Isprs J. Photogramm. Remote Sens. 2019, 149, 119–131. [Google Scholar] [CrossRef]
- Liu, L.X.; Coops, N.C.; Aven, N.W.; Pang, Y. Mapping urban tree species using integrated airborne hyperspectral and LiDAR remote sensing data. Remote Sens. Environ. 2017, 200, 170–182. [Google Scholar] [CrossRef]
- Valderrama-Landeros, L.; Flores-de-Santiago, F.; Kovacs, J.M.; Flores-Verdugo, F. An assessment of commonly employed satellite-based remote sensors for mapping mangrove species in Mexico using an NDVI-based classification scheme. Environ. Monit. Assess. 2017, 190, 23. [Google Scholar] [CrossRef]
- Persson, M.; Lindberg, E.; Reese, H. Tree species classification with multi-temporal Sentinel-2 data. Remote Sens. 2018, 10, 1794. [Google Scholar] [CrossRef]
- Sefrin, O.; Riese, F.M.; Keller, S. Deep Learning for Land Cover Change Detection. Remote Sens. 2020, 13, 78. [Google Scholar] [CrossRef]
- Russo, L.; Mauro, F.; Memar, B.; Sebastianelli, A.; Gamba, P.; Ullo, S.L. Using Multi-Temporal Sentinel-1 and Sentinel-2 data for water bodies mapping. arXiv 2024, arXiv:2402.00023. [Google Scholar] [CrossRef]
- Sukmono, A.; Hadi, F.; Widayanti, E.; Nugraha, A.L.; Bashit, N. Identifying Burnt Areas in Forests and Land Fire Using Multitemporal Normalized Burn Ratio (NBR) Index on Sentinel-2 Satellite Imagery. Int. J. Saf. Secur. Eng. 2023, 13, 469–477. [Google Scholar] [CrossRef]
- Tavus, B.; Kocaman, S.; Gokceoglu, C. Flood damage assessment with Sentinel-1 and Sentinel-2 data after Sardoba dam break with GLCM features and Random Forest method. Sci. Total Environ. 2022, 816, 151585. [Google Scholar] [CrossRef]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 Sen2Cor: L2A processor for users. In Proceedings of the Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016; pp. 1–8. [Google Scholar]
- Sentinel Application Platform (SNAP). Available online: https://step.esa.int/main/toolboxes/snap/ (accessed on 20 December 2024).
- Zheng, H.; Du, P.; Chen, J.; Xia, J.; Li, E.; Xu, Z.; Li, X.; Yokoya, N. Performance evaluation of downscaling Sentinel-2 imagery for land use and land cover classification by spectral-spatial features. Remote Sens. 2017, 9, 1274. [Google Scholar] [CrossRef]
- Qi, H.; Tian, W.; Zhang, X. Index System of Landform Regionalization for Highway in China. J. Chang. Univ. Nat. Sci. Ed. 2011, 31, 33–38. [Google Scholar]
- Rouse Jr, J.W.; Haas, R.H.; Deering, D.; Schell, J.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA: Washington, DC, USA, 1974. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Fitzgerald, G.; Rodriguez, D.; Christensen, L.; Belford, R.; Sadras, V.; Clarke, T. Spectral and thermal sensing for nitrogen and water status in rainfed and irrigated wheat environments. Precis. Agric. 2006, 7, 233–248. [Google Scholar] [CrossRef]
- Jiang, K.; Zhao, Q.; Wang, X.; Sheng, Y.; Tian, W. Tree Species Classification for Shelterbelt Forest Based on Multi-Source Remote Sensing Data Fusion from Unmanned Aerial Vehicles. Forests 2024, 15, 2200. [Google Scholar] [CrossRef]
- Tassi, A.; Vizzari, M. Object-Oriented LULC Classification in Google Earth Engine Combining SNIC, GLCM, and Machine Learning Algorithms. Remote Sens. 2020, 12, 3776. [Google Scholar] [CrossRef]
- Yang, S.; Gu, L.; Li, X.; Jiang, T.; Ren, R. Crop Classification Method Based on Optimal Feature Selection and Hybrid CNN-RF Networks for Multi-Temporal Remote Sensing Imagery. Remote Sens. 2020, 12, 3119. [Google Scholar] [CrossRef]
- Liu, G.; Jiang, X.; Tang, B. Application of feature optimization and convolutional neural network in crop classification. J. Geoinf. Sci. 2021, 23, 1071–1081. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Sun, L.; Chen, H.; Pan, J. Analysis of the land use spatiotemporal variation based on DEM—Beijing Yanqing County as an example. J. Mt. Res. 2004, 22, 762–766. [Google Scholar]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3D–2D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Zhong, Z.; Wang, J.; Wen, Y.; Zhang, Q. Research on the Resource Development and Industrialization Strategies of Chinese Torreya grandis. J. Zhejiang Agric. Sci. 2023, 64, 3020–3025. [Google Scholar]
- Wu, L.; Yang, L.; Li, Y.; Shi, J.; Zhu, X.; Zeng, Y. Evaluation of the Habitat Suitability for Zhuji Torreya Based on Machine Learning Algorithms. Agriculture 2024, 14, 1077. [Google Scholar] [CrossRef]
- Yang, X.; Yao, H.; Fan, F.; Yan, F.; Li, K.; Chen, C.; Wu, L. Effects of different altitudes on Torreya grandis ‘Merrillii’ fruit quality and its comprehensive evaluation. J. Anhui Agric. Univ. 2023, 50, 792–797. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).