Numerical Optimization of Root Blanket-Cutting Device for Rice Blanket Seedling Cutting and Throwing Transplanter Based on DEM-MBD
Abstract
1. Introduction
2. Materials and Methods
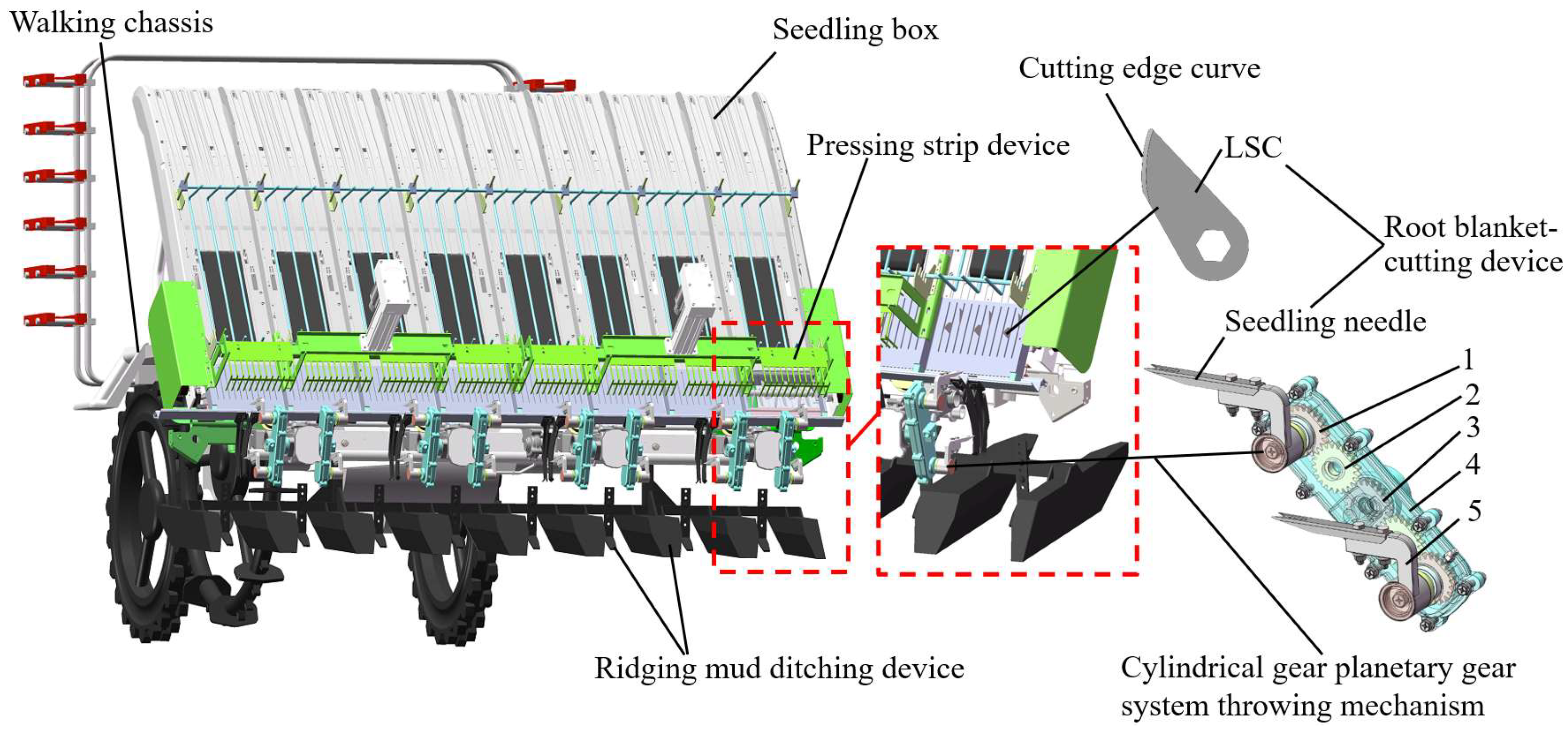
2.1. Introduction of Root Blanket-Cutting Device
2.1.1. Structure and Working Principle
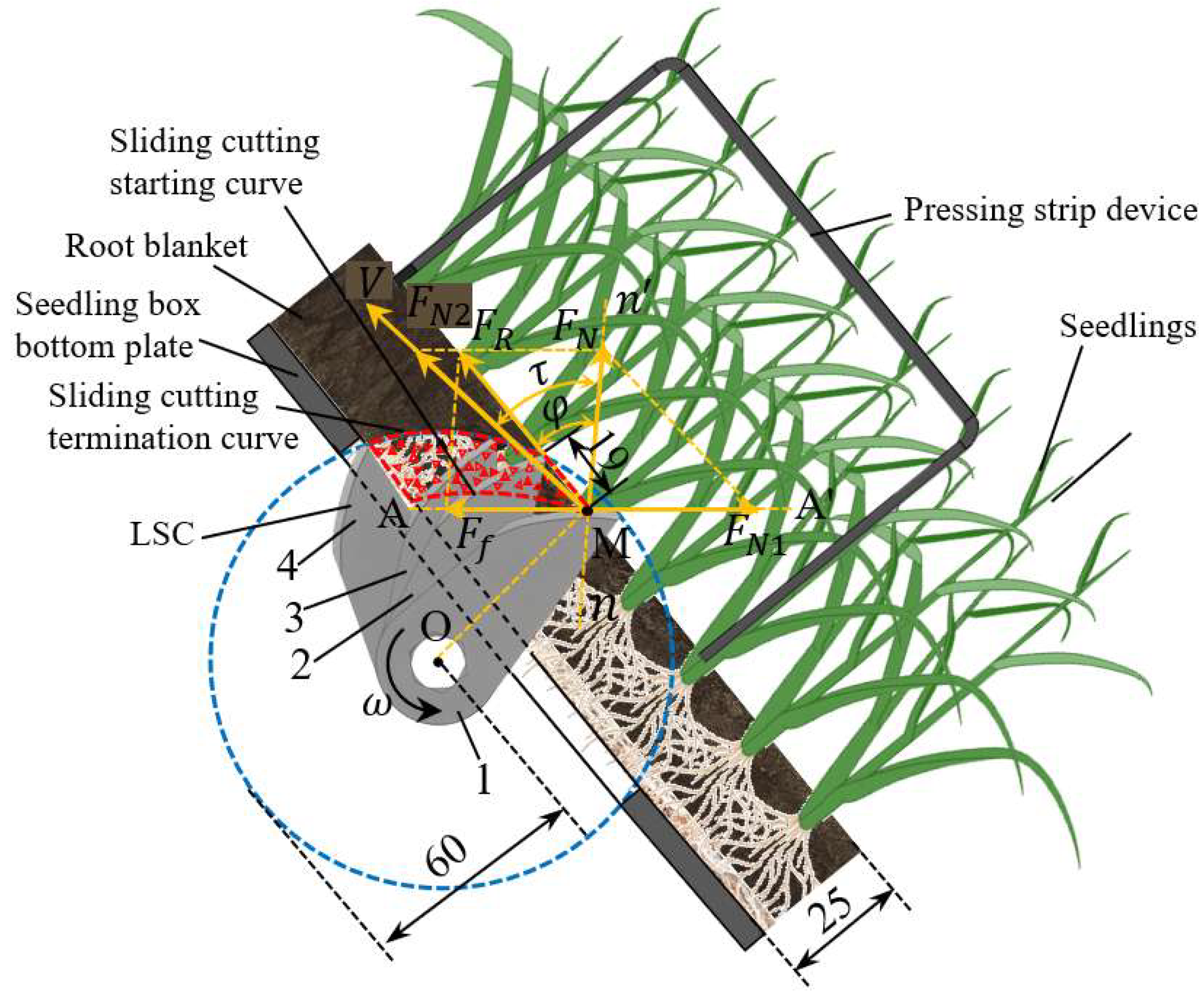
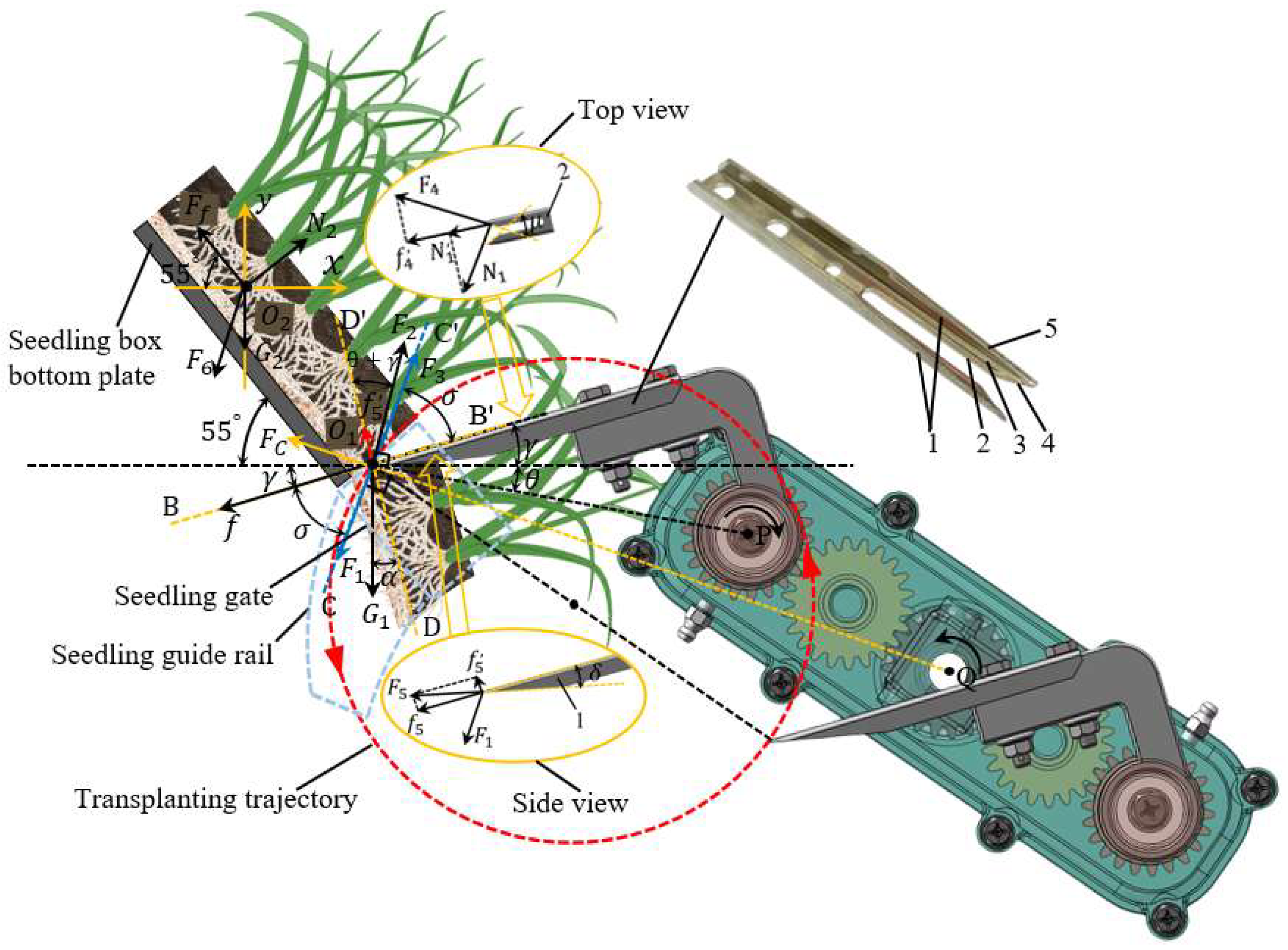
2.1.2. Force Analysis
2.1.3. Description of Three CA Arrangements of LSCs
2.1.4. Description of Seedling Needle Working Parameters
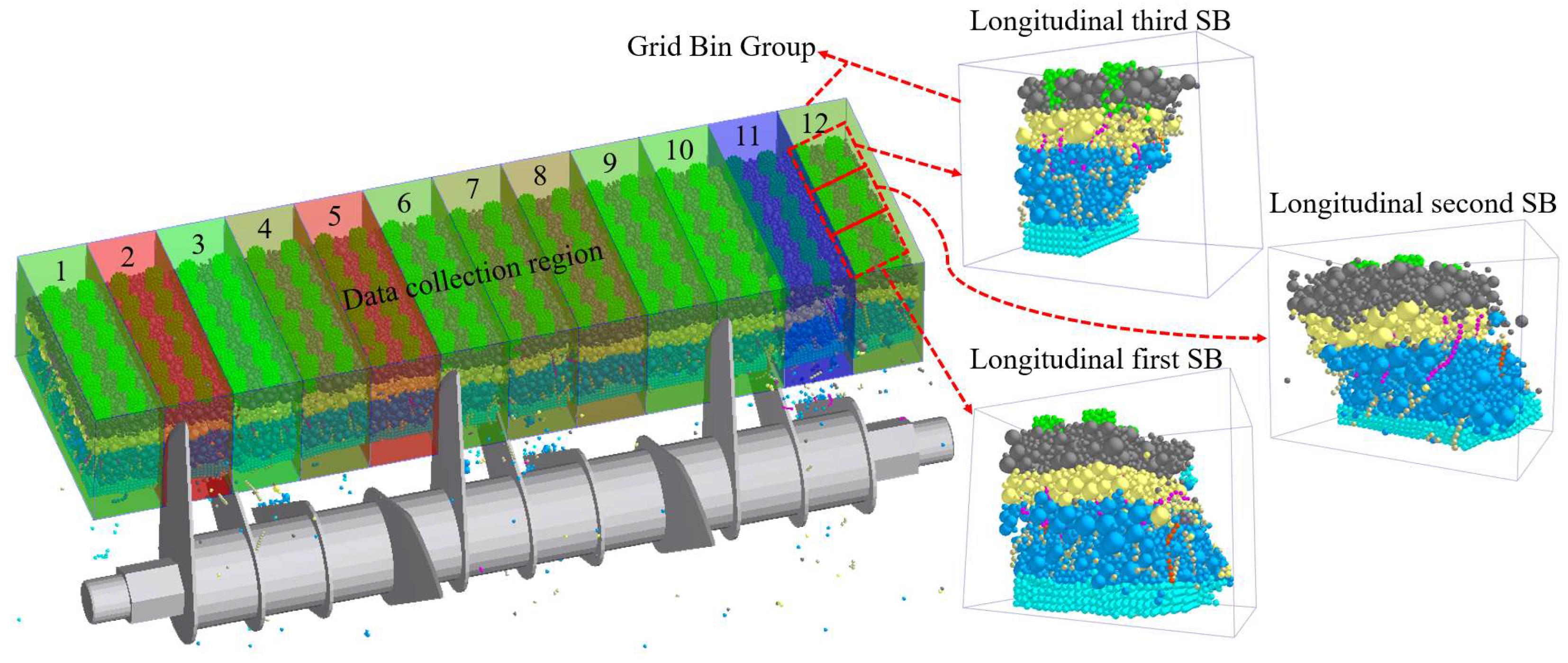
2.2. DEM-MDB Coupled Simulation Test
2.2.1. Establishment of DEM Flexible Model
2.2.2. Establishment of Coupled DEM-MBD Simulation Models
2.2.3. Design of Simulation Tests
- (1)
- In the longitudinal cutting simulation, the effects of different sliding angles and cutter shaft speeds on the performance of the three CA arrangements of the LSCs were investigated. The simulation tests were designed using the CCD method, with the levels of sliding angle (A) and cutter shaft speed (B) determined as shown in Table 1. The effects of the two factors and their interaction on the evaluation indicators of the maximum longitudinal cutting torque (TRBS), the RBS width (WRBS), the RBS breakage rate (MRBS), and the RBS root injury rate (SRBS) were analyzed.
- (2)
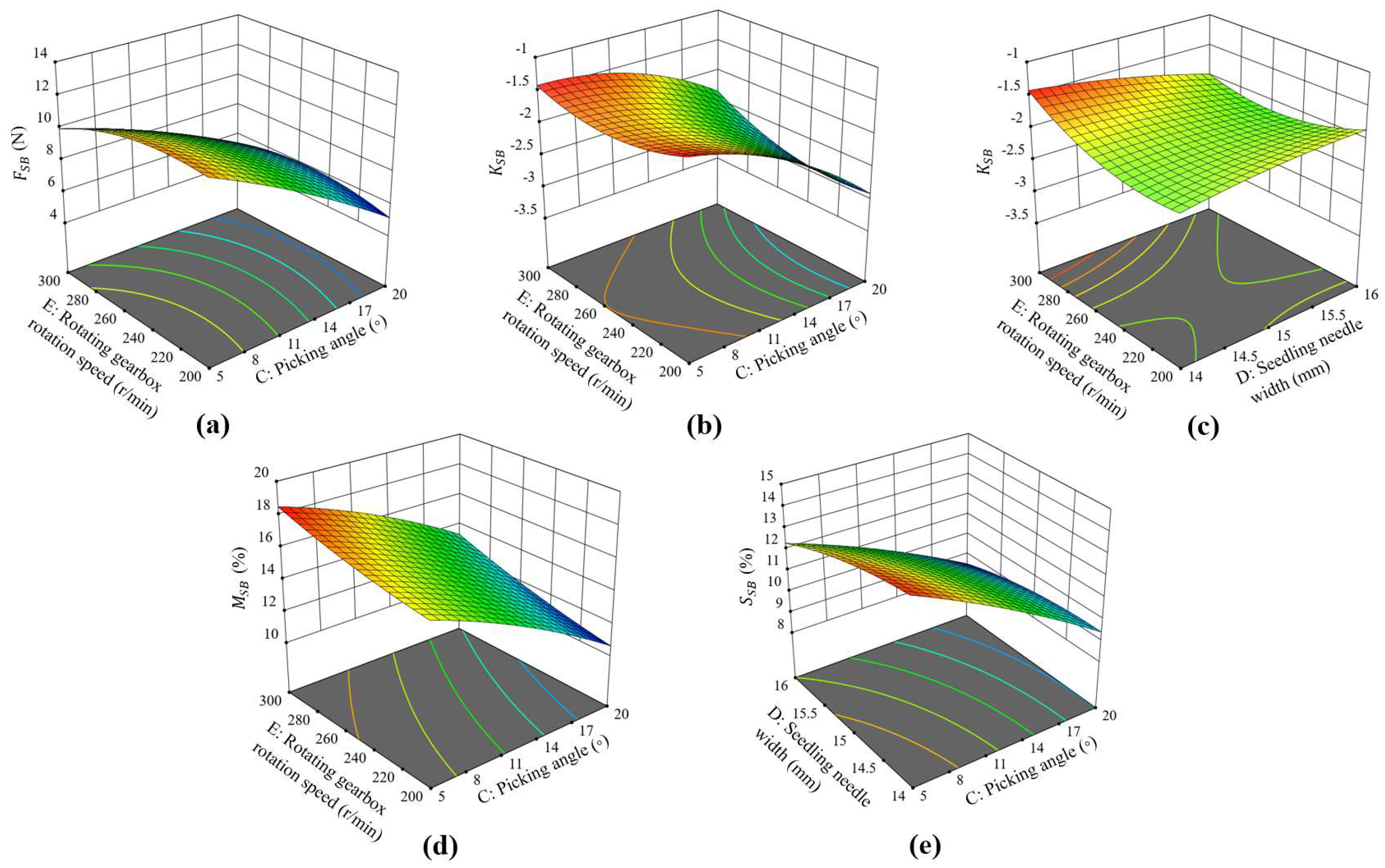
- When optimizing the working parameters of RBS lateral cutting, the picking angle (C), seedling needle width (D), and rotary gearbox speed (E) were considered, as detailed in Table 1. The simulation tests were conducted using the BBD method, employing the maximum lateral cutting resistance (FSB), the SB fracture surface contour fitting line slope (KSB), the SB breakage rate (MSB), and the SB root injury rate (SSB) as evaluation indicators. Regression models were established to determine the optimal parameter combinations.
| Factors | Symbol | Coded Levels | ||
|---|---|---|---|---|
| Low (−1) | Middle (0) | High (+1) | ||
| CCD test | ||||
| Sliding angle (°) | A | 45 | 51 | 57 |
| Cutter shaft speed (r/min) | B | 60 | 80 | 100 |
| BBD test | ||||
| Picking angle (°) | C | 5 | 12.5 | 20 |
| Seedling needle width (mm) | D | 14 | 15 | 16 |
| Rotary gearbox speed (r/min) | E | 200 | 250 | 300 |
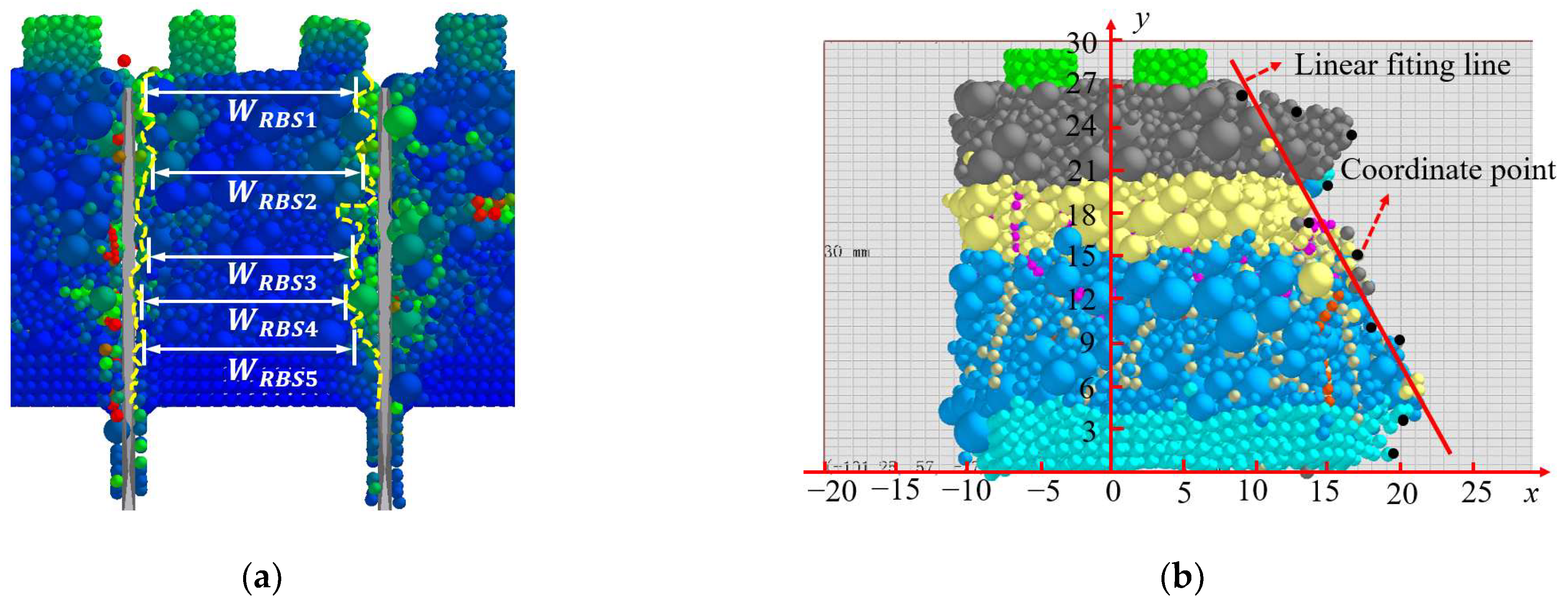
2.2.4. Measurement of Evaluation Indicators for Simulation Tests
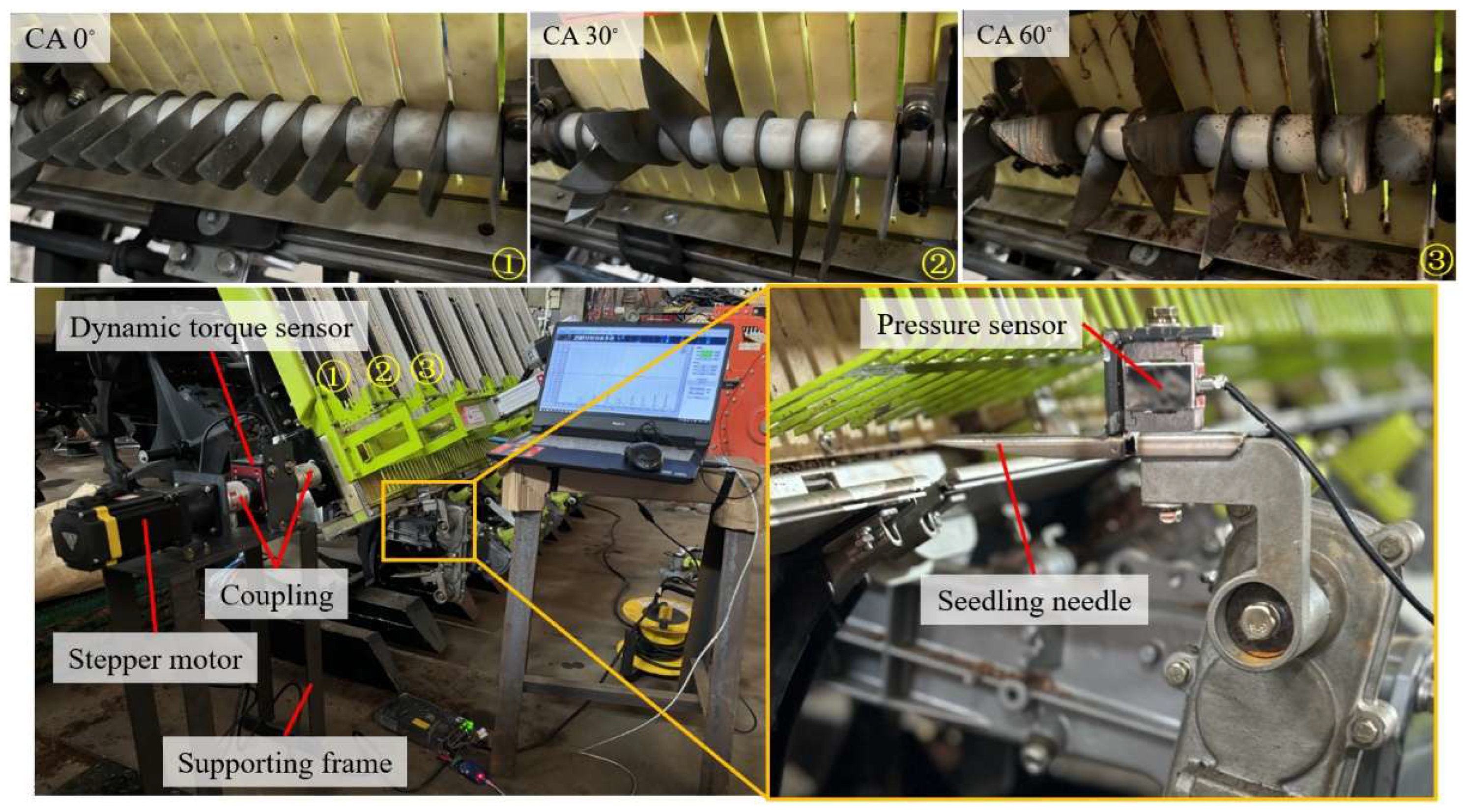
2.3. Physical Tests
2.3.1. Root Blanket Description
2.3.2. Test Equipment and Data Collection
2.4. Data Analysis
3. Results and Discussion
3.1. Analysis of Root Blanket Being Cut into SB Process
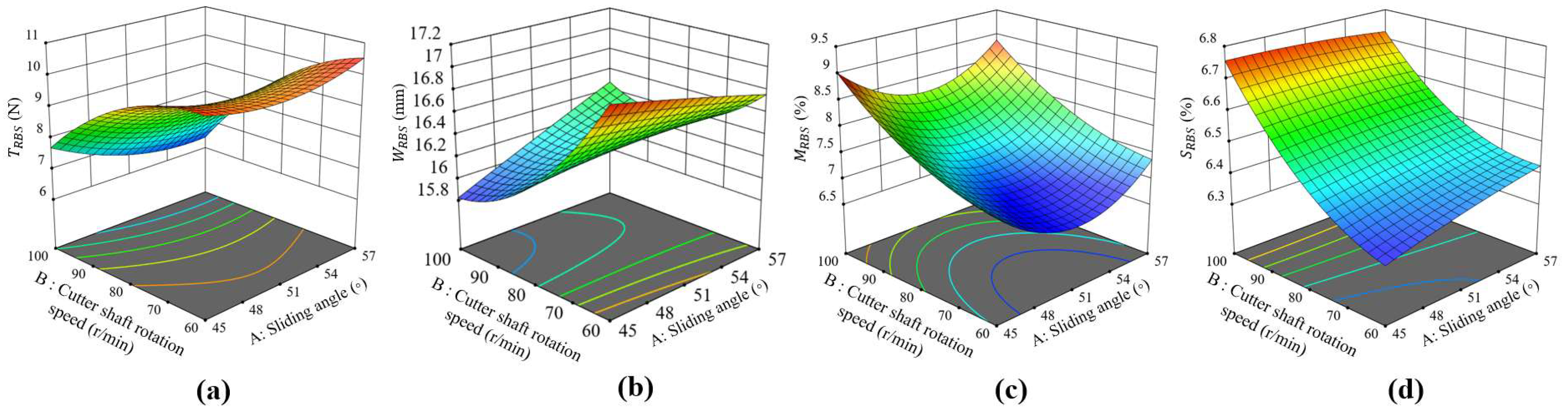
3.2. The Results of CCD Tests
3.2.1. The Test Results of LSCs Arranged at the CA 0°
3.2.2. The Test Results of LSCs Arranged at the CA 30°
3.2.3. The Test Results of LSCs Arranged at the CA 60°
3.2.4. Determination of the Optimal Value of the Longitudinal Cutting Parameters
3.2.5. CCD Optimal Parameter Verification Test
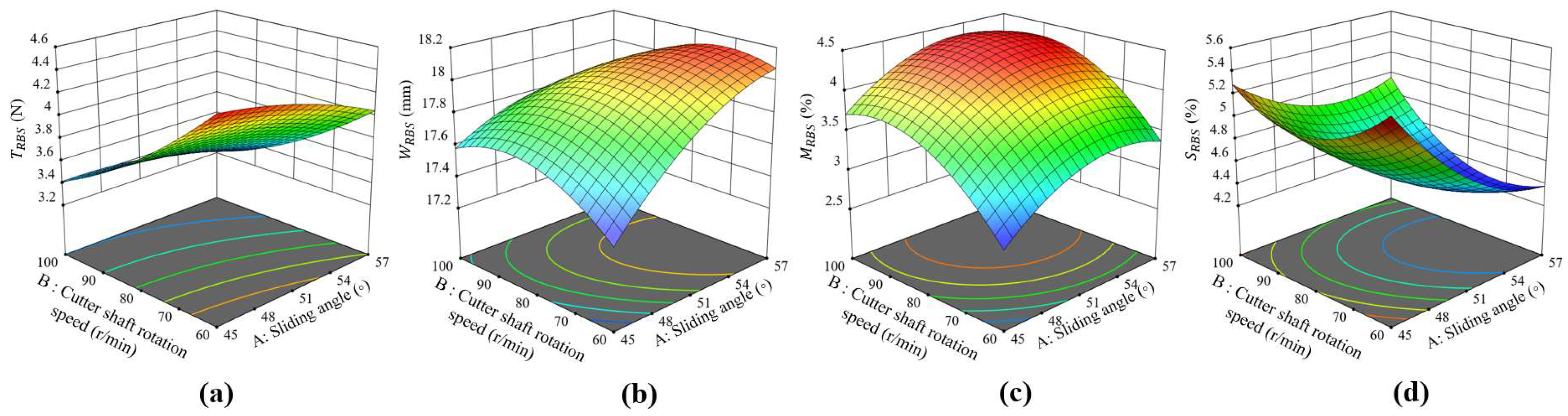
3.3. The Results of BBD Tests
3.3.1. Quadratic Regression Model
3.3.2. Factor Significance Analysis
3.3.3. Determination of the Optimal Value of the Lateral Cutting Parameters
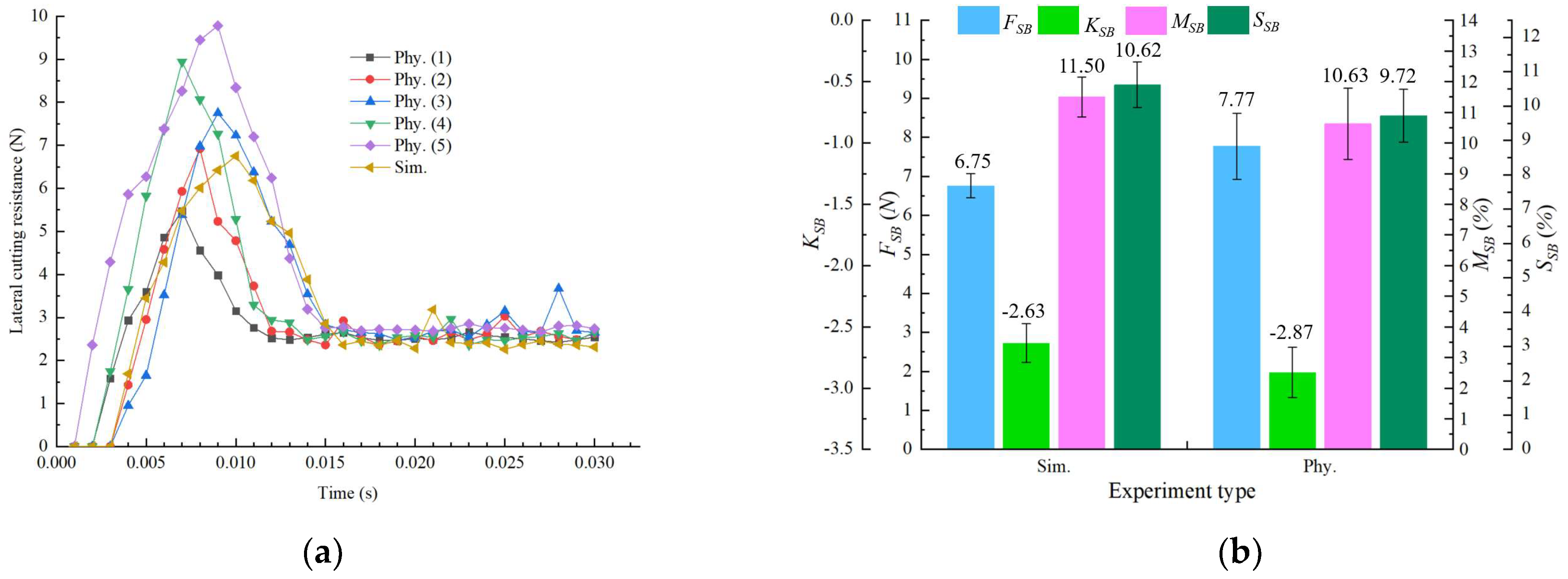
3.3.4. BBD Optimal Parameter Verification Test
4. Conclusions
- (1)
- Based on the DEM-MBD coupling method, the LSC–substrate–root interaction model was established to simulate the longitudinal cutting processes of the root blanket by the LSCs arranged at a CA of 0°, CA of 30°, and CA of 60°. The number of LSCs involved in cutting simultaneously was twelve, four and three, respectively. Based on the simulation tests of the CCD method and response surface analysis, the effects of the sliding cutting and cutter shaft speed on the maximum longitudinal cutting torque, RBS width, RBS breakage rate, and RBS root injury rate were studied. The quadratic regression models of the four performance evaluation indicators of the LSCs arranged at the three CAs were all significant, confirming the models’ high fitting accuracy and applicability in predicting slip cutting angle and cutter shaft speed. The cutting performance of the LSCs arranged at a CA of 0°, CA of 30°, and CA of 60° was significantly affected by the cutter shaft speed, the sliding angle and cutter shaft speed, and the sliding angle, respectively.
- (2)
- The LSCs’ CA arrangement significantly affected cutting performance. The cutting angles of the LSCs should be staggered to disperse the peak cutting force and reduce vibration. Among the tested configurations, LSCs arranged at a CA of 60° had the best cutting performance, which was recommended for root blanket longitudinal cutting. Based on multi-objective optimization, the optimal operating parameters were determined to be a sliding angle of 57° and a cutter shaft speed of 65.3 r/min. Under the optimal parameters, comparing the simulated data with the physical test data, the variation trend in the longitudinal cutting torque curves with the working time was basically the same, and the average deviation of the four peak values was less than 8%. The deviations of the RBS width, RBS breakage rate, and RBS root injury rate were 3.65%, 12.82%, and 13.19%, respectively, confirming the accuracy and reliability of the optimized parameters. These optimized parameters also provided a valuable reference for the subsequent parameter optimization of the cutting process of the seedling needle.
- (3)
- The coupled DEM–MBD method was used to establish a simulation model of the interaction between the seedling needle, substrate, and root, enabling the simulation of the lateral cutting process of the seedling needle. The SB fracture surface was uneven and showed a certain inclination angle. The simulation tests of the CCD method and response surface analysis were conducted to investigate the effects of picking angle, seedling needle width, and rotary gearbox speed on the four evaluation indicators: the maximum lateral cutting resistance, SB fracture surface contour fitting line slope, SB breakage rate, and SB root injury rate. All four second-order regression models were statistically significant, confirming that the optimal values of picking angle, seedling needle width, and rotary gearbox speed could be predicted. The picking angle had the highest F-value among the three factors, making it the most influential factor affecting the lateral cutting quality.
- (4)
- The optimal working parameters of the seedling needle were determined as follows: a picking angle of 20°, a seedling needle width of 15 mm, and a rotary gearbox speed of 209 r/min. Under these optimal parameters, the maximum physical lateral cutting resistance fluctuated between 5.47 N and 9.78 N. A comparison between simulated and physical test data showed that the variation laws of the lateral cutting resistance curves over time were highly consistent. The deviations of the maximum lateral cutting resistance, SB fracture surface contour fitting line slope, SB breakage rate, and SB root injury rate were 13.22%, 9.82%, 8.19%, and 9.33%, respectively. These results verified the reliability and accuracy of the model in predicting the lateral cutting performance of the seedling needle and confirmed that the optimized parameters effectively met the design requirements of the cutting device.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Item | Material | Value | Data Source | |
|---|---|---|---|---|
| Intrinsic parameters | ||||
| Density (kg·m−3) | Substrate (SI, SII, SIII) | 552 | [36] | |
| Steel | 7830 | EDEM, 2022 | ||
| PVC | 1400 | [58] | ||
| Stem | 789 | [36] | ||
| Root | 858 | [36] | ||
| Poisson’s ratio | Substrate | 0.30 | [59] | |
| Steel | 0.35 | EDEM, 2022 | ||
| PVC | 0.38 | [58] | ||
| Stem | 0.43 | [60] | ||
| Root | 0.20 | [61] | ||
| Shear modulus (Pa) | Substrate | 1.44 × 106 | [59] | |
| Steel | 7.90 × 1010 | EDEM, 2022 | ||
| PVC | 8.66 × 108 | [58] | ||
| Stem | 2.44 × 106 | [36] | ||
| Root | FR | 2.08 × 106 | [36] | |
| SR | 4.20 × 106 | [36] | ||
| TR | 2.45 × 106 | [36] | ||
| NL | 4.76 × 105 | [36] | ||
| Basic contact parameters | ||||
| Restitution coefficient | Substrate–substrate | 0.45 | [59] | |
| Substrate–steel | 0.40 | [59] | ||
| Root–root | 0.10 | [62] | ||
| Root–SII (SIII) | 0.20 | [61] | ||
| Root–steel | 0.145 | [10] | ||
| Root–PVC | 0.12 | [58] | ||
| Stem–stem | 0.30 | [63] | ||
| Stem–SI | 0.21 | [64] | ||
| Static friction coefficient | SI-SI | 0.726 | [36] | |
| SII-SII | 1.088 | [36] | ||
| SIII-SIII | 1.088 | [36] | ||
| SI–steel | 0.794 | [36] | ||
| SII (SIII)–steel | 0.986 | [39] | ||
| Root–root | 0.588 | [39] | ||
| Root–SII (SIII) | 0.650 | [36] | ||
| Root–steel | 0.484 | [36] | ||
| Root–PVC | 0.20 | [58] | ||
| Stem–stem | 0.371 | [36] | ||
| Stem–SI | 0.413 | [36] | ||
| Rolling friction coefficient | SI-SI | 0.229 | [36] | |
| SII-SII | 0.275 | [36] | ||
| SIII-SIII | 0.275 | [36] | ||
| SI–steel | 0.139 | [36] | ||
| SII (SIII)–steel | 0.069 | [36] | ||
| Root–root | 0.140 | [36] | ||
| Root–SII (SIII) | 0.161 | [39] | ||
| Root–steel | 0.196 | [39] | ||
| Root–PVC | 0.02 | [56] | ||
| Stem–stem | 0.019 | [36] | ||
| Stem–SI | 0.034 | [36] | ||
| Contact model parameters | ||||
| Normal stiffness per unit area (N·m−3) | Substrate | 107 | [36] | |
| Stem | 106 | [36] | ||
| FR | 106 | [36] | ||
| SR | 106 | [36] | ||
| TR | 106 | [36] | ||
| NL | 106 | [36] | ||
| Shear stiffness per unit area (N·m−3) | Substrate | 7.5 × 107 | [36] | |
| Stem | 106 | [36] | ||
| FR | 106 | [36] | ||
| SR | 106 | [36] | ||
| TR | 106 | [36] | ||
| NL | 106 | [36] | ||
| Normal strength (Pa) | SI | 38,468 | [36] | |
| SII | 47,323 | [36] | ||
| SIII | 105 | [36] | ||
| Stem | 105 | [36] | ||
| FR | 105 | [36] | ||
| SR | 105 | [36] | ||
| TR | 105 | [36] | ||
| NL | 105 | [36] | ||
| Shear strength (Pa) | SI | 83,653 | [36] | |
| SII | 88,216 | [36] | ||
| SIII | 105 | [36] | ||
| Stem | 105 | [36] | ||
| FR | 105 | [36] | ||
| SR | 105 | [36] | ||
| TR | 105 | [36] | ||
| NL | 104 | [36] | ||
| bonded disk scale | Substrate | 1.375 | [36] | |
| Stem | 1.2 | [62] | ||
| FR | 1.2 | [62] | ||
| SR | 1.2 | [62] | ||
| TR | 1.2 | [62] | ||
| NL | 1.2 | [62] | ||
| Interfacial ) | Stem–SI | 0.95 | [36] | |
| Root–SII | 2.12 | [36] | ||
| Root–SIII | 3.69 | [36] | ||
References
- Jia, X.; Li, Y.; Song, J.; Liu, C.; Cao, X.; Chen, L.; Wan, L.; Ma, X. Effects of Different Machine Transplanting Methods on the Physiological and Yield Characteristics of Late Rice in China. Int. J. Agric. Biol. Eng. 2023, 16, 37–47. [Google Scholar] [CrossRef]
- Xue, K.; Gao, K.; Kuang, F.; Zhang, S.; Liao, J.; Zhu, D. Machinery-Plant-Paddy Soil Coupling Model Based Numerical Simulation Method of Mechanical Transplanting Process of Big Rice Seedling. Comput. Electron. Agric. 2022, 198, 107053. [Google Scholar] [CrossRef]
- Deng, F.; He, L.; Chen, D.; Zhang, C.; Tian, Q.; Wu, Z.; Li, Q.; Zeng, Y.; Zhong, X.; Chen, H.; et al. Growth Characteristics and Grain Yield of Machine-Transplanted Medium Indica Hybrid Rice with High Daily Yield. J. Integr. Agric. 2022, 21, 2547–2558. [Google Scholar] [CrossRef]
- Jia, X.; Yang, Q.; Wen, X.; Wang, J.; Chen, Y.; Wu, A.; Song, J. Research and Application of Mechanized Seedling Raising and Transplanting Technology of Large-Bowl Blanket Seeding of Rice. China Rice 2022, 28, 18–22. [Google Scholar]
- Ye, C.; Li, Y.; Cao, Z.; Huang, J.; Sun, B.; Shu, S.; Wu, L. Effects of Different Seedling Raising Trays on Plant Type and Grain Yield of Machine-Transplanted Double Cropping Rice. Chin. J. Rice Sci. 2020, 34, 435–442. [Google Scholar]
- Jia, X.; Song, J.; Wang, J.; Cao, X.; Liu, C.; Wan, L.; Zheng, H.; Xu, Z. Effects of Seedling Age and Substrate Soil Ratio on the Population Quality and Yield of Late Rice of Machine-Transplanted Large-Pot Carpet Seedlings. Trans. Chin. Soc. Agric. Eng. 2022, 38, 1–11. [Google Scholar] [CrossRef]
- Wang, T.; Shi, M.; Xi, D.; Sun, D.; Kuang, F.; Xiong, W.; Zhang, S.; Zhu, D. Injury Mechanisms in High-Speed Transplanting of over Aged Rice Seedlings. Biosyst. Eng. 2024, 248, 142–155. [Google Scholar] [CrossRef]
- Chu, J.; Zhang, T.; Li, J.; Yin, Q.; Zhang, L.; Zhang, W. Design and Experiment of Automatic Planting Device for Root-Cut Grafted Seedlings. Trans. Chin. Soc. Agric. Mach. 2016, 47, 28–34. [Google Scholar]
- Cui, G.; Wei, Y.; Wen, S.; Zheng, X.; Wang, J.; Cui, Y. Experiment and Parameter Optimization of Root-Cutting for Trimming Postharvest Cabbage. Inmateh Agric. Eng. 2021, 63, 405–412. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Du, D.; Long, S.; Wang, Y.; Han, C.; Xu, Y. Optimization and Validation of Root-Cutting Device for Chinese Cabbage Harvester Based on Discrete Element Method. Comput. Electron. Agric. 2023, 214, 108314. [Google Scholar] [CrossRef]
- Wu, K.; Song, Y. Research Progress Analysis of Crop Stalk Cutting Theory and Method. Trans. Chin. Soc. Agric. Mach. 2022, 53, 1–20. [Google Scholar]
- Hou, S.; Chen, H.; Zou, Z.; Shi, N. Design and Test of Side-Direction Straw-Cleaning Blade for Seedbed Treatment of Original Stubble Planter. Trans. Chin. Soc. Agric. Mach. 2019, 50, 41–51+217. [Google Scholar]
- Mathanker, S.K.; Grift, T.E.; Hansen, A.C. Effect of Blade Oblique Angle and Cutting Speed on Cutting Energy for Energycane Stems. Biosyst. Eng. 2015, 133, 64–70. [Google Scholar] [CrossRef]
- Yan, L. Discussion on Sliding Cutting Angle of Working Parts of Agricultural Machinery. Acta Agric. Univ. Jiangxiensis 1991, 13, 64–68. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, X.; Xu, Y.; Li, P.; Chen, C.; Wu, S. Design and Experiment of Cutting Blade for Cane Straw. Trans. Chin. Soc. Agric. Eng. 2014, 30, 47–53. [Google Scholar]
- He, C.; You, Y.; Wang, D.; Wang, G.; Lu, D.; Morris Togo Kaji, J. The Effect of Tine Geometry During Vertical Movement on Soil Penetration Resistance Using Finite Element Analysis. Comput. Electron. Agric. 2016, 130, 97–108. [Google Scholar] [CrossRef]
- Zou, L.; Yan, D.; Niu, Z.; Yuan, J.; Cheng, H.; Zheng, H. Parametric Analysis and Numerical Optimisation of Spinach Root Vibration Shovel Cutting Using Discrete Element Method. Comput. Electron. Agric. 2023, 212, 108138. [Google Scholar] [CrossRef]
- Sun, L.; Jiang, K.; Zhou, B.; Yu, G.; Cui, R.; Xue, X. Design and Experiment of Regenerated Rice on Space Trajectory Transplantation Mechanism with Zero Lateral Offset. Trans. Chin. Soc. Agric. Mach. 2024, 55, 101–108. [Google Scholar]
- Xu, C.; Shan, Y.; Xin, L.; Xie, J.; Li, Z.; Zhao, Y. Design and Experiment of High-speed Rice Transplanter with Extensible Mulch Cutting Mechanism in Mulching Cultivation System. Trans. Chin. Soc. Agric. Mach. 2020, 51, 79–87. [Google Scholar]
- Xu, Y.; Zhu, Y.; Xue, X.; Wang, L.; Sun, L.; Yu, G. Optimal Design and Experiment on Gear Train Wide and Narrow Row Transplanting Mechanism of Spatial Direct Extraction and Large Offset of Ratooning Rice. Trans. Chin. Soc. Agric. Mach. 2022, 53, 83–90. [Google Scholar]
- Pradhan, N.C.; Sahoo, P.K.; Kushwaha, D.K.; Makwana, Y.; Mani, I.; Kumar, M.; Aruna, T.N.; Soumya, K.V. A Finite Element Modeling-Based Approach to Predict Vibrations Transmitted Through Different Body Segments of the Operator Within the Workspace of a Small Tractor. J. Field Robot. 2023, 40, 1543–1561. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Q.; Li, H.; He, J.; Wang, X.; Zhang, X.; He, D. Experimental Research on Vertical Straw Cleaning and Soil Tillage Device Based on Soil-Straw Composite Model. Comput. Electron. Agric. 2024, 216, 108510. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Y.; Liang, X.; Liu, X.; Tan, B.; He, S.; Zheng, J.; Hou, G.; Zhang, Y. Fragmentation of Soil-Root Complexes in Sloping Landscapes During Tillage and Soil Translocation. Biosyst. Eng. 2022, 223, 116–128. [Google Scholar] [CrossRef]
- Zhu, D.; Shi, M.; Yu, C.; Yu, Z.; Kuang, F.; Xiong, W.; Xue, K. Tool-Straw-Paddy Soil Coupling Model of Mechanical Rotary-Tillage Process Based on DEM-FEM. Comput. Electron. Agric. 2023, 215, 108410. [Google Scholar] [CrossRef]
- Zhang, L.; Zhai, Y.; Wu, C.; Huang, S.; Zhang, Z. Modeling the Interaction between a New Four-Bar Subsoiling Mechanism and Red Soil Using the Improved Differential Evolution Algorithm and DEM. Comput. Electron. Agric. 2023, 208, 107783. [Google Scholar] [CrossRef]
- Qian, J.; Ma, S.; Xu, Y.; Li, W.; Wang, C.; Yang, S.; Wang, F. Experimental Study on the Sugarcane Stubble Base-Cutting Mechanism. Biosyst. Eng. 2024, 245, 122–134. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Wang, C.; Xiang, Y.; Tang, H. Design and Simulation of a Trenching Device for Rice Straw Burial and Trenching Based on MBD-DEM. Comput. Electron. Agric. 2023, 207, 107722. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Zhang, X.; Zhong, X.; Wei, Z.; Geng, Y.; Cheng, X.; Zhao, K.; Bai, M. Determination and Verification of Parameters for the Discrete Element Modelling of Single Disc Covering of Flexible Straw with Soil. Biosyst. Eng. 2023, 233, 151–167. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, X.; Dong, J.; Wang, X.; Zhao, H.; Chen, X.; Zhang, Z.; Huang, Y.; Shi, J. Optimization of Operating Angles of Disc Coulters for Maize Residue Management Using Discrete Element Method. Comput. Electron. Agric. 2024, 218, 108691. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Zhang, X.; Cheng, X.; Wei, Z.; Zhou, H.; Zhao, K. The Impact of ‘T’-Shaped Furrow Opener of No-Tillage Seeder on Straw and Soil Based on Discrete Element Method. Comput. Electron. Agric. 2023, 213, 108278. [Google Scholar] [CrossRef]
- Lin, J.; Liao, Q.; Wang, X.; Kang, Y.; Du, W.; Zhang, Q. Exploring Straw Movement Through the Simulation of Shovel-Type Seedbed Preparation Machine-Straw-Soil Interaction Using the DEM-MBD Coupling Method. Comput. Electron. Agric. 2024, 226, 109465. [Google Scholar] [CrossRef]
- Xie, D.; He, J.; Liu, T.; Liu, C.; Zhao, G.; Chen, L. Establishment and Validation the DEM-MBD Coupling Model of Flexible Straw-Shajiang Black Soil-Walking Mechanism Interactions. Comput. Electron. Agric. 2024, 224, 109203. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Ma, L.; Zong, W.; Zhan, G.; Lin, Z. Design and test of static sliding Cut angle constant cut-ting machine for chain oil sunflower harvester header. Trans. Chin. Soc. Agric. Mach. 2021, 52, 99–108. [Google Scholar]
- Zhang, C.; Chen, L.; Xia, J.; Zhang, J. Effects of Blade Sliding Cutting Angle and Stem Level on Cutting Energy of Rice Stems. Int. J. Agric. Biol. Eng. 2019, 12, 75–81. [Google Scholar] [CrossRef]
- Zheng, K.; He, J.; Li, H.; Diao, P.; Wang, Q.; Zhao, H. Research on Polyline Soil-Breaking Blade Subsoiler Based on Subsoiling Soil Model Using Discrete Element Method. Trans. Chin. Soc. Agric. Mach. 2016, 47, 62–72. [Google Scholar] [CrossRef]
- Jia, X.; Zheng, X.; Chen, L.; Liu, C.; Song, J.; Zhu, C.; Xu, J.; Hao, S. Discrete Element Flexible Modeling and Experimental Verification of Rice Blanket Seedling Root Blanket. Comput. Electron. Agric. 2025, 233, 110155. [Google Scholar] [CrossRef]
- Ahmadi, I. A Torque Calculator for Rotary Tiller Using the Laws of Classical Mechanics. Soil. Tillage Res. 2017, 165, 137–143. [Google Scholar] [CrossRef]
- Vu, V.-D.; Ngo, Q.-H.; Nguyen, T.-T.; Nguyen, H.-C.; Nguyen, Q.-T.; Nguyen, V.-D. Multi-Objective Optimisation of Cutting Force and Cutting Power in Chopping Agricultural Residues. Biosyst. Eng. 2020, 191, 107–115. [Google Scholar] [CrossRef]
- Wu, G.; Yu, G.; Ye, B.; Yu, Y. Forward-Reverse Design Method for Rice Potted-Seedling Transplanting with Compound Planetary Gear Train. Trans. Chin. Soc. Agric. Mach. 2020, 51, 85–93+102. [Google Scholar] [CrossRef]
- Chen, Z.; Hua, G.; Li, S.; Ding, X.; Fang, X. Agricultural Machinery Design Handbook (First Volume); China Agricultural Science and Technology Press: Beijing, China, 2007. [Google Scholar]
- Song, X.; Dai, F.; Zhang, X.; Chen, H.; Zhang, F.; Zhao, W. Numerical Analyses Ridge-Forming for Whole Film-Mulching and Double Ridge-Furrow, a Discrete Element Method. Comput. Electron. Agric. 2023, 215, 108364. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, H.; Wang, X.; Dong, J.; Zhao, P.; Yang, F.; Chen, X.; Liu, F.; Huang, Y. Discrete Element Modeling and Shear Properties of the Maize Stubble-Soil Complex. Comput. Electron. Agric. 2023, 204, 107519. [Google Scholar] [CrossRef]
- Coetzee, C.J. Particle Upscaling: Calibration and Validation of the Discrete Element Method. Powder Technol. 2019, 344, 487–503. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R.; Cao, Q.; Zhang, Y.; Fu, J.; Wen, X.; Yuan, H. A Calibration Method for Contact Parameters of Agricultural Particle Mixtures Inspired by the Brazil Nut Effect (BNE): The Case of Tiger Nut Tuber-Stem-Soil Mixture. Comput. Electron. Agric. 2023, 212, 108112. [Google Scholar] [CrossRef]
- Pradhan, N.C.; Sahoo, P.K.; Kushwaha, D.K.; Mani, I.; Srivastava, A.; Sagar, A.; Kumari, N.; Sarkar, S.K.; Makwana, Y. A Novel Approach for Development and Evaluation of LiDAR Navigated Electronic Maize Seeding System Using Check Row Quality Index. Sensors 2021, 21, 5934. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Thoms, D.; Chen, Y.; Ma, X. Comparison of Soil and Corn Residue Cutting Performance of Different Discs Used for Vertical Tillage. Sci. Rep. 2021, 11, 2537. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, D.; Yang, L.; Cui, T.; Jing, H.; Zhong, X. Modeling the Interaction of Soil and a Vibrating Subsoiler Using the Discrete Element Method. Comput. Electron. Agric. 2020, 174, 105518. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Chen, L.; Li, H.; Huang, Y.; Li, J.; Luo, G.; Yao, J. Effects of Coupling of Nursing Seedling Densities and Seedling Fetching Area on Transplanting Quality and Yield of Hybrid Rice. Trans. Chin. Soc. Agric. Eng. 2019, 35, 20–30. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Pan, H.; Zheng, Z.; Huang, Y.; Zhu, R. Effect of Soil Particle Size on Soil-Subsoiler Interactions Using the Discrete Element Method Simulations. Biosyst. Eng. 2019, 182, 138–150. [Google Scholar] [CrossRef]
- Bono, F.M.; Cinquemani, S.; Radicioni, L.; Conese, C.; Tarabini, M. An Approach for Fault Detection Based on Multibody Simulations and Feature Selection Algorithm. In Proceedings of the NDE 4.0, Predictive Maintenance, and Communication and Energy Systems in a Globally Networked World, Long Beach, CA, USA, 6 March–11 April 2022; p. 6. [Google Scholar]
- Zheng, Z.; He, J.; Li, H.; Diao, P.; Wang, Q.; Zhang, X. Design and Experiment of Straw-Chopping Device with Chopping and Fixed Knife Supported Slide Cutting. Trans. Chin. Soc. Agric. Mach. 2016, 47, 108–116. [Google Scholar]
- Liu, X. Research on the Interaction Mechanism Between the Blade and the Maize Root-Soil Composite and Optimization of the Wing-Shaped Stubble-Breaking Device. Ph.D. Thesis, Jilin University, Hangzhou, China, 2025. [Google Scholar]
- Wang, X.; Gao, P.; Yue, B.; Shen, H.; Fu, Z.; Zheng, Z.; Zhu, R.; Huang, Y. Optimisation of Installation Parameters of Subsoiler’ Wing Using the Discrete Element Method. Comput. Electron. Agric. 2019, 162, 523–530. [Google Scholar] [CrossRef]
- Maraveas, C.; Tsigkas, N.; Bartzanas, T. Agricultural Processes Simulation Using Discrete Element Method: A Review. Comput. Electron. Agric. 2025, 237, 110733. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, A.; Liu, X.; Tong, Z.; Zhang, H. DEM/CFD-DEM Modelling of Non-Spherical Particulate Systems: Theoretical Developments and Applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]
- Zeng, Z.; Ma, X.; Chen, Y.; Qi, L. Modelling Residue Incorporation of Selected Chisel Ploughing Tools Using the Discrete Element Method (DEM). Soil. Tillage Res. 2020, 197, 104505. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, M.; Xie, J.; Cao, S.; Wu, A.; Wang, Z. Discrete Element Modeling and Physical Experiment Research on the Biomechanical Properties of Cotton Stalk. Comput. Electron. Agric. 2023, 204, 107502. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, Y.; Ma, L.; Ding, X.; Cao, D.; He, Z. Design and Experiment of Air-Suction Substrates Removal Device for Plug Lack of Seedlings Trays. Trans. Chin. Soc. Agric. Mach. 2022, 53, 140–151. [Google Scholar] [CrossRef]
- Wang, G.; Xue, Z.; Song, G.; Wang, Q.; Guo, C. Study on Spiral Stirring Process Simulation and Mixing Mechanism of Coconut Bran Substrate Based on Discrete Element Method. 2021. Available online: https://dost.hainan.gov.cn/kjcg/cggg/cggg2022/10/202204/t20220424_3180350.html (accessed on 20 February 2025).
- Xue, K.; Gao, K.; Wang, T.; Zhang, X.; Zhang, S.; Kuang, F.; Zhu, D. Biomechanical Modeling of Rice Seedling Stalk Based on Multi-Scale Structure and Heterogeneous Materials. Comput. Electron. Agric. 2023, 210, 107904. [Google Scholar] [CrossRef]
- Ma, G. Study on Enhancement Mechanism of Low Loss Seedling Picking in Biochar and Air Ejection-Package Clamping Pick-up Device. Ph.D. Thesis, Jiangsu University, Zhengjiang, China, 2021. [Google Scholar]
- Zhou, J.; Sun, W.; Liang, Z. Research on the Construction of Discrete Element Flexible Model for Jerusalem Artichoke Root-Tuber at Harvest Stage. Trans. Chin. Soc. Agric. Mach. 2023, 54, 124–132. [Google Scholar] [CrossRef]
- Hou, J.; Xie, F.; Wang, X.; Liu, D.; Chen, Z. Measurement of Contact Physical Parameters of Flexible Rice Straw and Discrete Element Simula Tion Calibration. Acta Agric. Univ. Jiangxiensis 2022, 44, 747–758. [Google Scholar]
- Liu, W.; Zhang, G.; Zhou, Y.; Liu, H.; Tang, N.; Kang, Q.; Zhao, Z. Establishment of Discrete Element Flexible Model of the Tiller Taro Plant and Clamping and Pulling Experiment. Front. Plant Sci. 2022, 13, 1019017. [Google Scholar] [CrossRef]







| Order | Factor | Simulation Data | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CA 0° | CA 30° | CA 60° | ||||||||||||
| A (°) | B (r/min) | (N·m) | (mm) | (%) | (mm) | (N·m) | (mm) | (%) | (mm) | (N·m) | (mm) | (%) | (mm) | |
| 1 | 45 | 60 | 10.52 | 16.96 | 7.28 | 6.33 | 7.35 | 16.95 | 5.28 | 4.98 | 4.45 | 17.43 | 2.89 | 5.36 |
| 2 | 57 | 60 | 10.49 | 16.72 | 7.24 | 6.41 | 6.91 | 17.41 | 3.92 | 4.76 | 4.04 | 18.09 | 3.45 | 4.33 |
| 3 | 45 | 100 | 7.63 | 15.83 | 8.94 | 6.78 | 6.12 | 16.28 | 6.95 | 5.54 | 3.45 | 17.56 | 3.78 | 5.18 |
| 4 | 57 | 100 | 6.04 | 16.58 | 8.82 | 6.72 | 5.15 | 17.43 | 6.07 | 5.17 | 3.24 | 17.68 | 4.28 | 4.89 |
| 5 | 45 | 80 | 9.55 | 16.31 | 8.15 | 6.42 | 6.93 | 16.55 | 6.43 | 5.15 | 3.81 | 17.62 | 3.52 | 5.24 |
| 6 | 57 | 80 | 9.57 | 16.28 | 8.05 | 6.52 | 5.95 | 17.32 | 5.42 | 4.85 | 3.52 | 18.15 | 4.08 | 4.48 |
| 7 | 51 | 60 | 9.80 | 17.12 | 6.95 | 6.38 | 6.52 | 16.84 | 4.98 | 4.91 | 4.33 | 17.78 | 3.27 | 4.82 |
| 8 | 51 | 100 | 7.03 | 16.05 | 8.36 | 6.73 | 5.43 | 16.95 | 6.58 | 5.34 | 3.32 | 17.89 | 4.18 | 5.07 |
| 9 | 51 | 80 | 8.97 | 16.15 | 7.07 | 6.49 | 6.01 | 16.51 | 6.84 | 5.21 | 3.76 | 17.94 | 4.34 | 4.41 |
| 10 | 51 | 80 | 8.97 | 16.27 | 7.07 | 6.49 | 6.01 | 16.51 | 6.84 | 5.21 | 3.76 | 17.97 | 4.34 | 4.41 |
| 11 | 51 | 80 | 8.97 | 16.38 | 7.07 | 6.49 | 6.01 | 16.52 | 6.84 | 5.21 | 3.76 | 18.01 | 4.34 | 4.41 |
| 12 | 51 | 80 | 8.97 | 16.26 | 7.07 | 6.49 | 6.01 | 16.64 | 6.84 | 5.21 | 3.76 | 18.05 | 4.34 | 4.41 |
| 13 | 51 | 80 | 8.97 | 16.19 | 7.07 | 6.49 | 6.01 | 16.66 | 6.84 | 5.21 | 3.76 | 18.08 | 4.34 | 4.41 |
| Source | CA 0° | CA 30° | CA 60° | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| 0.057 | 0.192 | 0.609 | 0.0625 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | |
| <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | 0.146 | <0.01 | <0.01 | <0.01 | 0.393 | <0.01 | 0.120 | |
| 0.030 | <0.01 | 0.846 | <0.01 | 0.043 | 0.038 | 0.328 | 0.724 | 0.016 | <0.01 | 0.825 | 0.038 | |
| 0.042 | 0.935 | <0.01 | 0.570 | <0.01 | 0.018 | <0.01 | 0.020 | 0.013 | 0.023 | <0.01 | 0.034 | |
| <0.01 | 0.011 | 0.047 | <0.01 | 0.499 | 0.037 | <0.01 | 0.793 | <0.01 | <0.01 | <0.01 | <0.01 | |
| Lack of Fit | / | 0.099 | / | / | / | 0.059 | / | / | / | 0.170 | / | |
| C.V.% | 3.230 | 0.829 | 2.600 | 0.340 | 1.730 | 0.802 | 3.720 | 1.230 | 0.845 | 0.427 | 3.330 | 3.070 |
| 0.971 | 0.918 | 0.957 | 0.985 | 0.982 | 0.925 | 0.967 | 0.948 | 0.995 | 0.936 | 0.960 | 0.916 | |
| 0.951 | 0.860 | 0.926 | 0.975 | 0.969 | 0.872 | 0.943 | 0.910 | 0.986 | 0.890 | 0.931 | 0.855 | |
| Adeq Precision | 21.276 | 13.818 | 17.404 | 29.254 | 29.652 | 12.421 | 19.678 | 17.792 | 57.390 | 14.063 | 16.885 | 11.047 |
| NO. | Factor | (N) | (%) | (%) | |||
|---|---|---|---|---|---|---|---|
(°) | (mm) | (r/min) | |||||
| 1 | 5 | 14 | 250 | 12.36 | −1.62 | 17.86 | 14.25 |
| 2 | 20 | 14 | 250 | 6.41 | −2.87 | 12.37 | 9.35 |
| 3 | 5 | 16 | 250 | 12.88 | −1.65 | 16.24 | 12.41 |
| 4 | 20 | 16 | 250 | 6.87 | −3.05 | 10.89 | 8.47 |
| 5 | 5 | 15 | 200 | 11.45 | −1.47 | 16.53 | 14.39 |
| 6 | 20 | 15 | 200 | 5.32 | −2.91 | 10.63 | 10.05 |
| 7 | 5 | 15 | 300 | 9.83 | −1.41 | 18.49 | 12.98 |
| 8 | 20 | 15 | 300 | 5.67 | −2.13 | 13.28 | 8.85 |
| 9 | 12.5 | 14 | 200 | 9.52 | −1.97 | 14.72 | 12.86 |
| 10 | 12.5 | 16 | 200 | 9.78 | −1.82 | 12.81 | 11.23 |
| 11 | 12.5 | 14 | 300 | 8.64 | −1.45 | 17.15 | 11.67 |
| 12 | 12.5 | 16 | 300 | 8.91 | −2.06 | 15.31 | 10.29 |
| 13 | 12.5 | 15 | 250 | 9.22 | −2.04 | 14.93 | 11.62 |
| 14 | 12.5 | 15 | 250 | 8.95 | −1.95 | 14.87 | 11.35 |
| 15 | 12.5 | 15 | 250 | 9.06 | −1.88 | 15.02 | 11.91 |
| 16 | 12.5 | 15 | 250 | 9.15 | −2.09 | 14.79 | 11.48 |
| 17 | 12.5 | 15 | 250 | 9.35 | −2.03 | 14.95 | 11.73 |
| Source | ||||||||
|---|---|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Model | 109.260 | <0.01 | 37.640 | <0.001 | 583.610 | <0.001 | 143.650 | <0.001 |
| 873.970 | <0.01 | 261.220 | <0.01 | 1022.490 | <0.01 | 1069.670 | <0.01 | |
| 4.030 | 0.085 | 4.860 | 0.063 | 391.750 | <0.01 | 117.210 | <0.01 | |
| 16.100 | <0.01 | 11.270 | 0.012 | 759.840 | <0.01 | 80.210 | <0.01 | |
| (AB) | 0.013 | 0.913 | 0.4876 | 0.508 | 0.32730 | 0.5852 | 6.580 | 0.037 |
| (AC) | 13.700 | <0.01 | 8.330 | 0.023 | 7.950 | 0.0258 | 0.315 | 0.592 |
| (BC) | 0.000 | 0.986 | 12.520 | <0.01 | 0.082 | 0.7831 | 0.446 | 0.525 |
| 6.500 | 0.038 | 20.980 | <0.01 | 49.250 | <0.01 | 5.900 | 0.045 | |
| 39.450 | <0.01 | 1.300 | 0.291 | 6.630 | 0.0368 | 9.190 | 0.019 | |
| 33.270 | <0.01 | 19.770 | <0.01 | 16.060 | <0.01 | 3.520 | 0.103 | |
| Lack of Fit | 5.78 | 0.062 | 2.580 | 0.191 | 3.310 | 0.139 | 0.399 | 0.762 |
| C.V.% | 2.950 | 5.290 | 0.829 | 1.630 | ||||
| 0.993 | 0.980 | 0.998 | 0.995 | |||||
| 0.984 | 0.954 | 0.997 | 0.988 | |||||
| 0.906 | 0.776 | 0.984 | 0.974 | |||||
| Adeq Precision | 36.474 | 18.164 | 83.888 | 41.084 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Hao, S.; Song, J.; Liu, C.; Zheng, X.; Chen, L.; Zhu, C.; Xu, J.; Liu, J. Numerical Optimization of Root Blanket-Cutting Device for Rice Blanket Seedling Cutting and Throwing Transplanter Based on DEM-MBD. Agriculture 2025, 15, 2105. https://doi.org/10.3390/agriculture15202105
Jia X, Hao S, Song J, Liu C, Zheng X, Chen L, Zhu C, Xu J, Liu J. Numerical Optimization of Root Blanket-Cutting Device for Rice Blanket Seedling Cutting and Throwing Transplanter Based on DEM-MBD. Agriculture. 2025; 15(20):2105. https://doi.org/10.3390/agriculture15202105
Chicago/Turabian StyleJia, Xuan, Shuaihua Hao, Jinyu Song, Cailing Liu, Xiaopei Zheng, Licai Chen, Chengtian Zhu, Jitong Xu, and Jianjun Liu. 2025. "Numerical Optimization of Root Blanket-Cutting Device for Rice Blanket Seedling Cutting and Throwing Transplanter Based on DEM-MBD" Agriculture 15, no. 20: 2105. https://doi.org/10.3390/agriculture15202105
APA StyleJia, X., Hao, S., Song, J., Liu, C., Zheng, X., Chen, L., Zhu, C., Xu, J., & Liu, J. (2025). Numerical Optimization of Root Blanket-Cutting Device for Rice Blanket Seedling Cutting and Throwing Transplanter Based on DEM-MBD. Agriculture, 15(20), 2105. https://doi.org/10.3390/agriculture15202105






