Quantification and Optimization of Straight-Line Attitude Control for Orchard Weeding Robots Using Adaptive Pure Pursuit
Abstract
1. Introduction
- An adaptive Pure Pursuit control strategy integrating yaw-rate feedback is proposed, further improving path-tracking accuracy and attitude stability.
- A set of time-series evaluation metrics tailored to attitude response is developed, providing a quantitative framework for straight-line control performance analysis.
- Comprehensive experiments in real orchard environments are conducted, systematically comparing attitude behaviors under different control strategies and demonstrating the effectiveness and application potential of the proposed method.
2. Materials and Methods
2.1. Experimental Data Acquisition
2.2. Quantitative Analysis and Optimization of Straight-Line Attitude Control
2.2.1. Pure Pursuit Control Algorithm
2.2.2. Adaptive Lookahead Pure Pursuit Control
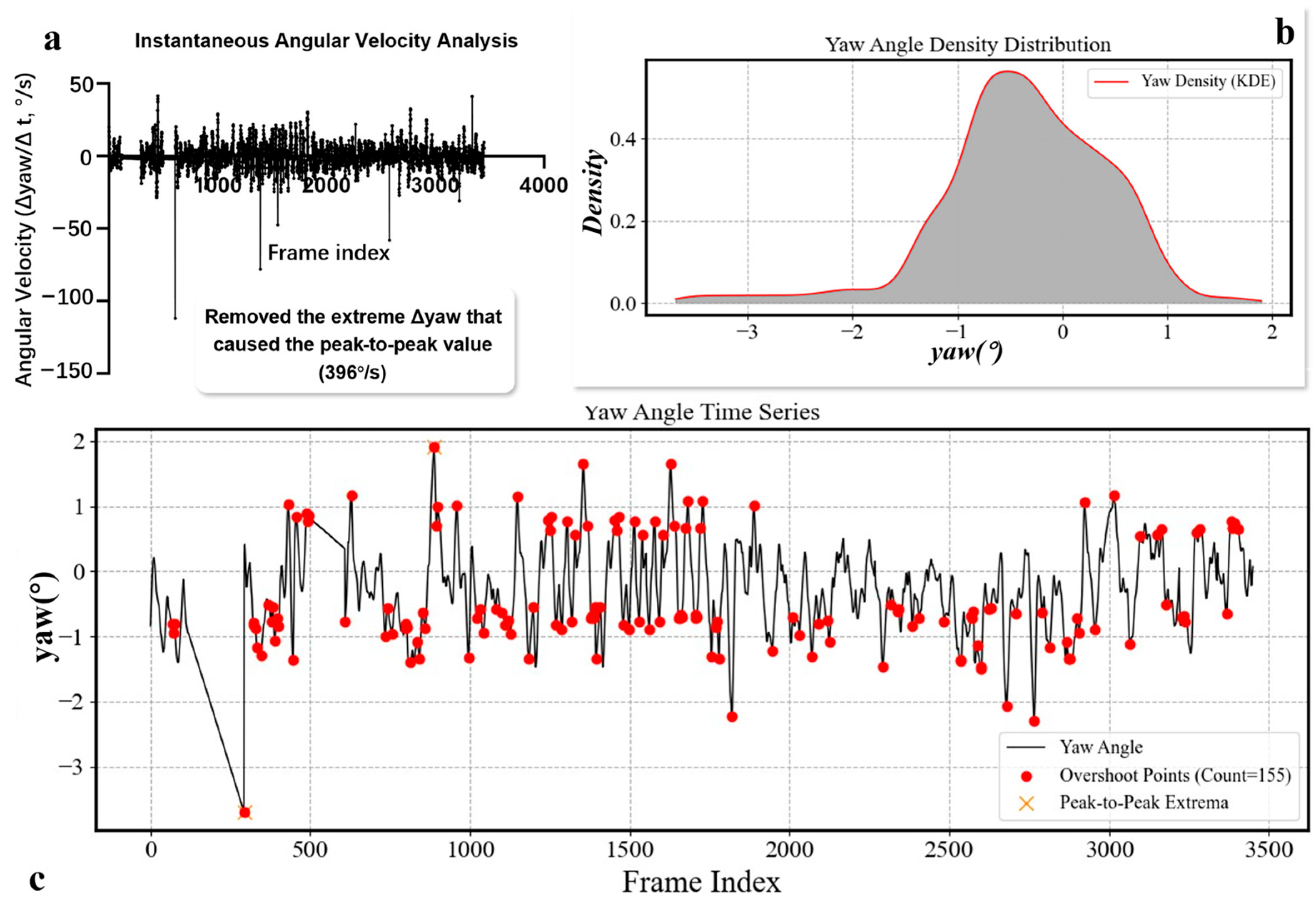
2.2.3. Quantitative Analysis of Straight-Line Attitude Response
3. Results and Discussion
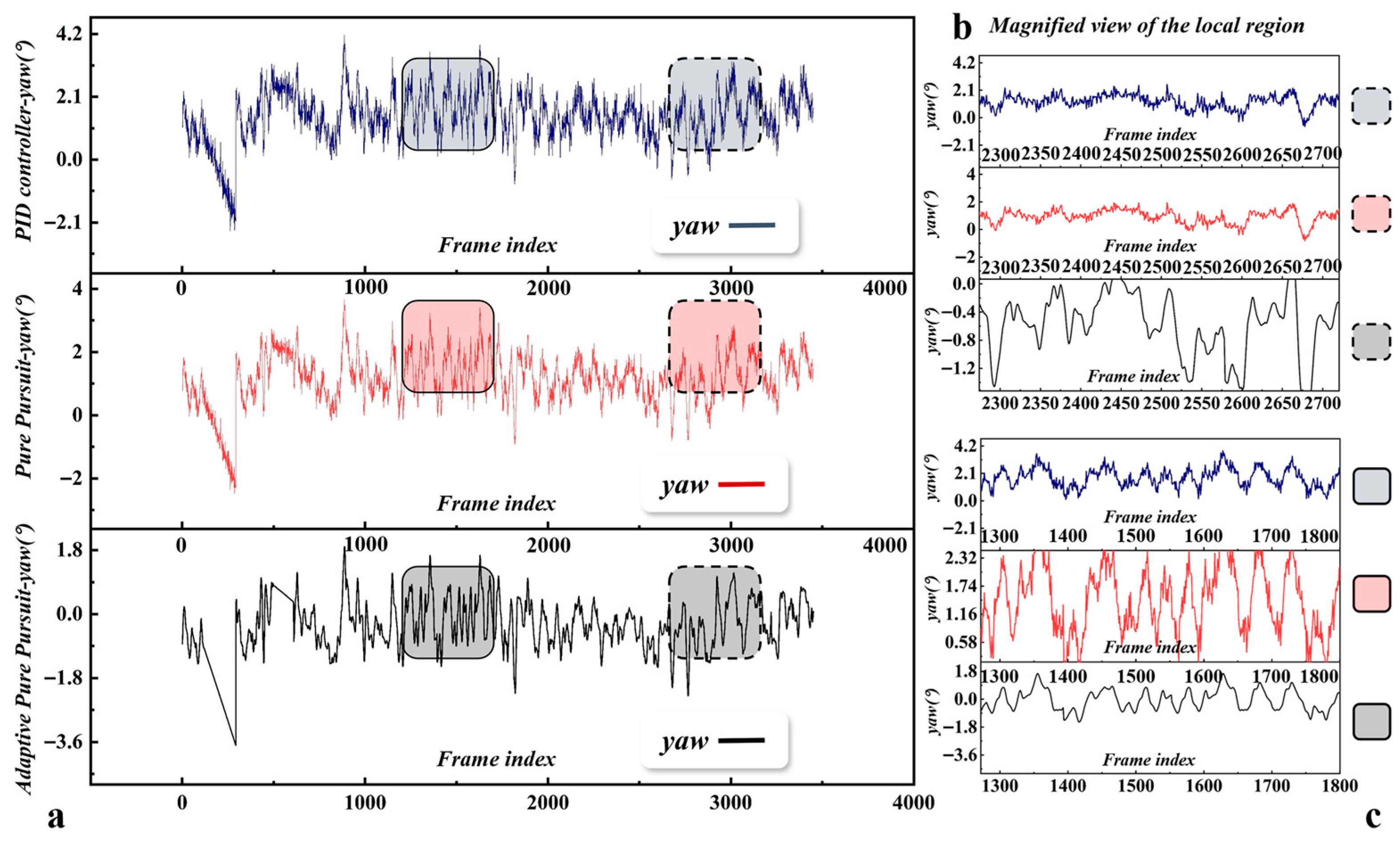
3.1. Analysis of Straight-Line Attitude Control Performance
3.2. Time-Series Behavior Analysis of Attitude Response Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Abbas, I.; Noor, R.S. Development of deep learning-based variable rate agrochemical spraying system for targeted weeds control in strawberry crop. Agronomy 2021, 11, 1480. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Tang, J.; Chen, X. Effects of weed management practices on orchard soil biological and fertility properties in southeastern China. Soil Tillage Res. 2007, 93, 179–185. [Google Scholar] [CrossRef]
- Hussain, S.; Sharma, M.K.; War, A.R.; Hussain, B. Weed management in apple cv. royal delicious by using different orchard floor management practices. Int. J. Fruit Sci. 2020, 20, 891–921. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Li, Y.; Hou, Y.; Zhao, Z.; Meng, L.; Wang, Z. Cover crops control weed and improve soil qualities in citrus orchard. J. Soil Sci. Plant Nutr. 2023, 23, 6827–6837. [Google Scholar] [CrossRef]
- Reiser, D.; Sehsah, E.S.; Bumann, O.; Morhard, J.; Griepentrog, H.W. Development of an autonomous electric robot implement for intra-row weeding in vineyards. Agriculture 2019, 9, 18. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Yang, Y.; Xie, H.; Zhang, K.; Wang, Y.; Li, Y.; Zhou, J.; Xu, L. Design, development, integration, and field evaluation of a ridge-planting strawberry harvesting robot. Agriculture 2024, 14, 2126. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, S.; Li, N.; Faheem, M.; Zhou, T.; Cai, W.; Zhao, M.; Zhu, X.; Li, P. Development and field test of an autonomous strawberry plug seeding transplanter for use in elevated cultivation. Appl. Eng. Agric. 2019, 35, 1067–1078. [Google Scholar] [CrossRef]
- Xiang, M.; Qu, M.; Wang, G.; Ma, Z.; Chen, X.; Zhou, Z.; Jia, H. Crop detection technologies, mechanical weeding executive parts and working performance of intelligent mechanical weeding: A review. Front. Plant Sci. 2024, 15, 1361002. [Google Scholar] [CrossRef]
- Ju, J.; Chen, G.; Lv, Z.; Zhao, M.; Sun, L.; Wang, Z.; Wang, J. Design and experiment of an adaptive cruise weeding robot for paddy fields based on improved YOLOv5. Comput. Electron. Agric. 2024, 219, 108824. [Google Scholar] [CrossRef]
- Zhao, P.; Chen, J.; Li, J.; Ning, J.; Chang, Y.; Yang, S. Design and Testing of an autonomous laser weeding robot for strawberry fields based on DIN-LW-YOLO. Comput. Electron. Agric. 2025, 229, 109808. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, J.; Liu, Y.; Zhang, T.; Meng, Y.; Chen, J.; Chen, X. An Ultrasonic Ridge-Tracking Method Based on Limiter Sliding Window Filter and Fuzzy Pure Pursuit Control for Ridge Transplanter. Agriculture 2024, 14, 1713. [Google Scholar] [CrossRef]
- Bao, X.; Mao, J.; Dai, P.; Gong, Z.; Li, S.; Chen, H. Research on trajectory planning and control system of general mobile platform for Mountain Orchard. J. Eng. 2022, 2022, 466–477. [Google Scholar] [CrossRef]
- Ma, Z.; Yang, S.; Li, J.; Qi, J. Research on slam localization algorithm for orchard dynamic vision based on YOLOD-SLAM2. Agriculture 2024, 14, 1622. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Zhang, W.; Li, H.; Zeng, Y.; Wang, T.; Cao, Y. Research on Path Tracking for an Orchard Mowing Robot Based on Cascaded Model Predictive Control and Anti-Slip Drive Control. Agronomy 2023, 13, 1395. [Google Scholar] [CrossRef]
- Bayar, G.; Bergerman, M.; Koku, A.B.; Ilhan Konukseven, E. Localization and control of an autonomous orchard vehicle. Comput. Electron. Agric. 2015, 115, 118–128. [Google Scholar] [CrossRef]
- Qu, J.; Li, H.; Zhang, Z.; Xi, X.; Zhang, R.; Guo, K. Performance analysis and optimization for steering motion mode switching of an agricultural four-wheel-steering mobile robot. Agronomy 2022, 12, 2655. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive sliding mode path tracking control of unmanned rice transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Hu, J.; Pan, J.; Dai, B.; Chai, X.; Sun, Y.; Xu, L. Development of an attitude adjustment crawler chassis for combine harvester and experiment of adaptive leveling system. Agronomy 2022, 12, 717. [Google Scholar] [CrossRef]
- Chai, X.; Hu, J.; Ma, T.; Liu, P.; Shi, M.; Zhu, L.; Xu, L. Construction and characteristic analysis of dynamic stress coupling simulation models for the attitude-adjustable chassis of a combine harvester. Agronomy 2024, 14, 1874. [Google Scholar] [CrossRef]
- Cui, L.; Le, F.; Xue, X.; Sun, T.; Jiao, Y. Design and experiment of an agricultural field management robot and its navigation control system. Agronomy 2024, 14, 654. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wen, X.; Zhang, G.; Ma, Q.; Cheng, S.; Chen, L. An optimal goal point determination algorithm for automatic navigation of agricultural machinery: Improving the tracking accuracy of the Pure Pursuit algorithm. Comput. Electron. Agric. 2022, 194, 106760. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Receding horizon lateral vehicle control for pure pursuit path tracking. J. Vib. Control 2018, 24, 619–642. [Google Scholar] [CrossRef]
- Ibrahim, A.E.B. Self-tuning look-ahead distance of pure-pursuit path-following control for autonomous vehicles using an automated curve information extraction method. Int. J. Intell. Transp. Syst. Res. 2022, 20, 709–719. [Google Scholar] [CrossRef]
- Chen, W.H.; Wu, J.C.; Davydov, Y.; Yeh, W.C.; Lin, Y.C. Impact of perception errors in vision-based detection and tracking pipelines on pedestrian trajectory prediction in autonomous driving systems. Sensors 2024, 24, 5066. [Google Scholar] [CrossRef] [PubMed]
- Fue, K.; Porter, W.; Barnes, E.; Li, C.; Rains, G. Autonomous navigation of a center-articulated and hydrostatic transmission rover using a modified pure pursuit algorithm in a cotton field. Sensors 2020, 20, 4412. [Google Scholar] [CrossRef]
- Boztaş, G.; Aydoğmuş, Ö. Implementation of pure pursuit algorithm for nonholonomic mobile robot using robot operating system. Balk. J. Electr. Comput. Eng. 2021, 9, 337–341. [Google Scholar] [CrossRef]
- Wang, Y.; Pang, Y.; Chen, O.; Iyer, H.N.; Dutta, P.; Menon, P.K.; Liu, Y. Uncertainty quantification and reduction in aircraft trajectory prediction using Bayesian-Entropy information fusion. Reliab. Eng. Syst. Saf. 2021, 212, 107650. [Google Scholar] [CrossRef]
- Wang, W.; Chen, M.; Peng, Y.; Ma, Y.; Dong, S. Unstructured environment navigation and trajectory calibration technology based on multi-data fusion. Comput. Electr. Eng. 2024, 120, 109658. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Z.; Wang, Y.; Zhang, C.; Zhao, B. Research on automobile four-wheel steering control system based on yaw angular velocity and centroid cornering angle. Meas. Control 2022, 55, 49–61. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Baseline lookahead distance | L0 | 1.00 | m |
| Coupling gain | k | 0.25 | m·s/° |
| Minimum lookahead distance | Lmin | 0.60 | m |
| Maximum lookahead distance | Lmax | 1.60 | m |
| Trial No. | Control Algorithm | Mean Absolute Yaw Error (°) | Maximum Yaw Deviation (°) | Steady-State Attitude Difference (°2) |
|---|---|---|---|---|
| 1 | Adaptive Pure Pursuit | 0.66 | 3.69 | 0.43488 |
| Pure Pursuit | 1.25 | 3.67 | 0.47084 | |
| PID controller | 1.53 | 4.15 | 0.52011 | |
| 2 | Adaptive Pure Pursuit | 0.62 | 3.55 | 0.42831 |
| Pure Pursuit | 1.19 | 3.60 | 0.46592 | |
| PID controller | 1.50 | 4.10 | 0.51235 | |
| 3 | Adaptive Pure Pursuit | 0.64 | 3.62 | 0.43214 |
| Pure Pursuit | 1.23 | 3.65 | 0.46918 | |
| PID controller | 1.56 | 4.20 | 0.52843 | |
| 4 | Adaptive Pure Pursuit | 0.61 | 3.50 | 0.42567 |
| Pure Pursuit | 1.20 | 3.55 | 0.46325 | |
| PID controller | 1.52 | 4.12 | 0.51794 | |
| 5 | Adaptive Pure Pursuit | 0.65 | 3.68 | 0.43129 |
| Pure Pursuit | 1.24 | 3.66 | 0.47121 | |
| PID controller | 1.54 | 4.18 | 0.52316 |
| Algorithm | Mean Absolute Yaw Error (°) | Maximum Yaw Deviation (°) | Steady-State Attitude Difference (°2) |
|---|---|---|---|
| Adaptive Pure Pursuit | 0.636 ± 0.021 (95% CI: 0.61–0.66) | 3.608 ± 0.082 (95% CI: 3.51–3.71) | 0.430 ± 0.004 (95% CI: 0.426–0.435) |
| Pure Pursuit | 1.222 ± 0.026 (95% CI: 1.19–1.26) | 3.626 ± 0.050 (95% CI: 3.56–3.69) | 0.468 ± 0.003 (95% CI: 0.464–0.472) |
| PID Controller | 1.529 ± 0.022 (95% CI: 1.50–1.56) | 4.151 ± 0.041 (95% CI: 4.10–4.20) | 0.520 ± 0.006 (95% CI: 0.513–0.528) |
| Adaptive Pure Pursuit | 0.636 ± 0.021 (95% CI: 0.61–0.66) | 3.608 ± 0.082 (95% CI: 3.51–3.71) | 0.430 ± 0.004 (95% CI: 0.426–0.435) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Zhang, Z.; Dong, X.; Ou, M.; Gao, R.; Wang, Y.; Yang, Q.; Wang, X. Quantification and Optimization of Straight-Line Attitude Control for Orchard Weeding Robots Using Adaptive Pure Pursuit. Agriculture 2025, 15, 2085. https://doi.org/10.3390/agriculture15192085
Jia W, Zhang Z, Dong X, Ou M, Gao R, Wang Y, Yang Q, Wang X. Quantification and Optimization of Straight-Line Attitude Control for Orchard Weeding Robots Using Adaptive Pure Pursuit. Agriculture. 2025; 15(19):2085. https://doi.org/10.3390/agriculture15192085
Chicago/Turabian StyleJia, Weidong, Zhenlei Zhang, Xiang Dong, Mingxiong Ou, Ronghua Gao, Yunfei Wang, Qizhi Yang, and Xiaowen Wang. 2025. "Quantification and Optimization of Straight-Line Attitude Control for Orchard Weeding Robots Using Adaptive Pure Pursuit" Agriculture 15, no. 19: 2085. https://doi.org/10.3390/agriculture15192085
APA StyleJia, W., Zhang, Z., Dong, X., Ou, M., Gao, R., Wang, Y., Yang, Q., & Wang, X. (2025). Quantification and Optimization of Straight-Line Attitude Control for Orchard Weeding Robots Using Adaptive Pure Pursuit. Agriculture, 15(19), 2085. https://doi.org/10.3390/agriculture15192085






