Grading and Detecting of Organic Matter in Phaeozem Based on LSVM-Stacking Model Using Hyperspectral Reflectance Data

Abstract

Phaeozem, which is recognized as one of the world’s most fertile soils, derives much of its productivity from soil organic matter (SOM). Because SOM strongly influences fertility, soil structure, and ecological functions, it is the SOM content that must be rapidly and accurately determined to ensure sustainable soil management. Traditional chemical methods are reliable but time-consuming and labor-intensive, which makes them inadequate for large-scale applications. Hyperspectral reflectance, which is highly sensitive to SOM variations, provides a non-destructive alternative for rapid SOM grading. This study proposes an ensemble learning strategy model based on phaeozem hyperspectral reference data for the rapid grading and detection of SOM content. First, the SOM content of the collected phaeozem samples was determined using the potassium dichromate volumetric method. Next, hyperspectral reflectance data of the phaeozem were collected using a hyperspectral imaging sensor, with a wavelength range of 400–1000 nm. Furthermore, stacking models were constructed by modifying the internal structure, with five classifiers (MLP, SVC, DTree, XGBoost, kNN) as the L1 layer. Then, global optimization was performed using the simulated annealing algorithm. Through comparative analysis, the LSVM-stacking model demonstrated the highest accuracy and generalization capabilities. The results demonstrated that the LSVM-stacking model not only achieved the highest overall accuracy (0.9488 on the independent test set) but also improved the classification accuracy of “Category 1” samples to 1.0. Compared with other models, this framework significantly improved generalization ability and robustness. It is therefore evident that combining hyperspectral reflectance with improved stacking strategies provides a novel and effective approach for the rapid grading and detection of SOM in phaeozem.

1. Introduction

Phaeozem is a clayey soil with significant swelling and shrinkage characteristics. The northeastern phaeozem region of China is one of the major phaeozem belts in the world. Phaeozem is a soil with favorable properties and high fertility, making it highly suitable for plant growth. It is an important non-renewable natural resource in agricultural production. The organic matter content in soil is directly related to crop growth and yield, serving as a crucial basis for many works such as fertility diagnosis, productivity evaluation, and land planning [1]. In China’s second national soil survey, soils were graded into six levels based on organic matter content: <0.6 g/kg, 0.6–10 g/kg, 10–20 g/kg, 20–30 g/kg, 30–40 g/kg, and 40 g/kg<. Based on the organic matter content of phaeozem, grid-based land management is implemented to guide farmers in scientific cultivation and appropriate fertilization. This approach ensures food security and supports sustainable agricultural development.

Traditional methods for SOM testing require extensive field sampling and laboratory chemical analysis of samples, and then the spatial distribution is plotted. While this approach yields accurate results, it is cumbersome, time-consuming, and labor-intensive, making it inadequate for large-scale, rapid, real-time, environmentally friendly, and dynamic monitoring needs [2]. Compared with traditional chemical analysis methods, hyperspectral technology offers advantages in terms of speed and non-destructive capabilities. Hyperspectral technology has found extensive use in multi-target classification and monitoring, including agricultural product classification [3], nutritional content detection of agricultural products [4], and soil organic carbon measurement [5]. Cheng et al. [6] confirmed as early as the early 20th century that hyperspectral information of soil contains a wealth of physicochemical information about the soil. Reis et al. [7] collected soil samples from eight depths near the COAMO experimental station in Southern Brazil. They acquired spectral images in the 380–2506 nm wavelength range and established a soil organic matter content estimation model using PLS. This study demonstrated that hyperspectral technology is both feasible and efficient for rapid monitoring of SOM. Therefore, hyperspectral sensing provides a promising solution for large-scale and non-destructive SOM assessment.

While hyperspectral technology offers comprehensive spectral information for soil organic matter detection, the inherent complexity, high dimensionality, and nonlinearity of such data necessitate advanced analytical techniques. Machine learning provides powerful tools to extract relevant features and model complex relationships; its integration with hyperspectral data has therefore become a pivotal approach for achieving rapid and accurate soil organic matter classification. Mainstream machine learning models can be broadly categorized into two types: linear and nonlinear models. Studies by Nawar S et al. [8], Zeraatpisheh M et al. [9], and Wei L et al. [10] have demonstrated that compared with linear models, nonlinear models constructed using machine learning algorithms are better suited for predicting soil organic matter content. Ensemble learners based on support vector machine (SVM) have demonstrated strong performance on high-dimensional hyperspectral data [11,12]. While the classification accuracy of decision tree models is comparable to that of SVMs, decision trees are more susceptible to noise interference [13]. Random Forest is another commonly used classification algorithm; however, its computational cost is significantly higher compared with that of other algorithms [14,15]. Wang H et al. [16] developed a three-layer neural network with an excitation module at the front end, assigning different weights to hyperspectral data to enhance the accuracy of the convolutional neural network. According to the balance theory of empirical risk and generalization risk, every standalone strong classifier has its own strengths and limitations. Ensemble learning can leverage the strengths of individual learners and integrate their prediction results. It compensates for the shortcomings of single models, such as sensitivity to perturbations from outliers and lack of robustness [17]. As a result, it has become a major focus of current research. Numerous past studies have demonstrated the effectiveness of ensemble learning methods for hyperspectral classification [15]. Common ensemble methods are predominantly homogeneous. Guo et al. [18] proposed a heterogeneous ensemble model comprising SVM, Kernel Extreme Learning Machine (KELM), and Multiple Linear Regression (MLR) using the bagging approach, demonstrating strong applicability. Additionally, Nguyen T et al. [19] showed that the ensemble learning model eXtreme Gradient Boosting (XGBoost) could also be applied to predict soil organic matter content, achieving better performance in certain aspects compared with Random Forest (RF) and SVM.

Since 2020, stacking ensemble strategies have attracted increasing attention. Song X et al. [20] implemented the stacking strategy to integrate three machine learning models, designing an equal-weight voting model and a weighted voting model based on climatic factors. Using nationwide soil data, they trained an ensemble learning model capable of monitoring soil organic matter content on a national scale. In 2022, Biney J et al. [21] utilized the stacking strategy to integrate one statistical method and three machine learning models, creating a weighted average voting model. They employed satellite hyperspectral data to study topsoil organic carbon content across three agricultural regions in different areas of the Czech Republic. In the same year, Lin N et al. [22] demonstrated that an ensemble learning model constructed using six machine learning models outperformed individual models in terms of predictive accuracy. Additionally, the stacking model exhibited relatively improved stability and generalization capabilities during comparative analyses. Zhou W et al. [23] advanced this approach by integrating multiple data preprocessing techniques, feature selection strategies, and models (RF, XGBoost, and SVM) to construct a stacking model, effectively extracting spectral features to enhance predictive accuracy. These studies indicate that machine learning algorithms, particularly nonlinear models, are more effective in addressing soil organic matter content grading tasks. Moreover, ensemble learning approaches, especially stacking strategies, have demonstrated superior performance in handling hyperspectral problems, excelling in terms of both accuracy and generalization. Consequently, the design and optimization of stacking ensemble models have become a prominent focus in current research.

Based on these insights, the present study focuses on developing a heterogeneous stacking ensemble model using phaeozem hyperspectral data. The remainder of this manuscript is structured as follows: Section 2 covers the collection and preparation of phaeozem samples and acquisition of hyperspectral data. In Section 3, we introduce the selection of models for each layer of the stacking model, the principles of ensemble learning and the simulated annealing algorithm, along with directions for algorithm improvement. In Section 4, an ensemble learning strategy model based on black soil hyperspectral data is developed to rapidly gradate the organic matter content of the SOM content. Nine stacking models were constructed and compared, with simulated annealing employed for hyperparameter optimization. The results show that the LSVM-stacking model outperforms the other models. Before optimization, its accuracy on the validation set was 0.6318, which increased to 0.8760 after optimization. On the independent test dataset, the LSVM-stacking model achieved an accuracy of 0.9488, higher than the other stacking models, demonstrating its superior applicability. Moreover, the model achieved a perfect classification accuracy of 1.0 for category “1”. This indicates that the LSVM-stacking model has the best applicability. Finally, we present the conclusions and future lines of research.

2. Materials and Methods

2.1. Determination of SOM

The phaeozem samples were collected from the Xiangyang Experimental Station in Heilongjiang Province, China (45°45′44″ N, 126°55′8″ E). The climate in this area is classified as temperate monsoon climate, with long, cold, and dry winters and short, hot, and rainy summers. The annual average precipitation is 569.1 mm. The geographical location information is shown in Figure 1a. In the experimental station’s layout, the blue area represents the land experimental zone, the red area represents the plant experimental zone, and the yellow area represents the paddy field. All of the samples in this manuscript were collected from the plant experimental zone, following the direction of plant cultivation, and the sampling locations were recorded using a handheld GPS; a total of 28 points were collected.

Since the crops grown in the experimental station absorb nutrients from the soil, the organic matter content in deep soil differs from that in surface soil. Collecting soil from different depths allows for obtaining soils with varying organic matter contents within a limited land area. During sampling, a handheld spiral digger was used to drill the hole, and a casing was installed to prevent the collapse of the well wall, ensuring the accuracy of the samples. The five-point composite sampling method was used to collect soil samples from four depths: 0–10 cm, 10–20 cm, 20–30 cm, and 30–40 cm. A total of 112 soil samples were collected; the sampling points are marked in Figure 1b. When bringing the samples back to the laboratory, the soil collected from each sampling point was thoroughly mixed. Impurities such as roots and stems were removed. The soil samples were air-dried naturally and then ground. They were sequentially passed through a 60-mesh sieve and a 100-mesh sieve. Particles with a diameter larger than 0.250 mm were removed by the 60-mesh sieve, which also eliminated most plant roots and seeds. Particles with a diameter smaller than 0.250 mm but larger than 0.150 mm were filtered out using the 100-mesh sieve and made into analytical samples for chemical analysis to obtain the true value of the organic matter content. Particles with a diameter smaller than 0.150 mm passed through the 100-mesh sieve for hyperspectral data acquisition. 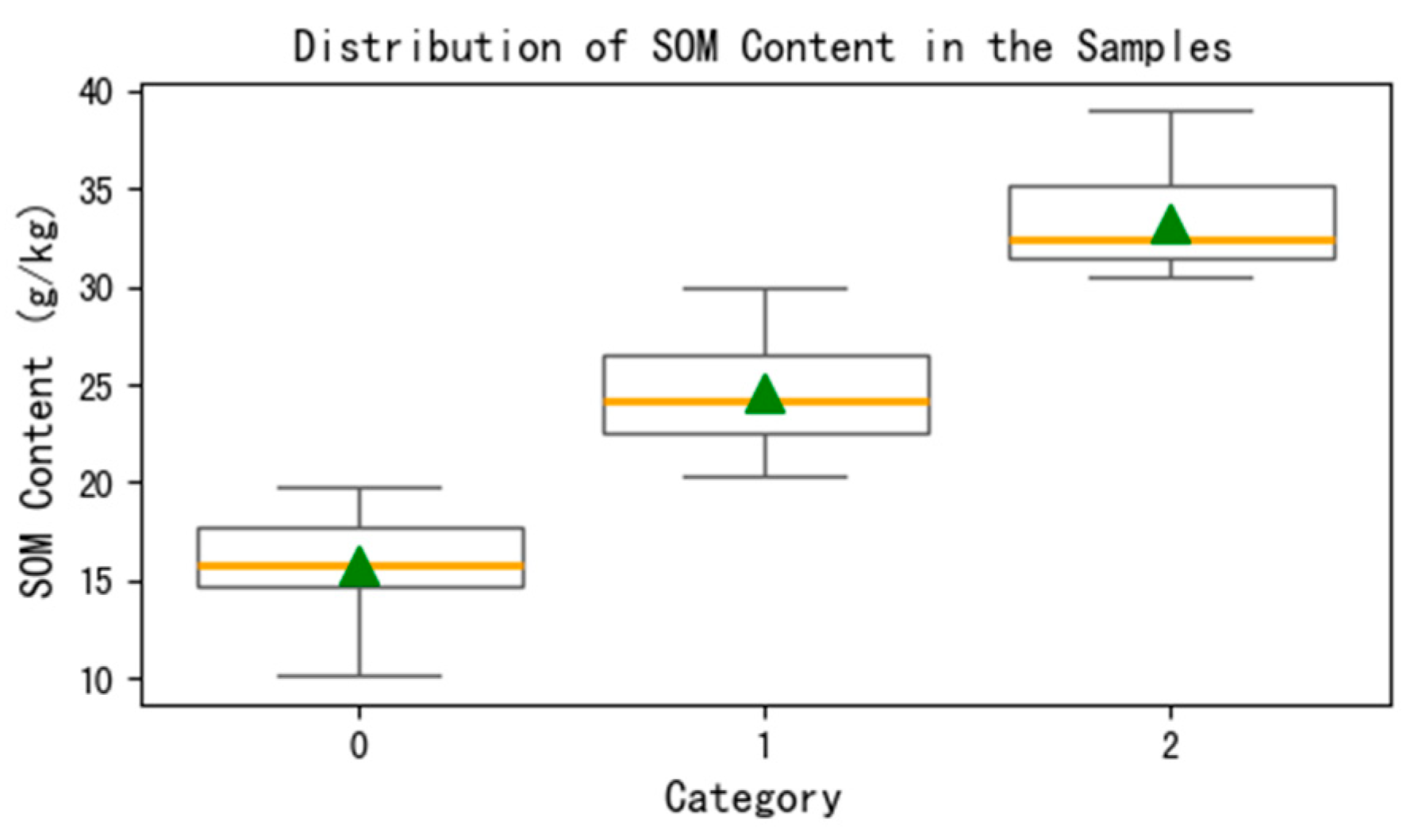The analysis of SOM was determined using the potassium dichromate volumetric method [24]. Excess potassium dichromate solution was mixed with the soil and heated in an oil bath. The potassium dichromate oxidized SOM. The remaining potassium dichromate was then titrated with a standard ferrous solution, and the organic matter content in the sample was calculated based on the amount of potassium dichromate consumed. SOM in the northeastern phaeozem region is higher than that of typical farmland, primarily ranging between 10 and 40 g/kg. Therefore, based on the relevant standards, the samples are categorized into three levels: Grade IV (10–20 g/kg), Grade III (20–30 g/kg), and Grade II (30–40 g/kg). The organic matter content of each sample is shown in

Table 1. Organic matter content of different soil samples.

	Code	Organic Matter	Code	Organic Matter	Code	Organic Matter	Code	Organic Matter
Category 0	C1-4	10.15	A2-4	12.40	A3-4	12.40	C3-4	12.97
	D2-4	13.53	D2-3	14.46	D1-4	14.66	F3-4	14.66
	B2-4	15.22	G1-4	15.22	E3-4	15.22	C2-4	15.79
	D1-1	15.79	A4-4	16.91	D1-2	16.91	C2-1	17.48
	F2-4	17.48	D4-4	18.04	E4-4	18.04	A2-2	18.60
	B3-4	19.17	G4-4	19.73	F3-3	19.73
Category 1	B3-3	20.30	G4-3	20.30	F4-4	20.30	C1-3	20.86
	G3-4	20.86	F2-1	20.86	C1-1	21.42	C3-2	21.42
	C4-4	21.42	C3-1	21.99	C3-3	21.99	G1-2	21.99
	G1-3	21.99	G3-2	21.99	D2-2	21.99	E2-4	21.99
	F1-4	21.99	B3-1	22.55	A2-3	22.55	G2-4	22.55
	D3-4	22.55	E1-1	22.55	E1-4	22.55	F1-3	22.55
	B1-1	23.68	B4-3	23.68	B1-4	23.68	A4-2	23.68
	C4-3	23.68	D1-3	23.68	D4-3	23.68	F2-3	23.68
	F4-3	23.68	B2-1	24.24	B4-2	24.24	B4-4	24.24
	G4-1	24.24	D2-1	24.24	A3-1	24.81	A1-4	24.81
	C1-2	24.81	A2-2	25.87	G2-3	25.87	B2-3	25.93
	A3-3	25.93	A4-3	25.93	C2-2	25.93	G1-1	25.93
	D3-3	25.93	F3-2	26.50	G2-1	26.50	G2-2	26.50
	D4-2	26.50	E2-2	26.50	F2-2	26.50	C4-1	27.06
	E1-3	27.06	E3-3	27.06	A1-2	27.62	D3-1	27.62
	E4-1	27.62	A4-1	28.19	A1-3	28.75	G4-2	28.75
	E2-3	29.32	B1-2	29.88	A2-1	29.88	C2-1	29.88
	E3-1	29.88
Category 2	C4-2	30.44	E2-1	30.44	E3-2	30.44	F3-1	30.44
	B4-1	31.01	B1-3	31.57	E4-2	31.57	B3-2	32.13
	D3-2	32.13	F1-1	32.13	F4-2	32.7	E4-3	33.26
	G3-2	33.83	F1-2	34.95	F1-2	34.95	A1-1	35.52
	E1-2	35.52	D4-1	36.08	G3-1	37.21	F3-2	38.97

, where the unit of organic matter content is g/kg. Figure 2 illustrates the distribution of organic matter content in soil samples of different grades, where the orange line represents the median and the green triangle denotes the mean.

2.2. Acquiring Spectral Data

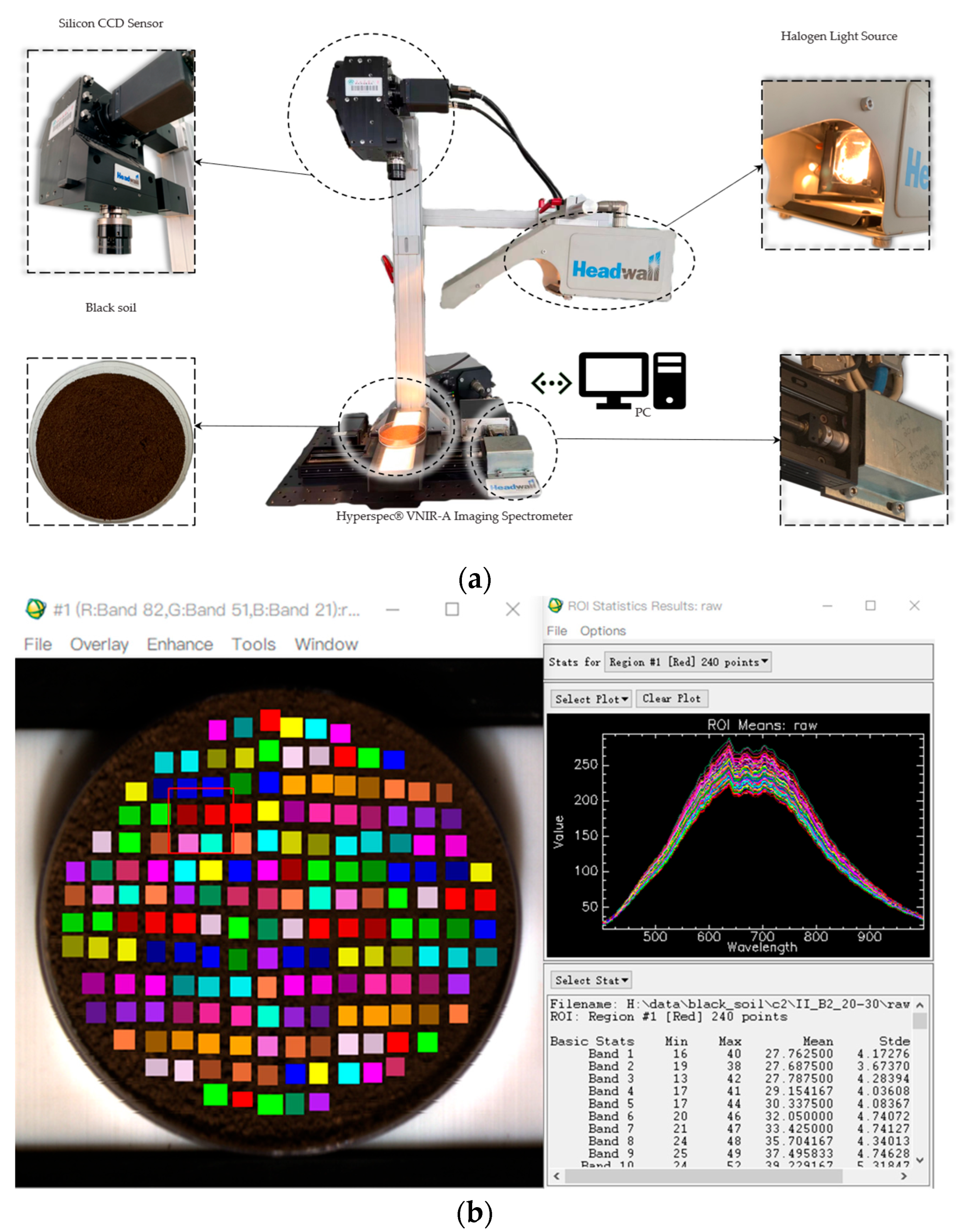
Since the soil samples have been air-dried and ground into a fine powder, directly placing them on the work platform for testing would cause the platform to malfunction. Therefore, we used selected Petri dishes with a diameter of 6 cm and a depth of 1 cm. The finely ground soil samples were classified, placed into the Petri dishes, and labeled accordingly. The soil samples were spread evenly to avoid shadows caused by the halogen lamp. Figure 3 shows the loading conditions of the selected samples.

Spectral data were collected using the VNIR-A series integrated hyperspectral imaging sensor produced by Headwall, MA, USA. The wavelength range of the sensor is 400–1000 nm. During data acquisition, a 50 W halogen lamp was adjusted to its maximum power, and the lamp housing was positioned such that the incident angle of illumination was 45°, resulting in an oblique distance of approximately 20 cm from the light source to the soil surface. The imaging sensor was mounted directly above the samples at a vertical distance of about 30 cm. The push-broom stage was operated at a moving speed of 5 mm/s, with an exposure time of 38.84 ms and a frame period of 0.04 ms. The final hyperspectral datacube was obtained with a spatial–spectral resolution of (1004, 812, 203). The data acquisition system is shown in Figure 4a. The imaging device and uneven light source generated noise. Radiometric correction was performed in ENVI Classic 5.3 using white (whitereference.hdr) and dark (darkreference.hdr) reference files. Regions of interest (ROIs) were then created in the central area of each Petri dish using the ROI_Type square function to minimize edge-reflection effects. Each ROI contained approximately 240 pixels on average. The mean spectral curve of each ROI was calculated by averaging the pixel spectra within the region, as shown in Figure 4b. Because some soil samples were partially lost during transportation or sieving, the number of ROIs varied among different soil types. After data cleaning, a total of 5894 valid spectral curves were obtained. Figure 4b shows the average reflectance spectra of the ROI marked. At some certain wavebands, the values vary greatly. The reasons for this could be the differences in the spatial distribution of the samples’ components (such as C-H, N-H, and O-H) [25]. Finally, a hyperspectral data matrix of 1013 × 203 was formed in this process, where the rows represented the number of samples and the columns represented the number of bands. There are some characteristic peaks and valleys in the spectral curve in Figure 4. We observed that all the spectral curves showed similar spectral characteristics with a similar curve shape, but some differences exist in terms of the magnitude of reflectance.

SOM in the northeastern phaeozem region is higher than that of typical farmland, primarily ranging between 10 and 40 g/kg. Therefore, it is classified into three levels according to the relevant standards. To train and test the model, a total of 112 phaeozem samples need to be randomly sampled without replacement to form two groups. The first group of samples was divided using the train_test_split function, and the spectral data extracted from these samples were used to construct the training and validation sets. The spectral data extracted from the second group of samples were used as an independent test set to evaluate the generalization performance of the model. The average spectral characteristic curves for the three sample categories are displayed in Figure 5. The vertical axis represents the instrument response values of the spectral camera, while the horizontal axis denotes the wavelength. The SOM range and specific quantities for each sample category are shown in

Table 2. Sample data distribution characteristics of each dataset.

	Organic Matter (g/kg)	Training Set	Validation Set	Total	Test Set	Total
Category 0	10.00–19.99	709	304	1013	704	1717
Category 1	20.00–29.99	721	309	1030	1069	2099
Category 2	30.00–45.00	714	306	1020	1058	2078
total		2144	919	3063	2831	5894

.

2.3. Ensemble Learning

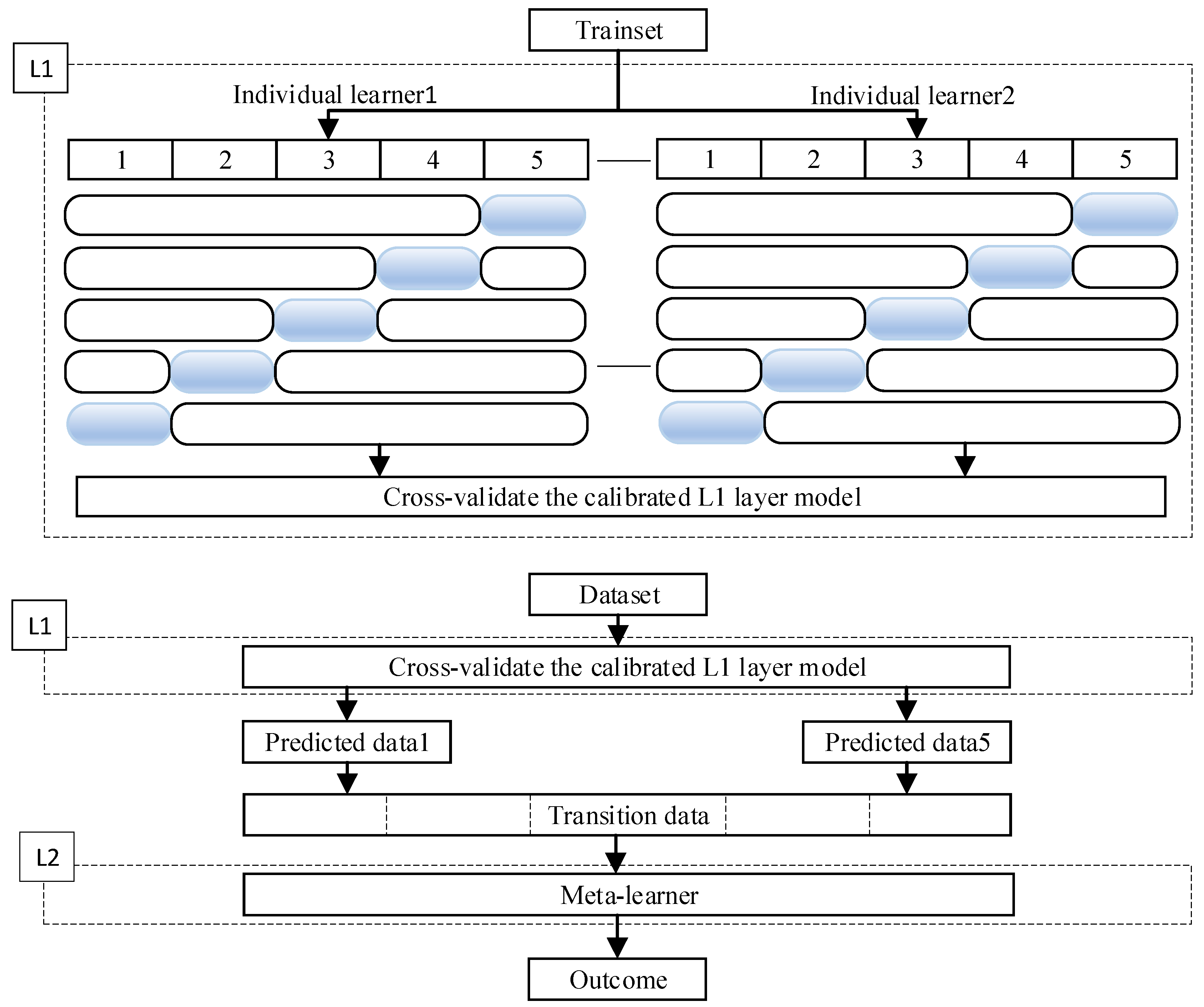
The combination strategy of ensemble learning refers to the coordination approach among individual learners. Common ensemble methods include boosting, bagging, and stacking [17]. The stacking strategy allows for greater flexibility in selecting different heterogeneous learners for integration. It first reduces variance through parallel training and then decreases bias through sequential training. In the stacking strategy, the model is primarily divided into two levels: the L1 layer, consisting of several base learners, and the L2 layer, which is the decision-making layer composed of a meta-learner. In the L1 layer, each learner performs supervised learning within the sample space. This process transforms the original data into n transitional data points S, which are then input into the L2 layer. The most basic form of the L2 layer is equal-weight voting (for classification problems) or equal-weight averaging (for regression problems). The workflow of the ensemble model can be simplified as shown in Figure 6.

The selection of meta-learners in the L1 layer must take into account the feature information within the sample space. Since the individual learners in this layer are responsible for direct feature extraction and decision-making, general feature engineering considerations are essential. Moreover, the sample subspace input into the L2 layer differs significantly from the original sample space, which shifts the focus of learner selection towards the features of the transformed data, S. Therefore, the diversification of meta-learners in the L1 layer becomes critical. In classification tasks, the output of the L1 layer can either be discrete sample labels or continuous values. The continuous values include class probabilities or information entropy, which represent the uncertainty or likelihood associated with the predicted classes. The main difference between the stacking strategy and other ensemble strategies lies in the presence of the L2 layer. Unlike Boosting and bagging, which focus on enhancing a single type of learner, stacking leverages multiple diverse meta-learners in the L1 layer. By subsequently selecting a strong learner in the L2 layer, this approach can significantly enhance the learning performance of the model. The pseudo code of stacking is as follows:

## stacking

Input: training set: $D=\{\left(x_1,y_1\right),\left(x_2,y_2\right), . . . ,\left(x_m,y_m\right)\}$;     individual learners: ${\eta }_1, {\eta }_2, . . . ,{\eta }_T$;     meta-learners: $\eta$.

1. for $\mathit{t}=1,2,...,\mathit{T}$ do 2. ${\mathit{h}}_{\mathit{t}}={\mathit{\eta }}_{\mathit{t}}\left(\mathit{D}\right)$; 3. end for 4. $\mathit{S}=\mathbf{\varnothing }$; 5. for $\mathit{i}=1,2,...,\mathit{m}$ do 6.  for $\mathit{t}=1,2,...,\mathit{T}$ do 7.   $s_{it}=h_t\left(x_i\right)$; 8.  end for 9.  $S=(\left(s_{i1},s_{i2}, . . . ,s_{iT}\right),y_i)$; 10. end for 11. $h^{\prime }=\eta \left(D^{\prime }\right)$;

Output: $H\left(x\right)=h^{\prime }(h_1\left(x\right),h_2\left(x\right), . . .,h_T\left(x\right))$

where D is a training set with m samples. L1 consists of T individual learners. L2 is meta-learner $\eta$. Trained model $h_t$ is received with the training set. For $x_i$ in D, $s_{it}=h_t\left(x_i\right)$, and then the secondary training set generated by $x_i$ is $s_i=\left(s_{i1},s_{i2},...,s_{iT}\right)$, where the label is $y_i$. The secondary training set produced by T individual learners is $S={\left\{\right(s_i,y_i\left)\right\}}_{i=1}^m$, which will be used for training meta-learner.

In conclusion, when choosing a stacking strategy to build an ensemble learning model, the diversity of L1 layer individual learners and the selection of L2 meta-learners are the two decisive aspects in this strategy.

2.4. Simulated Annealing

Hyperparameters are parameters used to control the behavior of algorithms when building models. These parameters cannot be obtained through regular training and must be manually set. One of the most challenging aspects of machine learning is finding the optimal hyperparameters for a model. The performance of the model is directly influenced by the hyperparameters. Their proper tuning can significantly enhance the model’s predictive capability. The idea of the simulated annealing algorithm was first proposed by N. Metropolis et al. [26]. The simulated annealing algorithm consists of two parts: the Metropolis criterion and the annealing process. The annealing process is understood as the process of finding the global optimal solution, and the purpose of the Metropolis criterion is to search for the global optimal solution out of the local optimal solution, which is the basis for annealing. The Metropolis criterion is generally expressed as follows:

$$P=\left\{\begin{array}{cc}\hfill 1,& E\left(x_{new}\right)<E\left(x_{old}\right)\hfill \\ \hfill \exp \left(-{\displaystyle \frac{E\left(x_{new}\right)-E\left(x_{old}\right)}{T}}\right),& E\left(x_{new}\right)\ge E\left(x_{old}\right)\hfill \end{array}\right.$$

(1)

The Metropolis criterion states that at temperature $T$, there is a probability $P(∆E)$ of cooling with an energy difference $∆E$, expressed as $P(∆E)=exp(∆E/(kT\left)\right)$, where $k$ is the Boltzmann constant, $exp$ is the natural exponent, and ΔE < 0. So, $P$ and $T$ are positively correlated. This formula means that the higher the temperature, the greater the probability of cooling with an energy difference of $∆E$; the lower the temperature, the lower the probability. If there is an energy attenuation, then this change will be accepted with 1. If the energy does not change or increases any more, this means that this change deviates from the direction of the global optimal solution, and this change will be accepted with $P$. Because the temperature gradually decreases during the annealing process, $\Delta E$ is always less than 0; therefore $∆E/kT<0$, so the range of $P(∆E)$ is $\left(\mathrm{0,1}\right)$. With the decrease in temperature $T$, $P(∆E)$ will gradually decrease and eventually stabilize to achieve the global optimal solution.

2.5. Algorithm Design

Research has shown that heterogeneous ensemble models can effectively reduce both variance and bias. This is achieved by combining diverse base learners, which enhances the model’s generalization ability. When selecting base learners, it is essential to consider the type of model, its functionality, and the specific problems it is best suited to address. To mitigate the risk of overcomplexity and excessive computational costs, the use of simpler base learners is recommended [27]. Consequently, the candidate models for the selection of functions in the L1 layer include neural network models (Multilayer Perceptron (MLP)), support vector machines (SVMs and Linear Support Vector Machine (LSVM)), basic decision tree models (Linear Support Vector Machine (Dtree)), nonlinear models (k-Nearest Neighbor (kNN) and Logistic), and linear models (Ridge and XGBoost with the booster = gblinear parameter, referred to as XGBl) [28]. These algorithms are widely used to address real-world problems involving hyperspectral techniques and have demonstrated their applicability in prior research. In addition, selecting these state-of-the-art (SOTA) methods requires balancing accuracy and fairness metrics. When accuracy differences are minimal, selecting models with a higher balance helps to reduce the variance in the L1 layer functions, thereby enhancing the model’s robustness and performance. To complete the construction of the model, different learners are employed in the L2 layer. After transforming the original data into transitional data, it is passed to the L2 layer for final model construction and decision-making.

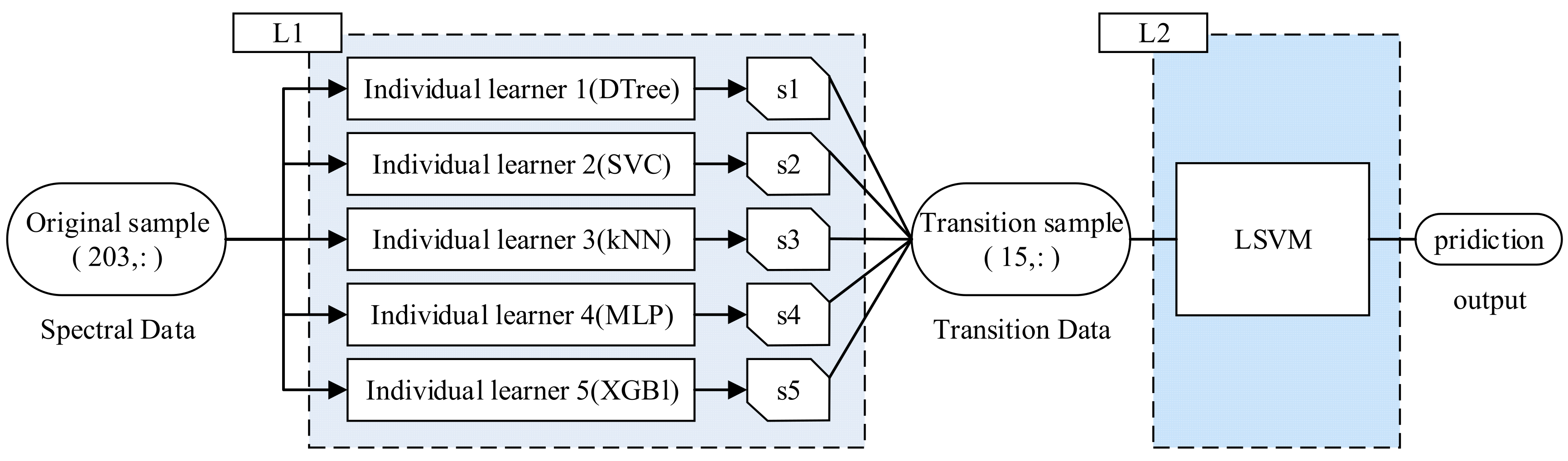
The Double-Stacking method exhibits a process structure analogous to that of multi-layer neural networks. Cross-validation randomly divides the training set into five mutually exclusive subsets of the same size. Each individual learner will use one subset as the prediction set, while the remaining four subsets are used as the training set. This process is repeated five times, ensuring that each subset is used as the prediction set once. The prediction results from all individual learners are then combined to form a new dataset, which is the transition data. In traditional stacking methods, the prediction results are used as transition data for the L2 layer. In contrast, the model designed in this manuscript uses the predicted probabilities as transition data for the L2 layer; that is, the probability of a sample being assigned to a particular class. Compared with directly inputting the prediction results into the L2 layer, using the predicted probabilities helps reduce errors. This is especially true for misclassifications from individual learners, making the overall model more reliable.

This manuscript mainly conducts comparative experiments on the model selection for the L2 layer. The candidate models for the L2 layer functions include nine models: Logistic Regression, MLP, kNN, XGBoost, decision tree, LSVM, Support Vector Classification (SVC), Random Forest, and Adaptive Boosting (AdaBoost). When selecting the L2 layer function, it is necessary to tune the hyperparameters of the objective function. Hyperparameter optimization is performed using the simulated annealing algorithm, with the optimal parameter solution selected after 1000 iterations. The optimal L2 layer function is selected by comparing the trained models on the test set. In addition, an independent validation set is used to assess the model’s applicability. The workflow diagram of the Double-Stacking model designed in this manuscript is shown in Figure 7.

2.6. Evaluation Indicators

For the grading of SOM, which is essentially a multi-classification problem in supervised learning, accuracy (ACC) can be used as the model evaluation index. Accuracy is calculated as follows (2):

$$\begin{array}{c}acc\left(y,y_{pred}\right)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=0}^N}I\left({y_{pred}}_i=y_i\right)\end{array}$$

(2)

where $y_i$ is the true category of the $i$ sample, ${y\_pred}_i$ is the predicted category of sample $i$, and $N$ is the total number of samples.

Class accuracy (C-ACC) for evaluating single-grade classification is a variant of accuracy, which indicates the proportion of a category that the model predicts correctly in the category. The formula is as follows (3):

$$\begin{array}{c}{acc}^j\left(y,y_{pred}\right)={\displaystyle \frac{1}{N^j}}{\displaystyle \sum _{i=0}^{N^j}}I\left({y_{pred}}_i=y_i\right),y_i\in label\left(j\right)\end{array}$$

(3)

where $y_i$ is the true category of the $i$ sample, ${y\_pred}_i$ is the predicted category of sample $i$, and $N^j$ is the total number of samples of this category.

The legal range of both of them is [0, 1]. The closer it is to 1, the higher the proof accuracy and the better the classification effect of the model. In this study, the number of samples in the three labels is basically balanced. So, for this three-category problem, the lowest limit of the total accuracy rate should be 0.33.

The F score, also known as the balance score, is the weighted average of precision and recall. In this grading problem, it is necessary to take into account the precision and recall; that is, the F1 score (F1) is quoted, and the formula is as follows (4):

$$\begin{array}{c}F1=2\times {\displaystyle \frac{precision\times recall}{precision+recall}}\end{array}$$

(4)

where precision and recall, respectively, represent the precision and recall within the category, and the formulas are as follows (5) and (6):

$$precision={\displaystyle \frac{TP}{TP+FP}}$$

(5)

$$recall={\displaystyle \frac{TP}{TP+FN}}$$

(6)

where TP represents the number of correctly predicted samples, FP represents the number of wrongly predicted samples from other grades as this grade, and FN represents the number of samples from this grade that are incorrectly predicted as other grades.

The legal range of the F score is [0, 1]; a larger value means a better model.

2.7. Computational Environment

The experiment was conducted in a Python 3.9 programming environment using Jupyter Notebook 6.2. The foundational dependencies included Scikit-learn v1.0.1, Pandas v1.3.3, and Numpy v1.18.5. The experimental environment and configurations are detailed in

Table 3. Experimental environment and equipment configuration.

Computing Environment		Algorithmic Environment
CPU	Intel® Core™ i5-10400 (2.90 GHz)	Scikit-learn 1.0.1, Pandas 1.3.3, Numpy 1.18.5 Scipy 1.5.0, Xgboost 1.4.2
GPU	NVIDIA GeForce RTX 3070
RAM	DDR4 3000 Mhz 16 GB = 2 × 8 GB
Operating system	Windows LTSC 99.99
Random state	615

.

3. Results and Analysis

3.1. Stacking Model Building

Table 4. L1 layer model selection evaluation index.

	LSVM	SVC	MLP	DTree	Logist	KNN	XGB1	Ridge
acc	0.4754	0.5511	0.5169	0.5429	0.6118	0.6238	0.5496	0.6696
f1	0.4238	0.5475	0.4033	0.5417	0.6008	0.6260	0.5286	0.6633
accp	0.4689	0.5538	0.5057	1.0000	0.5984	0.7425	0.5435	0.7064

presents the accuracy comparison results of various models. Specifically, ‘acc’ refers to the accuracy of each model on the validation set, with higher values indicating better model performance. ‘f1’ denotes the F1 score achieved by each model during training, with higher values indicating a more balanced prediction of the grades on the validation set. ‘accp’ represents the accuracy of each model on the training set, with higher values indicating a more thorough learning process on the training data.

For the two proposed support vector machine models, SVM is significantly better than LSVM. For the two nonlinear models, kNN and Logistic Regression (Logist) have little difference in terms of accuracy and equilibrium scores on the validation set. However, it is evident from the table that the kNN model achieves significantly higher accuracy on the training set compared with the Logistic Regression model, indicating that kNN learns the hyperspectral features in the training set more effectively. This is likely due to the preprocessing capability of kNN, where sample points can be pruned to eliminate less relevant data, enhancing the data’s overall coherence. In contrast, Logistic Regression relies solely on a simple gradient penalty function, which may limit its effectiveness when dealing with datasets with weak features and large sample sizes. Regarding the selection of linear models, the Ridge regression model significantly outperformed the XGBl.

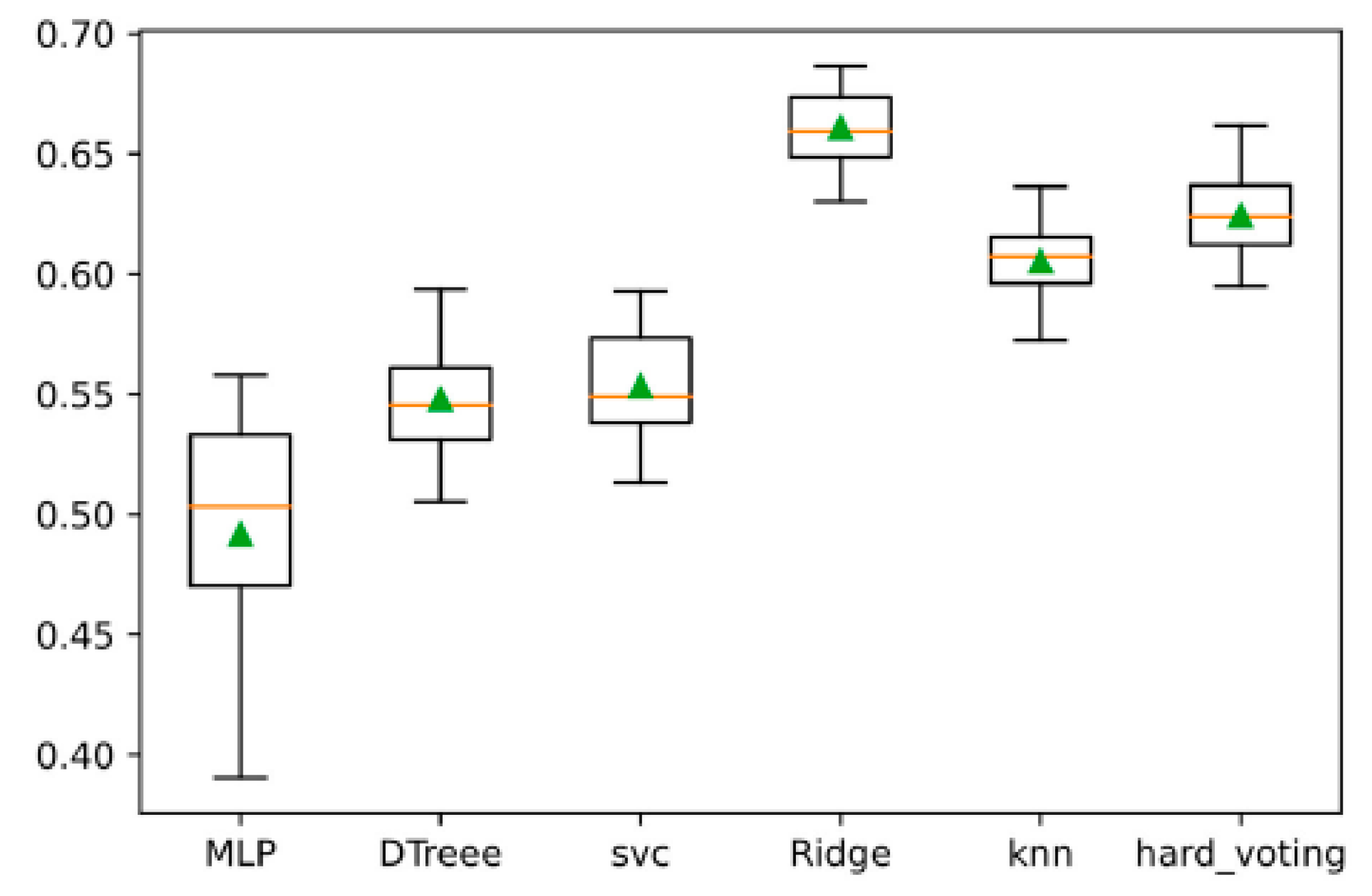
The independent test results of the five base learners in the L1 layer are shown in Figure 8. From the figure, it can be observed that among the five base learners, Ridge, kNN, and MLP achieve relatively high validation accuracies of 71.27%, 69.13%, and 68.70%, respectively. This indicates that these three base learners exhibit strong performance and can be initially classified as strong learners. In contrast, although kNN achieves a high accuracy, its balance score is 57.57%, further highlighting its robust learner characteristics within this sample space. On the other hand, theSVM and DTree models show lower accuracy values of 65.33% and 61.09%, respectively, suggesting that these two models can be preliminarily categorized as weak learners in the meta-model.

The accuracy and inter-grade accuracy comparison of the five base learners in the L1 layer are shown in Figure 8. From the figure, it is evident that the inter-grade classification performance varies across different base learners. ‘Acct’ represents the accuracy of the model on the validation set, while ‘acc_0’ and ‘acc_2’ denote the inter-grade accuracy for the four-level, three-level, and two-level soil samples, respectively. Higher values indicate better performance in terms of identifying samples from a particular level. ‘Accp’ refers to the accuracy of the models on the training set. The analysis reveals that the recognition of three-level soil samples is particularly challenging, with the highest recognition errors observed in this grade. Specifically, the MLP model performs the worst on the three-level soil samples, although it performs the best on the four-level samples. Excluding the MLP model, the other models demonstrate relatively balanced classification abilities, with misclassifications being fairly evenly distributed across the recognition tasks for different soil sample levels.

Based on the analysis of accuracy, F1 score, and the confusion matrix of the validation set, the base learners in the L1 layer can be summarized as follows: (1) The Ridge, kNN, and MLP models exhibit relatively high accuracy on the validation set. The misclassification distribution across different organic matter levels is fairly even, and the models perform particularly well in terms of grading soil samples with medium organic matter content. These three models can be considered strong learners and will be integrated into the L1 layer of the ensemble. (2) The SVM and DTree models show lower accuracy on the validation set and are prone to misclassifications of the two-level and four-level soil samples. These models exhibit weaker balance, making them less effective in terms of overall prediction stability. Therefore, they can be considered weak learners and will be included in the L1 layer of the ensemble.

The five individual learners are trained and integrated as the L1 under the same experimental environment. Each individual learner in the L1 predicts the sample and combines all the probabilistic prediction sets into a transition dataset S; then, the 203-dimensional raw data of the training set are output as a 15-dimensional S through the L1. S is input into the L2 alternative model to complete the model fitting analysis.

The prediction results of the base learners in the L1 layer are used as transition data S, and the L2 layer is set to a majority voting scheme with equal weights assigned to each learner (i.e., each learner’s weight is set to 1). The accuracy of the five base learners and the equal-weight voting model are compared, and the distribution of the prediction results is shown in Figure 9. The accuracy of the equal-weight majority voting stacking model is 62.4%. This suggests that the voting method, compared with individual models, can improve accuracy to some extent. However, in cases where linear models like Ridge Regression, which handle strong feature correlation, are used, the performance may degrade instead of improve. The primary limitation of the voting method is that if two models predict correctly while three models predict incorrectly, the final output label will be erroneous due to the majority-vote rule. To address this issue, this study proposes replacing the majority voting algorithm with a secondary learner, which will learn from the training patterns and override the ‘majority wins’ rule.

Table 5. Model evaluation results before and after optimization of each model.

	Before Optimization			After Optimization
	acc_b	f1_b	acc_a	acc_0	acc_1	acc_2	f1_a
DTree	0.6047	0.5959	0.8651	0.8520	0.7573	0.9869	0.8628
RF	0.6212	0.5809	0.8694	0.8553	0.7735	0.9804	0.8677
ada	0.5306	0.4467	0.8716	0.8520	0.7832	0.9804	0.8703
XGB	0.6059	0.5248	0.8760	0.8520	0.7961	0.9804	0.8749
LSVM	0.6318	0.5995	0.8760	0.8586	0.8026	0.9673	0.8754
SVC	0.6247	0.5910	0.8792	0.8586	0.7994	0.9804	0.8783
kNN	0.6153	0.5965	0.8825	0.8586	0.8252	0.9641	0.8822
MLP	0.6294	0.6007	0.8879	0.8750	0.8155	0.9739	0.8872
Logist	0.6459	0.6123	0.8912	0.8750	0.8252	0.9739	0.8905

and Figure 10 show the comparison of ACC and F1 of the nine stacking models before and after simulated annealing hyperparameter optimization. The ACC of the model after the simulated annealing hyperparameter optimization has been greatly improved, where the Logist-stacking model has the best performance with an ACC of 0.8923 and the DTree-stacking model has the worst performance with an ACC of 0.8651.

The C-ACC of the optimized nine models is drawn as Figure 10. The axis acct represents the accuracy of different meta-learners on the testing set, the axis acc_0-acc_2 represents the C-ACC effect of different meta-learners, the axis accp represents the ACC of different meta-learners on the training set. It can be clearly seen from the Figure 10 that the inter-grade classification capabilities of each learner are similar, the classification effects are similar, and they can complete the multi-classification task in the main.

3.2. Applicability Verification of Model

In order to further verify the ACC of the model in different samples, we introduced a new dataset, independent test set. In total, 2831 sample points in the test set inputted 9 stacking models.

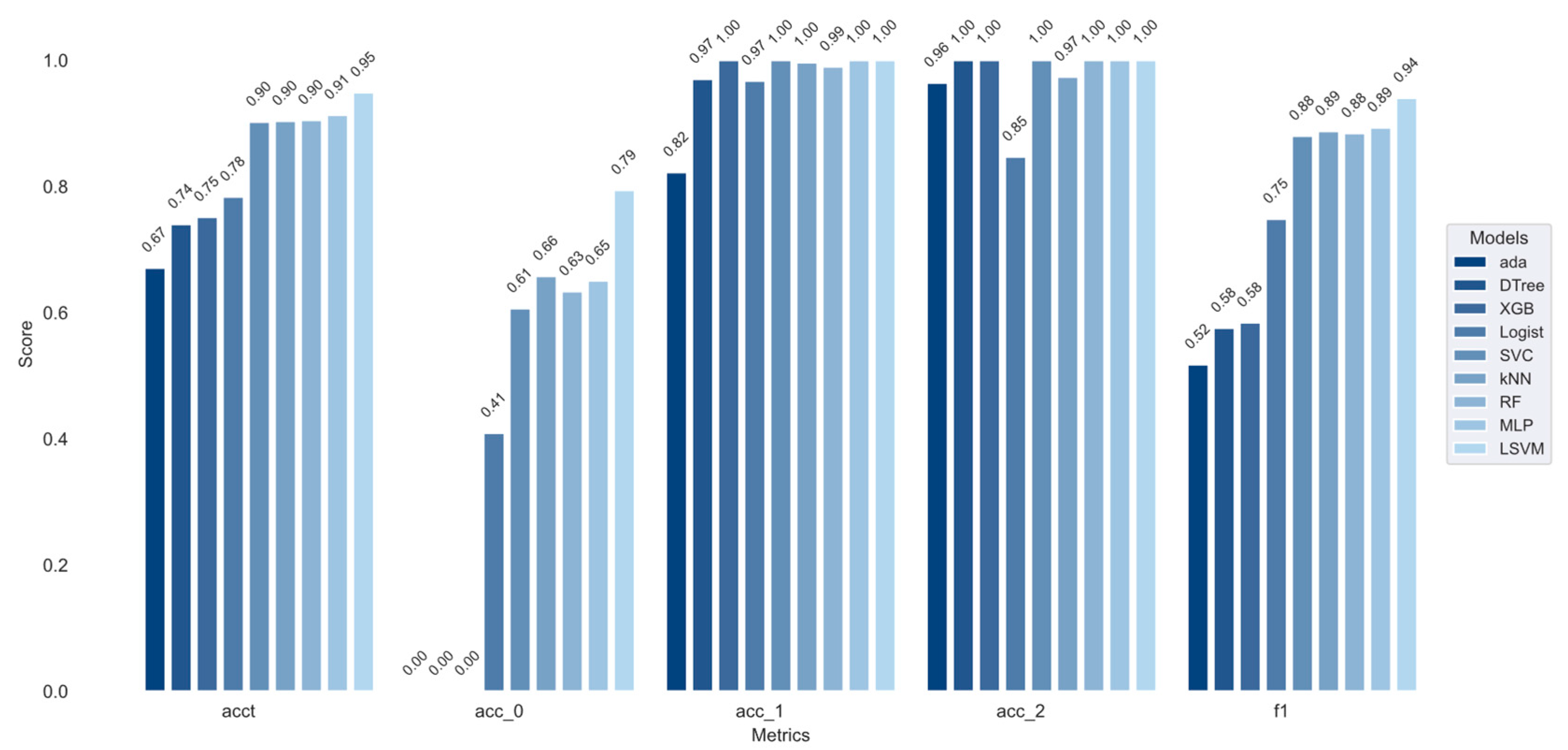
It can be seen from

Table 6. Accuracy of each stacking model on independent test set.

	acct	acc_0	acc_1	acc_2	f1
ada	0.6708	0.0000	0.8223	0.9641	0.5177
DTree	0.7400	0.0000	0.9701	1.0000	0.5756
XGB	0.7513	0.0000	1.0000	1.0000	0.5841
Logist	0.7835	0.4091	0.9673	0.8469	0.7483
SVC	0.9022	0.6065	1.0000	1.0000	0.8799
kNN	0.9036	0.6577	0.9963	0.9735	0.8874
RF	0.9050	0.6335	0.9897	1.0000	0.8842
MLP	0.9131	0.6506	1.0000	1.0000	0.8930
LSVM	0.9488	0.7940	1.0000	1.0000	0.9401

and Figure 11 that the ACC of the nine stacking models on the test set is quite different, where the LSVM-stacking model has the best performance with an ACC of 0.9488 and the ada-stacking model has the worst performance with an ACC of 0.6708. In addition, each classifier has significantly improved the recognition effect of “Category 1”, and the recognition effect of “Category 2” is also slightly improved. Instead, the main classification errors are concentrated in the recognition of “Category 0”. The C-ACC of the LSVM-stacking model in both “Category 1” and “Category 2” has reached 1.0, and the C-ACC in “Category 0” has also reached 0.7940, which is much higher than that of other stacking models, indicating that the LSVM-stacking model has the best applicability in the validation set.

Finally, the LSVM is determined to be an L2 function, and the final structure is shown in Figure 12.

3.3. Grading Results of a Single Model

Ten SOTA approaches were selected to verify the improvement in the stacking model proposed in this manuscript in the study of phaeozem organic matter grading based on hyperspectral technology. These include neural network model MLP; support vector machine models SVM and LSVM; decision tree model DTree; nonlinear models kNN and Logistic; linear models Ridge and XGBl; and homogeneous integration models Ada and XGBt. These algorithms are commonly used in the study of solving various real-world problems based on hyperspectral technology. The independent test results of the SOTA methods and LSVM-stacking model are shown in

Table 7. Accuracy analysis results of ten SOTA approaches and LSVM-stacking models.

	acc	acc_0	acc_1	acc_2	f1	accp	acct
MLP	0.5927	0.4792	0.9275	0.3689	0.5870	0.5910	0.7512
LSVM	0.6769	0.9682	0.0990	0.9684	0.5867	0.6819	0.7653
SVC	0.7279	0.7946	0.5628	0.8277	0.7250	0.7163	0.7169
DTree	0.6899	0.7555	0.5676	0.7476	0.6900	1.0000	0.7487
kNN	0.7223	0.8166	0.5773	0.7743	0.7211	0.7958	0.7416
Logist	0.8113	0.8631	0.7077	0.8641	0.8108	0.8017	0.7431
Ridge	0.7466	0.7848	0.6184	0.8374	0.7458	0.7240	0.7413
XGBl	0.7676	0.8729	0.6232	0.8083	0.7660	0.8014	0.6869
Ada	0.7433	0.7237	0.7729	0.7330	0.7488	0.9878	0.7293
XGBt	0.7854	0.8484	0.6908	0.8180	0.7858	1.0000	0.7265
LSVM-Stacking	0.8760	0.8586	0.8026	0.9673	0.8754	1.0000	0.9488

.

In Table 7, “acc” indicates the accuracy of each model in the testing set; the higher the number, the better the model performance. “accp” indicates the accuracy of each model in the training set, and the higher the number, the more fully the model learns from the training set. “acct” indicates the accuracy of each model in the test set, and the higher the number, the better the generalization of the model. It can be seen that the LSVM-stacking model proposed in this manuscript has better performance in the study of phaeozem organic matter grading, not only in the testing set but also in the validation set, indicating that LSVM-stacking has better generalization ability, sufficient learning ability of sample space, and more balanced and excellent identification of various types of soil.

4. Discussion

The representative Xgboost algorithm of ensemble learning is an excellent machine learning algorithm with better stability than a single individual learner, but not all ensemble learning or tree-based algorithms can complete the classification task well. As a machine learning model, its final performance is not necessarily better than traditional non-tree algorithms [29,30,31]. That is why the stacking model proposed in this manuscript is not entirely based on the tree model, and its final performance is not necessarily better than the traditional classifier model. However, using more types of individual learners in L1 can better take into account the diversity of the dataset; that is, improve the applicability ability of the model. This is why a brand-new validation set is introduced to validate the model. If we just want to choose a simple classification model, kNN can do the job well. When dealing with hyperspectral data, the data dimension is high and there is a lot of redundant information. It is necessary to filter the data information through L1. The preliminary judgment result of L1 is given to L2 for analysis and judgment, and this can also reduce the workload of L2 functions. It also explains why simpler models may serve for quick baseline tasks, but L1–L2 stacked architecture better leverages hyperspectral data structure for robust classification.

The majority of recent hyperspectral studies on soil organic matter (SOM) treat SOM as a continuous variable and focus on quantitative regression (e.g., PLSR, SVR, ridge-type and ensemble regressions) [10,32,33]. The physical basis for the hyperspectral detection of SOM has been well documented: organic matter generally darkens soil and reduces visible reflectance (notably in parts of the 400–700 nm range) and influences the VIS–NIR slope as well as specific near-infrared band correlations related to moisture and organic functional groups. Detailed correlation analyses and band-selection studies report strong SOM–reflectance correlations in the visible to NIR range and identify sensitive bands and transformed spectral indices that improve predictive power [34,35]. While these regression results confirm that SOM can be accurately estimated from spectra (supporting the physical basis of spectral detection), practical field management frequently relies on threshold-based decisions rather than on precise point estimates. Reviews and meta-analyses in soil science therefore commonly discuss SOM thresholds for management and fertilizer response [36,37]. For this reason, discretizing SOM into management-relevant grades, as achieved in this study, is a legitimate and useful objective: it maps continuous spectral information onto decision-ready categories while leveraging the strong spectral–SOM linkage demonstrated by regression studies.

This manuscript does not take into account the introduction of weather factors at the time of sample collection and instead only looks at the spectral data itself and also obtains reliable predictions. This is because the soil samples collected in this manuscript are naturally air-dried and ground before the hyperspectral data are collected. The proposed stacking algorithm does not require traditional spectral preprocessing of the raw data, such as multiplicative scatter correction (MSC) and standard normalized variate (SNV). The rationale is that these standalone preprocessing techniques usually require a large number of samples and full-range spectral data to avoid data shifts; otherwise, data shifts are still likely to occur. Mathematical transformations of individual spectral curves must be based on full-spectrum and full-sample information. Conducting full-spectrum transformations before the application phase may inadvertently introduce bias or misalignment, as information from the test set could be indirectly incorporated into the preprocessing procedure [38]. Additionally, the collected spectra had already been baseline-corrected using ENVI Classic 5.3 software, and measurements were taken during periods of minimal interference. Therefore, the spectral data adopted in this study exhibited negligible shifts. So, we think it was suitable for direct use in modeling.

Nevertheless, some limitations should be acknowledged in this paper. Only spectral data were considered, while environmental factors such as soil moisture and temperature at the time of sampling were not included. Moreover, the spectral range was limited to 400–1000 nm, which may omit important absorption features in the short-wave infrared region. Future studies should consider expanding the spectral range, incorporating environmental variables, and exploring advanced deep learning models (e.g., CNNs, Transformers) to further improve prediction accuracy and generalizability.

5. Conclusions

The results of this manuscript show that (1) the heterogeneous ensemble model based on stacking strategy is achievable and of research value. Compared with the single model, the single-sample recognition ability and generalization ability of the heterogeneous ensemble model with multiple algorithm principles proposed in this manuscript are also significantly improved. (2) It is remarkably necessary to perform hyperparameter optimization using the simulated annealing method, and the simulated annealing algorithm can greatly improve the accuracy of the model we design.

In this manuscript, an ensemble learning model based on phaeozem hyperspectral data is designed to quickly complete the grading of SOM content. Five different individual learners were integrated in the L1 layer to enhance the generalization ability of the model. The hyperparameters of each stacking model were optimized using simulated annealing with 500 iterations, resulting in significant improvements in the performance metrics, with gains ranging from 24.42% to 34.10%. On the independent test dataset, the LSVM-stacking model achieved an accuracy of 94.88%, outperforming the other models by 3.57–27.80%, indicating the highest generalizability. Moreover, the LSVM-stacking model achieved the highest F1 score, demonstrating the best balance in classification accuracy across all categories. Compared with ten SOTA models, LSVM-stacking consistently achieved better performance across all three datasets.

The new model of heterogeneous integration based on the stacking strategy proposed in this manuscript provides ideas for the future direction of algorithm enhancement and how to improve the effectiveness of the model for use.