Abstract
Maize (Zea mays L.) is a key global cereal crop with significant relevance to food security. Maize yield prediction is challenged by cultivar diversity and varying management practices. This preliminary study was conducted at Youyi Farm, Heilongjiang Province, China. Three maize cultivars (Songyu 438, Dika 1220, Dika 2188), two fertilization rates (700 and 800 kg·ha−1), and three planting densities (70,000, 75,000, and 80,000 plants·ha−1) were evaluated across 18 distinct cropping treatments. During the V6 (Vegetative 6-leaf stage), VT (Tasseling stage), R3 (Milk stage), and R6 (Physiological maturity) growth stages of maize, multi-temporal canopy spectral images were acquired using an unmanned aerial vehicle (UAV) equipped with a multispectral sensor. In situ measurements of key agronomic traits, including plant height (PH), stem diameter (SD), leaf area index (LAI), and relative chlorophyll content (SPAD), were conducted. The optimal vegetation indices (VIs) and agronomic traits were selected for developing a maize yield prediction model using the random forest (RF) algorithm. Results showed the following: (1) Vegetation indices derived from the red-edge band, particularly the normalized difference red-edge index (NDRE), exhibited a strong correlation with maize yield (R = 0.664), especially during the tasseling to milk ripening stage; (2) The integration of LAI and SPAD with NDRE improved model performance, achieving an R2 of 0.69—an increase of 23.2% compared to models based solely on VIs; (3) Incorporating SPAD values from middle-canopy leaves during the milk ripening stage further enhanced prediction accuracy (R2 = 0.74, RMSE = 0.88 t·ha−1), highlighting the value of vertical-scale physiological parameters in yield modeling. This study not only furnishes critical technical support for the application of UAV-based remote sensing in precision agriculture at the field-plot scale, but also charts a clear direction for the synergistic optimization of multi-dimensional agronomic traits and spectral features.
1. Introduction
Food security represents a critical global strategic priority, fundamentally linked to global stability, human well-being, and sustainable development. Maize, as one of the world’s major staple crops, is a key component of food security frameworks [1]. In China, a significant portion of maize production supports the food processing and animal feed industries, with an annual output of approximately 277 million tons, accounting for nearly 24% of global maize production. While continuous advancements in cultivar development and optimized agronomic management practices have led to substantial yield improvements, the increasing complexity of cropping systems introduces variability in plant phenotypic traits and growth patterns [2,3,4,5]. This complexity presents significant challenges to achieving accurate and timely yield predictions. Addressing this issue necessitates the development of robust, efficient, and adaptive yield prediction methodologies that can accommodate heterogeneous and dynamic cropping scenarios. Integrating remote sensing, big data analytics, and precision agricultural engineering offers promising avenues for enhancing the accuracy of maize yield forecasting. Such approaches are essential for providing actionable data to inform grain production strategies and to promote the intelligent, sustainable intensification of agricultural systems [6,7].
In addition to conventional field sampling methods, most contemporary yield prediction approaches rely primarily on crop growth models (CGMs) and remote sensing-based yield estimation models [3]. CGMs integrate climate data, management practices, and soil properties to mechanistically simulate crop growth, thereby enabling comprehensive simulation of crop growth processes [8]. For instance, Yang et al. (2004) successfully predicted maize LAI, dry matter accumulation, and yield using an improved CERES-Maize model [9]. Similarly, Folberth et al. (2013) employed the GEPIC model (GIS-based Environmental Policy Integrated Climate) to simulate maize yields under various cropping systems and identified optimal cultivation strategies [10]. These models, based on agronomic theory, offer a robust representation of crop physiological processes; however, they typically require extensive datasets to achieve reliable predictions, which poses significant challenges for data collection and model calibration. In contrast, remote sensing techniques enable non-destructive acquisition of crop canopy spectral data [11]. Remote sensing has become a mainstream, non-contact methodology widely applied in vegetation mapping, soil characterization, yield prediction, and vegetation classification [12,13,14,15]. VIs obtained from satellite or unmanned aerial vehicle (UAV) imagery have been widely employed for predicting crop yields. For example, Prasad et al. (2006) used satellite-derived normalized difference vegetation index (NDVI) to predict maize and soybean yields in Iowa [15], obtaining R2 values of 0.78 and 0.86, respectively. Saravia et al. (2022) demonstrated the effectiveness of UAV-based multispectral data, using ten derived vegetation indices to predict yields across four maize cultivars [16], underscoring the value of UAV data for timely yield estimation and monitoring. Wahab et al. (2018) used UAV-derived green normalized difference vegetation index (GNDVI) for yield prediction in the complex agricultural systems of South Africa [17], confirming a strong correlation between GNDVI and crop yield. While these remote sensing approaches offer rapid and non-invasive access to crop growth information, they often lack physiological interpretability and are limited in their ability to capture data from the lower canopy layers [16]. Consequently, integrating remote sensing data with mechanistic crop models is emerging as a promising approach for high-resolution agricultural monitoring at smaller spatial scales, combining the strengths of both methodologies.
The yield of field crops is influenced by both the quantity of harvested grains per unit land area and the average grain weight [18,19]. As a major field crop, maize yield represents a complex quantitative trait influenced by a multitude of factors [20,21]. For instance, leaf size and number directly affect light interception efficiency, which in turn is closely associated with dry matter accumulation and final yield [22]. Pendleton et al. (1968) demonstrated that maintaining an upright posture of leaves above the ear can significantly enhance grain yield under conditions of high LAI [23]. Large-leaf maize cultivars exhibit higher photosynthetic efficiency under optimal water and nutrient availability. In contrast, small-leaf cultivars display greater stress tolerance, making them more suitable for drought-prone or high-temperature environments. These traits directly or indirectly impact yield formation [24,25]. However, unlike crops such as rice, sorghum, or millet, maize has a unique source–sink relationship. In maize, yield is mainly determined by the efficiency of assimilate production and translocation from leaves surrounding the ear, rendering the middle canopy leaves particularly valuable for physiological and phenotyping studies [26]. Therefore, a detailed understanding of canopy structure and leaf function is critical for accurate yield assessment.
Nonetheless, limitations in remote sensing, such as spatial resolution constraints and sensor viewing geometry, impede the accurate monitoring of canopy substructure and lower-layer physiological traits [27,28]. Wiegand et al. (1979) showed that combining remote sensing with agronomic data improves model accuracy [28]. Luo et al. (2022) proposed integrating tassel change traits (TCT) with VIs to enhance the accuracy of rice yield prediction [29]. Han et al. (2021) estimated wheat LAI in experimental plots using UAV-derived multispectral VIs, subsequently predicting yield based on optimized models [30]. Guo et al. (2022) employed an RF algorithm, which combined spectral features, texture indices, and maize plant height for grain yield prediction [31]. Sharma et al. (2024) achieved significant results (R2 = 0.8) in predicting yields of 553 wheat genotypes using UAV-based plant height and VIs derived from multispectral imagery [32]. Liu et al. (2024) utilized multispectral UAV data to capture canopy spectral characteristics during critical wheat growth stages, integrating canopy volume features (CVF) for yield estimation [33]. These studies predominantly rely on remotely sensed VIs coupled with individual agronomic traits to construct yield prediction models. However, crop yield is a quintessential trait governed by polygenic inheritance, making it challenging for single agronomic parameters to comprehensively characterize its formation process. Furthermore, remote sensing data and their derived parameters face inherent limitations in model development, including error propagation, multicollinearity among variables, and the inability to accurately monitor sub-canopy structural characteristics. These constraints inevitably compromise prediction accuracy and model interpretability. Recently, Liu et al. (2025) successfully predicted potato yield by applying the fuzzy comprehensive evaluation (FCE) method to integrate multiple agronomic traits, which also demonstrates the reliability of multivariate trait integration [34]. Building upon this evidence, this study investigates the use of vegetation indices and agronomic trait data with the Random Forest algorithm to enhance yield prediction accuracy, as well as the application potential of agronomic traits in remote sensing-based yield forecasting.
In the study, we aimed to improve maize yield prediction accuracy by integrating VIs and agronomic trait data with machine learning algorithms, and to evaluate the contribution of agronomic data assimilation to enhancing the interpretability of remote sensing-based yield prediction models. To achieve this objective, a field experiment was conducted in 2024 with three maize cultivars—Songyu 438, Dika 1220, and Dika 2188—as experimental materials. The experimental design included two fertilization levels (700 and 800 kg·ha−1) and three planting densities (70,000, 75,000, and 80,000 plants·ha−1). By integrating remote sensing observations with agronomic trait parameters, we developed a field-scale maize yield prediction model suitable for complex cropping systems. Although the robustness and general applicability of the results require further validation, the methodological framework demonstrated in this study shows considerable potential for broader application in the future. It may provide theoretical support for optimizing cropping patterns and promoting sustainable agricultural development in complex planting regions, while also offering valuable insights for enhancing agricultural economic outcomes and advancing agricultural modernization.
2. Materials and Methods
2.1. Overview of the Study Area
Youyi County is located in the eastern part of Heilongjiang Province (131°27′ E–132°15′ E, 46°28′ N–46°59′ N), situated in the heart of the Sanjiang Plain, which is formed by the Heilongjiang, Songhua, and Ussuri Rivers. The terrain is flat and the soil is fertile, making it particularly suitable for agricultural production. The vast arable land area provides favorable natural conditions for crop cultivation. The regional climate system exhibits typical temperate monsoon characteristics, featuring clearly demarcated seasonal transitions. Summers are warm and humid, with concurrent rainfall and heat. The annual accumulated temperature is 2500–2700 °C, and the frost-free period is 143 days, which is conducive to the growth and maturity of crops. The thick, highly fertile black soil layer in Youyi County is suitable for growing a variety of staple and cash crops, including maize, soybean, and rice. It is an important agricultural production base (Figure 1).

Figure 1.
(a) Geographical location of Youyi County; (b) geographical location of the experimental field; (c) the experimental field with 18 treatments; (d) DEM of the experimental field and the layout of sampling points.
This study includes a total of 18 experimental treatments. We selected the main locally cultivated varieties. Due to their thermal accumulation requirements, these varieties can effectively reflect the planting characteristics and representativeness under the primary local production conditions. Maize was sown on 5 May 2024, following conventional local maize cultivation practices, and harvested on 28 September 2024. Throughout the maize-growing season, field inspections were conducted to monitor the occurrence of pests and diseases. No significant pests or diseases were observed during the growing period. Sampling areas were selected in regions with similar digital elevation model (DEM) characteristics to ensure data accuracy.
2.2. Data Acquisition and Preprocessing
2.2.1. Ground Data Collection
Maize phenotypic traits were measured manually in the field. For each experimental treatment, six sampling points were selected, and three representative plants were sampled at each point, resulting in a total of 108 sampling points. Guided by previous studies, we selected four critical growth stages for data acquisition: the V6 stage marks the vegetative transition point that determines canopy architecture and light-use efficiency; the VT stage initiates reproductive growth, with stem development influencing panicle differentiation and stress tolerance; the R3 stage is pivotal for yield formation, reflecting source–sink balance in regulating kernel weight; and the R6 stage, as the terminal phase, exhibits comparatively stable phenotypic parameters. Agronomic traits, including LAI, PH, SD, and SPAD, were measured on 20 June, 22 July, 26 August, and 23 September 2024. The study measured LAI using a portable LAI-2200C (Li-COR Inc, Lincoln, NE, USA) plant canopy analyzer. Measurements were performed between 16:00 and 18:00 local time to avoid direct sunlight. Light intensity was recorded in shaded areas prior to measurement, and 4A data were used for same-day calibration [35]. SPAD values were obtained using a portable SPAD-502 chlorophyll meter (Konica Minolta Inc, Tokyo, Japan). Measurements were conducted on three leaves per plant: the first fully expanded upper leaf, the middle leaf near the ear, and the first physiologically active leaf above the root zone [36]. PH and SD were measured using a plant height ruler and a vernier caliper, respectively. At each sampling area, we selected five representative maize plants to reflect the average PH and SD for that area (Table 1).

Table 1.
Selection of agronomic traits and their physiological relevance.
At physiological maturity, on 2 October 2024, 108 sampling points were selected for yield assessment. At each sampling point, two rows (narrow ridges) were sampled. The row length was calculated based on a sampling area of 10 m2 and a row spacing of 1.3 m, resulting in approximately 7.69 m per row. For each plot, the total number of ears, the total number of plants, and the number of barren stalks were recorded. From each row, 15 consecutive ears were collected (30 ears per sampling point). The ears were sorted by size, and 10 uniform ears from the middle were selected as standard samples. These ears were weighed, threshed, and the grain weight was recorded. Grain moisture content was also measured. Before threshing, five ears from each standard sample were used to record ear diameter, kernel number per row, ear length, and number of rows per ear. Additionally, 100 kernels were randomly selected and weighed using an electronic balance (accuracy ± 1 g) to determine hundred-kernel weight (HKW) [38].
n is the number of sampled plants; S is the sampling area (m2); Y is the yield per hectare (t·ha−1); R is the number of kernel rows per ear; K is the number of kernels per row; W is the hundred-kernel weight (g); P is the plant population per hectare.
2.2.2. UAV Data
UAV-based multispectral imagery was acquired using an integrated Phantom 4 Multispectral (P4M) UAV system manufactured by DJI Innovations, Shenzhen, China. The UAV was equipped with six 2.9-inch CMOS image sensors, including one RGB sensor for standard visible imagery and five monochromatic sensors for multispectral imaging. The spectral bands of the multispectral sensors are as follows: blue (B, 450 ± 16 nm), green (G, 560 ± 16 nm), red (R, 650 ± 16 nm), red edge (RE, 730 ± 16 nm), and near-infrared (NIR, 840 ± 26 nm) [39].
We conducted UAV flights between 10:00 and 13:00 local time under clear-sky and low-wind conditions (wind speed < 3 m/s) to ensure consistent illumination and reduce atmospheric interference (Table 2). The flight mode used hover-and-shoot image acquisition, with both forward and side overlap rates set at 80% [40]. To ensure geometric accuracy, imagery was orthorectified using a ground control point (GCP) approach. The experimental plots were then delineated and extracted in ArcGIS 10.8 to exclude extraneous features. Each UAV flight mission included approximately 1736 waypoints. At each waypoint, five single-band multispectral images were acquired, resulting in a total of approximately 10,416 images per flight. Due to the limited field of view of the UAV, image mosaicking and radiometric correction were required. Professional remote sensing software (DJI Terra 3.6.8) was used to perform image stitching, geographic correction, and radiometric calibration, ultimately generating five-band orthorectified reflectance mosaics of the entire experimental field [32]. Radiometric calibration was performed using three Spectralon reference panels with known reflectance values of 25%, 50%, and 75% (Figure 2). Images of the panels were captured before each flight to correct for variations in illumination. The raw digital numbers (DN) for each spectral band were subsequently converted to reflectance values.

Table 2.
Drone flight schedule.

Figure 2.
UAV and calibration targets: (a) UAV Platform—Phantom 4 Multispectral; (b) calibration targets.
2.3. Construction of Vegetation Indices
The original multispectral images of maize canopies acquired with UAVs exhibited clear differences among planting patterns. To enhance the predictive capability of the model, this study calculated multiple VIs from the multispectral images. VIs are essential tools for extracting remote sensing features of crops [41]. By integrating the spectral reflectance characteristics under different planting patterns, VIs helped algorithms better distinguish among treatments. Therefore, to capture canopy spectral characteristics across planting patterns, and based on previous studies [42], we selected VIs that did the following: clearly showed changes in canopy structure, leaf color, and chlorophyll content; effectively identified vegetation density; recognized and quantified the amount of exposed soil; and examined the relationship of light energy transformation. The relevant calculation formulas and references are shown in Table 3 [15,16,17,40,43,44].

Table 3.
Vegetation indices and formulas.
2.4. Yield Prediction Model
Random Forest (RF) is an ensemble learning method that combines multiple decision trees using the bagging technique [45]. The RF model was employed as the primary prediction approach owing to its ability to capture complex nonlinear relationships and accommodate diverse input features, including spectral indices and agronomic traits, while maintaining robustness even with relatively small sample sizes [46,47]. In this study, ten vegetation indices derived from UAV multispectral imagery and collected agronomic traits were used as independent variables, while the final measured plant yield served as the dependent variable. To improve the model’s predictive accuracy, the two key hyperparameters, mtry and ntree, were optimized. mtry denoted the number of features considered when splitting nodes during the construction of each decision tree, and ntree represented the total number of decision trees used to build the random forest. During model construction, ntree was increased incrementally from 5 to 500 with a step size of 5 over 100 iterations, while mtry was increased from 1 to n (the total number of variables) with a step size of 1 over n iterations. The final model was constructed using optimal hyperparameters: {‘n_estimators’: 629, ‘max_depth’: 54, ‘min_samples_split’: 4, ‘min_samples_leaf’: 1, ‘max_features’: 0.999}. This configuration achieved peak performance while maintaining stable error metrics.
2.5. Correlation Analysis
Pearson correlation analysis is a statistical technique that quantifies the linear association between two continuous variables [48]. It measures the linear relationship between variables through the computation of the Pearson correlation coefficient, typically denoted as R (ranging from −1 to 1). When R is close to 0, it indicates a weaker correlation. The strength of correlation is categorized based on the range of the correlation coefficient (Table 4). To improve model efficiency and reduce the time required for model training, this method was applied to analyze the VIs. Independent variables were selected according to the strength of their correlation with yield. Based on previous research, integrating features from different developmental stages yielded better predictive performance than using features from a single period. Therefore, this experiment selected the top two combinations of VIs with the highest correlation across the entire growth period for yield prediction. The Pearson correlation coefficient was calculated as follows:

Table 4.
Standard interpretation of Pearson’s correlation coefficient (R).
In the formula: and represent the measured values, and and represent the mean values of the measured samples.
2.6. Accuracy Assessment
The model performance was assessed through the determination of R2, RMSE, MAE, and NRMSE. Statistically, the closer R2 is to 1, the higher the accuracy of the model estimation. RMSE represented the dispersion of the data; lower RMSE values corresponded to greater predictive precision. MAE measured the average magnitude of errors. NRMSE intuitively reflected the relative magnitude of the error. The calculation formulas are as follows [45]:
In the formula, n is the number of samples; is the observed (measured) value; is the predicted value; is the mean of the observed values; is the mean of the predicted values; is the maximum value of the observations; and is the minimum value of the observations
2.7. Model Validation Strategies
2.7.1. Random 5-Fold Cross-Validation
In 5-fold cross-validation, the dataset was randomly partitioned into five equal subsets (folds). For each iteration, four folds were used as the training set while the remaining fold served as the validation set. This process was repeated five times to ensure each sample was validated exactly once. The final performance metrics were calculated by averaging the results across all iterations. By folding the dataset, overfitting of the model is prevented. As the training process is done every time with different training sets, the training process doesn’t get biased towards training data [49].
2.7.2. Group 6-Fold Cross-Validation
Group 6-fold cross-validation was employed to partition samples based on experimental treatments, ensuring that samples from the same group were not simultaneously included in both training and validation sets, thereby preventing data leakage from inflating model performance [50]. In each iteration, the dataset was divided into six groups, with five groups used for training and the remaining group for validation. This procedure was repeated six times, allowing each group to serve as the validation set once and ensuring comprehensive evaluation across the entire dataset.
2.7.3. Leave-One-Treatment-Out (LOTO)
The Leave-One-Treatment-Out (LOTO) strategy was applied to assess the model’s generalization to unseen treatment conditions [51]. This approach is particularly appropriate for experimental designs with a limited number of treatments that exhibit distinct variability. In each iteration, one treatment was excluded from the training set, while the remaining 17 treatments were used for model training. The procedure was repeated 18 times, enabling a comprehensive evaluation of predictive performance across all treatment conditions.
2.8. Technical Approach
We used drones to obtain multiple multispectral images in the research area from June 17th to September 25th. We harvested the maize on October 2nd of the same year. A Random Forest model was then applied to compare the accuracy of maize yield prediction at the field scale using vegetation indices calculated from these images. Building on this, measured agronomic traits were introduced as covariates in the model, and vertical-scale SPAD data were incorporated to further optimize the model. This approach aimed to evaluate the potential of agronomic traits in yield prediction research and to validate the feasibility of integrating plant physiology and remote sensing for field-scale yield forecasting. The overall technical workflow is illustrated in Figure 3.

Figure 3.
Spectral reflectance before and after the reproductive stage.
3. Results
3.1. Descriptive Data Analysis
3.1.1. Spectral Analysis at Key Growth Stages
By comparing spectral reflectance data between the V6 and R6 stages, significant differences were observed (Figure 4). Specifically, before the reproductive stage, the spectral reflectance in the B, G, and R bands exhibited relatively small variations across different planting patterns, with a range of 2.1% to 6.8%. In contrast, the NIR and RE bands exhibited more pronounced differences, with maximum variations of 28.7% and 31.2%, respectively. After entering the reproductive stage (R3 stage), the differences in spectral reflectance in the R band increased significantly, with a maximum difference of 19.5%, while differences in the RE band decreased, with the maximum difference dropping to 15.8%. Compared to the pre-reproductive stage, spectral reflectance in the R, RE, and NIR bands generally increased after the reproductive stage. This indicates that changes in internal physiological processes during the reproductive phase lead to a more complex canopy structure.

Figure 4.
Spectral reflectance before and after the reproductive stage: (a) before the reproductive stage; (b) after the reproductive stage.
Notably, the effects of fertilization rates and planting densities on spectral reflectance gradually weakened after the reproductive stage. Specifically, at a planting density of 85,000 plants·ha−1, the NIR reflectance under the 800 kg·ha−1 fertilization treatment was only 4.1% higher than that under the 700 kg·ha−1 treatment, significantly lower than the 7.3% difference observed before the reproductive stage. These findings suggest that changes in internal physiological processes during the reproductive phase result in a more complex canopy structure.
3.1.2. Correlation Between Vegetation Indices and Yield
Analysis of the correlations between VIs at different growth stages and maize yield (Figure 5) revealed significant variations in correlation strength across the growth cycle. These differences were mainly influenced by the type of VIs selected and the specific growth stage. Notably, the correlations between VIs and yield were strongest from VT—R6, highlighting this period as a critical window for yield prediction.

Figure 5.
Correlation analysis between vegetation indices and yield at different growth stages.
Our results also demonstrate that the optimal VIs vary across different phenological stages. Specifically, the most important VI at the V6, V12, VT, R3, and R6 stages was OSAVI, NDVI, NDVI, GNDVI, NDRE, and GNDVI, respectively, with corresponding correlation coefficients (R values) of 0.147, 0.397, 0.426, 0.664, 0.663, and 0.412. Based on these findings, we selected the two VI variables with the highest correlation to yield at each growth stage as input features for the yield prediction model to enhance the model’s predictive accuracy and reliability.
3.1.3. Statistical Analysis of Agronomic Traits
Statistical analysis of LAI, SPAD, PH, and SD under different planting patterns (Figure 6) revealed significant differences in agronomic traits across planting systems. In terms of different varieties, Dika 2188 had superior values in PH, LAI, and SPAD compared to the other two varieties. Compared to low-density planting, under high-density planting conditions, PH and SPAD values increased more rapidly in the early growth stage. They decreased more significantly during the late reproductive stage. Moreover, the effect of fertilization amount on agronomic traits was significant, with higher fertilization amounts generally promoting plant growth, especially under high-density planting patterns [52]. For example, for the variety Dika 1220, under a planting density of 85,000 plants per hectare, the PH, SD, SPAD, and LAI values for the treatment with 800 kg·ha−1 of fertilizer were 3.6%, 6.1%, 19.5%, and 5.7% higher, respectively, than those for the treatment with 700 kg·ha−1 of fertilizer. This indicates that increasing the fertilization rate can significantly improve the growth status of plants, especially under high-density planting conditions. Therefore, analyzing the effects of different planting patterns on agronomic traits can provide an important basis for optimizing the yield prediction model.

Figure 6.
Temporal dynamics of agronomic traits: (a) LAI; (b) PH; (c) SPAD; (d) SD.
3.2. Maize Yield Prediction Model Based on Remote Sensing Data
By analyzing data from six key growth stages, we constructed ten different input variables and evaluated their performance in yield prediction. The results showed variations in prediction accuracy among the datasets (Table 5), with R2 ranging from 0.16 to 0.54, RMSE ranging from 1.11 to 1.35 t·ha−1, MAE ranging from 0.83 to 1.15 t·ha−1, and NRMSE ranging from 0.093 to 0.115 t·ha−1. Among all datasets, the NDRE-based prediction model demonstrated superior performance with R2 = 0.54, RMSE = 1.11 t·ha−1, MAE = 0.88 t·ha−1, and NRMSE = 0.093, significantly outperforming models based on other Vis. Based on the assessment results of prediction accuracy, we selected the dataset with the highest accuracy as the basis for subsequent analysis to ensure that the model had robustness and predictive capability when introducing agronomic trait variables.

Table 5.
Accuracy of yield prediction models based on different vegetation indices.
3.3. Yield Prediction Model with the Introduction of Agronomic Traits
Based on the use of VIs as input variables, we further introduced agronomic traits as auxiliary variables to assess their contribution to the yield prediction model. According to the results presented in Table 6, the introduction of agronomic trait data significantly improved the model’s prediction accuracy. Throughout the prediction process, R2 ranged from 0.44 to 0.64, RMSE ranged from 0.91 to 1.10 t·ha−1, MAE ranged from 0.69 to 0.89 t·ha−1, and NRMSE ranged from 0.076 to 0.094. The best prediction performance was achieved when SPAD at the R3 stage was introduced, with R2 = 0.64, RMSE = 0.91 t·ha−1, MAE = 0.73 t·ha−1, and NRMSE = 0.0845. Photosynthesis-related traits (SPAD, LAI) demonstrated optimal predictive performance at the R3 stage (R2 = 0.64), while structural traits (PH, SD) showed greater predictive value during vegetative growth stages (V6-VT; R2 = 0.52–0.54). The predictive efficacy of these traits varied dynamically across the growth cycle. Specifically, SPAD values showed an 18.5% improvement in prediction accuracy from the V6 to the R3 stage, whereas plant height gradually lost its predictive capability during the reproductive phases (R6 stage: R2 = 0.48). These findings suggest that a single agronomic trait is insufficient to fully capture the driving factors of yield variation. Therefore, in practical applications, optimizing the combination of multiple agronomic traits is essential to further enhancing the accuracy of yield prediction.

Table 6.
Accuracy of yield prediction models with the introduction of single agronomic traits.
Table 7 provides a detailed overview of the prediction results for different combinations of agronomic traits. The results indicate that, compared to the introduction of a single agronomic trait, the use of multiple agronomic traits significantly enhances prediction accuracy. However, the degree of improvement varies among different combinations. Specifically, the introduction of multiple agronomic traits improves model accuracy by 7.8% to 23.2%, with RMSE ranging from 0.87 to 0.98 t·ha−1, MAE ranging from 0.66 to 0.78 t·ha−1, and NRMSE ranging from 0.0621 to 0.0952. Among these combinations, the combination of NDRE with LAI and SPAD performs the best, with R2 = 0.69, RMSE = 0.89 t·ha−1, MAE = 0.74 t·ha−1, and NRMSE = 0.0776, which is significantly better than other combinations. Feature-importance analysis of the RF model indicates that SPAD was the most influential predictor, followed closely by LAI, whereas PH and SD contributed comparatively little (Figure 7). These results demonstrate that integrating vegetation indices with multiple agronomic traits more effectively captures the complex processes underlying yield formation, yielding higher prediction accuracy and greater model stability than models based on single traits. Moreover, they underscore the pivotal roles of SPAD and LAI within the predictive framework.

Table 7.
Accuracy of yield prediction models with the introduction of multiple agronomic traits.

Figure 7.
Ranking of agronomic-trait importance.
3.4. Optimization of Yield Prediction Model by Introducing Vertical-Scale SPAD
In this study, the mean SPAD values in the prediction model were replaced with SPAD values measured at different growth stages and vertical canopy positions, and the prediction accuracy was evaluated, as shown in Table 8. The results indicated that SPAD values at different spatial vertical canopy positions had a significant impact on the model’s prediction accuracy. Compared with SPAD values at other canopy positions, middle-layer SPAD values generally exhibited better prediction performance, with the highest prediction accuracy occurring mainly in the time window from R3 to R6. Specifically, when using the middle-layer SPAD value at R3, the model achieved the best prediction accuracy, with the coefficient of determination R2 reaching 0.74, RMSE = 0.86 t·ha−1, MAE = 0.73 t·ha−1, and NRMSE = 0.0613. This represents a 7.2% increase in prediction accuracy compared with the mean SPAD value without vertical-scale segmentation, and a 13.8% to 25.4% increase in prediction accuracy compared with the combination of VT and R3. Figure 8 presents the residual plot of the predictive model, with residuals clustered around zero. Apart from a few outliers, no pronounced bias is evident; all residuals are randomly distributed. This result not only enhances the model’s prediction accuracy and stability but also highlights the importance of considering vertical-scale differences in crop growth monitoring.

Table 8.
Accuracy of yield prediction models based on SPAD at different vertical scales.

Figure 8.
Scatterplot of residuals versus predicted values.
3.5. Statistical Evaluation of Model Configuration and Cross-Validation
To further investigate differences among model configurations, we conducted the Friedman test on four evaluation metrics: R2, RMSE, MAE, and NRMSE, followed by pairwise comparisons using the Nemenyi post hoc test. The results indicated a progressive improvement in model accuracy from using only VIs to VIs combined with LAI and SPAD, and finally to the layered VIs + LAI + SPAD (Middle) configuration (Figure 9). The optimized models showed significant improvements over models using only VIs across all metrics (p < 0.05), with the 95% CIs demonstrating narrower intervals and reduced variability for the optimized models (Figure 10). In contrast, although some metrics improved when adding LAI and SPAD to VIs, the differences were not statistically significant. These findings suggest that incorporating multiple agronomic traits can enhance overall model performance, but the incremental benefit diminishes as more refined traits are added.

Figure 9.
Statistical significance test among models (Different letters denote significant differences, while the same letters indicate no significant difference). (a) R2; (b) RMSE; (c) MAE; (d) NRMSE.

Figure 10.
Confidence intervals of evaluation metrics.
To assess model robustness, the proposed maize yield prediction model was evaluated under progressively stringent cross-validation strategies, as shown in Figure 11. Overall, 5-fold cross-validation exhibited the most stable performance, whereas group 6-fold validation displayed greater variability. LOTO validation, in particular, showed larger deviations under extreme yield conditions. Figure 12 illustrates the relationship between predicted and observed values across the three validation methods, showing consistent overall trends, with most points closely aligned along the 1:1 reference line. Collectively, the evaluation metrics indicated relatively stable performance, demonstrating the feasibility and potential applicability of the proposed approach for field-scale yield prediction. At the same time, these results underscore the necessity of further transferability assessments across different locations and growing seasons to ensure broader applicability of the method.
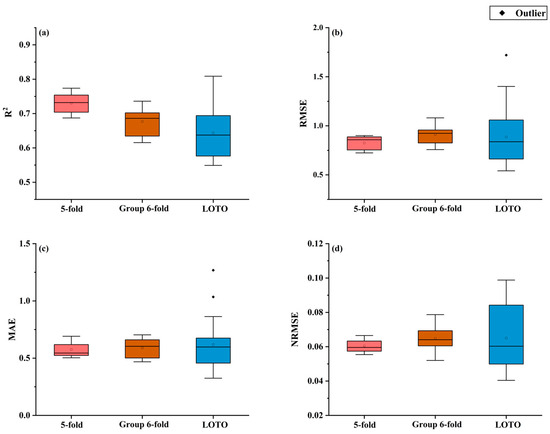
Figure 11.
Cross-validation results. (a) R2; (b) RMSE; (c) MAE; (d) NRMSE.

Figure 12.
Predicted vs. observed scatter plot. (A) 5-Fold Random Cross-Validation; (B) Group 6-Fold Cross-Validation; (C) LOTO.
4. Discussion
4.1. Advantages and Potential of Incorporating Agronomic Traits
Remote sensing technologies can provide large-scale, high-resolution spectral information; however, these data often lack direct descriptions of crop growth processes. Dynamic plant traits (such as LAI and SPAD) vary temporally across phenological stages, while structural traits (such as PH and SD) remain relatively stable after the reproductive phase. Combining both types of traits enables a comprehensive characterization of maize growth dynamics. Agronomic traits have explicit physical and biological meanings and can directly reflect crop growth status and yield potential [53,54]. Therefore, integrating agronomic traits with remote sensing data provides a more biologically meaningful approach to yield prediction.
In our study, the incorporation of agronomic traits reduced the RMSE of the yield prediction model by 20.7%, improving the prediction accuracy R2 from 0.54 to 0.74. Moreover, traditional yield prediction models based on remote sensing primarily rely on VIs and derived indicators [55,56]. Although these indices can reflect photosynthetic efficiency and environmental conditions, they fall short in explaining the underlying biological mechanisms driving yield variation. By utilizing field-measured agronomic data, this study avoided error propagation and multicollinearity commonly encountered during regression modeling, while emphasizing the importance of yield-determining factors. These findings are strongly supported by the “source–sink” relationships and yield formation mechanisms [23,24,57]. Compared to other leaf positions, incorporating mid-canopy leaf SPAD measurements as model inputs improved prediction accuracy by 13.8–22.6%. The inclusion of agronomic traits also enhanced the model’s adaptability to varying environmental conditions and cropping patterns.
Factors such as soil fertility, irrigation regimes, and planting density can significantly influence maize growth [58,59]. In the experiment, increasing fertilizer application improved key agronomic traits of DK1220 by 3.6–19.5%, with this effect being more significant under high-density conditions. The results showed distinct differences in agronomic performance under different planting patterns. These variations enable the model to better capture planting patterns, soil fertility, and moisture conditions. This advantage is particularly significant in drought-prone areas, where crop yield is more susceptible to agronomic trait influences, enabling the model to more accurately predict yield variations under environmental stress [60].
4.2. Impact of Data Scale on Practical Applications
This study validated the method’s effectiveness at a small spatial scale using field sampling data. Although field sampling can provide highly accurate agronomic trait data, its temporal and spatial coverage is limited, making it challenging to support large-scale and high-frequency monitoring needs [61]. Thus, alternative approaches are required to extend yield prediction beyond small-scale field experiments.
To enable large-scale remote sensing-based yield prediction, inversion methods must be optimized to accommodate multi-scale data inputs. Currently, certain agronomic traits, such as PH and LAI, can already be retrieved from remote sensing data with relatively high accuracy. However, due to “canopy shadowing effect”, the inversion of vertically stratified SPAD values remains underexplored and achieves lower accuracy [56,62]. Advances in deep learning-based crop phenotypic structure recognition and the application of LiDAR point cloud-based stem-leaf classification and segmentation models now offer promising avenues for retrieving such detailed agronomic trait information [63,64]. The inversion of agronomic traits not only enhances data acquisition efficiency but also enables continuous monitoring at large scales. Moreover, existing studies have demonstrated that incorporating specific indices at the field scale can significantly improve yield prediction accuracy. For example, Liu et al. (2022) successfully applied a lodging index to predict maize yield, achieving accurate prediction results [65]. García et al. (2020) highlighted that canopy coverage and volume, as structural indicators, substantially enhance the precision of field-scale yield prediction when integrated into modeling approaches [66].
However, due to data limitations, this study utilized data from a subset of the study area only. Future research should further explore the integration of multi-source data to achieve more precise and robust yield predictions.
4.3. Potential Limitations and Error Analysis
The core of this study lies in predicting crop yield using UAV-based multispectral data in combination with agronomic trait measurements. It should be emphasized, however, that model performance may still be constrained by multiple factors, which could lead to suboptimal outcomes under certain conditions. First, image quality can be compromised by sensor band discrepancies, flight parameters, and weather conditions, resulting in blurred imagery and reduced spatial resolution [67]. Second, the accuracy of agronomic traits also influences model performance, as field survey data may be affected by human measurement errors or limited temporal and spatial representativeness.
This study was conducted at the field scale and was based on a single growing season. In the experiment, varietal and topographic factors were fully considered during the design phase. However, data from a single growing season still impose limitations on the model’s transferability. Bongianino et al. (2024) observed that genotype and environment each account for roughly half of the variation in grain yield, indicating that the 18 treatment combinations applied to just three cultivars may not fully capture the complete trait–environment relationship [68]. Moreover, crop yield inherently exhibits substantial spatial heterogeneity as a result of its sensitivity to crop management practices and soil fertility conditions. Although these confounding effects were minimized in the present study through the implementation of standardized management practices, the predictive performance of the model may nonetheless deteriorate when extrapolated to regions characterized by distinct soil types and climatic conditions [69].
Our results indicated that PH and SD had limited direct effects on yield prediction—an observation somewhat divergent from previous findings [20,21]. Variability in plant height was primarily determined by cultivar characteristics, while fertilization and planting density also exerted an influence. However, the absence of significant nutrient or water stress during the growing season may have reduced the explanatory power of plant height for yield [70]. This finding aligns with the results of Huang et al. (2017), suggesting that plant height alone is not a definitive indicator of yield potential and that morphological characteristics of leaves at different canopy positions should be comprehensively analyzed [71]. Similarly, stem diameter showed little contribution, likely due to the absence of lodging in the trial. Under dense planting, shading also complicated the detection of structural traits from UAV imagery, further limiting its influence. Therefore, future studies will adopt a multi-site, multi-cultivar, and multi-year framework, integrated with soil–climate–crop modeling, to improve model generalizability and facilitate the transition from proof of concept to operational-scale application [72].
5. Conclusions
This study established 18 cultivation treatments through a factorial combination of three maize varieties, two fertilization levels, and three planting densities. The dynamic variations of LAI, PH, ST, SPAD, and VIs were systematically analyzed across different cultivation regimes. We proposed a remote sensing-based yield prediction approach that integrates spectral indices with field-measured agronomic traits, aiming to explore its feasibility for improving yield estimation accuracy in complex cropping systems. The main conclusions are as follows: (1) High fertilization rates significantly improved all agronomic traits, with particularly pronounced effects under high planting density. Although high-density cultivation accelerated trait development during early vegetative stages, it led to more rapid physiological decline during the late reproductive phase; (2) The VT–R3 period was identified as the optimal timing for data collection, while NDRE measured at the R3 stage showed relatively high correlation with maize yield; (3) NDRE together with concurrently measured middle-leaf SPAD values and LAI during the R3 period could serve as potentially effective input features; (4) the model’s prediction accuracy was further improved by introducing the SPAD values of middle-layer leaves during the grain-filling stage (R2 = 0.74, RMSE = 0.88 t·ha−1). This study demonstrates the potential of the proposed approach at the proof of concept level, providing preliminary insights for further investigation of field-scale yield prediction models and decision-making in precision agriculture. At the same time, its robustness and broader applicability still require validation across different locations, growing seasons, and management conditions.
Author Contributions
Conceptualization, M.Z. and H.L.; methodology, S.B. and Y.W.; software, S.B. and X.X.; validation, S.B. and Y.M.; formal analysis, X.X.; investigation, S.B. and S.M.; resources, H.L.; data curation, Y.M. and D.W.; writing—original draft preparation, S.B.; writing—review and editing, Y.W. and S.M.; visualization, X.X.; supervision, Y.W. and H.L.; project administration, M.Z. and H.L.; funding acquisition, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Low-carbon Green Agriculture of Grain Crops Project (LJGXCG2022-107).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author due to privacy concerns.
Acknowledgments
We thank the National Earth System Science Data Center for providing geographic information data.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Yu, Z.; Ning, Z.; Chang, W.-Y.; Chang, S.J.; Yang, H. Optimal harvest decisions for the management of carbon sequestration forests under price uncertainty and risk preferences. For. Policy Econ. 2023, 151, 102957. [Google Scholar] [CrossRef]
- Ku, L.; Zhao, W.; Zhang, J.; Wu, L.; Wang, C.; Wang, P.; Zhang, W.; Chen, Y. Quantitative trait loci mapping of leaf angle and leaf orientation value in maize (Zea mays L.). Theor. Appl. Genet. 2010, 121, 951–959. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned Aerial Vehicle Remote Sensing for Field-Based Crop Phenotyping: Current Status and Perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef]
- Habiba, R.M.M.; El-Diasty, M.Z.; Aly, R.S.H. Combining abilities and genetic parameters for grain yield and some agronomic traits in maize (Zea mays L.). Beni-Suef Univ. J. Basic Appl. Sci. 2022, 11, 108. [Google Scholar] [CrossRef]
- Bolaños, J.; Edmeades, G. The importance of the anthesis-silking interval in breeding for drought tolerance in tropical maize. Field Crops Res. 1996, 48, 65–80. [Google Scholar] [CrossRef]
- Qin, X.; Feng, F.; Li, Y.; Xu, S.; Siddique, K.H.M.; Liao, Y.; Lübberstedt, T. Maize yield improvements in China: Past trends and future directions. Plant Breed. 2016, 135, 166–176. [Google Scholar] [CrossRef]
- Epule, T.E.; Chehbouni, A.; Dhiba, D. Recent Patterns in Maize Yield and Harvest Area across Africa. Agronomy 2022, 12, 374. [Google Scholar] [CrossRef]
- Ai, Z.; Hanasaki, N.; Heck, V.; Hasegawa, T.; Fujimori, S. Simulating second-generation herbaceous bioenergy crop yield using the global hydrological model H08 (v.bio1). Geosci. Model Dev. 2020, 13, 6077–6092. [Google Scholar] [CrossRef]
- Yang, H.; Dobermann, A.; Lindquist, J.L.; Walters, D.T.; Arkebauer, T.J.; Cassman, K.G. Hybrid-maize—A maize simulation model that combines two crop modeling approaches. Field Crops Res. 2004, 87, 131–154. [Google Scholar] [CrossRef]
- Folberth, C.; Yang, H.; Gaiser, T.; Abbaspour, K.C.; Schulin, R. Modeling maize yield responses to improvement in nutrient, water and cultivar inputs in sub-Saharan Africa. Agric. Syst. 2013, 119, 22–34. [Google Scholar] [CrossRef]
- Ye, D.; Wang, B.; Wu, L.; Del Rio-Chanona, E.A.; Sun, Z. PO-SRPP: A decentralized pivoting path planning method for self-reconfigurable satellites. IEEE Trans. Ind. Electron. 2024, 71, 14318–14327. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Mulder, V.L.; de Bruin, S.; Schaepman, M.E.; Mayr, T.R. The use of remote sensing in soil and terrain mapping—A review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gamon, J.A. Remote sensing of plant functional types. New Phytol. 2010, 186, 795–816. [Google Scholar] [CrossRef]
- Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
- Saravia, D.; Salazar, W.; Valqui-Valqui, L.; Quille-Mamani, J.; Porras-Jorge, R.; Corredor, F.-A.; Barboza, E.; Vásquez, H.; Casas Diaz, A.; Arbizu, C. Yield Predictions of Four Hybrids of Maize (Zea mays) Using Multispectral Images Obtained from UAV in the Coast of Peru. Agronomy 2022, 12, 2630. [Google Scholar] [CrossRef]
- Wahab, I.; Hall, O.; Jirström, M. Remote Sensing of Yields: Application of UAV Imagery-Derived NDVI for Estimating Maize Vigor and Yields in Complex Farming Systems in Sub-Saharan Africa. Drones 2018, 2, 28. [Google Scholar] [CrossRef]
- Borrás, L.; Vitantonio-Mazzini, L.N. Maize reproductive development and kernel set under limited plant growth environments. J. Exp. Bot. 2018, 69, 3235–3243. [Google Scholar] [CrossRef]
- Vazin, F.; Hassanzadeh, M.; Madani, A.; Nassiri-Mahallati, M.; Nasri, M. Modeling light interception and distribution in mixed canopy of common cocklebur (Xanthium stramarium) in competition with corn. Planta Daninha 2010, 28, 455–462. [Google Scholar] [CrossRef]
- Nasar, J.; Khan, W.; Khan, M.Z.; Gitari, H.I.; Gbolayori, J.F.; Moussa, A.A.; Mandozai, A.; Rizwan, N.; Anwari, G.; Maroof, S.M. Photosynthetic Activities and Photosynthetic Nitrogen Use Efficiency of Maize Crop Under Different Planting Patterns and Nitrogen Fertilization. J. Soil Sci. Plant Nutr. 2021, 21, 2274–2284. [Google Scholar] [CrossRef]
- Jjagwe, J.; Chelimo, K.; Karungi, J.; Komakech, A.J.; Lederer, J. Comparative Performance of Organic Fertilizers in Maize (Zea mays L.) Growth, Yield, and Economic Results. Agronomy 2020, 10, 69. [Google Scholar] [CrossRef]
- Gardner, F.P.; Pearce, R.B.; Mitchell, R.L. Physiology of Crop Plants; Scientific Publishers: Jodhpur, India, 2017. [Google Scholar]
- Pendleton, J.W.; Smith, G.E.; Winter, S.R.; Johnston, T.J. Field Investigations of the Relationships of Leaf Angle in Corn (Zea mays L.) to Grain Yield and Apparent Photosynthesis. Agron. J. 1968, 60, 422–424. [Google Scholar] [CrossRef]
- Kandel, B.P. Spad value varies with age and leaf of maize plant and its relationship with grain yield. BMC Res. Notes 2020, 13, 475. [Google Scholar] [CrossRef] [PubMed]
- Bernhard, B.J.; Below, F.E. Plant population and row spacing effects on corn: Plant growth, phenology, and grain yield. Agron. J. 2020, 112, 2456–2465. [Google Scholar] [CrossRef]
- Yu, C.L.; Hui, D.; Deng, Q.; Wang, J.; Reddy, K.C.; Dennis, S. Responses of corn physiology and yield to six agricultural practices over three years in middle Tennessee. Sci. Rep. 2016, 6, 27504. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; White, J.C.; Wulder, M.A.; Næsset, E.; Achim, A. Remote sensing in forestry: Current challenges, considerations and directions. For. Int. J. For. Res. 2024, 97, 11–37. [Google Scholar] [CrossRef]
- Wiegand, C.L.; Richardson, A.J.; Kanemasu, E.T. Leaf Area Index Estimates for Wheat from LANDSAT and Their Implications for Evapotranspiration and Crop Modeling. Agron. J. 1979, 71, 336–342. [Google Scholar] [CrossRef]
- Luo, S.; Jiang, X.; Jiao, W.; Yang, K.; Li, Y.; Fang, S. Remotely sensed prediction of rice yield at different growth durations using UAV multispectral imagery. Agriculture 2022, 12, 1447. [Google Scholar] [CrossRef]
- Han, X.; Wei, Z.; Chen, H.; Zhang, B.; Li, Y.; Du, T. Inversion of winter wheat growth parameters and yield under different water treatments based on UAV multispectral remote sensing. Front. Plant Sci. 2021, 12, 609876. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, X.; Chen, S.; Wang, H.; Jayavelu, S.; Cammarano, D.; Fu, Y. Integrated UAV-based multi-source data for predicting maize grain yield using machine learning approaches. Remote Sens. 2022, 14, 6290. [Google Scholar] [CrossRef]
- Sharma, V.; Honkavaara, E.; Hayden, M.; Kant, S. UAV remote sensing phenotyping of wheat collection for response to water stress and yield prediction using machine learning. Plant Stress 2024, 12, 100464. [Google Scholar] [CrossRef]
- Liu, T.; Wu, F.; Mou, N.; Zhu, S.; Yang, T.; Zhang, W.; Wang, H.; Wu, W.; Zhao, Y.; Sun, C. The estimation of wheat yield combined with UAV canopy spectral and volumetric data. Food Energy Secur. 2024, 13, e527. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.; Fan, Y.; Yue, J.; Yang, F.; Fan, J.; Ma, Y.; Chen, R.; Bian, M.; Yang, G. Utilizing UAV-based hyperspectral remote sensing combined with various agronomic traits to monitor potato growth and estimate yield. Comput. Electron. Agric. 2025, 231, 109984. [Google Scholar] [CrossRef]
- Sebastiani, A.; Salvati, R.; Manes, F. Comparing leaf area index estimates in a Mediterranean forest using field measurements, Landsat 8, and Sentinel-2 data. Ecol. Process. 2023, 12, 28. [Google Scholar] [CrossRef]
- Shah, S.; Houborg, R.; McCabe, M. Response of Chlorophyll, Carotenoid and SPAD-502 Measurement to Salinity and Nutrient Stress in Wheat (Triticum aestivum L.). Agronomy 2017, 7, 61. [Google Scholar] [CrossRef]
- Lu, X.; Gao, H.; Liu, H. Effects of Different Water and Nitrogen Treatments on Corn. Int. Core J. Eng. 2021, 7, 593–602. [Google Scholar]
- Wang, Z.; Ling, J.; Liu, Z.; Zhao, D.; Li, Z.; Zhou, S.; Yuan, X.; Li, X.; Wen, Y. Effect of straw return practices on soil physico-chemical properties and maize yield. Chin. J. Eco-Agric. 2024, 32, 663–674. [Google Scholar] [CrossRef]
- Li, W.; Wang, J.; Zhang, Y.; Yin, Q.; Wang, W.; Zhou, G.; Huo, Z. Combining Texture, Color, and Vegetation Index from Unmanned Aerial Vehicle Multispectral Images to Estimate Winter Wheat Leaf Area Index during the Vegetative Growth Stage. Remote Sens. 2023, 15, 5715. [Google Scholar] [CrossRef]
- Yang, D. Gobi vegetation recognition based on low-altitude photogrammetry images of UAV. IOP Conf. Ser. Earth Environ. Sci. 2018, 186, 012053. [Google Scholar]
- Khanal, S.; Fulton, J.; Klopfenstein, A.; Douridas, N.; Shearer, S. Integration of high resolution remotely sensed data and machine learning techniques for spatial prediction of soil properties and corn yield. Comput. Electron. Agric. 2018, 153, 213–225. [Google Scholar] [CrossRef]
- Guo, A.; Ye, H.; Huang, W.; Qian, B.; Wang, J.; Lan, Y.; Wang, S. Inversion of maize leaf area index from UAV hyperspectral and multispectral imagery. Comput. Electron. Agric. 2023, 212, 108020. [Google Scholar] [CrossRef]
- Montero, D.; Aybar, C.; Mahecha, M.D.; Martinuzzi, F.; Söchting, M.; Wieneke, S. A standardized catalogue of spectral indices to advance the use of remote sensing in Earth system research. Sci. Data 2023, 10, 197. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Zheng, Z.; Yuan, J.; Yao, W.; Kwan, P.; Yao, H.; Liu, Q.; Guo, L. Fusion of UAV-acquired visible images and multispectral data by applying machine-learning methods in crop classification. Agronomy 2024, 14, 2670. [Google Scholar] [CrossRef]
- Park, B.; Kim, C.H.; Jun, J.K.; Suh, M.; Choi, K.S.; Choi, I.J.; Oh, H.J. A machine learning risk prediction model for gastric cancer with SHapley Additive exPlanations. Cancer Res. Treat. 2024, 57, 821–829. [Google Scholar] [CrossRef]
- Nyongesa, C.A.; Hogarth, M.; Pa, J. Artificial intelligence-driven natural language processing for identifying linguistic patterns in Alzheimer’s disease and mild cognitive impairment: A study of lexical, syntactic, and cohesive features of speech through picture description tasks. J. Alzheimer’s Dis. 2025, 106, 13872877251339756. [Google Scholar] [CrossRef] [PubMed]
- Janse, R.J.; Hoekstra, T.; Jager, K.J.; Zoccali, C.; Tripepi, G.; Dekker, F.W.; Van Diepen, M. Conducting correlation analysis: Important limitations and pitfalls. Clin. Kidney J. 2021, 14, 2332–2337. [Google Scholar] [CrossRef]
- Sejuti, Z.A.; Islam, M.S. A hybrid CNN–KNN approach for identification of COVID-19 with 5-fold cross validation. Sens. Int. 2023, 4, 100229. [Google Scholar] [CrossRef] [PubMed]
- Wolcott, N.S.; Sit, K.K.; Raimondi, G.; Hodges, T.; Shansky, R.M.; Galea, L.A.; Ostroff, L.E.; Goard, M.J. Automated classification of estrous stage in rodents using deep learning. Sci. Rep. 2022, 12, 17685. [Google Scholar] [CrossRef]
- Krupp, L.; Wiede, C.; Friedhoff, J.; Grabmaier, A. Explainable remaining tool life prediction for individualized production using automated machine learning. Sensors 2023, 23, 8523. [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.; Guo, T.; Xing, Y.; Mo, F.; Wang, H.; Fan, J.; Zhang, F. Effects of plastic mulch and nitrogen fertilizer on the soil microbial community, enzymatic activity and yield performance in a dryland maize cropping system. Eur. J. Soil Sci. 2020, 72, 400–412. [Google Scholar] [CrossRef]
- Wang, K.; Han, Y.; Zhang, Y.; Zhang, Y.; Wang, S.; Yang, F.; Liu, C.; Zhang, D.; Lu, T.; Zhang, L.; et al. Maize yield prediction with trait-missing data via bipartite graph neural network. Front. Plant Sci. 2024, 15, 1433552. [Google Scholar] [CrossRef] [PubMed]
- Kipkulei, H.K.; Bellingrath-Kimura, S.D.; Lana, M.; Ghazaryan, G.; Baatz, R.; Matavel, C.; Boitt, M.K.; Chisanga, C.B.; Rotich, B.; Moreira, R.M.; et al. Maize yield prediction and condition monitoring at the sub-county scale in Kenya: Synthesis of remote sensing information and crop modeling. Sci. Rep. 2024, 14, 14227. [Google Scholar] [CrossRef]
- Mokhtari, A.; Noory, H.; Vazifedoust, M. Improving crop yield estimation by assimilating LAI and inputting satellite-based surface incoming solar radiation into SWAP model. Agric. For. Meteorol. 2018, 250–251, 159–170. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Ata-Ui-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef]
- Hufford, M.B.; Seetharam, A.S.; Woodhouse, M.R.; Chougule, K.M.; Ou, S.; Liu, J.; Ricci, W.A.; Guo, T.; Olson, A.; Qiu, Y.; et al. De novo assembly, annotation, and comparative analysis of 26 diverse maize genomes. Science 2021, 373, 655–662. [Google Scholar] [CrossRef] [PubMed]
- Xue-jun, C.; Guang-cai, C.; Qun, S.; Dong-bin, W.; Jing, C.; Ya-xiong, Y.U.; Jie, L.; Wei, L. Altitude effects on maize growth period and quality traits. Acta Ecol. Sin. 2013, 33, 233–236. [Google Scholar] [CrossRef]
- Queiroz, M.S.; Oliveira, C.E.S.; Steiner, F.; Zuffo, A.M.; Zoz, T.; Vendruscolo, E.P.; Silva, M.V.; Mello, B.F.F.R.; Cabral, R.C.; Menis, F.T. Drought Stresses on Seed Germination and Early Growth of Maize and Sorghum. J. Agric. Sci. 2019, 11, 310–318. [Google Scholar] [CrossRef]
- Vadez, V.; Grondin, A.; Chenu, K.; Henry, A.; Laplaze, L.; Millet, E.J.; Carminati, A. Crop traits and production under drought. Nat. Rev. Earth Environ. 2024, 5, 211–225. [Google Scholar] [CrossRef]
- Ma, W.; Han, W.; Zhang, H.; Cui, X.; Zhai, X.; Zhang, L.; Shao, G.; Niu, Y.; Huang, S. UAV multispectral remote sensing for the estimation of SPAD values at various growth stages of maize under different irrigation levels. Comput. Electron. Agric. 2024, 227, 109566. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, G.; Lang, K.; Su, B.; Chen, X.; Xi, X.; Zhang, H. Integrated satellite, unmanned aerial vehicle (UAV) and ground inversion of the SPAD of winter wheat in the reviving stage. Sensors 2019, 19, 1485. [Google Scholar] [CrossRef]
- Yan, J.; Tan, F.; Li, C.; Jin, S.; Zhang, C.; Gao, P.; Xu, W. Stem–Leaf segmentation and phenotypic trait extraction of individual plant using a precise and efficient point cloud segmentation network. Comput. Electron. Agric. 2024, 220, 108839. [Google Scholar] [CrossRef]
- Qiao, G.; Zhang, Z.; Niu, B.; Han, S.; Yang, E. Plant stem and leaf segmentation and phenotypic parameter extraction using neural radiance fields and lightweight point cloud segmentation networks. Front. Plant Sci. 2025, 16, 1491170. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, C.; Zhang, Z.; Wang, Z.; Ming, B.; Xue, J.; Yang, H.; Xu, H.; Meng, L.; Cui, N.; et al. Evaluating how lodging affects maize yield estimation based on UAV observations. Front. Plant Sci. 2022, 13, 979103. [Google Scholar] [CrossRef]
- García-Martínez, H.; Flores-Magdaleno, H.; Ascencio-Hernández, R.; Khalil-Gardezi, A.; Tijerina-Chávez, L.; Mancilla-Villa, O.R.; Vázquez-Peña, M.A. Corn Grain Yield Estimation from Vegetation Indices, Canopy Cover, Plant Density, and a Neural Network Using Multispectral and RGB Images Acquired with Unmanned Aerial Vehicles. Agriculture 2020, 10, 277. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Bongianino, N.F.; Steffolani, M.E.; Morales, C.D.; Biasutti, C.A.; León, A.E. Semi-Arid Environmental Conditions and Agronomic Traits Impact on the Grain Quality of Diverse Maize Genotypes. Plants 2024, 13, 2482. [Google Scholar] [CrossRef] [PubMed]
- Tittonell, P.; Shepherd, K.D.; Vanlauwe, B.; Giller, K.E. Unravelling the effects of soil and crop management on maize productivity in smallholder agricultural systems of western Kenya—An application of classification and regression tree analysis. Agric. Ecosyst. Environ. 2008, 123, 137–150. [Google Scholar] [CrossRef]
- Djaman, K.; Allen, S.; Djaman, D.S.; Koudahe, K.; Irmak, S.; Puppala, N.; Darapuneni, M.K.; Angadi, S.V. Planting date and plant density effects on maize growth, yield and water use efficiency. Environ. Chall. 2022, 6, 100417. [Google Scholar] [CrossRef]
- Huang, S.; Gao, Y.; Li, Y.; Xu, L.; Tao, H.; Wang, P. Influence of plant architecture on maize physiology and yield in the Heilonggang River valley. Crop J. 2017, 5, 52–62. [Google Scholar] [CrossRef]
- Haque, M.A.; Sakimin, S.Z. Planting Arrangement and Effects of Planting Density on Tropical Fruit Crops—A Review. Horticulturae 2022, 8, 485. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).